Fractional-Order Sliding Mode Control for Hidden Semi-Markov Jump Systems Under DoS Attacks and Uncertain Emission Probabilities

Abstract

This paper addresses the stability analysis and control design for discrete-time hidden semi-Markov jump systems under the compounded challenges of denial-of-service (DoS) attacks and incomplete emission probabilities. Such conditions are prevalent in modern networked control systems, yet they pose significant hurdles for robust controller design. Existing control methods, typically based on integer-order dynamics, are inherently memoryless, struggling to effectively mitigate the long-term impact of mode observation uncertainties and intermittent cyberattacks. To overcome these challenges, we propose, for the first time, a fractional-order sliding mode control (FOSMC) strategy tailored for this class of systems. The core of our method is a novel sliding surface that leverages a discrete fractional-order sum to embed the system’s history—including observed modes and elapsed sojourn times—into the control logic. This memory-based approach enhances robustness against both mode observation uncertainties and adversarial packet losses. A corresponding FOSMC law is synthesized to ensure finite-time reachability of this surface. We derive sufficient conditions, formulated as linear matrix inequalities, to guarantee the mean-square stability of the resulting sliding mode dynamics.A numerical simulation validates the effectiveness of the proposed control scheme, demonstrating a convergence speed improvement ranging from 40% (under moderate attacks) to nearly 50% (under severe attacks) over its integer-order counterpart, conclusively validating its performance enhancement capability under compound uncertainties.

1. Introduction

Markov jump systems (MJSs) are governed by stochastic switching signals following Markov processes. They have been widely applied in various domains to handle parameter variations caused by internal or external disturbances, such as industrial control systems [1,2], power systems [3] and financial and economic systems [4,5]. However, the memoryless property of the underlying Markov chain constrains the sojourn time in each mode to follow a geometric distribution (exponential distribution in continuous time). Consequently, the transition probability remains time-invariant, independent of the duration for which the system has resided in the current mode. This assumption often fails to capture the time-varying or history-dependent switching behaviors prevalent in practical systems.

Semi-Markov jump systems (S-MJSs) overcome this limitation by permitting arbitrary sojourn time distributions, thus providing significantly enhanced modeling flexibility. Early work by [6] formulated the sojourn time probability density function (ST-PDF) as dependent only on the current mode and addressed stability for a subclass of continuous-time S-MJSs via interconnected algebraic Riccati equations. For controller design, ref. [7] employed linear matrix inequalities (LMIs) based on upper and lower bounds of sojourn time to ensure robustness against timing variations. A significant advancement was made by [8], who introduced the discrete-time semi-Markov kernel. This framework enables history-dependent switching dynamics by making the transition probability to the next mode explicitly dependent on both the current mode and the elapsed sojourn time. Such a feature enhances modeling accuracy for systems with time-varying or adaptive behaviors, as it allows transition rates from the same mode to vary based on their temporal history. Subsequent studies have explored various stability and control problems for discrete-time S-MJSs. Initial works focused on stability analysis, such as that provided by [9], and advanced concepts like input-to-state stabilization [10]. Later research extended this to complex scenarios, including fuzzy systems with unknown kernels [11] and asynchronous control under cyberattacks [12]. The presence of such temporal dependencies highlights that a control strategy capable of learning from past system behavior could be highly advantageous. Nevertheless, most existing works assume perfect knowledge of system modes, a condition difficult to satisfy in real-world scenarios involving packet losses or sensor degradation [13,14].

To address the issue of imperfect mode observation, hidden semi-Markov jump systems (HS-MJSs) have been proposed, in which the true system mode evolves according to a semi-Markov chain but is not directly observable. Instead, it must be inferred from observable outputs based on emission probabilities. Yet, a critical practical limitation remains: the emission probabilities are often partially known due to calibration errors, environmental changes, or limited training data. While many theoretical studies assume complete knowledge of these probabilities [15,16,17], their incompleteness directly undermines the reliability of mode estimation and, consequently, the performance of mode-dependent controllers.

Moreover, the integration of networked control systems (NCSs) introduces additional vulnerabilities. Although NCSs offer flexibility and cost efficiency, their reliance on shared communication networks exposes them to cyber threats, particularly denial-of-service (DoS) attacks [18,19]. Such attacks can disrupt data transmission, induce packet dropouts, and degrade system performance. Therefore, any controller for HS-MJSs must be robust not only to internal uncertainties (e.g., incomplete ST-PDFs and uncertain emission probabilities) but also to external malicious interference. This leads to the first key question: How can a unified system model and control framework be established for discrete-time HS-MJSs that simultaneously accommodates both incomplete emission probabilities and intermittent DoS attacks?

In the realm of controller design, intelligent and data-driven strategies have recently garnered significant attention due to their adaptability. Prominent examples include the sigmoid PID controller [20], which handles nonlinearities by adaptively adjusting gains; the neuroendocrine PID controller [21], which mimics hormonal regulation to improve transient responses; and the Brain Emotional Learning Based Intelligent Controller [22], which offers model-free adaptability. While PID-based regulation constitutes a widely adopted approach for stabilizing simple or uncertain systems where implementation simplicity is paramount, it is primarily favored for model-free scenarios. However, the HS-MJSs considered in this work represent a class of highly complex stochastic systems characterized by dual-layer uncertainties (hidden modes and cyberattacks). For such systems with well-characterized dynamic structures, model-based methods are generally preferred over heuristic PID schemes to achieve rigorous stability guarantees and enhanced control precision. A fundamental gap remains when applying standard PID schemes to this specific problem. First, strictly error-driven PID strategies generally lack the rigorous mathematical framework necessary to guarantee Mean-Square Stability (MSS) under the compounded randomness of hidden semi-Markov switching and stochastic DoS attacks. Second, unlike general purpose PID controllers, the proposed framework is specifically tailored to the structural dynamics of the HS-MJS, allowing for the explicit derivation of LMI-based conditions to ensure robustness against intermittent communication blackouts.

To address the issues of robustness and stability assurance, sliding mode control (SMC) is often preferred. SMC is inherently robust against matched uncertainties and disturbances [23,24,25,26,27,28,29,30], making it a promising candidate for stabilizing complex systems like HS-MJSs. While conventional SMC designs have been applied to MJSs [25], their direct extension to HS-MJSs faces significant challenges. Recent efforts have advanced SMC for uncertain discrete-time S-MJSs [29], and asynchronous SMC for networked HS-MJSs under cyberattacks has also been explored [30]. However, these approaches are based on integer-order dynamics and rely solely on instantaneous state feedback, thereby neglecting the temporal evolution of sojourn times and mode trajectories—information that is particularly valuable in HS-MJSs. In the presence of hidden modes, uncertain emission probabilities, and DoS-induced data losses, this lack of memory utilization exacerbates chattering, leading to excessive control effort and potential performance degradation. This motivates the second key question: How can a control strategy effectively exploit historical system dynamics, including sojourn and mode trajectories, to enhance robustness under incomplete and attacked observations?

To overcome the limitations of both data-driven PID (lack of stability proof) and integer-order SMC (IOSMC) (lack of memory), fractional-order calculus offers a transformative solution by inherently capturing the memory properties of dynamic systems. Unlike integer-order operators, fractional-order integrals encode the historical trajectory of a signal [31,32], making them uniquely suited for compensating for data unavailability. The efficacy of FOSMC in complex environments has been well-documented: Ref. [33] demonstrated its robustness in fuzzy Markovian jump systems, while [34,35] established the discrete-time theoretical framework essential for digital implementation. By incorporating historical dynamics, FOSMC can implicitly compensate for missing data during DoS attacks and utilize historical information to reduce mode observation errors. This leads to the third key question: How can the memory inherent in fractional-order calculus be systematically integrated into a sliding mode control framework for HS-MJSs to counteract the dual uncertainties from hidden modes and cyberattacks?

Building upon these foundations, this work aims to establish novel mean-square MSS conditions for HS-MJSs with incomplete emission probabilities and develop an advanced FOSMC scheme specifically tailored for HS-MJSs under DoS attacks. The key highlights of this study are summarized as the following three points:

• A Novel System Model: In contrast to existing works that either assume fully known system modes or operate in attack-free environments [9,10,11,12], this work introduces a more realistic framework for hidden semi-Markov jump systems by simultaneously accounting for both incomplete emission probabilities and DoS attacks. This integrated model captures the compounded uncertainties arising from partial observability and adversarial interference, significantly enhancing its applicability to real-world networked control systems under imperfect and insecure communication conditions.
• A Pioneering FOSMC Strategy: Departing from prior control designs [16,23,24], this paper proposes, to the best of our knowledge, the first FOSMC scheme for HS-MJSs. The core of this strategy is a novel sliding surface constructed using the Grünwald–Letnikov (G-L) difference operator, which actively leverages the entire history of system states and sojourn times. This inherent memory effect is the key to achieving accelerated convergence and enhanced robustness against the combined uncertainties of DoS attacks and incomplete emission probabilities.
• Demonstrated Superiority: Theoretical analysis and numerical simulations demonstrate that the proposed FOSMC law not only ensures MSS but also achieves significantly faster convergence compared to conventional IOSMC, thereby validating its effectiveness in enhancing dynamic performance under compound uncertainties.

To provide a clear, structured comparison and quantitatively validate the novelty of our approach,

Table 1. Comparison with the different references.

Ref.	System Model a	DoS Attacks	Incomplete Emission	Control Method b	LMI-Based Proof	Computational Complexity c
[28]	∘	√	×	∘	√	∘
[29]	□	×	×	□	√	∘
[30]	■	√	×	□	×	□
This paper	■	√	√	■	√	■

^a System Model: Other (∘)/S-MJS (□)/HS-MJS (Hidden Semi-Markov) (■). ^b Control Method: Other (e.g., State Feedback) (∘)/IOSMC (□)/FOSMC (■). ^c Computational Complexity: Low (Standard FOSMC) (∘)/Medium (SMC or HS-MJS) (□)/High (FOSMC + HS-MJS) (■). Symbols: √ (Considered); × (Not considered).

is presented. This table summarizes the key differences in system model, problem assumptions (DoS and incomplete emission), stability techniques, and associated computational complexity across both conventional IOSMC and Fractional-Order SMC methodologies. The comparison clearly demonstrates that our work is the first to establish a unified control framework that simultaneously accommodates HS-MJS dynamics, intermittent DoS attacks, incomplete emission probabilities, and fractional-order sliding surfaces.

For clarity and convenience, the main symbols and notation used throughout this paper are summarized in Abbreviations.

2. Preliminaries

2.1. System Description Under DoS Attacks and Uncertainties

Consider a class of discrete-time networked S-MJSs subject to parameter uncertainties and DoS attacks:

$$x(t+1)=(A_{\delta \left(t\right)}+\Delta A_{\delta \left(t\right)})x\left(t\right)+B_{\delta \left(t\right)}u\left(t\right),t\in \mathbf{N},$$

(1)

where $x\left(t\right)\in {\mathbf{R}}^{n_x}$ is the system state at the time instant t, $u\left(t\right)\in {\mathbf{R}}^{n_u}$ is the system control input at the time t and $\mathbf{N}$ represents the set of non-negative integers. The switching process $\left\{\delta \right(t),t\in \mathbf{N}\}$ is a discrete-time semi-Markov chain in $\mathcal{I}=\{1,2,\dots ,l\},l\in {\mathbf{N}}_{(0,\infty )}$ where ${\mathbf{N}}_{(a,b)}$ represents the set $\{x\in \mathbf{N}|a<x<b\}$. $A_{\delta \left(t\right)}$ and $B_{\delta \left(t\right)}$ are real known matrices and of compatible dimensions and matrix $B_{\delta \left(t\right)}$ is assumed to be of full column rank. The parameter uncertainty is structured as $\Delta A_{\delta \left(t\right)}=E_{\delta \left(t\right)}{F}_{\delta \left(t\right)}{G}_{\delta \left(t\right)}$, where $E_{\delta \left(t\right)}$, $G_{\delta \left(t\right)}$ are known, and $F_{\delta \left(t\right)}$ is an unknown matrix satisfying $F_{\delta \left(t\right)}^{\top }{F}_{\delta \left(t\right)}\le I$, where I denotes the identity matrix of appropriate dimension.

Let $t_n$ denote the time instant at the nth jump with $t_0=0$, and the index of $\delta \left(t\right)$ at the nth jump is denoted by $R_n$. $S_n\triangleq t_{n+1}-t_n$ represents the sojourn time of the current mode between the nth jump and the $(n+1)$th jump.

In practical networked environments, the true system mode $\delta \left(t\right)$ is often not directly accessible to the controller. Instead, an observed mode $\tilde{\delta }\left(t\right)\in \mathcal{M}=\{1,2,\dots ,M\}$ is available, which is stochastically related to $\delta \left(t\right)$ via emission probabilities:

$${\pi }_{ai\left(\kappa \right(t\left)\right)}\triangleq P_r(\tilde{\delta }\left(t\right)=i\left(\kappa \left(t\right)\right)\mid \delta \left(t\right)=a),$$

(2)

where $\kappa \left(t\right)$ denotes the elapsed sojourn time in the currently activated mode. The emission probabilities are partially unknown, meaning for each true mode $a\in \mathcal{I}$, the set $\mathcal{M}$ is partitioned into:

$$\begin{array}{cc}\hfill {\mathcal{M}}_a^a& =\{i\in \mathcal{M}\mid {\pi }_{ai\left(\kappa \right(t\left)\right)}\mathrm{is}\mathrm{known}\},\hfill \\ \hfill {\mathcal{M}}_a^u& =\{i\in \mathcal{M}\mid {\pi }_{ai\left(k\right(t\left)\right)}\mathrm{is}\mathrm{unknown}\},\hfill \end{array}$$

(3)

with $\mathcal{M}={\mathcal{M}}_a^a\cup {\mathcal{M}}_a^u$ and ${\mathcal{M}}_a^a\cap {\mathcal{M}}_a^u=\varnothing$, and if ${\mathcal{M}}_a^a\ne \varnothing$, we denote:

$${\mathcal{M}}_a^a=\{m_a^1,m_a^2,\dots ,m_a^{i^a}\},1\le i^a\le M.$$

This incompleteness in the emission probabilities fundamentally challenges the design of traditional mode-dependent control. Specifically, for a sliding mode controller, the accuracy of the equivalent control law—typically calculated based on the identified system mode—is directly compromised. Since the controller can only rely on the inaccurately estimated mode $\tilde{\delta }\left(t\right)$, a mismatch between the control input and the actual system dynamics $(A_{\delta \left(t\right)},B_{\delta \left(t\right)})$ is inevitable.

Furthermore, the communication channel from sensors to the controller is vulnerable to DoS attacks, which disrupt data transmission. Following [28], the state received by the controller is modeled as:

$$x_b\left(t\right)=\beta \left(t\right)x_b(t-1)+(1-\beta \left(t\right))x\left(t\right),$$

(4)

where the stochastic variable $\beta \left(t\right)$ follows a Bernoulli distribution, $P_r(\beta \left(t\right)=1)=\widehat{\beta },P_r(\beta \left(t\right)=0)=1-\widehat{\beta }$ and $\widehat{\beta }\in (0,1)$. Here, $\beta \left(t\right)=1$ indicates a successful DoS attack, which blocks the current data transmission and forces the controller to use the previously buffered state $x_b(t-1)$. Conversely, $\beta \left(t\right)=0$ signifies attack-free operation, allowing the timely reception of the current state $x\left(t\right)$.

Remark 1. 

The system formulation (1)–(4) establishes a unified modeling framework for discrete-time HS-MJSs under compound uncertainties, integrating (i) parameter perturbations, (ii) hidden modes with incomplete emission probabilities, and (iii) intermittent DoS attacks. This directly addresses the first key question posed in the Introduction regarding the establishment of a unified control framework.

2.2. Modeling Framework, Assumptions, and Signal Flow

To provide a clear and rigorous foundation for the modeling framework, this subsection details the signal flow of the networked control system and formally summarizes all key modeling assumptions. The closed-loop configuration, including the plant, sensors, controller, and actuator, is illustrated in Figure 1.

As depicted in Figure 1, the controller operates under significant informational constraints. The core assumptions underpinning this framework are formalized below.

• Assumption 1 (System Dynamics): The plant is modeled as the discrete-time S-MJS (1). The parameter uncertainty $\Delta A_{\delta \left(t\right)}$ is assumed to be structured as $\Delta A_{\delta \left(t\right)}=E_{\delta \left(t\right)}{F}_{\delta \left(t\right)}{G}_{\delta \left(t\right)}$, where $E_{\delta \left(t\right)}$ and $G_{\delta \left(t\right)}$ are known matrices, and $F_{\delta \left(t\right)}$ is an unknown matrix satisfying $F_{\delta \left(t\right)}^T{F}_{\delta \left(t\right)}\le I$. The input matrix $B_{\delta \left(t\right)}$ is assumed to be of full column rank for all modes $\delta \left(t\right)\in \mathcal{I}$.
• Assumption 2 (Hidden Semi-Markov Process): The true system mode $\delta \left(t\right)$, which evolves as a semi-Markov chain, is not directly accessible to the controller. Instead, the controller has access to two signals: (1) the observed mode $i=\left(t\right)\in \mathcal{M}$, and (2) the elapsed sojourn time $\kappa \left(t\right)$ of the activated mode.
• Assumption 3 (Incomplete Emission Probabilities): The relationship between the true mode $\delta \left(t\right)=a$ and the observed mode $\tilde{\delta }\left(t\right)=i\left(\kappa \left(t\right)\right)$ is governed by the emission probability ${\pi }_{ai\left(\kappa \right(t\left)\right)}$. These probabilities are partially unknown; for each true mode a, the set of observed modes $\mathcal{M}$ is partitioned into a known set ${\mathcal{M}}_a^a$ and an unknown set ${\mathcal{M}}_a^u$.
• Assumption 4 (DoS Attack Model): The communication channel from the sensor (measuring $x\left(t\right)$) to the controller’s buffer is vulnerable to DoS attacks. The attacks are modeled as a stochastic process governed by a Bernoulli variable $\beta \left(t\right)$ with a known probability $\widehat{\beta }=P_r(\beta \left(t\right)=1)$.

  –

  If $\beta \left(t\right)=0$ (no attack), the controller’s buffer receives the current state $x\left(t\right)$.

  –

  If $\beta \left(t\right)=1$ (attack occurs), the data packet is lost, and the controller must use the previously buffered state $x_b(t-1)$.

  The resulting state available to the controller is described by the buffer logic in (4): $x_b\left(t\right)=(1-\beta \left(t\right))x\left(t\right)+\beta \left(t\right)x_b(t-1)$.

Building upon the unified framework established in Remark 1, these assumptions (Assumptions 1–4) provide the formal specifications for this complex model. They define the precise informational constraints—such as hidden modes, partial probabilities, and DoS-induced data loss—that the FOSMC controller, proposed in Section 3, must be designed to overcome.

2.3. Mathematical Foundations of Hidden Semi-Markov Jump Systems

To facilitate the subsequent analysis, this subsection provides formal definitions and fundamentals of the hidden semi-Markov jump system (1).

Definition 1 

([16]). The stochastic process ${\left\{(R_n,t_n)\right\}}_{n\in \mathbf{N}}$ is a discrete-time homogeneous Markov renewal chain, if for any $b\in \mathcal{I},\varrho \in {\mathbf{N}}_{\ge 1},n\in \mathbf{N}$

$$\begin{array}{cc}& P_r\{R_{n+1}=b,S_n=\varrho \mid R_m,k_m,m\in {\mathbf{N}}_{[0,n]}\}\hfill \\ \hfill =& P_r\{R_{n+1}=b,S_n=\varrho \mid R_n\}\hfill \\ \hfill =& P_r(R_1=b,S_1=\varrho \mid R_0),\hfill \end{array}$$

holds.

In Definition 1, the stochastic process ${\left\{R_n\right\}}_{n\in \mathbf{N}}$ is named the embedded homogeneous Markov chain of the homogeneous Markov renewal chain ${\left\{(R_n,t_n)\right\}}_{n\in \mathbf{N}}$. For $\forall a,b\in \mathcal{I}$, the transition probabilities of ${\left\{R_n\right\}}_{n\in \mathbf{N}}$ are defined by ${\theta }_{ab}\triangleq P_r\{R_{n+1}=b\mid R_n=a\}$.

Definition 2 

([16]). The stochastic process ${\left\{\delta \left(t\right)\right\}}_{t\in \mathbf{N}}$ is called a homogeneous semi-Markov chain associated with homogeneous Markov renewal chain ${\left\{(R_n,t_n)\right\}}_{n\in \mathbf{N}}$, if the following condition holds:

$$\begin{array}{cc}& \delta \left(t\right)=R_{n\left(t\right)},\forall t\in \mathbf{N},n\left(t\right)\triangleq max\{n\in \mathbf{N}\mid t_n\le t\}.\hfill \end{array}$$

A key feature of the semi-Markov chain considered in this work is that the ST-PDF depends on both the current and the subsequent system mode. This is formally denoted as:

$${\omega }_{ab}\left(\varrho \right)=P_r(S_n=\varrho \mid R_n=a,R_{n+1}=b),\forall a,b\in \mathcal{I},\varrho \in {\mathbf{N}}_{[1,\infty )},$$

(5)

where $S_n=t_{n+1}-t_n$ is the sojourn time in mode a before jumping to mode b. Let ${\eta }_{ab}\left(\varrho \right)=P_r(R_{n+1}=b,S_n=\varrho \mid R_n=a)$ define the semi-Markov kernel, with the matrix form ${\Omega }_{ab}\left(\varrho \right)=\left[{\eta }_{ab}\left(\varrho \right)\right],a,b\in \mathcal{I}$. From the definitions of ${\eta }_{ab}\left(\varrho \right)$, ${\omega }_{ab}\left(\varrho \right)$, and ${\theta }_{ab}$, the following relationship is immediate:

$${\eta }_{ab}\left(\varrho \right)={\omega }_{ab}\left(\varrho \right){\theta }_{ab},\forall a,b\in \mathcal{I},\varrho \in {\mathbf{N}}_{[1,\infty )}.$$

(6)

Remark 2. 

The key distinction between the hidden semi-Markov model and semi-Markov model lies in the dual-layer uncertainty: the system mode evolves stochastically with memory (semi-Markovian), and its realization is only partially observable through an uncertain emission process. This dual uncertainty fundamentally distinguishes the control problem of HS-MJSs, necessitating controllers that are not only robust to parameter variations but also to errors in mode identification. Our subsequent controller design explicitly accounts for this by utilizing the observed mode $\tilde{\delta }\left(t\right)$ and the elapsed sojourn time $\kappa \left(t\right)$ as available information, rather than relying on the true, inaccessible mode $\delta \left(t\right)$.

Definition 3 

([16]). For any $a\in \mathcal{I}$, given the bound of sojourn time $T_{max}^a\in {\mathbf{N}}_{[1,\infty )}$, and any initial conditions $x\left(0\right)$, $\delta \left(0\right)$, system (1) is said to be MSS, if the following holds:

$$\begin{array}{c}\hfill \underset{t\to \infty }{lim}{\mathbb{E}\{\parallel x\left(t\right)\parallel }^2{\}}_{x\left(0\right),\delta \left(0\right),S_n\in [1,T_{max}^a]}=0.\end{array}$$

2.4. Fractional-Order Operators for Enhanced Control Design

The HS-MJS model established in Section 2.1 is characterized by dual-layer uncertainties and historical mode dependencies. Conventional IOSMC, which relies on instantaneous state feedback, is inherently memoryless and thus inadequate to fully leverage the temporal patterns embedded in such a system. To address this fundamental limitation, we turn to fractional-order calculus, whose intrinsic memory effect provides a natural mathematical framework for incorporating historical dynamics into the control design.

This paper adopts the G-L definition for the fractional-order difference, given its suitability for discrete-time analysis and digital implementation. The fractional-order difference of order $\lambda \in (0,1)$ for a discrete signal $x\left(t\right)$ is defined as:

$${\nabla }^{\lambda }x\left(t\right)\triangleq \sum _{j=0}^t{\psi }_j\left(\lambda \right)x(t-j),$$

where the binomial coefficients ${\psi }_j\left(\lambda \right)$ are given by:

$${\psi }_j\left(\lambda \right)={(-1)}^j\left({\displaystyle \genfrac{}{}{0pt}{}{\lambda }{j}}\right)={(-1)}^j{\displaystyle \frac{\Gamma (\lambda +1)}{\Gamma (j+1)\Gamma (\lambda -j+1)}},$$

(7)

and $\Gamma (·)$ is the Gamma function.

The inverse operator, the fractional-order sum, is defined as:

$${\nabla }^{-\lambda }x\left(t\right)=\sum _{j=0}^t{c}_j\left(\lambda \right)x(t-j).$$

The coefficients $c_j\left(\lambda \right)$ can be computed via the recurrence relation $c_0\left(\lambda \right)=1$ and $c_j\left(\lambda \right)=\frac{(j-1+\lambda )}{j}{c}_{j-1}\left(\lambda \right)$ for $j\ge 1$, which exhibits a power-law decay, assigning higher weights to recent states and non-zero weights to older states, thus encoding the history of the system.

A pivotal property of the fractional-order summation operator ${\nabla }^{-\lambda }$ for our subsequent stability analysis is that it constitutes a bounded linear operator [36]. Formally, there exists a positive constant $C\left(\lambda \right)$ such that for any square-summable signal $x\left(t\right)$, the following inequality holds:

$$\parallel {\nabla }^{-\lambda }x\left(t\right)\parallel \le C\left(\lambda \right)\underset{k\le t}{sup}\parallel x\left(k\right)\parallel .$$

(8)

Remark 3. 

The G-L operator’s dependence on the entire state history enables the controller to implicitly capture temporal patterns in mode transitions and sojourn times. This addresses the second key question in the Introduction regarding the exploitation of historical dynamics for robustness under incomplete and attacked observations.

2.5. A Key Stability Lemma

To analyze the stability of the closed-loop system, we employ the following lemma.

Lemma 1 

([15]). Consider the discrete-time mode switching system $x(t+1)=f\left(x\right(t),\delta (t\left)\right)$, where $\delta \left(t\right)$ is the hidden mode index associated with the switching instant $t_0,t_1,\dots ,t_q,\dots$ with $t_0=0$. If there exist Lyapunov functions $V(x,i):{\mathbf{R}}^{n_x}\times \mathcal{I}\mapsto {\mathbf{R}}_{(0,\infty )}$ and ${\mathcal{K}}_{\infty }$ functions ${\gamma }_1,{\gamma }_2,{\gamma }_3$, such that for any initial condition $x\left(0\right)=x_0\in {\mathbf{R}}^{n_x}$, $\delta \left(0\right)\in \mathcal{I}$ and given constants $h_a\in {\mathbf{R}}_{(0,\infty )}$, $a\in \mathcal{I}$, it holds that:

$$\begin{array}{cc}\hfill & {\gamma }_1(\parallel x\left(t\right)\parallel )\le V(x\left(t\right),\delta \left(t_n\right)))\le {\gamma }_2(\parallel x\left(t\right)\parallel ),\hfill \end{array}$$

(9)

$$\begin{array}{cc}\hfill & V(x\left(t\right),\delta \left(t_n\right))\le h_{\delta \left(t_n\right)}V(x\left(t_n\right),\delta \left(t_n\right)),t\in {\mathbf{Z}}_{[t_n+1,t_{n+1})},\hfill \end{array}$$

(10)

$$\begin{array}{cc}\hfill & \mathbb{E}[V(x\left(t_{n+1}\right),\delta \left(t_{n+1}\right))\mid x\left(t_n\right),\delta \left(t_n\right)]-V(x\left(t_n\right),\delta \left(t_n\right))\le -{\gamma }_3(\parallel x\left(t_n\right)\parallel ),\hfill \end{array}$$

(11)

where $\mathcal{K}=\left\{\alpha \right(·)\mid [0,\infty )\to [0,\infty ),\alpha (·)$ is continuous, strictly increasing and $\alpha \left(0\right)=0$}, ${\mathcal{K}}_{\infty }=\left\{\alpha (·)\right|\alpha (·)\in \mathcal{K}$ and $\alpha \left(x\right)\to \infty$ as $x\to \infty$} and $\mathbb{E}\{X\mid Y\}$ stands for the mathematical expectation of X conditioned on Y, then, the system is MSS.

Remark 4. 

Building upon the framework established in this section, the next section will propose a novel FOSMC that fuses the observed mode, sojourn time, and ${\nabla }^{-\lambda }x\left(t\right)$ to achieve robust stabilization. This will constitute the first systematic development of FOSMC for HS-MJSs under incomplete observations and DoS attacks, thereby addressing the third key question in the Introduction.

3. Fractional-Order Sliding Mode Controller

This section develops the core theoretical contributions of this work: the design and stability analysis of the proposed FOSMC. Building upon the established fractional-order framework, this section designs and analyzes a sliding mode control strategy for the system’s hybrid and uncertain dynamics. The development proceeds as follows: First, a novel fractional-order sliding surface is designed. Second, sufficient conditions for MSS of the closed-loop system are derived. Finally, a corresponding sliding mode control law is synthesized, and its reachability is rigorously analyzed to establish a quasi-sliding mode despite parameter uncertainties and intermittent DoS attacks.

3.1. Fractional-Order Sliding Surface Design

A fractional-order sliding surface is proposed to exploit the memory properties of fractional calculus, enhancing system robustness. It depends on the elapsed sojourn time $\kappa \left(t\right)$, and the full history of the state trajectory—utilizing the nonlocal characteristic to better handle uncertainties and partial observability. Inspired by the structure in [28], we propose the following sliding function:

$$\begin{array}{c}\hfill \varsigma \left(t\right)=(1-\widehat{\beta }){\mathcal{T}}_a{\nabla }^{-\lambda }x\left(t\right)+\widehat{\beta }{\mathcal{T}}_a(A_a+B_a{K}_{i\left(\kappa \right(t\left)\right)})\left({\nabla }^{-\lambda }{x}_b(t-2)\right),\end{array}$$

(12)

where ${\mathcal{T}}_a$ is a designed matrix ensuring $\mathcal{T}a{B}_a$ is nonsingular, $K_{i\left(\kappa \right(t\left)\right)}$ is a sojourn time dependent control gain to be determined via LMI optimization later in this section, and $\lambda \in (0,1)$ is the fractional order. The sliding manifold is given by $\varsigma \left(t\right)=0$.

Remark 5. 

The innovation of (12) stems from its use of fractional integrals, which mathematically represent a weighted sum over the entire history of the system states. This formulation effectively embeds memory into the sliding variable, allowing the controller to leverage past information for enhanced robustness against DoS attacks and observation uncertainties. Furthermore, this approach generalizes conventional designs, as the sliding function reduces to an integer-order surface when the fractional order λ approaches zero.

3.2. Sliding Mode Dynamics Under Fractional-Order Surface

The subsequent analysis leverages the linearity of the fractional-order operator. According to the system (1) and the sliding function (12), its dynamics are:

$$\begin{array}{cc}\hfill \varsigma (t+1)& =(1-\widehat{\beta }){\mathcal{T}}_a{\nabla }^{-\lambda }x(t+1)+\widehat{\beta }{\mathcal{T}}_a(A_a+B_a{K}_{i\left(\kappa \right(t\left)\right)}){\nabla }^{-\lambda }{x}_b(t-1)\hfill \\ \hfill & =(1-\widehat{\beta }){\mathcal{T}}_a{\nabla }^{-\lambda }\left[(A_a+\Delta A_a)x\left(t\right)+B_{a}u\left(t\right)\right]+\widehat{\beta }{\mathcal{T}}_a(A_a+B_a{K}_{i\left(\kappa \right(t\left)\right)}){\nabla }^{-\lambda }{x}_b(t-1)\hfill \end{array}$$

Under the ideal sliding motion, the system state is constrained to the sliding surface, satisfying:

$$\varsigma \left(t\right)=0,\forall t\ge t_0,$$

(13)

which implies $\varsigma (t+1)=\varsigma \left(t\right)=0$. Substituting the system dynamics (1) into the expression for $\varsigma (t+1)$, we obtain the following implicit relation that the control input must satisfy:

$$\begin{array}{cc}\hfill {\nabla }^{-\lambda }u\left(t\right)=& -{\left({\mathcal{T}}_a{B}_a\right)}^{-1}{\mathcal{T}}_a(A_a+\Delta A_a){\nabla }^{-\lambda }x\left(t\right)\hfill \\ \hfill & -{\displaystyle \frac{\widehat{\beta }}{1-\widehat{\beta }}}{\left({\mathcal{T}}_a{B}_a\right)}^{-1}{\mathcal{T}}_a(A_a+B_a{K}_{i\left(\kappa \right(t\left)\right)}){\nabla }^{-\lambda }{x}_b(t-1).\hfill \end{array}$$

(14)

This relation characterizes the dynamic constraint imposed by the sliding surface. Although it is not directly used for control implementation, it enables the derivation of the reduced-order sliding mode dynamics in the fractional-order domain.

3.3. Closed-Loop Dynamics and Stability Analysis

To establish a tractable stability analysis framework, we define the fractional-order state variables:

$$\begin{array}{c}\hfill z\left(t\right)\triangleq {\nabla }^{-\lambda }x\left(t\right),z_b\left(t\right)\triangleq {\nabla }^{-\lambda }{x}_b\left(t\right).\end{array}$$

Applying the fractional-order operator ${\nabla }^{-\lambda }$ to both sides of the system Equation (1) and utilizing its linearity property yields:

$$z(t+1)=(A_a+\Delta A_a)z\left(t\right)+B_a{\nabla }^{-\lambda }u\left(t\right)$$

(15)

Substituting the equivalent control ${\nabla }^{-\lambda }u\left(t\right)$ from (14) into (15), we obtain the closed-loop fractional-order dynamics:

$$z(t+1)=(A_a+\Delta A_a-\overline{A})z\left(t\right)+{\displaystyle \frac{\widehat{\beta }}{1-\widehat{\beta }}}{B}_a{\left({\mathcal{T}}_a{B}_a\right)}^{-1}{\mathcal{T}}_a(A_a+B_a{K}_{i\left(\kappa \right(t\left)\right)})z_b(t-1)$$

(16)

where $\overline{A}\triangleq B_a{\left({\mathcal{T}}_a{B}_a\right)}^{-1}{\mathcal{T}}_a(A_a+\Delta A_a)$.

For the buffered state, applying ${\nabla }^{-\lambda }$ to the buffer dynamics (4):

$$z_b\left(t\right)=\widehat{\beta }{z}_b(t-1)+(1-\widehat{\beta })z\left(t\right).$$

(17)

Let us define an augmented state vector that combines the fractional-order states:

$$\widehat{z}\left(t\right)\triangleq \left[\begin{array}{c}z\left(t\right)\\ z_b(t-1)\end{array}\right].$$

Combining (16) and (17), the augmented system dynamics are:

$$\widehat{z}(t+1)={\widehat{A}}_{ai\left(\kappa \right(t\left)\right)}\widehat{z}\left(t\right),$$

(18)

where the system matrix is given by:

$${\widehat{A}}_{ai\left(\kappa \right(t\left)\right)}\triangleq \left[\begin{array}{cc}{A}_a+\Delta A_a-\overline{A}& {\displaystyle \frac{\widehat{\beta }}{1-\widehat{\beta }}}{B}_a{\left({\mathcal{T}}_a{B}_a\right)}^{-1}{\mathcal{T}}_a(A_a+B_a{K}_{i\left(\kappa \right(t\left)\right)})\\ 1-\widehat{\beta }& \widehat{\beta }\end{array}\right].$$

Lemma 2. 

Let $z\left(t\right)\triangleq {\nabla }^{-\lambda }x\left(t\right)$ with $\lambda \in (0,1)$. If the fractional-order state $z\left(t\right)$ is MSS, then the original system state $x\left(t\right)$ is also MSS.

Proof. 

Assume $z\left(t\right)$ is MSS, which by definition means ${lim}_{k\to \infty }{\mathbb{E}\{\parallel z\left(k\right)\parallel }^2\}=0$. From the inverse relationship given by the G-L fractional-order difference, the state $x\left(t\right)$ is given by

$$x\left(t\right)={\nabla }^{\lambda }z\left(t\right)\triangleq \sum _{j=0}^t{\psi }_j\left(\lambda \right)z(t-j)$$

(19)

where ${\psi }_j\left(\lambda \right)$ are the binomial coefficients defined in (7). Taking the expectation of the squared norm yields the inequality:

$$\begin{array}{cc}\hfill \mathbb{E}\{\parallel x\left(t\right){\parallel }^2\}& \le C_{\psi }·\mathbb{E}\left\{\sum _{j=0}^t|{\psi }_j{|\parallel z(t-j)\parallel }^2\right\}\hfill \\ \hfill & =C_{\psi }\sum _{j=0}^t|{\psi }_j{\left|\mathbb{E}\right\{\parallel z(t-j)\parallel }^2\}\hfill \end{array}$$

(20)

where $C_{\psi }={\sum }_{j=0}^{\infty }\left|{\psi }_j\left(\lambda \right)\right|<\infty$ exists because the G-L coefficients are known to be absolutely summable for $\lambda \in (0,1)$.

Let $f\left(k\right)=\mathbb{E}\{\parallel z\left(k\right){\parallel }^2\}$ and $p_j=\left|{\psi }_j\right|$. Since $f\left(k\right)\to 0$ as $k\to \infty$, it is bounded, i.e., ${sup}_{k\ge 0}f\left(k\right)=M<\infty$. Also, ${\sum }_{j=0}^{\infty }{p}_j=C_{\psi }<\infty$. Given any $ϵ>0$, there exists an integer $K_1>0$ such that ${\sum }_{j=K_1+1}^{\infty }{p}_j<ϵ/\left(2M\right)$, and there exists an integer $K_2>0$ such that $f\left(k\right)<ϵ/\left(2C_{\psi }\right)$ for all $k>K_2$.

Now, let $T=K_1+K_2$. For any $t>T$, the convolution sum $g\left(t\right)$ is split as

$$g\left(t\right)=\sum _{j=0}^{K_1}|{\psi }_j{\left|\mathbb{E}\right\{\parallel z(t-j)\parallel }^2\}+\sum _{j=K_1+1}^t|{\psi }_j{\left|\mathbb{E}\right\{\parallel z(t-j)\parallel }^2\}$$

The second term is bounded using the boundedness M:

$$\sum _{j=K_1+1}^t|{\psi }_j{|\mathbb{E}\{\parallel z(t-j)\parallel }^2\}\le M\sum _{j=K_1+1}^t|{\psi }_j|\le M\sum _{j=K_1+1}^{\infty }|{\psi }_j|<M\left({\displaystyle \frac{ϵ}{2M}}\right)={\displaystyle \frac{ϵ}{2}}$$

For the first term, since $j\in [0,K_1]$ and $t>K_1+K_2$, the argument $t-j\ge t-K_1>K_2$. Thus, the convergence property can be applied:

$$\sum _{j=0}^{K_1}|{\psi }_j{|\mathbb{E}\{\parallel z(t-j)\parallel }^2\}<\sum _{j=0}^{K_1}|{\psi }_j|\left({\displaystyle \frac{ϵ}{2C_{\psi }}}\right)\le \left({\displaystyle \frac{ϵ}{2C_{\psi }}}\right)\sum _{j=0}^{\infty }|{\psi }_j|=\left({\displaystyle \frac{ϵ}{2C_{\psi }}}\right)C_{\psi }={\displaystyle \frac{ϵ}{2}}$$

Combining these bounds, for any $t>T$, it holds that $g\left(t\right)<ϵ/2+ϵ/2=ϵ$. By the formal definition of a limit, this proves ${lim}_{t\to \infty }g\left(t\right)=0$. Since $0\le {\mathbb{E}\{\parallel x\left(t\right)\parallel }^2\}\le C_{\psi }·g\left(t\right)$, the Squeeze Theorem implies

$$\underset{t\to \infty }{lim}{\mathbb{E}\{\parallel x\left(t\right)\parallel }^2\}=0$$

This completes the proof. □

Remark 6. 

As formally established in Lemma 2, the MSS of the fractional-order state $z\left(t\right)$ implies the MSS of the original system state $x\left(t\right)$. Therefore, the subsequent stability analysis can be focused on proving the MSS of the augmented system (17) without loss of generality, which rigorously addresses the transition from the fractional-order formulation to the Lyapunov proof.

3.4. Mean Square Stability Analysis

Theorem 1. 

For given constants $h_a\in {\mathbf{R}}_{(0,\infty )}$, $a\in \mathcal{I}$, if there exist matrices $P_a\succ 0$, $a\in \mathcal{I}$, such that for any $T_{max}^a\in {\mathbf{N}}_{[1,\infty )}$, $\varrho \in {\mathbf{N}}_{[1,T_{max}^a]}$, $t\in {\mathbf{N}}_{[1,T_{max}^a]}$ and $s\in {\mathbf{N}}_{[1,t]}$, the following inequalities hold:

$$\begin{array}{c}\hfill {(\prod _{s=1}^t{\widehat{A}}_{ai\left(s\right)})}^{\top }{\widehat{P}}_a\prod _{s=1}^t{\widehat{A}}_{ai\left(s\right)}-h_a{\widehat{P}}_a\prec 0,\end{array}$$

(21)

$$\begin{array}{cc}\hfill & \sum _{\varrho =1}^{T_{max}^a}[\sum _{i\left(1\right)\in {\mathcal{M}}_a^a}\dots \sum _{i\left(\varrho \right)\in {\mathcal{M}}_a^a}(\prod _{s=1}^{\varrho }{\pi }_{ai\left(s\right)}{\widehat{A}}_{ai\left(s\right)}^{\top }){\widehat{O}}_a\left(\varrho \right)\prod _{s=1}^{\varrho }{\widehat{A}}_{ai\left(s\right)}\hfill \\ \hfill & +\sum _{i\left(1\right)\in {\mathcal{M}}_a^u}\dots \sum _{i\left(\varrho \right)\in {\mathcal{M}}_a^u}(\prod _{s=1}^{\varrho }{\pi }_{ai\left(s\right)}{\widehat{A}}_{ai\left(s\right)}^{\top }){\widehat{O}}_a\left(\varrho \right)\prod _{s=1}^{\varrho }{\widehat{A}}_{ai\left(s\right)}^{\top }]\prec 0,\hfill \end{array}$$

(22)

where $O_a\left(\varrho \right)\triangleq {\sum }_{b\in \mathcal{I}}{\displaystyle \frac{{\eta }_{ab}\left(\varrho \right)}{{\sum }_{c\in \mathcal{I}}{\sum }_{v=1}^{T_{max}^a}{\eta }_{ac}\left(v\right)}}{P}_b$, ${\widehat{P}}_b\triangleq diag\{P_b,P_b\}$, $diag\{\dots \}$ stands for a block-diagonal matrix, ${\widehat{O}}_a\left(\varrho \right)\triangleq diag\{O_a\left(\varrho \right),O_a\left(\varrho \right)\}$ and ${\pi }_{ai\left(k\right)}$ is defined in (2), then, system (18) is MSS.

Proof. 

Construct the Lyapunov function

$$V(\widehat{z}\left(t\right),\delta \left(t\right))={\widehat{z}}^{\top }\left(t\right){\widehat{P}}_{\delta \left(t\right)}\widehat{z}\left(t\right).$$

(23)

Obviously, it follows from (23) that

$${\gamma }_1\parallel \widehat{z}{\left(t\right)\parallel }^2\le V(\widehat{z}\left(t\right),a)\le {\gamma }_2{\parallel \widehat{z}\left(t\right)\parallel }^2,$$

where ${\gamma }_1={min}_{a\in \mathcal{I}}\left\{{\lambda }_{min}\left({\widehat{P}}_a\right)\right\}$, ${\gamma }_2={max}_{a\in \mathcal{I}}\left\{{\lambda }_{max}\left({\widehat{P}}_a\right)\right\}$. Here, ${\lambda }_{min}\left({\widehat{P}}_a\right)$ and ${\lambda }_{max}\left({\widehat{P}}_a\right)$ represent the minimum and maximum eigenvalues of ${\widehat{P}}_a$, respectively. Consequently, condition (9) in Lemma 1 is satisfied.

For any $t\in {\mathbf{N}}_{[t_n+1,t_{n+1})}$, it can be obtained from (21) that

$$\begin{array}{cc}\hfill & V(\widehat{z}\left(t\right),\delta \left(t_n\right)\mid \widehat{z}\left(t_n\right),\delta \left(t_n\right)=a)-h_{a}V(\widehat{z}\left(\left(t_n\right)\right),\delta \left(t_n\right))\hfill \\ \hfill =& {\widehat{z}}^{\top }\left(t_n\right)\left[{(\prod _{s=1}^t{\widehat{A}}_{ai\left(s\right)})}^{\top }{\widehat{P}}_a\prod _{s=1}^t{\widehat{A}}_{ai\left(s\right)}\right]\widehat{z}\left(t_n\right)-h_a{\widehat{z}}^{\top }\left(t_n\right){\widehat{P}}_a\widehat{z}\left(t_n\right)\hfill \\ \hfill =& {\widehat{z}}^{\top }\left(t_n\right)\left[{(\prod _{s=1}^t{\widehat{A}}_{ai\left(s\right)})}^{\top }{\widehat{P}}_a\prod _{s=1}^t{\widehat{A}}_{ai\left(s\right)}-h_a{\widehat{P}}_a\right]\widehat{z}\left(t_n\right)\prec 0,\hfill \end{array}$$

which implies that condition (10) of Lemma 1 holds.

For any $n\in \mathbf{N}$, from (22) and the definition of ${\widehat{O}}_a\left(\varrho \right)$, one can derive that

$$\begin{array}{cc}\hfill & \mathbb{E}[V(\widehat{z}(t_{n+1}),\delta (t_{n+1}))\mid \widehat{z}(t_n),\delta (t_n)=a]-V\left(\widehat{z}(t_n),\delta (t_n)\right)\hfill \\ \hfill =& {\widehat{z}}^{\top }(t_n)\{\sum _{\varrho =1}^{T_{max}^a}[\sum _{i(1)\in {\mathcal{M}}_a^a}\dots \sum _{i(\varrho )\in {\mathcal{M}}_a^a}(\prod _{s=1}^{\varrho }{\pi }_{ai(s)}{\widehat{A}}_{ai(s)}^{\top }){\widehat{O}}_a(\varrho )\prod _{s=1}^{\varrho }{\widehat{A}}_{ai(s)}\hfill \\ \hfill & +\sum _{i(1)\in {\mathcal{M}}_a^u}\dots \sum _{i(\varrho )\in {\mathcal{M}}_a^u}(\prod _{s=1}^{\varrho }{\pi }_{ai(s)}{\widehat{A}}_{ai(s)}^{\top }){\widehat{O}}_a(\varrho )\prod _{s=1}^{\varrho }{\widehat{A}}_{ai(s)}]\}\widehat{z}(t_n)-{\widehat{z}}^{\top }(t_n){\widehat{P}}_a\widehat{z}(t_n)\hfill \\ \hfill \le & -{\sigma }_{min}\{-\sum _{\varrho =1}^{T_{max}^a}[\sum _{i(1)\in {\mathcal{M}}_a^a}\dots \sum _{i(\varrho )\in {\mathcal{M}}_a^a}(\prod _{s=1}^{\varrho }{\pi }_{ai(s)}{\widehat{A}}_{ai(s)}^{\top }){\widehat{O}}_a(\varrho )\prod _{s=1}^{\varrho }{\widehat{A}}_{ai(s)}+\sum _{i(1)\in {\mathcal{M}}_a^u}\dots \sum _{i(\varrho )\in {\mathcal{M}}_a^u}\hfill \\ \hfill & (\prod _{s=1}^{\varrho }{\widehat{A}}_{ai(s)}^{\top }{\widehat{O}}_a(\varrho )(\varrho )\prod _{s=1}^{\varrho }{\widehat{A}}_{ai(s)}]+{\widehat{P}}_a\}\parallel \widehat{z}(t_n){\parallel }^2,\hfill \end{array}$$

where ${\displaystyle \tilde{\lambda }\triangleq \underset{a\in \mathcal{I}}{inf}{\sigma }_{min}\{-\sum _{\varrho =1}^{T_{max}^a}[\sum _{i(1)\in {\mathcal{M}}_a^a}\dots \sum _{i(\varrho )\in {\mathcal{M}}_a^a}(\prod _{s=1}^{\varrho }{\pi }_{ai(s)}{\widehat{A}}_{ai(s)}^{\top }){\widehat{O}}_a(\prod _{s=1}^{\varrho }{\widehat{A}}_{ai(s)})+\sum _{i(1)\in {\mathcal{M}}_a^u}\dots }$  ${\displaystyle \times \sum _{i(\varrho )\in {\mathcal{M}}_a^u}(\prod _{s=1}^{\varrho }{\widehat{A}}_{ai(s)}^{\top }){\widehat{O}}_a(\varrho )(\prod _{s=1}^{\varrho }{\widehat{A}}_{ai(s)})+{\widehat{P}}_a\}}$ and ${\displaystyle {\widehat{O}}_a(\varrho )}$ is defined in (22), which can guarantee that condition (11) holds of Lemma 1. Therefore, system (18) is MSS. The proof of the Theorem is completed. □

Remark 7. 

Theorem 1 establishes a sufficient condition for MSS. However, its practical application is limited by non-convex terms such as ${\prod }_{s=1}^t{\widehat{A}}_{ai\left(s\right)}$, which complicate the solution process. To address this, we introduce an auxiliary variable to transform the condition into a convex framework amenable to efficient computation.

Theorem 2. 

For given constants $h_a\in {\mathbf{R}}_{(0,\infty )}$, $T_{max}^a\in {\mathbf{N}}_{[1,\infty )}$, $a\in \mathcal{I}$, if there exist matrices $P_a\succ 0$, $O_a(\varrho ,m),\varrho \in {\mathbf{N}}_{[1,T_{max}^a]},m\in {\mathbf{N}}_{[1,T_{max}^a]}$ and $X_{i,t,p}\succ 0$, $t\in {\mathbf{N}}_{[1,T_{max}^a]}$, $p={\mathbf{N}}_{[1,t]}$, $t\ne q$, such that when $T_{max}^a\in {\mathbf{N}}_{[2,\infty )}$, the following conditions hold:

$$\begin{array}{cc}\hfill & A_{ai(t-p)}^{\top }{\widehat{X}}_{a,t,p+1}{\widehat{A}}_{ai(t-p)}-{\widehat{X}}_{a,t,p}\prec 0,\hfill \end{array}$$

(24)

$$\begin{array}{cc}\hfill & {\widehat{A}}_{ai\left(t\right)}{\widehat{X}}_{a,t,1}{A}_{ai\left(t\right)}-h_a{\widehat{P}}_a\prec 0,\hfill \end{array}$$

(25)

$$\begin{array}{cc}\hfill & \sum _{i\left(s\right)\in {\mathcal{M}}_a^a}{\pi }_{ai\left(s\right)}{\widehat{A}}_{ai\left(s\right)}^{\top }({\mathbf{L}}_{am+1}^{\top }\mathbf{P}{\mathbf{L}}_{am+1}+{\mathbf{O}}_{a,m+1}){\widehat{A}}_{ai\left(s\right)}-{\pi }_a^{\mathcal{U}}{\mathbf{O}}_{a,m}\prec 0,\hfill \end{array}$$

(26)

$$\begin{array}{cc}\hfill & {\widehat{A}}_{ai\left(s\right)}^{\top }({\mathbf{L}}_{am+1}^{\top }\mathbf{P}{\mathbf{L}}_{am+1}+{\mathbf{O}}_{a,m+1}){\widehat{A}}_{ai\left(s\right)}-{\mathbf{O}}_{a,m}\prec 0,i\left(s\right)\in {\mathcal{M}}_a^u,\hfill \end{array}$$

(27)

$$\begin{array}{cc}\hfill & \sum _{i\left(1\right)\in {\mathcal{M}}_a^a}{\pi }_{ai}{\widehat{A}}_{ai\left(1\right)}^{\top }({\mathbf{L}}_{a1}^{\top }\mathbf{P}{\mathbf{L}}_{a1}+{\mathbf{O}}_{a,1}){\widehat{A}}_{ai\left(1\right)}-{\pi }_a^{\mathcal{U}}{\widehat{P}}_a\prec 0,\hfill \end{array}$$

(28)

$$\begin{array}{cc}\hfill & {\widehat{A}}_{ai\left(1\right)}^{\top }({\mathbf{L}}_{a1}^{\top }\mathbf{P}{\mathbf{L}}_{a1}+{\mathbf{O}}_{a,1}){\widehat{A}}_{ai\left(1\right)}-{\widehat{P}}_a\prec 0,i\left(1\right)\in {\mathcal{M}}_a^u,\hfill \end{array}$$

(29)

and when $T_{max}^a=1$, (25), (28) and (29) hold, where ${\pi }_{ai\left(\kappa \right)\left(t\right)}$ and ${\widehat{O}}_a\left(\varrho \right)$ are defined in (2) and (25), respectively,

$$\begin{array}{ccc}& & {\pi }_a^{\mathcal{U}}\triangleq \sum _{i\left(s\right)\in {\mathcal{M}}_a^u}{\pi }_{ai\left(s\right)},\mathbf{P}=diag\{P_1,P_2,\dots ,P_l,P_1,P_2,\dots ,P_l\},\hfill \\ & & O_a(\varrho ,\varrho )\triangleq O_a\left(\varrho \right),{\mathbf{O}}_{am}\triangleq \sum _{\varrho =m+1}^{T_{max}^a}{O}_a(\varrho ,m),X_{a,l,l}\triangleq X_a,{\widehat{X}}_{a,c,d}\triangleq diag\{X_{a,c,d},X_{a,c,d}\}\hfill \\ & & {\mathbf{L}}_{am}\triangleq \{\sqrt{O_{a1\left(m\right)}}I,\dots ,\sqrt{O_{al\left(m\right)}}I,{\sqrt{O}}_{a1\left(m\right)}I,\dots ,\sqrt{O_{al\left(m\right)}}I\},\hfill \end{array}$$

then, system (18) is MSS.

Proof. 

When $T_{max}^a=1$, for this case, the above definition of with the above ${\widehat{X}}_{a,l,l}$, it is easy to see that (25) is equivalent to (21). Consequently, (22) follows immediately from (28) and (29), which completes the proof for $T_{max}^a=1$.

When $T_{max}^a\in {\mathbf{N}}_{[2,\infty )}$, we denote

$$\begin{array}{cc}\hfill & I_1\triangleq \sum _{\varrho =1}^{T_{max}^a}\sum _{i\left(1\right)\in {\mathcal{M}}_a^a}\dots \sum _{i_{\varrho }\in {\mathcal{M}}_a^a}\left(\prod _{s=1}^{\varrho }{\pi }_{ai\left(s\right)}{\widehat{A}}_{ai\left(s\right)}^{\top }\right){\widehat{O}}_a\left(\varrho \right)\prod _{s=1}^{\varrho }{\widehat{A}}_{ai\left(s\right)},\hfill \\ \hfill & I_2\triangleq \sum _{\varrho =1}^{T_{max}^a}\sum _{i\left(1\right)\in {\mathcal{M}}_a^u}\dots \sum _{i_{\varrho }\in {\mathcal{M}}_a^u}\left(\prod _{s=1}^{\varrho }{\pi }_{ai\left(s\right)}{\widehat{A}}_{ai\left(s\right)}^{\top }\right){\widehat{O}}_a\left(\varrho \right)\times \prod _{s=1}^{\varrho }{\widehat{A}}_{ai\left(s\right)}.\hfill \end{array}$$

Then, we have

$$\begin{array}{cc}\hfill I_1=& \sum _{i(1)\in {\mathcal{M}}_a^a}{\pi }_{ai(1)}{\widehat{A}}_{ai(1)}^{\top }{\widehat{O}}_a(1){\widehat{A}}_{ai(1)}+\sum _{\varrho =2}^{T_{max}^a}\sum _{m=1}^{\varrho -1}[\sum _{i(1)\in {\mathcal{M}}_a^a}\dots \sum _{i(m)\in {\mathcal{M}}_a^a}(\prod _{s=1}^m{\pi }_{ai(s)}{\widehat{A}}_{ai(s)}^{\top })\hfill \\ & (\sum _{i(m+1)\in {\mathcal{M}}_a^a}{\pi }_{ai(m+1)}{\widehat{A}}_{ai(m+1)}^{\top }{\widehat{O}}_a(\varrho ,m+1){\widehat{A}}_{ai(m+1)}-{\widehat{O}}_a(\varrho ,m))\prod _{s=1}^m{\widehat{A}}_{ai(s)}]\hfill \\ & +\sum _{\varrho =2}^{T_{max}^a}\sum _{i(1)\in {\mathcal{M}}_a^a}{\pi }_{ai(1)}{\widehat{A}}_{ai(1)}^{\top }{\widehat{O}}_a(\varrho ,1){\widehat{A}}_{ai(1)}\hfill \\ \hfill =& \sum _{i(1)\in {\mathcal{M}}_a^a}{\pi }_{ai(1)}{\widehat{A}}_{ai(1)}^{\top }{\widehat{O}}_a(1){\widehat{A}}_{ai(1)}+\sum _{m=1}^{T_{max}^a-1}\sum _{i(1)\in {\mathcal{M}}_a^a}\dots \sum _{i(m)\in {\mathcal{M}}_a^a}(\prod _{s=1}^m{\pi }_{ai(s)}{\widehat{A}}_{ai(s)}^{\top })\hfill \\ \hfill & \times \left[\sum _{i(m+1){\mathcal{M}}_a^a}{\pi }_{ai(m+1)}{\widehat{A}}_{ai(m+1)}^{\top }\times (\sum _{\varrho =m+1}^{T_{max}^a}{\widehat{O}}_a(\varrho ,m+1)){\widehat{A}}_{ai(m+1)}-\sum _{\varrho =m+1}^{T_{max}^a}{\widehat{O}}_a(\varrho ,m)\right]\prod _{s=1}^m{\widehat{A}}_{ai(s)}\hfill \\ \hfill & +\sum _{i(1)\in {\mathcal{M}}_a^a}{\pi }_{ai(1)}{\widehat{A}}_{ai(1)}^{\top }{\widehat{O}}_a(\varrho ,1){\widehat{A}}_{ai(1)}\hfill \\ \hfill =& \sum _{m=1}^{T_{max}^a-1}\sum _{i(1)\in {\mathcal{M}}_a^a}\dots \sum _{i(m)\in {\mathcal{M}}_a^a}(\prod _{s=1}^m{\widehat{\pi }}_{ai(s)}{\widehat{A}}_{ai(s)}^{\top })[\sum _{i(m+1)\in {\mathcal{M}}_a^a}{\pi }_{ai(m+1)}{\widehat{A}}_{ai(m+1)}^{\top }({\widehat{O}}_a(\varrho )\hfill \\ \hfill & +\sum _{\varrho =m+2}^{T_{max}^a}{\widehat{O}}_a(\varrho ,m+1)){\widehat{A}}_{ai(m+1)}-\sum _{\varrho =m+1}^{T_{max}^a}{\widehat{O}}_a(\varrho ,m)]\prod _{s=1}^m{\widehat{A}}_{ai(s)}+\sum _{i(1)\in {\mathcal{M}}_a^a}{\pi }_{ai(1)}{\widehat{A}}_{ai(1)}^{\top }{\widehat{O}}_a(1,1)\hfill \\ \hfill & \times {\widehat{A}}_{ai(1)}+\sum _{i(1)\in {\mathcal{M}}_a^a}{\pi }_{ai(1)}{\widehat{A}}_{ai(1)}(\sum _{\varrho =2}^{T_{max}^a}{\widehat{O}}_a(\varrho ,1)){\widehat{A}}_{ai(1)}\hfill \\ \hfill =& \sum _{m=1}^{T_{max}^a-1}\sum _{i(1)\in {\mathcal{M}}_a^a}\dots \sum _{i(m)\in {\mathcal{M}}_a^a}(\prod _{s=1}^m{\widehat{A}}_{ai(s)}^{\top })[\sum _{i(m+1)\in \mathcal{M}}{\pi }_{ai(m+1)}{\widehat{A}}_{ai(m+1)}^{\top }({\mathbf{L}}_{a_{m+1}}^{\top }\mathbf{P}{\mathbf{L}}_{a_{m+1}}+{\mathbf{O}}_{a_{m+1}})\hfill \\ & {\widehat{A}}_{ai(m+1)}-{\mathbf{O}}_{am}]\prod _{s=1}^m{\widehat{A}}_{ai(s)}+\sum _{i(1)\in {\mathcal{M}}_a^a}{\pi }_{ai(1)}{\widehat{A}}_{ai(1)}^{\top }({\mathbf{L}}_{a1}^{\top }\mathbf{P}{\mathbf{L}}_{a1}+{\mathbf{O}}_{ai(1)}){\widehat{A}}_{ai(1)}.\hfill \end{array}$$

(30)

Based on (26), (28) and (30), it can be concluded that $I_1-{\pi }_a^u{\widehat{P}}_a\prec 0$. This result, together with (27) and (29), implies that condition (22) of Theorem 1 holds for all $T_{max}^a\in {\mathbf{N}}_{[2,\infty )}$.

Binding conditions (24) and (25), we have

$$\begin{array}{cc}\hfill & {\left(\prod _{s=1}^t{\widehat{A}}_{ai\left(s\right)}\right)}^{\top }\widehat{P_a}\prod _{s=1}^t{\widehat{A}}_{ai\left(s\right)}-h_a{\widehat{P}}_a\hfill \\ \hfill =& \sum _{p=1}^{t-1}\{{\left(\prod _{l=t-p+1}^t{\widehat{A}}_{ai\left(l\right)}\right)}^{\top }[A_{ai(t-p)}^{\top }{\widehat{X}}_{a,t,p+1}{\widehat{A}}_{ai(t-p)}-{\widehat{X}}_{a,t,p}]\hfill \\ \hfill & \times \prod _{l=t-p+1}^t{\widehat{A}}_{ai\left(l\right)}\}+{\widehat{A}}_{ai\left(t\right)}{\widehat{X}}_{a,t,1}-h_a{\widehat{P}}_a\prec 0,\hfill \end{array}$$

(31)

and so the condition (21) holds in Theorem 1 for all $T_{max}^a\in {\mathbf{N}}_{[2,\infty )}$. Therefore, by Theorem 1, the system (18) is MSS. This completes the proof. □

The preceding content undertakes a series of stability analyses on the system, subsequently leading to the controller design based on Theorem 3.

Theorem 3. 

For given constants $h_a\in {\mathbf{R}}_{(0,\infty )}$ and $T_{max}^a\in {\mathbf{N}}_{[1,\infty )},a\in \mathcal{I}$, if there exist matrices ${\widehat{\mathbf{X}}}_{a,t,p},\widehat{\mathbf{P}},{\widehat{\mathbf{O}}}_{am},V,U_a$, $t\in {\mathbf{R}}_{[1,T_{max}^a]},p\in {\mathbf{R}}_{[1,t]},p\ne t,m\in {\mathbf{R}}_{[1,T_{max}^a]}$, $a\in \mathcal{I}$, such that when $T_{max}^a\in {\mathbf{N}}_{[2,\infty )}$, the following LMIs hold:

$$\left[\begin{array}{cc}{\widehat{\mathbf{X}}}_{a,t,p+1}-Sym\left(\widehat{V}\right)& {\widehat{\mathbf{A}}}_{ai(t-p)}\\ \ast & -{\widehat{X}}_{a,t,p}\end{array}\right]\prec 0$$

(32)

$$\left[\begin{array}{cc}{\widehat{\mathbf{X}}}_{a,t,1}-Sym\left(\widehat{V}\right)& {\widehat{\mathbf{A}}}_{ai\left(t\right)}\\ \ast & -h_a{\widehat{P}}_a\end{array}\right]\prec 0$$

(33)

$$\left[\begin{array}{ccccccc}\widehat{\mathbf{P}}-Sym\left(\mathbf{V}\right)& 0& \dots & 0& \dots & 0& \sqrt{{\pi }_{a{m}_a^1}}{\mathbf{L}}_{am+1}{\widehat{\mathbf{A}}}_{a{m}_a^1}\\ \ast & \ddots & ⋮& ⋮& ⋮& ⋮& ⋮\\ \ast & \ast & \widehat{\mathbf{P}}-Sym\left(\mathbf{V}\right)& 0& \dots & 0& \sqrt{{\pi }_{a{m}_a^1}}{\mathbf{L}}_{am+1}{\widehat{\mathbf{A}}}_{a{m}_a^{i^a}}\\ \ast & \ast & \ast & {\widehat{\mathbf{O}}}_{a,m}-Sym\left(V\right)& \dots & ⋮& \sqrt{{\pi }_{a{m}_a^1}}{\mathbf{L}}_{am+1}{\widehat{\mathbf{A}}}_{a{m}_a^1}\\ \ast & \ast & \ast & \ast & \ddots & 0& ⋮\\ \ast & \ast & \ast & \ast & \ast & {\widehat{\mathbf{O}}}_{a,m}-Sym\left(V\right)& \sqrt{{\pi }_{a{m}_a^1}}{\mathbf{L}}_{am+1}{\widehat{\mathbf{A}}}_{a{m}_a^{i^a}}\\ \ast & \ast & \ast & \ast & \ast & \ast & -{\widehat{\mathbf{O}}}_{am}\end{array}\right]\prec 0,$$

(34)

$$\left[\begin{array}{ccc}\widehat{\mathbf{P}}-Sym\left(\mathbf{V}\right)& 0& {\mathbf{L}}_{am+1}{\widehat{\mathbf{A}}}_{ai\left(s\right)}\\ 0& {\widehat{\mathbf{O}}}_{am+1}-Sym\left(\widehat{V}\right)& {\widehat{\mathbf{A}}}_{ai\left(s\right)}\\ \ast & \ast & -{\widehat{\mathbf{O}}}_{am}\end{array}\right]\prec 0,$$

(35)

$$\left[\begin{array}{ccccccc}\widehat{\mathbf{P}}-Sym\left(\mathbf{V}\right)& 0& \dots & 0& \dots & 0& \sqrt{{\pi }_{a{m}_a^1}}{\mathbf{L}}_{a1}{\widehat{\mathbf{A}}}_{a{m}_a^1}\\ \ast & \ddots & ⋮& ⋮& ⋮& ⋮& ⋮\\ \ast & \ast & \widehat{\mathbf{P}}-Sym\left(\mathbf{V}\right)& 0& \dots & 0& \sqrt{{\pi }_{a{m}_a^1}}{\mathbf{L}}_{a1}{\widehat{\mathbf{A}}}_{a{m}_a^{i^a}}\\ \ast & \ast & \ast & {\widehat{\mathbf{O}}}_{a,m}-Sym\left(\widehat{V}\right)& \dots & ⋮& \sqrt{{\pi }_{a{m}_a^1}}{\mathbf{L}}_{a1}{\widehat{\mathbf{A}}}_{a{m}_a^1}\\ \ast & \ast & \ast & \ast & \ddots & 0& ⋮\\ \ast & \ast & \ast & \ast & \ast & {\widehat{\mathbf{O}}}_{a,m}-Sym\left(\widehat{V}\right)& \sqrt{{\pi }_{a{m}_a^1}}{\mathbf{L}}_{a1}{\widehat{\mathbf{A}}}_{a{m}_a^{i^a}}\\ \ast & \ast & \ast & \ast & \ast & \ast & -{\pi }_a^{\mathcal{K}}{\widehat{\mathbf{O}}}_{am}\end{array}\right]\prec 0,$$

(36)

$$\left[\begin{array}{ccc}\widehat{\mathbf{P}}-Sym\left(\mathbf{V}\right)& 0& L_{a1}{\widehat{\mathbf{A}}}_{ai\left(1\right)}\\ 0& {\widehat{\mathbf{O}}}_{am+1}-Sym\left(\widehat{V}\right)& {\widehat{\mathbf{A}}}_{ai\left(1\right)}\\ \ast & \ast & -{\widehat{\mathbf{O}}}_{am}\end{array}\right]\prec 0,$$

(37)

and when $T_{max}^a$ = 1, conditions (33), (35) and (37) hold, in which $\widehat{\mathbf{V}}\triangleq dia{g}_{2l}\left\{V\right\},\widehat{V}\triangleq diag\{V,V\}$, ${\widehat{\mathbf{A}}}_{ai\left(\kappa \right(t\left)\right)}\triangleq \left[\begin{array}{cc}(A_a+\Delta A_a-\overline{A})V& {\displaystyle \frac{\widehat{\beta }}{1-\widehat{\beta }}}{B}_a{\left({\mathcal{T}}_a{B}_a\right)}^{-1}{\mathcal{T}}_a(A_a+B_a{U}_{i\left(\kappa \right(t\left)\right)})\\ (1-\widehat{\beta })V& \widehat{\beta }V\end{array}\right]$,  $dia{g}_N\left\{X\right\}$ denotes an $N\times N$ block-diagonal matrix, then, system (18) is MSS with the controller gains matrix

$$K_{i\left(\kappa \right(t\left)\right)}=U_{i\left(\kappa \right(t\left)\right)}{V}^{-1},$$

Proof. 

When $T_{max}^a\in {\mathbf{N}}_{[2,\infty )}$, we first prove that condition (35) can guarantee that (27) holds.

Since $\widehat{\mathbf{P}}\succ 0$ and ${\widehat{\mathbf{O}}}_{am}\succ 0$ ensure $\widehat{\mathbf{P}}-Sym\left(\mathbf{V}\right)\succ -{\mathbf{V}}^{\top }{\widehat{\mathbf{P}}}^{-1}\mathbf{V}$ and ${\widehat{\mathbf{O}}}_{am+1}-Sym\left(\widehat{V}\right)\succ -{\widehat{V}}^{\top }{\widehat{\mathbf{O}}}_{am+1}^{-1}\widehat{V}$, (35) implies:

$$\left[\begin{array}{ccc}-{\mathbf{V}}^{\top }{\widehat{\mathbf{P}}}^{-1}\mathbf{V}& 0& {\mathbf{L}}_{am+1}{\widehat{\mathbf{A}}}_{ai\left(s\right)}\\ 0& -{\widehat{V}}^{\top }{\widehat{\mathbf{O}}}_{am+1}^{-1}\widehat{V}& {\widehat{\mathbf{A}}}_{ai\left(s\right)}\\ \ast & \ast & -{\widehat{\mathbf{O}}}_{am}\end{array}\right]\prec 0.$$

Applying the congruence transformation to above inequality by $diag\{{\mathbf{V}}^{-1},{\widehat{V}}^{-1},{\widehat{V}}^{-1}\}$, we have

$$\left[\begin{array}{ccc}-{\widehat{\mathbf{P}}}^{-1}& 0& {\left({\mathbf{V}}^{-1}\right)}^{\top }{\mathbf{L}}_{am+1}{\widehat{A}}_{ai\left(s\right)}\\ 0& -{\widehat{\mathbf{O}}}_{am+1}^{-1}& {\left({\widehat{V}}^{-1}\right)}^{\top }{\widehat{A}}_{ai\left(s\right)}\\ \ast & \ast & -{\left({\widehat{V}}^{-1}\right)}^{\top }{\widehat{\mathbf{O}}}_{am}{\widehat{V}}^{-1}\end{array}\right]\prec 0.$$

It follows from the Schur complement lemma that

$${\left({\widehat{V}}^{-1}\right)}^{\top }{\widehat{\mathbf{O}}}_{am}{\widehat{V}}^{-1}+\left[\begin{array}{cc}{\widehat{A}}_{ai\left(s\right)}{\mathbf{L}}_{am+1}^{\top }{\mathbf{V}}^{-1}& {\widehat{A}}_{ai\left(s\right)}{\widehat{V}}^{-1}\end{array}\right]\left[\begin{array}{cc}\widehat{\mathbf{P}}& 0\\ 0& {\widehat{\mathbf{O}}}_{am+1}\end{array}\right]\left[\begin{array}{c}{\left({\mathbf{V}}^{-1}\right)}^{\top }{\mathbf{L}}_{am+1}{\widehat{A}}_{ai\left(s\right)}\\ {\left({\widehat{V}}^{-1}\right)}^{\top }{\widehat{A}}_{ai\left(s\right)}\end{array}\right]\prec 0$$

Let

$$\widehat{\mathbf{P}}=\mathbf{V}\mathbf{P}{\left(\mathbf{V}\right)}^{\top },{\widehat{\mathbf{O}}}_{am}=\widehat{V}{\mathbf{O}}_{am}{\left(\widehat{V}\right)}^{\top }$$

we have

$${\widehat{A}}_{ai\left(s\right)}^{\top }{\mathbf{L}}_{am+1}^{\top }{\mathbf{V}}^{-1}\mathbf{V}\mathbf{P}{\mathbf{V}}^{\top }{\left({\mathbf{V}}^{-1}\right)}^{\top }{\mathbf{L}}_{am+1}{\widehat{A}}_{ai\left(s\right)}+{\widehat{A}}_{ai\left(s\right)}{\widehat{V}}^{-1}\widehat{V}{\mathbf{O}}_{am+1}{\widehat{V}}^{\top }{\left({\widehat{V}}^{-1}\right)}^{\top }{\widehat{A}}_{ai\left(s\right)}-{\mathbf{O}}_{am}\prec 0$$

that is

$${\widehat{A}}_{ai\left(s\right)}^{\top }{\mathbf{L}}_{am+1}^{\top }\mathbf{P}{\mathbf{L}}_{am+1}{\widehat{A}}_{ai\left(s\right)}+{\widehat{A}}_{ai\left(s\right)}{\mathbf{O}}_{am+1}{\widehat{A}}_{ai\left(s\right)}-{\mathbf{O}}_{am}\prec 0$$

which implies that condition (27) of Theorem 2.

Since ${\widehat{\mathbf{X}}}_{a,t,p}\succ 0$ ensures ${\widehat{\mathbf{X}}}_{a,t,p}-Sym\left(\widehat{V}\right)\succ {\widehat{V}}^{\top }{\widehat{\mathbf{X}}}_{a,t,p}^{-1}\widehat{V}$, then we have

$$\left[\begin{array}{cc}{\widehat{V}}^{\top }{\widehat{\mathbf{X}}}_{a,t,p}^{-1}\widehat{V}& {\widehat{\mathbf{A}}}_{ai(t-p)}\\ \ast & -{\widehat{X}}_{a,t,p}\end{array}\right]\prec 0$$

Performing a congruence transformation to above inequality by $diag\{{\widehat{V}}^{-1},\mathbf{I}\}$, we obtain

$$\left[\begin{array}{cc}{\widehat{\mathbf{X}}}_{a,t,p}^{-1}& {\left({\widehat{V}}^{-1}\right)}^{\top }{\widehat{A}}_{ai(t-p)}\\ \ast & -{\widehat{X}}_{a,t,p}\end{array}\right]\prec 0$$

Let ${\widehat{\mathbf{X}}}_{a,t,p}=\widehat{V}{\widehat{X}}_{a,t,p+1}{\left(\widehat{V}\right)}^{\top }$, it follows from Schur complement that

$${\widehat{A}}_{ai(t-p)}^{\top }{\widehat{X}}_{a,t,p+1}{\widehat{A}}_{ai(t-p)}-{\widehat{X}}_{a,t,p}\prec 0.$$

Thus, condition (32) can guarantee that condition (24) holds. Following an identical methodology (i.e., applying the standard matrix inequality, followed by a congruence transformation and the Schur Complement lemma), it can be shown that the LMI conditions (33), (34), (28) and (37) are sufficient for (25), (26), (28) and (29), respectively. When $T_{max}^a=1$, following a similar reasoning to that above, it can be rigorously shown that the system (4) is also MSS. Thus, we complete the proof of this theorem. □

3.5. Reachability Analysis

In this subsection, we design a sliding mode control law to drive the system trajectories toward the predefined sliding surface (12), and prove that they enter and remain within a neighborhood of the surface in finite time.

Theorem 4. 

Consider the system under the uncertainty structure $\Delta A_a=E_a{F}_a{G}_a$ with $\parallel F_a\parallel \le I$. The sliding surface (12) is reachable in finite time under the following sliding mode control law:

$$u\left(t\right)=-{\left({\mathcal{T}}_a{B}_a\right)}^{-1}\left[{\mathcal{T}}_a{A}_a{\nabla }^{-\lambda }x\left(t\right)+\eta \left(t\right)·\mathrm{sign}\left(\varsigma \left(t\right)\right)\right],$$

(38)

where the adaptive gain $\eta \left(t\right)$ is given by

$$\eta \left(t\right)=\parallel {\mathcal{T}}_a{E}_a\parallel \parallel G_a\parallel \parallel {\nabla }^{-\lambda }x\left(t\right)\parallel +{\eta }_{\mathrm{res}}\left(t\right)+\tau ,$$

with $\tau >0$ being a design constant, and ${\eta }_{\mathrm{res}}\left(t\right)$ defined as

$${\eta }_{\mathrm{res}}\left(t\right)={\displaystyle \frac{\widehat{\beta }}{1-\widehat{\beta }}}\left(\parallel {\mathcal{T}}_a{A}_a\parallel +\parallel {\mathcal{T}}_a{B}_a{K}_{i\left(\kappa \right(t\left)\right)}\parallel \right)\parallel {\nabla }^{-\lambda }{x}_b(t-1)\parallel .$$

Then, the sliding variable $\varsigma \left(t\right)$ converges in finite time to the bounded region

$$\Omega =\left\{\varsigma \left(t\right)|\parallel \varsigma (t)\parallel \le \rho \right\},$$

where the bound ρ is

$$\rho ={(1-\widehat{\beta })}^{-1}{\sigma }_{max}\left({\mathcal{T}}_a\right)\left(\parallel \Delta A_a\parallel \parallel x\left(t\right)\parallel +{\eta }_{\mathrm{res}}\left(t\right)\right)/\tau ,$$

and ${\sigma }_{max}\left({\mathcal{T}}_a\right)$ denotes the maximum singular value of the matrix ${\mathcal{T}}_a$.

Proof. 

Consider the Lyapunov function candidate:

$$V\left(t\right)={\displaystyle \frac{1}{2}}{\varsigma }^{\top }\left(t\right)\varsigma \left(t\right).$$

Defining $\Delta \varsigma \left(t\right)=\varsigma (t+1)-\varsigma \left(t\right)$, the difference of $V\left(t\right)$ along the closed-loop trajectories is:

$$\begin{array}{cc}\hfill \Delta V\left(t\right)& =V(t+1)-V\left(t\right)\hfill \\ \hfill & =\varsigma {\left(t\right)}^{\top }\Delta \varsigma \left(t\right)+{\displaystyle \frac{1}{2}}\Delta \varsigma {\left(t\right)}^{\top }\Delta \varsigma \left(t\right)\hfill \\ \hfill & =\varsigma {\left(t\right)}^{\top }\varsigma (t+1)-\varsigma {\left(t\right)}^{\top }\varsigma \left(t\right)+{\displaystyle \frac{1}{2}}\Delta \varsigma {\left(t\right)}^{\top }\Delta \varsigma \left(t\right)\hfill \end{array}$$

From the definition of $\varsigma \left(t\right)$ in (12) and the system dynamics, its evolution satisfies:

$$\begin{array}{c}\hfill \varsigma (t+1)=\varsigma \left(t\right)+(1-\widehat{\beta }){\mathcal{T}}_a\left[\Delta A_{a}x\left(t\right)+B_{a}u\left(t\right)\right].\end{array}$$

Substituting the control law (38) yields:

$$\begin{array}{c}\hfill \varsigma (t+1)=\varsigma \left(t\right)+(1-\widehat{\beta }){\mathcal{T}}_a\Delta A_{a}x\left(t\right)-(1-\widehat{\beta }){\mathcal{T}}_a{A}_a{\nabla }^{-\lambda }x\left(t\right)-(1-\widehat{\beta })\eta \left(t\right)\mathrm{sign}\left(\varsigma \left(t\right)\right).\end{array}$$

Now, examine the inner product ${\varsigma }^{\top }\left(t\right)\varsigma (t+1)$:

$$\begin{array}{cc}\hfill {\varsigma }^{\top }\left(t\right)\varsigma (t+1)={\parallel \varsigma \left(t\right)\parallel }^2& +(1-\widehat{\beta }){\varsigma }^{\top }\left(t\right){\mathcal{T}}_a\Delta A_{a}x\left(t\right)\hfill \\ \hfill & -(1-\widehat{\beta }){\varsigma }^{\top }\left(t\right){\mathcal{T}}_a{A}_a{\nabla }^{-\lambda }x\left(t\right)-(1-\widehat{\beta })\eta \left(t\right)\parallel \varsigma \left(t\right)\parallel .\hfill \end{array}$$

Applying the Cauchy–Schwarz inequality and the bounds $\parallel \Delta A_a\parallel \le \parallel E_a\parallel \parallel G_a\parallel$ and $\parallel F_a\parallel \le I$:

$$\begin{array}{cc}\hfill {\varsigma }^{\top }\left(t\right)\varsigma (t+1)\le {\parallel \varsigma \left(t\right)\parallel }^2& +(1-\widehat{\beta })\parallel \varsigma \left(t\right)\parallel \left(\parallel {\mathcal{T}}_a{E}_a\parallel \parallel G_a\parallel \parallel x\left(t\right)\parallel +\parallel {\mathcal{T}}_a{A}_a\parallel \parallel {\nabla }^{-\lambda }x\left(t\right)\parallel \right)\hfill \\ \hfill & -(1-\widehat{\beta })\eta \left(t\right)\parallel \varsigma \left(t\right)\parallel .\hfill \end{array}$$

By construction, the gain $\eta \left(t\right)$ dominates the uncertainty terms, ensuring:

$$\begin{array}{c}\hfill {\varsigma }^{\top }\left(t\right)\varsigma (t+1)\le {\parallel \varsigma \left(t\right)\parallel }^2-(1-\widehat{\beta })\tau \parallel \varsigma \left(t\right)\parallel .\end{array}$$

This inequality guarantees that $\Delta V\left(t\right)<0$ whenever $\parallel \varsigma \left(t\right)\parallel$ is sufficiently large, confirming finite-time convergence to the region $\Omega$. □

Remark 8. 

The results presented in Theorem 4 provide a complete solution to the third key problem raised in the introduction: the design of a robust sliding mode control law under DoS attacks. Specifically, the control law (38) explicitly incorporates the DoS attack probability $\widehat{\beta }$, system uncertainties, and quantized historical information, ensuring that the system trajectories are driven into a bounded neighborhood of the predefined sliding surface. Combined with the MSS of the sliding mode dynamics established in Theorem 3, this guarantees both the reachability and asymptotic stability of the closed-loop system. Thus, the proposed SMC framework fully addresses the control objective under unreliable communication environments.

Remark 9. 

It is crucial to distinguish between the offline design and the online implementation. The LMI conditions in Theorem 3, while involving a number of matrix variables that scales with the system order ($n_x$), number of modes (l), and maximum sojourn time ($T_{max}^a$), are solved offline one-time using convex optimization solvers (as noted in Section 4.2). The online implementation of the control law (38) involves two main tasks: (1) the matrix-vector multiplications of the control law itself, which are computationally light (approx. $O\left(n_x^2\right)$), and (2) the computation of the fractional-order sum ${\nabla }^{-\lambda }x\left(t\right)$ (Equation (7)). The sum ${\nabla }^{-\lambda }x\left(t\right)={\sum }_{j=0}^t{c}_j\left(\lambda \right)x(t-j)$ presents a “growing memory” problem as t increases. For practical implementability, this is commonly and effectively addressed by applying the “Short Memory Principle”. The infinite-history sum is approximated using a fixed-size sliding window of length L, i.e., ${\nabla }^{-\lambda }x\left(t\right)\approx {\sum }_{j=0}^L{c}_j\left(\lambda \right)x(t-j)$. This standard approximation bounds the memory requirement to $O(L·n_x)$ and the computational complexity of the sum to $O(L·n_x)$ per time step, making the proposed FOSMC strategy perfectly feasible for real-time implementation.

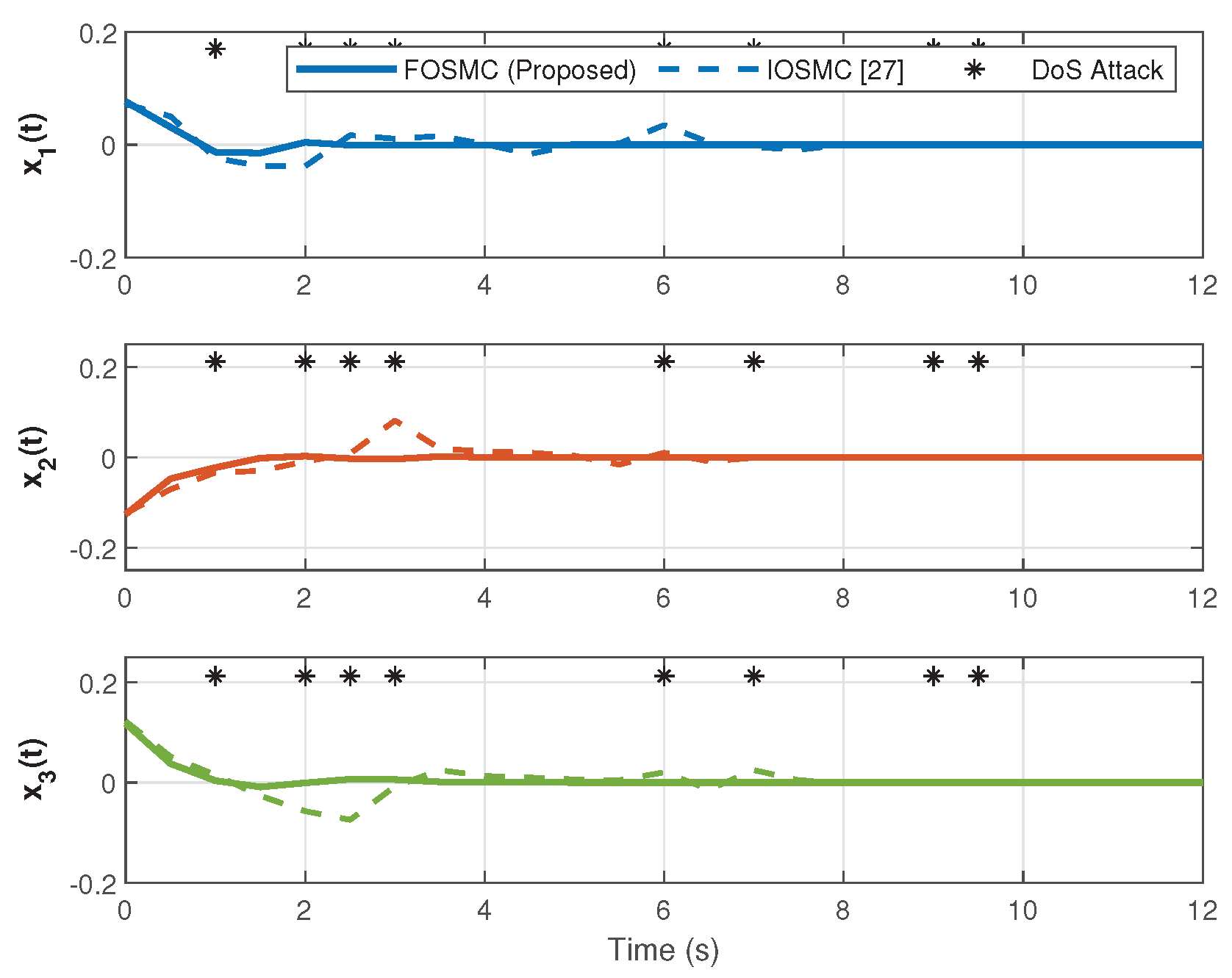
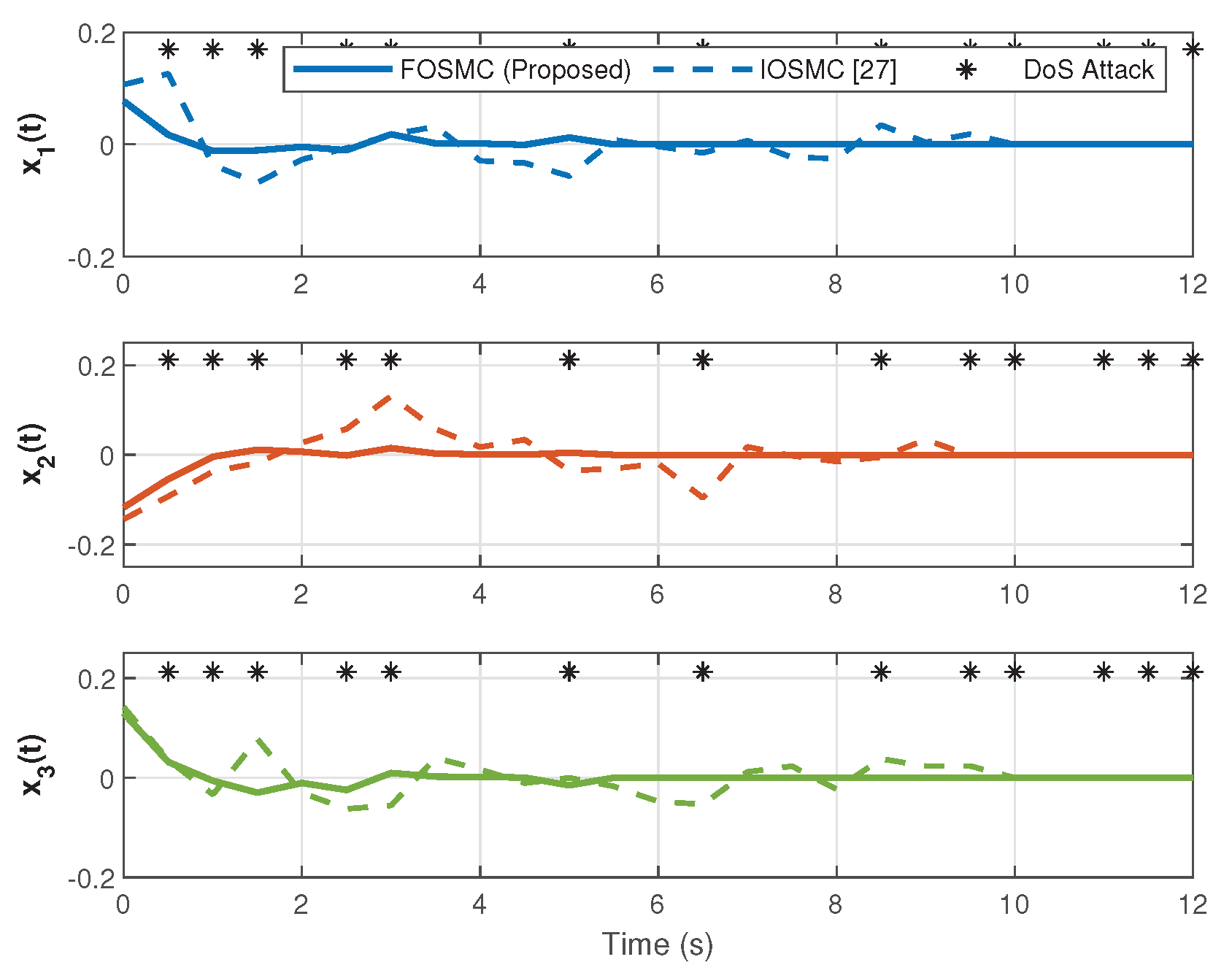
4. Numerical Simulation

This section presents a numerical simulation to validate the effectiveness of the proposed FOSMC scheme for HS-MJSs under DoS attacks. A case study of the benchmark F-404 aircraft engine system [29] is provided, which represents a practical cyber-physical system where network-induced vulnerabilities and unobservable operational modes are critical concerns.

To provide a comprehensive quantitative assessment of the proposed control scheme, the following three performance indices are explicitly defined and evaluated throughout the simulation studies:

• Settling Time ($T_s$): Defined as the time required for the system state norm $\parallel x\left(t\right)\parallel$ to enter and permanently remain within a bounded error band (set as $\pm 5\%$ of the initial deviation) of the equilibrium point. This index evaluates the convergence speed of the system.
• Integral Square Error (ISE): Calculated as $\mathrm{ISE}={\sum }_{t=0}^{T_f}{\parallel x\left(t\right)\parallel }^2$, where $T_f$ is the simulation duration. This index serves as a cumulative measure of the transient response quality and steady-state precision.
• Control Effort (U): Defined as $U={\sum }_{t=0}^{T_f}{\parallel u\left(t\right)\parallel }^2$. This index reflects the total energy consumption required by the controller to stabilize the system, characterizing the cost-effectiveness of the control strategy.

4.1. System Configuration and Parameters

The F-404 aircraft engine system is modeled as a discrete-time HS-MJS with three operational modes ($\mathcal{I}=\{1,2,3\}$), described by the following state equation:

$$x(t+1)=(A_a+\Delta A_a)x\left(t\right)+B_{a}u\left(t\right),$$

where the state vector $x={[x_1,x_2,x_3]}^{\top }$ represents the sideslip angle, roll rate, and yaw rate, respectively. The system is sampled at $T=0.5$ s. The system matrices for each mode $a\in \{1,2,3\}$ are given by:

$$A_a=\left(\begin{array}{ccc}1-1.46T& 0& 2.438T\\ (0.163+0.5{\gamma }_a)T& 1-(0.4+{\gamma }_a)T& -0.3788T\\ 0.3107T& 0& 1-2.23T\end{array}\right),$$

with mode-dependent parameters ${\gamma }_1=0.5$, ${\gamma }_2=0.8$, and ${\gamma }_3=1.2$,

$$B_1=\left(\begin{array}{cc}0.15T& 0.2T\\ 0.11T& -1.5T\\ 0.5T& -0.5T\end{array}\right),B_2=\left(\begin{array}{cc}0.1T& -0.2T\\ 0.05T& 0.3T\\ 0.2T& 0.3T\end{array}\right),B_3=\left(\begin{array}{cc}0.15T& 0.12T\\ 0.15T& -1.5T\\ 0.2T& -0.2T\end{array}\right).$$

The parameter uncertainty is structured as $\Delta A_a=E_a{F}_a{G}_a$, where

$$E_a=\left(\begin{array}{c}0.01\\ 0.01\\ 0.01\end{array}\right),F_a=sin\left(t\right),G_a=\left[0.20.10.1\right].$$

The communication channel from the sensor to the controller is vulnerable to cyber attacks. The system experiences intermittent DoS attacks that prevent the transmission of true state measurements $x\left(t\right)$ at random time instants. The DoS attack process is modeled by the Bernoulli random variable $\beta \left(t\right)$ in (4), with an attack probability of $\widehat{\beta }=0.3$. This means that on average, 30% of the data packets containing the state information are lost, and the controller must use the last available buffered state $x_b(t-1)$ during these attacks ($\beta \left(t\right)=1$).

The stochastic process ${\left\{\delta \left(t\right)\right\}}_{t\in {\mathbf{N}}_{[0,\infty )}}$ is a discrete-time semi-Markov chain with transition probability matrix

$$\begin{array}{c}\hfill \left(\begin{array}{ccc}0& 0.7& 0.3\\ 0.4& 0& 0.6\\ 0.5& 0.5& 0\end{array}\right),\end{array}$$

and sojourn-time probability density functions for $\varrho =1,2,\dots ,10$:

$$\begin{array}{ccc}& & {\omega }_{12}\left(\varrho \right)={\displaystyle \frac{0.2^{\varrho }0.8^{(10-\varrho )}10!}{(10-\varrho )!\varrho !}},\hfill \\ & & {\omega }_{13}\left(\varrho \right)={\displaystyle \frac{0.4^{\varrho }0.6^{(10-\varrho )}10!}{(10-\varrho )!\varrho !}},\hfill \\ & & {\omega }_{21}\left(\varrho \right)={\displaystyle \frac{0.3^{\varrho }0.7^{(10-\varrho )}10!}{(10-\varrho )!\varrho !}},\hfill \\ & & {\omega }_{23}\left(\varrho \right)=0.2^{{(\varrho -1)}^{0.8}}-0.2^{{\varrho }^{0.8}},\hfill \\ & & {\omega }_{31}\left(\varrho \right)=0.4^{{(\varrho -1)}^{1.3}}-0.4^{{\varrho }^{1.3}},\hfill \\ & & {\omega }_{32}\left(\varrho \right)=0.3^{{(\varrho -1)}^{0.8}}-0.3^{{\varrho }^{0.8}}.\hfill \end{array}$$

The emission probability matrix for mode observation contains partially unknown elements:

$$\begin{array}{c}\hfill \left(\begin{array}{ccc}0.7& 0.24& 0.06\\ 0.12& {\pi }_{22}& {\pi }_{23}\\ {\pi }_{31}& 0.06& {\pi }_{33}\end{array}\right),\end{array}$$

(39)

where ${\pi }_{22}\in [0.7,0.8]$, ${\pi }_{23}\in [0.08,0.18]$, ${\pi }_{31}\in [0,0.05]$, ${\pi }_{33}\in [0.89,0.92]$.

Remark 10. 

The simulation scenario incorporates four major practical challenges simultaneously: hidden semi-Markov dynamics, partially unknown emission probabilities, system parameter uncertainties, and stochastic DoS attacks. This comprehensive setup exceeds the typical assumptions in existing works [9,10] and provides a rigorous validation environment for the proposed control scheme.

4.2. Simulation Results and Analysis

To provide a rigorous quantitative evaluation, we define the Settling Time ($T_s$) as the time required for all system state trajectories to enter and permanently remain within a $\pm 5\%$ band of the equilibrium (zero).

The proposed FOSMC law (38) is designed with fractional order $\lambda =0.7$. The sliding surface (12) incorporates the fractional-order integral term ${\nabla }^{-\lambda }{x}_b(t-2)$ and ${\nabla }^{-\lambda }x\left(t\right)$ to enhance resilience against DoS attacks by utilizing historical state information. Controller gains $K_{i\left(\kappa \right(t\left)\right)}$ are obtained by solving the LMIs in Theorem 3 with parameters $h_1=1.8$, $h_2=1.2$, $h_3=1.5$, and maximum sojourn times $T_{max}^a=3$ for $a=1,2,3$. Specifically, the parameters $h_a$ represent the upper bounds on the Lyapunov function’s growth during sojourn periods (as defined in Lemma 1). These values are selected as tuning parameters to ensure that the LMI conditions in Theorem 3 remain feasible.

The LMI conditions in Theorem 3 were solved using the YALMIP toolbox in MATLAB (version R2023a), with SeDuMi as the convex optimization solver. The variable dimensions scale with the system order ($n_x$), the number of modes ($l=3$), and the maximum sojourn time ($T_{max}^a=3$). As the LMIs represent a convex problem, no special initialization procedure is required.

For comparison, an IOSMC strategy [30] is implemented under identical conditions, corresponding to the case $\lambda \to 0$ in our framework. The initial condition is set to x(0) = [0.08, −0.12, 0.1${]}^{\top }$.

The simulation results are organized into two figures and two tables to systematically demonstrate the control performance under various scenarios.

Figure 2 and Figure 3 visually present the performance comparison between the proposed FOSMC and the IOSMC [27] plotted within the same axes for direct contrast. Figure 2 illustrates the state trajectories under a moderate DoS attack probability ($\widehat{\beta }=0.3$). As observed, the FOSMC (solid curves) achieves faster convergence and significantly smaller oscillations compared to the IOSMC (dashed curves), which exhibits a longer recovery time due to the intermittent data loss. Figure 3 depicts the results under a more severe attack condition ($\widehat{\beta }=0.5$). In this scenario, the advantage of the proposed method is even more pronounced. The FOSMC maintains robust performance with smooth convergence, whereas the IOSMC suffers from significant degradation, characterized by large overshoots and a prolonged settling time. This distinct contrast visually confirms the effectiveness of the fractional-order memory effect in compensating for missing data.

To provide a rigorous quantitative validation, Monte Carlo simulations (N = 100 runs) were conducted to evaluate the statistical performance of both controllers under different DoS probabilities. Three key performance indices were measured: Settling Time ($T_s$), Integral Square Error (ISE), and Control Effort (U). The results are summarized in

Table 2. Quantitative Performance Comparison (N = 100, $\widehat{\beta }=0.3$).

Performance Index	FOSMC (This Work) (Mean ± Std)	IOSMC [30] (Mean ± Std)
Settling Time ($T_s$)	$4.52\pm 0.31$	$7.48\pm 0.55$
Error (ISE)	$0.95\pm 0.12$	$1.61\pm 0.25$
Control Effort (U)	$1.15\pm 0.20$	$1.05\pm 0.18$

and

Table 3. Quantitative Performance Comparison (N = 100, $\widehat{\beta }=0.5$).

Performance Index	FOSMC (This Work) (Mean ± Std)	IOSMC [30] (Mean ± Std)
Settling Time ($T_s$)	$5.05\pm 0.45$	$9.85\pm 1.15$
Error (ISE)	$1.25\pm 0.22$	$2.80\pm 0.65$
Control Effort (U)	$1.30\pm 0.28$	$1.55\pm 0.40$

.

Table 2 presents the mean and standard deviation under the moderate attack probability ($\widehat{\beta }=0.3$). The proposed FOSMC achieves an average settling time of $4.52$ s, which is nearly 40% faster than the $7.48$ s of the SMC. Furthermore, the FOSMC demonstrates higher precision, with its average ISE (0.95) being approximately 41% lower than that of the IOSMC (1.61). The control efforts (U) are comparable, indicating that the superior performance of FOSMC does not come at the cost of excessive control energy.

Table 3 shows the results under the higher attack probability ($\widehat{\beta }=0.5$). Here, the performance gap widens significantly. The FOSMC average settling time ($T_s=5.05$ s) is now almost 50% shorter than the IOSMC ($T_s=9.85$ s). The average ISE of the FOSMC is less than half that of the IOSMC, underscoring its enhanced robustness. Notably, under this high-attack scenario, the FOSMC is not only more accurate but also more efficient, with its average control effort being lower than that of the SMC This clearly demonstrates the critical advantage of the ’memory’ effect introduced by the fractional-order, which allows the controller to effectively mitigate the impact of DoS-induced data blackouts more effectively.

Remark 11. 

The proposed strategy exhibits superior overall control performance, yielding a convergence speed enhancement of at least 40% (for $\widehat{\beta }=0.3$) over its integer-order counterpart. This advantage becomes more pronounced under more severe attack conditions ($\widehat{\beta }=0.5$), where the performance enhancement increases to nearly 50%. The key mechanism is the predictive compensation afforded by the fractional-order memory effect during DoS-induced data dropouts ($\beta \left(t\right)=1$). This capability to utilize historical data results in a more stable response and quicker recovery post-attack, conclusively validating the theoretical framework.

The simulation results provide comprehensive validation of the proposed FOSMC scheme. The controller ensures robust MSS and delivers significantly faster convergence compared to conventional methods, demonstrating effective performance under challenging conditions including hidden modes, uncertain observations, parameter variations, and persistent DoS attacks.

5. Conclusions

This paper has presented a fractional-order sliding mode control strategy for hidden semi-Markov jump systems subject to DoS attacks and incomplete mode information. The primary contribution is a sliding surface design that leverages the non-local memory of fractional calculus to enhance system resilience, particularly during communication outages. The proposed controller guarantees finite-time reachability and MSS. Simulations confirmed a decisive performance advantage over conventional integer-order methods, showcasing superior transient response and a significantly faster convergence rate under both moderate and severe DoS attacks. This robust performance profile, driven by the fractional-order memory effect, fully validates the effectiveness of the proposed control framework. Future research will focus on extending this framework to address deception attacks and more complex nonlinear system dynamics. Furthermore, it is worth noting that the proposed FOSMC structure possesses inherent adaptability regarding attack characteristics. Future work will therefore investigate its application to scenarios with time-varying bounds on $\beta \left(t\right)$ or mode-dependent attack rates, by appropriately extending the stochastic stability conditions. Finally, the limitations of this work, including the focus on a single linear plant model (the F-404 engine) and the assumption of norm-bounded uncertainties ($\Delta A_a$), should also be addressed in future validation efforts.