On the Stability and Synchronization of Distributed-Order Coupled Delayed Neural Networks: A Novel Halanay Inequality Technique
Abstract
1. Introduction
2. Preliminaries
3. Main Results
3.1. Stability Theory of Distributed-Order Nonlinear Systems
3.2. Stability Analysis of the DOCDNNs
3.3. Synchronization Analysis of DOCDNNs
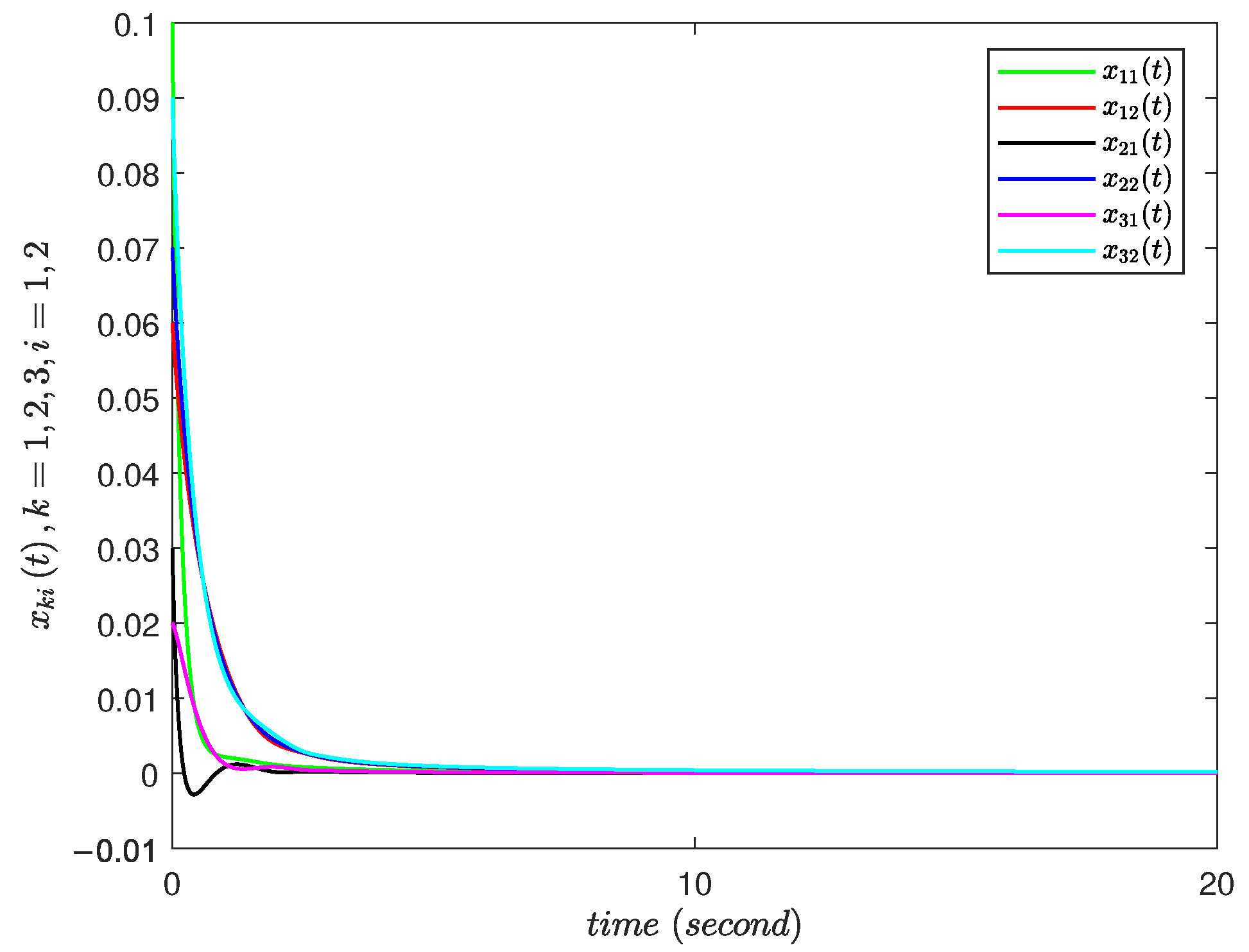
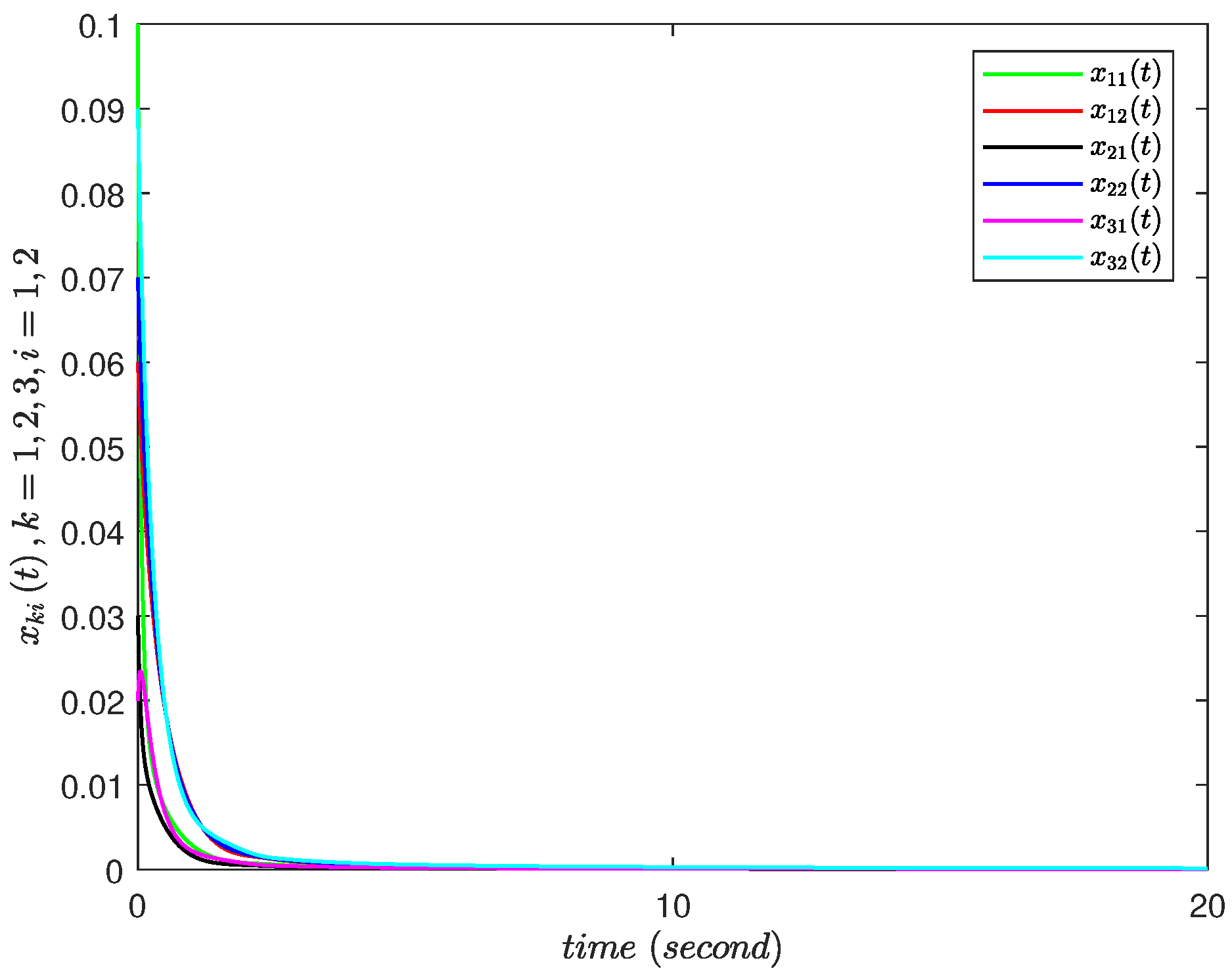
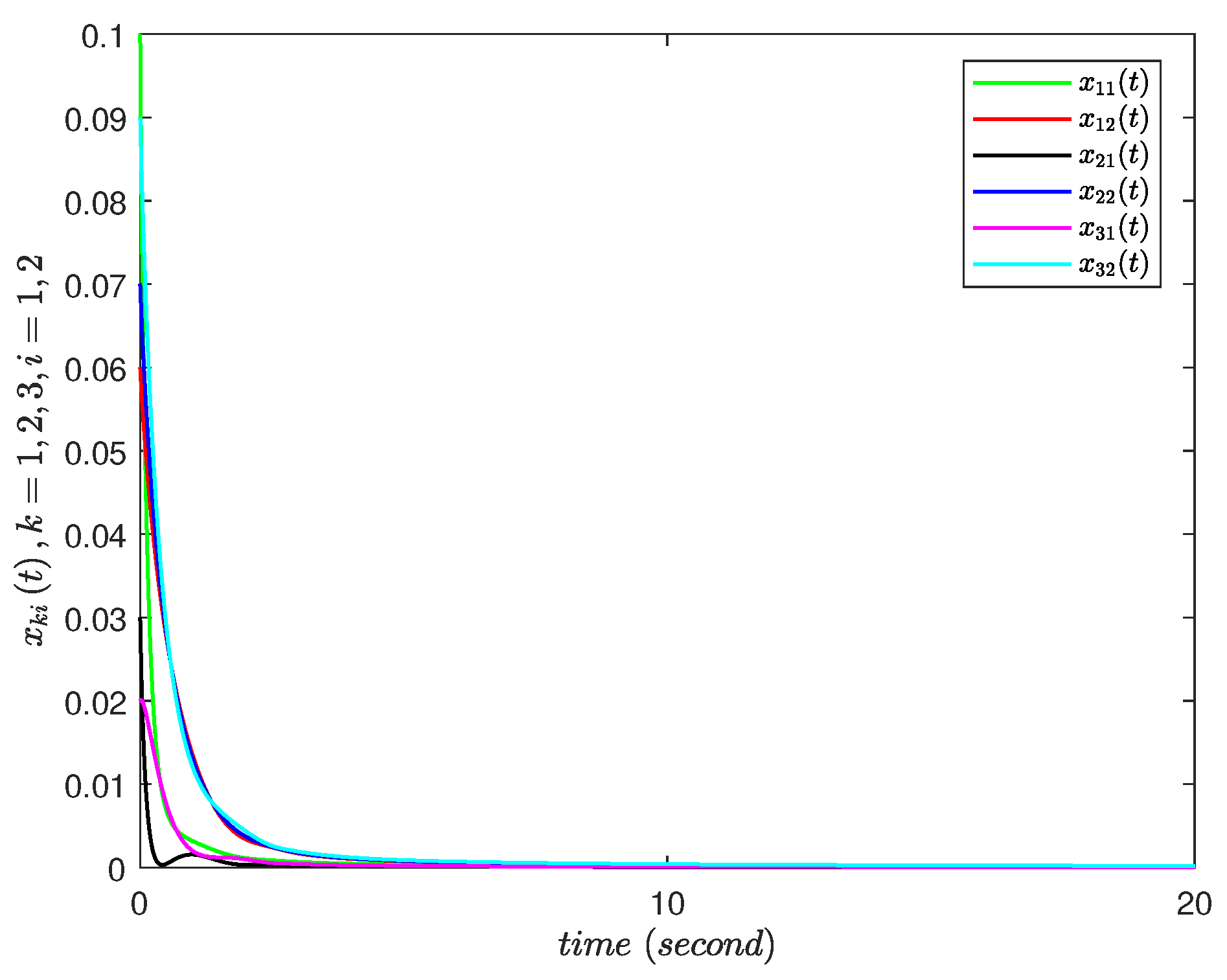
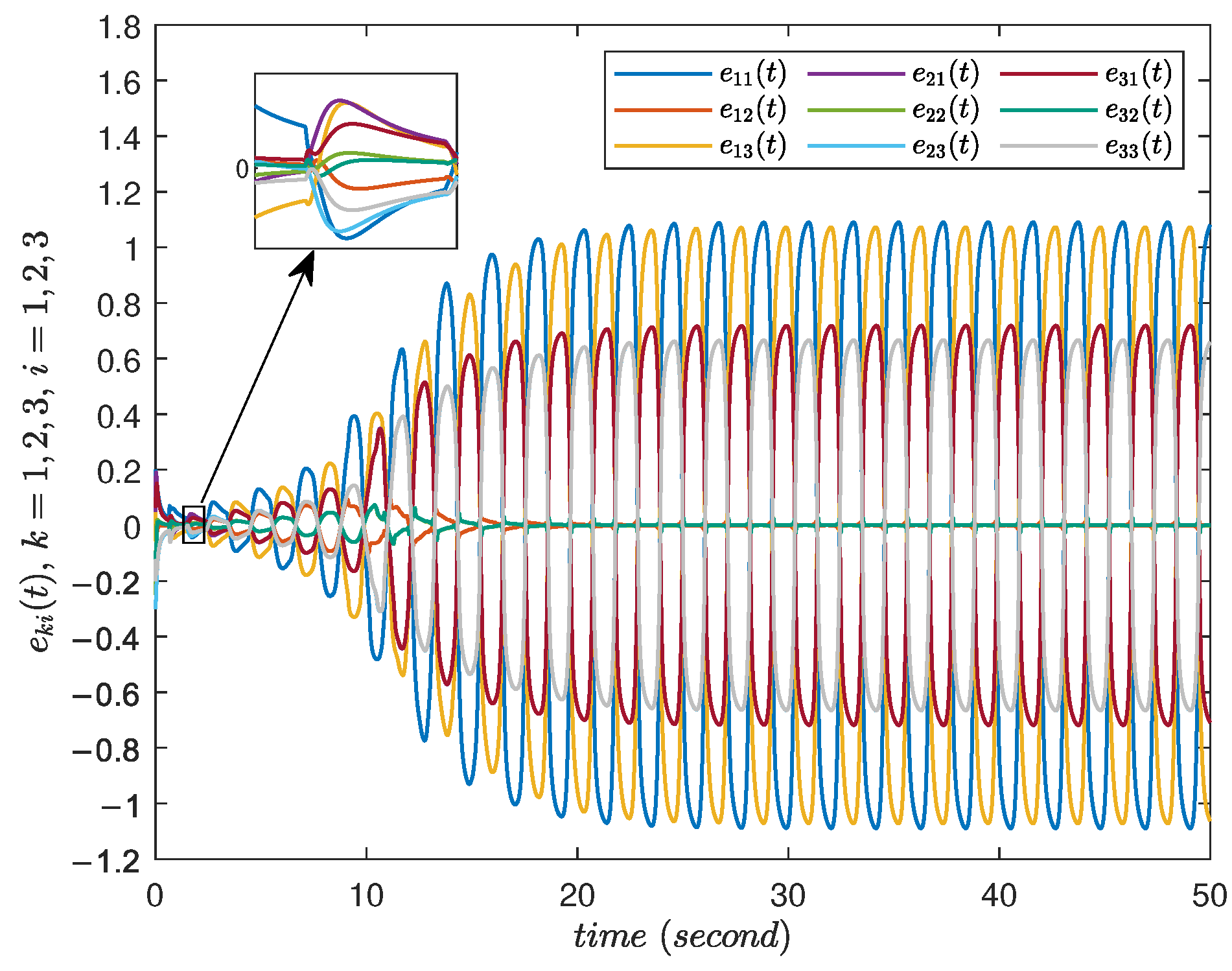
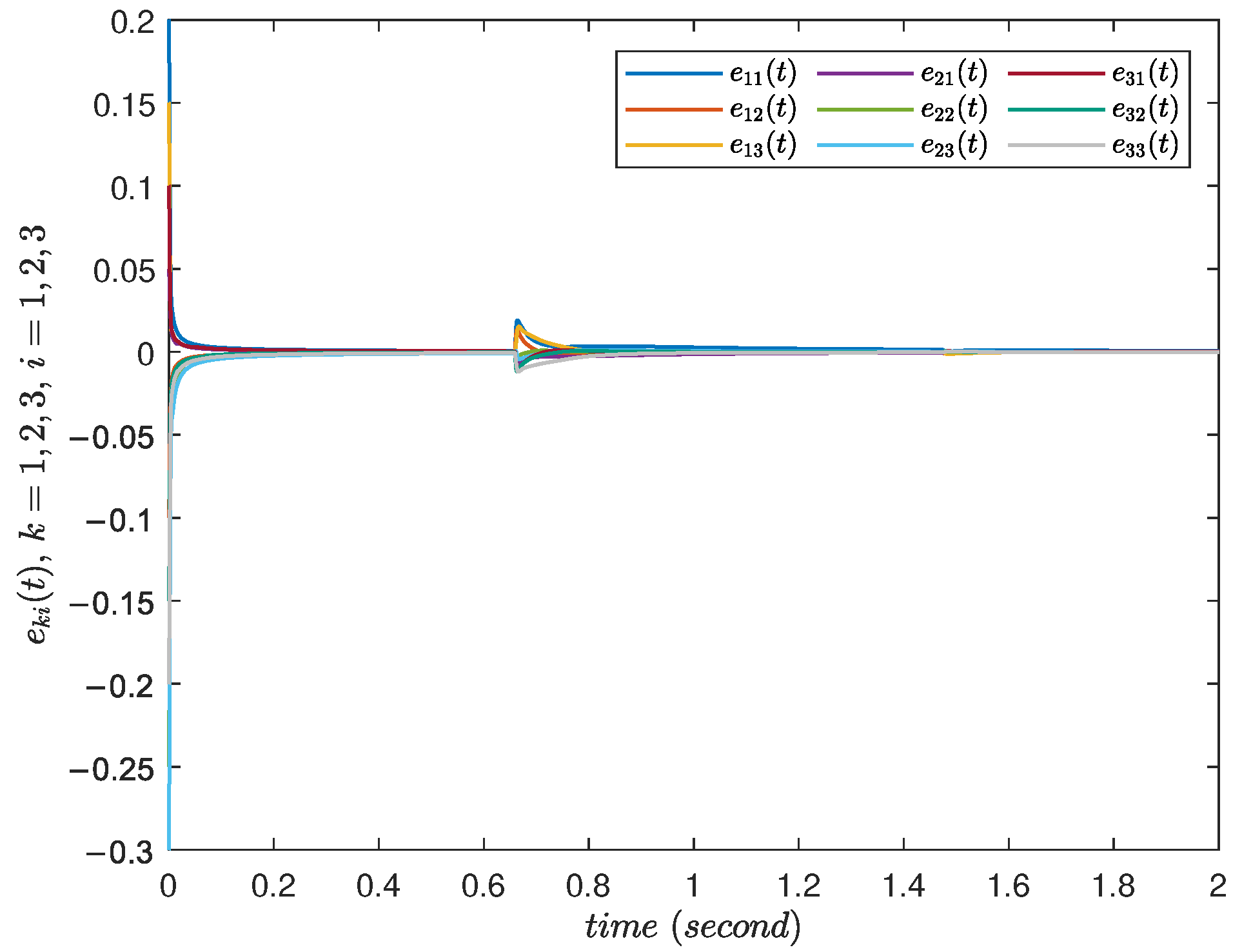
4. Numerical Examples
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| DOCDNNs | Distributed-order coupled delayed neural networks |
References
- Podlubny, I. Fractional Differential Equations; Academic Press: Cambridge, MA, USA, 1999. [Google Scholar]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations; Elsevier: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Ates, A.; Kavuran, G.; Alagoz, B.B.; Yeroglu, C. Improvement of IIR filter discretization for fractional order filter by discrete stochastic optimization. In Proceedings of the 2016 39th International Conference on Telecommunications and Signal Processing (TSP), Vienna, Austria, 27–29 June 2016; pp. 583–586. [Google Scholar]
- Machado, J.A.T.; Jesus, I.S.; Galhano, A.; Cunha, J.B. Fractional order electromagnetics. Signal Process. 2006, 86, 2637–2644. [Google Scholar] [CrossRef]
- Stamova, I.; Stamov, G.; Li, X. Advances in Fractional-Order Neural Networks, Volume II. Fractal Fract. 2023, 7, 845. [Google Scholar] [CrossRef]
- Li, Z.; Yu, J.; Liu, Y.; Zhang, X.; Zhang, B.; Elmaimouni, L. Determination of fractional order for layered viscoelastic materials in cement grouted resin anchor bolt by using guided wave technology. Mech. Syst. Signal Process. 2025, 224, 112101. [Google Scholar] [CrossRef]
- Hakmi, S.H.; Alnami, H.; Ginidi, A.; Shaheen, A.; Alghamdi, T.A.H. A Fractional Order-Kepler Optimization Algorithm (FO-KOA) for single and double-diode parameters PV cell extraction. Heliyon 2024, 10, e35771. [Google Scholar] [CrossRef] [PubMed]
- Zagirnyak, M.; Serhiienko, S.; Serhiienko, I. Improvement of the qualitative characteristics of an automatic control system with a fractional-order PID-controller. In Proceedings of the 2017 18th International Conference on Computational Problems of Electrical Engineering (CPEE), Lviv, Ukraine, 5–8 September 2017; pp. 1–4. [Google Scholar]
- Wang, Z.; Yang, D.; Zhang, H. Stability analysis on a class of nonlinear fractional-order systems. Nonlinear Dyn. 2016, 86, 1023–1033. [Google Scholar] [CrossRef]
- Wang, Z.; Huang, X.; Zhao, Z. Synchronization of nonidentical chaotic fractional-order systems with different orders of fractional derivatives. Nonlinear Dyn. 2012, 69, 999–1007. [Google Scholar] [CrossRef]
- Wei, H.; Li, R.; Li, N. Dissipative and dissipativity analysis for quaternion-valued fractional-order discrete-time memristive neural networks. Math. Control Relat. Fields 2025, 15, 845. [Google Scholar] [CrossRef]
- Demircioğlu, B.; Kuru, Ş.; Önder, M.; Verçin, A. Two families of superintegrable and isospectral potentials in two dimensions. J. Math. Phys. 2002, 43, 2133–2150. [Google Scholar] [CrossRef]
- Caputo, M. Elasticità e Dissipazione; Zanichelli: Bologna, Italy, 1969. [Google Scholar]
- Caputo, M. Mean fractional-order-derivatives differential equations and filters. Ann. Univ. Ferrara 1995, 41, 73–84. [Google Scholar] [CrossRef]
- Liu, L.; Chen, S.; Feng, L.; Zhu, J.; Zhang, J.; Zheng, L.; Xie, C. A novel distributed-order time fractional model for heat conduction, anomalous diffusion, and viscoelastic flow problems. Comput. Fluids 2023, 265, 105991. [Google Scholar] [CrossRef]
- Zhou, F.; Zhao, Y.; Li, Y.; Chen, Y.Q. Design, implementation and application of distributed-order PI control. ISA Trans. 2013, 52, 429–437. [Google Scholar] [CrossRef]
- Chen, Y.; Fiorentino, A.; Dal Negro, L. A fractional diffusion random laser. Sci. Rep. 2019, 9, 8686. [Google Scholar] [CrossRef] [PubMed]
- Khan, M.; Alhowaity, A.; Imran, M.; Hussien, M.; Alroobaea, R.; Anwar, M.S. Advanced numerical simulation techniques in MHD fluid flow analysis using distributed fractional-order derivatives and Cattaneo heat-flux model. Z. Angew. Math. Mech. 2024, 104, e202300622. [Google Scholar] [CrossRef]
- Li, Y.; Chen, Y.Q.; Podlubny, I. Mittag–Leffler stability of fractional-order nonlinear dynamic systems. Automatica 2009, 45, 1965–1969. [Google Scholar] [CrossRef]
- Taghavian, H.; Tavazoei, M.S. Stability analysis of distributed-order nonlinear dynamic systems. Int. J. Syst. Sci. 2018, 49, 523–536. [Google Scholar] [CrossRef]
- Wang, C.; Zhu, T.; Chen, Y.Q. Stability analysis of the nabla distributed-order nonlinear systems. Fractal Fract. 2022, 6, 228. [Google Scholar] [CrossRef]
- Aminikhah, H.; Refahi Sheikhani, A.H.; Rezazadeh, H. Stability analysis of distributed-order fractional Chen system. Sci. World J. 2013, 2013, 645080. [Google Scholar] [CrossRef]
- Medoff, D.R.; Tagamets, M.A. Neural networks: Neural systems III. Am. J. Psychiatry 2000, 157, 1571. [Google Scholar] [CrossRef]
- Dutt, A.; Pellerin, D.; Quénot, G. Coupled ensembles of neural networks. Neurocomputing 2020, 396, 346–357. [Google Scholar] [CrossRef]
- Sun, H.; Li, N.; Chen, Z.; Miao, S. Exponential stochastic synchronization of coupled neural networks with adaptive intermittent control. In Proceedings of the 36th Chinese Control Conference (CCC), Dalian, China, 26–28 July 2017; pp. 995–1000. [Google Scholar]
- Song, Q.; Zhao, Z. Cluster, local and complete synchronization in coupled neural networks with mixed delays and nonlinear coupling. Neural Comput. Appl. 2014, 24, 1101–1113. [Google Scholar] [CrossRef]
- Sun, Y.; Hu, C.; Yu, J. Bipartite leaderless synchronization of fractional-order coupled neural networks via edge-based adaptive pinning control. J. Franklin Inst. 2024, 361, 1303–1317. [Google Scholar] [CrossRef]
- Zhang, L.; Yang, Y. Impulsive effects on bipartite quasi-synchronization of extended Caputo fractional-order coupled networks. J. Franklin Inst. 2020, 357, 4328–4348. [Google Scholar] [CrossRef]
- Wang, J.-L. Output synchronization analysis and PD control for coupled fractional-order neural networks with multiple weights. In Dynamical Behaviors of Fractional-Order Complex Dynamical Networks; Springer: Cham, Switzerland, 2024; pp. 91–112. [Google Scholar]
- Liu, K.; Jiang, W. Uniform stability of fractional neutral systems: A Lyapunov–Krasovskii functional approach. Adv. Differ. Equ. 2013, 2013, 379. [Google Scholar] [CrossRef]
- Humphries, A.R.; Magpantay, F.M.G. Lyapunov–Razumikhin techniques for state-dependent delay differential equations. J. Differ. Equ. 2021, 304, 287–325. [Google Scholar] [CrossRef]
- Xu, D.; Yang, Z. Impulsive delay differential inequality and stability of neural networks. J. Math. Anal. Appl. 2005, 305, 107–120. [Google Scholar] [CrossRef]
- Yang, B.; Wang, J.; Wang, J. Stability analysis of delayed neural networks via a new integral inequality. Neural Netw. 2017, 88, 49–57. [Google Scholar] [CrossRef]
- Chen, Y.; Zhu, S.; Li, Y.; Liu, X.; Wen, S. Finite-time synchronization for delayed NNs via generalized Halanay inequalities. IEEE Trans. Syst. Man Cybern. Syst. 2025, 55, 4742–4751. [Google Scholar] [CrossRef]
- Thi Thu Huong, N.; Nhu Thang, N.; Dinh Ke, T. An improved fractional Halanay inequality with distributed delays. Math. Methods Appl. Sci. 2023, 46, 19083–19099. [Google Scholar] [CrossRef]
- Yang, D.; Yu, Y.; Wang, H.; Ren, G.; Zhang, X. Successive lag synchronization of heterogeneous distributed-order coupled neural networks with unbounded delayed coupling. Chaos Solitons Fractals 2024, 178, 114337. [Google Scholar] [CrossRef]
- Carvalho, A.N.; Langa, J.A.; Robinson, J.C. Non-autonomous dynamical systems. Discret. Contin. Dyn. Syst. Ser. B 2015, 20, 3–22. [Google Scholar] [CrossRef]
- Fernández-Anaya, G.; Nava-Antonio, G.; Jamous-Galante, J.; Muñoz-Vega, R.; Hernández-Martínez, E.G. Asymptotic Stability of Distributed Order Nonlinear Dynamical Systems. Commun. Nonlinear Sci. Numer. Simul. 2017, 48, 541–549. [Google Scholar] [CrossRef]
- Chen, Y.Q.; Podlubny, I. Distributed-Order Dynamic Systems: Stability, Simulation, Applications and Perspectives; Springer: London, UK, 2012. [Google Scholar]
- Diethelm, K.; Ford, N.J. The Analysis of Fractional Differential Equations; Lecture Notes in Mathematics; Springer: New York, NY, USA, 2010; Volume 2004. [Google Scholar]
- Zhang, S.; Tang, M.; Liu, X.; Zhang, X.-M. Mittag–Leffler stability and stabilization of delayed fractional-order memristive neural networks based on a new Razumikhin-type theorem. J. Franklin Inst. 2024, 361, 1211–1226. [Google Scholar] [CrossRef]
- Pepe, P.; Fridman, E. On global exponential stability preservation under sampling for globally Lipschitz time-delay systems. Automatica 2017, 82, 295–300. [Google Scholar] [CrossRef]
- Thinh, L.V.; Tuan, H.T. A generalized fractional Halanay inequality and its applications. SIAM J. Control Optim. 2025, 63, 916–935. [Google Scholar] [CrossRef]
- Nguyen, T.T.H.; Nguyen, N.T.; Tran, M.N. Global fractional Halanay inequalities approach to finite-time stability of nonlinear fractional-order delay systems. J. Math. Anal. Appl. 2023, 525, 127145. [Google Scholar] [CrossRef]
- Muñoz-Vázquez, A.J.; Fernández-Anaya, G.; Sánchez-Torres, J.D.; Meléndez-Vázquez, F. Predefined-time control of distributed-order systems. Nonlinear Dyn. 2021, 103, 2689–2700. [Google Scholar] [CrossRef]
- Miller, K.S. A note on the complete monotonicity of the generalized Mittag–Leffler function. Real Anal. Exch. 1999, 23, 753–756. [Google Scholar] [CrossRef]
- Górska, K.; Horzela, A.; Garrappa, R. Some results on the complete monotonicity of Mittag–Leffler functions of Le Roy type. Fract. Calc. Appl. Anal. 2019, 22, 1284–1306. [Google Scholar] [CrossRef]
- Ke, T.D.; Thang, N.N. An optimal Halanay inequality and decay rate of solutions to some classes of nonlocal functional differential equations. J. Dyn. Differ. Equ. 2024, 36, 1617–1634. [Google Scholar] [CrossRef]
- Li, Y.; Chen, Y.Q.; Podlubny, I. Stability of fractional-order nonlinear dynamic systems: Lyapunov direct method and generalized Mittag–Leffler stability. Comput. Math. Appl. 2010, 59, 1810–1821. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, F.; Liang, X.; Chen, R.; Liu, X. On the Stability and Synchronization of Distributed-Order Coupled Delayed Neural Networks: A Novel Halanay Inequality Technique. Fractal Fract. 2025, 9, 769. https://doi.org/10.3390/fractalfract9120769
Wang F, Liang X, Chen R, Liu X. On the Stability and Synchronization of Distributed-Order Coupled Delayed Neural Networks: A Novel Halanay Inequality Technique. Fractal and Fractional. 2025; 9(12):769. https://doi.org/10.3390/fractalfract9120769
Chicago/Turabian StyleWang, Fengxian, Xiaoyu Liang, Ruidong Chen, and Xinge Liu. 2025. "On the Stability and Synchronization of Distributed-Order Coupled Delayed Neural Networks: A Novel Halanay Inequality Technique" Fractal and Fractional 9, no. 12: 769. https://doi.org/10.3390/fractalfract9120769
APA StyleWang, F., Liang, X., Chen, R., & Liu, X. (2025). On the Stability and Synchronization of Distributed-Order Coupled Delayed Neural Networks: A Novel Halanay Inequality Technique. Fractal and Fractional, 9(12), 769. https://doi.org/10.3390/fractalfract9120769




