Ulam-Type Stability and Krasnosel’skii’s Fixed Point Approach for φ-Caputo Fractional Neutral Differential Equations with Iterated State-Dependent Delays

Abstract

This work analyses the existence, uniqueness, and Ulam-type stability of neutral fractional functional differential equations with recursively defined state-dependent delays. Employing the Caputo fractional derivative of order $\alpha \in (0,1)$ with respect to a strictly increasing function $\phi$, the analysis extends classical results to nonuniform memory. The neutral term and delay chain are defined recursively by the solution, with arbitrary continuous initial data. Existence and uniqueness of solutions are established using Krasnosel’skii’s fixed point theorem. Sufficient conditions for Ulam–Hyers stability are obtained via the Volterra-type integral form and a $\phi$-fractional Grönwall inequality. Examples illustrate both standard and nonlinear time scales, including a Hopfield neural network with iterated delays, which has not been previously studied even for integer-order equations. Fractional neural networks with iterated state-dependent delays provide a new and effective model for the description of AI processes—particularly machine learning and pattern recognition—as well as for modelling the functioning of the human brain.

1. Introduction

Fractional differential equations with delay terms have played a fundamental role in modelling memory-dependent processes across various fields of science and engineering, including viscoelasticity, control theory, population dynamics, neuroscience, and signal processing [1,2,3,4]. The Caputo derivative is regarded as providing a robust framework for describing such dynamics; nevertheless, the majority of classical results concerning existence, uniqueness, and stability are predicated on the assumption of constant delays or restrictive initial data [5,6]. Analytical techniques such as the fixed point theorems, Laplace transform methods [7], and fractional generalizations of Grönwall’s lemma [8] have been adapted to address models with variable delays and more complex memory structures. Further developments have included the application of Krasnosel’skii’s fixed point theorem on generalized sequential boundary value problems [9], integro-differential equations with state-dependent delays [10], and stability analyses for fractional systems governed by Caputo derivatives [11], Riemann–Liouville derivatives [12], and distributed delays [13], as well as the important results concerning iterated delays in functional differential equations [14,15], which may also be found in [16,17]. Recent developments have extended these analyses to fractional differential equations with iterated delays, in which the delay arguments are recursively defined by the evolving state of the system [18,19].

Nevertheless, most existing studies in the literature have not systematically addressed the influence of the specific choice of an initial function on the qualitative behavior of certain solutions, an issue highlighted in works such as [20,21]. Those considerations have motivated the present investigation, which aims to establish the rigorous Ulam stability results for some neutral-type equations [22,23] involving the Caputo derivatives with respect to another function [24,25,26]. That approach has enabled a precise connection between the solution of the considered equation and the associated differential inequality within a generalized fractional framework, ensuring that the behaviour of the solution of the differential equation is consistently and accurately reflected in the corresponding inequality [27].

In this context, a class of neutral fractional functional differential equations with iterated state-dependent delays, governed by the $\phi$-Caputo derivative of order $\alpha \in (0,1)$, is investigated.

$${}_{\phi }{}^C\mathcal{D}_{0+}^{\alpha }(x\left(t\right)-g\left(t,x\left({\tau }_0^x\left(t\right)\right)\right))=f\left(t,x\left(t\right),x\left({\tau }_0^x\left(t\right)\right)\right),t\in (0,T],$$

(1)

where the delays are recursively defined by

$$\begin{array}{cc}\hfill {\tau }_m^x\left(t\right)& :={\theta }_m\left(t,x\left(t\right)\right),\hfill \\ \hfill {\tau }_{m-1}^x\left(t\right)& :={\theta }_{m-1}\left(t,x\left(t\right),x\left({\tau }_m^x\left(t\right)\right)\right),\hfill \\ \hfill & ⋮\hfill \\ \hfill {\tau }_1^x\left(t\right)& :={\theta }_1\left(t,x\left(t\right),x\left({\tau }_2^x\left(t\right)\right)\right),\hfill \\ \hfill {\tau }_0^x\left(t\right)& :={\theta }_0\left(t,x\left(t\right),x\left({\tau }_1^x\left(t\right)\right)\right),\hfill \end{array}$$

(2)

and the initial function is given by

$$x\left(t\right)=\varphi \left(t\right),t\le 0,$$

(3)

where $\varphi :(-\infty ,0]\to \mathbb{R}$ is continuous and bounded on $(-\infty ,0].$

The problem under investigation has been characterised as describing processes exhibiting hereditary dependencies, adaptive temporal responses, and hierarchically structured feedback interactions. Applications of such structures have been reported in associative-memory neural networks, viscoelastic modelling, and neural systems incorporating long-memory mechanisms and time delays [28,29,30].

A distinctive feature of the present equation is the potential for nonlinearity to appear not only in the right-hand side but also within the neutral term and the recursively defined state-dependent delays. Through these mechanisms, a highly nonlocal and structurally intricate dynamical system is generated. The combined effects of fractional memory, neutral-type dependence, and nonlinear delay operators have been observed to impose substantial analytical difficulties. Classical transform-based methods and series-type expansions have been shown to be effective only under restrictive structural assumptions concerning delay regularity or separability of nonlinearities, conditions that are seldom met in systems incorporating state-dependent or iterated delays [31]. Recent developments in symbolic computation have been shown to provide further support for analytic investigations of nonlinear fractional models [32].

Although classical transform-based techniques, such as the Laplace or Fourier transform, are applicable in certain simplified subclasses of problems (typically when delays are constant or exogenous and nonlinearities exhibit specific separability properties) [33], their utility is severely constrained by the presence of iterated state-dependent delays and neutral nonlinearities. In parallel, symbolic methods have been successfully employed to derive structural reductions, such as auto-Bäcklund transformations and related analytical constructions in complex nonlinear systems, thereby offering additional insight into fractional and neutral-type dynamics [34]. Likewise, series-type analytical approaches, including generalized Taylor expansions, Adomian decomposition, and homotopy perturbation methods, may be employed under suitable structural assumptions [3], but their convergence and reliability are highly sensitive to the behaviour of the underlying nonlinearities and delay functions. Consequently, for the general class of problems considered here, explicit closed-form analytical solutions are seldom attainable. As a result, qualitative techniques—such as fixed-point formulations, integral-equation methods, stability analysis, and numerical schemes tailored to fractional and state-dependent operators—have typically been employed to examine well-posedness and dynamical behaviour. Such approaches have been demonstrated to be effective in the study of composite relaxation processes, passivity analysis of networks with diffusion and delay, and the behaviour of fractional neutral systems arising in physics and engineering applications [30,35]. Although the present investigation remains theoretical, the mathematical structures under consideration correspond closely to phenomena in viscoelasticity, hereditary control processes, anomalous transport, neural signalling with memory, and electrical systems characterised by nonlocal responses. These connections provide a foundation for future analytical and empirical developments. Moreover, symbolic computational tools play a central role in several applied domains, including nonlinear quantum theory, plasma physics, fluid dynamics, and magnetic-wave propagation, where explicit solution forms are essential for understanding the underlying physical phenomena [36].

To facilitate the analysis, for each $r>0$ the closed ball ${\mathcal{B}}_r$ in $C\left(\right[0,T\left]\right)$ of radius r is introduced, and the norm is defined by ${\parallel x\parallel }_{\infty }:={sup}_{t\in [0,T]}\left|x\left(t\right)\right|.$

The following hypotheses are imposed throughout the work:

(As.1)

For every admissible trajectory x, the iterated delays defined by (2) satisfy the condition

$${\tau }_k^x\left(t\right)\le t,k=0,1,\dots ,m,t\in [0,T].$$

The mappings ${\theta }_m:[0,T]\times \mathbb{R}\to [0,T]$ and ${\theta }_k:[0,T]\times {\mathbb{R}}^2\to [0,T],k=0,1,\dots m-1$ are continuous and Lipschitz in the state variables, i.e., there exist $L_{\theta }\ge 0$ such that the following hold:

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill & |{\theta }_m(t,u)-{\theta }_m(t,\tilde{u})|\le L_{\theta }|u-\tilde{u}|\hfill \\ \hfill & |{\theta }_k(t,u,v)-{\theta }_k(t,\tilde{u},\tilde{v})|\le L_{\theta }\left(\right|u-\tilde{u}|+|v-\tilde{v}\left|\right).\hfill \end{array}\end{array}$$

(As.2)

The function $g:[0,T]\times \mathbb{R}\to \mathbb{R}$ is continuous, and there exists $L_g>0$ such that

$$\begin{array}{c}\hfill |g(t,u)-g(t,v)|\le L_g|u-v|,t\in [0,T],u,v\in \mathbb{R}.\end{array}$$

and ${sup}_{t\in [0,T]}\left|g(t,0)\right|<\infty .$

(As.3)

The function $f:[0,T]\times {\mathbb{R}}^2\to \mathbb{R}$ is continuous, and there exist constants $L_f\ge 0$ and $M_f\ge 0$ such that

$$|f(t,u,v)-f(t,\tilde{u},\tilde{v})|\le L_f\left(\right|u-\tilde{u}|+|v-\tilde{v}\left|\right),$$

and ${sup}_{t\in [0,T]}\left|f(t,0,0)\right|\le M_f.$

(As.4)

For each $r>0$ there exists $L_x\left(r\right)\ge 0$ such that any $x\in C\left(\right[0,T\left]\right)$ with ${\parallel x\parallel }_{\infty }\le r$ satisfies

$$|x\left(t\right)-x\left(s\right)|\le L_x\left(r\right)|t-s|,s,t\in [0,T].$$

(As.5)

The inequality

$${\displaystyle \frac{|\varphi \left(0\right)-g(0,\varphi ({\tau }_0^{\varphi }(0)))|+{sup}_{t\in [0,T]}\left|g(t,0)\right|+{\displaystyle \frac{{(\phi (T)-\phi (0))}^{\alpha }}{\mathsf{\Gamma }(\alpha +1)}}{M}_f}{1-L_g-{\displaystyle \frac{2L_f{(\phi (T)-\phi (0))}^{\alpha }}{\mathsf{\Gamma }(\alpha +1)}}}}\le r.$$

holds for $L_g+{\displaystyle \frac{2L_f{(\phi \left(T\right)-\phi \left(0\right))}^{\alpha }}{\mathsf{\Gamma }(\alpha +1)}}<1.$

(As.6)

The following conditions hold:

$$q\left(r\right):=L_g{\mathsf{\Lambda }}_{\tau }\left(r\right)+{\displaystyle \frac{L_f\left(1+{\mathsf{\Lambda }}_{\tau }\left(r\right)\right)}{\mathsf{\Gamma }(\alpha +1)}}{\left(\phi \left(T\right)-\phi \left(0\right)\right)}^{\alpha }<1,L_g{\mathsf{\Lambda }}_{\tau }\left(r\right)<1$$

where ${\mathsf{\Lambda }}_{\tau }\left(r\right)=(1+L_x\left(r\right)L_{\theta }){\sum }_{\ell =0}^m{\left(L_x\left(r\right)L_{\theta }\right)}^{\ell }.$

This study departs from earlier works such as [18] in several principal aspects. Firstly, it admits general nontrivial initial data, thereby extending the conventional focus on zero histories. Secondly, the analysis is conducted in the broader setting of the $\phi$-Caputo fractional derivative, necessitating the development of integral representations and kernel estimates on nonlinear time domains [24]. Thirdly, existence and uniqueness are established via Krasnosel’skii’s fixed point theorem, which accommodates operators lacking global contractivity. Finally, the theoretical framework is applied to construct a novel example involving a Hopfield neural network with iterated delays—a configuration that, to the best of our knowledge, has not been previously explored in either the fractional or classical (integer-order) context.

The initial value problem ($\mathcal{IVP}$) (1), (3) is reformulated in Volterra integral form via the left-inverse formula for the $\phi$-Caputo derivative. The solution operator is decomposed into a contraction and a compact integral operator, and the existence of solutions is established using Krasnosel’skii’s fixed point theorem. Uniqueness is demonstrated by showing that the operator is a strict contraction. The analysis of Ulam–Hyers stability follows the general methodology of [27]; however, the present framework departs from that setting in a fundamental way, owing to the neutral structure of the equation and the inclusion of state-dependent, and in particular iterated, delays, which introduce additional nonlocal effects that require a refined treatment.

The remainder of the paper is structured as follows. Section 2 presents preliminary results, including delay-chain estimates, the $\phi$-fractional integral and Caputo derivative, the left-inverse identity, and a $\phi$-Grönwall lemma. Section 3 develops the Volterra representation and operator decomposition, establishes continuity and compactness properties, and proves existence and uniqueness via Krasnosel’ski’s theorem. Section 4 addresses Ulam–Hyers stability. Section 5 provides illustrative examples, numerical results, and graphical representations.

2. Preliminaries

Let $0<T<\infty$ be fixed. Throughout the paper, a function $\phi :[0,T]\to \mathbb{R}$ is fixed, which is continuously differentiable and increasing, with ${\phi }^{\prime }\left(t\right)\ne 0$ almost everywhere on $[0,T]$; see, for example, [1,4,24].

Definition 1.

Let $\alpha >0$. For a locally integrable function $h:[0,T]\to \mathbb{R}$, the $\phi$–fractional integral of order α is defined by

$$\left({\mathcal{I}}_{0+}^{\alpha ,\phi }h\right)\left(t\right)={\displaystyle \frac{1}{\mathsf{\Gamma }\left(\alpha \right)}}{\int }_0^t{\left(\phi \left(t\right)-\phi \left(s\right)\right)}^{\alpha -1}{\phi }^{\prime }\left(s\right)h\left(s\right)ds,t\in [0,T].$$

Definition 2.

Let $\alpha \in (0,1).$ The $\phi$–Caputo derivative of order α of a function $h\in C^1\left([0,T]\right)$ is defined by

$$\begin{array}{cc}\hfill \left({}_{\phi }{}^C\mathcal{D}_{0+}^{\alpha }h\right)\left(t\right)& :=\left({\mathcal{I}}_{0+}^{1-\alpha ,\phi }\right)\left({\displaystyle \frac{1}{{\phi }^{\prime }\left(t\right)}}{\displaystyle \frac{\mathrm{d}}{\mathrm{d}t}}h\left(t\right)\right)\hfill \\ & ={\displaystyle \frac{1}{\mathsf{\Gamma }(1-\alpha )}}{\int }_0^t{(\phi \left(t\right)-\phi \left(s\right))}^{-\alpha }{h}^{\prime }\left(s\right)\mathrm{d}s,t\in (0,T],\hfill \end{array}$$

Lemma 1.

Let $h\in C^1\left([0,T]\right)$ and $0<\alpha <1$. Then, for all $t\in [0,T]$,

$$\left({\mathcal{I}}_{0+}^{\alpha ,\phi }\left({}_{\phi }{}^C\mathcal{D}_{0+}^{\alpha }h\right)\right)\left(t\right)=h\left(t\right)-h\left(0\right),$$

and, for all $t\in (0,T]$, $\left({}_{\phi }{}^C\mathcal{D}_{0+}^{\alpha }\left({\mathcal{I}}_{0+}^{\alpha ,\phi }h\right)\right)\left(t\right)=h\left(t\right).$

Lemma 2.

For $\alpha >0$ and $t\in [0,T]$, ${\displaystyle \frac{1}{\mathsf{\Gamma }\left(\alpha \right)}}{\int }_0^t{(\phi \left(t\right)-\phi \left(s\right))}^{\alpha -1}{\phi }^{\prime }\left(s\right)ds={\displaystyle \frac{{(\phi \left(t\right)-\phi \left(0\right))}^{\alpha }}{\mathsf{\Gamma }(\alpha +1)}}.$

For completeness, we recall two auxiliary results that will be useful in the subsequent analysis. The first is a $\phi$–fractional Grönwall inequality [37,38,39,40], which is not required for the main stability proofs but provides an alternative route for obtaining a priori bounds. The second is Krasnosel’skii’s fixed point theorem [41,42], which is the key tool in establishing the existence of solutions via an operator decomposition. Related uniqueness results for nonlinear equations can be found, for example, in the context of the generalized Choquard equation [43].

Lemma 3.

Let $u,v$ be integrable functions on $[a,b]$, and let $g:[a,b]\to [0,\infty )$ be continuous. Assume that

1.

u and v are nonnegative;

2.

g is nonnegative and nondecreasing.

If

$$u\left(t\right)\le v\left(t\right)+g\left(t\right){\int }_a^t{\phi }^{\prime }\left(s\right){\left(\phi \left(t\right)-\phi \left(s\right)\right)}^{\alpha -1}u\left(s\right)ds,t\in [a,b],$$

then

$$u\left(t\right)\le v\left(t\right)+{\int }_a^t\sum _{k=1}^{\infty }{\displaystyle \frac{{\left(g\left(t\right)\mathsf{\Gamma }\left(\alpha \right)\right)}^k}{\mathsf{\Gamma }\left(\alpha k\right)}}{\phi }^{\prime }\left(s\right){\left(\phi \left(t\right)-\phi \left(s\right)\right)}^{\alpha k-1}v\left(s\right)ds,t\in [a,b].$$

Moreover, if v is nondecreasing, then

$$u\left(t\right)\le v\left(t\right)E_{\alpha }(g\left(t\right)\mathsf{\Gamma }\left(\alpha \right){[\phi \left(t\right)-\phi \left(a\right)]}^{\alpha }),$$

where

$$E_{\alpha }\left(z\right)=\sum _{k=0}^{\infty }{\displaystyle \frac{z^k}{\mathsf{\Gamma }(\alpha k+1)}},\alpha >0.$$

Theorem 1.

Let $(X,\parallel ·\parallel )$ be a Banach space and let $\mathsf{\Omega }\subset X$ be a nonempty, bounded, closed, and convex set. Suppose that ${\mathcal{F}}_1,{\mathcal{F}}_2:\mathsf{\Omega }\to X$ are operators such that:

1.

${\mathcal{F}}_1$ is a contraction, i.e., there exists $\kappa \in [0,1)$ with

$$\parallel {\mathcal{F}}_1\left(x\right)-{\mathcal{F}}_1\left(y\right)\parallel \le \kappa \parallel x-y\parallel ,\forall x,y\in \mathsf{\Omega };$$

2.

${\mathcal{F}}_2$ is completely continuous (that is, continuous and maps bounded subsets of X into relatively compact subsets);

3.

For every $x\in \mathsf{\Omega }$ one has

$${\mathcal{F}}_1\left(x\right)+{\mathcal{F}}_2\left(x\right)\in \mathsf{\Omega }.$$

Then there exists at least one $x^{*}\in \mathsf{\Omega }$ such that

$$x^{*}={\mathcal{F}}_1\left(x^{*}\right)+{\mathcal{F}}_2\left(x^{*}\right).$$

The iterated state-dependent delays ${\tau }_k^x\left(t\right)$, $0\le k\le m$, must be controlled in terms of the sup–norm distance between trajectories. The following lemma provides such an estimate; its proof follows by induction, as presented in [18], through the resolution of a linear difference inequality. We subsequently derive Lipschitz-type estimates on bounded sets, which will be essential for the fixed-point analysis.

Lemma 4.

Let $r>0$ and let ${\mathcal{B}}_r:={\{x\in C\left([0,T]\right): \parallel x\parallel }_{\infty }\le r\}$. Under assumptions (As.1) and (As.4), the following inequalities hold for all $x,y\in {\mathcal{B}}_r$:

$$|x\left({\tau }_k^x\left(t\right)\right)-y\left({\tau }_k^y\left(t\right)\right)|\le {\mathsf{\Lambda }}_{\tau }\left(r\right){\parallel x-y\parallel }_{\infty },0\le k\le m,t\in [0,T],$$

where

$${\mathsf{\Lambda }}_{\tau }\left(r\right)=(1+L_x\left(r\right)L_{\theta })\sum _{\ell =0}^m{\left(L_x\left(r\right)L_{\theta }\right)}^{\ell }=\left\{\begin{array}{cc}{\displaystyle (1+L_x\left(r\right)L_{\theta })\frac{1-{\left(L_x\left(r\right)L_{\theta }\right)}^{m+1}}{1-L_x\left(r\right)L_{\theta }},}\hfill & L_x\left(r\right)L_{\theta }\ne 1,\hfill \\ 2(m+1),\hfill & L_x\left(r\right)L_{\theta }=1.\hfill \end{array}\right.$$

Proof. 

Only a sketch of the proof is given, as the details follow [18]. For $k=m$, using (As.1) and (As.4) one obtains

$$|x\left({\tau }_m^x\left(t\right)\right)-y\left({\tau }_m^y\left(t\right)\right)|\le {\parallel x-y\parallel }_{\infty }+L_x\left(r\right)L_{\theta }{\parallel x-y\parallel }_{\infty }.$$

Set $E_k\left(t\right):=|x\left({\tau }_k^x\left(t\right)\right)-y\left({\tau }_k^y\left(t\right)\right)|$. Then $E_m\left(t\right)\le (1+L_x\left(r\right)L_{\theta }){\parallel x-y\parallel }_{\infty }$.

For the induction step, suppose that $E_j\left(t\right)\le {\beta }_j{\parallel x-y\parallel }_{\infty }$ for some ${\beta }_j\ge 0$. By (As.1) and (As.4),

$$E_{j-1}\left(t\right)\le (1+L_x\left(r\right)L_{\theta }){\parallel x-y\parallel }_{\infty }+L_x\left(r\right)L_{\theta }{E}_j\left(t\right).$$

Hence the sequence $\left\{{\beta }_k\right\}$ satisfies the following linear difference inequality:

$${\beta }_{j-1}\le (1+L_x\left(r\right)L_{\theta })+L_x\left(r\right)L_{\theta }{\beta }_j,1\le j\le m.$$

Solving this recurrence gives

$${\beta }_0\le (1+L_x\left(r\right)L_{\theta })\sum _{\ell =0}^m{\left(L_x\left(r\right)L_{\theta }\right)}^{\ell },$$

which gives the claimed bound with ${\mathsf{\Lambda }}_{\tau }\left(r\right)$. A detailed induction proof can be found in [18]. □

Corollary 1.

If conditions (As.1)–(As.4) hold, then for all $x,y\in B_r$ and $t\in [0,T]$,

$$|g(t,x\left({\tau }_0^x\left(t\right)\right))-g(t,y\left({\tau }_0^y\left(t\right)\right))| \le L_g{\mathsf{\Lambda }}_{\tau }\left(r\right){\parallel x-y\parallel }_{\infty },$$

(4)

$$|f(t,x\left(t\right),x\left({\tau }_0^x\left(t\right)\right))-f(t,y\left(t\right),y\left({\tau }_0^y\left(t\right)\right))| \le L_f\left(1+{\mathsf{\Lambda }}_{\tau }\left(r\right)\right){\parallel x-y\parallel }_{\infty },$$

(5)

where ${\mathsf{\Lambda }}_{\tau }\left(r\right)$ is is given by Lemma 4.

Proof. 

The inequalities follow immediately from Lemma 4 together with assumptions (As.2) and (As.3). □

Lemma 5.

Let $f\in C([0,T]\times {\mathbb{R}}^2,\mathbb{R})$, and let $x:(-\infty ,T]\to \mathbb{R}$ satisfy the neutral fractional initial value problem (1), (3). Then the problem (1)–(3) is equivalent to the fractional Volterra integral equation:

$$\begin{array}{cc}\hfill x\left(t\right)& =\varphi \left(0\right)-g\left(0,\varphi \left({\tau }_0^{\varphi }\left(0\right)\right)\right)+g\left(t,x\left({\tau }_0^x\left(t\right)\right)\right)\hfill \\ \hfill & +{\displaystyle \frac{1}{\mathsf{\Gamma }\left(\alpha \right)}}{\int }_0^t{(\phi \left(t\right)-\phi \left(s\right))}^{\alpha -1}{\phi }^{\prime }\left(s\right)f\left(s,x\left(s\right),x\left({\tau }_0^x\left(s\right)\right)\right)ds,t\in [0,T].\hfill \end{array}$$

(6)

with $x\left(t\right)=\varphi \left(t\right)$ for $t\le 0$. Both formulations are considered for functions x such that the operator ${}_{\phi }{}^{C}D_{0+}^{\alpha }x$ exists on $(0,T]$, ensuring a well-defined φ-Caputo derivative of the neutral term.

Proof. 

Applying Lemma 1 to the neutral fractional Equation (1) gives

$$\begin{array}{cc}\hfill \left({\mathcal{I}}_{0+}^{\alpha ,\phi }{}_{\phi }{}^C\mathcal{D}_{0+}^{\alpha }\right(x\left(t\right)& -g\left(t,x\left({\tau }_0^x\left(t\right)\right)\right)\left)\right)\left(t\right)\hfill \\ \hfill & ={\displaystyle \frac{1}{\mathsf{\Gamma }\left(\alpha \right)}}{\int }_0^t{(\phi \left(t\right)-\phi \left(s\right))}^{\alpha -1}{\phi }^{\prime }\left(s\right)f\left(s,x\left(s\right),x\left({\tau }_0^x\left(s\right)\right)\right)\mathrm{d}s.\hfill \end{array}$$

Therefore, using the initial condition (3), we obtain

$$\begin{array}{cc}\hfill x\left(t\right)-g\left(t,x\left({\tau }_0^x\left(t\right)\right)\right)& - \varphi \left(0\right)+g\left(0,\varphi \left({\tau }_0^{\varphi }\left(0\right)\right)\right)\hfill \\ & ={\displaystyle \frac{1}{\mathsf{\Gamma }\left(\alpha \right)}}{\int }_0^t{(\phi \left(t\right)-\phi \left(s\right))}^{\alpha -1}{\phi }^{\prime }\left(s\right)f\left(s,x\left(s\right),x\left({\tau }_0^x\left(s\right)\right)\right)\mathrm{d}s,\hfill \end{array}$$

which yields (6). Assume that x satisfies the Volterra representation (6). Applying ${}_{\phi }{}^{C}D_{0+}^{\alpha }$ to both sides of (6) and using linearity of the operator gives

$$\begin{array}{cc}\hfill {}_{\phi }{}^C\mathcal{D}_{0+}^{\alpha }(x\left(t\right)& - g(t,x\left({\tau }_0^x\left(t\right)\right)))\hfill \\ & ={}_{\phi }{}^C\mathcal{D}_{0+}^{\alpha }\left(\varphi \left(0\right)-g\left(0,\varphi \left({\tau }_0^{\varphi }\left(0\right)\right)\right)+{\mathcal{I}}_{0+}^{\alpha ,\phi }\left(f(s,x\left(s\right),x\left({\tau }_0^x\left(s\right)\right))\right)\left(t\right)\right).\hfill \end{array}$$

The term $\varphi \left(0\right)-g\left(0,\varphi \left({\tau }_0^{\varphi }\left(0\right)\right)\right)$ is constant and therefore its $\phi$–Caputo derivative vanishes.

It follows from Lemma 1 that ${}_{\phi }{}^{C}D_{0+}^{\alpha }\left(x\left(t\right)-g(t,x\left({\tau }_0^x\left(t\right)\right))\right)=f\left(t,x\left(t\right),x\left({\tau }_0^x\left(t\right)\right)\right),$ which is precisely the differential Equation (1). Finally, evaluating (6) at $t=0$ shows that the integral term vanishes, which confirms the initial condition in (3). □

Remark 1.

For clarity of exposition, we assume throughout this paper that the unknown function $x\in C^1([0,T],\mathbb{R})$. In particular, it is assumed that the φ–Caputo derivative of the neutral term $x\left(t\right)-g\left(t,x\left({\tau }_0^x\left(t\right)\right)\right)$ exists on $(0,T]$. This is consistent with the regularity assumptions (As. 1)–(As. 4). Furthermore, the existence of the φ–fractional integral can be verified under a Lebesgue measurable right-hand side by means of Hölder’s inequality (see [23]). The problem may alternatively be formulated within the framework of absolutely continuous functions, where the φ-Caputo derivative is defined almost everywhere. Under assumptions (As.1)–(As.4) and additional regularity of the function g, the existence of the φ–Caputo derivative for the neutral term can be established within the standard theory of fractional calculus for absolutely continuous functions (see, e.g., [2,5,44] and the references therein). In the present work, we remain in the $C^1$ setting for simplicity of presentation.

3. Existence via Krasnosel’skii’s Fixed Point Theorem

We establish the existence of a solution to the $\mathcal{IVP}$ (1), (3) on the time interval $[0,T]$ by applying Krasnosel’skii’s theorem [41,42], following the approach in [22,24].

Consider the Banach space $X:=C\left(\right[0,T];\mathbb{R})$, endowed with the supremum norm ${\parallel x\parallel }_{\infty }:={sup}_{t\in [0,T]}\left|x\left(t\right)\right|$. For any $r>0$, define the closed and convex subset ${\mathcal{B}}_r:=\left\{x\in {X:\parallel x\parallel }_{\infty }\le r\right\}.$

Using Lemma 5, we define the operator decomposition $\mathcal{F}={\mathcal{F}}_1+{\mathcal{F}}_2$ on ${\mathcal{B}}_r$ as follows:

$$\left({\mathcal{F}}_{1}x\right)\left(t\right) := \varphi \left(0\right)-g\left(0,\varphi \left({\tau }_0^{\varphi }\left(0\right)\right)\right)+g\left(t,x\left({\tau }_0^x\left(t\right)\right)\right),$$

(7)

$$\left({\mathcal{F}}_{2}x\right)\left(t\right) := {\displaystyle \frac{1}{\mathsf{\Gamma }\left(\alpha \right)}}{\int }_0^t{\left(\phi \left(t\right)-\phi \left(s\right)\right)}^{\alpha -1}{\phi }^{\prime }\left(s\right)f\left(s,x\left(s\right),x\left({\tau }_0^x\left(s\right)\right)\right)ds.$$

(8)

Lemma 6.

Assume (As.1), (As.2), and (As.4). If the inequality $L_g{\mathsf{\Lambda }}_{\tau }\left(r\right)<1$ holds, where ${\mathsf{\Lambda }}_{\tau }\left(r\right)=(1+L_x\left(r\right)L_{\theta }){\sum }_{\ell =0}^m{\left(L_x\left(r\right)L_{\theta }\right)}^{\ell }$, then ${\mathcal{F}}_1$ is a contraction mapping on ${\mathcal{B}}_r$, satisfying $\parallel {\mathcal{F}}_{1}x-{\mathcal{F}}_{1}y\parallel \le L_g{\mathsf{\Lambda }}_{\tau }\left(r\right){\parallel x-y\parallel }_{\infty }.$

Proof. 

For any $x,y\in {\mathcal{B}}_r$, the Lipschitz continuity of g with respect to its second argument (see (As.2)), together with assumptions (As.1), (As.4), and Corollary 1, yields

$$|\left({\mathcal{F}}_{1}x\right)\left(t\right)-\left({\mathcal{F}}_{1}y\right)\left(t\right)|\le L_g|x\left({\tau }_0^x\left(t\right)\right)-y\left({\tau }_0^y\left(t\right)\right)|\le L_g{\mathsf{\Lambda }}_{\tau }\left(r\right){\parallel x-y\parallel }_{\infty }.$$

Taking the supremum over $t\in [0,T]$ gives the claim. □

Lemma 7.

Assume (As.1), (As.3), and (As.4). Then the operator ${\mathcal{F}}_2$ is completely continuous on ${\mathcal{B}}_r$.

Proof. 

To prove continuity, let $\left\{x_n\right\}$ be a sequence in ${\mathcal{B}}_r$ converging uniformly to x. By Corollary 1,

$$\begin{array}{cc}\hfill & |{\mathcal{F}}_2{x}_n-{\mathcal{F}}_{2}x|\le {\displaystyle \frac{1}{\mathsf{\Gamma }\left(\alpha \right)}}{\int }_0^t{\left(\phi \left(t\right)-\phi \left(s\right)\right)}^{\alpha -1}{\phi }^{\prime }\left(s\right)|f\left(s,x_n\left(s\right),x_n\left({\tau }_0^{x_n}\left(s\right)\right)\right)-f\left(s,x\left(s\right),x\left({\tau }_0^x\left(s\right)\right)\right)|ds\hfill \\ \hfill & \le {\displaystyle \frac{1}{\mathsf{\Gamma }\left(\alpha \right)}}{\int }_0^t{(\phi \left(t\right)-\phi \left(s\right))}^{\alpha -1}{\phi }^{\prime }\left(s\right)L_f\left(|x_n\left(s\right)-x\left(s\right)|+|x_n\left({\tau }_0^{x_n}\left(s\right)\right)-x\left({\tau }_0^x\left(s\right)\right)|\right)ds\hfill \\ \hfill & \le {\displaystyle \frac{L_f(1+{\mathsf{\Lambda }}_{\tau }\left(r\right))}{\mathsf{\Gamma }(\alpha +1)}}{\left(\phi \left(T\right)-\phi \left(0\right)\right)}^{\alpha }{\parallel x_n-x\parallel }_{\infty }.\hfill \end{array}$$

Therefore,

$$\parallel {\mathcal{F}}_2{x}_n-{\mathcal{F}}_{2}x\parallel \le {\displaystyle \frac{L_f(1+{\mathsf{\Lambda }}_{\tau }\left(r\right))}{\mathsf{\Gamma }(\alpha +1)}}{\left(\phi \left(T\right)-\phi \left(0\right)\right)}^{\alpha }{\parallel x_n-x\parallel }_{\infty }.$$

Thus, $\parallel {\mathcal{F}}_2{x}_n-{\mathcal{F}}_{2}x\parallel \to 0,n\to \infty$ which proves the continuity of ${\mathcal{F}}_2$.

Fix $x\in {\mathcal{B}}_r$. From (As.3) and ${\parallel x\parallel }_{\infty }\le r,$ we have

$$\begin{array}{cc}\hfill \left|f\right(s,x\left(s\right),x\left({\tau }_0^x\left(s\right)\right)\left)\right|& =\left|f\right(s,x\left(s\right),x\left({\tau }_0^x\left(s\right)\right))-f(s,0,0)|+\left|f(s,0,0)\right|\hfill \\ & \le M_f+L_f\left(\right|x\left(s\right)|+|x\left({\tau }_0^x\left(s\right)\right)\left|\right)\hfill \\ & \le M_f+2L_{f}r=:M_r.\hfill \end{array}$$

It follows from Lemma 2,

$$|\left({\mathcal{F}}_{2}x\right)\left(t\right)| \le {\displaystyle \frac{M_r}{\mathsf{\Gamma }\left(\alpha \right)}}{\int }_0^t{\left(\phi \left(t\right)-\phi \left(s\right)\right)}^{\alpha -1}{\phi }^{\prime }\left(s\right)ds={\displaystyle \frac{M_r}{\mathsf{\Gamma }(\alpha +1)}}{\left(\phi \left(t\right)-\phi \left(0\right)\right)}^{\alpha },$$

which shows that ${\mathcal{F}}_2\left({\mathcal{B}}_r\right)$ is uniformly bounded.

For equicontinuity, consider $0\le t<t^{\prime }\le T.$ Then estimate the difference

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill & |\left({\mathcal{F}}_{2}x\right)\left(t^{\prime }\right)-\left({\mathcal{F}}_{2}x\right)\left(t\right)|={\displaystyle \frac{1}{\mathsf{\Gamma }\left(\alpha \right)}}{\int }_0^t\left[{(\phi \left(t^{\prime }\right)-\phi \left(s\right))}^{\alpha -1}-{(\phi \left(t\right)-\phi \left(s\right))}^{\alpha -1}\right]{\phi }^{\prime }\left(s\right)\hfill \\ \hfill & \times |f(s,x\left(s\right),x\left({\tau }_0^x\left(s\right)\right))|ds+{\displaystyle \frac{1}{\mathsf{\Gamma }\left(\alpha \right)}}{\int }_t^{t^{\prime }}{(\phi \left(t^{\prime }\right)-\phi \left(s\right))}^{\alpha -1}{\phi }^{\prime }\left(s\right)\left|f(s,x\left(s\right),x\left({\tau }_0^x\left(s\right)\right))\right|ds.\hfill \\ \hfill & \le {\displaystyle \frac{M_r}{\mathsf{\Gamma }\left(\alpha \right)}}\left[{\int }_0^t\left({(\phi \left(t^{\prime }\right)-\phi \left(s\right))}^{\alpha -1}-{(\phi \left(t\right)-\phi \left(s\right))}^{\alpha -1}\right){\phi }^{\prime }\left(s\right)ds+{\int }_t^{t^{\prime }}{(\phi \left(t^{\prime }\right)-\phi \left(s\right))}^{\alpha -1}{\phi }^{\prime }\left(s\right)ds\right].\hfill \end{array}\end{array}$$

Hence, by Lemma 2

$$|\left({\mathcal{F}}_{2}x\right)\left(t^{\prime }\right)-\left({\mathcal{F}}_{2}x\right)\left(t\right)|\le {\displaystyle \frac{M_r}{\mathsf{\Gamma }(\alpha +1)}}\left({(\phi \left(t^{\prime }\right)-\phi \left(0\right))}^{\alpha }-{(\phi \left(t\right)-\phi \left(0\right))}^{\alpha }\right).$$

Since the right-hand side $\to 0$ as $t^{\prime }\to t$, uniformly in $x\in {\mathcal{B}}_r,$${\mathcal{F}}_2\left({\mathcal{B}}_r\right)$ is equicontinuous by Arzelà–Ascoli, ${\mathcal{F}}_2$ is compact.

Thus, $\parallel {\mathcal{F}}_{2}x-{\mathcal{F}}_2{y\parallel }_{\infty }\le {\displaystyle \frac{L_f(1+{\mathsf{\Lambda }}_{\tau }\left(r\right))}{\mathsf{\Gamma }(\alpha +1)}}{\left(\phi \left(T\right)-\phi \left(0\right)\right)}^{\alpha }{\parallel x-y\parallel }_{\infty }$ on ${\mathcal{B}}_r$ and the operator ${\mathcal{F}}_2$ is completely continuous.

Moreover, for $x,y\in {\mathcal{B}}_r$, by (As.3) and Corollary 1,

$$\begin{array}{cc}\hfill & |{\mathcal{F}}_{2}x-{\mathcal{F}}_{2}y|\le {\displaystyle \frac{1}{\mathsf{\Gamma }\left(\alpha \right)}}{\int }_0^t{\left(\phi \left(t\right)-\phi \left(s\right)\right)}^{\alpha -1}{\phi }^{\prime }\left(s\right)|f(s,x\left(s\right),x\left({\tau }_0^x\left(s\right)\right)-f\left(s,y\left(s\right),y\left({\tau }_0^y\left(s\right)\right)|\right)ds\hfill \\ \hfill & \le {\displaystyle \frac{1}{\mathsf{\Gamma }\left(\alpha \right)}}{\int }_0^t{(\phi \left(t\right)-\phi \left(s\right))}^{\alpha -1}{\phi }^{\prime }\left(s\right)L_f\left(|x\left(s\right)-y\left(s\right)|+|x\left({\tau }_0^x\left(s\right)\right)-y\left({\tau }_0^y\left(s\right)\right)|\right)ds\hfill \\ \hfill & \le {\displaystyle \frac{L_f(1+{\mathsf{\Lambda }}_{\tau }\left(r\right))}{\mathsf{\Gamma }(\alpha +1)}}{\left(\phi \left(T\right)-\phi \left(0\right)\right)}^{\alpha }{\parallel x-y\parallel }_{\infty }.\hfill \end{array}$$

□

Lemma 8.

Assume (As.2) and (As.3). Then, for all $x,y\in {\mathcal{B}}_r$, the sum ${\mathcal{F}}_{1}x+{\mathcal{F}}_{2}y$ belongs to ${\mathcal{B}}_r$ provided that

$$|\varphi \left(0\right)-g(0,\varphi \left({\tau }_0^{\varphi }\left(0\right)\right))|+\underset{t\in [0,T]}{sup}|g(t,0)|+L_{g}r+{\displaystyle \frac{{\left(\phi \left(T\right)-\phi \left(0\right)\right)}^{\alpha }}{\mathsf{\Gamma }(\alpha +1)}}\left(M_f+2L_{f}r\right)\le r.$$

(9)

Proof. 

By the triangle inequality, using (7)–(8)

$$\begin{array}{cc}\hfill |{\mathcal{F}}_{1}x+{\mathcal{F}}_{2}y|& \le |\varphi (0)-g\left(0,\varphi ({\tau }_0^{\varphi }(0))\right)|+\left|g\left(t,x({\tau }_0^x(t))\right)\right|\hfill \\ \hfill & +{\displaystyle \frac{1}{\mathsf{\Gamma }(\alpha )}}{\int }_0^t{\left(\phi (t)-\phi (s)\right)}^{\alpha -1}{\phi }^{\prime }(s)|f\left(s,y(s),y({\tau }_0^y(s))\right)|ds.\hfill \\ \hfill & \le |\varphi (0)-g\left(0,\varphi ({\tau }_0^{\varphi }(0))\right)|+|g\left(t,x({\tau }_0^x(t))\right)-g(t,0)|+\left|g(t,0)\right|\hfill \\ \hfill & +{\displaystyle \frac{1}{\mathsf{\Gamma }(\alpha )}}{\int }_0^t{\left(\phi (t)-\phi (s)\right)}^{\alpha -1}{\phi }^{\prime }(s)|f\left(s,y(s),y({\tau }_0^y(s))\right)-f\left(s,0,0\right)|+|f\left(s,0,0\right)|ds.\hfill \end{array}$$

Consequently, using assumption (As.2), $|g\left(t,x({\tau }_0^x(t))\right)-g(t,0)|+\left|g(t,0)\right|\le L_g|x({\tau }_0^x(t))|+|g(t,0)|.$ Thus, $g\left(t,x({\tau }_0^x(t))\right)\le {sup}_{t\in [0,T]}|g(t,0)|+L_{g}r$, with $|x(·)|\le r$ on $[0,T]$, $|g(t,x\left({\tau }_0^x\left(t\right)\right))|\le {sup}_{t\in [0,T]}|g(t,0)|+L_{g}r.$

Moreover, by (As.3), $y\in {\mathcal{B}}_r$ and Lemma 2, $|f\left(s,y\left(s\right),y\left({\tau }_0^y\left(s\right)\right)\right)-f\left(s,0,0\right)|+|f\left(s,0,0\right)|\le L_f(|y\left(s\right)|+|y\left({\tau }_0^y\left(s\right)\right)|)+M_f\le 2L_{f}r+M_f.$ Taking the supremum in t and using the radius condition (9), yields

$$\begin{array}{cc}\hfill \parallel {\mathcal{F}}_{1}x+{\mathcal{F}}_{2}y\parallel & \le |\varphi \left(0\right)-g(0,\varphi \left({\tau }_0^{\varphi }\left(0\right)\right))|+\underset{t\in [0,T]}{sup}|g(t,0)|\hfill \\ & +L_{g}r+{\displaystyle \frac{{\left(\phi \left(T\right)-\phi \left(0\right)\right)}^{\alpha }}{\mathsf{\Gamma }(\alpha +1)}}\left(M_f+2L_{f}r\right)\le r.\hfill \end{array}$$

Accordingly, the proof is complete. □

Theorem 2.

Assume (As.1)–(As.5). Then the neutral fractional $\mathcal{IVP}$ (1), (3) admits at least one solution $x^{*}\in {\mathcal{B}}_r$ on $[0,T].$

Proof. 

The set ${\mathcal{B}}_r$ is non-empty, bounded, convex, and closed. Lemma 6 ensures that ${\mathcal{F}}_1$ is a contraction, Lemma 7 establishes that ${\mathcal{F}}_2$ is completely continuous, and Lemma 8 guarantees invariance of ${\mathcal{B}}_r$. The hypotheses of Krasnosel’skii’s fixed point Theorem 1 are thus satisfied, which yields the existence of a fixed point $x^{*}\in {\mathcal{B}}_r$ with $x^{*}={\mathcal{F}}_1{x}^{*}+{\mathcal{F}}_2{x}^{*}$. □

Theorem 3.

Under the hypotheses of Theorem 2, if condition (As.6) is satisfied, then the solution in ${\mathcal{B}}_r$ on $[0,T]$ is unique.

Proof. 

Suppose $x,y\in {\mathcal{B}}_r$ are both fixed points of $\mathcal{F}$. By the contraction and Lipschitz properties established in Lemmas 6 and 7, we have

$$\begin{array}{cc}\hfill {\parallel \mathcal{F}x-\mathcal{F}y\parallel }_{\infty }& \le \parallel {\mathcal{F}}_{1}x-{\mathcal{F}}_1{y\parallel }_{\infty }+{\parallel {\mathcal{F}}_{2}x-{\mathcal{F}}_{2}y\parallel }_{\infty }\hfill \\ & \le L_g{\mathsf{\Lambda }}_{\tau }{\left(r\right)\parallel x-y\parallel }_{\infty }+{\displaystyle \frac{L_f(1+{\mathsf{\Lambda }}_{\tau }\left(r\right))}{\mathsf{\Gamma }(\alpha +1)}}{\left(\phi \left(T\right)-\phi \left(0\right)\right)}^{\alpha }{\parallel x-y\parallel }_{\infty }\hfill \\ & \le {q\left(r\right)\parallel x-y\parallel }_{\infty }.\hfill \end{array}$$

for some $q\left(r\right)<1$. It follows that ${\parallel x-y\parallel }_{\infty }=0$, and thus $x\equiv y$ on $[0,T]$. □

4. Ulam–Hyers Stability

In this section, we establish the Ulam–Hyers stability of the initial value problem (1), (3) on the interval $[0,T]$, under Assumptions (As.1)–(As.6), in the sense of the stability concept for fractional differential equations introduced in [20,27].

Definition 3.

The $\mathcal{IVP}$ (1), (3) is said to be Ulam–Hyers stable if there exists a constant $C>0$ such that, for every $\epsilon >0$ and for every function $\zeta :(-\infty ,T]\to \mathbb{R}$ satisfying

$$\left|{}_{\phi }{}^C\mathcal{D}_{0+}^{\alpha }\left(\zeta \left(t\right)-g(t,\zeta \left({\tau }_0^{\zeta }\left(t\right)\right))\right)-f\left(t,\zeta \left(t\right),\zeta \left({\tau }_0^{\zeta }\left(t\right)\right)\right)\right|\le \epsilon ,t\in (0,T],$$

(10)

there exists a solution $x:(-\infty ,T]\to \mathbb{R}$ of the $\mathcal{IVP}$ (1), (3) such that

$$|x(t)-\zeta (t)|\le C\epsilon ,t\in (-\infty ,T].$$

In what follows, we suppose that $\zeta \in C^1\left([0,T]\right)$. In particular, we assume that the $\phi$–Caputo derivative of the neutral term $\zeta \left(t\right)-g\left(t,\zeta \left({\tau }_0^{\zeta }\left(t\right)\right)\right)$ admits a well-defined $\phi$–Caputo derivative for all $t\in (0,T]$.

Theorem 4.

Assume (As.1)–(As.6). Then the $\mathcal{IVP}$ (1), (3) is Ulam–Hyers stable.

Proof. 

Let $\epsilon >0$ and let $\zeta :(-\infty ,T]\to \mathbb{R}$ satisfy the perturbed inequality (10). In general, $\zeta$ need not satisfy (3). By (10), there exists a function $\eta (·)\in C\left(\right[0,T],\mathbb{R}):|\eta (t)|\le \epsilon$, such that

$${}_{\phi }{}^C\mathcal{D}_{0+}^{\alpha }\left(\zeta \left(t\right)-g(t,\zeta \left({\tau }_0^{\zeta }\left(t\right)\right))\right)=f\left(t,\zeta \left(t\right),\zeta \left({\tau }_0^{\zeta }\left(t\right)\right)\right)+\eta \left(t\right),t\in (0,T].$$

By Lemma 1, this yields the integral representation

$$\begin{array}{cc}\hfill \zeta \left(t\right)& -g\left(t,\zeta \left({\tau }_0^{\zeta }\left(t\right)\right)\right)=\zeta \left(0\right)-g\left(0,\zeta \left({\tau }_0^{\zeta }\left(0\right)\right)\right)\hfill \\ \hfill & +{\displaystyle \frac{1}{\mathsf{\Gamma }\left(\alpha \right)}}{\int }_0^t{(\phi \left(t\right)-\phi \left(s\right))}^{\alpha -1}{\phi }^{\prime }\left(s\right)\left[f\left(s,\zeta \left(s\right),\zeta \left({\tau }_0^{\zeta }\left(s\right)\right)\right)+\eta \left(s\right)\right]ds,\hfill \end{array}$$

(11)

for $t\in [0,T]$, with $|\eta (s)|\le \epsilon$.

By Theorem 3, there exists a unique solution $x:(-\infty ,T]\to \mathbb{R}$ associated with the initial function $\varphi$. We define the initial function by $\varphi =\zeta$ on $(-\infty ,0]$, so that the solution x satisfies the integral equation (by Lemma 5):

$$\begin{array}{cc}\hfill x\left(t\right)& =\zeta \left(0\right)-g\left(0,\zeta \left({\tau }_0^{\zeta }\left(0\right)\right)\right)+g\left(t,x\left({\tau }_0^x\left(t\right)\right)\right)\hfill \\ \hfill & +{\displaystyle \frac{1}{\mathsf{\Gamma }\left(\alpha \right)}}{\int }_0^t{(\phi \left(t\right)-\phi \left(s\right))}^{\alpha -1}{\phi }^{\prime }\left(s\right)f\left(s,x\left(s\right),x\left({\tau }_0^x\left(s\right)\right)\right)ds.\hfill \end{array}$$

(12)

Since $x=\zeta$ on $(-\infty ,0]$ by construction, the delayed initial terms coincide, so $g\left(0,\varphi \left({\tau }_0^{\varphi }\left(0\right)\right)\right)=g\left(0,\zeta \left({\tau }_0^{\zeta }\left(0\right)\right)\right)$. Subtracting the two integral equations, we obtain

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill x\left(t\right)-\zeta \left(t\right)& =g\left(t,x\left({\tau }_0^x\left(t\right)\right)\right)-g\left(t,\zeta \left({\tau }_0^{\zeta }\left(t\right)\right)\right)-g\left(0,x\left({\tau }_0^x\left(0\right)\right)\right)+g\left(0,\zeta \left({\tau }_0^{\zeta }\left(0\right)\right)\right)\hfill \\ \hfill & +{\displaystyle \frac{1}{\mathsf{\Gamma }\left(\alpha \right)}}{\int }_0^t{(\phi \left(t\right)-\phi \left(s\right))}^{\alpha -1}{\phi }^{\prime }\left(s\right)\left[f\left(s,x\left(s\right),x\left({\tau }_0^x\left(s\right)\right)\right)-f\left(s,\zeta \left(s\right),\zeta \left({\tau }_0^{\zeta }\left(s\right)\right)\right)\right]ds\hfill \\ \hfill & -{\displaystyle \frac{1}{\mathsf{\Gamma }\left(\alpha \right)}}{\int }_0^t{(\phi \left(t\right)-\phi \left(s\right))}^{\alpha -1}{\phi }^{\prime }\left(s\right)\eta \left(s\right)ds.\hfill \end{array}\end{array}$$

Therefore, by the assumptions (As.2), (As.3) and Corollary 1, for $t\in [0,T]$,

$$\begin{array}{cc}\hfill |x(t)-\zeta (t)|& \le |g\left(t,x\left({\tau }_0^x\left(t\right)\right)\right)-g\left(t,\zeta \left({\tau }_0^{\zeta }\left(t\right)\right)\right)|\hfill \\ & +{\displaystyle \frac{1}{\mathsf{\Gamma }\left(\alpha \right)}}{\int }_0^t{(\phi \left(t\right)-\phi \left(s\right))}^{\alpha -1}{\phi }^{\prime }\left(s\right)|f\left(s,x\left(s\right),x\left({\tau }_0^x\left(s\right)\right)\right)-f\left(s,\zeta \left(s\right),\zeta \left({\tau }_0^{\zeta }\left(s\right)\right)\right)|ds\hfill \\ & +{\displaystyle \frac{1}{\mathsf{\Gamma }\left(\alpha \right)}}{\int }_0^t{(\phi \left(t\right)-\phi \left(s\right))}^{\alpha -1}{\phi }^{\prime }\left(s\right)|\eta \left(s\right)|ds\hfill \\ & \le L_g{\mathsf{\Lambda }}_{\tau }\left(r\right)\parallel x-\zeta \parallel +{\displaystyle \frac{L_f\left(1+{\mathsf{\Lambda }}_{\tau }\left(r\right)\right)\parallel x-\zeta \parallel }{\mathsf{\Gamma }\left(\alpha \right)}}{\int }_0^t{(\phi \left(t\right)-\phi \left(s\right))}^{\alpha -1}{\phi }^{\prime }\left(s\right)ds\hfill \\ & +{\displaystyle \frac{1}{\mathsf{\Gamma }\left(\alpha \right)}}{\int }_0^t{(\phi \left(t\right)-\phi \left(s\right))}^{\alpha -1}{\phi }^{\prime }\left(s\right)|\eta \left(s\right)|ds\hfill \\ & \le L_g{\mathsf{\Lambda }}_{\tau }\left(r\right)\parallel x-\zeta \parallel +{\displaystyle \frac{L_f\left(1+{\mathsf{\Lambda }}_{\tau }\left(r\right)\right){(\phi \left(T\right)-\phi \left(0\right))}^{\alpha }\parallel x-\zeta \parallel }{\mathsf{\Gamma }(\alpha +1)}}+{\displaystyle \frac{{(\phi \left(T\right)-\phi \left(0\right))}^{\alpha }}{\mathsf{\Gamma }(\alpha +1)}}\epsilon .\hfill \end{array}$$

Consequently,

$$|x\left(t\right)-\zeta \left(t\right)|\le q\left(r\right)\parallel x-\zeta \parallel +{\displaystyle \frac{{(\phi \left(T\right)-\phi \left(0\right))}^{\alpha }}{\mathsf{\Gamma }(\alpha +1)}}\epsilon ,t\in [0,T],$$

where

$$q\left(r\right):=L_g{\mathsf{\Lambda }}_{\tau }\left(r\right)+{\displaystyle \frac{{(\phi \left(T\right)-\phi \left(0\right))}^{\alpha }{L}_f\left(1+{\mathsf{\Lambda }}_{\tau }\left(r\right)\right)}{\mathsf{\Gamma }(\alpha +1)}}.$$

Taking the supremum over $t\in [0,T]$ and using $q\left(r\right)<1$ yields that

$${\parallel x\left(t\right)-\zeta \left(t\right)\parallel }_{\infty }\le {\displaystyle \frac{{(\phi \left(T\right)-\phi \left(0\right))}^{\alpha }}{(1-q(r\left)\right)\mathsf{\Gamma }(\alpha +1)}}\epsilon .$$

Hence the $\mathcal{IVP}$ is Ulam–Hyers stable with $C={\displaystyle \frac{{(\phi \left(T\right)-\phi \left(0\right))}^{\alpha }}{(1-q(r\left)\right)\mathsf{\Gamma }(\alpha +1)}}.$ □

Remark 2.

In the context of the proof of Theorem 4, consider the auxiliary functions:

$$u\left(t\right):=|x\left(t\right)-\zeta \left(t\right)|,v\left(t\right):={\displaystyle \frac{{(\phi \left(T\right)-\phi \left(0\right))}^{\alpha }}{\mathsf{\Gamma }(\alpha +1)}}\epsilon ,g\left(t\right):=q\left(r\right),$$

with $q\left(r\right)$ as defined in assumption (As.6).

The resulting inequality can be reformulated as

$$u\left(t\right)\le v\left(t\right)+g\left(t\right){\int }_0^t{\phi }^{\prime }\left(s\right){\left(\phi \left(t\right)-\phi \left(s\right)\right)}^{\alpha -1}u\left(s\right)ds,t\in [0,T],$$

which is precisely the structure addressed by Lemma 3. Application of this lemma yields the explicit estimate:

$$u\left(t\right)\le v\left(t\right)+{\int }_0^t\sum _{k=1}^{\infty }{\displaystyle \frac{\left(g\left(t\right)\mathsf{\Gamma }(\alpha \right){)}^k}{\mathsf{\Gamma }\left(\alpha k\right)}}{\phi }^{\prime }\left(s\right){\left(\phi \left(t\right)-\phi \left(s\right)\right)}^{\alpha k-1}v\left(s\right)ds,t\in [0,T].$$

Since $v\left(s\right)$ is constant and given by $v\left(s\right)\equiv {\displaystyle \frac{{(\phi \left(T\right)-\phi \left(0\right))}^{\alpha }}{\mathsf{\Gamma }(\alpha +1)}}\epsilon$, and since by direct computation,

$${\displaystyle \frac{1}{\mathsf{\Gamma }\left(\alpha k\right)}}{\int }_0^t{\phi }^{\prime }\left(s\right){\left(\phi \left(t\right)-\phi \left(s\right)\right)}^{\alpha k-1}ds={\displaystyle \frac{{(\phi \left(t\right)-\phi \left(0\right))}^{\alpha k}}{\mathsf{\Gamma }(\alpha k+1)}},$$

we deduce the refined stability bound

$$|x\left(t\right)-\zeta \left(t\right)|\le {\displaystyle \frac{{(\phi \left(T\right)-\phi \left(0\right))}^{\alpha }}{\mathsf{\Gamma }(\alpha +1)}}{E}_{\alpha }\left(q\left(r\right)\mathsf{\Gamma }\left(\alpha \right){(\phi \left(t\right)-\phi \left(0\right))}^{\alpha }\right)\epsilon ,t\in [0,T],$$

where $E_{\alpha }(·)$ denotes the Mittag–Leffler function. Therefore, Lemma 3 provides an alternative Ulam–Hyers stability estimate to that of Theorem 4, in which the geometric factor ${\displaystyle \frac{1}{1-q\left(r\right)}}$ is refined to by a Mittag-Leffler type bound.

5. Illustrative Examples

To demonstrate the applicability of the main theoretical results, namely, existence (Theorem 2), uniqueness (Theorem 3), and Ulam–Hyers stability (Theorem 4), we present three examples. For each example, the initial value problem is first formulated. Subsequently, the validity of assumptions (As.1)–(As.6) is established. Thereafter, analytical conclusions are drawn and substantiated by graphical illustrations of Ulam–Hyers stability. Finally, additional discussion and remarks concerning the proposed examples and their associated graphics are provided.

Throughout this section, we employ the notation

$$C_{\alpha }\left(T\right):={\displaystyle \frac{{\left(\phi \left(T\right)-\phi \left(0\right)\right)}^{\alpha }}{\mathsf{\Gamma }(\alpha +1)}},{\mathcal{B}}_r:={\{x\in C([0,T];\mathbb{R}):\parallel x\parallel }_{\infty }\le r\}.$$

and the one-parameter Mittag–Leffler function

$$E_{\alpha }\left(z\right):=\sum _{k=0}^{\infty }{\displaystyle \frac{z^k}{\mathsf{\Gamma }(\alpha k+1)}},\alpha >0.$$

In the context of the Mittag–Leffler stability estimate (cf. Remark 2), the relevant parameter is

$$z_T:=q_T\left(r\right)\mathsf{\Gamma }\left(\alpha \right){\left(\phi \left(T\right)-\phi \left(0\right)\right)}^{\alpha },$$

(13)

and the corresponding stability bound is given by

$${\parallel x-\zeta \parallel }_{\infty }\le {\displaystyle \frac{{\left(\phi \left(T\right)-\phi \left(0\right)\right)}^{\alpha }}{\mathsf{\Gamma }(\alpha +1)}}{E}_{\alpha }\left(z_T\right)\epsilon ,$$

(14)

Additionally, $q_T\left(r\right)<1$, the geometric stability estimate of Theorem 4 applies:

$${\parallel x-\zeta \parallel }_{\infty }\le {\displaystyle \frac{{\left(\phi \left(T\right)-\phi \left(0\right)\right)}^{\alpha }}{(1-q_T\left(r\right))\mathsf{\Gamma }(\alpha +1)}}\epsilon .$$

(15)

5.1. Example 1

Consider the following $\mathcal{IVP}$ for a fractional functional differential equations with variable delays

$$\begin{array}{cc}\hfill & {}_t{}^C\mathcal{D}_{0+}^{\alpha }\left(x\left(t\right)-{\displaystyle \frac{1}{4}}x({\tau }_0^x(t)))\right)=\frac{1}{6}sint+\frac{1}{6}(x\left(t\right)+x\left({\tau }_0^x\left(t\right)\right)),t\in (0,T],\hfill \\ \hfill & x\left(t\right)=\varphi \left(t\right)\equiv 1t\le 0\hfill \end{array}$$

(16)

with ${\tau }_0^x\left(t\right)=\frac{t}{2},\phi \left(t\right)=t$ and $T\in \{1,2\}.$

Assumptions (As.1)–(As.6) are satisfied with $L_{\theta }=0$, $L_g=\frac{1}{4}$, ${sup}_t|g(t,0)|=0,$ $L_f=\frac{1}{6}$, $M_f=\frac{1}{6}$, and $C_{1/2}\left(T\right)=T^{1/2}/\mathsf{\Gamma }(3/2)$. Ball invariance holds for

$$r\ge r_{min}\left(T\right)={\displaystyle \frac{0.75+\frac{1}{6}{C}_{1/2}\left(T\right)}{1-\frac{1}{4}-\frac{1}{3}{C}_{1/2}\left(T\right)}}.$$

Numerically, $r_{min}\left(1\right)=2.509$ and $r_{min}\left(2\right)=4.659$. The contraction parameter is $q_T\left(r\right)=\frac{1}{4}+\frac{1}{3}{C}_{\alpha }\left(T\right)$, so $q_1=0.626$, $q_2=0.782<1$. Therefore, Theorems 2, 3 and 4 apply, guaranteeing existence, uniqueness, and Ulam–Hyers stability for $T\in \{1,2\}$.

We note that for the particular choice of $\phi \left(t\right)=t$, the generalized $\phi$-Caputo derivative reduces to the classical Caputo fractional derivative. Consequently, the considered problem becomes a classical fractional neutral functional differential equation with variable delay.

5.2. Example 2

Consider the following $\mathcal{IVP}$ for a neutral fractional functional differential equation with iterated state-dependent delays:

$$\begin{array}{cc}\hfill & {}_{t^2}{}^C\mathcal{D}_{0+}^{\alpha }\left(x\left(t\right)-{\displaystyle \frac{1}{5}}x({\tau }_0^x(t)))\right)=\frac{1}{10}(x\left(t\right)-x\left({\tau }_0^x\left(t\right)\right)),t\in (0,T],\hfill \\ \hfill & x\left(t\right)=\varphi \left(t\right)\equiv 1,t\le 0\hfill \end{array}$$

(17)

with ${\tau }_1\left(t\right)=t-ax{\left(t\right)}^2,{\tau }_0^x\left(t\right)=t-bx{\left({\tau }_1\left(t\right)\right)}^2,a=b=0.05$ and $\phi \left(t\right)=t^2,T\in \{1,2\}.$

Assumptions (As.1)–(As.6) hold on ${\mathcal{B}}_r$ with $L_{\theta }=max\{2ar,2br\}=0.1r$, $L_g=\frac{1}{5}$, ${sup}_t|g(t,0)|=0,$ $L_f={\displaystyle \frac{1}{10}}$, $M_f=0$, and $C_{1/2}\left(T\right)={\displaystyle \frac{T}{\mathsf{\Gamma }(3/2)}}$. The ball invariance condition is satisfied for

$$r\ge r_{min}(T,\alpha ):={\displaystyle \frac{0.8}{1-L_g-2L_f{C}_{\alpha }\left(T\right)}}={\displaystyle \frac{0.8}{0.8-0.2C_{\alpha }\left(T\right)}}.$$

Numerically, for $\alpha =\frac{1}{2},$ $r_{min}\left(1\right)=1.393$ and $r_{min}\left(2\right)=2.295$. Therefore, $q_T\left(r\right)=L_g{\mathsf{\Lambda }}_{\tau }\left(r\right)+L_f{C}_{\alpha }\left(T\right)(1+{\mathsf{\Lambda }}_{\tau }\left(r\right))=0.2{\mathsf{\Lambda }}_{\tau }\left(r\right)+0.1C_{\alpha }\left(T\right)(1+{\mathsf{\Lambda }}_{\tau }\left(r\right)).$ With $r=r_{min}\left(T\right),$ we fix $L_x\left(r\right)=1$: ${\mathsf{\Lambda }}_{\tau }\left(1\right)=1.298$, ${\mathsf{\Lambda }}_{\tau }\left(2\right)=1.512$; hence, $q_{T=1}=0.519<1$, $q_{T=2}=0.868<1$. Thus, Theorems 2, 3 and 4 ensure existence, uniqueness, and Ulam–Hyers stability.

5.3. Example 3

Consider the following $\mathcal{IVP}$ for a neutral fractional functional differential equations with iterated state-dependent delays:

$${}_t{}^C\mathcal{D}_{0+}^{\alpha }\left(x\left(t\right)-{\displaystyle \frac{1}{10}}x({\tau }_0^x\left(t\right)))\right)=\beta sin\left(t\right)+\mu (x\left(t\right)+x\left({\tau }_0^x\left(t\right)\right)),t\in (0,T],$$

(18)

with $\beta =0.01,\mu =0.01,$ ${\tau }_1\left(t\right)=t-a{x}^2\left(t\right),{\tau }_0^x\left(t\right)=t-b{x}^2\left(t\right)-c{x}^2\left({\tau }_1\left(t\right)\right),a=b=c=0.1$ and $\phi \left(t\right)=t,t\in (0,T],\varphi \left(t\right)\equiv 1(t\le 0),T=3.$

Assumptions (As.1)–(As.6) are fulfilled on ${\mathcal{B}}_r$ with $|{\theta }_1(t,u)-{\theta }_1(t,v)|\le 2ar|u-v|,$ $|{\theta }_0(t,u,v)-{\theta }_0(t,u,v)|\le 2(b+c)r\parallel u-v\parallel ,$ $L_{\theta }=max\{2ar,2(b+c)r\}=0.4r$, $L_g=\frac{1}{10}$, $L_f=0.01$, $M_f=0.01$, and $C_{1/2}\left(T\right)=T^{1/2}/\mathsf{\Gamma }(3/2)$. Ball invariance is achieved for $r\ge r_{min}(3,\alpha ):={\displaystyle \frac{0.9+C_{\alpha }\left(3\right)M_f}{1-L_g-2L_f{C}_{\alpha }\left(3\right)}}.$ For $\alpha =\frac{1}{2}$, we have $C_{1/2}\left(3\right)=\sqrt{3}/\mathsf{\Gamma }\left(1.5\right)\approx 1.956$; hence, $r_{min}=1.119$; we fix $L_x\left(r\right)=2$ on ${\mathcal{B}}_r$. Thus, $q_{T=3}=0.479.$ Accordingly, Theorems 2–4 guarantee existence, uniqueness, and Ulam–Hyers stability.

5.4. Example 4: Fractional Hopfield Network with Iterated State-Dependent Delays

Consider, for $i=1,2$, the following two-layer neuron neutral fractional Hopfield system:

$$\begin{array}{cc}\hfill & {}_{\phi }{}^C\mathcal{D}_{0+}^{\alpha }\left(x_i\left(t\right)-c{x}_i({\tau }_{0,i}\left(t\right)))\right)=-a{x}_j\left({\tau }_{0,j}\left(t\right)\right)+\sum _{j=1}^2{w}_{ij}tanh\left(x_i\left(t\right)\right)+I_i\left(t\right),t\in (0,T]\hfill \\ \hfill & x_i\left(t\right)={\varphi }_i\left(t\right)\equiv 1,t\le 0\hfill \end{array}$$

(19)

with parameters ${\tau }_{1,i}\left(t\right)=t-b_1{x}_i{\left(t\right)}^2,{\tau }_{0,i}\left(t\right)=t-b_0{x}_i{\left({\tau }_{1,i}\left(t\right)\right)}^2$ and $\phi \left(t\right)=t^{\frac{1}{3}},T\in \{1,2\}$. $a=0.1,c=0.05,W=\left\{w_{ij}\right\}=a{E}_2,$ where $E_2$ is the 2-by-2 identity matrix. Let $b_0=b_1=0.02,I_i\left(t\right)=0.05sint.$ Since $W=a{E}_2$, the system reduces to two identical scalar equations. The analysis below applies to each neuron.

Assumptions (As.1)–(As.6) are satisfied on ${\mathcal{B}}_r$ with $L_{\theta }=2max\{b_0,b_1\}r=0.04r$. Here, $g(t,u)=cu$ ($L_g=0.05$), and using $|tanhu-tanhv|\le |u-v|$, so $L_f=a=0.1$ and $M_f=0.05$. Since ${(\phi \left(T\right)-\phi \left(0\right))}^{\alpha }=T^{1/6}$, $C_{\alpha }\left(T\right)=T^{1/6}/\mathsf{\Gamma }(3/2)$. At $t=0$, $|1-g(0,\varphi \left({\tau }_{0,i}\left(0\right)\right))|=|1-0.05|=0.95$. Numerically, $r_{min}\left(1\right)=1.389$ and $r_{min}\left(2\right)=1.454$, and at these radii, with $L_x\left(r\right)=1$, ${\mathsf{\Lambda }}_{\tau }\left(r\right)={(1+0.04r)}^2$, $q_1=0.294<1$, $q_2=0.324<1$. Therefore, existence, uniqueness, and Ulam–Hyers stability follow from Theorems 2–4.

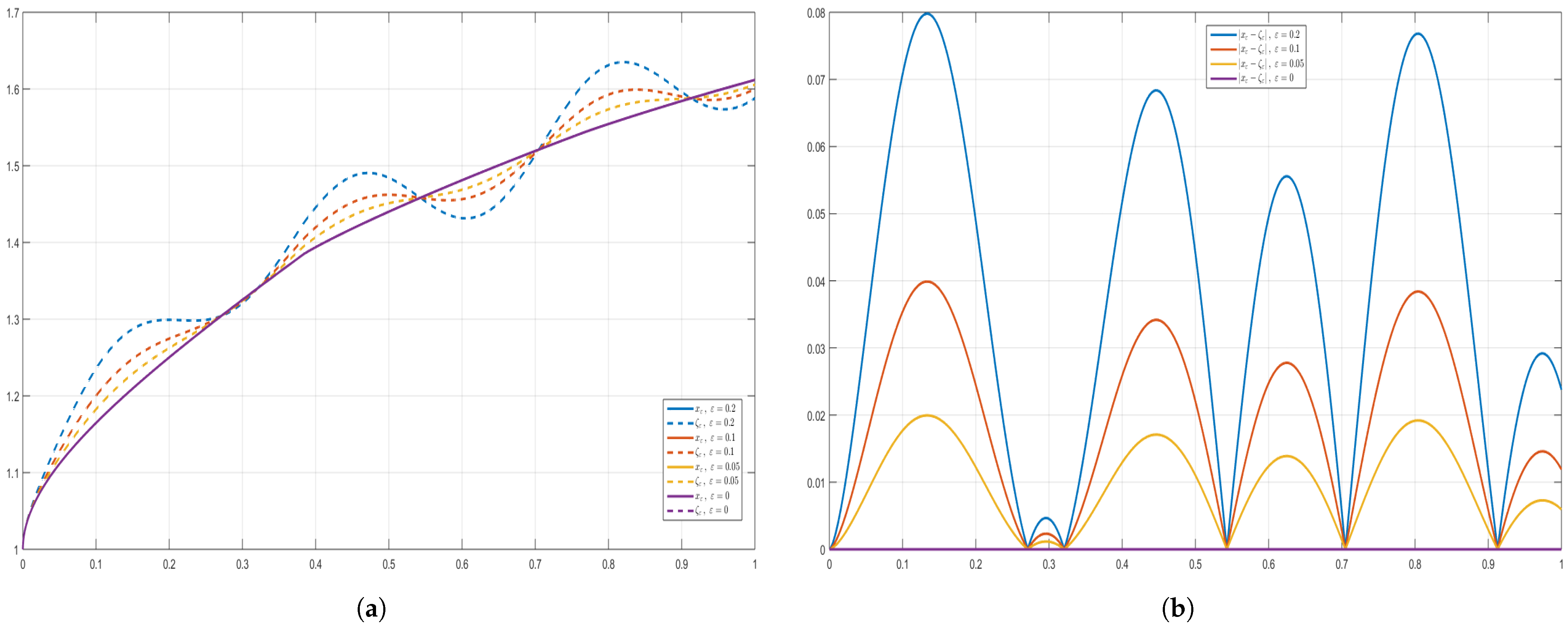
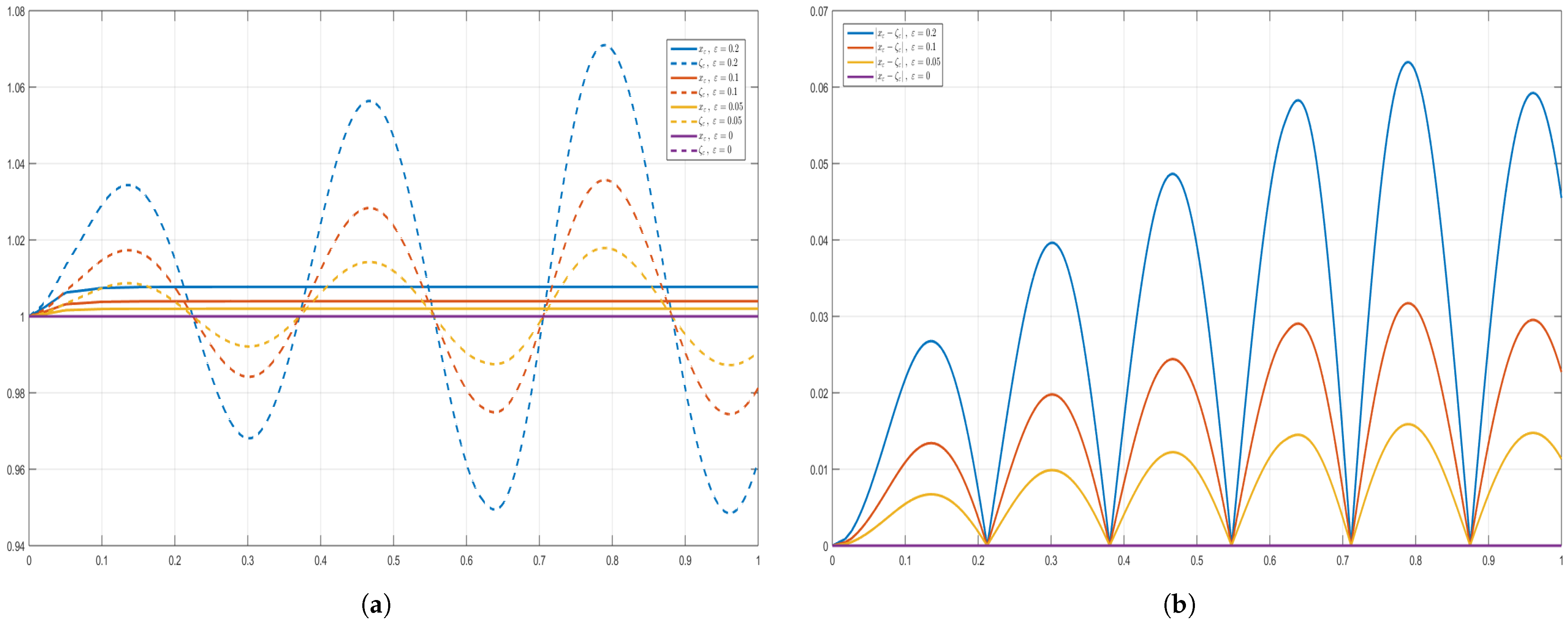
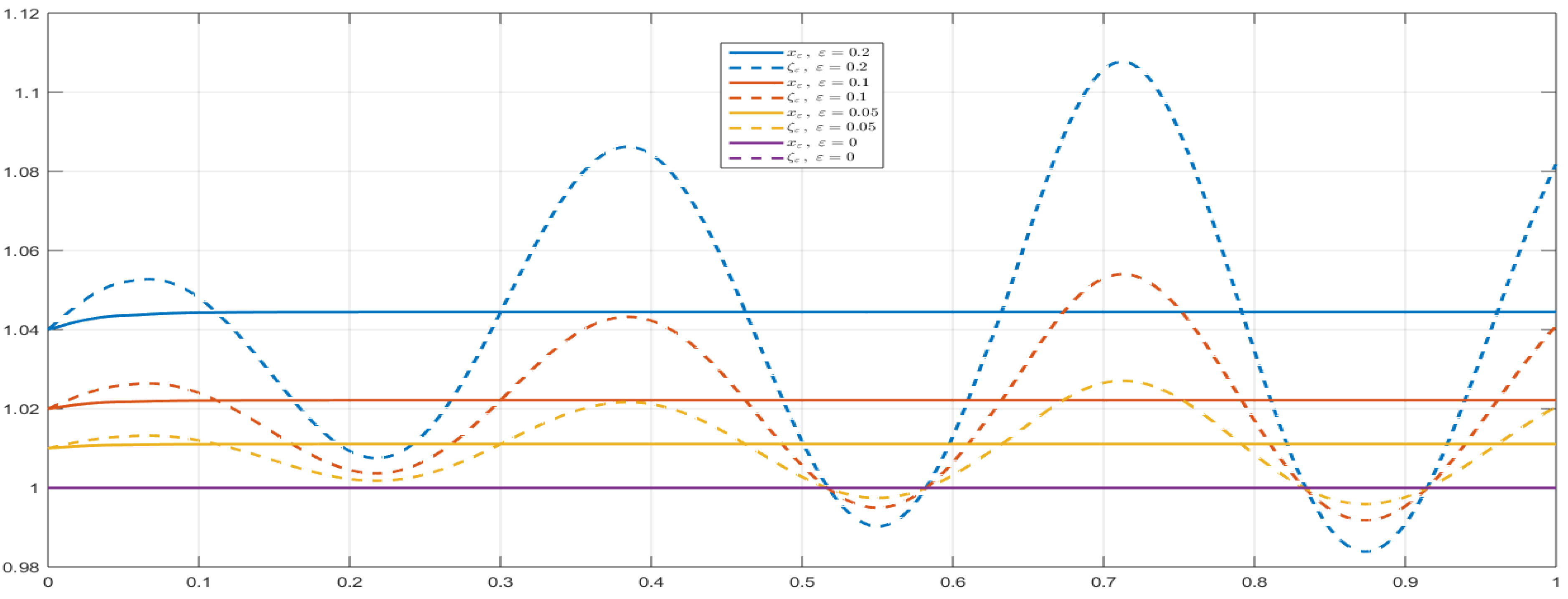
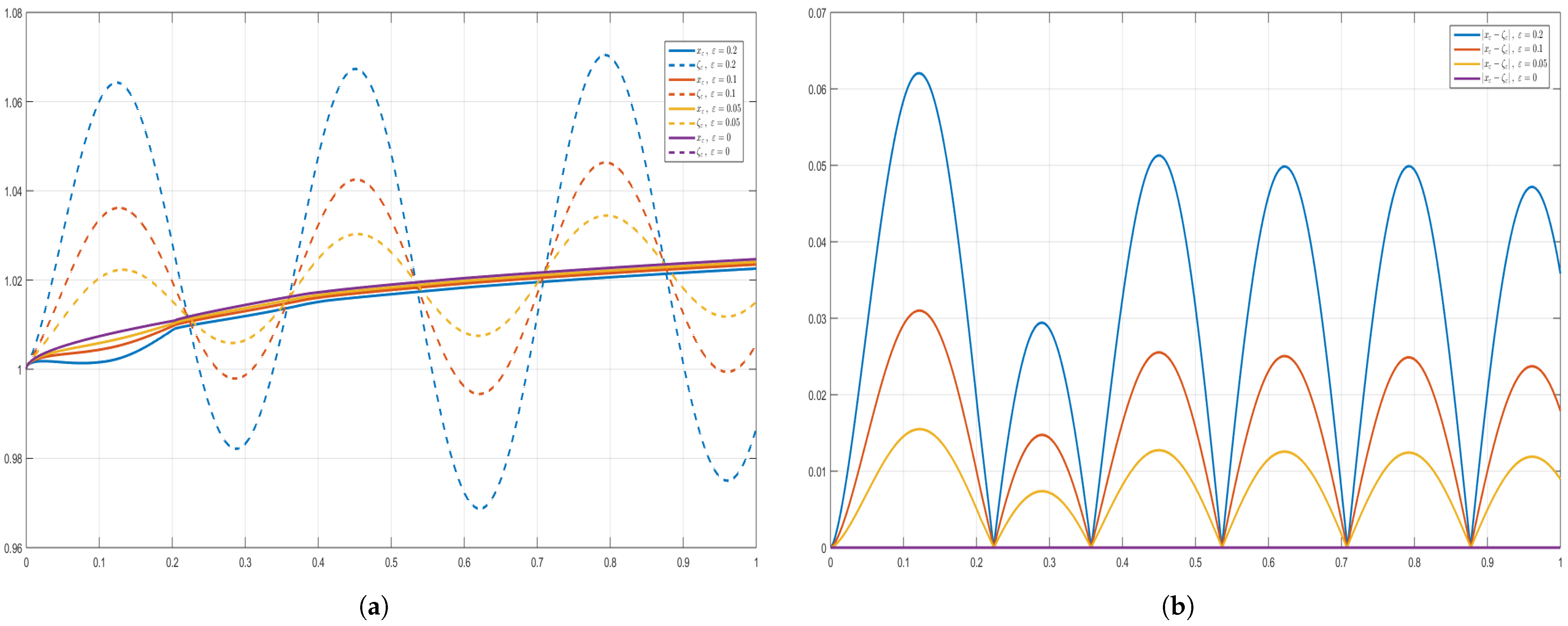
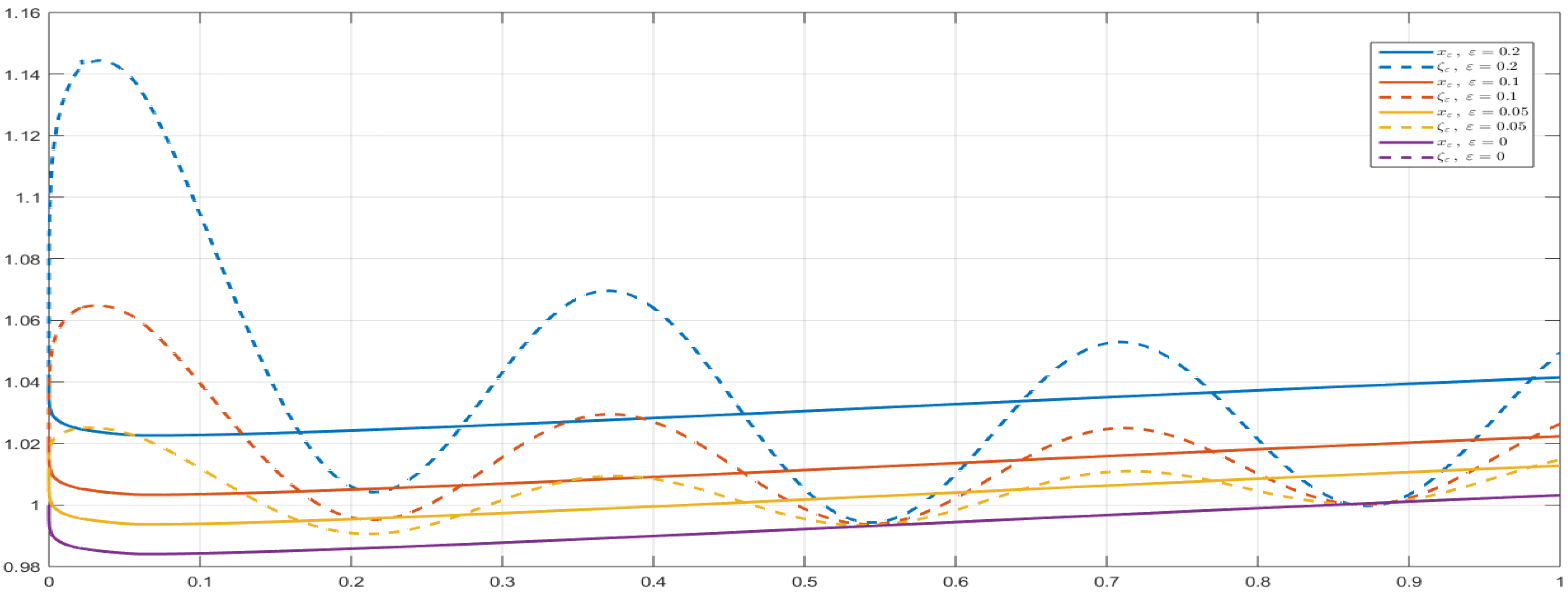
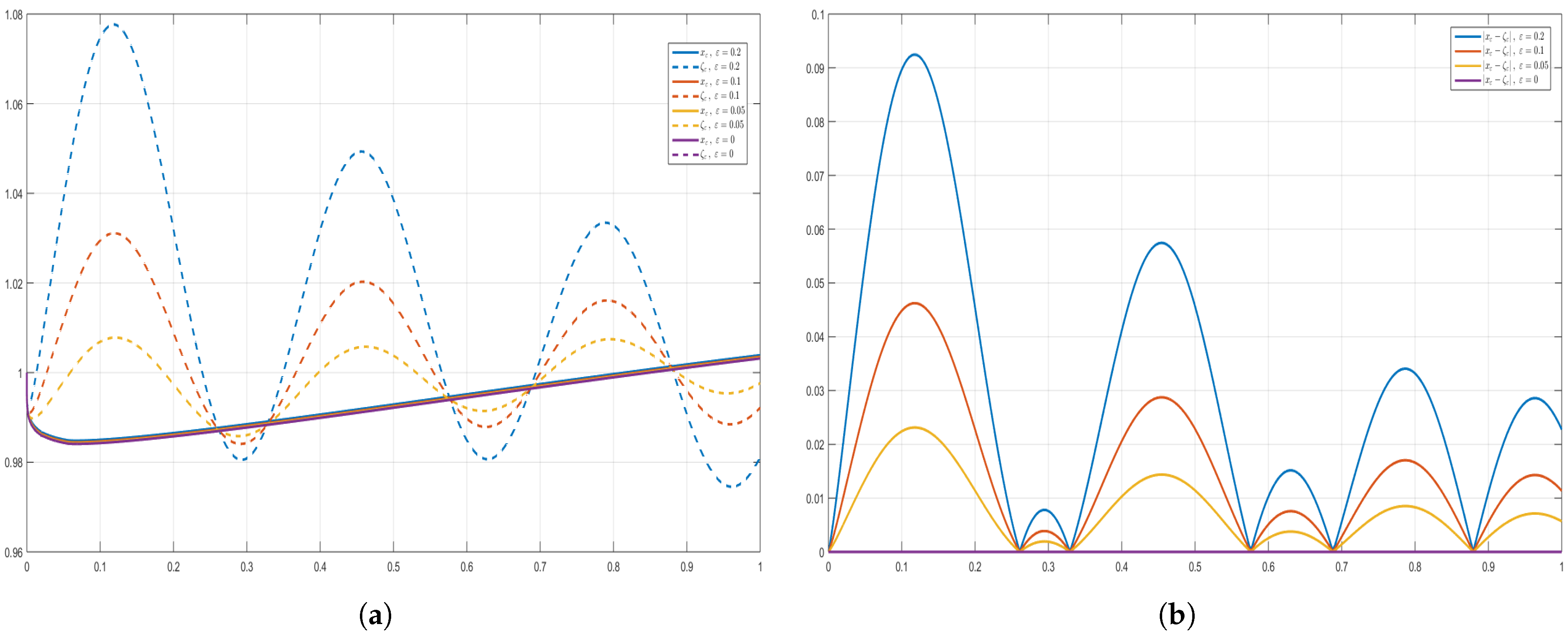
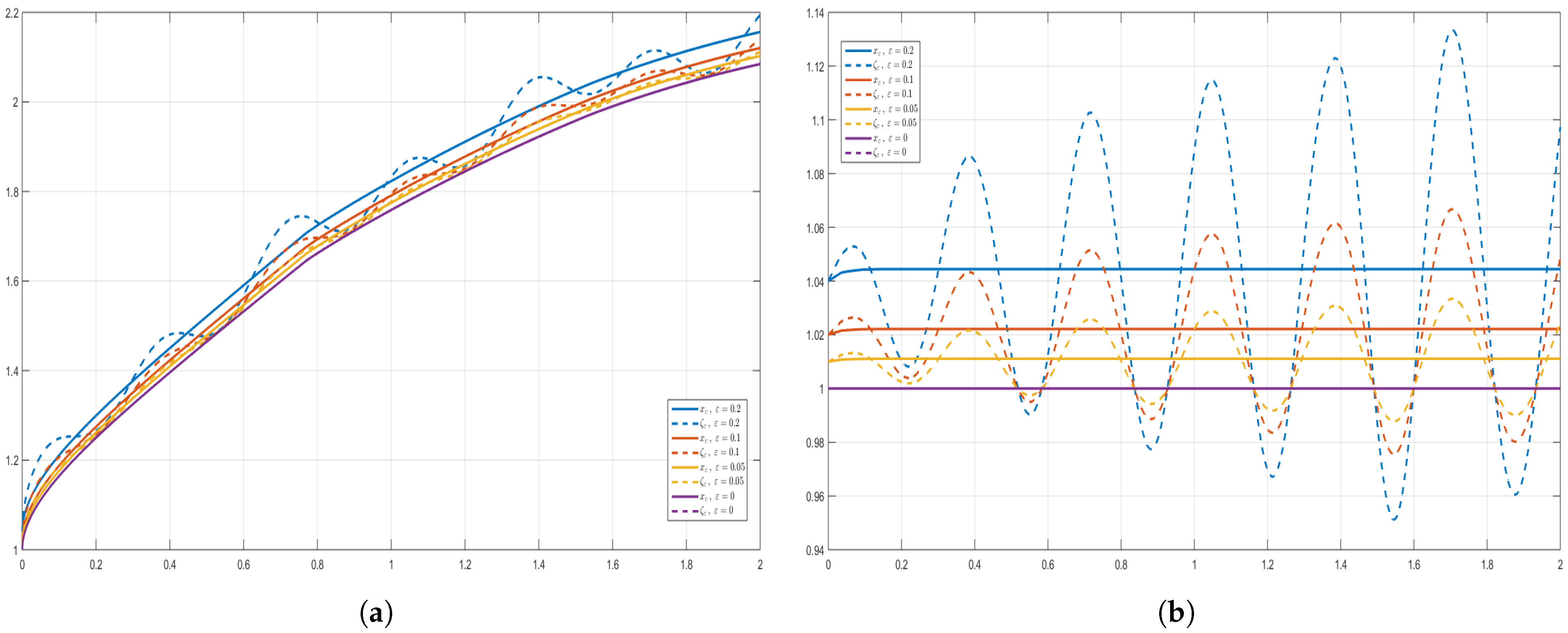
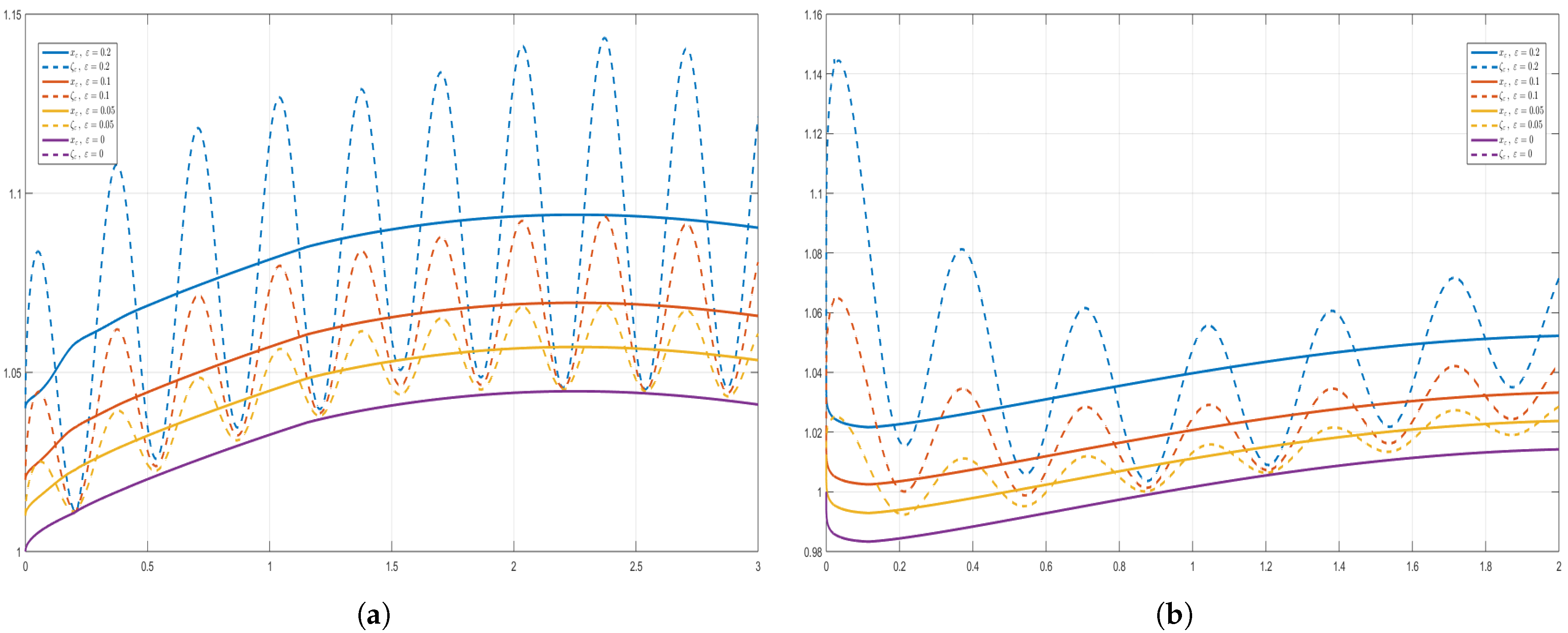
5.5. Remarks and Comments on the Proposed Examples and Graphics

All values of the Mittag–Leffler function reported below are obtained via direct series evaluation of $E_{1/2}$. The resulting Ulam–Hyers stability bounds, as given by Equations (14) and (15), are collected in Table 1.

Table 1. Ulam–Hyers stability bounds for $\alpha =\frac{1}{2}$ and $T\in \{1,2\}$. Geometric bound: ${\parallel x-\zeta \parallel }_{\infty }\le {\displaystyle \frac{C_{\alpha }\left(T\right)}{1-q_T\left(r\right)}}\epsilon$, Mittag–Leffler bound: ${\parallel x-\zeta \parallel }_{\infty }\le C_{\alpha }\left(T\right)E_{1/2}\left(z_T\right)\epsilon$, where $E_{1/2}\left(z\right)={\sum }_{k=0}^{\infty }{\displaystyle \frac{z^k}{\mathsf{\Gamma }(\frac{k}{2}+1)}}$.

Example	T	${\mathit{q}}_{\mathit{T}}\left(\mathit{r}\right)$	${\mathit{z}}_{\mathit{T}}$	${\displaystyle \frac{{\mathit{C}}_{\mathit{\alpha }}\left(\mathit{T}\right)}{1-{\mathit{q}}_{\mathit{T}}\left(\mathit{r}\right)}}$	${\mathit{C}}_{\mathit{\alpha }}\left(\mathit{T}\right){\mathit{E}}_{1/2}\left({\mathit{z}}_{\mathit{T}}\right)$
Example 1 (Section 5.1)	1	0.626	1.110	3.018	7.283
	2	0.782	1.960	7.317	148.306
Example 2 (Section 5.2)	1	0.519	0.920	2.345	4.750
	2	0.869	3.081	17.242	$5.982\times {10}^4$
Example 3 (Section 5.3)	1	0.439	0.778	2.011	3.571
	2	0.461	1.157	2.963	11.542
	3	0.479	1.470	3.750	33.272
Example 4 (Section 5.4)	1	0.294	0.522	1.599	2.280
	2	0.324	0.646	1.875	3.149

Remark 3 (Comparison of Stability Bounds).

For all examples considered in Table 1, the explicit computations demonstrate that the geometric bound ${\displaystyle \frac{C_{1/2}\left(T\right)}{1-q_T\left(r\right)}}$ is strictly less than the Grönwall-type (Mittag–Leffler) bound $C_{1/2}\left(T\right)·E_{1/2}\left(z_T\right),$ where all quantities are as previously defined. Accordingly, the geometric estimates yield a more precise bound for the Ulam–Hyers stability of the fractional neutral functional differential equations with state-dependent delays. This outcome is consistent with theoretical expectations, given the rapid growth rate of the Mittag–Leffler function.

Remark 4 (Note on the choice of $L_x\left(r\right)$).

Due to the lack of an explicit form of the solution of the $\mathcal{IVP}$ for Equations (16)–(19), as an alternative to fixing $L_x$ in Assumption (As.4), the inequality in Assumption (As.6) for uniqueness can be verified with respect to $L_x$, and one can obtain all values $L_x$ for which it is satisfied, as was done in the work [18].

In Examples 2–4 (Section 5.2, Section 5.3 and Section 5.4), explicit admissible values $L_x\left(r\right)=1$ and $L_x\left(r\right)=2$ are selected on ${\mathcal{B}}_r$ to ensure transparency and reproducibility of constants. Any finite Lipschitz modulus on ${\mathcal{B}}_r$ is admissible in the estimation; a smaller choice reduces ${\mathsf{\Lambda }}_{\tau }\left(r\right)$ and $q_T\left(r\right)$, thereby enlarging the admissible interval T or decreasing the minimal radius $r_{min}$. In Example 1 (Section 5.1), since $L_{\theta }=0$, $L_x\left(r\right)$ is arbitrary.

Remark 5 (On the choice of perturbation and the role of $\zeta$ in the graphics).

(a) 

In the proof of Theorem 4, the perturbation term η is arbitrary, subject only to ${\parallel \eta \parallel }_{\infty }\le \epsilon$. For the numerical illustrations in Figure 1, Figure 2, Figure 3, Figure 4, Figure 5 and Figure 6, we fix

$$\eta \left(t\right)=\epsilon sin\left(\omega t\right),(or\epsilon cos(\omega t\left)\right)\omega =6\pi ,$$

to construct explicit ε-approximate solutions ζ, where ζ denotes the numerical solution of the perturbed problem. The purple curves in the figures correspond to the reference solution x ($\epsilon =0$), computed via the fractional Adams-Bashforth-Moulton predictor-corrector method [45,46,47] using MATLAB^®, Version 9.9 (R2020b), on a laptop Lenovo X1 Carbon 7th Generation Ultrabook, while the colored curves depict perturbed solutions ζ for various values of ε. This choice of η is non-restrictive; any bounded perturbation with ${\parallel \eta \parallel }_{\infty }\le \epsilon$ is admissible in theory. The sinusoidal form is adopted for clarity of visualization, as it highlights the effect of Ulam–Hyers stability in the plots. For different perturbation levels, the approximate solutions remain uniformly close to the analytic solution x, in full agreement with Theorem 4. All three examples satisfy Assumptions (As.1)–(As.6) and yield a contraction constant $q\left(r\right)<1$, so existence, uniqueness, and Ulam–Hyers stability are guaranteed. The colored curves represent ε-perturbed approximate solutions, which converge uniformly to the reference solution as $\epsilon \to 0$.

Figure 1. Graphs of the solutions illustrating Ulam-type stability for Example 1 (Section 5.1) on $[0,1]$ with varying $\epsilon =0, 0.1, 0.05, 0.01$ and $\eta \left(t\right)=\epsilon \ast sin\left(6\pi t\right)$: (a) $x_{\epsilon }\left(t\right)$ and ${\zeta }_{\epsilon }\left(t\right)$ (b) $|x_{\epsilon }\left(t\right)-{\zeta }_{\epsilon }\left(t\right)|$.

Figure 2. Graphs of the solutions illustrating Ulam-type stability for Example 2 (Section 5.2) on $[0,1]$ with varying $\epsilon =0, 0.1, 0.05, 0.01$ and $\eta \left(t\right)=\epsilon \ast sin\left(6\pi t\right)$: (a) $x_{\epsilon }\left(t\right)$ and ${\zeta }_{\epsilon }\left(t\right)$ (b) $|x_{\epsilon }\left(t\right)-{\zeta }_{\epsilon }\left(t\right)|$.

Figure 3. Graphs of the solutions illustrating Ulam-type stability for Example 2 (Section 5.2) on $[0,1]$ with varying $\epsilon =0, 0.1, 0.05, 0.01$ and $\eta \left(t\right)=\epsilon \ast cos\left(6\pi t\right)$: (a) $x_{\epsilon }\left(t\right)$ and ${\zeta }_{\epsilon }\left(t\right)$ (b) $|x_{\epsilon }\left(t\right)-{\zeta }_{\epsilon }\left(t\right)|$.

Figure 4. Graphs of the solutions illustrating Ulam-type stability for Example 3 (Section 5.3) on $[0,1]$ with varying $\epsilon =0, 0.1, 0.05, 0.01$ $\eta \left(t\right)=\epsilon \ast sin\left(6\pi t\right)$: (a) $x_{\epsilon }\left(t\right)$ and ${\zeta }_{\epsilon }\left(t\right)$ (b) $|x_{\epsilon }\left(t\right)-{\zeta }_{\epsilon }\left(t\right)|$.

Figure 5. Graphs of the solutions illustrating Ulam-type stability for Example 4 (Section 5.4) on $[0,1]$ with varying $\epsilon =0, 0.1, 0.05, 0.01$ and $\eta \left(t\right)=\epsilon \ast cos\left(6\pi t\right)$: (a) $x_{\epsilon }\left(t\right)$ and ${\zeta }_{\epsilon }\left(t\right)$ (b) $|x_{\epsilon }\left(t\right)-{\zeta }_{\epsilon }\left(t\right)|$.

Figure 6. Graphs of the solutions illustrating Ulam-type stability for Example 4 (Section 5.4) on $[0,1]$ with varying $\epsilon =0.1, 0.05, 0.01$ and $\eta \left(t\right)=\epsilon \ast sin\left(6\pi t\right)$: (a) $x_{\epsilon }\left(t\right)$ and ${\zeta }_{\epsilon }\left(t\right)$ (b) $|x_{\epsilon }\left(t\right)-{\zeta }_{\epsilon }\left(t\right)|$.

(b) 

In accordance with Definition 3 and Remark 4 of [27], we illustrate the Ulam–Hyers stability for the ψ–Caputo fractional initial value problem by considering, for each $\epsilon >0$, the ε–dependent initial function (${\varphi }_{\epsilon }={\zeta }_{\epsilon }$) for the differential inequality (10)

$${\varphi }_{\epsilon }\left(t\right)=1+0.2\epsilon cos\left(6\pi t\right),t\le 0,(or1+0.2\epsilon sin\left(6\pi t\right)).$$

 and the perturbation

$${\eta }_{\epsilon }\left(t\right)=\epsilon sin\left(6\pi t\right)(or\epsilon cos\left(6\pi t\right)).$$

The differential inequality is considered for $t>0$; therefore, the perturbation does not affect the initial point, and in the IVP setup the change of the initial condition of the Equation (1) is illustrated through the choice of the ε-dependent initial function for the inequality. By Theorem 2, for each choice of the initial function ${\zeta }_{\epsilon }$ of the inequality, there exists a corresponding solution $x_{\epsilon }$ of the φ–Caputo equation with the same ε–dependent initial function.

In the numerical results, the perturbation effect at $t=0$ is not visible in Figure 1, Figure 2, Figure 4 and Figure 6 due to the value of $sin\left(6\pi t\right)$ at that point; however, Figure 3, Figure 5, Figure 7 and Figure 8 explicitly confirm the existence of solutions of the equation for each ε-dependent initial function chosen for the inequality.

Figure 7. Graphs of the solutions illustrating Ulam-type stability for Examples 1 and 2 (Section 5.1 and Section 5.2 on $[0,2]$ with varying $\epsilon =0, 0.1, 0.05, 0.01$ and $\eta \left(t\right)=\epsilon \ast cos\left(6\pi t\right)$: (a) $x_{\epsilon }\left(t\right)$ and ${\zeta }_{\epsilon }\left(t\right)$ of Example 1 (Section 5.1) (b) $x_{\epsilon }\left(t\right)$ and ${\zeta }_{\epsilon }\left(t\right)$ of Example 2 (Section 5.2).

Figure 8. Graphs of the solutions illustrating Ulam-type stability for Examples 3 and 4 (Section 5.3 and Section 5.4) with varying $\epsilon =0, 0.1, 0.05, 0.01$ and $\eta \left(t\right)=\epsilon \ast cos\left(6\pi t\right)$: (a) $x_{\epsilon }\left(t\right)$ and ${\zeta }_{\epsilon }\left(t\right)$ of Example 3 (Section 5.3) on $[0,3]$ (b) $x_{\epsilon }\left(t\right)$ and ${\zeta }_{\epsilon }\left(t\right)$ of Example 4 (Section 5.4) on $[0,2]$.

6. Conclusions

In this work, we have analysed a novel class of neutral fractional functional differential equations characterised by iterated state-dependent delays, governed by the $\phi$-Caputo derivative of order $\alpha \in (0,1)$. The problem was posed on a general compact interval $[0,T]$ with nontrivial initial data. This framework extends existing results on equations with constant or state-dependent delays and those involving the standard Caputo derivative.

The principal advances of this work may be summarized as follows:

1.

Formulation and rigorous analysis of a new class of neutral fractional functional differential equations with recursively defined, state-dependent delays, governed by the $\phi$-Caputo derivative.

2.

Establishment of existence and uniqueness results through Krasnosel’skii’s fixed point theorem and refined contraction arguments, supported by new inequalities tailored to the iterated delay structure.

3.

Derivation of explicit, quantitative criteria for Ulam–Hyers stability within this generalized fractional framework. A comparative analysis of geometric and Grönwall-type stability estimates is provided.

4.

Demonstration of the theoretical findings via illustrative examples and computational simulations.

5.

Introduction of a Hopfield neural network model incorporating iterated delays, thereby extending the applicability of the developed theory to a novel domain not previously addressed in the literature.

Future research directions include extending the analysis to systems in ${\mathbb{R}}^n$ with infinitely many iterated delays, investigating boundary problems [21], and exploring the existence of global solutions. Additionally, further study is warranted on the influence of the time-scale function $\phi$ on the qualitative properties of solutions. Finally, we mention the works [48,49] (and references therein) for different kinds of stability involving nonlinear evolution-type equations.