Hardware-in-the-Loop Experimental Validation of a Fault-Tolerant Control System for Quadcopter UAV Motor Faults
Abstract
1. Introduction
2. Literature Review
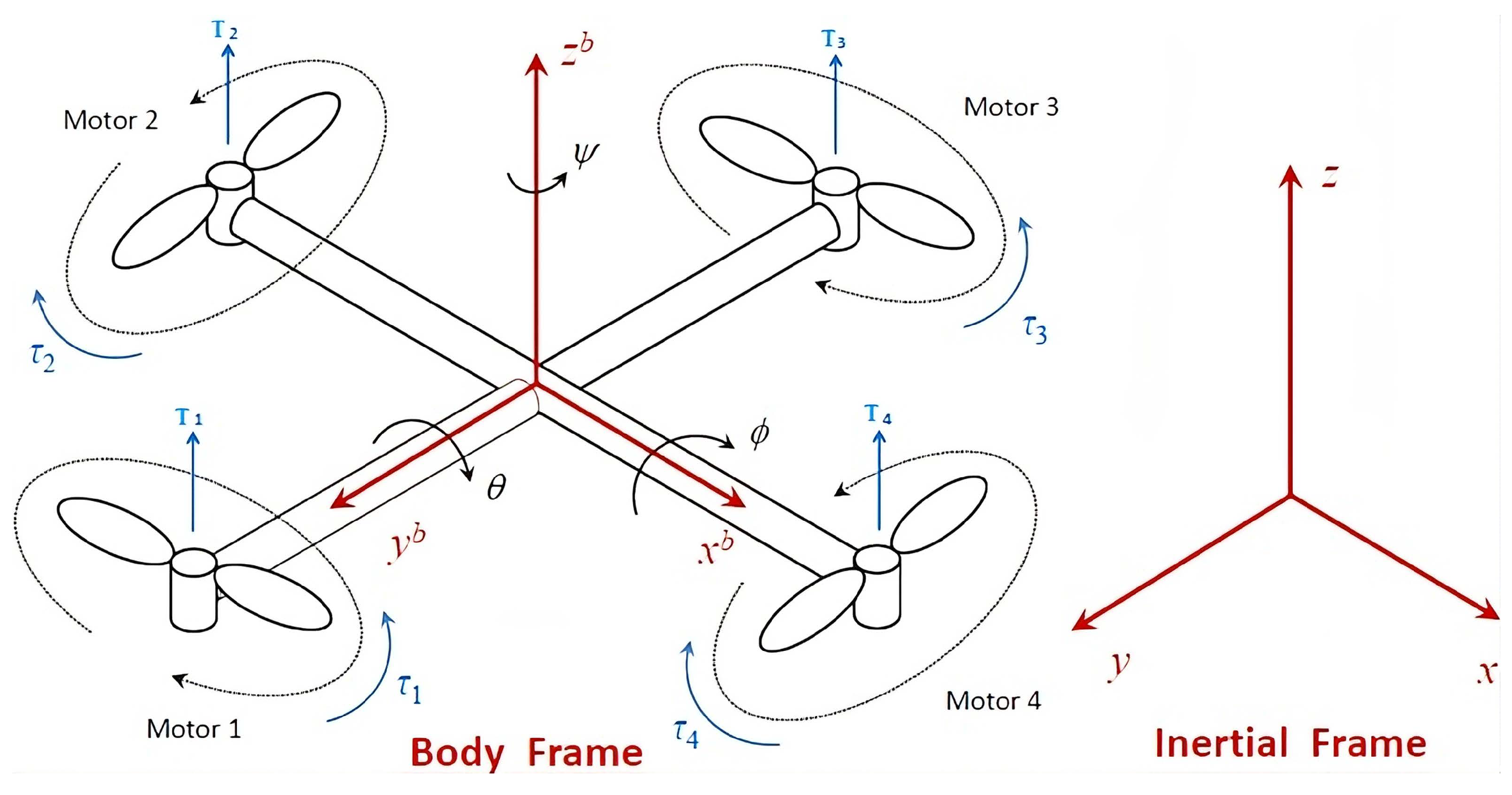
3. Mathematical Modeling of the Quadcopter
3.1. Fault Modeling
3.2. Quadcopter Parameters
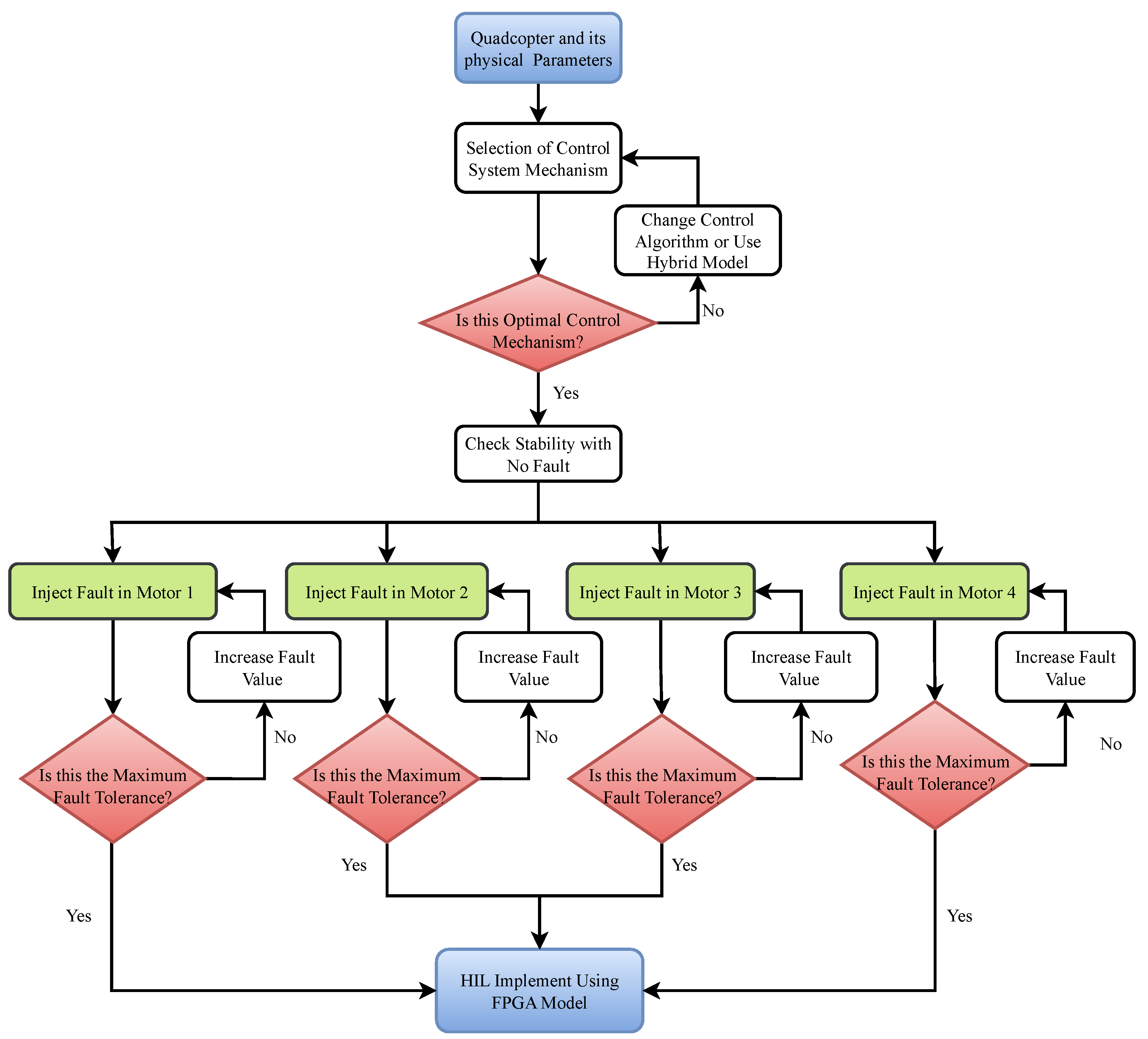
4. Proposed Methodology
4.1. Integral Backstepping-Based Controller for Translational Motion Monitoring and Controlling
4.2. Nonlinear Disturbance Observer Sliding Mode (NLDO-SM)-Based Controller for Rotational Motion Monitoring and Controlling
- Look-up Tables: 31,800;
- Block RAMs used: 26BRAM;
- Number of Flip Flops: 4998;
- Digital signal-processing blocks used: 240.
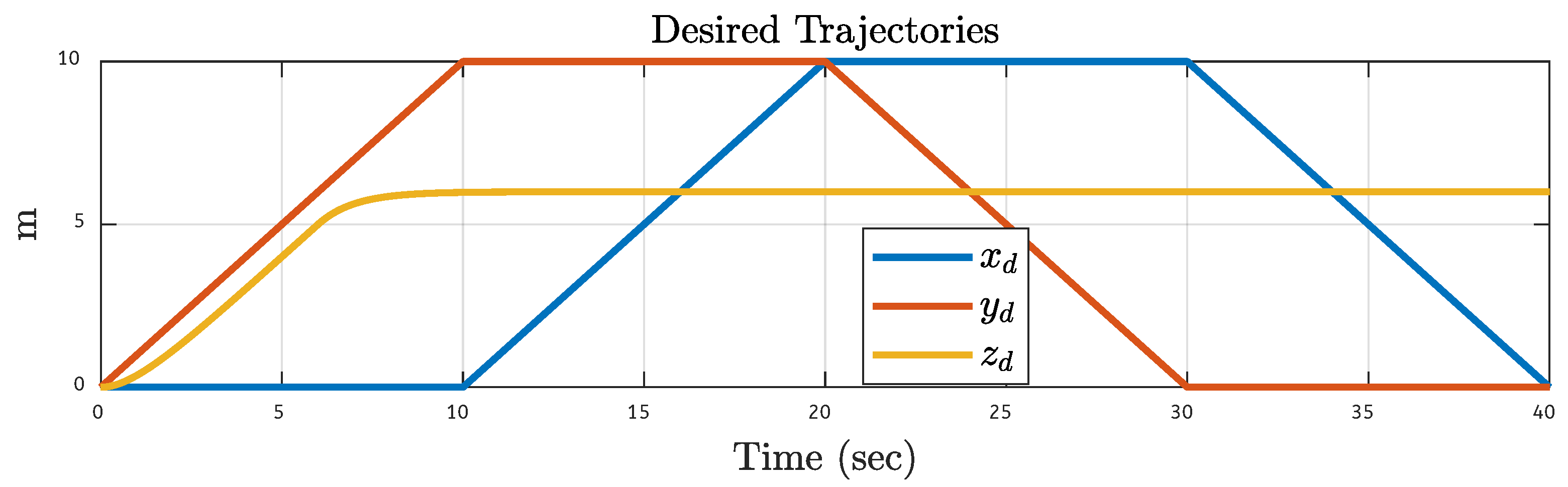
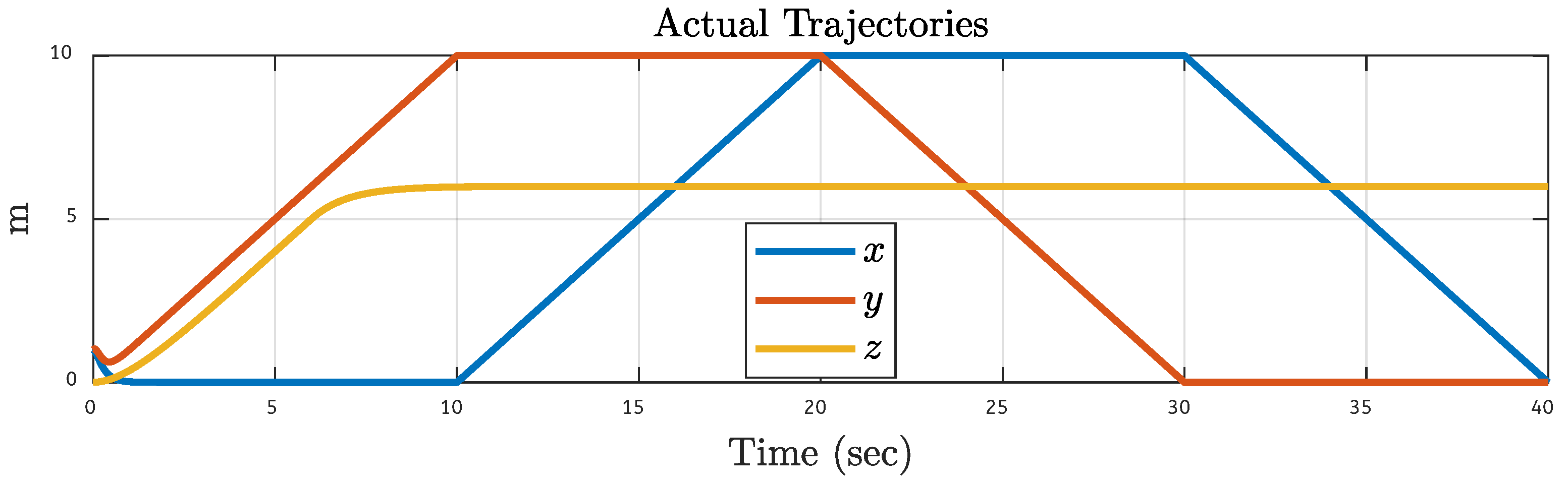
5. Results
5.1. Quadcopter Trajectory Under Various Faults on Motor 1 of the Quadcopter
5.2. Quadcopter Trajectory Under Various Faults on Motor 2 of the Quadcopter
5.3. Quadcopter Trajectory Under Various Faults on Motor 3 of the Quadcopter
5.4. Quadcopter Trajectory Under Various Faults on Motor 4 of the Quadcopter
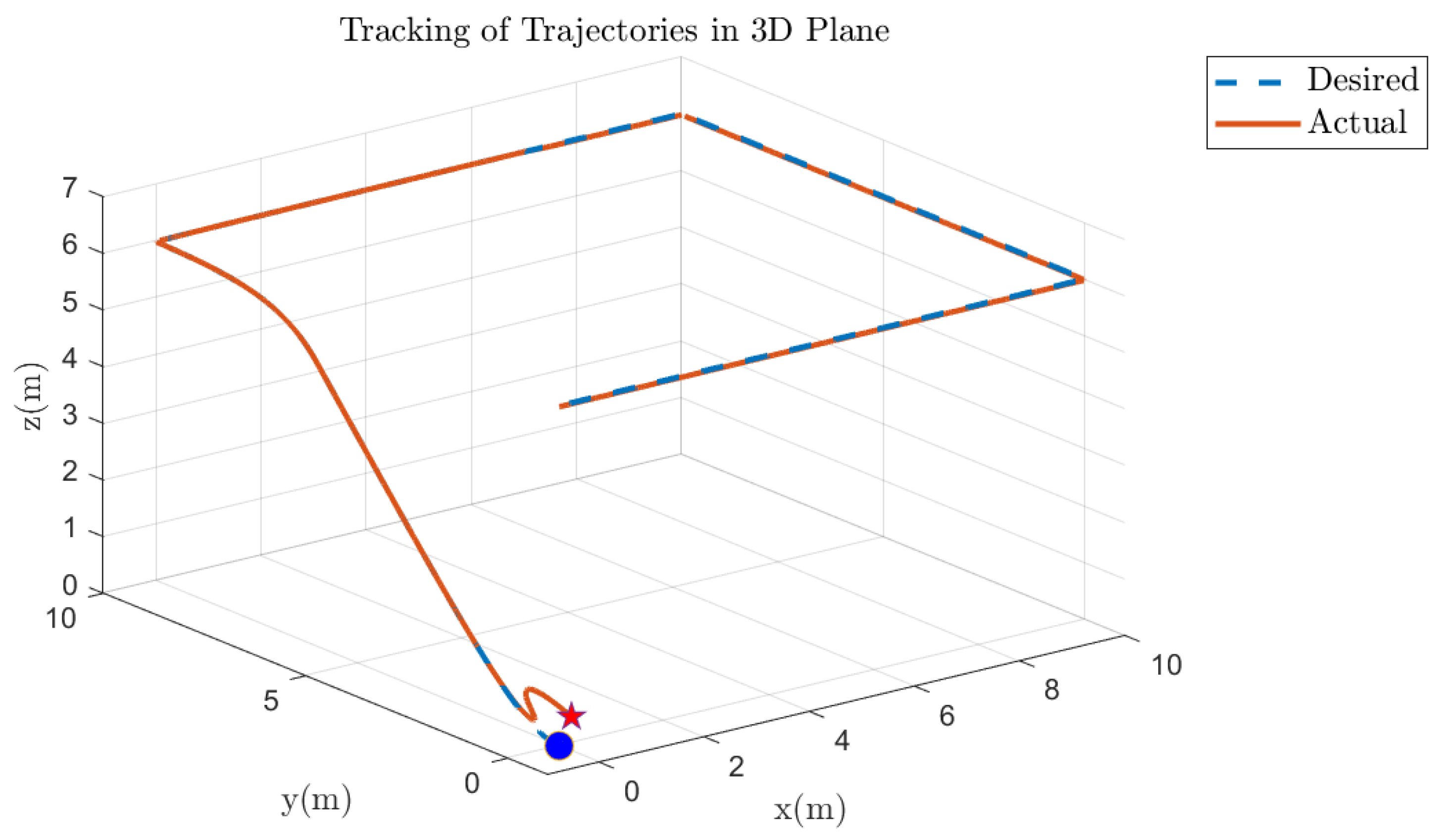
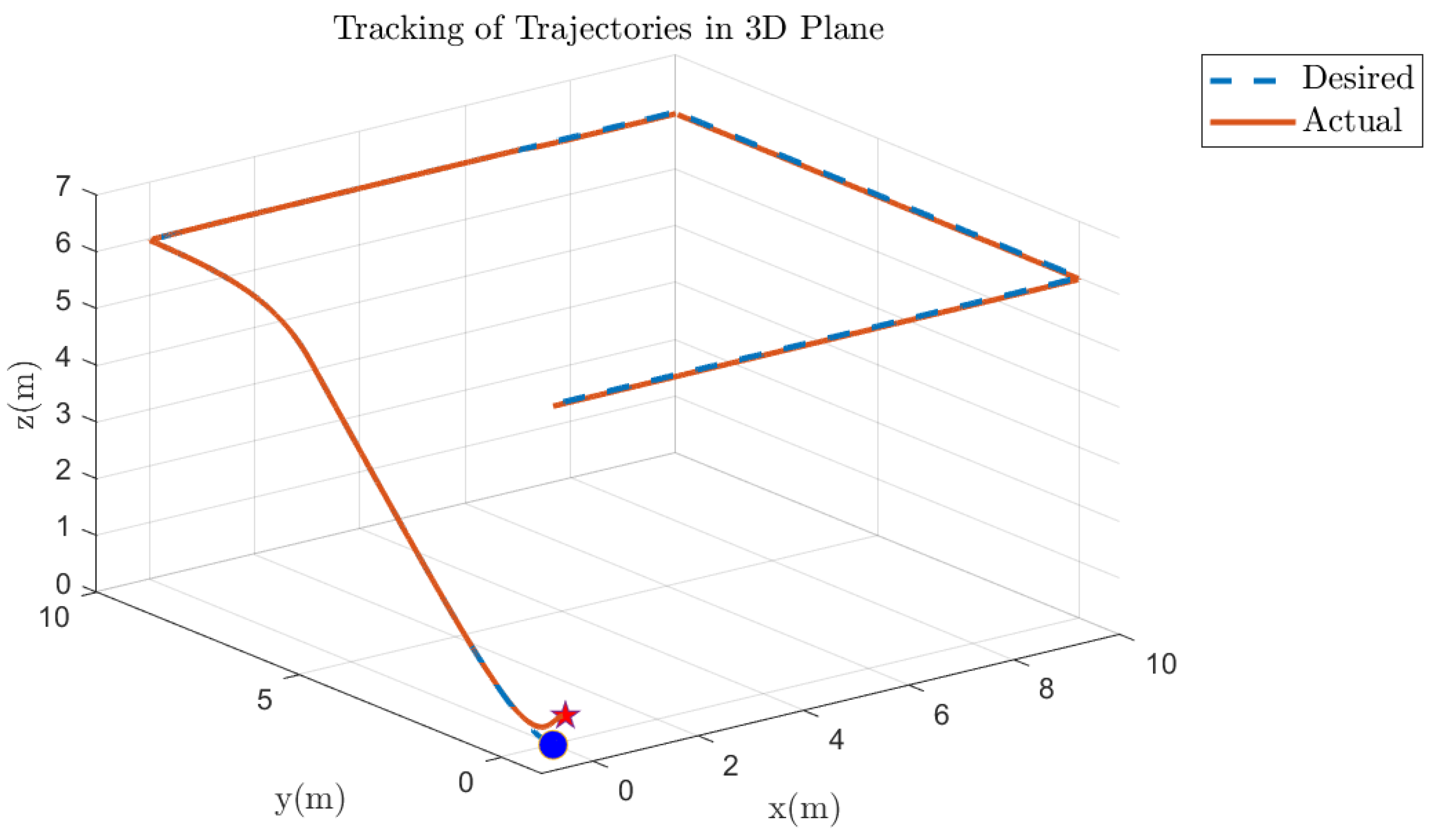
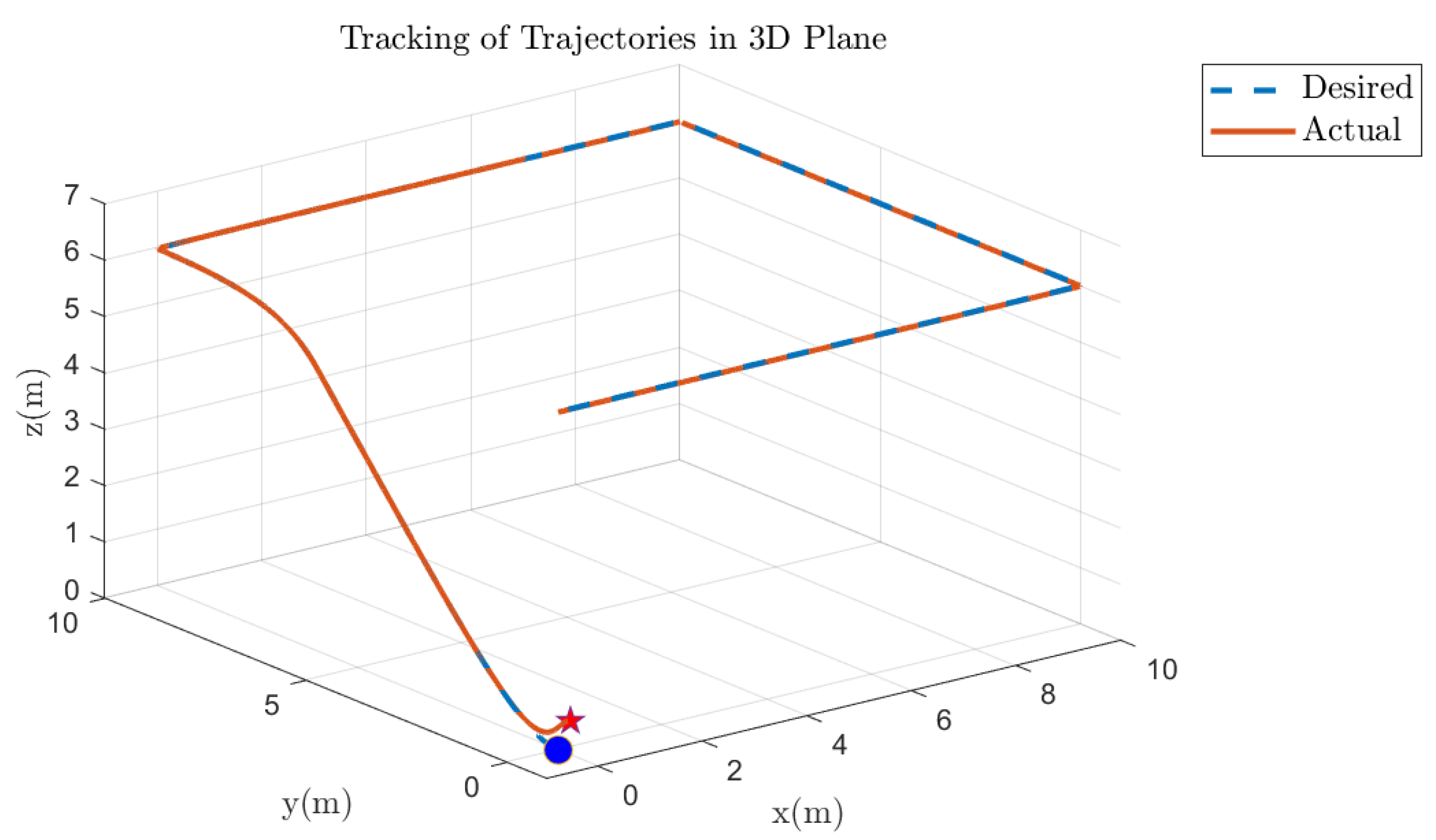
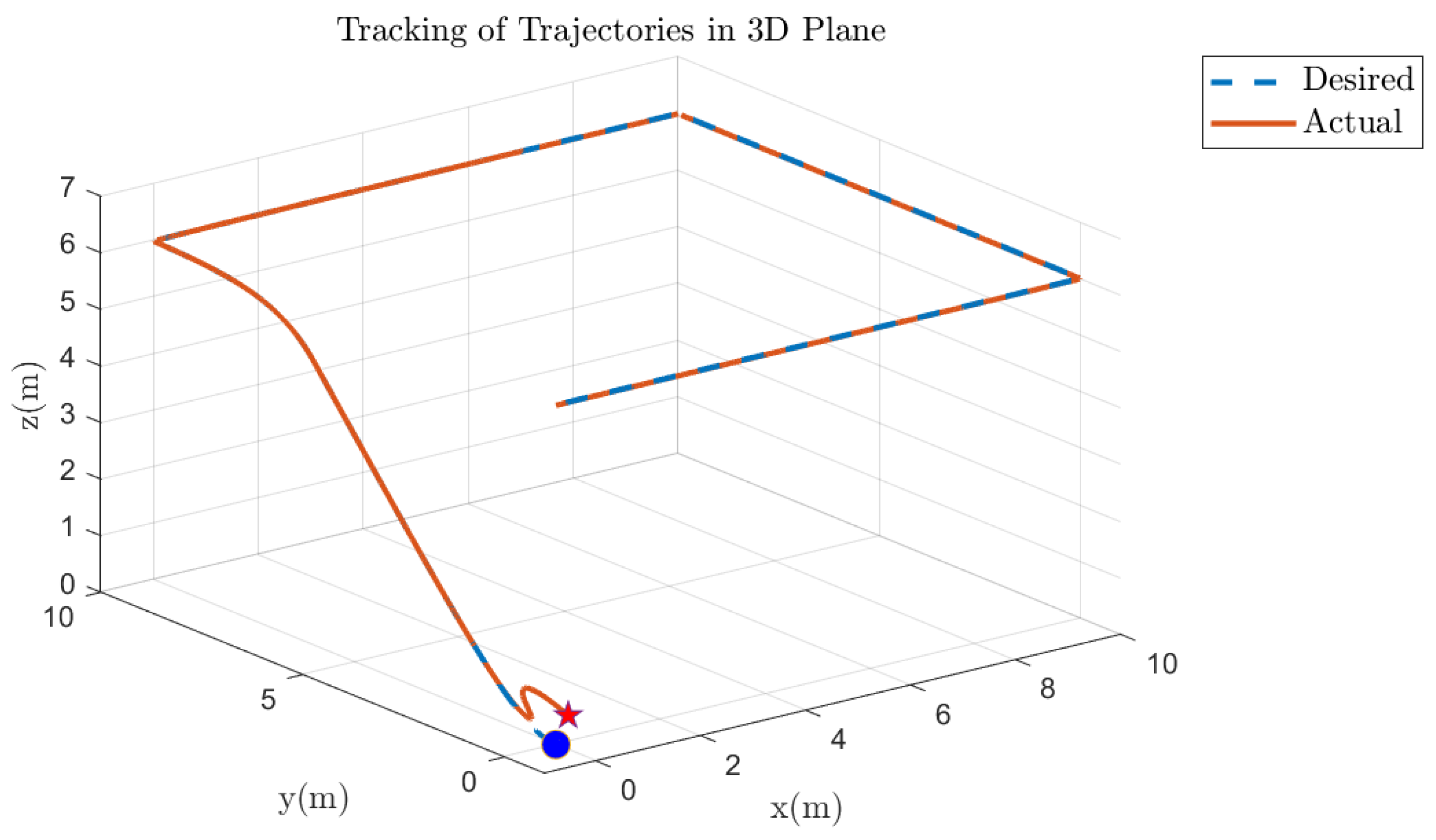
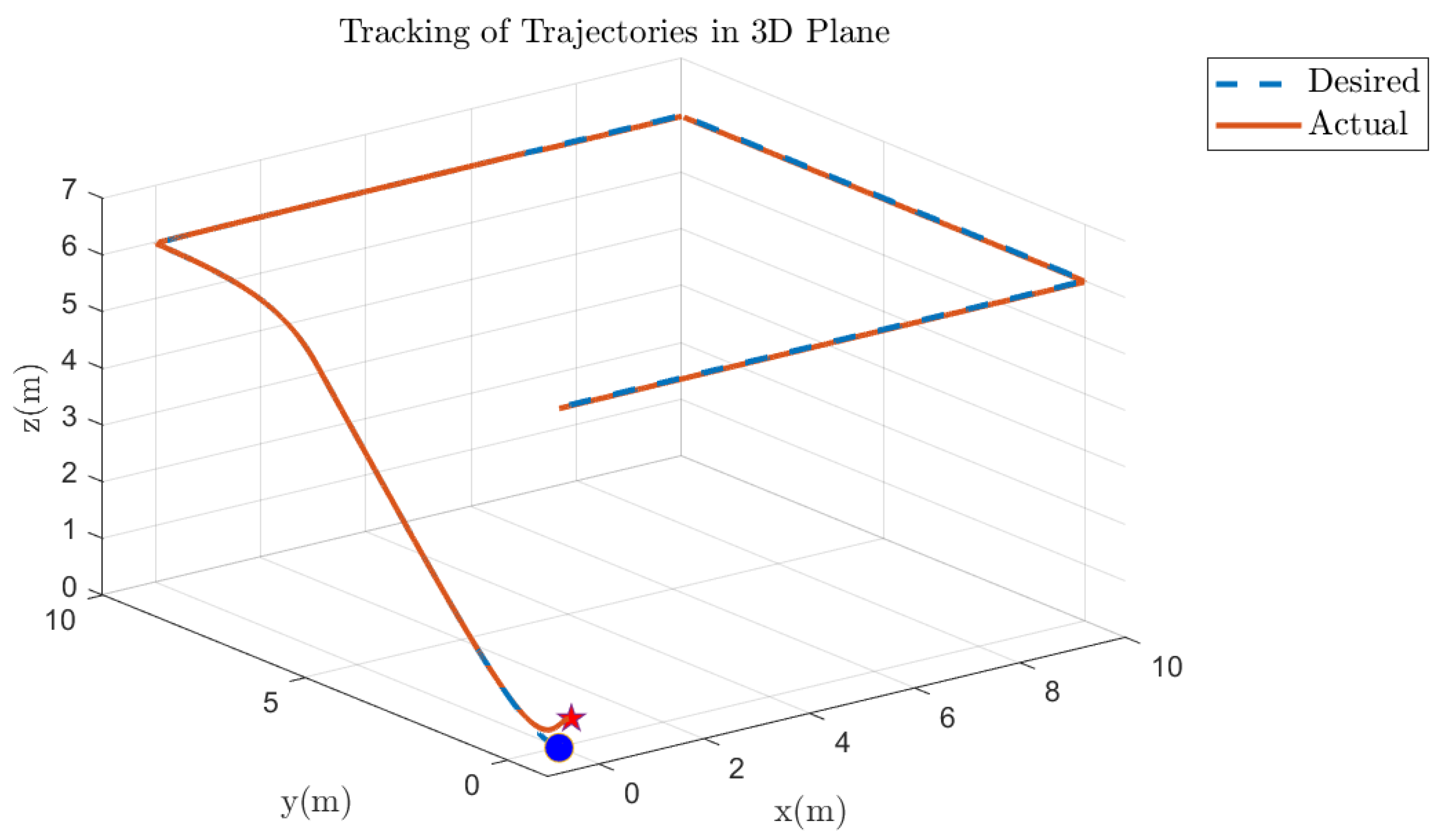
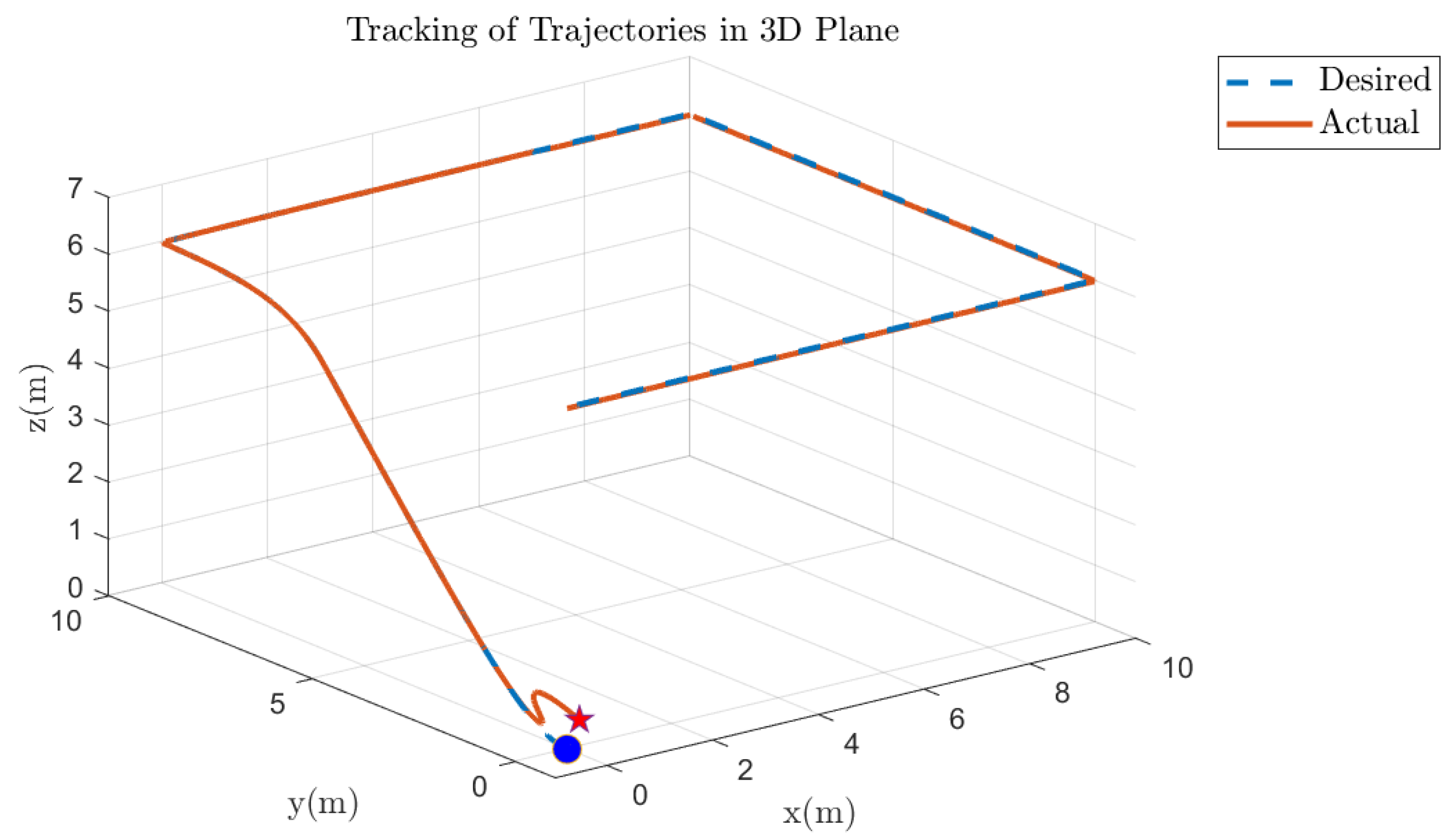
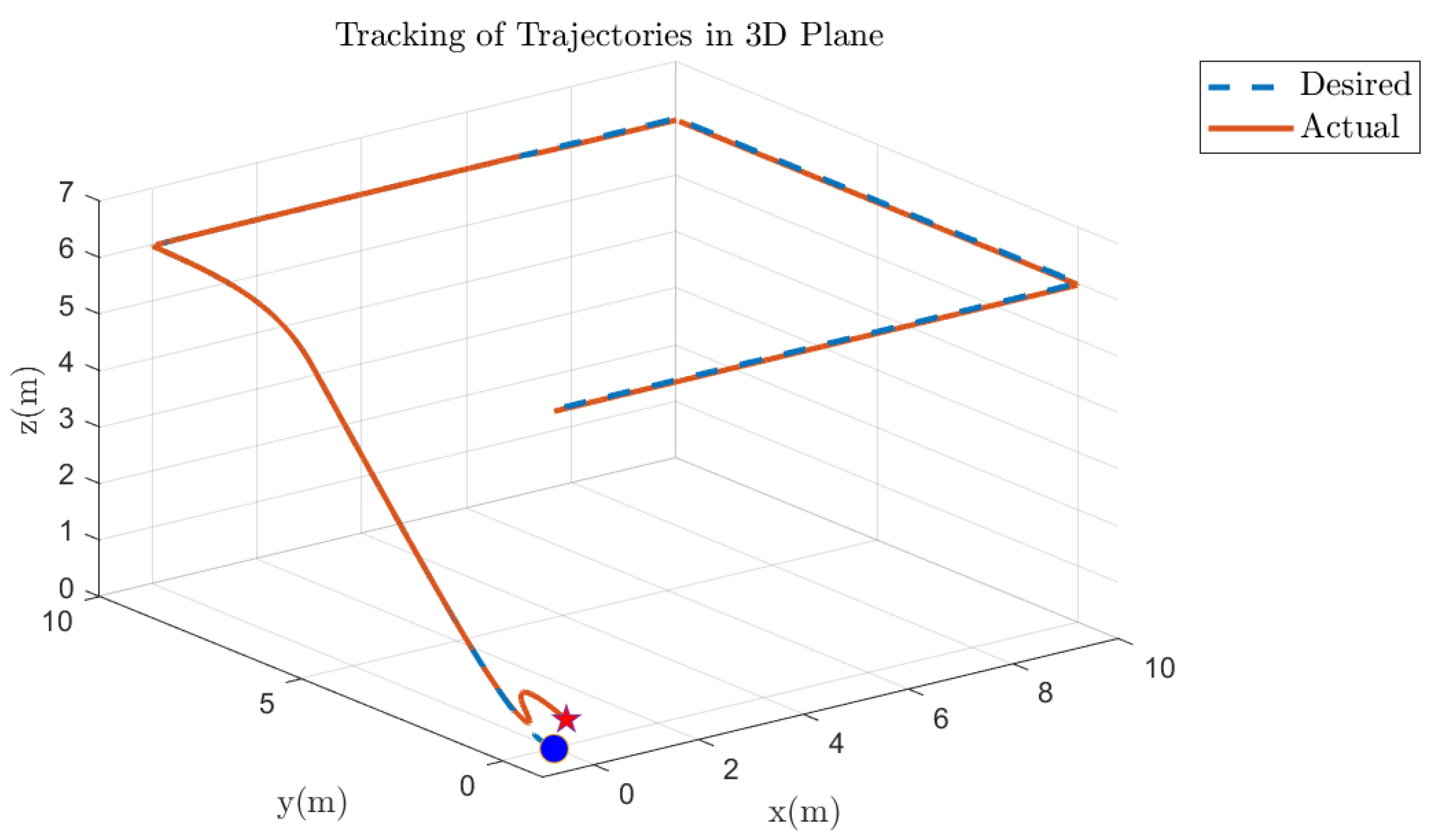
5.5. Quadcopter 3D Track Followed Under Various Faults on Motor 1 of the Quadcopter
5.6. Quadcopter 3D Track Followed Under Various Faults on Other Motors of the Quadcopter
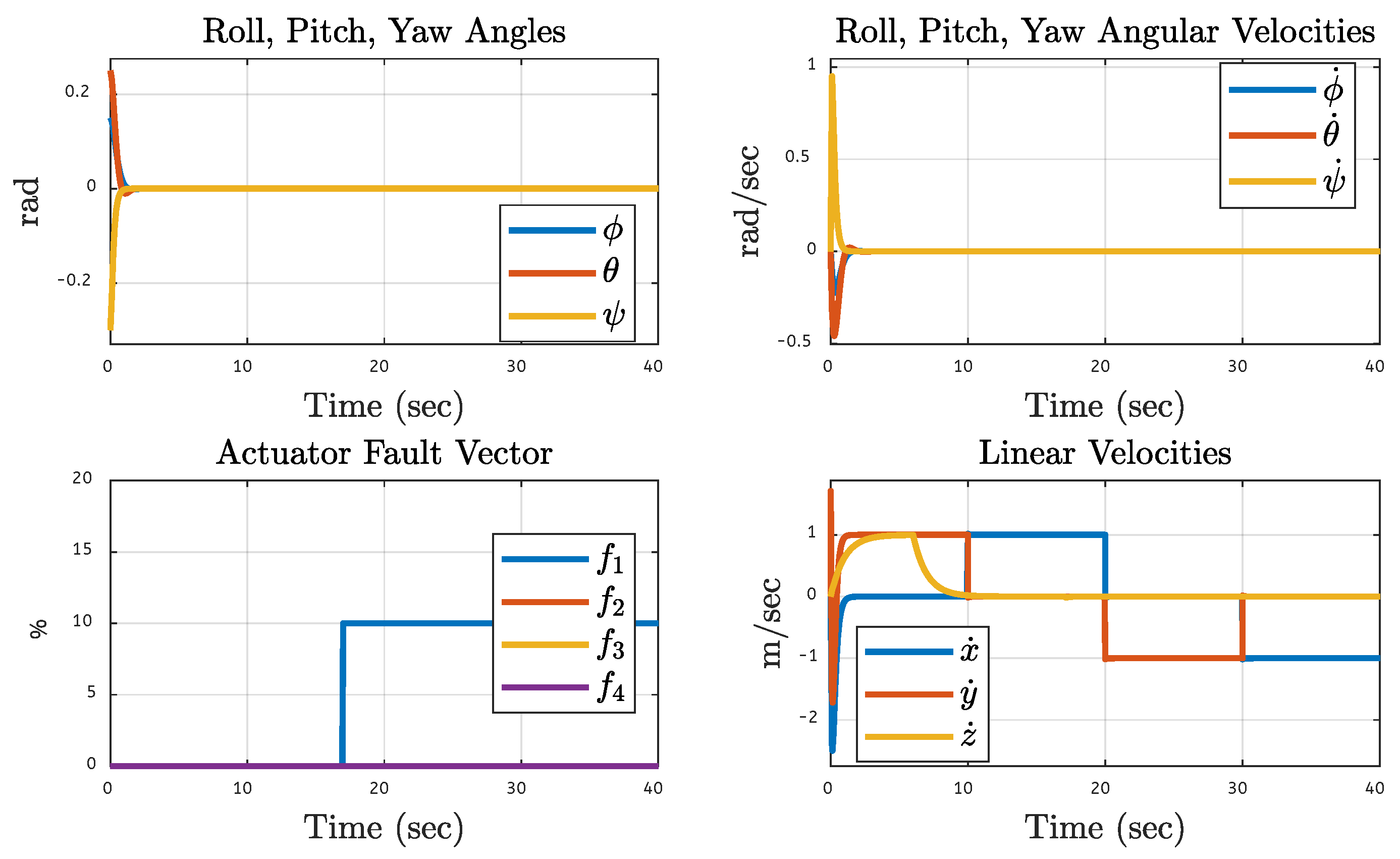
5.7. Quadcopter System Orientation Under Various Faults on the Motor of the Quadcopter
5.8. Quadcopter System Orientation Under Various Faults on the Other Motors of the Quadcopter
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Valianti, P.; Kolios, P.; Ellinas, G. Energy-aware tracking and jamming rogue UAVs using a swarm of pursuer UAV agents. IEEE Syst. J. 2022, 17, 1524–1535. [Google Scholar] [CrossRef]
- Kwon, D.; Son, S.; Kim, M.H.; Lee, J.Y.; Das, A.K.; Park, Y. A Secure Self-Certified Broadcast Authentication Protocol for Intelligent Transportation Systems in UAV-Assisted Mobile Edge Computing Environments. IEEE Trans. Intell. Transp. Syst. 2024, 25, 19004–19017. [Google Scholar] [CrossRef]
- Mukhamediev, R.I.; Yakunin, K.; Aubakirov, M.; Assanov, I.; Kuchin, Y.; Symagulov, A.; Levashenko, V.; Zaitseva, E.; Sokolov, D.; Amirgaliyev, Y. Coverage Path Planning Optimization of Heterogeneous UAVs Group for Precision Agriculture. IEEE Access 2023, 11, 5789–5803. [Google Scholar] [CrossRef]
- Hu, S.; Yuan, X.; Ni, W.; Wang, X.; Jamalipour, A. Visual-Based Moving Target Tracking with Solar-Powered Fixed-Wing UAV: A New Learning-Based Approach. IEEE Trans. Intell. Transp. Syst. 2024, 25, 9115–9129. [Google Scholar] [CrossRef]
- Alhafnawi, M.; Salameh, H.A.B.; Masadeh, A.E.; Al-Obiedollah, H.; Ayyash, M.; El-Khazali, R.; Elgala, H. A Survey of Indoor and Outdoor UAV-Based Target Tracking Systems: Current Status, Challenges, Technologies, and Future Directions. IEEE Access 2023, 11, 68324–68339. [Google Scholar] [CrossRef]
- Song, L.; Wan, N.; Gahlawat, A.; Tao, C.; Hovakimyan, N.; Theodorou, E.A. Generalization of Safe Optimal Control Actions on Networked Multiagent Systems. IEEE Trans. Control Netw. Syst. 2022, 10, 491–502. [Google Scholar] [CrossRef]
- Kusmirek, S.; Socha, V.; Malich, T.; Socha, L.; Hylmar, K.; Hanakova, L. Dynamic Flight Tracking: Designing System for Multirotor UAVs with Pixhawk Autopilot Data Verification. IEEE Access 2024, 12, 109806–109821. [Google Scholar] [CrossRef]
- Zhou, Z.; Liu, Y. A Smart Landing Platform with Data-Driven Analytic Procedures for UAV Preflight Safety Diagnosis. IEEE Access 2021, 9, 154876–154891. [Google Scholar] [CrossRef]
- Ventura, J.O.; Morales, D.B.; Oliver, J.P.O.; Quesada, E.S.E. Dynamic Sliding Mode Control with PID Surface for Trajectory Tracking of a Multirotor Aircraft. IEEE Access 2023, 11, 99878–99888. [Google Scholar] [CrossRef]
- Liu, B.; Wang, Y.; Mofid, O.; Mobayen, S.; Khooban, M.H. Barrier Function-Based Backstepping Fractional-Order Sliding Mode Control for Quad-Rotor Unmanned Aerial Vehicle under External Disturbances. IEEE Trans. Aerosp. Electron. Syst. 2023, 60, 716–728. [Google Scholar] [CrossRef]
- Xu, L.X.; Wang, Y.L.; Wang, X.; Peng, C. Distributed Active Disturbance Rejection Formation Tracking Control for Quadrotor UAVs. IEEE Trans. Cybern. 2023, 54, 4678–4689. [Google Scholar] [CrossRef]
- Gai, W.; Zhou, Y.; Zhong, M.; Sheng, C.; Zhang, J. Simple Adaptive Control with an Adaptive Anti-Windup Compensator for the Unmanned Aerial Vehicle Attitude Control. IEEE Access 2020, 8, 52323–52332. [Google Scholar] [CrossRef]
- Chen, B.-S.; Hung, T.-W. Integrating Local Motion Planning and Robust Decentralized Fault-Tolerant Tracking Control for Search and Rescue Task of Hybrid UAVs and Biped Robots Team System. IEEE Access 2023, 11, 45888–45909. [Google Scholar] [CrossRef]
- Nguyen, D.-T.; Saussie, D.; Saydy, L. Design and experimental validation of robust self-scheduled fault-tolerant control laws for a multicopter UAV. IEEE/ASME Trans. Mechatronics 2020, 26, 2548–2557. [Google Scholar] [CrossRef]
- Avram, R.C.; Zhang, X.; Muse, J. Nonlinear adaptive fault-tolerant quadrotor altitude and attitude tracking with multiple actuator faults. IEEE Trans. Control Syst. Technol. 2017, 26, 701–707. [Google Scholar] [CrossRef]
- Yu, Z.; Zhang, Y.; Jiang, B. PID-type fault-tolerant prescribed performance control of fixed-wing UAV. J. Syst. Eng. Electron. 2021, 32, 1053–1061. [Google Scholar]
- Mofid, O.; Mobayen, S.; Wong, W.-K. Adaptive terminal sliding mode control for attitude and position tracking control of quadrotor UAVs in the existence of external disturbance. IEEE Access 2020, 9, 3428–3440. [Google Scholar] [CrossRef]
- Cohen, M.R.; Abdulrahim, K.; Forbes, J.R. Finite-horizon LQR control of quadrotors on SE2(3). IEEE Robot. Autom. Lett. 2020, 5, 5748–5755. [Google Scholar] [CrossRef]
- Aliyari, M.; Wong, W.-K.; Bouteraa, Y.; Najafinia, S.; Fekih, A.; Mobayen, S. Design and implementation of a constrained model predictive control approach for unmanned aerial vehicles. IEEE Access 2022, 10, 91750–91762. [Google Scholar] [CrossRef]
- Gu, J.; Sun, R.; Chen, J. Improved back-stepping control for nonlinear small UAV systems with transient prescribed performance design. IEEE Access 2021, 9, 128786–128798. [Google Scholar] [CrossRef]
- Du, Y.; Huang, P.; Cheng, Y.; Fan, Y.; Yuan, Y. Fault tolerant control of a quadrotor unmanned aerial vehicle based on active disturbance rejection control and two-stage Kalman filter. IEEE Access 2023, 11, 67556–67566. [Google Scholar] [CrossRef]
- Zou, Y.; Xia, K. Robust fault-tolerant control for underactuated takeoff and landing UAVs. IEEE Trans. Aerosp. Electron. Syst. 2020, 56, 3545–3555. [Google Scholar] [CrossRef]
- Ortiz-Torres, G.; Castillo, P.; Sorcia-Vázquez, F.D.; Rumbo-Morales, J.Y.; Brizuela-Mendoza, J.A.; De La Cruz-Soto, J.; Martínez-García, M. Fault estimation and fault tolerant control strategies applied to VTOL aerial vehicles with soft and aggressive actuator faults. IEEE Access 2020, 8, 10649–10661. [Google Scholar] [CrossRef]
- Lee, D.; Park, H.J.; Lee, D.; Lee, S.; Choi, J.-H. A Novel Kalman Filter-Based Prognostics Framework for Performance Degradation of Quadcopter Motors. IEEE Trans. Instrum. Meas. 2023, 73, 3501312. [Google Scholar] [CrossRef]
- Freire, V.; Xu, X. Flatness-Based Quadcopter Trajectory Planning and Tracking with Continuous-Time Safety Guarantees. IEEE Trans. Control Syst. Technol. 2023, 31, 2319–2334. [Google Scholar] [CrossRef]
- Miloš, M.; Mirosavljević, P. Analysis of the Performance and Kinematics of the Movement of UAV. FME Trans. 2023, 51, 627–636. [Google Scholar] [CrossRef]
- Ullah, S. Design a Nonlinear Controller for a Quadcopter. Ph.D. Thesis, COMSATS Institute of Information Technology, Chak Shahzad, Pakistan, 2016. [Google Scholar]
- Su, Y.; Yu, P.; Gerber, M.J.; Ruan, L.; Tsao, T.C. Fault-Tolerant Control of an Overactuated UAV Platform Built on Quadcopters and Passive Hinges. IEEE/ASME Trans. Mechatronics 2023, 29, 602–613. [Google Scholar] [CrossRef]
- Bao, C.; Guo, Y.; Luo, L.; Su, G. Design of a Fixed-Wing UAV Controller Based on Adaptive Backstepping Sliding Mode Control Method. IEEE Access 2021, 9, 157825–157841. [Google Scholar] [CrossRef]
- Gaufan, K.S.B.; El-Ferik, S.; Alyazidi, N.M. Fractional Model-Based Formation Control of Quad-Rotor UAVs Using Sliding Mode Backstepping. IEEE Access 2024, 12, 166460–166473. [Google Scholar] [CrossRef]
- Esmail, M.S.; Merzban, M.H.; Khalaf, A.A.; Hamed, H.F.; Hussein, A.I. Attitude and Altitude Tracking Controller for Quadcopter Dynamical Systems. IEEE Access 2022, 10, 53344–53358. [Google Scholar] [CrossRef]
- Gavgani, A.K.; Talaeizadeh, A.; Heidarzadeh, S.; Alasty, A.; Pishkenari, H.N. Dynamic Modeling and Sliding Mode Control of an Over-Actuated Quadrotor with Variable Hedral Angle of Propeller Axes. In Proceedings of the 2024 2nd International Conference on Unmanned Vehicle Systems-Oman (UVS), Muscat, Oman, 12–14 February 2024; IEEE: Piscataway, NJ, USA, 2024; pp. 1–6. [Google Scholar]
- Liu, Y.; Wang, H.; Liu, B.; Chen, L.; Wang, Y.; Chen, H. Learning-Based Compound Docking Control for UAV Aerial Recovery: Methodology and Implementation. IEEE/ASME Trans. Mechatronics 2022, 28, 1706–1717. [Google Scholar] [CrossRef]
- Huang, J.; Ma, X.; Wang, B.; Zhang, Y.; Xin, G.; Zhang, Y. Trajectory Tracking Control of a Quadrotor UAV by Cascaded Inner-Outer-Loop Backstepping Sliding Mode Control. In Proceedings of the 2022 34th Chinese Control and Decision Conference (CCDC), Hefei, China, 15–17 August 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 4725–4730. [Google Scholar]
- Chen, X. Terminal Sliding Mode Controller Design Based on Barrier for UAVs With Mismatched Disturbances. IEEE Access 2024, 12, 137942–137951. [Google Scholar] [CrossRef]
- Gai, W.; Song, H.; Zhang, G.; Jing, G. An Automatic Collision Avoidance with Disturbance Interval Observer for Unmanned Aerial Vehicle. In Proceedings of the 2023 2nd Conference on Fully Actuated System Theory and Applications (CFASTA), Qingdao, China, 14–16 July 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 1085–1090. [Google Scholar]



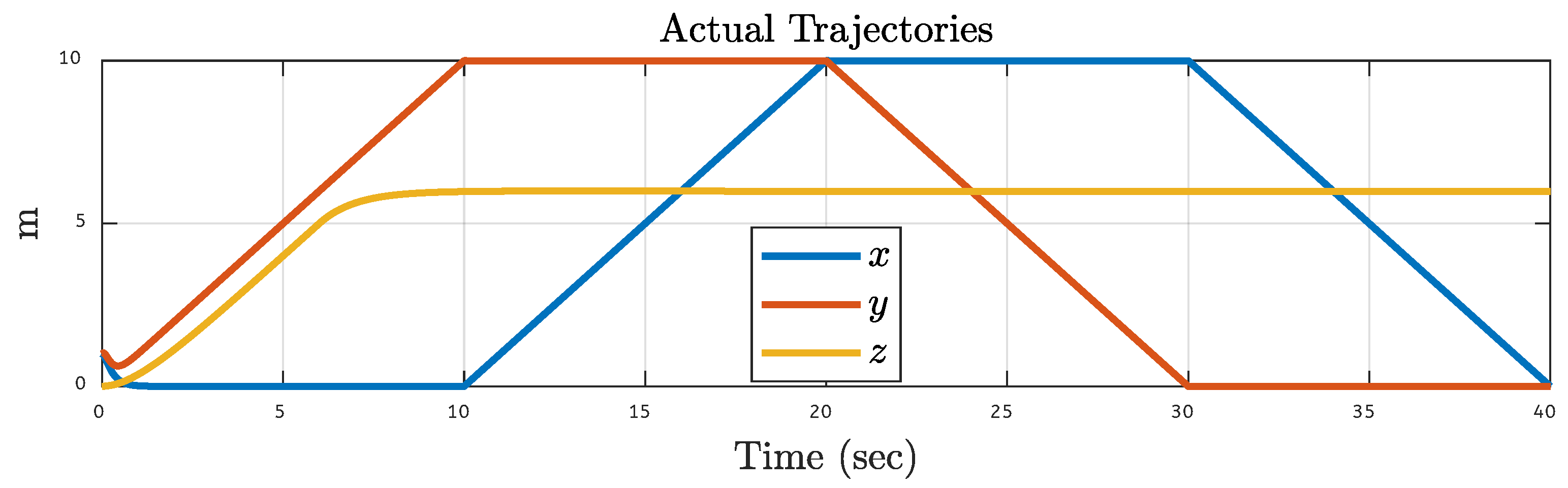
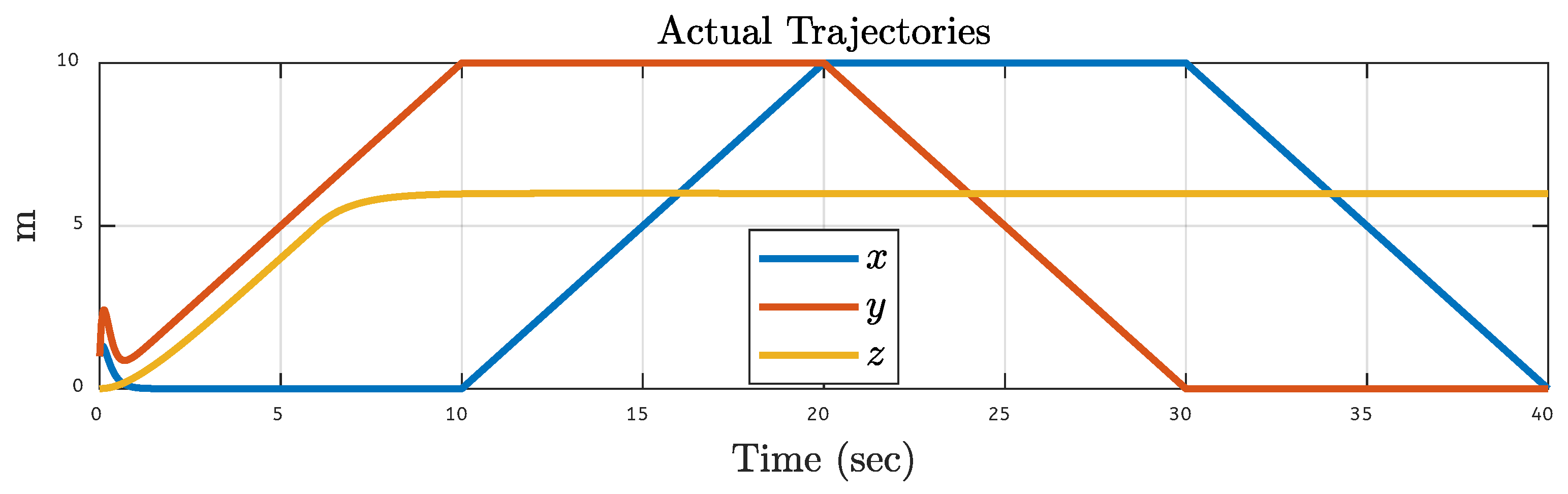

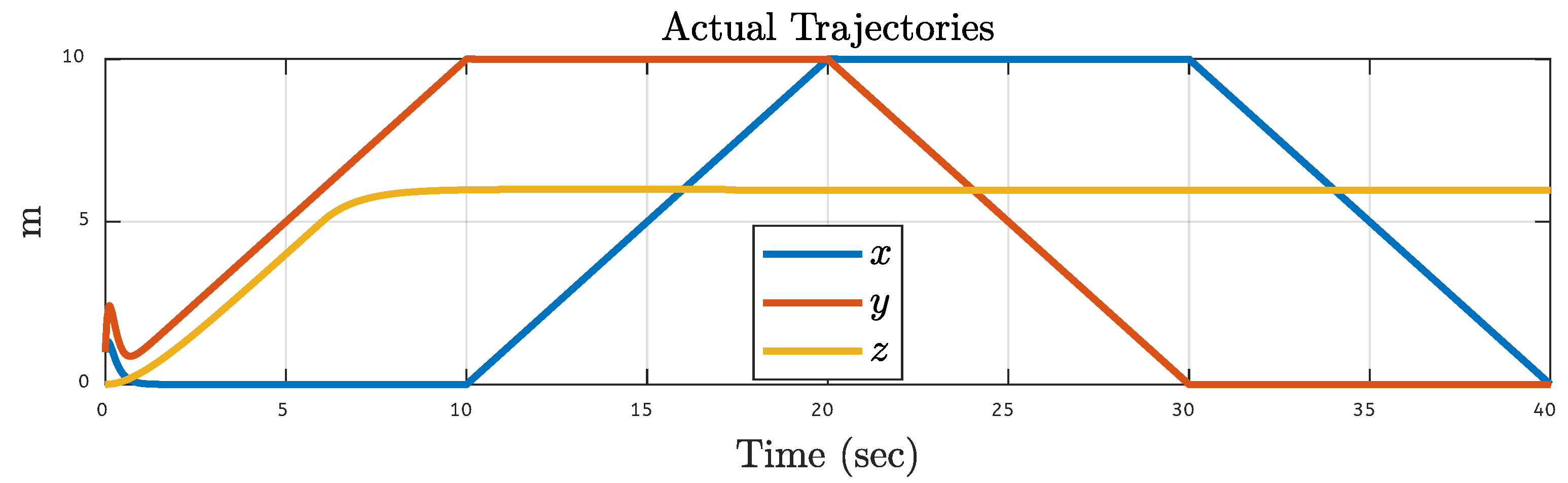
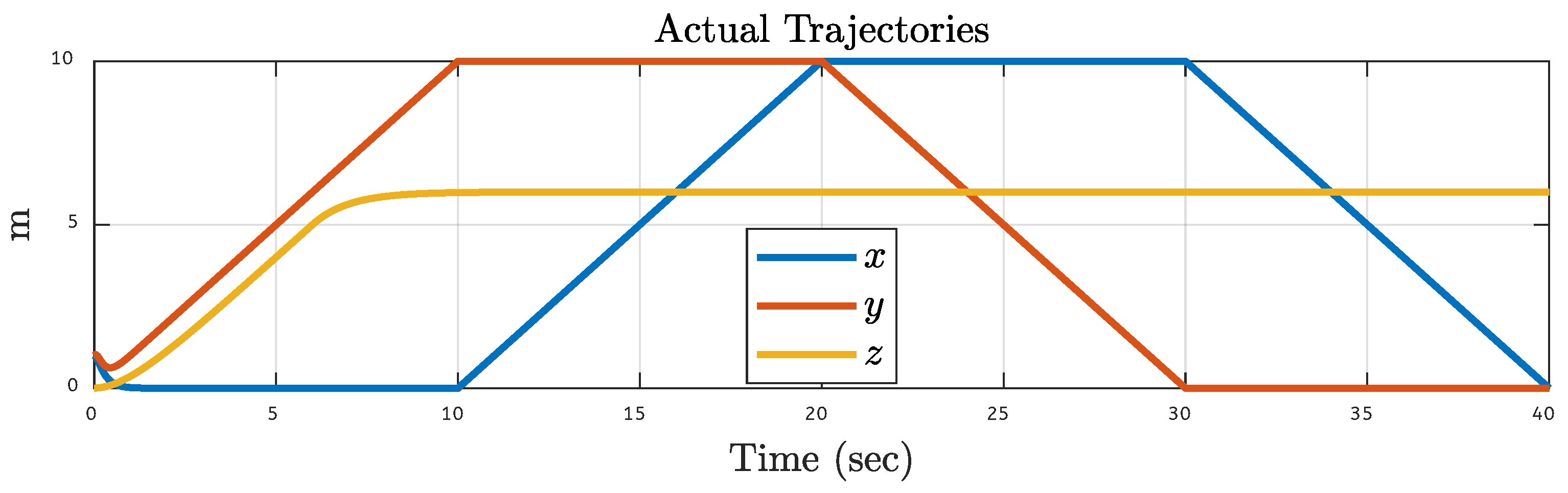
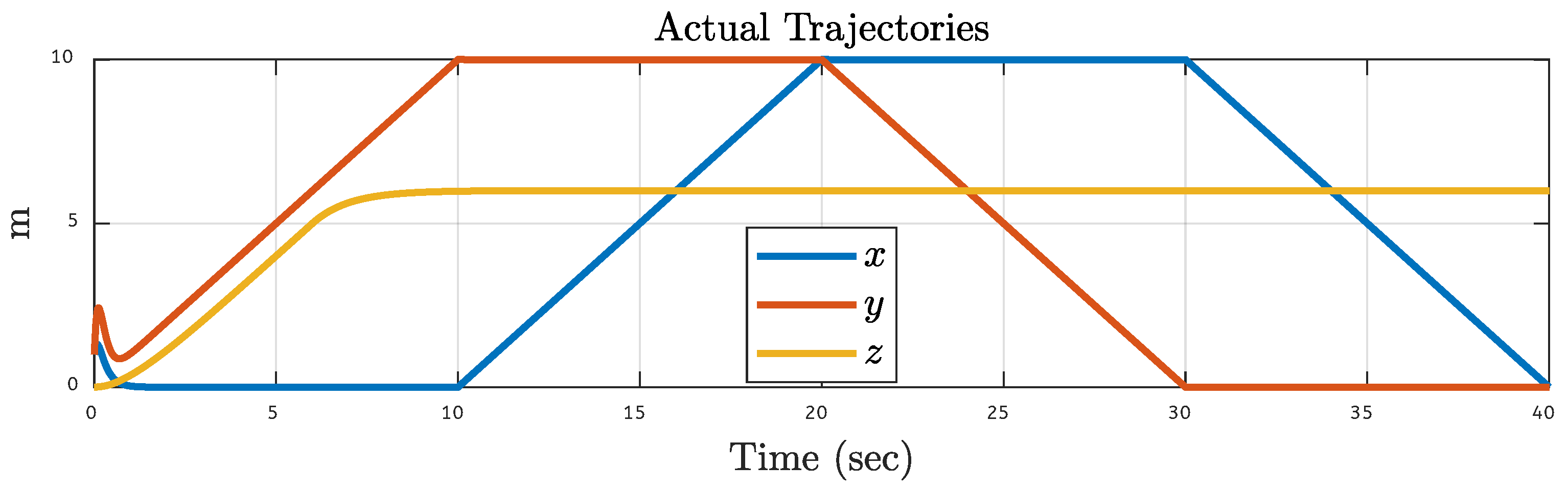
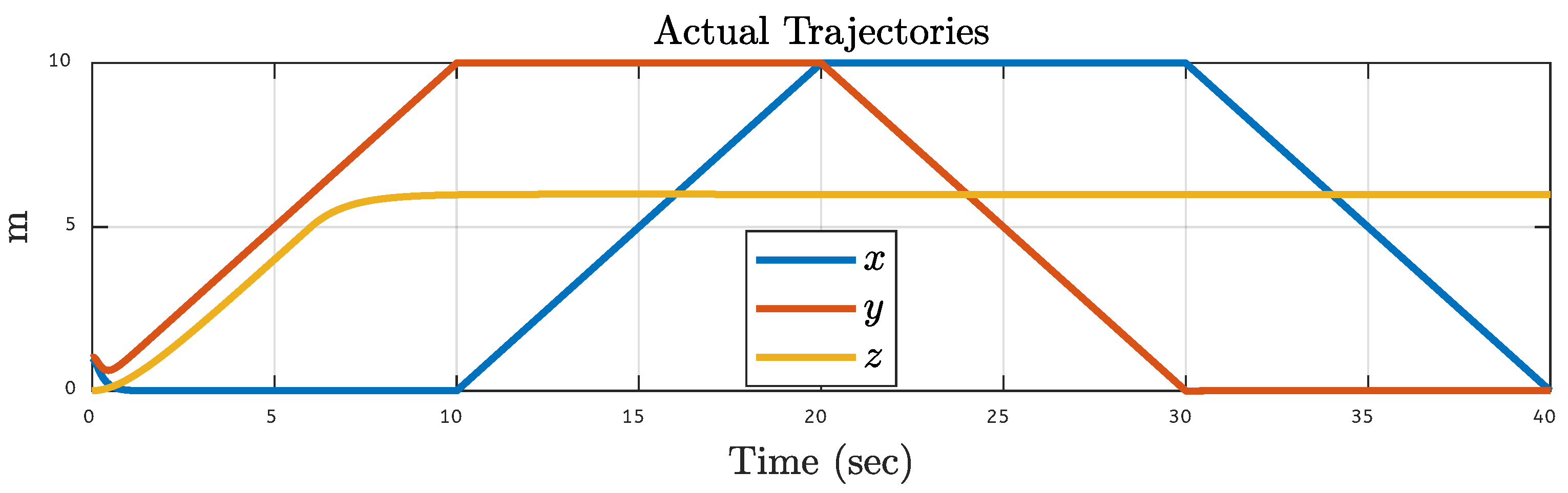
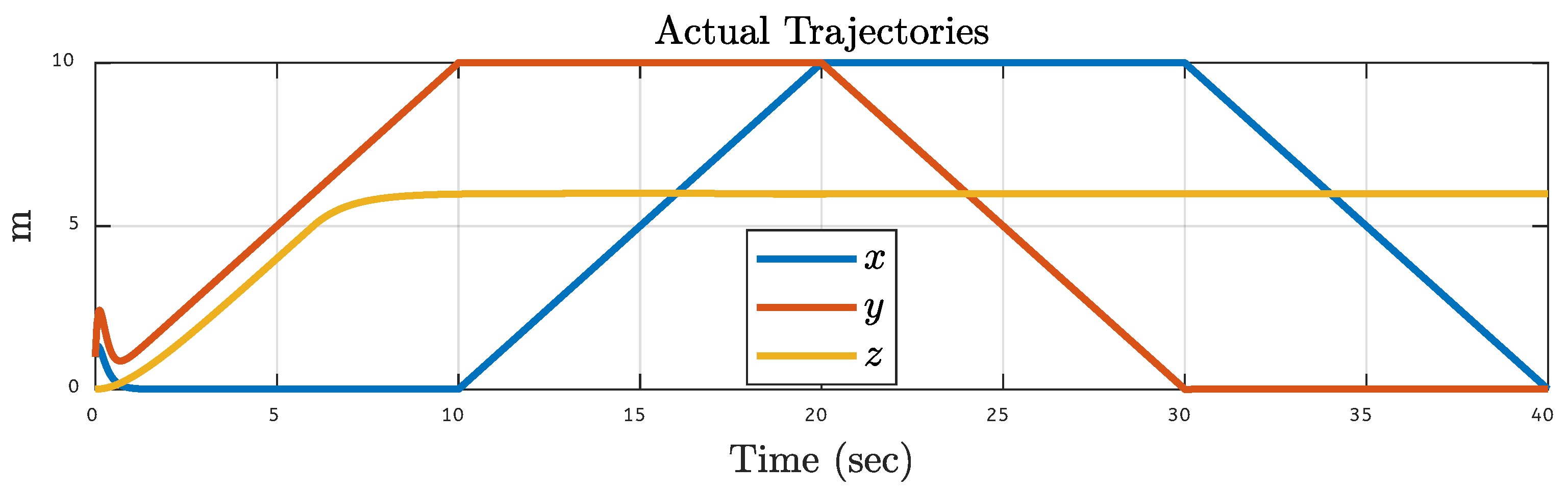
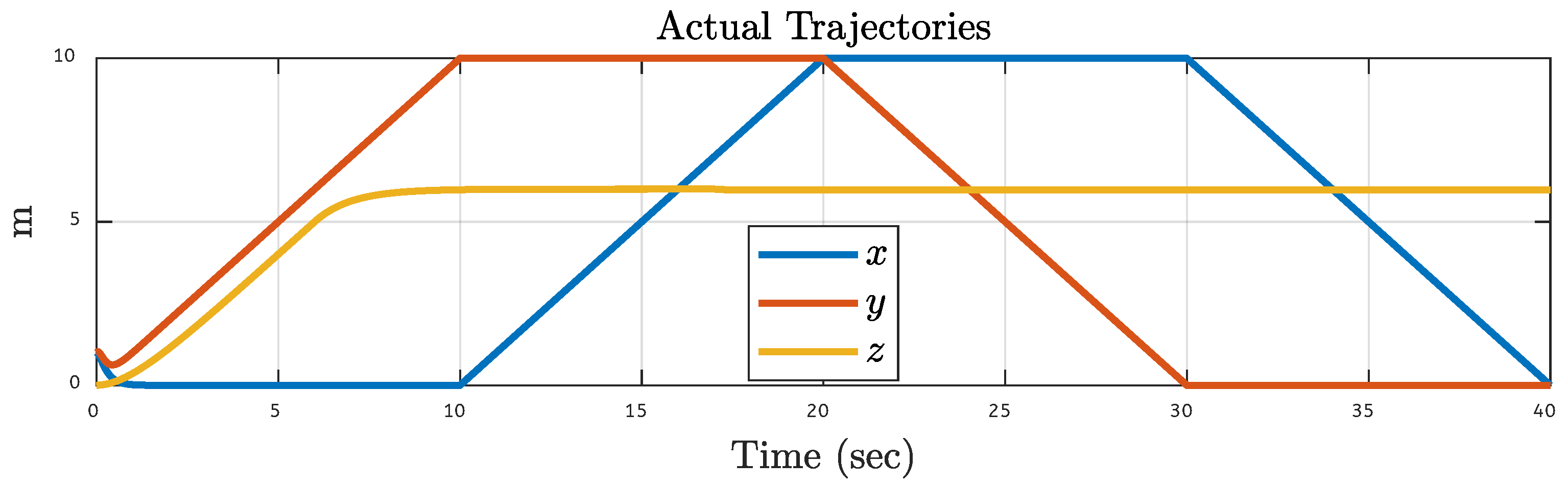
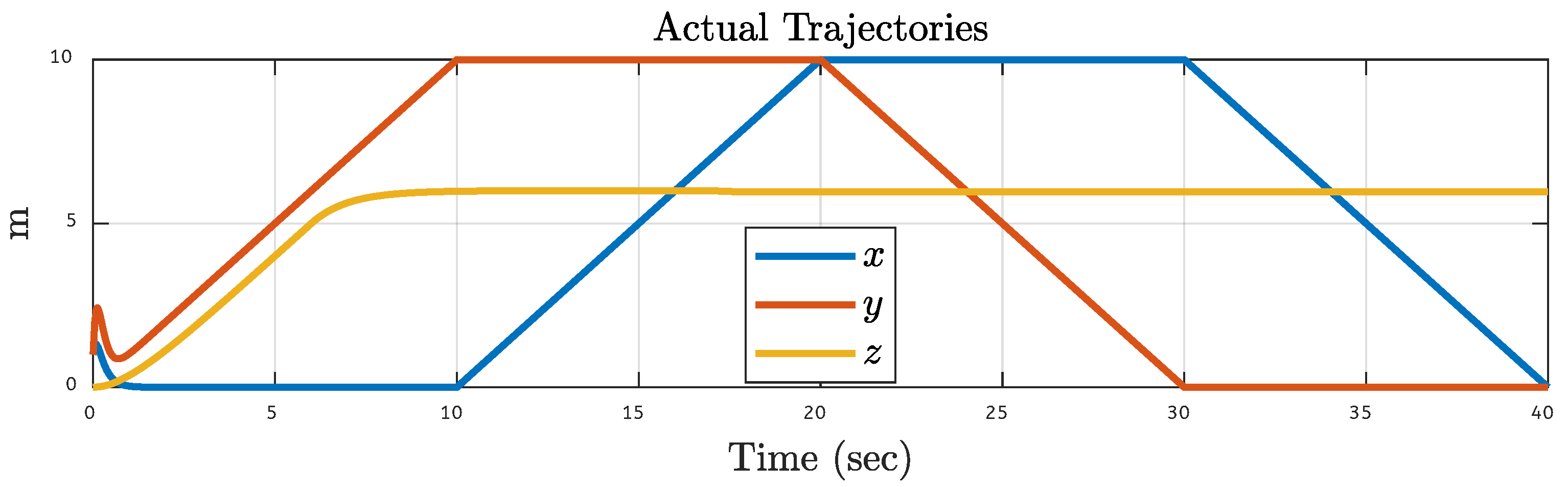

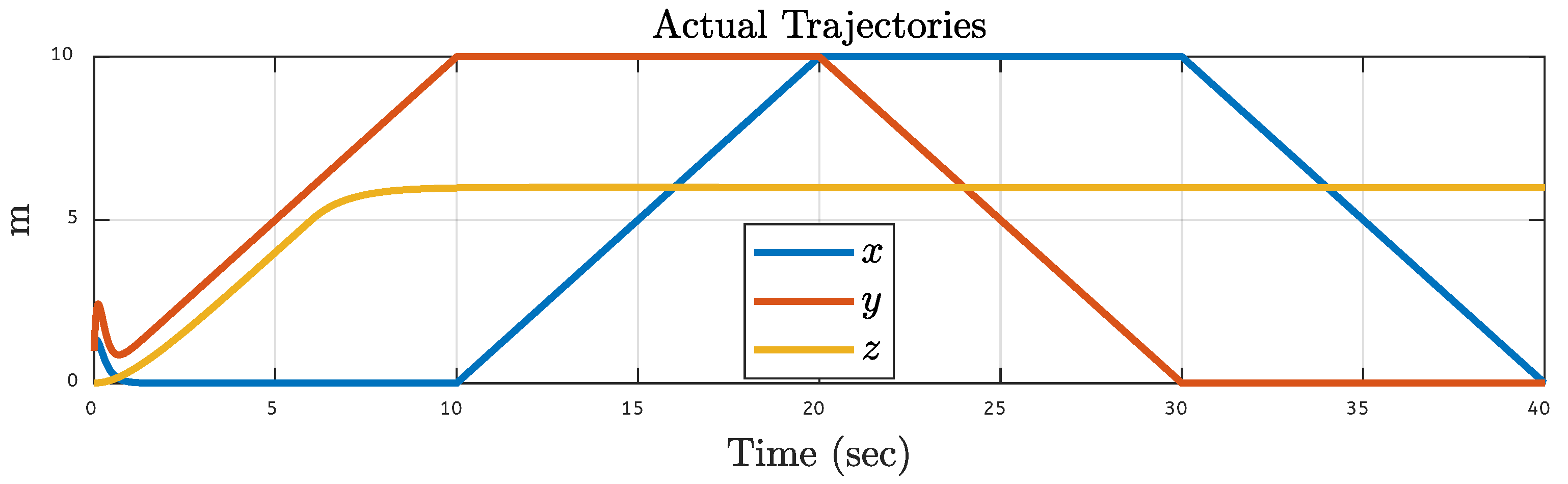
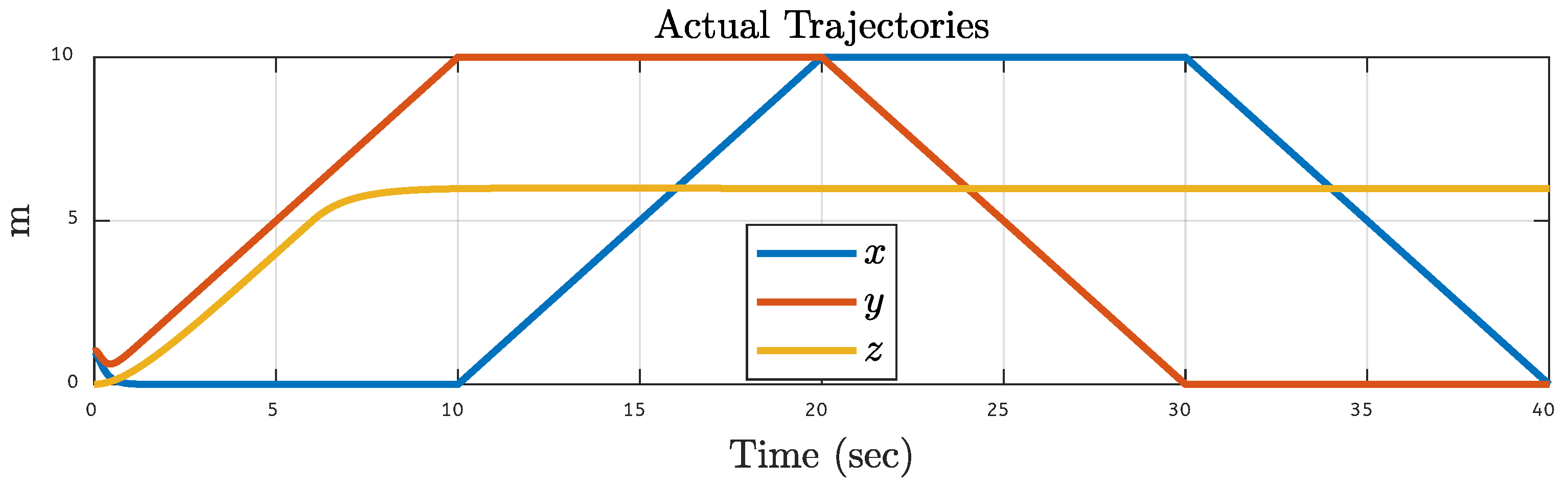
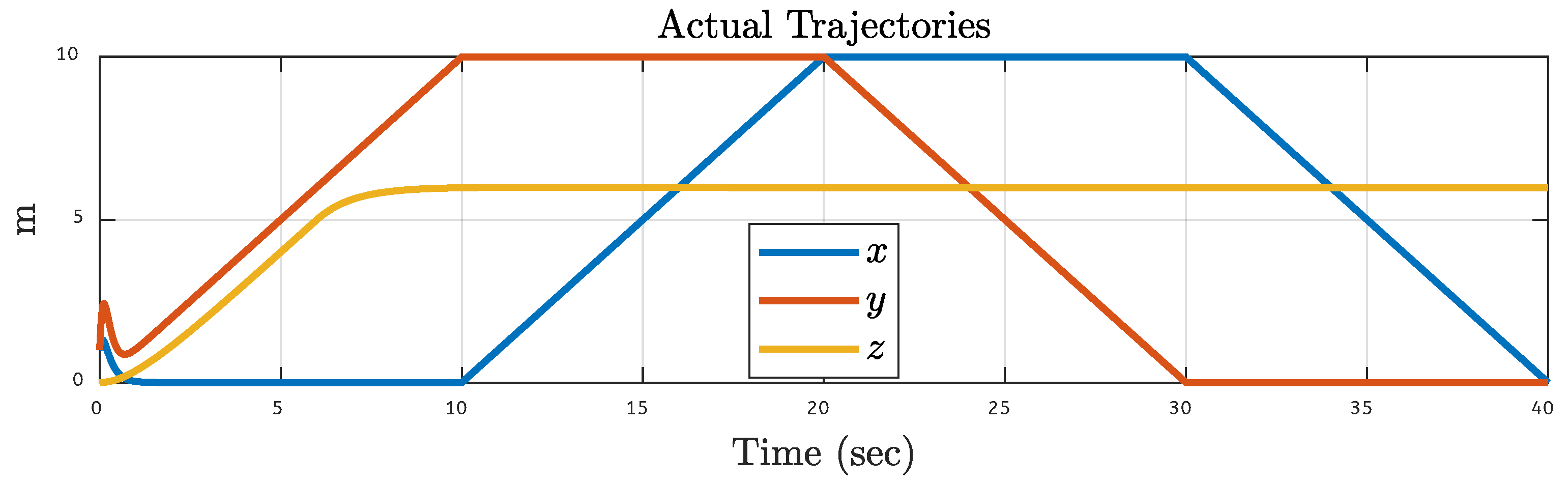
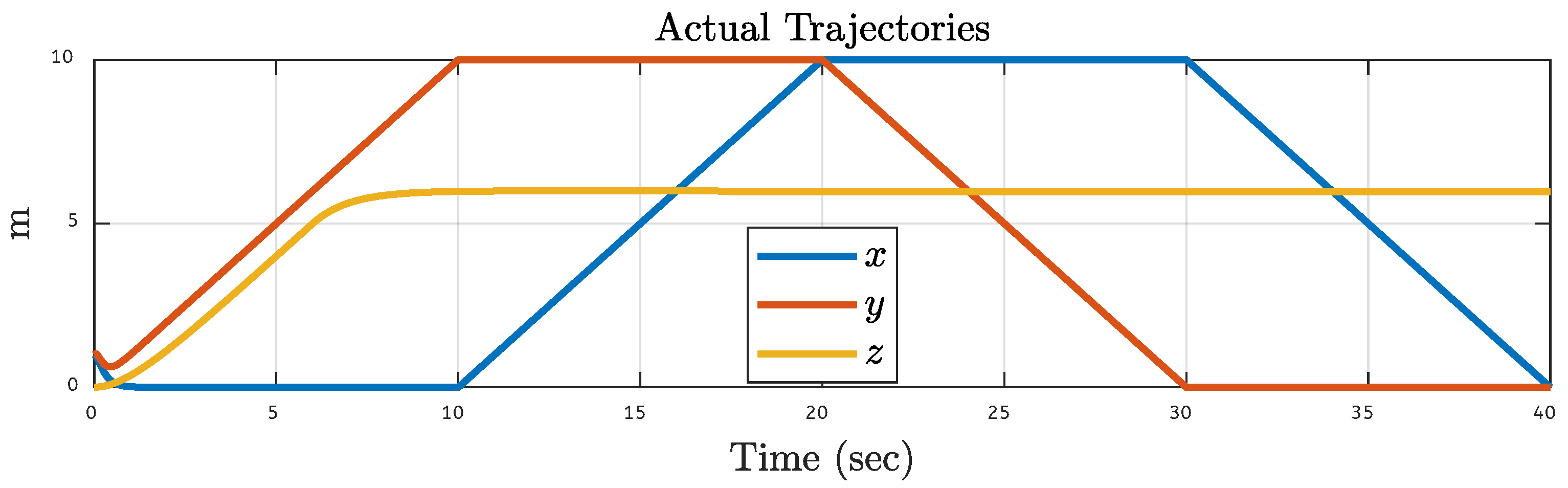
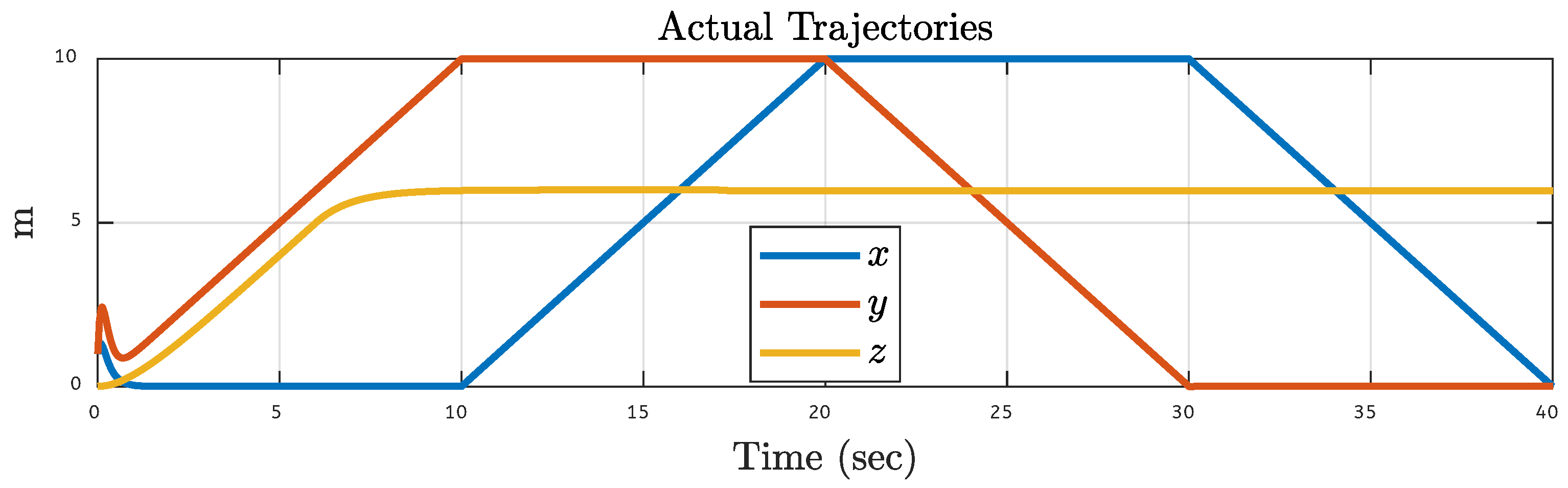
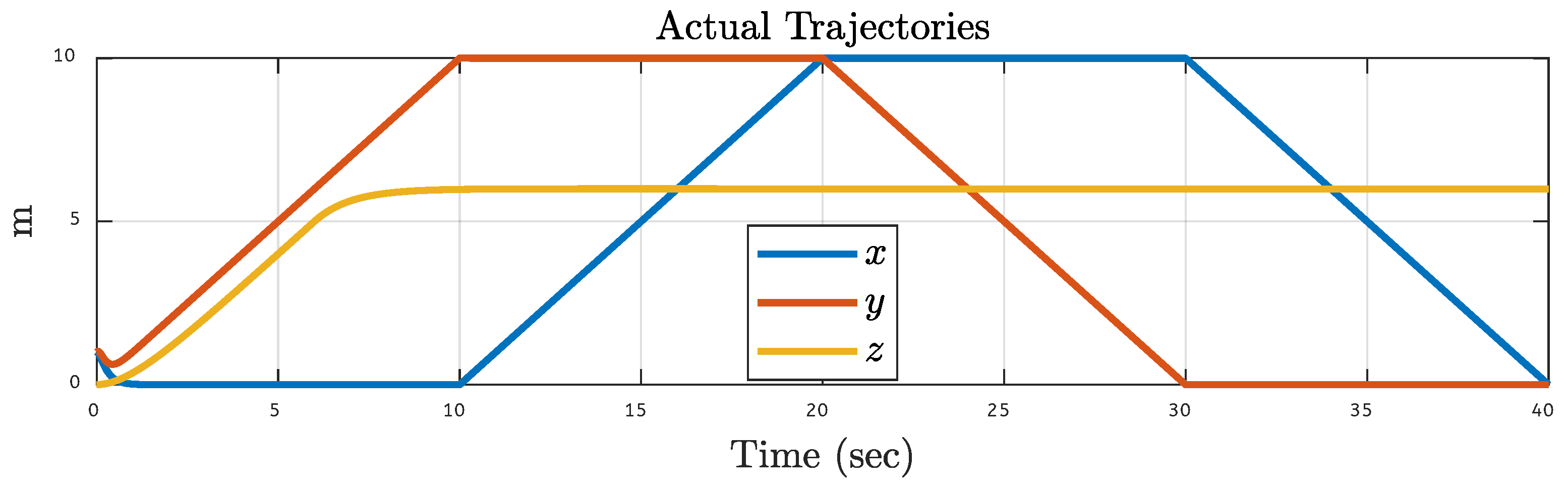
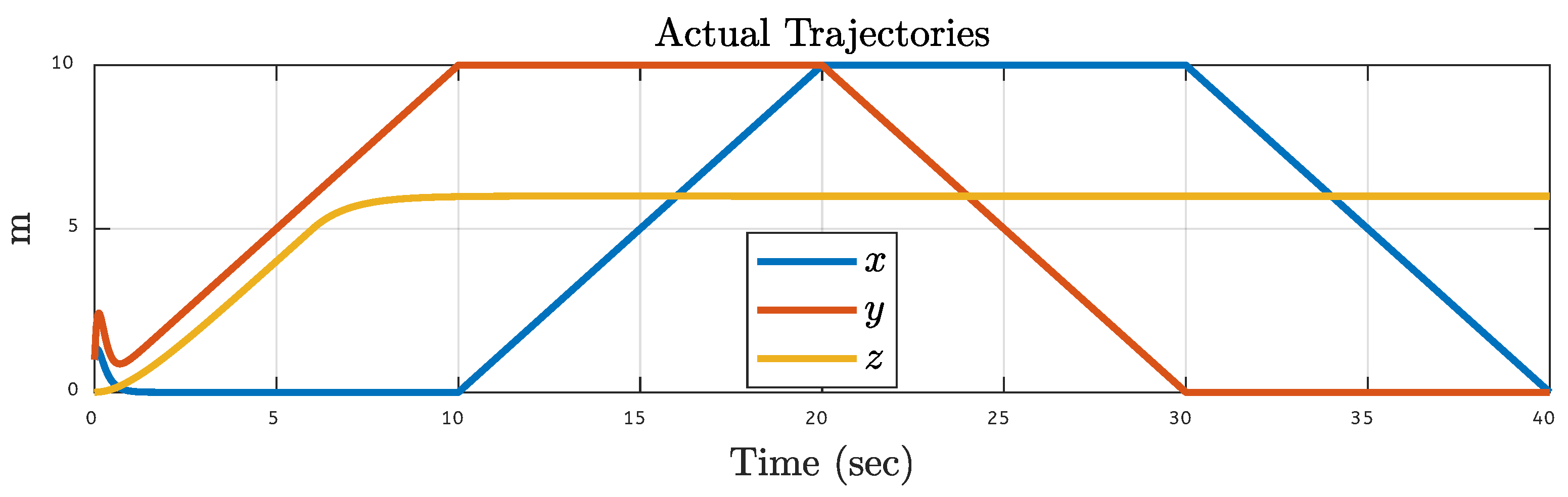


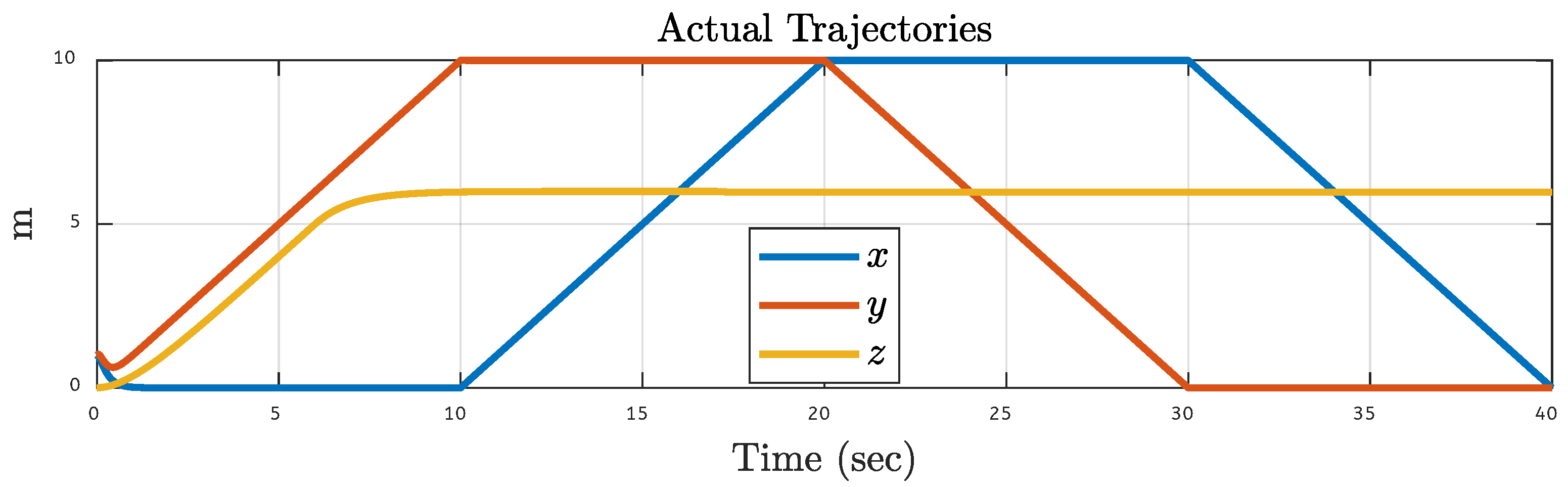
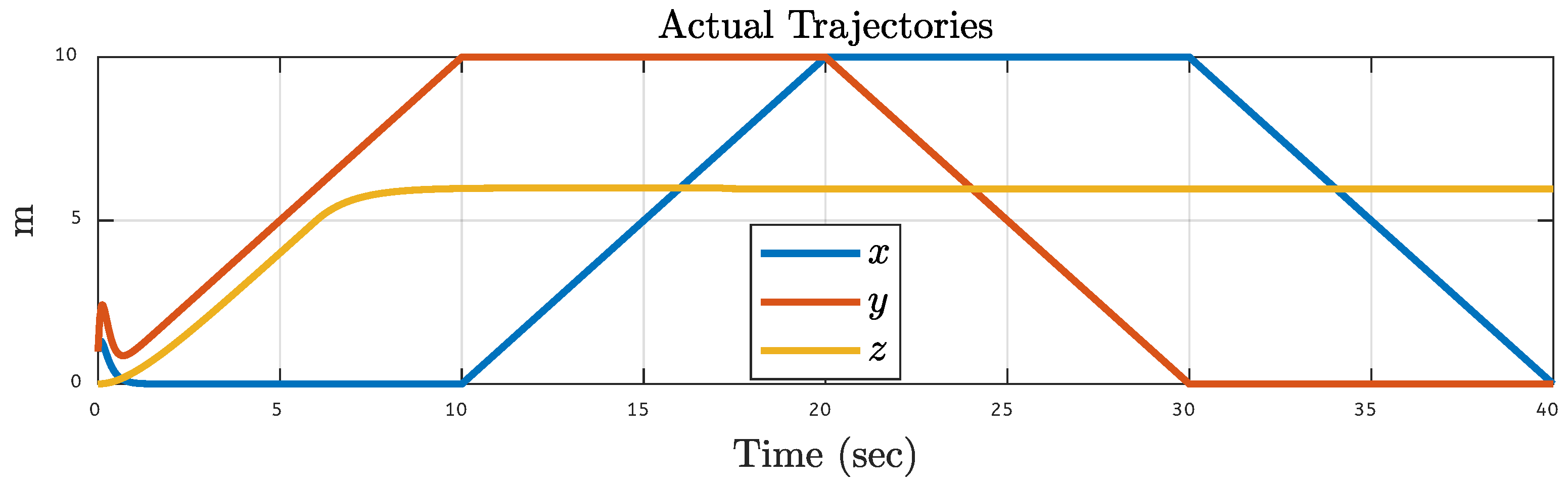

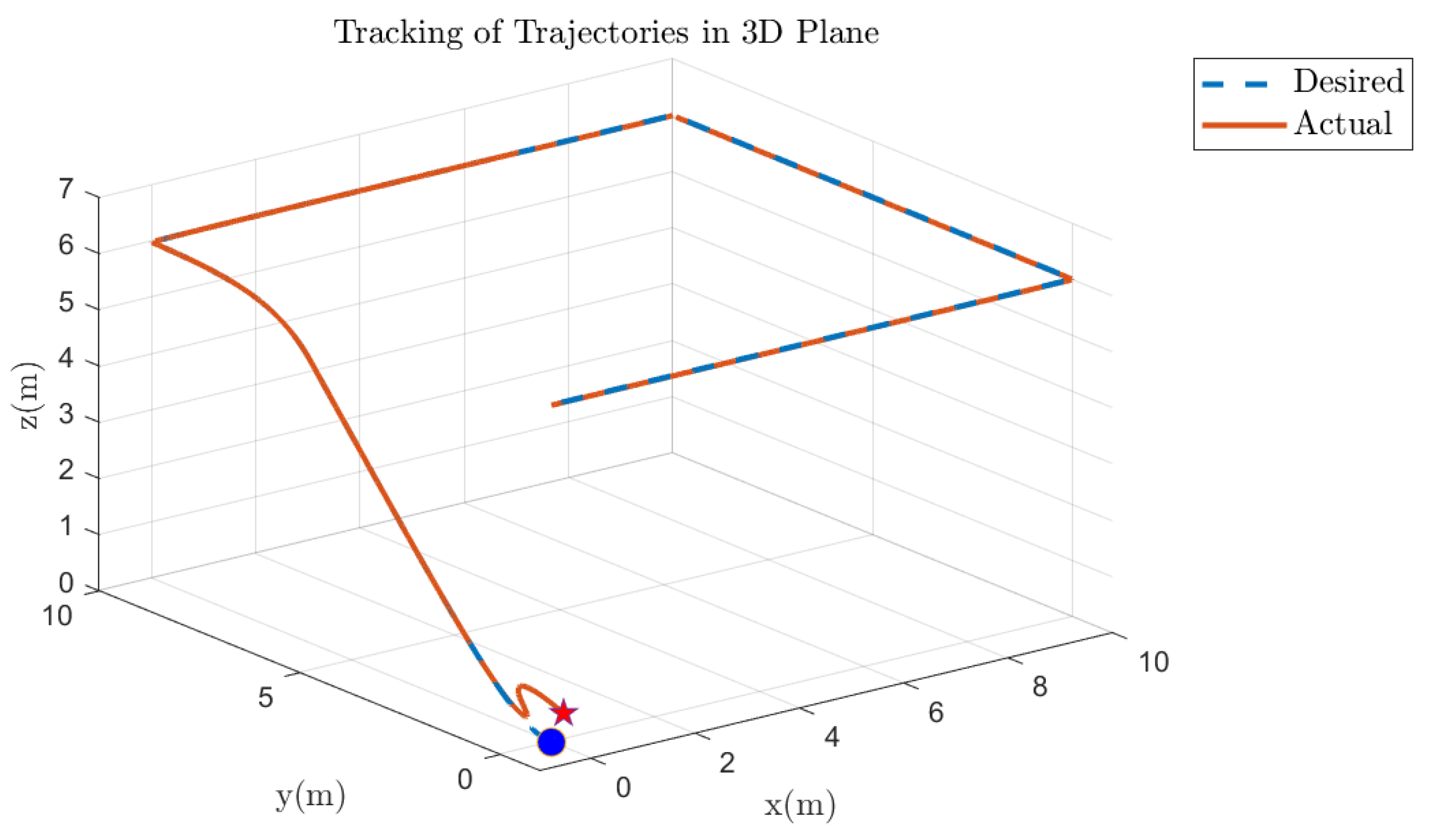
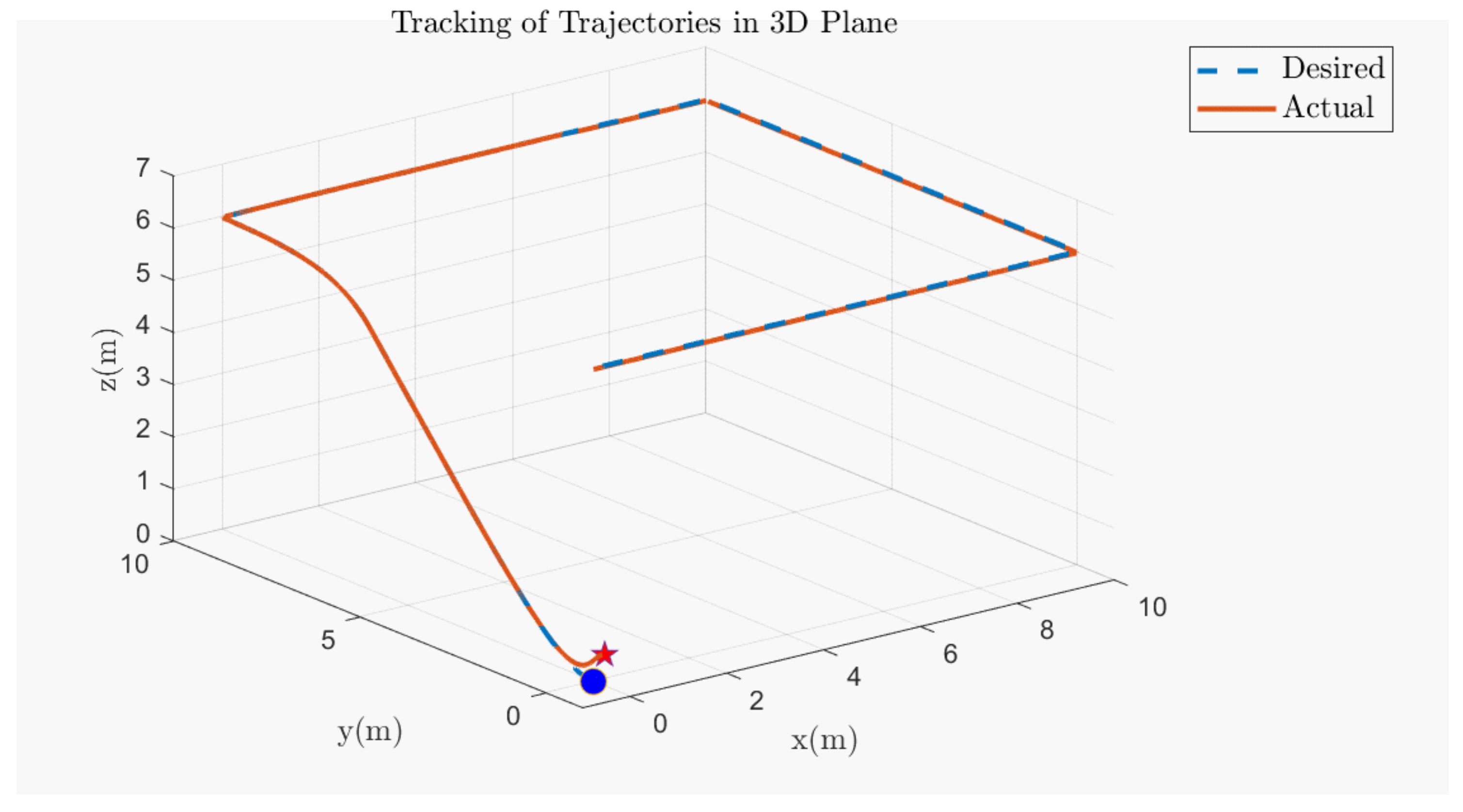


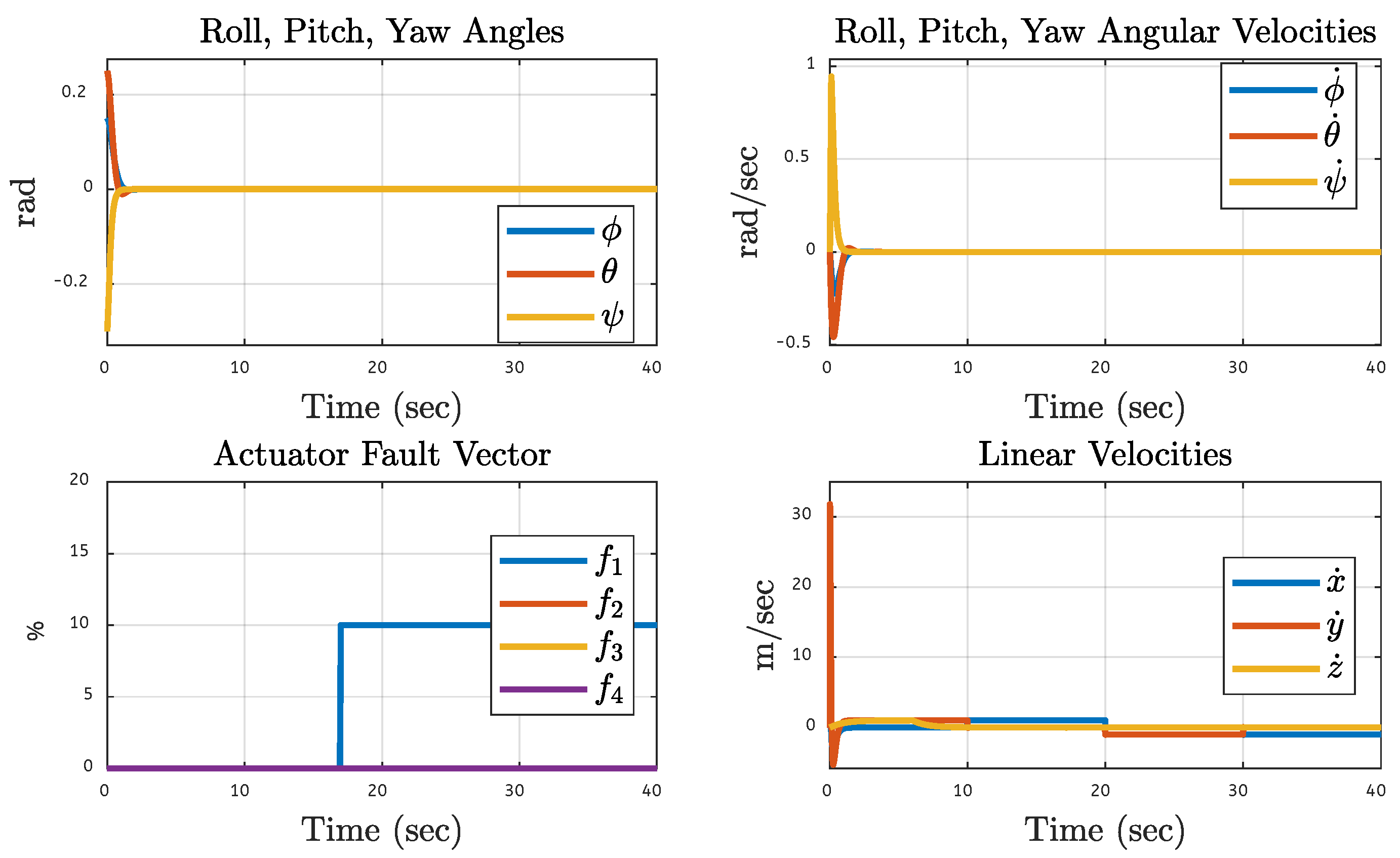
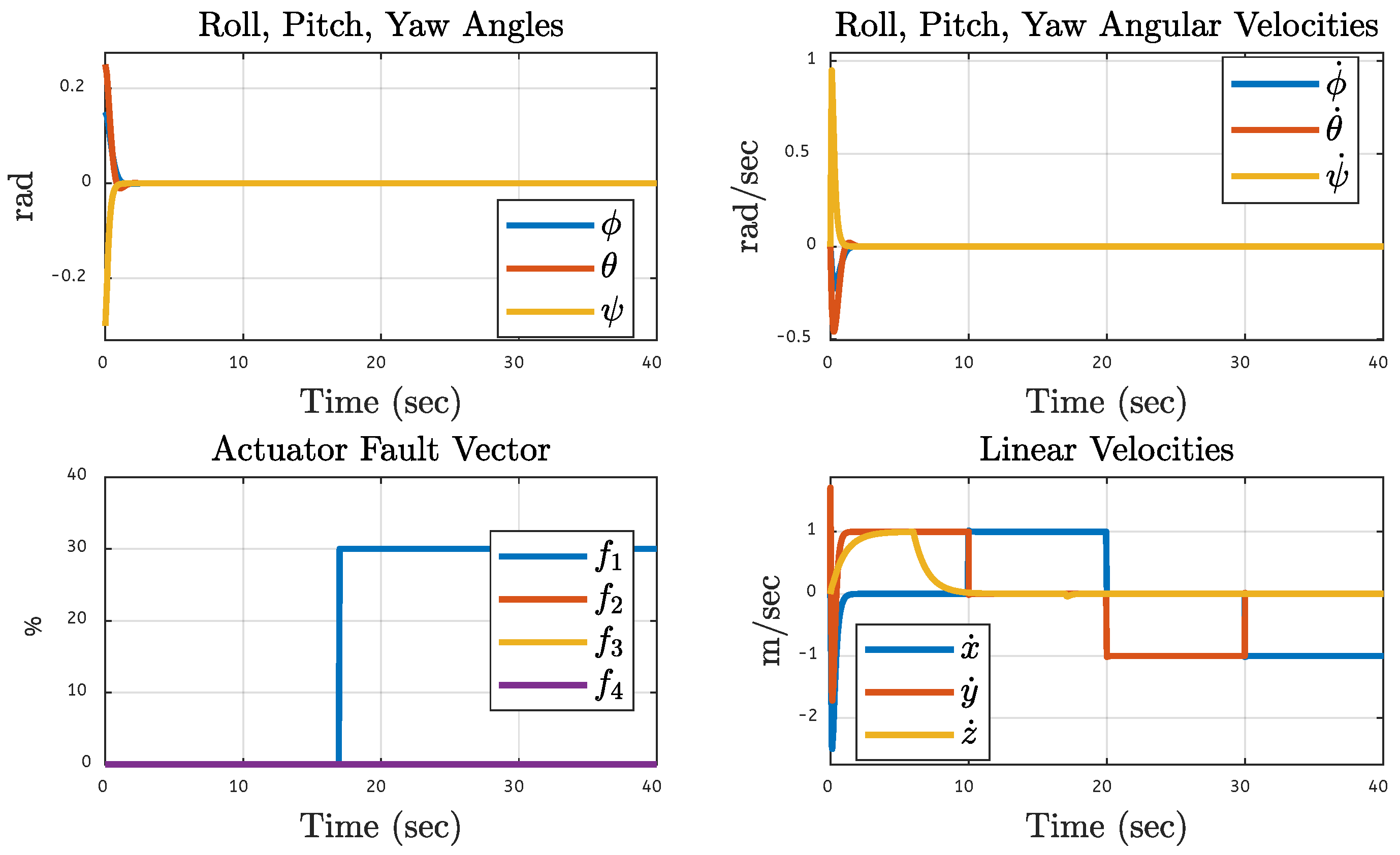
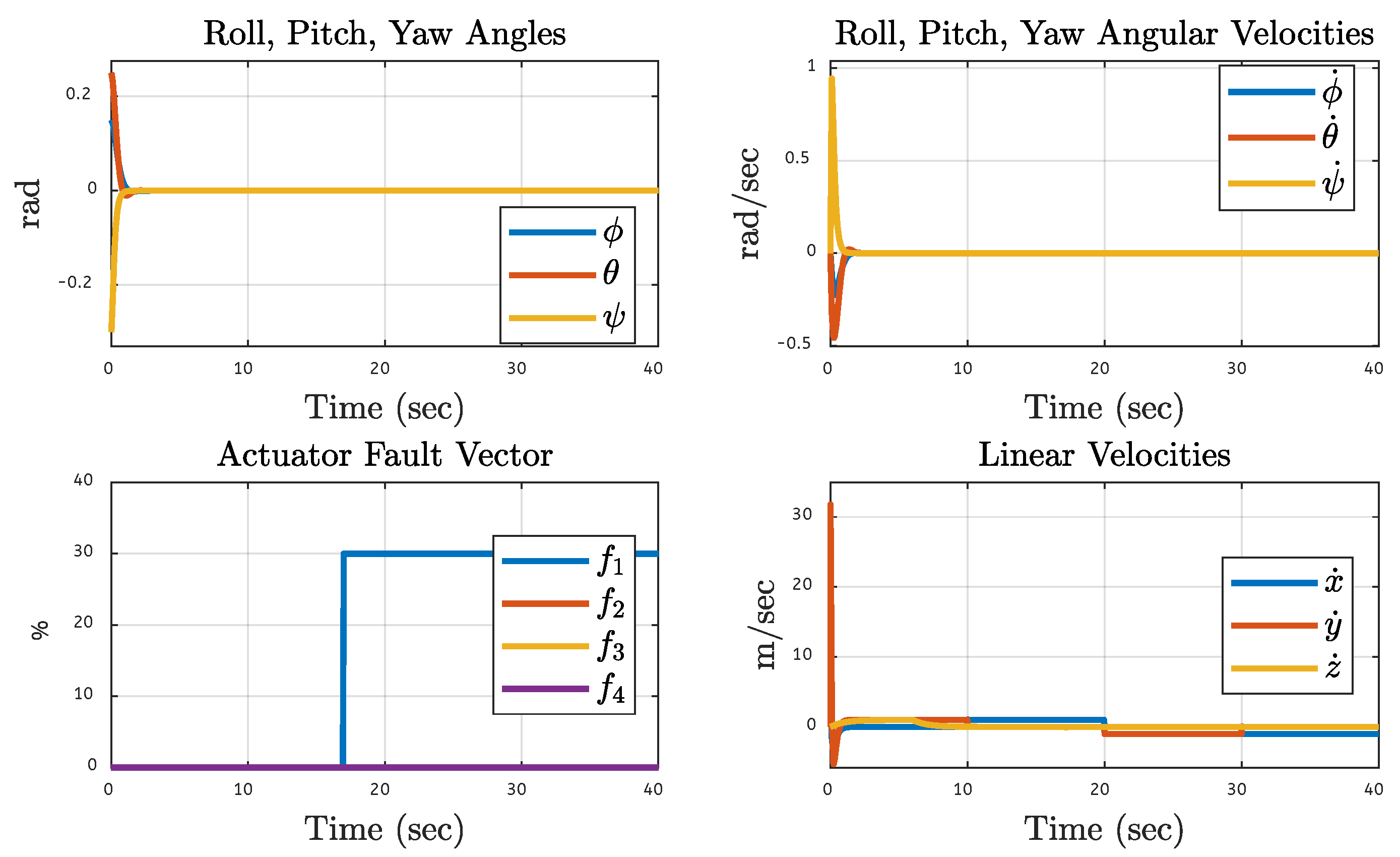
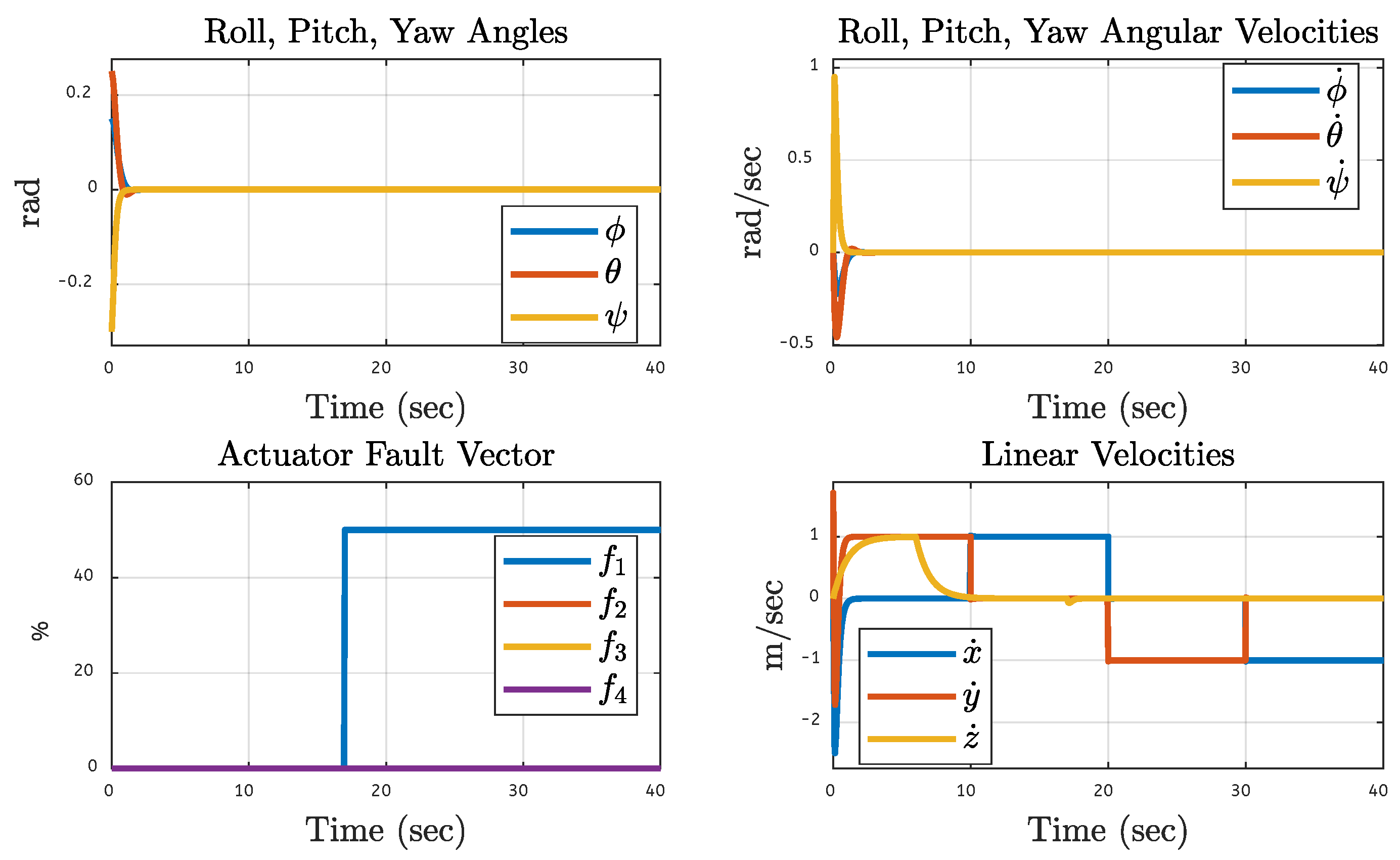
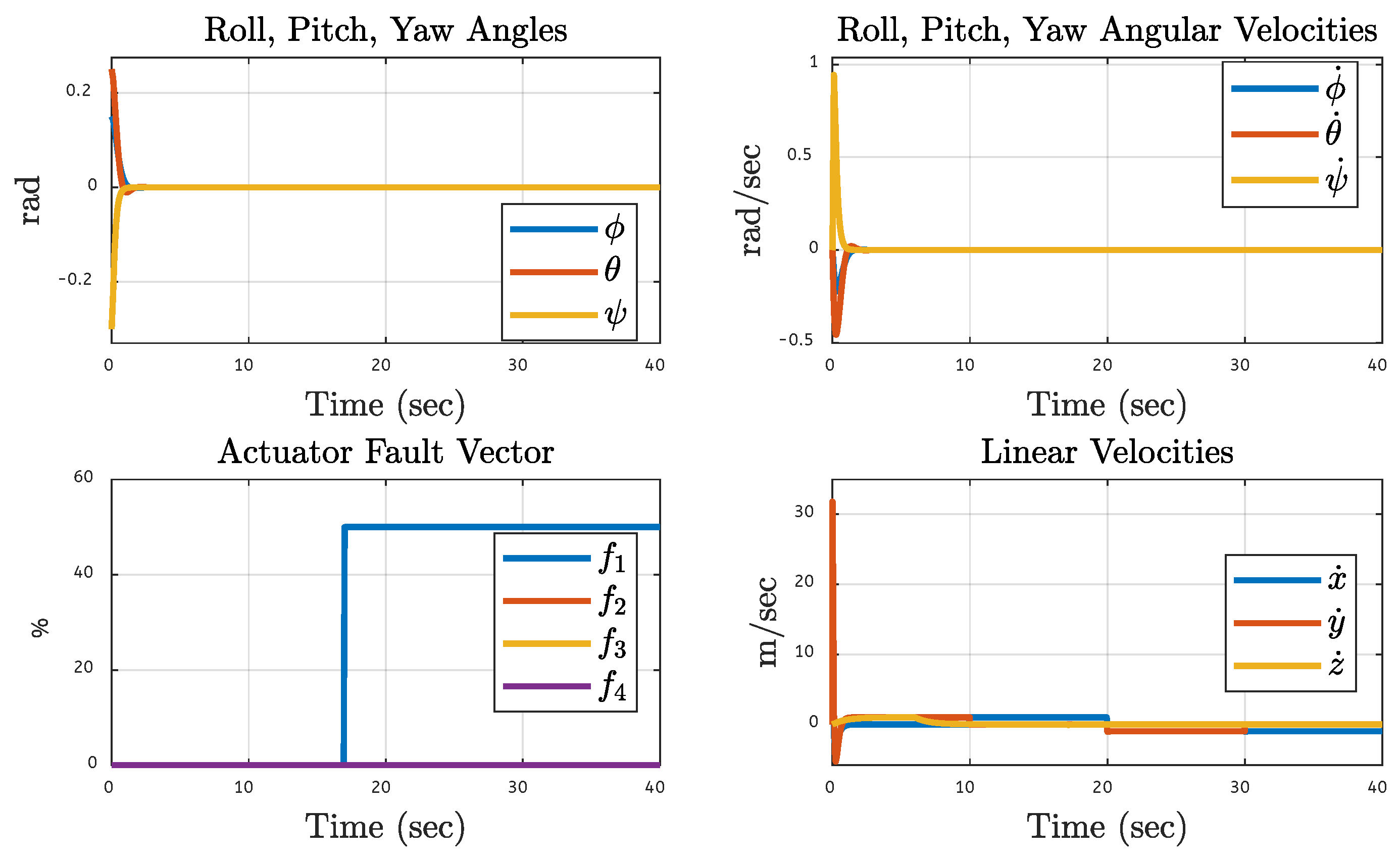
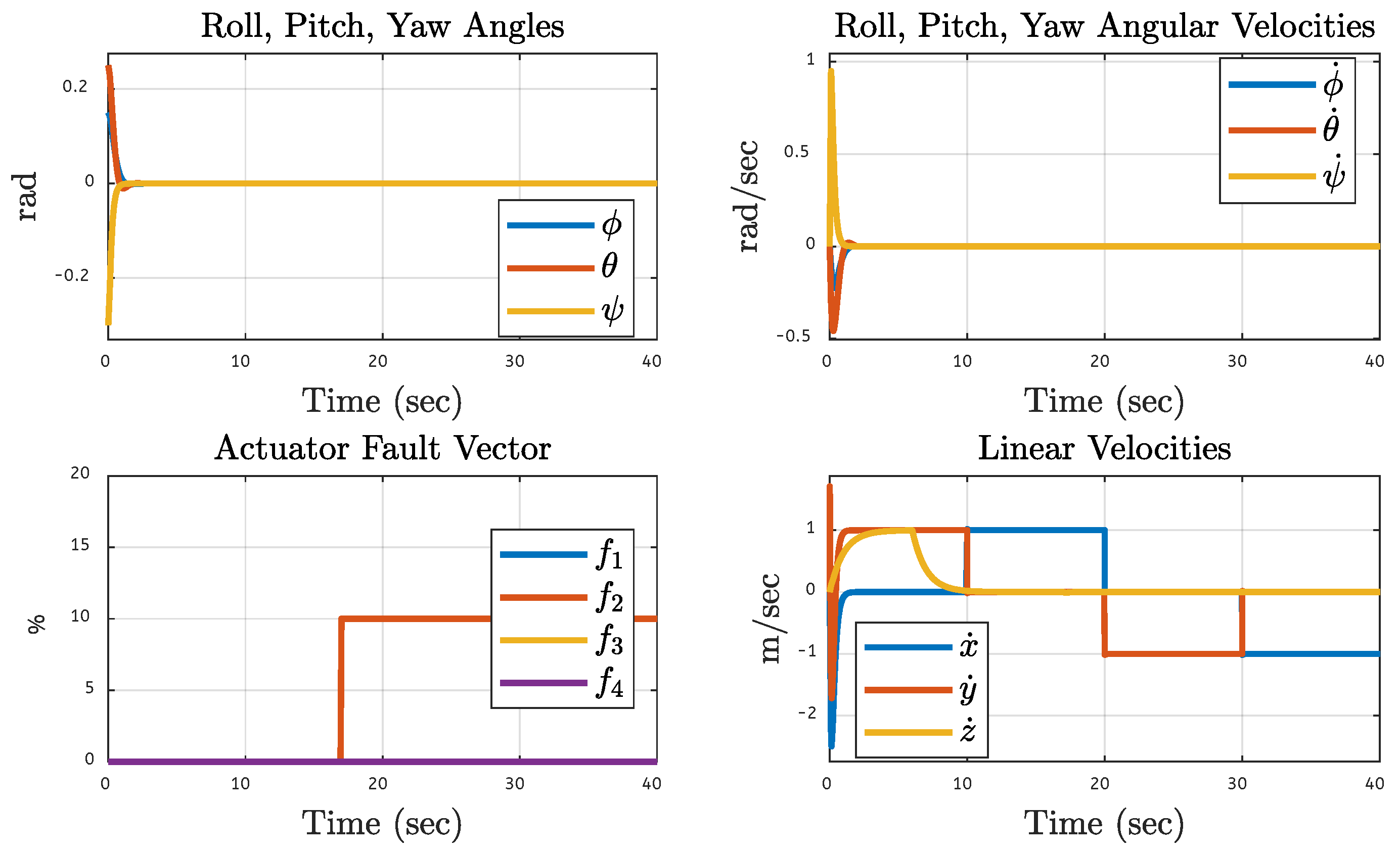
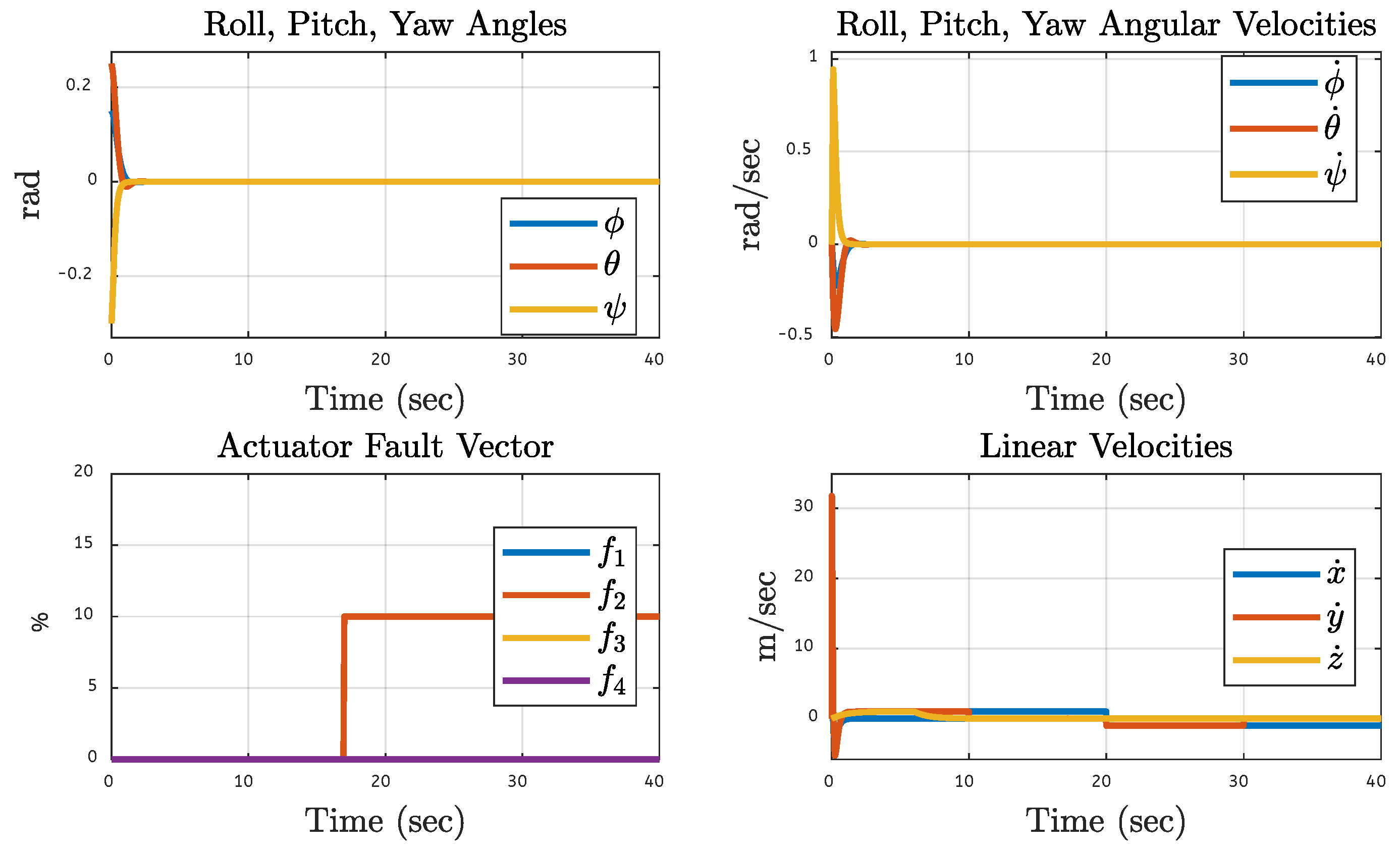
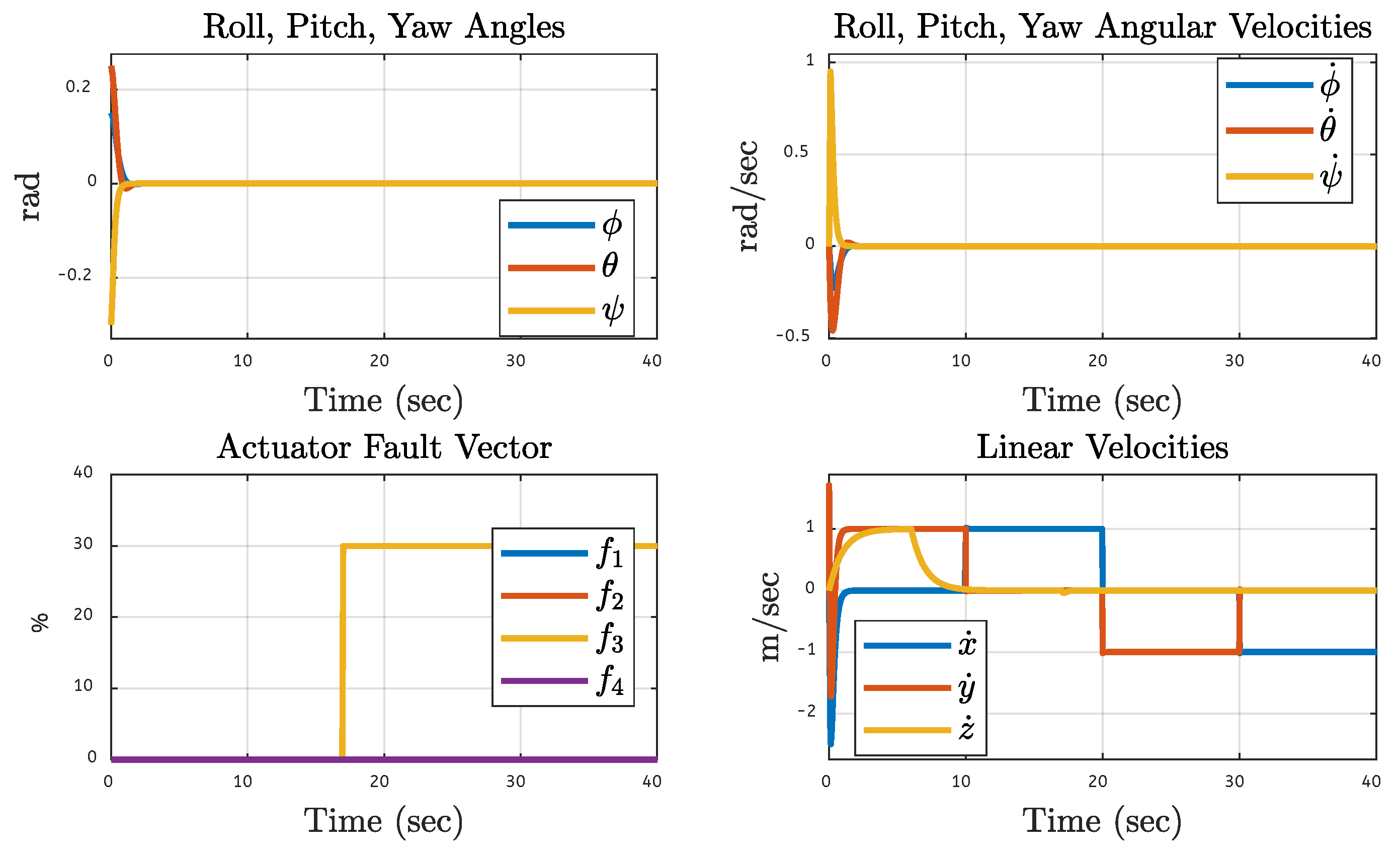
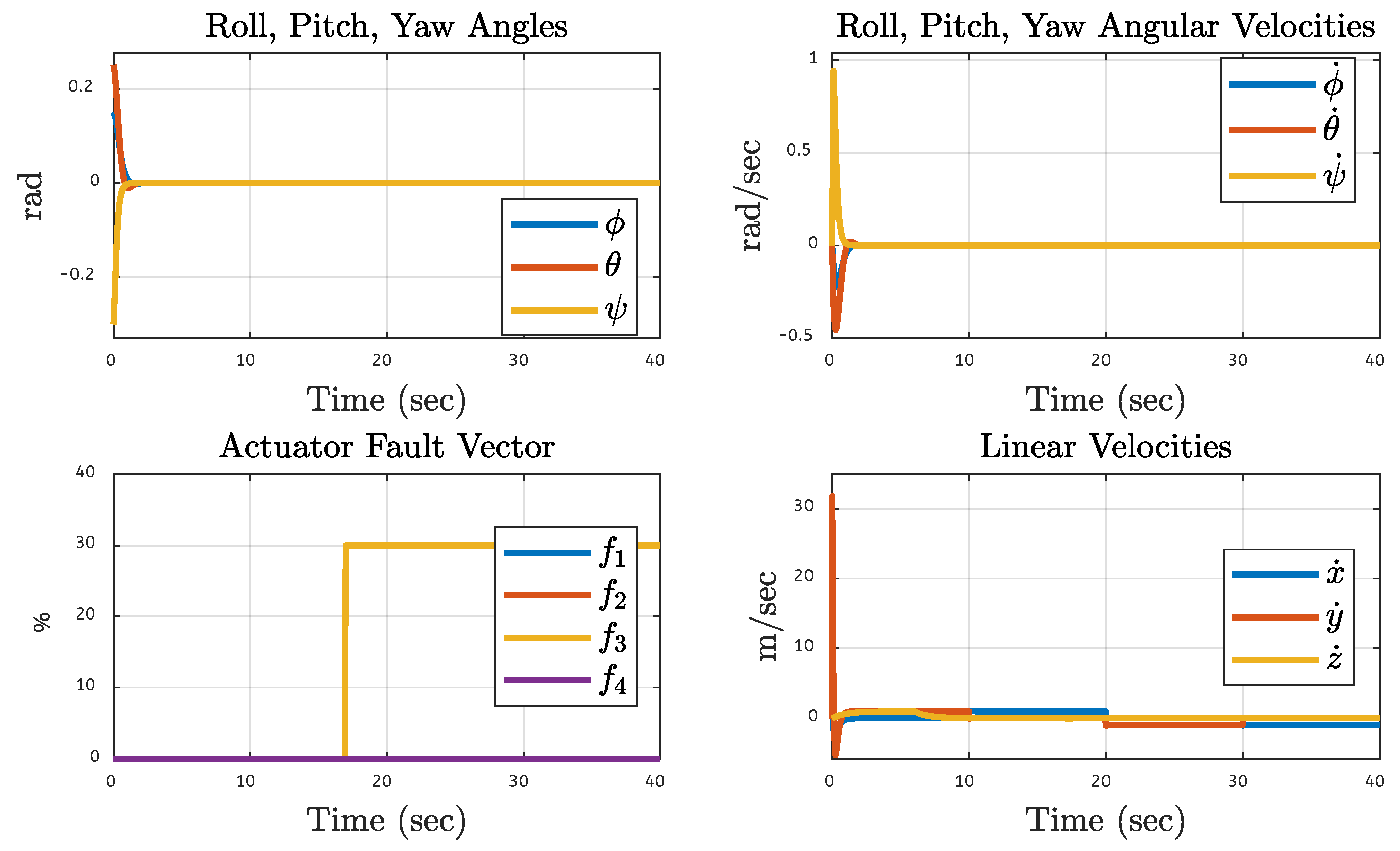
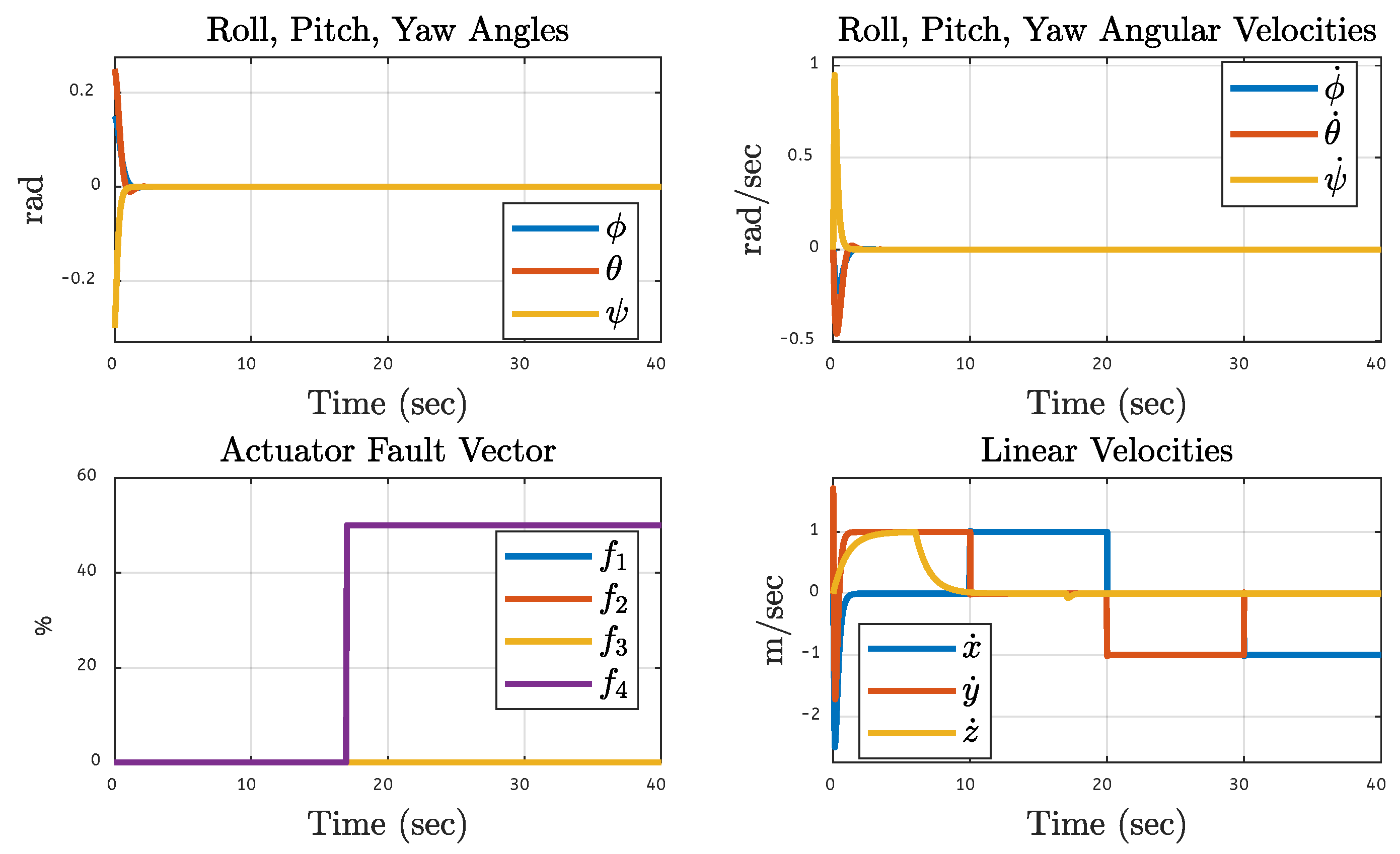
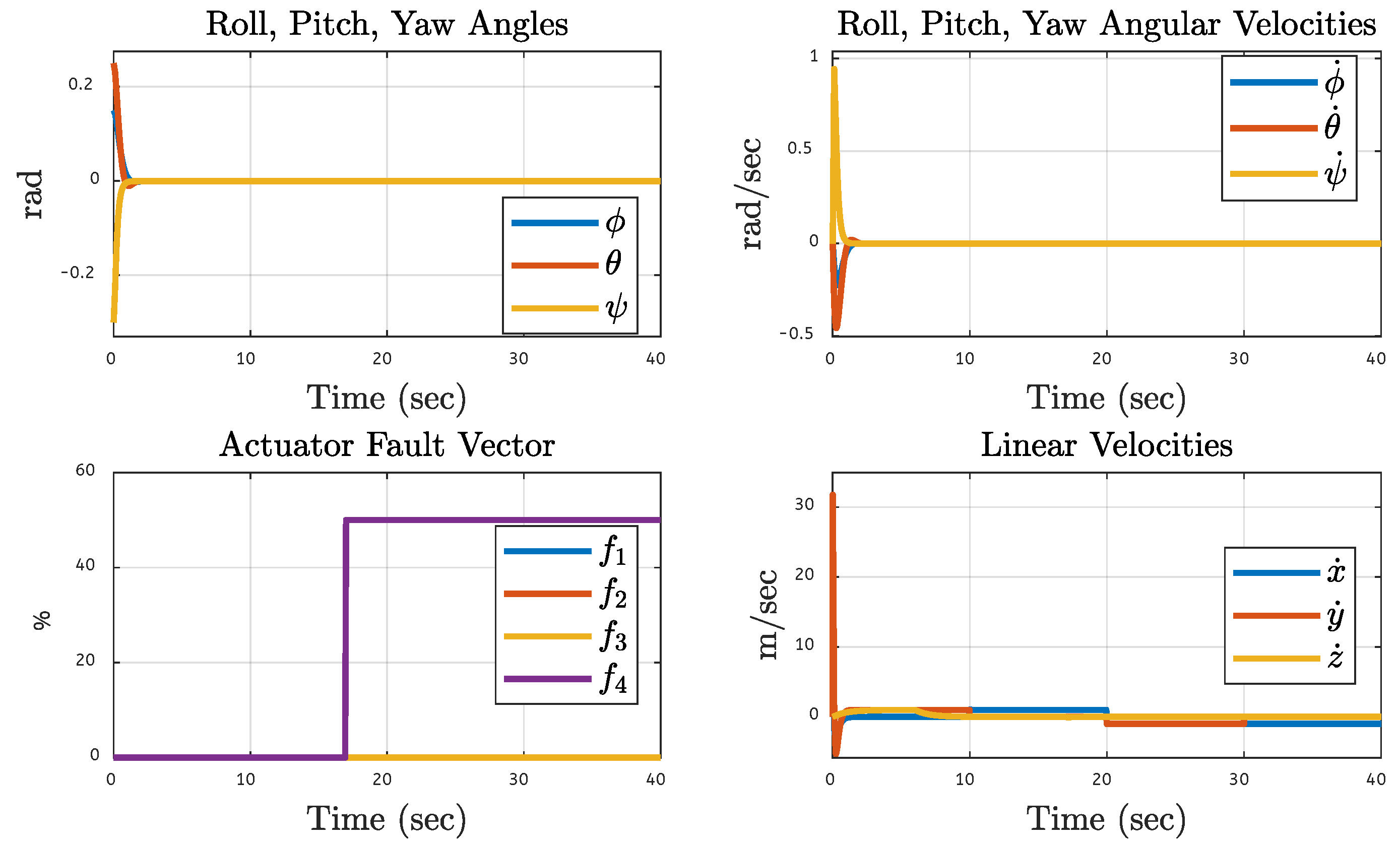
| Translational Gain | Rotational Gain | Initial Point | Tuning Factor |
|---|---|---|---|
| Numerical Results | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Simulation-Based Results | FPGA-Based Results | |||||||||
| After Injecting 10% Fault | Motor 1 | Motor 2 | Motor 3 | Motor 4 | Motor 1 | Motor 2 | Motor 3 | Motor 4 | ||
| 1.02 | 1.02 | 1.02 | 1.02 | 1.02 | 1.02 | 1.02 | 1.02 | |||
| 9.15 | 9.15 | 9.15 | 9.15 | 9.34 | 9.34 | 9.34 | 9.34 | |||
| 0.10341 | 0.10341 | 0.10341 | 0.10341 | 0.10340 | 0.10340 | 0.10340 | 0.10340 | |||
| 0 | 0 | 0 | 0 | 1.57 | 1.57 | 1.57 | 1.57 | |||
| 0 | 0 | 0 | 0 | 1.69 | 1.69 | 1.69 | 1.69 | |||
| 0 | 0 | 0 | 0 | 1.90 | 1.90 | 1.90 | 1.90 | |||
| After Injecting 30% Fault | Motor 1 | Motor 2 | Motor 3 | Motor 4 | Motor 1 | Motor 2 | Motor 3 | Motor 4 | ||
| 1.02 | 1.02 | 1.02 | 1.02 | 1.02 | 1.02 | 1.02 | 1.02 | |||
| 9.20 | 9.20 | 9.20 | 9.20 | 9.34 | 9.34 | 9.34 | 9.34 | |||
| 0.33022 | 0.33022 | 0.33022 | 0.33022 | 0.3302 | 0.3302 | 0.3302 | 0.3302 | |||
| 0 | 0 | 0 | 0 | 1.58 | 1.58 | 1.58 | 1.58 | |||
| 0 | 0 | 0 | 0 | 2.06 | 1.90 | 1.90 | 1.90 | |||
| 0 | 0 | 0 | 0 | 1.90 | 1.90 | 1.90 | 1.90 | |||
| After Injecting 50% Fault | Motor 1 | Motor 2 | Motor 3 | Motor 4 | Motor 1 | Motor 2 | Motor 3 | Motor 4 | ||
| 1.26 | 1.26 | 1.26 | 1.26 | 5.8 | 5.9 | 5.8 | 5.9 | |||
| 5.34 | 5.34 | 5.34 | 5.34 | 2.66 | 2.72 | 2.60 | 2.71 | |||
| 0.58293 | 0.58293 | 0.58293 | 0.58293 | 0.5839 | 0.5839 | 0.5839 | 0.5839 | |||
| 0 | 0 | 0 | 0 | 1.59 | 1.59 | 1.59 | 1.59 | |||
| 0 | 0 | 0 | 0 | 2.73 | 1.90 | 1.90 | 1.90 | |||
| 0 | 0 | 0 | 0 | 1.90 | 1.90 | 1.90 | 1.90 | |||
| Fault_Lvl | Metric | Mean_Sim | Mean_FPGA | Mean_Diff | p_ttest | p_wilcoxon | N_eff | CI_low |
|---|---|---|---|---|---|---|---|---|
| 10% | 0.000102 | 0.000102 | 0 | 1 | 1 | 4 | ||
| 0.0000915 | 0.0000934 | −1.9 | 0 | 0 | 4 | −1.9 | ||
| 0.10341 | 0.1034 | 1 | 0 | 0 | 4 | 1 | ||
| 0 | 0.0000157 | −0.0000157 | 0 | 0 | 4 | −0.0000157 | ||
| 0 | 0.0000169 | −0.0000169 | 0 | 0 | 4 | −0.0000169 | ||
| 0 | 0.000019 | −0.000019 | 0 | 0 | 4 | −0.000019 | ||
| 30% | 0.000102 | 0.000102 | 0 | 1 | 1 | 4 | ||
| 0.000092 | 0.0000934 | −1.4 | 0 | 0 | 4 | −1.4 | ||
| 0.33022 | 0.3302 | 2 | 0 | 0 | 4 | 2 | ||
| 0 | 0.0000158 | −0.0000158 | 0 | 0 | 4 | −0.0000158 | ||
| 0 | 0.0000194 | −0.0000194 | 1.93 | 0.125 | 4 | −2.0673 | ||
| 0 | 0.000019 | −0.000019 | 0 | 0 | 4 | −0.000019 | ||
| 50% | 1.26 | 5.85 | −4.59 | 5.49 | 0.125 | 4 | −4.68187 | |
| 5.34 | 2.6725 | −2.6725 | 2.4 | 0.125 | 4 | −2.76002 | ||
| 0.58293 | 0.5839 | −0.00097 | 0 | 0 | 4 | −0.00097 | ||
| 0 | 0.0000159 | −0.0000159 | 0 | 0 | 4 | −0.0000159 | ||
| 0 | 0.000021075 | −0.000021075 | 0.002034 | 0.125 | 4 | −2.76786 | ||
| 0 | 0.000019 | −0.000019 | 0 | 0 | 4 | −0.000019 |
| Fault_Lvl | Metric | Mean_Sim | Mean_FPGA | Mean_Diff | p_anova | p_kruskal | N_total |
|---|---|---|---|---|---|---|---|
| 10% | 0.000102 | 0.000102 | 0 | 1 | 1 | 8 | |
| 0.0000915 | 0.0000934 | −1.9 | 0 | 0 | 8 | ||
| 0.10341 | 0.1034 | 1 | 0 | 0 | 8 | ||
| 0 | 0.0000157 | −1.57 | 0 | 0 | 8 | ||
| 0 | 0.0000169 | −1.69 | 0 | 0 | 8 | ||
| 0 | 0.000019 | −0.000019 | 0 | 0 | 8 | ||
| 30% | 0.000102 | 0.000102 | 0 | 1 | 1 | 8 | |
| 0.000092 | 0.0000934 | −1.4 | 0 | 0 | 8 | ||
| 0.33022 | 0.3302 | 2 | 0 | 0 | 8 | ||
| 0 | 0.0000158 | −1.58 | 0 | 0 | 8 | ||
| 0 | 0.0000194 | −1.94 | 5.15168 | 0.011412036 | 8 | ||
| 0 | 0.000019 | −0.000019 | 0 | 0 | 8 | ||
| 50% | 1.26 | 5.85 | −4.59 | 4.17459 | 0.012615667 | 8 | |
| 5.34 | 2.6725 | −2.6725 | 7.99963 | 0.013874406 | 8 | ||
| 0.58293 | 0.5839 | −0.00097 | 0 | 0 | 8 | ||
| 0 | 0.0000159 | −0.0000159 | 0 | 0 | 8 | ||
| 0 | 2.1075 | −0.000021075 | 5.30041 | 0.011412036 | 8 | ||
| 0 | 0.000019 | −0.000019 | 0 | 0 | 8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abdullah, M.; Zulfiqar, A.; Zeeshan Babar, M.; Arman, J.H.; Hafeez, G.; Alsafran, A.S.; Rawa, M. Hardware-in-the-Loop Experimental Validation of a Fault-Tolerant Control System for Quadcopter UAV Motor Faults. Fractal Fract. 2025, 9, 682. https://doi.org/10.3390/fractalfract9110682
Abdullah M, Zulfiqar A, Zeeshan Babar M, Arman JH, Hafeez G, Alsafran AS, Rawa M. Hardware-in-the-Loop Experimental Validation of a Fault-Tolerant Control System for Quadcopter UAV Motor Faults. Fractal and Fractional. 2025; 9(11):682. https://doi.org/10.3390/fractalfract9110682
Chicago/Turabian StyleAbdullah, Muhammad, Adil Zulfiqar, Muhammad Zeeshan Babar, Jamal Hussain Arman, Ghulam Hafeez, Ahmed S. Alsafran, and Muhyaddin Rawa. 2025. "Hardware-in-the-Loop Experimental Validation of a Fault-Tolerant Control System for Quadcopter UAV Motor Faults" Fractal and Fractional 9, no. 11: 682. https://doi.org/10.3390/fractalfract9110682
APA StyleAbdullah, M., Zulfiqar, A., Zeeshan Babar, M., Arman, J. H., Hafeez, G., Alsafran, A. S., & Rawa, M. (2025). Hardware-in-the-Loop Experimental Validation of a Fault-Tolerant Control System for Quadcopter UAV Motor Faults. Fractal and Fractional, 9(11), 682. https://doi.org/10.3390/fractalfract9110682








