Computational and Parameter-Sensitivity Analysis of Dual-Order Memory-Driven Fractional Differential Equations with an Application to Animal Learning
Abstract
1. Introduction
- Memory-dependent materials, where the stress–strain relationship is influenced by prior deformations [17].
- Anomalous diffusion processes, commonly observed in transport through heterogeneous media, deviating from classical Brownian motion [18].
- Biological and artificial intelligence models, where adaptive behavior arises from accumulated past inputs [19].
- Neural dynamics and population growth models, where historical states exert a long-term influence on system evolution [20].
2. Preliminaries
- 1.
- , for all .
- 2.
- is compact and continuous.
- 3.
- is a contraction mapping.
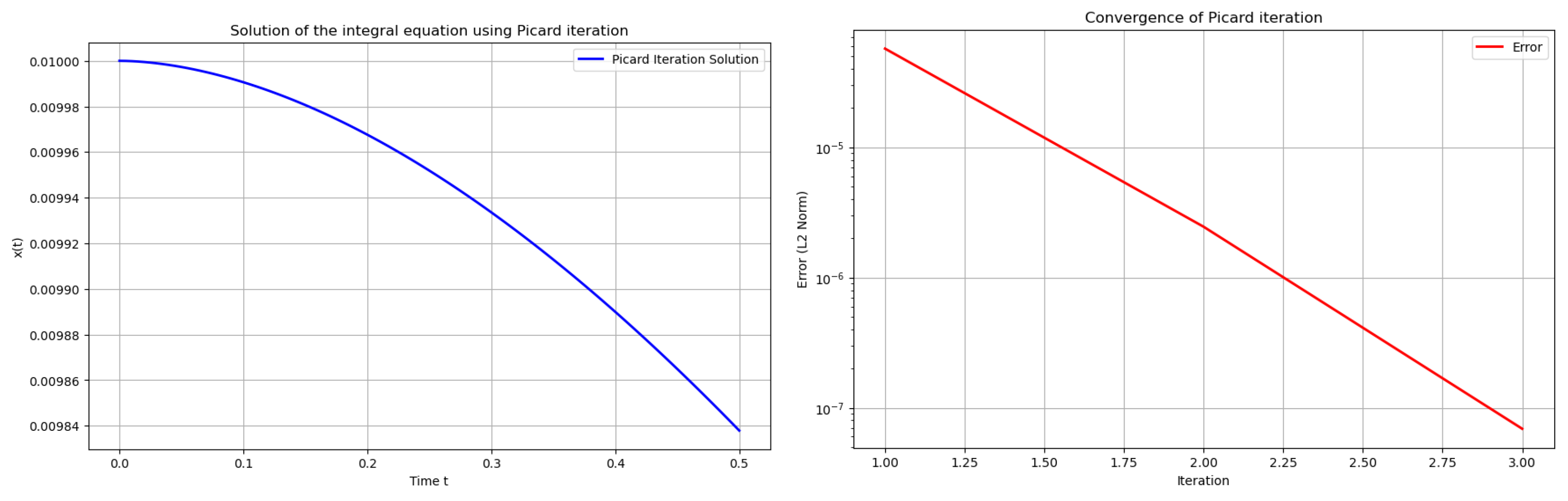
3. Analytical Investigation
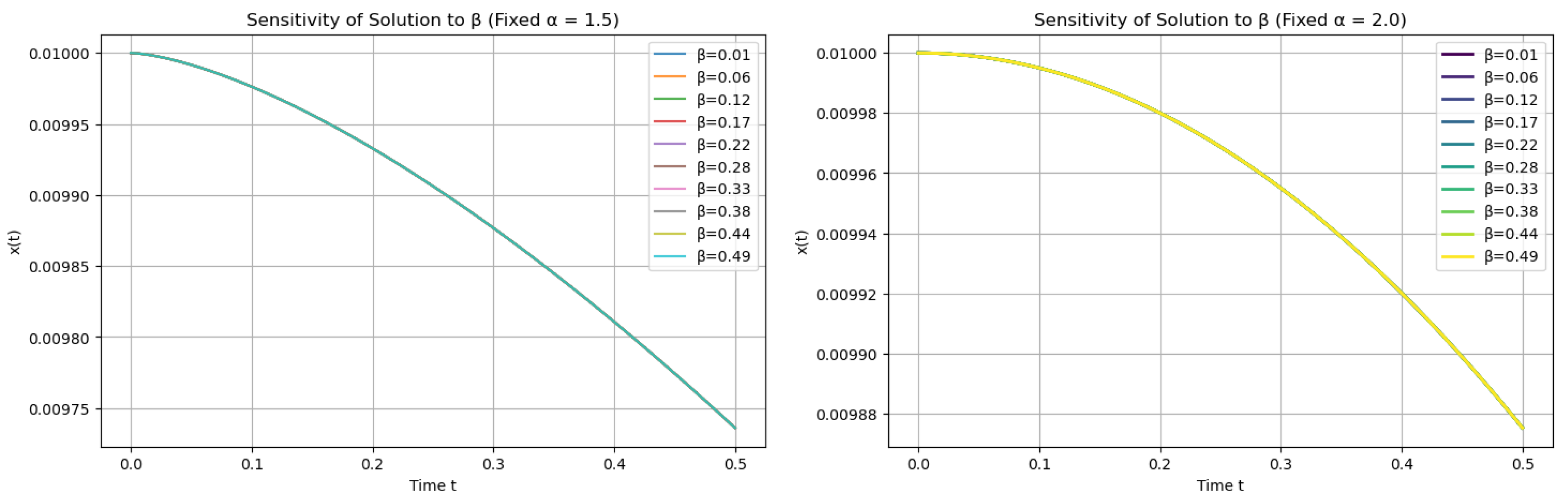
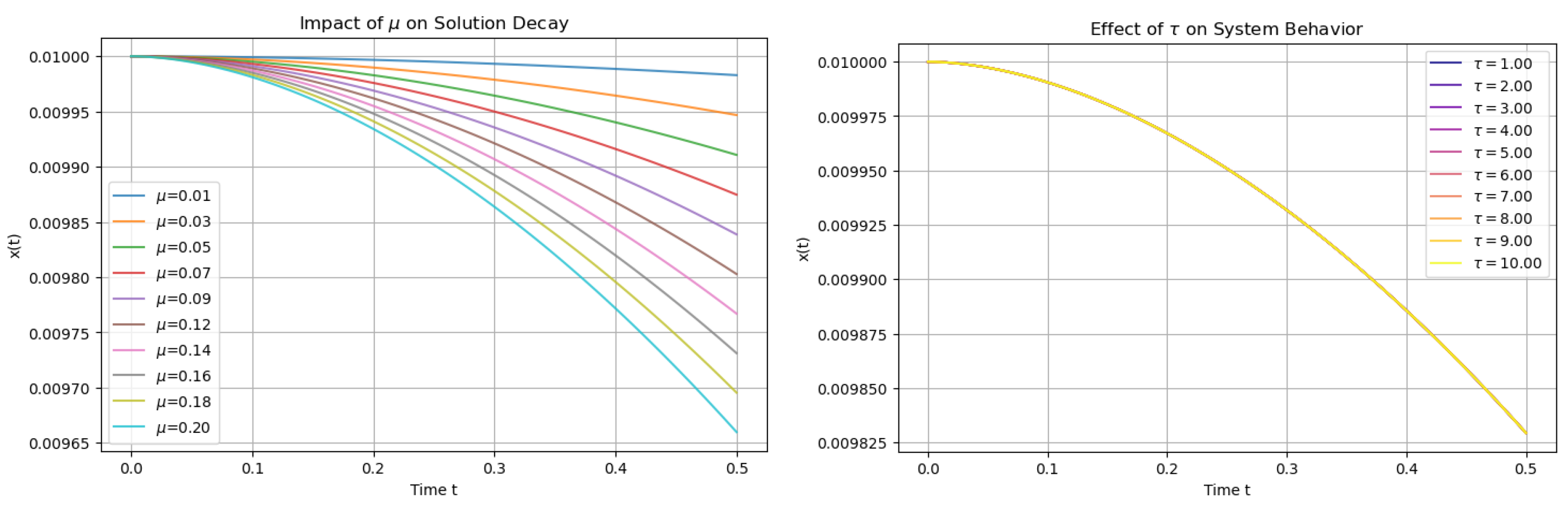
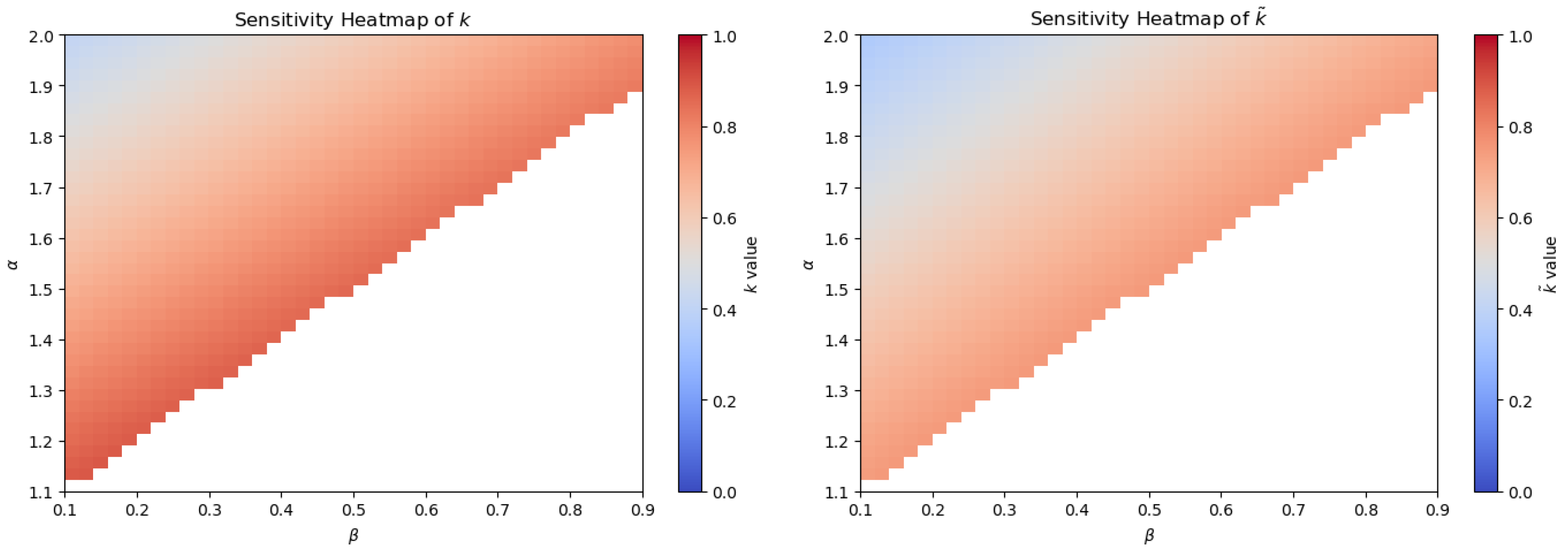
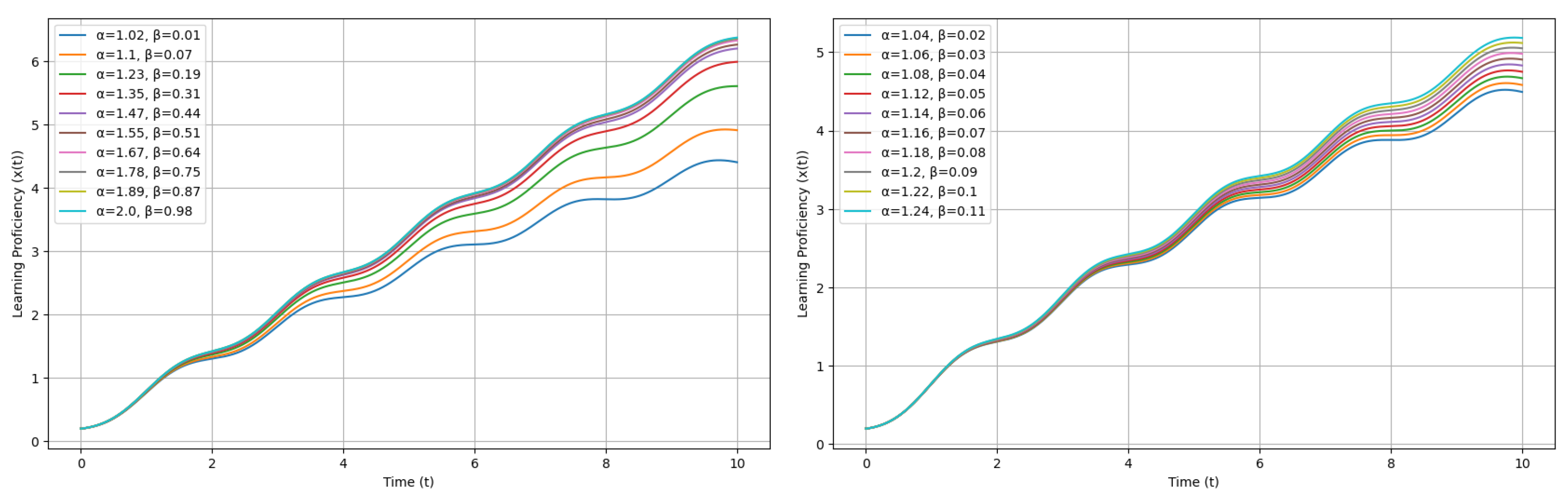
4. Parameter Sensitivity Analysis
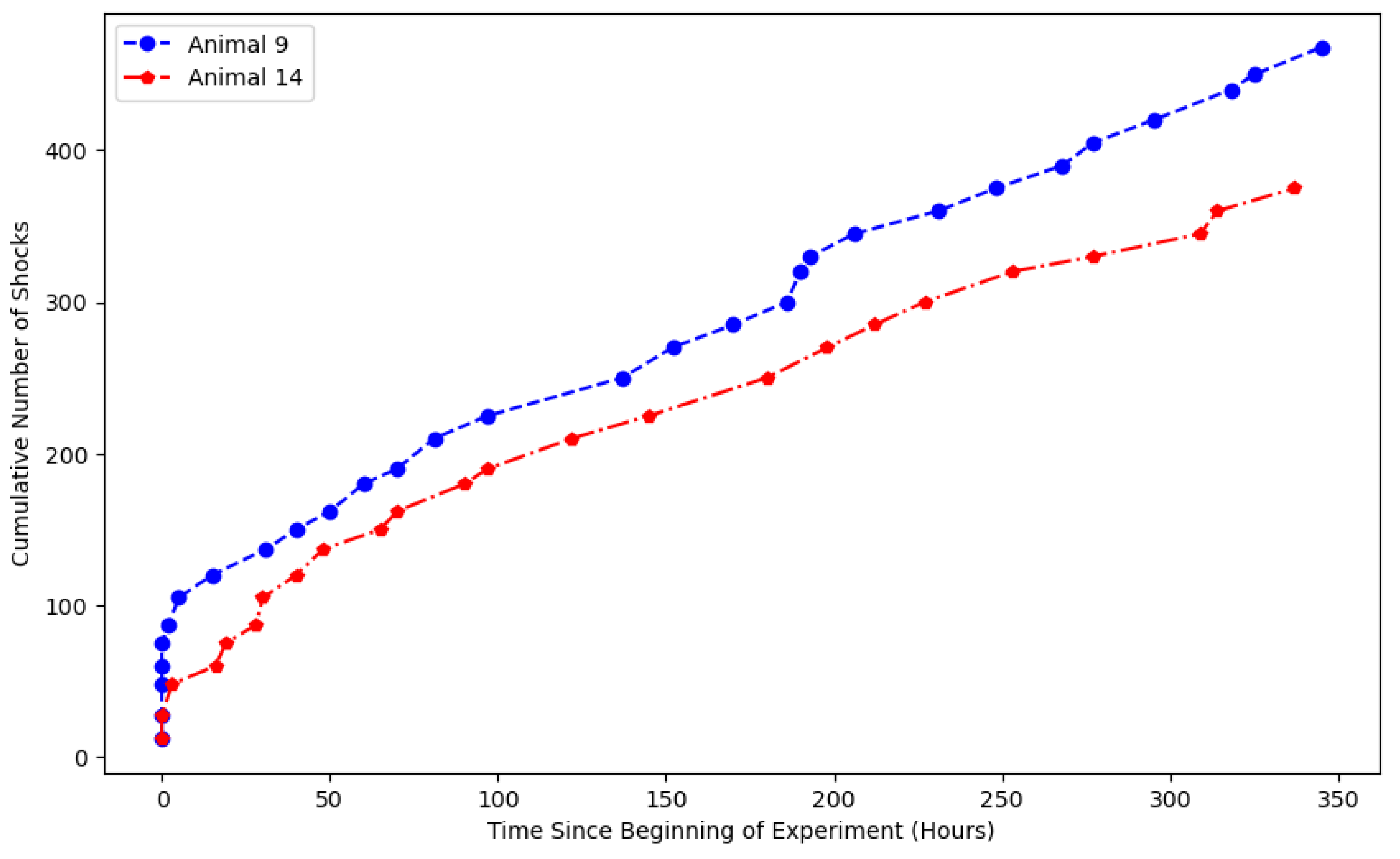
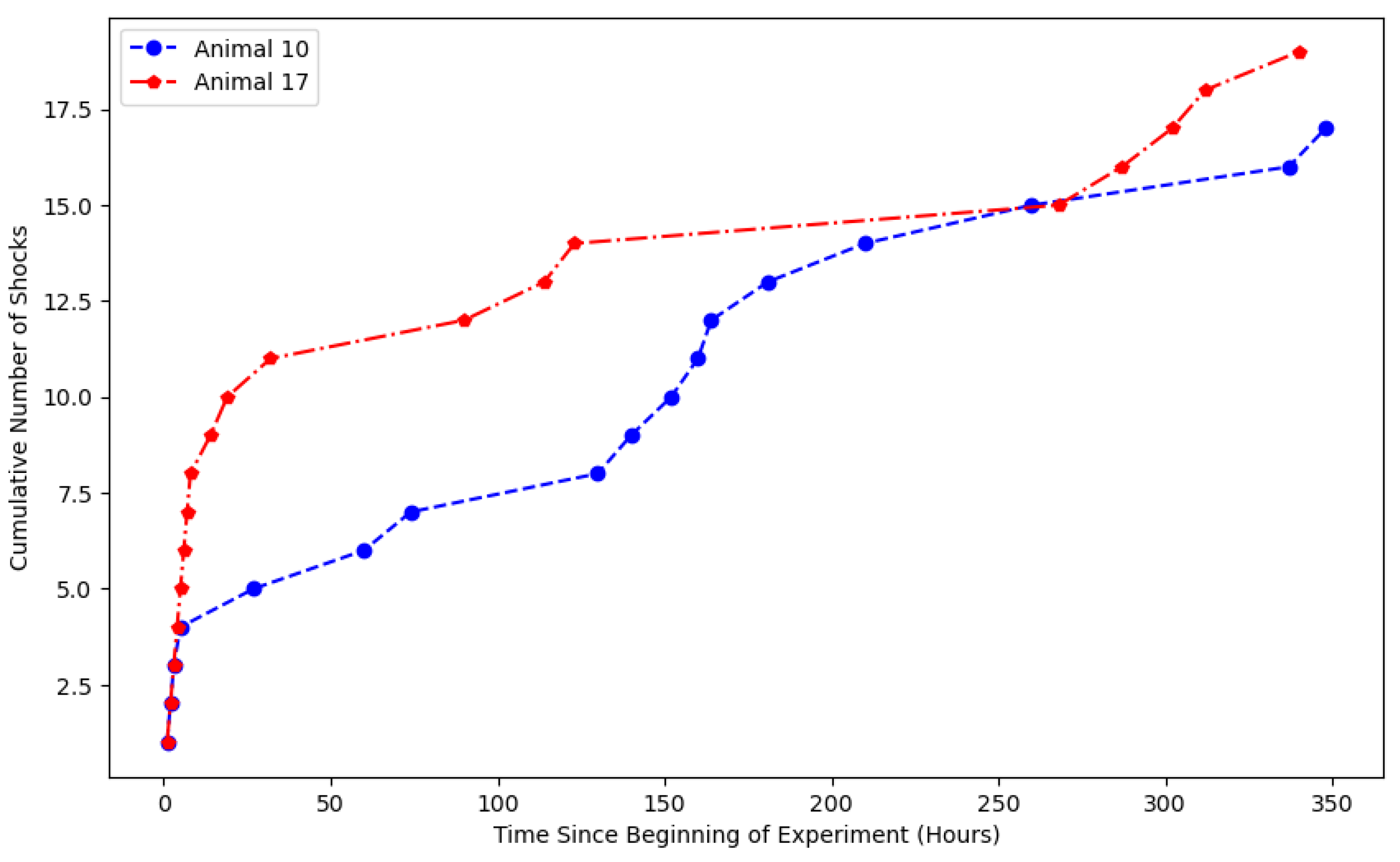
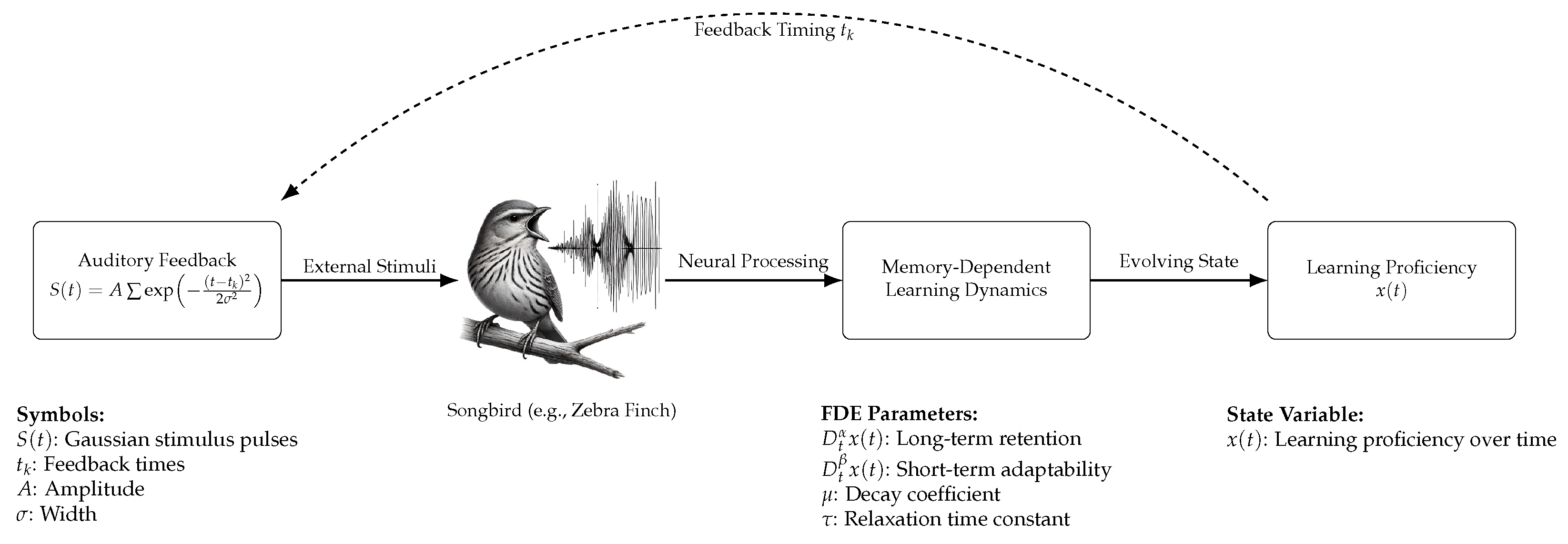
5. Memory-Dependent Learning and Behavioral Adaptation in Animals: An Application
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Whitby, M.; Cardelli, L.; Kwiatkowska, M.; Laurenti, L.; Tribastone, M.; Tschaikowski, M. PID control of biochemical reaction networks. IEEE Trans. Autom. Control 2021, 67, 1023–1030. [Google Scholar] [CrossRef]
- Fröhlich, F.; Sorger, P.K. Fides: Reliable trust-region optimization for parameter estimation of ordinary differential equation models. PLoS Comput. Biol. 2022, 18, e1010322. [Google Scholar] [CrossRef] [PubMed]
- Linot, A.J.; Burby, J.W.; Tang, Q.; Balaprakash, P.; Graham, M.D.; Maulik, R. Stabilized neural ordinary differential equations for long-time forecasting of dynamical systems. J. Comput. Phys. 2023, 474, 111838. [Google Scholar] [CrossRef]
- Turab, A.; Sintunavarat, W. A unique solution of the iterative boundary value problem for a second-order differential equation approached by fixed point results. Alex. Eng. J. 2021, 60, 5797–5802. [Google Scholar] [CrossRef]
- He, L.; Valocchi, A.J.; Duarte, C.A. A transient global-local generalized FEM for parabolic and hyperbolic PDEs with multi-space/time scales. J. Comput. Phys. 2023, 488, 112179. [Google Scholar] [CrossRef]
- Zúñiga-Aguilar, C.J.; Gómez-Aguilar, J.F.; Romero-Ugalde, H.M.; Escobar-Jiménez, R.F.; Fernández-Anaya, G.; Alsaadi, F.E. Numerical solution of fractal-fractional Mittag–Leffler differential equations with variable-order using artificial neural networks. Eng. Comput. 2022, 38, 2669–2682. [Google Scholar] [CrossRef]
- Lakzian, H.; Gopal, D.; Sintunavarat, W. New fixed point results for mappings of contractive type with an application to nonlinear fractional differential equations. J. Fixed Point Theory Appl. 2016, 18, 251–266. [Google Scholar] [CrossRef]
- Rezaei, M.M.; Zohoor, H.; Haddadpour, H. Analytical solution for nonlinear dynamics of a rotating wind turbine blade under aerodynamic loading and yawed inflow effects. Thin-Walled Struct. 2025, 212, 113164. [Google Scholar] [CrossRef]
- Magazev, A.A.; Boldyreva, M.N. Schrödinger equations in electromagnetic fields: Symmetries and noncommutative integration. Symmetry 2021, 13, 1527. [Google Scholar] [CrossRef]
- Liu, Y.; Yang, Z.; Yu, Z.; Liu, Z.; Liu, D.; Lin, H.; Li, M.; Ma, S.; Avdeev, M.; Shi, S. Generative artificial intelligence and its applications in materials science: Current situation and future perspectives. J. Mater. 2023, 9, 798–816. [Google Scholar] [CrossRef]
- Hsu, S.B.; Chen, K.C. Ordinary Differential Equations with Applications; World Scientific: Singapore, 2022; Volume 23. [Google Scholar]
- Kai, Y.; Yin, Z. Linear structure and soliton molecules of Sharma-Tasso-Olver-Burgers equation. Phys. Lett. A 2022, 452, 128430. [Google Scholar] [CrossRef]
- Turab, A.; Montoyo, A.; Nescolarde-Selva, J.A. Stability and numerical solutions for second-order ordinary differential equations with application in mechanical systems. J. Appl. Math. Comput. 2024, 70, 5103–5128. [Google Scholar] [CrossRef]
- Brady, J.P.; Marmasse, C. Analysis of a simple avoidance situation: I. Experimental paradigm. Psychol. Rec. 1962, 12, 361. [Google Scholar] [CrossRef]
- Turab, A.; Montoyo, A.; Nescolarde-Selva, J.-A. Computational and analytical analysis of integral-differential equations for modeling avoidance learning behavior. J. Appl. Math. Comput. 2024, 70, 4423–4439. [Google Scholar] [CrossRef]
- Marmasse, C.; Brady, J.P. Analysis of a simple avoidance situation. II. A model. Bull. Math. Biophys. 1964, 26, 77–81. [Google Scholar] [CrossRef] [PubMed]
- Zhang, D.; Zhang, L.; Lan, T.; Wen, J.; Gao, L. A memory-dependent three-dimensional creep model for concrete. Case Stud. Constr. Mater. 2024, 20, e03289. [Google Scholar] [CrossRef]
- Ribeiro, H.V.; Tateishi, A.A.; Lenzi, E.K.; Magin, R.L.; Perc, M. Interplay between particle trapping and heterogeneity in anomalous diffusion. Commun. Phys. 2023, 6, 244. [Google Scholar] [CrossRef]
- Maurizi, M.; Gao, C.; Berto, F. Predicting stress, strain and deformation fields in materials and structures with graph neural networks. Sci. Rep. 2022, 12, 21834. [Google Scholar] [CrossRef]
- Lenzi, M.K.; Lenzi, E.K.; Guilherme, L.M.S.; Evangelista, L.R.; Ribeiro, H.V. Transient anomalous diffusion in heterogeneous media with stochastic resetting. Phys. A Stat. Mech. Its Appl. 2022, 588, 126560. [Google Scholar] [CrossRef]
- Hattaf, K. On the stability and numerical scheme of fractional differential equations with application to biology. Computation 2022, 10, 97. [Google Scholar] [CrossRef]
- Jajarmi, A.; Baleanu, D.; Sajjadi, S.S.; Nieto, J.J. Analysis and some applications of a regularized Ψ–Hilfer fractional derivative. J. Comput. Appl. Math. 2022, 415, 114476. [Google Scholar] [CrossRef]
- Özköse, F.; Yavuz, M.; Şenel, M.T.; Habbireeh, R. Fractional order modelling of omicron SARS-CoV-2 variant containing heart attack effect using real data from the United Kingdom. Chaos Solitons Fractals 2022, 157, 111954. [Google Scholar] [CrossRef] [PubMed]
- Sintunavarat, W.; Turab, A. A unified fixed point approach to study the existence of solutions for a class of fractional boundary value problems arising in a chemical graph theory. PLoS ONE 2022, 17, e0270148. [Google Scholar] [CrossRef]
- Almeida, R. A Caputo fractional derivative of a function with respect to another function. Commun. Nonlinear Sci. Numer. Simul. 2017, 44, 460–481. [Google Scholar] [CrossRef]
- Banach, S. Sur les opérations dans les ensembles abstraits et leur application aux équations intégrales. Fundam. Math. 1922, 3, 133–181. [Google Scholar] [CrossRef]
- Burton, T.A. A fixed-point theorem of Krasnoselskii. Appl. Math. Lett. 1998, 11, 85–88. [Google Scholar] [CrossRef]
- Kawamura, K.; Koshimizu, H.; Miura, T. Norms on C 1 ([0, 1]) and their isometries. Acta Sci. Math. 2018, 84, 239–261. [Google Scholar] [CrossRef]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations; Elsevier: Amsterdam, The Netherlands, 2006; Volume 204. [Google Scholar]
- Zhu, T. Global attractivity for fractional differential equations of Riemann-Liouville type. Fract. Calc. Appl. Anal. 2023, 26, 2264–2280. [Google Scholar] [CrossRef]
- Vu, H.; Rassias, J.M.; Hoa, N.V. Hyers–Ulam stability for boundary value problem of fractional differential equations with κ-Caputo fractional derivative. Math. Methods Appl. Sci. 2023, 46, 438–460. [Google Scholar] [CrossRef]
- Wang, X.; Luo, D.; Zhu, Q. Ulam-Hyers stability of caputo type fuzzy fractional differential equations with time-delays. Chaos Solitons Fractals 2022, 156, 111822. [Google Scholar] [CrossRef]
- Rosenfeld, J.A.; Dixon, W.E. Convergence rate estimates for the kernelized predictor corrector method for fractional order initial value problems. Fract. Calc. Appl. Anal. 2021, 24, 1879–1898. [Google Scholar] [CrossRef]
- Karaman, B. The global stability investigation of the mathematical design of a fractional-order HBV infection. J. Appl. Math. Comput. 2022, 68, 4759–4775. [Google Scholar] [CrossRef] [PubMed]



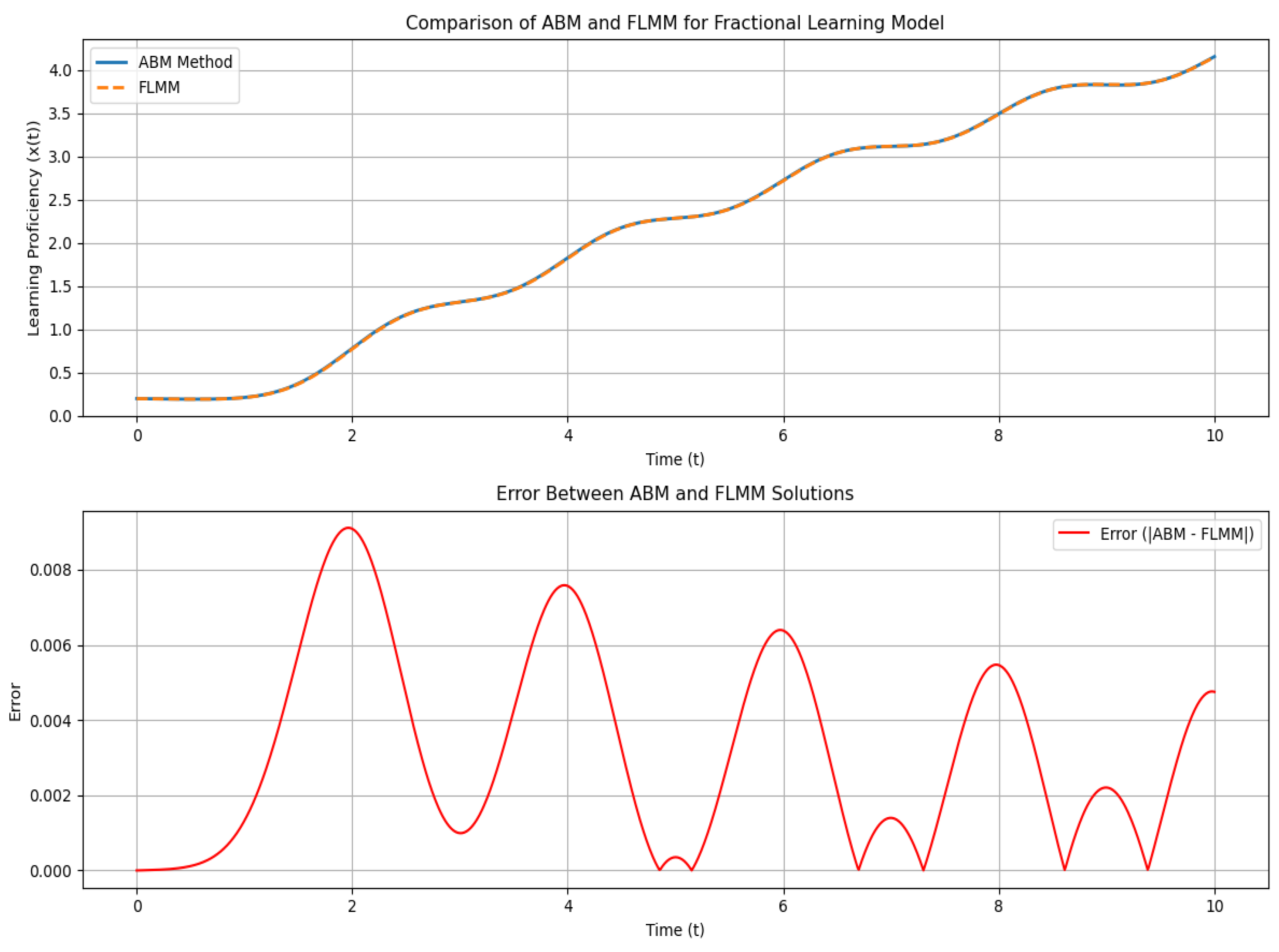
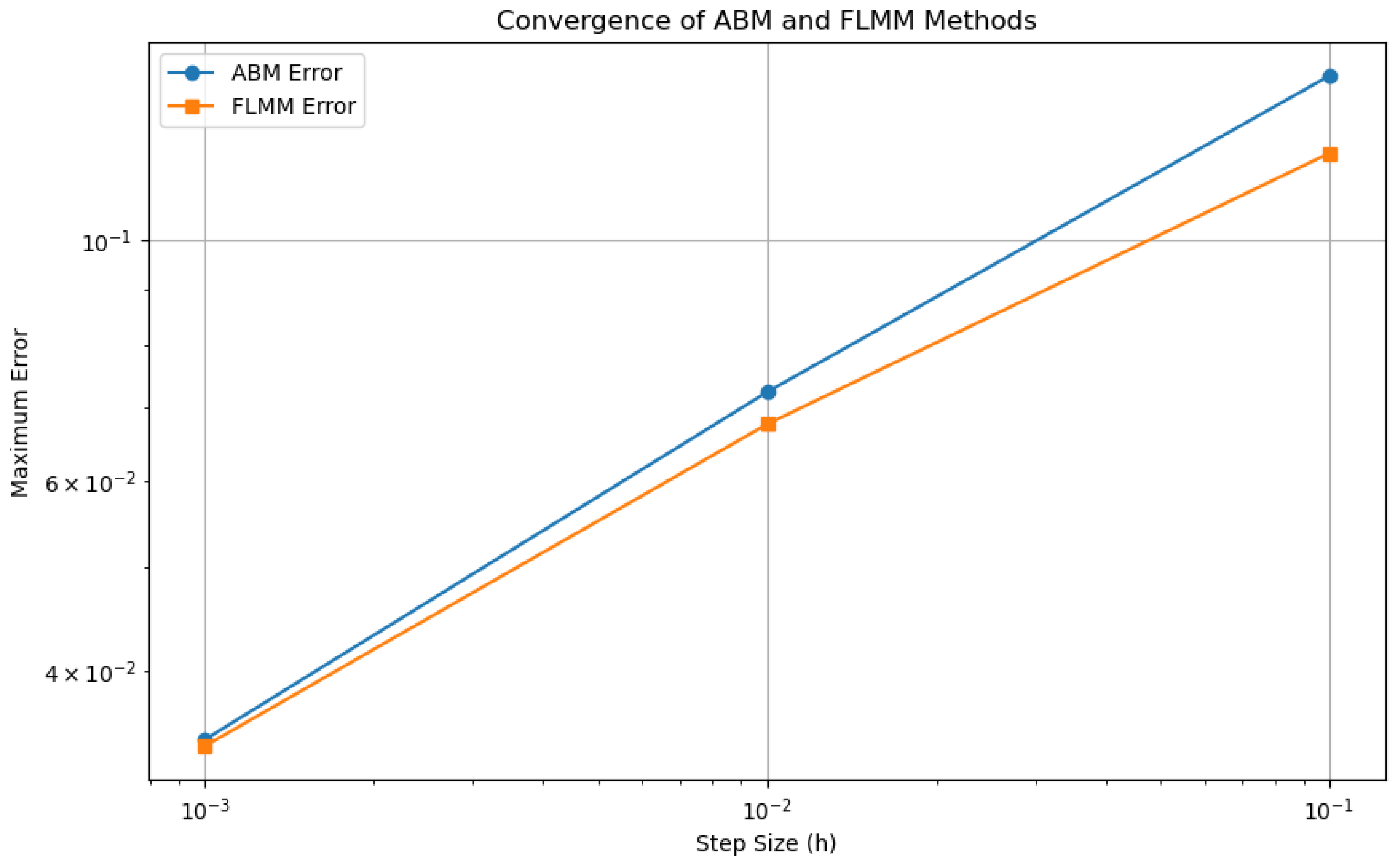

| ABM Solution | FLMM Solution | Max Error | RMSE | ABM Runtime (s) | FLMM Runtime (s) | |
|---|---|---|---|---|---|---|
| (1.02, 0.01) | 2.5751219 | 2.5732136 | 0.0078374 | 0.0035339 | 0.026154 | 0.0068009 |
| (1.10, 0.07) | 2.7576885 | 2.7551044 | 0.0080098 | 0.0038441 | 0.012748 | 0.0054479 |
| (1.23, 0.19) | 3.0060839 | 3.0024821 | 0.0082594 | 0.0044978 | 0.01372 | 0.005466 |
| (1.35, 0.31) | 3.1443561 | 3.1401566 | 0.0084149 | 0.0049633 | 0.0126553 | 0.0052679 |
| (1.47, 0.44) | 3.2219551 | 3.217426 | 0.0085116 | 0.0052406 | 0.0125911 | 0.0052991 |
| (1.55, 0.51) | 3.2456856 | 3.2410621 | 0.0085431 | 0.0053228 | 0.0128849 | 0.0054393 |
| (1.67, 0.64) | 3.2711351 | 3.2664217 | 0.0085757 | 0.0054027 | 0.0126472 | 0.0052738 |
| (1.78, 0.75) | 3.2818758 | 3.2771353 | 0.0085856 | 0.0054279 | 0.0125711 | 0.0053248 |
| (1.89, 0.87) | 3.2878896 | 3.2831445 | 0.0085848 | 0.0054333 | 0.0146072 | 0.00545 |
| (2.00, 0.98) | 3.2906774 | 3.2859394 | 0.0085775 | 0.0054279 | 0.013361 | 0.005218 |
| ABM Solution | FLMM Solution | Max Error | RMSE | ABM Runtime (s) | FLMM Runtime (s) | |
|---|---|---|---|---|---|---|
| (1.02, 0.01) | 2.1691824 | 2.1663326 | 0.0091103 | 0.0040994 | 0.0190721 | 0.0071342 |
| (1.10, 0.07) | 2.3100524 | 2.3065317 | 0.0093127 | 0.0045493 | 0.0123508 | 0.0051861 |
| (1.23, 0.19) | 2.5013948 | 2.496891 | 0.009605 | 0.0053443 | 0.0122812 | 0.0052679 |
| (1.35, 0.31) | 2.6081881 | 2.603116 | 0.0097861 | 0.0058601 | 0.0123289 | 0.0051851 |
| (1.47, 0.44) | 2.6685079 | 2.6631236 | 0.0098981 | 0.0061581 | 0.0126269 | 0.0051892 |
| (1.55, 0.51) | 2.6870838 | 2.6816098 | 0.0099347 | 0.0062459 | 0.0122221 | 0.0052018 |
| (1.67, 0.64) | 2.7071442 | 2.7015849 | 0.009973 | 0.0063315 | 0.0127382 | 0.0052538 |
| (1.78, 0.75) | 2.7156904 | 2.7101053 | 0.0099856 | 0.0063591 | 0.0125258 | 0.0052421 |
| (1.89, 0.87) | 2.7205179 | 2.7149287 | 0.0099865 | 0.0063658 | 0.0126369 | 0.0057559 |
| (2.00, 0.98) | 2.7227754 | 2.7171935 | 0.0099801 | 0.006361 | 0.0131481 | 0.005378 |
| ABM Solution | FLMM Solution | Max Error | RMSE | ABM Runtime (s) | FLMM Runtime (s) | |
|---|---|---|---|---|---|---|
| (1.04, 0.02) | 2.6086714 | 2.6066441 | 0.0078689 | 0.0035803 | 0.0265877 | 0.0055413 |
| (1.06, 0.03) | 2.6409399 | 2.6387959 | 0.0078992 | 0.0036294 | 0.01248 | 0.0052299 |
| (1.08, 0.04) | 2.6719501 | 2.6696918 | 0.0079285 | 0.0036806 | 0.0123467 | 0.0052569 |
| (1.12, 0.05) | 2.7017267 | 2.6993569 | 0.0079566 | 0.0037338 | 0.0123818 | 0.005203 |
| (1.14, 0.06) | 2.7302967 | 2.7278182 | 0.0079837 | 0.0037884 | 0.0130999 | 0.0055909 |
| (1.16, 0.07) | 2.7576885 | 2.7551044 | 0.0080098 | 0.0038441 | 0.0126798 | 0.0053079 |
| (1.18, 0.08) | 2.7839322 | 2.7812454 | 0.0080351 | 0.0039006 | 0.0126419 | 0.0052891 |
| (1.20, 0.09) | 2.8090587 | 2.8062725 | 0.0080597 | 0.0039575 | 0.0127132 | 0.0053508 |
| (1.22, 0.10) | 2.8330999 | 2.8302176 | 0.0080834 | 0.0040146 | 0.0131898 | 0.0064509 |
| (1.24, 0.11) | 2.8560886 | 2.8531133 | 0.0081061 | 0.0040715 | 0.0133493 | 0.0055439 |
| ABM Solution | FLMM Solution | Max Error | RMSE | ABM Runtime (s) | FLMM Runtime (s) | |
|---|---|---|---|---|---|---|
| (1.04, 0.02) | 2.1951016 | 2.1921322 | 0.0091468 | 0.004173 | 0.0279031 | 0.008374 |
| (1.06, 0.03) | 2.2200158 | 2.2169299 | 0.0091825 | 0.0042477 | 0.0123689 | 0.005197 |
| (1.08, 0.04) | 2.2439456 | 2.240746 | 0.0092169 | 0.0043231 | 0.012358 | 0.0052168 |
| (1.12, 0.05) | 2.2669126 | 2.2636028 | 0.00925 | 0.0043987 | 0.0123022 | 0.005199 |
| (1.14, 0.06) | 2.2889402 | 2.2855233 | 0.0092819 | 0.0044742 | 0.0129232 | 0.0053151 |
| (1.16, 0.07) | 2.3100524 | 2.3065317 | 0.0093127 | 0.0045493 | 0.0126967 | 0.00528 |
| (1.18, 0.08) | 2.330274 | 2.326653 | 0.0093423 | 0.0046237 | 0.0126362 | 0.0052989 |
| (1.20, 0.09) | 2.3496307 | 2.3459127 | 0.0093707 | 0.0046973 | 0.012629 | 0.0052691 |
| (1.22, 0.10) | 2.3681484 | 2.3643369 | 0.0093984 | 0.0047696 | 0.0126758 | 0.0052612 |
| (1.24, 0.11) | 2.3858535 | 2.3819518 | 0.0094252 | 0.0048406 | 0.012702 | 0.0053277 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Turab, A.; Nescolarde-Selva, J.-A.; Ali, W.; Montoyo, A.; Tiang, J.-J. Computational and Parameter-Sensitivity Analysis of Dual-Order Memory-Driven Fractional Differential Equations with an Application to Animal Learning. Fractal Fract. 2025, 9, 664. https://doi.org/10.3390/fractalfract9100664
Turab A, Nescolarde-Selva J-A, Ali W, Montoyo A, Tiang J-J. Computational and Parameter-Sensitivity Analysis of Dual-Order Memory-Driven Fractional Differential Equations with an Application to Animal Learning. Fractal and Fractional. 2025; 9(10):664. https://doi.org/10.3390/fractalfract9100664
Chicago/Turabian StyleTurab, Ali, Josué-Antonio Nescolarde-Selva, Wajahat Ali, Andrés Montoyo, and Jun-Jiat Tiang. 2025. "Computational and Parameter-Sensitivity Analysis of Dual-Order Memory-Driven Fractional Differential Equations with an Application to Animal Learning" Fractal and Fractional 9, no. 10: 664. https://doi.org/10.3390/fractalfract9100664
APA StyleTurab, A., Nescolarde-Selva, J.-A., Ali, W., Montoyo, A., & Tiang, J.-J. (2025). Computational and Parameter-Sensitivity Analysis of Dual-Order Memory-Driven Fractional Differential Equations with an Application to Animal Learning. Fractal and Fractional, 9(10), 664. https://doi.org/10.3390/fractalfract9100664






