Electrical Analogy Approach to Fractional Heat Conduction Models
Abstract
1. Introduction
2. Fractional Differential Operators Caputo and Atangana–Balenau
2.1. Caputo Fractional Derivative
2.2. Atangana–Baleanu (AB) Fractional Operator
2.3. Comparative Remarks: Caputo vs. Atangana–Baleanu Operators
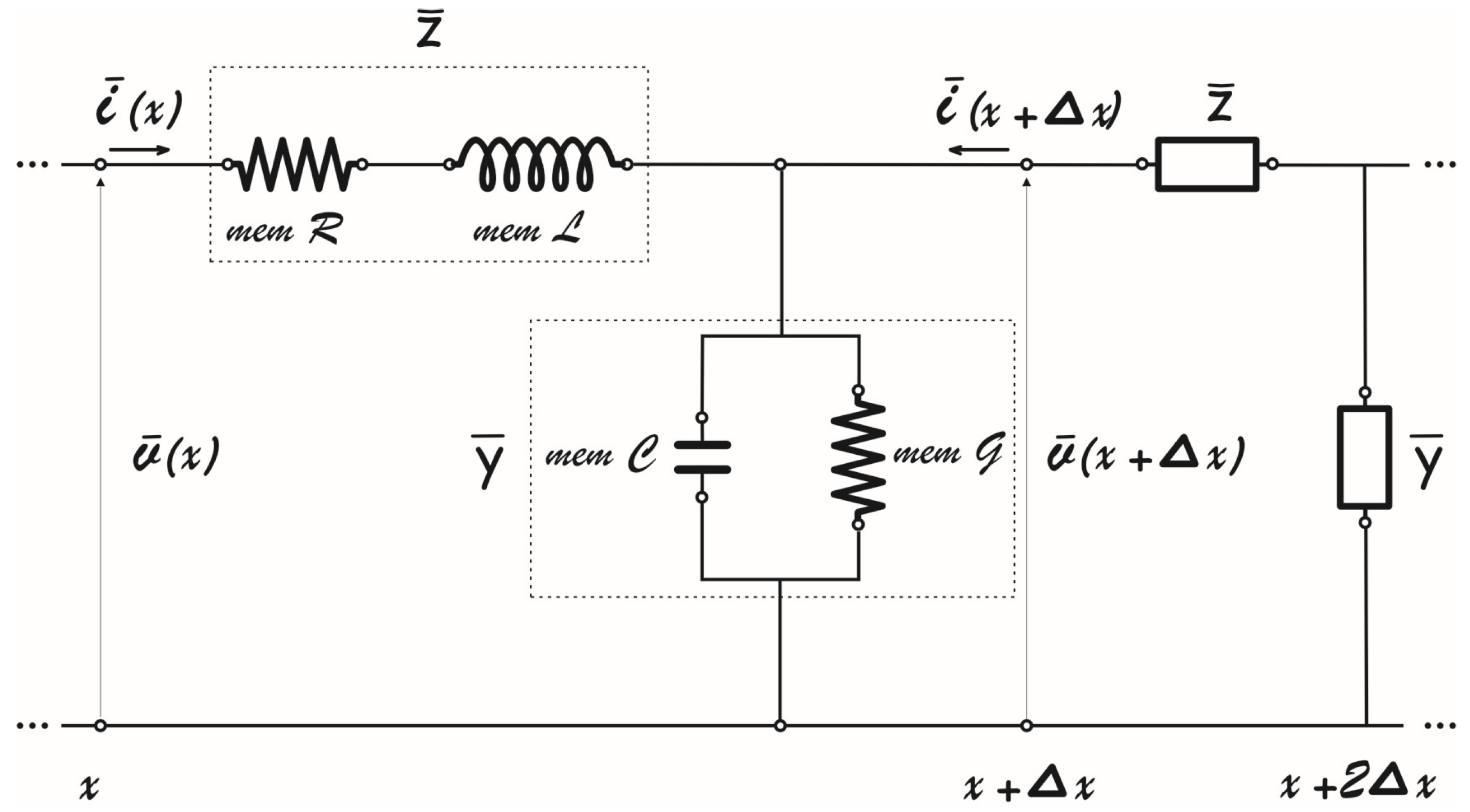
3. Generalized Fractional Heat Conduction Theories and Analogy with Voltage and Current Propagation in a Transmission Line
3.1. Theoretical Framework of Classical Heat Conduction via Constitutive Relations and Energy Conservation
3.2. Fractional Heat Conduction Theories
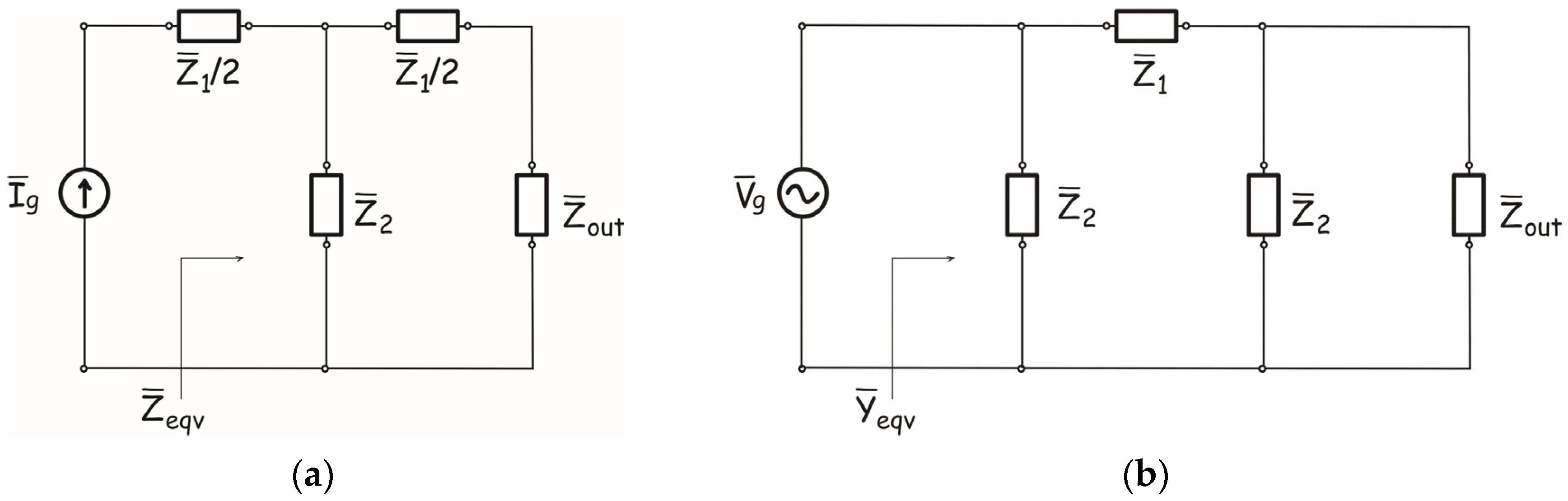
3.3. Generalized Heat Conduction Theories with Fractional Temporal Operators in Laplace Space and Electrical Analogy
Electro-Thermal Analogy
4. Application of Electro-Thermal Analogy for Experimentally Relevant Fractional Heat Conduction Problems
4.1. The Mathematical Description of the Problem
4.2. Surface Temperature Variations in a Semi-Infinite Sample and Spectral Properties of the Characteristic Thermal Impedance
4.3. Analysis and Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Carslaw, H.S.; Jaeger, J.C. Conduction of Heat in Solids; Oxford University Press: Cary, NC, USA, 1959. [Google Scholar]
- Bialkowski, S.E.; Astrath, N.G.C.; Proskurnin, M.A. Photothermal Spectroscopy Methods; John Wiley & Sons: Hoboken, NJ, USA, 2019. [Google Scholar]
- Bertolotti, M.; Voti, R.L. A note on the history of photoacoustic, thermal lensing, and photothermal deflection techniques. J. Appl. Phys. 2020, 128, 23. [Google Scholar] [CrossRef]
- Dubyk, K.; Borisova, T.; Paliienko, K.; Krisanova, N.; Isaiev, M.; Alekseev, S.; Skryshevsky, V.; Lysenko, V.; Geloen, A. Bio-distribution of Carbon Nanoparticles Studied by Photoacoustic Measurements. Nanoscale Res. Lett. 2022, 17, 127. [Google Scholar] [CrossRef]
- Galovic, S.P.; Djordjevic, K.L.; Nesic, M.V.; Popovic, M.N.; Markushev, D.K.; Todorovic, D.M. Time-domain minimum-volume cell photoacoustic of thin semiconductor layer. I. Theory. J. Appl. Phys. 2023, 133, 245701. [Google Scholar] [CrossRef]
- Galovic, S.; Stanimirovic, Z.; Stanimirovic, I.; Djordjevic, K.; Milicevic, D.; Suljovrujic, E. Time-resolved photoacoustic response of thin solids measured using minimal volume cell. Int. Commun. Heat Mass Transf. 2024, 155, 107574. [Google Scholar] [CrossRef]
- Crank, J. The Mathematics of Diffusion; Oxford University Press: London, UK, 1957. [Google Scholar]
- Wunderlich, B. Thermal Analysis of Polymeric Materialse; Springer: Berlin/Heidelberg, Germany, 2005. [Google Scholar]
- Garden, J.-L.; Guillou, H.; Lopeandia, A.; Richard, J.; Heron, J.-S.; Souche, G.; Ong, F.; Vianay, B.; Bourgeois, O. Thermodynamics of small systems by nanocalorimetry: From physical to biological nano-objects. Thermochim. Acta 2009, 492, 16–28. [Google Scholar] [CrossRef]
- Varma-Nair, M.; Wunderlich, B. Non isothermal heat capacities and chemical reactions using a modulated DSC. J. Therm. Anal. 1996, 46, 879–892. [Google Scholar] [CrossRef]
- Saiter, A.; Couderc, H.; Grenet, J. Characterisation of structural relaxation phenomena in polymeric materials from thermal analysis investigations. J. Therm. Anal. Calorim. 2007, 88, 483–488. [Google Scholar] [CrossRef]
- Toda, A.; Saruyama, Y. A modeling of the irreversible melting kinetics of polymer crystals responding to temperature modulation with retardation of melting rate coefficient. Polymer 2001, 42, 4727–4730. [Google Scholar] [CrossRef]
- Saruyama, Y. AC calorimetry at the first order phase transition point. J. Therm. Anal. 1995, 38, 1827–1833. [Google Scholar] [CrossRef]
- Birge, N.O.; Nagel, S.R. Wide-frequency specific heat spectrometer. Rev. Sci. Instrum. 1987, 58, 1464–1470. [Google Scholar] [CrossRef]
- Dixon, P.K. Specific-heat spectroscopy and dielectric susceptibility measurements of salol at the glass transition. Phys. Rev. B 1990, 42, 8179–8186. [Google Scholar] [CrossRef] [PubMed]
- Scott, E.P.; Tilahun, M.; Vick, B. The question of thermal waves in heterogeneous and biological materials. J. Biomech. Eng. 2009, 131, 074518. [Google Scholar] [CrossRef] [PubMed]
- Mitra, K.; Kumar, S.; Vedavarz, A.; Moallemi, M.K. Experimental Evidence of Hyperbolic Heat Conduction in Processed Meat. J. Heat Transf. 1995, 117, 568–573. [Google Scholar] [CrossRef]
- Roetzel, W.; Putra, N.; Das, S. Experiment and analysis for non-Fourier conduction in materials with non-homogeneous inner structure. Int. J. Therm. Sci. 2003, 42, 541–552. [Google Scholar] [CrossRef]
- Forghani, P.; Ahmadikia, H.; Karimipour, A. Non-Fourier Boundary Conditions Effects on the Skin Tissue Temperature Response. Heat Transf. Res. 2017, 46, 29–48. [Google Scholar] [CrossRef]
- Herwig, H.; Beckert, K. Experimental evidence about the controversy concerning Fourier or non-Fourier heat conduction in materials with a nonhomogeneous inner structure. Heat Mass Transf. Und Stoffuebertragung 2000, 36, 387–392. [Google Scholar] [CrossRef]
- Evangelista, L.R.; Lenzi, E.K. Fractional Diffusion Equations and Anomalous Diffusion; Cambridge University Press: Cambidge, UK, 2018. [Google Scholar]
- Norregaard, K.; Metzler, R.; Ritter, C.M.; Berg-Sørensen, K.; Oddershede, L.B. Manipulation and Motion of Organelles and Single Molecules in Living Cells. Chem. Rev. 2017, 117, 4342–4375. [Google Scholar] [CrossRef] [PubMed]
- Mainardi, F. Fractional Calculus and Waves in Linear Viscoelasticity; Imperial College Press: London, UK, 2010. [Google Scholar]
- Podlubny, I. Fractional Differential Equations: An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of Their Solution and Some of Their Applications; Elsevier: Amsterdam, The Netherlands, 1998; Volume 198. [Google Scholar]
- Metzler, R.; Jeon, J.H.; Cherstvy, A.G.; Barkai, E. Anomalous diffusion models and their properties: Non-stationarity, non-ergodicity, and ageing at the centenary of single particle tracking. Phys. Chem. Chem. Phys. 2014, 16, 24128–24164. [Google Scholar] [CrossRef]
- Metzler, R.; Klafter, J. The Random Walk’s Guide to Anomalous Diffusion: A Fractional Dynamics Approach. Phys. Rep. 2000, 339, 1–77. [Google Scholar] [CrossRef]
- Compte, A.; Metzler, R. The generalized Cattaneo equation for the description of anomalous transport processes. J. Phys. A Math. Gen. 1997, 30, 7277–7289. [Google Scholar] [CrossRef]
- Korabel, N.; Klages, R.; Chechkin, A.V.; Sokolov, I.M.; Gonchar, V.Y. Fractal properties of anomalous diffusion in intermittent maps. Phys. Rev. E 2007, 75, 36213. [Google Scholar] [CrossRef]
- Barkai, E. CTRW pathways to the fractional diffusion equation. Chem. Phys. 2002, 284, 13–27. [Google Scholar] [CrossRef]
- Caputo, M.; Fabrizio, M. Applications of new time and spatial fractional derivatives with exponential kernels. Prog. Fract. Differ. Appl. 2016, 2, 1–11. [Google Scholar] [CrossRef]
- Zwanzig, R. Nonequilibrium Statistical Mechanics; Oxford University Press: Oxford, UK, 2001. [Google Scholar]
- Kumar, M.; Rai, K.N.; Rajeev, A. A study of fractional order dual-phase-lag bioheat transfer model. J. Therm. Biol. 2020, 93, 102661. [Google Scholar] [CrossRef]
- Xu, H.Y.; Jiang, X.Y. Time fractional dual-phase-lag heat conduction equation. Chin. Phys. B 2015, 24, 034401. [Google Scholar] [CrossRef]
- Atanackovic, T.M.; Pilipovic, S. On a constitutive equation of heat conduction with fractional derivatives of complex order. Acta Mech. 2018, 229, 1111–1121. [Google Scholar] [CrossRef]
- Somer, A.; Camilotti, F.; Costa, G.F.; Bonardi, C.; Novatski, A.; Andrade, A.V.C.; Kozlowski, V.A.; Cruz, G.K. The thermoelastic bending and thermal diffusion processes influence on photoacoustic signal generation using open photoacoustic cell technique. J. Appl. Phys. 2013, 114, 063503. [Google Scholar] [CrossRef]
- Somer, A.; Galovic, S.P.; Lenzi, E.K.; Novatski, A.; Djordjevic, K. Temperature Profile and Thermal Piston Component of Photoacoustic Response Calculated by the Fractional Dual-Phase-Lag Heat Conduction Theory. SSRN Electron. J. 2022, 203, 123801. [Google Scholar] [CrossRef]
- Somer, A.; Popovic, M.N.; da Cruz, G.K.; Novatski, A.; Lenzi, E.K.; Galovic, S.P. Anomalous thermal diffusion in two-layer system: The temperature profile and photoacoustic signal for rear light incidence. Int. J. Therm. Sci. 2022, 179, 107661. [Google Scholar] [CrossRef]
- Tateishi, A.A.; Ribeiro, H.V.; Lenzi, E.K. The role of fractional time-derivative operators on anomalous diffusion. Front. Phys. 2017, 5, 52. [Google Scholar] [CrossRef]
- Lenzi, E.K.; Somer, A.; Zola, R.S.; da Silva, L.R.; Lenzi, M.K. A Generalized Diffusion Equation: Solutions and Anomalous Diffusion. Fluids 2023, 8, 34. [Google Scholar] [CrossRef]
- Alawaideh, Y.M.; Alkhamiseh, B.M.; Alawideh, S.E.; Baleanu, D.; Abu-Izneid, B.; Asad, J. Hamiltonian Formulation of Generalized Classical Field Systems Using Linear fields’ variables(ϕ, Ai,Aj). J. Stat. Appl. Probab. 2023, 12, 503–518. [Google Scholar] [CrossRef]
- Alawaideh, Y.M. A fractional approach to Hamiltonian-generalized classical fields: The Hamilton-Jacob technique Amman 17110 Amman Lebanon Romania. J. Interdiscip. Math. 2010, 0502, 12. [Google Scholar]
- Suszyński, Z. Thermal model based on the electrical analogy of the thermal processes. AIP Conf. Proc. 1999, 463, 197–199. [Google Scholar] [CrossRef]
- Galović, S.P.; Šoškić, Z.N.; Popović, M.N. Analysis of photothermal response of thin solid films by analogy with passive linear electric networks. Therm. Sci. 2009, 13, 129–142. [Google Scholar] [CrossRef]
- Galovic, S.P.; Markushev, D.K.; Markushev, D.D.; Djordjevic, K.L. Time-Resolved Photoacoustic Response of Thin Semiconductors Measured with Minimal Volume Cell: Influence of Photoinduced Charge Carriers. Appl. Sci. 2025, 15, 7290. [Google Scholar] [CrossRef]
- Krapez, J.-C.; Dohou, E. Thermal quadrupole approaches applied to improve heat transfer computations in multilayered materials with internal heat sources. Int. J. Therm. Sci. 2014, 81, 38–51. [Google Scholar] [CrossRef]
- Maillet, D.; Andre, S.; Batsale, J.C.; Degiovanni, A.; Moyne, C. Thermal Quandupoles Solving the Heat Equation through Integral Transforms; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2000. [Google Scholar]
- Caputo, M. Linear Models of Dissipation whose Q is almost Frequency Independent-II. Geophys. J. R. Astron. Soc. 1967, 13, 529–539. [Google Scholar] [CrossRef]
- Atangana, A.; Baleanu, D. New Fractional Derivatives with Non-Singular Kernel: Theory and Application to Heat Transfer Model. Int. J. Therm. Sci. 2016, 20, 763–769. [Google Scholar] [CrossRef]
- Atangana, A. On the new fractional derivative and application to nonlinear Fisher’s reaction–diffusion equation. Appl. Math. Comput. 2015, 273, 948–956. [Google Scholar] [CrossRef]
- Fahmy, M.A.; Almutlg, A. Boundary element method solution of a fractional bioheat equation for memory-driven heat transfer in biological tissues. Fractal Fract. 2025, 9, 565. [Google Scholar] [CrossRef]
- Hobiny, A.; Abbas, I. The Effect of Fractional Derivatives on Thermo-Mechanical Interaction in Biological Tissues during Hyperthermia Treatment Using Eigenvalues Approach. Fractal Fract. 2023, 7, 432. [Google Scholar] [CrossRef]
- Zhang, Q.; Sun, Y.; Yang, J. Thermoelastic responses of biological tissue under thermal shock based on three phase lag model. Case Stud. Therm. Eng. 2021, 28, 101376. [Google Scholar] [CrossRef]
- Fahmy, M.A.; Almehmadi, M.M. Fractional Dual-Phase-Lag Model for Nonlinear Viscoelastic Soft Tissues. Fractal Fract. 2023, 7, 66. [Google Scholar] [CrossRef]
- Shah, N.A.; Almutairi, B.; Vieru, D.; Lee, B.; Chung, J.D. Bioheat Transfer with Thermal Memory and Moving Thermal Shocks. Fractal Fract. 2023, 7, 629. [Google Scholar] [CrossRef]
- Xu, M.; Tan, W. Intermediate processes and critical phenomena: Theory, method and progress of fractional operators and their applications to modern mechanics. Sci. China Ser. G 2006, 49, 257–272. [Google Scholar] [CrossRef]
- Oldham, K.B.; Spanier, J. The Fractional Calculus Theory and Applications of Differentiation and Integration to Arbitrary Order; Academic press: Cambridge, MA, USA, 1974. [Google Scholar]
- Samko, S.G.; Kilbas, A.A.; Marichev, O.I. Fractional Integrals and Derivatives Theory and Applications; Gordon and Breach Science Publishers: London, UK, 2020. [Google Scholar]
- Cichon, M.; Shammakh, W.; Salem, H.A.H. A Unified Framework for Fractional and Non-Fractional Operators in Some Function Spaces. Fractal Fract. 2025, 9, 441. [Google Scholar] [CrossRef]
- Yang, S.; Song, H.; Zhou, H.; Xie, S.; Zhang, L.; Zhou, W. A Fractional Derivative Insight into Full-Stage Creep Behavior in Deep Coal. Fractal Fract. 2025, 9, 473. [Google Scholar] [CrossRef]
- Abramowitz, M.; Stegun, I. Handbook of Mathematical Functions; Dover Publications, Inc.: New York, NY, USA, 1970. [Google Scholar]
- Rogosin, S.; Gorenflo, R.; Kilbas, A.A.; Mainardi, F. Mittag-Leffler Function, Related Topics and Applications; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Biolek, D.; Garrappa, R.; Mainardi, F.; Popolizio, M. Derivatives of Mittag-Leffler functions: Theory, computation and applications. Nonlinear Dyn. 2025. [Google Scholar] [CrossRef]
- Mainardi, F. Why the mittag-leffler function can be considered the queen function of the fractional calculus? Entropy 2020, 22, 1359. [Google Scholar] [CrossRef]
- Popovic, A.; Šoškic, Z.; Stojanovic, Z.; Cevizovic, D.; Galovic, S. On the applicability of the effective medium approximation to the photoacoustic response of multilayered structures. Phys. Scr. 2012, 2012, 014066. [Google Scholar] [CrossRef]
- Liu, L.; Zheng, L.; Liu, F.; Zhang, X. An improved heat conduction model with Riesz fractional derivatives for biological tissues. Int. J. Heat Mass Transf. 2016, 103, 1191–1197. [Google Scholar] [CrossRef]
- Beybalaev, V.D.; Aliverdiev, A.A.; Yakubov, A.Z.; Ninalalov, S.A.; Amirova, A.A. Mathematical model of heat conduction for a semi-infinite body, taking into account memory effects and spatial correlations. Fractal Fract. 2023, 7, 265. [Google Scholar] [CrossRef]
- Migdal, A. Topological vortexes, asymptotic freedom, and multifractals. Fractal Fract. 2023, 7, 351. [Google Scholar] [CrossRef]
- Migdal, A. To the theory of decaying turbulence. Fractal Fract. 2023, 7, 754. [Google Scholar] [CrossRef]
- Novikov, I.A.; Kolpashipov, V.I.; Shnipp, A.I. Reophysics and Thermophysics of Nonequliubrium Systems; Science and Technology: Minsk, Russia, 1991. [Google Scholar]
- Galovic, S.; Djordjevic, A.I.; Kovacevic, B.Z.; Djordjevic, K.L.; Chevizovich, D. Influence of Local Thermodynamic Non-Equilibrium to Photothermally Induced Acoustic Response of Complex Systems. Fractal Fract. 2024, 8, 399. [Google Scholar] [CrossRef]
- Joseph, D.D.; Preziosi, L. Heat waves. Rev. Mod. Phys. 1989, 61, 41–73. [Google Scholar] [CrossRef]
- Novikov, I.A. Harmonic thermal waves in materials with thermal memory. J. Appl. Phys. 1997, 81, 1067–1072. [Google Scholar] [CrossRef]
- Galović, S.; Kostoski, D. Photothermal wave propagation in media with thermal memory. J. Appl. Phys. 2003, 93, 3063–3070. [Google Scholar] [CrossRef]
- Zhukovsky, K. Operational Approach and Solutions of Hyperbolic Heat Conduction Equations. Axioms 2016, 5, 28. [Google Scholar] [CrossRef]
- Galovic, S.; Čukić, M.; Chevizovich, D. Inertial Memory Effects in Molecular Transport Across Nanoporous Membranes. Membranes 2025, 15, 11. [Google Scholar] [CrossRef]
- Garden, J. Macroscopic non-equilibrium thermodynamics in dynamic calorimetry. Thermochim. Acta 2007, 452, 85–105. [Google Scholar] [CrossRef]
- Garden, J.; Richard, J.; Saruyama, Y. Entropy production in TMDSC. J. Therm. Anal. Calorim. 2008, 94, 585–590. [Google Scholar] [CrossRef]
- Sobolev, S.L. Local non-equilibrium transport models. Physics-Uspekhi 1997, 40, 1043–1053. [Google Scholar] [CrossRef]
- Sobolev, S.L.; Dai, W. Heat Transport on Ultrashort Time and Space Scales in Nanosized Systems: Diffusive or Wave-like? Materials 2022, 15, 4287. [Google Scholar] [CrossRef]
- Prigogine, I. Introduction to Thermodynamics of Irreversible Processes; Interscience Publishers: Geneva, Switzerland, 1961. [Google Scholar]
- Cattaneo, C. Sur une forme de l’equation de la chaleur eliminant la paradoxe d’une propagation instantantee. Compt. Rendu 1958, 247, 431–433. [Google Scholar]
- Vernotte, M. La veritable equation de chaleur. Comptes Rendus Hebd. Des Séances L’academie Des Sci. 1958, 247, 2103–2105. [Google Scholar]
- Landau, L. Theory of the Superfluidity of Helium II. Phys. Rev. 1941, 60, 356–358. [Google Scholar] [CrossRef]
- Peshkov, V.P. SECOND SOUND IN HELIUM II. Sov. Phys. Jetp 1960, 11, 799–805. [Google Scholar]
- Ackerman, C.C.; Guyer, R.A. Temperature pulses in dielectric solids. Ann. Phys. 1968, 50, 128–185. [Google Scholar] [CrossRef]
- Narayanamurti, V.; Dynes, R.C. Observation of Second Sound in Bismuth. Phys. Rev. Lett. 1972, 28, 1461–1465. [Google Scholar] [CrossRef]
- McNelly, T.F.; Rogers, S.J.; Channin, D.J.; Rollefson, R.J.; Goubau, W.M.; Schmidt, G.E.; Krumhansl, J.A.; Pohl, R.O. Heat Pulses in NaF: Onset of Second Sound. Phys. Rev. Lett. 1970, 24, 100–102. [Google Scholar] [CrossRef]
- Huberman, S.; Duncan, R.A.; Chen, K.; Song, B.; Chiloyan, V.; Ding, Z.; Maznev, A.A.; Chen, G.; Nelson, K.A. Observation of second sound in graphite at temperatures above 100 K. Science 2019, 364, 375–379. [Google Scholar] [CrossRef]
- Ding, Z.; Chen, K.; Song, B.; Shin, J.; Maznev, A.A.; Nelson, K.A.; Chen, G. Observation of second sound in graphite over 200 K. Nat. Commun. 2022, 13, 285. [Google Scholar] [CrossRef]
- Tzou, D.Y. A Unified Field Approach for Heat Conduction From Macro- to Micro-Scales. J. Heat. Transf. Asme 1995, 117, 8–16. [Google Scholar] [CrossRef]
- Tzou, D.Y. Macro- to Microscale Heat Transfer: The Lagging Behavior; John Wiley & Sons: Hoboken, NJ, USA, 2014. [Google Scholar]
- Djordjevic, K.L. Photothermal Response of Polymeric Materials Including Complex Heat Capacity. Int. J. Thermophys. 2022, 43, 68. [Google Scholar] [CrossRef]
- Liu, K.-C.; Wang, Y.-N.; Chen, Y.-S. Investigation on the Bio-Heat Transfer with the Dual-Phase-Lag Effect. Int. J. Therm. Sci. 2012, 58, 29–35. [Google Scholar] [CrossRef]
- Askarizadeh, H.; Ahmadikia, H. Analytical analysis of the dual-phase-lag model of bioheat transfer equation during transient heating of skin tissue. Heat Mass Transf. 2014, 50, 1673–1684. [Google Scholar] [CrossRef]
- Sobolev, S.L. Discrete heat conduction equation: Dispersion analysis and continuous limits. Int. J. Heat. Mass. Transf. 2024, 221, 2023–2024. [Google Scholar] [CrossRef]
- Sobolev, S.L. Non-Fourier heat conduction: Discrete vs. continuum approaches. Mech. Res. Commun. 2025, 149, 104512. [Google Scholar] [CrossRef]
- Cole, K.S.; Cole, R.H. Dispersion and absorption in dielectrics I. Alternating current characteristics. J. Chem. Phys. 1941, 9, 341–351. [Google Scholar] [CrossRef]
- Galović, S.; Šoškić, Z.; Popović, M.; Cevizović, D.; Stojanović, Z. Theory of photoacoustic effect in media with thermal memory. J. Appl. Phys. 2014, 116, 024901. [Google Scholar] [CrossRef]
- Popovic, M.N.; Galovic, S.P.; Lenzi, E.K. The Thermoelastic Component of the Photoacoustic Response in a 3D-Printed Polyamide Coated with Pigment Dye: A Two-Layer Model Incorporating Fractional Heat Conduction Theories. Fractal Fract. 2025, 9, 456. [Google Scholar] [CrossRef]
- Somer, A. Photoacoustic Signal of Optically Opaque Two-Layer Samples: Influence of Anomalous Thermal Diffusion. Int. J. Thermophys. 2025, 46, 84. [Google Scholar] [CrossRef]
- Herrera, L. Causal heat conduction contravening the fading memory paradigm. Entropy 2019, 21, 950. [Google Scholar] [CrossRef]
- Telenkov, S.A.; Mandelis, A. Photothermoacoustic imaging of biological tissues: Maximum depth characterization comparison of time and frequency-domain measurements. J. Biomed. Opt. 2009, 14, 044025. [Google Scholar] [CrossRef]
- Pellegrino, N.; Ecclestone, B.R.; Fieguth, P.; Hajireza, P. Time-domain feature extraction for target-specificity in Photoacoustic Remote Sensing Microscopy. arXiv 2022. [Google Scholar] [CrossRef]

| Feature | Caputo Operator | Atangana–Baleanu (ABC) Operator |
|---|---|---|
| Kernel type | Singular kernel with power-law decay (t − τ)−α | Non-singular kernel based on one-parameter Mittag–Leffler function |
| Memory structure | Long-tailed (slowly decaying) memory: strong influence of the distant past | Exponentially tempered memory: smooth fading of past influence |
| Physical meaning | Suitable for systems with slow relaxation | Suitable for systems with multiple relaxation scales |
| Initial conditions | Require classical initial conditions (integer-order derivatives), physically intuitive and practically applicable | Same treatment of initial conditions as Caputo, but extended to nonsingular memory kernels |
| Spectral response | Pure power-law frequency response | Modified spectral response with exponential damping |
| Examples of applications | Tansport of mass, energy or charge in glassy and polymeric systems, biological tissues, amorphous porous materials; | Transport in heterogeneous media with hierarchical structure; neural and cardiac tissue modeling |
| Heat Conduction Theory | Thermal Conductivity | Heat Capacity | Microscopic Picture | Energy (Thermodynamic) Effect |
|---|---|---|---|---|
| Classical parabolic (without memory) | Real, frequency-independent | Real, frequency-independent | Fast localized modes (molecular rotations, bond vibrations). Energy transported by short-lived collective modes (phonons, collective vibrations). | Energy stored in fast local modes; dissipation along the flux due to scattering of collective modes. |
| Debye relaxation (exponentially decaying kinetic memory) | Real, frequency independent | Real + imaginary, frequency-dependent, imaginary part vanishes at low frequencies. | Slow localized modes may be trapped in metastable states; energy transported by short-lived collective modes | Local accumulation in fast modes; additional dissipation within the local volume (imaginary part of complex heat capacity) feeding the entropic reservoir; dissipation along the flux due to scattering. |
| Fractional subdiffusive theory (kinetic memory via fractional operator kernel) | Real, frequency-independent | Real + imaginary, frequency dependent | Describes the full spectrum of localized modes, from those that relax at infinite speed to those with long-lived relaxation; Energy still transported by short-lived collective modes (phonons, collective vibrations). | Frequency-dependent accumulation and dissipation in the local volume; frequency-independent dissipation along the flux due to scattering of collective modes |
| Hyperbolic/damped-wave theory (second sound, SPL; inertial memory via fading kernel) | Real + imaginary, frequency-dependent, imaginary part vanishes at low frequencies. | Real, frequency independent | Energy oscillates between fast localized modes and long-lived delocalized modes (phonons, collective vibrations); wave-like effects arise; no metastable trapping (all local modes infinitely fast). | Accumulation in local modes + additional accumulation in the flux; dissipation, if present, occurs only along the flux. |
| Fractional wave-like theory (inertial memory via fractional operator kernel) | Real + imaginary, frequency dependent | Real, frequency independent | Oscillations between fast localized and multiscale living delocalized modes; hierarchical energy oscillations. No metastable trapping. | Frequency-dependent accumulation in the flux, frequency-independent accumulation in local volume; frequency-dependent dissipation along the energy flux (short-lived and long-lived collective modes) |
| Classical dual-phase-lag (DPL) theory | Real + imaginary, frequency-dependent, imaginary part vanishes at low frequencies. | Real + imaginary, frequency-dependent, imaginary part vanishes at low frequencies. | Combined influence of slow localized and long-lived collective modes. Wave-like effects may be damped or lost depending on collective mode lifetime and local mode relaxation time. | Accumulation in local modes and in the flux; dissipation both in the local volume and along the flux |
| Fractional DPL models | Real+ imaginary, frequency-dependent. | Real + imaginary, frequency-dependent | Influence of fast/slow localized modes and short-/long-lived collective modes. Wave-like effects at high frequency and subdiffusive effects at low frequencies. | Frequency-dependent accumulation in local modes and in the flux; frequency-dependent dissipation in the local volume and along the flux |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Galovic, S.; Popovic, M.N.; Chevizovich, D. Electrical Analogy Approach to Fractional Heat Conduction Models. Fractal Fract. 2025, 9, 653. https://doi.org/10.3390/fractalfract9100653
Galovic S, Popovic MN, Chevizovich D. Electrical Analogy Approach to Fractional Heat Conduction Models. Fractal and Fractional. 2025; 9(10):653. https://doi.org/10.3390/fractalfract9100653
Chicago/Turabian StyleGalovic, Slobodanka, Marica N. Popovic, and Dalibor Chevizovich. 2025. "Electrical Analogy Approach to Fractional Heat Conduction Models" Fractal and Fractional 9, no. 10: 653. https://doi.org/10.3390/fractalfract9100653
APA StyleGalovic, S., Popovic, M. N., & Chevizovich, D. (2025). Electrical Analogy Approach to Fractional Heat Conduction Models. Fractal and Fractional, 9(10), 653. https://doi.org/10.3390/fractalfract9100653







