Abstract
Fractional heat conduction models extend classical formulations by incorporating fractional differential operators that capture multiscale relaxation effects. In this work, we introduce an electrical analogy that represents the action of these operators via generalized longitudinal impedance and admittance elements, thereby clarifying their physical role in energy transfer: fractional derivatives account for the redistribution of heat accumulation and dissipation within micro-scale heterogeneous structures. This analogy unifies different classes of fractional models—diffusive, wave-like, and mixed—as well as distinct fractional operator types, including the Caputo and Atangana–Baleanu forms. It also provides a general computational methodology for solving heat conduction problems through the concept of thermal impedance, defined as the ratio of surface temperature variations (relative to ambient equilibrium) to the applied heat flux. The approach is illustrated for a semi-infinite sample, where different models and operators are shown to generate characteristic spectral patterns in thermal impedance. By linking these spectral signatures of microstructural relaxation to experimentally measurable quantities, the framework not only establishes a unified theoretical foundation but also offers a practical computational tool for identifying relaxation mechanisms through impedance analysis in microscale thermal transport.
1. Introduction
The classical theory of heat conduction, formulated in the early 19th century, is one of the most widely used models in physics and engineering [1]. For more than 150 years, it has been successfully applied in various domains—from civil engineering and geophysics to electronics, biomedicine, and the development of modern experimental techniques based on the photothermal (PT) effect [2,3,4,5,6]. This theory is based on the principle of energy conservation and on Fourier’s constitutive relation between the temperature gradient and the heat flux, a phenomenological relation consistent with the Second Law of Thermodynamics [1]. This formulation leads to a diffusion-type partial differential equation (a parabolic PDE), which describes the temporal and spatial distribution of temperature variations (relative to the ambient temperature) in a system [1,7].
Despite its wide applicability, the classical model exhibits significant limitations in explaining heat transfer in media with complex internal structures such as polymeric [8,9,10,11,12] or glassy materials [13,14,15] and biological tissues [16,17,18,19,20], where anomalous diffusion and wave-like effects emerge as a consequence of the complex dynamics of internal degrees of freedom. To overcome this shortcoming, various fractional models have been developed [21,22,23,24,25].
The literature generally distinguishes several classes of fractional models of heat conduction. Some are derived from probabilistic approaches, most notably the Continuous Time Random Walk (CTRW) framework [25,26,27,28,29], which describes subdiffusion type of anomalous diffusion through a nonlinear dependence of the mean-square displacement on time, , . Most fractional models, however, are based on phenomenological considerations. Among them there are formulations that introduce the concept of inertia in heat flow via fractional time-delayed heat flux [23,30,31], enabling the description of wave-like features of heat transfer. Besides, there are fractional dual phase lag models [32,33,34] that introduce the influence of the thermal displacement in time-delayed heat flux, enabling description of wave-like and anomalous diffusive effects. Another important group consists of time-fractional telegraph models, often referred to as Generalized Cattaneo equations [27], which capture both subdiffusive and superdiffusive anomalous effects as well as wave-like propagation of thermal disturbances by replacing the integer time differential operator with fractional operators [35,36,37,38,39]. Finally, some formulations are derived from Hamilton–Jacobi-type formalisms [40,41], offering alternative perspectives on fractional thermal transport.
However, to the best of our knowledge, the literature still lacks a unified framework for fractional heat-conduction models that would enable systematic comparison and evaluation of their thermodynamic consistency, treatment of irreversibility and dissipation, and their macroscopic, experimentally measurable consequences. Establishing such a framework would be highly valuable, both for advancing the fundamental understanding of internal relaxation processes in complex materials and for interpreting experimentally observed phenomena—such as anomalous diffusion or wave-like effects.
In this work, we demonstrate that identifying two distinct types of memory effects, kinetic memory and inertial memory in energy balance, provides a framework that explains the thermodynamic consistency of fractional models by introducing concept of complex heat capacity and complex thermal conductivity. This motivates the use of analogical methods, in particular electrical analogies [42,43,44,45,46], which provide both a powerful and intuitive framework to clarify the role of fractional differential operators and to enable systematic comparison of different fractional models. We further show that this analogy establishes a general platform for solving spatiotemporal temperature distributions in media where heat conduction is governed by time-fractional models. The framework not only yields deeper physical insight into how different internal relaxation processes related to material memory affect energy storage and dissipation, but also facilitates analytical and numerical solutions through the definition of thermal impedance concept.
Within this framework, we analyze the boundary value problem of a photothermally excited sample using three groups of fractional theories with time-fractional differential operators. The derived expressions allow the determination of surface temperature variations, which are particularly relevant for the interpretation of experimental results in photothermal techniques and other methods based on thermal wave propagation. Special attention is devoted to the role of different fractional operators, with the Caputo [47] and Atangana–Baleanu (in the Caputo sense) [48,49] operators analyzed in detail, emphasizing their distinct implications for the evolution of surface temperature variations. We focused on the Caputo and Atangana–Baleanu–Caputo (ABC) operators because they are most commonly used in interpreting experimental results for materials with complex internal structures and naturally incorporate physically meaningful initial conditions [50,51,52,53,54].
Although the present analysis focuses on Caputo and Atangana–Baleanu–Caputo operators, the framework itself is general and applies to other fractional operators as well. The primary aim is to demonstrate that both the type of memory (kinetic vs. inertial) and the choice of fractional operator crucially affect the thermal impedance and, consequently, the measurable system response to thermal excitation. This highlights the role of thermal impedance as a unifying tool for developing fractional heat conduction models and comparing them with experimental results.
The structure of the paper is as follows. After this introductory section, Section 2 briefly reviews the mathematical properties of the Caputo (C) and Atangana–Baleanu in the Caputo sense (ABC) operators. Section 3 introduces the heat conduction model in the Laplace domain, which, by incorporating two new parameters—complex heat capacity and complex thermal conductivity that depend on the choice of fractional operators—encompasses all fractional heat conduction models with time-fractional differential operators. The analogy with current and voltage propagation in transmission lines is then discussed, and the concept of thermal impedance as a transfer function is defined, describing thermal disturbance propagation in direct relation to complex heat capacity and thermal conductivity. In Section 4, the thermal impedance of a semi-infinite sample is analyzed to avoid boundary condition effects, and spectral analysis is performed to separate the system’s intrinsic response from the temporal shape of the excitation. This illustrates how the presented approach enables a systematic investigation of how kinetic and inertial memory effects, represented by different fractional operators, influence the response. Finally, Section 5 summarizes the main conclusions and discusses the implications of the results for interpreting photothermal experiments and for the further development of fractional heat conduction theories.
2. Fractional Differential Operators Caputo and Atangana–Balenau
Fractional calculus extends the classical notions of differentiation and integration to non-integer orders [55,56,57,58,59] and has proven especially powerful for describing systems with long-term memory and temporal nonlocality [24]. These features are important when modeling anomalous transport of mass, energy, or charge, which cannot be fully captured by integer-order equations.
In this work, we focus on two types of time-fractional operators. The first is the Caputo operator [47,56,57], widely used in physical applications because it incorporates initial conditions in a straightforward manner. The second is the Atangana–Baleanu operator in the Caputo sense (ABC) [48,49], which employs nonsingular kernels and provides a smoother representation of memory effects across multiple time scales.
Physically, the Caputo operator is suited for processes with long-lasting memory, while the ABC operator can capture transient responses with gradually fading memory. Both operators are relevant for transport in complex systems, such as glassy materials, polymers, neural tissue, cell membranes, and disordered porous media.
2.1. Caputo Fractional Derivative
The Caputo fractional derivative of order α ∈ (0, 1) for a sufficiently smooth function f(t) on the interval [0, T] is defined as
where Γ( ) denotes the Gamma function [60].
This operator introduces a power-law memory with a singular kernel, meaning that the present state of the system depends on its entire history, weighted by a slowly decaying function of the form (t − τ)−α. This long-tailed memory describes subdiffusive processes and slow relaxation of subsystems (internal degree og freedom) in complex systems.
An important advantage of the Caputo derivative is that it allows the formulation of initial conditions in terms of integer-order derivatives of f(t), which is consistent with physical intuition and simplifies both numerical implementation and analytical interpretation. In the limiting cases,
The Laplace transform of the Caputo derivative is given by
where
Since the Laplace transform of the Caputo operator is expressed in terms of the function value and its integer-order derivatives at the initial time—quantities that are typically known or can be determined from physical arguments—this formalism enables an efficient analysis of frequency-domain characteristics and provides a convenient tool for solving fractional differential and partial differential equations in which Caputo-type operators appear.
2.2. Atangana–Baleanu (AB) Fractional Operator
The Atangana–Baleanu (AB) operator is a more recent approach to fractional modeling of dynamical systems with memory. Unlike the Caputo operator, it employs a non-singular kernel based on the Mittag–Leffler (ML) function [61,62,63]. This avoids singularities at t = 0 and describes intermediate relaxation regimes not captured by power-law memory.
To allow the use of classical initial conditions expressed in terms of integer-order derivatives, the AB operator is used here in the Caputo sense (the so-called ABC operator), which represents a significant practical advantage for solving real-world problems.
For a sufficiently smooth function f(t), the AB and ABC fractional derivatives of order α ∈ (0, 1) are defined as
where Eα(⋅) is the one parmeter Mittag–Leffler function and B(α) is a normalization coefficient [61,62,63].
The kernel of this operator is a smooth function, which implies that the system possesses exponentially tempered memory—in contrast to the long-tailed power-law memory of the Caputo operator. This property makes it particularly suitable for describing systems with multiple characteristic time scales and intermediate relaxation regimes, phenomena often encountered in biological tissues, polymers, and amorphous materials.
In the limiting cases, the AB operator reduces to the same integer-order forms as the Caputo operator:
The Laplace transform of the ABC operator is given by
which highlights a relaxation dynamics with a spectral response modified by an exponential-type factor, in contrast to the pure power-law spectrum of Caputo-type models.
2.3. Comparative Remarks: Caputo vs. Atangana–Baleanu Operators
Both operators generalize classical derivatives to non-integer orders, but differ in memory type and physical applicability (Table 1).

Table 1.
Systematic overview of properties of Caputo and ABC types of operators.
In summary, the Caputo operator provides a framework for describing systems with persistent long-term memory and anomalous subdiffusive dynamics, while the ABC operator offers additional flexibility for modeling materials and processes characterized by tempered memory effects and multiple characteristic time scales.
3. Generalized Fractional Heat Conduction Theories and Analogy with Voltage and Current Propagation in a Transmission Line
The electro-thermal analogies presented in this paper unify almost all linear heat conduction models, from the classical Fourier law, through generalized non-fractional models (such as second sound, the hyperbolic Cattaneo model, and dual-phase-lag theory), to various fractional models with time-fractional operators. The same principle could, in theory, be extended to nonlinear or nonlinear-fractional models or to spatially non-uniform linear problems at larger scales (e.g., with position-dependent conductivity or heat capacity, similar to the multilayer approach used in non-fractional theories [64]). However, such cases fall outside the present scope. Likewise, linear fractional models involving spatial-fractional operators—such as those based on the fractional Laplacian (superdiffusive transport) [65,66]—would require further development of the analogy, potentially building on approaches applied in the treatment of turbulence [67,68]. These extensions lie beyond the scope of the current work.
3.1. Theoretical Framework of Classical Heat Conduction via Constitutive Relations and Energy Conservation
From a thermodynamic perspective, the first law of thermodynamics (energy balance) for a system excited by an external energy source can be written as [69,70]:
together with the constitutive relations:
Here, denotes the Dirac delta function, f(t) is a dimensionless temporal profile of the heat flux source of intensity S0 [W/m3], u(x,t) [J/m3] represents the change in internal energy density associated with temperature variations [K], [W/m2] is the heat flux. Temperature variation is defined by where is the initial temperature of the system in equilibrium with ambient and ambiental temperature (before the action of thermal source).
In classical heat conduction, both constitutive relations are linear and temporally local:
where is volumetric heat capacity [J/(K·m3)], is mass density [kg/m3], is specific heat at constant pressure [J/(K·kg)], and k is thermal conductivity [W/(m·K)].
Substituting Equations (11) and (12) into Equation (8) yields the classical diffusion equation:
Equation (13) predicts that temperature disturbances propagate instantaneously across the system, implying infinite speed of heat propagation [71,72,73,74,75]. This unphysical result arises from the temporal locality of the constitutive relation in Equation (12), which assumes that the heat flux at a given point depends only on the temperature gradient at the same point and time, neglecting any effects from previous times—i.e., the inertial memory of energy carriers in the system [71,73,74,75].
Mathematically, accounting for these memory effects leads to wave-like or damped wave models instead of the parabolic diffusion description of classical theory, allowing for finite-speed propagation [71,72,73,74]. However, temporal nonlocality in the heat flux relation alone does not resolve another limitation of classical theory: it still treats system evolution as an ergodic process in phase space [9,76,77].
From a thermodynamic viewpoint, with the first law (Equation (8)) and a local constitutive link between internal energy and temperature (Equation (11)), the temperature gradient acts as the sole affinity driving the system toward global equilibrium, regardless of energy carrier inertia [9]. It means that hyperbolic theories, like the classical diffusion equation, assume that infinitesimal system volumes instantaneously reach local equilibrium. In other words, temporal locality of constitutive relation between density of internal energy and scalar temperature field (Equation (11)) neglects the kinetic memory of the system.
From these considerations, two types of memory emerge: (i) inertial memory: associated with temporal nonlocality in the relation between heat flux and temperature gradient, giving rise to wave-like propagation and (ii) kinetic memory associated with temporal nonlocality in the relation between internal energy and temperature, producing an additional thermodynamic driving force that guides the system toward global equilibrium, not necessarily through a sequence of local equilibrium states [76,77,78,79,80].
This distinction provides a foundation for fractional heat conduction models, where temporal nonlocality of the energy conservation law arises naturally from introducing fractional derivatives in one or both constitutive relations (Equations (9) and (10)).
3.2. Fractional Heat Conduction Theories
The temporal nonlocality of the constitutive relation in Equation (9), reflecting the kinetic memory of the system, can be modeled by introducing a fractional differential operator:
Here, the memory kernel of the fractional operator is a dimensionless function describing the kinetic memory, and is the fractional volumetric heat capacity with dimensions [Jsα/m3K].
Substituting Equation (14) for Equation (9) in the energy conservation law (Equation (8)) leads to a nonlocal energy balance, which, together with Equation (10), gives the first type of fractional heat conduction theory, mathematically expressed as a linear fractional diffusion equation:
Typically, the Caputo fractional derivative is used (Section 2.1), while more recently the ABC derivative has become popular (Section 2.2). Equation (15) with Caputo type of operator corresponds to subdiffusion, which can also be derived from the stochastic CTRW approach, where the mean squared displacement of energy carriers is nonlinearly dependent on time [27,28]. This links anomalous diffusion effects to the kinetic memory of the system.
The effect of inertial memory can similarly be introduced in the relation between the temperature gradient (thermodynamic force) and its conjugate heat flux (Equation (10)) via a fractional differential operator:
Substituting Equation (16) into Equation (8), while assuming a local relation between internal energy change and temperature (Equation (11)), yields the second type of fractional heat conduction theory:
Analogous to the hyperbolic Cattaneo–Vernotte equation [81,82], Equation (17) can not describe subdiffusion or local-non-equilibrium movement of the system towards global equilibrium with surroundings. Therefore, inertial memory is associated only with sharper thermal wavefronts, superdiffusive behavior, and finite-speed propagation, i.e., wave-like effects.
If both constitutive relations (Equations (9) and (10)) are generalized using fractional operators (Equations (14) and (16)), the resulting theory incorporates both kinetic and inertial memory effects, allowing for the description of anomalous diffusion and wave-like propagation simultaneously, as well as local non-equilibrium movement of the system across phase space:
From this point of view, it is important to note that fractional DPL models [32,33] introduce inertial memory explicitly and kinetic memory implicitly, via complex nonlocal relations between heat flux, temperature gradient and thermal displacement. They can be linked to Equation (18) by choosing appropriate fractional operators or combining fractional derivatives with phase delays between generalized thermodynamic forces (temperature gradient and scalar temperature field) and their conjugate fluxes (heat flux and internal energy).
Similarly, fractional telegraph-equation models (known in the literature as Generalized Cattaneo Equations (GCE) [27] or models derived via Hamilton–Jacobi formalism [45,46] follow the same thermodynamic consistency and could be considered from point of view memory effects caused kinetic and inertial memory of the system.
Interestingly, Equation (15), which represents a fractional generalization of the internal energy–temperature relation, reduces to the classical Debye relaxation theory when the power-law kernel (Caputo) or Mittag–Leffler kernel (ABC) is replaced by an exponentially decaying kernel. In this case, a phase lag appears between the internal energy density and the scalar temperature field, a feature commonly used to describe thermal propagation in glasses and amorphous materials [14].
Similarly, Equation (17) reduces to the Cattaneo–Vernotte hyperbolic model when the convolution kernel in Equation (9) is replaced by an exponentially decaying kernel [72,73]. The Cattaneo–Vernotte model was originally developed as a generalization of the second-sound model of heat conduction (undamped wave propagation) [83] at low temperatures close to liquid helium temperature [84,85,86,87], and it has more recently been applied to 2D materials in the 100–200 K range [88,89].
Finally, if exponentially decaying kernels are chosen in both relations, the resulting framework recovers the dual-phase-lag (DPL) theory [90,91], which has been widely employed in the analysis of polymers, macromolecular structures, nanostructures, and biological tissues [92,93,94].
3.3. Generalized Heat Conduction Theories with Fractional Temporal Operators in Laplace Space and Electrical Analogy
In this subsection, an electrical analogy is introduced, which relates thermal memory effects to electrical elements (memory resistors, memory capacitors, and memory inductors) and clarifies the physical meaning of fractional operators in thermodynamics.
These operators cause a frequency-dependent redistribution of energy accumulation and dissipation in a thermally excited system, influencing temperature evolution and phenomena observed in calorimetric and photothermal experiments [2,3].
Electro-Thermal Analogy
Applying the Laplace transform to Equation (15), and assuming , gives a linear differential equation in the complex domain describing the first type of fractional heat conduction
where denotes the Laplace transform of f(t). The complex heat capacity in Equation (19) is defined as:
As can be seen from Equation (20), the spectrum of complex heat capacity depends on the spectral properties of memory kernel of fractional differential operator, . For the Caputo derivative, the complex heat capacity is:
while for the ABC derivative, it is:
The real and imaginary parts are obtained by mapping from the s-plane to the jω axis (j is the imaginary unit) and depend on the type of fractional operator. For Caputo and ABC operators, the real and imaginary parts of complex heat capacity are given by:
where .
Similarly, applying the Laplace transform to Equation (17), assuming the system was initially at equilibrium (), yields the equation describing the second type of fractional heat conduction:
where the complex thermal conductivity is
For Caputo and ABC operators, complex thermal conductivities are given by:
Real and imaginary parts of complex thermal conductivity for Caputo and ABC operators are:
Applying the Laplace transform to Equation (18) gives:
where complex heat capacities and complex thermal conductivities for different operators are given by Equations (21), (22), (25) and (26) and their real and imaginary parts by Equations (23), (24), (31) and (32) for Caputo type of operator and Equations (25), (26), (33) and (34) for ABC type of operator.
Each fractional theory (Equations (12), (20) and (28)) is formally analogous to current and voltage propagation in an electrical line, where energy conservation law corresponds to Kirchhoff’s current law and the heat-flux-temperature gradient relation corresponds to Kirchhoff’s voltage law (spatially local and global).
In this analogy, temperature variation corresponds to potential difference , heat flux corresponds to current , and internal energy density corresponds to charge storage. Longitudinal impedance and admittance define the relations between temperature variations and heat flux (see Figure 1, compare to discrete model in [95,96]).
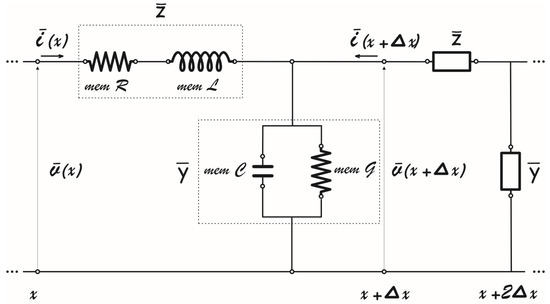
Figure 1.
Electrical analogue of fractional heat propagation: transmission line in continuum approximation.
The longitudinal impedances and admittances differ for each type of theory.
For the first group of fractional theories (Equation (19)), which include only kinetic memory effects, we obtain real longitudinal impedance and complex longitudinal admittance:
For second group of fractional theories (Equation (27)) that include only inertial memory effect, we obtain
For third group of fractional theories (Equation (35)) that include both kinetic and inertial memory effects, we obtain:
In summary, introducing the effect of kinetic memory leads to the first class of theories, which describe media with real thermal conductivity but complex heat capacity. Considering only inertial memory gives rise to the second class of theories, which describe media with real heat capacity but complex thermal conductivity. Finally, when both types of memory are taken into account, one arrives at the third class of theories, which describe heat conduction in media characterized by both complex heat capacity and complex thermal conductivity.
Applying the electro-thermal analogy to classical parabolic heat conduction theory, it can be concluded that the real heat capacity describes reversible energy storage in fast local modes (such as molecular rotations, bond stretching, or intramolecular vibrations), while the real thermal conductivity accounts for irreversible dissipation along the flux (primarily through scattering of collective carriers such as phonons or related excitations).
When kinetic memory is introduced (Equations (36) and (37)), an additional dissipative channel appears, represented by the imaginary part of the heat capacity. Microscopically, this corresponds to local vibrational modes that become trapped and partially converted into metastable states, thereby feeding the entropic reservoir.
By contrast, inertial memory contributes a reversible accumulation channel, expressed by the imaginary part of the thermal conductivity (Equations (38) and (39)). This reversible accumulation arises due to the inertia of long-lived collective modes, which temporarily store energy within the heat flux before it is redistributed or dissipated. Together with standard storage in the local volume, this mechanism allows oscillatory energy exchange between different types of internal degrees of freedom, ultimately enabling the formation of a propagating temperature wavefront with finite speed.
The full picture thus combines scattering, metastable-state formation, and oscillatory energy transfer between distinct internal degrees of freedom, with reversible flux accumulation physically linked to the inertia of long-lived collective modes.
A comparison with generalized non-fractional models of heat conduction—such as the Debye relaxation model, the hyperbolic Cattaneo model, and the Dual-Phase-Lag (DPL) model—shows that exponentially decaying (fading) kinetic and inertial memory produces effects similar to those obtained with fractional operators. These include additional dissipative channels in the local volume or reversible energy accumulation in the heat flux, associated with trapped vibrational modes and oscillatory energy exchange between distinct internal degrees of freedom. The essential difference, however, lies in the way memory is represented. In non-fractional models, exponentially decaying kernels describe fading finite-time memory, characterized by a single relaxation delay between thermodynamic forces and their conjugate fluxes. By contrast, fractional operators introduce complex frequency-dependent equivalent electrical elements—analogous to those in dielectric Cole–Cole models [97]—that capture long-tailed or tempered memory effects involving multiple characteristic time scales. In this way, they describe hierarchical multiscale relaxations of internal degrees of freedom and the multiscale lifetimes of collective modes, which together govern the complex dynamics of thermal conduction in structurally heterogeneous materials.
Finally, the table review of this consideration is given below (Table 2).

Table 2.
Systematic overview of kinetic and inertial memory effects, based on the electrical-analogy approach.
4. Application of Electro-Thermal Analogy for Experimentally Relevant Fractional Heat Conduction Problems
Heat conduction problems in practical experiments can be efficiently analyzed using the electro-thermal analogy introduced in Section 3. In this analogy (Figure 1), the heat conduction equations are treated in the same way as wave propagation in a transmission line, governed by two key parameters: the propagation coefficient (wave vector) and the characteristic impedance of the line [5,73,98,99,100].
In this paper, we apply this analogy, together with the transfer function concept, to solve the problem of heat propagation and calculate surface temperature variations. This approach proves to be efficient for analyzing fractional memory effects and, consequently, the complex dynamics of internal degrees of freedom in experimentally measured signals from biological membranes, tissues, glassy systems, and polymeric materials.
4.1. The Mathematical Description of the Problem
To solve the heat conduction problem in a way suitable for practical thermal experiments, we use the analogy shown in Figure 1. Within this framework, heat conduction can be described by the following relations:
Here, the influence of an external energy source is described through the boundary condition at x = 0. The excitation of the sample can be represented either as an analog current source when the excitation is an external heat flux, as in photothermal methods:
or as an analog voltage source when the excitation is a temperature variation at the sample surface:
In the above equations (Equations (44) and (45)), denotes the Laplace transform of a dimensionless, time-dependent function describing the temporal evolution of the excitation. Symbol represents the variation in surface temperature relative to the equilibrium temperature, and S0 denotes the excitation heat flux.
Based on Equations (42) and (43), the propagation coefficient (wave vector) and the characteristic thermal impedance can be defined as:
In experiments, typically only the heat flux or surface temperature variations at the sample boundary are measured (either directly or indirectly). Therefore, it is particularly important to determine these quantities, rather than the complete space–time distribution. Using the analogy shown in Figure 1 and the expressions (46) and (47), the relation between surface variations in temperature and heat flux can be determined through the equivalent two-port network (T or Π network) shown in Figure 2, where the impedances of the equivalent circuits can be expressed via the propagation coefficient (Equation (46)) and the characteristic thermal impedance (Equation (47)) [42,43,44].
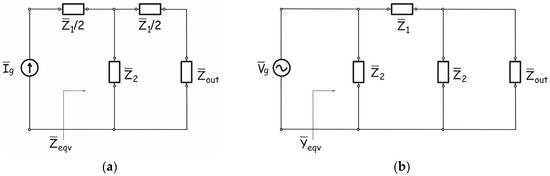
Figure 2.
Equivalent quadripoles used for calculating surface variations in temperature or heat flux. (a) Equivalent (symmetric two-port) network for temperature (T-network); (b) Equivalent (symmetric two-port) network for heat flux (П network). Symbol denotes the equivalent thermal impedance of the sample backing, allowing the representation of different boundary conditions.
The surface temperature variations at the boundary subjected to an external heat flux, as in PT methods, can be described by:
where denotes the equivalent thermal impedance of the system. This depends on the thermal properties of the sample (complex heat capacity and complex thermal conductivity, see Figure 2a, Equations (46)–(49), and Figure 1), on the boundary condition at x = L (the thermal impedance of the backing, see Figure 2a), as well as on the temporal dependence of the excitation (see Figure 2a, Equations (44) and (45). Variable L represents the thickness of the sample.
The heat flux variations at the surface excited by a time-dependent temperature change (as in AC calorimetric methods) can be described by:
where denotes the equivalent thermal admittance of the system. Similarly to , it depends on the thermal properties of the sample, the boundary condition at x = L, and the temporal form of the excitation (see Figure 2b).
It is important to note that the equivalent thermal impedance and admittance seen by the heat source depend on the boundary conditions at x = L, through the concept of the backing thermal impedance (see Figure 2). If , the case corresponds to an adiabatic boundary (zero heat flux). If , the case corresponds to zero temperature variation at the boundary. For a semi-infinite sample, reduces to the characteristic thermal impedance of the medium, (Equation (47)). More generally, all other cases involving more complex boundary conditions can also be described consistently through the concept of the backing thermal impedance.
In the following, we will analyze the surface temperature variations in a semi-infinite sample.
4.2. Surface Temperature Variations in a Semi-Infinite Sample and Spectral Properties of the Characteristic Thermal Impedance
For a semi-infinite sample uniformly excited by a surface heat flux, as in photothermal methods [98], the boundary conditions are:
Based on Equations (48) and (49) and equivalent circuit in Figure 2a, the equivalent thermal impedance of a semi-infinite sample equals the characteristic thermal impedance of the material [73]. In that case, the corresponding electrical scheme is simplified to that shown in Figure 3.
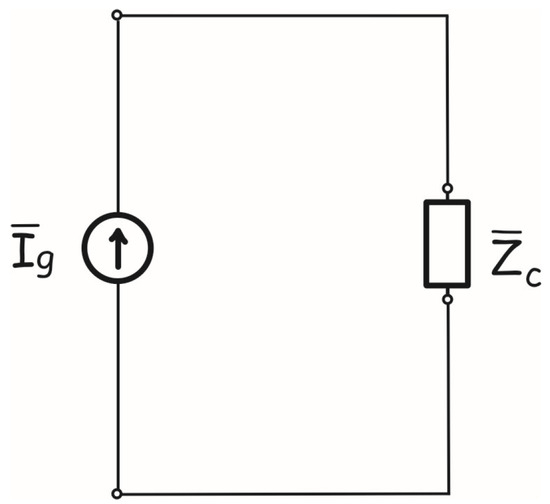
Figure 3.
Equivalent electrical scheme for calculating surface temperature variations in a semi-infinite sample.
According to Figure 3, the surface temperature variations in a semi-infinite sample can be expressed as:
Equation (54) models the surface temperature variations as the system’s response to a time-dependent excitation applied at the sample surface. The equivalent thermal impedance is determined by the characteristic thermal impedance of the system (Equation (45)), which depends on both the complex thermal conductivity and complex heat capacity.
The time-domain evolution of the surface temperature can be obtained by performing the inverse Laplace transform of Equation (54), representing the convolution of the characteristic thermal impedance with the Laplace-transformed excitation signal [5,44]. This approach is general and can be applied to different temporal profiles of excitations used in various time-domain experimental methods, including finite-length samples (where the transfer function corresponds to the equivalent thermal impedance seen by the source, see Figure 2).
In the following, we analyze the spectral properties of the characteristic thermal impedance for each fractional theory and for different fractional operators within each theory. This is equivalent to analyzing the spectral properties of the Green’s function for surface temperature variations, which fully characterizes the system’s frequency response regardless of the specific excitation, corresponding to frequency-domain spectroscopy methods such as those used in photothermal techniques.
Starting from Equations (28)–(33) and Equation (45), and transforming from the Laplace domain (s) to the frequency domain (jω), one can derive expressions for the characteristic thermal impedance of systems with long-tailed or tempered memory.
The first group of fractional theories, for both Caputo and Atangana–Baleanu (ABC) types of fractional operators, predicts the following spectral dependence of the thermal impedance:
For the second group of theories, the spectral characteristics of the characteristic thermal impedance for Caputo and ABC operators are given as:
Finally, for the third group of fractional theories, the corresponding models of the characteristic thermal impedance for Caputo and ABC operators are:
or their combinations, e.g., when the kinetic memory is represented by a long-tail memory (Caputo-type operator) while the inertial memory is represented by tempered memory (the ABC-type operator) (Equation (61)), or in other combinations (Equation (62)):
4.3. Analysis and Discussion
The characteristic thermal impedance predicted by the first group of theories (Equations (55) and (56)) that consider only fractional kinetic memory reduces to the characteristic thermal impedance predicted by the classical parabolic diffusion theory of heat conduction for . The modulus of this impedance tends to infinity when and asymptotically approaches zero when , as [73]. The phase of the characteristic thermal impedance is constant (frequency-independent) in this case and indicates that, as in the classical diffusion theory, there exists a phase shift between the excitation heat flux and the surface thermal variations, which is equal to , and independent of the type of fractional operator.
When in Equation (55), the characteristic thermal impedance predicted by the fractional model from the first group (complex thermal capacitance and real thermal conductivity) with the Caputo-type operator yields a constant and real thermal impedance over the entire frequency range, i.e., without any phase shift. In other words, in this case the characteristic thermal impedance reduces to the equivalent thermal resistance equal to .
If, within the first group of fractional theories, the ABC operator is used instead of the Caputo operator, then according to Equation (56) for , one obtains a frequency-dependent thermal impedance
When , the modulus of this impedance tends to infinity, while for , the modulus of this impedance tends to a finite constant value different from zero, . The phase of the characteristic thermal impedance is also frequency-dependent and varies from for to when , indicating that the ABC-type operator at high frequencies essentially predicts a phase lag of surface thermal variations that is nearly the same as in the classical model, while at low frequencies it predicts for larger phase lag.
Based on the above considerations, it can be concluded that the differences between Caputo and ABC-type operators are reflected in the amplitude and phase spectra of the thermal impedance. In other words, variations in the dynamics of multiscale relaxations within spatially local modes manifest as distinct signatures in the characteristic thermal impedance of the sample. When the order of the fractional operator approaches one, these differences diminish, and the characteristic thermal impedance predicted by the first group of fractional models converges toward that predicted by classical diffusion theory.
The characteristic thermal impedance predicted by the second group of theories (Equations (57) and (58)), which consider only fractional inertial memory, reduces to the characteristic thermal impedance of the classical parabolic diffusion theory of heat conduction if as well as to that of the first group of fractional theories for .
For , the Caputo-type operator in the second group of theories (Equation (57)) predicts a frequency-dependent characteristic thermal impedance whose modulus tends to infinity when , while for the modulus asymptotically approaches zero as , i.e., this model exhibits a much faster convergence than the classical diffusion model. The phase of the characteristic thermal impedance is constant in this case and equal to , which means that the second group of theories with the Caputo operator predicts that the characteristic thermal impedance behaves as an equivalent frequency-dependent inductance.
The ABC-type operator for in the second group of theories (Equation (58)) predicts an infinite amplitude of the characteristic thermal impedance and a phase equal to at all frequencies. Interestingly, such a characteristic thermal impedance is predicted by undamped wave-type hyperbolic models, such as the second sound model or the hyperbolic Cattaneo–Vernotte model in the limit of infinite thermal relaxation time. These models are associated with long-time inertial memory that does not decay with time [101], and can be microscopically linked to long-lived degrees of freedom that prevent the energy introduced into the system from dissipating into the entropic reservoir, instead allowing its resonant transfer through the system.
In the third group of models, which considers both fractional memory, we analyze only the case in order to examine how different fractional operators affect the complex thermal impedance. In this case, Equations (59)–(62) reduce to the following expressions:
From the analysis of Equation (64) for , it follows that the model with the Caputo operator from the third group predicts the same characteristic thermal impedance as the Caputo operator from the first group of models for (i.e., the characteristic thermal impedance behaves as a frequency-independent equivalent thermal resistance equal to . For , the result coincides with the characteristic thermal impedance obtained in the first group of theories for or in the second group of theories for , namely the same impedance as predicted by the classical diffusion theory. For , the third group of models yields the same characteristic thermal impedance as the second group of theories with the Caputo operator and , which corresponds to a frequency-dependent amplitude of the characteristic thermal impedance, where the modulus tends to infinity when , while for the modulus asymptotically approaches zero as . The phase of the characteristic thermal impedance in this case is constant and equal to .
For the ABC-type operator and , Equation (65) reduces to Equation (63), which means that the modulus of the characteristic thermal impedance tends to infinity when while for the modulus approaches a constant value different from zero, . The phase of the characteristic thermal impedance varies from for to when . This is exactly the same behavior of the characteristic thermal impedance as that predicted by the first group of theories with the ABC operator and .
For , Equation (58) reduces to
which is not equal to the characteristic thermal impedance predicted by either the first group of theories with the ABC operator and , or the second group of theories for , i.e., it does not reduce to the characteristic thermal impedance given by the classical diffusion theory. The only similarity is that, also in this model, the amplitude of the characteristic thermal impedance ranges from infinitely large values when to zero when . This model predicts a complex frequency dependence of the phase of the characteristic thermal impedance for .
For , the ABC operator predicts an infinite amplitude of the characteristic thermal impedance and a constant phase equal to at all frequencies, as in the second group of theories with the ABC operator for , i.e., in the same way as wave-type models (the second-sound model or the hyperbolic Cattaneo–Vernotte model in the limit of infinite thermal relaxation time).
Based on the above considerations, it can be concluded that in the amplitude and phase spectra of the thermal impedance in the third group of theories, a pronounced difference is observed between the effects of the Caputo and ABC operators. Nevertheless, both operators in the third group of models predict that the characteristic thermal impedance reflects the complex dynamics of spatially localized and spatially nonlocal internal degrees of freedom.
If, in the third group of theories, the inertial and kinetic memory are described by different types of fractional operators, for α = β = γ two distinct models of the characteristic thermal impedance are obtained, Equations (59) and (60).
If the kinetic memory is described by the Caputo-type operator and the inertial memory by the ABC operator, then from Equation (66) for the thermal impedance is found to be frequency-independent and real (equivalent to a thermal resistance), identical to the result obtained in the first group of theories with the Caputo operator and . For , this model predicts a complex frequency dependence of the characteristic thermal impedance, whose amplitude tends to infinity when and asymptotically approaches zero when . For , the model predicts an infinite amplitude of the characteristic thermal impedance and a constant phase equal to at all frequencies, just as in the second group of theories with the ABC operator for , or equivalently, as in undamped wave-type models, or the third group of theories with the ABC operator and .
If the kinetic memory is described by the ABC operator and the inertial memory by the Caputo operator, then for Equation (67) yields a characteristic thermal impedance identical to that of the first group of theories with the ABC operator and . For , this model predicts a complex frequency dependence of the characteristic thermal impedance, whose amplitude tends to infinity when and asymptotically approaches zero when . For , this theory predicts a frequency-dependent characteristic thermal impedance whose modulus tends to infinity when and asymptotically decays to zero as , with a constant phase equal to , exactly as in the second group of theories with the Caputo operator when .
Finally, each of the theories—whether involving a single type of fractional operator or a combination thereof—leaves a unique signature in the characteristic thermal impedance. This indicates that thermal impedance spectroscopy can be employed to identify the theory that best captures the dynamics of the internal degrees of freedom in a given material, as well as to monitor the complex dynamics of these internal modes.
5. Conclusions
We unify diverse fractional heat conduction models through the fundamental concepts of kinetic and inertial memory, capturing the thermodynamic foundation of fractional models. Building on this unification, we introduce an electrical analogy in which fractional operators are mapped onto complex heat capacity and complex thermal conductivity. This mapping demonstrates that long-living and slowly relaxing internal degrees of freedom govern the redistribution of accumulated and dissipated energy in the excited system.
Within this framework, thermal impedance emerges as an experimentally measurable property directly linked to the complex heat capacity and conductivity of the material, providing access to the multiscale relaxation dynamics of microscopically heterogeneous systems. Using a semi-infinite sample as a case study, we demonstrated how the interplay of kinetic and inertial memory, described by different fractional models and operator types, affects the characteristic thermal impedance.
Three linear fractional theories were analyzed, each formulated with time-fractional operators of Caputo and ABC type. Every theory, and every operator within it, leaves a unique signature in the spectrum of the characteristic thermal impedance, demonstrating the sensitivity of thermal impedance spectroscopy to different fractional models. Importantly, the proposed framework can be extended to other linear fractional theories with time fractional differential operators, as well as to additional fractional differential operators reported in the literature, including the Riemann–Liouville (RL) operator. This enables a comprehensive and systematic analysis of fractional models and their experimental signatures, supporting the selection of the most appropriate theoretical description for a given material.
Beyond the semi-infinite case analyzed here, a natural extension of the framework is the study of finite-size samples, particularly relevant for frequency-domain techniques where boundary effects cannot be neglected. Such analyses, combined with systematic experimental comparison, will provide further validation of the framework and refine the connection between fractional operators, the underlying type of memory (kinetic or inertial), the relaxation dynamics and lifetimes of internal degrees of freedom, and measurable system responses—thus bridging theoretical predictions with experimental observables in realistic geometries.
Future work may also extend this approach to the analysis of time-domain responses for various combinations of fractional models and operators. In practice, many experimental techniques operate in the time domain (e.g., AC calorimetry, time-domain photoacoustics, time-domain radiometry) on micron-scale samples [102,103]. To interpret such measurements and capture the role of relaxation processes in materials with complex internal structures, forthcoming studies should develop a methodology for the inverse Laplace transform of the convolution between excitation signals and the transfer function (equivalent thermal impedance or admittance seen by the source, Figure 2). Applying this methodology to specific types of impulse excitations will enable deeper insights into the relaxation times of cooperative processes underlying wave-like and anomalous diffusive effects in glassy solids, nanoporous and biological membranes, and biological tissues.
Author Contributions
Conceptualization, S.G.; methodology, S.G.; validation, M.N.P. and D.C.; formal analysis, S.G., M.N.P. and D.C.; investigation, S.G., D.C. and M.N.P.; resources, S.G. and D.C.; writing—original draft preparation, S.G.; writing—review and editing, S.G., M.N.P. and D.C.; visualization, D.C.; All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Ministry of Science, Technological Development and Innovation of the Republic of Serbia, Contract No. 451-03-136/2025-03/200017.
Data Availability Statement
The authors declare that the data supporting the findings of this study are available upon reasonable request. The research is theoretical in nature, involving the proposal of a model and the analysis of its results. No databases were used in this study.
Acknowledgments
We would like to express our gratitude for the assistance received in improving the clarity and coherence of the manuscript. However, it is important to clarify that the authors retain full responsibility for all content, analyses, and conclusions presented in this work. The role of artificial intelligence in this context was limited to providing language enhancement and stylistic suggestions, and does not imply that any part of the manuscript was generated by AI.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Carslaw, H.S.; Jaeger, J.C. Conduction of Heat in Solids; Oxford University Press: Cary, NC, USA, 1959. [Google Scholar]
- Bialkowski, S.E.; Astrath, N.G.C.; Proskurnin, M.A. Photothermal Spectroscopy Methods; John Wiley & Sons: Hoboken, NJ, USA, 2019. [Google Scholar]
- Bertolotti, M.; Voti, R.L. A note on the history of photoacoustic, thermal lensing, and photothermal deflection techniques. J. Appl. Phys. 2020, 128, 23. [Google Scholar] [CrossRef]
- Dubyk, K.; Borisova, T.; Paliienko, K.; Krisanova, N.; Isaiev, M.; Alekseev, S.; Skryshevsky, V.; Lysenko, V.; Geloen, A. Bio-distribution of Carbon Nanoparticles Studied by Photoacoustic Measurements. Nanoscale Res. Lett. 2022, 17, 127. [Google Scholar] [CrossRef]
- Galovic, S.P.; Djordjevic, K.L.; Nesic, M.V.; Popovic, M.N.; Markushev, D.K.; Todorovic, D.M. Time-domain minimum-volume cell photoacoustic of thin semiconductor layer. I. Theory. J. Appl. Phys. 2023, 133, 245701. [Google Scholar] [CrossRef]
- Galovic, S.; Stanimirovic, Z.; Stanimirovic, I.; Djordjevic, K.; Milicevic, D.; Suljovrujic, E. Time-resolved photoacoustic response of thin solids measured using minimal volume cell. Int. Commun. Heat Mass Transf. 2024, 155, 107574. [Google Scholar] [CrossRef]
- Crank, J. The Mathematics of Diffusion; Oxford University Press: London, UK, 1957. [Google Scholar]
- Wunderlich, B. Thermal Analysis of Polymeric Materialse; Springer: Berlin/Heidelberg, Germany, 2005. [Google Scholar]
- Garden, J.-L.; Guillou, H.; Lopeandia, A.; Richard, J.; Heron, J.-S.; Souche, G.; Ong, F.; Vianay, B.; Bourgeois, O. Thermodynamics of small systems by nanocalorimetry: From physical to biological nano-objects. Thermochim. Acta 2009, 492, 16–28. [Google Scholar] [CrossRef][Green Version]
- Varma-Nair, M.; Wunderlich, B. Non isothermal heat capacities and chemical reactions using a modulated DSC. J. Therm. Anal. 1996, 46, 879–892. [Google Scholar] [CrossRef]
- Saiter, A.; Couderc, H.; Grenet, J. Characterisation of structural relaxation phenomena in polymeric materials from thermal analysis investigations. J. Therm. Anal. Calorim. 2007, 88, 483–488. [Google Scholar] [CrossRef]
- Toda, A.; Saruyama, Y. A modeling of the irreversible melting kinetics of polymer crystals responding to temperature modulation with retardation of melting rate coefficient. Polymer 2001, 42, 4727–4730. [Google Scholar] [CrossRef]
- Saruyama, Y. AC calorimetry at the first order phase transition point. J. Therm. Anal. 1995, 38, 1827–1833. [Google Scholar] [CrossRef]
- Birge, N.O.; Nagel, S.R. Wide-frequency specific heat spectrometer. Rev. Sci. Instrum. 1987, 58, 1464–1470. [Google Scholar] [CrossRef]
- Dixon, P.K. Specific-heat spectroscopy and dielectric susceptibility measurements of salol at the glass transition. Phys. Rev. B 1990, 42, 8179–8186. [Google Scholar] [CrossRef] [PubMed]
- Scott, E.P.; Tilahun, M.; Vick, B. The question of thermal waves in heterogeneous and biological materials. J. Biomech. Eng. 2009, 131, 074518. [Google Scholar] [CrossRef] [PubMed]
- Mitra, K.; Kumar, S.; Vedavarz, A.; Moallemi, M.K. Experimental Evidence of Hyperbolic Heat Conduction in Processed Meat. J. Heat Transf. 1995, 117, 568–573. [Google Scholar] [CrossRef]
- Roetzel, W.; Putra, N.; Das, S. Experiment and analysis for non-Fourier conduction in materials with non-homogeneous inner structure. Int. J. Therm. Sci. 2003, 42, 541–552. [Google Scholar] [CrossRef]
- Forghani, P.; Ahmadikia, H.; Karimipour, A. Non-Fourier Boundary Conditions Effects on the Skin Tissue Temperature Response. Heat Transf. Res. 2017, 46, 29–48. [Google Scholar] [CrossRef]
- Herwig, H.; Beckert, K. Experimental evidence about the controversy concerning Fourier or non-Fourier heat conduction in materials with a nonhomogeneous inner structure. Heat Mass Transf. Und Stoffuebertragung 2000, 36, 387–392. [Google Scholar] [CrossRef]
- Evangelista, L.R.; Lenzi, E.K. Fractional Diffusion Equations and Anomalous Diffusion; Cambridge University Press: Cambidge, UK, 2018. [Google Scholar]
- Norregaard, K.; Metzler, R.; Ritter, C.M.; Berg-Sørensen, K.; Oddershede, L.B. Manipulation and Motion of Organelles and Single Molecules in Living Cells. Chem. Rev. 2017, 117, 4342–4375. [Google Scholar] [CrossRef] [PubMed]
- Mainardi, F. Fractional Calculus and Waves in Linear Viscoelasticity; Imperial College Press: London, UK, 2010. [Google Scholar]
- Podlubny, I. Fractional Differential Equations: An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of Their Solution and Some of Their Applications; Elsevier: Amsterdam, The Netherlands, 1998; Volume 198. [Google Scholar]
- Metzler, R.; Jeon, J.H.; Cherstvy, A.G.; Barkai, E. Anomalous diffusion models and their properties: Non-stationarity, non-ergodicity, and ageing at the centenary of single particle tracking. Phys. Chem. Chem. Phys. 2014, 16, 24128–24164. [Google Scholar] [CrossRef]
- Metzler, R.; Klafter, J. The Random Walk’s Guide to Anomalous Diffusion: A Fractional Dynamics Approach. Phys. Rep. 2000, 339, 1–77. [Google Scholar] [CrossRef]
- Compte, A.; Metzler, R. The generalized Cattaneo equation for the description of anomalous transport processes. J. Phys. A Math. Gen. 1997, 30, 7277–7289. [Google Scholar] [CrossRef]
- Korabel, N.; Klages, R.; Chechkin, A.V.; Sokolov, I.M.; Gonchar, V.Y. Fractal properties of anomalous diffusion in intermittent maps. Phys. Rev. E 2007, 75, 36213. [Google Scholar] [CrossRef]
- Barkai, E. CTRW pathways to the fractional diffusion equation. Chem. Phys. 2002, 284, 13–27. [Google Scholar] [CrossRef]
- Caputo, M.; Fabrizio, M. Applications of new time and spatial fractional derivatives with exponential kernels. Prog. Fract. Differ. Appl. 2016, 2, 1–11. [Google Scholar] [CrossRef]
- Zwanzig, R. Nonequilibrium Statistical Mechanics; Oxford University Press: Oxford, UK, 2001. [Google Scholar]
- Kumar, M.; Rai, K.N.; Rajeev, A. A study of fractional order dual-phase-lag bioheat transfer model. J. Therm. Biol. 2020, 93, 102661. [Google Scholar] [CrossRef]
- Xu, H.Y.; Jiang, X.Y. Time fractional dual-phase-lag heat conduction equation. Chin. Phys. B 2015, 24, 034401. [Google Scholar] [CrossRef]
- Atanackovic, T.M.; Pilipovic, S. On a constitutive equation of heat conduction with fractional derivatives of complex order. Acta Mech. 2018, 229, 1111–1121. [Google Scholar] [CrossRef]
- Somer, A.; Camilotti, F.; Costa, G.F.; Bonardi, C.; Novatski, A.; Andrade, A.V.C.; Kozlowski, V.A.; Cruz, G.K. The thermoelastic bending and thermal diffusion processes influence on photoacoustic signal generation using open photoacoustic cell technique. J. Appl. Phys. 2013, 114, 063503. [Google Scholar] [CrossRef]
- Somer, A.; Galovic, S.P.; Lenzi, E.K.; Novatski, A.; Djordjevic, K. Temperature Profile and Thermal Piston Component of Photoacoustic Response Calculated by the Fractional Dual-Phase-Lag Heat Conduction Theory. SSRN Electron. J. 2022, 203, 123801. [Google Scholar] [CrossRef]
- Somer, A.; Popovic, M.N.; da Cruz, G.K.; Novatski, A.; Lenzi, E.K.; Galovic, S.P. Anomalous thermal diffusion in two-layer system: The temperature profile and photoacoustic signal for rear light incidence. Int. J. Therm. Sci. 2022, 179, 107661. [Google Scholar] [CrossRef]
- Tateishi, A.A.; Ribeiro, H.V.; Lenzi, E.K. The role of fractional time-derivative operators on anomalous diffusion. Front. Phys. 2017, 5, 52. [Google Scholar] [CrossRef]
- Lenzi, E.K.; Somer, A.; Zola, R.S.; da Silva, L.R.; Lenzi, M.K. A Generalized Diffusion Equation: Solutions and Anomalous Diffusion. Fluids 2023, 8, 34. [Google Scholar] [CrossRef]
- Alawaideh, Y.M.; Alkhamiseh, B.M.; Alawideh, S.E.; Baleanu, D.; Abu-Izneid, B.; Asad, J. Hamiltonian Formulation of Generalized Classical Field Systems Using Linear fields’ variables(ϕ, Ai,Aj). J. Stat. Appl. Probab. 2023, 12, 503–518. [Google Scholar] [CrossRef]
- Alawaideh, Y.M. A fractional approach to Hamiltonian-generalized classical fields: The Hamilton-Jacob technique Amman 17110 Amman Lebanon Romania. J. Interdiscip. Math. 2010, 0502, 12. [Google Scholar]
- Suszyński, Z. Thermal model based on the electrical analogy of the thermal processes. AIP Conf. Proc. 1999, 463, 197–199. [Google Scholar] [CrossRef]
- Galović, S.P.; Šoškić, Z.N.; Popović, M.N. Analysis of photothermal response of thin solid films by analogy with passive linear electric networks. Therm. Sci. 2009, 13, 129–142. [Google Scholar] [CrossRef]
- Galovic, S.P.; Markushev, D.K.; Markushev, D.D.; Djordjevic, K.L. Time-Resolved Photoacoustic Response of Thin Semiconductors Measured with Minimal Volume Cell: Influence of Photoinduced Charge Carriers. Appl. Sci. 2025, 15, 7290. [Google Scholar] [CrossRef]
- Krapez, J.-C.; Dohou, E. Thermal quadrupole approaches applied to improve heat transfer computations in multilayered materials with internal heat sources. Int. J. Therm. Sci. 2014, 81, 38–51. [Google Scholar] [CrossRef]
- Maillet, D.; Andre, S.; Batsale, J.C.; Degiovanni, A.; Moyne, C. Thermal Quandupoles Solving the Heat Equation through Integral Transforms; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2000. [Google Scholar]
- Caputo, M. Linear Models of Dissipation whose Q is almost Frequency Independent-II. Geophys. J. R. Astron. Soc. 1967, 13, 529–539. [Google Scholar] [CrossRef]
- Atangana, A.; Baleanu, D. New Fractional Derivatives with Non-Singular Kernel: Theory and Application to Heat Transfer Model. Int. J. Therm. Sci. 2016, 20, 763–769. [Google Scholar] [CrossRef]
- Atangana, A. On the new fractional derivative and application to nonlinear Fisher’s reaction–diffusion equation. Appl. Math. Comput. 2015, 273, 948–956. [Google Scholar] [CrossRef]
- Fahmy, M.A.; Almutlg, A. Boundary element method solution of a fractional bioheat equation for memory-driven heat transfer in biological tissues. Fractal Fract. 2025, 9, 565. [Google Scholar] [CrossRef]
- Hobiny, A.; Abbas, I. The Effect of Fractional Derivatives on Thermo-Mechanical Interaction in Biological Tissues during Hyperthermia Treatment Using Eigenvalues Approach. Fractal Fract. 2023, 7, 432. [Google Scholar] [CrossRef]
- Zhang, Q.; Sun, Y.; Yang, J. Thermoelastic responses of biological tissue under thermal shock based on three phase lag model. Case Stud. Therm. Eng. 2021, 28, 101376. [Google Scholar] [CrossRef]
- Fahmy, M.A.; Almehmadi, M.M. Fractional Dual-Phase-Lag Model for Nonlinear Viscoelastic Soft Tissues. Fractal Fract. 2023, 7, 66. [Google Scholar] [CrossRef]
- Shah, N.A.; Almutairi, B.; Vieru, D.; Lee, B.; Chung, J.D. Bioheat Transfer with Thermal Memory and Moving Thermal Shocks. Fractal Fract. 2023, 7, 629. [Google Scholar] [CrossRef]
- Xu, M.; Tan, W. Intermediate processes and critical phenomena: Theory, method and progress of fractional operators and their applications to modern mechanics. Sci. China Ser. G 2006, 49, 257–272. [Google Scholar] [CrossRef]
- Oldham, K.B.; Spanier, J. The Fractional Calculus Theory and Applications of Differentiation and Integration to Arbitrary Order; Academic press: Cambridge, MA, USA, 1974. [Google Scholar]
- Samko, S.G.; Kilbas, A.A.; Marichev, O.I. Fractional Integrals and Derivatives Theory and Applications; Gordon and Breach Science Publishers: London, UK, 2020. [Google Scholar]
- Cichon, M.; Shammakh, W.; Salem, H.A.H. A Unified Framework for Fractional and Non-Fractional Operators in Some Function Spaces. Fractal Fract. 2025, 9, 441. [Google Scholar] [CrossRef]
- Yang, S.; Song, H.; Zhou, H.; Xie, S.; Zhang, L.; Zhou, W. A Fractional Derivative Insight into Full-Stage Creep Behavior in Deep Coal. Fractal Fract. 2025, 9, 473. [Google Scholar] [CrossRef]
- Abramowitz, M.; Stegun, I. Handbook of Mathematical Functions; Dover Publications, Inc.: New York, NY, USA, 1970. [Google Scholar]
- Rogosin, S.; Gorenflo, R.; Kilbas, A.A.; Mainardi, F. Mittag-Leffler Function, Related Topics and Applications; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Biolek, D.; Garrappa, R.; Mainardi, F.; Popolizio, M. Derivatives of Mittag-Leffler functions: Theory, computation and applications. Nonlinear Dyn. 2025. [Google Scholar] [CrossRef]
- Mainardi, F. Why the mittag-leffler function can be considered the queen function of the fractional calculus? Entropy 2020, 22, 1359. [Google Scholar] [CrossRef]
- Popovic, A.; Šoškic, Z.; Stojanovic, Z.; Cevizovic, D.; Galovic, S. On the applicability of the effective medium approximation to the photoacoustic response of multilayered structures. Phys. Scr. 2012, 2012, 014066. [Google Scholar] [CrossRef]
- Liu, L.; Zheng, L.; Liu, F.; Zhang, X. An improved heat conduction model with Riesz fractional derivatives for biological tissues. Int. J. Heat Mass Transf. 2016, 103, 1191–1197. [Google Scholar] [CrossRef]
- Beybalaev, V.D.; Aliverdiev, A.A.; Yakubov, A.Z.; Ninalalov, S.A.; Amirova, A.A. Mathematical model of heat conduction for a semi-infinite body, taking into account memory effects and spatial correlations. Fractal Fract. 2023, 7, 265. [Google Scholar] [CrossRef]
- Migdal, A. Topological vortexes, asymptotic freedom, and multifractals. Fractal Fract. 2023, 7, 351. [Google Scholar] [CrossRef]
- Migdal, A. To the theory of decaying turbulence. Fractal Fract. 2023, 7, 754. [Google Scholar] [CrossRef]
- Novikov, I.A.; Kolpashipov, V.I.; Shnipp, A.I. Reophysics and Thermophysics of Nonequliubrium Systems; Science and Technology: Minsk, Russia, 1991. [Google Scholar]
- Galovic, S.; Djordjevic, A.I.; Kovacevic, B.Z.; Djordjevic, K.L.; Chevizovich, D. Influence of Local Thermodynamic Non-Equilibrium to Photothermally Induced Acoustic Response of Complex Systems. Fractal Fract. 2024, 8, 399. [Google Scholar] [CrossRef]
- Joseph, D.D.; Preziosi, L. Heat waves. Rev. Mod. Phys. 1989, 61, 41–73. [Google Scholar] [CrossRef]
- Novikov, I.A. Harmonic thermal waves in materials with thermal memory. J. Appl. Phys. 1997, 81, 1067–1072. [Google Scholar] [CrossRef]
- Galović, S.; Kostoski, D. Photothermal wave propagation in media with thermal memory. J. Appl. Phys. 2003, 93, 3063–3070. [Google Scholar] [CrossRef]
- Zhukovsky, K. Operational Approach and Solutions of Hyperbolic Heat Conduction Equations. Axioms 2016, 5, 28. [Google Scholar] [CrossRef]
- Galovic, S.; Čukić, M.; Chevizovich, D. Inertial Memory Effects in Molecular Transport Across Nanoporous Membranes. Membranes 2025, 15, 11. [Google Scholar] [CrossRef]
- Garden, J. Macroscopic non-equilibrium thermodynamics in dynamic calorimetry. Thermochim. Acta 2007, 452, 85–105. [Google Scholar] [CrossRef]
- Garden, J.; Richard, J.; Saruyama, Y. Entropy production in TMDSC. J. Therm. Anal. Calorim. 2008, 94, 585–590. [Google Scholar] [CrossRef]
- Sobolev, S.L. Local non-equilibrium transport models. Physics-Uspekhi 1997, 40, 1043–1053. [Google Scholar] [CrossRef]
- Sobolev, S.L.; Dai, W. Heat Transport on Ultrashort Time and Space Scales in Nanosized Systems: Diffusive or Wave-like? Materials 2022, 15, 4287. [Google Scholar] [CrossRef]
- Prigogine, I. Introduction to Thermodynamics of Irreversible Processes; Interscience Publishers: Geneva, Switzerland, 1961. [Google Scholar]
- Cattaneo, C. Sur une forme de l’equation de la chaleur eliminant la paradoxe d’une propagation instantantee. Compt. Rendu 1958, 247, 431–433. [Google Scholar]
- Vernotte, M. La veritable equation de chaleur. Comptes Rendus Hebd. Des Séances L’academie Des Sci. 1958, 247, 2103–2105. [Google Scholar]
- Landau, L. Theory of the Superfluidity of Helium II. Phys. Rev. 1941, 60, 356–358. [Google Scholar] [CrossRef]
- Peshkov, V.P. SECOND SOUND IN HELIUM II. Sov. Phys. Jetp 1960, 11, 799–805. [Google Scholar]
- Ackerman, C.C.; Guyer, R.A. Temperature pulses in dielectric solids. Ann. Phys. 1968, 50, 128–185. [Google Scholar] [CrossRef]
- Narayanamurti, V.; Dynes, R.C. Observation of Second Sound in Bismuth. Phys. Rev. Lett. 1972, 28, 1461–1465. [Google Scholar] [CrossRef]
- McNelly, T.F.; Rogers, S.J.; Channin, D.J.; Rollefson, R.J.; Goubau, W.M.; Schmidt, G.E.; Krumhansl, J.A.; Pohl, R.O. Heat Pulses in NaF: Onset of Second Sound. Phys. Rev. Lett. 1970, 24, 100–102. [Google Scholar] [CrossRef]
- Huberman, S.; Duncan, R.A.; Chen, K.; Song, B.; Chiloyan, V.; Ding, Z.; Maznev, A.A.; Chen, G.; Nelson, K.A. Observation of second sound in graphite at temperatures above 100 K. Science 2019, 364, 375–379. [Google Scholar] [CrossRef]
- Ding, Z.; Chen, K.; Song, B.; Shin, J.; Maznev, A.A.; Nelson, K.A.; Chen, G. Observation of second sound in graphite over 200 K. Nat. Commun. 2022, 13, 285. [Google Scholar] [CrossRef]
- Tzou, D.Y. A Unified Field Approach for Heat Conduction From Macro- to Micro-Scales. J. Heat. Transf. Asme 1995, 117, 8–16. [Google Scholar] [CrossRef]
- Tzou, D.Y. Macro- to Microscale Heat Transfer: The Lagging Behavior; John Wiley & Sons: Hoboken, NJ, USA, 2014. [Google Scholar]
- Djordjevic, K.L. Photothermal Response of Polymeric Materials Including Complex Heat Capacity. Int. J. Thermophys. 2022, 43, 68. [Google Scholar] [CrossRef]
- Liu, K.-C.; Wang, Y.-N.; Chen, Y.-S. Investigation on the Bio-Heat Transfer with the Dual-Phase-Lag Effect. Int. J. Therm. Sci. 2012, 58, 29–35. [Google Scholar] [CrossRef]
- Askarizadeh, H.; Ahmadikia, H. Analytical analysis of the dual-phase-lag model of bioheat transfer equation during transient heating of skin tissue. Heat Mass Transf. 2014, 50, 1673–1684. [Google Scholar] [CrossRef]
- Sobolev, S.L. Discrete heat conduction equation: Dispersion analysis and continuous limits. Int. J. Heat. Mass. Transf. 2024, 221, 2023–2024. [Google Scholar] [CrossRef]
- Sobolev, S.L. Non-Fourier heat conduction: Discrete vs. continuum approaches. Mech. Res. Commun. 2025, 149, 104512. [Google Scholar] [CrossRef]
- Cole, K.S.; Cole, R.H. Dispersion and absorption in dielectrics I. Alternating current characteristics. J. Chem. Phys. 1941, 9, 341–351. [Google Scholar] [CrossRef]
- Galović, S.; Šoškić, Z.; Popović, M.; Cevizović, D.; Stojanović, Z. Theory of photoacoustic effect in media with thermal memory. J. Appl. Phys. 2014, 116, 024901. [Google Scholar] [CrossRef]
- Popovic, M.N.; Galovic, S.P.; Lenzi, E.K. The Thermoelastic Component of the Photoacoustic Response in a 3D-Printed Polyamide Coated with Pigment Dye: A Two-Layer Model Incorporating Fractional Heat Conduction Theories. Fractal Fract. 2025, 9, 456. [Google Scholar] [CrossRef]
- Somer, A. Photoacoustic Signal of Optically Opaque Two-Layer Samples: Influence of Anomalous Thermal Diffusion. Int. J. Thermophys. 2025, 46, 84. [Google Scholar] [CrossRef]
- Herrera, L. Causal heat conduction contravening the fading memory paradigm. Entropy 2019, 21, 950. [Google Scholar] [CrossRef]
- Telenkov, S.A.; Mandelis, A. Photothermoacoustic imaging of biological tissues: Maximum depth characterization comparison of time and frequency-domain measurements. J. Biomed. Opt. 2009, 14, 044025. [Google Scholar] [CrossRef]
- Pellegrino, N.; Ecclestone, B.R.; Fieguth, P.; Hajireza, P. Time-domain feature extraction for target-specificity in Photoacoustic Remote Sensing Microscopy. arXiv 2022. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).