Global Funnel Control of Nonlinear Systems with Unknown and Time-Varying Fractional Powers
Abstract
1. Introduction
2. Problem Formulation
2.1. System Description
2.2. Control Objective
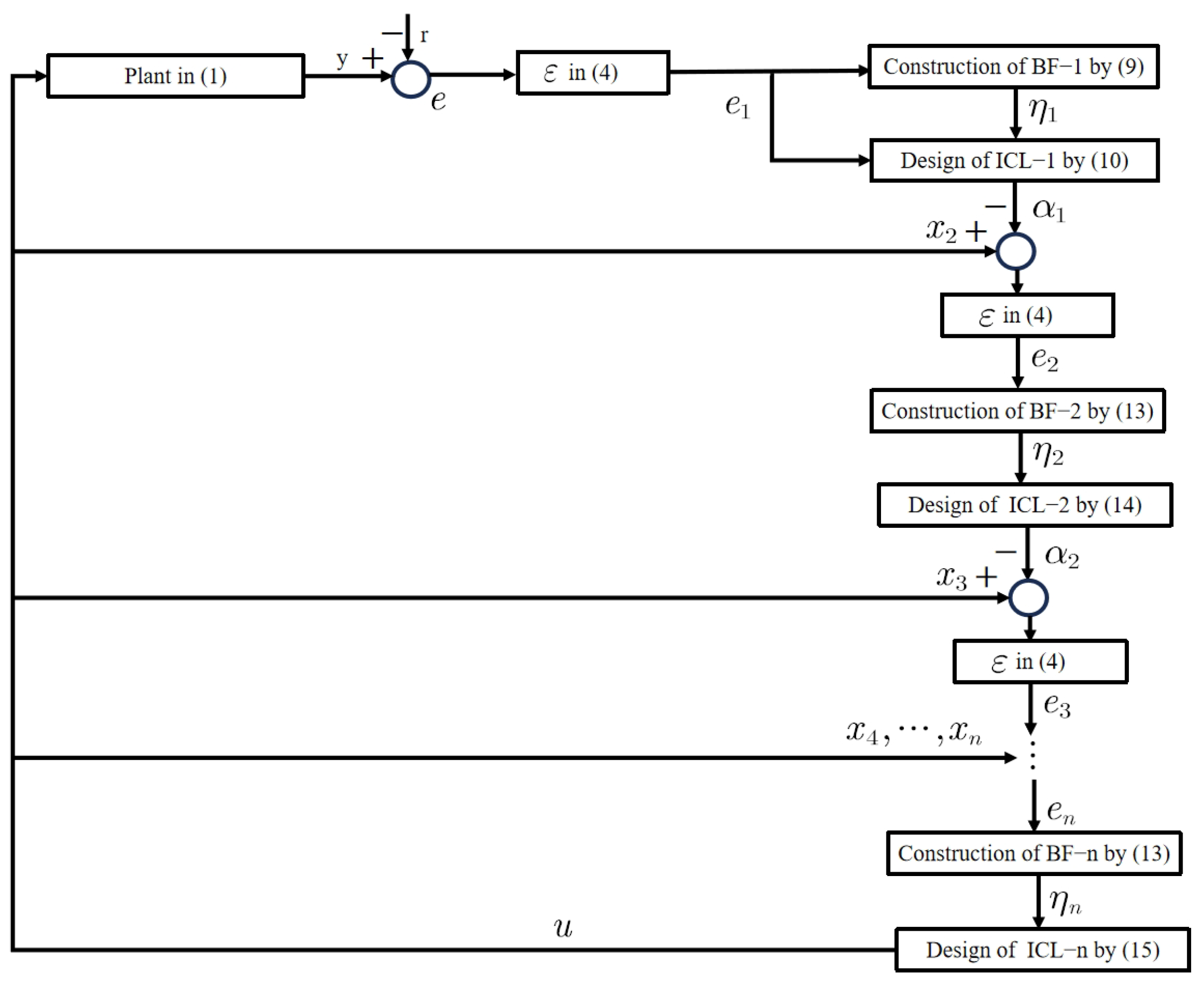
3. Control Development
4. Performance Analysis
- evolves inside and keeps at a distance from and during ;
- and are both bounded during .
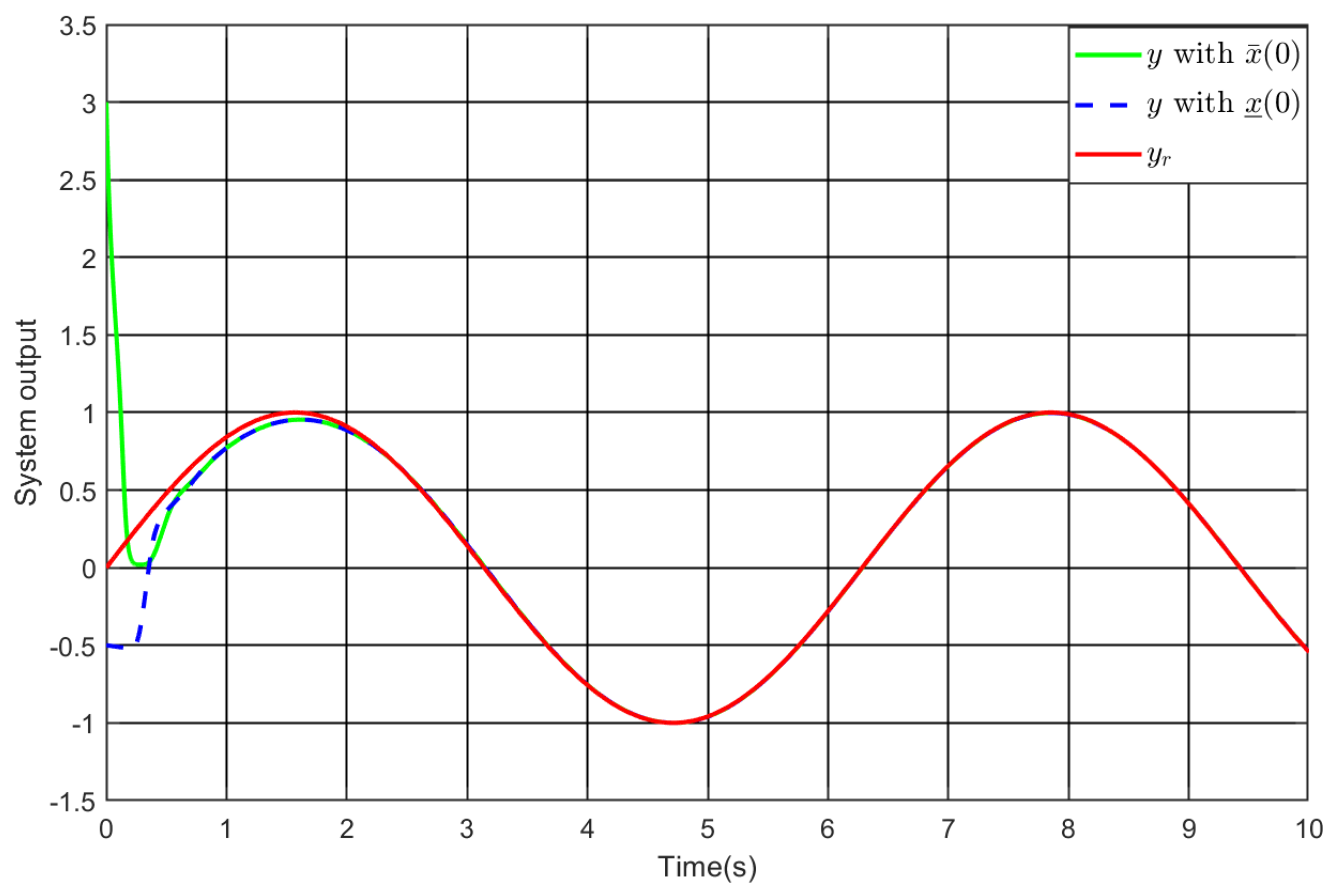
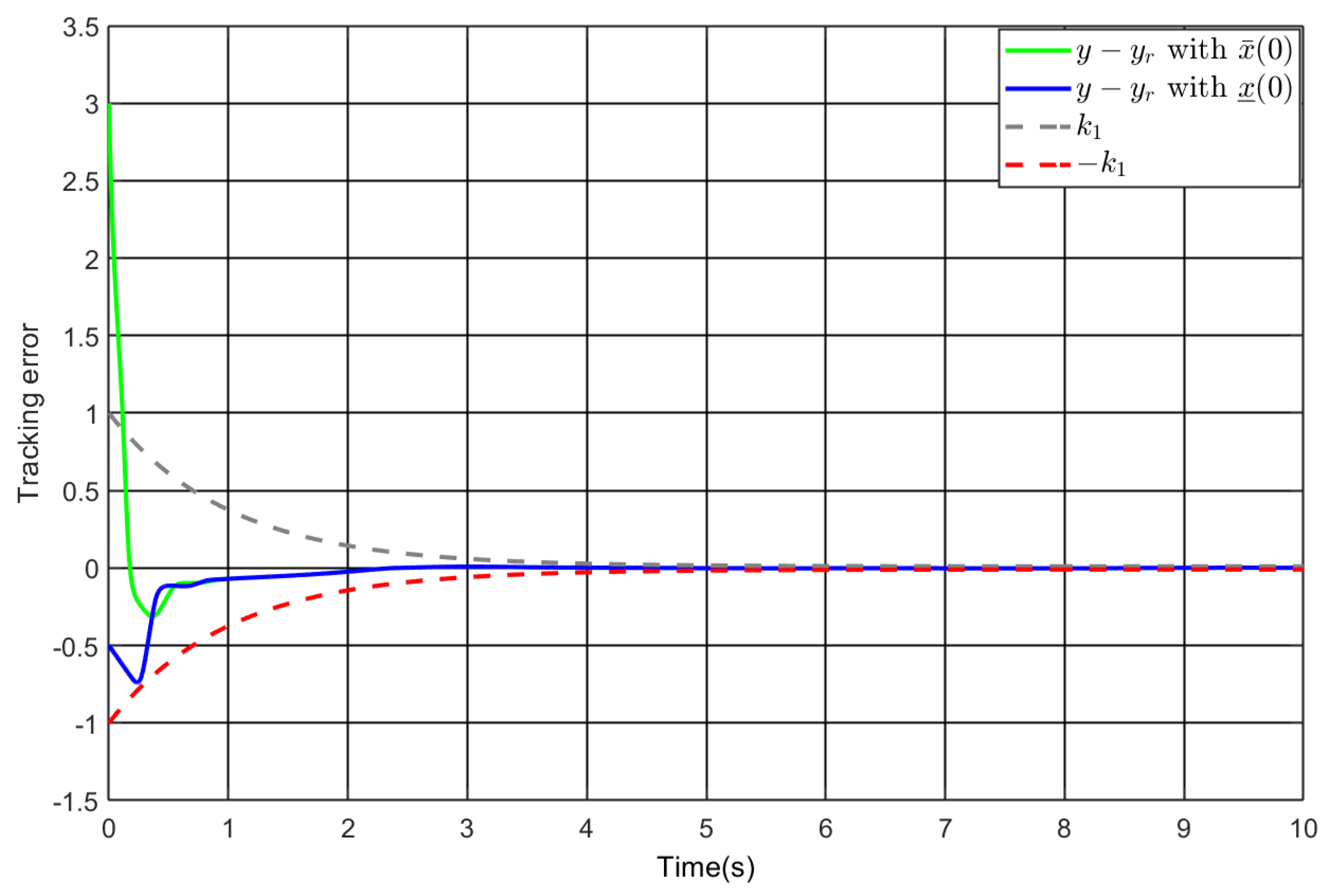
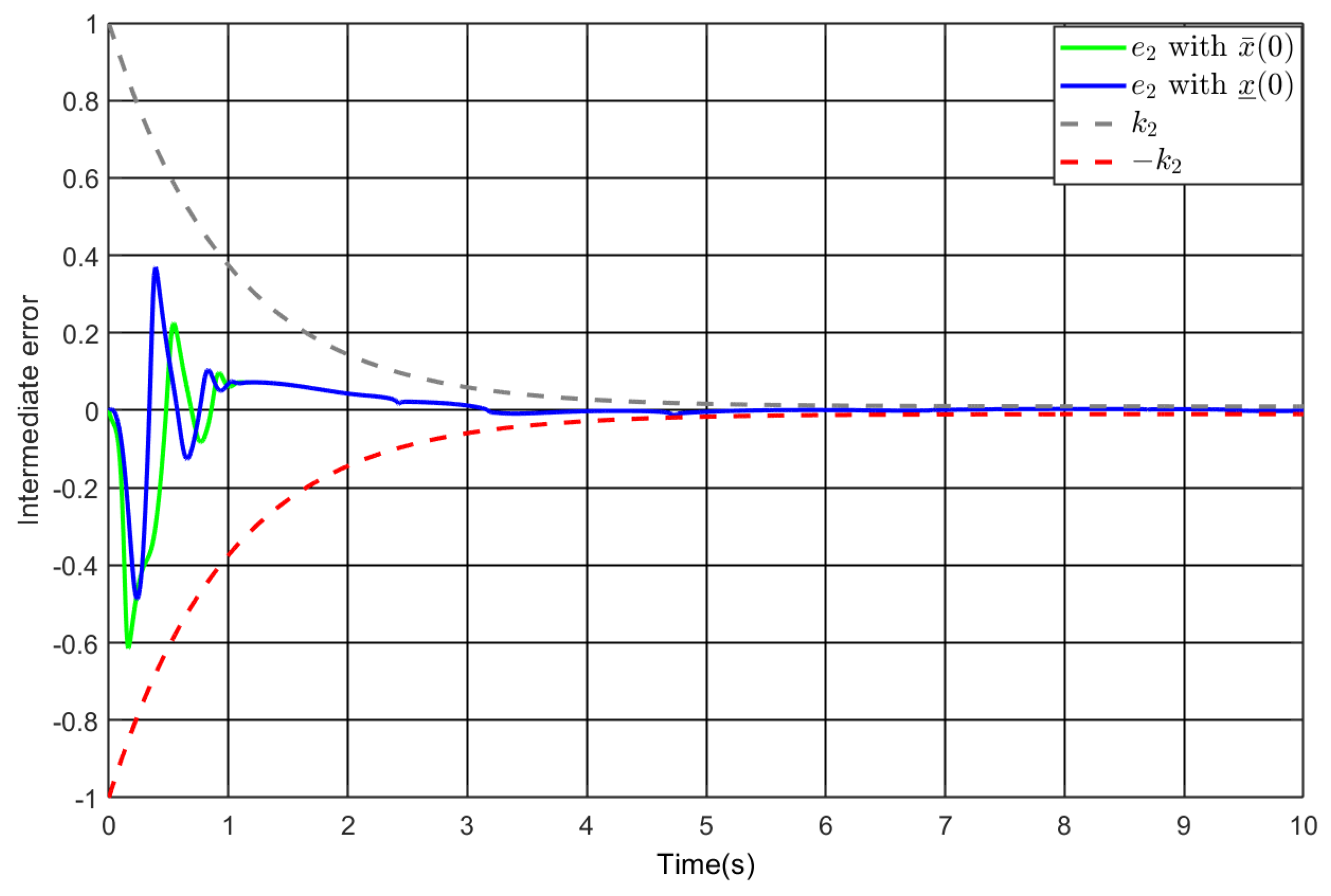
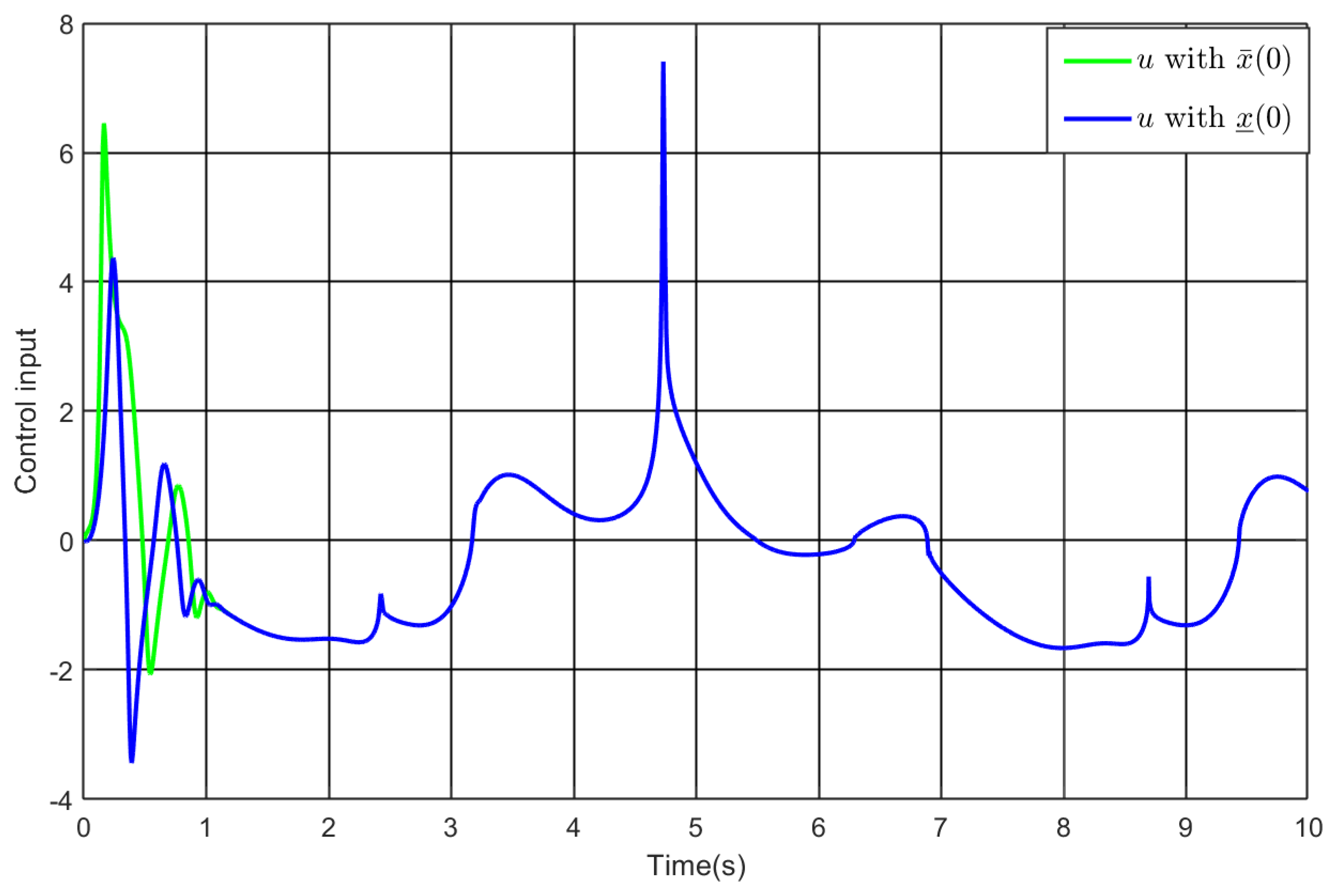
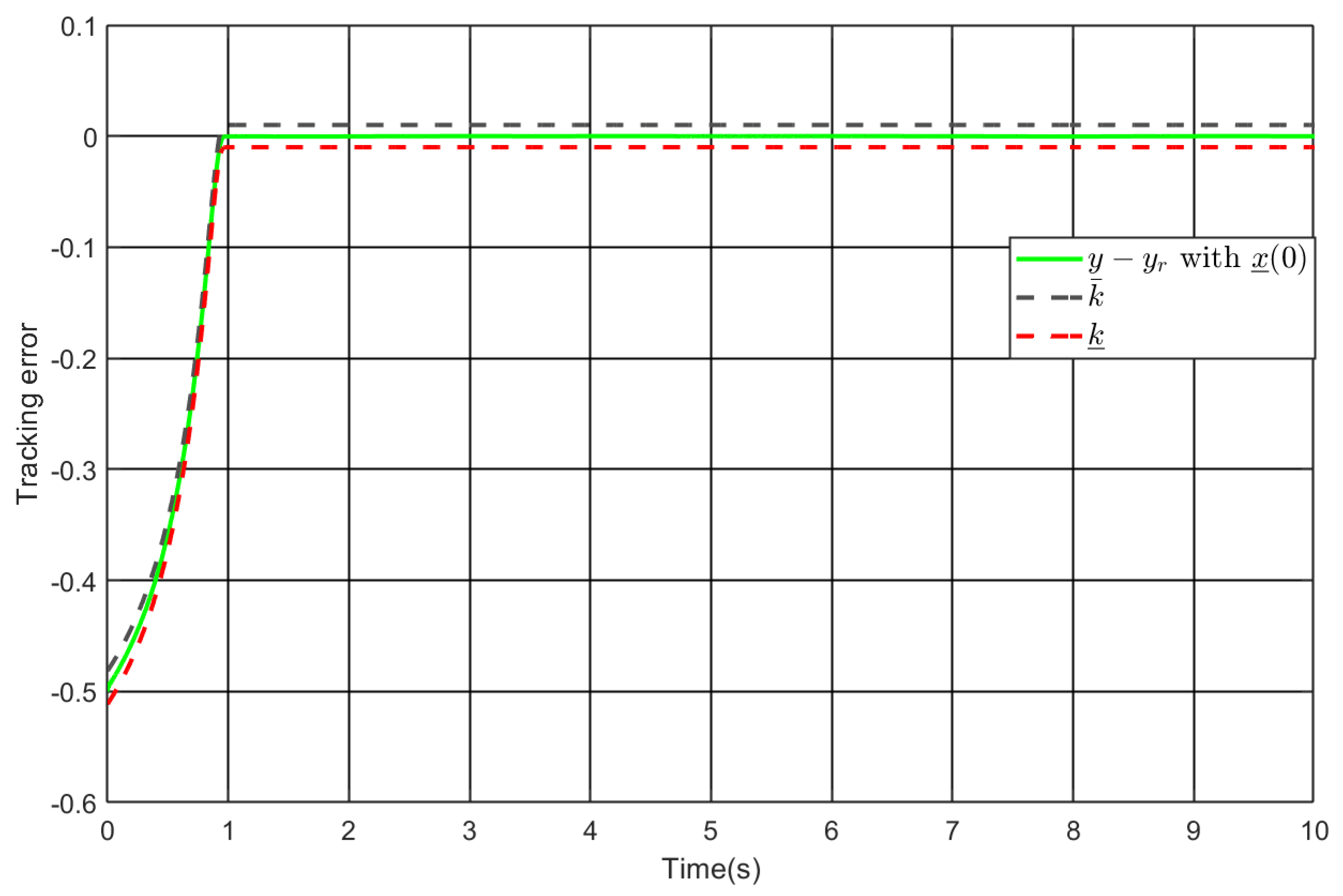
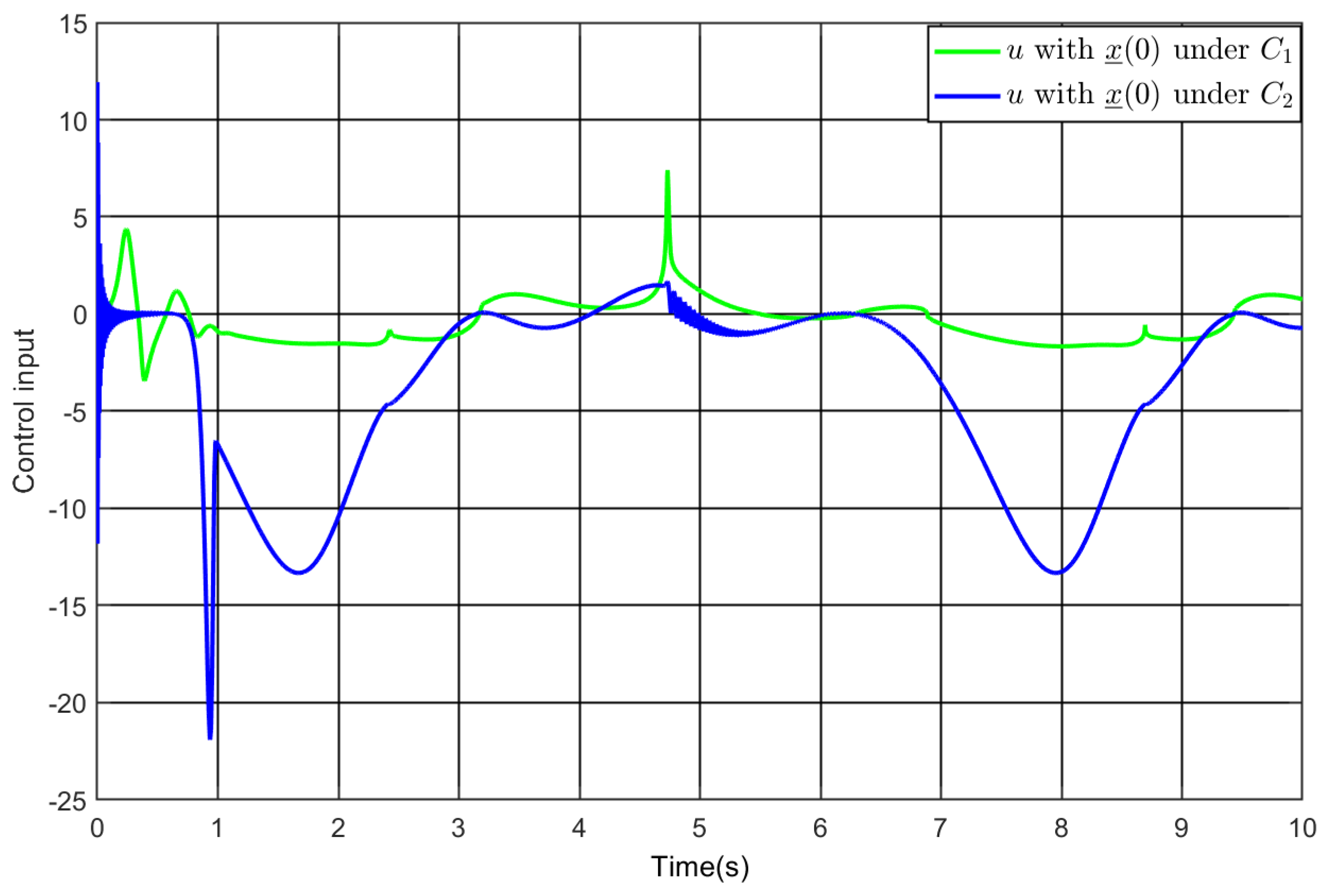
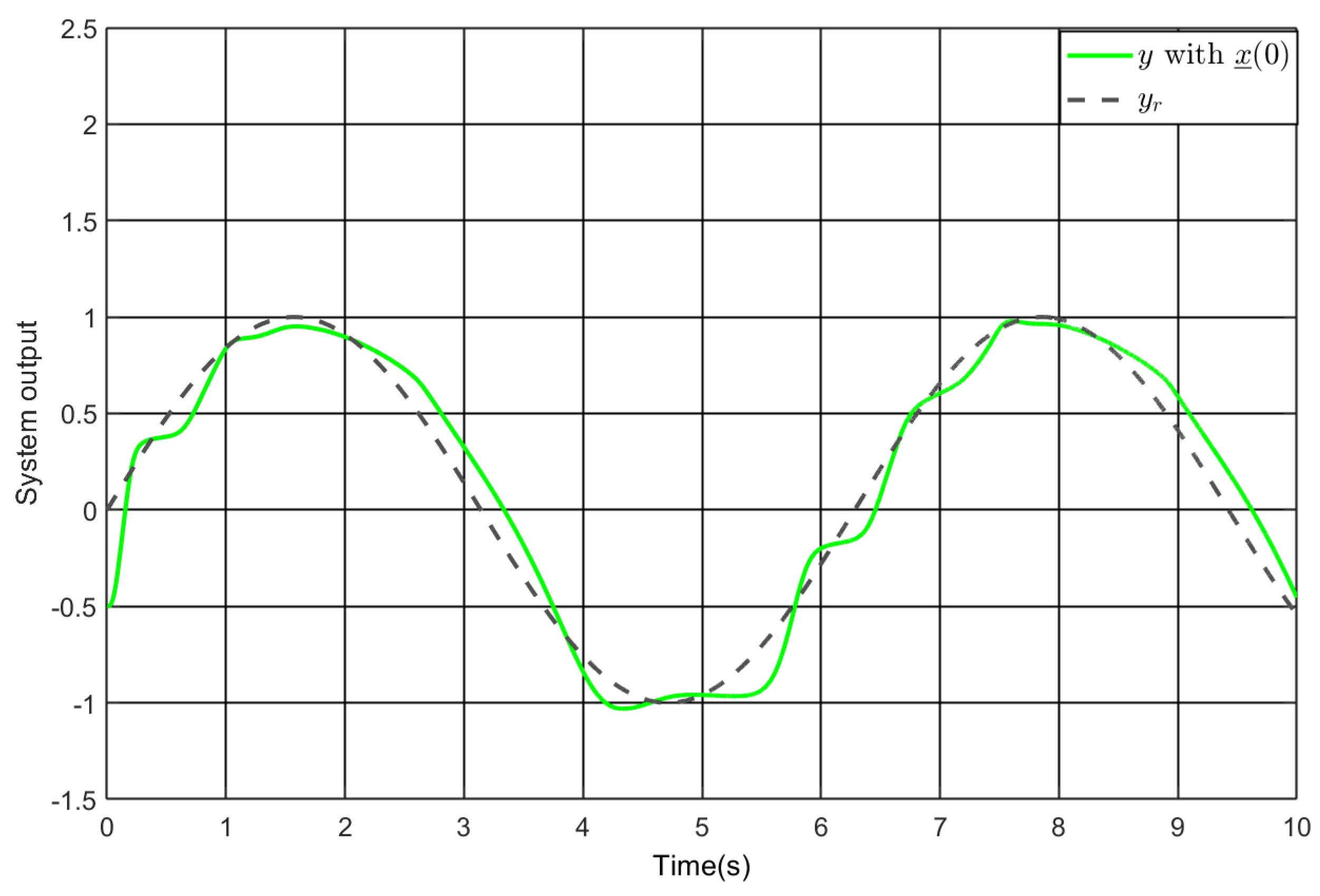
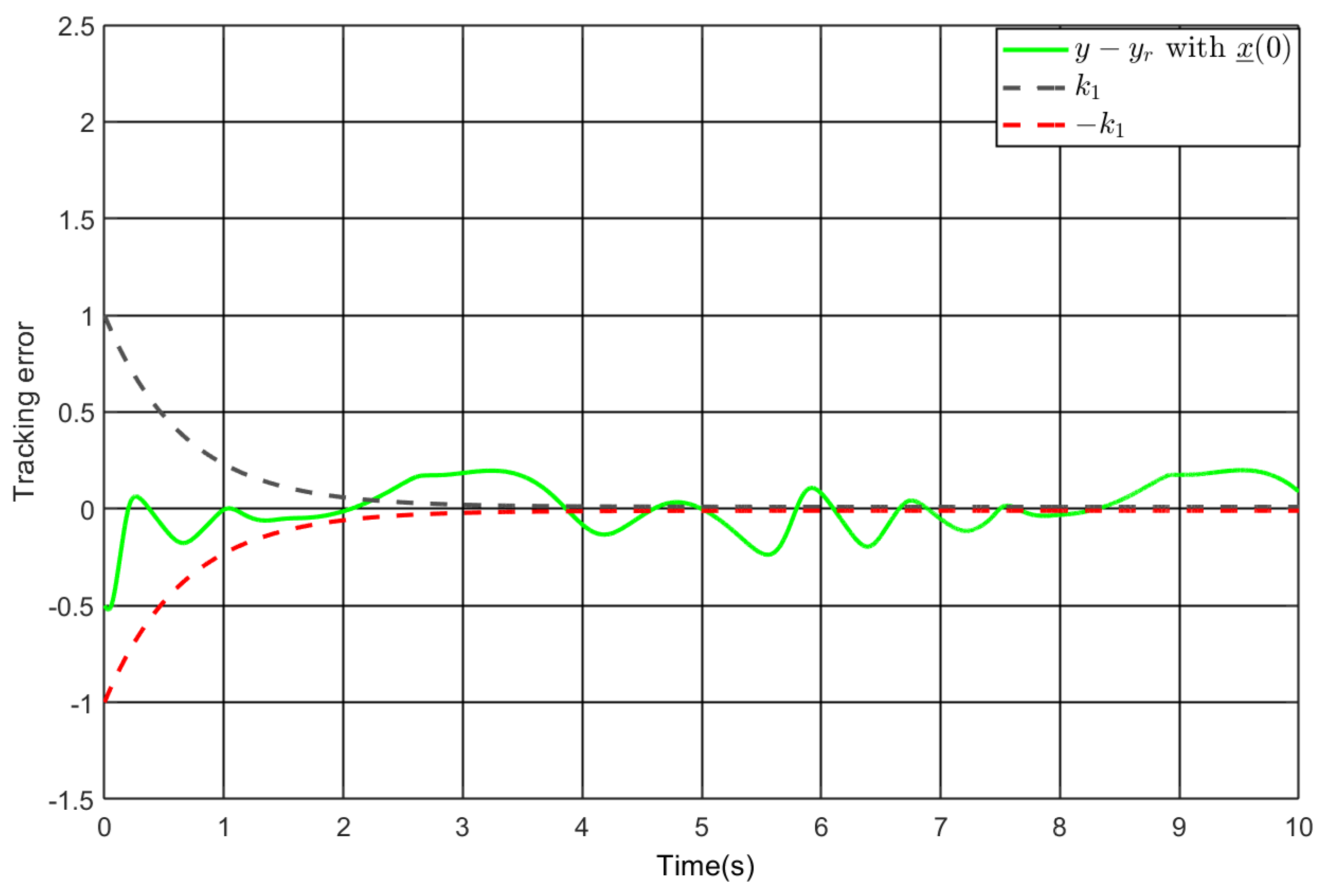
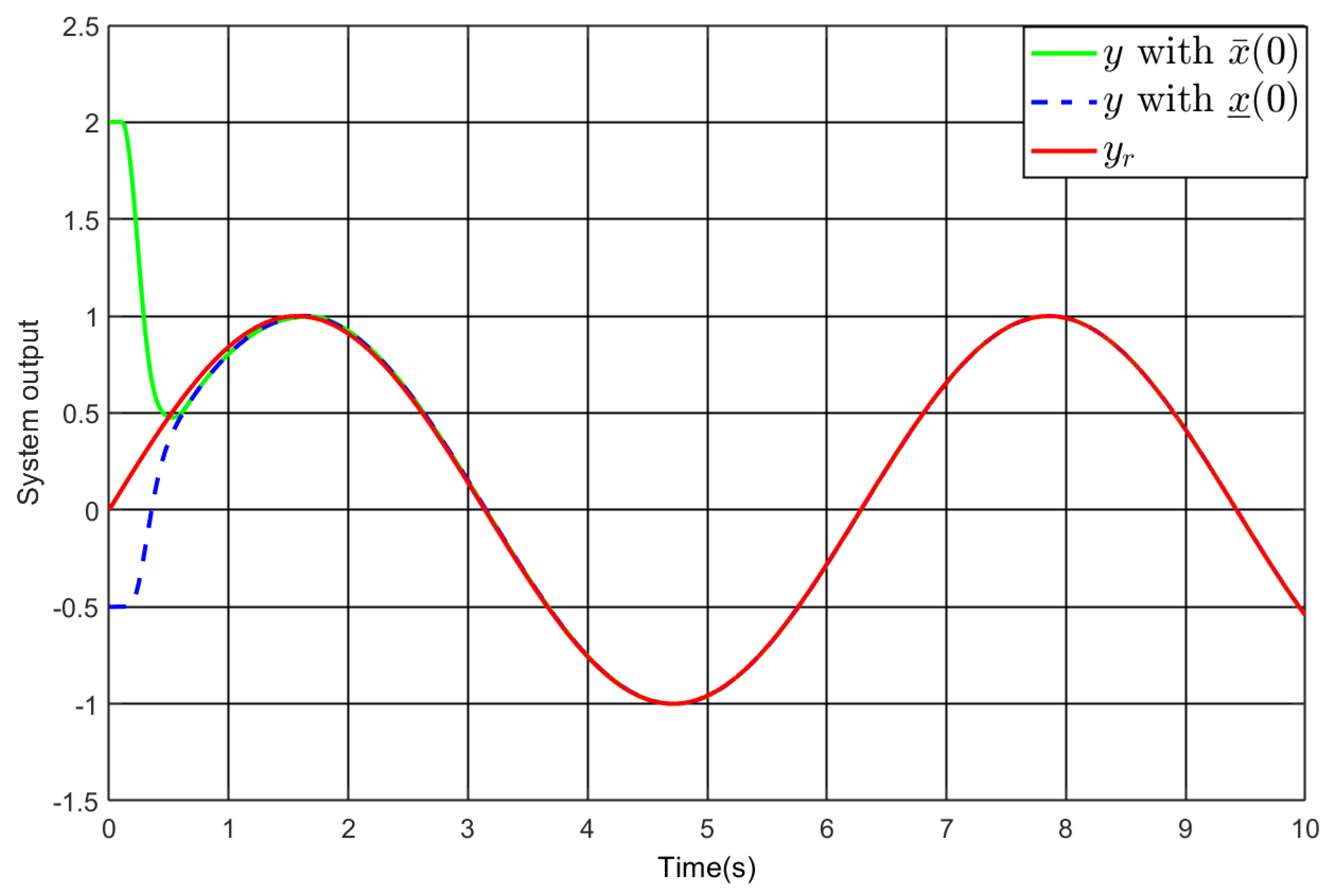
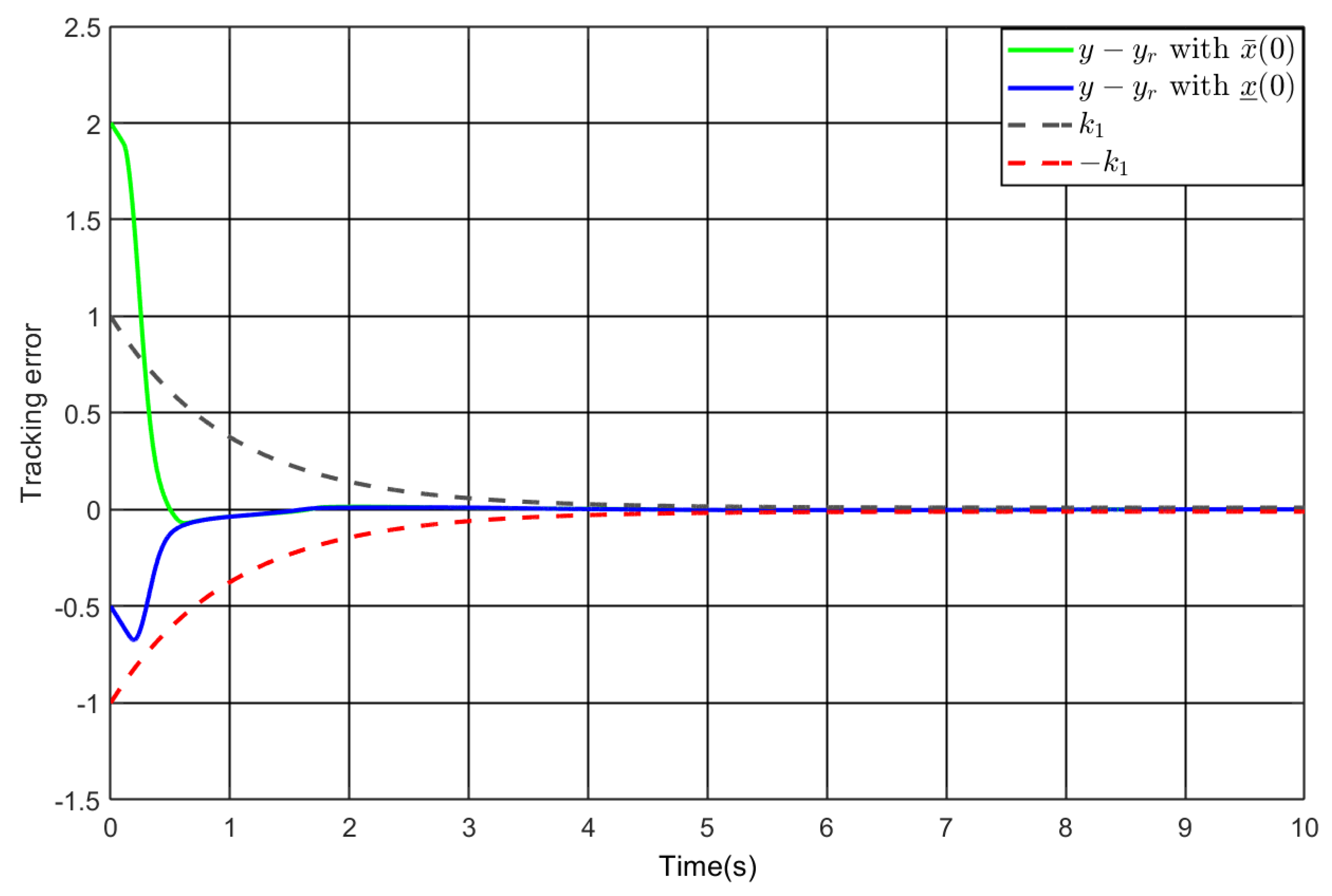
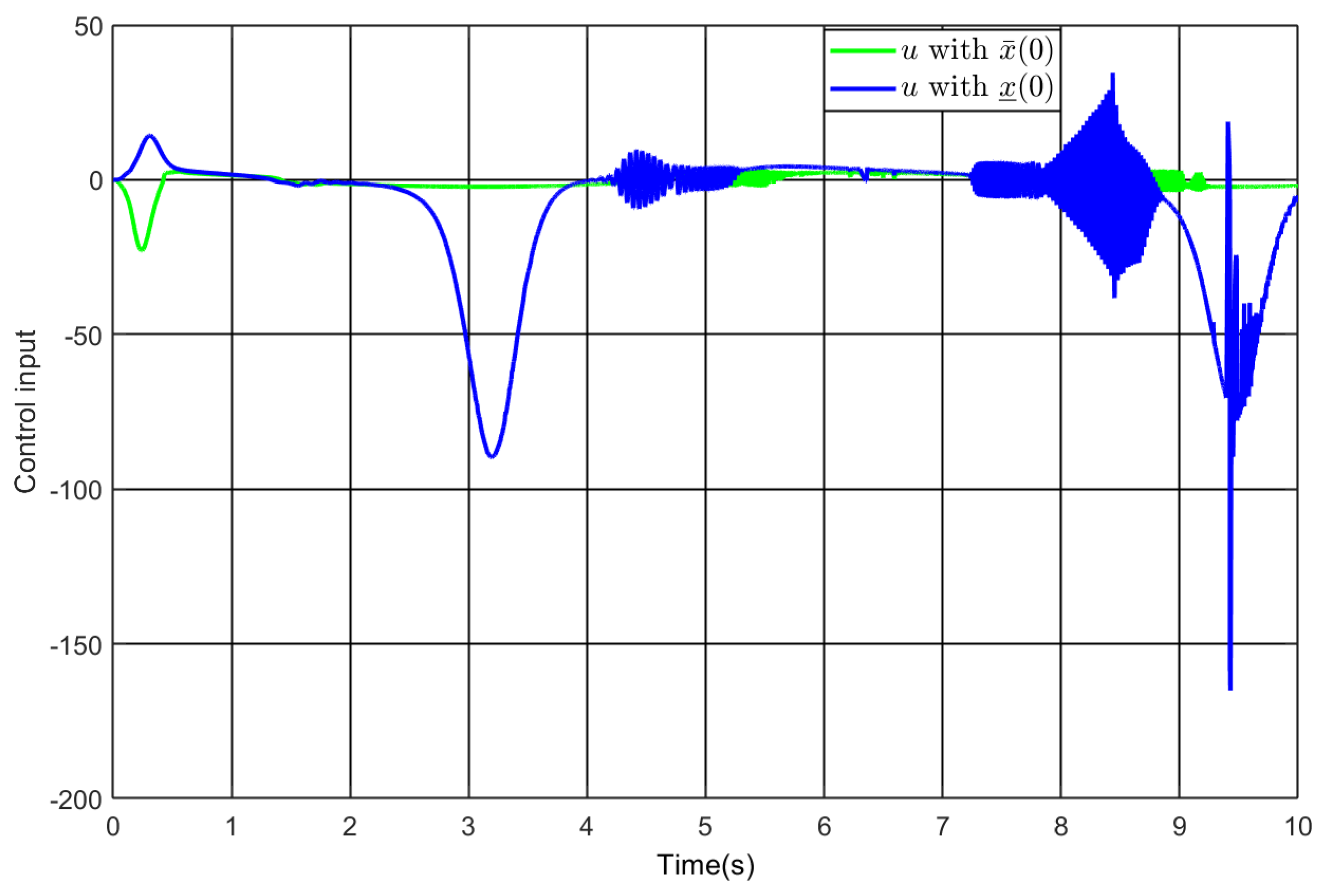
5. Simulation Study
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Xie, X.J.; Duan, N. Output tracking of high-order stochastic nonlinear systems with application to benchmark mechanical system. IEEE Trans. Autom. Control 2010, 55, 1197–1202. [Google Scholar]
- Liu, J.Z.; Yan, S.; Zeng, D.L.; Hu, Y.; Lv, Y. A dynamic model used for controller design of a coal fired once-through boiler-turbine unit. Energy 2015, 93, 2069–2078. [Google Scholar] [CrossRef]
- Zhang, X.; Liu, R.; Ren, J.; Gui, Q. Adaptive Fractional Image Enhancement Algorithm Based on Rough Set and Particle Swarm Optimization. Fractal Fract. 2022, 6, 100. [Google Scholar] [CrossRef]
- Xie, X.J.; Tian, J. Adaptive state-feedback stabilization of high-order stochastic systems with nonlinear parameterization. Automatica 2009, 45, 126–133. [Google Scholar] [CrossRef]
- Li, W.; Jing, Y.; Zhang, S. Adaptive state-feedback stabilization for a large class of high-order stochastic nonlinear systems. Automatica 2011, 47, 819–828. [Google Scholar] [CrossRef]
- Li, W.; Liu, X.; Zhang, S. Further results on adaptive state-feedback stabilization for stochastic high-order nonlinear systems. Automatica 2012, 48, 1667–1675. [Google Scholar] [CrossRef]
- Liu, L.; Yin, S.; Gao, H.; Alsaadi, F.; Hayat, T. Adaptive partial-state feedback control for stochastic high-order nonlinear systems with stochastic input-to-state stable inverse dynamics. Automatica 2015, 51, 285–291. [Google Scholar] [CrossRef]
- Sun, Z.Y.; Xue, L.R.; Zhang, K. A new approach to finite-time adaptive stabilization of high-order uncertain nonlinear system. Automatica 2015, 58, 60–66. [Google Scholar] [CrossRef]
- Man, Y.; Liu, Y. Global adaptive stabilization and practical tracking for nonlinear systems with unknown powers. Automatica 2019, 100, 171–181. [Google Scholar] [CrossRef]
- Ma, J.; Wang, H.; Su, Y.; Liu, C.; Chen, M. Adaptive neural fault-tolerant control for nonlinear fractional-order systems with positive odd rational powers. Fractal Fract. 2022, 6, 622. [Google Scholar] [CrossRef]
- Wang, N.; Wang, Y. Fuzzy adaptive quantized tracking control of switched high-order nonlinear systems: A new fixed-Time prescribed performance method. IEEE Trans. Circuits Syst. II Exp. Briefs 2022, 69, 3279–3283. [Google Scholar] [CrossRef]
- Fu, Z.; Wang, N.; Song, S.; Wang, T. Adaptive fuzzy finite-Time tracking control of stochastic high-order nonlinear systems with a class of prescribed performance. IEEE Trans. Fuzzy Syst. 2022, 30, 88–96. [Google Scholar] [CrossRef]
- Lin, W.; Qian, C. Adding one power integrator: A tool for global stabilization of high-order lower-triangular systems. Syst. Control Lett. 2000, 39, 339–351. [Google Scholar] [CrossRef]
- Chen, C.C.; Qian, C.; Lin, X.; Sun, Z.Y.; Liang, Y.W. Smooth output feedback stabilization for a class of nonlinear systems with time-varying powers. Int. J. Robust Nonlinear Control 2017, 27, 5113–5128. [Google Scholar] [CrossRef]
- Su, Z.; Qian, C.; Shen, J. Interval homogeneity-based control for a class of nonlinear systems with unknown power drifts. IEEE Trans. Autom. Control 2017, 62, 1445–1450. [Google Scholar] [CrossRef]
- Xie, X.J.; Guo, C.; Cui, R.H. Removing feasibility conditions on tracking control of full-State constrained nonlinear systems with time-varying powers. IEEE Trans. Syst. Man Cybern. Syst. 2021, 51, 6535–6543. [Google Scholar] [CrossRef]
- Zhang, L.; Liu, X.; Hua, C. Prescribed-time control for stochastic high-order nonlinear systems with parameter uncertainty. IEEE Trans. Circuits Syst. II Exp. Briefs 2023, 70, 4083–4087. [Google Scholar] [CrossRef]
- Lv, M.; De Schutter, B.; Cao, J.; Baldi, S. Adaptive prescribed performance asymptotic tracking for high-order odd-rational-power nonlinear systems. IEEE Trans. Autom. Control 2023, 68, 1047–1053. [Google Scholar] [CrossRef]
- Sui, S.; Chen, C.L.P.; Tong, S. Finite-time adaptive fuzzy prescribed performance control for high-order stochastic nonlinear systems. IEEE Trans. Fuzzy Syst. 2022, 30, 2227–2240. [Google Scholar] [CrossRef]
- Zhao, C.R.; Xie, X.J. Global stabilization of stochastic high-order feedforward nonlinear systems with time-varying delay. Automatica 2014, 50, 203–210. [Google Scholar] [CrossRef]
- Chowdhury, D.; Khalil, H.K. Funnel control for nonlinear systems with arbitrary relative degree using high-gain observers. Automatica 2019, 105, 107–116. [Google Scholar] [CrossRef]
- Dimanidis, I.S.; Bechlioulis, C.P.; Rovithakis, G.A. Output feedback approximation-free prescribed performance tracking control for uncertain MIMO nonlinear systems. IEEE Trans. Autom. Control 2020, 65, 5058–5069. [Google Scholar] [CrossRef]
- Bechlioulis, C.P.; Rovithakis, G.A. Robust partial-state feedback prescribed performance control of cascade systems with unknown nonlinearities. IEEE Trans. Autom. Control 2011, 56, 2224–2230. [Google Scholar] [CrossRef]
- Zhang, J.X.; Ding, J.; Chai, T. Cyclic performance monitoring-based fault-tolerant funnel control of unknown nonlinear systems with actuator failures. IEEE Trans. Autom. Control 2025, 70, 6111–6118. [Google Scholar] [CrossRef]
- Zhang, J.X.; Yang, G.H. Low-complexity tracking control of strict-feedback systems with unknown control directions. IEEE Trans. Autom. Control 2019, 64, 5175–5182. [Google Scholar] [CrossRef]
- Zhang, J.X.; Liu, Y.Q.; Chai, T. Singularity-free low-complexity fault-tolerant prescribed performance control for spacecraft attitude stabilization. IEEE Trans. Autom. Sci. Eng. 2025, 22, 15408–15419. [Google Scholar] [CrossRef]
- Zhang, J.X.; Yang, G.H. Robust Adaptive fault-tolerant control for a class of unknown nonlinear systems. IEEE Trans. Ind. Electron. 2017, 64, 585–594. [Google Scholar] [CrossRef]
- Zhang, J.X.; Yang, G.H. Adaptive asymptotic stabilization of a class of unknown nonlinear systems with specified convergence rate. Int. J. Robust Nonlinear Control 2019, 29, 238–251. [Google Scholar] [CrossRef]
- Song, Y.D.; Zhou, S. Tracking control of uncertain nonlinear systems with deferred asymmetric time-varying full state constraints. Automatica 2018, 98, 314–322. [Google Scholar] [CrossRef]
- Zhou, S.; Song, Y.; Luo, X. Fault-tolerant tracking control with guaranteed performance for nonlinearly parameterized systems under uncertain initial conditions. J. Frankl. Inst. 2020, 357, 6805–6823. [Google Scholar] [CrossRef]
- Zhao, K.; Song, Y.; Chen, C.L.P.; Chen, L. Adaptive asymptotic tracking with global performance for nonlinear systems with unknown control directions. IEEE Trans. Autom. Control 2022, 67, 1566–1573. [Google Scholar] [CrossRef]
- Zhao, K.; Chen, L.; Chen, C.L.P. Event-based adaptive neural control of nonlinear systems with deferred constraint. IEEE Trans. Syst. Man Cybern. Syst. 2022, 52, 6273–6282. [Google Scholar] [CrossRef]
- Berger, T.; Lê, H.H.; Reis, T. Funnel control for nonlinear systems with known strict relative degree. Automatica 2018, 87, 345–357. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, Y. Global practical tracking via adaptive output feedback for uncertain nonlinear systems without polynomial constraint. IEEE Trans. Autom. Control 2021, 66, 1848–1855. [Google Scholar] [CrossRef]
- Jiang, Z.P.; Mareels, I.; Hill, D.; Huang, J. A unifying framework for global regulation via nonlinear output feedback: From ISS to iISS. IEEE Trans. Autom. Control 2004, 49, 549–562. [Google Scholar] [CrossRef]
- Chen, W.; Wen, C.; Wu, J. Global exponential/finite-time stability of nonlinear adaptive switching systems with applications in controlling systems with unknown control direction. IEEE Trans. Autom. Control 2018, 63, 2738–2744. [Google Scholar] [CrossRef]
- Liu, L.; Huang, J. Global robust stabilization of cascade-connected systems with dynamic uncertainties without knowing the control direction. IEEE Trans. Autom. Control 2006, 51, 1693–1699. [Google Scholar] [CrossRef]
- Zhou, Y.; Zhou, Y.; Wan, P. Prescribed finite-time stabilization of fuzzy neural networks with time-varying controller. J. Autom. Intell. 2024, 3, 176–184. [Google Scholar] [CrossRef]
- Shi, Y.; Yi, B.; Xie, W.; Zhang, W. Enhancing prescribed performance of tracking control using monotone tube boundaries. Automatica 2024, 159, 111304. [Google Scholar] [CrossRef]



| Item of Comparison | [9] | [10] | [13] | [29] | [32] | [33] | [36] | This Paper |
|---|---|---|---|---|---|---|---|---|
| Global property | ✘ | ✘ | ✘ | ✔ | ✔ | ✔ | ✔ | ✔ |
| Time-varying fractional powers | ✔ | ✔ | ✔ | ✘ | ✘ | ✘ | ✘ | ✔ |
| Nonparametric uncertainty | ✘ | ✔ | ✘ | ✘ | ✘ | ✘ | ✘ | ✔ |
| FC/PPC | ✘ | ✘ | ✘ | ✔ | ✔ | ✔ | ✘ | ✔ |
| Adaptive control | ✔ | ✘ | ✘ | ✔ | ✘ | ✘ | ✔ | ✘ |
| Power integrator technique | ✔ | ✘ | ✔ | ✘ | ✘ | ✘ | ✘ | ✘ |
| Neural network control | ✘ | ✔ | ✘ | ✘ | ✔ | ✘ | ✘ | ✘ |
| Item of Comparison | The Comparative Controller | Our Controller |
|---|---|---|
| Overshoot | 0.006 | 0.008 |
| Settling time | 0.921 | 2.181 |
| Accuracy | 0.004 | 0.002 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, R.-B.; Zhang, X.; Ahn, H.-S.; Antonis, V. Global Funnel Control of Nonlinear Systems with Unknown and Time-Varying Fractional Powers. Fractal Fract. 2025, 9, 648. https://doi.org/10.3390/fractalfract9100648
Gao R-B, Zhang X, Ahn H-S, Antonis V. Global Funnel Control of Nonlinear Systems with Unknown and Time-Varying Fractional Powers. Fractal and Fractional. 2025; 9(10):648. https://doi.org/10.3390/fractalfract9100648
Chicago/Turabian StyleGao, Rui-Bo, Xuefeng Zhang, Hyo-Sung Ahn, and Vardulakis Antonis. 2025. "Global Funnel Control of Nonlinear Systems with Unknown and Time-Varying Fractional Powers" Fractal and Fractional 9, no. 10: 648. https://doi.org/10.3390/fractalfract9100648
APA StyleGao, R.-B., Zhang, X., Ahn, H.-S., & Antonis, V. (2025). Global Funnel Control of Nonlinear Systems with Unknown and Time-Varying Fractional Powers. Fractal and Fractional, 9(10), 648. https://doi.org/10.3390/fractalfract9100648







