A Novel Method to Determine the Grain Size and Structural Heterogeneity of Fine-Grained Sedimentary Rocks
Abstract
1. Introduction
2. Samples and Methods
2.1. Samples
2.2. Methodology
2.2.1. Sample Pretreatment and Image Capture
2.2.2. Image Processing
- a.
- Mosaic and Fusion of Images
- b.
- Grain Recognition by Image Analysis Method
2.2.3. Process of Grain Size Distribution (GSD) Analysis
2.2.4. Local GSD Analysis Process
2.2.5. Laser Granulometry
2.2.6. Multifractal Method
3. Results and Discussion
3.1. Comparison of the New Image-Based Method and Laser Particle Size Analysis Method
3.1.1. Results of the Image Recognition Based on the New Method
3.1.2. Comparison of the New Method and Laser Particle Size Analysis Method
3.2. Implications to the Hydrodynamic Difference in the Fine-Grained Sedimentary Rocks
3.3. Multifractal Characteristics
3.4. Comparison with Other Non-Destructive Methods
- -
- Siltstones (4–63 μm): Silt particles show clear grayscale contrast in polarized images, with >93% recognition accuracy;
- -
- Marlstones (carbonate-rich): Carbonate minerals exhibit strong birefringence (cross-polarized light), enabling >90% differentiation from clays;
- -
- Organic-rich shales (TOC > 5%): Organic matter appears dark in single-polarized light—adjusting k-means k = 4 reduces grayscale overlap with clays, improving accuracy to 88% (further enhanced to >95% with Raman spectroscopy for organic identification).
4. Conclusions
- (1)
- The proposed non-destructive workflow effectively retains sedimentary fabric, enabling accurate grain size analysis via polarized image mosaicking, clustering, and watershed segmentation without sample disaggregation.
- (2)
- Localized grain size statistical analysis across ten defined sub-regions successfully captures internal heterogeneity, enhancing understanding of depositional variability.
- (3)
- Validation confirms high accuracy (absolute error −5% to 3%) when compared to conventional laser granulometry, particularly for particles larger than 0.039 mm.
- (4)
- The method discriminates lithofacies effectively, clearly distinguishing laminated shale, characterized by alternating coarse siliceous and fine clay laminae, from more homogeneous massive mudstone.
- (5)
- Application of multifractal parameters (Dq, α~f(α)) quantifies spatial complexity and enhances the geological interpretation of depositional conditions—specifically pore size distribution, connectivity, and spatial heterogeneity. For example, D0 (capacity dimension) reflects pore size range (laminated shale: D0 = 1.8328 > massive mudstone: D0 = 1.7055), while Δα (αmax-αmin) indicates spatial heterogeneity (laminated shale: Δα = 1.5308 > massive mudstone: Δα = 1.4367).
- (6)
- Overall, this image-based grain size analysis significantly advances facies differentiation, providing robust constraints for shale reservoir characterization and enhancing predictive reservoir modeling. For industrial-scale routine characterization, the workflow can be optimized by performing the following: Automating image stitching (via Python 3.11 OpenCV) to reduce manual time from 8 h to 2 h per sample; Integrating with robotic sample stages to eliminate manual movement; Developing a user-friendly GUI (e.g., MATLAB App) for non-experts. These optimizations make the method feasible for batch processing of 50+ samples/month, meeting industrial demands.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Picard, M.D. Classification of fine-grained sedimentary rocks. J. Sediment. Res. 1971, 41, 179–195. [Google Scholar] [CrossRef]
- Owens, P.N.; Batalla, R.J.; Collins, A.J.; Gomez, B.; Hicks, D.M.; Horowitz, A.J.; Kondolf, G.M.; Marden, M.; Page, M.J.; Peacock, D.H.; et al. Fine-grained sediment in river systems: Environmental significance and management issues. River Res. Appl. 2005, 21, 693–717. [Google Scholar] [CrossRef]
- Stow, D.A.V.; Piper, D.J.W. Deep-water fine-grained sediments: Facies models. Geol. Soc. Lond. Spec. Publ. 1984, 15, 611–646. [Google Scholar] [CrossRef]
- Liu, B.; Wang, H.; Fu, X.; Bai, Y.; Bai, L.; Jia, M.; He, B. Lithofacies and depositional setting of a highly prospective lacustrine shale oil succession from the Upper Cretaceous Qingshankou Formation in the Gulong sag, northern Songliao Basin, northeast China. AAPG Bull. 2019, 103, 405–432. [Google Scholar] [CrossRef]
- Tian, S.; Bowen, L.; Liu, B.; Zeng, F.; Xue, H.; Erastova, V.; Greenwell, H.C.; Dong, Z.; Zhao, R.; Liu, J. A method for automatic shale porosity quantification using an Edge-Threshold Automatic Processing (ETAP) technique. Fuel 2021, 304, 121319. [Google Scholar] [CrossRef]
- Guo, H.; Shi, J.; Fu, S.; Liu, Z.; Cai, L.; Yin, S. Lithofacies Characteristics of Continental Lacustrine Fine-Grained Sedimentary Rocks and Their Coupling Relationship with Sedimentary Environments: Insights from the Shahejie Formation, Dongying Sag. Minerals 2024, 14, 479. [Google Scholar] [CrossRef]
- McCave, I.N.; Syvitski, J.P.M. Principles and methods of geological particle size analysis. In Principles, Methods and Application of Particle Size Analysis; Cambridge University Press: Cambridge, UK, 1991; pp. 3–21. [Google Scholar]
- Visher, G.S. Grain size distributions and depositional processes. J. Sediment. Res. 1969, 39, 1074–1106. [Google Scholar] [CrossRef]
- Sun, D.; Bloemendal, J.; Rea, D.K.; Vandenberghe, J.; Jiang, F.; An, Z.; Su, R. Grain-size distribution function of polymodal sediments in hydraulic and aeolian environments, and numerical partitioning of the sedimentary components. Sediment. Geol. 2002, 152, 263–277. [Google Scholar] [CrossRef]
- Chen, Y.; Wei, L.; Mastalerz, M.; Schimmelmann, A. The effect of analytical particle size on gas adsorption porosimetry of shale. Int. J. Coal Geol. 2015, 138, 103–112. [Google Scholar] [CrossRef]
- Liu, B.; He, S.; Meng, L.; Fu, X.; Gong, L.; Wang, H. Sealing mechanisms in volcanic faulted reservoirs in Xujiaweizi extension, northern Songliao Basin, northeastern China. AAPG Bull. 2021, 105, 1721–1743. [Google Scholar] [CrossRef]
- Al-Mudhafar, W.J.; Hasan, A.A.; Abbas, M.A.; Wood, D.A. Machine learning with hyperparameter optimization applied in facies-supported permeability modeling in carbonate oil reservoirs. Sci. Rep. 2025, 15, 12939. [Google Scholar] [CrossRef]
- Folk, R.L. Petrology of Sedimentary Rocks; Hemphill Publishing Company: Elmhurst, NY, USA, 1980. [Google Scholar]
- Gee, G.W. 2.4 Particle-size analysis. In Methods of Soil Analysis: Part 4 Physical Methods; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2002; Volume 5, pp. 255–293. [Google Scholar]
- Konert, M.; Vandenberghe, J.E.F. Comparison of laser grain size analysis with pipette and sieve analysis: A solution for the underestimation of the clay fraction. Sedimentology 1997, 44, 523–535. [Google Scholar] [CrossRef]
- Yuan, H.; Wang, L.; Yu, Y.; Zhang, D.J.; Xu, F.M.; Liu, H.T. Review of sedimentary grain size analysis methods. J. Jilin Univ. (Earth Sci. Ed.) 2019, 49, 380–393. [Google Scholar]
- Buscombe, D. Estimation of grain-size distributions and associated parameters from digital images of sediment. Sediment. Geol. 2008, 210, 1–10. [Google Scholar] [CrossRef]
- Bankole, S.A.; Buckman, J.; Stow, D.; Lever, H. Grain-size analysis of mudrocks: A new semi-automated method from SEM images. J. Pet. Sci. Eng. 2019, 174, 244–256. [Google Scholar] [CrossRef]
- Izadi, H.; Sadri, J.; Mehran, N.A. A new intelligent method for minerals segmentation in thin sections based on a novel incremental color clustering. Comput. Geosci. 2015, 81, 38–52. [Google Scholar] [CrossRef]
- Cuddy, S. The benefits and dangers of using artificial intelligence in petrophysics. Artif. Intell. Geosci. 2021, 2, 1–10. [Google Scholar] [CrossRef]
- Bhattacharya, S. A Primer on Machine Learning in Subsurface Geosciences; Springer: Cham, Switzerland, 2021. [Google Scholar] [CrossRef]
- Leblanc, C.; Picek, L.; Deneu, B.; Bonnet, P.; Servajean, M.; Palard, R.; Joly, A. Mapping biodiversity at very-high resolution in Europe. In Proceedings of the 2025 IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), Nashville, TN, USA, 11–12 June 2025; pp. 2349–2358. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention Is All You Need. In Proceedings of the Advances in Neural Information Processing Systems 30 (NeurIPS 2017), Long Beach, CA, USA, 4–9 December 2017; pp. 5998–6008. [Google Scholar]
- Johnson, M.R. Thin section grain size analysis revisited. Sedimentology 1994, 41, 985–999. [Google Scholar] [CrossRef]
- Tarquini, S.; Favalli, M. A microscopic information system (MIS) for petrographic analysis. Comput. Geosci. 2010, 36, 665–674. [Google Scholar] [CrossRef]
- Tang, D.G.; Milliken, K.L.; Spikes, K.T. Machine learning for point counting and segmentation of arenite in thin section. Mar. Pet. Geol. 2020, 120, 104518. [Google Scholar] [CrossRef]
- Han, W.; Zhao, X.; Pu, X.; Chen, S.; Wang, H.; Liu, Y.; Shi, Z.; Zhang, W.; Wu, J. Fine-grained rock fabric facies classification and its control on shale oil accumulation: A case study from the Paleogene Kong 2 Member, Bohai Bay Basin. Front. Earth Sci. 2021, 15, 423–437. [Google Scholar] [CrossRef]
- Bian, C.; Guo, B.; Pu, X.; Zeng, X.; Liu, W.; Li, Y.; Zhou, K.; Tian, Q.; Ma, C. Lithofacies Characteristics and Their Effects on Shale Oil Enrichment: A Case Study from Shahejie Formation of the Qibei Sag, Bohai Bay Basin, China. Energies 2023, 16, 2107. [Google Scholar] [CrossRef]
- Udden, J.A. The Mechanical Composition of Wind Deposits; Augustana College Library: Rock Island, IL, USA, 1898; pp. 838–839. [Google Scholar]
- Miall, A.D. A review of the braided-river depositional environment. Earth-Sci. Rev. 1977, 13, 1–62. [Google Scholar] [CrossRef]
- Blott, S.J.; Pye, K. GRADISTAT: A grain size distribution and statistics package for the analysis of unconsolidated sediments. Earth Surf. Process. Landf. 2001, 26, 1237–1248. [Google Scholar] [CrossRef]
- Bjørlykke, K. Relationships between depositional environments, burial history and rock properties. Some principal aspects of diagenetic process in sedimentary basins. Sediment. Geol. 2014, 301, 1–14. [Google Scholar] [CrossRef]
- Loog, A.; Kurvits, T.; Aruvali, J.; Petersell, V. Grain size analysis and mineralogy of the Tremadocian Dictyonema shale in Estonia. Oil Shale 2001, 18, 281–297. [Google Scholar] [CrossRef]
- Wentworth, C.K. A scale of grade and class terms for clastic sediments. J. Geol. 1922, 30, 377–392. [Google Scholar] [CrossRef]
- Krumbein, W.C. Size frequency distributions of sediments. J. Sediment. Res. 1934, 4, 65–77. [Google Scholar] [CrossRef]
- Allen, G.P.; Castaing, P.; Klingebiel, A. Distinction of elementary sand populations in the Gironde Estuary (France) by R-mode factor analysis of grain-size data. Sedimentology 1972, 19, 21–35. [Google Scholar] [CrossRef]
- Folk, R.L.; Ward, W.C. A study in the significance of grain size parameters. J. Sediment. Res. 1957, 27, 3–26. [Google Scholar] [CrossRef]
- Beuselinck, L.; Govers, G.; Poesen, J.; Degraer, G.; Froyen, L. Grain-size analysis by laser diffractometry: Comparison with the sieve–pipette method. Catena 1998, 32, 193–208. [Google Scholar] [CrossRef]
- Loucks, R.G.; Reed, R.M.; Ruppel, S.C.; Hammes, U. Spectrum of pore types and networks in mudrocks and a descriptive classification for matrix-related mudrock pores. AAPG Bull. 2012, 96, 1071–1098. [Google Scholar] [CrossRef]

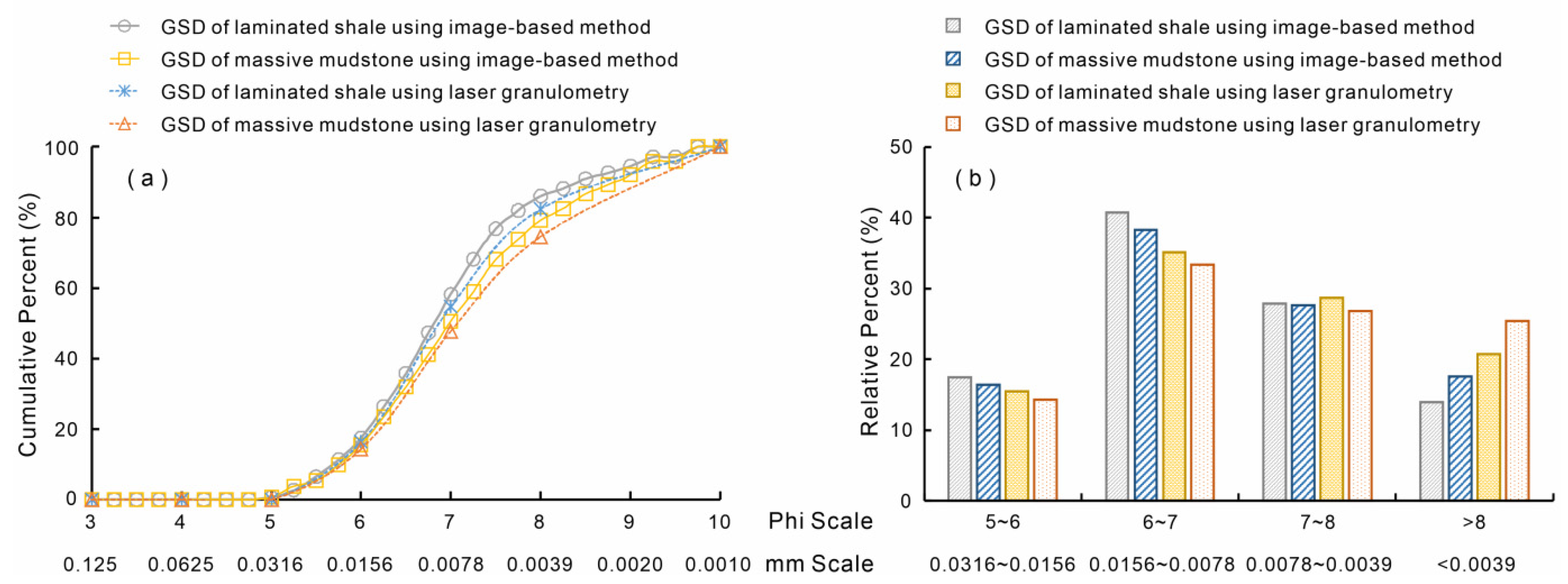


| Different Method | GSD Using Image-Based Method (%) | GSD Using Laser Granulometry (%) | Absolute Error (%) | Relative Error (%) | |||||
|---|---|---|---|---|---|---|---|---|---|
| Phi Scale | LS | MM | LS | MM | LS | MM | LS | MM | |
| 5~6 | 17.439 | 15.523 | 16.397 | 14.361 | 1.042 | 1.162 | 6.355 | 8.093 | |
| 6~7 | 40.746 | 35.083 | 38.294 | 33.420 | 2.452 | 1.663 | 6.404 | 4.976 | |
| 7~8 | 27.883 | 28.657 | 27.684 | 26.813 | 0.199 | 1.844 | 0.719 | 6.878 | |
| >8 | 13.932 | 20.737 | 17.625 | 25.406 | −3.693 | −4.669 | −20.955 | −18.379 | |
| Particles in Different Region | D0 | D1 | D2 | αmin | αmax | α0 | Δα | A | Db |
|---|---|---|---|---|---|---|---|---|---|
| Blue region of laminated shale | 1.8328 | 1.7851 | 1.7645 | 1.6505 | 3.1813 | 1.9161 | 1.5308 | 0.2099 | 1.7057 |
| Blue region of massive shale | 1.7055 | 1.5972 | 1.5280 | 1.2954 | 2.7322 | 1.8264 | 1.4367 | 0.5863 | 1.5818 |
| Red region of laminated shale | 1.2077 | 1.0118 | 0.9123 | 0.7052 | 2.1418 | 1.4298 | 1.4366 | 1.0178 | 1.2737 |
| Red region of massive shale | 1.8018 | 1.7223 | 1.6699 | 1.4752 | 2.8902 | 1.8945 | 1.4150 | 0.4212 | 1.5223 |
| Method | Resolution | Reliability (Accuracy) | Scalability (Single-Sample Processing Time) | Core Advantages | Core Disadvantages |
|---|---|---|---|---|---|
| Proposed method | 0.97 μm | 92–95% | 8 h (including sample preparation) | Non-destructive, preserves sedimentary structures, large field of view (3 × 3 mm) | Cannot identify particles <0.2 μm |
| micro-CT | >0.5 μm | 90–93% | >24 h (including sample preparation) | Characterizes three-dimensional pore structure | High cost (~5 million RMB/unit), small sample volume |
| SEM | 0.01 μm | 95–98% | 12 h (including sample preparation) | High resolution, accurate mineral identification | Small field of view (<0.1 × 0.1 mm), lacks macro-scale analysis |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zeng, F.; Tian, S.; Dong, H.; Dong, Z.; Liu, B.; Liu, H. A Novel Method to Determine the Grain Size and Structural Heterogeneity of Fine-Grained Sedimentary Rocks. Fractal Fract. 2025, 9, 642. https://doi.org/10.3390/fractalfract9100642
Zeng F, Tian S, Dong H, Dong Z, Liu B, Liu H. A Novel Method to Determine the Grain Size and Structural Heterogeneity of Fine-Grained Sedimentary Rocks. Fractal and Fractional. 2025; 9(10):642. https://doi.org/10.3390/fractalfract9100642
Chicago/Turabian StyleZeng, Fang, Shansi Tian, Hongli Dong, Zhentao Dong, Bo Liu, and Haiyang Liu. 2025. "A Novel Method to Determine the Grain Size and Structural Heterogeneity of Fine-Grained Sedimentary Rocks" Fractal and Fractional 9, no. 10: 642. https://doi.org/10.3390/fractalfract9100642
APA StyleZeng, F., Tian, S., Dong, H., Dong, Z., Liu, B., & Liu, H. (2025). A Novel Method to Determine the Grain Size and Structural Heterogeneity of Fine-Grained Sedimentary Rocks. Fractal and Fractional, 9(10), 642. https://doi.org/10.3390/fractalfract9100642






