Finite-Time Adaptive Cluster Synchronization of Heterogeneous Fractional-Order Dynamic Networks with Community Structure and Co-Competition Interactions
Abstract
1. Introduction
2. Preliminaries and Model Description
2.1. Preliminaries
2.2. Model Description
3. Main Results
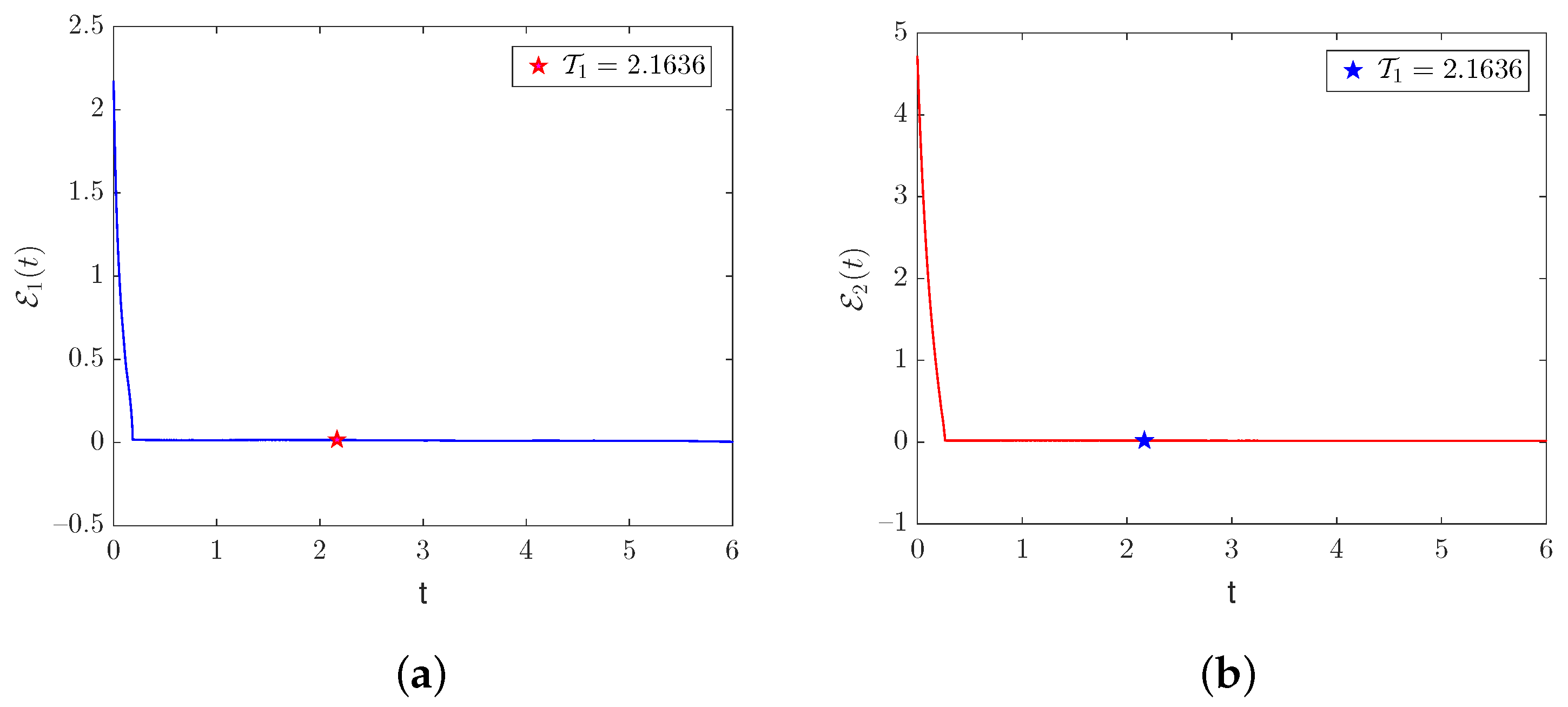
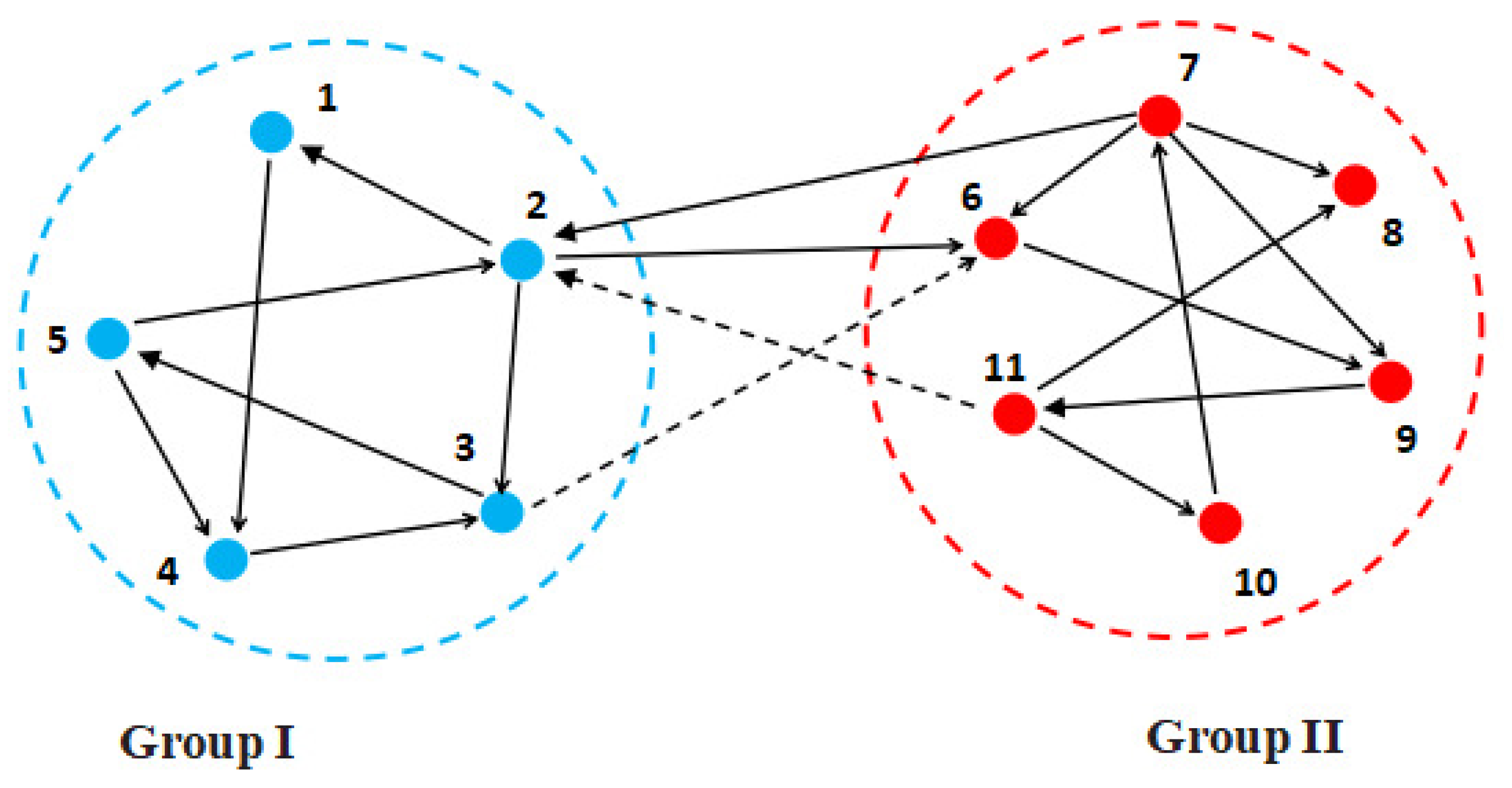
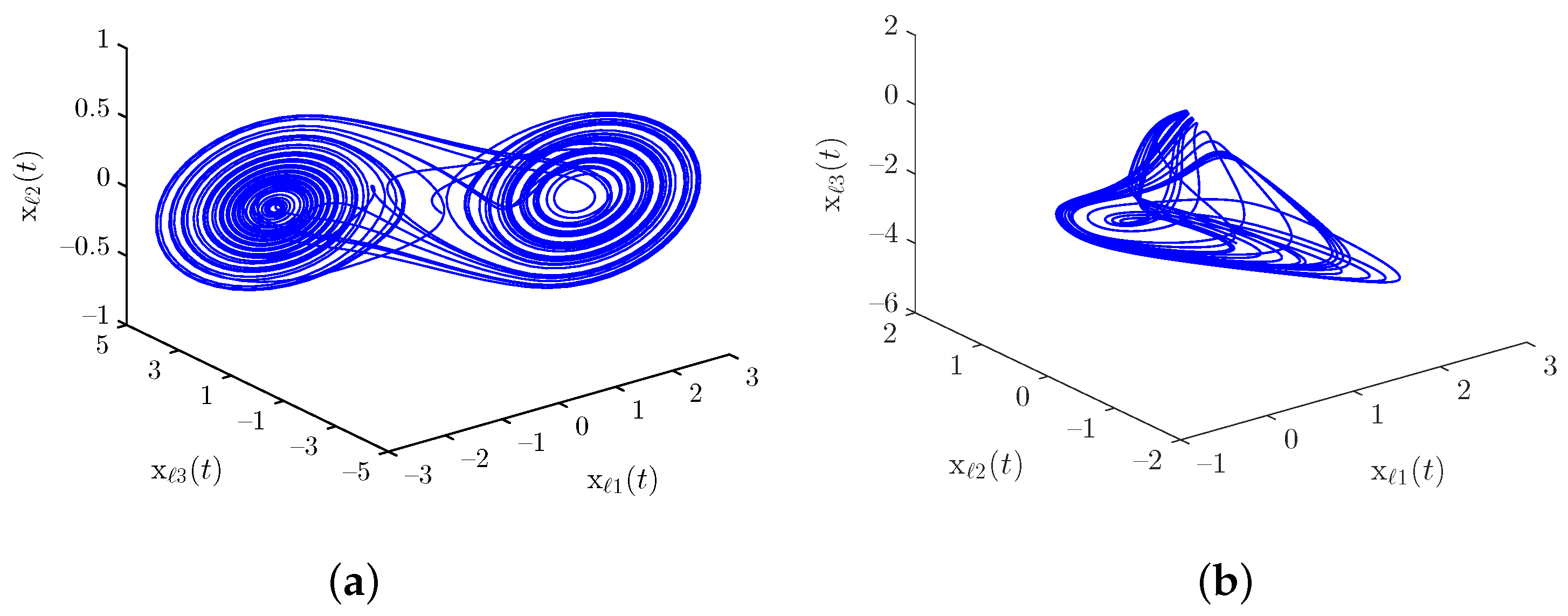
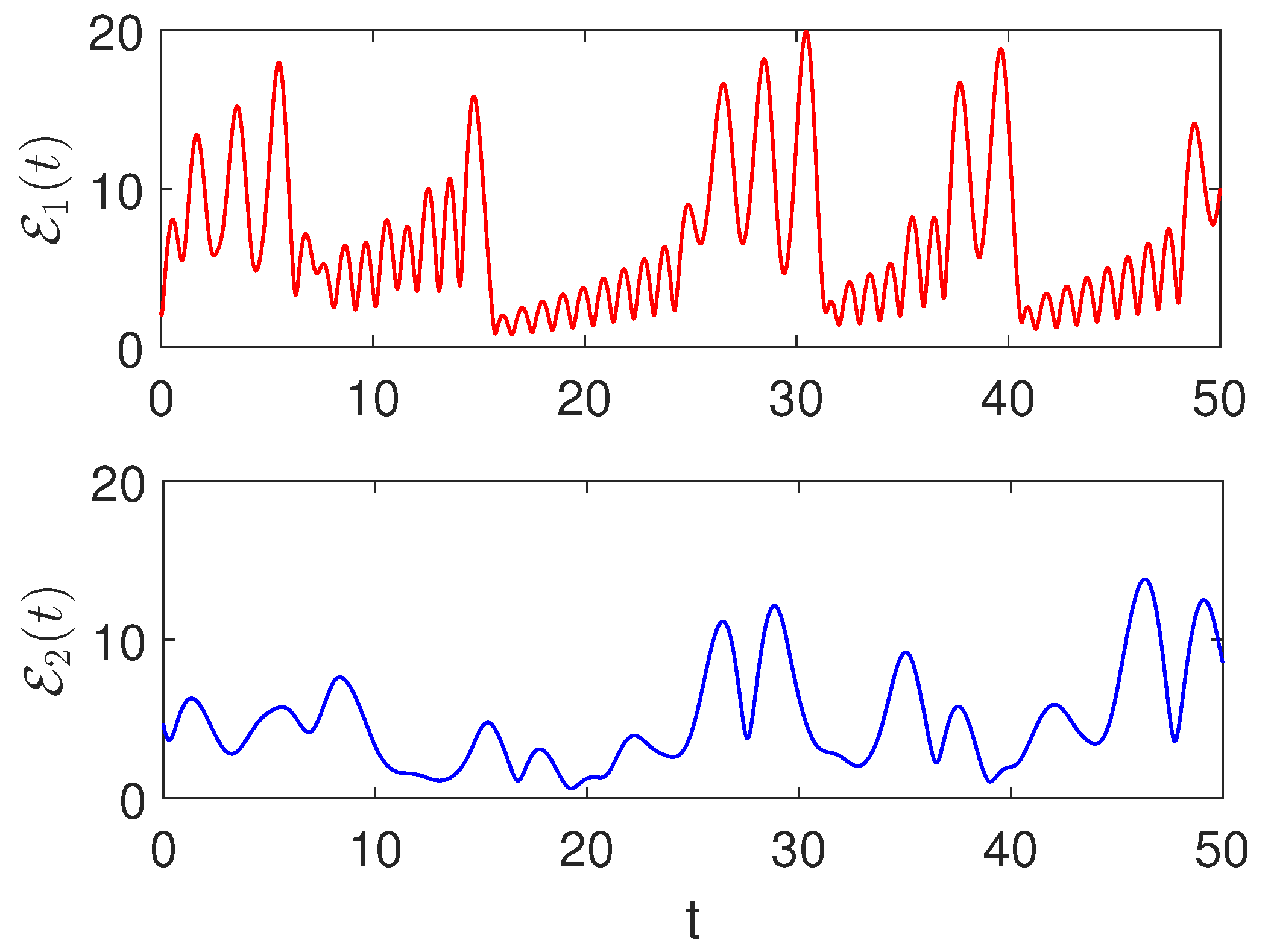
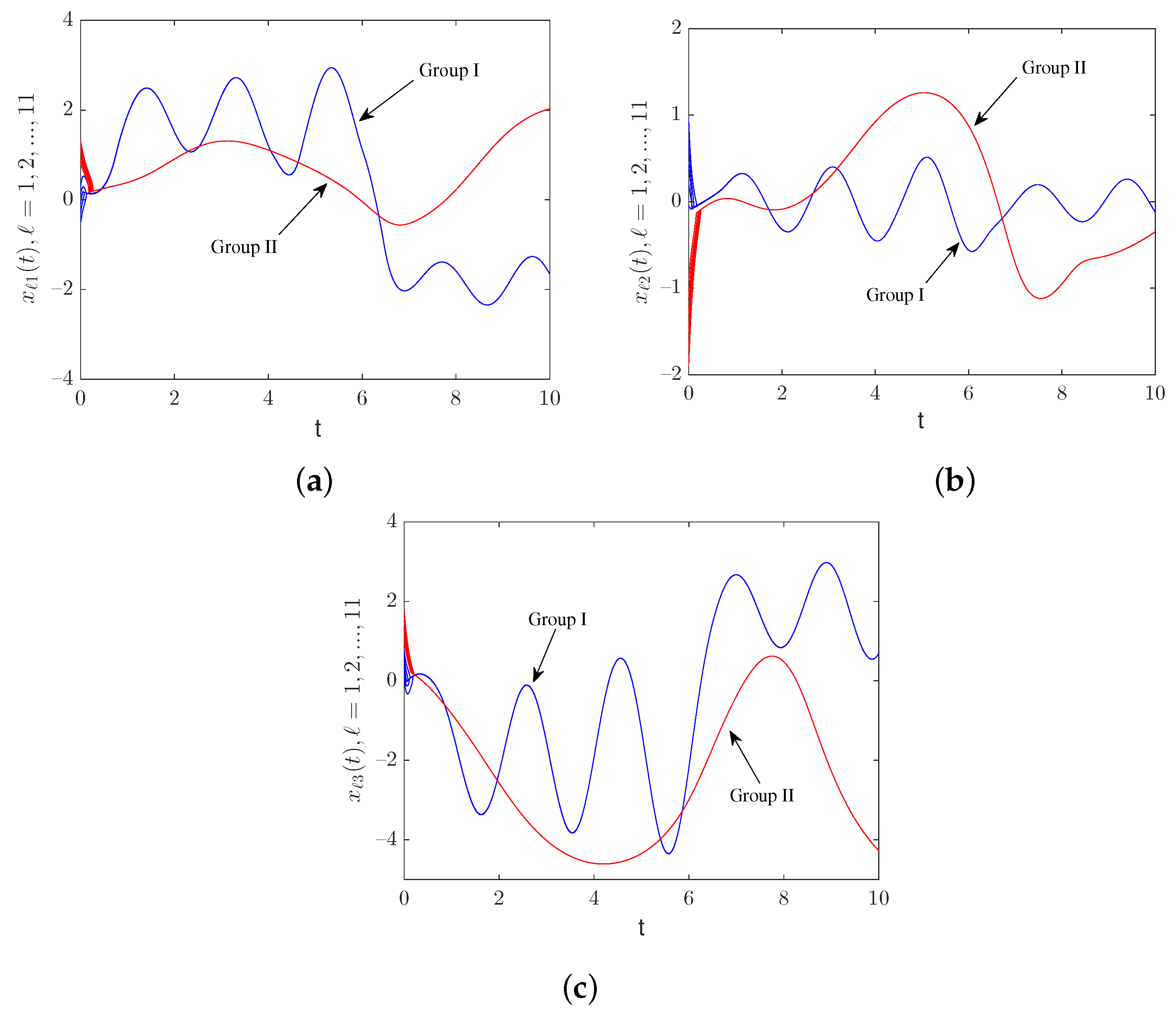
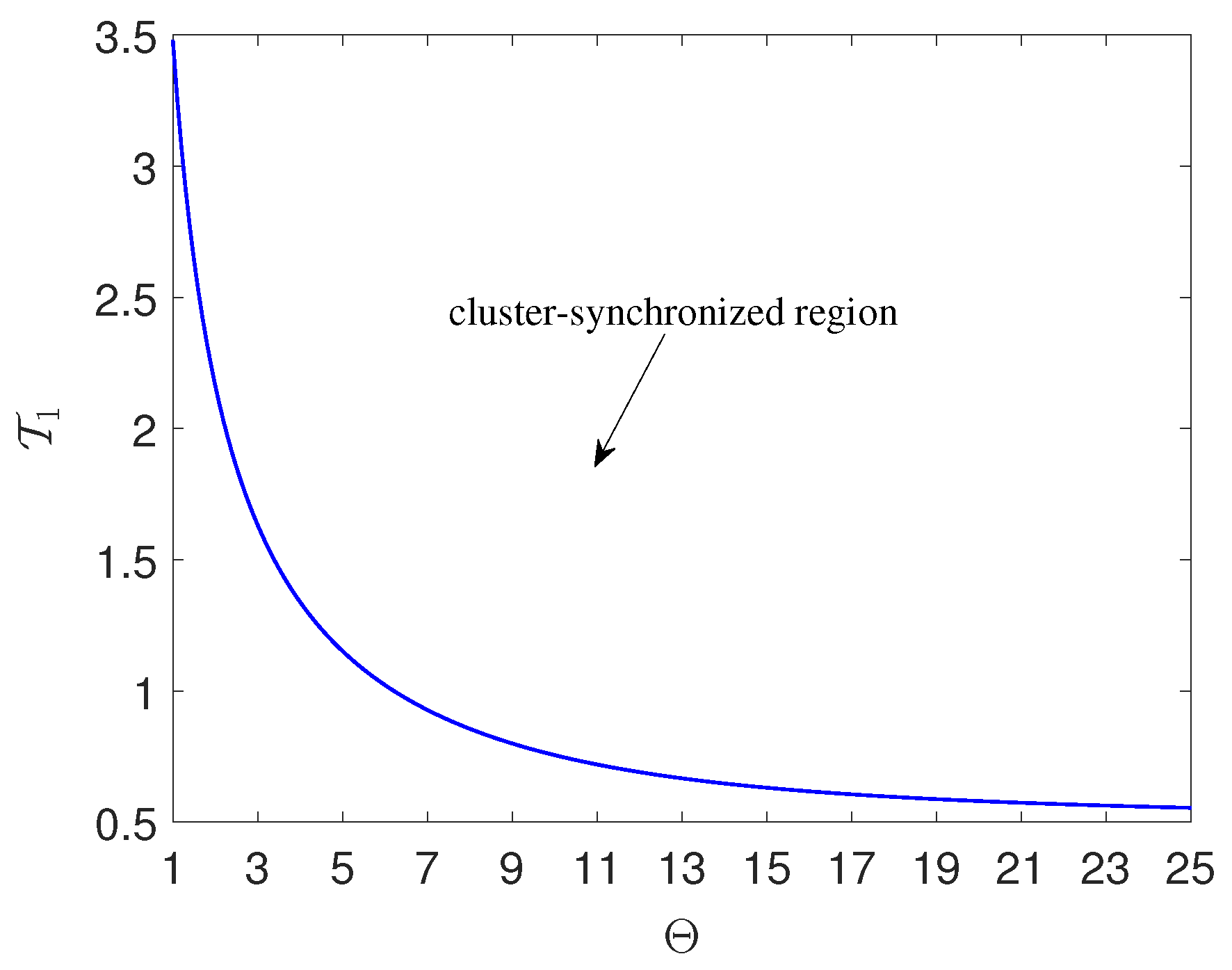
4. Numerical Simulations
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Newman, M.E.J. Communities, modules and large-scale structure in networks. Nat. Phys. 2012, 8, 25–31. [Google Scholar] [CrossRef]
- Benson, A.R.; Gleich, D.F.; Leskovec, J. Higher-order organization of complex networks. Science 2016, 353, 163–166. [Google Scholar] [CrossRef]
- Schaub, M.T.; Li, J.; Peel, L. Hierarchical community structure in networks. Phys. Rev. E 2023, 107, 054305. [Google Scholar] [CrossRef]
- Liu, C.; Ma, Y.; Zhao, J.; Nussinov, R.; Zhang, Y.-C.; Cheng, F.; Zhang, Z.-K. Computational network biology: Data, models, and applications. Phys. Rep. 2020, 846, 1–66. [Google Scholar] [CrossRef]
- Bardoscia, M.; Barucca, P.; Battiston, S.; Caccioli, F.; Cimini, G.; Garlaschelli, D.; Saracco, F.; Squartini, T.; Caldarelli, G. The physics of financial networks. Nat. Rev. Phys. 2021, 3, 490–507. [Google Scholar] [CrossRef]
- Wang, K.; Fu, X.; Li, K. Cluster synchronization in community networks with nonidentical nodes. Chaos 2009, 19, 023106. [Google Scholar] [CrossRef] [PubMed]
- Boccaletti, S.; Pisarchik, A.N.; Del Genio, C.I.; Amann, A. Synchronization: From Coupled Systems to Complex Networks; Cambridge University Press: New York, NY, USA, 2018. [Google Scholar]
- Ma, Z.; Liu, Z.; Zhang, G. A new method to realize cluster synchronization in connected chaotic networks. Chaos 2006, 16, 023103. [Google Scholar] [CrossRef]
- Wu, W.; Chen, T. Partial synchronization in linearly and symmetrically coupled ordinary differential systems. Phys. D 2009, 238, 355–364. [Google Scholar] [CrossRef]
- Schnitzler, A.; Gross, J. Normal and pathological oscillatory communication in the brain. Nat. Rev. Neurosci. 2005, 6, 285–296. [Google Scholar] [CrossRef]
- Lynn, C.W.; Bassett, D.S. The physics of brain network structure, function, and control. Nat. Rev. Phys. 2019, 1, 318–332. [Google Scholar]
- Jaiswal, A.K.; Sharma, B.B. Cluster synchronization of networks of chaotic systems: A comprehensive review of theory and applications. IETE Tech. Rev. 2024, 41, 537–556. [Google Scholar] [CrossRef]
- Lu, W.; Liu, B.; Chen, T. Cluster synchronization in networks of coupled nonidentical dynamical systems. Chaos 2010, 20, 013120. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.; Chen, T. Cluster synchronization in directed networks via intermittent pinning control. IEEE Trans. Neural Netw. 2011, 22, 1009–1020. [Google Scholar] [PubMed]
- Zhang, J.; Ma, Z.; Zhang, G. Cluster synchronization induced by one-node clusters in networks with asymmetric negative couplings. Chaos 2013, 23, 043128. [Google Scholar] [CrossRef]
- Wu, Z.; Fu, X. Cluster synchronization in community networks with nonidentical nodes via edge-based adaptive pinning control. J. Frankl. Inst. 2014, 351, 1372–1385. [Google Scholar] [CrossRef]
- Cai, S.; Jia, Q.; Liu, Z. Cluster synchronization for directed heterogeneous dynamical networks via decentralized adaptive intermittent pinning control. Nonlinear Dyn. 2015, 82, 689–702. [Google Scholar] [CrossRef]
- Zhou, P.; Cai, S.; Shen, J.; Liu, Z. Adaptive exponential cluster synchronization in colored community networks via aperiodically intermittent pinning control. Nonlinear Dyn. 2018, 92, 905–921. [Google Scholar] [CrossRef]
- Jiang, S.; Qi, Y.; Cai, S.; Lu, X. Light fixed-time control for cluster synchronization of complex networks. Neurocomputing 2021, 424, 63–70. [Google Scholar] [CrossRef]
- Wang, J.; Liu, X. Cluster synchronization for multi-weighted and directed complex networks via pinning control. IEEE Trans. Circuits Syst. II 2022, 69, 1347–1351. [Google Scholar] [CrossRef]
- Zhu, X.; Tang, Z.; Feng, J.; Park, J.H. Aperiodically intermittent event-triggered pinning control on cluster synchronization of directed complex networks. ISA Trans. 2023, 138, 281–290. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Differential Equations; Academic Press: San Diego, CA, USA, 1999. [Google Scholar]
- Jin, B. Fractional Differential Equations: An Approach via Fractional Derivatives; Springer: Cham, Switzerland, 2021. [Google Scholar]
- Chen, W.; Sun, H.G.; Li, X. Fractional Derivative Modeling in Mechanics and Engineering; Springer Nature: Berlin/Heidelberg, Germany, 2022. [Google Scholar]
- He, Y.; Peng, J.; Zheng, S. Fractional-order financial system and fixed-time synchronization. Fractal Fract. 2022, 6, 507. [Google Scholar] [CrossRef]
- Wang, G.-S.; Xiao, J.-W.; Wang, Y.-W.; Yi, J.-W. Adaptive pinning cluster synchronization of fractional-order complex dynamical networks. Appl. Math. Comput. 2014, 231, 347–356. [Google Scholar] [CrossRef]
- Zhou, J.; Zhao, Y.; Wu, Z. Cluster synchronization of fractional-order directed networks via intermittent pinning control. Phys. A 2019, 519, 22–33. [Google Scholar] [CrossRef]
- Wang, J.; Liu, X. Cluster synchronization for multiweighted and directed fractional-order Networks with cooperative-competitive interactions. IEEE Trans. Circuits Syst. II 2022, 69, 4359–4363. [Google Scholar] [CrossRef]
- Wang, Y.; Wu, Z. Cluster synchronization in fractional-order network with nondelay and delay coupling. Int. J. Mod. Phys. C 2022, 33, 2250006. [Google Scholar] [CrossRef]
- Liu, P.; Zeng, Z.; Wang, J. Asymptotic and finite-time cluster synchronization of coupled fractional-order neural networks with time delay. IEEE Trans. Neural Netw. Learn. Syst. 2020, 33, 4956–4967. [Google Scholar] [CrossRef]
- Li, H.-L.; Cao, J.; Jiang, H.; Alsaedi, A. Finite-time synchronization of fractional-order complex dynamical networks via hybrid feedback control. Neurocomputing 2018, 320, 69–75. [Google Scholar] [CrossRef]
- Ding, Z.; Zeng, Z.; Wang, L. Robust finite-time synchronization of fractional-order neural networks with discontinuous and continuous activation functions under uncertainty. IEEE Trans. Neural Netw. Learn. Syst. 2018, 29, 1471–1490. [Google Scholar] [CrossRef]
- Yang, S.; Hu, C.; Yu, J.; Jiang, H. Projective synchronization in finite-time for fully quaternion-valued memristive networks with fractional-order. Chaos Solitons Fract. 2021, 147, 110911. [Google Scholar] [CrossRef]
- Li, H.-L.; Hu, C.; Zhang, L.; Jiang, H.; Cao, J. Complete and finite-time synchronization of fractional-order fuzzy neural networks via nonlinear feedback control. Fuzzy Set. Syst. 2022, 443, 50–69. [Google Scholar] [CrossRef]
- Yang, S.; Hu, C.; Yu, J.; Jiang, H. Finite-time cluster synchronization in complex-varible networks with fractional-order and nonlinear coupling. Neural Netw. 2021, 135, 212–224. [Google Scholar] [CrossRef]
- Cai, S.; Hou, M. Quasi-synchronization of fractional-order heterogeneous dynamical networks via aperiodic intermittent pinning control. Chaos Solitons Fract. 2021, 146, 110901. [Google Scholar] [CrossRef]
- Shi, J.; Zhou, P.; Jia, Q.; Cai, S. Fixed-time synchronization of multilayered complex dynamic networks via quantized variable-gain saturated control. Inf. Sci. 2024, 681, 121206. [Google Scholar] [CrossRef]
- Jiang, S.; Song, Y.; Zeng, W.; Zhang, H.; Cai, S.; Lu, X. New results on adaptive fixed-time control for convex-delayed neural networks. ISA Trans. 2023, 134, 134–143. [Google Scholar] [CrossRef]
- Xu, Y.; Li, Y.; Li, W. Adaptive finite-time synchronization control for fractional-order complex-valued dynamical networks with multiple weights. Commun. Nonlinear Sci. Numer. Simulat. 2020, 85, 105239. [Google Scholar] [CrossRef]
- Kao, Y.; Li, Y.; Park, J.H.; Chen, X. Mittag-Leffler synchronization of delayed fractional memristor neural networks via adaptive control. IEEE Trans. Neural Netw. Learn. Syst. 2021, 32, 2279–2284. [Google Scholar] [CrossRef]
- Duarte-Mermoud, M.A.; Aguila-Camacho, N.; Gallegos, J.A.; Castro-Linares, R. Using general quadratic Lyapunov functions to prove Lyapunov uniform stability for fractional order systems. Commun. Nonlinear Sci. Numer. Simulat. 2015, 22, 650–659. [Google Scholar] [CrossRef]
- Yu, J.; Hu, C.; Jiang, H. Corrigendum to “Projective synchronization for fractional neural networks”. Neural Netw. 2015, 67, 152–154. [Google Scholar] [CrossRef]
- Li, Y.; Chen, Y.; Podlubny, I. Stability of fractional-order nonlinear dynamic systems: Lyapunov direct method and generalized Mittag-Leffler stability. Comput. Math. Appl. 2010, 59, 1810–1821. [Google Scholar] [CrossRef]
- Li, H.-H.; Hu, C.; Cao, J.; Jiang, H.; Alsaedi, A. Quasi-projective and complete synchronization of fractional-order complex-valued neural networks with time delays. Neural Netw. 2019, 118, 102–109. [Google Scholar] [CrossRef] [PubMed]
- Zhu, Z.; Xia, Y.; Fu, M. Attitude stabilization of rigid spacecraft with finite time convergence. Int. J. Robust. Nonlinear Control 2011, 21, 686–702. [Google Scholar] [CrossRef]
- Ni, J.; Liu, L.; Liu, C.; Hu, X. Fractional order fixed-time nonsingular terminal sliding mode synchronization and control of fractional order chaotic systems. Nonlinear Dyn. 2017, 89, 2065–2083. [Google Scholar] [CrossRef]
- Qin, X.; Jiang, H.; Qiu, J.; Hu, C.; Ren, Y. Strictly intermittent quantized control for fixed/predefined-time cluster lag synchronization of stochastic multi-weighted complex networks. Neural Netw. 2023, 158, 258–271. [Google Scholar] [CrossRef]
- Wu, Z.; Fu, X. Cluster lag synchronisation in community networks via linear pinning control with local intermittent effect. Phys. A 2014, 395, 487–498. [Google Scholar] [CrossRef]
- Cai, S.; Zhou, F.; He, Q. Fixed-time cluster lag synchronization in directed heterogeneous community networks. Phys. A 2019, 525, 128–142. [Google Scholar] [CrossRef]
- Lu, J. Chaotic dynamics and synchronization of fractional-order Chua’s circuit with a piecewise-linear nonlinearity. Int. J. Mod. Phys. B 2005, 19, 3249–3259. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, P.; Cai, S. Finite-Time Adaptive Cluster Synchronization of Heterogeneous Fractional-Order Dynamic Networks with Community Structure and Co-Competition Interactions. Fractal Fract. 2025, 9, 641. https://doi.org/10.3390/fractalfract9100641
Zhou P, Cai S. Finite-Time Adaptive Cluster Synchronization of Heterogeneous Fractional-Order Dynamic Networks with Community Structure and Co-Competition Interactions. Fractal and Fractional. 2025; 9(10):641. https://doi.org/10.3390/fractalfract9100641
Chicago/Turabian StyleZhou, Peipei, and Shuiming Cai. 2025. "Finite-Time Adaptive Cluster Synchronization of Heterogeneous Fractional-Order Dynamic Networks with Community Structure and Co-Competition Interactions" Fractal and Fractional 9, no. 10: 641. https://doi.org/10.3390/fractalfract9100641
APA StyleZhou, P., & Cai, S. (2025). Finite-Time Adaptive Cluster Synchronization of Heterogeneous Fractional-Order Dynamic Networks with Community Structure and Co-Competition Interactions. Fractal and Fractional, 9(10), 641. https://doi.org/10.3390/fractalfract9100641