Integrated Analysis of Mapping, Path Planning, and Advanced Motion Control for Autonomous Robotic Navigation
Abstract
1. Introduction
2. Environment Representation Using Occupancy-Based Mapping
2.1. Binary Occupancy Maps
2.2. Probabilistic Occupancy Maps
3. Sampling-Driven Path Planning Algorithms
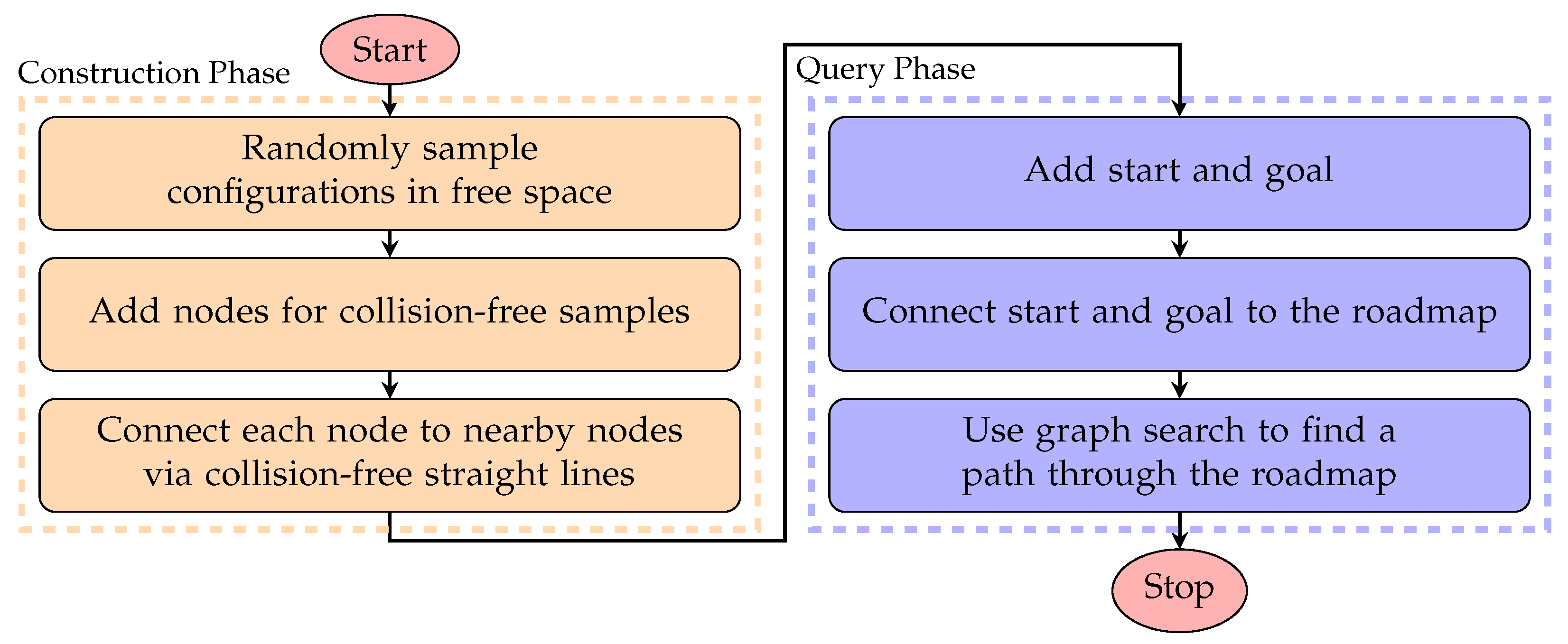
3.1. Probabilistic Roadmap (PRM)
3.2. A* and Hybrid A* Algorithms
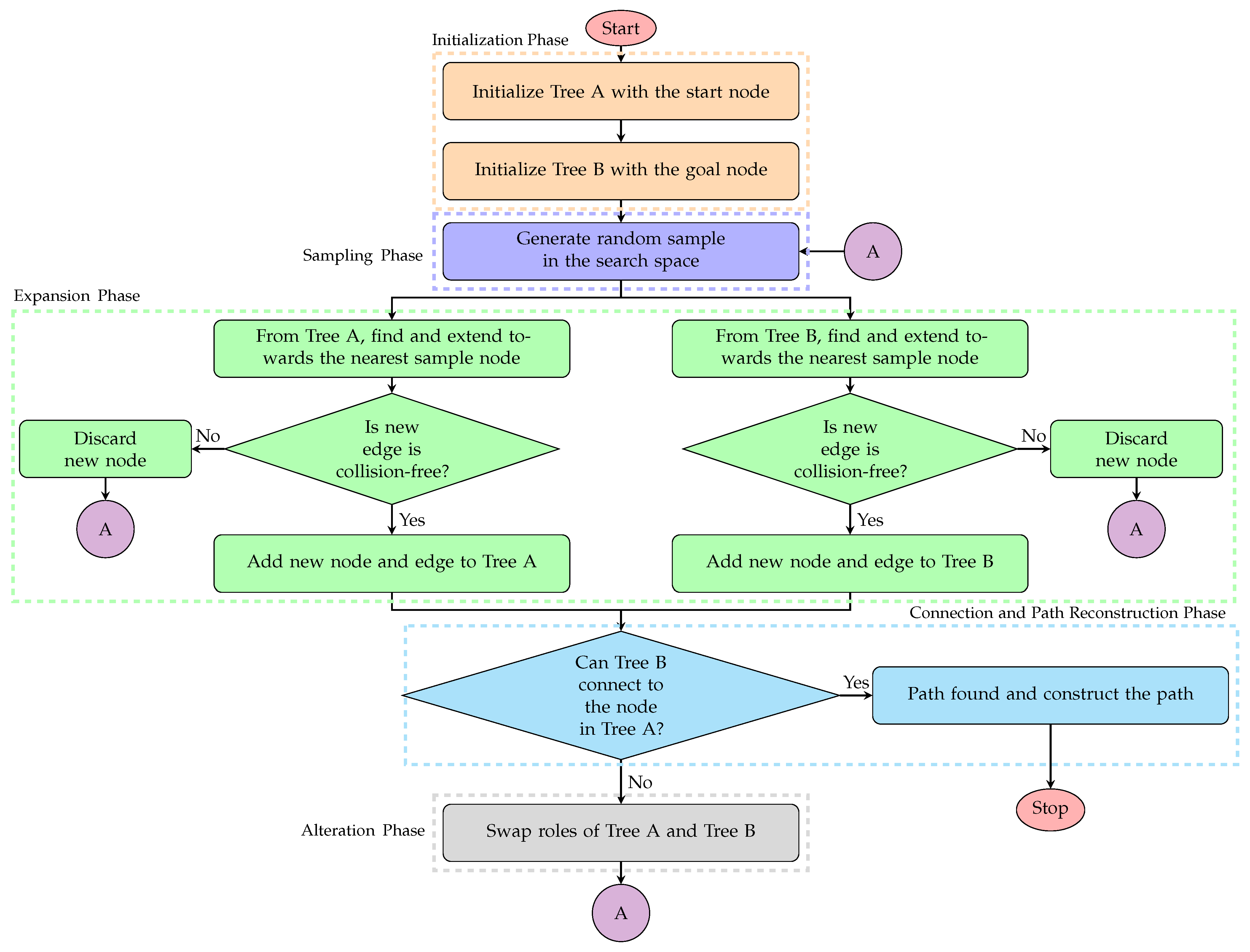
3.3. Rapidly Exploring Random Tree (RRT)
4. Advanced Motion Control Techniques
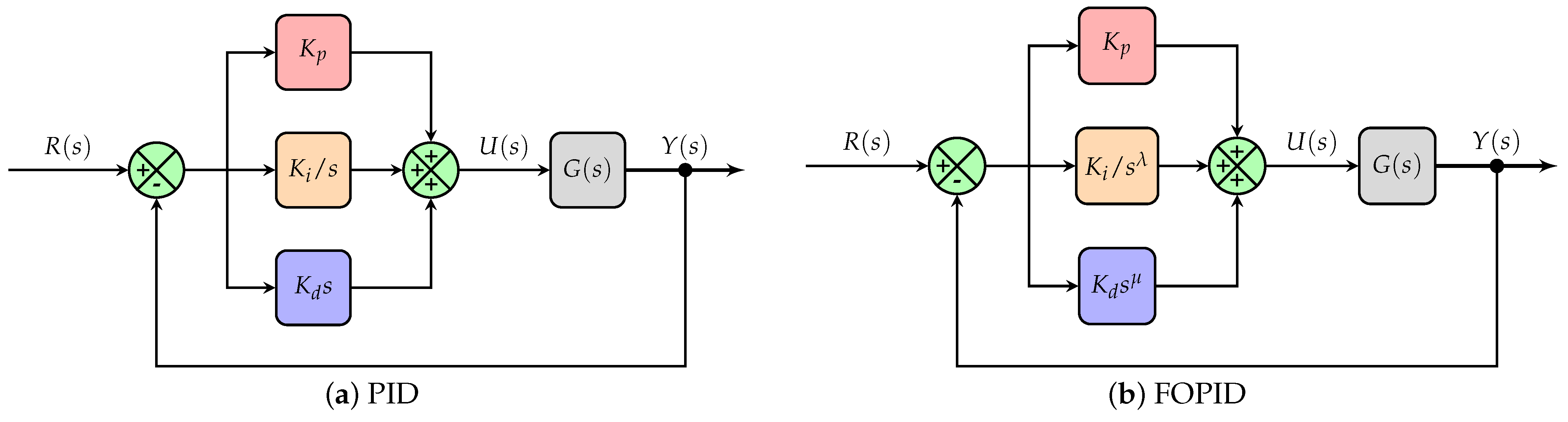
4.1. PID and Fractional-Order PID Controllers (FOPIDs)
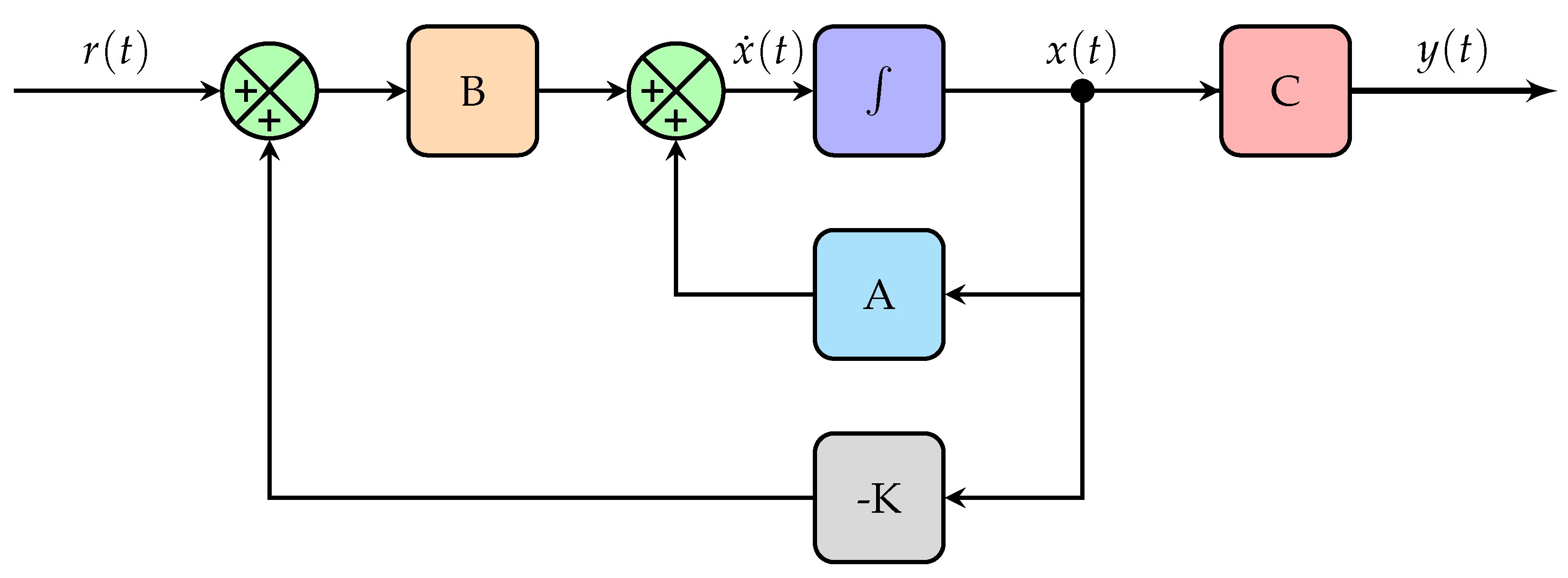
4.2. State Feedback Controller (SFC)
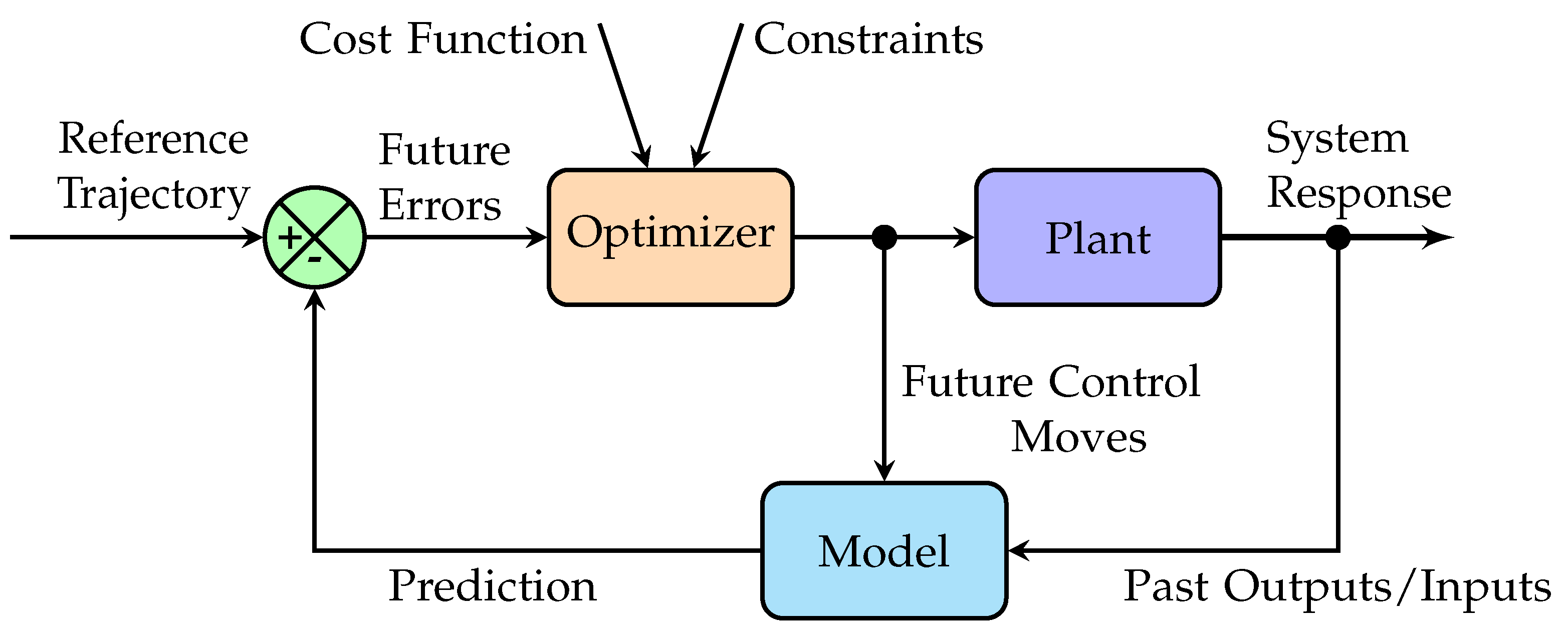
4.3. Model Predictive Controller (MPC)
5. Results and Discussions
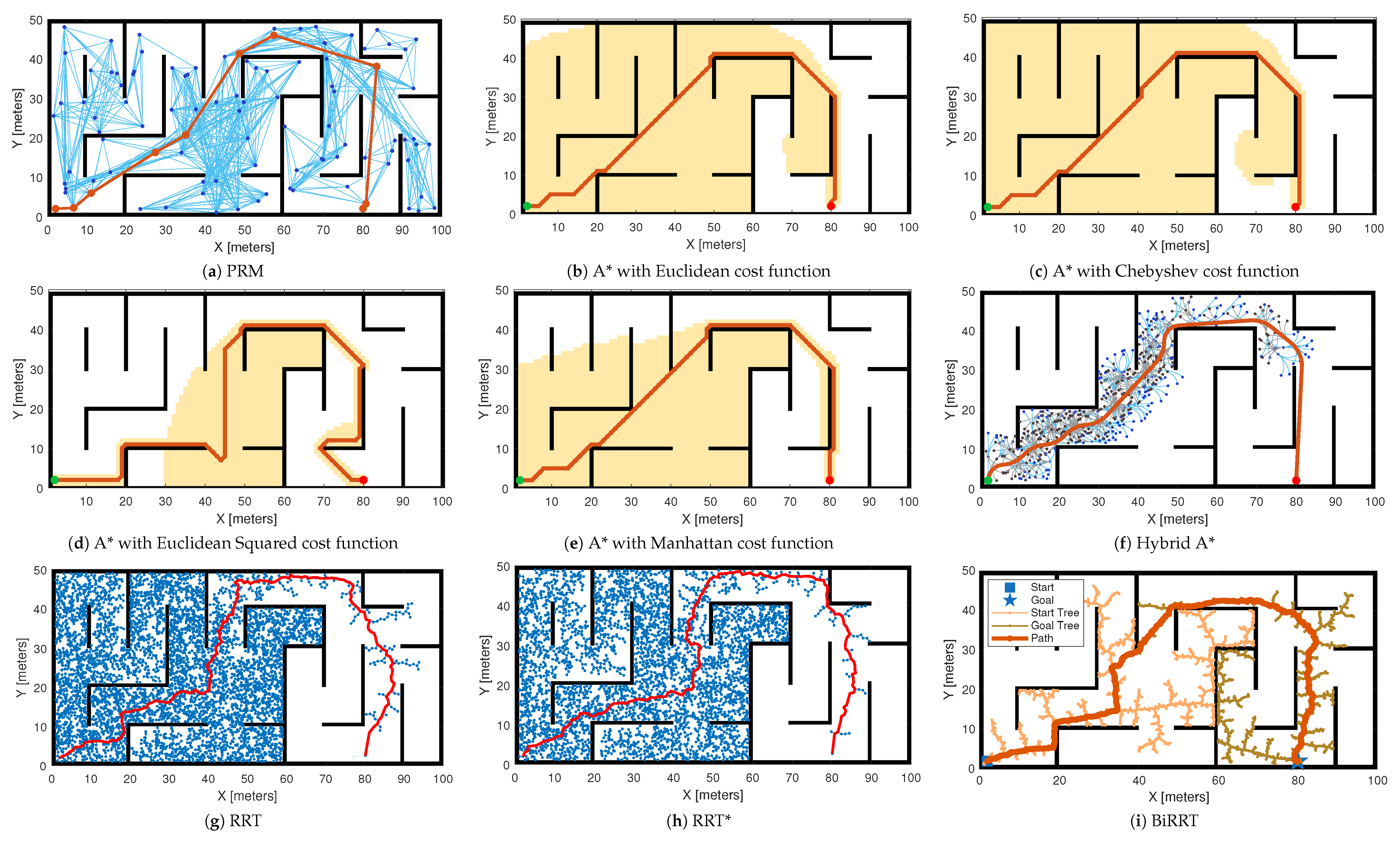
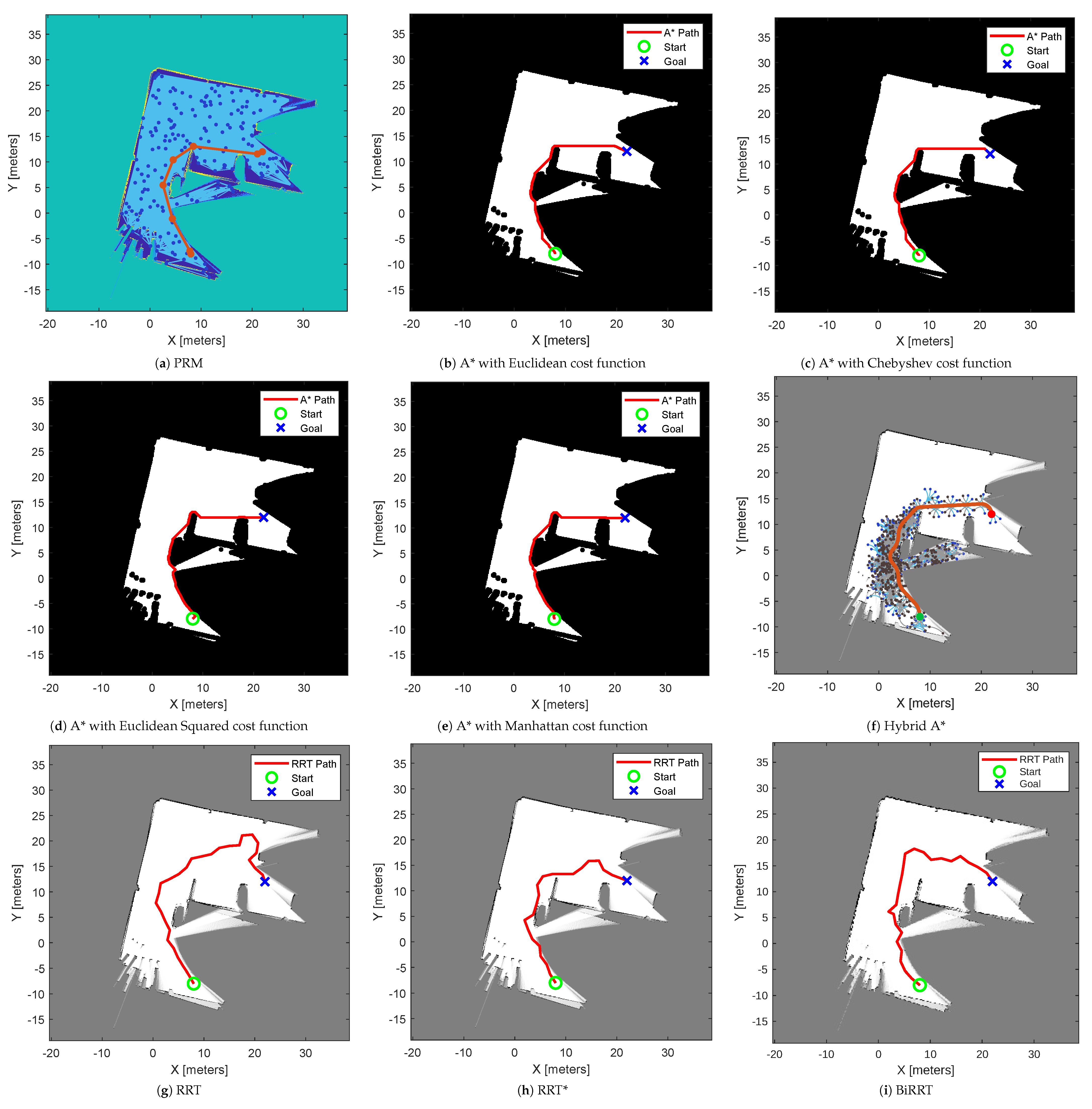
5.1. Performance Analysis of Path Planning Algorithms
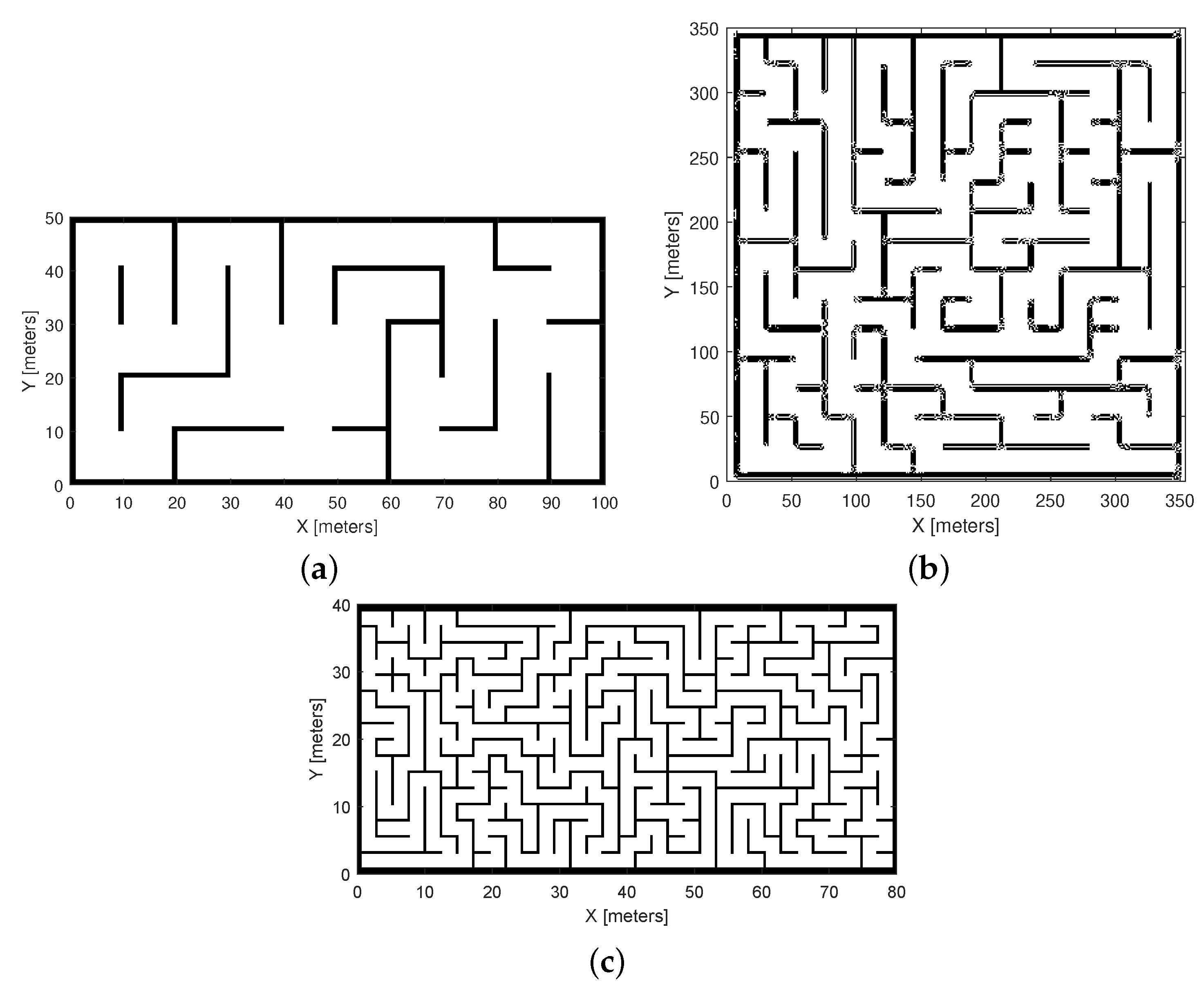
5.1.1. Case 1: Manually Defined Map
5.1.2. Case 2: Map Created from Image
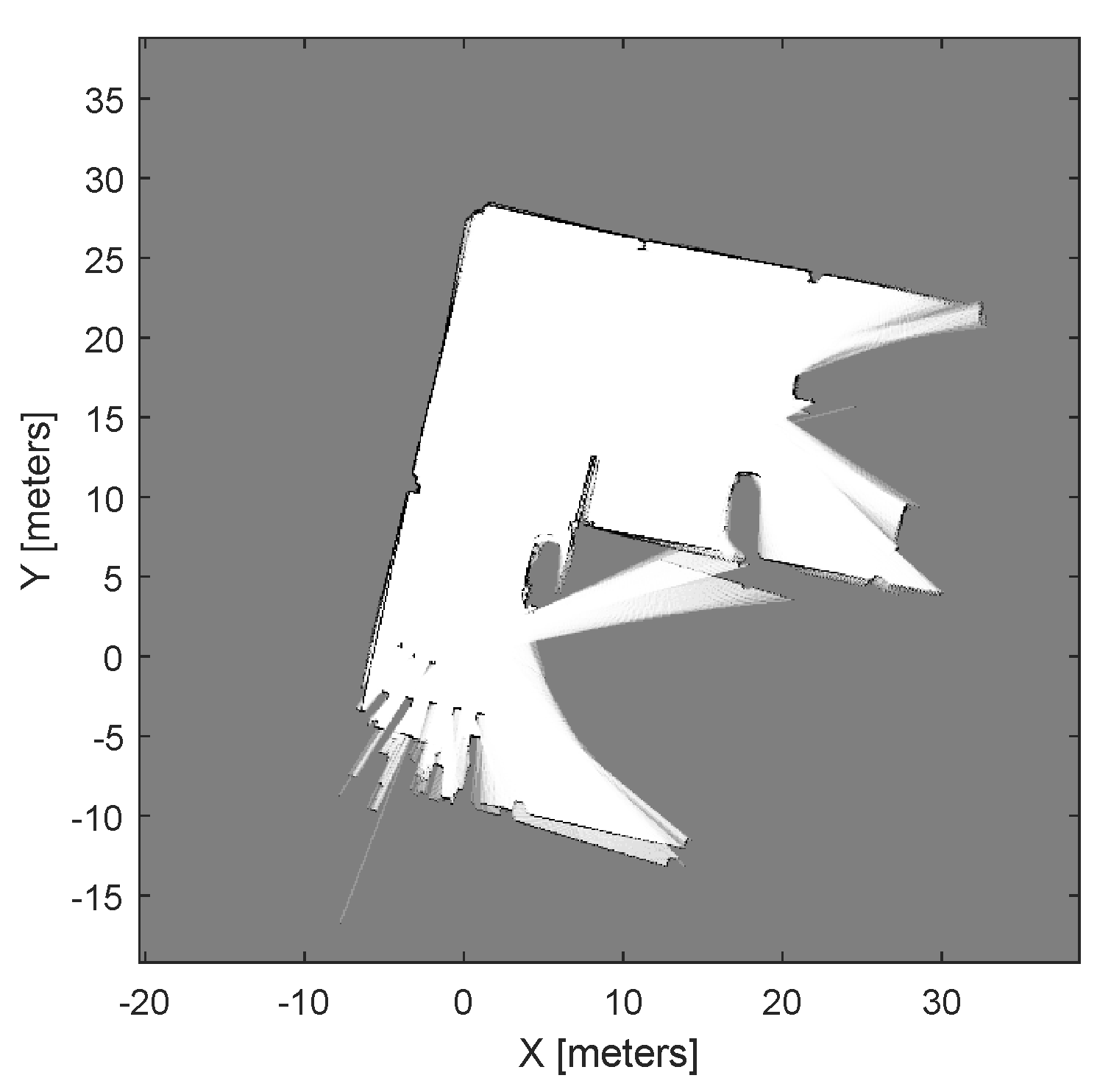
5.1.3. Case 3: Map Created from LiDAR Scans and Poses
5.1.4. Case 4: Randomly Generated Map
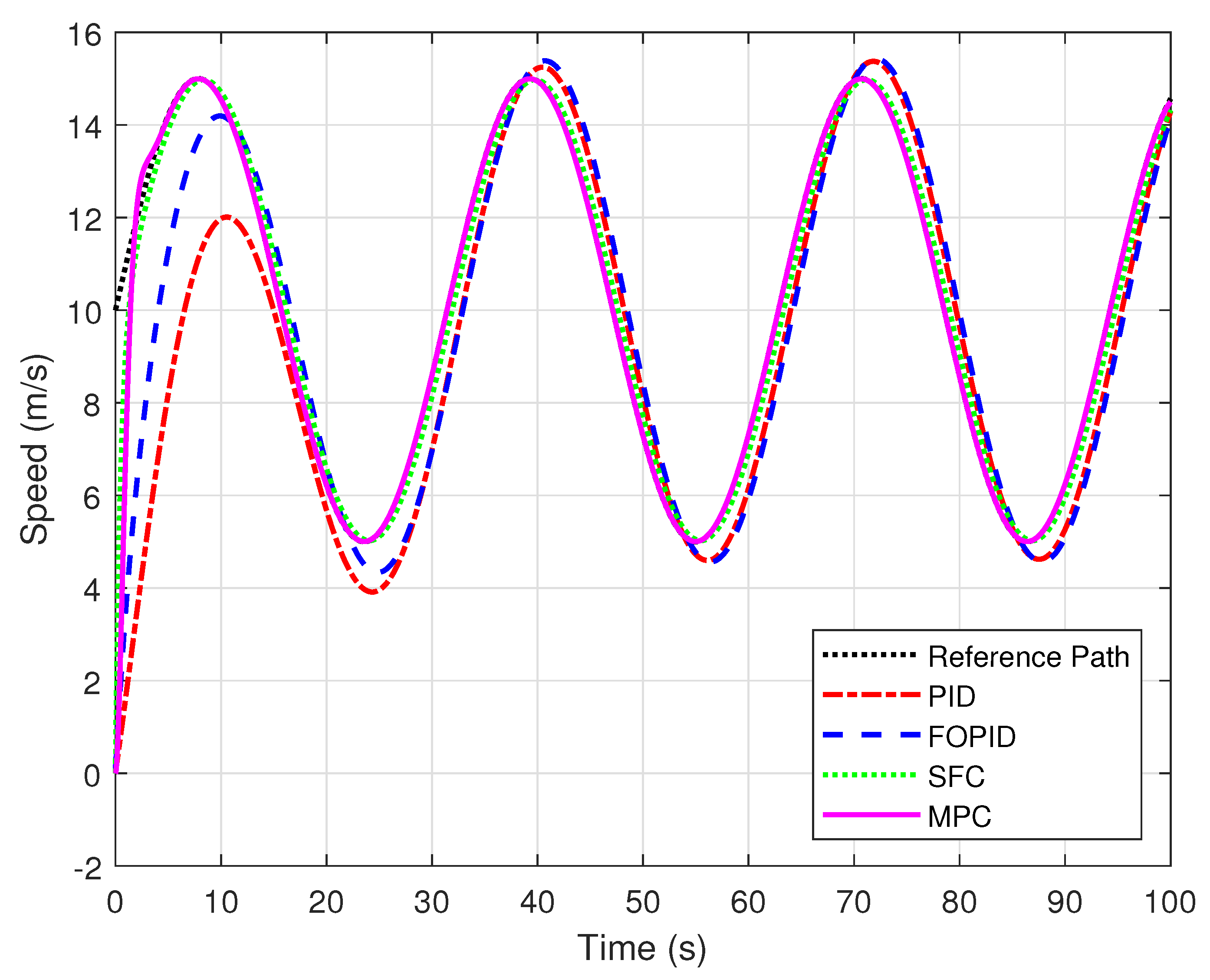
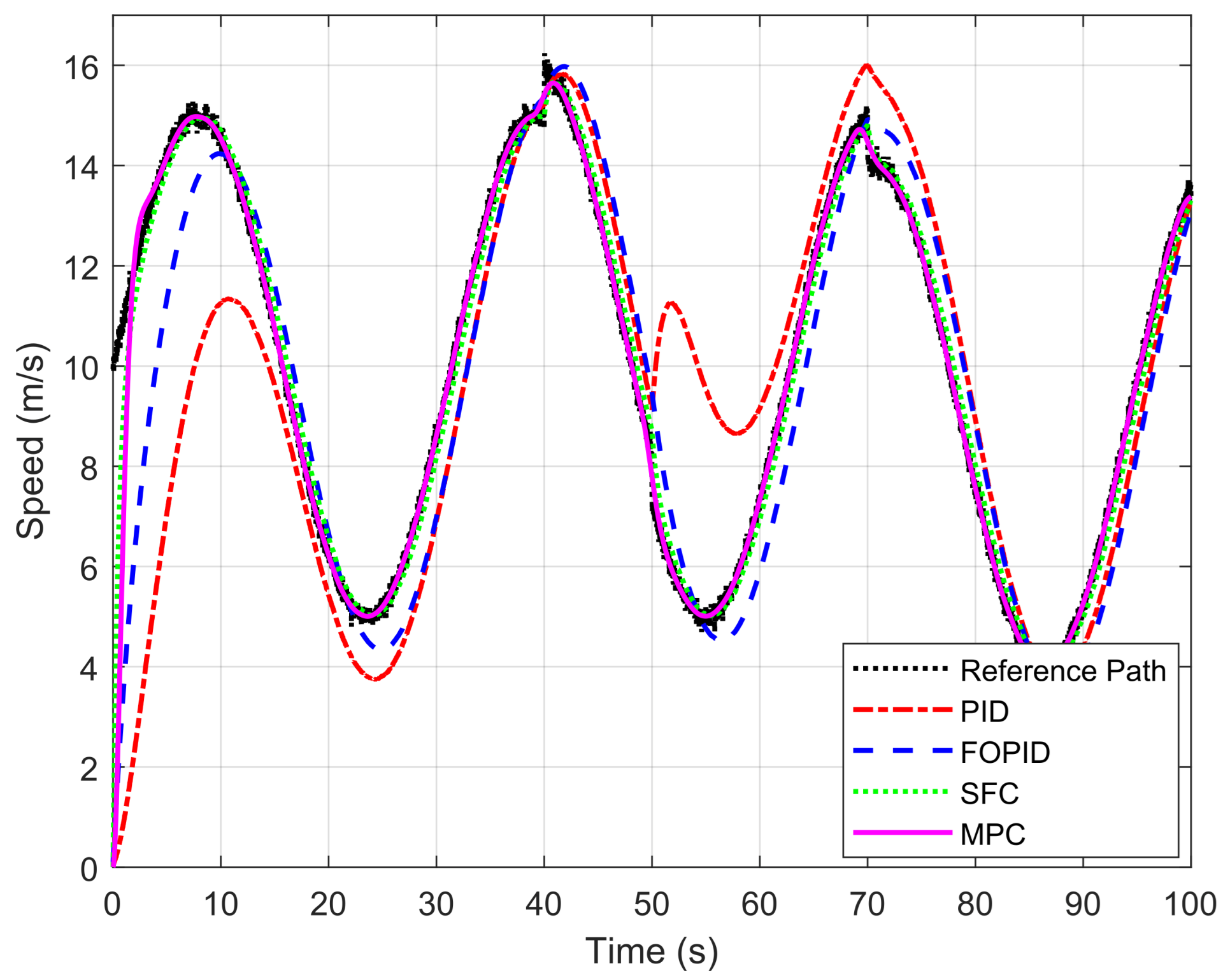
5.2. Performance Analysis of Motion Control Techniques
- —longitudinal position of the vehicle [m];
- —longitudinal velocity of the vehicle [m/s];
- —longitudinal acceleration of the vehicle [m/s2];
- m—mass of the vehicle [kg];
- —net tractive/braking force applied at the wheels [N];
- —air density [kg/m3];
- —aerodynamic drag coefficient;
- A—frontal cross-sectional area of the vehicle [m2];
- g—gravitational acceleration ( m/s2);
- —road slope angle [rad];
- —rolling resistance coefficient;
- —measured output, taken as the vehicle longitudinal velocity [m/s].
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| ARA* | Anytime Repairing A* |
| BiRRT | Bidirectional Rapidly Exploring Random Tree |
| BIT | Batch Informed Trees |
| FOPID | Fractional-order PID |
| IAE | Integral of Absolute Error |
| LiDAR | Light Detection and Ranging |
| MAE | Mean Absolute Error |
| MPC | Model Predictive Control |
| PID | Proportional-Integral-Derivative |
| PRM | Probabilistic Roadmaps |
| RMSE | Root Mean Square Error |
| ROS | Robot Operating System |
| RRT | Rapidly Exploring Random Tree |
| RTAB | Real-Time Appearance-Based Mapping |
| SFC | State Feedback Control |
| SLAM | Simultaneous Localisation and Mapping |
References
- Chen, W.; Chi, W.; Ji, S.; Ye, H.; Liu, J.; Jia, Y.; Yu, J.; Cheng, J. A survey of autonomous robots and multi-robot navigation: Perception, planning and collaboration. Biomim. Intell. Robot. 2025, 5, 100203. [Google Scholar] [CrossRef]
- Liu, L.; Wang, X.; Yang, X.; Liu, H.; Li, J.; Wang, P. Path planning techniques for mobile robots: Review and prospect. Expert Syst. Appl. 2023, 227, 120254. [Google Scholar] [CrossRef]
- Crespo, J.; Castillo, J.C.; Mozos, O.M.; Barber, R. Semantic information for robot navigation: A survey. Appl. Sci. 2020, 10, 497. [Google Scholar] [CrossRef]
- Lluvia, I.; Lazkano, E.; Ansuategi, A. Active mapping and robot exploration: A survey. Sensors 2021, 21, 2445. [Google Scholar] [CrossRef]
- Sánchez-Ibáñez, J.R.; Pérez-del Pulgar, C.J.; García-Cerezo, A. Path planning for autonomous mobile robots: A review. Sensors 2021, 21, 7898. [Google Scholar] [CrossRef]
- Aggarwal, S.; Kumar, N. Path planning techniques for unmanned aerial vehicles: A review, solutions, and challenges. Comput. Commun. 2020, 149, 270–299. [Google Scholar] [CrossRef]
- Zhang, H.y.; Lin, W.m.; Chen, A.x. Path planning for the mobile robot: A review. Symmetry 2018, 10, 450. [Google Scholar] [CrossRef]
- Tang, Y.; Zakaria, M.A.; Younas, M. Path planning trends for autonomous mobile robot navigation: A review. Sensors 2025, 25, 1206. [Google Scholar] [CrossRef]
- Tzafestas, S.G. Mobile robot control and navigation: A global overview. J. Intell. Robot. Syst. 2018, 91, 35–58. [Google Scholar] [CrossRef]
- Xiao, X.; Liu, B.; Warnell, G.; Stone, P. Motion planning and control for mobile robot navigation using machine learning: A survey. Auton. Robot. 2022, 46, 569–597. [Google Scholar] [CrossRef]
- Hornung, A.; Wurm, K.M.; Bennewitz, M.; Stachniss, C.; Burgard, W. OctoMap: An efficient probabilistic 3D mapping framework based on octrees. Auton. Robot. 2013, 34, 189–206. [Google Scholar] [CrossRef]
- Wang, H.; Zhang, G.; Cao, H.; Hu, K.; Wang, Q.; Deng, Y.; Gao, J.; Tang, Y. Geometry-Aware 3D Point Cloud Learning for Precise Cutting-Point Detection in Unstructured Field Environments. J. Field Robot. 2025, 42, 3063–3076. [Google Scholar] [CrossRef]
- Labbé, M.; Michaud, F. RTAB-Map as an open-source lidar and visual simultaneous localization and mapping library for large-scale and long-term online operation. J. Field Robot. 2019, 36, 416–446. [Google Scholar] [CrossRef]
- Mur-Artal, R.; Tardós, J.D. Orb-slam2: An open-source slam system for monocular, stereo, and rgb-d cameras. IEEE Trans. Robot. 2017, 33, 1255–1262. [Google Scholar] [CrossRef]
- Campos, C.; Elvira, R.; Rodríguez, J.J.G.; Montiel, J.M.; Tardós, J.D. Orb-slam3: An accurate open-source library for visual, visual–inertial, and multimap slam. IEEE Trans. Robot. 2021, 37, 1874–1890. [Google Scholar] [CrossRef]
- Yilmaz, Ö.; KarakuŞ, F. Stereo and Kinect Fusion for continuous 3D reconstruction and visual odometry. Turk. J. Electr. Eng. Comput. Sci. 2016, 24, 2756–2770. [Google Scholar] [CrossRef]
- Qin, H.; Shao, S.; Wang, T.; Yu, X.; Jiang, Y.; Cao, Z. Review of autonomous path planning algorithms for mobile robots. Drones 2023, 7, 211. [Google Scholar] [CrossRef]
- Gul, F.; Mir, I.; Abualigah, L.; Sumari, P.; Forestiero, A. A consolidated review of path planning and optimization techniques: Technical perspectives and future directions. Electronics 2021, 10, 2250. [Google Scholar] [CrossRef]
- Borkar, K.K.; Aljrees, T.; Pandey, S.K.; Kumar, A.; Singh, M.K.; Sinha, A.; Singh, K.U.; Sharma, V. Stability analysis and navigational techniques of wheeled mobile robot: A review. Processes 2023, 11, 3302. [Google Scholar] [CrossRef]
- Iqbal, M.; Zhang, K.; Iqbal, S.; Tariq, I. A fast and reliable Dijkstra algorithm for online shortest path. Int. J. Comput. Sci. Eng. 2018, 5, 24–27. [Google Scholar] [CrossRef]
- Erke, S.; Bin, D.; Yiming, N.; Qi, Z.; Liang, X.; Dawei, Z. An improved A-Star based path planning algorithm for autonomous land vehicles. Int. J. Adv. Robot. Syst. 2020, 17, 1729881420962263. [Google Scholar] [CrossRef]
- Eskandarian, A.; Wu, C.; Sun, C. Research advances and challenges of autonomous and connected ground vehicles. IEEE Trans. Intell. Transp. Syst. 2019, 22, 683–711. [Google Scholar] [CrossRef]
- Bagad, P.; Dahatonde, P.; Gagare, R.; Athare, I.; Ghule, G. Optimizing Pathfinding in Dynamic Environments: A Comparative Study of A* and D-Lite Algorithms. In Proceedings of the 2024 IEEE Pune Section International Conference (PuneCon), Pune, India, 13–15 December 2024; pp. 1–11. [Google Scholar]
- Sandakalum, T.; Ang, M.H., Jr. Motion planning for mobile manipulators—a systematic review. Machines 2022, 10, 97. [Google Scholar] [CrossRef]
- Chen, G.; Luo, N.; Liu, D.; Zhao, Z.; Liang, C. Path planning for manipulators based on an improved probabilistic roadmap method. Robot.-Comput.-Integr. Manuf. 2021, 72, 102196. [Google Scholar]
- Ravankar, A.A.; Ravankar, A.; Emaru, T.; Kobayashi, Y. HPPRM: Hybrid potential based probabilistic roadmap algorithm for improved dynamic path planning of mobile robots. IEEE Access 2020, 8, 221743–221766. [Google Scholar] [CrossRef]
- Qiao, L.; Luo, X.; Luo, Q. An optimized probabilistic roadmap algorithm for path planning of mobile robots in complex environments with narrow channels. Sensors 2022, 22, 8983. [Google Scholar] [CrossRef]
- Wei, K.; Ren, B. A method on dynamic path planning for robotic manipulator autonomous obstacle avoidance based on an improved RRT algorithm. Sensors 2018, 18, 571. [Google Scholar] [CrossRef]
- Ma, G.; Duan, Y.; Li, M.; Xie, Z.; Zhu, J. A probability smoothing Bi-RRT path planning algorithm for indoor robot. Future Gener. Comput. Syst. 2023, 143, 349–360. [Google Scholar]
- Zhang, H.; Wang, Y.; Zheng, J.; Yu, J. Path planning of industrial robot based on improved RRT algorithm in complex environments. IEEE Access 2018, 6, 53296–53306. [Google Scholar] [CrossRef]
- Wang, J.; Chi, W.; Li, C.; Wang, C.; Meng, M.Q.H. Neural RRT*: Learning-based optimal path planning. IEEE Trans. Autom. Sci. Eng. 2020, 17, 1748–1758. [Google Scholar] [CrossRef]
- Gammell, J.D.; Barfoot, T.D.; Srinivasa, S.S. Batch informed trees (bit*): Informed asymptotically optimal anytime search. Int. J. Robot. Res. 2020, 39, 543–567. [Google Scholar] [CrossRef]
- Pérez-Juárez, J.G.; García-Martínez, J.R.; Medina Santiago, A.; Cruz-Miguel, E.E.; Olmedo-García, L.F.; Barra-Vázquez, O.A.; Rojas-Hernández, M.A. Kinematic Fuzzy Logic-Based Controller for Trajectory Tracking of Wheeled Mobile Robots in Virtual Environments. Symmetry 2025, 17, 301. [Google Scholar] [CrossRef]
- Bingul, Z.; Gul, K. Intelligent-PID with PD feedforward trajectory tracking control of an autonomous underwater vehicle. Machines 2023, 11, 300. [Google Scholar] [CrossRef]
- Acosta, D.; Fariña, B.; Toledo, J.; Acosta, L. Improving mobile robot maneuver performance using fractional-order controller. Sensors 2023, 23, 3191. [Google Scholar] [CrossRef]
- Zhang, X.; Li, J.; Ma, Z.; Chen, D.; Zhou, X. Lateral trajectory tracking of self-driving vehicles based on sliding mode and fractional-order proportional-integral-derivative control. Actuators 2023, 13, 7. [Google Scholar]
- Wang, Z.; Sun, K.; Ma, S.; Sun, L.; Gao, W.; Dong, Z. Improved linear quadratic regulator lateral path tracking approach based on a real-time updated algorithm with fuzzy control and cosine similarity for autonomous vehicles. Electronics 2022, 11, 3703. [Google Scholar] [CrossRef]
- Villalba-Aguilera, E.; Blesa, J.; Ponsa, P. Model-based predictive control for position and orientation tracking in a multilayer architecture for a three-wheeled omnidirectional mobile robot. Robotics 2025, 14, 72. [Google Scholar]
- Chen, G.; Dong, W.; Peng, P.; Alonso-Mora, J.; Zhu, X. Continuous occupancy mapping in dynamic environments using particles. IEEE Trans. Robot. 2023, 40, 64–84. [Google Scholar] [CrossRef]
- Wang, Y.; Zhao, L.; Huang, S. Occupancy-slam: An efficient and robust algorithm for simultaneously optimizing robot poses and occupancy map. IEEE Trans. Robot. 2025, 41, 4057–4077. [Google Scholar] [CrossRef]
- Bingi, K.; Ibrahim, R.; Karsiti, M.N.; Hassan, S.M.; Harindran, V.R. Fractional-Order Systems and PID Controllers; Springer: Berlin/Heidelberg, Germany, 2020; Volume 264. [Google Scholar]
- Singh, A.P.; Bingi, K. Applications of fractional-order calculus in robotics. Fractal Fract. 2024, 8, 403. [Google Scholar] [CrossRef]
- Bingi, K.; Rajanarayan Prusty, B.; Pal Singh, A. A review on fractional-order modelling and control of robotic manipulators. Fractal Fract. 2023, 7, 77. [Google Scholar] [CrossRef]
- Popescu, M.; Mronga, D.; Bergonzani, I.; Kumar, S.; Kirchner, F. Experimental investigations into using motion capture state feedback for real-time control of a humanoid robot. Sensors 2022, 22, 9853. [Google Scholar] [CrossRef] [PubMed]
- Benotsmane, R.; Kovács, G. Optimization of energy consumption of industrial robots using classical PID and MPC controllers. Energies 2023, 16, 3499. [Google Scholar] [CrossRef]






| Aspect | Description |
|---|---|
| Structure | Grid (2D or 3D) of discrete cells. |
| Cell Values | 0: free space; 1: occupied (obstacle); : probability of occupancy. |
| Binary Occupancy Map | Each cell is either free (0) or occupied (1). |
| Probabilistic Occupancy Map | Each cell stores a probability value for occupancy. |
| 3D Occupancy Map (Octomap) | Extends to 3D using voxel-based representation. |
| Technique/Metrics | Case 1 | Case 2 | Case 3 | Case 4 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| PL | CT | SM | PL | CT | SM | PL | CT | SM | PL | CT | SM | |
| PRM | 136.89 | 0.082 | 0.75 | 738.37 | 64.731 | 3.50 | 38.39 | 0.721 | 0.18 | 480.72 | 64.40 | 0.20 |
| A* with Euclidean | 129.30 | 0.008 | 1.26 | 735.46 | 0.131 | 0.51 | 39.59 | 0.143 | 1.03 | 421.00 | 0.142 | 0.00 |
| A* with Chebyshev | 129.30 | 0.008 | 1.24 | 737.22 | 0.125 | 0.51 | 39.59 | 0.165 | 1.02 | 422.29 | 0.139 | 0.00 |
| A* with Euclidean Squared | 166.08 | 0.006 | 1.52 | 860.98 | 0.061 | 0.51 | 40.58 | 0.112 | 1.06 | 463.73 | 0.101 | 0.00 |
| A* with Manhattan | 129.30 | 0.007 | 1.26 | 756.17 | 0.114 | 0.51 | 39.83 | 0.115 | 1.06 | 429.90 | 0.144 | 0.00 |
| Hybrid A* | 131.86 | 0.325 | 1.29 | 726.05 | 22.58 | 3.28 | 40.29 | 20.766 | 1.59 | 700.82 | 136.39 | 0.18 |
| RRT | 169.82 | 3.227 | 1.07 | 973.55 | 7.198 | 3.73 | 55.36 | 0.054 | 3.11 | – | – | – |
| RRT* | 170.07 | 3.150 | 1.54 | 953.04 | 6.589 | 4.06 | 43.10 | 0.065 | 1.27 | – | – | – |
| BiRRT | 160.12 | 5.008 | 1.58 | 922.11 | 5.884 | 3.97 | 49.05 | 0.031 | 1.53 | – | – | – |
| Controller | Sinusoidal Path Without Disturbances | Sinusoidal Path with Dynamic Disturbances | ||||
|---|---|---|---|---|---|---|
| MAE | RMSE | IAE | MAE | RMSE | IAE | |
| PID | 1.40 | 2.26 | 140.19 | 1.98 | 2.89 | 198.03 |
| FOPID | 1.19 | 1.68 | 119.65 | 1.21 | 1.69 | 121.72 |
| SFC | 0.37 | 0.64 | 37.01 | 0.38 | 0.80 | 38.81 |
| MPC | 0.09 | 0.59 | 9.89 | 0.19 | 0.65 | 19.46 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bingi, K.; Singh, A.P.; Ibrahim, R.; Rajamallaiah, A.; Shaik, N.B. Integrated Analysis of Mapping, Path Planning, and Advanced Motion Control for Autonomous Robotic Navigation. Fractal Fract. 2025, 9, 640. https://doi.org/10.3390/fractalfract9100640
Bingi K, Singh AP, Ibrahim R, Rajamallaiah A, Shaik NB. Integrated Analysis of Mapping, Path Planning, and Advanced Motion Control for Autonomous Robotic Navigation. Fractal and Fractional. 2025; 9(10):640. https://doi.org/10.3390/fractalfract9100640
Chicago/Turabian StyleBingi, Kishore, Abhaya Pal Singh, Rosdiazli Ibrahim, Anugula Rajamallaiah, and Nagoor Basha Shaik. 2025. "Integrated Analysis of Mapping, Path Planning, and Advanced Motion Control for Autonomous Robotic Navigation" Fractal and Fractional 9, no. 10: 640. https://doi.org/10.3390/fractalfract9100640
APA StyleBingi, K., Singh, A. P., Ibrahim, R., Rajamallaiah, A., & Shaik, N. B. (2025). Integrated Analysis of Mapping, Path Planning, and Advanced Motion Control for Autonomous Robotic Navigation. Fractal and Fractional, 9(10), 640. https://doi.org/10.3390/fractalfract9100640








