Relating the Morphology of Bipolar Neurons to Fractal Dimension
Abstract
:1. Introduction
2. Materials and Methods
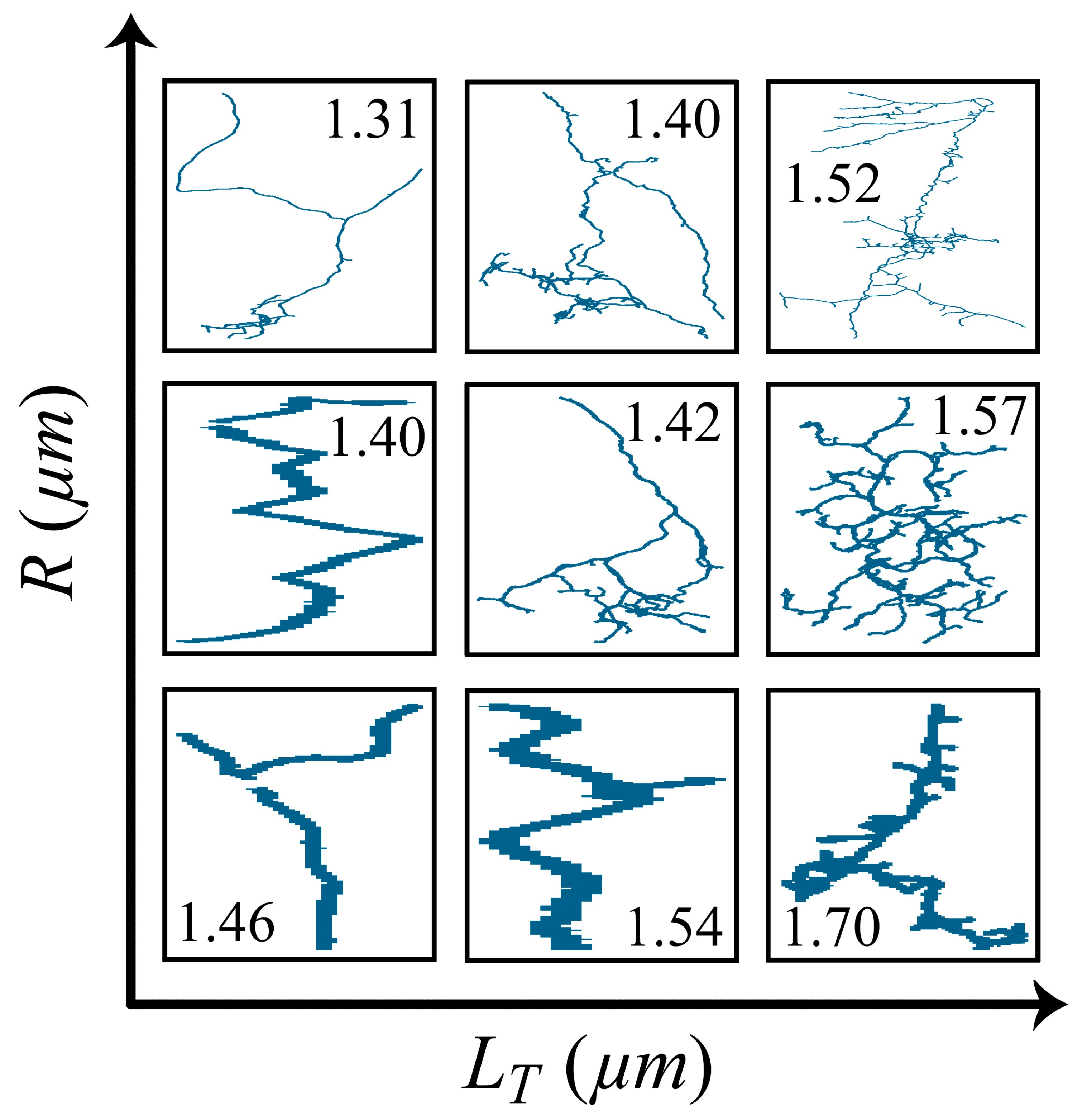
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chklovskii, D.B. Synaptic Connectivity and Neuronal Morphology: Two Sides of the Same Coin. Neuron 2004, 43, 609–617. [Google Scholar] [CrossRef] [PubMed]
- Hill, S.L.; Wang, Y.; Riachi, I.; Schürmann, F.; Markram, H. Statistical Connectivity Provides a Sufficient Foundation for Specific Functional Connectivity in Neocortical Neural Microcircuits. Proc. Natl. Acad. Sci. USA 2012, 109, E2885–E2894. [Google Scholar] [CrossRef]
- van Ooyen, A.; Carnell, A.; de Ridder, S.; Tarigan, B.; Mansvelder, H.D.; Bijma, F.; de Gunst, M.; van Pelt, J. Independently Outgrowing Neurons and Geometry-Based Synapse Formation Produce Networks with Realistic Synaptic Connectivity. PLoS ONE 2014, 9, e85858. [Google Scholar] [CrossRef]
- Laughlin, S.B.; de Ruyter van Steveninck, R.R.; Anderson, J.C. The Metabolic Cost of Neural Information. Nat. Neurosci. 1998, 1, 36–41. [Google Scholar] [CrossRef] [PubMed]
- Dukkipati, S.S.; Garrett, T.L.; Elbasiouny, S.M. The Vulnerability of Spinal Motoneurons and Soma Size Plasticity in a Mouse Model of Amyotrophic Lateral Sclerosis. J. Physiol. 2018, 596, 1723–1745. [Google Scholar] [CrossRef] [PubMed]
- Kemper, T.L.; Bauman, M. Neuropathology of Infantile Autism. J. Neuropathol. Exp. Neurol. 1998, 57, 645–652. [Google Scholar] [CrossRef]
- Goikolea-Vives, A.; Stolp, H.B. Connecting the Neurobiology of Developmental Brain Injury: Neuronal Arborisation as a Regulator of Dysfunction and Potential Therapeutic Target. Int. J. Mol. Sci. 2021, 22, 8220. [Google Scholar] [CrossRef] [PubMed]
- Arikkath, J. Molecular Mechanisms of Dendrite Morphogenesis. Front. Cell. Neurosci. 2012, 6, 61. [Google Scholar] [CrossRef] [PubMed]
- Kalisman, N.; Silberberg, G.; Markram, H. Deriving Physical Connectivity from Neuronal Morphology. Biol. Cybern. 2003, 88, 210–218. [Google Scholar] [CrossRef] [PubMed]
- Stepanyants, A.; Chklovskii, D.B. Neurogeometry and Potential Synaptic Connectivity. Trends Neurosci. 2005, 28, 387–394. [Google Scholar] [CrossRef]
- McAssey, M.P.; Bijma, F.; Tarigan, B.; van Pelt, J.; van Ooyen, A.; de Gunst, M. A Morpho-Density Approach to Estimating Neural Connectivity. PLoS ONE 2014, 9, e86526. [Google Scholar] [CrossRef] [PubMed]
- Wen, Q.; Stepanyants, A.; Elston, G.N.; Grosberg, A.Y.; Chklovskii, D.B. Maximization of the Connectivity Repertoire as a Statistical Principle Governing the Shapes of Dendritic Arbors. Proc. Natl. Acad. Sci. USA 2009, 106, 12536–12541. [Google Scholar] [CrossRef] [PubMed]
- Moslehi, S.; Rowland, C.; Smith, J.H.; Watterson, W.J.; Miller, D.; Niell, C.M.; Alemán, B.J.; Perez, M.-T.; Taylor, R.P. Controlled Assembly of Retinal Cells on Fractal and Euclidean Electrodes. PLoS ONE 2022, 17, e0265685. [Google Scholar] [CrossRef] [PubMed]
- Moslehi, S.; Rowland, C.; Smith, J.H.; Griffiths, W.; Watterson, W.J.; Niell, C.M.; Alemán, B.J.; Perez, M.-T.; Taylor, R.P. Comparison of Fractal and Grid Electrodes for Studying the Effects of Spatial Confinement on Dissociated Retinal Neuronal and Glial Behavior. Sci. Rep. 2022, 12, 17513. [Google Scholar] [CrossRef]
- Schröter, M.; Paulsen, O.; Bullmore, E.T. Micro-Connectomics: Probing the Organization of Neuronal Networks at the Cellular Scale. Nat. Rev. Neurosci. 2017, 18, 131–146. [Google Scholar] [CrossRef] [PubMed]
- Erickson, P.A.; Fisher, S.K.; Anderson, D.H.; Stern, W.H.; Borgula, G.A. Retinal Detachment in the Cat: The Outer Nuclear and Outer Plexiform Layers. Investig. Ophthalmol. Vis. Sci. 1983, 24, 927–942. [Google Scholar]
- Wu, S.M. Feedback Connections and Operation of the Outer Plexiform Layer of the Retina. Curr. Opin. Neurobiol. 1992, 2, 462–468. [Google Scholar] [CrossRef] [PubMed]
- Karamali, F.; Behtaj, S.; Babaei-Abraki, S.; Hadady, H.; Atefi, A.; Savoj, S.; Soroushzadeh, S.; Najafian, S.; Nasr Esfahani, M.H.; Klassen, H. Potential Therapeutic Strategies for Photoreceptor Degeneration: The Path to Restore Vision. J. Transl. Med. 2022, 20, 572. [Google Scholar] [CrossRef] [PubMed]
- Phelan, J.K.; Bok, D. A Brief Review of Retinitis Pigmentosa and the Identified Retinitis Pigmentosa Genes. Mol. Vis. 2000, 6, 116–124. [Google Scholar]
- Kralik, J.; Kleinlogel, S. Functional Availability of ON-Bipolar Cells in the Degenerated Retina: Timing and Longevity of an Optogenetic Gene Therapy. Int. J. Mol. Sci. 2021, 22, 11515. [Google Scholar] [CrossRef]
- Jones, B.W.; Pfeiffer, R.L.; Ferrell, W.D.; Watt, C.B.; Marmor, M.; Marc, R.E. Retinal Remodeling in Human Retinitis Pigmentosa. Exp. Eye Res. 2016, 150, 149–165. [Google Scholar] [CrossRef]
- Chichagova, V.; Hallam, D.; Collin, J.; Zerti, D.; Dorgau, B.; Felemban, M.; Lako, M.; Steel, D.H. Cellular Regeneration Strategies for Macular Degeneration: Past, Present and Future. Eye 2018, 32, 946–971. [Google Scholar] [CrossRef] [PubMed]
- Zhang, C.-J.; Ma, Y.; Jin, Z.-B. The Road to Restore Vision with Photoreceptor Regeneration. Exp. Eye Res. 2021, 202, 108283. [Google Scholar] [CrossRef] [PubMed]
- Palanker, D.; Goetz, G. Restoring Sight with Retinal Prostheses. Phys. Today 2018, 71, 26–32. [Google Scholar] [CrossRef] [PubMed]
- Jang, J.; Kim, H.; Song, Y.M.; Park, J.-U. Implantation of Electronic Visual Prosthesis for Blindness Restoration. Opt. Mater. Express OME 2019, 9, 3878–3894. [Google Scholar] [CrossRef]
- Chenais, N.A.L.; Airaghi Leccardi, M.J.I.; Ghezzi, D. Photovoltaic Retinal Prosthesis Restores High-Resolution Responses to Single-Pixel Stimulation in Blind Retinas. Commun. Mater. 2021, 2, 28. [Google Scholar] [CrossRef]
- Wang, B.-Y.; Chen, Z.C.; Bhuckory, M.; Huang, T.; Shin, A.; Zuckerman, V.; Ho, E.; Rosenfeld, E.; Galambos, L.; Kamins, T.; et al. Electronic Photoreceptors Enable Prosthetic Visual Acuity Matching the Natural Resolution in Rats. Nat. Commun. 2022, 13, 6627. [Google Scholar] [CrossRef]
- Keremane, S.; Rowland, C.; Brouse, B.; Uehara, H.; Ambati, B.K.; Taylor, R. Quantification of Neuronal Dendrite Structure in Mouse Retinal Bipolar Cells Using Fractal Dimension, D. Investig. Ophthalmol. Vis. Sci. 2024, 65, 6685. [Google Scholar]
- Golestanirad, L.; Elahi, B.; Molina Arribere, A.; Mosig, J.R.; Pollo, C.; Graham, S.J. Analysis of Fractal Electrodes for Efficient Neural Stimulation. Front. Neuroeng. 2013, 6, 3. [Google Scholar] [CrossRef]
- Watterson, W.J.; Montgomery, R.D.; Taylor, R.P. Modeling the Improved Visual Acuity Using Photodiode Based Retinal Implants Featuring Fractal Electrodes. Front. Neurosci. 2018, 12, 277. [Google Scholar] [CrossRef]
- De Berg, M.; Cheong, O.; Van Kreveld, M.; Overmars, M. Computational Geometry: Algorithms and Applications; Springer: Berlin/Heidelberg, Germany, 2008; ISBN 978-3-540-77973-5. [Google Scholar]
- Morigiwa, K.; Tauchi, M.; Fukuda, Y. Fractal Analysis of Ganglion Cell Dendritic Branching Patterns of the Rat and Cat Retinae. Neurosci. Res. Suppl. 1989, 10, S131–S139. [Google Scholar] [CrossRef] [PubMed]
- Takeda, T.; Ishikawa, A.; Ohtomo, K.; Kobayashi, Y.; Matsuoka, T. Fractal Dimension of Dendritic Tree of Cerebellar Purkinje Cell during Onto- and Phylogenetic Development. Neurosci. Res. 1992, 13, 19–31. [Google Scholar] [CrossRef]
- Bassingthwaighte, J.B.; Liebovitch, L.S.; West, B.J. Fractal Physiology; American Physiological Society: Rockville, MD, USA, 1994; ISBN 978-0-19-508013-1. [Google Scholar]
- Caserta, F.; Eldred, W.D.; Fernandez, E.; Hausman, R.E.; Stanford, L.R.; Bulderev, S.V.; Schwarzer, S.; Stanley, H.E. Determination of Fractal Dimension of Physiologically Characterized Neurons in Two and Three Dimensions. J. Neurosci. Methods 1995, 56, 133–144. [Google Scholar] [CrossRef] [PubMed]
- Iannaccone, P.M.; Khokha, M. Fractal Geometry in Biological Systems: An Analytical Approach; CRC Press: Boca Raton, FL, USA, 1996; ISBN 978-0-8493-7636-8. [Google Scholar]
- Smith, T.G.; Lange, G.D.; Marks, W.B. Fractal Methods and Results in Cellular Morphology--Dimensions, Lacunarity and Multifractals. J. Neurosci. Methods 1996, 69, 123–136. [Google Scholar] [CrossRef] [PubMed]
- Isaeva, V.V.; Pushchina, E.V.; Karetin, Y.A. The Quasi-Fractal Structure of Fish Brain Neurons. Russ. J. Mar. Biol. 2004, 30, 127–134. [Google Scholar] [CrossRef]
- Wearne, S.L.; Rodriguez, A.; Ehlenberger, D.B.; Rocher, A.B.; Henderson, S.C.; Hof, P.R. New Techniques for Imaging, Digitization and Analysis of Three-Dimensional Neural Morphology on Multiple Scales. Neuroscience 2005, 136, 661–680. [Google Scholar] [CrossRef] [PubMed]
- Milosević, N.T.; Ristanović, D. Fractality of Dendritic Arborization of Spinal Cord Neurons. Neurosci. Lett. 2006, 396, 172–176. [Google Scholar] [CrossRef] [PubMed]
- Werner, G. Fractals in the Nervous System: Conceptual Implications for Theoretical Neuroscience. Front. Physiol. 2010, 1, 15. [Google Scholar] [CrossRef] [PubMed]
- Kim, J.; Kwon, N.; Chang, S.; Kim, K.-T.; Lee, D.; Kim, S.; Yun, S.J.; Hwang, D.; Kim, J.W.; Hwu, Y.; et al. Altered Branching Patterns of Purkinje Cells in Mouse Model for Cortical Development Disorder. Sci. Rep. 2011, 1, 122. [Google Scholar] [CrossRef] [PubMed]
- Di Ieva, A.; Grizzi, F.; Jelinek, H.; Pellionisz, A.J.; Losa, G.A. Fractals in the Neurosciences, Part I: General Principles and Basic Neurosciences. Neuroscientist 2014, 20, 403–417. [Google Scholar] [CrossRef] [PubMed]
- Jelinek, H.F.; Cornforth, D.J.; Roberts, A.J.; Landini, G.; Bourke, P.; Iorio, A. Image Processing of Finite Size Rat Retinal Ganglion Cells Using Multifractal and Local Connected Fractal Analysis. In AI 2004: Advances in Artificial Intelligence; Webb, G.I., Yu, X., Eds.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2004; Volume 3339, pp. 961–966. ISBN 978-3-540-24059-4. [Google Scholar]
- Murray, J.D. Use and Abuse of Fractal Theory in Neuroscience. J. Comp. Neurol. 1995, 361, 369–371. [Google Scholar] [CrossRef] [PubMed]
- Cuntz, H.; Mathy, A.; Häusser, M. A Scaling Law Derived from Optimal Dendritic Wiring. Proc. Natl. Acad. Sci. USA 2012, 109, 11014–11018. [Google Scholar] [CrossRef]
- Rowland, C.; Moslehi, S.; Smith, J.H.; Harland, B.; Dalrymple-Alford, J.; Taylor, R.P. Fractal Resonance: Can Fractal Geometry Be Used to Optimize the Connectivity of Neurons to Artificial Implants? Adv. Neurobiol. 2024, 36, 877–906. [Google Scholar] [CrossRef] [PubMed]
- Smith, J.H.; Rowland, C.; Harland, B.; Moslehi, S.; Montgomery, R.D.; Schobert, K.; Watterson, W.J.; Dalrymple-Alford, J.; Taylor, R.P. How Neurons Exploit Fractal Geometry to Optimize Their Network Connectivity. Sci. Rep. 2021, 11, 2332. [Google Scholar] [CrossRef] [PubMed]
- Ascoli, G.A.; Donohue, D.E.; Halavi, M. NeuroMorpho.Org: A Central Resource for Neuronal Morphologies. J. Neurosci. 2007, 27, 9247–9251. [Google Scholar] [CrossRef] [PubMed]
- Helmstaedter, M.; Briggman, K.L.; Turaga, S.C.; Jain, V.; Seung, H.S.; Denk, W. Connectomic Reconstruction of the Inner Plexiform Layer in the Mouse Retina. Nature 2013, 500, 168–174. [Google Scholar] [CrossRef]
- Denk, W.; Horstmann, H. Serial Block-Face Scanning Electron Microscopy to Reconstruct Three-Dimensional Tissue Nanostructure. PLoS Biol. 2004, 2, e329. [Google Scholar] [CrossRef]
- Berning, M.; Boergens, K.M.; Helmstaedter, M. SegEM: Efficient Image Analysis for High-Resolution Connectomics. Neuron 2015, 87, 1193–1206. [Google Scholar] [CrossRef]
- Inglis, A.; Cruz, L.; Roe, D.L.; Stanley, H.E.; Rosene, D.L.; Urbanc, B. Automated Identification of Neurons and Their Locations. J. Microsc. 2008, 230, 339–352. [Google Scholar] [CrossRef] [PubMed]
- Pilgrim, I.; Taylor, R. Fractal Analysis of Time-Series Data Sets: Methods and Challenges. In Fractal Analysis; IntechOpen: London, UK, 2018; ISBN 978-1-78985-433-6. [Google Scholar]
- Rowland, C.; Harland, B.; Smith, J.H.; Moslehi, S.; Dalrymple-Alford, J.; Taylor, R.P. Investigating Fractal Analysis as a Diagnostic Tool That Probes the Connectivity of Hippocampal Neurons. Front. Physiol. 2022, 13, 932598. [Google Scholar] [CrossRef]
- Rowland, C.; Smith, J.H.; Moslehi, S.; Harland, B.; Dalrymple-Alford, J.; Taylor, R.P. Neuron Arbor Geometry Is Sensitive to the Limited-Range Fractal Properties of Their Dendrites. Front. Netw. Physiol. 2023, 3, 1072815. [Google Scholar] [CrossRef] [PubMed]
- Dillon, A.P.; Moslehi, S.; Brouse, B.; Keremane, S.; Philliber, S.; Griffiths, W.; Rowland, C.; Smith, J.H.; Taylor, R.P. Evolution of Retinal Neuron Fractality When Interfacing with Carbon Nanotube Electrodes. Bioengineering 2024, 11, 823. [Google Scholar] [CrossRef]
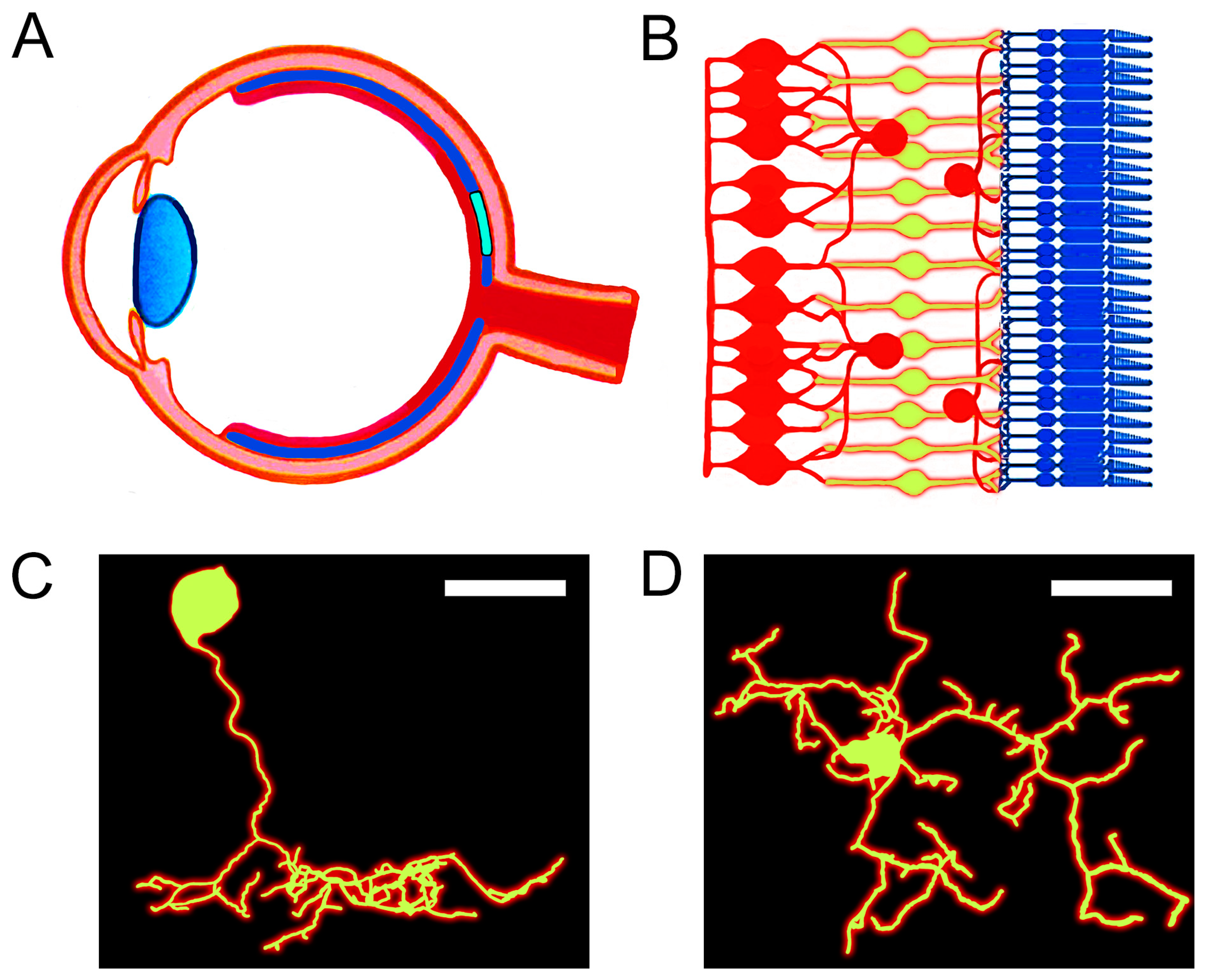
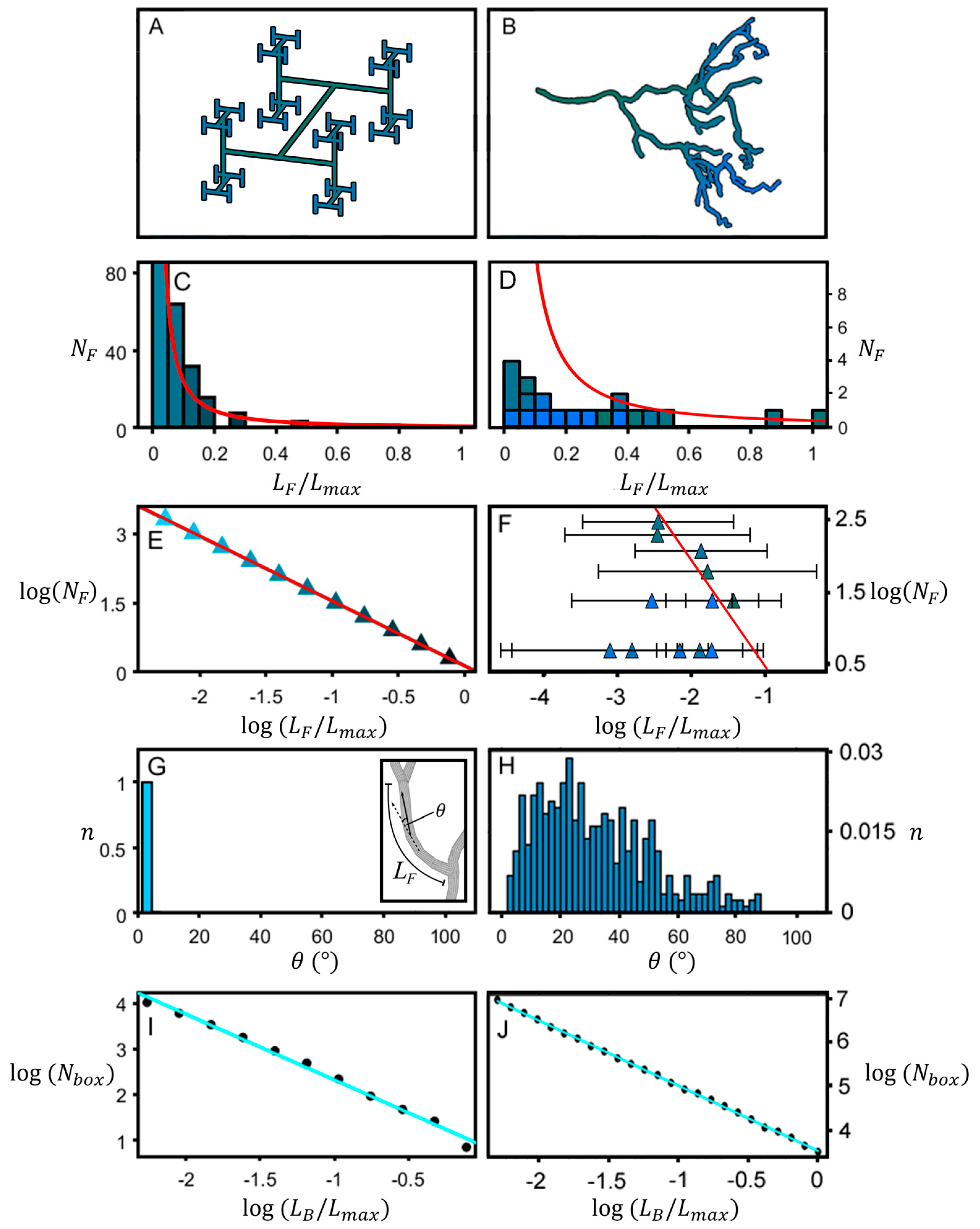
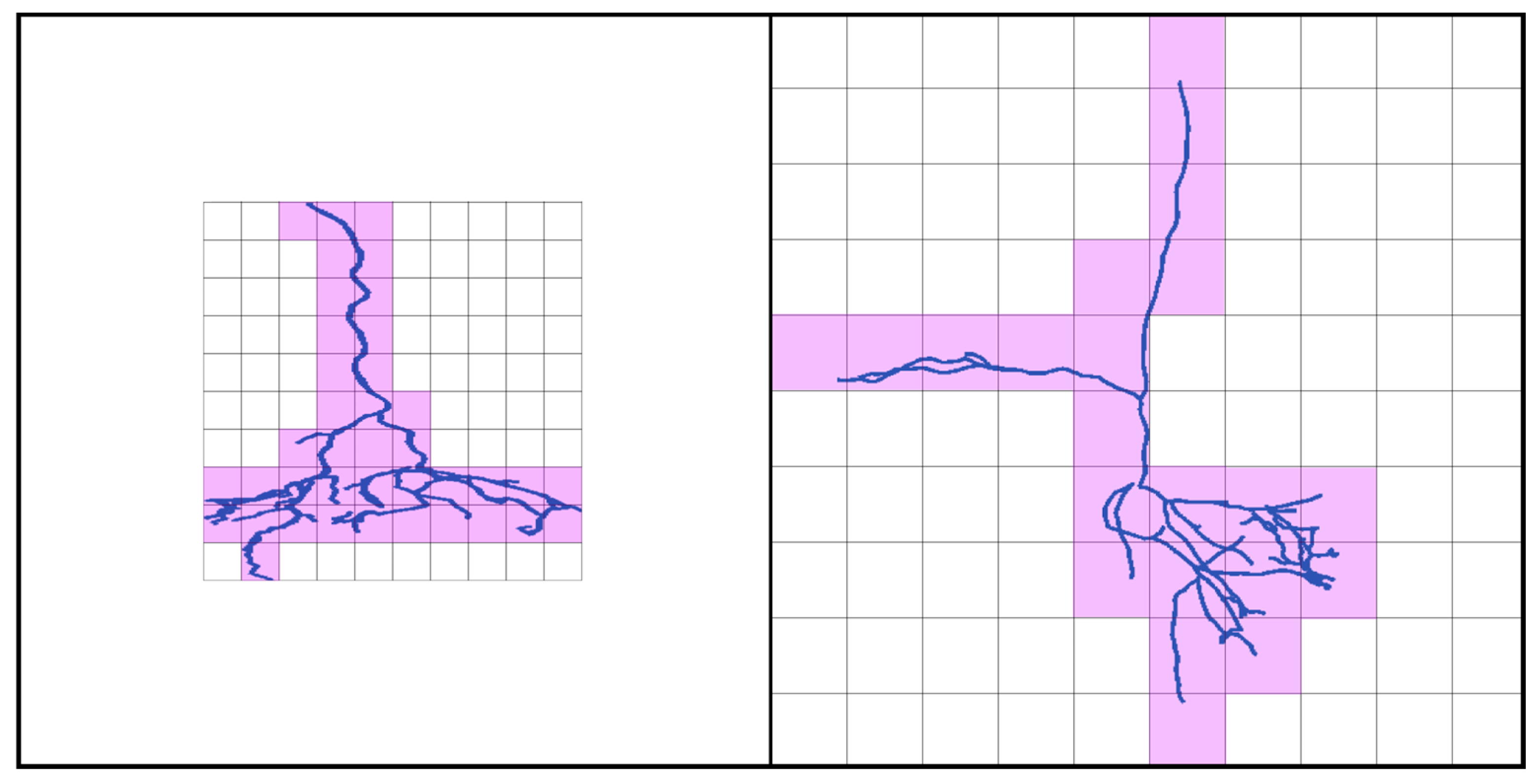
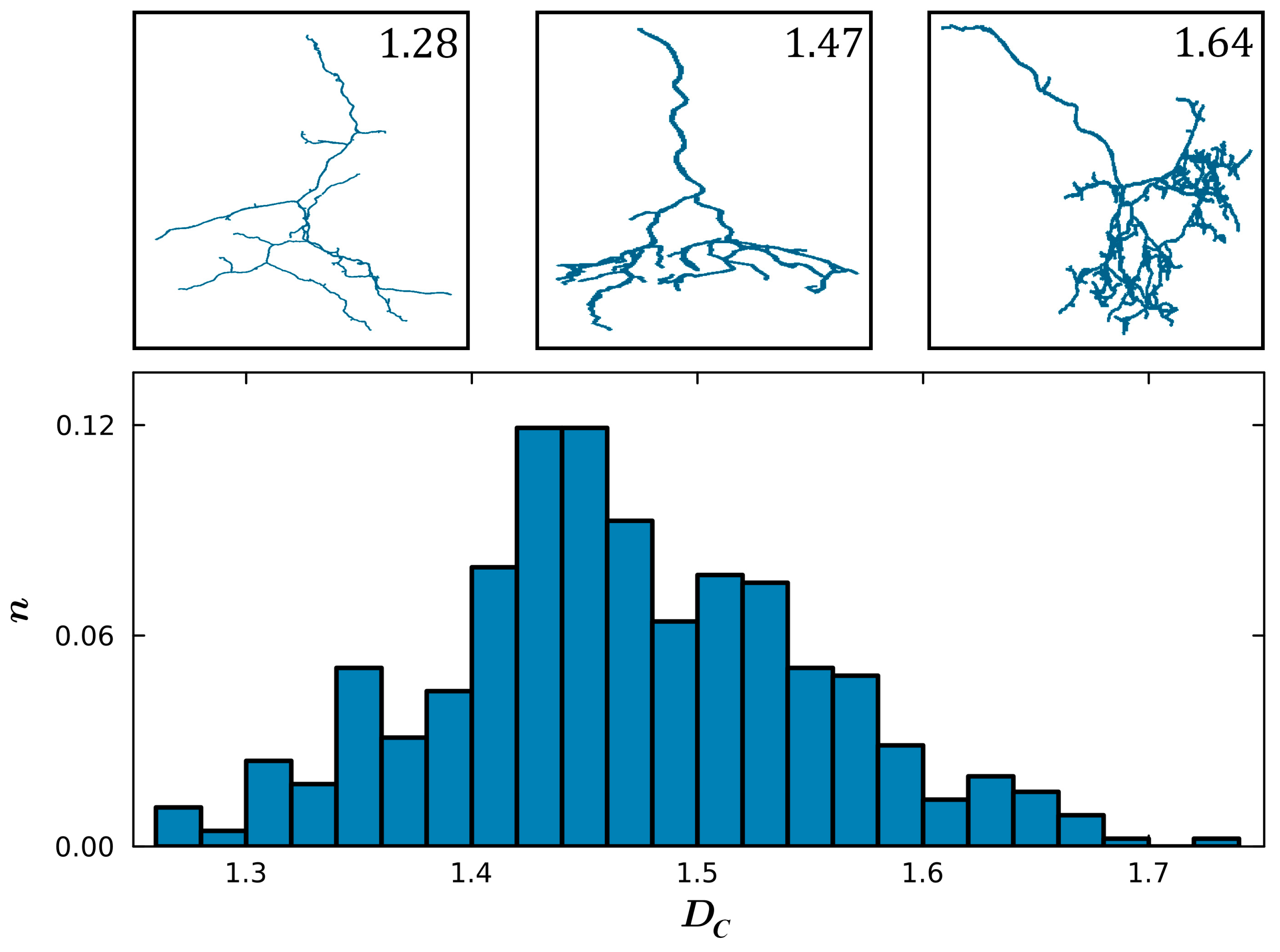
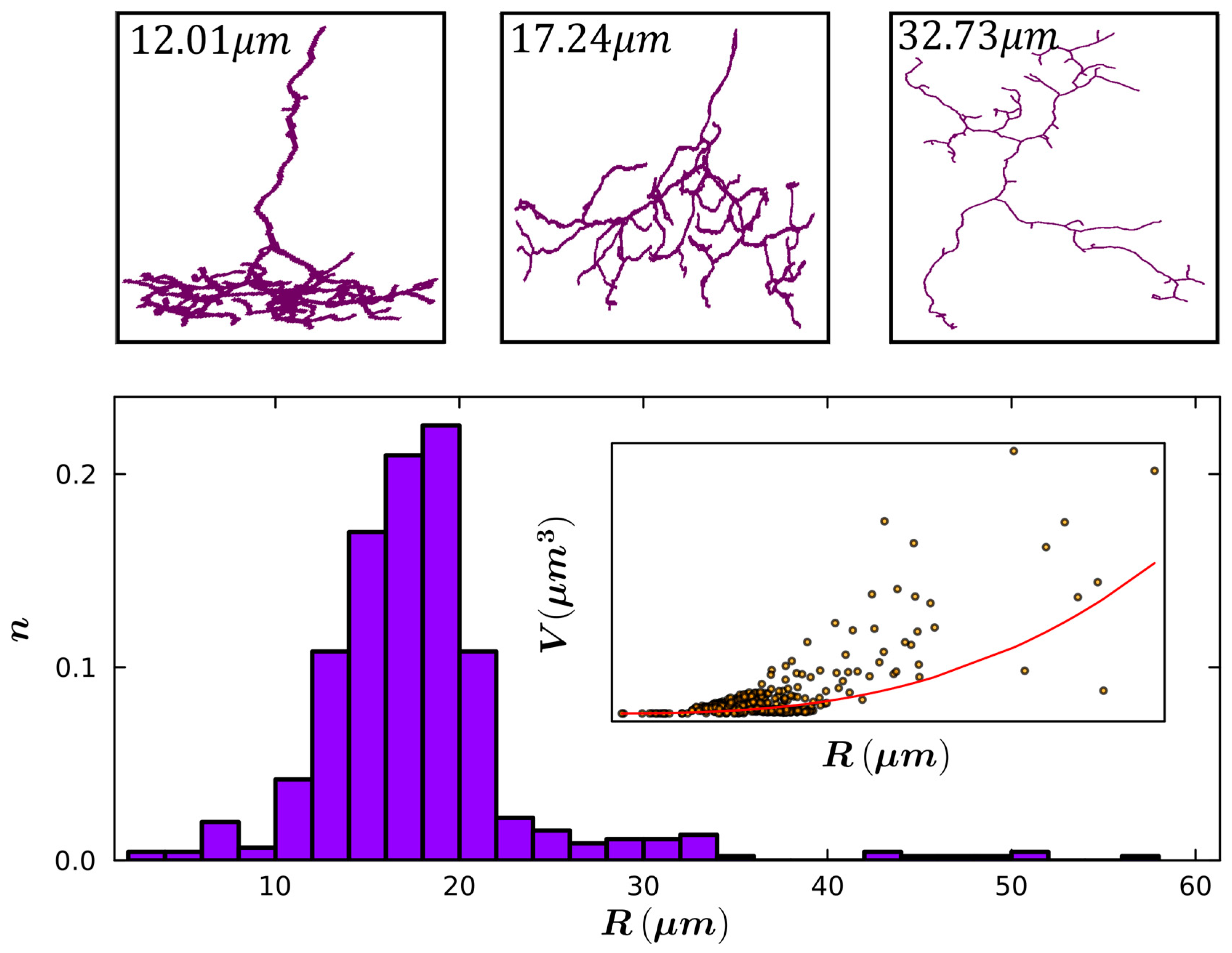
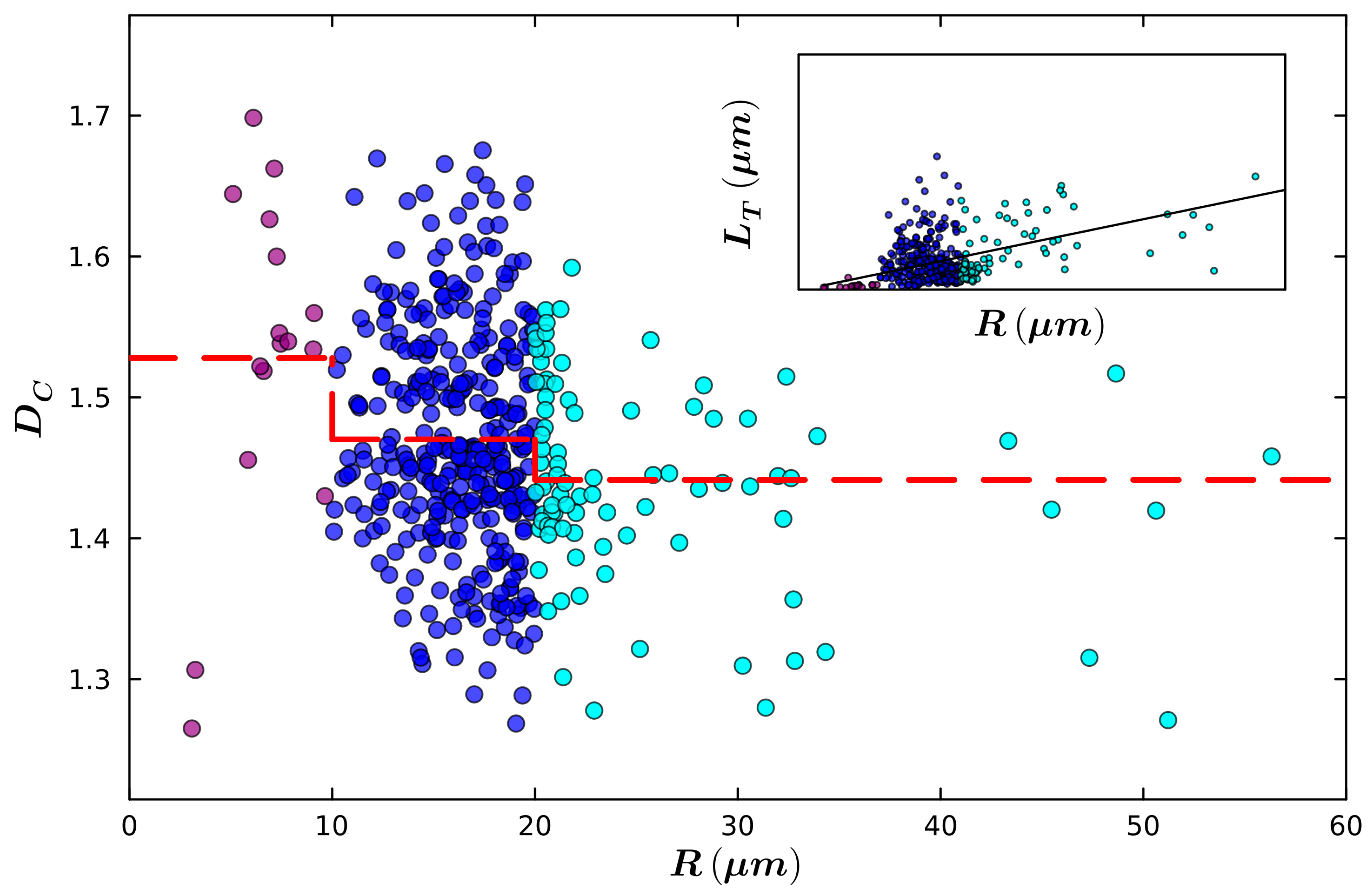
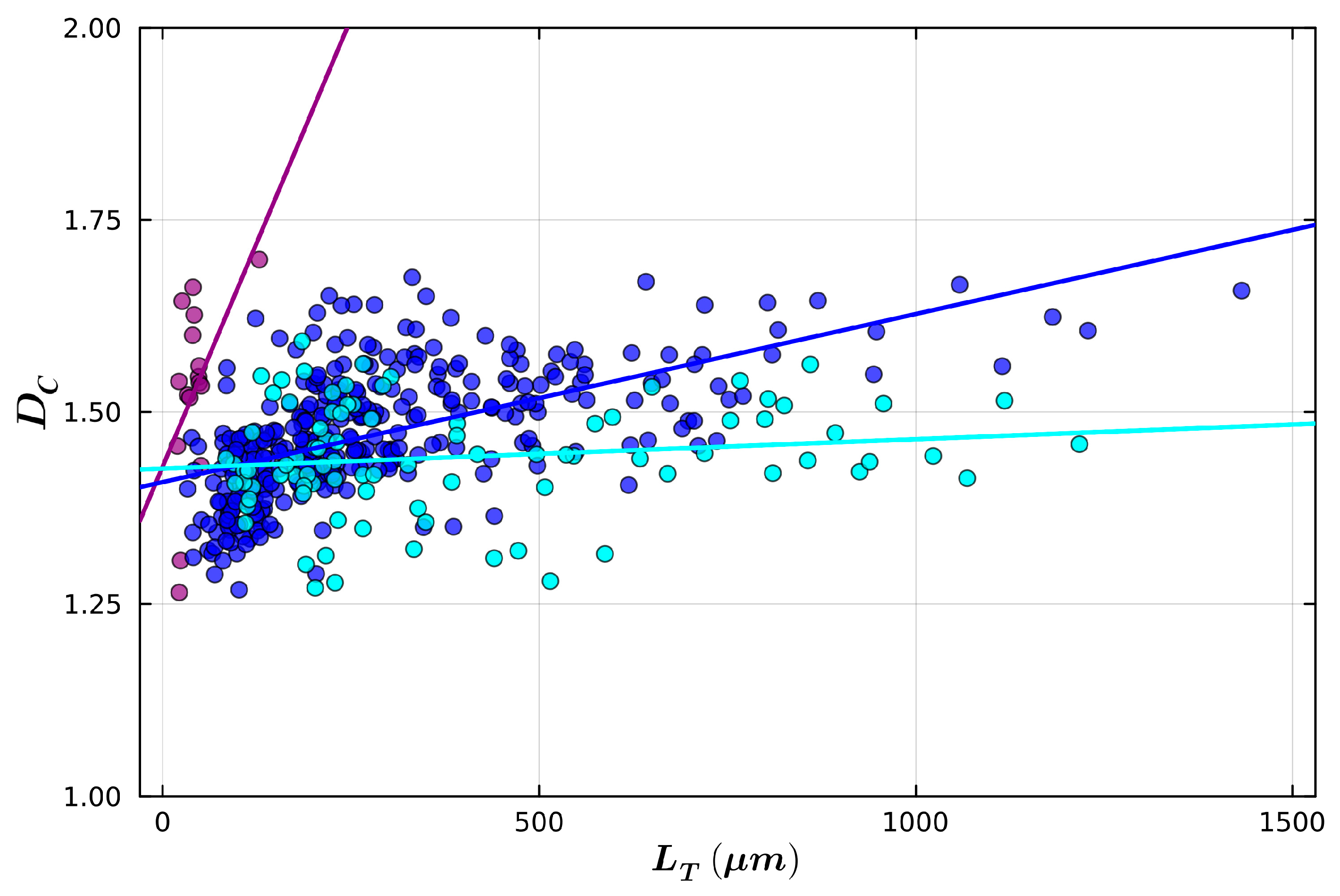
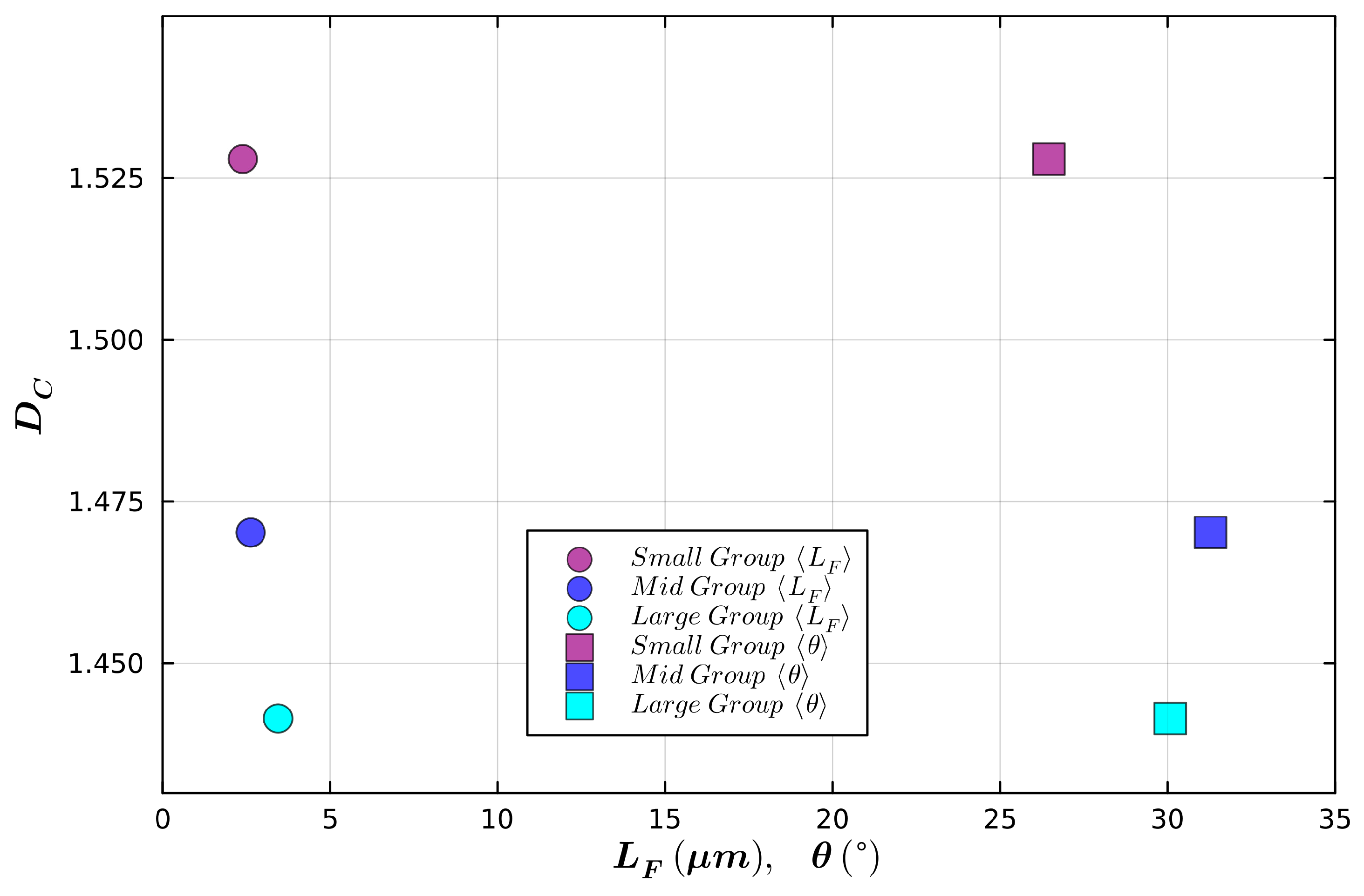
| Small Radius | Medium Radius | Large Radius | |
|---|---|---|---|
| Mean Radius (µm) | 6.8 | 16.2 | 25.6 |
| Mean Total Length (µm) | 42.6 | 281.0 | 394.0 |
| Mean Fork Length (µm) | 2.2 | 2.6 | 3.4 |
| Mean Weave Angle (°) | 26.5 | 31.3 | 30.1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Brouse, B., Jr.; Rowland, C.; Taylor, R.P. Relating the Morphology of Bipolar Neurons to Fractal Dimension. Fractal Fract. 2025, 9, 9. https://doi.org/10.3390/fractalfract9010009
Brouse B Jr., Rowland C, Taylor RP. Relating the Morphology of Bipolar Neurons to Fractal Dimension. Fractal and Fractional. 2025; 9(1):9. https://doi.org/10.3390/fractalfract9010009
Chicago/Turabian StyleBrouse, Bret, Jr., Conor Rowland, and Richard P. Taylor. 2025. "Relating the Morphology of Bipolar Neurons to Fractal Dimension" Fractal and Fractional 9, no. 1: 9. https://doi.org/10.3390/fractalfract9010009
APA StyleBrouse, B., Jr., Rowland, C., & Taylor, R. P. (2025). Relating the Morphology of Bipolar Neurons to Fractal Dimension. Fractal and Fractional, 9(1), 9. https://doi.org/10.3390/fractalfract9010009






