Finite-Time Synchronization of Fractional-Order Complex-Valued Multi-Layer Network via Adaptive Quantized Control Under Deceptive Attacks
Abstract
1. Introduction
- (1)
- The designed AQC strategy combines the merits of adaptive control and quantized control. Considering the vulnerability of network systems to stochastic DPAs, a random variable that follows the Bernoulli distribution has been designed, which is more practical.
- (2)
- This article introduces new sign functions and quantization functions in the complex domain and establishes some related formulas for the complex-valued domain. It studies the FITS of FOCVMLNs, and the settling time of FITS is sufficiently evaluated.
- (3)
- A sufficient criterion for FITS of FOCVMLNs under stochastic DPAs is designed based on Lyapunov functions and graph theory methods. The numerical simulation presented at the end demonstrates the dependability of theoretical deductions.
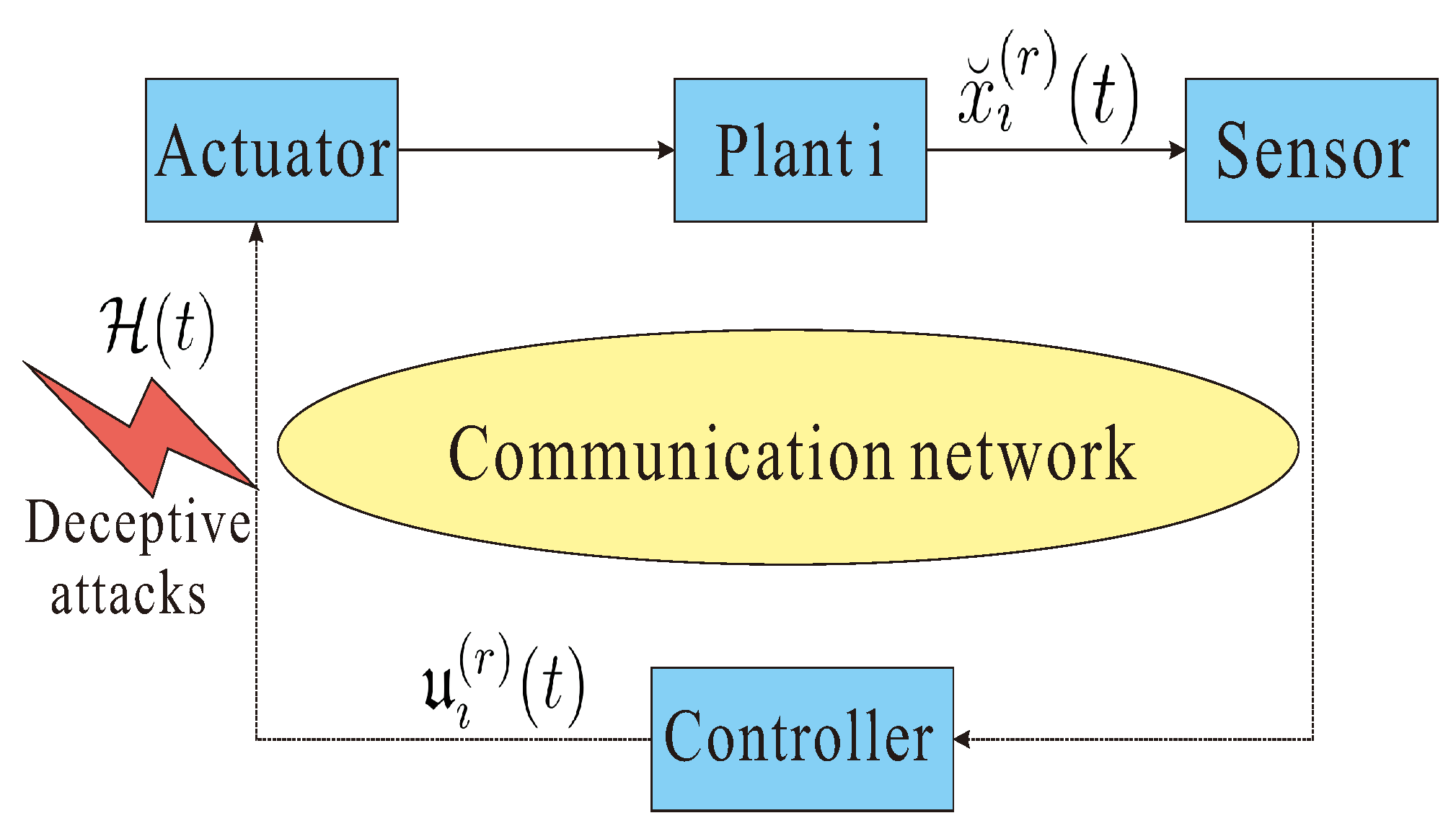
2. Preliminaries and Problem Description
- (1)
- .
- (2)
- .
- (3)
- .
- (4)
- .
3. Main Results
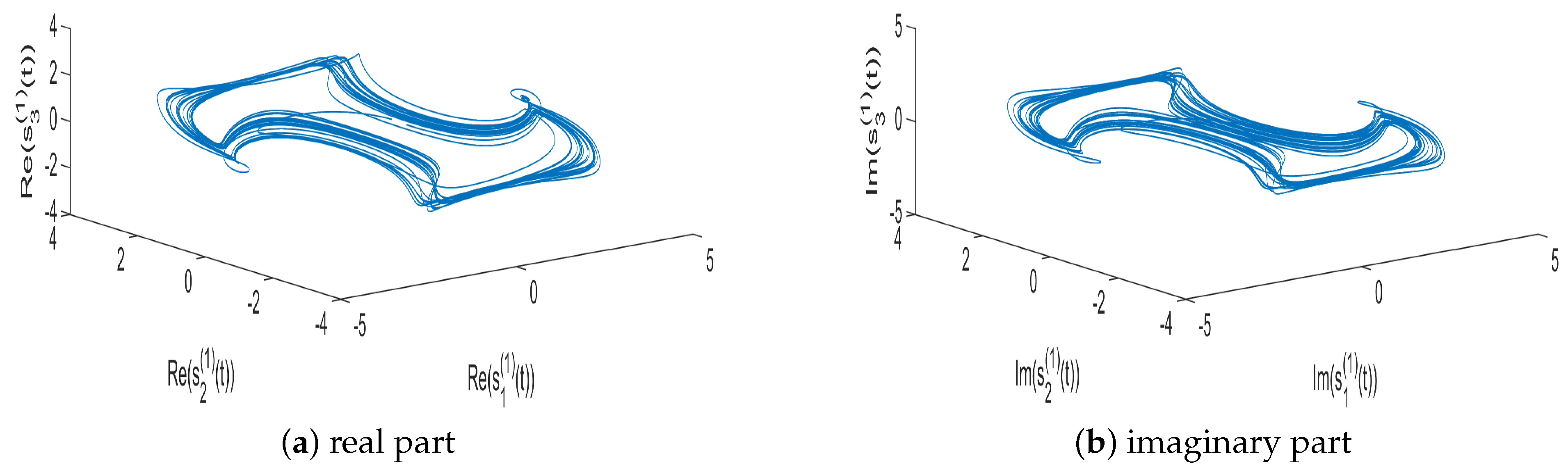
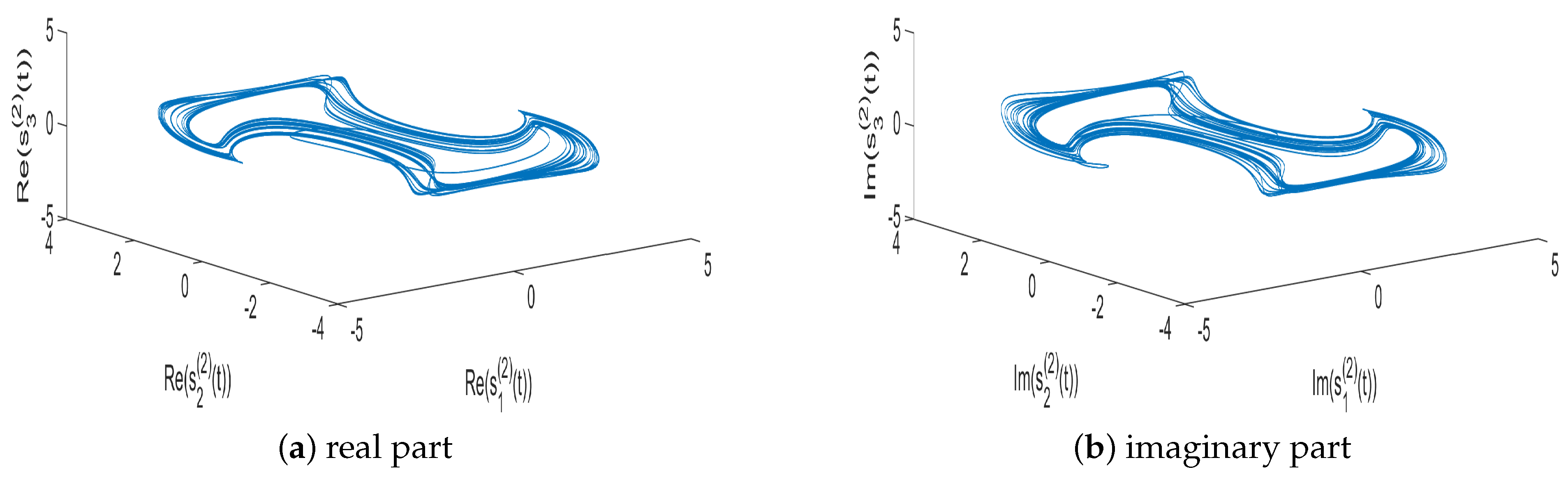
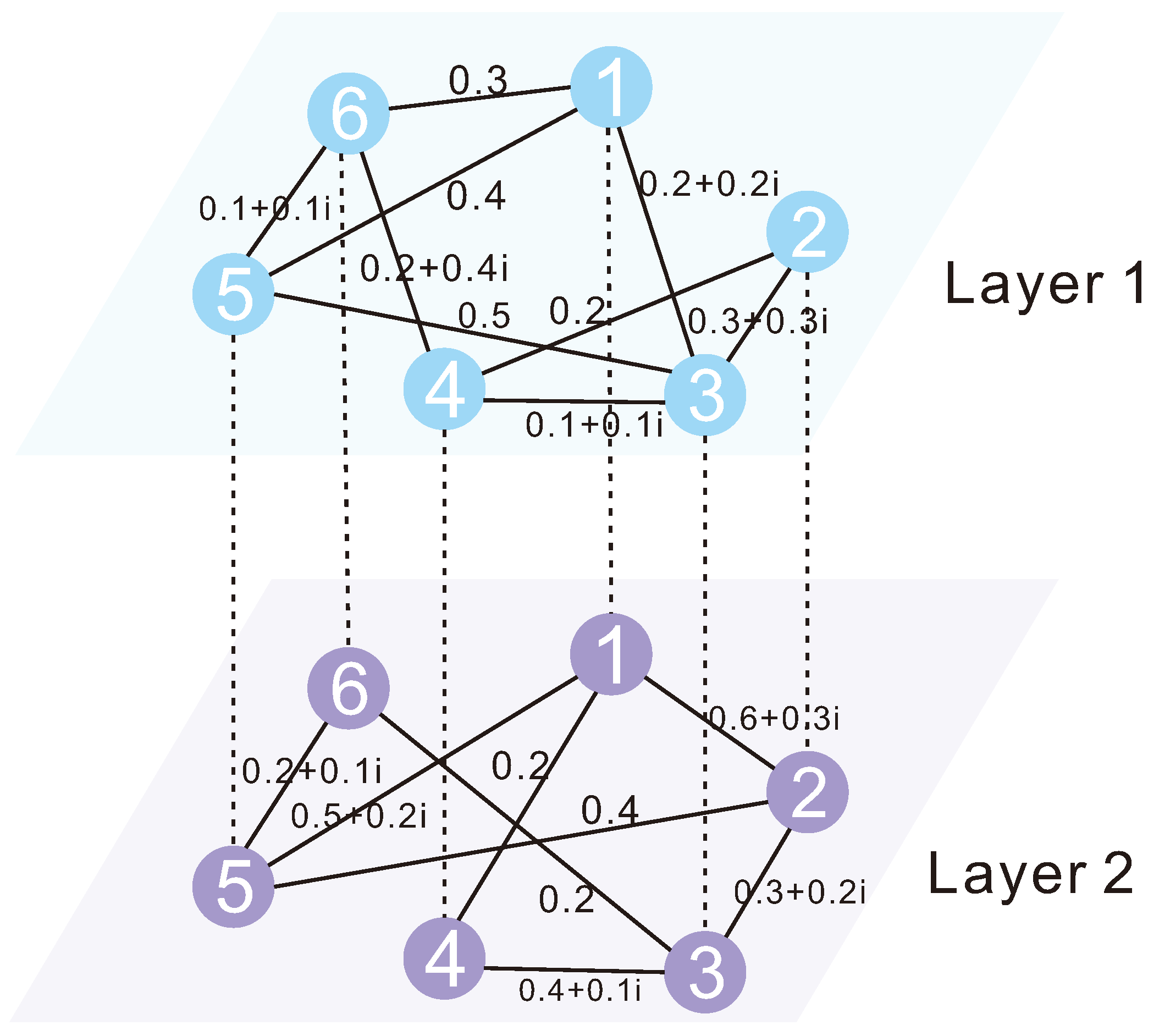
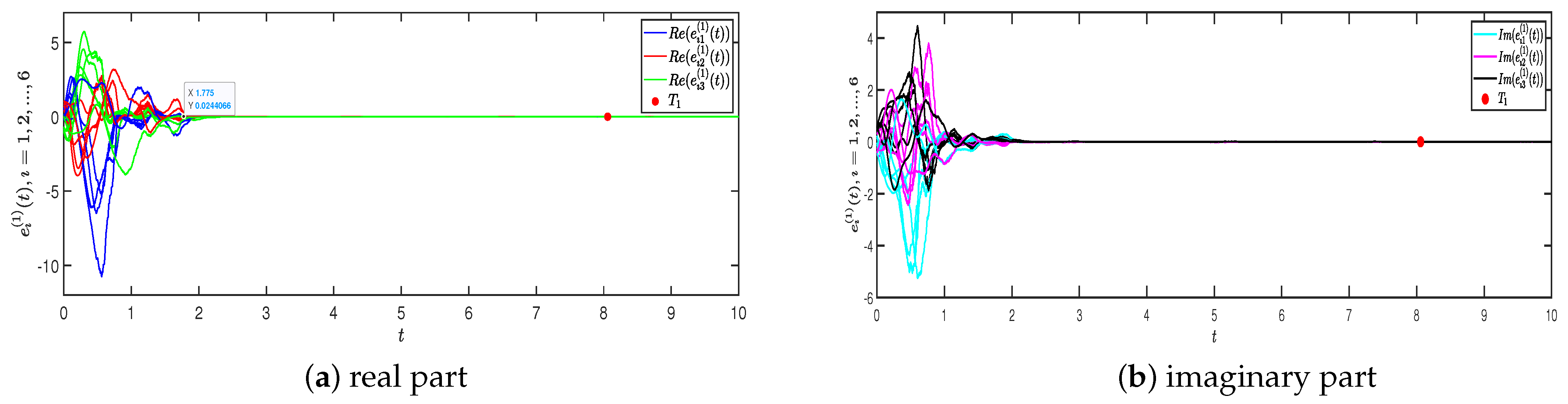
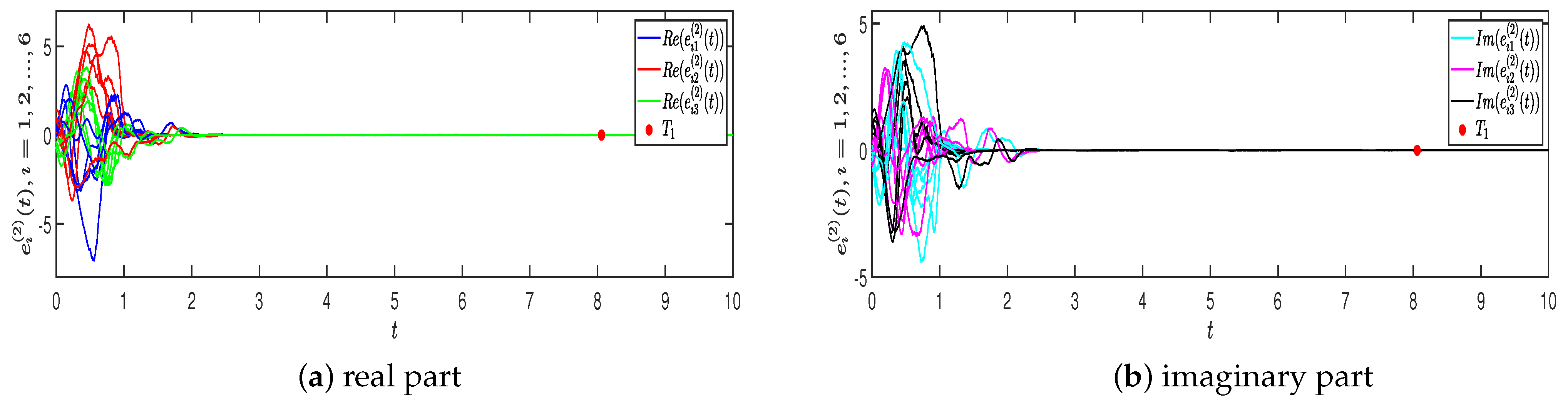
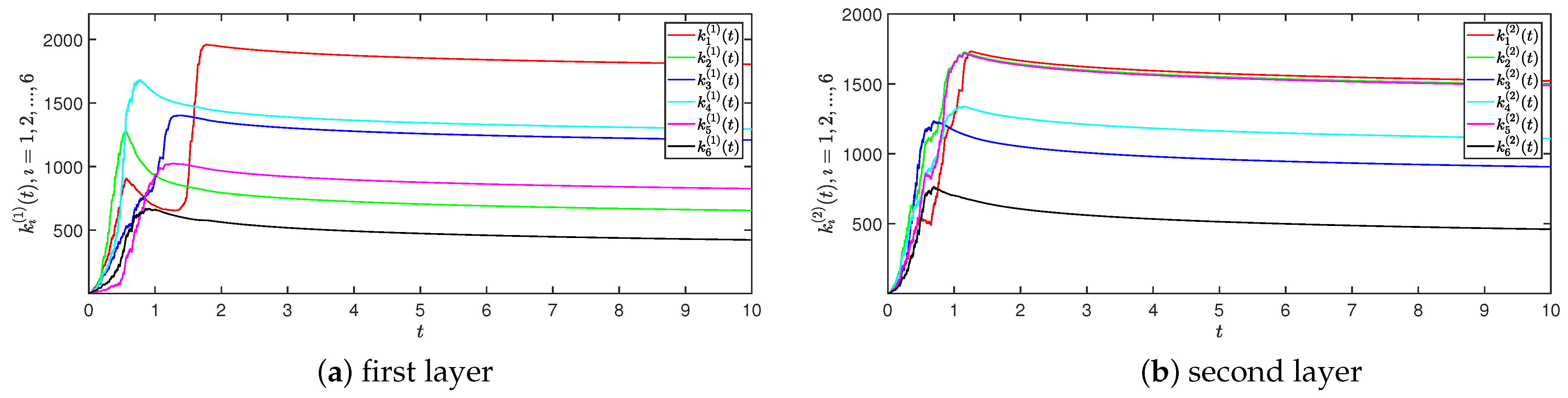
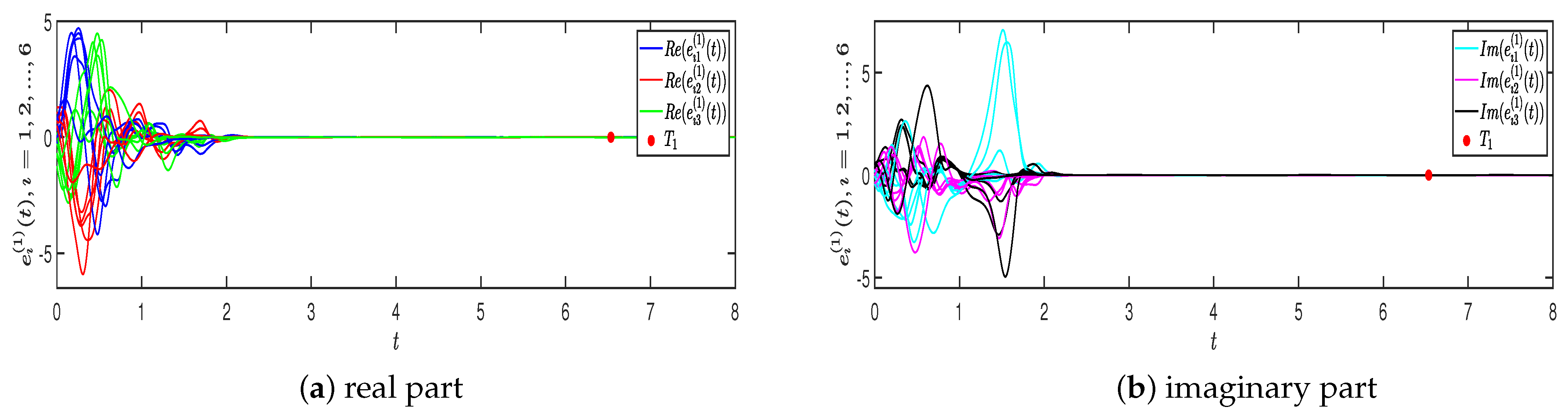
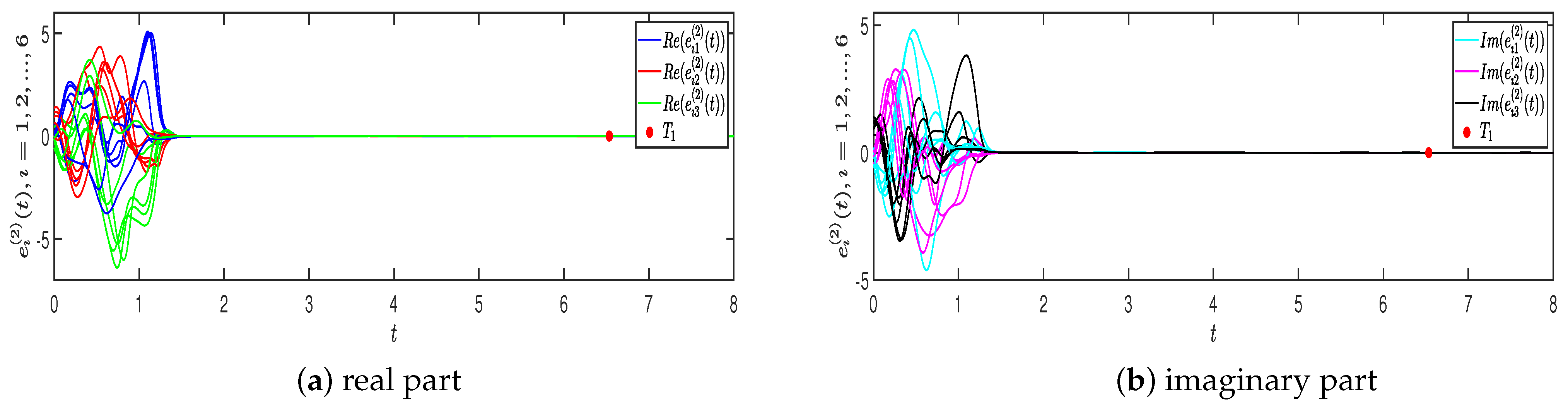
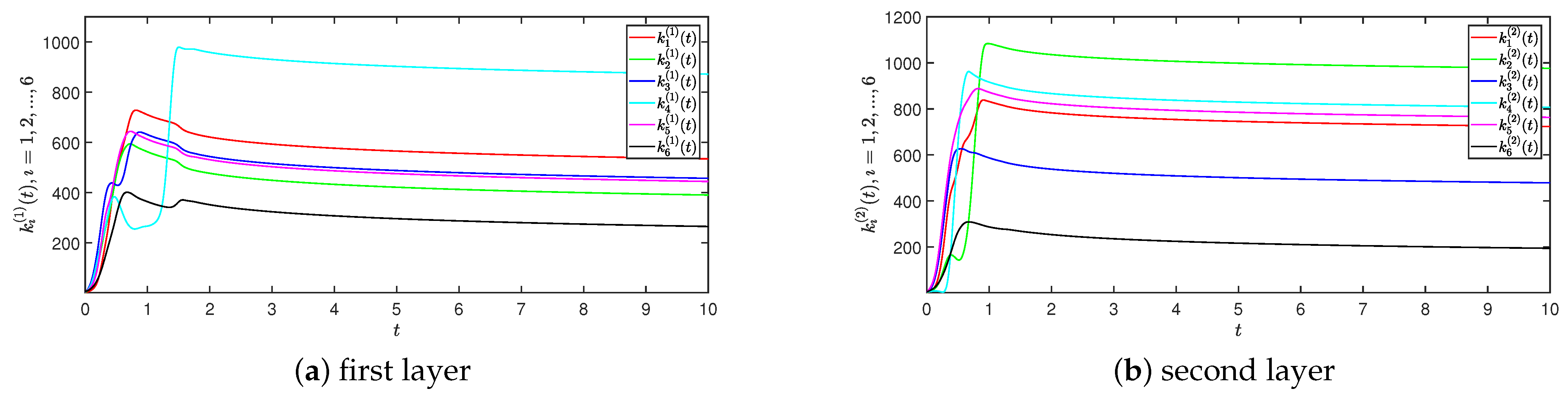
4. Numerical Simulations
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Tran, T.H.; Nguyen, T.B.; Le, H.S.; Phung, D.C. Formulation and solution technique for agricultural waste collection and transport network design. Eur. J. Oper. Res. 2024, 313, 1152–1169. [Google Scholar] [CrossRef]
- Wang, S.L.; Guo, Z.Y.; Huang, X.D.; Zhang, J.H. A three-stage model of quantifying and analyzing power network resilience based on network theory. Reliab. Eng. Syst. Saf. 2024, 241, 109681. [Google Scholar] [CrossRef]
- Barabási, A.L.; Albert, R. Emergence of scaling in random networks. Science 1999, 286, 509–512. [Google Scholar] [CrossRef]
- Sun, Y.P.; Jia, R.Y.; Razzaq, A.; Bao, Q. Social network platforms and climate change in China: Evidence from TikTok. Technol. Forecast. Soc. Change 2024, 200, 123197. [Google Scholar] [CrossRef]
- Elfarhani, M.; Jarraya, A.; Abid, S.; Haddar, M. Fractional derivative and hereditary combined model for memory effects on flexible polyurethane foam. Mech.-Time-Depend. Mater. 2016, 20, 197–217. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Differential Equations: An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of Their Solution and Some of Their Applications; Elsevier: Berkeley, CA, USA, 1998. [Google Scholar]
- Hilfer, R. Applications of Fractional Calculus in Physics; Word Scientific Press: Singapore, 2000. [Google Scholar]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations; Elsevier: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Gibbon, J.D.; McGuinness, M.J. The real and complex Lorenz equations in rotating fluids and lasers. Phys. D Nonlinear Phenomena 1982, 5, 108–122. [Google Scholar] [CrossRef]
- Rauh, A.; Hannibal, L.; Abraham, N.B. Global stability properties of the complex Lorenz model. Phys. D Nonlinear Phenomena 1996, 99, 45–58. [Google Scholar] [CrossRef]
- Tripathi, B.K.; Kalra, P.K. On efficient learning machine with root-power mean neuron in complex domain. IEEE Trans. Neural Netw. 2011, 22, 727–738. [Google Scholar] [CrossRef]
- Adali, T.; Schreier, P.J.; Scharf, L.L. Complex-valued signal processing: The proper way to deal with impropriety. IEEE Trans. Signal Process. 2011, 59, 5101–5125. [Google Scholar] [CrossRef]
- Wu, K.; Tang, M.; Liu, Z.H.; Ren, H.; Zhao, L. Pinning synchronization of multiple fractional-order fuzzy complex-valued delayed spatiotemporal neural networks. Chaos Solitons Fractals 2024, 182, 114801. [Google Scholar] [CrossRef]
- Ren, Y.; Jiang, H.J.; Hu, C.; Qin, X.J. Discontinuous control for exponential synchronization of complex-valued stochastic multi-layer networks. Chaos Solitons Fractals 2023, 174, 113792. [Google Scholar] [CrossRef]
- Li, S.; Ren, X.N.; Li, W.X. Inter-layer noise-based topology of complex-valued multi-layer networks: Almost sure stability via time-varying hybrid intermittent pinning control. IEEE Trans. Netw. Sci. Eng. 2022, 9, 1477–1492. [Google Scholar] [CrossRef]
- He, X.Y.; Li, L.S.; Mo, Y.F.; Huang, J.X.; Qin, S.J. A distributed route network planning method with congestion pricing for drone delivery services in cities. Transp. Res. Part C Emerg. Technol. 2024, 160, 104536. [Google Scholar] [CrossRef]
- Li, C.D.; Liao, X.F.; Wong, K.W. Lag synchronization of hyperchaos with application to secure communications. Chaos Solitons Fractals 2005, 23, 183–193. [Google Scholar] [CrossRef]
- Tang, L.K.; Wu, X.Q.; Lv, J.H.; Lu, J.A.; D’Souza, R.M. Master stability functions for complete, intralayer, and interlayer synchronization in multiplex networks of coupled Rössler oscillators. Phys. Rev. E 2019, 99, 012304. [Google Scholar] [CrossRef]
- Li, Z.W.; Tang, L.K.; Zhuang, J.S. Bounded intra-layer synchronization of multilayer heterogeneous networks without external controllers. Nonlinear Dyn. 2024, 112, 14497–14512. [Google Scholar] [CrossRef]
- Shi, J.Y.; Zhou, P.P.; Cai, S.M. On fixed-time interlayer synchronization of two-layer multiweighted complex dynamic networks: An economic and practical non-chattering adaptive control approach. Chaos Solitons Fractals 2024, 182, 114835. [Google Scholar] [CrossRef]
- Yin, Y.W.; Yu, J.; Hu, C.; Shi, T.T. Pinning synchronization of fractional-order two-layer networks: From inter-layer synchronization to cluster synchronization. In Proceedings of the International Conference on Neuromorphic Computing (ICNC2023), Wuhan, China, 15–17 December 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 297–302. [Google Scholar]
- Sun, J.W.; Wu, Y.Y.; Cui, G.Z.; Wang, Y.F. Finite-time real combination synchronization of three complex-variable chaotic systems with unknown parameters via sliding mode control. Nonlinear Dyn. 2017, 88, 1677–1690. [Google Scholar] [CrossRef]
- Du, F.F.; Lu, J.G.; Zhang, Q.H. Delay-dependent finite-time synchronization criterion of fractional-order delayed complex networks. Commun. Nonlinear Sci. Numer. Simul. 2023, 119, 107072. [Google Scholar] [CrossRef]
- Zhang, H.W.; Cheng, R.; Ding, D.W. Finite-time synchronization of uncertain fractional-order multi-weighted complex networks with external disturbances via adaptive quantized control. Chin. Phys. B 2022, 31, 100504. [Google Scholar] [CrossRef]
- Zheng, B.B.; Hu, C.; Yu, J.; Jiang, H.J. Finite-time synchronization of fully complex-valued neural networks with fractional-order. Neurocomputing 2020, 373, 70–80. [Google Scholar] [CrossRef]
- Hou, T.Q.; Yu, J.; Hu, C.; Jiang, H.J. Finite-time synchronization of fractional-order complex-variable dynamic networks. IEEE Trans. Syst. Man Cybern. Syst. 2019, 51, 4297–4307. [Google Scholar] [CrossRef]
- Fan, H.G.; Chen, X.J.; Shi, K.B.; Liang, Y.H.; Wang, Y.; Wen, H. Mittag-Leffler synchronization in finite time for uncertain fractional-order multi-delayed memristive neural networks with time-varying perturbations via information feedback. Fractal Fract. 2024, 8, 422. [Google Scholar] [CrossRef]
- Wu, E.; Wang, Y.; Li, Y.D.; Li, K.L.; Luo, F. Fixed-time synchronization of complex-valued coupled networks with hybrid perturbations via quantized control. Mathematics 2023, 11, 3845. [Google Scholar] [CrossRef]
- Pan, C.N.; Bao, H.B. Exponential synchronization of complex-valued memristor-based delayed neural networks via quantized intermittent control. Neurocomputing 2020, 404, 317–328. [Google Scholar] [CrossRef]
- Xu, Y.; Li, Y.Z.; Li, W.X. Adaptive finite-time synchronization control for fractional-order complex-valued dynamical networks with multiple weights. Commun. Nonlinear Sci. Numer. Simul. 2020, 85, 105239. [Google Scholar] [CrossRef]
- Xiang, K.Q.; Kang, Q.K.; Chang, H.; Yang, J. Adaptive control for finite-time cluster synchronization of fractional-order fully complex-valued dynamical networks. Fractal Fract. 2023, 7, 645. [Google Scholar] [CrossRef]
- Chen, S.L.; Luo, X.P.; Yang, J.K.; Li, Z.M.; Li, H.L. Adaptive synchronization of fractional-order uncertain complex-valued competitive neural networks under the non-decomposition method. Fractal Fract. 2024, 8, 449. [Google Scholar] [CrossRef]
- Yang, J.P.; Li, H.L.; Zhang, L.; Hu, C.; Jiang, H.J. Quasi-projective and finite-time synchronization of delayed fractional-order BAM neural networks via quantized control. Math. Methods Appl. Sci. 2023, 46, 197–214. [Google Scholar] [CrossRef]
- Bai, J.; Wu, H.Q.; Cao, J.D. Secure synchronization and identification for fractional complex networks with multiple weight couplings under DoS attacks. Comput. Appl. Math. 2022, 41, 187. [Google Scholar] [CrossRef]
- Lu, Y.; Wu, X.R.; Wang, Y.N.; Huang, L.H.; Wei, Q.J. Quantization-based event-triggered H∞ consensus for discrete-time Markov Jump fractional-order multiagent systems with DoS Attacks. Fractal Fract. 2024, 8, 147. [Google Scholar] [CrossRef]
- Sakthivel, R.; Kwon, O.M.; Park, M.J.; Sakthivel, R. Event-triggered synchronization control for fractional-order IT2 fuzzy multi-weighted complex dynamical networks with deception attacks. Commun. Nonlinear Sci. Numer. Simul. 2024, 136, 108091. [Google Scholar] [CrossRef]
- Liu, X.; Chen, L.L.; Zhao, Y.F.; Li, H.L. Event-triggered hybrid impulsive control for synchronization of fractional-order multilayer signed networks under cyber attacks. Neural Netw. 2024, 172, 106124. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Differential Equations; Academic Press: New York, NY, USA, 1999. [Google Scholar]
- Yang, S.; Yu, J.; Hu, C.; Jiang, H.J. Quasi-projective synchronization of fractional-order complex-valued recurrent neural networks. Neural Netw. 2018, 104, 104–113. [Google Scholar] [CrossRef]
- Ji, G.J.; Hu, C.; Yu, J.; Jiang, H.J. Finite-time and fixed-time synchronization of discontinuous complex networks: A unified control framework design. J. Frankl. Inst. 2018, 355, 4665–4685. [Google Scholar] [CrossRef]
- Xu, C.; Yang, X.S.; Lu, J.Q.; Feng, J.W.; Alsaadi, F.E.; Hayat, T. Finite-time synchronization of networks via quantized intermittent pinning control. IEEE Trans. Cybern. 2017, 48, 3021–3027. [Google Scholar] [CrossRef]
- He, J.J.; Chen, H.; Ge, M.F.; Ding, T.F.; Wang, L.M.; Liang, C.D. Adaptive finite-time quantized synchronization of complex dynamical networks with quantized time-varying delayed couplings. Neurocomputing 2021, 431, 90–99. [Google Scholar] [CrossRef]
- Tan, F.; Zhou, L.L.; Lu, J.W.; Quan, H.Z.; Liu, K.Y. Adaptive quantitative control for finite time synchronization among multiplex switched nonlinear coupling complex networks. Eur. J. Control 2023, 70, 100764. [Google Scholar] [CrossRef]
- Tan, F.; Xu, S.Y.; Li, Y.M.; Chu, Y.M.; Zhang, Z.Q. Adaptive quantitative control for robust H∞ synchronization between multiplex neural networks under stochastic cyber attacks. Neurocomputing 2022, 493, 129–142. [Google Scholar] [CrossRef]
- Bai, Y.Z.; Yu, J.; Hu, C. Adaptive quantized synchronization of fractional-order output-coupling multiplex networks. Fractal Fract. 2022, 7, 22. [Google Scholar] [CrossRef]
- Song, X.N.; Man, J.T.; Song, S.; Zhang, Y.J.; Ning, Z.K. Finite/fixed-time synchronization for Markovian complex-valued memristive neural networks with reaction-diffusion terms and its application. Neurocomputing 2020, 414, 131–142. [Google Scholar] [CrossRef]
- Zhang, Y.L.; Deng, S.F. Fixed-time synchronization of complex-valued memristor-based neural networks with impulsive effects. Neural Process. Lett. 2020, 52, 1263–1290. [Google Scholar] [CrossRef]
- Ding, D.W.; Yan, J.; Wang, N.; Liang, D. Adaptive synchronization of fractional order complex-variable dynamical networks via pinning control. Commun. Theor. Phys. 2017, 68, 366. [Google Scholar] [CrossRef]
- Xu, Q.; Xu, X.H.; Zhuang, S.X.; Xiao, J.X.; Song, C.H.; Che, C. New complex projective synchronization strategies for drive-response networks with fractional complex-variable dynamics. Appl. Math. Comput. 2018, 338, 552–566. [Google Scholar] [CrossRef]
- Shi, J.Y.; Zhou, P.P.; Jia, Q.; Cai, S.M. Fixed-time synchronization of multilayered complex dynamic networks via quantized variable-gain saturated control. Inf. Sci. 2024, 681, 121206. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, L.; Yu, J.; Hu, C.; Xiong, K.; Shi, T. Finite-Time Synchronization of Fractional-Order Complex-Valued Multi-Layer Network via Adaptive Quantized Control Under Deceptive Attacks. Fractal Fract. 2025, 9, 47. https://doi.org/10.3390/fractalfract9010047
Xu L, Yu J, Hu C, Xiong K, Shi T. Finite-Time Synchronization of Fractional-Order Complex-Valued Multi-Layer Network via Adaptive Quantized Control Under Deceptive Attacks. Fractal and Fractional. 2025; 9(1):47. https://doi.org/10.3390/fractalfract9010047
Chicago/Turabian StyleXu, Lulu, Juan Yu, Cheng Hu, Kailong Xiong, and Tingting Shi. 2025. "Finite-Time Synchronization of Fractional-Order Complex-Valued Multi-Layer Network via Adaptive Quantized Control Under Deceptive Attacks" Fractal and Fractional 9, no. 1: 47. https://doi.org/10.3390/fractalfract9010047
APA StyleXu, L., Yu, J., Hu, C., Xiong, K., & Shi, T. (2025). Finite-Time Synchronization of Fractional-Order Complex-Valued Multi-Layer Network via Adaptive Quantized Control Under Deceptive Attacks. Fractal and Fractional, 9(1), 47. https://doi.org/10.3390/fractalfract9010047





