Dynamic Behavior and Fixed-Time Synchronization Control of Incommensurate Fractional-Order Chaotic System
Abstract
1. Introduction
2. Preliminaries, Modeling, and Algorithms
2.1. Preliminaries
2.2. Modeling and Algorithms
3. Dynamic Analysis
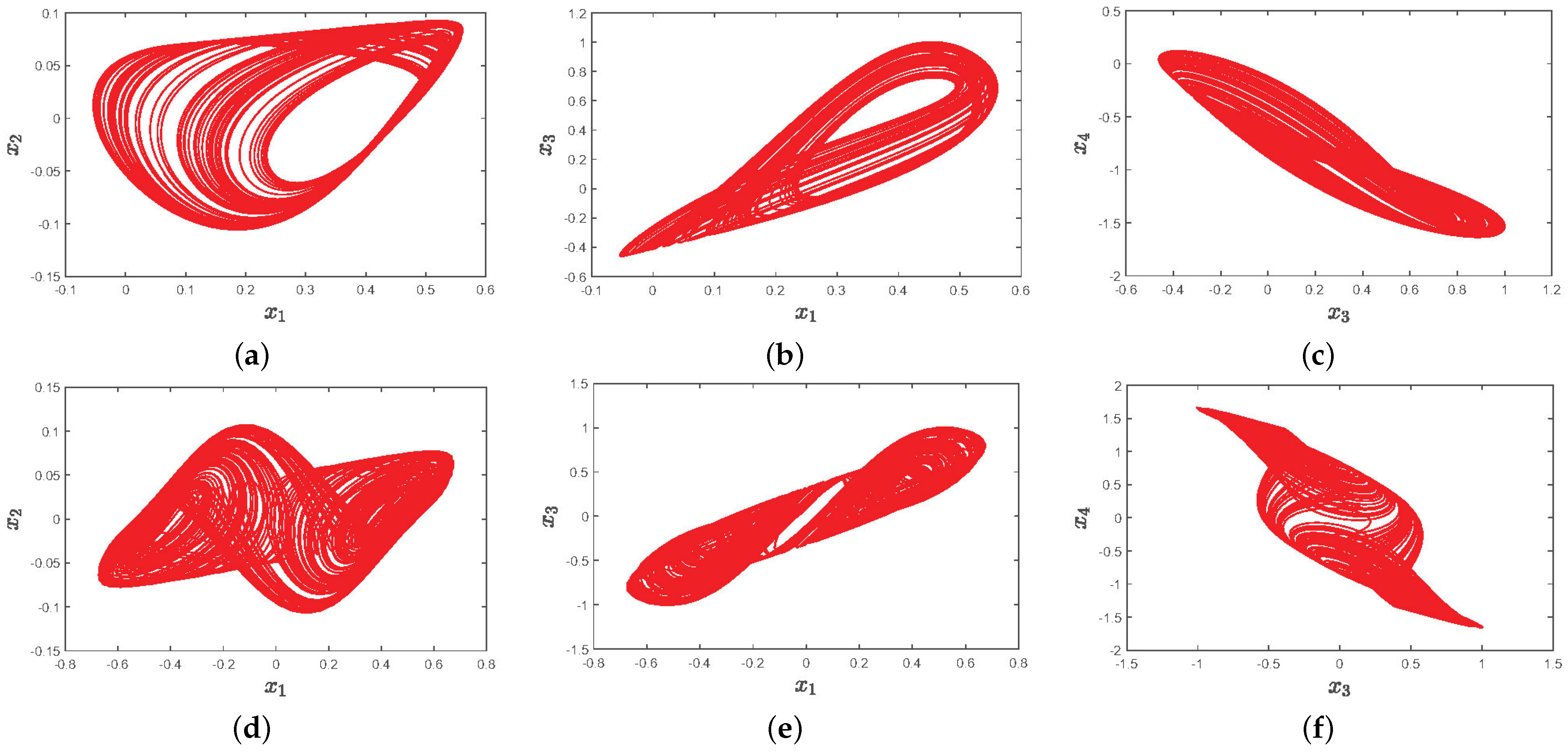
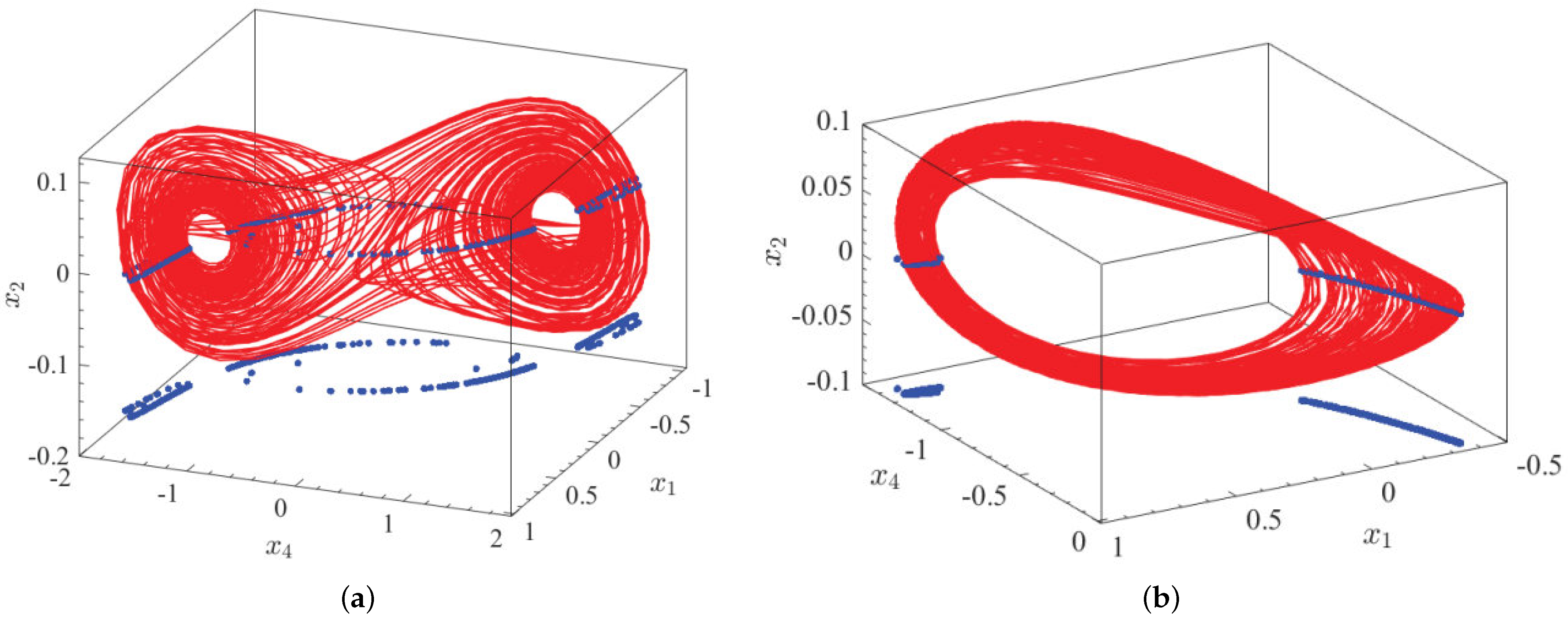
3.1. Incommensurate Aystem Phase Diagram and Poincaré Analysis
3.2. Dynamic Analysis of Fractional Orders Change in Incommensurate System
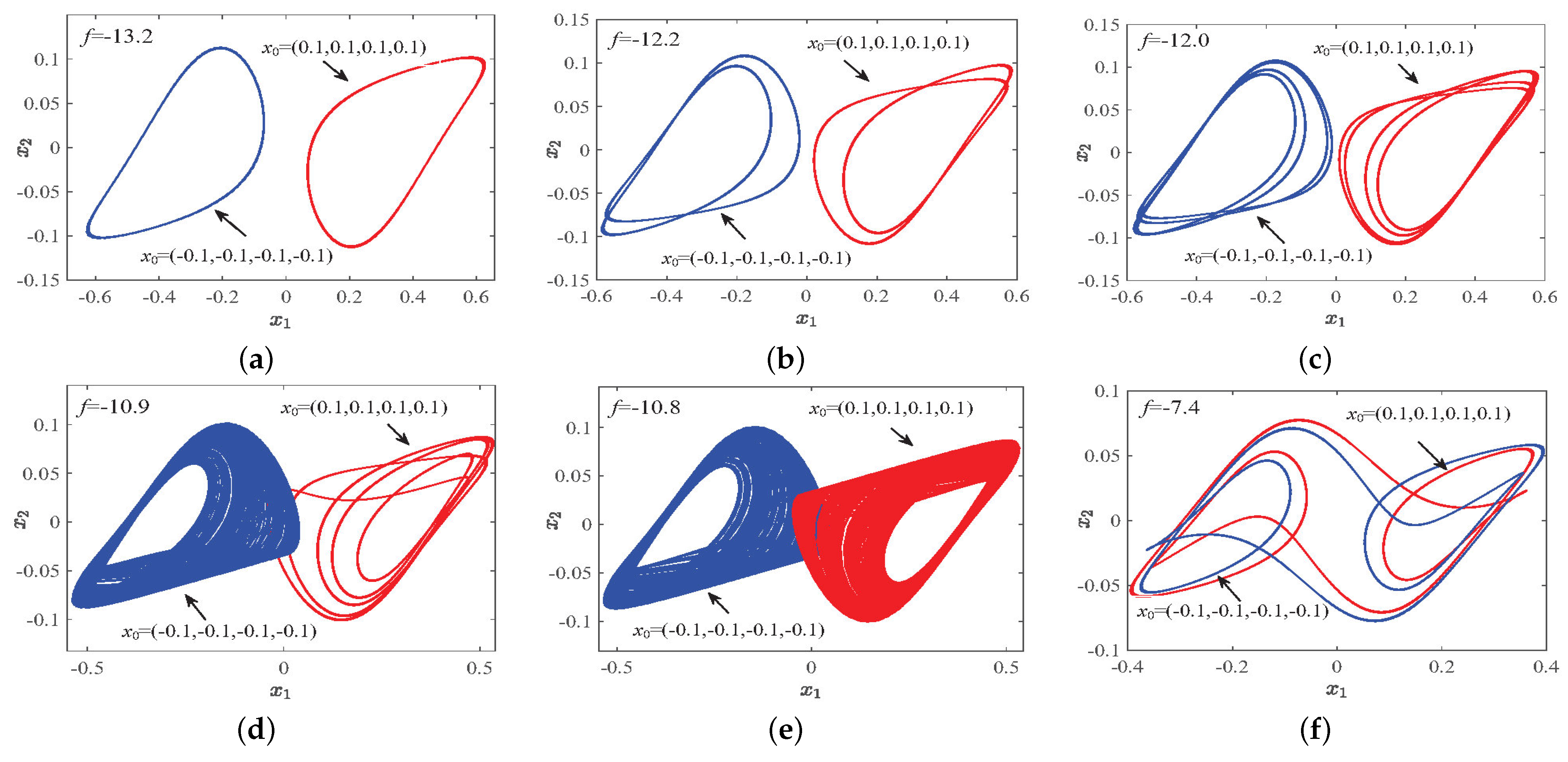
3.3. Coexistence Dynamics Phenomenon of Incommensurate System Parameter Changes
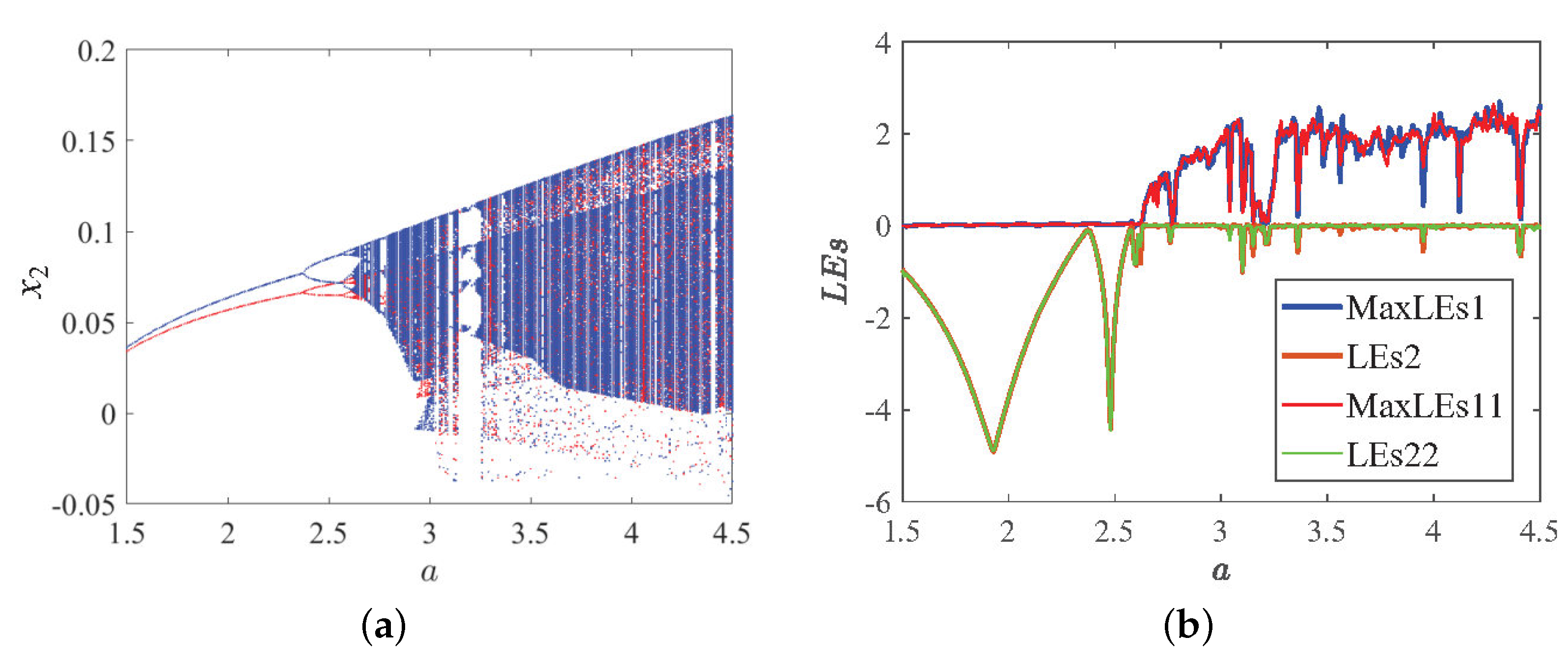
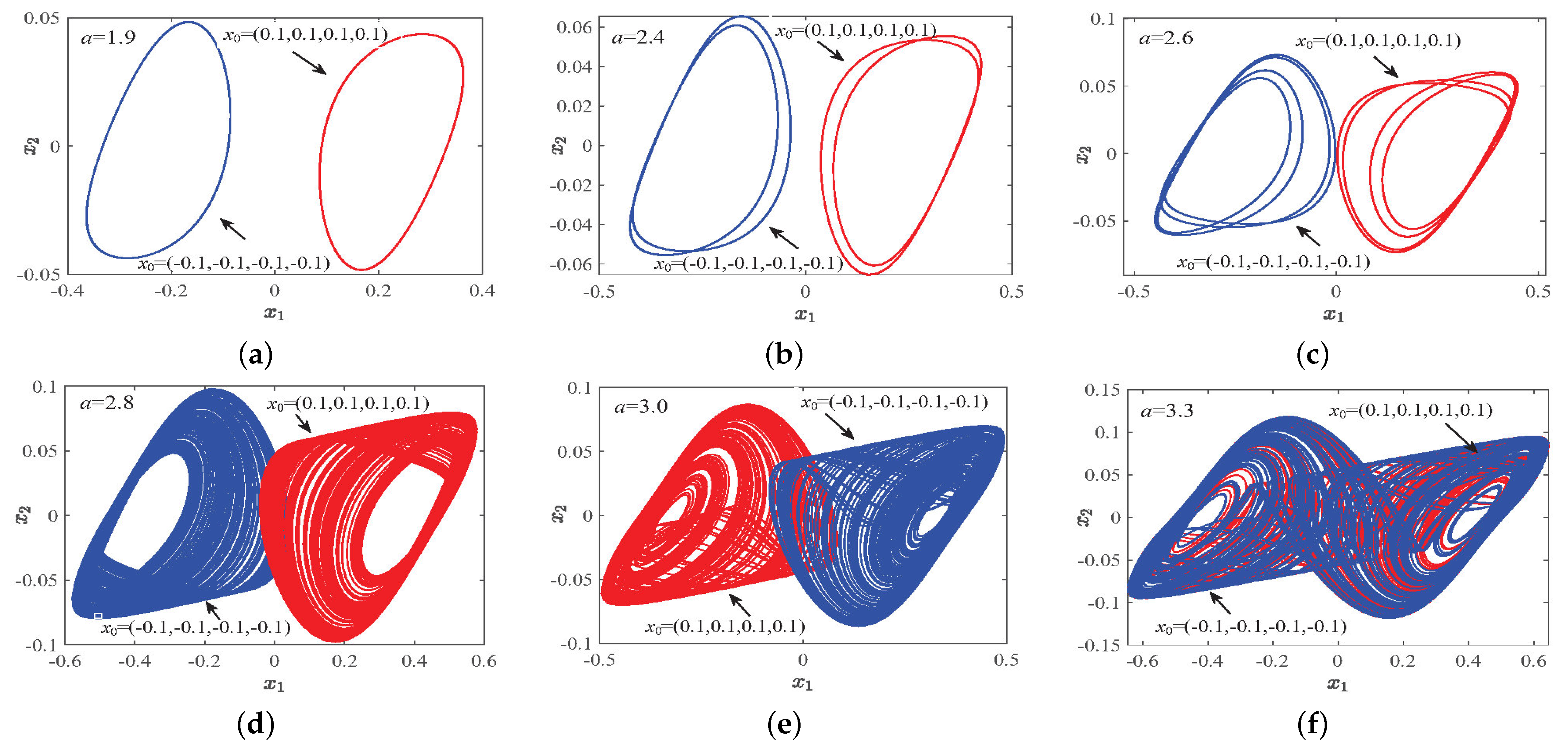
3.3.1. Dynamic Phenomena of Parameter a Change
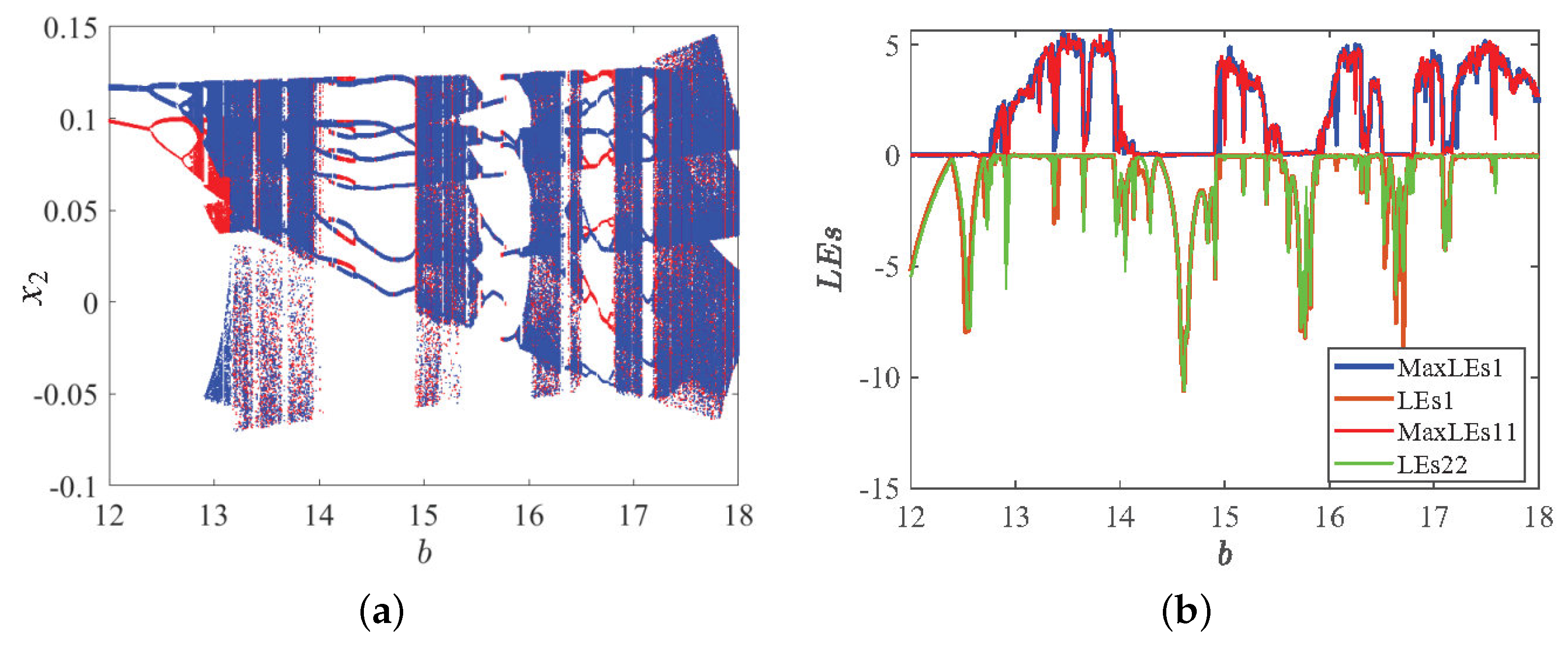
3.3.2. Dynamic Phenomena of Parameter b Change
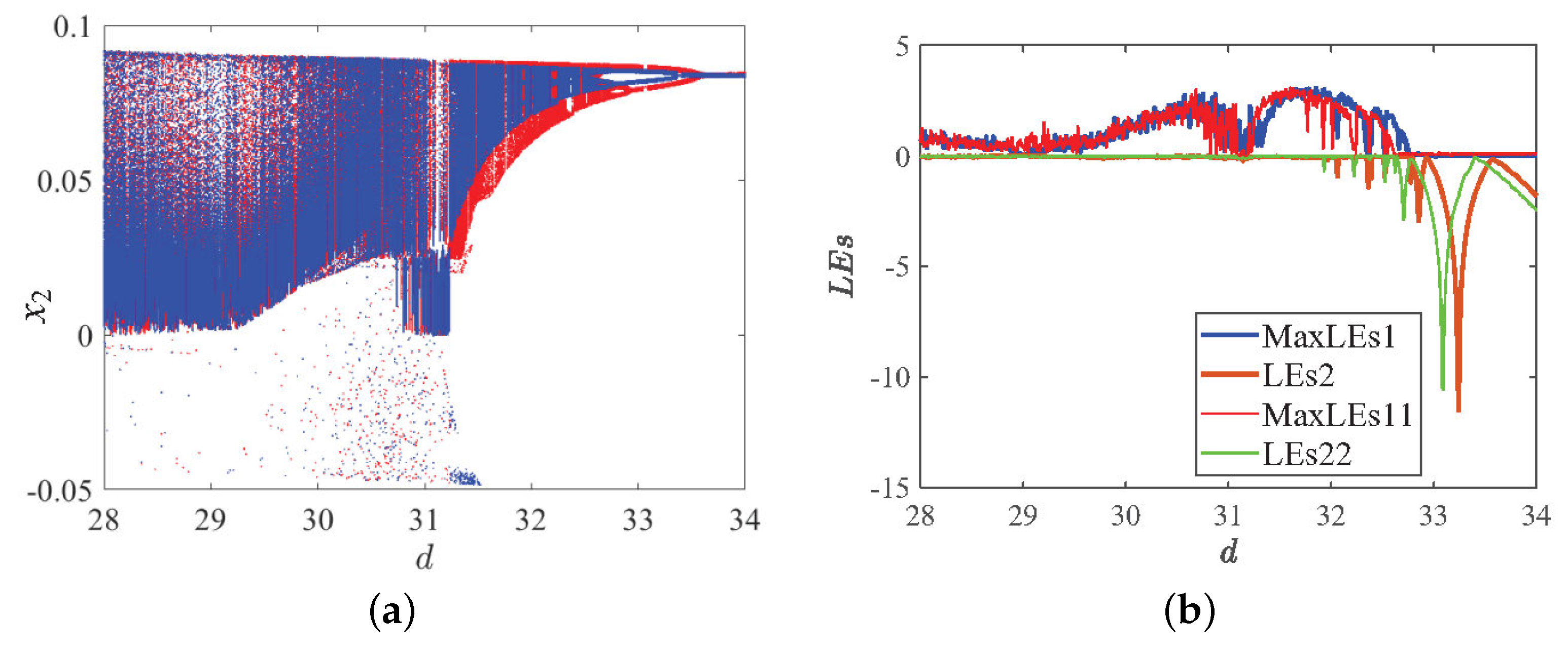
3.3.3. Dynamic Phenomena of Parameter d Change
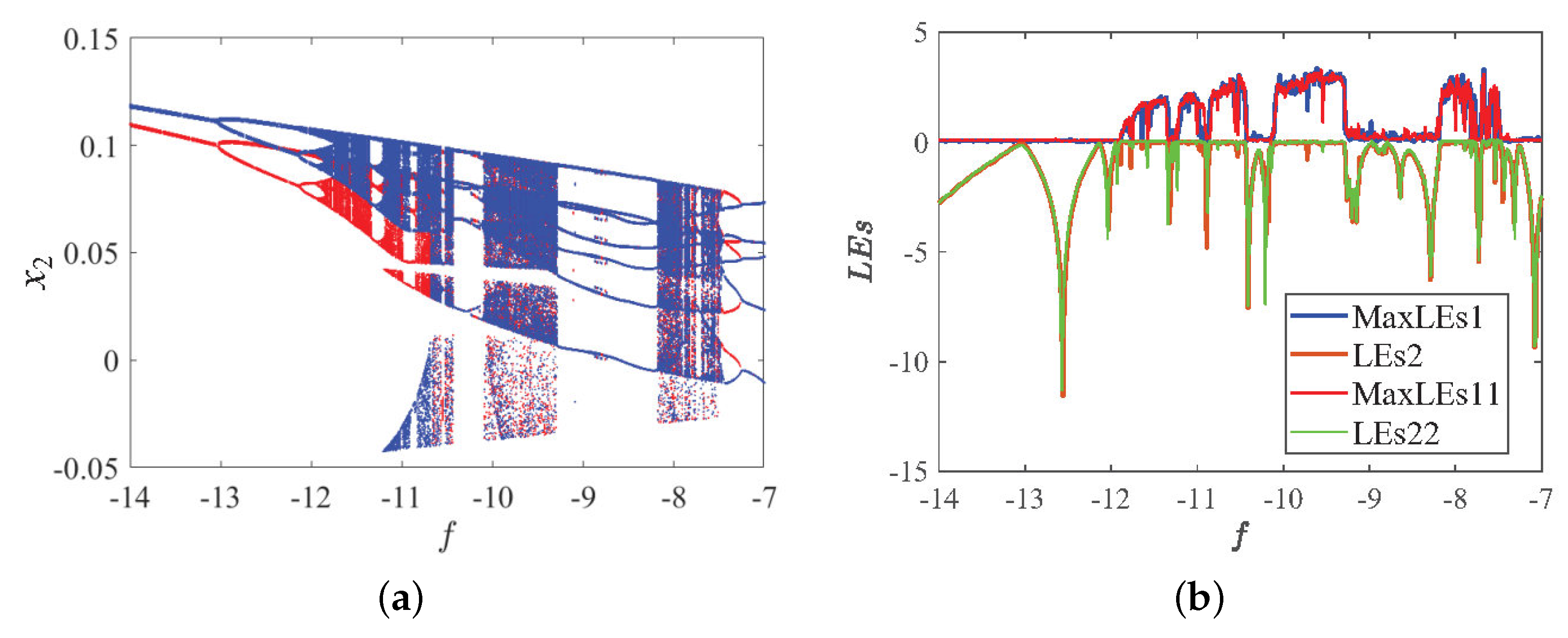
3.3.4. Dynamic Phenomena of Parameter f Change
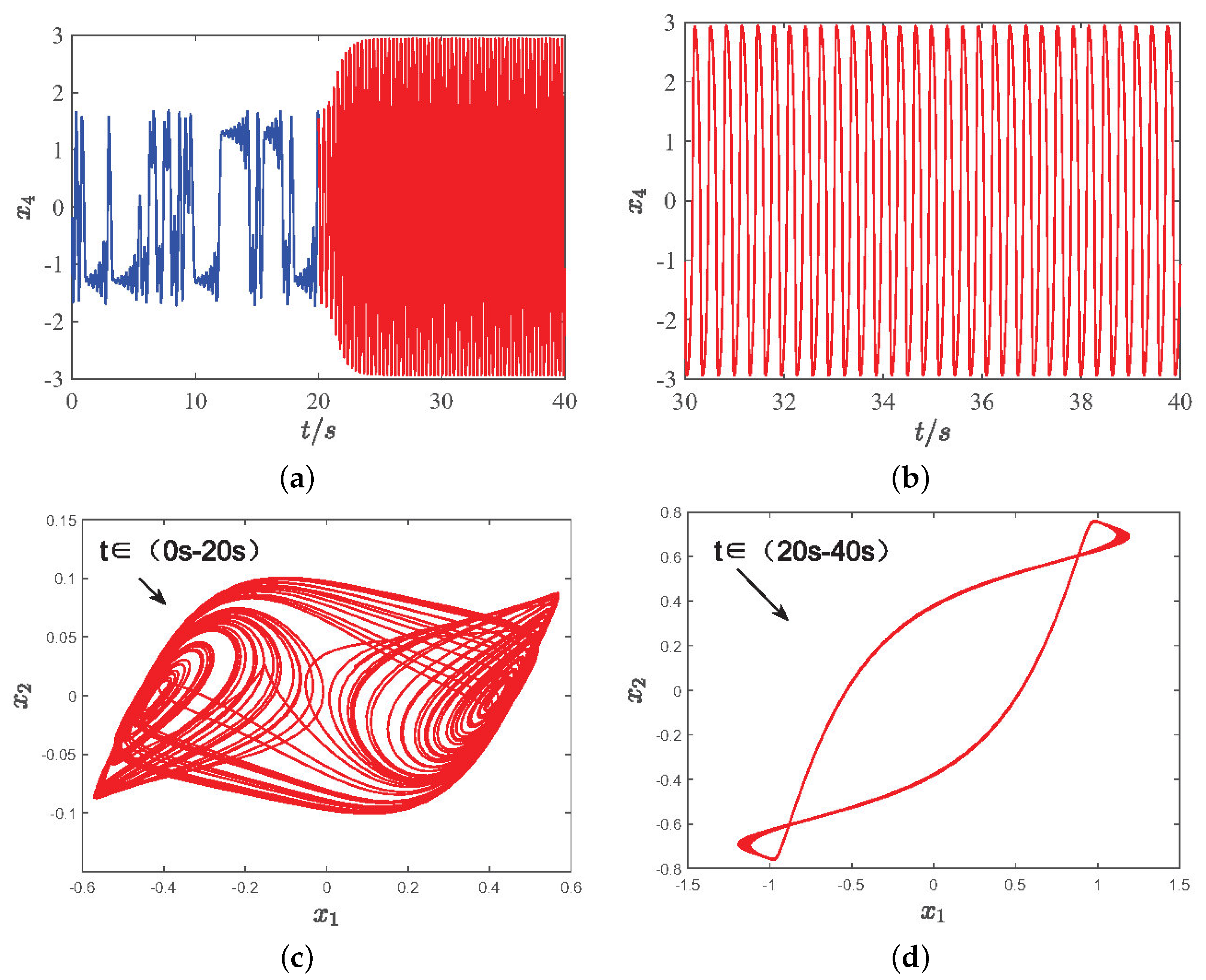
3.4. Dynamic Behavior of Chaotic Degeneration in Incommensurate Fractional-Order System
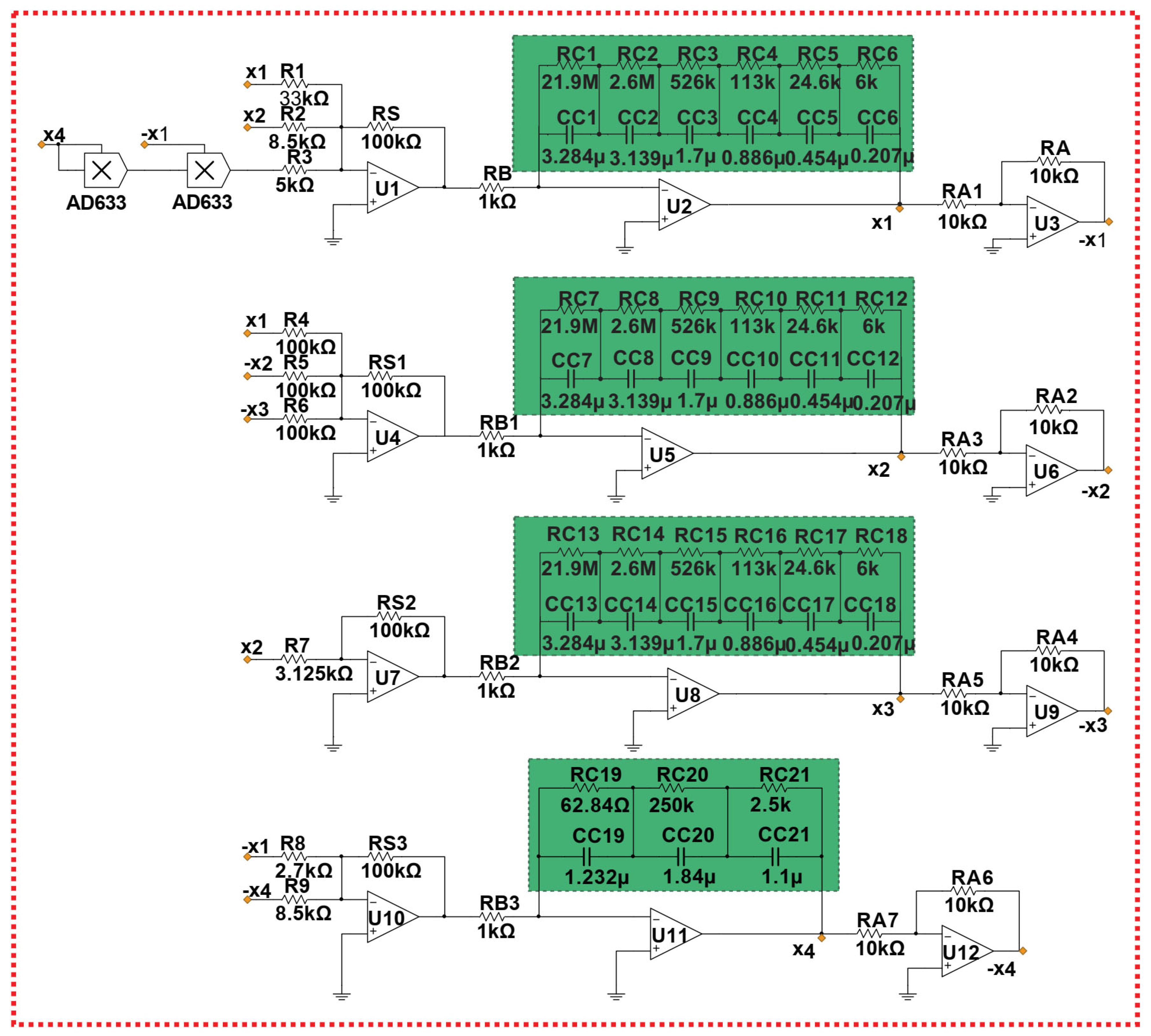
4. Analog Circuit Implementation of Incommensurate System
5. Fixed-Time Synchronization Control of Incommensurate System
5.1. Main Discussion
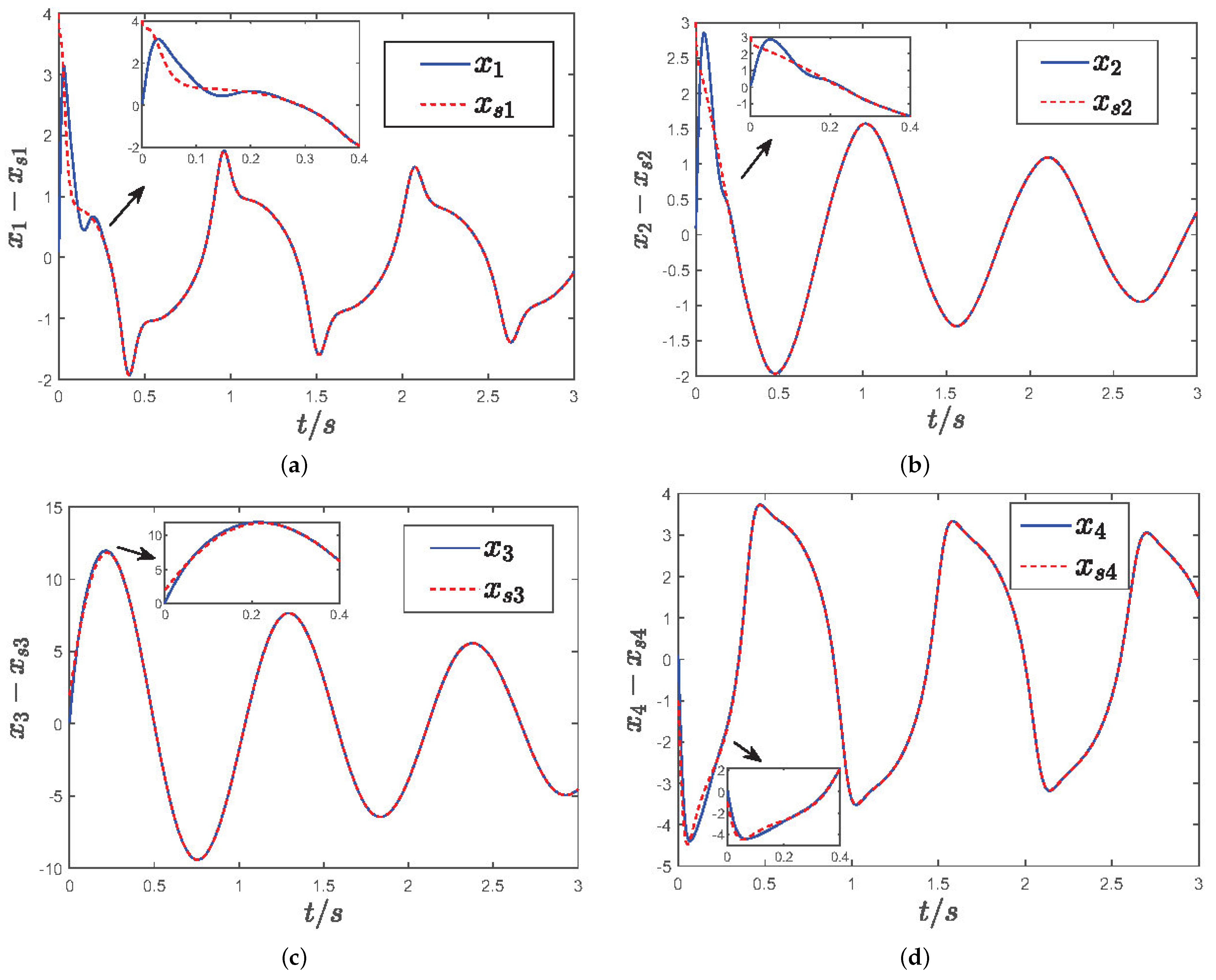
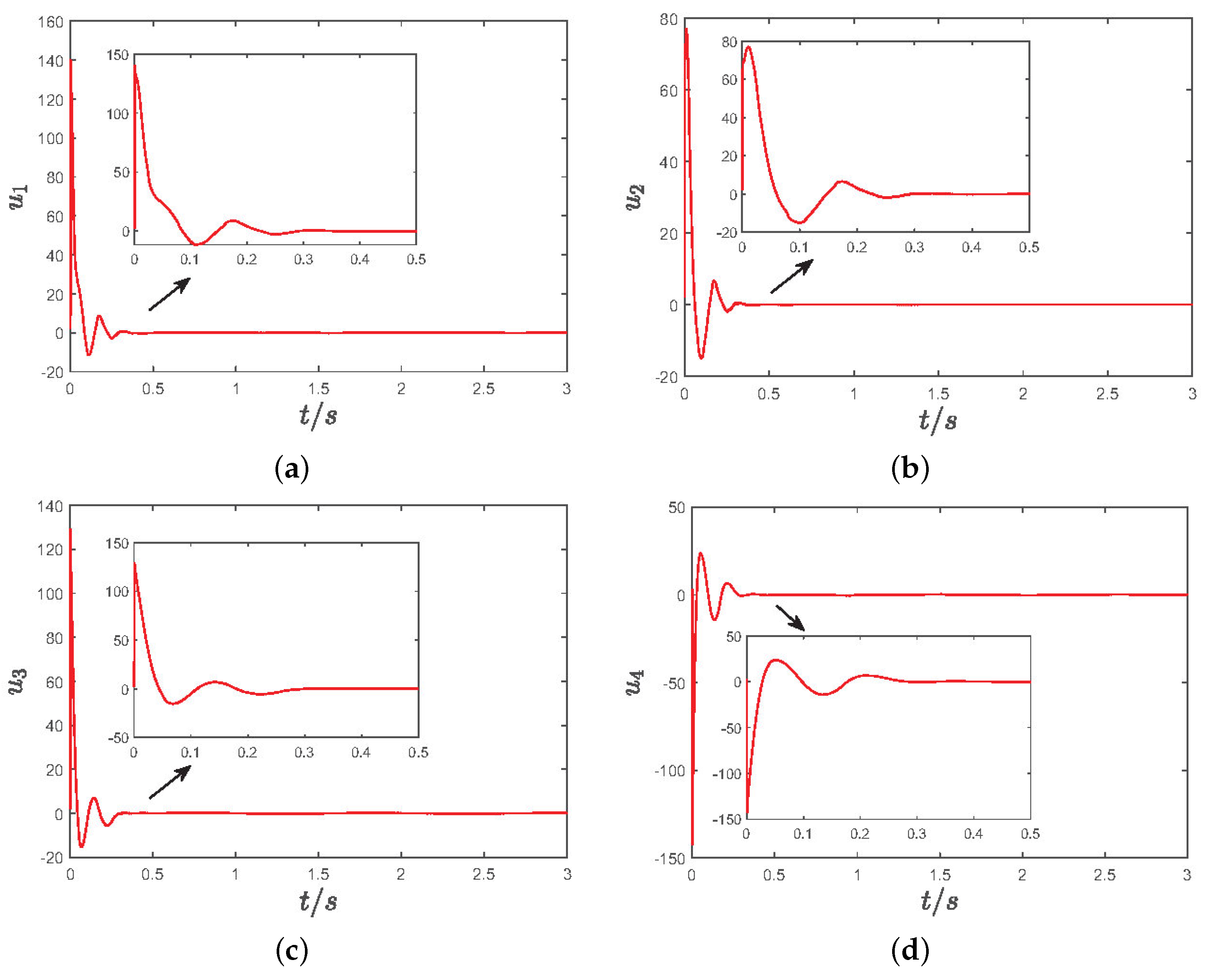
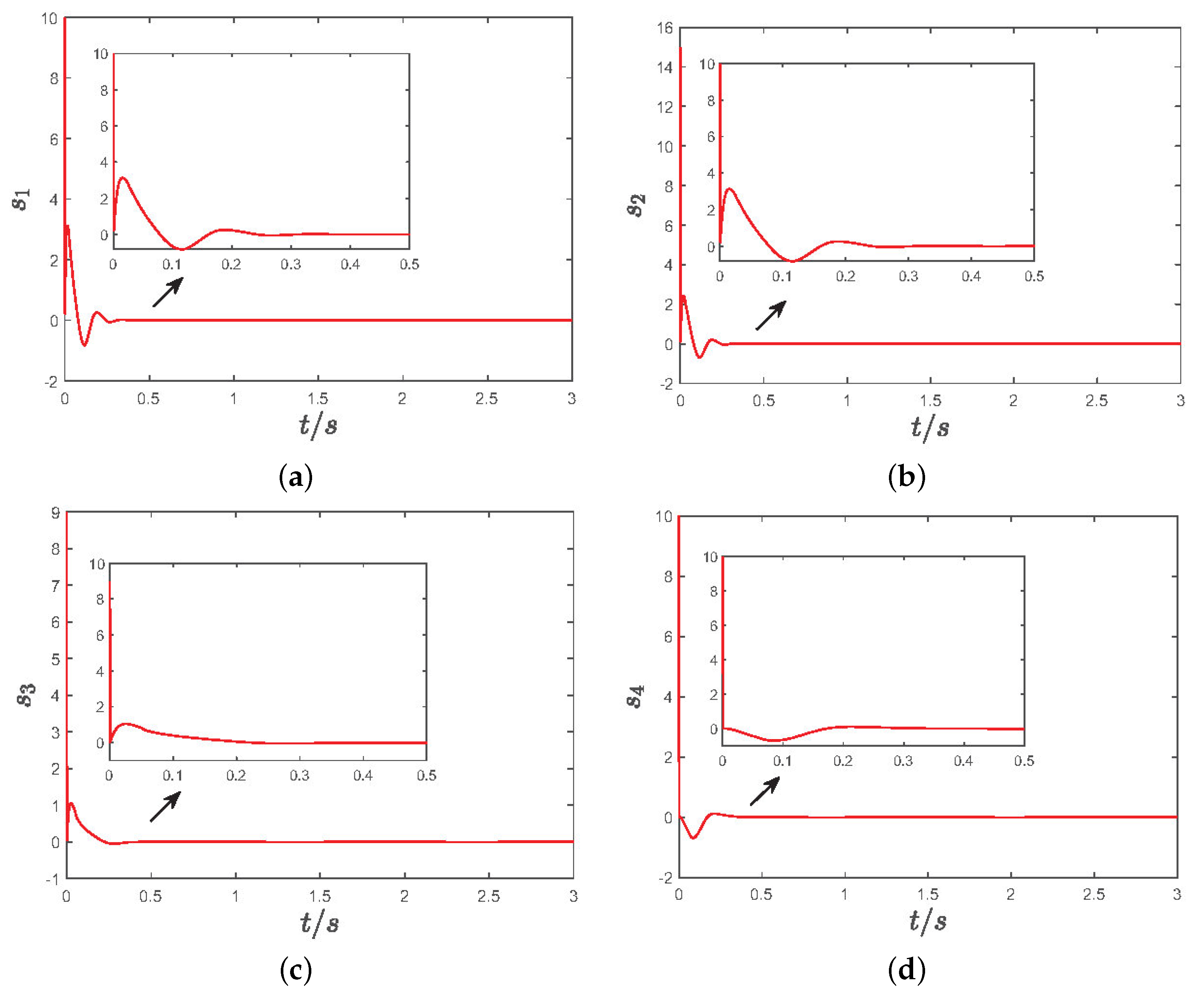
5.2. Simulation Results
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lin, H.; Wang, C.; Cui, L.; Sun, Y.; Zhang, X.; Yao, W. Hyperchaotic memristive ring neural network and application in medical image encryption. Nonlinear Dyn. 2022, 110, 841–855. [Google Scholar] [CrossRef]
- Yang, J.; Xiong, J.; Cen, J.; He, W. Finite-time generalized synchronization of non-identical fractional order chaotic systems and its application in speech secure communication. PLoS ONE 2022, 17, e0263007. [Google Scholar] [CrossRef]
- Wang, Z.; Hu, W. Chaos of a single-walled carbon nanotube resulting from periodic parameter perturbation. Int. J. Bifurc. Chaos 2021, 31, 2150130. [Google Scholar] [CrossRef]
- Wang, Z.; Hu, W. Resonance analysis of a single-walled carbon nanotube. Chaos Solitons Fractals 2021, 142, 110498. [Google Scholar] [CrossRef]
- Wang, Z.; Yang, Y.; Parastesh, F.; Cao, S.; Wang, J. Chaotic dynamics of a carbon nanotube oscillator with symmetry-breaking. Phys. Scr. 2025, 100, 015225. [Google Scholar] [CrossRef]
- Tian, H.; Wang, Z.; Zhang, H.; Cao, Z.; Zhang, P. Dynamical analysis and fixed-time synchronization of a chaotic system with hidden attractor and a line equilibrium. Eur. Phys. J. Spec. Top. 2022, 231, 2455–2466. [Google Scholar] [CrossRef]
- Tian, H.; Zhao, M.; Liu, J.; Wang, Q.; Yu, X.; Wang, Z. Dynamic Analysis and Sliding Mode Synchronization Control of Chaotic Systems with Conditional Symmetric Fractional-Order Memristors. Fractal Fract. 2024, 8, 307. [Google Scholar] [CrossRef]
- Li, G.; Xu, X.; Zhong, H. A image encryption algorithm based on coexisting multi-attractors in a spherical chaotic system. Multimed. Tools Appl. 2022, 81, 32005–32031. [Google Scholar] [CrossRef]
- Yang, N.; Xu, C.; Wu, C.; Jia, R.; Liu, C. Modeling and analysis of a fractional-order generalized memristor-based chaotic system and circuit implementation. Int. J. Bifurc. Chaos 2017, 27, 1750199. [Google Scholar] [CrossRef]
- Said, L.A.; Radwan, A.G.; Madian, A.H.; Soliman, A.M. Three fractional-order-capacitors-based oscillators with controllable phase and frequency. J. Circuits Syst. Comput. 2017, 26, 1750160. [Google Scholar] [CrossRef]
- Ghanbari, B.; Atangana, A. A new application of fractional Atangana–Baleanu derivatives: Designing ABC-fractional masks in image processing. Phys. A Stat. Mech. Its Appl. 2020, 542, 123516. [Google Scholar] [CrossRef]
- Jahanshahi, H.; Yousefpour, A.; Munoz-Pacheco, J.M.; Kacar, S.; Pham, V.T.; Alsaadi, F.E. A new fractional-order hyperchaotic memristor oscillator: Dynamic analysis, robust adaptive synchronization, and its application to voice encryption. Appl. Math. Comput. 2020, 383, 125310. [Google Scholar] [CrossRef]
- Qureshi, S.; Yusuf, A.; Shaikh, A.A.; Inc, M.; Baleanu, D. Fractional modeling of blood ethanol concentration system with real data application. Chaos Interdiscip. J. Nonlinear Sci. 2019, 29, 013143. [Google Scholar] [CrossRef] [PubMed]
- Yusuf, A.; Qureshi, S.; Inc, M.; Aliyu, A.I.; Baleanu, D.; Shaikh, A.A. Two-strain epidemic model involving fractional derivative with Mittag-Leffler kernel. Chaos Interdiscip. J. Nonlinear Sci. 2018, 28, 123121. [Google Scholar] [CrossRef] [PubMed]
- Xu, Y.; Sun, K.; He, S.; Zhang, L. Dynamics of a fractional-order simplified unified system based on the Adomian decomposition method. Eur. Phys. J. Plus 2016, 131, 186. [Google Scholar] [CrossRef]
- Gul, T.; Alghamdi, W.; Khan, I.; Ali, I. New similarity variable to transform the fluid flow from PDEs into fractional-order ODEs: Numerical study. Phys. Scr. 2021, 96, 084009. [Google Scholar] [CrossRef]
- Danca, M.F. Hopfield neuronal network of fractional order: A note on its numerical integration. Chaos Solitons Fractals 2021, 151, 111219. [Google Scholar] [CrossRef]
- Ramani, P.; Khan, A.M.; Suthar, D.L.; Kumar, D. Approximate analytical solution for non-linear Fitzhugh–Nagumo equation of time fractional order through fractional reduced differential transform method. Int. J. Appl. Comput. Math. 2022, 8, 61. [Google Scholar] [CrossRef]
- Atangana, A.; Araz, S. New numerical approximation for Chua attractor with fractional and fractal-fractional operators. Alex. Eng. J. 2020, 59, 3275–3296. [Google Scholar] [CrossRef]
- Atangana, A.; Araz, S.İ. Fractional stochastic modelling illustration with modified Chua attractor. Eur. Phys. J. Plus 2019, 134, 160. [Google Scholar] [CrossRef]
- Wang, Z.; Sun, W.; Wei, Z.; Zhang, S. Dynamics and delayed feedback control for a 3D jerk system with hidden attractor. Nonlinear Dyn. 2015, 82, 577–588. [Google Scholar] [CrossRef]
- Wang, Z.; Wei, Z.; Xi, X.; Li, Y. Dynamics of a 3D autonomous quadratic system with an invariant algebraic surface. Nonlinear Dyn. 2014, 77, 1503–1518. [Google Scholar] [CrossRef]
- Chen, C.; Min, F. ReLU-type memristor-based Hopfield neural network. Eur. Phys. J. Spec. Top. 2022, 231, 2979–2992. [Google Scholar] [CrossRef]
- Chang, H.; Li, Y.; Chen, G.; Yuan, F. Extreme multistability and complex dynamics of a memristor-based chaotic system. Int. J. Bifurc. Chaos 2020, 30, 2030019. [Google Scholar] [CrossRef]
- Al-Nassir, S. Dynamic analysis of a harvested fractional-order biological system with its discretization. Chaos Solitons Fractals 2021, 152, 111308. [Google Scholar] [CrossRef]
- Ma, C.; Mou, J.; Yang, F.; Yan, H. A fractional-order hopfield neural network chaotic system and its circuit realization. Eur. Phys. J. Plus 2020, 135, 100. [Google Scholar] [CrossRef]
- Tavazoei, M.S.; Haeri, M. Synchronization of chaotic fractional-order systems via active sliding mode controller. Phys. A Stat. Mech. Its Appl. 2008, 387, 57–70. [Google Scholar] [CrossRef]
- Almatroud, A.O. On the anti-synchronization of fractional-order chaotic and hyperchaotic systems via modified adaptive sliding-mode control. Turk. J. Comput. Math. Educ. (TURCOMAT) 2021, 12, 1112–1123. [Google Scholar]
- Chen, L.; Fang, J.A. Adaptive continuous sliding mode control for fractional-order systems with uncertainties and unknown control gains. Int. J. Control Autom. Syst. 2022, 20, 1509–1520. [Google Scholar] [CrossRef]
- Zambrano-Serrano, E.; Bekiros, S.; Platas-Garza, M.A.; Posadas-Castillo, C.; Agarwal, P.; Jahanshahi, H.; Aly, A.A. On chaos and projective synchronization of a fractional difference map with no equilibria using a fuzzy-based state feedback control. Phys. A Stat. Mech. Its Appl. 2021, 578, 126100. [Google Scholar] [CrossRef]
- Wang, L.; Dong, J. Reset event-triggered adaptive fuzzy consensus for nonlinear fractional-order multiagent systems with actuator faults. IEEE Trans. Cybern. 2022, 53, 1868–1879. [Google Scholar] [CrossRef] [PubMed]
- Alattas, K.A.; Mostafaee, J.; Sambas, A.; Alanazi, A.K.; Mobayen, S.; Vu, M.T.; Zhilenkov, A. Nonsingular integral-type dynamic finite-time synchronization for hyper-chaotic systems. Mathematics 2021, 10, 115. [Google Scholar] [CrossRef]
- Aghababa, M.P. Design of a chatter-free terminal sliding mode controller for nonlinear fractional-order dynamical systems. Int. J. Control 2013, 86, 1744–1756. [Google Scholar] [CrossRef]
- Wang, Y.L.; Jahanshahi, H.; Bekiros, S.; Bezzina, F.; Chu, Y.M.; Aly, A.A. Deep recurrent neural networks with finite-time terminal sliding mode control for a chaotic fractional-order financial system with market confidence. Chaos Solitons Fractals 2021, 146, 110881. [Google Scholar] [CrossRef]
- Ni, J.; Liu, L.; Liu, C.; Hu, X. Fractional order fixed-time nonsingular terminal sliding mode synchronization and control of fractional order chaotic systems. Nonlinear Dyn. 2017, 89, 2065–2083. [Google Scholar] [CrossRef]
- Wang, C.; Liu, C.L.; Chen, Y.Y.; Zhang, Y. Fixed-time consensus tracking for second-order leader-follower multi-agent systems with nonlinear dynamics under directed topology. Int. J. Control Autom. Syst. 2021, 19, 2697–2705. [Google Scholar] [CrossRef]
- Wang, Z.; Parastesh, F.; Natiq, H.; Li, J.; Xi, X.; Mehrabbeik, M. Synchronization patterns in a network of diffusively delay-coupled memristive Chialvo neuron map. Phys. Lett. A 2024, 514, 129607. [Google Scholar] [CrossRef]
- Wang, Z.; Chen, M.; Xi, X.; Tian, H.; Yang, R. Multi-chimera states in a higher order network of FitzHugh–Nagumo oscillators. Eur. Phys. J. Spec. Top. 2024, 233, 779–786. [Google Scholar] [CrossRef]
- Delgado, B.B.; Macías-Díaz, J.E. On the general solutions of some non-homogeneous Div-Curl systems with Riemann–Liouville and Caputo fractional derivatives. Fractal Fract. 2021, 5, 117. [Google Scholar] [CrossRef]
- Yusuf, A.; Acay, B.; Inc, M. Analysis of fractional-order nonlinear dynamic systems under Caputo differential operator. Math. Methods Appl. Sci. 2021, 44, 10861–10880. [Google Scholar] [CrossRef]
- Liu, J.; Wang, Z.; Chen, M.; Zhang, P.; Yang, R.; Yang, B. Chaotic system dynamics analysis and synchronization circuit realization of fractional-order memristor. Eur. Phys. J. Spec. Top. 2022, 231, 3095–3107. [Google Scholar] [CrossRef]
- Cafagna, D.; Grassi, G. Hyperchaos in the fractional-order Rössler system with lowest-order. Int. J. Bifurc. Chaos 2009, 19, 339–347. [Google Scholar] [CrossRef]
- Dutta, M.; Roy, B.K. A new memductance-based fractional-order chaotic system and its fixed-time synchronisation. Chaos Solitons Fractals 2021, 145, 110782. [Google Scholar] [CrossRef]
- Hardy, G.H.; Littlewood, J.E.; Pólya, G. Inequalities; Cambridge University Press: Cambridge, UK, 1952. [Google Scholar]
- He, X.; Li, X.; Song, S. Prescribed-time stabilization of nonlinear systems via impulsive regulation. IEEE Trans. Syst. Man, Cybern. Syst. 2022, 53, 981–985. [Google Scholar] [CrossRef]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Wang, Z.; Dang, S. Dynamic Behavior and Fixed-Time Synchronization Control of Incommensurate Fractional-Order Chaotic System. Fractal Fract. 2025, 9, 18. https://doi.org/10.3390/fractalfract9010018
Wang X, Wang Z, Dang S. Dynamic Behavior and Fixed-Time Synchronization Control of Incommensurate Fractional-Order Chaotic System. Fractal and Fractional. 2025; 9(1):18. https://doi.org/10.3390/fractalfract9010018
Chicago/Turabian StyleWang, Xianchen, Zhen Wang, and Shihong Dang. 2025. "Dynamic Behavior and Fixed-Time Synchronization Control of Incommensurate Fractional-Order Chaotic System" Fractal and Fractional 9, no. 1: 18. https://doi.org/10.3390/fractalfract9010018
APA StyleWang, X., Wang, Z., & Dang, S. (2025). Dynamic Behavior and Fixed-Time Synchronization Control of Incommensurate Fractional-Order Chaotic System. Fractal and Fractional, 9(1), 18. https://doi.org/10.3390/fractalfract9010018








