Abstract
In this paper, a novel fractal model for the contact resistance based on axisymmetric sinusoidal asperity is proposed, which focuses on the resistance characteristics of the rough interface at a microscopic scale. By introducing the unique geometric shape of axisymmetric sinusoidal asperity, and combining it with a three-dimensional fractal theory, the micro-morphology characteristics of the rough interface can be characterized more precisely. Subsequently, by conducting a theoretical analysis and numerically solving the deformation mechanisms of asperities on the rough interface, a refined model for contact resistance is constructed. This research comprehensively employs theoretical analysis, numerical simulation, and experimental testing methods to deeply explore the current transmission mechanisms during the contact process of the rough interface. The findings suggest that the proposed model is capable of precisely capturing the intricate interplay of various factors, including contact area, contact load, and material properties, with the contact resistance. Compared to the existing models, the presented model demonstrates significant advantages in terms of prediction accuracy and practicality. This research provides an important theoretical basis and design guidance for optimizing the electrical performance of the rough interface, which has great significance for engineering applications.
1. Introduction
As a key parameter of electrical connection, contact resistance has a significant impact on the conductivity, signal transmission quality, and overall performance of equipment. In components such as switches, relays, and connectors, contact resistance is crucial for the normal operation and lifespan of the equipment [1]. In the automotive industry, contact resistance is essential for the stability and reliability of the vehicle’s electrical system [2]. Meanwhile, in fields such as measurement and control, and materials science research, contact resistance also plays an important role [3]. To summarize, contact resistance holds a crucial position across numerous fields, and the ongoing exploration and refinement of contact resistance technology is immensely important for driving progress in industries like electronics, automotive, and measurement and control.
Research on contact resistance has consistently been a focal point for scholars in the field [4,5]. In 1981, Holm [6] pioneeringly derived the Laplace potential equation, based on an ideal cylindrical conductor within a circular contraction region, thereby obtaining an analytical expression for contact resistance. Building upon this, taking into account the actual surface roughness characteristics, Greenwood [7] proposed a statistical equation for calculating contact resistance in 1966. Persson [8] explored the relationship between contact resistance and mechanical contact stiffness, and demonstrated how these two distinctly different methods are interrelated. Subsequent research [9,10] has shown that contact models established based on statistics do not possess objective uniqueness. The surface roughness parameters obtained through statistical methods can vary with changes in instrument resolution [11]. In comparison, the fractal dimension in fractal theory describes geometric contours based on geometric self-similarity, which is not influenced by measurement instruments. Consequently, utilizing fractal theory to represent the rough surface successfully addresses the problem of non-uniqueness encountered in statistical models.
In the 1970s, Mandelbrot and Bhushan [12] proposed the two-dimensional fractal model (M–B model), providing a novel theoretical framework for describing these random and irregular geometric phenomena. Kogut and Komvopoulos [13] determined the functional correlation between contact resistance and contact load for isotropic fractal surfaces, showing that both an elevated fractal dimension and a diminished fractal roughness contribute to a decrease in contact resistance. Following this, a computational model for contact resistance, which incorporates an insulating film, was formulated [9], affirming that contact resistance is exclusively influenced by current density and film thickness. Hu [14] utilized the Weierstrass–Mandelbrot fractal function (W–M function) to establish copper–indium contact surface morphologies with different surface characteristics, and analyzed the impact of pressure on contact thermal resistance using the finite element method. Li [15] constructed an electrical contact model for the rough surface, which considers the interactions between asperities, using the rough surface generated by the two-dimensional W–M function.
The aforementioned model employs two-dimensional fractal theory to simulate actual three-dimensional morphology, which inherently has limitations [16]. To address this, Ausloos [17] extended the W–M function to the A–B function by introducing multiple variables, enabling a description of three-dimensional fractal morphology. Yan [18] further derived the A–B function and obtained the function for a three-dimensional fractal surface in the spatial Cartesian coordinate system, also known as the Y–K function. The fractal representation serves as a widely utilized method for describing rough surfaces, and numerous discoveries have been made in the examination of the contact characteristics for uneven joint surfaces [19,20]. Zhao [21] proposed a three-dimensional fractal model grounded in thermal contact conductance and devised an experimental apparatus featuring a ring-shaped interface to verify the proposed model of thermal contact conductance. Zhang [22] employed the Y–K function to generate the rough surface and developed a contact resistance model that incorporated both basic thermal resistance and contraction thermal resistance. Li [23] established a multi-physical finite element model considering multi-scale and three-dimensional fractal surfaces for the contact resistance and temperature rise, and analyzed the multi-physical coupling process of electrical-thermal-stress at conductive points. Jiang [24] applied fractal theory to establish a contact model for the electrical contact resistance between a rigid plane and a cylindrical surface, predicting the dynamic characteristics of contact between a graphite cylinder and a copper electrode in the welding core of the heating cables. Li [25] developed a fractal model to forecast the thermal contact resistance at the liquid–solid interface, taking into account the self-affine fractal geometry of the rough surface. Utilizing the fractal traits of the rough structure, both morphological and mechanical analyses were conducted to ascertain the location of the liquid–solid interface and the corresponding thermal contact resistance. Taking into account the coefficient of friction, Sun [26] proposed a fractal model for the TCC of two spherical joint surfaces based on a three-dimensional fractal theory. Xiao [27] formulated a model utilizing fractal theory to predict the permeability and effective thermal conductivity of bidirectional (2-D) fiber porous materials, providing an improved characterization of the pore size randomness and distribution typically observed in commercially available fibrous materials. Sun [28] proposed a fractal model for the thermal contact conductance considering substrate deformation. The model considers the three contact deformation modes of the asperities, including elastic deformation, elasto-plastic deformation, and fully plastic deformation, and studies the effects of the contact load, fractal dimension, and fractal roughness on thermal contact conductance. Based on a three-dimensional fractal theory, Sun [29] established a thermal contact conductance model for the inclined rough surface and used numerical simulations to study the effects of the contact load, inclination angle, fractal dimension, and fractal roughness on thermal contact conductance. Shen [30] utilized the Y–K function to generate fractal surfaces and subsequently developed a novel fractal contact model for evaluating contact resistance. Zhang [31] introduced a mechanical model that addresses the interface between a lithium metal anode and a polymer-coated solid-state electrolyte, incorporating factors such as lithium creep, the viscoelastic nature of the polymer, and electrochemistry driven by pressure.
From the aforementioned research, it is clear that there has been substantial investigation into contact resistance models that are grounded in three-dimensional fractal theory. The focus of these studies has been on several issues within the contact deformation mechanism, material properties, and application scenarios. Nevertheless, a prevalent limitation across these accomplishments is the oversight of the impact of asperity geometric shape on contact resistance. Specifically, the asperities employed in the rough interface are commonly assumed to be hemispherical. The assumption of the hemispherical asperity with a single radius of curvature will introduce errors into the contact deformation of asperity, which subsequently introduces errors into the analytical calculation of contact resistance. With the deepening research on the contact resistance of the rough interface, related studies [32,33,34] have found that the geometric shape of asperity has a significant impact on contact resistance. Xu [35] categorized asperities into different levels by constructing cosine wave scales of the surface micro-morphologies and established a contact model for the rough interface based on multi-level asperities. Zhang [36] introduced ellipsoidal asperity by analyzing the actual surface morphology of the contact points, more realistically achieving numerical reconstruction and representation of the contact surface, and proposed a numerical modeling method for contact resistance, exploring theoretical methods to reduce the contact resistance. Sun [37] proposed a fractal model for thermal contact conductance based on conical asperity, investigating the effects of the contact load, fractal dimension, fractal roughness, and material properties on thermal contact conductance. Sun [4] proposed a fractal model for thermal contact conductance based on elliptical asperity and studied the effects of the contact load, fractal dimension, fractal roughness, and eccentricity on the thermal contact conductance through numerical simulations.
It is worth noting that the aforementioned scholars have recognized the significant impact of asperity on contact resistance and attempted to simulate the rough surface using an asperity with different geometric shapes. However, none of these models have delved into the geometric shapes of asperity in conjunction with the measured rough surface. In previous studies [38,39,40], by gathering and analyzing micro-morphology data, we have verified that the geometric shape of asperities on rough surfaces more closely resembles an axisymmetric sinusoidal form. Consequently, we will introduce a new fractal model for contact resistance, grounded in both axisymmetric sinusoidal asperity and three-dimensional fractal theory. The presented model is anticipated to enhance the accuracy of contact resistance calculations, possessing significant theoretical and practical value in improving electrical contact performance, optimizing the design of electronic devices, and ensuring the stable operation of power systems.
2. Current Transmission Mechanism of the Rough Interface
This section provides a detailed elaboration of the current transmission mechanism of the rough interface at the microscopic scale. Holm [6] pioneeringly derived the analytical expression for contraction resistance Rc obtained from the Laplace potential equation within the circular contraction region of an ideal cylindrical conductor, as shown in Equation (1).
where Rc denotes the contact resistance; ρ1 and ρ2 represent the resistivity of the materials (assuming ρ1 = ρ2 = ρ for simplicity); and rΩ signifies the radius of the conductive area, which corresponds to the actual contact area radius of the asperity.
The formation mechanism of contraction resistance is shown in Figure 1. Combining the analysis with Figure 1a, due to the roughness characteristics and geometric diversity of the surface micro-morphology, the current will not be distributed uniformly across the entire contact surface. Instead, it flows concentratedly through those extremely small conductive spots (also known as the asperity). The contact resistance at these conductive spots is much smaller than that of the non-contact areas, resulting in a contraction phenomenon of the current at the contact asperities.
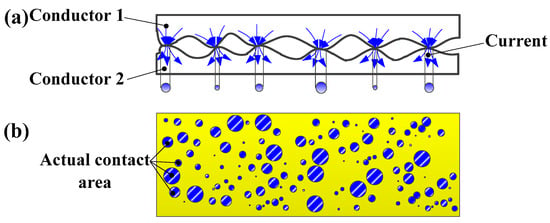
Figure 1.
The formation mechanism of contraction resistance: (a) the contact between two conductors; (b) the actual contact area.
Taking into account the roughness characteristics of the actual surfaces, Greenwood [7] proposed a calculation equation for the contact resistance of multiple spots within a single cluster, without considering the size and distribution of these spots. According to Figure 1b, due to the fact that the two contacting surfaces are not completely smooth, the essence of the contact is the interaction between asperities on the rough interface. The actual contact area is indicated by the blue area in Figure 1b. The current is transmitted through the contact of these asperities, indicating that the actual contact area of asperities on the rough interface has a significant impact on contact resistance.
Combining Holm’s theory, the actual contact area of asperities on the rough interface is one of the important factors affecting contact resistance. Furthermore, with the in-depth research of our research group [38,39,40], it has been found that the geometric shape of the single asperity has a significant impact on the actual contact area of the rough interface, and using axisymmetric sinusoidal to characterize the geometric shape of an asperity is closer to the actual working conditions. Figure 2 illustrates the contact diagram of the single asperity on the rough interface. In conjunction with Figure 2, the influence mechanism of asperity geometry on contact resistance is further elaborated.
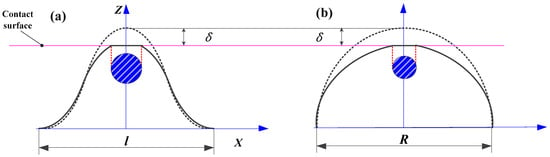
Figure 2.
The contact diagram of the single asperity on the rough interface: (a) the axisymmetric sinusoidal asperity; (b) the hemispherical asperity.
Based on the analysis of Figure 2, which shows the contact deformation diagram under the contact load for the axisymmetric sinusoidal asperity and the hemispherical asperity, respectively. It is evident that the actual contact area generated by the deformation of asperities differs under the same indentation depth. Considering the formation mechanism of contact resistance, the difference in the actual contact area will directly lead to the difference in contact resistance. The precise determination of the contact resistance of a rough interface hinges on the accurate representation of asperity geometry. An incorrect geometric shape can lead to inaccuracies in the calculation of contact resistance. Furthermore, as depicted in Figure 1b, the actual contact process is not a two-dimensional interaction but a three-dimensional one. Pertinent research suggests [18] that there are constraints in utilizing two-dimensional fractal theory to emulate real three-dimensional morphologies, and it is not logical to compute contact resistance parameters for three-dimensional surfaces using two-dimensional fractal theory. Furthermore, considering the contact deformation mechanism of the asperities, the actual contact area of asperities also changes with the different contact loads.
In summary, the current transmission mechanism during contact is a complex process, which is influenced by various factors such as micro-morphology, the contact load, and the material parameters. Therefore, in this paper, we construct a contact resistance model for the rough interface, grounded in the axisymmetric sinusoidal asperity tailored to actual operating conditions and integrated with three-dimensional fractal theory.
3. Modeling Method for the Contact Resistance
Combining the analysis of the current transmission mechanism of the rough interface in Section 2, it can be found that the geometric shape of the single asperity has a significant impact on contact resistance. Furthermore, with the in-depth research of our research group [38,39,40], it is found that using axisymmetric sinusoidal to characterize the geometric shape of an asperity is closer to the actual working conditions. Therefore, based on the axisymmetric sinusoidal asperity, the contact resistance of the single asperity under contact load will be solved in this section. Following this, by integrating a three-dimensional fractal theory, we will proceed to construct the contact resistance model for the rough interface.
3.1. Parametric Characterization of the Rough Surface
To obtain the analytical model for the contact resistance, it is necessary to perform parameterized characterization of the rough surface. The characterization process necessitates an investigation into both the geometric shape of the single asperity and the distribution of these asperities across the rough surface.
At the outset, the geometric configuration of the single asperity is redefined. An axisymmetric sinusoidal shape is employed to depict the geometry of the single asperity, and its contour diagram is presented in Figure 3.
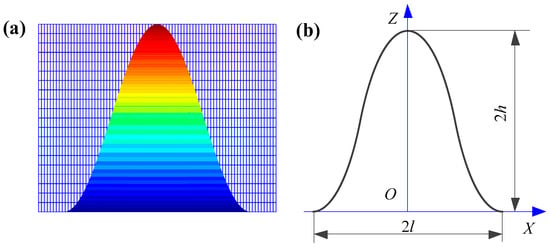
Figure 3.
The contour schematic of the single asperity: (a) the sectional drawing; (b) the two-dimensional profile.
Figure 3 illustrates that the contour of the single asperity adheres to an axisymmetric sinusoidal shape. Therefore, the geometric shape of the asperity can be defined in a functional form, and the functional expression of the asperity contour can be obtained [41].
where h represents the height, and l represents the width.
There exists a proportional relationship between the asperity’s height and width. To streamline the ensuing equation calculations, we introduce the parameter k here.
Following the definition of the geometric shape of the single asperity, the distribution of asperities is characterized using parameters. Due to the limitation of the two-dimensional fractal theory, a three-dimensional fractal theory is adopted to characterize the rough surface. The three-dimensional fractal surface can be generated by the Y–K function proposed by Yan [18], and the expression of the Y–K function is shown in Equation (3).
where x, y, z are the coordinates of the three-dimensional rough surface in the space cartesian coordinate system; L is the sampling length; D is the fractal dimension (2 < D < 3); G is the scale coefficient; M is the number of overlapping ridges on the constructed three-dimensional surface (1 < M < 100); γ represents the frequency density parameter (commonly, γ is taken as 1.5); n represents the frequency index (n = int[ln(1/La)/lnγ], where La is the value within the sampling length range); and nmax = int[log(L/Ls)/log γ]; φm,n represents the random phase.
3.2. The Contact Resistance of the Single Asperity
Based on Equation (1), it is known that, given the resistivity of the material, contact resistance depends on the actual contact area of the rough interface under the contact load. The actual contact area is essentially the aggregate of the contact areas of the asperities present within the interface. Consequently, after parameterizing the rough surface, this section will address the determination of the actual contact area of a single asperity under a given contact load. Furthermore, by combining Equation (1), the contact resistance of the single asperity can be obtained.
As a result of the redefined geometric shape of the single asperity, this section will undertake a revised exploration of the contact deformation mechanisms of the single asperity throughout the three deformation stages: elastic, elasto-plastic, and fully plastic. Figure 4 shows the contact diagram of the single asperity.
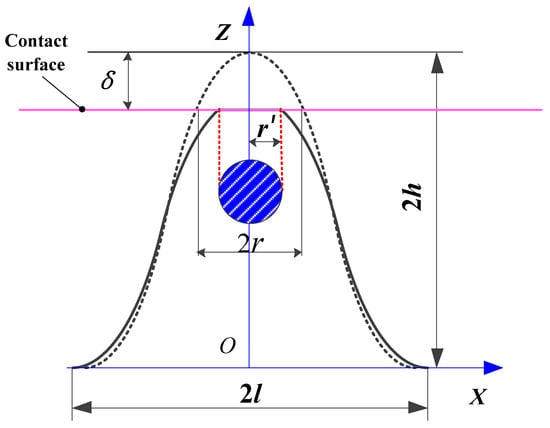
Figure 4.
The contact diagram of the single asperity.
When proposing the Y–K function, Yan [18] derived the functional expression of the indentation depth δ and the fractal parameters D and G.
where r represents the cross-sectional radius at the indentation depth δ, and r’ represents the actual radius of the contact surface at the indentation depth δ.
When the indentation depth is δ, through geometric calculations based on Figure 4, the relationship between the indentation depth δ and the geometric shape parameters h and l of the asperity can be obtained.
After combining Equations (5) and (6), the relationship between the geometric shape parameter and the cross-sectional radius r can be obtained.
Then, perform the first-order Taylor expansion on the cos(πr/l), which is represented as follows:
By combining Equations (3) and (8), and further by combining Equations (3) and (8) and deriving Equation (7), the following relationship can be obtained:
Meanwhile, as can be seen from Figure 4, a relationship exists between the cross-sectional area a at the indentation depth δ and the cross-sectional radius r.
Therefore, by substituting Equation (10) into Equation (9), the relationship between the geometric shape parameters h and the cross-sectional area a can be obtained.
As the contact load intensifies, the asperity will progress through three deformation stages: elastic deformation, elasto-plastic deformation, and ultimately, full plastic deformation. The following is the analysis of these three deformation processes, respectively.
3.2.1. Elastic Deformation Process
Utilizing Hertz contact theory [42] as a foundation, an analysis of the asperity’s contact deformation during the elastic deformation stage can be performed to derive the relationship between the indentation depth δ and the average contact pressure pea, as shown in Equation (12).
where, Pea represents the average pressure during the elastic deformation process; E is the equivalent elastic modulus, E = ((1 − ν12)/E1 + (1 − ν22)/E2)−1, where E1, E2, ν1, and ν2 are the elastic moduli and Poisson’s ratios of the materials on both sides of the rough interface; and R is the radius of the curvature at the contact point of the asperity, which can be obtained from Equation (2).
By merging Equations (12) and (13), the average contact pressure Pea during the elastic deformation stage can be determined.
Based on the Hertz contact theory, due to the deformation of the asperity, the actual contact area ae during the elastic deformation process is half of the cross-sectional area a at the indentation depth of the undeformed asperity.
Combining Equations (12)–(15), the contact load Fne of the single asperity during the elastic deformation process can be obtained.
As stated in reference [43], plastic deformation in the asperity initiates when Pea = 1.1kμσy, where σy is the yield strength of the softer material on both sides of the rough interface. Therefore, using Equation (12) as a basis, the critical indentation depth δec when the asperity enters the elasto-plastic deformation process can be determined.
where kμ represents the correction factor for friction. For 0 ≤ μ ≤ 0.3, kμ = 1 − 0.228μ; whereas for 0 < μ < 0.3, kμ = 0.932e−1.58(μ−0.3). In this context, μ denotes the friction coefficient between the rough interfaces. For the convenience of the calculation, the material coefficient φ is defined as φ = σy/E.
Combining Equations (15) and (17), the cross-sectional area aec at the critical indentation depth when the asperity enters the elasto-plastic deformation process can be obtained.
Drawing upon Holm’s contact resistance theory, an expression for the contact resistance of a single asperity can be formulated.
3.2.2. Full Plastic Deformation Process
As the contact load increases, the asperity undergoes a transition from the elastic deformation process to the elasto-plastic deformation process. Currently, there is a lack of analytical analysis based on the contact mechanics theory for the elasto-plastic deformation process. The analysis of the elasto-plastic deformation process mainly relies on combining the contact deformation of the elastic deformation process with that of the plastic deformation process to perform a transitional treatment. Therefore, this section will analyze the stress and deformation process of the asperity during the fully plastic deformation process.
According to the plastic mechanics theory [44], the actual contact area ap of the asperity during the fully plastic deformation process is equal to the cross-sectional area at the indentation depth of the undeformed asperity.
By consulting the reference [16], the relationship between the average contact pressure Ppa during the plastic deformation process and the yield strength σy can be obtained.
where H represents the material hardness.
Based on Equations (20) and (21), the contact load Fnp during the full plastic deformation process can be obtained.
In the contact mechanics theory [42], the relationship between the cross-sectional radius rpc and the average contact pressure Ppa when the asperity enters the full plastic deformation process is given.
Combining Figure 4 with Equation (2), the parameters in Equation (23) are derived.
Then, after combining that with Equation (24), the critical contact cross-sectional radius rpc when the asperity enters the full plastic deformation process can be obtained.
Subsequently, based on Equations (10) and (25), the cross-sectional area apc at the critical indentation depth when the asperity enters the full plastic deformation process can be obtained.
Similarly, the first-order Taylor expansion on the is performed, which is represented as follows:
Substituting Equation (27) into Equation (26), the apc can be rewritten in the following form:
By combining Equations (1) and (20), the contact resistance Rcp of the single asperity within the fully plastic deformation process can be derived.
3.2.3. Elasto-Plastic Deformation Process
Combining the analysis from Section 3.2.1 and Section 3.2.2, the analytical expressions for the contact resistance of the asperity during the elastic and full plastic deformation processes are obtained. The transitional process between these two processes, where the asperity undergoes both elastic and plastic deformation, is referred to as the elasto-plastic deformation process. When the asperity is in this deformation process, the deformation becomes more complex. In this model, the limit average pressure method [45] will be adopted to transition the elasto-plastic deformation process.
During this transitional deformation process, solving for the normal elasto-plastic average pressure becomes extremely complex. The material hardness H varies with the indentation depth, making H not a constant value in this context. Assuming the limiting average pressure function for the elasto-plastic deformation process is HG(a), an empirical equation for fitting this function using the power function is given as follows:
where c1 and c are undetermined coefficients.
From this, the expressions for the average contact pressure Pepa and the contact load Fnep of the asperity during the elasto-plastic deformation process can be obtained.
where aep represents the actual contact area during the elasto-plastic deformation process.
By substituting Equation (30), Equations (31) and (32) can be transformed into the following forms:
where c2 and c3 are undetermined coefficients.
According to the form shown in Equation (30), the average contact pressure Pea and the contact load Fne of the asperity during the elastic deformation process can be rewritten. Equations (14) and (16) can be transformed into the following unified form:
where the coefficient K = 0.4kμ. Similarly, according to the form shown in Equation (30), the average contact pressure Ppa and the contact load Fpe of the asperity during the elastic deformation process can be rewritten. Equations (21) and (22) can be transformed into the following unified form:
At the two endpoints of the elasto-plastic deformation process for the asperity, the average contact pressure Pepa must meet the critical conditions for both elastic deformation and full plastic deformation.
After substituting the average contact pressures at the two critical deformation points, the two coefficients c and c1 can be obtained.
Subsequently, by substituting the contact loads at the two critical points, the contact load Fep during the elasto-plastic deformation process satisfies the following equation:
From this, the two coefficients c2 and c3 can be obtained.
Moreover, there is the following relationship between apc and aec:
By substituting the obtained four parameters c, c1, c2, and c3 into Equations (37) and (38), the Pepa and the Fnpe of the asperity during the elasto-plastic deformation process can be obtained.
With further derivation, the actual contact area aep of the asperity during the elasto-plastic deformation process can be derived.
By combining Equations (1) and (50), the contact resistance Rcep of the single asperity within the elasto-plastic deformation process can be derived.
3.3. The Contact Resistance of the Rough Interface
Building upon the analysis conducted in Section 3.2, which explored the deformation mechanism of a single asperity on a rough surface, this section will establish the contact resistance for the rough interface by integrating the distribution of asperities on a three-dimensional fractal surface. According to the literature [18], the density function for the cross-sectional area of distribution of the asperities on the three-dimensional fractal surface is provided below.
where aL denotes the maximum actual contact area of the asperities.
The contact load on the rough interface can be derived by multiplying the contact load of the single asperity by its cross-sectional area distribution density function. Hence, utilizing Equations (16), (22) and (49), and combining them with Equation (52), when D ≠ 2.5, the contact load Fn on the rough interface can be expressed as follows:
Meanwhile, under the condition of D = 2.5, the contact load Fn on the rough interface has the following expression:
After contact, the asperities in the rough interface form a parallel relationship, and the contact resistance of the entire rough interface is represented by the parallel resistance Rc of all the asperities within the interface, which exhibits the following relationship:
Substitute the analytical equations for the contact resistance in the three deformation processes, which are equations Rce, Rcep and Rcp, into Equation (55). Meanwhile, split and display Equation (55) into different parts.
At the end of model construction, to facilitate a comparison with other models, dimensionless processing is performed on the contact load Fn and the contact resistance Rc. When D ≠ 2.5, the dimensionless contact load Fn* on the rough interface can be expressed as follows:
where Fn* = Fn/(EAa), G* = G/Aa0.5, aL* = aL/Aa, aec* = aec/Aa, apc* = apc/Aa, as* = as/Aa, Aa is the nominal contact area of the interface at the macroscopic scale.
Under the condition of D = 2.5, the dimensionless contact load Fn* has the following expression.
Similarly, the expression for Rc* is as follows:
where Rc* = Rc Aa0.5/ρ.
Based on the preceding analysis, analytical expressions have been derived for the contact resistance of the rough interface across different deformation processes, culminating in the development of an analytical model for contact resistance. In the forthcoming section, experimental tests will be undertaken to verify the accuracy of the model presented in this paper.
4. Experimental Verification and Simulation Analysis
The experimental verification of the contact resistance for the rough interface will be conducted in this section. Subsequently, a comparison will be made between the simulation results obtained from the presented model, the experimental results, and the simulation results reported in the existing literature. Furthermore, a numerical simulation and analysis of the presented model will be performed, elucidating the influence of the mechanism of micro-morphology on contact resistance.
4.1. Construction of the Experimental Test Platform
In this section, an experimental test platform for contact resistance will be constructed to measure the contact resistance of the rough interfaces. Figure 5 displays the schematic diagram of the experimental test platform.
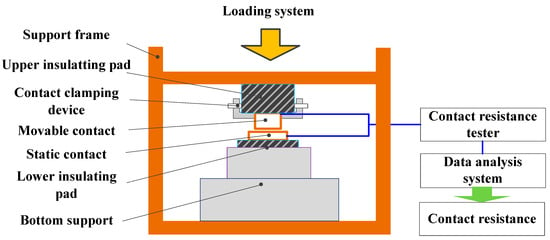
Figure 5.
The schematic diagram of the experimental test platform.
The experimental test platform primarily consists of two components: the actuating mechanism and the data acquisition system. The actuating mechanism employs a vertical structure that includes the loading system, overall support frame, upper and lower insulating pads, contact clamping device, movable contact, static contact, and bottom support. Notably, the loading system utilizes the ZWICKZ005 electronic universal testing machine (manufactured by ZWICK Corporation in Bavaria, Germany) for applying loads. This universal testing machine is equipped with the KAP-TC pressure sensor (manufactured by Kewill GmbH in Hamburg, Germany) to measure the applied pressure during loading. The pressure sensor has a load range of 5000 N and exhibits a pressure measurement accuracy of 0.5%FS. The data acquisition system comprises two parts: the contact resistance tester and the data analysis system. For testing of the contact resistance, the GSZRC-10B DC resistance tester (manufactured by Wuhan Guoshi Electrical Equipment Co., Ltd. in Wuhan City, China) was employed. It offers a range of 0.05 mΩ, a test accuracy of 0.02%FS, and a sampling rate of 50 times per second.
Utilizing this experimental test platform, both the contact load and the contact resistance signals are collected, enabling the acquisition of the contact resistance variation curve under different contact loads. Importantly, to ensure the authenticity of the experimental results, three specimens of each type are tested, and the average value is reported as the final result.
4.2. Parameter Acquisition of the Tested Specimen
Before proceeding with the contact resistance experiment, the specimen must be processed to acquire the pertinent parameters for model simulation. To guarantee complete contact between the upper and lower test pieces, cylindrical test pieces with diameters of ϕ10 mm and ϕ30 mm were utilized for testing. Prior to conducting the experimental tests, the micro-morphology of the specimens was measured using the ZYGO-Nexview device (manufactured by ZYGO Corporation in Middlefield, CT, USA), and the measurement results are presented in Figure S1. Subsequently, the fractal characteristic parameters of the measured surfaces were determined using the box counting method, as described in reference [46]. In ascending order of roughness Sa, the fractal parameters obtained from the three surfaces are D = 2.589, G* = 6.29 × 10−8; D = 2.547, G* = 1.821 × 10−7; and D = 2.523, G* = 5.477 × 10−7, respectively.
Furthermore, the rough interface is composed of a copper material, and its material parameters were tested using the universal testing machine (manufactured by ZWICK Corporation in Bavaria, Germany). The material parameters of the specimen are presented in Table 1. Specifically, the specimen exhibits an elastic modulus of 115 GPa and a Poisson’s ratio of 0.34, resulting in an equivalent elastic modulus E of 65 GPa for the interface. Additionally, the specimen has a yield strength of 220 MPa, leading to the parameter φ of 0.0034. The friction coefficient μ is measured to be 0.19, and the resistivity ρ is determined to be 1.78 × 10−8 Ω·m.

Table 1.
The material parameters of the specimen.
4.3. Comparison and Analysis of the Contact Resistance
Based on the analysis conducted in Section 4.2, the parameters of the tested specimen were acquired, which provided a parameter basis for the numerical simulation of the model in this paper. By inputting the obtained parameters into the calculation equation of the contact resistance model and using MATLAB 2018b software to program, the numerical simulation results for contact resistance can be derived.
4.3.1. Comparison with Experimental Results
To illustrate and validate the benefits of the model presented in this paper, a comparison of the results was augmented with the Pan model for the hemispherical asperity [43] and the Y–K model without considering the elasto-plastic deformation of the asperity [18]. A comparison of the results of the three models with the experimental results is shown in Figure 6. As depicted in Figure 6, the comparative results present the contact resistance and relative error under different roughness levels. Specifically, Figure 6a,c,e, respectively, showcase the comparison results of the contact resistance at Sa 0.017 μm, Sa 0.057 μm, and Sa 0.096 μm. Figure 6b,d,f displays the comparative results of relative error at Sa 0.017 μm, Sa 0.057 μm, and Sa 0.096 μm, respectively.
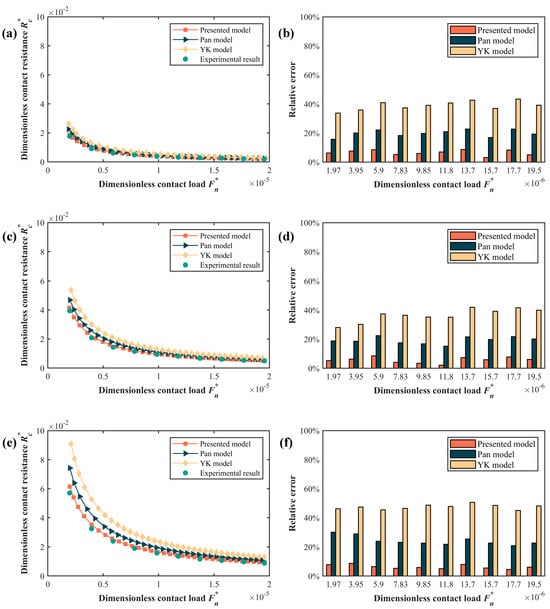
Figure 6.
The comparison results: (a) the contact resistance at Sa 0.017 μm; (b) the relative error at Sa 0.017 μm; (c) the contact resistance at Sa 0.057 μm; (d) the relative error at Sa 0.057 μm; (e) the contact resistance at Sa 0.096 μm; (f) the relative error at Sa 0.096 μm.
Based on the comprehensive analysis of Figure 6a,c,e, it is evident that the contact resistance gradually decreases with increasing contact load across different roughness levels. Moreover, the numerical simulation results of the three models exhibit the same trend as the experimental results. In conjunction with Figure 4, as the contact load rises, the actual contact area of the asperity progressively expands. Furthermore, with an increasing contact load, the number of asperities engaging in contact gradually grows, leading to an enlargement of the total contact area of the rough interface. According to Equation (1), contact resistance is inversely proportional to the actual contact area; hence the contact resistance gradually decreases as the contact load increases. Furthermore, under identical contact load conditions, the contact resistance gradually rises as the surface roughness increases. This phenomenon is consistent with the latest research findings in the literature [47]. Surfaces with higher surface roughness have more irregular asperity sizes and distributions, resulting in a smaller actual contact area under the same contact load conditions, which ultimately leads to an increase in contact resistance as the roughness increases.
It is noteworthy that the presented model in this paper is closer to the experimental results compared to the other two models. Analyzing the comparison of the results of the relative errors, the relative error values for the three models are presented in Tables S1–S3 of the Supplementary Materials. Upon examining these errors, it is evident that the model introduced in this paper exhibits a relative error of approximately 8%, whereas the relative errors for the other two models surpass 20% and 40%, respectively. As depicted in Figure 6, the highest error observed in our model is 8.74%, compared to the maximum errors of 30.11% and 50.62% in the other two models.
Analyzing the relative errors of the model in this paper and the Pan model in conjunction with Figure 2, the difference between the two models lies in the geometry shape of the asperity. The model in this paper adopts the axisymmetric sinusoidal asperity, while the Pan model uses the hemispherical asperity. Combining with the previous research results of the team [39], under the same contact load conditions, the axisymmetric sinusoidal asperity has a larger actual contact area compared to the hemispherical asperity, which results in a smaller contact resistance for the model in this paper compared to the Pan model.
Additionally, the method for handling the elasto-plastic deformation process can also lead to an increase in relative errors. Reference can be made to the literature [48] for a comparison of the results of the elasto-plastic transition methods used for asperity. Neglecting the elasto-plastic deformation process will reduce the value of the actual contact area in the rough interface, thereby introducing a larger relative error into the contact resistance.
4.3.2. Numerical Simulation and Analysis
After confirming the accuracy of the presented model, the focus will shift to exploring the influence of the mechanism of micro-morphology on contact resistance. Factors related to micro-morphology are specifically manifested through parameters. Therefore, the discussion will revolve around the impact of these parameters on contact resistance. The material parameters required for the simulation are detailed in Section 4.2. Furthermore, the specific value ranges for both the fractal dimension and the scale coefficient will be clearly defined in their respective sections.
As two crucial parameters for characterizing surface micro-morphology, this section delves into the impact of these parameters on the contact resistance of the rough interface. Specifically, D denotes the fractal dimension of the fractal surface, which determines the contributions of the high- and low-frequency components on surface function. Meanwhile, G represents the scale coefficient of the fractal surface, signifying the height scaling parameter that is independent of the frequency.
- (1)
- The contact resistance across diverse fractal dimensions
The fractal dimension D serves as the quantitative parameter that describes the complexity of the rough surface. It more accurately reflects the self-similarity and irregularity of the rough surface across different scales. A larger D value indicates a rougher, more complex surface that contains greater details and variations. Consequently, this section conducts a numerical simulation to investigate the influence of the fractal dimension D on the interface contact resistance. The fractal dimension D varies within the range of 2.5 to 2.7, while the scale coefficient is fixed at G* = 1 × 10−8. The variation of contact resistance across diverse fractal dimensions is shown in Figure 7.
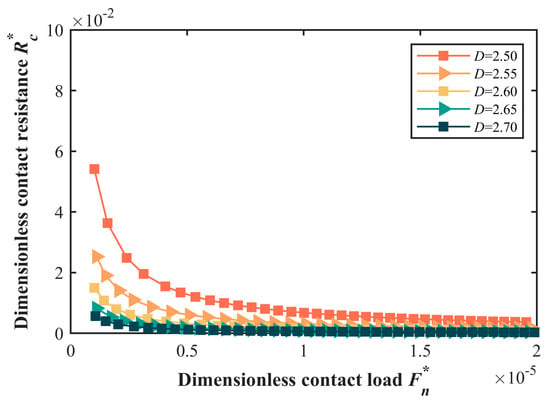
Figure 7.
The variation of the contact resistance across diverse fractal dimensions.
The variation curve of the dimensionless contact resistance Rc* with respect to the dimensionless contact load Fn* across different fractal dimensions is presented in Figure 7. Generally, the Rc* exhibits a similar trend to the Fn* under varying fractal dimensions. Specifically, contact resistance diminishes as the contact load escalates, with the decrement rate progressively decelerating. According to Equation (53), as the contact load increases, the conductive area of asperities within the interface gradually expands, leading to a consistent reduction in contact resistance. Concurrently, the decrement rate of the contact resistance slows down due to the gradually diminishing rate of increase in the conductive area.
It is noteworthy that, under the consistent contact load, the contact resistance varies across different fractal dimensions. The higher fractal dimensions correspond to the lower contact resistances. The fractal dimension affects the density and height of the asperities on the rough surface. Larger fractal dimensions are associated with smaller asperity amplitudes and higher asperity densities. Under the identical contact loads, smaller asperity amplitudes augment the actual contact area at the interface, resulting in decreased contact resistance. Furthermore, increased asperity densities result in a higher number of asperities coming into contact. Given that the contact resistances between single asperities are in parallel, this leads to a decrease in overall contact resistance.
- (2)
- The contact resistance across diverse scale coefficients
The scale coefficient G serves as the characteristic scale parameter for the rough surface, offering a quantitative assessment of surface roughness. It encapsulates the height characteristics of the surface contour curve, which signifies the extent of undulation in the surface micro-morphology. By determining or calculating the value of G, an objective assessment of the surface’s roughness level can be made.
Hence, this section delves into a numerical simulation to investigate the impact of the scale coefficient G on the interface contact resistance. The values of the G* span from 1 × 10−10 to 1 × 10−6, with the fractal dimension fixed at D = 2.6. The variation in contact resistance across diverse scale coefficients is shown in Figure 8.
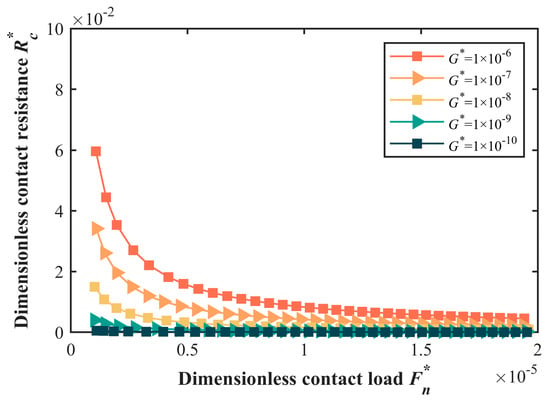
Figure 8.
The variation in contact resistance across diverse scale coefficients.
The variation curve of the dimensionless contact resistance Rc* with respect to the dimensionless contact load Fn* under varying scale coefficients is presented in Figure 8. Generally, the Rc* exhibits a similar trend as the Fn* across different scale coefficients. Specifically, contact resistance diminishes as the contact load escalates, with the decrement rate progressively decelerating. Akin to the simulation results under varying fractal dimensions, as the contact load intensifies, the conductive area of the asperities within the interface gradually expands, leading to a consistent reduction in contact resistance. Concurrently, the decrement rate of contact resistance slows down due to the gradually diminishing rate of increase in the conductive area.
Notably, under the consistent contact load, the contact resistance varies with different scale coefficients. A larger scale coefficient corresponds to an elevated contact resistance. The scale coefficient affects the height of the asperities on the rough surface, with a larger scale coefficient correlating to taller asperity amplitudes. Under the identical contact loads, larger asperity amplitudes reduce the actual contact area at the interface, resulting in an increased contact resistance.
5. Conclusions
A novel fractal model for contact resistance based on the axisymmetric sinusoidal asperity is proposed in this paper, which can more accurately capture the electrical resistance characteristics of the rough interface. The main conclusions are summarized below:
- (1)
- A parametric characterization method for the rough surface is proposed. Starting from the current transmission mechanism of the rough interface, the influence mechanism of the asperity on contact resistance is revealed. Afterwards, the asperity geometry is redefined by employing an axisymmetric sinusoidal function, and the asperity distribution is described using a three-dimensional fractal function, ultimately leading to a new characterization of the rough interface.
- (2)
- A fractal model for contact resistance based on the axisymmetric sinusoidal asperity is constructed. A theoretical analysis and numerical solution of the basic deformation mechanism of the axisymmetric sinusoidal asperity are carried out. The analytical expressions for the contact resistance of the single asperity and the rough interface during elastic, elasto-plastic, and full plastic deformation processes are solved, ultimately achieving a refined modeling of the contact resistance.
- (3)
- An experimental test platform is built to verify the accuracy of the model. A comparison of the results shows that the presented model in this paper is closer to the experimental results than the other two models. The maximum error of the model in this paper is 8.74%, while the maximum errors of the other two models are 30.11% and 50.62%. Moreover, the mechanism by which micro-morphology influences contact resistance is elucidated. The presented model offers significant theoretical and practical value for enhancing electrical contact performance, refining electronic device design, and ensuring the stable operation of power systems.
However, the presented model in this paper delves deeply into the impact of axisymmetric sinusoidal asperity on the contact resistance. In practical scenarios, when a current flows through the contacts, the resistive heat generated during the relay contact will affect the contact resistance. In addition, in the process of contact resistance formation, the interaction of the asperities on the rough interface cannot be ignored. Further exploration will be conducted in subsequent work to investigate the influence of temperature factors on contact resistance for the rough interface.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/fractalfract8090544/s1, Figure S1: The micro-topography under different roughness: (a) Sa 0.017 μm; (b) Sa 0.057 μm; (c) Sa 0.096 μm; Table S1: The relative errors under Sa 0.017 μm; Table S2: The relative errors under Sa 0.057 μm; Table S3: The relative errors under Sa 0.096 μm.
Author Contributions
Conceptualization and methodology, Y.L., Q.A. and W.W.; validation, Q.A., M.H. and S.S.; writing—original draft preparation and visualization, S.Y., Q.A., S.W. and Y.L. All authors have read and agreed to the published version of this manuscript.
Funding
This study is financially supported by the National Key Research and Development Program of China (No. 2017YFF0108101), and the Beijing Information Science & Technology University Research Foundation (No. 2024XJJ01).
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Dong, Y.; Zhang, P.; Chen, M.; Lian, W. Numerical study of thermal contact resistance considering spots and gap conduction effects. Tribol. Int. 2024, 193, 109304. [Google Scholar] [CrossRef]
- Jiang, C.Y.; Liang, X.M. An incremental contact model for hyperelastic solids with rough surfaces. Tribol. Lett. 2024, 72, 1. [Google Scholar] [CrossRef]
- Cai, Z.-B.; Li, C.-L.; You, L.; Chen, X.-D.; He, L.-P.; Cao, Z.-Q.; Zhang, Z.-N. Prediction of contact resistance of electrical contact wear using different machine learning algorithms. Friction 2024, 12, 1250–1271. [Google Scholar] [CrossRef]
- Sun, X.G.; Xing, W.C. Fractal model of thermal contact conductance of rough surfaces based on elliptical asperity. Ind. Lubr. Tribol. 2023, 75, 424–431. [Google Scholar] [CrossRef]
- Zhang, M.L.; Zuo, X.; Zhou, Y.K. Fractal contact resistance model of wind pitch slip ring considering wear and self-excited vibration. Ind. Lubr. Tribol. 2024, 76, 214–230. [Google Scholar] [CrossRef]
- Holm, R. Electric Contacts: Theory and Applications; Springer: Berlin, Germany, 1981. [Google Scholar]
- Greenwood, J.A. Constriction resistance and the real area of contact. Br. J. Appl. Phys. 1966, 17, 1621. [Google Scholar] [CrossRef]
- Persson, B.N.J. On the electric contact resistance. Tribol. Lett. 2022, 70, 88. [Google Scholar] [CrossRef]
- Kogut, L.; Komvopoulos, K. Electrical contact resistance theory for conductive rough surfaces separated by a thin insulating film. J. Appl. Phys. 2004, 95, 576–585. [Google Scholar] [CrossRef]
- Müser, M.H.; Dapp, W.B.; Bugnicourt, R.; Sainsot, P.; Lesaffre, N.; Lubrecht, T.A.; Persson, B.N.J.; Harris, K.; Bennett, A.; Schulze, K.; et al. Meeting the contact-mechanics challenge. Tribol. Lett. 2017, 65, 118. [Google Scholar] [CrossRef]
- Zhang, X.; Jackson, R. An analysis of the multi-scale structure of surfaces with various finishes. Tribol. Trans. 2016, 60, 121–134. [Google Scholar] [CrossRef]
- Majumdar, A.; Bhushan, B. Fractal model of elastic-plastic contact between rough surfaces. Tribol. Trans. Asme. 1991, 113, 1–11. [Google Scholar] [CrossRef]
- Kogut, L.; Komvopoulos, K. Electrical contact resistance theory for conductive rough surfaces. J. Appl. Phys. 2003, 94, 3153–3162. [Google Scholar] [CrossRef]
- Hu, J.; Feng, C.; Shen, B.; Hu, Z.; Zhu, F. Investigation Regarding the Influence of Contact Condition on the Thermal Contact Resistance Between Copper and Indium. IEEE Trans. Electron Devices 2021, 68, 4028–4032. [Google Scholar] [CrossRef]
- Li, Y.-H.; Shen, F.; Güler, M.A.; Ke, L.-L. A rough surface electrical contact model considering the interaction between asperities. Tribol. Int. 2023, 190, 109044. [Google Scholar] [CrossRef]
- Pan, W.; Sun, Y.; Li, X.; Song, H.; Guo, J. Contact mechanics modeling of fractal surface with complex multi-stage actual loading deformation. Appl. Math. Model. 2024, 128, 58–81. [Google Scholar] [CrossRef]
- Ausloos, M.; Berman, D.H. A multivariate Weierstrass–Mandelbrot function. Proc. R. Soc. A Math. Phys. Eng. Sci. 1985, 400, 331–350. [Google Scholar] [CrossRef]
- Yan, W.; Komvopoulos, K. Contact analysis of elastic-plastic fractal surfaces. J. Appl. Phys. 1998, 84, 3617–3624. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, Y.; Chen, X.; Yu, H. A spherical conformal contact model considering frictional and microscopic factors based on fractal theory. Chaos Solitons Fractals 2018, 111, 96–107. [Google Scholar] [CrossRef]
- Zheng, J.; Liu, X.; Jin, Y.; Dong, J.; Wang, Q. Effects of surface geometry on advection-diffusion process in rough fractures. Chem. Eng. J. 2021, 414, 128745. [Google Scholar] [CrossRef]
- Zhao, Y.; Fang, C.; Cai, L.; Liu, Z. A three-dimensional fractal theory based on thermal contact conductance model of rough surfaces. Proc. Inst. Mech. Eng. Part E J. Process Mech. Eng. 2018, 232, 528–539. [Google Scholar] [CrossRef]
- Zhang, J.; Liu, Y.; Yan, K.; Fang, B. A fractal model for predicting thermal contact conductance considering elasto-plastic deformation and base thermal resistances. J. Mech. Sci. Technol. 2019, 33, 475–484. [Google Scholar] [CrossRef]
- Li, R.Y.; Yang, W.Y.; Liang, H.M. Multi-physics finite element model of relay contact resistance and temperature rise considering multi-scale and 3D fractal surface. IEEE Access 2020, 8, 122241–122250. [Google Scholar] [CrossRef]
- Jiang, Y.L.; Gao, Y.Z.; Feng, Z.G. A contact model for electrical contact resistance between a rigid plane and a cylindrical surface. J. Mech. Sci. Technol. 2021, 35, 4125–4134. [Google Scholar] [CrossRef]
- Li, J.M.; Zhu, Q.Y.; Sun, J.J. Study on thermal contact resistance at liquid-solid interface based on fractal theory. AIP Adv. 2021, 11, 125308. [Google Scholar] [CrossRef]
- Wang, H.; Liu, Y.; Cai, Y.; Liu, Z.; Yang, Y. Fractal analysis of the thermal contact conductance for mechanical interface. Int. J. Heat Mass Transf. 2021, 169, 120942. [Google Scholar] [CrossRef]
- Xiao, T.; Guo, J.; Yang, X.; Hooman, K.; Lu, T.J. On the modelling of heat and fluid transport in fibrous porous media: Analytical fractal models for permeability and thermal conductivity. Int. J. Therm. Sci. 2022, 172, 107270. [Google Scholar] [CrossRef]
- Sun, X.G. Fractal model of thermal contact conductance of rough surfaces considering substrate deformation. Ind. Lubr. Tribol. 2023, 75, 895–903. [Google Scholar] [CrossRef]
- Sun, X.G. Thermal contact conductance model of rough surfaces with inclination based on three-dimensional fractal theory. Aircr. Eng. Aerosp. Technol. 2024, 96, 265–272. [Google Scholar] [CrossRef]
- Shen, F.; Li, Y.H.; Ke, L.L. A novel fractal contact model based on size distribution law. Int. J. Mech. Sci. 2023, 249, 108255. [Google Scholar] [CrossRef]
- Shen, F.; Li, Y.-H.; Ke, L.-L. Pressure and polymer selections for solid-state batteries investigated with high-throughput simulations. Cell Rep. Phys. Sci. 2023, 4, 101328. [Google Scholar] [CrossRef]
- Liu, M. Finite element analysis of large contact deformation of an elastic-plastic sinusoidal asperity and a rigid flat. Int. J. Solids Struct. 2014, 51, 3642–3652. [Google Scholar] [CrossRef]
- Mishra, T.; de Rooij, M.; Schipper, D.J. The effect of asperity geometry on the wear behaviour in sliding of an elliptical asperity. Wear 2021, 470, 203615. [Google Scholar] [CrossRef]
- Jackson, R.L.; Angadi, S. Electrical contact during a rolling vibratory motion considering mixed lubrication. J. Tribol. 2023, 145, 082201. [Google Scholar] [CrossRef]
- Xu, K.; Yuan, Y.; Zhang, L.H. A normal contact stiffness model of joint surface based on fractal theory. Comput. Model. Eng. Sci. 2019, 119, 459–480. [Google Scholar] [CrossRef]
- Zhang, C.; Ren, W. Modeling of 3D surface morphologies for predicting the mechanical contact behaviors and associated electrical contact resistance. Tribol. Lett. 2021, 69, 20. [Google Scholar] [CrossRef]
- Sun, X.; Xing, W. Fractal model of thermal contact conductance of rough surfaces based on cone asperity. Aircr. Eng. Aerosp. Technol. 2023, 95, 966–973. [Google Scholar] [CrossRef]
- An, Q.; Suo, S.; Lin, F.; Shi, J. A novel micro-contact stiffness model for the grinding surfaces of steel materials based on cosine curve-shaped asperities. Materials 2019, 12, 3561. [Google Scholar] [CrossRef]
- Wang, W.; An, Q.; Suo, S.; Meng, G.; Yu, Y.; Bai, Y. A novel three-dimensional fractal model for the normal contact stiffness of mechanical interface based on axisymmetric cosinusoidal asperity. Fractal Fract. 2023, 7, 279. [Google Scholar] [CrossRef]
- An, Q.; Liu, Y.; Huang, M.; Suo, S. A novel contact stiffness model for grinding joint surface based on the generalized ubiquitiformal sierpinski carpet theory. Fractal Fract. 2024, 8, 351. [Google Scholar] [CrossRef]
- Wang, X.; Xu, Y.; Jackson, R.L. Elastic–plastic sinusoidal waviness contact under combined normal and tangential loading. Tribol. Lett. 2017, 65, 45. [Google Scholar] [CrossRef]
- Johnson, K.L. Contact Mechanics; Cambridge University Press: Cambridge, UK, 1985. [Google Scholar]
- Pan, W.; Li, X.; Wang, L.; Guo, N.; Mu, J. A normal contact stiffness fractal prediction model of dry-friction rough surface and experimental verification. Eur. J. Mech. A/Solids 2017, 66, 94–102. [Google Scholar] [CrossRef]
- Abbott, E.J.; Firestone, F.A. Specifying surface quantity—A method based on accurate measurement and comparison. ASME J. Mech. Eng. 1933, 55, 569–572. [Google Scholar]
- Tian, H.; Chen, B.; He, K.; Dong, Y.; Zhong, X.; Wang, X.; Xi, N. A new fractal model of elastic, elastoplastic and plastic normal contact stiffness for slow sliding interface considering dynamic friction and strain hardening. J. Shanghai Jiaotong Univ. 2017, 22, 589–601. [Google Scholar] [CrossRef]
- Freiberg, U.; Kohl, S. Box dimension of fractal attractors and their numerical computation. Commun. Nonlinear Sci. Numer. Simul. 2021, 95, 105615. [Google Scholar] [CrossRef]
- Li, Y.-H.; Shen, F.; Güler, M.A.; Ke, L.-L. Modeling multi-physics electrical contact on rough surfaces considering elastic-plastic deformation. Int. J. Mech. Sci. 2024, 269, 109066. [Google Scholar] [CrossRef]
- Zhang, Y.; Lu, H.; Zhang, X.; Ling, H.; Fan, W.; Bao, L.; Guo, Z. A normal contact stiffness model of machined joint surfaces considering elastic, elasto-plastic and plastic factors. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2020, 234, 1007–1016. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).