A High-Order Numerical Method Based on a Spatial Compact Exponential Scheme for Solving the Time-Fractional Black–Scholes Model
Abstract
1. Introduction
2. Construction of the High-Order Numerical Method
3. Stability and Convergence Analysis
3.1. Stability Analysis
3.2. Convergence Analysis
4. Numerical Examples
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Podlubny, I. Fractional Differential Equations; Academic Press: San Diego, CA, USA, 1999. [Google Scholar]
- Hilfer, R. Applications of Fractional Calculus in Physics; World Scientific: Singapore, 2000. [Google Scholar]
- Magin, R.L. Fractional Calculus in Bioengineering; Begell House Publishers: Danbury, CT, USA, 2006. [Google Scholar]
- Black, F.; Scholes, M. The pricing of options and corporate liabilities. J. Polit. Econ. 1973, 81, 637–654. [Google Scholar] [CrossRef]
- Merton, R.C. Theory of rational option pricing. Bell J. Econ. Manag. Sci. 1973, 4, 141–183. [Google Scholar] [CrossRef]
- Zhang, H.; Liu, F.; Turner, I.; Yang, Q. Numerical solution of the time fractional Black–Scholes model governing European options. Comput. Math. Appl. 2016, 69, 1772–1783. [Google Scholar] [CrossRef]
- Cartea, A.; del-Castillo-Negrete, D. Fractional diffusion models of option prices in markets with jumps. Physical A 2007, 374, 749–763. [Google Scholar] [CrossRef]
- Jumarie, G. Stock exchange fractional dynamics defined as fractional exponential growth driven by (usual) Gaussian white noise. Application to fractional Black–Scholes equations. Insurance Math. Econom. 2008, 42, 271–287. [Google Scholar] [CrossRef]
- Liang, J.R.; Wang, J.; Zhang, W.J.; Qiu, W.Y.; Ren, F.Y. The solutions to a bi-fractional black-scholes-merton differential equation. Int. J. Pure Appl. Math. 2010, 58, 99–112. [Google Scholar]
- Chen, W.; Xu, X.; Zhu, S. Analytically pricing double barrier options based on a time-fractional Black–Scholes equation. Comput. Math. Appl. 2015, 69, 1407–1419. [Google Scholar] [CrossRef]
- Zhang, H.M.; Zhang, M.C.; Liu, F.W.; Shen, M. Review of the fractional Black-Scholes equations and their solution techniques. Fractal Fract. 2024, 8, 101. [Google Scholar] [CrossRef]
- Liu, F.; Zhuang, P.; Liu, Q. Numerical Methods of Fractional Partial Differential Equations and Applications; Science Press: Beijing, China, 2015. [Google Scholar]
- Cai, M.; Li, C.P. Theory and Numerical Approximations of Fractional Integrals and Derivatives; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2019. [Google Scholar]
- Yu, B.; Jiang, X. Numerical Identification of the Fractional Derivatives in the Two-Dimensional Fractional Cable Equation. J. Sci. Comput. 2016, 68, 252–272. [Google Scholar] [CrossRef]
- Yu, B.; Jiang, X. Temperature prediction by a fractional heat conduction model for the bi-layered spherical tissue in the hyperthermia experiment. Int. J. Therm. Sci. 2019, 145, 105990. [Google Scholar] [CrossRef]
- Yu, B. High-order efficient numerical method for solving a generalized fractional Oldroyd-B fluid model. J. Appl. Math. Comput. 2021, 66, 749–768. [Google Scholar] [CrossRef]
- Yu, B. High-order compact finite difference method for the multi-term time fractional mixed diffusion and diffusion-wave equation. Math. Meth. Appl. Sci. 2021, 44, 6526–6539. [Google Scholar] [CrossRef]
- De Staelen, R.H.; Hendy, A.S. Numerically pricing double barrier options in a time-fractional Black-Scholes model. Comput. Math. Appl. 2017, 74, 1166–1175. [Google Scholar] [CrossRef]
- Roul, P.; Goura, V.M.K.P. A compact finite difference scheme for fractional Black-Scholes option pricing model. Appl. Numer. Math. 2021, 166, 40–60. [Google Scholar] [CrossRef]
- Roul, P. A high accuracy numerical method and its convergence for time-fractional Black-Scholes equation governing European options. Appl. Numer. Math. 2020, 151, 472–493. [Google Scholar] [CrossRef]
- An, X.Y.; Liu, F.W.; Zheng, M.L.; Anh, V.; Turner, I.W. A space-time spectral method for time-fractional Black-Scholes equation. Appl. Numer. Math. 2021, 165, 152–166. [Google Scholar] [CrossRef]
- Song, K.; Lyu, P. A high-order and fast scheme with variable time steps for the time-fractional Black-Scholes equation. Math. Meth. Appl. Sci. 2023, 46, 1990–2011. [Google Scholar] [CrossRef]
- Abdi, N.; Aminikhah, H.; Sheikhani, A.H.R. High-order compact finite difference schemes for the time-fractional Black-Scholes model governing European options. Chaos Solitons Fractals 2022, 162, 112423. [Google Scholar] [CrossRef]
- Taghipour, M.; Aminikhah, H. A spectral collocation method based on fractional Pell functions for solving time–fractional Black–Scholes option pricing model. Chaos Solitons Fractals 2022, 163, 112571. [Google Scholar] [CrossRef]
- Kaur, J.; Natesan, S. A novel numerical scheme for time-fractional Black-Scholes PDE governing European options in mathematical finance. Numer Algor. 2023, 94, 1519–1549. [Google Scholar] [CrossRef]
- Zhang, M.; Zheng, X. Numerical approximation to a variable-order time-fractional Black–Scholes model with applications in option pricing. Comput. Econ. 2023, 62, 1155–1175. [Google Scholar] [CrossRef]
- Kazmi, K. A second order numerical method for the time-fractional Black-Scholes European option pricing model. J. Comput. Appl. Math. 2023, 418, 114647. [Google Scholar] [CrossRef]
- Tian, Z.; Dai, S. High-order compact exponential finite difference methods for convection–diffusion type problems. J. Comput. Phys. 2007, 220, 952–974. [Google Scholar] [CrossRef]
- Tian, Z.; Yu, P. A high-order exponential scheme for solving 1D unsteady convection–diffusion equations. J. Comput. Appl. Math. 2011, 235, 2477–2491. [Google Scholar] [CrossRef]
- Sun, Z.; Wu, X. A fully discrete difference scheme for a diffusion-wave system. Appl. Numer. Math. 2006, 56, 193–209. [Google Scholar] [CrossRef]
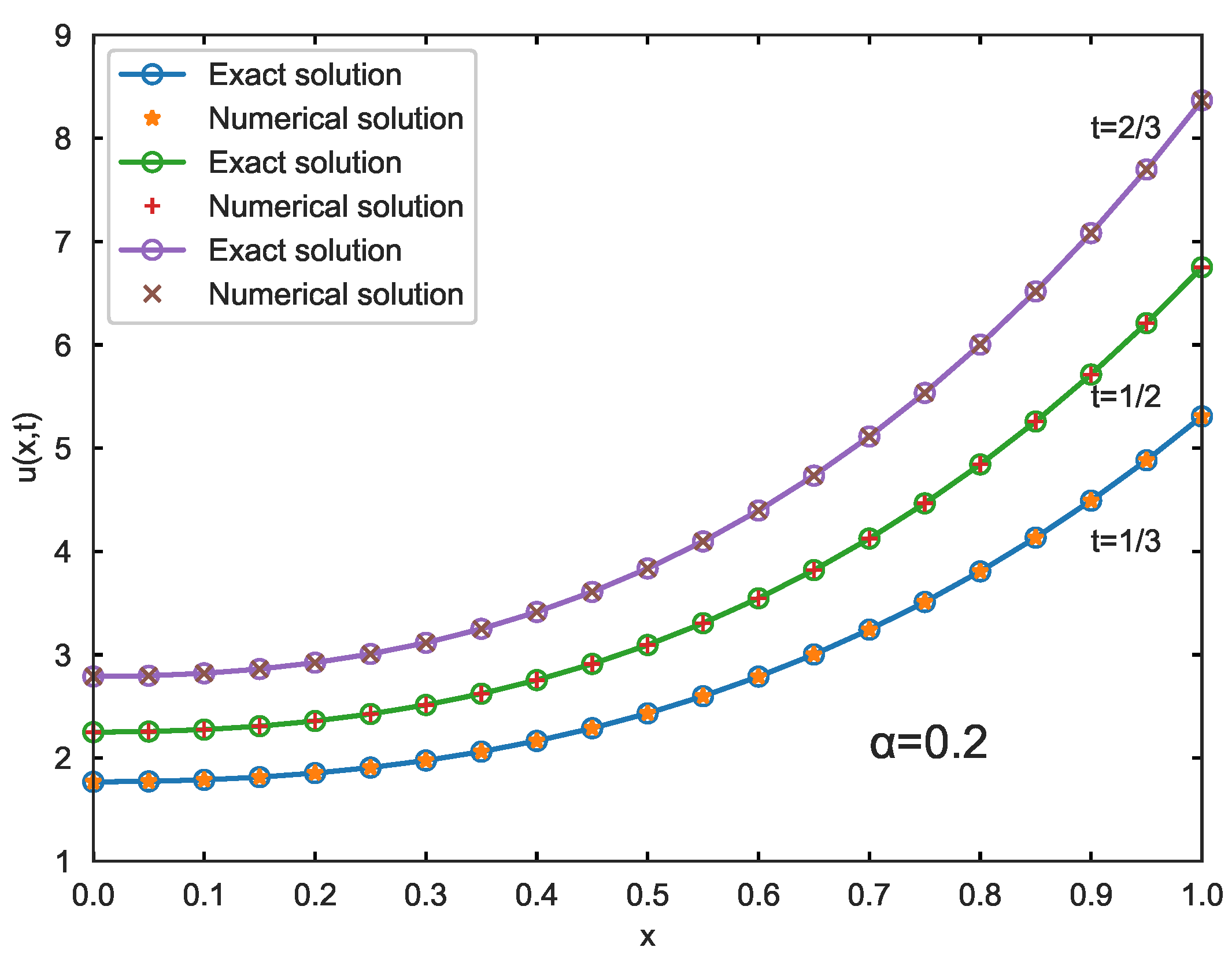
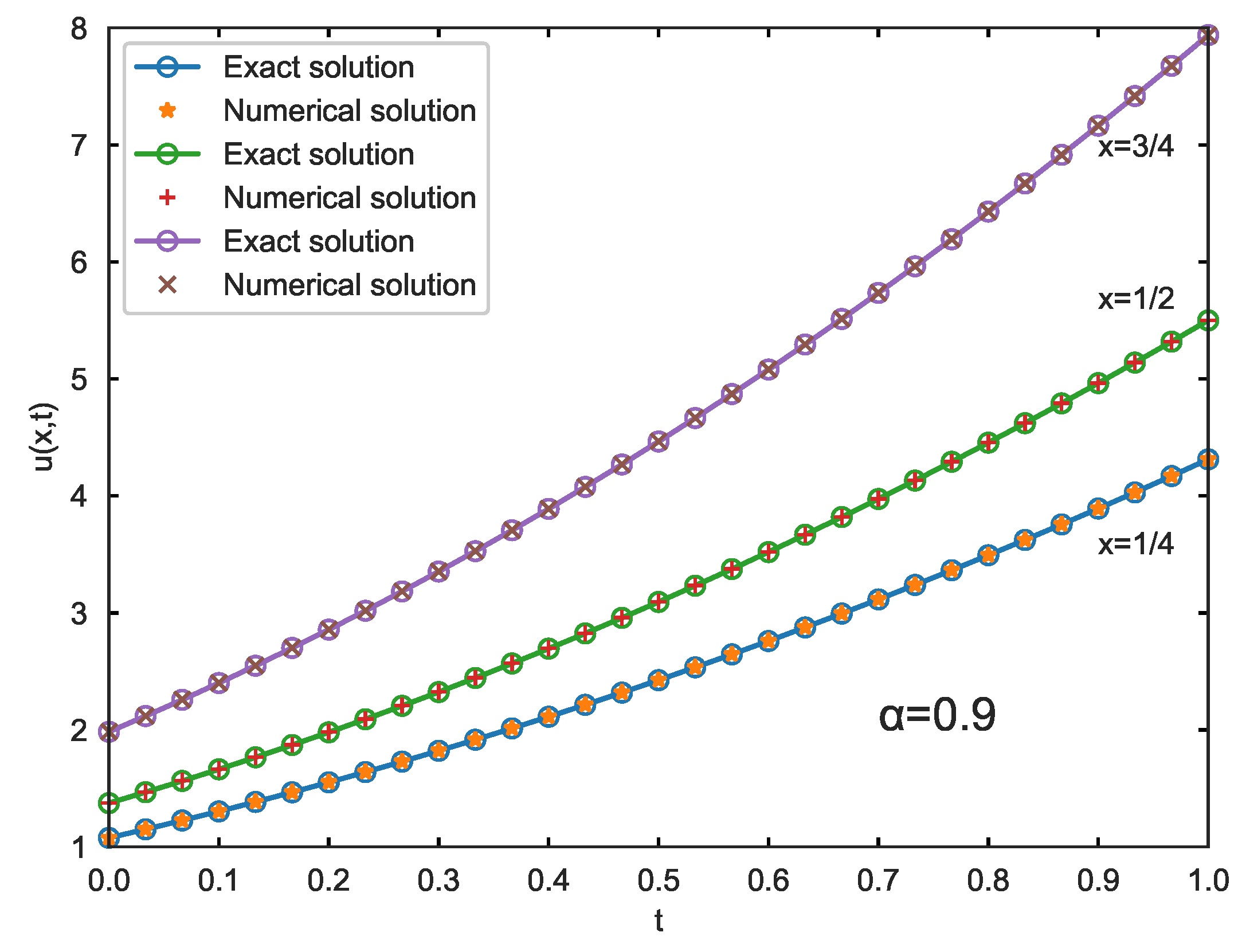
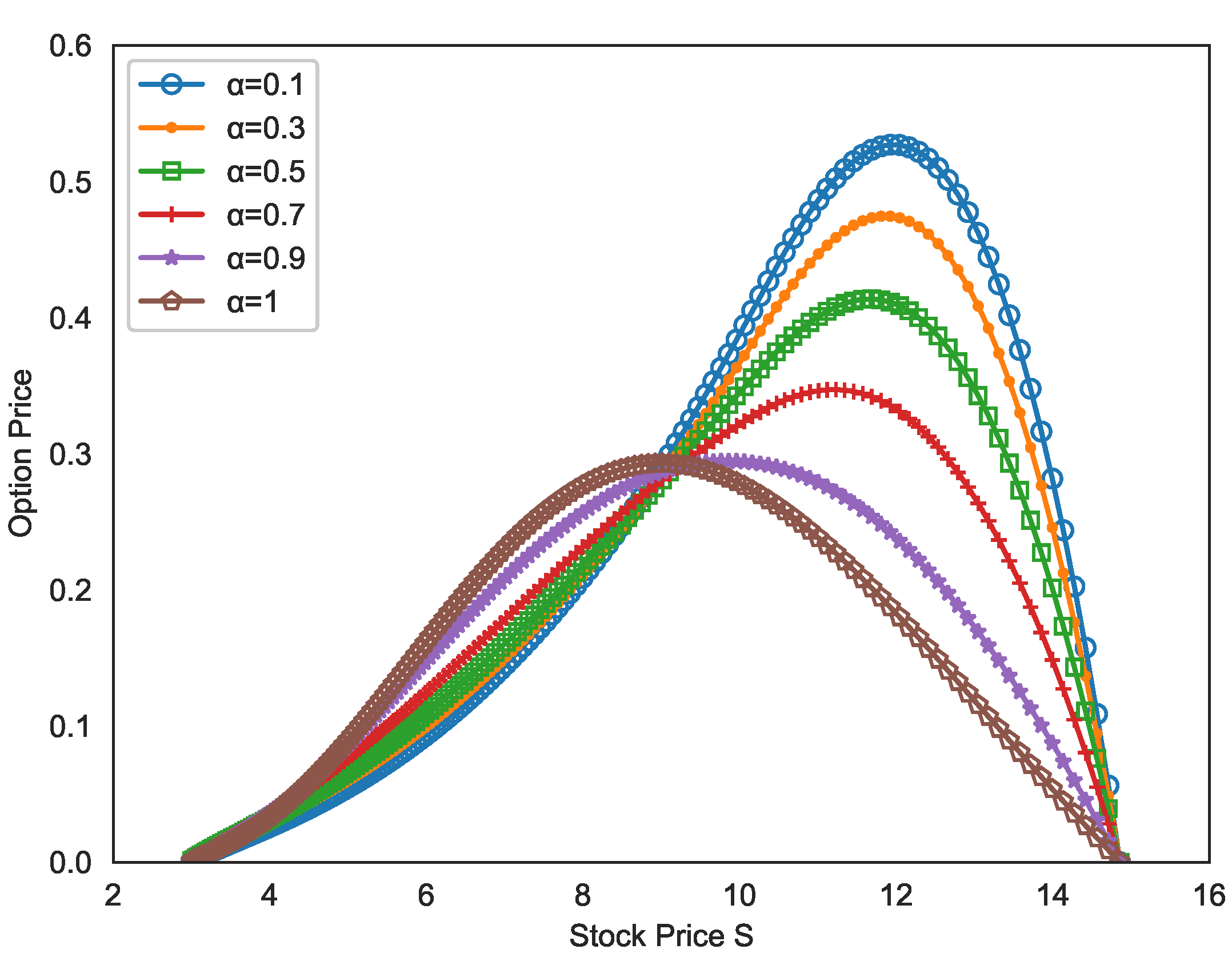
| h | Error | Order | ||
|---|---|---|---|---|
| h | Error | Order | ||
|---|---|---|---|---|
| 100,000 | ||||
| 100,000 | ||||
| 1/100,000 | ||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, X.; Yu, B. A High-Order Numerical Method Based on a Spatial Compact Exponential Scheme for Solving the Time-Fractional Black–Scholes Model. Fractal Fract. 2024, 8, 465. https://doi.org/10.3390/fractalfract8080465
Huang X, Yu B. A High-Order Numerical Method Based on a Spatial Compact Exponential Scheme for Solving the Time-Fractional Black–Scholes Model. Fractal and Fractional. 2024; 8(8):465. https://doi.org/10.3390/fractalfract8080465
Chicago/Turabian StyleHuang, Xinhao, and Bo Yu. 2024. "A High-Order Numerical Method Based on a Spatial Compact Exponential Scheme for Solving the Time-Fractional Black–Scholes Model" Fractal and Fractional 8, no. 8: 465. https://doi.org/10.3390/fractalfract8080465
APA StyleHuang, X., & Yu, B. (2024). A High-Order Numerical Method Based on a Spatial Compact Exponential Scheme for Solving the Time-Fractional Black–Scholes Model. Fractal and Fractional, 8(8), 465. https://doi.org/10.3390/fractalfract8080465






