Two-Dimensional Time-Fractional Nonlinear Drift Reaction–Diffusion Equation Arising in Electrical Field
Abstract
1. Introduction
2. Preliminaries
2.1. Caputo Fractional Derivative
2.2. Airfoil Polynomial
3. Description of the Proposed Method
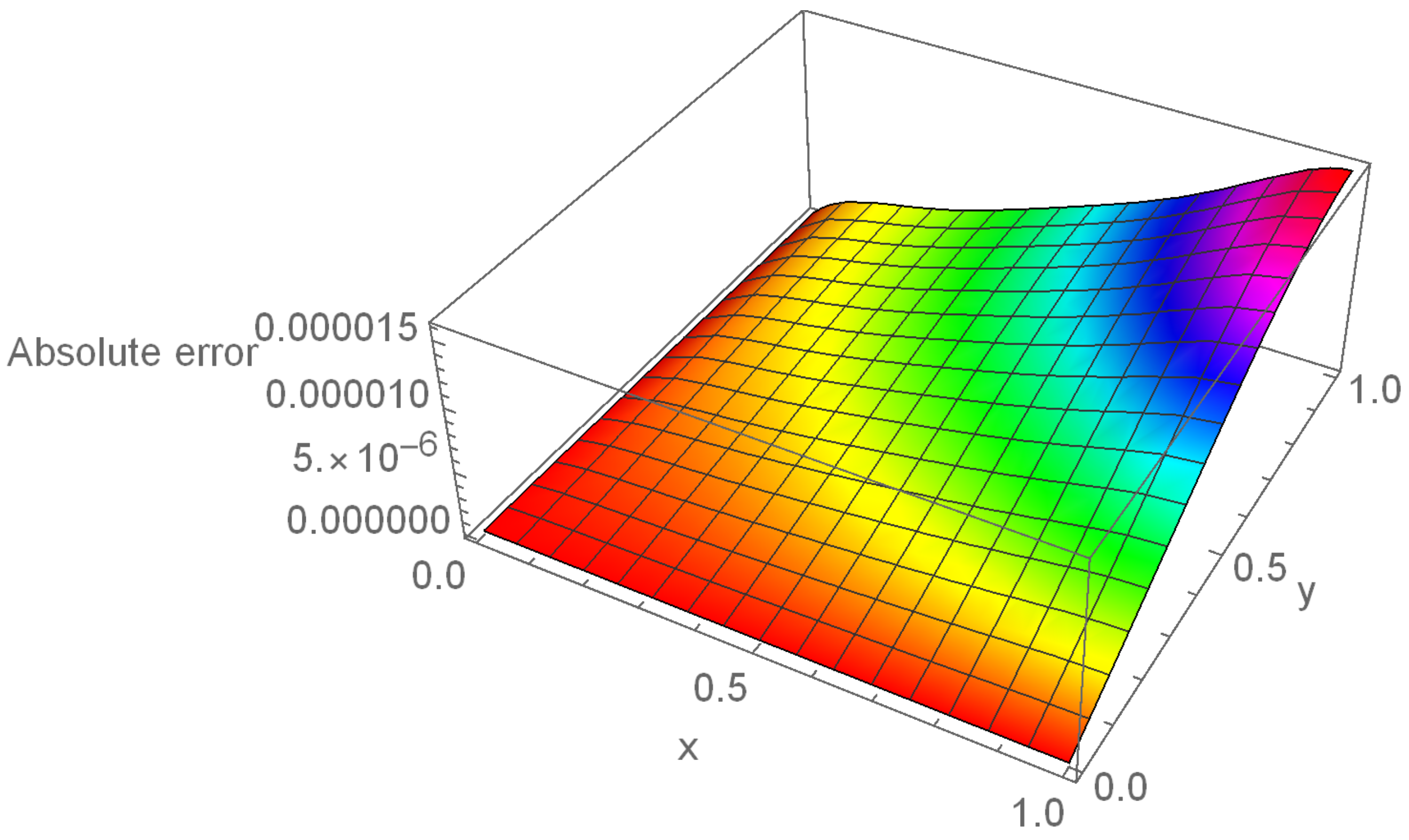
4. Numerical Analysis
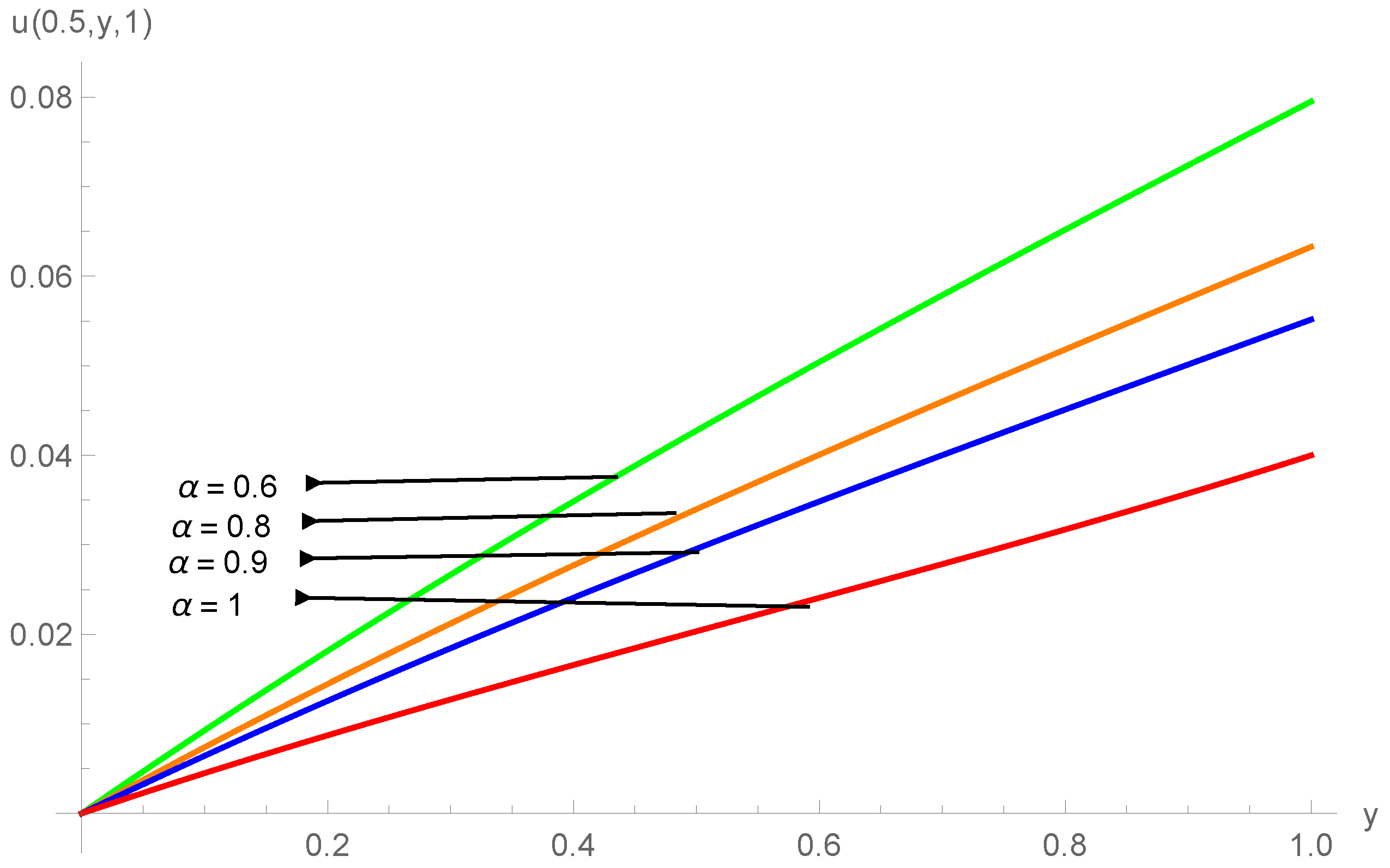
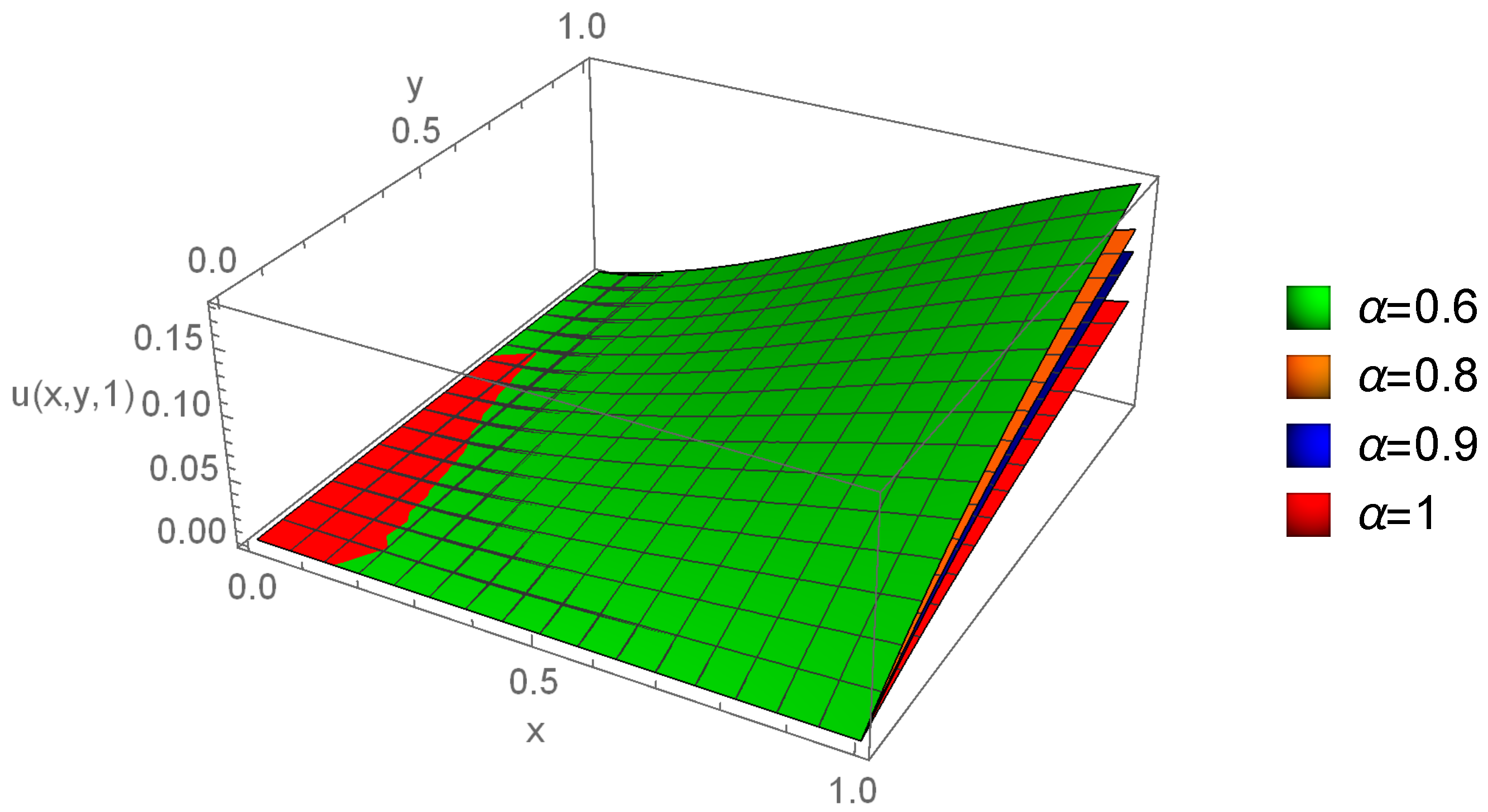
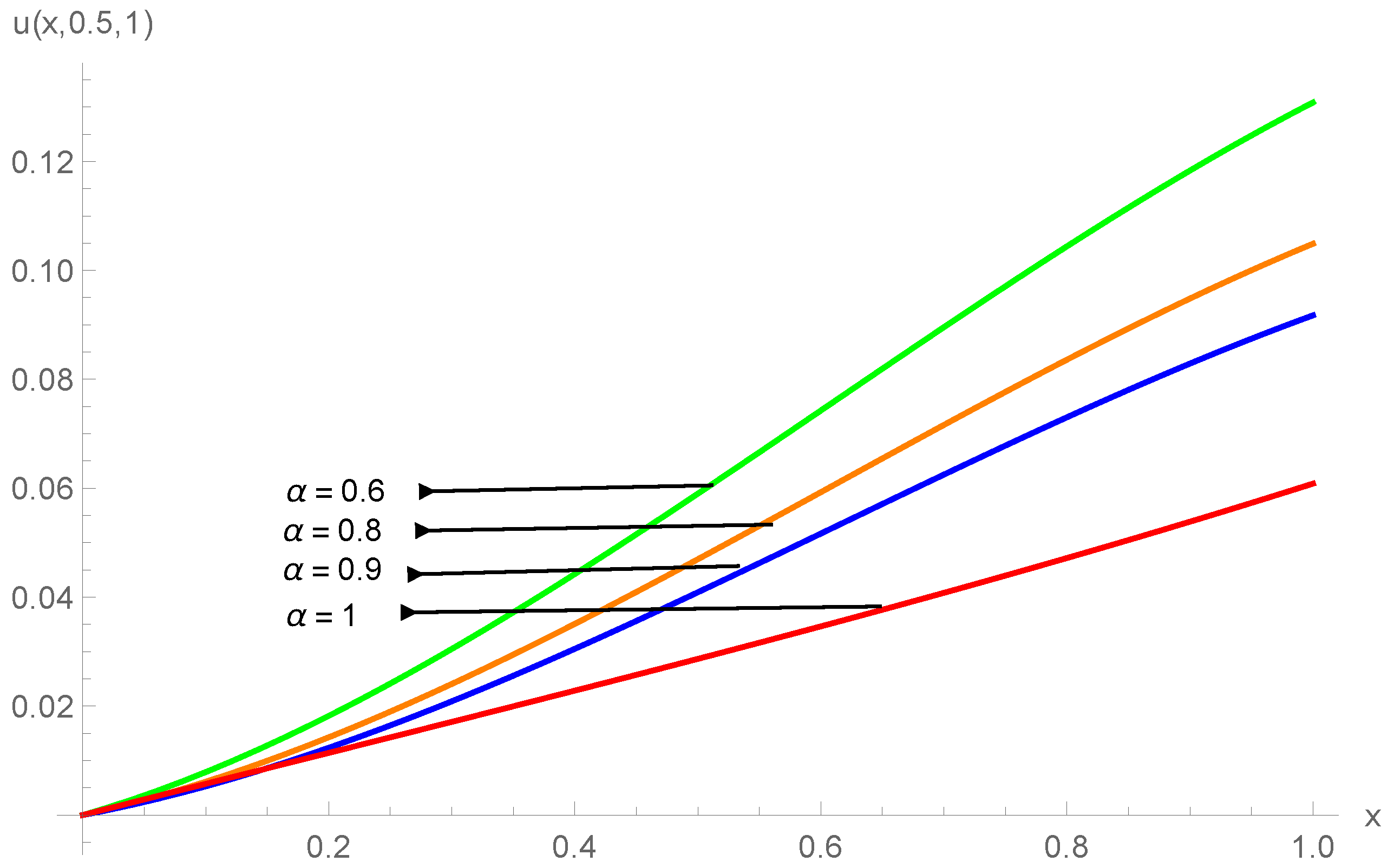
5. Application
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Nikerov, D.; Korolev, N.; Nikitenko, V.; Tyutnev, A. Theoretical analysis of the drift and diffusion of charge carriers in thin layers of organic crystals. Chem. Phys. 2019, 517, 1–5. [Google Scholar] [CrossRef]
- Gorenflo, R.; Mainardi, F. Fractional diffusion processes: Probability distributions and continuous time random walk. In Processes with Long-Range Correlations; Springer: Berlin/Heidelberg, Germany, 2003; pp. 148–166. [Google Scholar]
- Gorenflo, R.; Mainardi, F.; Vivoli, A. Continuous-time random walk and parametric subordination in fractional diffusion. Chaos Solitons Fractals 2007, 34, 87–103. [Google Scholar] [CrossRef]
- Das, S. Analytical solution of a fractional diffusion equation by variational iteration method. Comput. Math. Appl. 2009, 57, 483–487. [Google Scholar] [CrossRef]
- Vishal, K.; Kumar, S.; Das, S. Application of homotopy analysis method for fractional Swift Hohenberg equation–revisited. Appl. Math. Model. 2012, 36, 3630–3637. [Google Scholar] [CrossRef]
- Biswas, C.; Das, S.; Singh, A.; Altenbach, H. Solution of variable-order partial integro-differential equation using Legendre wavelet approximation and operational matrices. ZAMM-J. Appl. Math. Mech. Angew. Math. Mech. 2023, 103, e202200222. [Google Scholar] [CrossRef]
- Das, S.; Gupta, P. A mathematical model on fractional Lotka–Volterra equations. J. Theor. Biol. 2011, 277, 1–6. [Google Scholar] [CrossRef]
- Choo, K.; Muniandy, S.; Woon, K.; Gan, M.; Ong, D. Modeling anomalous charge carrier transport in disordered organic semiconductors using the fractional drift-diffusion equation. Org. Electron. 2017, 41, 157–165. [Google Scholar] [CrossRef]
- Zamani, S. Reaction-diffusion equations with polynomial drifts driven by fractional Brownian motions. Stoch. Anal. Appl. 2010, 28, 1020–1039. [Google Scholar] [CrossRef]
- Abdelkawy, M.; Alyami, S. Legendre-Chebyshev spectral collocation method for two-dimensional nonlinear reaction-diffusion equation with Riesz space-fractional. Chaos Solitons Fractals 2021, 151, 111279. [Google Scholar] [CrossRef]
- Jafari, H.; Babaei, A.; Banihashemi, S. A novel approach for solving an inverse reaction–diffusion–convection problem. J. Optim. Theory Appl. 2019, 183, 688–704. [Google Scholar] [CrossRef]
- Askar, A.H.; Nagy, Á.; Barna, I.F.; Kovács, E. Analytical and Numerical Results for the Diffusion-Reaction Equation When the Reaction Coefficient Depends on Simultaneously the Space and Time Coordinates. Computation 2023, 11, 127. [Google Scholar] [CrossRef]
- Rashidinia, J.; Momeni, A.; Molavi-Arabshahi, M. Solution of convection-diffusion model in groundwater pollution. Sci. Rep. 2024, 14, 2075. [Google Scholar] [CrossRef] [PubMed]
- Postavaru, O. An efficient numerical method based on Fibonacci polynomials to solve fractional differential equations. Math. Comput. Simul. 2023, 212, 406–422. [Google Scholar] [CrossRef]
- Sadeghi, S.; Jafari, H.; Nemati, S. Operational matrix for Atangana–Baleanu derivative based on Genocchi polynomials for solving FDEs. Chaos Solitons Fractals 2020, 135, 109736. [Google Scholar] [CrossRef]
- Mező, I. A new formula for the Bernoulli polynomials. Results Math. 2010, 58, 329–335. [Google Scholar] [CrossRef]
- Youssri, Y.H.; Atta, A.G. Spectral collocation approach via normalized shifted Jacobi polynomials for the nonlinear Lane-Emden equation with fractal-fractional derivative. Fractal Fract. 2023, 7, 133. [Google Scholar] [CrossRef]
- Singh, A.K.; Mehra, M. Wavelet collocation method based on Legendre polynomials and its application in solving the stochastic fractional integro-differential equations. J. Comput. Sci. 2021, 51, 101342. [Google Scholar] [CrossRef]
- Srivastava, H.M.; Adel, W.; Izadi, M.; El-Sayed, A.A. Solving some physics problems involving fractional-order differential equations with the Morgan-Voyce polynomials. Fractal Fract. 2023, 7, 301. [Google Scholar] [CrossRef]
- Zogheib, B.; Tohidi, E. Modal Hermite spectral collocation method for solving multi-dimensional hyperbolic telegraph equations. Comput. Math. Appl. 2018, 75, 3571–3588. [Google Scholar] [CrossRef]
- Dolapçi, İ.T. Chebyshev collocation method for solving linear differential equations. Math. Comput. Appl. 2004, 9, 107–115. [Google Scholar] [CrossRef]
- Mirkov, N.; Rašuo, B. Bernstein polynomial collocation method for elliptic boundary value problems. PAMM 2013, 13, 421–422. [Google Scholar] [CrossRef]
- Cui, T.; Xu, C. Müntz Legendre polynomials: Approximation properties and applications. Math. Comput. 2024, 93. [Google Scholar] [CrossRef]
- Bakhet, A.; Hussain, S.; Niyaz, M.; Zakarya, M.; AlNemer, G. On the Two-Variable Analogue Matrix of Bessel Polynomials and Their Properties. Axioms 2024, 13, 202. [Google Scholar] [CrossRef]
- Eid, A.; Khader, M.; Megahed, A.M. Vieta-Lucas Collocation Technique for Examination of the Flow of Casson Fluid over a Slippery Stretching Sheet Which Is Impacted by Thermal Slip, Ohmic Dissipation, and Variable Thermal Conductivity. J. Math. 2023, 2023, 8723343. [Google Scholar] [CrossRef]
- Biswas, C.; Singh, A.; Chopra, M.; Das, S. Study of fractional-order reaction-advection-diffusion equation using neural network method. Math. Comput. Simul. 2023, 208, 15–27. [Google Scholar] [CrossRef]
- Srivastava, H.M.; Izadi, M. Generalized shifted airfoil polynomials of the second kind to solve a class of singular electrohydrodynamic fluid model of fractional order. Fractal Fract. 2023, 7, 94. [Google Scholar] [CrossRef]


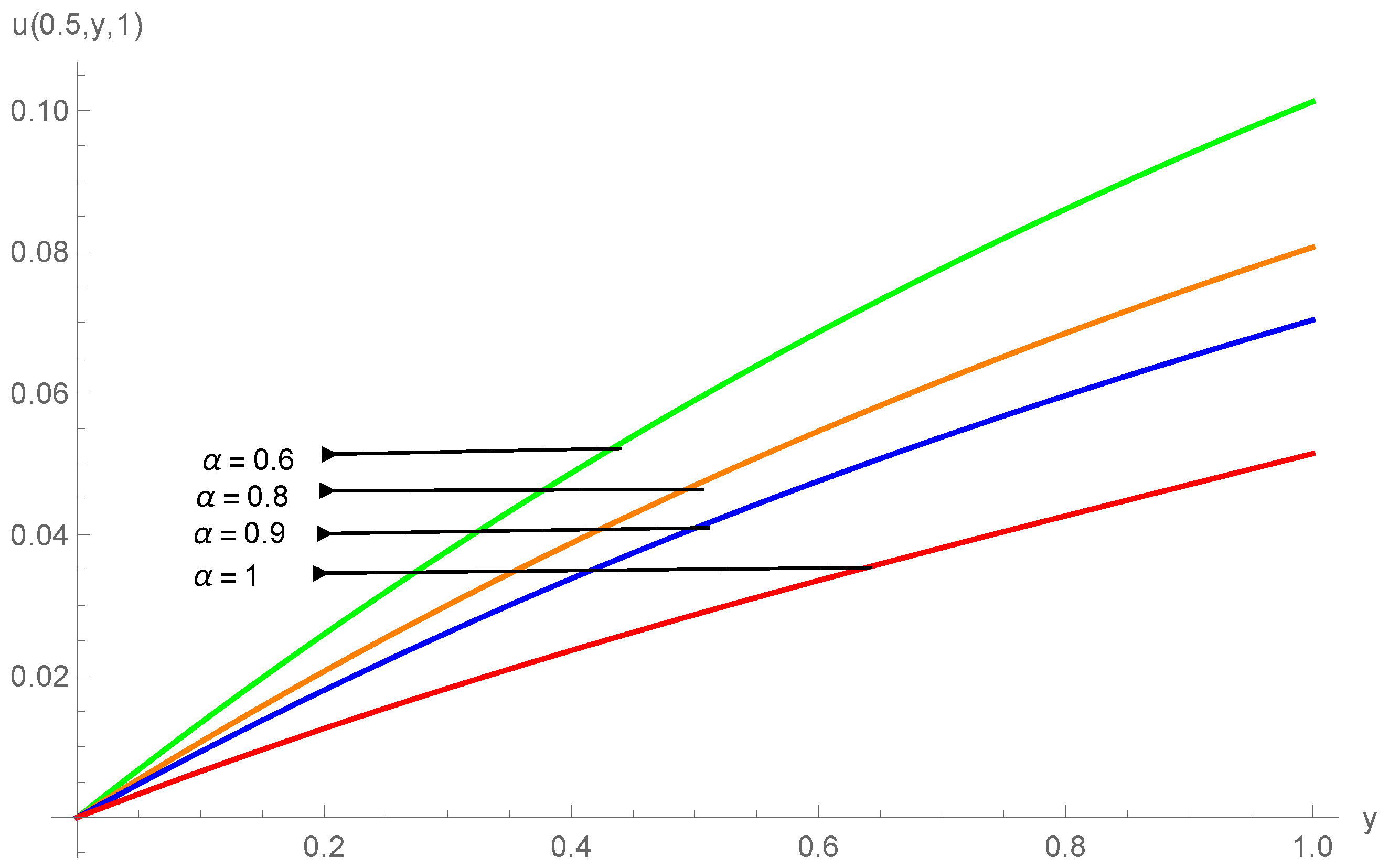

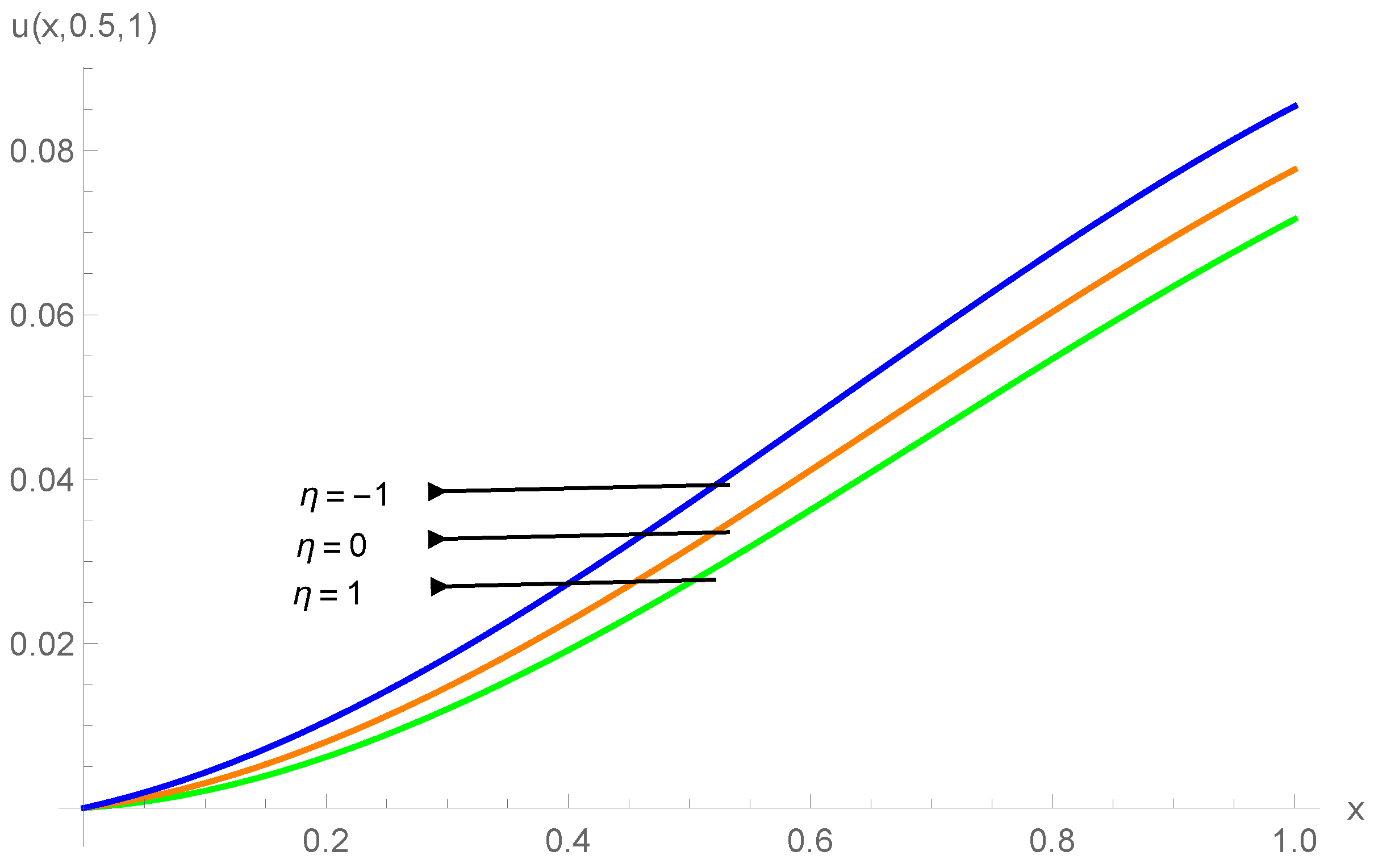
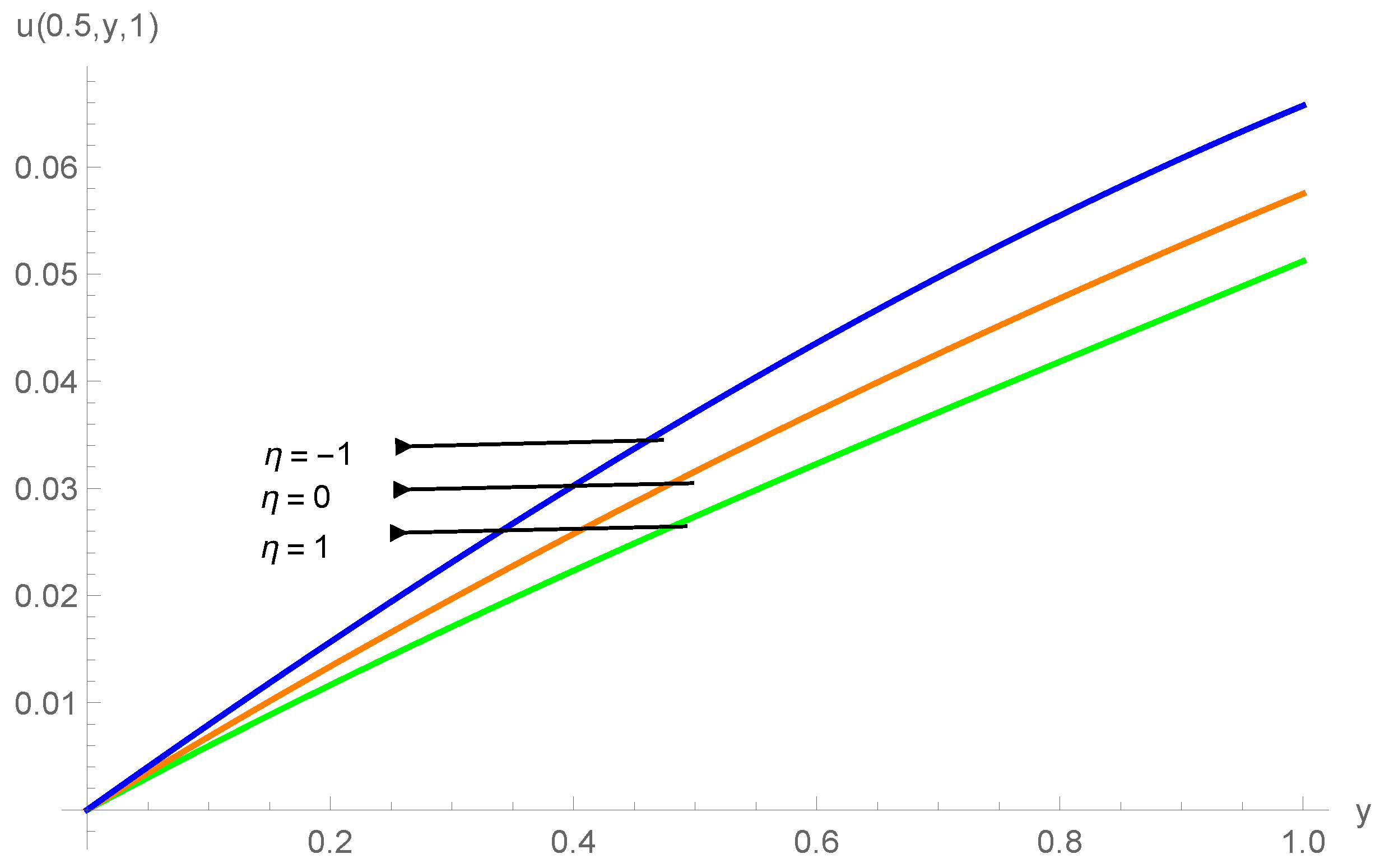
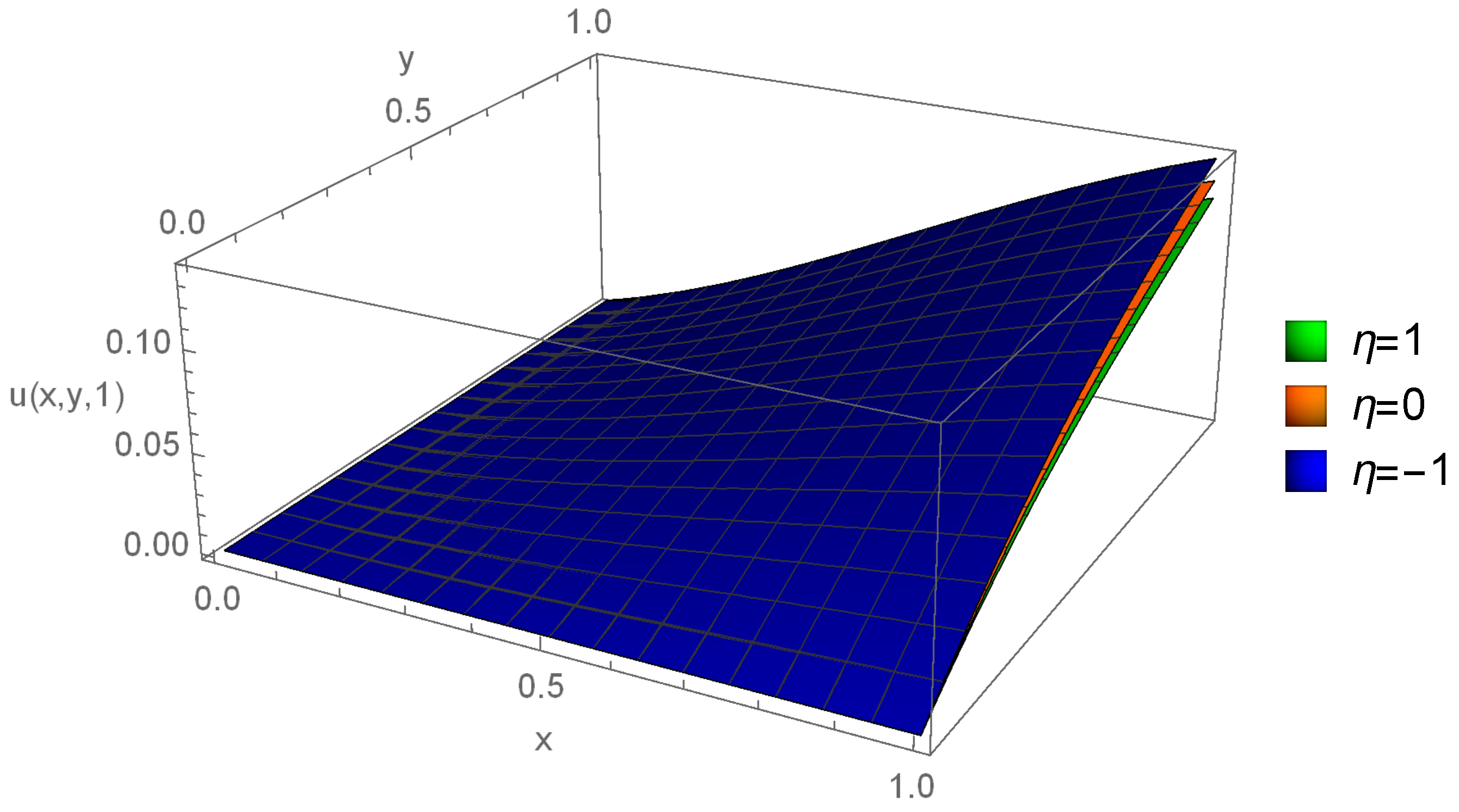
| () | |
|---|---|
| (3, 3, 3) | |
| (4, 4, 4) | |
| (5, 5, 4) | |
| (5, 5, 5) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Anjuman; Leung, A.Y.T.; Das, S. Two-Dimensional Time-Fractional Nonlinear Drift Reaction–Diffusion Equation Arising in Electrical Field. Fractal Fract. 2024, 8, 456. https://doi.org/10.3390/fractalfract8080456
Anjuman, Leung AYT, Das S. Two-Dimensional Time-Fractional Nonlinear Drift Reaction–Diffusion Equation Arising in Electrical Field. Fractal and Fractional. 2024; 8(8):456. https://doi.org/10.3390/fractalfract8080456
Chicago/Turabian StyleAnjuman, Andrew Y. T. Leung, and Subir Das. 2024. "Two-Dimensional Time-Fractional Nonlinear Drift Reaction–Diffusion Equation Arising in Electrical Field" Fractal and Fractional 8, no. 8: 456. https://doi.org/10.3390/fractalfract8080456
APA StyleAnjuman, Leung, A. Y. T., & Das, S. (2024). Two-Dimensional Time-Fractional Nonlinear Drift Reaction–Diffusion Equation Arising in Electrical Field. Fractal and Fractional, 8(8), 456. https://doi.org/10.3390/fractalfract8080456






