A Fast Second-Order ADI Finite Difference Scheme for the Two-Dimensional Time-Fractional Cattaneo Equation with Spatially Variable Coefficients

Abstract

This paper presents an efficient finite difference method for solving the time-fractional Cattaneo equation with spatially variable coefficients in two spatial dimensions. The main idea is that the original equation is first transformed into a lower system, and then the graded mesh-based fast L2-$1_{\sigma }$ formula and second-order spatial difference operator for the Caputo derivative and the spatial differential operator are applied, respectively, to derive the fully discrete finite difference scheme. By adding suitable perturbation terms, we construct an efficient fast second-order ADI finite difference scheme, which significantly improves computational efficiency for solving high-dimensional problems. The corresponding stability and error estimate are proved rigorously. Extensive numerical examples are shown to substantiate the accuracy and efficiency of the proposed numerical scheme.

1. Introduction

In this paper, we study the efficient numerical scheme for solving the time-fractional Cattaneo equation with spatially variable coefficients:

$${\partial }_{t}u(\mathbf{x},t)+\kappa {\hspace{0.25em}}_C{D}_{0,t}^{\alpha }u(\mathbf{x},t)=\mathcal{L}u(\mathbf{x},t)+f(\mathbf{x},t),\mathrm{in}\Omega \times (0,T),$$

(1)

where the boundary and initial conditions are $u(\mathbf{x},t)=0$ on $\partial \Omega \times (0,T]$, and $u(\mathbf{x},0)=u_0\left(\mathbf{x}\right),{\partial }_{t}u(\mathbf{x},0)=u_1\left(\mathbf{x}\right)$ in $\Omega$, respectively. Here, the coefficient $\kappa$ is positive, $\mathbf{x}=(x_1,x_2)\in \Omega \subset {\mathbb{R}}^2$ with a bounded rectangle domain $\Omega$, and T is a fixed time.

The spatial differential operator $\mathcal{L}={\mathcal{L}}_1+{\mathcal{L}}_2$, where ${\mathcal{L}}_{k}u={\partial }_{x_k}\left(d_k{\partial }_{x_k}u\right)$ with $d_k:=d_k(x_1,x_2)(k=1,2)$. The coefficient $d_k$ is supposed to satisfy $0<\underline{d}\le d_k\le \overline{d}$, where $\underline{d}$ and $\overline{d}$ are the proper lower and upper bounds of $d_k$, respectively. In addition, the coefficient $d_k$ and the source term f are assumed to be sufficiently smooth with respect to their arguments, ensuring that our methods can achieve the claimed convergence accuracy and consistency. The Caputo derivative ${\hspace{0.25em}}_C{D}_{0,t}^{\alpha }u(\mathbf{x},t)$ with $\alpha \in (1,2)$ is defined by

$${\hspace{0.25em}}_C{D}_{0,t}^{\alpha }u(\mathbf{x},t)={\displaystyle \frac{1}{\Gamma (2-\alpha )}}{\int }_0^t{(t-s)}^{1-\alpha }{\displaystyle \frac{{\partial }^{2}u(\mathbf{x},s)}{\partial s^2}}\mathrm{d}s.$$

The fractional model (1) or its variants plays an important role in the description of anomalous transport and has been studied extensively in recent decades; see [1,2,3,4,5] and the references therein for more details. In our recent paper [6], we constructed an efficient difference scheme for solving the fractional model (1) with constant diffusion coefficients (i.e., the case $d_1=d_2=constant$). We applied the fast L2-$1_{\sigma }$ formula and the compact difference operator to discrete the Caputo derivative and the Laplacian appearing in the lower-order system, which is transformed by the original equation, and then combined with the fast discrete Sine transform (DST) technique to further improve the computational efficiency. However, it seems that the DST technique is not applicable for the fractional model (1) considered here, because of the appearance of the spatial variable coefficients in (1). In order to address this issue, we need to resort to other fast solvers.

It is well known that the ADI (alternating direction implicit) technique is effective in dealing with high-dimensional problems, since it can reduce the original problems to a series of independent one-dimensional problems, significantly improving the computational efficiency with lower computational complexity and CPU time. There have been many various numerical schemes based on the ADI technique for solving high-dimensional fractional models in recent years; see [7,8,9,10,11,12], just to name a few. As far as we know, for the ADI numerical study of the model (1), there is little work available on this subject [13,14,15]. In [13], Ren and Gao developed an efficient compact ADI scheme for (1) with constant coefficients. In [14], Zhao and Sun proposed a compact Crank-Nicolson scheme for (1) with $d_1=d_1\left(x_1\right)$ and $d_2=d_2\left(x_2\right)$. In addition, the numerical methods obtained in the previous two papers have lower temporal accuracy, since the L1 formula is used. In [15], Chen and Li considered a two-dimensional time-fractional partial differential equation with damping and proposed an ADI finite element method based on the L2-$1_{\sigma }$ formula. It is worth noting that the numerical schemes mentioned above are derived based on the temporally uniform meshes, which may lead to a lower accuracy for the less regular solution problems.

Furthermore, for the computational efficiency of the corresponding numerical scheme, apart from the high spatial dimensionality, which has a significant impact on it, the fractional derivative also has a strong influence over it, because this fractional derivative is non-local. So, the corresponding numerical scheme needs to store all the historical numerical solutions when calculating the current numerical solutions, which makes it extremely difficult to numerically simulate high-dimensional fractional models. There have been some efforts made on this topic; see [16,17,18] and the corresponding references therein. However, to the best of our knowledge, it seems that studies on the fast solver of the time-fractional model with spatially variable coefficients (1) are quite sparse.

In this paper, we aim to develop such numerical scheme solving (1) that can effectively handle the problem of initial weak singular solutions while overcoming the computational efficiency problems arising from the nonlocality of fractional derivatives and high dimensionality in space. By applying the graded mesh-based fast L2-$1_{\sigma }$ formula and the ADI technique for the equivalent lower system of the original equation, we can derive a fast second-order ADI finite difference scheme for the high-dimensional fractional model with spatially variable coefficients (1). The contributions of this paper are listed as follows: First, we develop an efficient ADI finite difference scheme based on the temporally graded meshes. By the graded mesh-based sum-of-exponential (SOE) and ADI techniques, the proposed scheme’s computational efficiency is greatly improved. Second, we present the rigorous proof of the corresponding stability and error estimate for the case of temporally uniform meshes. Third, extensive numerical examples are given to verify the numerical theories.

The structure of this paper is as follows. Section 2 derives the fast second-order finite difference scheme by applying the graded meshes-based fast L2-$1_{\sigma }$ formula. In Section 3, in order to deal with the high-dimensional problems, an efficient ADI difference scheme is constructed. The stability and error estimate of the proposed ADI difference scheme are given in Section 4. Numerical examples and the conclusions are provided in Section 5 and Section 6, respectively.

2. Derivation of the Difference Scheme

By setting $\varphi (\mathbf{x},t)={\partial }_{t}u(\mathbf{x},t)$ for (1), we get the following lower-order system:

$$\varphi (\mathbf{x},t)+\kappa {\hspace{0.25em}}_C{D}_{0,t}^{\alpha -1}\varphi (\mathbf{x},t)=\mathcal{L}u(\mathbf{x},t)+f(\mathbf{x},t).$$

(2)

In the following, we shall derive the difference scheme based on this equivalent lower-order system.

Suppose the rectangle domain $\Omega =[x_1^L,x_1^R]\times [x_2^L,x_2^R]$. Let the spatial stepsize be $h_k=(x_k^R-x_k^L)/M_k$ and the grid points be $x_{k,j_k}=x_k^L+j_k{h}_k(j_k=0,1,\cdots ,M_k)$, where $M_k(k=1,2)$ is a positive integer. The fully discrete grids on $\Omega$ are given by ${\overline{\Omega }}_h=\{{\mathbf{x}}_h=(x_{1,j_1},x_{2,j_2})|0\le j_k\le M_k(k=1,2)\}$. The inner and boundary grids are denoted by ${\Omega }_h={\overline{\Omega }}_h\cap \Omega$ and $\partial {\Omega }_h={\overline{\Omega }}_h\cap \partial \Omega$, respectively. We denote the space of grid function as $V_h=\left\{v\right|v={\left(v_h\right)}_{{\mathbf{x}}_h}\mathrm{and}{v}_h=0\mathrm{for}{\mathbf{x}}_h\in \partial {\Omega }_h\}$.

For the grid function $v_h=v\left({\mathbf{x}}_h\right)$ with the index vector $h=(i_1,i_2)$ at the kth position $(k=1,2)$, we define the spatial difference operator as ${\mathcal{L}}_h={\mathcal{L}}_1^h+{\mathcal{L}}_2^h$, where

$${\mathcal{L}}_k^h{v}_{i_k}={\displaystyle \frac{1}{h_k}}\left[{\left(d_k\right)}_{i_k+\frac{1}{2}}{\delta }_k{v}_{i_k+\frac{1}{2}}-{\left(d_k\right)}_{i_k-\frac{1}{2}}{\delta }_k{v}_{i_k-\frac{1}{2}}\right].$$

Here, $k=1,2$, and

$${\delta }_k{v}_{i_k+\frac{1}{2}}={\displaystyle \frac{v_{i_k+1}-v_{i_k}}{h_k}}.$$

So, for ${\mathbf{x}}_h\in {\Omega }_h$, we have $\mathcal{L}v\left({\mathbf{x}}_h\right)={\mathcal{L}}_h{v}_h+O\left({\mathbf{h}}^2\right)$ where $\mathbf{h}=(h_1,h_2)$ [19].

Since the solution of the time-fractional differential equation is not always sufficiently smooth at the initial time layer, in this paper, we adopt the graded meshes $t_n=T{\left({\displaystyle \frac{n}{N_t}}\right)}^{\gamma }$ in time. Here, $n=0,\cdots ,N_t$, $N_t$ is a positive integer, and $\gamma \ge 1$ is a proper chosen temporal mesh grading parameter. Denote the time stepsize ${\tau }_k=t_k-t_{k-1}$. Set $t_{k+\sigma }=t_k+\sigma {\tau }_{k+1}$ and $D_{{\tau }_k}{g}^k={\displaystyle \frac{g^k-g^{k-1}}{{\tau }_k}}$ with $g^k=g\left(t_k\right)$. The graded meshes-based fast L2-1_σ formula for the approximation of the Caputo derivative ${\hspace{0.25em}}_C{D}_{0,t}^{\beta }g\left(t\right)$ with $\beta \in (0,1)$ at the grid point $t=t_{n+\sigma }$ is defined as

$${\hspace{0.25em}}^F{\overline{D}}_{{\tau }_n}^{\beta }{g}^{n+\sigma }={\varpi }_0{D}_{{\tau }_{n+1}}{g}^{n+1}+\sum _{k=1}^{N_{exp}}{\varpi }_k{e}^{-s_k\sigma {\tau }_{n+1}}{H}_k\left(t_n\right),$$

(3)

where $\sigma =1-\beta /2,{\varpi }_0={\displaystyle \frac{{\left(\sigma {\tau }_1\right)}^{1-\beta }}{\Gamma (2-\beta )}}$ and $H_k\left(t_j\right)(j\ge 0)$ are obtained by the following recurrence:

$$H_k\left(t_j\right)=e^{-s_k{\tau }_j}{H}_k\left(t_{j-1}\right)+a_{k,j}{D}_{{\tau }_j}{g}^j+b_{k,j}(D_{{\tau }_{j+1}}{g}^{j+1}-D_{{\tau }_j}{g}^j),$$

(4)

with the initial value $H_k\left(t_0\right)=0$. Here, the coefficients $a_{k,j}={\displaystyle \frac{1}{s_k}}(1-e^{-s_k{\tau }_j})$ and $b_{k,j}={\displaystyle \frac{2}{{\tau }_j+{\tau }_{j+1}}}{\int }_{t_{j-1}}^{t_j}(t-t_{j-\frac{1}{2}})e^{-s_k(t_j-t)}dt$. The weights ${\varpi }_k$ and the points $s_k$ are chosen to satisfy

$$\left|{\displaystyle \frac{t^{-\beta }}{\Gamma (1-\beta )}}-\sum _{k=1}^{N_{exp}}{\varpi }_k{e}^{-s_{k}t}\right|\le ϵ,\forall t\in [t_1,T],$$

where $ϵ$ is the absolute tolerance error and the number of exponentials $N_{exp}$ satisfies

$$N_{exp}=O\left(log{\displaystyle \frac{1}{ϵ}}\left(loglog{\displaystyle \frac{1}{ϵ}}+log{\displaystyle \frac{T}{{\tau }_1}}\right)+log{\displaystyle \frac{1}{{\tau }_1}}\left(loglog{\displaystyle \frac{1}{ϵ}}+log{\displaystyle \frac{1}{{\tau }_1}}\right)\right).$$

We omit the details of the derivation in (3), since one may refer to [20].

So, replacing ${\hspace{0.25em}}_C{D}_{0,t}^{\alpha -1}$ and $\mathcal{L}$ in the Equation (2) with the difference operator ${\hspace{0.25em}}^F{\overline{D}}_{{\tau }_n}^{\alpha -1}$ and ${\mathcal{L}}_h$, respectively, we obtain

$$\left\{\begin{array}{cc}\hfill & {\varphi }_h^{n+\sigma }+\kappa {\hspace{0.25em}}^F{\overline{D}}_{{\tau }_n}^{\alpha -1}{\varphi }_h^{n+\sigma }={\mathcal{L}}_h{u}_h^{n+\sigma }+f_h^{n+\sigma }+R^n,\hfill \\ \hfill & {\delta }_t{u}_h^{\frac{1}{2}}={\varphi }_h^{\frac{1}{2}}+r^0,\hfill \\ \hfill & {\widehat{\delta }}_t{u}_h^n={\varphi }_h^{n+\sigma }+r^n,\hfill \end{array}\right.$$

(5)

where $n\ge 0$, ${\varphi }_h^{n+\sigma }$ and $f_h^{n+\sigma }$ are the grid functions defined by ${\varphi }_h^{n+\sigma }=\sigma \varphi ({\mathbf{x}}_h,t_{n+1})+(1-\sigma )\varphi ({\mathbf{x}}_h,t_n)$ and $f_h^{n+\sigma }=f({\mathbf{x}}_h,t_{n+\sigma })$, respectively. $u_h^{n+\sigma }$ is similarly defined as ${\varphi }_h^{n+\sigma }$. In addition, ${\delta }_t{u}_h^{\frac{1}{2}}=(u({\mathbf{x}}_h,t_1)-u({\mathbf{x}}_h,t_0))/{\tau }_1$, ${\varphi }_h^{\frac{1}{2}}=(\varphi ({\mathbf{x}}_h,t_1)+\varphi ({\mathbf{x}}_h,t_0))/2$, and

$${\widehat{\delta }}_t{u}_h^n={\displaystyle \frac{u({\mathbf{x}}_h,t_{n+1})-u({\mathbf{x}}_h,t_n)}{C_1}}-C_2{\displaystyle \frac{u({\mathbf{x}}_h,t_n)-u({\mathbf{x}}_h,t_{n-1})}{{\tau }_n}},$$

where $C_1={\displaystyle \frac{{\tau }_{n+1}({\tau }_n+{\tau }_{n+1})}{{\tau }_n+2\sigma {\tau }_{n+1}}}$ and $C_2={\displaystyle \frac{(2\sigma -1){\tau }_{n+1}}{{\tau }_n+{\tau }_{n+1}}}$. The expressions of the above local truncation errors $R^n$ and $r^n(n\ge 0)$ in (5) are a little bit complex. If setting the grading parameter to $\gamma =1$, they have the simple expressions $R^n=O({\tau }^2+{\mathbf{h}}^2+ϵ)$ and $r^n=O\left({\tau }^2\right)$ for $n\ge 0$, where $\tau ={\displaystyle \frac{T}{N_t}}$. One may partly refer to other papers [21,22] for the temporal truncation errors in $R^n$ and $r^n$, respectively.

In the following, for simplicity and convenience, we shall use the same notations as in (5) if there is no ambiguity. Dropping the small terms $R^n$ and $r^n$, we have the following fast second-order difference scheme for solving (1): Find the numerical solution ${\varphi }_h^n$ of $\varphi ({\mathbf{x}}_h,t_n)$ for $n\ge 1$, such that

$$\left\{\begin{array}{cc}\hfill & {\varphi }_h^{n+\sigma }+\kappa {\hspace{0.25em}}^F{\overline{D}}_{{\tau }_n}^{\alpha -1}{\varphi }_h^{n+\sigma }={\mathcal{L}}_h{u}_h^{n+\sigma }+f_h^{n+\sigma },\hfill \\ \hfill & {\delta }_t{u}_h^{1/2}={\varphi }_h^{1/2},\hfill \\ \hfill & {\widehat{\delta }}_t{u}_h^n={\varphi }_h^{n+\sigma },\hfill \end{array}\right.$$

(6)

where $u_h^0=u_0\left({\mathbf{x}}_h\right),{\varphi }_h^0=u_1\left({\mathbf{x}}_h\right)$, and $u\left({\mathbf{x}}_h\right){|}_{{\mathbf{x}}_h\in \partial {\Omega }_h}=0$. The corresponding numerical solution to (1) is then computed by $u_h^1=u_h^0+{\tau }_1({\varphi }_h^1+{\varphi }_h^0)/2$ and for $n\ge 1$,

$$u_h^{n+1}=u_h^n+C_1\left(C_2{\displaystyle \frac{u_h^n-u_h^{n-1}}{{\tau }_n}}+\sigma {\varphi }_h^{n+1}+(1-\sigma ){\varphi }_h^n\right).$$

(7)

Remark 1. 

There are various alternative approaches for computing the numerical solution at the first time layer. For example, following [23], one can consider the temporal discretization at $t=t_{\frac{1}{2}}$ to derive the following difference scheme:

$$\left\{\begin{array}{cc}\hfill & {\varphi }_h^{\frac{1}{2}}+\kappa {\overline{D}}_{{\tau }_1}^{\alpha -1}{\varphi }_h^{\frac{1}{2}}={\mathcal{L}}_h{u}_h^{\frac{1}{2}}+f_h^{\frac{1}{2}},\hfill \\ \hfill & {\delta }_t{u}_h^{\frac{1}{2}}={\varphi }_h^{\frac{1}{2}},\hfill \end{array}\right.$$

 where

$${\overline{D}}_{{\tau }_1}^{\alpha -1}{\varphi }_h^{\frac{1}{2}}=w_0{D}_{{\tau }_1}{\varphi }_h^1,$$

 with $w_0=t_{\frac{1}{2}}^{2-\alpha }/\Gamma (3-\alpha )$. The corresponding numerical theoretical analyses may be more straightforward. However, it will impact the proposed difference scheme’s overall theoretical convergence order, since the numerical solution’s convergence order at the first time layer is less than two. There are some strategies to improve the temporal accuracy of the numerical solution at the first time layer, e.g., by refining the first time interval [24] or by using Hermite interpolation polynomials [25]. Nevertheless, these strategies have some limitations, such as increasing the computational complexity of the numerical scheme or requiring highly regular problem solutions. So, we prefer to consider the temporal discretization of fractional model (1) at $t=t_{\sigma }$ instead of $t=t_{\frac{1}{2}}$ when computing the numerical solution at the first time layer.

3. The Derivation of the Fast ADI Difference Scheme

In this part, we use the ADI technique to further reduce the computational complexity of the numerical scheme (6). To this end, for the case of $n\ge 1$, we rewrite the expression of (5) as

$$\begin{array}{ccc}\hfill \hspace{0.25em}& & (\sigma +{\displaystyle \frac{\kappa ({\varpi }_0+\tilde{\varpi })}{{\tau }_{n+1}}}){\varphi }_h^{n+1}-{\sigma }^2{C}_1{\mathcal{L}}_h{\varphi }_h^{n+1}\hfill \\ & =& -\kappa \sum _{k=1}^{N_{exp}}{\varpi }_k{e}^{-s_k\sigma {\tau }_{n+1}}\left(e^{-s_k{\tau }_n}{H}_k\left(t_{n-1}\right)+a_{k,n}{D}_{{\tau }_n}{\varphi }_h^n-b_{k,n}{D}_{{\tau }_n}{\varphi }_h^n\right)\hfill \\ & & -(1-\sigma -{\displaystyle \frac{\kappa ({\varpi }_0+\tilde{\varpi })}{{\tau }_{n+1}}}){\varphi }_h^n+\sigma (1-\sigma )C_1{\mathcal{L}}_h{\varphi }_h^n\hfill \\ & & +{\mathcal{L}}_h{u}_h^n+\sigma {\displaystyle \frac{C_1{C}_2}{{\tau }_n}}({\mathcal{L}}_h{u}_h^n-{\mathcal{L}}_h{u}_h^{n-1})+f_h^{n+\sigma }+R^n=:F_h^n,\hfill \end{array}$$

(8)

from which we obtain a compact form

$${\varphi }_h^{n+1}-{\mu }_1{\mathcal{L}}_h{\varphi }_h^{n+1}=b_h^n.$$

(9)

Here, $\tilde{\varpi }={\sum }_{k=1}^{N_{exp}}{\varpi }_k{e}^{-s_k\sigma {\tau }_{n+1}}{b}_{k,n}$, ${\mu }_1={\displaystyle \frac{{\sigma }^2{C}_1}{{\mu }_{10}}}$ and $b_h^n={\displaystyle \frac{F_h^n}{{\mu }_{10}}}$ with ${\mu }_{10}=\sigma +{\displaystyle \frac{\kappa ({\varpi }_0+\tilde{\varpi })}{{\tau }_{n+1}}}$.

Similarly, for the case $n=0$ in (6), we have

$$\begin{array}{ccc}\hfill \hspace{0.25em}& & (\sigma +{\displaystyle \frac{\kappa {\varpi }_0}{{\tau }_1}}){\varphi }_h^1-\sigma {\displaystyle \frac{{\tau }_1}{2}}{\mathcal{L}}_h{\varphi }_h^1\hfill \\ & =& -(1-\sigma -{\displaystyle \frac{\kappa {\varpi }_0}{{\tau }_1}}){\varphi }_h^0+\sigma {\displaystyle \frac{{\tau }_1}{2}}{\mathcal{L}}_h{\varphi }_h^0+{\mathcal{L}}_h{u}_h^0+f_h^{\sigma }+R^0=:F_h^0.\hfill \end{array}$$

(10)

That is,

$${\varphi }_h^1-{\mu }_0{\mathcal{L}}_h{\varphi }_h^1=b_h^0,$$

(11)

where ${\mu }_0={\displaystyle \frac{\sigma {\tau }_1}{2{\mu }_{00}}}$ and $b_h^0={\displaystyle \frac{F_h^0}{{\mu }_{00}}}$ with ${\mu }_{00}=\sigma +{\displaystyle \frac{\kappa {\varpi }_0}{{\tau }_1}}$.

Adding the perturbation terms ${\displaystyle \frac{{\mu }_1^2}{\sigma }}{\mathcal{L}}_1^h{\mathcal{L}}_2^h{\varphi }_h^{n+\sigma }$ and $2{\mu }_0^2{\mathcal{L}}_1^h{\mathcal{L}}_2^h{\varphi }_h^{\frac{1}{2}}$ on both sides of (9) and (11), respectively, we have the following fast second-order ADI finite difference scheme:

$$(I-\mu {\mathcal{L}}_1^h)(I-\mu {\mathcal{L}}_2^h){\varphi }_h^{n+1}={\tilde{b}}_h^n,$$

(12)

with $\mu ={\mu }_1,{\tilde{b}}_h^n=b_h^n-{\mu }_1^2{\displaystyle \frac{1-\sigma }{\sigma }}{\mathcal{L}}_1^h{\mathcal{L}}_2^h{\varphi }_h^n$ for $n\ge 1$ and $\mu ={\mu }_0,{\tilde{b}}_h^n=b_h^0-{\mu }_0^2{\mathcal{L}}_1^h{\mathcal{L}}_2^h{\varphi }_h^0$ for $n=0$. Here, I is an identity operator. Note that we have omitted the small terms on the right-hand side of (12), that is, $R^n(n\ge 0)$ and the perturbation terms, to obtain a fully discrete finite difference scheme. More details for the small terms shall be discussed in the next section.

By introducing the intermediate variable ${\varphi }_h^{★}=(I-\mu {\mathcal{L}}_2^h){\varphi }_h^{n+1}$, we can solve the original scheme (6) through two sets of independent one-dimensional systems:

• First, the intermediate variables ${\varphi }_h^{★}$ are obtained by computing the system

  $$(I-\mu {\mathcal{L}}_1^h){\varphi }_h^{★}={\tilde{b}}_h^n;$$
• Then, we obtain the numerical solution ${\varphi }_h^n$ by solving

  $$(I-\mu {\mathcal{L}}_2^h){\varphi }_h^{n+1}={\left({\varphi }_h^{★}\right)}^T.$$

The numerical solutions $u_h^n(n\ge 1)$ of the fractional model (1) are thus obtained by ${\varphi }_h^{n+1}$; see (7).

4. Stability and Error Estimate

This part presents the stability and error estimate for the fast second-order ADI finite difference scheme (12). For the ease of presentation, here and thereafter, we assume that the variable coefficients $d_k$ in the fractional model (1) satisfy $d_k=d_k\left(x_k\right)$ with $k=1,2$, unless otherwise noted. Note that we consider the central difference method for the approximation of the spatial differential operator $\mathcal{L}$ in this paper. Indeed, under the above assumptions, one may further use the compact difference method instead; see [26] for more details. We remark that the numerical theory for the corresponding compact finite difference scheme can be derived from the ideas presented here, so we restrict ourselves to the central difference method.

Some notations and lemmas are introduced first. For any grid functions $u,v\in V_h$, we define the discrete inner products and norms:

$$\begin{array}{ccc}\hfill (u,v)& =& h_1{h}_2\sum _{{\mathbf{x}}_h\in {\Omega }_h}{u}_h{v}_h,\parallel u\parallel =\sqrt{(u,u)},\hfill \\ \hfill ({\delta }_{k}u,{\delta }_{k}v)& =& h_1{h}_2\sum _{{\mathbf{x}}_h\in {\Omega }_h}{\delta }_k{u}_{i_k+\frac{1}{2}}{\delta }_k{v}_{i_k+\frac{1}{2}},\parallel {\delta }_{k}u\parallel =\sqrt{({\delta }_{k}u,{\delta }_{k}u)},\hfill \\ \hfill {({\delta }_{k}u,{\delta }_{k}v)}_{d_k}& =& h_1{h}_2\sum _{{\mathbf{x}}_h\in {\Omega }_h}{\left(d_k\right)}_{i_k+\frac{1}{2}}{\delta }_k{u}_{i_k+\frac{1}{2}}{\delta }_k{v}_{i_k+\frac{1}{2}},{\parallel {\delta }_{k}u\parallel }_{d_k}=\sqrt{{({\delta }_{k}u,{\delta }_{k}u)}_{d_k}},\hfill \\ \hfill ({\delta }_1{\delta }_{2}u,{\delta }_1{\delta }_{2}v)& =& h_1{h}_2\sum _{i=1}^{M_1}\sum _{j=1}^{M_2}{\delta }_1{\delta }_2{u}_{i-\frac{1}{2},j-\frac{1}{2}}{\delta }_1{\delta }_2{v}_{i-\frac{1}{2},j-\frac{1}{2}},\hfill \\ \hfill {({\delta }_1{\delta }_{2}u,{\delta }_1{\delta }_{2}v)}_d& =& h_1{h}_2\sum _{i=1}^{M_1}\sum _{j=1}^{M_2}{\left(d_1\right)}_{i-\frac{1}{2}}{\left(d_2\right)}_{j-\frac{1}{2}}{\delta }_1{\delta }_2{u}_{i-\frac{1}{2},j-\frac{1}{2}}{\delta }_1{\delta }_2{v}_{i-\frac{1}{2},j-\frac{1}{2}},\hfill \\ \hfill {\left|u\right|}_1& =& \sqrt{\parallel {\delta }_1{u\parallel }^2+{\parallel {\delta }_{2}u\parallel }^2},{\parallel u\parallel }_1=\sqrt{{\parallel u\parallel }^2+{\left|u\right|}_1^2},\hfill \\ \hfill {\left|u\right|}_{★}& =& \sqrt{\parallel {\delta }_1{u\parallel }_{d_1}^2+{\parallel {\delta }_{2}u\parallel }_{d_2}^2},\parallel {\delta }_1{\delta }_{2}u\parallel =\sqrt{({\delta }_1{\delta }_{2}u,{\delta }_1{\delta }_{2}u)},\hfill \\ \hfill \parallel {\delta }_1{\delta }_2{u\parallel }_d& =& \sqrt{{({\delta }_1{\delta }_{2}u,{\delta }_1{\delta }_{2}u)}_d}.\hfill \end{array}$$

Note that we use the notation $v_{i,j}$ here instead of $v_{i_k}(k=1,2)$, introduced in Section 2, for the definition of ${({\delta }_1{\delta }_{2}u,{\delta }_1{\delta }_{2}v)}_d$. We will use one of the two symbols below for expression when needed. In the following, we present some useful results.

Lemma 1. 

Consider the spatial grid functions $u,v\in V_h$; then, for $d_k=d_k(x_1,x_2)(k=1,2)$, we have

$$({\mathcal{L}}_{h}u,v)=-{({\delta }_{1}u,{\delta }_{1}v)}_{d_1}-{({\delta }_{2}u,{\delta }_{2}v)}_{d_2}.$$

(13)

 Especially, for $d_k=d_k\left(x_k\right)(k=1,2)$, we further have

$$({\mathcal{L}}_1^h{\mathcal{L}}_2^{h}u,v)={({\delta }_1{\delta }_{2}u,{\delta }_1{\delta }_{2}v)}_d.$$

(14)

Proof. 

It follows from the definition of ${\mathcal{L}}_k^h(k=1,2)$ that

$$\begin{array}{ccc}\hfill ({\mathcal{L}}_1^{h}u,v)& =& h_1{h}_2\sum _{{\mathbf{x}}_h\in {\Omega }_h}{\mathcal{L}}_1^h{u}_h{v}_h\hfill \\ & =& h_1{h}_2\sum _{i=1}^{M_1-1}\sum _{j=1}^{M_2-1}{\displaystyle \frac{1}{h_1}}\left({\left(d_1{\delta }_{1}u\right)}_{i+\frac{1}{2},j}-{\left(d_1{\delta }_{1}u\right)}_{i-\frac{1}{2},j}\right)·v_{i,j}\hfill \\ & =& h_1{h}_2\sum _{i=2}^{M_1}\sum _{j=1}^{M_2-1}{\displaystyle \frac{1}{h_1}}{\left(d_1{\delta }_{1}u\right)}_{i-\frac{1}{2},j}{v}_{i-1,j}-h_1{h}_2\sum _{i=1}^{M_1-1}\sum _{j=1}^{M_2-1}{\displaystyle \frac{1}{h_1}}{\left(d_1{\delta }_{1}u\right)}_{i-\frac{1}{2},j}{v}_{i,j}\hfill \\ & =& -h_1{h}_2\sum _{i=1}^{M_1}\sum _{j=1}^{M_2-1}{\displaystyle \frac{1}{h_1}}{\left(d_1{\delta }_{1}u\right)}_{i-\frac{1}{2},j}(v_{i,j}-v_{i-1,j})\hfill \\ & & -h_1{h}_2\sum _{j=1}^{M_2-1}{\displaystyle \frac{1}{h_1}}{\left(d_1{\delta }_{1}u\right)}_{\frac{1}{2},j}{v}_{0,j}+h_1{h}_2\sum _{j=1}^{M_2-1}{\displaystyle \frac{1}{h_1}}{\left(d_1{\delta }_{1}u\right)}_{M-\frac{1}{2},j}{v}_{M,j}\hfill \\ & =& -h_1{h}_2\sum _{i=1}^{M_1}\sum _{j=1}^{M_2-1}{\left(d_1{\delta }_{1}u\right)}_{i-\frac{1}{2},j}{\delta }_1{v}_{i-\frac{1}{2},j}=-{({\delta }_{1}u,{\delta }_{1}v)}_{d_1},\hfill \end{array}$$

where the homogeneous boundary conditions of the grid functions are applied in the above last equality. Similarly, we have $({\mathcal{L}}_2^{h}u,v)=-{({\delta }_{2}u,{\delta }_{2}v)}_{d_2}$. Note that ${\mathcal{L}}_h={\mathcal{L}}_1^h+{\mathcal{L}}_2^h$, so we readily have the desired identity (13).

For the identity (14), we have

$$\begin{array}{ccc}& & ({\mathcal{L}}_1^h{\mathcal{L}}_2^{h}u,v)\hfill \\ & =& -h_1{h}_2\sum _{i=1}^{M_1}\sum _{j=1}^{M_2-1}{\left(d_1{\delta }_1{\mathcal{L}}_2^{h}u\right)}_{i-\frac{1}{2},j}{\delta }_1{v}_{i-\frac{1}{2},j}\hfill \\ & =& -h_1{h}_2\sum _{i=1}^{M_1}\sum _{j=1}^{M_2-1}{\left(d_1\right)}_{i-\frac{1}{2}}\left({\delta }_1{\mathcal{L}}_2^h{u}_{i-\frac{1}{2},j}\right)\left({\delta }_1{v}_{i-\frac{1}{2},j}\right)\hfill \\ & =& -h_1{h}_2\sum _{i=1}^{M_1}\sum _{j=1}^{M_2-1}{\left(d_1\right)}_{i-\frac{1}{2}}{\delta }_1{\displaystyle \frac{1}{h_2}}({\left(d_2\right)}_{j+\frac{1}{2}}{\delta }_2{u}_{i-\frac{1}{2},j+\frac{1}{2}}\hfill \\ & & -{\left(d_2\right)}_{j-\frac{1}{2}}{\delta }_2{u}_{i-\frac{1}{2},j-\frac{1}{2}})\left({\delta }_1{v}_{i-\frac{1}{2},j}\right)\hfill \\ & =& -h_1{h}_2\sum _{i=1}^{M_1}\sum _{j=2}^{M_2}{\left(d_1\right)}_{i-\frac{1}{2}}{\left(d_2\right)}_{j-\frac{1}{2}}{\displaystyle \frac{1}{h_2}}{\displaystyle \frac{{\delta }_2{u}_{i,j-\frac{1}{2}}-{\delta }_2{u}_{i-1,j-\frac{1}{2}}}{h_1}}\left({\delta }_1{v}_{i-\frac{1}{2},j-1}\right)\hfill \\ & & +h_1{h}_2\sum _{i=1}^{M_1}\sum _{j=1}^{M_2-1}{\left(d_1\right)}_{i-\frac{1}{2}}{\left(d_2\right)}_{j-\frac{1}{2}}{\displaystyle \frac{1}{h_2}}{\displaystyle \frac{{\delta }_2{u}_{i,j-\frac{1}{2}}-{\delta }_2{u}_{i-1,j-\frac{1}{2}}}{h_1}}\left({\delta }_1{v}_{i-\frac{1}{2},j}\right)\hfill \\ & =& h_1{h}_2\sum _{i=1}^{M_1}\sum _{j=1}^{M_2}{\left(d_1\right)}_{i-\frac{1}{2}}{\left(d_2\right)}_{j-\frac{1}{2}}{\displaystyle \frac{{\delta }_2{u}_{i,j-\frac{1}{2}}-{\delta }_2{u}_{i-1,j-\frac{1}{2}}}{h_1}}·{\displaystyle \frac{{\delta }_1{v}_{i-\frac{1}{2},j}-{\delta }_1{v}_{i-\frac{1}{2},j-1}}{h_2}}\hfill \\ & & +h_1{h}_2\sum _{i=1}^{M_1}{\left(d_1\right)}_{i-\frac{1}{2}}{\left(d_2\right)}_{\frac{1}{2}}{\displaystyle \frac{1}{h_2}}{\displaystyle \frac{{\delta }_2{u}_{i,\frac{1}{2}}-{\delta }_2{u}_{i-1,\frac{1}{2}}}{h_1}}\left({\delta }_1{v}_{i-\frac{1}{2},0}\right)\hfill \\ & & -h_1{h}_2\sum _{i=1}^{M_1}{\left(d_1\right)}_{i-\frac{1}{2}}{\left(d_2\right)}_{M_2-\frac{1}{2}}{\displaystyle \frac{1}{h_2}}{\displaystyle \frac{{\delta }_2{u}_{i,M_2-\frac{1}{2}}-{\delta }_2{u}_{i-1,M_2-\frac{1}{2}}}{h_1}}\left({\delta }_1{v}_{i-\frac{1}{2},M_2}\right)\hfill \\ & =& h_1{h}_2\sum _{i=1}^{M_1}\sum _{j=1}^{M_2}{\left(d_1\right)}_{i-\frac{1}{2}}{\left(d_2\right)}_{j-\frac{1}{2}}{\delta }_1{\delta }_2{u}_{i-\frac{1}{2},j-\frac{1}{2}}{\delta }_1{\delta }_2{v}_{i-\frac{1}{2},j-\frac{1}{2}}.\hfill \end{array}$$

Here, the last equality holds, since the boundary conditions of the grid functions are homogeneous. Thus, the proof is completed. □

The following lemma gives the error bounds for ${|·|}_{★}$ and ${\parallel ·\parallel }_d$.

Lemma 2. 

The following two inequalities hold.

$$\begin{array}{ccc}& & {\parallel u\parallel }^2\le {\displaystyle \frac{1}{6L}}{\left|u\right|}_1^2\le {\displaystyle \frac{1}{6L\underline{d}}}{\left|u\right|}_{★}^2,\hfill \\ & & \underline{d}\parallel {\delta }_1{\delta }_2{u\parallel }_1\le \parallel {\delta }_1{\delta }_2{u\parallel }_d\le \overline{d}{\parallel {\delta }_1{\delta }_{2}u\parallel }_1,\hfill \end{array}$$

where $L={\displaystyle \frac{L_1^2+L_2^2}{L_1^2{L}_2^2}}$ with $L_k=x_k^R-x_k^L(k=1,2)$.

Proof. 

One can readily have the first inequality according to Lemma 2.7 in [27]. In view of the definition ${\parallel ·\parallel }_d$, the second inequality can be obtained by trivial deduction. So, we complete the proof. □

Here and later in this paper, for the sake of presentation, we shall consider the temporally uniform meshes in the numerical theories unless otherwise noted.

We first rewrite the fast L2-$1_{\sigma }$ Formula (3) based on uniform meshes as the following equivalent form [20]:

$${\hspace{0.25em}}^F{\overline{D}}_{\tau }^{\beta }{g}^{n+\sigma }=\sum _{j=0}^n{\widehat{\varpi }}_{n-j}^{(n+1)}(g\left(t_{j+1}\right)-g\left(t_j\right)),$$

(15)

where the weights ${\widehat{\varpi }}_{n-j}^{(n+1)}$ are defined by ${\widehat{\varpi }}_0^{\left(1\right)}={\tau }^{-1}{\varpi }_0$ if $n=0$, and if $n\ge 1$,

$${\widehat{\varpi }}_k^{(n+1)}=\left\{\begin{array}{cc}{A}_0+B_1,\hfill & k=0,\hfill \\ A_k+B_{k+1}-B_k,\hfill & k=1,2,\cdots ,n-1,\hfill \\ A_n-B_n,\hfill & k=n.\hfill \end{array}\right.$$

(16)

Here, $A_0={\tau }^{-1}{\varpi }_0$, $A_{n-k}={\displaystyle \frac{1}{\tau }}{\int }_{t_k}^{t_{k+1}}{\sum }_{j=1}^{N_{exp}}{\varpi }_j{e}^{-s_j(t_{n+\sigma }-s)}ds$, and

$$B_{n-k}={\displaystyle \frac{1}{{\tau }^2}}{\int }_{t_k}^{t_{k+1}}\sum _{j=1}^{N_{exp}}{\varpi }_j{e}^{-s_j(t_{n+\sigma }-s)}(s-t_{k-\frac{1}{2}})ds.$$

Note that the subscript n of the symbol ${\tau }_n$ in (3) has been ignored, since the temporal uniform grids are considered.

The weights ${\widehat{\varpi }}_{n-k}^{(n+1)}$ in the equivalent form (15) have the following properties (Lemma 1 in [6]), which are crucial in the proof of stability and the error estimate.

Lemma 3. 

Suppose the weights ${\widehat{\varpi }}_k^{(n+1)}$ are given by (16); then, we have

$$\sum _{k=1}^{m-1}({\widehat{\varpi }}_{k-1}^{(k+1)}-{\widehat{\varpi }}_k^{(k+1)})\le {\displaystyle \frac{9ϵ(m-1)}{4\Gamma (1-\beta )}}+{\displaystyle \frac{4-3\beta }{{\tau }^{\beta }\Gamma (3-\beta )}}{(m-1+\sigma )}^{1-\beta },$$

and

$$\sum _{k=1}^{m-1}{\widehat{\varpi }}_k^{(k+1)}\le {\displaystyle \frac{ϵ(m-1)}{\Gamma (1-\beta )}}+{\displaystyle \frac{{(m-1+\sigma )}^{1-\beta }}{{\tau }^{\beta }\Gamma (2-\beta )}}.$$

We state the truncation error estimate for the fast L2-$1_{\sigma }$ Formula (3) with the temporally uniform meshes below.

Lemma 4 

([21]). If $v\left(t\right)\in C^3[0,T]$ and $\beta \in (0,1)$, then the fast L2-$1_{\sigma }$ Formula (3) with the temporally uniform meshes has the following error estimate:

$${\hspace{0.25em}}_C{D}_{0,t}^{\beta }v\left(t_{n+\sigma }\right)={\hspace{0.25em}}^F{\overline{D}}_{\tau }^{\beta }{v}^{n+\sigma }+O({\tau }^{3-\beta }+ϵ).$$

Here, ϵ is an absolute tolerance error set in (3).

Lemma 5. 

Consider the grid functions $u^n\in V_h(n\ge 0)$; then, we have

$$({\mathcal{L}}_h{\widehat{\delta }}_t{u}_h^n,u_h^{n+\sigma })\le -{\displaystyle \frac{1}{4\tau }}(E_d^{n+1}-E_d^n),n\ge 1,$$

(17)

where $E_d^{n+1}=(2\sigma +1)|u_h^{n+1}{|}_{★}^2-(2\sigma -1)|u_h^n{|}_{★}^2+(2{\sigma }^2+\sigma -1){|u_h^{n+1}-u_h^n|}_{★}^2$. Furthermore, the term $E_d^{n+1}$ has the following estimate:

$$E_d^{n+1}\ge {\displaystyle \frac{1}{\sigma }}{\left|u_h^{n+1}\right|}_{★}^2,n\ge 0.$$

(18)

Proof. 

In view of the definition of ${\mathcal{L}}_h$, one has

$$\begin{array}{ccc}& & ({\mathcal{L}}_h{\widehat{\delta }}_t{u}_h^n,u_h^{n+\sigma })\hfill \\ & =& -{({\widehat{\delta }}_t{\delta }_1{u}_h^n,{\delta }_1{u}_h^n)}_{d_1}-{({\widehat{\delta }}_t{\delta }_2{u}_h^n,{\delta }_2{u}_h^n)}_{d_2}\hfill \\ & \le & -{\displaystyle \frac{1}{4\tau }}\left(E_{d_1}^{n+1}-E_{d_1}^n+E_{d_2}^{n+1}-E_{d_2}^n\right),\hfill \end{array}$$

where $E_{d_k}^{n+1}=(2\sigma +1)|{\delta }_k{u}_h^{n+1}{|}_{d_k}^2-(2\sigma -1)|{\delta }_k{u}_h^n{|}_{d_k}^2+(2{\sigma }^2+\sigma -1){|{\delta }_k{u}_h^{n+1}-{\delta }_k{u}_h^n|}_{d_k}^2$ with $k=1,2$. Here, we have used Lemma 3.5 in [22]. So, the desired result (17) can be readily obtained by setting $E_d^n=E_{d_1}^n+E_{d_2}^n$. The inequality (18) can be obtained by Cauchy–Schwarz inequality, or see Lemma 3.5 in [22] for more details. Thus, the proofs are all completed. □

The fast L2-$1_{\sigma }$ formula has the following estimate, which can be seen as the special case of Corollary 3.1 in [20].

Lemma 6. 

For any grid function $v^n\in V_h(n\ge 1)$, the following inequality holds:

$$\sum _{k=0}^n{\widehat{\varpi }}_{n-k}^{(n+1)}((v_h^{k+1}-v_h^k),v_h^{n+\sigma })\ge {\displaystyle \frac{1}{2}}\sum _{k=0}^n{\widehat{\varpi }}_{n-k}^{(n+1)}(\parallel v_h^{k+1}{\parallel }^2-\parallel v_h^k{\parallel }^2).$$

Using the equivalent form of (3) in (15) and the definitions of the parameters $C_1$ and $C_2$, we obtain the equivalent form of (12):

$$\begin{array}{ccc}\hfill & & {\varphi }_h^1-{\displaystyle \frac{\tau \sigma }{2(\sigma +\kappa {\widehat{\varpi }}_0^{\left(1\right)})}}{\mathcal{L}}_h{\varphi }_h^1+{\left({\displaystyle \frac{\tau \sigma }{2(\sigma +\kappa {\widehat{\varpi }}_0^{\left(1\right)})}}\right)}^2{\mathcal{L}}_1^h{\mathcal{L}}_2^h{\varphi }_h^1\hfill \\ & =& {\displaystyle \frac{1}{\sigma +\kappa {\widehat{\varpi }}_0^{\left(1\right)}}}\left(-(1-\sigma -\kappa {\widehat{\varpi }}_0^{\left(1\right)}){\varphi }_h^0+\sigma {\displaystyle \frac{\tau }{2}}{\mathcal{L}}_h{\varphi }_h^0+{\mathcal{L}}_h{u}_h^0+f_h^{\sigma }\right)\hfill \\ & & -{\left({\displaystyle \frac{\tau \sigma }{2(\sigma +\kappa {\widehat{\varpi }}_0^{\left(1\right)})}}\right)}^2{\mathcal{L}}_1^h{\mathcal{L}}_2^h{\varphi }_h^0,n=0,\hfill \\ & & {\varphi }_h^{n+1}-{\displaystyle \frac{2\tau {\sigma }^2}{(1+2\sigma )(\sigma +\kappa {\widehat{\varpi }}_0^{(n+1)})}}{\mathcal{L}}_h{\varphi }_h^{n+1}+{\left({\displaystyle \frac{2\tau {\sigma }^2}{(1+2\sigma )(\sigma +\kappa {\widehat{\varpi }}_0^{(n+1)})}}\right)}^2{\mathcal{L}}_1^h{\mathcal{L}}_2^h{\varphi }_h^{n+1}\hfill \\ & =& {\displaystyle \frac{1}{\sigma +\kappa {\widehat{\varpi }}_0^{(n+1)}}}(-\kappa \sum _{k=1}^{n-1}{\widehat{\varpi }}_{n-k}^{(n+1)}({\varphi }_h^{k+1}-{\varphi }_h^k)\hfill \\ & & -(1-\sigma -\kappa {\widehat{\varpi }}_0^{(n+1)}){\varphi }_h^n+\sigma (1-\sigma ){\displaystyle \frac{2\tau }{1+2\sigma }}{\mathcal{L}}_h{\varphi }_h^n\hfill \\ & & +{\mathcal{L}}_h{u}_h^n+{\displaystyle \frac{\sigma (2\sigma -1)}{1+2\sigma }}({\mathcal{L}}_h{u}_h^n-{\mathcal{L}}_h{u}_h^{n-1})+f_h^{n+\sigma })\hfill \\ & & -{\displaystyle \frac{1-\sigma }{\sigma }}{\left({\displaystyle \frac{2\tau {\sigma }^2}{(1+2\sigma )(\sigma +\kappa {\widehat{\varpi }}_0^{(n+1)})}}\right)}^2{\mathcal{L}}_1^h{\mathcal{L}}_2^h{\varphi }_h^n,n\ge 1.\hfill \end{array}$$

(19)

We remark that the corresponding temporally uniform mesh-based form of the two small terms $2{\mu }_0^2{\mathcal{L}}_1^h{\mathcal{L}}_2^h{\varphi }_h^{\frac{1}{2}}$ and ${\displaystyle \frac{{\mu }_1^2}{\sigma }}{\mathcal{L}}_1^h{\mathcal{L}}_2^h{\varphi }_h^{n+\sigma }$, shown in (12), are actually given by

$$2{\left({\displaystyle \frac{\tau \sigma }{2(\sigma +\kappa {\widehat{\varpi }}_0^{\left(1\right)})}}\right)}^2{\mathcal{L}}_1^h{\mathcal{L}}_2^h{\varphi }_h^{\frac{1}{2}}\mathrm{and}{\displaystyle \frac{1}{\sigma }}{\left({\displaystyle \frac{2\tau {\sigma }^2}{(1+2\sigma )(\sigma +\kappa {\widehat{\varpi }}_0^{(n+1)})}}\right)}^2{\mathcal{L}}_1^h{\mathcal{L}}_2^h{\varphi }_h^{n+\sigma },$$

respectively.

Thus, we can rewrite (19) as the following compact form:

$$\begin{array}{ccc}\hfill & & {\varphi }_h^{\sigma }+\kappa {\widehat{\varpi }}_0^{\left(1\right)}({\varphi }_h^1-{\varphi }_h^0)+{\displaystyle \frac{{\tau }^2{\sigma }^2}{2(\sigma +\kappa {\widehat{\varpi }}_0^{\left(1\right)})}}{\mathcal{L}}_1^h{\mathcal{L}}_2^h{\varphi }_h^{\frac{1}{2}}={\mathcal{L}}_h{u}_h^{\sigma }+f_h^{\sigma },n=0,\hfill \\ & & {\varphi }_h^{n+\sigma }+\kappa \sum _{k=0}^n{\widehat{\varpi }}_{n-k}^{(n+1)}({\varphi }_h^{k+1}-{\varphi }_h^k)+{\displaystyle \frac{4{\tau }^2{\sigma }^4}{{(1+2\sigma )}^2(\sigma +\kappa {\widehat{\varpi }}_0^{(n+1)})}}{\mathcal{L}}_1^h{\mathcal{L}}_2^h{\varphi }_h^{n+\sigma }\hfill \\ & =& {\mathcal{L}}_h{u}_h^{n+\sigma }+f_h^{n+\sigma },n\ge 1.\hfill \end{array}$$

(20)

In the following, we use the notation C to denote a positive constant that may differ in different occurrences, but is always independent of $\tau$ and $\mathbf{h}$.

Theorem 1. 

Suppose that the grid functions $u^n,{\varphi }^n\in V_h(n\ge 0)$ satisfy

$$\begin{array}{ccc}& & {\varphi }_h^{\sigma }+\kappa {\widehat{\varpi }}_0^{\left(1\right)}({\varphi }_h^1-{\varphi }_h^0)+{\displaystyle \frac{{\tau }^2{\sigma }^2}{2(\sigma +\kappa {\widehat{\varpi }}_0^{\left(1\right)})}}{\mathcal{L}}_1^h{\mathcal{L}}_2^h{\varphi }_h^{\frac{1}{2}}={\mathcal{L}}_h{u}_h^{\sigma }+f_h^{\sigma },\hfill \\ & & {\varphi }_h^{n+\sigma }+\kappa \sum _{k=0}^n{\widehat{\varpi }}_{n-k}^{(n+1)}({\varphi }_h^{k+1}-{\varphi }_h^k)+{\displaystyle \frac{4{\tau }^2{\sigma }^4}{{(1+2\sigma )}^2(\sigma +\kappa {\widehat{\varpi }}_0^{(n+1)})}}{\mathcal{L}}_1^h{\mathcal{L}}_2^h{\varphi }_h^{n+\sigma }\hfill \end{array}$$

(21)

$$\begin{array}{ccc}& & ={\mathcal{L}}_h{u}_h^{n+\sigma }+f_h^{n+\sigma },n\ge 1,\hfill \end{array}$$

(22)

$$\begin{array}{ccc}& & {\delta }_t{u}_h^{\frac{1}{2}}={\varphi }_h^{\frac{1}{2}}+{\epsilon }_h^0,\hfill \end{array}$$

(23)

$$\begin{array}{ccc}& & {\widehat{\delta }}_t{u}_h^n={\varphi }_h^{n+\sigma }+{\epsilon }_h^{n+\sigma },\hfill \end{array}$$

(24)

$$\begin{array}{ccc}& & u_h^0=u_0\left({\mathbf{x}}_h\right),{\varphi }_h^0=u_1\left({\mathbf{x}}_h\right).\hfill \end{array}$$

(25)

Then, the following inequality holds.

$$|u_h^n{|}_{★}^2\le C\left(|u_h^0{|}_{★}^2+\parallel {\varphi }_h^0{\parallel }^2+{\tau }^2\sum _{m=0}^{n-1}\parallel {\mathcal{L}}_h{\tilde{\epsilon }}_h^{m+\sigma }{\parallel }^2+\tau \sum _{m=0}^{n-1}{\parallel {\tilde{f}}_h^{m+\sigma }\parallel }^2\right),$$

where $n\ge 1$. Here, the notations are ${\tilde{\epsilon }}_h^{\sigma }={\epsilon }_h^0$ for $m=0$ and ${\tilde{\epsilon }}_h^{m+\sigma }={\epsilon }_h^{m+\sigma }$ for $m\ge 1$.

Proof. 

We first consider the case $n=0$. Taking the discrete inner product of (21) with ${\varphi }_h^{\frac{1}{2}}$, one has

$$\begin{array}{ccc}& & ({\varphi }_h^{\sigma },{\varphi }_h^{\frac{1}{2}})+\kappa {\widehat{\varpi }}_0^{\left(1\right)}({\varphi }_h^1-{\varphi }_h^0,{\varphi }_h^{\frac{1}{2}})+{\displaystyle \frac{{\tau }^2{\sigma }^2}{2(\sigma +\kappa {\widehat{\varpi }}_0^{\left(1\right)})}}({\mathcal{L}}_1^h{\mathcal{L}}_2^h{\varphi }_h^{\frac{1}{2}},{\varphi }_h^{\frac{1}{2}})\hfill \\ & =& ({\mathcal{L}}_h{u}_h^{\sigma },{\varphi }_h^{\frac{1}{2}})+(f_h^{\sigma },{\varphi }_h^{\frac{1}{2}}),\hfill \end{array}$$

from which we have

$$\begin{array}{ccc}\hfill & & ({\varphi }_h^{\sigma },{\varphi }_h^{\frac{1}{2}})+\kappa {\displaystyle \frac{{\widehat{\varpi }}_0^{\left(1\right)}}{2\tau }}(\parallel {\varphi }_h^1{\parallel }^2-\parallel {\varphi }_h^0{\parallel }^2)+{\displaystyle \frac{{\tau }^2{\sigma }^2}{2(\sigma +\kappa {\widehat{\varpi }}_0^{\left(1\right)})}}{|{\delta }_1{\delta }_2{\varphi }_h^{\frac{1}{2}}|}_d^2\hfill \\ & =& ({\mathcal{L}}_h{u}_h^{\sigma },{\varphi }_h^{\frac{1}{2}})+(f_h^{\sigma },{\varphi }_h^{\frac{1}{2}}).\hfill \end{array}$$

(26)

From Equation (23), we can obtain

$$({\mathcal{L}}_h{\delta }_t{u}_h^{\frac{1}{2}},u_h^{\sigma })=({\mathcal{L}}_h{\varphi }_h^{\frac{1}{2}},u_h^{\sigma })+({\mathcal{L}}_h{\epsilon }_h^0,u_h^{\sigma }).$$

So, using the Cauchy–Schwarz inequality, we derive that

$$\begin{array}{ccc}& & ({\mathcal{L}}_h{\varphi }_h^{\frac{1}{2}},u_h^{\sigma })\hfill \\ & =& ({\mathcal{L}}_h{\delta }_t{u}_h^{\frac{1}{2}},u_h^{\sigma })-({\mathcal{L}}_h{\epsilon }_h^0,u_h^{\sigma })\hfill \\ & =& {\displaystyle \frac{1}{\tau }}({\mathcal{L}}_h{u}_h^1-{\mathcal{L}}_h{u}_h^0,\sigma u_h^1+(1-\sigma )u_h^0)-({\mathcal{L}}_h{\epsilon }_h^0,\sigma u_h^1+(1-\sigma )u_h^0)\hfill \\ & =& {\displaystyle \frac{1}{\tau }}\left(-\sigma |u_h^1{|}_{★}^2+(1-\sigma ){|u_h^0|}_{★}^2+(1-2\sigma )({\mathcal{L}}_h{u}_h^0,u_h^1)\right)\hfill \\ & & -({\mathcal{L}}_h{\epsilon }_h^0,\sigma u_h^1+(1-\sigma )u_h^0)\hfill \\ & =& {\displaystyle \frac{1}{\tau }}\left(-\sigma |u_h^1{|}_{★}^2+(1-\sigma ){|u_h^0|}_{★}^2+(2\sigma -1)\left({({\delta }_1{u}_h^0,{\delta }_1{u}_h^1)}_{d_1}+{({\delta }_2{u}_h^0,{\delta }_2{u}_h^1)}_{d_2}\right)\right)\hfill \\ & & -\sigma ({\mathcal{L}}_h{\epsilon }_h^0,u_h^1)-(1-\sigma )({\mathcal{L}}_h{\epsilon }_h^0,u_h^0)\hfill \\ & \le & {\displaystyle \frac{1}{\tau }}\left(-\sigma |u_h^1{|}_{★}^2+(1-\sigma )|u_h^0{|}_{★}^2+(2\sigma -1)({ϵ}_0|u_h^0{|}_{★}^2+{\displaystyle \frac{1}{4{ϵ}_0}}|u_h^1{|}_{★}^2)\right)\hfill \\ & & +\sigma \left({ϵ}_1\parallel {\mathcal{L}}_h{\epsilon }_h^0{\parallel }^2+{\displaystyle \frac{1}{4{ϵ}_1}}{\parallel u_h^1\parallel }^2\right)+(1-\sigma )\left({ϵ}_2\parallel {\mathcal{L}}_h{\epsilon }_h^0{\parallel }^2+{\displaystyle \frac{1}{4{ϵ}_2}}{\parallel u_h^0\parallel }^2\right)\hfill \\ & \le & {\displaystyle \frac{1}{\tau }}\left(-\sigma |u_h^1{|}_{★}^2+(1-\sigma )|u_h^0{|}_{★}^2+(2\sigma -1)({ϵ}_0|u_h^0{|}_{★}^2+{\displaystyle \frac{1}{4{ϵ}_0}}|u_h^1{|}_{★}^2)\right)\hfill \\ & & +\sigma \left({ϵ}_1\parallel {\mathcal{L}}_h{\epsilon }_h^0{\parallel }^2+{\displaystyle \frac{1}{24L\underline{d}{ϵ}_1}}{|u_h^1|}_{★}^2\right)+(1-\sigma )\left({ϵ}_2\parallel {\mathcal{L}}_h{\epsilon }_h^0{\parallel }^2+{\displaystyle \frac{1}{24L\underline{d}{ϵ}_2}}{|u_h^0|}_{★}^2\right),\hfill \end{array}$$

where the last inequality holds in view of Lemma 2. We can set ${ϵ}_0={\displaystyle \frac{2\sigma -1}{4\sigma -2}}$ and ${ϵ}_1={ϵ}_2={\displaystyle \frac{\sigma \tau }{6L\underline{d}}}$ to obtain

$$({\mathcal{L}}_h{\varphi }_h^{\frac{1}{2}},u_h^{\sigma })\le -{\displaystyle \frac{1}{4\tau }}|u_h^1{|}_{★}^2+{\displaystyle \frac{1+\sigma }{4\sigma \tau }}|u_h^0{|}_{★}^2+{\displaystyle \frac{\sigma \tau }{6L\underline{d}}}{\parallel {\mathcal{L}}_h{\epsilon }_h^0\parallel }^2.$$

(27)

Notice that $({\mathcal{L}}_h{\varphi }_h^{\frac{1}{2}},u_h^{\sigma })=({\mathcal{L}}_h{u}_h^{\sigma },{\varphi }_h^{\frac{1}{2}})$ and ${\displaystyle \frac{{\tau }^2{\sigma }^2}{2(\sigma +\kappa {\widehat{\varpi }}_0^{\left(1\right)})}}{\parallel {\delta }_1{\delta }_2{\varphi }_h^{\frac{1}{2}}\parallel }_d^2>0$, so combining (26) with (27), we have

$$\begin{array}{ccc}& & ({\varphi }_h^{\sigma },{\varphi }_h^{\frac{1}{2}})+\kappa {\displaystyle \frac{{\widehat{\varpi }}_0^{\left(1\right)}}{2\tau }}(\parallel {\varphi }_h^1{\parallel }^2-\parallel {\varphi }_h^0{\parallel }^2)\hfill \\ & \le & -{\displaystyle \frac{1}{4\tau }}|u_h^1{|}_{★}^2+{\displaystyle \frac{1+\sigma }{4\sigma \tau }}|u_h^0{|}_{★}^2+{\displaystyle \frac{\sigma \tau }{6L\underline{d}}}{\parallel {\mathcal{L}}_h{\epsilon }_h^0\parallel }^2+(f_h^{\sigma },{\varphi }_h^{\frac{1}{2}}).\hfill \end{array}$$

Using the identity $({\varphi }_h^{\sigma },{\varphi }_h^{\frac{1}{2}})=2\sigma {\parallel {\varphi }_h^{\frac{1}{2}}\parallel }^2-(2\sigma -1)({\varphi }_h^0,{\varphi }_h^{\frac{1}{2}})$, one can derive that

$$\begin{array}{ccc}& & 2\sigma \parallel {\varphi }_h^{\frac{1}{2}}{\parallel }^2+\kappa {\displaystyle \frac{{\widehat{\varpi }}_0^{\left(1\right)}}{2\tau }}\parallel {\varphi }_h^1{\parallel }^2+{\displaystyle \frac{1}{4\tau }}{|u_h^1|}_{★}^2\hfill \\ & \le & \kappa {\displaystyle \frac{{\widehat{\varpi }}_0^{\left(1\right)}}{2\tau }}\parallel {\varphi }_h^0{\parallel }^2+{\displaystyle \frac{1+\sigma }{4\sigma \tau }}|u_h^0{|}_{★}^2+{\displaystyle \frac{\sigma \tau }{6L\underline{d}}}{\parallel {\mathcal{L}}_h{\epsilon }_h^0\parallel }^2+(2\sigma -1)({\varphi }_h^0,{\varphi }_h^{\frac{1}{2}})+(f_h^{\sigma },{\varphi }_h^{\frac{1}{2}})\hfill \\ & \le & \kappa {\displaystyle \frac{{\widehat{\varpi }}_0^{\left(1\right)}}{2\tau }}\parallel {\varphi }_h^0{\parallel }^2+{\displaystyle \frac{1+\sigma }{4\sigma \tau }}|u_h^0{|}_{★}^2+{\displaystyle \frac{\sigma \tau }{6L\underline{d}}}{\parallel {\mathcal{L}}_h{\epsilon }_h^0\parallel }^2\hfill \\ & & +(2\sigma -1)\left({ϵ}_3\parallel {\varphi }_h^0{\parallel }^2+{\displaystyle \frac{1}{4{ϵ}_3}}\parallel {\varphi }_h^{\frac{1}{2}}\parallel \right)+{ϵ}_4\parallel f_h^{\sigma }{\parallel }^2+{\displaystyle \frac{1}{4{ϵ}_4}}{\parallel {\varphi }_h^{\frac{1}{2}}\parallel }^2.\hfill \end{array}$$

By setting ${ϵ}_3={\displaystyle \frac{2\sigma -1}{4\sigma }}$ and ${ϵ}_4={\displaystyle \frac{1}{4\sigma }}$, we obtain

$$\begin{array}{ccc}& & \kappa {\displaystyle \frac{{\widehat{\varpi }}_0^{\left(1\right)}}{2\tau }}\parallel {\varphi }_h^1{\parallel }^2+{\displaystyle \frac{1}{4\tau }}{\left|u_h^1\right|}_{★}^2\hfill \\ & \le & (\kappa {\displaystyle \frac{{\widehat{\varpi }}_0^{\left(1\right)}}{2\tau }}+{\displaystyle \frac{{(2\sigma -1)}^2}{4\sigma }})\parallel {\varphi }_h^0{\parallel }^2+{\displaystyle \frac{1+\sigma }{4\sigma \tau }}|u_h^0{|}_{★}^2+{\displaystyle \frac{\sigma \tau }{6L\underline{d}}}\parallel {\mathcal{L}}_h{\epsilon }_h^0{\parallel }^2+{\displaystyle \frac{1}{4\sigma }}{\parallel f_h^{\sigma }\parallel }^2,\hfill \end{array}$$

from which yields

$$\begin{array}{ccc}& & 2\kappa {\widehat{\varpi }}_0^{\left(1\right)}\parallel {\varphi }_h^1{\parallel }^2+{\left|u_h^1\right|}_{★}^2\hfill \\ & \le & \left(2\kappa {\widehat{\varpi }}_0^{\left(1\right)}+{\displaystyle \frac{{(2\sigma -1)}^2}{\sigma }}\tau \right)\parallel {\varphi }_h^0{\parallel }^2+{\displaystyle \frac{1+\sigma }{\sigma }}|u_h^0{|}_{★}^2+{\displaystyle \frac{2\sigma {\tau }^2}{3L\underline{d}}}\parallel {\mathcal{L}}_h{\epsilon }_h^0{\parallel }^2+{\displaystyle \frac{\tau }{\sigma }}{\parallel f_h^{\sigma }\parallel }^2.\hfill \end{array}$$

Since ${\widehat{\varpi }}_0^{\left(1\right)}>0$, from the above inequality, one can readily obtain the desired result for the case $n=0$.

What remains to be shown is the case $n\ge 1$. Taking the discrete inner product of (21) with ${\varphi }_h^{n+\sigma }$, one has

$$\begin{array}{ccc}& & ({\varphi }_h^{n+\sigma },{\varphi }_h^{n+\sigma })+\kappa \sum _{k=0}^n{\widehat{\varpi }}_{n-k}^{(n+1)}(({\varphi }_h^{k+1}-{\varphi }_h^k),{\varphi }_h^{n+\sigma })\hfill \\ & & +{\displaystyle \frac{4{\tau }^2{\sigma }^4}{{(1+2\sigma )}^2(\sigma +\kappa {\widehat{\varpi }}_0^{(n+1)})}}({\mathcal{L}}_1^h{\mathcal{L}}_2^h{\varphi }_h^{n+\sigma },{\varphi }_h^{n+\sigma })\hfill \\ & =& ({\mathcal{L}}_h{u}_h^{n+\sigma },{\varphi }_h^{n+\sigma })+(f_h^{n+\sigma },{\varphi }_h^{n+\sigma }).\hfill \end{array}$$

Using Lemmas 1 and 2, we have

$$\begin{array}{ccc}& & \parallel {\varphi }_h^{n+\sigma }{\parallel }^2+\kappa \sum _{k=0}^n{\widehat{\varpi }}_{n-k}^{(n+1)}(({\varphi }_h^{k+1}-{\varphi }_h^k),{\varphi }_h^{n+\sigma })\hfill \\ & & +{\displaystyle \frac{4{\tau }^2{\sigma }^4}{{(1+2\sigma )}^2(\sigma +\kappa {\widehat{\varpi }}_0^{(n+1)})}}{\left|{\delta }_1{\delta }_2{\varphi }_h^{n+\sigma }\right|}_d^2\hfill \\ & =& ({\mathcal{L}}_h{u}_h^{n+\sigma },{\varphi }_h^{n+\sigma })+(f_h^{n+\sigma },{\varphi }_h^{n+\sigma }).\hfill \end{array}$$

According to Lemma 6 and the positive term ${\displaystyle \frac{4{\tau }^2{\sigma }^4}{{(1+2\sigma )}^2(\sigma +\kappa {\widehat{\varpi }}_0^{(n+1)})}}{\parallel {\delta }_1{\delta }_2{\varphi }_h^{n+\sigma }\parallel }_d^2$, it follows that

$$\begin{array}{ccc}& & \parallel {\varphi }_h^{n+\sigma }{\parallel }^2+{\displaystyle \frac{1}{2}}\kappa \sum _{k=0}^n{\widehat{\varpi }}_{n-k}^{(n+1)}(\parallel {\varphi }_h^{k+1}{\parallel }^2-\parallel {\varphi }_h^k{\parallel }^2)\hfill \\ & \le & ({\mathcal{L}}_h{u}_h^{n+\sigma },{\varphi }_h^{n+\sigma })+(f_h^{n+\sigma },{\varphi }_h^{n+\sigma }).\hfill \end{array}$$

By (24), we can obtain the following equation.

$$({\mathcal{L}}_h{\widehat{\delta }}_t{u}_h^n,u_h^{n+\sigma })=({\mathcal{L}}_h{\varphi }_h^{n+\sigma },u_h^{n+\sigma })+({\mathcal{L}}_h{\epsilon }_h^{n+\sigma },u_h^{n+\sigma }).$$

Thanks to Lemma 5, we further have

$$({\mathcal{L}}_h{\varphi }_h^{n+\sigma },u_h^{n+\sigma })+({\mathcal{L}}_h{\epsilon }_h^{n+\sigma },u_h^{n+\sigma })\le -{\displaystyle \frac{1}{4\tau }}(E_d^{n+1}-E_d^n).$$

So,

$$\begin{array}{ccc}& & \parallel {\varphi }_h^{n+\sigma }{\parallel }^2+{\displaystyle \frac{1}{2}}\kappa \sum _{k=0}^n{\widehat{\varpi }}_{n-k}^{(n+1)}(\parallel {\varphi }_h^{k+1}{\parallel }^2-\parallel {\varphi }_h^k{\parallel }^2)\hfill \\ & \le & -{\displaystyle \frac{1}{4\tau }}(E_d^{n+1}-E_d^n)-({\mathcal{L}}_h{\epsilon }_h^{n+\sigma },u_h^{n+\sigma })+(f_h^{n+\sigma },{\varphi }_h^{n+\sigma }),\hfill \end{array}$$

that is,

$$\begin{array}{ccc}& & \parallel {\varphi }_h^{n+\sigma }{\parallel }^2+{\displaystyle \frac{1}{4\tau }}{E}_d^{n+1}+{\displaystyle \frac{1}{2}}\kappa {\widehat{\varpi }}_0^{(n+1)}\parallel {\varphi }_h^{n+1}{\parallel }^2+{\displaystyle \frac{1}{2}}\kappa \sum _{k=1}^n({\widehat{\varpi }}_{n-k+1}^{(n+1)}-{\widehat{\varpi }}_{n-k}^{(n+1)}){\parallel {\varphi }_h^k\parallel }^2\hfill \\ & \le & {\displaystyle \frac{1}{4\tau }}{E}_d^n+{\displaystyle \frac{1}{2}}\kappa {\widehat{\varpi }}_n^{(n+1)}{\parallel {\varphi }_h^0\parallel }^2-({\mathcal{L}}_h{\epsilon }_h^{n+\sigma },u_h^{n+\sigma })+(f_h^{n+\sigma },{\varphi }_h^{n+\sigma }).\hfill \end{array}$$

Summing up n from $n=1$ to $n=m-1$, for the above inequality, we get

$$\begin{array}{ccc}& & \sum _{n=1}^{m-1}\parallel {\varphi }_h^{n+\sigma }{\parallel }^2+{\displaystyle \frac{1}{4\tau }}{E}_d^m+{\displaystyle \frac{1}{2}}\kappa \sum _{n=1}^{m-1}{\widehat{\varpi }}_0^{(n+1)}{\parallel {\varphi }_h^{n+1}\parallel }^2\hfill \\ & & +{\displaystyle \frac{1}{2}}\kappa \sum _{n=1}^{m-1}\sum _{k=1}^n({\widehat{\varpi }}_{n-k+1}^{(n+1)}-{\widehat{\varpi }}_{n-k}^{(n+1)}){\parallel {\varphi }_h^k\parallel }^2\hfill \\ & \le & {\displaystyle \frac{1}{4\tau }}{E}_d^1+{\displaystyle \frac{1}{2}}\kappa \sum _{n=1}^{m-1}{\widehat{\varpi }}_n^{(n+1)}{\parallel {\varphi }_h^0\parallel }^2-\sum _{n=1}^{m-1}({\mathcal{L}}_h{\epsilon }_h^{n+\sigma },u_h^{n+\sigma })+\sum _{n=1}^{m-1}(f_h^{n+\sigma },{\varphi }_h^{n+\sigma }).\hfill \end{array}$$

Exchanging the order of summation for the double summation term on the above inequality and performing some straightforward calculations yields, we obtain

$$\begin{array}{ccc}& & \sum _{n=1}^{m-1}\parallel {\varphi }_h^{n+\sigma }{\parallel }^2+{\displaystyle \frac{1}{4\tau }}{E}_d^m+{\displaystyle \frac{\kappa }{2}}\sum _{n=1}^{m-1}{\widehat{\varpi }}_0^{(n+1)}{\parallel {\varphi }_h^{n+1}\parallel }^2\hfill \\ & & +{\displaystyle \frac{\kappa }{2}}\sum _{k=2}^{m-1}({\widehat{\varpi }}_{m-k}^{\left(m\right)}-{\widehat{\varpi }}_0^{(k+1)})\parallel {\varphi }_h^k{\parallel }^2+\sum _{n=1}^{m-1}({\widehat{\varpi }}_n^{(n+1)}-{\widehat{\varpi }}_{n-1}^{(n+1)}){\parallel {\varphi }_h^1\parallel }^2\hfill \\ & =& \sum _{n=1}^{m-1}\parallel {\varphi }_h^{n+\sigma }{\parallel }^2+{\displaystyle \frac{1}{4\tau }}{E}_d^m+{\displaystyle \frac{\kappa }{2}}\sum _{n=2}^m{\widehat{\varpi }}_{m-n}^{\left(m\right)}\parallel {\varphi }_h^n{\parallel }^2+\sum _{n=1}^{m-1}({\widehat{\varpi }}_n^{(n+1)}-{\widehat{\varpi }}_{n-1}^{(n+1)}){\parallel {\varphi }_h^1\parallel }^2\hfill \\ & \le & {\displaystyle \frac{1}{4\tau }}{E}_d^1+{\displaystyle \frac{\kappa }{2}}\sum _{n=1}^{m-1}{\widehat{\varpi }}_n^{(n+1)}{\parallel {\varphi }_h^0\parallel }^2-\sum _{n=1}^{m-1}({\mathcal{L}}_h{\epsilon }_h^{n+\sigma },u_h^{n+\sigma })+\sum _{n=1}^{m-1}(f_h^{n+\sigma },{\varphi }_h^{n+\sigma }).\hfill \end{array}$$

Notice that the weights ${\widehat{\varpi }}_{m-n}^{\left(m\right)}$ satisfy ${\widehat{\varpi }}_{m-n}^{\left(m\right)}\ge c_f=min\{{\widehat{\varpi }}_n^{(n+1)},{\varpi }_0\}>0$ for $n=1,2,\cdots ,m$ (see Lemma 4.1 in [21]); this, together with Lemmas 3 and 5, yields

$$\begin{array}{ccc}& & \sum _{n=1}^{m-1}\parallel {\varphi }_h^{n+\sigma }{\parallel }^2+{\displaystyle \frac{1}{4\tau \sigma }}|u_h^m{|}_{★}^2+{\displaystyle \frac{\kappa c_f}{2}}\sum _{n=2}^m{\parallel {\varphi }_h^n\parallel }^2\hfill \\ & & -\left({\displaystyle \frac{9ϵ(m-1)}{4\Gamma (1-\beta )}}+{\displaystyle \frac{4-3\beta }{{\tau }^{\beta }\Gamma (3-\beta )}}{(m-1+\sigma )}^{1-\beta }\right){\parallel {\varphi }_h^1\parallel }^2\hfill \\ & \le & {\displaystyle \frac{1}{4\tau }}{E}_d^1+{\displaystyle \frac{\kappa }{2}}\left({\displaystyle \frac{ϵ(m-1)}{\Gamma (1-\beta )}}+{\displaystyle \frac{{(m-1+\sigma )}^{1-\beta }}{{\tau }^{\beta }\Gamma (2-\beta )}}\right){\parallel {\varphi }_h^0\parallel }^2\hfill \\ & & -\sum _{n=1}^{m-1}({\mathcal{L}}_h{\epsilon }_h^{n+\sigma },u_h^{n+\sigma })+\sum _{n=1}^{m-1}(f_h^{n+\sigma },{\varphi }_h^{n+\sigma }),\hfill \end{array}$$

from which we have

$$\begin{array}{ccc}& & \sum _{n=1}^{m-1}\parallel {\varphi }_h^{n+\sigma }{\parallel }^2+{\displaystyle \frac{1}{4\tau \sigma }}{\left|u_h^m\right|}_{★}^2\hfill \\ & \le & {\displaystyle \frac{1}{4\tau }}{E}_d^1+{\displaystyle \frac{\kappa }{2}}\left({\displaystyle \frac{ϵ(m-1)}{\Gamma (1-\beta )}}+{\displaystyle \frac{{(m-1+\sigma )}^{1-\beta }}{{\tau }^{\beta }\Gamma (2-\beta )}}\right){\parallel {\varphi }_h^0\parallel }^2\hfill \\ & & +\left({\displaystyle \frac{9ϵ(m-1)}{4\Gamma (1-\beta )}}+{\displaystyle \frac{4-3\beta }{{\tau }^{\beta }\Gamma (3-\beta )}}{(m-1+\sigma )}^{1-\beta }\right){\parallel {\varphi }_h^1\parallel }^2\hfill \\ & & -\sum _{n=1}^{m-1}({\mathcal{L}}_h{\epsilon }_h^{n+\sigma },u_h^{n+\sigma })+\sum _{n=1}^{m-1}(f_h^{n+\sigma },{\varphi }_h^{n+\sigma }).\hfill \end{array}$$

Multiplying both sides of the above inequality by $4\tau$ and observing that ${\tau }^{1-\beta }{(m-1+\sigma )}^{1-\beta }=t_{m-1+\sigma }$, we can deduce that

$$\begin{array}{ccc}& & 4\tau \sum _{n=1}^{m-1}\parallel {\varphi }_h^{n+\sigma }{\parallel }^2+{\displaystyle \frac{1}{\sigma }}{\left|u_h^m\right|}_{★}^2\hfill \\ & \le & E_d^1+2\kappa \left({\displaystyle \frac{t_{m-1}ϵ}{\Gamma (1-\beta )}}+{\displaystyle \frac{t_{m-1+\sigma }^{1-\beta }}{\Gamma (2-\beta )}}\right){\parallel {\varphi }_h^0\parallel }^2\hfill \\ & & +\left({\displaystyle \frac{9ϵt_{m-1}}{\Gamma (1-\beta )}}+{\displaystyle \frac{4-3\beta }{\Gamma (3-\beta )}}{t}_{m-1+\sigma }^{1-\beta }\right){\parallel {\varphi }_h^1\parallel }^2\hfill \\ & & -4\tau \sum _{n=1}^{m-1}({\mathcal{L}}_h{\epsilon }_h^{n+\sigma },u_h^{n+\sigma })+4\tau \sum _{n=1}^{m-1}(f_h^{n+\sigma },{\varphi }_h^{n+\sigma })\hfill \\ & \le & E_d^1+2\kappa \left({\displaystyle \frac{t_{m-1}ϵ}{\Gamma (1-\beta )}}+{\displaystyle \frac{t_{m-1+\sigma }^{1-\beta }}{\Gamma (2-\beta )}}\right){\parallel {\varphi }_h^0\parallel }^2\hfill \\ & & +\left({\displaystyle \frac{9ϵt_{m-1}}{\Gamma (1-\beta )}}+{\displaystyle \frac{4-3\beta }{\Gamma (3-\beta )}}{t}_{m-1+\sigma }^{1-\beta }\right){\parallel {\varphi }_h^1\parallel }^2\hfill \\ & & +4\sum _{n=1}^{m-1}\left({ϵ}_2{\tau }^2\parallel {\mathcal{L}}_h{\epsilon }_h^{n+\sigma }{\parallel }^2+{\displaystyle \frac{1}{4{ϵ}_2}}{\parallel u_h^{n+\sigma }\parallel }^2\right)\hfill \\ & & +4\tau \sum _{n=1}^{m-1}\left({ϵ}_3\parallel f_h^{n+\sigma }{\parallel }^2+{\displaystyle \frac{1}{4{ϵ}_3}}{\parallel {\varphi }_h^{n+\sigma }\parallel }^2\right),\hfill \end{array}$$

where we have used the Cauchy–Schwarz inequality in the last inequality. Here, the two positive parameters ${ϵ}_2$ and ${ϵ}_3$ will be given later on. Since $\sigma =1-\beta /2\in (0.5,1)$, one can deduce that

$$\begin{array}{ccc}\hfill E_d^1& =& (2\sigma +1)|u_h^1{|}_{★}^2-(2\sigma -1)|u_h^0{|}_{★}^2+(2{\sigma }^2+\sigma -1){|u_h^1-u_h^0|}_{★}^2\hfill \\ & \le & (2\sigma +1)|u_h^1{|}_{★}^2-(2\sigma -1)|u_h^0{|}_{★}^2+2(2{\sigma }^2+\sigma -1)(|u_h^1{|}_{★}^2+|u_h^0{|}_{★}^2)\hfill \\ & =& (4{\sigma }^2+4\sigma -1)|u_h^1{|}_{★}^2+(4{\sigma }^2-1){|u_h^0|}_{★}^2,\hfill \end{array}$$

and

$$\begin{array}{ccc}\hfill \sum _{n=1}^{m-1}{\parallel u_h^{n+\sigma }\parallel }^2& =& \sum _{n=1}^{m-1}\parallel \sigma u_h^{n+1}+(1-\sigma )u_h^n{\parallel }^2\le 2\sum _{n=1}^{m-1}(\parallel u_h^{n+1}{\parallel }^2+\parallel u_h^n{\parallel }^2)\hfill \\ & \le & {\displaystyle \frac{1}{3L\underline{d}}}\sum _{n=1}^{m-1}(|u_h^{n+1}{|}_{★}^2+|u_h^n{|}_{★}^2)\hfill \\ & =& {\displaystyle \frac{1}{3L\underline{d}}}\left(|u_h^m{|}_{★}^2+2\sum _{n=1}^{m-1}|u_h^n{|}_{★}^2-{|u_h^1|}_{★}^2\right).\hfill \end{array}$$

So,

$$\begin{array}{ccc}& & 4\tau \sum _{n=1}^{m-1}\parallel {\varphi }_h^{n+\sigma }{\parallel }^2+{\displaystyle \frac{1}{\sigma }}{|u_h^m|}_{★}^2\hfill \\ & \le & \left(4{\sigma }^2+4\sigma -1-{\displaystyle \frac{1}{3L\underline{d}{ϵ}_2}}\right)|u_h^1{|}_{★}^2+(4{\sigma }^2-1)|u_h^0{|}_{★}^2+{\displaystyle \frac{1}{3L\underline{d}{ϵ}_2}}|u_h^m{|}_{★}^2+{\displaystyle \frac{2}{3L\underline{d}{ϵ}_2}}\sum _{n=1}^{m-1}{|u_h^n|}_{★}^2\hfill \\ & & +2\kappa \left({\displaystyle \frac{t_{m-1}ϵ}{\Gamma (1-\beta )}}+{\displaystyle \frac{t_{m-1+\sigma }^{1-\beta }}{\Gamma (2-\beta )}}\right)\parallel {\varphi }_h^0{\parallel }^2+\left({\displaystyle \frac{9ϵt_{m-1}}{\Gamma (1-\beta )}}+{\displaystyle \frac{4-3\beta }{\Gamma (3-\beta )}}{t}_{m-1+\sigma }^{1-\beta }\right){\parallel {\varphi }_h^1\parallel }^2\hfill \\ & & +4{ϵ}_2{\tau }^2\sum _{n=1}^{m-1}{\parallel {\mathcal{L}}_h{\epsilon }_h^{n+\sigma }\parallel }^2+4\tau \sum _{n=1}^{m-1}\left({ϵ}_3\parallel f_h^{n+\sigma }{\parallel }^2+{\displaystyle \frac{1}{4{ϵ}_3}}{\parallel {\varphi }_h^{n+\sigma }\parallel }^2\right).\hfill \end{array}$$

We can choose ${ϵ}_2={\displaystyle \frac{2\sigma }{3L\underline{d}}}$ and ${ϵ}_3={\displaystyle \frac{1}{4}}$ to obtain

$$\begin{array}{ccc}\hfill {\displaystyle \frac{1}{\sigma }}{|u_h^m|}_{★}^2& \le & \left(4{\sigma }^2+4\sigma -1-{\displaystyle \frac{1}{2\sigma }}\right)|u_h^1{|}_{★}^2+(4{\sigma }^2-1)|u_h^0{|}_{★}^2+{\displaystyle \frac{1}{\sigma }}\sum _{n=1}^{m-1}{|u_h^n|}_{★}^2\hfill \\ & & +2\kappa \left({\displaystyle \frac{ϵt_{m-1}}{\Gamma (1-\beta )}}+{\displaystyle \frac{t_{m-1+\sigma }^{1-\beta }}{\Gamma (2-\beta )}}\right)\parallel {\varphi }_h^0{\parallel }^2+\left({\displaystyle \frac{9ϵt_{m-1}}{\Gamma (1-\beta )}}+{\displaystyle \frac{4-3\beta }{\Gamma (3-\beta )}}{t}_{m-1+\sigma }^{1-\beta }\right){\parallel {\varphi }_h^1\parallel }^2\hfill \\ & & +{\displaystyle \frac{8\sigma {\tau }^2}{3L\underline{d}}}\sum _{n=1}^{m-1}\parallel {\mathcal{L}}_h{\epsilon }_h^{n+\sigma }{\parallel }^2+\tau \sum _{n=1}^{m-1}{\parallel f_h^{n+\sigma }\parallel }^2.\hfill \end{array}$$

Combining the above inequality with the estimate for the case $n=0$, one can obtain

$$\begin{array}{ccc}\hfill |u_h^m{|}_{★}^2& \le & C(|u_h^0{|}_{★}^2+\sum _{n=1}^{m-1}|u_h^n{|}_{★}^2+{\parallel {\varphi }_h^0\parallel }^2\hfill \\ & & +{\tau }^2\sum _{n=0}^{m-1}\parallel {\mathcal{L}}_h{\tilde{\epsilon }}_h^{n+\sigma }{\parallel }^2+\tau \sum _{n=0}^{m-1}{\parallel {\tilde{f}}_h^{n+\sigma }\parallel }^2),\hfill \end{array}$$

from which the desired result holds by the Gronwall inequality.

Thereby, all the proofs are completed. □

In view of Theorem 1, we can conclude the following stability of the fast second-order ADI finite difference scheme (12).

Theorem 2. 

The fast second-order ADI finite difference scheme (12) is unconditionally stable with respect to the initial values $u_0$, $u_1$, and the right-hand-side function f.

Finally, the error estimate of the difference scheme (12) is presented below.

Theorem 3. 

Suppose that $u(\mathbf{x},t)\in C_{\mathbf{x},t}^{4,3}(\Omega \times [0,T])$ is the exact solution of (1), and $u_h^n$ is the solution of the finite difference scheme (12). Then, for the case of temporally uniform meshes and $n>1$, the following error estimate holds:

$$|u({\mathbf{x}}_h,t_n)-u_h^n{|}_{★}\le C({\tau }^2+{\mathbf{h}}^2+ϵ),$$

where ϵ is an absolute tolerance error set in the fast L2-$1_{\sigma }$ Formula (3).

Proof. 

From (5) and (20), we can obtain the following error equations:

$$\begin{array}{ccc}& & {\tilde{e}}_h^{\frac{1}{2}}+\kappa {\tau }^{-1}{w}_0({\tilde{e}}_h^1-{\tilde{e}}_h^0)+{\displaystyle \frac{{\tau }^2{\sigma }^2}{2(\sigma +\kappa {\widehat{\varpi }}_0^{\left(1\right)})}}{\mathcal{L}}_1^h{\mathcal{L}}_2^h{\varphi }_h^{\frac{1}{2}}={\mathcal{L}}_h{e}_h^{\frac{1}{2}}+{\tilde{R}}^0,\hfill \\ & & {\tilde{e}}_h^{n+\sigma }+\kappa \sum _{k=0}^n{\widehat{\varpi }}_{n-k}^{(n+1)}({\tilde{e}}_h^{k+1}-{\tilde{e}}_h^k)+{\displaystyle \frac{4{\tau }^2{\sigma }^4}{{(1+2\sigma )}^2(\sigma +\kappa {\widehat{\varpi }}_0^{(n+1)})}}{\mathcal{L}}_1^h{\mathcal{L}}_2^h{\varphi }_h^{n+\sigma }\hfill \\ & & ={\mathcal{L}}_h{e}_h^{n+\sigma }+{\tilde{R}}^n,n\ge 1,\hfill \\ & & {\delta }_t{e}_h^{\frac{1}{2}}={\tilde{e}}_h^{\frac{1}{2}}+r^0,\hfill \\ & & {\widehat{\delta }}_t{e}_h^n={\tilde{e}}_h^{n+\sigma }+r^n,\hfill \end{array}$$

where $e_h^n=u({\mathbf{x}}_h,t_n)-u_h^n$ and ${\tilde{e}}_h^n=\varphi ({\mathbf{x}}_h,t_n)-{\varphi }_h^n$.

Since the small term ${\displaystyle \frac{4{\tau }^2{\sigma }^4}{{(1+2\sigma )}^2(\sigma +\kappa {\widehat{\varpi }}_0^{(n+1)})}}{\mathcal{L}}_1^h{\mathcal{L}}_2^h{\varphi }_h^{n+\sigma }=O\left({\tau }^2\right)$ for $n\ge 1$, we can get the temporally uniform mesh-based local truncation error ${\tilde{R}}^n=R^n+O\left({\tau }^2\right)=O({\tau }^2+{\mathbf{h}}^2+ϵ)$. In addition, one has ${\displaystyle \frac{{\tau }^2{\sigma }^2}{2(\sigma +\kappa {\widehat{\varpi }}_0^{\left(1\right)})}}{\mathcal{L}}_1^h{\mathcal{L}}_2^h{\varphi }_h^{\frac{1}{2}}=O\left({\tau }^2\right)$. So, for the case $n=0$, one has the local truncation error ${\tilde{R}}^0=R^0+O\left({\tau }^2\right)=O({\tau }^2+{\mathbf{h}}^2)$.

Using Lemma 4 and Theorem 1, we have

$$\begin{array}{ccc}\hfill |e_h^n{|}_{★}& \le & C\sqrt{{\tau }^2\sum _{m=0}^{n-1}\parallel {\mathcal{L}}_h{r}^m{\parallel }^2+\tau \sum _{m=0}^{n-1}{\parallel {\tilde{R}}^m\parallel }^2}\hfill \\ & \le & C({\tau }^2+{\mathbf{h}}^2+ϵ).\hfill \end{array}$$

Thus, we complete the proof. □

Remark 2. 

Although we only provide the stability and error estimate for one case of variable coefficients, in practical numerical tests, we observe that our numerical scheme can be applied to other cases of variable coefficients problems, such as separable coefficients and non-separable coefficients, whose corresponding numerical theories are beyond the scope of this paper, and need to be further investigated.

5. Numerical Examples

In this section, we present numerical examples to verify the accuracy and efficiency of the proposed fast second-order ADI finite difference scheme (12). In view of Lemma 2, we measure the errors as

$$e(N_t,M)=\underset{n\ge 1}{max}\parallel u({\mathbf{x}}_h,t_n)-u_h^n\parallel$$

with $M=M_1=M_2$. The corresponding convergence orders in time and space are calculated by $log(e(N_t,M)/e(2N_t,M))$ and $log(e(N_t,M)/e(N_t,2M))$, respectively. The absolute tolerance error $ϵ$ in Theorem 3 is chosen to be $ϵ={10}^{-10}$ so that it does not affect the temporal and spatial accuracy of the scheme (12). Without a loss in generality, we always set $\Omega =(0,1)\times (0,1),T=1$ and $\kappa =1$ in (1).

Example 1 

(Accuracy). Consider the following three cases of spatially variable coefficients for the problem (1) with zero Dirichlet boundary conditions:

(a) 

$d_1\left(x\right)=e^x$ and $d_2\left(y\right)=e^y$;

(b) 

$d_1(x,y)=d_2(x,y)=e^{x+y}$;

(c) 

$d_1(x,y)=d_2(x,y)=e^{xy}$;

(d) 

$d_1(x,y)=2-0.01sin(x+y)$ and $d_2(x,y)=2-0.01cos(x+y)$.

We first consider the problem solution sufficiently smooth. By suitably choosing the source term f, one can obtain the exact solution $u(x,y,t)=(1+t^{4.1})x^2{(1-x)}^2{y}^2{(1-y)}^2$ of the problem (1). For different fractional orders $\alpha =1.1,1.5$, and 1.9, we choose the fixed spatial stepsize $M=512$ to make the spatial errors not affect the temporal errors, and then apply the fast second-order ADI finite difference scheme (12) to compute the temporal accuracy and the convergence orders by varying the number of temporal nodes $N_t$, see

Table 1. The $L^2$-norm errors in time for the smooth case in Example 1 with $M=512$.

Cases	${\mathit{N}}_{\mathit{t}}$	$\mathit{\alpha }=1.1$		$\mathit{\alpha }=1.5$		$\mathit{\alpha }=1.9$
		${\mathit{L}}^{\mathbf{2}}$ Error	Rate	${\mathit{L}}^{\mathbf{2}}$ Error	Rate	${\mathit{L}}^{\mathbf{2}}$ Error	Rate
(a)	4	3.88 × ${10}^{-4}$	-	2.88 × ${10}^{-4}$	-	2.10 × ${10}^{-4}$	-
	8	1.27 × ${10}^{-4}$	1.61	7.16 × ${10}^{-5}$	2.01	4.69 × ${10}^{-5}$	2.16
	16	3.35 × ${10}^{-5}$	1.92	1.53 × ${10}^{-5}$	2.23	1.03 × ${10}^{-5}$	2.19
	32	8.22 × ${10}^{-6}$	2.03	3.14 × ${10}^{-6}$	2.28	2.32 × ${10}^{-6}$	2.15
(b)	4	6.05 × ${10}^{-4}$	-	4.47 × ${10}^{-4}$	-	2.95 × ${10}^{-4}$	-
	8	2.27 × ${10}^{-4}$	1.42	1.20 × ${10}^{-4}$	1.90	6.27 × ${10}^{-5}$	2.23
	16	6.31 × ${10}^{-5}$	1.85	2.55 × ${10}^{-5}$	2.23	1.27 × ${10}^{-5}$	2.30
	32	1.58 × ${10}^{-5}$	2.00	5.14 × ${10}^{-6}$	2.31	2.70 × ${10}^{-6}$	2.24
(c)	4	2.95 × ${10}^{-4}$	-	2.24 × ${10}^{-4}$	-	1.74 × ${10}^{-4}$	-
	8	9.22 × ${10}^{-5}$	1.68	5.46 × ${10}^{-5}$	2.04	3.99 × ${10}^{-5}$	2.13
	16	2.40 × ${10}^{-5}$	1.94	1.17 × ${10}^{-5}$	2.22	8.98 × ${10}^{-6}$	2.15
	32	5.85 × ${10}^{-6}$	2.04	2.42 × ${10}^{-6}$	2.27	2.07 × ${10}^{-6}$	2.12
(d)	4	4.48 × ${10}^{-4}$	-	3.29 × ${10}^{-4}$	-	2.32 × ${10}^{-4}$	-
	8	1.50 × ${10}^{-4}$	1.58	8.28 × ${10}^{-5}$	1.99	5.12 × ${10}^{-5}$	2.18
	16	4.00 × ${10}^{-5}$	1.91	1.77 × ${10}^{-5}$	2.23	1.11 × ${10}^{-5}$	2.21
	32	9.93 × ${10}^{-6}$	2.01	3.83 × ${10}^{-6}$	2.21	2.76 × ${10}^{-6}$	2.00

. Similarly, we also obtain the numerical results for the spatial accuracy and the convergence orders; see

Table 2. The $L^2$-norm errors in space for the smooth case in Example 1 with $N_t=1024$.

Cases	M	$\mathit{\alpha }=1.1$		$\mathit{\alpha }=1.5$		$\mathit{\alpha }=1.9$
		${\mathit{L}}^{\mathbf{2}}$ Error	Rate	${\mathit{L}}^{\mathbf{2}}$ Error	Rate	${\mathit{L}}^{\mathbf{2}}$ Error	Rate
(a)	4	7.93 × ${10}^{-4}$	-	7.65 × ${10}^{-4}$	-	7.01 × ${10}^{-4}$	-
	8	2.00 × ${10}^{-4}$	1.99	1.93 × ${10}^{-4}$	1.98	1.76 × ${10}^{-4}$	1.99
	16	5.02 × ${10}^{-5}$	2.00	4.85 × ${10}^{-5}$	1.99	4.41 × ${10}^{-5}$	2.00
	32	1.26 × ${10}^{-5}$	2.00	1.21 × ${10}^{-5}$	2.00	1.10 × ${10}^{-5}$	2.00
(b)	4	8.19 × ${10}^{-4}$	-	8.01 × ${10}^{-4}$	-	7.22 × ${10}^{-4}$	-
	8	2.06 × ${10}^{-4}$	1.99	2.02 × ${10}^{-4}$	1.99	1.85 × ${10}^{-4}$	1.96
	16	5.17 × ${10}^{-5}$	2.00	5.06 × ${10}^{-5}$	2.00	4.68 × ${10}^{-5}$	1.99
	32	1.29 × ${10}^{-5}$	2.00	1.27 × ${10}^{-5}$	2.00	1.17 × ${10}^{-5}$	2.00
(c)	4	7.74 × ${10}^{-4}$	-	7.38 × ${10}^{-4}$	-	7.12 × ${10}^{-4}$	-
	8	1.94 × ${10}^{-4}$	2.00	1.85 × ${10}^{-4}$	2.00	1.78 × ${10}^{-4}$	2.00
	16	4.86 × ${10}^{-5}$	2.00	4.64 × ${10}^{-5}$	2.00	4.45 × ${10}^{-5}$	2.00
	32	1.21 × ${10}^{-5}$	2.00	1.16 × ${10}^{-5}$	2.00	1.11 × ${10}^{-5}$	2.00
(d)	4	8.15 × ${10}^{-4}$	-	7.90 × ${10}^{-4}$	-	7.34 × ${10}^{-4}$	-
	8	2.03 × ${10}^{-4}$	2.00	1.97 × ${10}^{-4}$	2.00	1.83 × ${10}^{-4}$	2.01
	16	5.09 × ${10}^{-5}$	2.00	4.94 × ${10}^{-5}$	2.00	4.57 × ${10}^{-5}$	2.00
	32	1.28 × ${10}^{-5}$	1.99	1.24 × ${10}^{-5}$	1.99	1.15 × ${10}^{-5}$	2.00

. From Table 1 and Table 2, we can observe that the convergence order in both time and space is second-order accuracy for the four different cases (a)–(d). It is worth mentioning that the numerical results of the first case (a) coincide with the error estimate of Theorem 3, while those for the last three cases (b)–(d) require further theoretical investigation.

Next, we consider the solution of (1) not sufficiently smooth. In a similar manner, we can construct the analytical solution $u(x,y,t)=(1+t^{1.1})x^2{(1-x)}^2{y}^2{(1-y)}^2$ by suitably choosing the term f. We note that the temporal first-order partial derivative of u is unbounded at the initial time layer, which suggests that the regularity of the solution in this case is lower than that of the previous example. The numerical results obtained by the fast second-order ADI finite difference scheme (12) for the four cases (a)–(d) are demonstrated in

Table 3. The $L^2$-norm errors in time for the nonsmooth case in Example 1 with $M=1024$ and $\alpha =1.5$.

Cases	${\mathit{N}}_{\mathit{t}}$	$\mathit{\gamma }=1$		$\mathit{\gamma }=1.5$		$\mathit{\gamma }=2$
		${\mathit{L}}^{\mathbf{2}}$ Error	Rate	${\mathit{L}}^{\mathbf{2}}$ Error	Rate	${\mathit{L}}^{\mathbf{2}}$ Error	Rate
(a)	4	1.22 × ${10}^{-4}$	-	1.85 × ${10}^{-4}$	-	2.72 × ${10}^{-4}$	-
	8	6.31 × ${10}^{-5}$	0.96	4.43 × ${10}^{-5}$	2.06	7.70 × ${10}^{-5}$	1.82
	16	3.80 × ${10}^{-5}$	0.73	1.77 × ${10}^{-5}$	1.33	1.68 × ${10}^{-5}$	2.20
	32	2.38 × ${10}^{-5}$	0.67	8.58 × ${10}^{-6}$	1.04	3.35 × ${10}^{-6}$	2.32
(b)	4	1.69 × ${10}^{-4}$	-	3.05 × ${10}^{-4}$	-	4.19 × ${10}^{-4}$	-
	8	5.94 × ${10}^{-5}$	1.51	7.69 × ${10}^{-5}$	1.99	1.31 × ${10}^{-4}$	1.67
	16	3.28 × ${10}^{-5}$	0.85	1.56 × ${10}^{-5}$	2.30	2.95 × ${10}^{-5}$	2.15
	32	2.15 × ${10}^{-5}$	0.61	7.62 × ${10}^{-6}$	1.04	5.85 × ${10}^{-6}$	2.33
(c)	4	1.22 × ${10}^{-4}$	-	1.42 × ${10}^{-4}$	-	2.15 × ${10}^{-4}$	-
	8	6.62 × ${10}^{-5}$	0.88	3.81 × ${10}^{-5}$	1.90	5.85 × ${10}^{-5}$	1.88
	16	4.17 × ${10}^{-5}$	0.67	1.89 × ${10}^{-5}$	1.01	1.27 × ${10}^{-5}$	2.20
	32	2.58 × ${10}^{-5}$	0.69	9.15 × ${10}^{-6}$	1.04	3.58 × ${10}^{-6}$	1.83
(d)	4	1.25 × ${10}^{-4}$	-	2.15 × ${10}^{-4}$	-	3.11 × ${10}^{-4}$	-
	8	6.15 × ${10}^{-5}$	1.02	5.19 × ${10}^{-5}$	2.05	8.97 × ${10}^{-5}$	1.79
	16	3.58 × ${10}^{-5}$	0.78	1.70 × ${10}^{-5}$	1.61	1.96 × ${10}^{-5}$	2.20
	32	2.32 × ${10}^{-5}$	0.63	8.33 × ${10}^{-6}$	1.03	4.05 × ${10}^{-6}$	2.27

. We can see that by choosing a suitable grading parameter γ, the numerical scheme (12) is able to maintain the desired second-order accuracy. This fact demonstrates that the temporally graded mesh-based (12) has great advantages in dealing with nonsmooth solutions, yet the corresponding numerical theory needs to be further investigated, as the numerical scheme is more complicated than that of the uniform meshes case.

Example 2 

(Efficiency). This numerical test focuses on the computational efficiency of the fast second-order ADI finite difference scheme (12). For the sake of comparison, we present the following numerical scheme using the original L2-$1_{\sigma }$ formula:

$$\left\{\begin{array}{cc}\hfill & {\varphi }_h^{n+\sigma }+\kappa {\overline{D}}_{\tau }^{\alpha -1}{\varphi }_h^{n+\sigma }={\mathcal{L}}_h{u}_h^{n+\sigma }+f_h^{n+\sigma },\hfill \\ \hfill & {\delta }_t{u}_h^{1/2}={\varphi }_h^{1/2},\hfill \\ \hfill & {\widehat{\delta }}_t{u}_h^n={\varphi }_h^{n+\sigma },\hfill \end{array}\right.$$

(28)

where the L2-$1_{\sigma }$ difference operator ${\overline{D}}_{\tau }^{\beta }$ with $\beta =\alpha -1$ is given by

$${\overline{D}}_{\tau }^{\beta }{g}^{n+\sigma }=\sum _{k=0}^n{\overline{\varpi }}_{n-k}^{(n+1)}(g\left(t_{k+1}\right)-g\left(t_k\right)).$$

(29)

Here, ${\overline{\varpi }}_0^{\left(1\right)}=a_0{\tau }^{-\beta }/\Gamma (2-\beta )$ if $n=0$; otherwise,

$${\overline{\varpi }}_k^{(n+1)}={\displaystyle \frac{{\tau }^{-\beta }}{\Gamma (2-\beta )}}\left\{\begin{array}{cc}{a}_0+b_1,\hfill & k=0,\hfill \\ a_k+b_{k+1}-b_k,\hfill & k=1,2,\cdots ,n-1,\hfill \\ a_n-b_n,\hfill & k=n,\hfill \end{array}\right.$$

where $a_0={\sigma }^{1-\beta },a_k={(k+\sigma )}^{1-\beta }-{(k-1+\sigma )}^{1-\beta },k\ge 1$, and

$$b_k={\displaystyle \frac{{(k+\sigma )}^{2-\beta }-{(k-1+\sigma )}^{2-\beta }}{2-\beta }}-{\displaystyle \frac{{(k+\sigma )}^{1-\beta }-{(k-1+\sigma )}^{1-\beta }}{2}},k\ge 1.$$

Notice that the structure of the L2-$1_{\sigma }$ Formula (29) is very similar to that of (15). So, the original numerical scheme (28) can be proved to be unconditionally stable with an accuracy of $O({\tau }^2+{\mathbf{h}}^2)$.

We can see that the computational complexity of the original numerical scheme (28) is $O\left(N_t^2{M}^4\right)$, which is much higher than that of the fast ADI finite difference scheme (12). Note that the computational complexity of (12) is only $O\left(N_t{N}_{exp}{M}^2\right)$, which suggests that our method has a great advantage in computational efficiency. This will be further verified in numerical test presented here. One may refer to Section 3 in [6] and Section 3.2 in [23] for more discussions about the computational complexity of the SOE and ADI methods, respectively.

By using numerical schemes (12) and (28), fixing the spatial stepsize $M=64$ and varying the temporal stepsize $N_t$, we present the numerical tests for case (a) in Example 1; see

Table 4. Comparison of $L^2$ errors and CPU time of the two schemes (28) and (12) for case (a) in Example 1 with a smooth solution (fixed $M=64$).

$\mathit{\alpha }$	Scheme	${\mathit{N}}_{\mathit{t}}=500$		${\mathit{N}}_{\mathit{t}}=1000$		${\mathit{N}}_{\mathit{t}}=2000$		${\mathit{N}}_{\mathit{t}}=4000$
		${\mathit{L}}^{\mathbf{2}}$ Error	CPU (s)	${\mathit{L}}^{\mathbf{2}}$ Error	CPU (s)	${\mathit{L}}^{\mathbf{2}}$ Error	CPU (s)	${\mathit{L}}^{\mathbf{2}}$ Error	CPU (s)
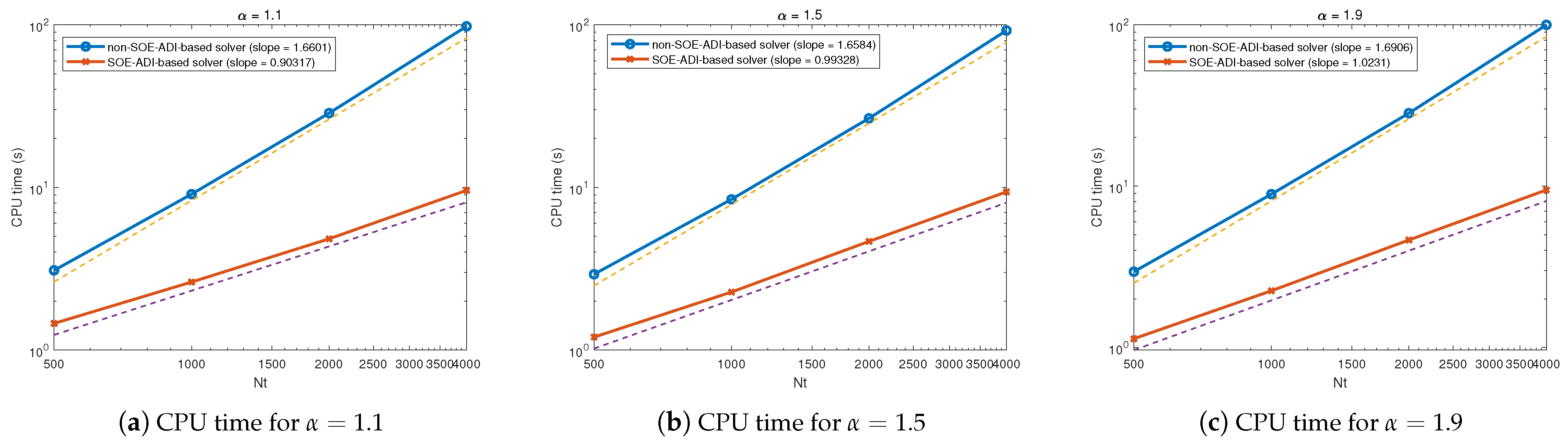
1.1	(28)	3.1413 × ${10}^{-6}$	3.09	3.1405 × ${10}^{-6}$	9.09	3.1402 × ${10}^{-6}$	28.60	3.1402 × ${10}^{-6}$	97.70
	(12)	3.1159 × ${10}^{-6}$	1.46	3.1344 × ${10}^{-6}$	2.62	3.1388 × ${10}^{-6}$	4.83	3.1398 × ${10}^{-6}$	9.59
1.5	(28)	3.0285 × ${10}^{-6}$	2.93	3.0320 × ${10}^{-6}$	8.45	3.0329 × ${10}^{-6}$	26.58	3.0331 × ${10}^{-6}$	92.12
	(12)	3.0265 × ${10}^{-6}$	1.20	3.0317 × ${10}^{-6}$	2.27	3.0328 × ${10}^{-6}$	4.66	3.0331 × ${10}^{-6}$	9.39
1.9	(28)	2.7571 × ${10}^{-6}$	2.95	2.7576 × ${10}^{-6}$	8.91	2.7577 × ${10}^{-6}$	28.30	2.7577 × ${10}^{-6}$	99.73
	(12)	2.7571 × ${10}^{-6}$	1.13	2.7576 × ${10}^{-6}$	2.25	2.7577 × ${10}^{-6}$	4.63	2.7577 × ${10}^{-6}$	9.46

and Figure 1. Here, for observation and comparison, we denote the two numerical schemes (28) and (12) as the non-SOE-ADI-based solver and SOE-ADI-based solver in Figure 1, respectively. From Table 4, it can be seen that for the same temporal and spatial steps, the two numerical schemes (12) and (28) have almost the same errors, but the former takes less time than that of the latter. In addition, it is found from Figure 1 that in different α cases, when the spatial step is fixed, the slope of the increase in computation time is much smaller for (12) than for (28), as the temporal step keeps getting smaller. Similar results, which we do not present here for brevity, are also observed for the other three cases in Example 1. These numerical results further verify that the fast ADI finite difference scheme (12) has better computational efficiency.

6. Conclusions

In this paper, we propose a fast second-order ADI finite difference scheme based on temporally graded meshes for solving the two-dimensional time-fractional Cattaneo equation with spatially variable coefficients. The corresponding stability and error estimates for the case of temporally uniform meshes are presented. Numerical examples further verify the accuracy and efficiency of the constructed difference scheme.