Numerical Performance of the Fractional Direct Spreading Cholera Disease Model: An Artificial Neural Network Approach
Abstract
1. Introduction
- The numerical solutions of the FO direct spreading cholera disease model are presented through the neuro-computing BR neural network process;
- The FO derivative based on the CD is used to present more reliable solutions of the mathematical model;
- Three cases based on FO values between 0 and 1 are presented to solve the mathematical model given in system (2);
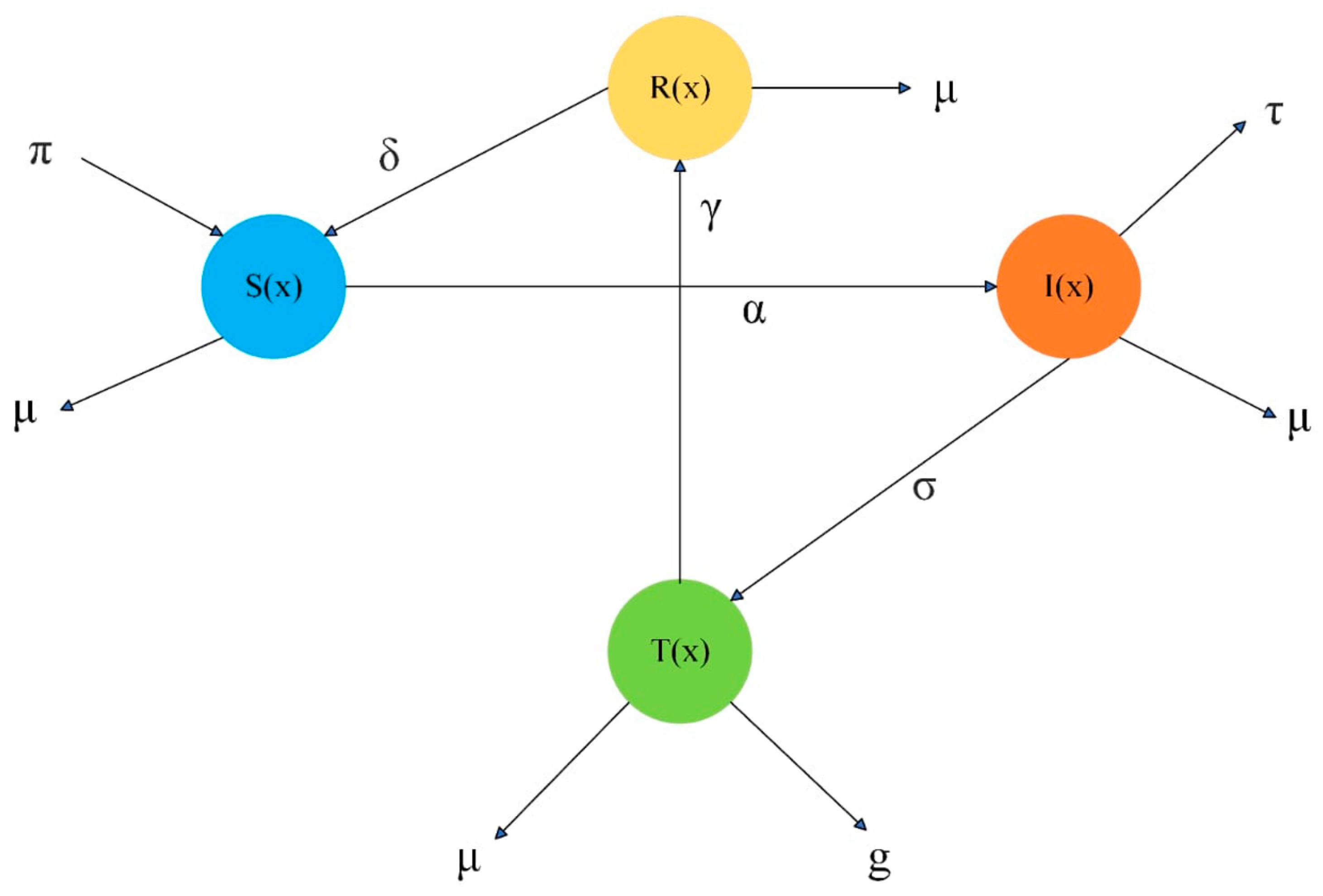
- The direct spreading cholera disease model is a nonlinear system that contains four different categories, while the numerical solutions are obtained through the BR neural network;
- A fitness function based on the sigmoid function is presented by taking twenty-two neurons in the hidden layer to obtain the results of the FO model;
- The correctness of the solver is authenticated through the matching of the outcomes and absolute error (AE).
2. Mathematical Formulation
3. Materials and Methods
BR Procedure
4. Results
5. Conclusions
- The solutions of the FO endemic disease model based on the direct spreading of cholera have been successfully obtained by applying the proposed structure method.
- The aim was to implement the FO derivatives for the precise solution of the model as compared to the integer-order case.
- A dataset has been constructed through the implicit Runge–Kutta method, which is used to reduce the M.S.E., by using 74% of the data for training, while 8% is used for both validation and testing.
- Twenty-two neurons and the log-sigmoid fitness function in the hidden layer have been used via the stochastic neural network process.
- Optimization has been performed through the BR scheme in order to solve the direct spreading cholera disease model.
- The accuracy of the BR stochastic process has been authenticated through the valuation of the outputs, along with a negligible AE.
- The FO values of 0.7, 0.8, and 0.9 have been used in three cases, and the value of 0.9 is found to be more precise as compared to other two cases.
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Brooks, S.; Weston, D.; Greenberg, N. Psychological impact of infectious disease outbreaks on pregnant women: Rapid evidence review. Public Health 2020, 189, 26–36. [Google Scholar] [CrossRef] [PubMed]
- Chowdhury, F.; Ross, A.G.; Islam, T.; McMillan, N.A.J.; Qadri, F. Diagnosis, Management, and Future Control of Cholera. Clin. Microbiol. Rev. 2022, 35, e0021121. [Google Scholar] [CrossRef] [PubMed]
- Beryl, M.; George, L.; Fredrick, N. Mathematical Analysis of A Cholera Transmission Model Incorporating Media Coverage. Int. J. Pure Appl. Math. 2016, 111, 219–331. [Google Scholar] [CrossRef]
- Helmi, A.M.; Mukti, A.T.; Soegianto, A.; Effendi, M.H. A review of vibriosis in fisheries: Public health importance. Syst. Rev. Pharm. 2020, 11, 51–58. [Google Scholar]
- Lopez, A.L.; Dutta, S.; Qadri, F.; Sovann, L.; Pandey, B.D.; Bin Hamzah, W.M.; Memon, I.; Iamsirithaworn, S.; Dang, D.A.; Chowdhury, F.; et al. Cholera in selected countries in Asia. Vaccine 2020, 38, A18–A24. [Google Scholar] [CrossRef]
- Fatima, S.; Krishnarajah, I.; Jaffar, M.; Adam, M.B. A Mathematical Model for the Control of Cholera in Nigeria. Res. J. Environ. Earth Sci. 2014, 6, 321–325. [Google Scholar] [CrossRef]
- Fakai, S.A.; Ibrahim, M.O.; Siddiqui, A.M. A deterministic mathematical model on cholera dynamics and some control strategies. Int. J. Sci. Eng. Technol. 2014, 8, 1115–1118. [Google Scholar]
- Bakare, E.A.; Hoskova-Mayerova, S. Optimal Control Analysis of Cholera Dynamics in the Presence of Asymptotic Transmission. Axioms 2021, 10, 60. [Google Scholar] [CrossRef]
- Sweileh, W.M. Global research activity on mathematical modeling of transmission and control of 23 selected infectious disease outbreak. Glob. Health 2022, 18, 4. [Google Scholar] [CrossRef]
- Siettos, C.I.; Russo, L. Mathematical modeling of infectious disease dynamics. Virulence 2013, 4, 295–306. [Google Scholar] [CrossRef]
- Codeço, C.T. Endemic and epidemic dynamics of cholera: The role of the aquatic reservoir. BMC Infect. Dis. 2001, 1, 1. [Google Scholar] [CrossRef]
- Wang, J.; Wang, J. Analysis of a reaction–diffusion cholera model with distinct dispersal rates in the human population. J. Dyn. Differ. Equ. 2021, 33, 549–575. [Google Scholar] [CrossRef]
- Sabir, Z.; Raja, M.A.; Mumtaz, N.; Fathurrochman, I.; Sadat, R.; Ali, M.R. An investigation through stochastic procedures for solving the fractional order computer virus propagation mathematical model with kill signals. Neural Process. Lett. 2023, 55, 1783–1797. [Google Scholar] [CrossRef]
- Sabir, Z.; Baleanu, D.; Raja, M.A.Z.; Alshomrani, A.S.; Hincal, E. Meyer wavelet neural networks procedures to investigate the numerical performances of the computer virus spread with kill signals. Fractals 2023, 31, 2340025. [Google Scholar] [CrossRef]
- Umar, M.; Sabir, Z.; Raja, M.A.Z. Intelligent computing for numerical treatment of nonlinear prey–predator models. Appl. Soft Comput. 2019, 80, 506–524. [Google Scholar] [CrossRef]
- Umar, M.; Sabir, Z.; Raja, M.A.Z.; Amin, F.; Saeed, T.; Sanchez, Y.G. Design of intelligent computing solver with Morlet wavelet neural networks for nonlinear predator–prey model. Appl. Soft Comput. 2023, 134, 109975. [Google Scholar] [CrossRef]
- Sabir, Z. Stochastic numerical investigations for nonlinear three-species food chain system. Int. J. Biomath. 2022, 15, 2250005. [Google Scholar] [CrossRef]
- Chen, Q.; Sabir, Z.; Raja, M.A.Z.; Gao, W.; Baskonus, H.M. A fractional study based on the economic and environmental mathematical model. Alex. Eng. J. 2023, 65, 761–770. [Google Scholar] [CrossRef]
- AbuAli, N.; Sabir, Z. Designing a heuristic computing structure to solve the human balancing model. J. King Saud Univ.-Comput. Inf. Sci. 2024, 36, 101890. [Google Scholar] [CrossRef]
- Sabir, Z.; Ben Said, S.; Al-Mdallal, Q. An artificial neural network approach for the language learning model. Sci. Rep. 2023, 13, 22693. [Google Scholar] [CrossRef]
- Umar, M.; Sabir, Z.; Raja, M.A.Z.; Baskonus, H.M.; Ali, M.R.; Shah, N.A. Heuristic computing with sequential quadratic programming for solving a nonlinear hepatitis B virus model. Math. Comput. Simul. 2023, 212, 234–248. [Google Scholar] [CrossRef]
- Tilahun, G.T.; Woldegerima, W.A.; Wondifraw, A. Stochastic and deterministic mathematical model of cholera disease dynamics with direct transmission. Adv. Differ. Equ. 2020, 2020, 670. [Google Scholar] [CrossRef]
- Rezapour, S.; Etemad, S.; Mohammadi, H. A mathematical analysis of a system of Caputo–Fabrizio fractional differential equations for the anthrax disease model in animals. Adv. Differ. Equ. 2020, 2020, 481. [Google Scholar] [CrossRef]
- Western, B.; Jackman, S. Bayesian Inference for Comparative Research. Am. Political-Sci. Rev. 1994, 88, 412–423. [Google Scholar] [CrossRef]
- Girosi, F.; Jones, M.; Poggio, T. Regularization Theory and Neural Networks Architectures. Neural Comput. 1995, 7, 219–269. [Google Scholar] [CrossRef]
- Sariev, E.; Germano, G. Bayesian regularized artificial neural networks for the estimation of the probability of default. Quant. Financ. 2020, 20, 311–328. [Google Scholar] [CrossRef]
- Marcos, F.L.; Plangklang, B. A high accurate user-friendly energy audit platform of a university building using ANN Bayesian regularization and Levenberg-Marquardt algorithm. Energy Rep. 2024, 11, 2220–2235. [Google Scholar] [CrossRef]
- Ahmad, Z.; Bonanomi, G.; Cardone, A.; Iuorio, A.; Toraldo, G.; Giannino, F. Fractalfractional sirs model for the disease dynamics in both prey and predator with singular and nonsingular kernels. J. Biol. Syst. 2024, 1–34. [Google Scholar] [CrossRef]
- Umar, M.; Sabir, Z.; Raja, M.A.Z.; Sánchez, Y.G. A stochastic numerical computing heuristic of SIR nonlinear model based on dengue fever. Results Phys. 2020, 19, 103585. [Google Scholar] [CrossRef]
- Lu, H.; Giannino, F.; Tartakovsky, D.M. Parsimonious models of in-host viral dynamics and immune response. Appl. Math. Lett. 2023, 145, 108781. [Google Scholar] [CrossRef]
- Junswang, P.; Sabir, Z.; Raja, M.A.Z.; Salahshour, S.; Botmart, T.; Weera, W. An Advanced Stochastic Numerical Approach for Host-Vector-Predator Nonlinear Model. Comput. Mater. Contin. 2022, 72, 5823–5843. [Google Scholar] [CrossRef]
- Ahmad, Z.; Bonanomi, G.; di Serafino, D.; Giannino, F. Transmission dynamics and sensitivity analysis of pine wilt disease with asymptomatic carriers via fractal-fractional differential operator of Mittag-Leffler kernel. Appl. Numer. Math. 2023, 185, 446–465. [Google Scholar] [CrossRef]
- Yusuf, A.; Acay, B.; Mustapha, U.T.; Inc, M.; Baleanu, D. Mathematical modeling of pine wilt disease with Caputo fractional operator. Chaos Solitons Fractals 2021, 143, 110569. [Google Scholar] [CrossRef]
- Khan, M.A.; Ullah, S.; Okosun, K.O.; Shah, K. A fractional order pine wilt disease model with Caputo–Fabrizio derivative. Adv. Differ. Equ. 2018, 2018, 410. [Google Scholar] [CrossRef]







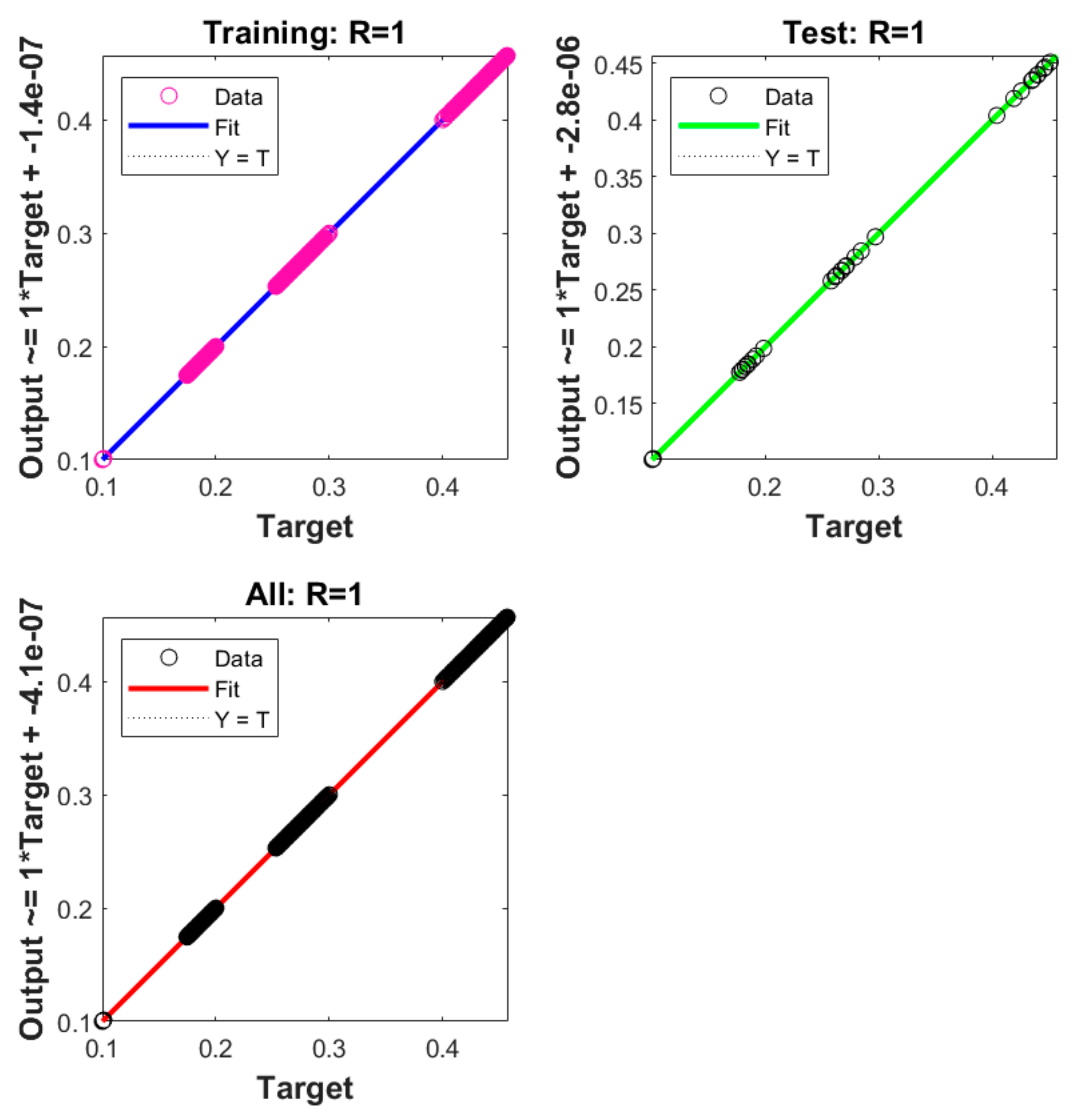



| Case | M.S.E. | Performance | Gradient | Iterations | Time | |
|---|---|---|---|---|---|---|
| Test | Train | |||||
| 1 | 1.20103 × 10−10 | 1.07270 × 10−10 | 1.07 × 10−10 | 5.58 × 10−8 | 07 | 1 s |
| 2 | 8.16973 × 10−11 | 3.12398 × 10−11 | 3.12 × 10−11 | 1.60 × 10−8 | 07 | 1 s |
| 3 | 8.25530 × 10−12 | 2.76863 × 10−12 | 2.77 × 10−12 | 1.13 × 10−8 | 07 | 1 s |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Malik, S. Numerical Performance of the Fractional Direct Spreading Cholera Disease Model: An Artificial Neural Network Approach. Fractal Fract. 2024, 8, 432. https://doi.org/10.3390/fractalfract8070432
Malik S. Numerical Performance of the Fractional Direct Spreading Cholera Disease Model: An Artificial Neural Network Approach. Fractal and Fractional. 2024; 8(7):432. https://doi.org/10.3390/fractalfract8070432
Chicago/Turabian StyleMalik, Saadia. 2024. "Numerical Performance of the Fractional Direct Spreading Cholera Disease Model: An Artificial Neural Network Approach" Fractal and Fractional 8, no. 7: 432. https://doi.org/10.3390/fractalfract8070432
APA StyleMalik, S. (2024). Numerical Performance of the Fractional Direct Spreading Cholera Disease Model: An Artificial Neural Network Approach. Fractal and Fractional, 8(7), 432. https://doi.org/10.3390/fractalfract8070432







