Understanding the Role of Intraspecific Disease Transmission and Quarantine on the Dynamics of Eco-Epidemiological Fractional Order Model
Abstract
1. Introduction
2. Model Formulation
- The population of prey is divided into three compartments, namely susceptible prey, infected prey, and quarantine prey, which, respectively, are denoted by S, I, and Q.
- The birth rate of susceptible prey is assumed contantly symbolized by .
- The susceptible prey is infected by disease with the disease transmission provided by a bilinear term βSI.
- As a human effort in protecting the ecological system, the infected prey is captured and quarantined with the quarantine rate proportional to the density of infected prey denoted by the linear term ηI. If the quarantined prey recovers, they will be returned to their natural habitat so that there is a risk of being reinfected. We denote the recovery rate by ζQ.
- The natural death rate of prey is provided by μ, and, hence, we have a natural death rate for each compartment symbolized by μS, μI, and μQ.
- The death rates caused by disease for infected and quarantined prey are, respectively, denoted by κI and φQ.
- The predator denoted by P only hunts the weak prey, in this case, the infected prey, and, hence, the susceptible prey is not being chased by the predator. The quarantine prey is also free from predation because it is in a place with human protection. We denote the predation rate of infected prey by ξIP.
- The birth rate of the predator is converted from the predation process provided by IP and the death rate of the predator provided by δP.
- Since the predator can only attack the infected prey, there is limited food availability for the predator. As an impact, there exists intraspecific competition regarding the predator with the death rate P2.
3. Analytical Results
3.1. Existence and Uniqueness of Solutions
3.2. Non-Negativity and Boundedness of Solutions
3.3. The Predator-Disease-Free Point and Basic Reproduction Number
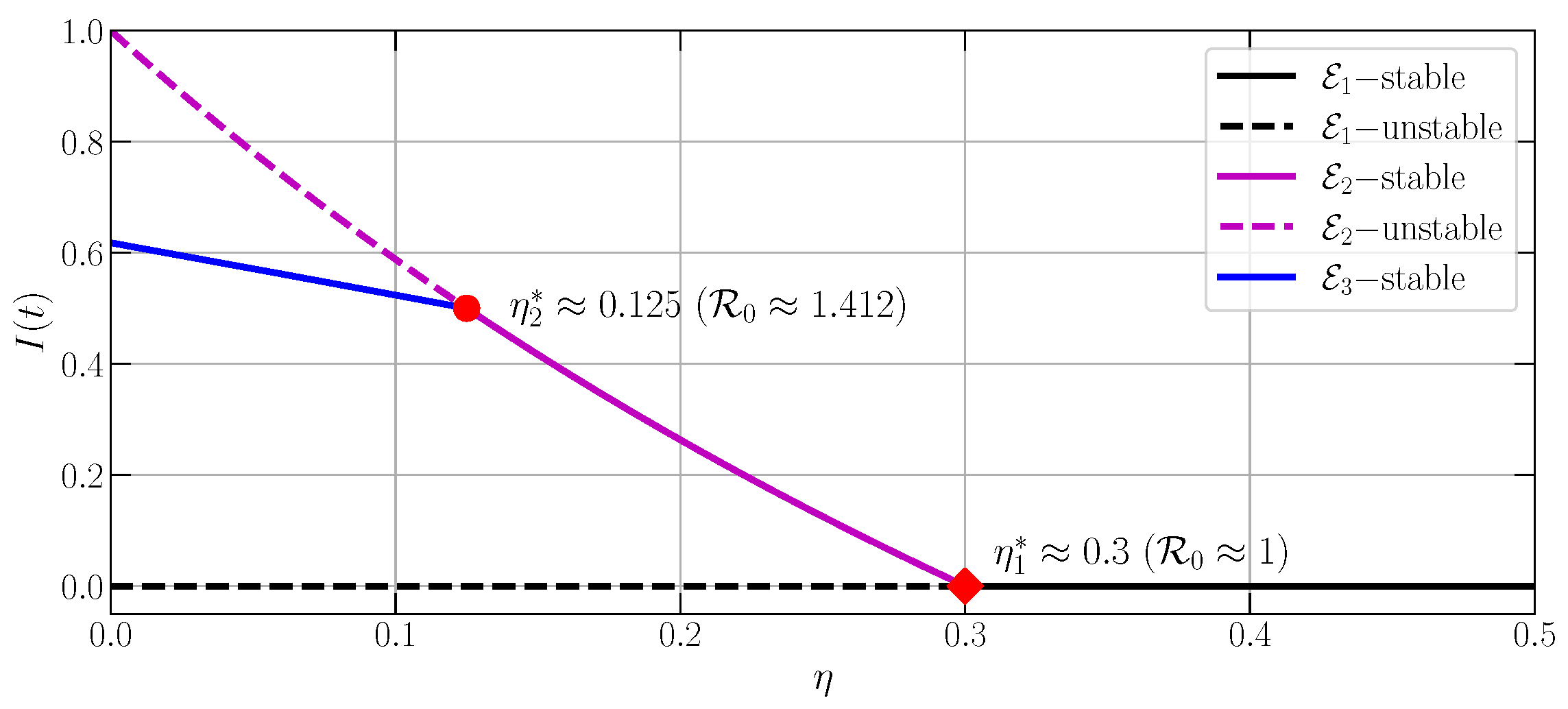
3.4. The Predator-Free-Endemic Point
3.5. The Predator-Endemic Point
- (i)
- unique if .
- (ii)
- a pair if and .
4. Numerical Results
4.1. Global Sensitivity Analysis
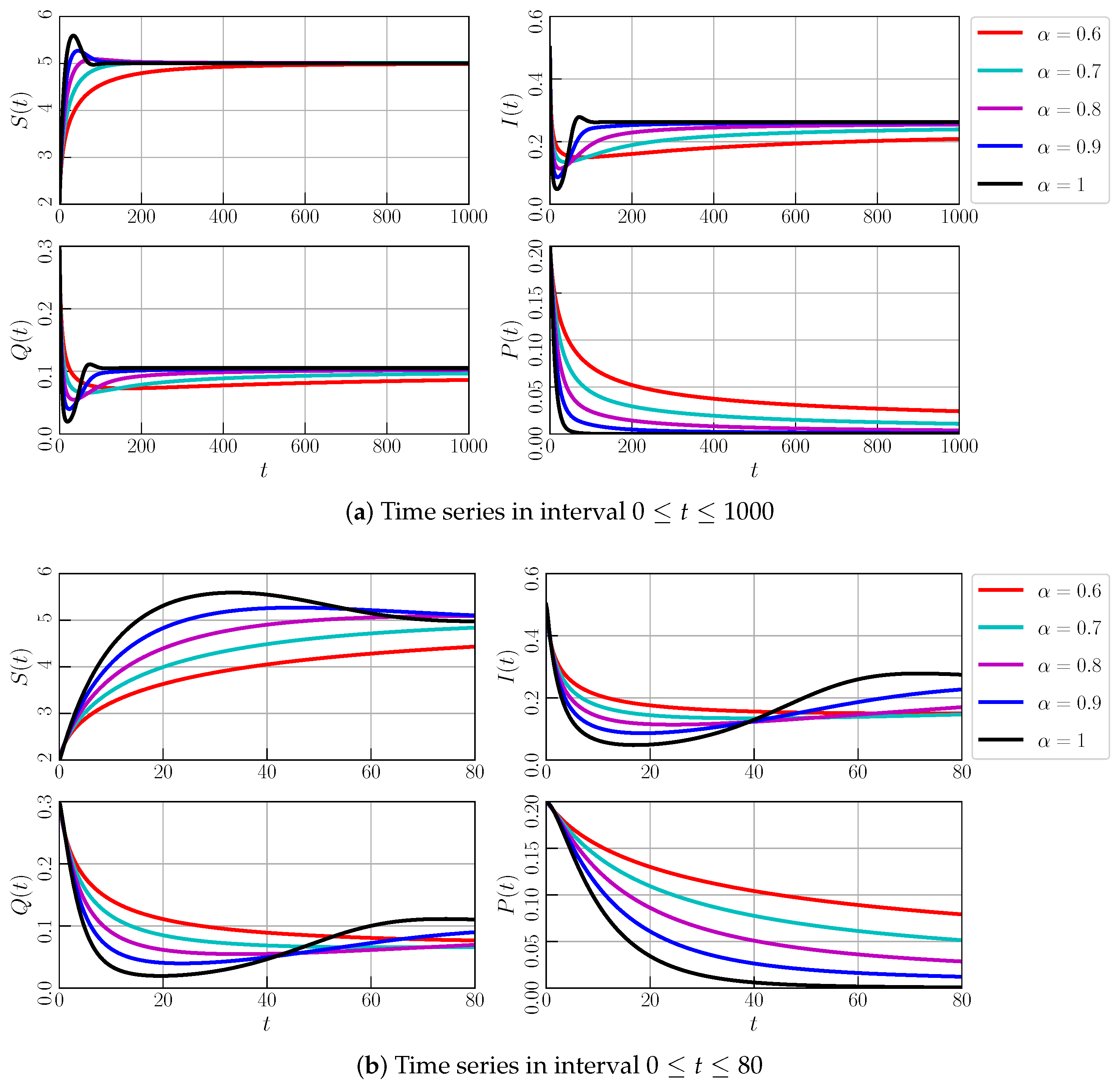
4.2. Dynamical Behaviors
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| LAS | Locally asymptotically stable |
| GAS | Globally asymptotically stable |
| PDFP | Predator-disease-free point |
| PFEP | The predator-free-endemic point |
| PEP | The Predator-Endemic Point |
References
- Anderson, R.M.; May, R.M.; Joysey, K.; Mollison, D.; Conway, G.R.; Cartwell, R.; Thompson, H.V.; Dixon, B. The Invasion, Persistence and Spread of Infectious Diseases within Animal and Plant Communities. Philos. Trans. R. Soc. B Biol. Sci. 1986, 314, 533–570. [Google Scholar] [CrossRef]
- Chattopadhyay, J.; Arino, O. A predator-prey model with disease in the prey. Nonlinear Anal. Theory Methods Appl. 1999, 36, 747–766. [Google Scholar] [CrossRef]
- Venturino, E. Epidemics in predator–prey models: Disease in the predators. J. Math. Appl. Med. Biol. 2002, 19, 185–205. [Google Scholar] [CrossRef]
- Siekmann, I. On competition in ecology, epidemiology and eco-epidemiology. Ecol. Complex. 2013, 14, 166–179. [Google Scholar] [CrossRef]
- Rahmi, E.; Darti, I.; Suryanto, A.; Trisilowati, T. A Fractional-Order Eco-Epidemiological Leslie–Gower Model with Double Allee Effect and Disease in Predator. Int. J. Differ. Equ. 2023, 2023, 5030729. [Google Scholar] [CrossRef]
- Naji, R.K.; Mustafa, A.N. The Dynamics of an Eco-Epidemiological Model with Nonlinear Incidence Rate. J. Appl. Math. 2012, 2012, 852631. [Google Scholar] [CrossRef]
- Rahman, M.S.; Chakravarty, S. A predator-prey model with disease in prey. Nonlinear Anal. Model. Control 2013, 18, 191–209. [Google Scholar] [CrossRef]
- Kant, S.; Kumar, V. Dynamics of a prey-predator system with infection in prey. Electron. J. Differ. Equ. 2017, 2017, 1–27. [Google Scholar]
- Greenhalgh, D.; Khan, Q.J.A.; Al-kharousi, F.A. Eco-epidemiological model with fatal disease in the prey. Nonlinear Anal. Real World Appl. 2020, 53, 103072. [Google Scholar] [CrossRef]
- Moustafa, M.; Mohd, M.H.; Ismail, A.I.; Abdullah, F.A. Dynamical analysis of a fractional-order eco-epidemiological model with disease in prey population. Adv. Differ. Equ. 2020, 2020. [Google Scholar] [CrossRef]
- Lopez, L.K.; Cortez, M.H.; Deblieux, T.S.; Hall, S.R.; Menel, I.A.; Brien, B.O.; Carla, E.C.; Duffy, M.A. A healthy but depleted herd: Predators decrease prey disease and density. Ecology 2023, 104, e4063. [Google Scholar] [CrossRef]
- Mbava, W.; Mugisha, J.Y.T.; Gonsalves, J.W. Prey, Predator and Super-Predator Model with Disease in the Super-Predator. Appl. Math. Comput. 2017, 297, 92–114. [Google Scholar] [CrossRef]
- Bate, A.M.; Hilker, F.M. Complex Dynamics in an Eco-epidemiological Model. Bull. Math. Biol. 2013, 75, 2059–2078. [Google Scholar] [CrossRef] [PubMed]
- Kang, A.; Xue, Y.; Fu, J. Dynamic Behaviors of a Leslie-Gower Ecoepidemiological Model. Discret. Dyn. Nat. Soc. 2015, 2015, 169242. [Google Scholar] [CrossRef]
- Shaikh, A.A.; Das, H.; Ali, N. Study of LG-Holling type III predator–prey model with disease in predator. J. Appl. Math. Comput. 2018, 58, 235–255. [Google Scholar] [CrossRef]
- Mondal, A.; Pal, A.K.; Samanta, G.P. On the dynamics of evolutionary Leslie-Gower predator-prey eco-epidemiological model with disease in predator. Ecol. Genet. Genom. 2019, 10, 100034. [Google Scholar] [CrossRef]
- Herrera, J.; Nunn, C.L. Behavioural ecology and infectious disease: Implications for conservation of biodiversity. Philos. Trans. R. Soc. B Biol. Sci. 2019, 374, 20180054. [Google Scholar] [CrossRef]
- Perumal, R.; Munigounder, S.; Mohd, M.H.; Balachandran, K. Stability analysis of the fractional-order prey-predator model with infection. Int. J. Model. Simul. 2021, 41, 434–450. [Google Scholar] [CrossRef]
- Bhattacharjee, D.; Kashyap, A.J.; Sarmah, H.K.; Paul, R. Dynamics in a ratio-dependent eco-epidemiological predator-prey model having cross species disease transmission. Commun. Math. Biol. Neurosci. 2021, 2021, 15. [Google Scholar] [CrossRef]
- pada Das, K. A study of harvesting in a predator—Prey model with disease in both populations. Math. Methods Appl. Sci. 2016, 39, 2853–2870. [Google Scholar] [CrossRef]
- Sharma, S.; Samanta, G.P. A Leslie-Gower predator-prey model with disease in prey incorporating a prey refuge. Chaos Solitons Fractals 2015, 70, 69–84. [Google Scholar] [CrossRef]
- Wang, S.; Ma, Z.; Wang, W. Dynamical behavior of a generalized eco-epidemiological system with prey refuge. Adv. Differ. Equ. 2018, 2018, 244. [Google Scholar] [CrossRef]
- Bhattacharyya, R.; Mukhopadhyay, B. On an Eco-Epidemiological Model with Prey Harvesting and Predator Switching: Local and Global Perspectives. Nonlinear Anal. Real World Appl. 2010, 11, 3824–3833. [Google Scholar] [CrossRef]
- Meng, X.Y.; Qin, N.N.; Huo, H.F. Dynamics analysis of a predator–prey system with harvesting prey and disease in prey species. J. Biol. Dyn. 2018, 12, 342–374. [Google Scholar] [CrossRef]
- Cojocaru, M.; Migot, T.; Jaber, A. Controlling infection in predator-prey systems with transmission dynamics. Infect. Dis. Model. 2020, 5, 1–11. [Google Scholar] [CrossRef]
- Bezabih, A.F.; Edessa, G.K.; Rao, K.P. Ecoepidemiological Model and Analysis of Prey-Predator System. J. Appl. Math. 2021, 2021, 6679686. [Google Scholar] [CrossRef]
- Kang, Y.; Kumar Sasmal, S.; Ranjan Bhowmick, A.; Chattopadhyay, J. Dynamics of a predator-prey system with prey subject to Allee effects and disease. Math. Biosci. Eng. 2014, 11, 877–918. [Google Scholar] [CrossRef]
- Saifuddin, M.; Biswas, S.; Samanta, S.; Sarkar, S.; Chattopadhyay, J. Complex dynamics of an eco-epidemiological model with different competition coefficients and weak Allee in the predator. Chaos Solitons Fractals 2016, 91, 270–285. [Google Scholar] [CrossRef]
- Wang, L.; Qiu, Z.; Feng, T.; Kang, Y. An eco-epidemiological model with social predation subject to a component Allee effect. Appl. Math. Model. 2022, 101, 111–131. [Google Scholar] [CrossRef]
- Babaei, A.; Ahmadi, M.; Jafari, H.; Liya, A. A mathematical model to examine the effect of quarantine on the spread of coronavirus. Chaos Solitons Fractals 2021, 142, 33–37. [Google Scholar] [CrossRef]
- Shah, N.H.; Sheoran, N.; Jayswal, E. Z-Control on COVID-19-Exposed Patients in Quarantine. Int. J. Differ. Equ. 2020, 2020. [Google Scholar] [CrossRef]
- Aronna, M.S.; Guglielmi, R.; Moschen, L.M. A model for COVID-19 with isolation, quarantine and testing as control measures. Epidemics 2021, 34, 100437. [Google Scholar] [CrossRef]
- Farman, M.; Akgül, A.; Fahad Aldosary, S.; Nisar, K.S.; Ahmad, A. Fractional order model for complex Layla and Majnun love story with chaotic behaviour. Alex. Eng. J. 2022, 61, 6725–6738. [Google Scholar] [CrossRef]
- Coronel-Escamilla, A.; Gómez-Aguilar, J.; López-López, M.; Alvarado-Martínez, V.; Guerrero-Ramírez, G. Triple pendulum model involving fractional derivatives with different kernels. Chaos Solitons Fractals 2016, 91, 248–261. [Google Scholar] [CrossRef]
- Almeida, R.; Brito da Cruz, A.M.; Martins, N.; Monteiro, M.T.T. An epidemiological MSEIR model described by the Caputo fractional derivative. Int. J. Dyn. Control. 2019, 7, 776–784. [Google Scholar] [CrossRef]
- Chen, S.B.; Jahanshahi, H.; Alhadji Abba, O.; Solís-Pérez, J.E.; Bekiros, S.; Gómez-Aguilar, J.F.; Yousefpour, A.; Chu, Y.M. The effect of market confidence on a financial system from the perspective of fractional calculus: Numerical investigation and circuit realization. Chaos Solitons Fractals 2020, 140, 110223. [Google Scholar] [CrossRef]
- Acay, B.; Inc, M. Fractional modeling of temperature dynamics of a building with singular kernels. Chaos Solitons Fractals 2021, 142, 110482. [Google Scholar] [CrossRef]
- Srivastava, H.M.; Dubey, V.P.; Kumar, R.; Singh, J.; Kumar, D.; Baleanu, D. An efficient computational approach for a fractional-order biological population model with carrying capacity. Chaos Solitons Fractals 2020, 138, 109880. [Google Scholar] [CrossRef]
- Barman, D.; Roy, J.; Alam, S. Modelling hiding behaviour in a predator-prey system by both integer order and fractional order derivatives. Ecol. Inform. 2022, 67, 101483. [Google Scholar] [CrossRef]
- Abdullah, F.A.; Moustafa, M.; Ismail, A.I.; Mohd, M.H. Global stability of a fractional order eco-epidemiological system with infected prey. Int. J. Math. Model. Numer. Optim. 2021, 11, 53. [Google Scholar] [CrossRef]
- Ogunrinde, R.B.; Nwajeri, U.K.; Fadugba, S.E.; Ogunrinde, R.R.; Oshinubi, K.I. Dynamic model of COVID-19 and citizens reaction using fractional derivative. Alex. Eng. J. 2021, 60, 2001–2012. [Google Scholar] [CrossRef]
- Djilali, S.; Ghanbari, B. The influence of an infectious disease on a prey-predator model equipped with a fractional-order derivative. Adv. Differ. Equ. 2021, 2021, 20. [Google Scholar] [CrossRef]
- Jurczynski, K.; Lyashchenko, K.P.; Gomis, D.; Journal, S.; Medicine, W.; June, N. Pinniped Tuberculosis In Malayan Tapirs (Tapirus indicus) and Its Transmission to Other Terrestrial Mammals. J. Zoo Wildl. Med. 2011, 42, 222–227. [Google Scholar] [CrossRef]
- Martin, C.; Pastoret, P.P.; Brochier, B.; Humblet, M.F.; Saegerman, C. A survey of the transmission of infectious diseases/infections between wild and domestic ungulates in Europe. Vet. Res. 2011, 42, 70. [Google Scholar] [CrossRef] [PubMed]
- Woodford, M.H. Quarantine and Health Screening Protocols for Wildlife Prior to Translocation and Release into the Wild; IUCN Species Survival Commission’s Veterinary Specialist Group, Gland, the Office International des Epizooties (OIE), Paris, Care for the Wild and the European Association of Zoo and Wildlife Veterinarians. 2000. Available online: https://digitalcommons.unl.edu/zoonoticspub/32/ (accessed on 20 February 2023).
- Petras, I. Fractional-Order Nonlinear Systems: Modeling, Analysis and Simulation; Springer: Berlin, Heidelberg, 2011. [Google Scholar] [CrossRef]
- Poria, S.; Dhiman, A. Existence and uniqueness of solution to ODEs: Lipschitz continuity. Resonance 2017, 22, 491–507. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Differential Equations; Academic Press: London, UK, 1999. [Google Scholar]
- Cresson, J.; Szafrańska, A. Discrete and continuous fractional persistence problems—The positivity property and applications. Commun. Nonlinear Sci. Numer. Simul. 2017, 44, 424–448. [Google Scholar] [CrossRef]
- Anbalagan, P.; Hincal, E.; Ramachandran, R.; Baleanu, D.; Cao, J.; Niezabitowski, M. A Razumikhin approach to stability and synchronization criteria for fractional order time delayed gene regulatory networks. AIMS Math. 2021, 6, 4526–4555. [Google Scholar] [CrossRef]
- Choi, S.K.; Kang, B.; Koo, N. Stability for Caputo Fractional Differential Systems. Abstr. Appl. Anal. 2014, 2014, 631419. [Google Scholar] [CrossRef]
- Matignon, D. Stability results for fractional differential equations with applications to control processing. In Proceedings of the CESA’96 IMACS Multiconference: Computational Engineering in Systems Applications, Lille, France, 9–12 July 1996; Volume 2, pp. 963–968. [Google Scholar]
- Huo, J.; Zhao, H.; Zhu, L. The effect of vaccines on backward bifurcation in a fractional order HIV model. Nonlinear Anal. Real World Appl. 2015, 26, 289–305. [Google Scholar] [CrossRef]
- Okyere, S.; Ackora-Prah, J. Modeling and analysis of monkeypox disease using fractional derivatives. Results Eng. 2023, 17, 100786. [Google Scholar] [CrossRef]
- Peter, O.J.; Panigoro, H.S.; Abidemi, A.; Ojo, M.M.; Oguntolu, F.A. Mathematical Model of COVID-19 Pandemic with Double Dose Vaccination. Acta Biotheor. 2023, 71, 9. [Google Scholar] [CrossRef] [PubMed]
- Peter, O.J.; Panigoro, H.S.; Ibrahim, M.A.; Otunuga, O.M.; Ayoola, T.A.; Oladapo, A.O. Analysis and dynamics of measles with control strategies: A mathematical modeling approach. Int. J. Dyn. Control 2023. [Google Scholar] [CrossRef]
- Diekmann, O.; Heesterbeek, J.; Metz, J. On the definition and the computation of the basic reproduction ratio R 0 in models for infectious diseases in heterogeneous populations. J. Math. Biol. 1990, 28, 365–382. [Google Scholar] [CrossRef]
- Sinan, M.; Shah, K.; Kumam, P.; Mahariq, I.; Ansari, K.J.; Ahmad, Z.; Shah, Z. Fractional order mathematical modeling of typhoid fever disease. Results Phys. 2022, 32, 105044. [Google Scholar] [CrossRef]
- Anggriani, N.; Beay, L.K. Modeling of COVID-19 spread with self-isolation at home and hospitalized classes. Results Phys. 2022, 36, 105378. [Google Scholar] [CrossRef]
- Vargas-De-León, C. Volterra-type Lyapunov functions for fractional-order epidemic systems. Commun. Nonlinear Sci. Numer. Simul. 2015, 24, 75–85. [Google Scholar] [CrossRef]
- Ahmed, E.; El-Sayed, A.; El-Saka, H.A. On some Routh–Hurwitz conditions for fractional order differential equations and their applications in Lorenz, Rössler, Chua and Chen systems. Phys. Lett. A 2006, 358, 1–4. [Google Scholar] [CrossRef]
- Pratap, A.; Raja, R.; Agarwal, R.P.; Alzabut, J.; Niezabitowski, M.; Hincal, E. Further results on asymptotic and finite-time stability analysis of fractional-order time-delayed genetic regulatory networks. Neurocomputing 2022, 475, 26–37. [Google Scholar] [CrossRef]
- Diethelm, K.; Ford, N.J.; Freed, A.D. A Predictor-Corrector Approach for the Numerical Solution of Fractional Differential Equations. Nonlinear Dyn. 2002, 29, 3–22. [Google Scholar] [CrossRef]
- Marino, S.; Hogue, I.B.; Ray, C.J.; Kirschner, D.E. A methodology for performing global uncertainty and sensitivity analysis in systems biology. J. Theor. Biol. 2008, 254, 178–196. [Google Scholar] [CrossRef]
- Saltelli, A. Making best use of model evaluations to compute sensitivity indices. Comput. Phys. Commun. 2002, 145, 280–297. [Google Scholar] [CrossRef]
- Saltelli, A.; Annoni, P.; Azzini, I.; Campolongo, F.; Ratto, M.; Tarantola, S. Variance based sensitivity analysis of model output. Design and estimator for the total sensitivity index. Comput. Phys. Commun. 2010, 181, 259–270. [Google Scholar] [CrossRef]
- Herman, J.; Usher, W. SALib: An open-source Python library for Sensitivity Analysis. J. Open Source Softw. 2017, 2, 97. [Google Scholar] [CrossRef]

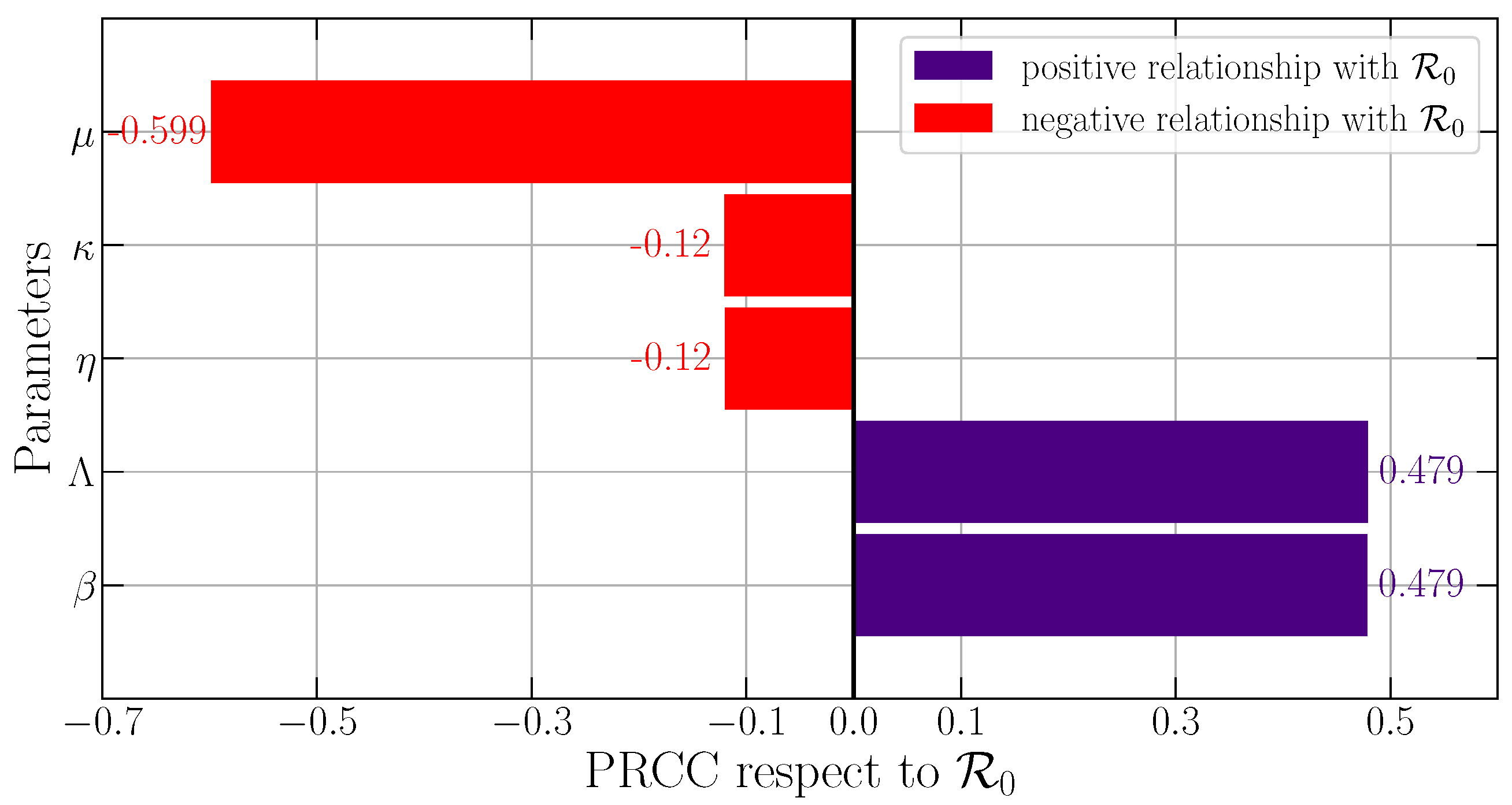


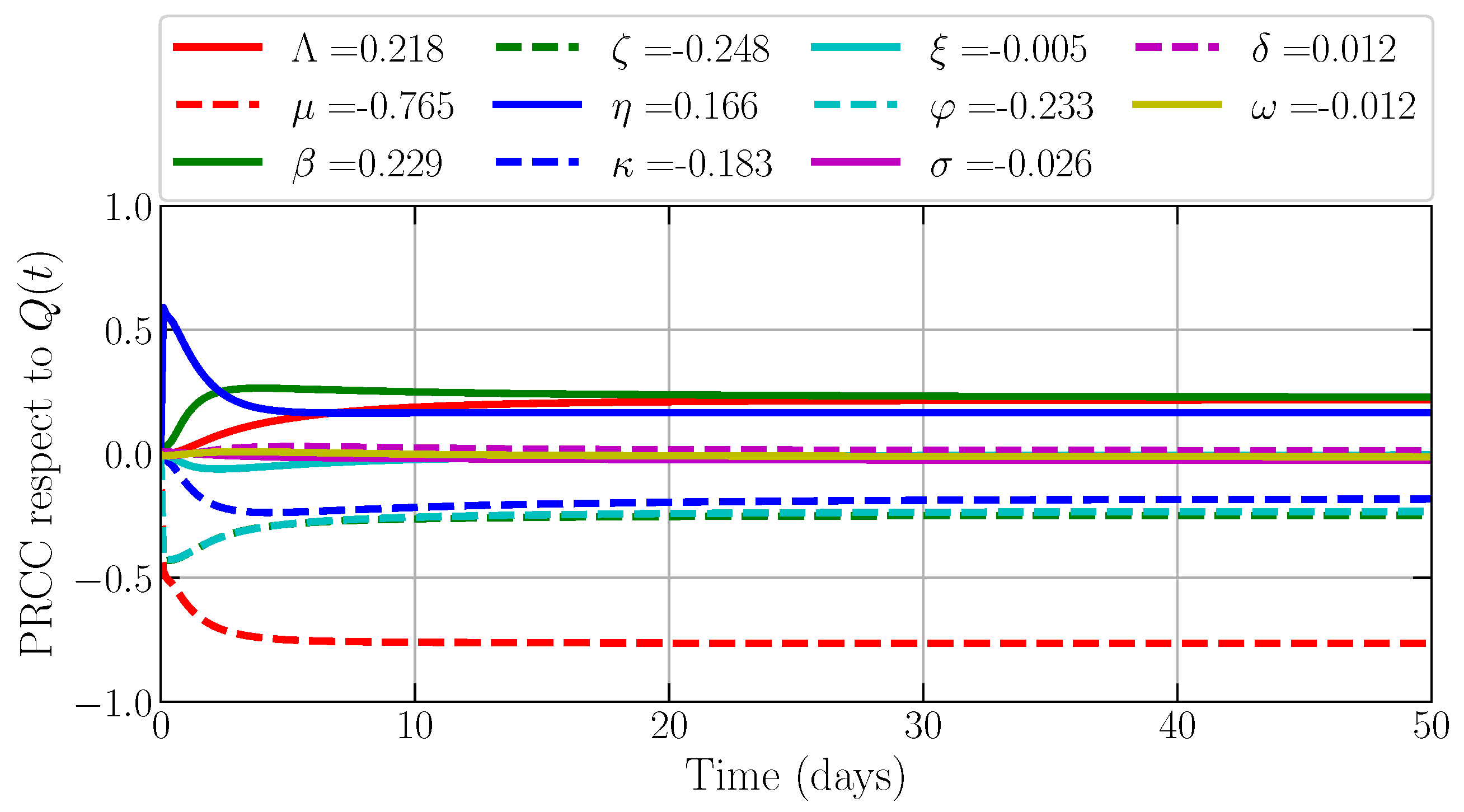

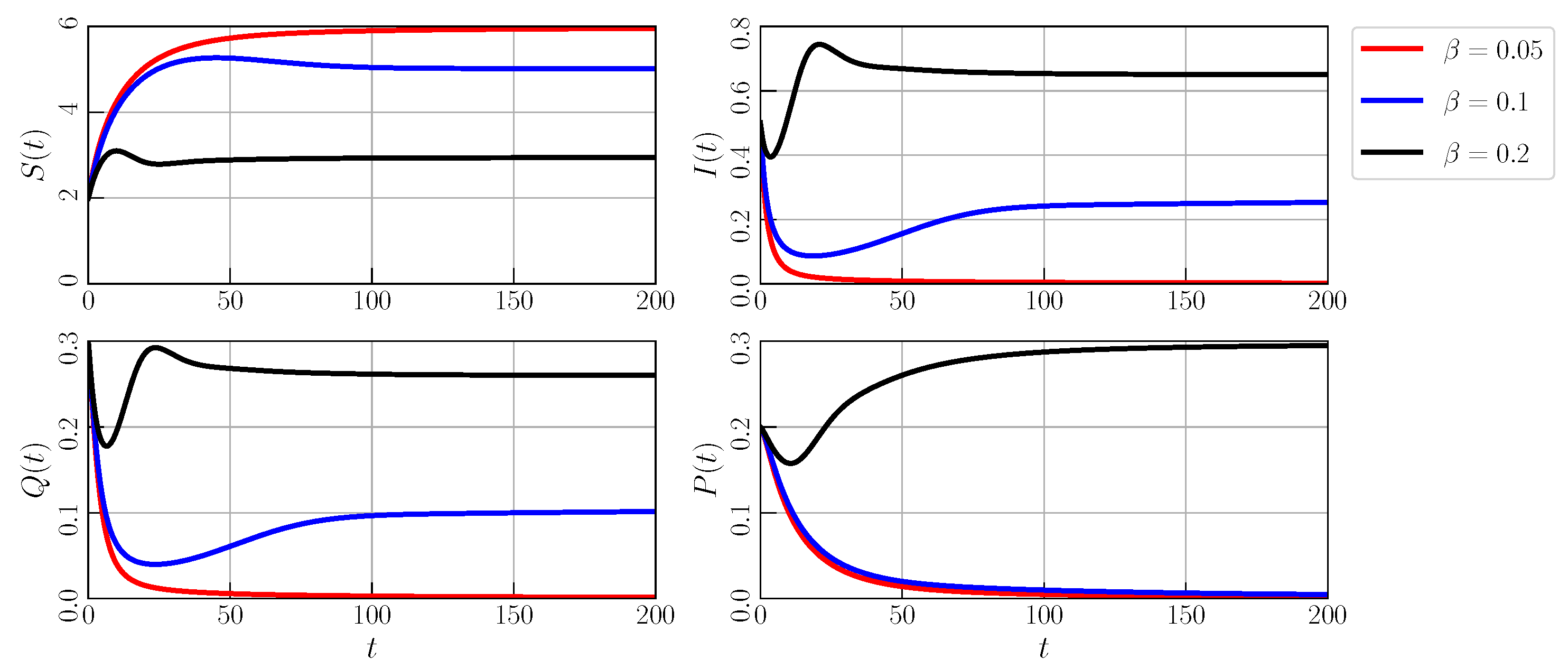
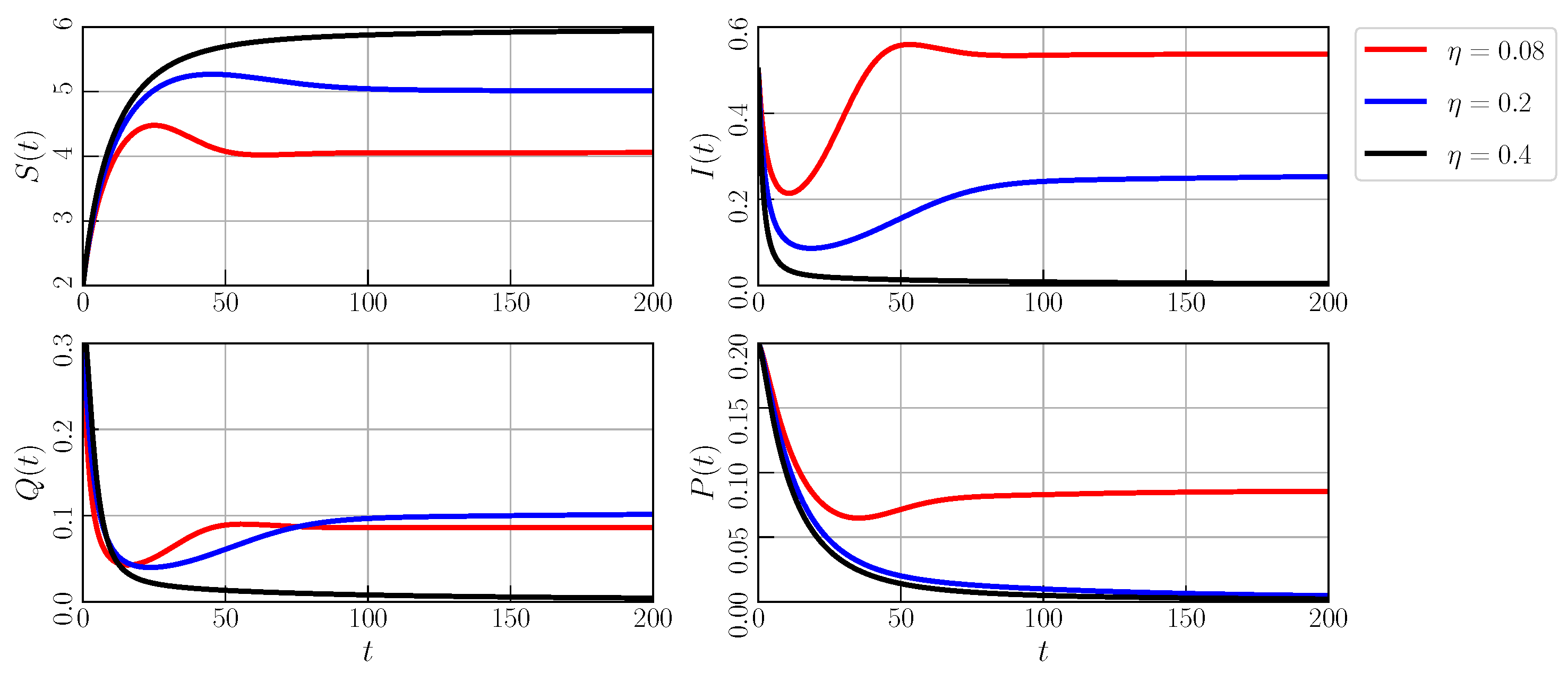
| Objective Functions | Most Influential Parameter | Biological Interpretation |
|---|---|---|
| The disease transmission rate has the greatest influence on increasing or decreasing the basic reproduction number. The disease transmission rate is directly proportional to basic reproduction number. | ||
| The disease transmission rate has the greatest influence on increasing or decreasing the density of the susceptible prey. The disease transmission rate is inversely proportional to the density of the susceptible prey. | ||
| The quarantine rate has the greatest influence on increasing or decreasing the density of the infected prey. The quarantine rate is inversely proportional to the density of the infected prey. | ||
| The recovery rate has the greatest influence on increasing or decreasing the density of the quarantine prey. The recovery rate is inversely proportional to the density of the quarantine prey. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Panigoro, H.S.; Anggriani, N.; Rahmi, E. Understanding the Role of Intraspecific Disease Transmission and Quarantine on the Dynamics of Eco-Epidemiological Fractional Order Model. Fractal Fract. 2023, 7, 610. https://doi.org/10.3390/fractalfract7080610
Panigoro HS, Anggriani N, Rahmi E. Understanding the Role of Intraspecific Disease Transmission and Quarantine on the Dynamics of Eco-Epidemiological Fractional Order Model. Fractal and Fractional. 2023; 7(8):610. https://doi.org/10.3390/fractalfract7080610
Chicago/Turabian StylePanigoro, Hasan S., Nursanti Anggriani, and Emli Rahmi. 2023. "Understanding the Role of Intraspecific Disease Transmission and Quarantine on the Dynamics of Eco-Epidemiological Fractional Order Model" Fractal and Fractional 7, no. 8: 610. https://doi.org/10.3390/fractalfract7080610
APA StylePanigoro, H. S., Anggriani, N., & Rahmi, E. (2023). Understanding the Role of Intraspecific Disease Transmission and Quarantine on the Dynamics of Eco-Epidemiological Fractional Order Model. Fractal and Fractional, 7(8), 610. https://doi.org/10.3390/fractalfract7080610







