Abstract
The dynamical behavior of the double-chain deoxyribonucleic acid (DNA) system holds significant implications for advancing the understanding of DNA transmission laws in the realms of biology and medicine. This study delves into the investigation of chaos patterns and solitary wave solutions for the (2+1) Beta-fractional double-chain DNA system, employing the theory of planar dynamical systems and the method of complete discrimination system for polynomials (CDSP). The results demonstrate a diverse spectrum of solitary wave solutions, sensitivity to perturbations, and manifestations of chaotic behavior within the system. Through the utilization of the complete discrimination system for polynomials, a multitude of novel solitary wave solutions, encompassing periodic, solitary wave, and Jacobian elliptic function solutions, were systematically constructed. The influence of Beta derivatives on the solutions was elucidated through parameter comparison analysis, emphasizing the innovative nature of this study. These findings underscore the potential of this system in unraveling various biologically significant DNA transmission mechanisms.
1. Introduction
Nowadays, nonlinear partial differential equations (PDEs) play a crucial role in various scientific disciplines such as physics, chemistry, optics and biology [1,2,3]. In addition, they are also used in fields such as fluid dynamics, engineering, and even financial markets [4,5].
The dynamics of deoxyribonucleic acid (DNA) molecules have emerged as a cutting-edge research area with applications extending beyond humans to the development of vaccines and viruses. Advanced vaccine technologies encompass DNA, ribonucleic acid (RNA), subunits, and virus-like particles [6,7]. Double-chain DNA stands as a pivotal molecular structure in biology, finding applications across diverse fields including biology, medicine, and bioinformatics.
Researchers from the disciplines of mathematics, physics, and biology have formulated numerous mathematical models pertaining to double-chain DNA to investigate the operational mechanisms of DNA and the evolutionary dynamics of genetic regulation within organisms. The application of mathematical models and analytical methods to explore biological processes involving DNA has become a tangible reality. Numerous studies have demonstrated that these mathematical models can effectively delineate DNA sequence evolution, gene expression regulation, and protein synthesis. Various mathematical tools such as dynamic models [8] and network analysis [9] have been established to study double-chain DNA systems.
Mathematical physicists leverage mathematical methodologies to simulate the structure, mechanical properties, and dynamic behaviors of DNA. Drawing upon theories including elasticity, fluid dynamics, and statistical mechanics, extensive research has been conducted on phenomena such as the double helical structure of DNA, double-strand unwinding, and supercoiling formation. The diverse characteristics of DNA dynamic systems render mathematical modeling a highly challenging endeavor. Nonlinear partial differential equations have proven to be effective tools for constructing mathematical models that elucidate the physical properties and behaviors of DNA. Analysis of DNA behavior reveals that nonlinear structures within DNA can give rise to local waves that transmit energy without dissipation. The simplest nonlinear partial differential equation model is the (1+1)-dimensional model [10], which elucidates the motion of DNA chains, facilitating the study of bending, twisting, and stretching movements of DNA chains to unravel the structural and functional aspects of DNA within organisms. The (2+1)-dimensional model accounts for interactions between the two DNA strands [11], offering a more realistic representation. This model is instrumental in investigating processes such as DNA unwinding, replication, and repair, unveiling the intricate regulatory mechanisms of DNA replication. The most intricate DNA model, the (3+1)-dimensional model [12], incorporates the three-dimensional structure of DNA chains and their interactions with other molecules. This model enables the study of the spatial arrangement of DNA and its interactions with other molecules, such as DNA-protein binding, thereby providing deeper insights into the functional role of DNA within cells.
Solitary wave solutions and chaotic behavior [13] play pivotal roles in understanding wave propagation. Solitary wave solutions refer to isolated waves formed by information on DNA chains that propagate without deformation or loss. These solutions are crucial for studying the stable transmission and protection of DNA information, aiding in our comprehension of the role of DNA in cell division and genetic transmission. Chaotic behavior pertains to the spatially random and unpredictable dynamic behavior of information on DNA chains. It is essential for studying the nonlinear dynamical behavior and stability of DNA, facilitating our understanding of the role of DNA in genetic variation and evolution. In conclusion, through the study of double-stranded DNA models and their wave solutions, solitary wave solutions, and chaotic behavior, we can deepen our understanding of the structure and function of DNA, unveil the dynamic behavior and genetic regulatory processes of DNA within organisms, and furnish potent mathematical tools and theoretical foundations for biological research.
Several attractive solutions have already been adopted to study nonlinear DNA systems. Using the expansion method [10], various types of wave solutions have been obtained, including composite solitons, hyperbolic, plane waves, trigonometric, and elliptic function solutions. By utilizing multi-wave techniques, [11] studies the multi-wave interaction behavior of DNA systems. Yao and his collaborators used the Lie transformation approach to construct one-soliton solutions, multiple-soliton and periodic solutions for (3+1) DNA systems in [12]. In addition, references [14,15,16] study the dynamic properties and optical soliton solutions [17] of DNA systems. Perturbation techniques are employed to independently study the interaction behavior of DNA systems in [18,19]. It is worth mentioning that many new methods have been developed to construct more new solitary solutions in double-chain DNA systems. Researchers utilize the auxiliary function method [20], the new auxiliary equation method [21], the generalized Kudryashov method [22], and the generalized exponential rational function method [23] to construct solutions for nonlinear DNA systems.
Fractional order calculus has made rapid development in recent years. Compared with integer-order partial differential equations, fractional-order partial differential equations are more advantageous in describing nonlinear behavior, nonlocal behavior, and multiscale coupling problems, and thus can better simulate complex phenomena. Fractional-order partial differential equations have a wide range of applications in the fields of image processing, signal processing, and financial engineering [24,25,26]. In order to deepen the research, researchers have incorporated fractional-order derivatives into DNA models [27] and conducted related studies. Among the many definitions of fractional derivatives, a Beta-fractional derivative is also a highly practical and valuable one. The -order Beta-fractional derivative of is defined as
If the -order Beta-fractional derivative of exists, then function is said to be -order Beta differentiable.
According to the definition of Beta-fractional derivative, if and are differentiable, then is -order Beta-differentiable, and the following formula holds:
The Beta-fractional derivative has been successfully applied to multiple nonlinear partial differential equation models [28,29,30]. In this article, we investigate double-chain DNA models with Beta-fractional derivatives, which provide new insights into the dynamic characteristics of double-chain DNA unwinding and the development of biomedical and biotechnology.
The structure of this paper is as follows: In Section 2, we perform a traveling wave transformation on the double-chain DNA system and reduce it to a nonlinear ordinary differential equation. In Section 3, we investigate the branches of this equation and its chaotic behavior under periodic perturbations. In Section 4, we employ the complete discrimination method to obtain soliton solutions. In Section 5, we provide graphical illustrations of these solutions and compare them with previously published papers to demonstrate the novelty of this work. At last, the paper ends with a conclusion based on the analysis of the chaotic behaviour of a double-chain DNA model within the framework of Beta-fractional derivatives.
2. Mathematical Analysis
This research aims to investigate the chaotic behavior and the solitary solutions of the double-chain DNA equation with a Beta-fractional derivative, which represents a specific mathematical model, in the context of (2+1)-dimensional stochastic gene evolution. The dynamics of DNA molecules can be described by the following nonlinear dynamical equations:
where v shows the difference of transverse displacements of top and bottom strands, u interprets for the difference of longitudinal displacements of top and bottom strands, stands for the Beta derivative of u and . The constants , , , , , , , , , and are defined as
The meanings of the variables and symbols involved are listed below:
- *
- denotes the area of the transverse cross-section,
- *
- denotes Young’s modulus,
- *
- represents the rigidity of the elastic membrane,
- *
- is the mass density,
- *
- F denotes the tension density of the strand,
- *
- represents the height of the membrane in its equilibrium position,
- *
- is the distance between the two strands.
The two equations of Equation (4) are similar if
Consequently, , and Equation (4) is converted to
where .
We take wave transformation
where
Equation (5) is reduced to
where , , , and .
3. Phase Portraits and Chaotic Analysis
3.1. Phase Portraits
Based on the equilibrium points of nonlinear differential equations and planar dynamic systems, phase portrait analysis is a powerful qualitative analysis technique for nonlinear ordinary differential equations.
Equation (8) is equivalent to the following differential equation system:
with the first integration
where is a constant. The equilibrium point of Equation (9) refers to the constant solution of . The type of equilibrium point and the stability of the system near the equilibrium point can be determined by the eigenvalues of the Jacobian matrix, which is defined as
If all the eigenvalues of the Jacobian matrix J are pure imaginary, the equilibrium point is a center. If the eigenvalues have non-zero real parts and are complex roots, the equilibrium point is a focus. If the eigenvalues have both positive and negative real parts, the equilibrium point is a saddle point. If the eigenvalues are two real roots with the same sign, the equilibrium point is a node. If the eigenvalues are 0, the equilibrium point is a degenerate equilibrium point. Furthermore, we can determine the stability of System (9) around the equilibrium points: If the real parts of the eigenvalues are all negative, then the equilibrium point is stable. If the real parts of the eigenvalues are all positive, then the equilibrium point is unstable. If the real parts of the eigenvalues are both positive and negative, then the equilibrium point is unstable.
We denote . According to the theory of planar dynamical systems, when , is the center point. When , is the saddle point. When and the Poincaré index is zero, is a cusp point.
We let .
If and , the system has three equilibrium points , and . It is easy to infer that when , is the saddle point. When , is the center point. When , is a cusp point. Meanwhile, both and are the cusp points.
If and , the system has two equilibrium points and . We can infer that when , is the saddle point. When , is the center point. When , is a sharp point. Meanwhile, both is the cusp points.
If and , the system has a unique equilibrium point . Similarly, when , is the saddle point. When , is the center point. When , is a sharp point.
If and , the system has two equilibrium points , . It is easy to find that , so when , is the saddle point and is the center point. When , is the center point and is the saddle point. When , both and are the cusp points.
If , the system has one equilibrium point .
The phase portraits are crucial for analyzing the dynamic behavior of Equation (9). According to the theory of planar dynamical systems and utilizing symbols , , , and , the classification of trajectories near the equilibrium point can be obtained. With the help of the symbol calculation package Maple 23, these phase portraits are listed in Figure 1, Figure 2, Figure 3 and Figure 4). Symbols in these figures denote , and . Each color in the figure represents the same set of trajectories. It is evident that in certain graphs, trajectories of two branches share the same color, indicating that Equation (9) possesses the double periodic function, also known as the elliptic function. Additionally, closed curves are observed in some graphs, leading to periodic solutions for Equation (9). Importantly, these graphs also illustrate abundant homoclinic orbits, signifying the existence of solitary wave solutions. Therefore, System (9) has solitary wave solutions, periodic solutions, and other forms of solutions.

Figure 1.
The phase portraits of (9) for .
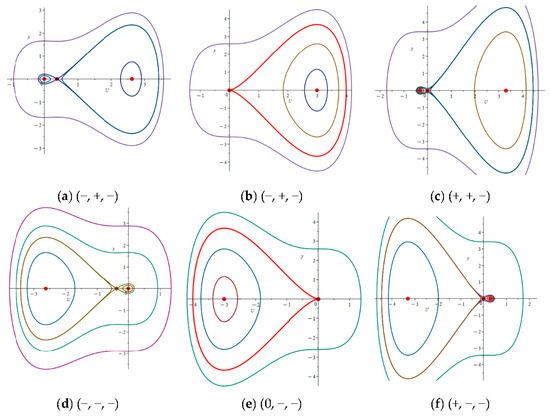
Figure 2.
The phase portraits of (9) for .
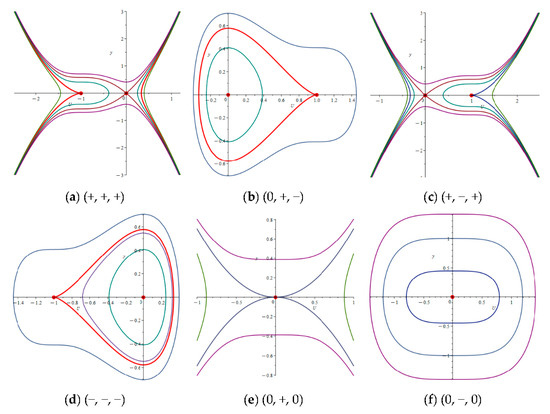
Figure 3.
The phase portraits of (9) for .
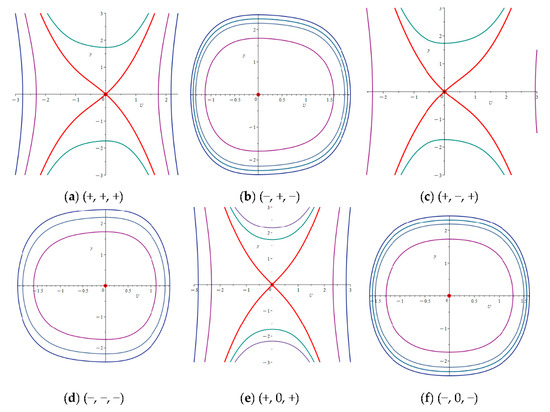
Figure 4.
The phase portraits of (9) for .
3.2. Sensitivity Analysis
This section discusses the sensitivity behavior of Equation (9) to initial values. In Figure 5, the parameters are set as and . Figure 5a,b illustrate the 3D and 2D trajectories with initial values of . This shows that Equation (9) has a periodic solution. In Figure 5c, two independent initial conditions are considered: the blue solid line corresponds to an initial value of , while the red dashed line corresponds to an initial value of . It can be seen that a slight change in the initial state can have a significant effect on nonlinear Equation (9), leading to the disordered behavior of the solution. This sensitive behavior of the solution motivates one to analyze this equation under discussion from multiple perspectives.
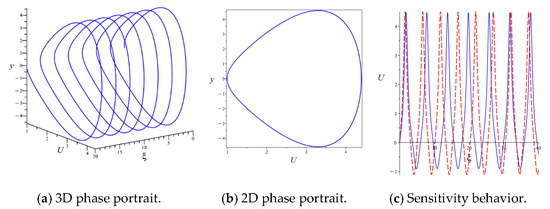
Figure 5.
Sensitivity analysis of Equation (9) with and .
3.3. Quasiperiodic and Chaotic Behaviors
Due to the complexity of the real environment, periodic disturbances often exist. Therefore, a periodic perturbation term, , is introduced in Equation (9) as follows:
where represents disturbance intensity, represents disturbance frequency. We keep parameters and fixed, and consider the effects of and on the behavior of the solution. In Figure 6 and Figure 7, the influence of perturbations on the behavior of solutions is demonstrated using 3D trajectories, 2D trajectories, time series, and Poincaé cross-sections. The initial values corresponding to the time series diagram are the same as those in Figure 5. As shown in the figures, slight changes in the intensity and frequency of external disturbances can lead to chaotic behavior in the system.
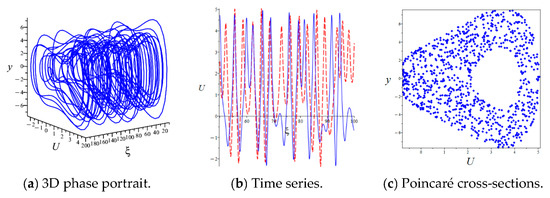
Figure 6.
Chaotic behavior of Equation (9) with and .
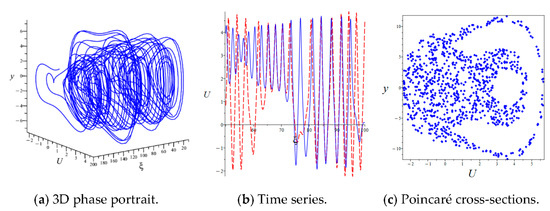
Figure 7.
Chaotic behavior of Equation (9) with and .
4. Traveling Wave Solution of Equation (2)
In the following, we use the complete discriminant system to find the traveling wave solution of Equation (2). We integrate Equation (8) once to obtain
where is the constant of integration.
Equation (12) can be rewritten into an equivalent form:
Once Equation (13) is solved, the solution to Equation (2) can be constructed by combining Equations (3), (6), and (7). However, the presence of parameters poses difficulties in solving Equation (13). Therefore, we use the complete discriminant method to solve Equation (13).
4.1. Set 1:
When , Equation (8) is equivalent to
where is the constant of integration.
Equation (14) is equivalent to
where is the constant of integration.
Case 1.1. .
In this case, Equation (2) exhibits the following hyperbolic sine function solutions:
where .
Case 1.2. .
Equation (2) possesses periodic solutions as follows:
where .
Case 1.3. .
Equation (2) possesses the exponential function solution as shown below:
Case 1.4. .
Equation (2) possesses another form of exponential function solution:
4.2. Set 2:
Substitution converts Equation (12) to
where , , is a integral constant, and . The complete discriminant system for is as follows:
Case 2.1. .
In this situation, . This leads to a singular isolated wave solution of Equation (2) as follows:
Case 2.2. .
We factorize to obtain , where and are different real numbers.
When , Equation (2) has the triangle solution of the following form:
where .
Case 2.3. .
It is easy to draw the following conclusion: , where are different real numbers.
Case 2.4. .
In this situation, , where are real numbers and .
The Jacobian elliptic function solutions of Equation (2) can be constructed as follows:
where and .
4.3. Set 3:
Substitution , converts Equation (12) to
where if , we take ; if , we take , ; is the constant of integration; ; ; and .
To solve Equation (29), the complete discriminant system of is introduced as follows:
Case 3.1. .
It is easy to conclude that . This leads to a singular solitary wave solution of Equation (2) as follows:
where .
Case 3.2. .
It can be concluded that .
If , when or , we obtain the solitary wave solution of Equation (2) as follows:
If , when , we obtain the solitary wave solution of Equation (2) as follows:
Case 3.3. .
Based on the parameter values, it is not difficult to obtain .
If , when or , we obtain the solitary wave solution of Equation (2) as follows:
If , when , we obtain the solitary wave solution of Equation (2) as follows:
where .
Case 3.4. .
In the situation, .
If , we obtain the periodic wave solution of Equation (2) as follows:
Case 3.5. .
In this situation, , where and are different real numbers, and .
If , when or , we obtain the solitary wave solution of Equation (2) as follows:
When , we obtain the solitary wave solution of Equation (2) as follows:
where .
If , when , we obtain the solitary wave solution of Equation (2) as follows:
When , we obtain the solitary wave solution of Equation (2) as follows:
where .
Case 3.6. .
In this situation, , where and are real numbers.
If , we obtain the solitary wave solution of Equation (2) as follows:
where .
Case 3.7. .
In this situation, , where and are real numbers. The elliptic function solution of Equation (2) can be constructed as follows:
where , , , , and .
Case 3.8. .
In this situation, , where are real numbers, . If , the elliptic function solution of Equation (2) can be constructed as follows:
where , , , , .
5. Results and Discussion
In this study, the dynamical behavior and exact solutions of the fractional-order double-chain DNA system were comprehensively investigated. Firstly, the phase portrait analysis method based on the theory of planar dynamical systems was employed for a qualitative analysis of the planar dynamics and chaotic behavior of the double-chain DNA system. The phase portrait analysis reveals that System (2) exhibits important geometric features such as periodic orbits and homoclinic orbits. Perturbation analysis demonstrates that the system is sensitive to perturbation strength and initial conditions, leading to chaotic behavior. Secondly, the complete discrimination method was successfully utilized to construct traveling wave solutions of System (2), including rich periodic solutions and solitary wave solutions.
5.1. Graphical Presentation
Figure 8 illustrates a three-dimensional visualization, contour plots, and two-dimensional waveforms of periodic solution , with parameters set as . Additionally, a solitary wave solution is depicted in Figure 9. It is well known that as , , and as , . This implies that as , periodic functions also exist in the solutions represented by elliptic functions, such as , , , etc. Figure 10 and Figure 11 then display the constructed soliton solutions, and . Similarly, more solitary solutions can be constructed from those represented by these elliptic functions.
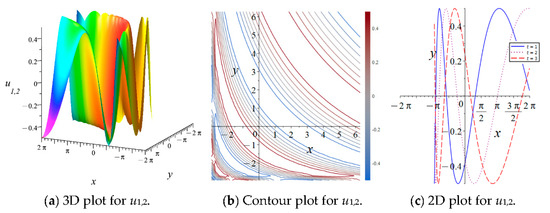
Figure 8.
Graphical view of periodic solution for with , and .
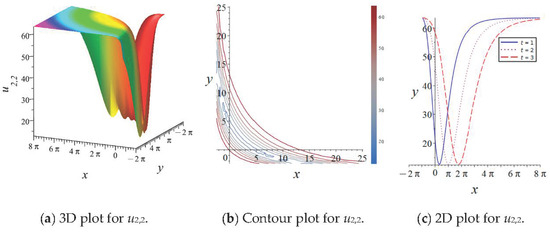
Figure 9.
Graphical view of soliton solution for with , , and .
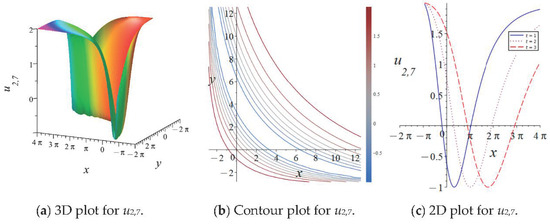
Figure 10.
Graphical view of soliton solution for with , , and .

Figure 11.
Graphical view of soliton solution for with , and .
5.2. Influence of Fractional Derivative
In this study, a novel approach was employed to investigate the propagation of DNA models using Beta-fractional derivatives. Figure 12 illustrates the 2D waveforms of , , and for different values of , specifically , , and 1. The physical implications of these solutions are used to elucidate the influence of Beta on periodic solutions and solitary wave solutions.
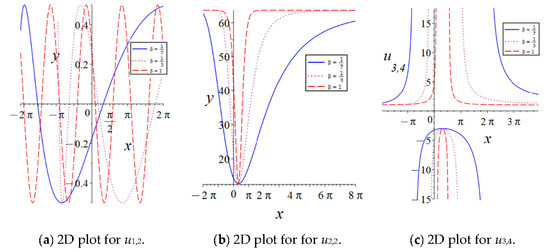
Figure 12.
The influence of fractional derivatives on solutions from a 2D perspective at .
Figure 12a indicates that, with other parameters held constant, an increase in Beta from small to large values results in no change in the amplitude of the periodic solution but a decrease in the period. Figure 12b,c demonstrate that, under unchanged parameters, an increase in Beta leads to no variation in the amplitude of the solitary wave solution but a decrease in its width. Consequently, for smaller Beta, the oscillations of solutions become smoother.
Therefore, it is crucial to accurately interpret the effects of Beta on different types of wave solutions in the context of DNA models.
5.3. Literature Comparison
In comparison with the most recent publications [10,12,25], this paper exhibits innovativeness. Firstly, the introduction of fractional-order derivatives in the model of this paper is innovative, thus possessing broader theoretical and practical significance. Secondly, this paper provides the first analysis of the dynamical properties of DNA models. Lastly, in terms of the types of traveling wave solutions constructed, the conclusions of this paper are more diverse. Reference [10] employed the method to construct solutions containing tanh, sech, coth, and sinh functions; [12] utilized Lie group methods to construct solutions in the forms of sn, cd, tan, tanh. This paper employed CDSP to construct solutions of more diverse solutions, including sin, tan, exp, sn, cn, sinh, tanh, coth, and rational function solutions.
6. Conclusions
This study investigates the chaotic behavior of a double-chain DNA model within the framework of Beta-fractional derivatives and utilizes the CDSP method to construct solitary wave solutions. Initially, Equation (2) is transformed into a nonlinear ordinary differential equation using a traveling wave substitution. Subsequently, a detailed analysis of the trajectory distribution near equilibrium points is conducted using the method of planar dynamical systems, showcasing the chaotic behavior of the perturbed system through sensitivity analysis and Poincaré sections. Furthermore, plenty of novel traveling wave solutions and solitary wave solutions for Equation (2) are constructed using the CDSP method, encompassing periodic solutions, solitary wave solutions, and Jacobian elliptic function solutions. The paper concludes by visually presenting the dynamic properties of selected representative solutions and examining the influence of fractional-order derivatives on these solutions. These findings contribute to a deeper understanding of the dynamic processes involved in genetic information transmission and the evolution of DNA sequences.
Author Contributions
T.H.: Investigation, writing—original draft. K.Z.: Review, graphic drawing. Y.J.: Critical review. H.R.: Methodology, critical review. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by Sichuan Science and Technology Program (No.2023 NSFSC0078), Ecological Security and Protection Sichuan Provincial Key Laboratory Open Fund Project (ESP2303).
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare that there is no conflict of interest regarding the publication of this paper. The authors declare that they have no competing interests.
References
- Zhang, K.; Li, Z.; Cao, J. Qualitative analysis and modulation instability for the extended (3+1)-dimensional nonlinear Schrödinger equation with conformable derivative. Results Phys. 2024, 61, 107713. [Google Scholar] [CrossRef]
- Wang, J.; Li, Z. A Dynamical Analysis and New TravelingWave Solution of the Fractional Coupled Konopelchenko CDubrovsky Model. Fractal Fract. 2024, 8, 341. [Google Scholar] [CrossRef]
- Liu, C.; Li, Z. The dynamical behavior analysis and the traveling wave solutions of the stochastic Sasa-Satsuma Equation. Qual. Theory Dyn. Syst. 2024, 23, 157. [Google Scholar] [CrossRef]
- Gu, M.; Peng, C.; Li, Z. Traveling wave solution of (3+1)-dimensional negative-order KdV-Calogero-Bogoyavlenskii-Schiff equation. Aims Math. 2024, 9, 6699–6708. [Google Scholar] [CrossRef]
- Tang, C.; Li, X.; Wang, Q. Mean-field stochastic linear quadratic optimal control for jump-diffusion systems with hybrid disturbances. Symmetry 2024, 16, 642. [Google Scholar] [CrossRef]
- Wang, Z.; Fang, T.; Fang, Y.; Xie, P.; Liu, Y. Harnessing single fluorescent probe to image deoxyribonucleic acid and ribonucleic acid in cells. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2023, 303, 123216. [Google Scholar] [CrossRef] [PubMed]
- Zhao, T.; Dong, F.; Hu, X.; Xu, Y.; Wei, W.; Liu, R.; Yu, F.; Fang, W.; Shen, Y.; Zhang, Z. Dynamic tracking of p21 mRNA in living cells by sticky-flares for the visual evaluation of the tumor treatment effect. Nanoscale 2022, 14, 1733–1741. [Google Scholar] [CrossRef] [PubMed]
- Forinash, K.; Bishop, A.R.; Lomdahl, P.S. Nonlinear dynamics in a double-chain model of DNA. Phys. Rev. B 1991, 43, 10743. [Google Scholar] [CrossRef]
- Okaly, J.B.; Mvogo, A.; Woulache, R.L.; Kofane, T.C. Semi-discrete breather in a helicoidal DNA double chain-model. Wave Motion 2018, 82, 1–15. [Google Scholar] [CrossRef]
- Seadawy, A.R.; Bilal, M.; Younis, M.; Rizvi, S.T.R.; Althobaiti, S.; Makhlouf, M.M. Analytical mathematical approaches for the double-chain model of DNA by a novel computational technique. Chaos Solitons Fractals 2021, 144, 110669. [Google Scholar] [CrossRef]
- Seadawy, A.R.; Ahmed, S.; Rizvi, S.T.R.; Ali, K. Lumps, breathers, interactions and rogue wave solutions for a stochastic gene evolution in double chain deoxyribonucleic acid system. Chaos Solitons Fractals 2022, 161, 112307. [Google Scholar] [CrossRef]
- Yao, S.; Mabrouk, S.M.; Inc, M.; Rashed, A.S. Analysis of double-chain deoxyribonucleic acid dynamical system in pandemic confrontation. Results Phys. 2022, 42, 105966. [Google Scholar] [CrossRef]
- Han, T.; Li, Z.; Li, C. Bifurcation analysis, stationary optical solitons and exact solutions for generalized nonlinear Schrödinger equation with nonlinear chromatic dispersion and quintuple power-law of refractive index in optical fibers. Phys. Stat. Mech. Appl. 2023, 615, 128599. [Google Scholar] [CrossRef]
- Qian, X.; Lou, S.-Y. Exact solutions of nonlinear dynamics equation in a new double-chain model of DNA. Commun. Theor. Phys. 2003, 39, 501–505. [Google Scholar]
- Shi, D.; Hamood, U.R.; Ifrah, I.; Vivas-Cortez, M.; Saleem, M.S.; Zhang, X. Analytical study of the dynamics in the double-chain model of DNA. Results Phys. 2023, 52, 106787. [Google Scholar] [CrossRef]
- Ouyang, Z.Y.; Zheng, S. Travelling wave solutions of nonlinear dynamical equations in a double-chain model of DNA. Abstr. Appl. Anal. 2014, 317543. [Google Scholar] [CrossRef]
- Ouahid, L.; Abdou, M.A.; Owyed, S.; Kumar, S. New optical soliton solutions via two distinctive schemes for the DNA Peyrard-Bishop equation in fractal order. Mod. Phys. Lett. B 2021, 35, 2150444. [Google Scholar] [CrossRef]
- Hai, W.-H.; Yi, X.; Fang, J.-S.; Zhang, X.-L.; Huang, W.-L. Chaotic Solitons in Deoxyribonucleic Acid (DNA) Interacting with a Plane Wave. Commun. Theor. Phys. 2021, 36, 503. [Google Scholar]
- Kong, D.; Lou, S.-Y.; Zeng, J. Nonlinear dynamics in a new double chain-model of DNA. Commun. Theor. Phys. 2021, 36, 737–742. [Google Scholar]
- Abdou, M.A.; Ouahid, L.; Al Shahrani, J.S.; Alanazi, M.M.; Kumar, S. New analytical solutions and efficient methodologies for DNA (Double-Chain Model) in mathematical biology. Mod. Phys. Lett. B 2022, 36, 2250124. [Google Scholar] [CrossRef]
- Usman, Y.; Ren, J.; Lanre, A.; Rezazadeh, H. On the multiple explicit exact solutions to the double-chain DNA dynamical system. Math. Methods Appl. Sci. 2023, 46, 6309–6323. [Google Scholar]
- Bilal, M.; Younas, U.; Ren, J. Dynamics of exact soliton solutions in the double-chain model of deoxyribonucleic acid. Math. Methods Appl. Sci. 2021, 44, 13357–13375. [Google Scholar] [CrossRef]
- Kumar, S.; Kumar, A.; Kharbanda, H. Abundant exact closed-form solutions and solitonic structures for the double-chain deoxyribonucleic acid (DNA) model. Braz. J. Phys. 2021, 51, 1043–1068. [Google Scholar] [CrossRef]
- Han, T.; Jiang, Y. Bifurcation, chaotic pattern and traveling wave solutions for the fractional Bogoyavlenskii equation with multiplicative noise. Phys. Scr. 2024, 99, 035207. [Google Scholar] [CrossRef]
- Shi, D.; Li, Z.; Han, T. New traveling solutions, phase portrait and chaotic pattern for the generalized (2+1)-dimensional nonlinear conformable fractional stochastic Schrödinger equations forced by multiplicative Brownian motion. Results Phys. 2023, 52, 106837. [Google Scholar] [CrossRef]
- Han, T.; Jiang, Y.; Lyu, J. Chaotic behavior and optical soliton for the concatenated model arising in optical communication. Results Phys. 2024, 58, 107467. [Google Scholar] [CrossRef]
- Kolebaje, O.; Bonyah, E.; Mustapha, L. The first integral method for two fractional non-linear biological models. Discret. Contin. Dyn. Syst. Ser. S 2019, 12, 487–502. [Google Scholar] [CrossRef]
- Li, Z.; Peng, C. Bifurcation, phase portrait and traveling wave solution of time-fractional thin-film ferroelectric material equation with beta fractional derivative. Phys. Lett. A 2023, 484, 129080. [Google Scholar] [CrossRef]
- Chakrabarty, A.K.; Roshid, M.M.; Rahaman, M.M.; Abdeljawad, T.; Osman, M.S. Dynamical analysis of optical soliton solutions for CGL equation with Kerr law nonlinearity in classical, truncated M-fractional derivative, beta fractional derivative, and conformable fractional derivative types. Results Phys. 2024, 60, 107636. [Google Scholar] [CrossRef]
- Tripathy, A.; Sahoo, S. New wave dynamics of the time-fractional Kaup-Kupershmidt model of seventh-order arises in shallow water waves. Opt. Quantum Electron. 2024, 56, 472. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).