Robust Consensus Analysis in Fractional-Order Nonlinear Leader-Following Systems with Delays: Incorporating Practical Controller Design and Nonlinear Dynamics

Abstract

This article investigates the resilient-based consensus analysis of fractional-order nonlinear leader-following systems with distributed and input lags. To enhance the practicality of the controller design, an incorporation of a disturbance term is proposed. Our modeling framework provides a more precise and flexible approach that considers the memory and heredity aspects of agent dynamics through the utilization of fractional calculus. Furthermore, the leader and follower equations of the system incorporate nonlinear functions to explore the resulting changes. The leader-following system is expressed by a weighted graph, which can be either undirected or directed. Analyzed using algebraic graph theory and the fractional-order Razumikhin technique, the case of leader-following consensus is presented algebraically. To increase robustness in multi-agent systems, input and distributive delays are used to accommodate communication delays and replicate real-time varying environments. This study lays the groundwork for developing control methods that are more robust and flexible in complex networked systems. It does so by advancing our understanding and practical application of fractional-order multi-agent systems. Additionally, experiments were conducted to show the effectiveness of the design in achieving consensus within the system.

1. Introduction

There are different fields in which great importance has been achieved through cooperative control due to vast applications, e.g., many car collaborative commands [1], spacecraft group traveling [2], and unmanned aerial vehicles [3]. Great focus has been obtained by multi-agent system consensus. Remarkable investigation has been conducted on the consensus of leader-following systems [4,5] and consensus of non-leader-following systems [6,7]. Integer-order dynamical standards are very important according to some researchers [8,9,10]. This means that fractional derivatives play an important role in the description of many phenomena that are very complicated and processes that are compared with integer-order classical derivatives [11]. Graph theory and the Lyapunov function approach were used by Yu et al. [12] to assume a group of fractional-order leaders following consensus. On multi-agent system consensus, an investigation was conducted by Bai et al. through designing a useful controller [13,14]. Xu et al. applied the suggested lemma and an appropriate Lyapunov function to analyze the fractional-order challenging system replica [15,16,17]. In the case of a real dynamical system, we can say that a delay in time can be considered a common phenomenon that can affect the dynamical standard’s behavioral system and even make the system risky [18,19].

Research on the consensus of the fractional-order delayed system can now be performed using the frequency-domain analysis method. For instance, in [20], fractional-order system consensus with input delay was considered. Directed multi-agent systems with delay in non-uniform input and communication were studied in [21,22] to explore the well-posedness and iterative formula for fractional oscillator equations characterized by dual fractional orders and temporal delays. Concerning heterogeneous input, an undirected multi-agent system with delay was considered in [23,24] in order to find adherence and complicated dynamical system consensus in time domain analysis. The most suitable approach was presented by Liu et al. for dealing with adherence to differential equations of fractional order [25,26]. Certain stability criteria are obtained using the proposed lemma in many systems of fractional order [27].

Current research has primarily concentrated on the nonlinear dynamics of fractional-order multi-agent systems, often overlooking the impact of delay effects. For instance, Refs. [28,29] illustrated the effectiveness of nonlinear control methods in enhancing the robustness and stability of fractional-order multi-agent systems. Similarly, Refs. [30,31] developed advanced nonlinear synchronization techniques that highlighted the superior performances of fractional-order systems compared to traditional models. The literature still has a notable gap concerning the integration of delayed nonlinear functions into the dynamics of fractional-order multi-agent systems. Despite the crucial role that delays play in real-world systems’ sensing, actuation, and communication processes, there has not been sufficient focus on incorporating them into fractional-order models. This is a critical lag because delays can significantly impact the synchronization, stability, and overall performance of multi-agent systems.

In this article, we present an resilient-based consensus analysis of a fractional order nonlinear multi-agent system with distributed and input lags. We use the nonlinear delayed function in the dynamics of the system. Using algebraic graph theory and the fractional Razumikhin approach, certain algebraic manipulations on leader-following consensus are presented. Finally, we express some examples to show that the cases described are suitable for checking consensus. The layout of our paper is described in Figure 1.

2. Preliminaries

First of all, we offer some definitions, including several crucial lemmas. We will use them subsequently. Let directed weighted graph $B=(V,ϵ)$ consist of a collection of faces $V=\{v_1,v_2,v_3,\dots ,v_P\}$ and $ϵ\subset \{\{v_i,v_z\}:v_i,v_z\in V\}$ be the directed edge’s set, where every directed edge ${ϵ}_{iz}$ is a vertex ordered pair $(v_i,v_z)$ that illustrates an edge that starts at vertex $v_z$ and terminates at vertex $v_i$, where $v_i$ is called the tail and $v_z$ is the head. $P_i=\left\{v_z\right|(v_z,v_i):v_i,v_z\in ϵ\}$ displays the neighbor’s collection of corners. Let $D={\left(d_{iz}\right)}_{P\times P}$ be a weighted adjacency matrix, where $d_{iz}>0$ for $(v_i,v_z)\in ϵ$; else, $d_{iz}=0$. If B defines a directed graph, then its directed spanning tree is a subgraph of B such that the root vertices can reach every other vertex by following the directed edge. Let $E={\left(I_{iz}\right)}_{P\times P}$ be the Laplacian matrix of the graph B:

$$\left\{\begin{array}{c}{I}_{iz}=-d_{iz},y\ne z\hfill \\ I_{ii}=\sum _{z=1,z\ne y}^P{d}_{iz}i=z.\hfill \end{array}\right.$$

Obviously, we can say that ${\sum }_{z=1}^P{I}_{iz}=0fori=1,2,\dots ,P$.

Lemma 1. 

If and only if one eigenvalue of the Laplacian matrix E is 0 and the other eigenvalue real components are positive, the directed graph B has a directed spanning tree.

Definition 1 

([8]). Let $l\left(n\right)$ be a function. Then, we can define Caputo’s derivative with order γ as

$${ }_{n_0}^C{D}_n^{\gamma }l\left(n\right)=\frac{1}{\beta (w-\gamma )}{\int }_{n_0}^n\frac{l^w\left(v\right)}{{(n-v)}^{\gamma -w+1}}dv$$

(1)

where $0\le w-1<\gamma \le w,w\in Z^{+}$.

Definition 2 

([8]). The function $l:R^p\times R\to R^p$ is $QUAD(\delta ,u)$ if $\delta \in R^{p\times p}$ and $u>0$ exist, which satisfy

$${(i-j)}^T[l(n,i)-l(n,j)]-{(i-j)}^T\delta (i-j)\le -u{(i-j)}^T(i-j),foranyi,j\in R^p.$$

(2)

where δ is a diagonal matrix, and u is any constant.

Lemma 2 

([8]). Let F, G, H be three matrices. Then, the inequality

$$\left(\begin{array}{cc}F& G\\ F^T& H\end{array}\right)<0$$

(3)

and inequalities

$$F<0andH-G^T{F}^{-1}G<0$$

(4)

are equivalent.

Lemma 3 

([8]). Take $i\left(n\right)\in R^p$ as a continuous and also differentiable function, $I>0$. Then, the following inequality holds:

$$\frac{1}{2}{ }_{n_0}^C{D}_n^{\gamma }(i^n\left(n\right)Ii\left(n\right)\le i^T\left(n\right)I{ }_{n_0}^C{D}_n^{\gamma }i\left(n\right),\forall \gamma \in (0,1).$$

(5)

Let $H=\left\{\xi \right|\xi :[-s_1,0]\to R^{p}iscontinous\}$ be expressed as the Banach space, which is paired via the supreme norm. With the delay in time, consider a general fractional nonlinear equation:

$${ }_{n_0}^C{D}_n^{\gamma }r\left(n\right)=l(n,r_n),n\ge n_0$$

(6)

If $0<\gamma \le 1$ $r_n\left(\varpi \right)=r(n+\varpi )$, and $\varpi \in [-s_1,0]$, then $lis from theRX$$\left(boundedsetsofH\right)$ to the $\left(boundedsetsof{R}^p\right)$, and this satisfies $l(n,0)=0$.

Lemma 4 

([8]). Let ${\beta }_1,{\beta }_2,{\beta }_3:R\to R$ be continuous increasing functions; ${\beta }_1\left(v\right)$ and ${\beta }_2\left(v\right)$ are non-negative if v is greater than zero, and ${\beta }_1\left(0\right)={\beta }_2\left(0\right)=0$, ${\dot{\beta }}_2>0$ if differential function $K:RX{R}^p\to R$ and continuous increasing function $\mu \left(v\right)$ are greater when compared to v for $v>0$, such that for $\xi \in H$ and $r\in R^p$,

$${\beta }_1\left(\right|\left|r\right|\left|\right)\le K(n,r)\le {\beta }_2\left(\right|\left|r\right|\left|\right),$$

(7)

if

$$\begin{array}{c}\hfill K(n+\psi ,\xi (\psi \left)\right)\le \mu \left(K\right(n,\xi \left(0\right)\left)\right)\end{array}$$

$${ }_{n_0}^C{D}_n^{\gamma }K(n,\xi \left(0\right))\le -{\beta }_3\left(\right|\left|\xi \left(0\right)\right|\left|\right),n\ge n_0$$

(8)

The solution of Equation (6) is asymptotically stable if $r=0$ for $\psi \in [-\varpi ,0]$, and if ${\beta }_1\left(v\right)\to \infty as$v→∞, then $r=0$ is called globally stable.

Lemma 5 

([23]). Let ${\upsilon }_1,{\upsilon }_2,\dots ,{\upsilon }_w$ be the eigenvalues of matrix $F\in R^{wxw}$ and ${\varpi }_1,{\varpi }_2,\dots ,{\varpi }_p$ be the eigenvalues of matrix $G\in R^{pxp}$. Then, the eigenvalues of $F\otimes G$ are ${\upsilon }_i{\varpi }_z(i=1,2,\dots ,w,$$z=1,2,\dots ,p)$.

3. Problem Formulation

The fractional-order nonlinear multi-agent system’s resilient-based consensus analysis with distributed and input delay is explained in this section. Many convenient conditions will be shown using the fractional-order Razumikhin approach.

Let the state of yth agent be

$$\begin{array}{cc}\hfill { }_{n_0}^C{D}_n^{\gamma }{r}_i\left(n\right)& =G{r}_i\left(n\right)+l(n,r_i\left(n\right))+l_1(n,r_i(n-s_2))+H{\int }_{-s_1}^0{r}_i(n+\psi )d\psi \hfill \\ \hfill & +i_i\left(n\right)+\delta {\widehat{i}}_i\left(n\right)\hfill \end{array}$$

(9)

where $i=1,2,\dots ,P.$ Here, $r_i\left(n\right)={(r_{i1}\left(n\right),r_{i2}\left(n\right),\dots ,r_{ip}\left(n\right))}^T$ represent the states of agents. Here, $s_2$ is the input delay, $s_1$ is the distributed delay, $l(n,.)\in R^w$ and $l_1(n,.)\in R^w$ are given nonlinear functions, and G and H are constant matrices. ${\widehat{i}}_i\left(n\right)$ is a controller, and $\delta {\widehat{i}}_i\left(n\right)$ is disturbance in the controller, and $\delta {\widehat{i}}_i\left(n\right)=sinn$, which is taken to be bounded in this case. The leader satisfies

$${ }_{n_0}^C{D}_n^{\gamma }{r}_0\left(n\right)=G{r}_0\left(n\right)+l(n,r_0\left(n\right))+l_0(n,r_0(n-s_2))+H{\int }_{-s_1}^0{r}_0(n+\psi )d\psi .$$

(10)

Let the controller be designed as follows:

$$\begin{array}{cc}\hfill {\widehat{i}}_i\left(n\right)& =L\sum _{z=1}^P{d}_{iz}(r_z(n-s_2)-r_i(n-s_2))+L{d}_{i0}(r_0(n-s_2)-r_i(n-s_2))+\delta {\widehat{i}}_i\left(n\right)\hfill \\ \hfill & i=1,2,\dots ,P,\hfill \end{array}$$

(11)

Here, L is taken to be a constant matrix, and it is assumed that its eigenvalues are non-negative. If there is a directed connection from $r_z\left(n\right)$ to $r_i\left(n\right),$ where $i=1,2,\dots ,P$ and $z=0,1,\dots ,P$, then $F={\left(d_{iz}\right)}_{P\times P}$, and $d_{iz}=0$ otherwise.

Definition 3 

([23]). The system that is defined by (9) and (10) under controlling rule (11) gains leader-following consensus if any $i=1,2,\dots ,P$, where

$$\underset{n\to \infty }{lim}\left|\right|r_i\left(n\right)-r_0\left(n\right)\left|\right|=0$$

(12)

To obtain results, some lemmas and assumptions are needed.

Assumption 1. 

In incorporating delays into the utility evaluation process, the QUAD function plays a crucial role in enhancing decision-making processes within multi-agent systems. This, in turn, bolsters the resilience and efficiency of agent interactions, so we assume that l is $QUAD(\delta ,u)$.

Assumption 2. 

For efficient communication between agents, assume that the corresponding digraph of a multi-agent system with a rooted leader contains a spanning tree.

Assumption 3. 

As we require stability in a multi-agent systems (9) and (10), assume that $l_i$ is Lipschitz continuous; that is, there exist two scalars $k_i>0$ such that for any ξ, $\gamma \in R^p$,

$$\left|\right|l_i(n,\xi )-l_i(\xi ,\gamma )\left|\right|\le k_i\left|\right|\xi -\gamma \left|\right|,i=1,2.$$

(13)

Lemma 6 

([8]). Consider $M=E+B_0$, $B_0=diag(d_{10},\dots ,d_{P0})$. Assumption 2 is satisfied if and only if the real part of all eigenvalues of matrix M are non-negative.

Lemma 7 

([8]). If Assumption 2 is satisfied according to Lemma 5, then the real portion of the eigenvalues of matrix $M\otimes L$ are positive.

Lemma 8 

([8]). Let u, $\xi \in R^p$ and $\nu >0$. Then, inequality $2u^T\xi \le \nu u^{T}u+\frac{1}{\nu }{\xi }^T\xi$ holds.

Remark 1. 

Our proposed fractional-order leader-following consensus algorithm offers significant improvements over existing methods. Unlike [21], which involves multiple leaders, coordination is more straightforward with a single leader, simplifying the control strategy and communication protocols, thereby enhancing efficiency. Compared to the method of [22], which uses nonlinear functions to handle system dynamics, our method uses nonlinear delayed functions, further stabilizing the system by damping oscillations and allowing agents to synchronize actions over time, leading to more robust and realistic modeling. Moreover, in contrast to the approach of [26], which defines system dynamics using ordinary differential equations, our approach employs fractional differential equations. This captures memory and hereditary properties, enabling a more accurate modeling of complex interactions, improving convergence speed, stability, and overall robustness. These enhancements demonstrate the superior effectiveness of our proposed technique.

4. Leader-Following Consensus

The fractional-order nonlinear multi-agent system’s resilient-based consensus analysis with distributed and input delay is explained in this section. Many convenient conditions will be shown using the fractional-order Razumikhin approach.

Theorem 1. 

If Assumptions 1 and 2 are satisfied and scalars $\alpha >0$ and $\varrho >0$ and a positive definite matrix $R>0$ exist, then the system that is defined by (9) and (10) under control law (11) achieves leader-following consensus if

$$I_P\otimes (G+G^T+2\delta -2u{I}_p+\alpha I_p+R+{\nu }_1{I}_p+\frac{f_2^2}{{\nu }_1}{I}_p+\frac{4\delta \widehat{i}\left(n\right)}{\varrho })+\frac{1}{\alpha }(M^T\otimes L^T)(M\otimes L)<0$$

(14)

$$I_P\otimes (\alpha I_p-\frac{1}{s_1}R)+\frac{1}{\alpha }(I_P\otimes H^T)(I_P\otimes H)<0$$

(15)

where ${\nu }_1>0$ and $f_2>0$, which are scalars, and both u and δ are defined in Definition 2. Also, $\varrho =w\left(n\right)$.

Proof. 

Through using Equation (11) in Equation (9),

$$\begin{array}{cc}\hfill { }_{n_0}^C{D}_n^{\gamma }{r}_i\left(n\right)& =G{r}_i\left(n\right)+l(n,r_i\left(n\right))+l_1(n,r_i(n-s_2))+H{\int }_{-s_1}^0{r}_i(n+\psi )d\psi \hfill \\ \hfill & +L\sum _{z=1}^P{d}_{iz}(r_z(n-s_2)-r_i(n-s_2))+L{d}_{i0}(r_0(n-s_2)-r_i(n-s_2))\hfill \\ \hfill & +\delta {\widehat{i}}_i\left(n\right)+\delta {\widehat{i}}_i\left(n\right)).\hfill \end{array}$$

(16)

In subtracting Equation (10) from Equation (16),

$$\begin{array}{cc}\hfill { }_{n_0}^C{D}_n^{\gamma }{r}_i\left(n\right){-}_{n_0}^C{D}_n^{\gamma }{r}_0\left(n\right)& =G{r}_i\left(n\right)+l(n,r_i\left(n\right))+l_1(n,r_i(n-s_2))+H{\int }_{-s_1}^0{r}_i(n+\psi )d\psi \hfill \\ \hfill & +L\sum _{z=1}^P{d}_{iz}(r_z(n-s_2)-r_i(n-s_2))+L{d}_{i0}(r_0(n-s_2)-r_i(n-s_2))\hfill \\ \hfill & +2\delta {\widehat{i}}_i\left(n\right)-G{r}_0\left(n\right)-l(n,r_0\left(n\right))-l_1(n,r_0(n-s_2))-H{\int }_{-s_1}^0{r}_0(n+\psi )d\psi \hfill \\ \hfill { }_{n_0}^C{D}_n^{\gamma }[r_i\left(n\right)-r_0\left(n\right)]& =G[r_i\left(n\right)-r_0\left(n\right)]+l(n,r_i\left(n\right))-l(n,r_0\left(n\right))+[l_1(n,r_i(n-s_2))\hfill \\ & -l_1(n,r_0(n-s_2))]+H{\int }_{-s_1}^0[r_i(n+\psi )-r_0(n+\psi )]d\psi \hfill \\ & +L\sum _{z=1}^P{d}_{iz}[r_z(n-s_2)-r_0(n-s_2)+r_0(n-s_2)\hfill \\ \hfill & -r_i(n-s_2)]-L{d}_{i0}[r_i(n-s_2)-r_0(n-s_2)]+2\delta {\widehat{i}}_i\left(n\right)\hfill \end{array}$$

$$\begin{array}{cc}\hfill { }_{n_0}^C{D}_n^{\gamma }[r_i\left(n\right)-r_0\left(n\right)]& =G[r_i\left(n\right)-r_0\left(n\right)]+l(n,r_i\left(n\right))-l(n,r_0\left(n\right))+\left[l_1\right(n,r_i\hfill \\ \hfill & (n-s_2))-l_1(n,r_0(n-s_2))]+H{\int }_{-s_1}^0[r_i(n+\psi )-r_0(n+\psi )]d\psi \hfill \\ \hfill & +L\sum _{z=1}^P{d}_{iz}[r_z(n-s_2)-r_0(n-s_2)]-L\sum _{z=1}^P{d}_{iz}[r_i(n-s_2)-r_0(n-s_2)]\hfill \\ \hfill & -L{d}_{i0}[r_i(n-s_2)-r_0(n-s_2)]+2\delta {\widehat{i}}_i\left(n\right)\hfill \end{array}$$

(17)

Suppose that

$$w_i\left(n\right)=r_i\left(n\right)-r_0\left(n\right),i=1,2,\dots ,P$$

(18)

Here, $w_i\left(n\right)$ represents the error term in the system defined by Equations (9) and (10). Then, Equation (17) takes the form

$$\begin{array}{ccc}\hfill { }_{n_0}^C{D}_n^{\gamma }{w}_i\left(n\right)& =& G{w}_i\left(n\right)+l(n,r_i\left(n\right))-l(n,r_0\left(n\right))+l_1(n,r_i(n-s_2))-l_1(n,r_0(n-s_2))\hfill \\ \hfill & & +H{\int }_{-s_1}^0{w}_i(n+\psi )d\psi +L\sum _{z=1}^P{d}_{iz}(w_z(n-s_2)\hfill \\ & & -w_i(n-s_2))-L{d}_{i0}{w}_i(n-s_2)+2\delta {\widehat{i}}_i\left(n\right)\hfill \end{array}$$

(19)

Let a quadratic Lyapunov function be chosen as follows:

$$K\left(n\right)=\sum _{i=1}^P{w}_i^T\left(n\right)w_i\left(n\right)$$

(20)

By using Lemma 3 and along with the solutions of Equation (18), we find the $\gamma$-order derivative of $K\left(n\right)$:

$${ }_{n_0}^C{D}_n^{\gamma }K\left(n\right)\le 2\sum _{i=1}^P{w}_i^T{\left(n\right)}_{n_0}^C{D}_n^{\gamma }{w}_i\left(n\right)$$

(21)

In substituting Equation (19) into Equation (21),

$$\begin{array}{ccc}\hfill { }_{n_0}^C{D}_n^{\gamma }K\left(n\right)& \le & 2\sum _{i=1}^P{w}_i^T\left(n\right)[G{w}_i\left(n\right)+l(n,r_i\left(n\right))-l(n,r_0\left(n\right))+l_1(n,r_i\hfill \\ \hfill & & (n-s_2))-l_1(n,r_0(n-s_2))+H{\int }_{-s_1}^0{w}_i(n+\psi )d\psi \hfill \\ & & +L\sum _{z=1}^P{d}_{iz}(w_z(n-s_2)-w_i(n-s_2))-L{d}_{i0}{w}_i(n-s_2)+2\delta {\widehat{i}}_i\left(n\right)]\hfill \end{array}$$

(22)

From Assumption 1, we have

$$\begin{array}{c}\hfill w_i^T\left(n\right)[l(n,r_i\left(n\right))-l(n,r_0\left(n\right))]-w_i^T\left(n\right)\delta w_i\left(n\right)\le -u{w}_i^T\left(n\right)w_i\left(n\right)\end{array}$$

Then,

$$\begin{array}{c}\hfill w_i^T\left(n\right)[l(n,r_i\left(n\right))-l(n,r_0\left(n\right))]\le w_i^T\left(n\right)\delta w_i\left(n\right)-u{I}_p{w}_i^T\left(n\right)w_i\left(n\right)\end{array}$$

Then, we obtain

$$w_i^T\left(n\right)[l(n,r_i\left(n\right))-l(n,r_0\left(n\right)]\le w_i^T\left(n\right)(\delta -u{I}_p)w_i\left(n\right).$$

(23)

Notice that

$$\begin{array}{c}\hfill I_{iz}=-d_{iz},y\ne zand{I}_{ii}=\sum _{z=1,z\ne y}^P{d}_{iz},\end{array}$$

We obtain

$$\begin{array}{ccc}\hfill \sum _{z=1}^P{d}_{iz}(w_z\left(n\right)-w_i\left(n\right))& =& \sum _{z=1,z\ne y}^P{d}_{iz}(w_z\left(n\right)-w_i\left(n\right))=\sum _{z=1,z\ne y}^P{d}_{iz}{w}_z\left(n\right)-\sum _{z=1,z\ne y}^P{d}_{iz}{w}_i\left(n\right)\hfill \\ \hfill & =& -\sum _{z=1,z\ne y}^P{I}_{iz}{w}_z\left(n\right)-I_{ii}{w}_i\left(n\right)\hfill \end{array}$$

Then, we obtain

$$\sum _{z=1}^P{d}_{iz}(w_z\left(n\right)-w_i\left(n\right))=-\sum _{z=1}^P{I}_{iz}{w}_z\left(n\right)$$

(24)

Now, in substituting values into Equation (22),

$$\begin{array}{ccc}\hfill { }_{n_0}^C{D}_n^{\gamma }K\left(n\right)& \le & 2w_i^T\left(n\right)\sum _{i=1}^P[G{w}_i\left(n\right)+l(n,r_i\left(n\right))-l(n,r_0\left(n\right))+l_1(n,r_i\hfill \\ \hfill & & (n-s_2))-l_1(n,r_0(n-s_2))+H{\int }_{-s_1}^0{w}_i(n+\psi )d\psi \hfill \\ \hfill & & +L\sum _{z=1}^P{d}_{iz}(w_z(n-s_2)-w_i(n-s_2))-L{d}_{i0}{w}_i(n-s_2)+2\delta {\widehat{i}}_i\left(n\right)]\hfill \\ \hfill & \le & 2\sum _{i=1}^P[w_i^T\left(n\right)G{w}_i\left(n\right)+w_i^T\left(n\right)(l(n,r_i\left(n\right))-l(n,r_0\left(n\right)))+w_i^T\left(n\right)(l_1(n,r_i(n-s_2))\hfill \\ \hfill & & -l_1(n,r_0(n-s_2))\left)\right]+2{\int }_{-s_1}^0\sum _{i=1}^P{w}_i^T\left(n\right)H{w}_i(n+\psi )d\psi +2\sum _{i=1}^P{w}_i^T\hfill \\ \hfill & & \left(n\right)L\sum _{z=1}^P{d}_{iz}(w_z(n-s_2)-w_i(n-s_2))\hfill \\ \hfill & & -2\sum _{i=1}^P{w}_i^T\left(n\right)L{d}_{i0}{w}_i(n-s_2)+2\sum _{i=1}^P{w}_i^T\left(n\right)\left[2\delta {\widehat{i}}_i\left(n\right)\right]].\hfill \end{array}$$

In using Equation (23),

$$\begin{array}{cc}\hfill { }_{n_0}^C{D}_n^{\gamma }K\left(n\right)& \le 2\sum _{i=1}^P[w_i^T\left(n\right)G{w}_i\left(n\right)+w_i^T\left(n\right)(\delta -2u{I}_p)w_i\left(n\right)]\hfill \\ \hfill & +2{\int }_{-s_1}^0\sum _{i=1}^P{w}_i^T\left(n\right)H{w}_i(n+\psi )d\psi +2\sum _{i=1}^P{w}_i^T\left(n\right)L\sum _{z=1}^P{d}_{iz}(w_z(n-s_2)-w_i(n-s_2))\hfill \\ \hfill & -2\sum _{i=1}^P{w}_i^T\left(n\right)L{d}_{i0}{w}_i(n-s_2)+4\delta \widehat{i}\left(n\right)w^T\left(n\right)+2\sum _{i=1}^P[w_i^T\left(n\right)\left[\right(l_1(n,r_i(n-s_2)\hfill \\ & -\left(l_1(n,r_0(n-s_2))\right)].\hfill \end{array}$$

$$\begin{array}{ccc}\hfill { }_{n_0}^C{D}_n^{\gamma }K\left(n\right)& \le & 2\sum _{i=1}^P{w}_i^T\left(n\right)(G+\delta -u{I}_p)w_i\left(n\right)+2{\int }_{-s_1}^0\sum _{i=1}^P{w}_i^T\left(n\right)H{w}_i(n+\psi )d\psi \hfill \\ \hfill & & +2\sum _{i=1}^P{w}_i^T\left(n\right)L(-\sum _{z=1}^P{I}_{iz}{w}_z(n-s_2))-2\sum _{i=1}^P{w}_i^T\left(n\right)L{d}_{i0}{w}_i(n-s_2)\hfill \\ \hfill & & +\delta {\widehat{i}}_i\left(n\right)w_i(n-s_2)+4\delta \widehat{i}\left(n\right)w^T\left(n\right)+2\sum _{i=1}^P[w_i^T\left(n\right)\left[\right(l_1(n,r_i(n-s_2)\hfill \\ \hfill & & -\left(l_1(n,r_0(n-s_2))\right)].\hfill \end{array}$$

(25)

$$\begin{array}{ccc}\hfill & \le & 2\sum _{i=1}^P{w}_i^T\left(n\right)(G+\delta -u{I}_p)w_i\left(n\right)+2{\int }_{-s_1}^0\sum _{i=1}^P{w}_i^T\left(n\right)w_i(n+\psi )d\psi \hfill \\ \hfill & & -2\sum _{i=1}^P{w}_i^T\left(n\right)L\sum _{z=1}^P{I}_{iz}{w}_z(n-s_2)-2\sum _{i=1}^P{w}_i^T\left(n\right)L{d}_{i0}{w}_i(n-s_2)+4\delta \widehat{i}{w}^T\left(n\right)\hfill \\ \hfill & & +2\sum _{i=1}^P[w_i^T\left(n\right)\left[\right(l_1(n,r_i(n-s_2)-\left(l_1(n,r_0(n-s_2))\right)].\hfill \end{array}$$

$$\begin{array}{ccc}\hfill & \le & 2w^T\left(n\right)(I_P\otimes (G+\delta -u{I}_p)w\left(n\right)+2{\int }_{-s_1}^0{w}^T\left(n\right)(I_P\otimes H)w(n+\psi )d\psi \hfill \\ \hfill & & -2w^T\left(n\right)(E\otimes L)w(n-s_2)-2w^T\left(n\right)(B_0\otimes L)w(n-s_2)+4\delta \widehat{i}\left(n\right)w^T\left(n\right)(I_P\otimes I_p)\hfill \\ & & +2w^T\left(n\right)[{\Re }_1(n,r(n-s_2))-{\Re }_1(n,r_0(n-s_2))].\hfill \\ \hfill where{\Re }_i(n,r)& =& {(l_i^T(n,r_1),\dots ,l_i^T(n,r_P))}^T\hfill \\ \hfill and{\Re }_i(n,r_0)& =& {(l_i^T(n,r_0),\dots ,l_i^T(n,r_0))}^T\hfill \end{array}$$

(26)

$$\begin{array}{ccc}\hfill & \le & 2w^T\left(n\right)(I_P\otimes (G+\delta -u{I}_p)w\left(n\right)+2{\int }_{-s_1}^0{w}^T\left(n\right)(I_P\otimes H)w(n+\psi )d\psi \hfill \\ \hfill & & -2w^T\left(n\right)(E+B_0)\otimes Lw(n-s_2)+4\delta \widehat{i}\left(n\right)w^T\left(n\right)(I_P\otimes I_p)\hfill \\ \hfill & & +2w^T\left(n\right)[{\Re }_1(n,r(n-s_2))-{\Re }_1(n,r_0(n-s_2))].\hfill \end{array}$$

(27)

In using Lemma 6,

$$\begin{array}{cc}\hfill { }_{n_0}^C{D}_n^{\gamma }K\left(n\right)& \le 2w^T\left(n\right)(I_P\otimes (G+\delta -u{I}_p)w\left(n\right)+2{\int }_{-s_1}^0{w}^T\left(n\right)(I_P\otimes H)w(n+\psi )d\psi \hfill \\ \hfill & -w^T\left(n\right)(M\otimes L)w(n-s_2)+4\delta \widehat{i}\left(n\right)w^T\left(n\right)(I_P\otimes I_p)+2w^T\left(n\right)[{\Re }_1(n,r(n-s_2))\hfill \\ \hfill & -{\Re }_1(n,r_0(n-s_2))]+2w^T\left(n\right)[{\Re }_1(n,r(n-s_2))-{\Re }_1(n,r_0(n-s_2))].\hfill \\ \hfill & \le w^T\left(n\right)(I_P\otimes (2G+2\delta -2u{I}_p)w\left(n\right)+2{\int }_{-s_1}^0{w}^T\left(n\right)(I_P\otimes H)w(n+\psi )d\psi \hfill \\ \hfill & -2w^T\left(n\right)(M\otimes L)w(n-s_2)+4\delta \widehat{i}\left(n\right)w^T\left(n\right)(I_P\otimes I_p)+\hfill \\ \hfill & 2w^T\left(n\right)[{\Re }_1(n,r(n-s_2))-{\Re }_1(n,r_0(n-s_2))].\hfill \\ \hfill & \le w^T\left(n\right)(I_P\otimes (G+G^T+2\delta -2u{I}_p)w\left(n\right)+2{\int }_{-s_1}^0{w}^T\left(n\right)(I_P\otimes H)w(n+\psi )d\psi \hfill \\ \hfill & -2w^T\left(n\right)(M\otimes L)w(n-s_2)+4\delta \widehat{i}\left(n\right)w^T\left(n\right)(I_P\otimes I_p)+\hfill \\ \hfill & +2w^T\left(n\right)[{\Re }_1(n,r(n-s_2))-{\Re }_1(n,r_0(n-s_2))].\hfill \end{array}$$

where

$$w^T\left(n\right)={(w_1^T\left(n\right),\dots ,w_P^T\left(n\right))}^T$$

Whenever

$$K(n+\varpi ,r(n+\varpi \left)\right)<\mu K(n,r(n\left)\right),forall-s\le \varpi <0$$

in this case, $s=max\{s_1,s_2\}$, for any scalar $\alpha >0$, and for some positive $\mu >1$,

$$\begin{array}{cc}\hfill { }_{n_0}^C{D}_n^{\gamma }K\left(n\right)& \le w^T\left(n\right)(I_P\otimes (G+G^T+2\delta -2u{I}_p)w\left(n\right)+2{\int }_{-s_1}^0{w}^T\left(n\right)(I_P\otimes H)w(n+\psi )d\psi \hfill \\ \hfill & -2w^T\left(n\right)(M\otimes L)w(n-s_2)+4\delta \widehat{i}\left(n\right)w^T\left(n\right)(I_P\otimes I_p)\hfill \\ \hfill & +\alpha [\mu w^T\left(n\right)(I_P\otimes I_p)w\left(n\right)-w^T(n-s_2)(I_P\otimes I_p)w(n-s_2)]\hfill \\ \hfill & +{\int }_{-s_1}^0\alpha [\mu w^T\left(n\right)(I_P\otimes I_p)w\left(n\right)-w^T(n+\psi )(I_P\otimes I_p)w(n+\psi )]d\psi \hfill \\ \hfill & +2w^T\left(n\right)[{\Re }_1(n,r(n-s_2))-{\Re }_1(n,r_0(n-s_2))].\hfill \end{array}$$

(28)

In using Lemma 8,

$$\begin{array}{cc}\hfill { }_{n_0}^C{D}_n^{\gamma }K\left(n\right)& \le w^T\left(n\right)[I_P\otimes (G+G^T+2\delta -2u{I}_p+\alpha \mu I_p+R)]w\left(n\right)-2w^T\left(n\right)(M\otimes L)w(n-s_2)\hfill \\ \hfill & -\alpha w^T(n-s_2)(I_P\otimes I_p)w(n-s_2)+{\int }_{-s_1}^0[w^T\left(n\right)(I_P\otimes (\alpha \mu I_p-\frac{1}{s_1}R)w(n)))\hfill \\ \hfill & +2w^T\left(n\right)(I_P\otimes H)w(n+\psi )-\alpha w^T(n+\psi )(I_P\otimes I_p)w(n+\psi )]d\psi \hfill \\ \hfill & +\frac{4\delta \widehat{i}\left(n\right)w^T\left(n\right)(I_P\otimes I_p)w\left(n\right)}{w\left(n\right)}+{\nu }_1{w}^T\left(n\right)w\left(n\right)\hfill \\ \hfill & +\frac{1}{{\nu }_1}{[{\Re }_1(n,r(n-s_2))-{\Re }_1(n,r_0(n-s_2))]}^T[{\Re }_1(n,r(n-s_2))-{\Re }_1(n,u_0(n-s_2))]\hfill \end{array}$$

In using Assumption 3,

$$\begin{array}{cc}\hfill { }_{n_0}^C{D}_n^{\gamma }K\left(n\right)& \le w^T\left(n\right)[I_P\otimes (G+G^T+2\delta -2u{I}_p+\alpha \mu I_p+R)]w\left(n\right)-2w^T\left(n\right)(M\otimes L)w(n-s_2)\hfill \\ \hfill & -\alpha w^T(n-s_2)(I_P\otimes I_p)w(n-s_2)+{\int }_{-s_1}^0[w^T\left(n\right)(I_P\otimes (\alpha \mu I_p-\frac{1}{s_1}R)w(n)))\hfill \\ \hfill & +2w^T\left(n\right)(I_P\otimes H)w(n+\psi )-\alpha w^T(n+\psi )(I_P\otimes I_p)w(n+\psi )]d\psi \hfill \\ \hfill & +\frac{4\delta \widehat{i}\left(n\right)(w^T\left(n(I_P\otimes I_p)\right)w\left(n\right)}{w\left(n\right)}+{\nu }_1{w}^T\left(n\right)w\left(n\right)+\frac{f_2^2}{{\nu }_1}{w}^T(n-s_2)w(n-s_2).\hfill \end{array}$$

$$\begin{array}{cc}\hfill { }_{n_0}^C{D}_n^{\gamma }K\left(n\right)& \le {\chi }_{s2}^T\left(\begin{array}{cc}{I}_P\otimes (G+G^T+2\delta -2u{I}_p+\alpha \mu I_p+R+{\nu }_{1}Ip+\frac{f_2^2}{{\nu }_1}Ip+\frac{4\delta \widehat{i}\left(n\right)I_p}{w\left(n\right)})& -M\otimes L\\ -M^T\otimes L^T& -\alpha I_P\otimes I_p\end{array}\right)\hfill \\ \hfill {\chi }_{s2}& +{\int }_{-s1}^0{\chi }_{\psi }^T\left(\begin{array}{cc}{I}_P\otimes (\alpha \mu I_p-\frac{1}{s_1}R& I_P\otimes H\\ I_P\otimes H^T& \alpha I_P\otimes I_p\end{array}\right){\chi }_{\psi }d\psi .\hfill \end{array}$$

(29)

where ${\chi }_{s2}={(w^T\left(n\right),w^T(n-s_2))}^T$, ${\chi }_{\psi }={(w^T\left(n\right),w^T(n+\psi ))}^T$, $\varrho =w\left(n\right)$, and $\psi \in [-s_1,0]$.

Suppose that $\mu \to +1$:

$$\begin{array}{cc}\hfill { }_{n_0}^C{D}_n^{\gamma }K\left(n\right)& \le {\chi }_{s2}^T\left(\begin{array}{cc}{I}_P\otimes (G+G^T+2\delta -2u{I}_p+\alpha I_p+R+{\nu }_{1}Ip+\frac{f_2^2}{{\nu }_1}Ip+\frac{4\delta \widehat{i}\left(n\right)I_p}{\varrho })& -M\otimes L\\ -M^T\otimes L^T& -\alpha I_P\otimes I_p\end{array}\right)\hfill \\ & {\chi }_{s2}+{\int }_{-s1}^0{\chi }_{\psi }^T\left(\begin{array}{cc}{I}_P\otimes (\alpha I_p-\frac{1}{s_1}R)& I_M\otimes G\\ I_P\otimes H^T& -\alpha I_P\otimes I_p\end{array}\right){\chi }_{\psi }d\psi .\hfill \end{array}$$

In using inequalities (14) and (15) and Lemma 2,

$$\left(\begin{array}{cc}{I}_P\otimes (G+G^T+2\delta -2u{I}_p+\alpha I_p+R+{\nu }_{1}Ip+\frac{f_2^2}{{\nu }_1}Ip+\frac{4\delta \widehat{i}\left(n\right)I_p}{\varrho })& -M\otimes L\\ -M^T\otimes L^T& -\alpha I_P\otimes I_p\end{array}\right)<0$$

(30)

and

$$\begin{array}{c}\hfill \left(\begin{array}{cc}{I}_p\otimes (\alpha I_p-\frac{1}{s_1}R)& I_P\otimes H\\ I_P\otimes H^T& -\alpha I_P\otimes I_p\end{array}\right)<0\end{array}$$

(31)

Systems (14) and (15) are satisfied in based on Lemma 2; this provides evidence that if $K(n+\varpi ,$$r(n+\varpi ))<\mu K(n,r\left(n\right))$, then ${ }_{n_0}^C{D}_n^{\gamma }K\left(n\right)<0$ for some $\varpi \in [-s,0]$ and $\mu >1$. Hence, according to Lemma 4, it can be said that system (19) is asymptotically stable. The system that is defined by (9) and (10) under control law (11) achieves leader-following consensus. □

Remark 2. 

The criteria for the consensus of the fractional-order multi-agent system used above describe the achievement of the leader-following consensus with delays and disturbance in the controller. But when there is a larger delay and disturbance occurs, then there is more chance to increase in error, which can reduce the accuracy of the system.

Corollary 1. 

If Assumptions 1 and 2 hold and a ${\nu }_1>0$, $f_2>0$, $\varrho >0$, and $R>0$ exist, where ${\nu }_1$, $f_2$, and ϱ are scalars and R is a positive definite matrix, then the system that is defined by (9) and (10) under control law (11) achieves leader-following consensus if

$$\begin{array}{c}\hfill {\upsilon }_{max}[I_P\otimes (G+G^T+2\delta -2u{I}_p+\alpha I_p+R+{\nu }_{1}Ip+\frac{f_2^2}{{\nu }_1}Ip+\frac{4\delta \widehat{i}\left(n\right)I_p}{\varrho })\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+\frac{1}{\alpha }(M^T\otimes L^T)(M\otimes L)]<0\hfill \end{array}$$

(32)

and

$${\upsilon }_{max}(\alpha I_p-\frac{1}{s_1}R+\frac{1}{\alpha }{H}^{T}H)<0$$

(33)

Lemma 9. 

Our criteria will be much better for determining the consensus of the leader-follower system. The system that is analyzed in this article results from a weighted directed graph as well as from having a distributed input delay. Our standards apply to broader leader-follower systems, as the criteria employed apply only to directed graphs. If “$w^T\left(n\right)(I_P\otimes R)w\left(n\right)$” is used in place of $s_1{w}^T\left(n\right)(I_P\otimes R)w{\left(n\right)}^{\prime }$ in the first equation of Formula (24), then the following result can be obtained.

Lemma 10. 

If Assumptions 1 and 2 hold and a ${\nu }_1>0,$ $f_2>0$, $\varrho >0$, and $R>0$ exist, where ${\nu }_1, f_2,$ and ϱ are scalars and R is a positive definite matrix, then the system that is defined by (9) and (10) under control law (11) achieves leader-following consensus if

$$\begin{array}{c}\hfill I_P\otimes (G+G^T+2\delta -2u{I}_p+\alpha I_p+s_{1}R+{\nu }_{1}Ip+\frac{f_2^2}{{\nu }_1}Ip+\frac{4\delta \widehat{i}\left(n\right)I_p}{\varrho })\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+\frac{1}{\alpha }(M^T\otimes L^T)(M\otimes L)<0\hfill \end{array}$$

(34)

$$I_P\otimes (\alpha I_p-R)+\frac{1}{\alpha }(I_P\otimes H^T)(I_P\otimes H)<0$$

(35)

The results that are being obtain must be suitable for the leader-follower systems of the fractional order, which have undirected topology.

Lemma 11. 

The graph B is connected if and only if Laplacian matrix E is a graph that is undirected. B is a positive semi-definite matrix. Moreover, it can be said that E has a simple eigenvalue of zero and that the other eigenvalues are non-negative.

Lemma 12. 

Based on Theorem 1, the system generates a directed graph or weighted graph. Only Lemma 1 needs to be modified, and the proof is completed in a similar manner as if the system’s topology is a connected undirected graph.

Remark 3. 

Our work has limitations due to our reliance on particular model assumptions, which cannot be applied to other multi-agent systems or variations in delays and disturbances. We did not examine different network topologies or broader disturbance types, or analyze computational complexity and parameter sensitivity. Furthermore, practical validation through experiments or simulations is necessary to verify our theoretical results. Future research should focus on addressing these issues to improve the robustness and applicability of our control strategy.

5. Examples

To determine the effectiveness of the results, consider some numerical examples.

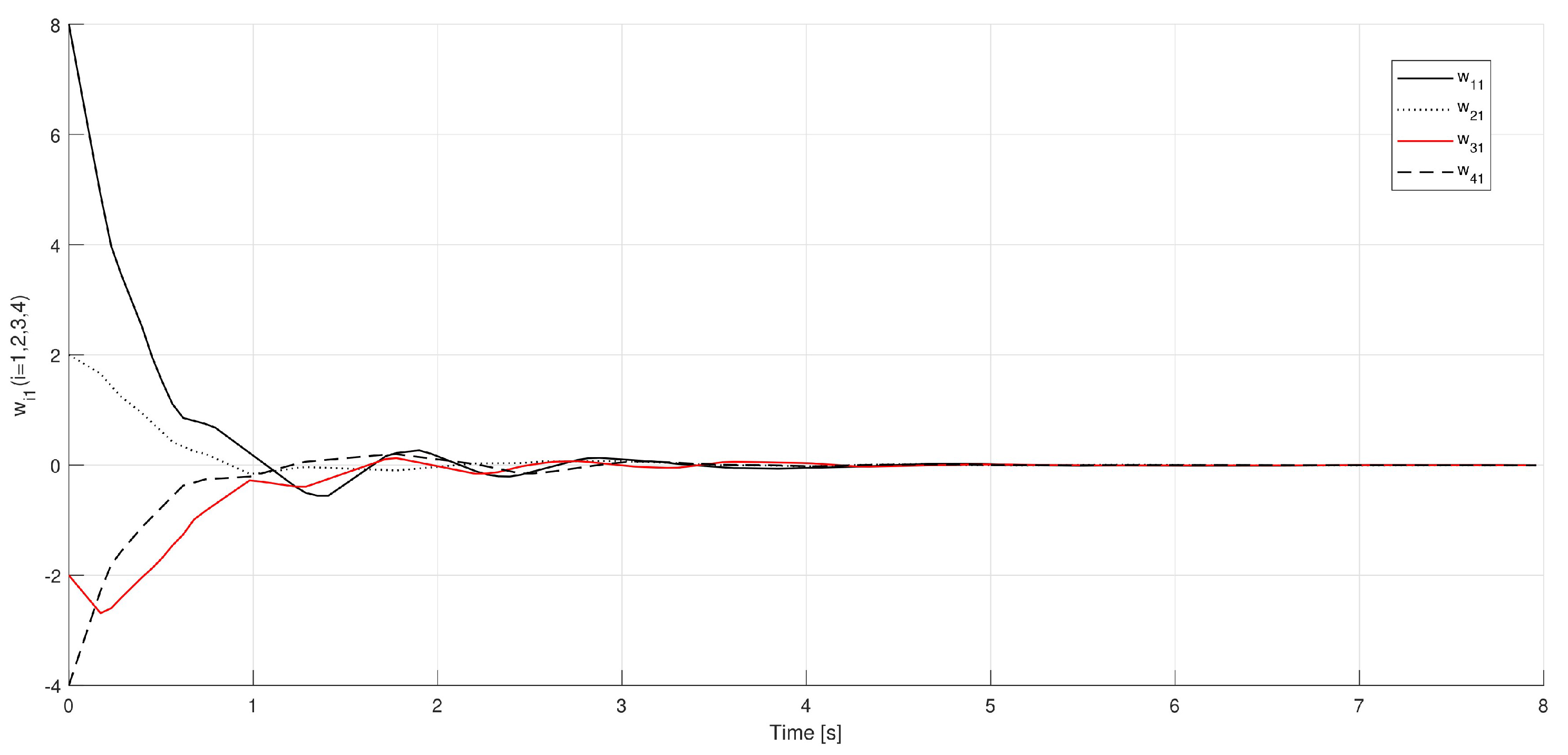
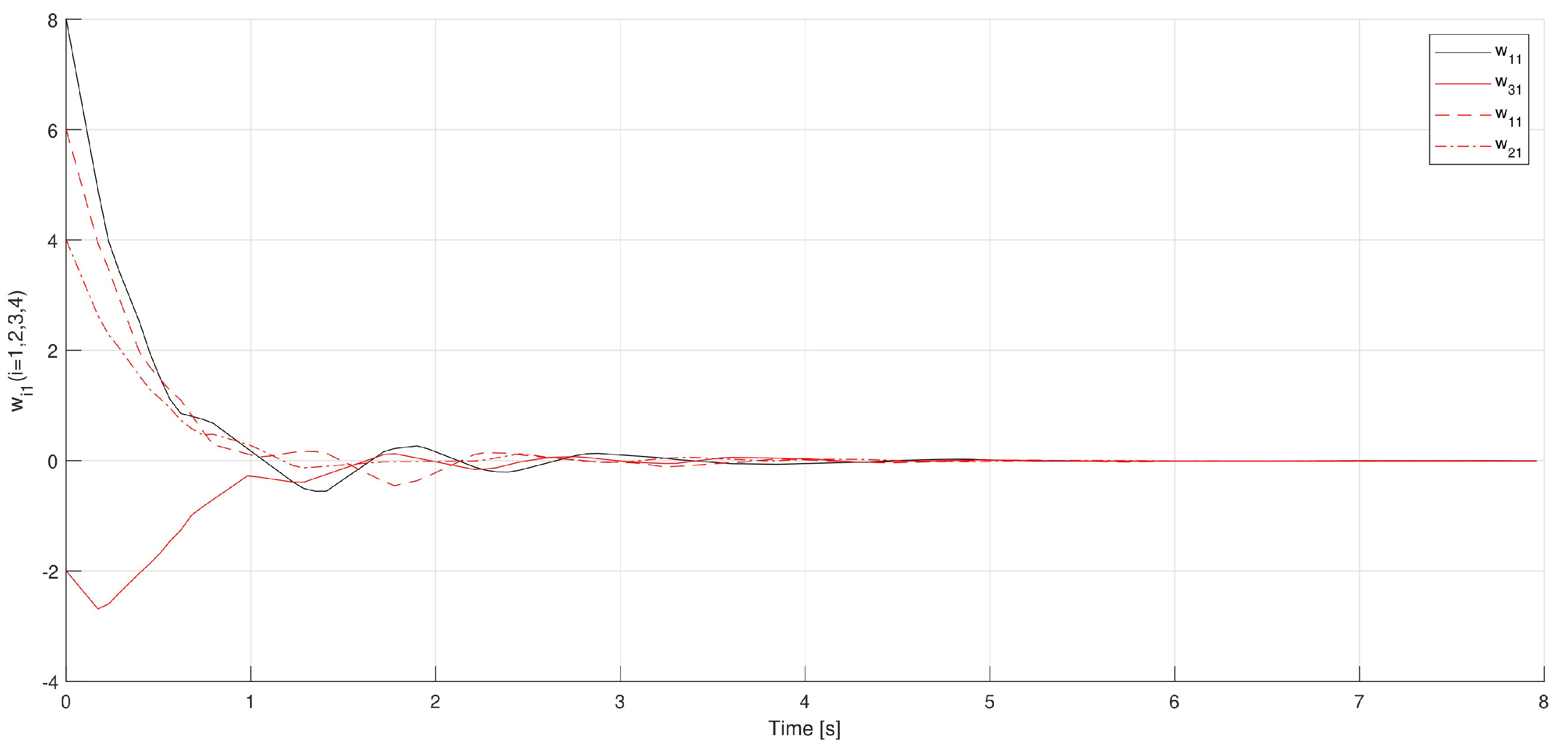
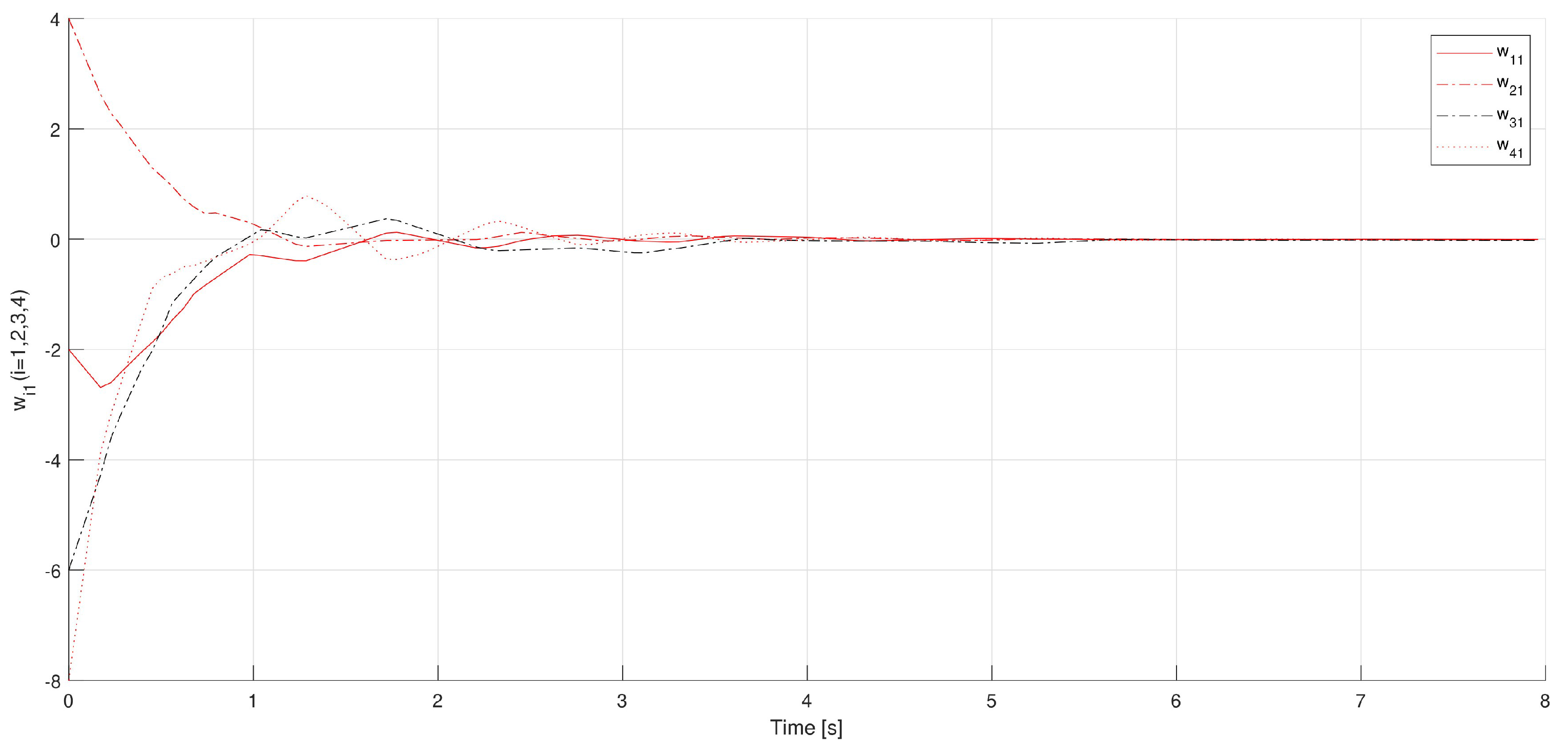
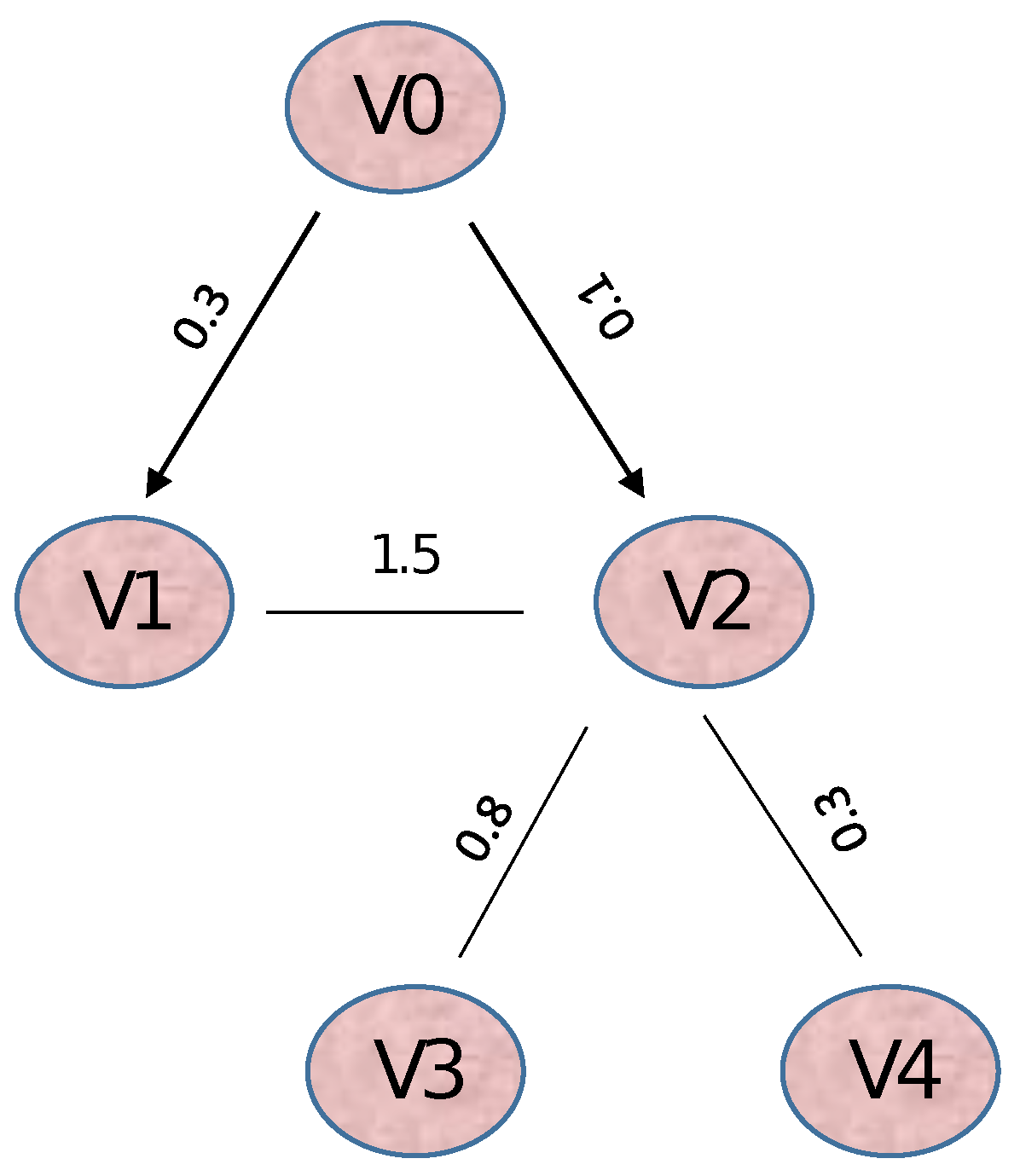
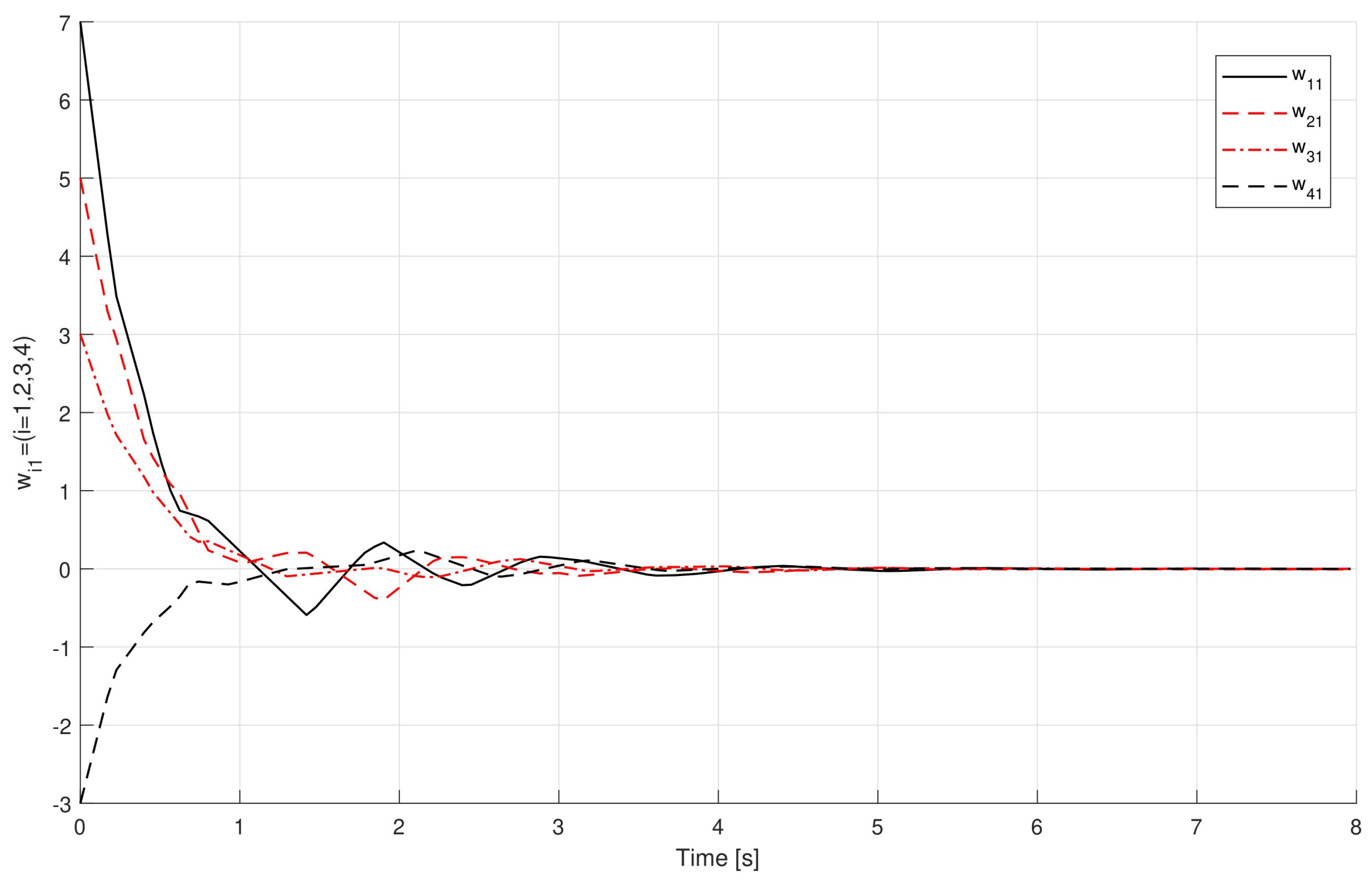
Example 1. 

Consider a multi-agent system that is defined by (9) and (10) under control law (11) with one leader V0 and four followers V1, V2, V3, and V4 as shown in Figure 2. Consider the following matrices G and H:

$$G=\left(\begin{array}{ccc}-4.15& 0& 2.8\\ 0& -4.1& 0\\ 3.4& 0.1& -4.25\end{array}\right),$$

and

$$H=\left(\begin{array}{ccc}0.1& 0& 0\\ 0.05& 0.15& 0\\ 0& 0& 0.075\end{array}\right)$$

From Figure 2,

$$F=\left(\begin{array}{cccc}0& 0& 0& 0.3\\ 0.7& 0& 0& 0\\ 0& 0& 0& 0.25\\ 0& 0& 0.45& 0\end{array}\right)$$

$$B_0=\left(\begin{array}{cccc}0.1& 0& 0& 0\\ 0& 0& 0& 0\\ 0& 0& 0& 0\\ 0& 0& 0& 0.25\end{array}\right)$$

$$E=\left(\begin{array}{cccc}0.3& 0& 0& -0.3\\ -0.7& 0.7& 0& 0\\ 0& 0& 0.25& -0.25\\ 0& 0& -0.45& 0.45\end{array}\right)$$

$$M=\left(\begin{array}{cccc}0.4& 0& 0& -0.3\\ -0.7& 0.7& 0& 0\\ 0& 0& 0.25& -0.25\\ 0& 0& -0.45& 0.7\end{array}\right)+\left(\begin{array}{cccc}0.1& 0& 0& 0\\ 0& 0& 0& 0\\ 0& 0& 0& 0\\ 0& 0& 0& 0.25\end{array}\right)$$

which implies that

$$M=\left(\begin{array}{cccc}0.4& 0& 0& -0.3\\ -0.7& 0.7& 0& 0\\ 0& 0& 0.25& -0.25\\ 0& 0& -0.45& 0.7\end{array}\right)$$

Here, $l(n,r_i\left(n\right))=cos\left(r_i\left(n\right)\right)$, $l_1(n,r_i(n-s_2))=\frac{3}{10}sin{r}_i(n-s_2)$, $y=0,1,\dots ,4$, $\gamma =0.6$, $s_1=0.7$, ${\nu }_1=0.2$, $f_2=0.2$, and $s_2=0.6$.

Let $u=0.3$ by considering Assumption 1:

$$\delta =\left(\begin{array}{ccc}0.3& 0& 0\\ 0& 0.3& 0\\ 0& 0& 0.3\end{array}\right)$$

Let $\alpha =0.25$. Then, according to Equation (15),

$I_P\otimes (\alpha I_p-\frac{1}{s_1}R)+\frac{1}{\alpha }(I_P\otimes H^T)(I_P\otimes H)$

=$I_P\otimes (\alpha I_p-\frac{1}{s_1}R)+I_P\otimes \frac{1}{\alpha }{H}^{T}H$

=$I_P\otimes (\alpha I_p+\frac{1}{\alpha }{H}^{T}H-\frac{1}{s_1}R)<0$

That is,

$$\alpha s_1{I}_p+\frac{s_1}{\alpha }{H}^{T}H-R<0$$

(36)

So,

$$R=\left(\begin{array}{ccc}0.36& 0& 0.04\\ 0& 0.28& 0\\ 0.04& 0& 0.32\end{array}\right)$$

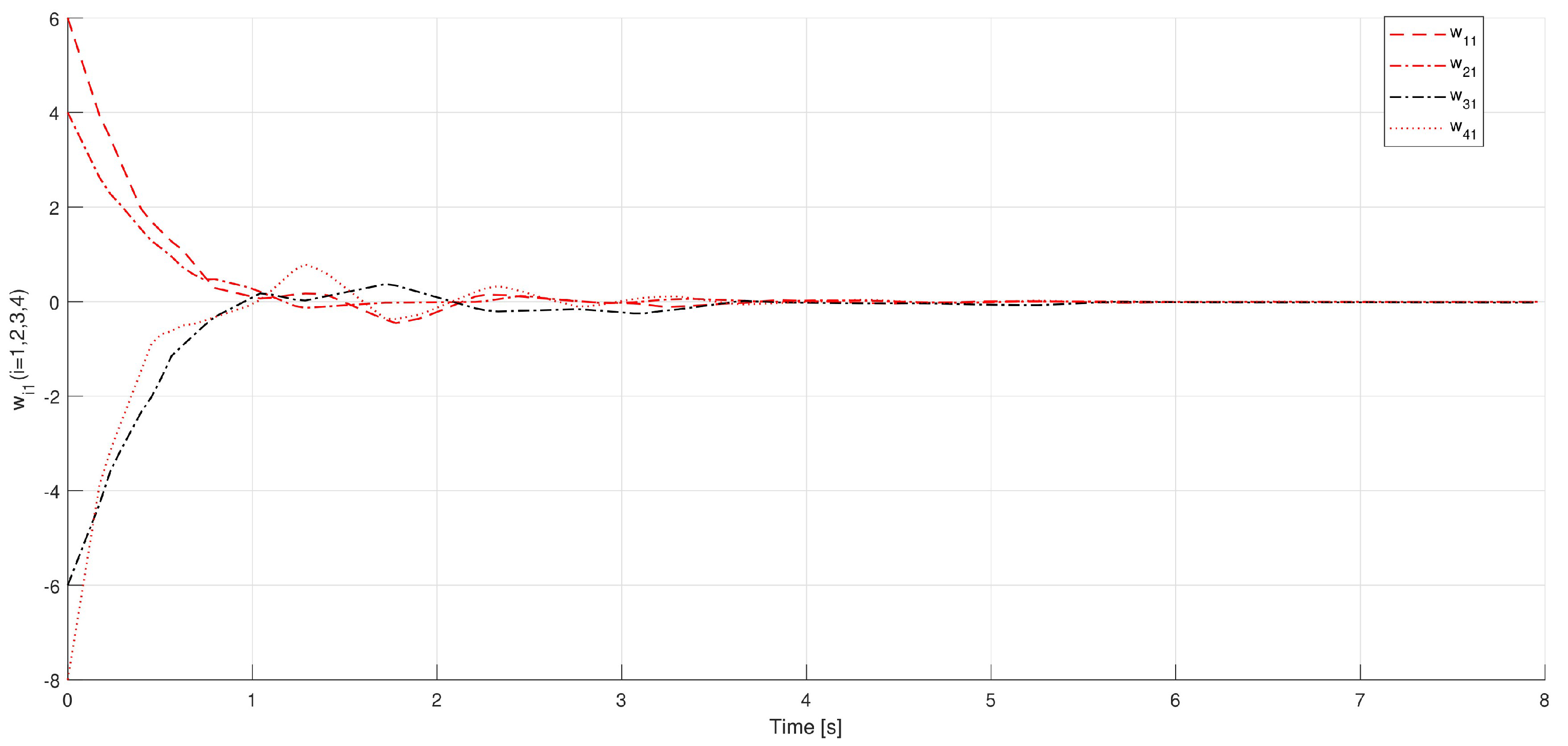
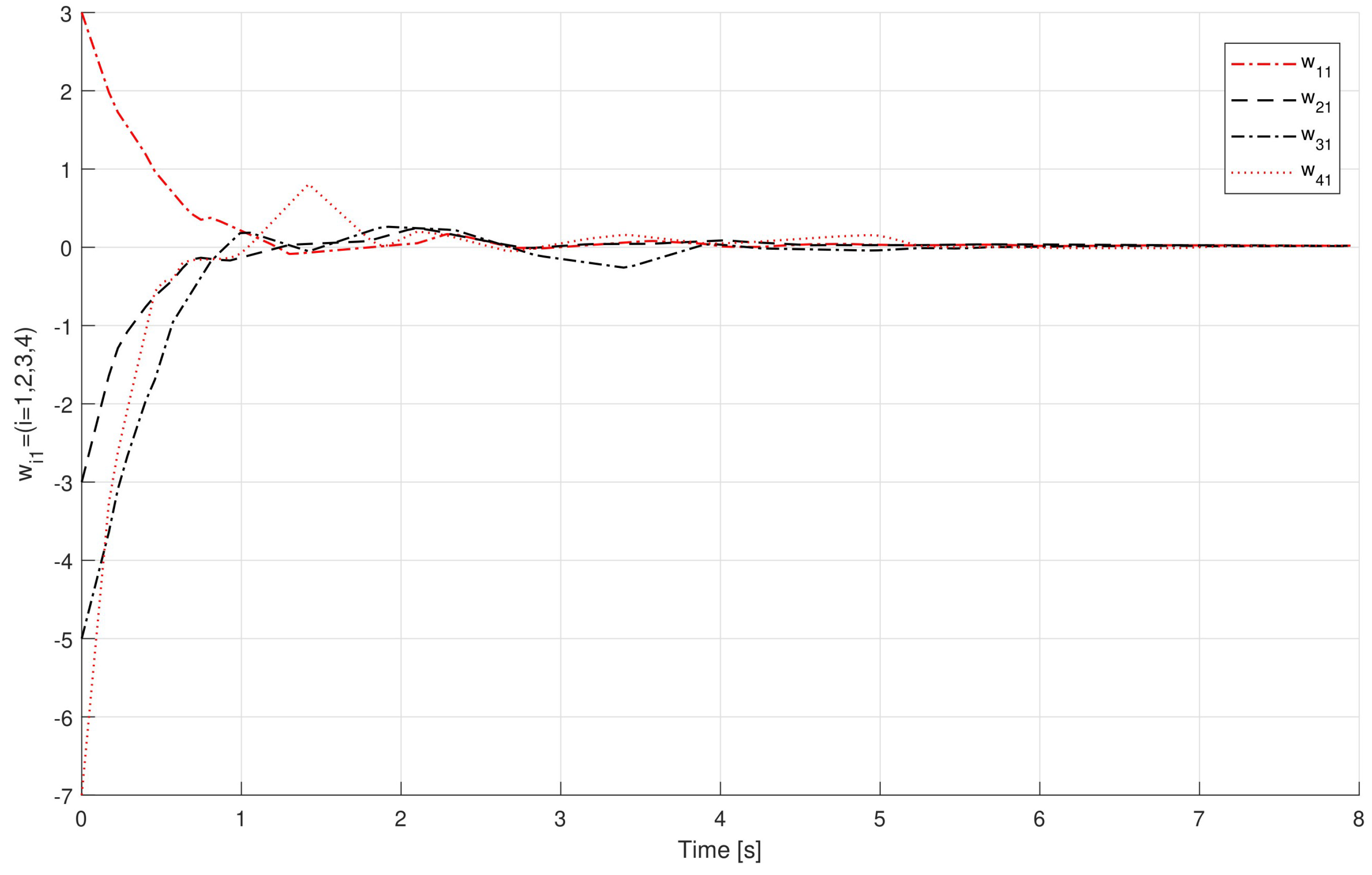
satisfying (36) can be chosen.

Similarly, (14) implies that

$$\alpha I_P\otimes (G+G^T+2\delta -2u{I}_p+R+{\nu }_1{I}_p+\frac{f_2^2}{{\nu }_1}{I}_p+\frac{4\delta \widehat{i}\left(n\right)I_p}{\varrho }{I}_p)+M^{T}M\otimes L^{T}L<0$$

(37)

where $\delta \widehat{i}\left(n\right)=10cos\left(0.1\right)$, and $\varrho =0.1$. Therefore,

$$L=\left(\begin{array}{ccc}0.1& 0& 0\\ 0.15& 0.25& 0\\ 0& 0& 0.05\end{array}\right)$$

can be chosen in order to satisfy (37). In using Theorem 1, the leader-following consensus of systems (9) and (10) on the basis of control law (11) is achieved, and in Figure 3, Figure 4, Figure 5 and Figure 6, the states of the errors $w_i\left(n\right)$ are explained.

Example 2. 

Consider a multi-agent system that is defined by (9) and (10) under control law (11) with one leader V0 and four followers V1, V2, V3, and V4 as shown in Figure 7. Let the matrices G and H be taken as follows:

$$G=\left(\begin{array}{ccc}-10.6& 0& 1.5\\ 0& -8.5& 0\\ 1& 0& -9.7\end{array}\right),H=\left(\begin{array}{ccc}1.8& 0& 0\\ 2.9& 1.5& 0\\ 0& 0& 2.7\end{array}\right)$$

From Figure 7,

$$F=\left(\begin{array}{cccc}0& 1.5& 0& 0\\ 1.5& 0& 0.8& 0.3\\ 0& 0.8& 0& 0\\ 0& 0.3& 0& 0\end{array}\right)$$

and

$$B_0=\left(\begin{array}{cccc}0.3& 0& 0& 0\\ 0& 0.1& 0& 0\\ 0& 0& 0& 0\\ 0& 0& 0& 0\end{array}\right)$$

$$E=\left(\begin{array}{cccc}1.5& -1.5& 0& 0\\ -1.5& 2.6& -0.8& -0.3\\ 0& -0.8& 0.8& 0\\ 0& -0.3& 0& 0.3\end{array}\right)$$

and

$$M=\left(\begin{array}{cccc}1.5& -1.5& 0& 0\\ -1.5& 2.6& -0.8& -0.3\\ 0& -0.8& 0.8& 0\\ 0& -0.3& 0& 0.3\end{array}\right)+\left(\begin{array}{cccc}0.3& 0& 0& 0\\ 0& 0.1& 0& 0\\ 0& 0& 0& 0\\ 0& 0& 0& 0\end{array}\right)$$

which implies that

$$M=\left(\begin{array}{cccc}1.8& -1.5& 0& 0\\ -1.5& 2.7& -0.8& -0.3\\ 0& -0.8& 0.8& 0\\ 0& -0.3& 0& 0.3\end{array}\right)$$

Here, $l(n,r_i\left(n\right))=\frac{1}{4}tanh{r}_i\left(n\right)$, $l_1(n,r_i(n-s_2))=\frac{1}{10}sin{r}_i(n-s_2)$, $y=0,1,\dots ,4$, $\gamma =0.5$, $s_1=0.3$, $s_2=0.6$, ${\nu }_1=0.3$, and $f_2=0.2$.

Consider $u=2.5$ and $\delta \widehat{i}\left(n\right)=10sin\left(0.1\right)$:

$$\delta =\left(\begin{array}{ccc}0.3& 0& 0\\ 0& 0.3& 0\\ 0& 0& 0.3\end{array}\right)$$

Let $\alpha =0.2$. In order to fulfill consensus conditions,

$$R=\left(\begin{array}{ccc}0.38& 0& 0.54\\ 0& 0.12& 0\\ 0.24& 0& 0.16\end{array}\right)$$

and

$$L=\left(\begin{array}{ccc}0.05& 0& 0\\ 0.25& 0.4& 0\\ 0& 0& 0.1\end{array}\right)$$

can be taken. According to Theorem 1, leader-following consensus of system (9) and (10) under control law (11) with undirected topology is achieved. In Figure 8, Figure 9, Figure 10 and Figure 11, the states of errors $w_i\left(n\right)$ under different values of $s_2$ are presented.

Remark 4. 

In this work, we constructed the error trajectories of the system using MATLAB software. The equations for the error system were solved using the ADAMS predictor–corrector approach. Due to its accuracy and stability when handling fractional order dynamics, this approach works well for solving fractional differential equations. Furthermore, the ADAMS predictor–corrector approach makes it easier to compute precise error trajectories by expecting future solution values and frequently correcting them.

5.1. Significance and Evaluation of Performance Metrics

In the research of fractional-order leader-following consensus in multi-agent systems, the following performance metrics have significance for evaluating system performance:

• ISE—integral of the squared error;
• IAE—integral of the absolute error;
• ITAE—integral of the time-weighted absolute error.

The ISE concentrates on larger errors by squaring the error term, which is very important for ensuring stability by significantly disciplining major variations. On the other side, the IAE offers an unbiased perspective of overall system performance by treating all errors equally, providing insights into the total collective error over time. The ITAE, by weighting errors with time, emphasizes the swift correction of errors, thus emphasizing the system’s responsiveness and robustness, specifically in the face of input and distribution delays. Collectively, these metrics offer the capability to retain accuracy, stability, and efficiency in dynamic, delay-vulnerable conditions through the analysis of the control strategies.

5.2. ISE (Integral of Squared Error)

Mathematically, the integral of the squared error (ISE) is calculated using the following formula:

$$\mathrm{ISE}A=\int w{\left(n\right)}^{2}dn$$

5.3. IAE (Integral of Absolute Error)

The integral of the absolute error (IAE) is calculated using the following formula:

$$\mathrm{IAE}=\int |w(n)|dn$$

5.4. ITAE (Integral of Time-Weighted Absolute Error)

The ITAE is determined by summing the product of time and the absolute values of the errors over the given period.

$$\mathrm{ITAE}=\int n·|w(n)|dn$$

In

Table 1. Performance comparison summary.

Iteration NO.	ISE	IAE	ITAE
50	2.55 $\times {10}^{-2}$	$3.50\times {10}^{-2}$	4.50 $\times {10}^{-2}$
100	1.30 $\times {10}^{-2}$	2.05 $\times {10}^{-2}$	3.25 $\times {10}^{-2}$
150	0.14 $\times {10}^{-2}$	0.67 $\times {10}^{-2}$	1.30 $\times {10}^{-2}$

, you can see the performance metrics (ISE, IAE, and ITAE) for the proposed fractional-order leader-following consensus algorithm at different iterations. As the iterations advance, there is a noticeable pattern of decreasing values for all three metrics. The reduction in ISE over the iterations indicates an improvement in the system’s ability to handle large deviations and stabilize more effectively. The decreasing IAE values show a consistent decrease in the overall accumulated error, demonstrating continuous performance improvement. In addition, the significant decline in the ITAE highlights the system’s enhanced ability to promptly correct errors with each iteration, indicating an improved responsiveness and robustness to delays. The following table effectively presents the progressive enhancement in the system’s performance, emphasizing the effectiveness of our control strategy throughout each iteration.

6. Conclusions

Nonlinear leader and follower systems in the fractional format with source and distributed lags resilient-based consensus analysis are discussed in this article. By integrating a delayed nonlinear function into the dynamics of the leader and follower states, we introduced a more realistic and complex model for analysis using the Razumikhin approach used, and with the help of this approach, some suitable conditions were obtained. Utilizing the Lyapunov function method, we rigorously proved the stability of the system, demonstrating that the proposed control strategy effectively mitigates the impact of delays and disturbances. The criteria are expressed as linear matrix inequalities. This provides a suitable way for the calculation of consensus. This leader and follower system is ahead of the weighted directed graph and the results that are acquired are sufficient for drawing an undirected graph. Hence, it can be said that our standard is more than suitable for extensive leader and follower networks. The results of our study validate the practicality and strength of the control method and also establishe a strong basis for future explorations. Prospective routes for future research could involve analyzing the effects of different network structures, adapting the method for various disturbance classes and expanding the framework to encompass additional types of fractional-order systems. The fractional-order leader-following consensus algorithm for multi-agent systems, when assessed with the performance metrics ISE, IAE, and ITAE, showcased remarkable stability, well-rounded error reduction, and improved adaptability to time delays. This will broaden the scope of application and support the robustness of multi-agent networks.