Fractal Tent Map with Application to Surrogate Testing
Abstract
1. Introduction
- A novel fractal chaotic map is presented, being a generalization of the chaotic tent map with a fractal structure.
- A pseudorandom number generator (PRNG) was developed based on the fractal tent map proposed in this paper. The developed generator successfully passes all NIST tests.
- The developed PRNG was applied to the surrogate data testing task. The test results show that the use of the PRNG based on the fractal tent map shows better accuracy when testing data sequences for nonlinearity than the standard approach.
2. Materials and Methods
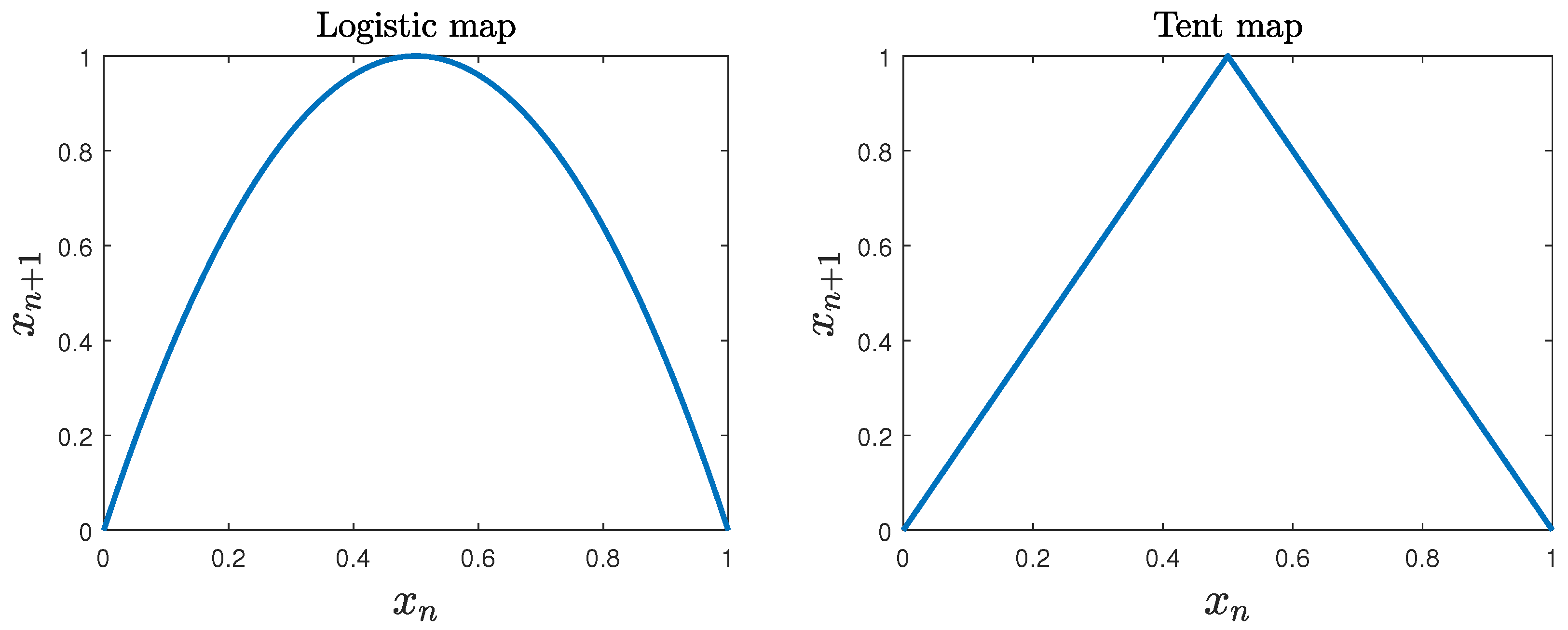
2.1. Logistic and Tent Maps
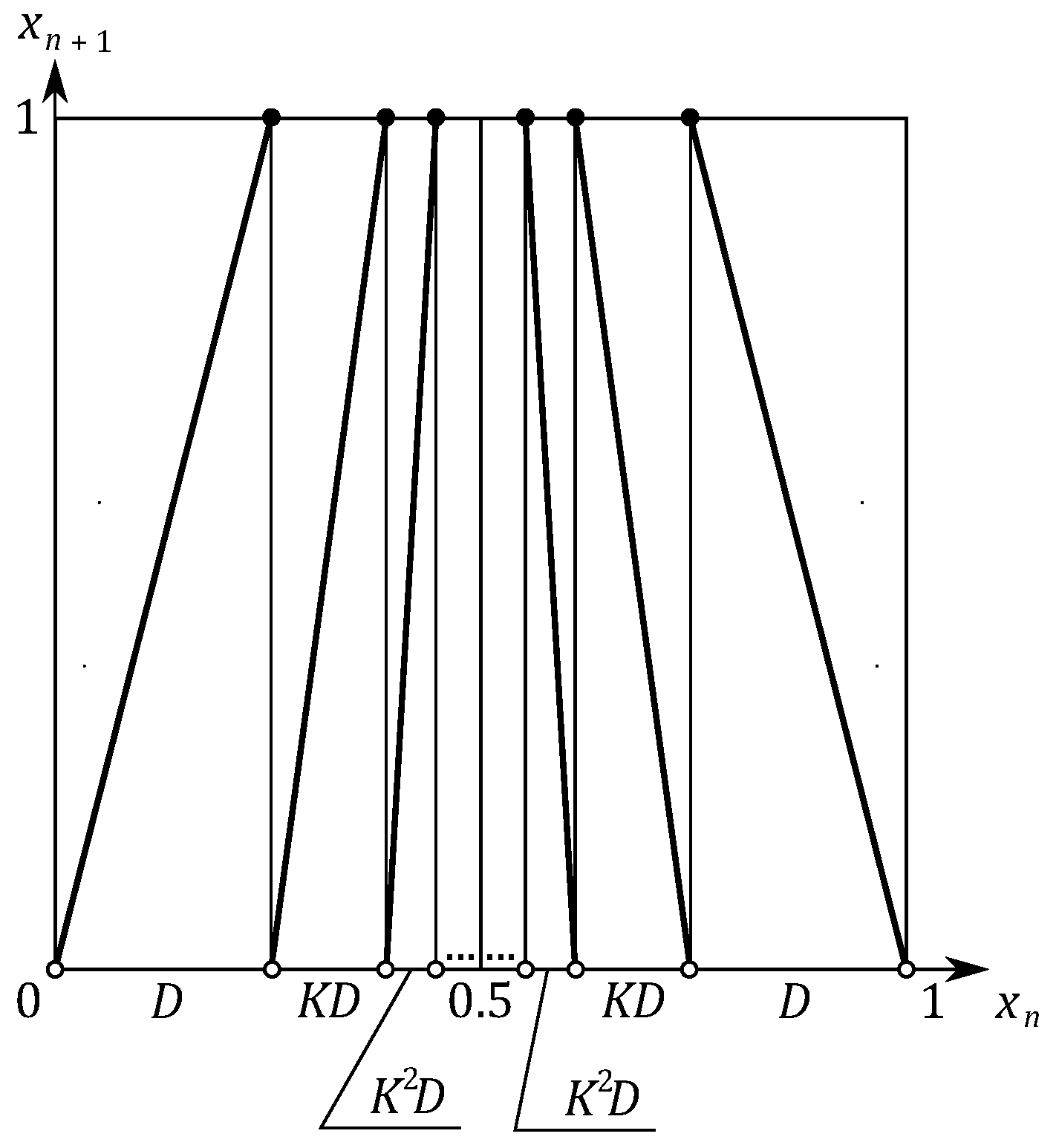
2.2. Proposed Fractal Tent Map
| Algorithm 1: Evaluation of . |
 |
2.3. Surrogate Data Testing
3. Results
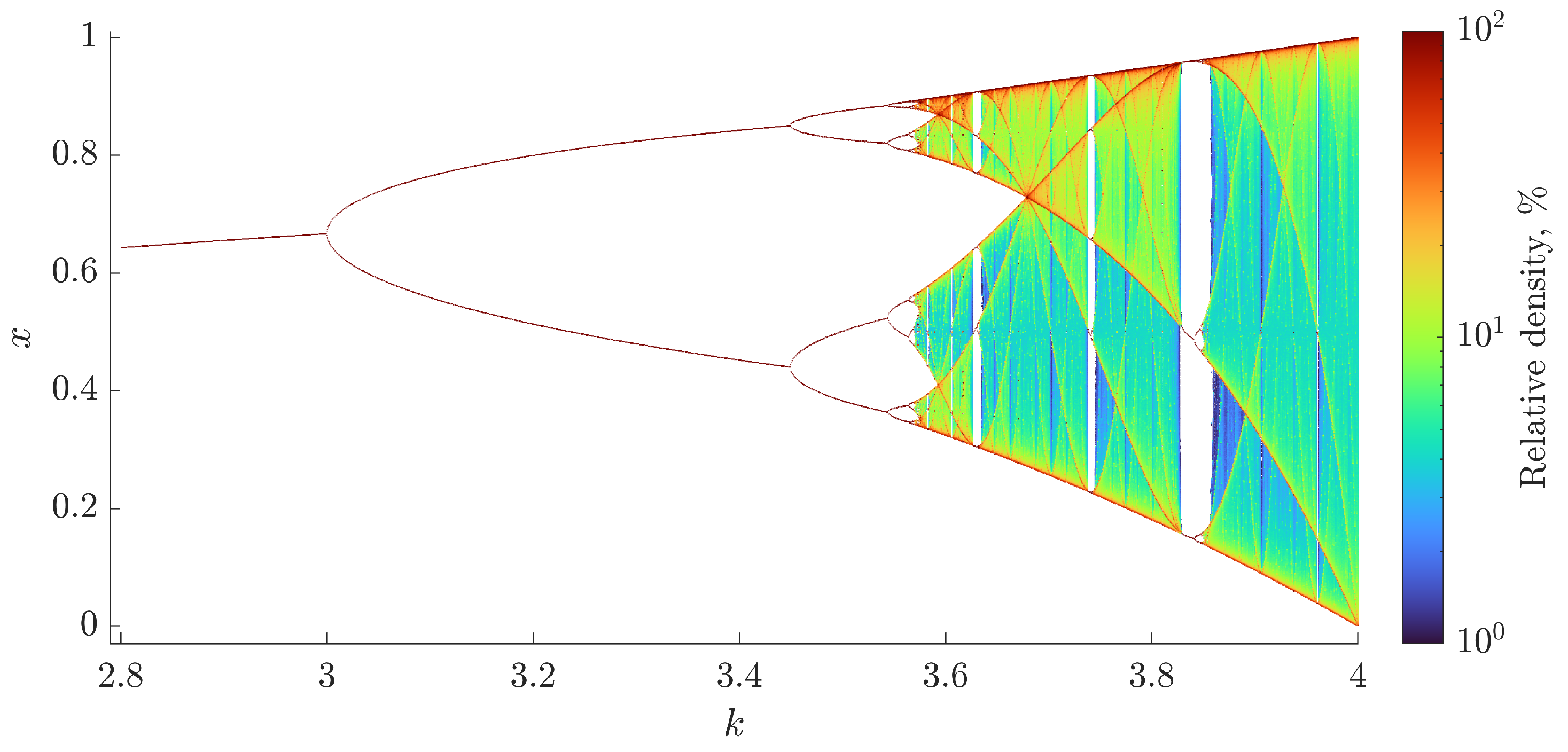
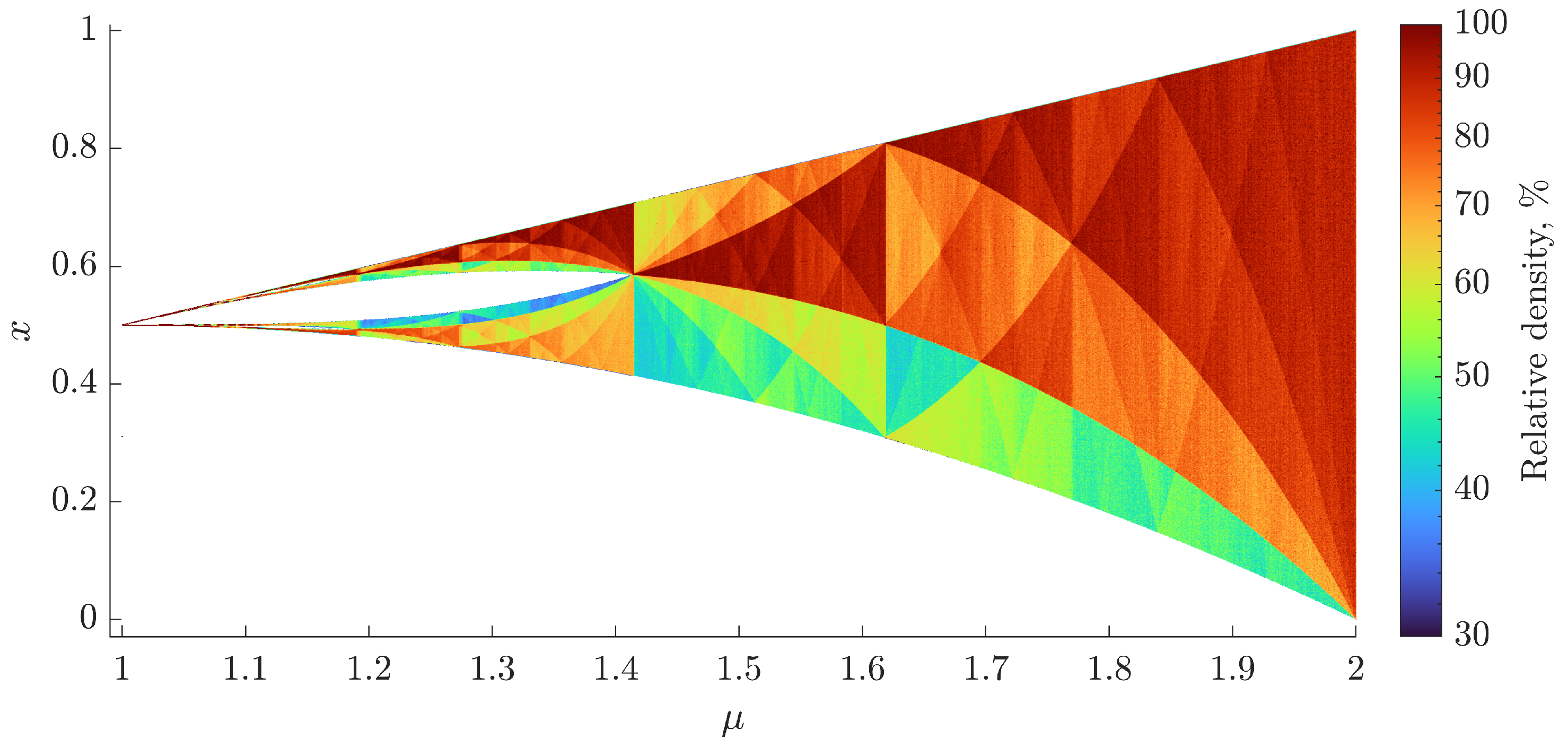
3.1. Bifurcation Analysis
3.2. NIST Tests
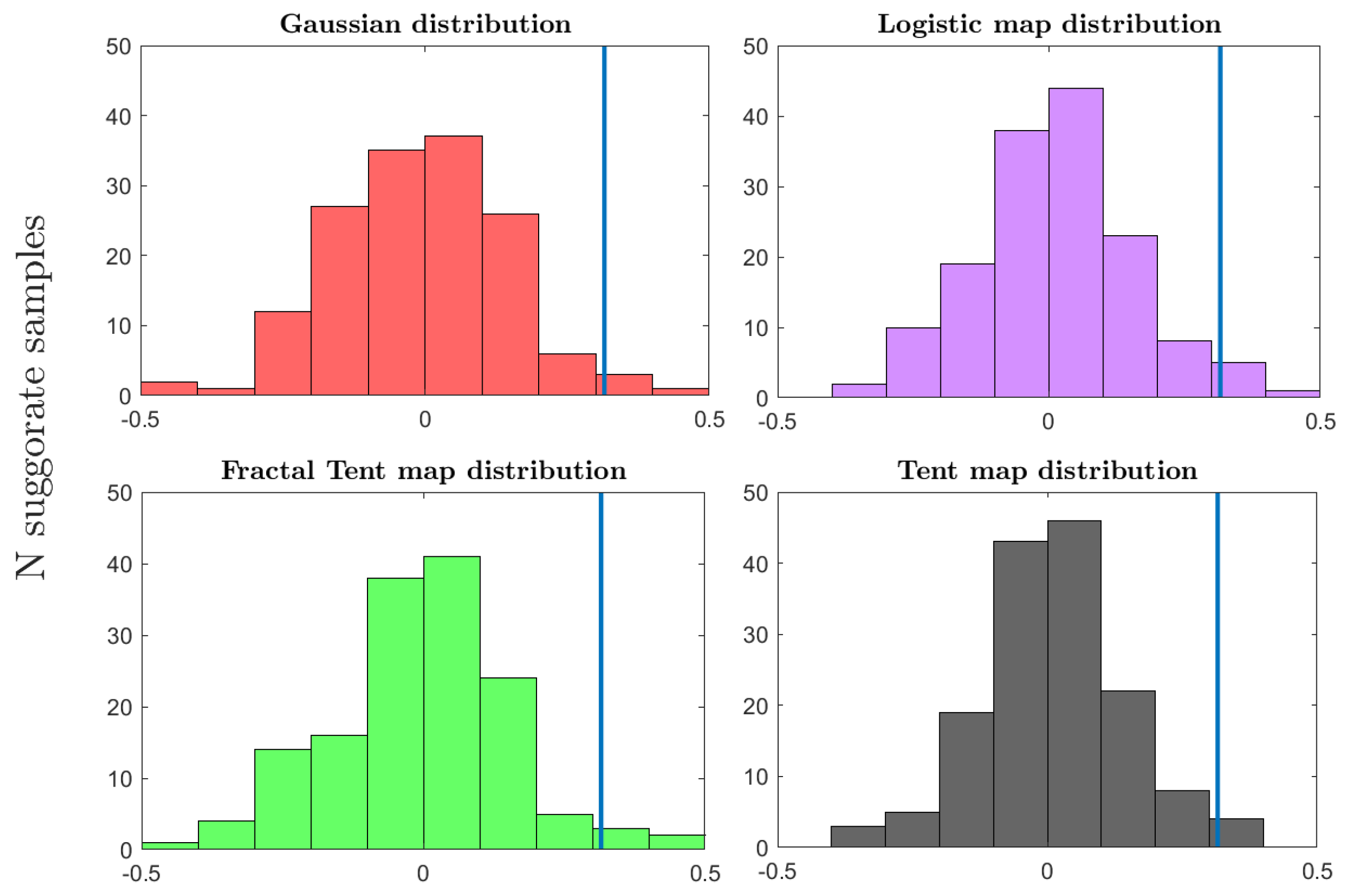
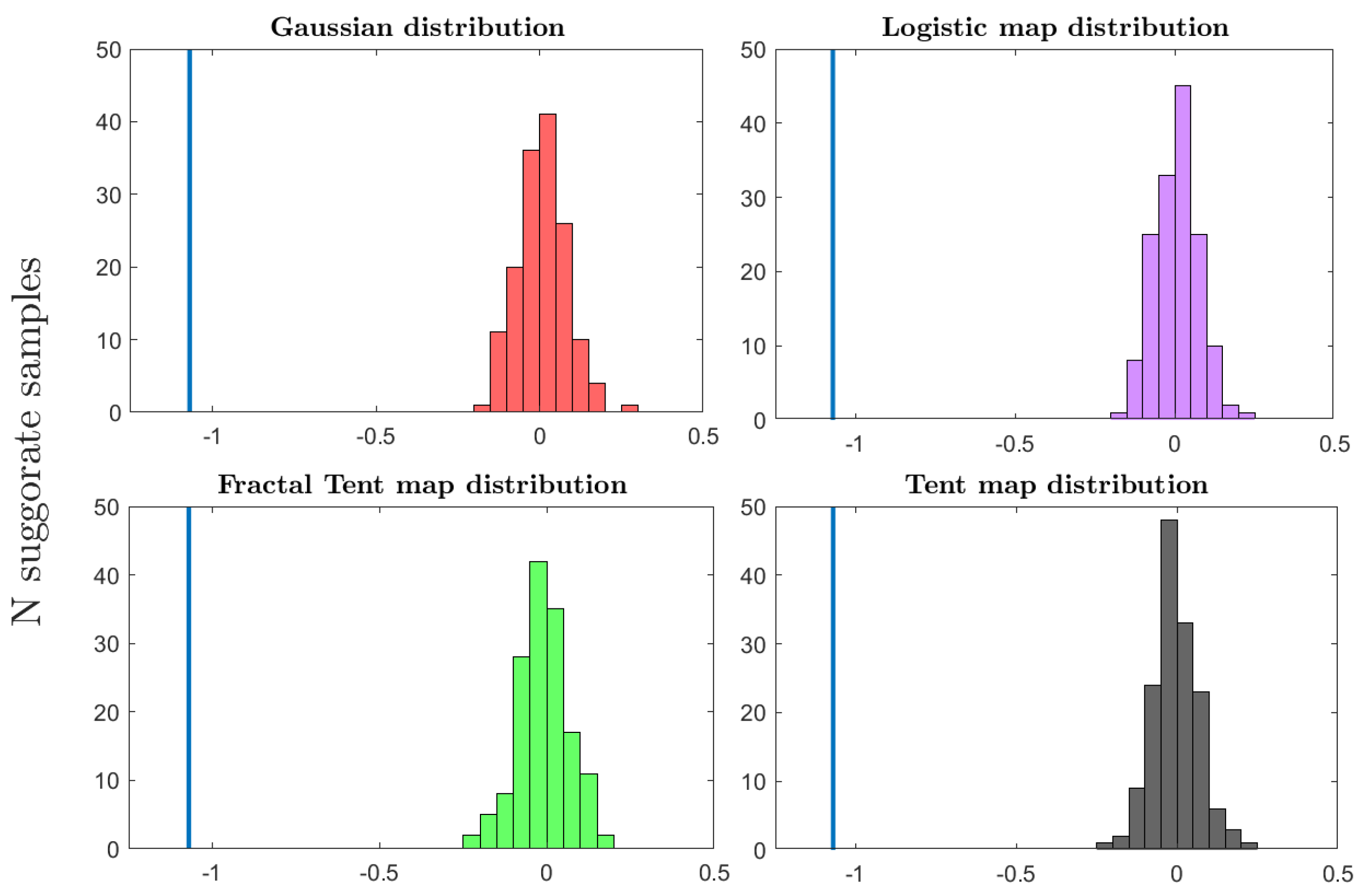
3.3. Surrogate Testing Results
- A linear signal that is generated by the AR process.
- A nonlinear chaotic signal generated by the logistic map (for k = 4).
- A biological signal that is taken from a dataset of 81 recordings of sperm whale clicks. It is generally a linear signal, but quite noisy.
4. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Biswas, H.R.; Hasan, M.M.; Bala, S.K. Chaos theory and its applications in our real life. Barishal Univ. J. Part 2018, 1, 123–140. [Google Scholar]
- Alnajim, A.M.; Abou-Bakr, E.; Alruwisan, S.S.; Khan, S.; Elmanfaloty, R.A. Hybrid chaotic-based PRNG for secure cryptography applications. Appl. Sci. 2023, 13, 7768. [Google Scholar] [CrossRef]
- Cao, W.; Cai, H.; Hua, Z. n-Dimensional Chaotic Map with application in secure communication. Chaos Solitons Fractals 2022, 163, 112519. [Google Scholar] [CrossRef]
- Naik, R.B.; Singh, U. A review on applications of chaotic maps in pseudo-random number generators and encryption. Ann. Data Sci. 2024, 11, 25–50. [Google Scholar] [CrossRef]
- Haliuk, S.; Krulikovskyi, O.; Vovchuk, D.; Corinto, F. Memristive structure-based chaotic system for prng. Symmetry 2022, 14, 68. [Google Scholar] [CrossRef]
- Yu, F.; Li, L.; He, B.; Liu, L.; Qian, S.; Zhang, Z.; Shen, H.; Cai, S.; Li, Y. Pseudorandom number generator based on a 5D hyperchaotic four-wing memristive system and its FPGA implementation. Eur. Phys. J. Spec. Top. 2021, 230, 1763–1772. [Google Scholar] [CrossRef]
- Fellet, M. Pseudorandom number generator uses true chaos to generate sequences with random behavior. Scilight 2018, 2018, 440001. [Google Scholar] [CrossRef]
- Rezk, A.A.; Madian, A.H.; Radwan, A.G.; Soliman, A.M. Reconfigurable chaotic pseudo random number generator based on FPGA. AEU-Int. J. Electron. Commun. 2019, 98, 174–180. [Google Scholar] [CrossRef]
- Elmanfaloty, R.A.; Abou-Bakr, E. Random property enhancement of a 1D chaotic PRNG with finite precision implementation. Chaos Solitons Fractals 2019, 118, 134–144. [Google Scholar] [CrossRef]
- Kadir, A.; Hamdulla, A.; Guo, W.Q. Color image encryption using skew tent map and hyper chaotic system of 6th-order CNN. Optik 2014, 125, 1671–1675. [Google Scholar] [CrossRef]
- Hasler, M.; Maistrenko, Y.L. An introduction to the synchronization of chaotic systems: Coupled skew tent maps. IEEE Trans. Circuits Syst. I Fundam. Theory Appl. 1997, 44, 856–866. [Google Scholar] [CrossRef]
- Tan, Z.; Wu, Q. Study of linearly cross-coupled chaotic systems for a random bit generator. In Proceedings of the 2008 International Conference on Computational Intelligence and Security, Suzhou, China, 13–17 December 2008; IEEE: New York, NY, USA, 2008; Volume 2, pp. 267–272. [Google Scholar]
- Saito, A.; Yamaguchi, A. Pseudorandom number generator based on the Bernoulli map on cubic algebraic integers. Chaos Interdiscip. Nonlinear Sci. 2018, 28, 103122. [Google Scholar] [CrossRef] [PubMed]
- Moysis, L.; Tutueva, A.; Christos, K.; Butusov, D. A chaos based pseudo-random bit generator using multiple digits comparison. Chaos Theory Appl. 2020, 2, 58–68. [Google Scholar]
- Moysis, L.; Volos, C.; Jafari, S.; Munoz-Pacheco, J.M.; Kengne, J.; Rajagopal, K.; Stouboulos, I. Modification of the logistic map using fuzzy numbers with application to pseudorandom number generation and image encryption. Entropy 2020, 22, 474. [Google Scholar] [CrossRef] [PubMed]
- Kvitko, D.; Rybin, V.; Bayazitov, O.; Karimov, A.; Karimov, T.; Butusov, D. Chaotic Path-Planning Algorithm Based on Courbage–Nekorkin Artificial Neuron Model. Mathematics 2024, 12, 892. [Google Scholar] [CrossRef]
- Murillo-Escobar, D.; Murillo-Escobar, M.Á.; Cruz-Hernández, C.; Arellano-Delgado, A.; López-Gutiérrez, R.M. Pseudorandom number generator based on novel 2D Hénon-Sine hyperchaotic map with microcontroller implementation. Nonlinear Dyn. 2023, 111, 6773–6789. [Google Scholar] [CrossRef] [PubMed]
- Garcia-Bosque, M.; Pérez-Resa, A.; Sánchez-Azqueta, C.; Aldea, C.; Celma, S. Chaos-based bitwise dynamical pseudorandom number generator on FPGA. IEEE Trans. Instrum. Meas. 2018, 68, 291–293. [Google Scholar] [CrossRef]
- Tutueva, A.V.; Karimov, T.I.; Moysis, L.; Nepomuceno, E.G.; Volos, C.; Butusov, D.N. Improving chaos-based pseudo-random generators in finite-precision arithmetic. Nonlinear Dyn. 2021, 104, 727–737. [Google Scholar] [CrossRef]
- Zhao, W.; Chang, Z.; Ma, C.; Shen, Z. A pseudorandom number generator based on the chaotic map and quantum random walks. Entropy 2023, 25, 166. [Google Scholar] [CrossRef]
- Hocine, M.; Lahcene, M.; Larbi, T.; Adda, A.P. A PRNG based on an improved chaotic map using a self-perturbation mechanism. Rom. J. Inf. Technol. Autom. Control 2023, 33, 47–60. [Google Scholar] [CrossRef]
- Massopust, P.R. Fractal functions and their applications. Chaos, Solitons Fractals 1997, 8, 171–190. [Google Scholar] [CrossRef]
- Lorenz, E.N. The problem of deducing the climate from the governing equations. Tellus 1964, 16, 1–11. [Google Scholar] [CrossRef]
- Collet, P.; Eckmann, J.P. Iterated Maps on the Interval as Dynamical Systems; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Wu, J.; Jin, X.; Mi, S.; Tang, J. An effective method to compute the box-counting dimension based on the mathematical definition and intervals. Results Eng. 2020, 6, 100106. [Google Scholar] [CrossRef]
- Theiler, J.; Eubank, S.; Longtin, A.; Galdrikian, B.; Farmer, J.D. Testing for nonlinearity in time series: The method of surrogate data. Phys. D Nonlinear Phenom. 1992, 58, 77–94. [Google Scholar] [CrossRef]
- Schreiber, T.; Schmitz, A. Surrogate time series. Phys. D Nonlinear Phenom. 2000, 142, 346–382. [Google Scholar] [CrossRef]
- Theiler, J.; Prichard, D. Using ‘surrogate surrogate data’to calibrate the actual rate of false positives in tests for nonlinearity in time series. Fields Inst. Commun. 1997, 11, 99. [Google Scholar]
- Schreiber, T.; Schmitz, A. Improved surrogate data for nonlinearity tests. Phys. Rev. Lett. 1996, 77, 635. [Google Scholar] [CrossRef] [PubMed]
- Prichard, D.; Theiler, J. Generating surrogate data for time series with several simultaneously measured variables. Phys. Rev. Lett. 1994, 73, 951. [Google Scholar] [CrossRef] [PubMed]
- Stoica, P.; Friedlander, B.; Söderström, T. A high-order Yule-Walker method for estimation of the AR parameters of an ARMA model. Syst. Control Lett. 1988, 11, 99–105. [Google Scholar] [CrossRef]
- Cohen, L. The generalization of the Wiener-Khinchin theorem. In Proceedings of the 1998 IEEE International Conference on Acoustics, Speech and Signal Processing, ICASSP’98 (Cat. No. 98CH36181), Seattle, WA, USA, 12–15 May 1998; IEEE: New York, NY, USA, 1998; Volume 3, pp. 1577–1580. [Google Scholar]
- Moysis, L.; Lawnik, M.; Volos, C. Density-Colored Bifurcation Diagrams—A Complementary Tool for Chaotic Map Analysis. Int. J. Bifurc. Chaos 2023, 33, 2330036. [Google Scholar] [CrossRef]
- Tutueva, A.V.; Nepomuceno, E.G.; Karimov, A.I.; Andreev, V.S.; Butusov, D.N. Adaptive chaotic maps and their application to pseudo-random numbers generation. Chaos Solitons Fractals 2020, 133, 109615. [Google Scholar] [CrossRef]
- Stinson, D.R. Classical Cryptography. In Cryptography Theory and Practice; CRC-Press: Boca Raton, FL, USA, 1995; pp. 1–20. [Google Scholar]
- Alvarez, G.; Li, S. Some basic cryptographic requirements for chaos-based cryptosystems. Int. J. Bifurc. Chaos 2006, 16, 2129–2151. [Google Scholar] [CrossRef]
- Pearson, K.X. On the criterion that a given system of deviations from the probable in the case of a correlated system of variables is such that it can be reasonbly supposed to have arisen from random sampling. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1900, 50, 157–175. [Google Scholar] [CrossRef]







| Statistic Tests | randn() Function | Logistic Map | Fractal Tent Map | Tent Map | ||||
|---|---|---|---|---|---|---|---|---|
| Pvalue | Pass Rate | Pvalue | Pass Rate | Pvalue | Pass Rate | Pvalue | Pass Rate | |
| FT | 0.457 | 0.98 | 0.478 | 1 | 0.480 | 0.99 | 0.543 | 0.98 |
| BFT | 0.525 | 0.99 | 0.466 | 0.99 | 0.470 | 0.99 | 0.492 | 0.99 |
| RT | 0.513 | 1 | 0.515 | 1 | 0.543 | 1 | 0.527 | 0.99 |
| LROT | 0.502 | 1 | 0.505 | 0.99 | 0.568 | 0.98 | 0.487 | 1 |
| MRT | 0.498 | 0.98 | 0.517 | 0.98 | 0.464 | 0.99 | 0.482 | 1 |
| SPT | 0.462 | 1 | 0.504 | 0.99 | 0.542 | 0.99 | 0.521 | 0.99 |
| NTMT | 0.461 | 0.99 | 0.502 | 1 | 0.535 | 0.99 | 0.519 | 0.99 |
| OTMT | 0.393 | 0.97 | 0.529 | 0.97 | 0.512 | 1 | 0.474 | 1 |
| MUST | 0.474 | 1 | 0.473 | 1 | 0.499 | 1 | 0.490 | 1 |
| LCT | 0.459 | 0.99 | 0.546 | 0.98 | 0.536 | 1 | 0.497 | 0.99 |
| ST0 | 0.475 | 0.98 | 0.541 | 1 | 0.514 | 1 | 0.520 | 1 |
| ST1 | 0.465 | 1 | 0.535 | 0.99 | 0.475 | 1 | 0.553 | 1 |
| AET | 0.494 | 0.98 | 0.468 | 0.99 | 0.542 | 1 | 0.493 | 0.99 |
| CSTF | 0.457 | 0.98 | 0.444 | 1 | 0.498 | 0.99 | 0.524 | 0.98 |
| CSTR | 0.456 | 0.99 | 0.440 | 0.99 | 0.486 | 0.99 | 0.539 | 0.98 |
| RET | 0.505 | 0.99 | 0.501 | 0.98 | 0.537 | 0.99 | 0.454 | 0.98 |
| REVT | 0.470 | 0.99 | 0.543 | 0.98 | 0.504 | 0.99 | 0.488 | 0.95 |
| Fractal Tent Map | Logistic Map | Tent Map | |
|---|---|---|---|
| Key Space |
| Fractal Tent Map | Logistic Map | Tent | |||||||
|---|---|---|---|---|---|---|---|---|---|
| D = 1/2 | D = 1/3 | Sum (Row) | k = 4 | k = 3.8 | Sum (Row) | u = | u = 1.5 | Sum (Row) | |
| Ones | 500,765 | 1,000,509 | 1,501,274 | 500,316 | 999,435 | 1,499,751 | 500,141 | 1,000,064 | 1,500,205 |
| Zeroes | 499,235 | 999,491 | 1,498,726 | 499,684 | 1,000,565 | 1,500,249 | 499,859 | 999,936 | 1,499,795 |
| Sum (Col) | 1,000,000 | 2,000,000 | 3,000,000 | 1,000,000 | 2,000,000 | 3,000,000 | 1,000,000 | 2,000,000 | 3,000,000 |
| Chi-Square Value | |||||||||
| Type of Signal | randn() Function | Logistic Map | Fractal Tent Map | Tent Map |
|---|---|---|---|---|
| Linear signal (AR) | 0.99 | 1 | 1 | 1 |
| Nonlinear signal (logistic map) | 1 | 1 | 1 | 1 |
| Biological signal (sperm whale) | 0.93 | 0.96 | 1 | 1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kopets, E.; Rybin, V.; Vasilchenko, O.; Butusov, D.; Fedoseev, P.; Karimov, A. Fractal Tent Map with Application to Surrogate Testing. Fractal Fract. 2024, 8, 344. https://doi.org/10.3390/fractalfract8060344
Kopets E, Rybin V, Vasilchenko O, Butusov D, Fedoseev P, Karimov A. Fractal Tent Map with Application to Surrogate Testing. Fractal and Fractional. 2024; 8(6):344. https://doi.org/10.3390/fractalfract8060344
Chicago/Turabian StyleKopets, Ekaterina, Vyacheslav Rybin, Oleg Vasilchenko, Denis Butusov, Petr Fedoseev, and Artur Karimov. 2024. "Fractal Tent Map with Application to Surrogate Testing" Fractal and Fractional 8, no. 6: 344. https://doi.org/10.3390/fractalfract8060344
APA StyleKopets, E., Rybin, V., Vasilchenko, O., Butusov, D., Fedoseev, P., & Karimov, A. (2024). Fractal Tent Map with Application to Surrogate Testing. Fractal and Fractional, 8(6), 344. https://doi.org/10.3390/fractalfract8060344







