Unveiling the Complexity of HIV Transmission: Integrating Multi-Level Infections via Fractal-Fractional Analysis
Abstract
1. Introduction
2. Development of the Model
Model Description
3. Basic Preliminaries
- (i)
- ,
- (ii)
- There is a compact and continuous operator ,
- (iii)
- A contraction mapping is defined by .
- (i)
- for all , hence, does not decrease.
- (ii)
- for all , hence does not increase.
4. Fractional Formulation of the Proposed Model
5. Exploring Theoretical Aspects of the Proposed Model
5.1. Existence and Uniqueness Results
5.2. Ulam-Hyers Stability Analysis
- for
6. Numerical Method for Fractal-Fractional Model
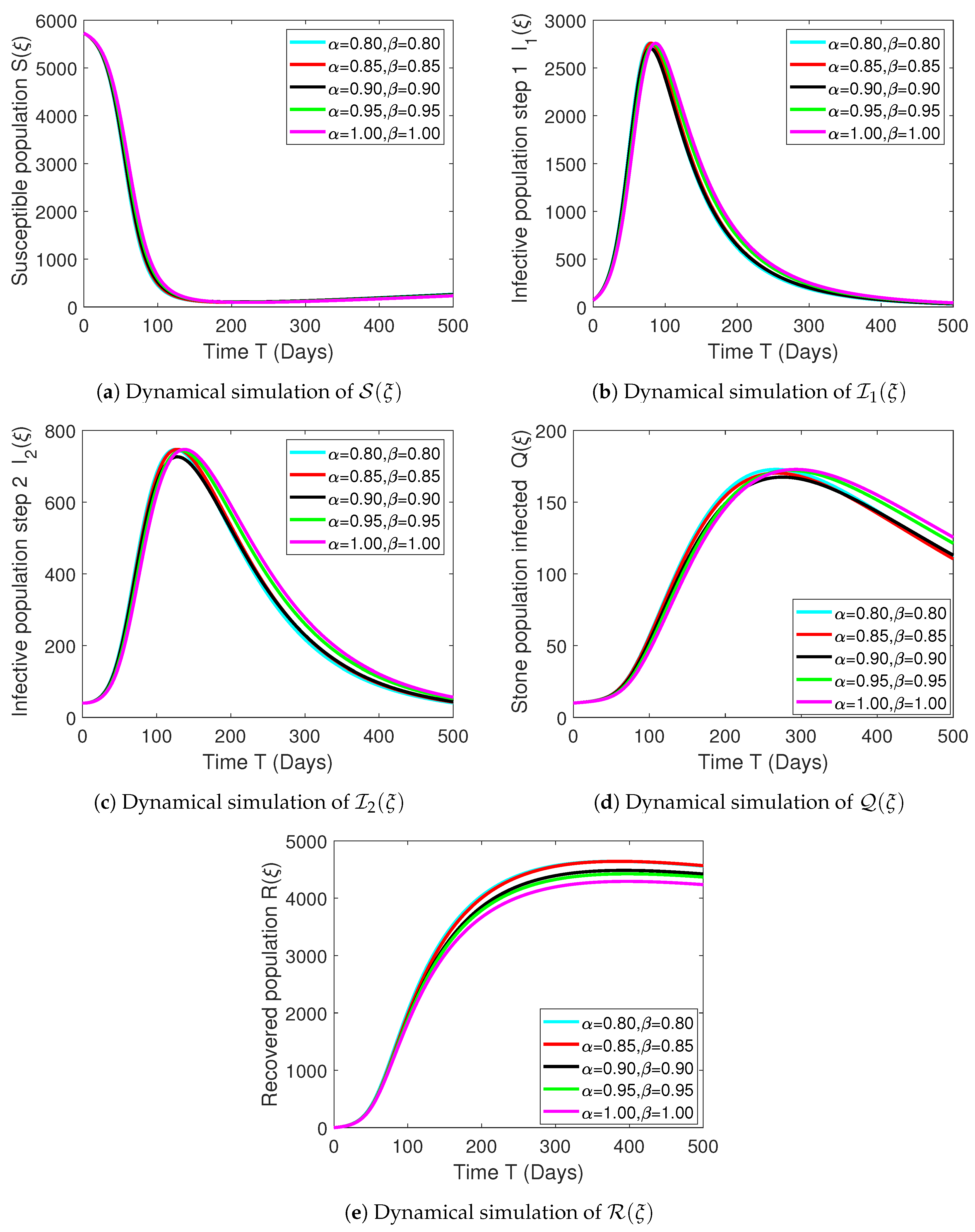
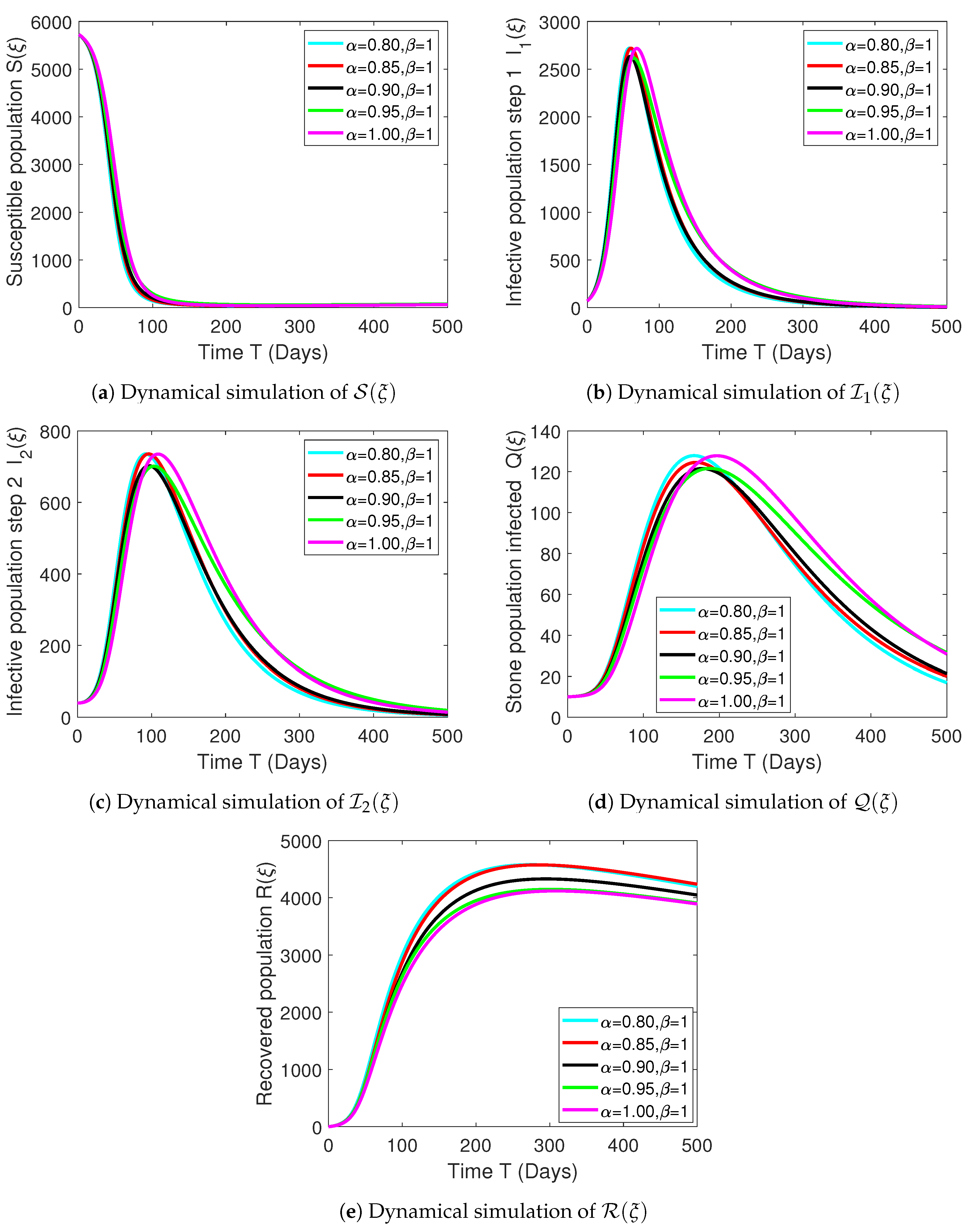
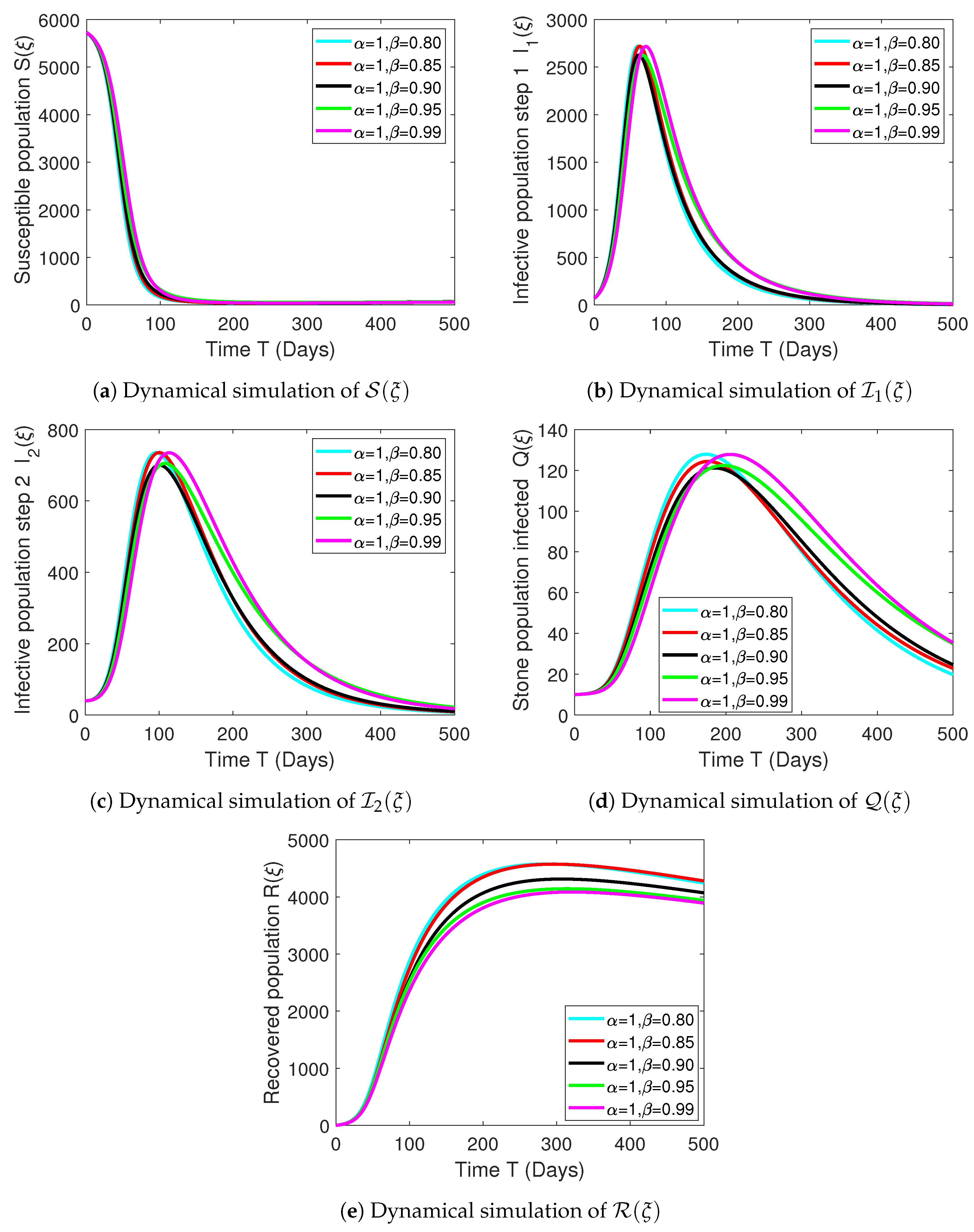
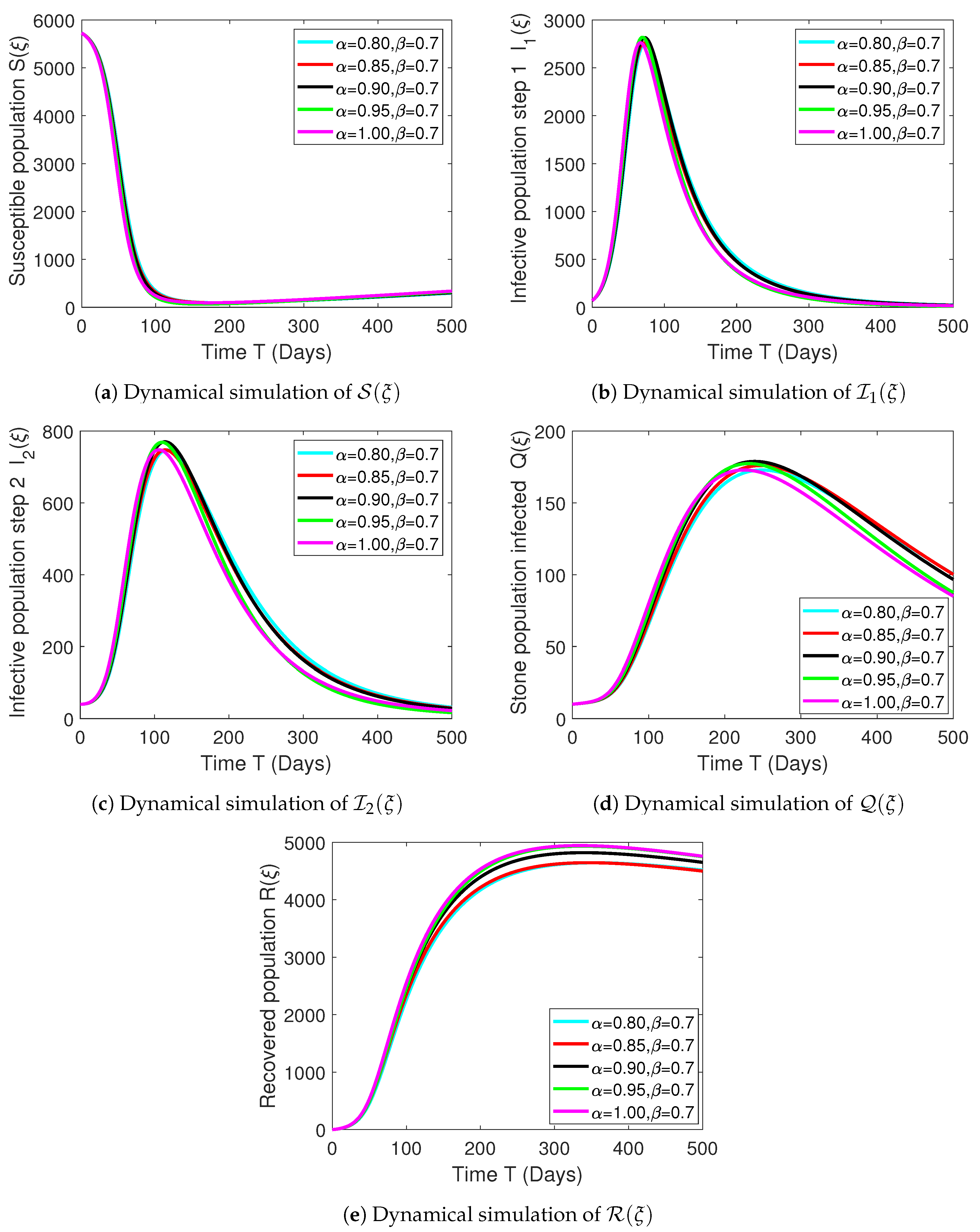
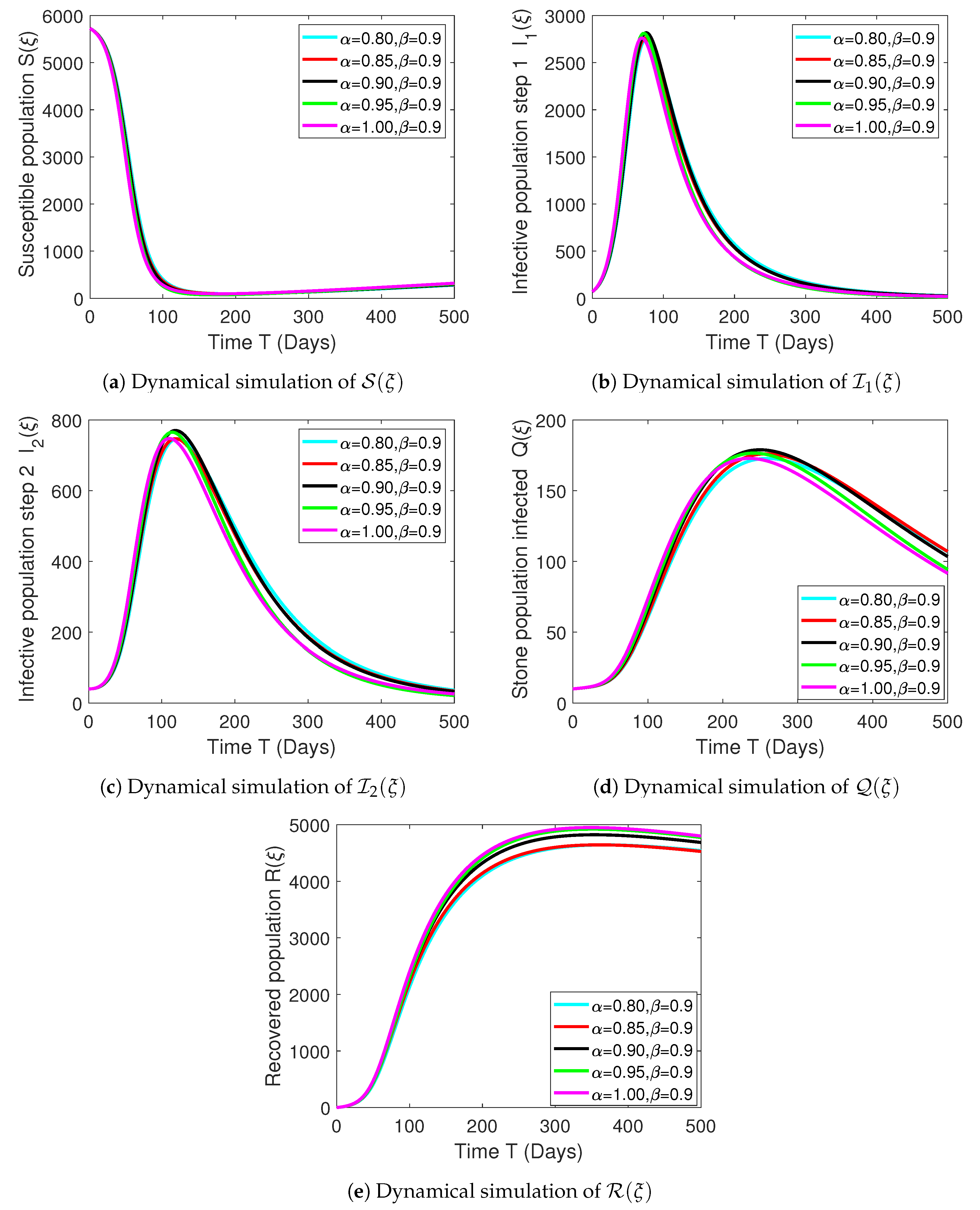
Numerical Experimentation and Discussion
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Anderson, R.M. The role of mathematical models in the study of HIV transmission and the epidemiology of AIDS. J. Acquir. Immune Defic. Syndr. 1988, 1, 241–256. [Google Scholar] [PubMed]
- Sakkoum, A.; Lhous, M.; Magri, E.M. A mathematical simulation and optimal control of a VIH model with different infectious level. J. Math. Comput. Sci. 2022, 12, 117. [Google Scholar]
- Anderson, R.M.; Blythe, S.P.; Gupta, S.; Konings, E. The transmission dynamics of the human immunodeficiency virus type 1 in the male homosexual community in the United Kingdom: The influence of changes in sexual behaviour. Philos. Trans. R. Soc. Lond. B Biol. Sci. 1989, 325, 45–98. [Google Scholar] [PubMed]
- Nisar, K.S.; Farman, M.; Abdel-Aty, M.; Cao, J. A review on epidemic models in sight of fractional calculus. Alex. Eng. J. 2023, 75, 81–113. [Google Scholar] [CrossRef]
- Chen, Y.; Liu, F.; Yu, Q.; Li, T. Review of fractional epidemic models. Appl. Math. Model. 2021, 97, 281–307. [Google Scholar] [CrossRef]
- Ngina, P.; Mbogo, R.W.; Luboobi, L.S. Modelling optimal control of in-host HIV dynamics using different control strategies. Comput. Math. Methods Med. 2018, 2018, 9385080. [Google Scholar] [CrossRef] [PubMed]
- Silva, C.J.; Torres, D.F. Modeling and optimal control of HIV/AIDS prevention through PrEP. Discret. Contin. Dyn. Syst.-S 2018, 11, 119–141. [Google Scholar] [CrossRef]
- Shirazian, M.; Farahi, M.H. Optimal control strategy for a fully determined HIV model. Intell. Control. Autom. 2010, 1, 15–19. [Google Scholar] [CrossRef]
- Li, Z.; Teng, Z.; Miao, H. Modeling and control for HIV/AIDS transmission in China based on data from 2004 to 2016. Comput. Math. Methods Med. 2017, 2017, 8935314. [Google Scholar] [CrossRef]
- Shen, M.; Xiao, Y.; Rong, L. Global stability of an infection-age structured HIV-1 model linking within-host and between-host dynamics. Math. Biosci. 2015, 263, 37–50. [Google Scholar] [CrossRef]
- Shi, S.; Nguyen, P.K.; Cabral, H.J.; Diez-Barroso, R.; Derry, P.J.; Kanahara, S.M.; Kumar, V.A. Development of peptide inhibitors of HIV transmission. Bioact. Mater. 2016, 1, 109–121. [Google Scholar] [CrossRef] [PubMed]
- Huo, H.F.; Chen, R.; Wang, X.Y. Modelling and stability of HIV/AIDS epidemic model with treatment. Appl. Math. Model. 2016, 40, 6550–6559. [Google Scholar] [CrossRef]
- Zhai, X.; Li, W.; Wei, F.; Mao, X. Dynamics of an HIV/AIDS transmission model with protection awareness and fluctuations. Chaos Solitons Fractals 2023, 169, 113224. [Google Scholar] [CrossRef]
- Zafar, Z.U.A.; Ali, N.; Younas, S.; Abdelwahab, S.F.; Nisar, K.S. Numerical investigations of stochastic HIV/AIDS infection model. Alex. Eng. J. 2021, 60, 5341–5363. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, R.; Kuniya, T. Global dynamics for a class of age-infection HIV models with nonlinear infection rate. J. Math. Anal. Appl. 2015, 432, 289–313. [Google Scholar] [CrossRef]
- Singh, R.; Ali, S.; Jain, M. Epidemic model of HIV/AIDS transmission dynamics with different latent stages based on treatment. Am. J. Appl. Math. 2016, 4, 222–234. [Google Scholar] [CrossRef][Green Version]
- Alyobi, S.; Jan, R. Qualitative and quantitative analysis of fractional dynamics of infectious diseases with control measures. Fractal Fract. 2023, 7, 400. [Google Scholar] [CrossRef]
- Anjam, Y.N.; Yavuz, M.; ur Rahman, M.; Batool, A. Analysis of a fractional pollution model in a system of three interconnecting lakes. AIMS Biophys. 2023, 10, 220–240. [Google Scholar] [CrossRef]
- Qureshi, S.; Atangana, A. Fractal-fractional differentiation for the modeling and mathematical analysis of nonlinear diarrhea transmission dynamics under the use of real data. Chaos Solitons Fractals 2020, 136, 109812. [Google Scholar] [CrossRef]
- Anjam, Y.N.; Shahid, I.; Emadifar, H.; Arif Cheema, S.; ur Rahman, M. Dynamics of the optimality control of transmission of infectious disease: A sensitivity analysis. Sci. Rep. 2024, 14, 1041. [Google Scholar] [CrossRef]
- Anjam, Y.N.; Shafqat, R.; Sarris, I.E.; Ur Rahman, M.; Touseef, S.; Arshad, M. A fractional order investigation of smoking model using Caputo-Fabrizio differential operator. Fractal Fract. 2022, 6, 623. [Google Scholar] [CrossRef]
- Caputo, M.; Fabrizio, M. On the singular kernels for fractional derivatives. Some applications to partial differential equations. Progr. Fract. Differ. Appl. 2021, 7, 79–82. [Google Scholar]
- Caputo, M.; Fabrizio, M. A new definition of fractional derivative without singular kernel. Prog. Fract. Differ. Appl. 2015, 1, 73–85. [Google Scholar]
- Atangana, A. Fractal-fractional differentiation and integration: Connecting fractal calculus and fractional calculus to predict complex system. Chaos Solitons Fractals 2017, 102, 396–406. [Google Scholar] [CrossRef]
- ur Rahman, M.; Ahmad, S.; Matoog, R.T.; Alshehri, N.A.; Khan, T. Study on the mathematical modelling of COVID-19 with Caputo-Fabrizio operator. Chaos Solitons Fractals 2021, 500, 111121. [Google Scholar] [CrossRef]
- Zhang, T.; Zhao, Y.; Xu, X.; Wu, S.; Gu, Y. Solution and dynamics analysis of fractal-fractional multi-scroll Chen chaotic system based on Adomain decomposition method. Chaos, Solitons Fractals 2024, 178, 114268. [Google Scholar] [CrossRef]
- Almutairi, N.; Saber, S. Application of a time-fractal fractional derivative with a power-law kernel to the Burke-Shaw system based on Newton’s interpolation polynomials. MethodsX 2024, 12, 102510. [Google Scholar] [CrossRef] [PubMed]
- Asifa; Anwar, T.; Kumam, P.; Sitthithakerngkiet, K.; Muhammad, S. A fractal-fractional model-based investigation of shape influence on thermal performance of tripartite hybrid nanofluid for channel flows. Numer. Heat Transf. Part A Appl. 2024, 85, 155–186. [Google Scholar] [CrossRef]
- Adom-Konadu, A.; Bonyah, E.; Sackitey, A.L.; Anokye, M.; Asamoah, J.K.K. A fractional order Monkeypox model with protected travelers using the fixed point theorem and Newton polynomial interpolation. Healthc. Anal. 2023, 3, 100191. [Google Scholar] [CrossRef]
- Atangana, A.; Qureshi, S. Modeling attractors of chaotic dynamical systems with fractal–fractional operators. Chaos Solitons Fractals 2019, 123, 320–337. [Google Scholar] [CrossRef]
- Li, Z.; Liu, Z.; Khan, M.A. Fractional investigation of bank data with fractal-fractional Caputo derivative. Chaos Solitons Fractals 2020, 131, 109528. [Google Scholar] [CrossRef]
- Owolabi, K.M.; Shikongo, A. Fractal fractional operator method on HER2+ breast cancer dynamics. Int. J. Appl. Comput. Math. 2021, 7, 85. [Google Scholar] [CrossRef]
- Ahmad, S.; Ullah, A.; Abdeljawad, T.; Akgül, A.; Mlaiki, N. Analysis of fractal-fractional model of tumor-immune interaction. Results Phys. 2021, 25, 104178. [Google Scholar] [CrossRef]
- Anjam, Y.N.; Arshad, A.; Alqahtani, R.T.; Arshad, M. Unveiling the dynamics of drug transmission: A fractal-fractional approach integrating criminal law perspectives. AIMS Math. 2024, 9, 13102–13128. [Google Scholar] [CrossRef]
- Liu, X.; ur Rahmamn, M.; Ahmad, S.; Baleanu, D.; Nadeem Anjam, Y. A new fractional infectious disease model under the non-singular Mittag–Leffler derivative. Waves Random Complex Media 2022, 1–27. [Google Scholar] [CrossRef]
- Ali, Z.; Rabiei, F.; Shah, K.; Khodadadi, T. Qualitative analysis of fractal-fractional order COVID-19 mathematical model with case study of Wuhan. Alex. Eng. J. 2021, 60, 477–489. [Google Scholar] [CrossRef]
- Qureshi, S.; Rangaig, N.A.; Baleanu, D. New numerical aspects of Caputo-Fabrizio fractional derivative operator. Mathematics 2019, 7, 374. [Google Scholar] [CrossRef]
- Atangana, A. Modelling the spread of COVID-19 with new fractal-fractional operators: Can the lockdown save mankind before vaccination? Chaos Solitons Fractals 2020, 136, 109860. [Google Scholar] [CrossRef] [PubMed]
- Farman, M.; Sarwar, R.; Akgul, A. Modeling and analysis of sustainable approach for dynamics of infections in plant virus with fractal fractional operator. Chaos Solitons Fractals 2023, 170, 113373. [Google Scholar] [CrossRef]
- Granas, A.; Dugundji, J. Fixed Point Theory; Springer: New York, NY, USA, 2003; Volume 14, pp. 15–16. [Google Scholar]
- Kongson, J.; Sudsutad, W.; Thaiprayoon, C.; Alzabut, J.; Tearnbucha, C. On analysis of a nonlinear fractional system for social media addiction involving Atangana-Baleanu-Caputo derivative. Adv. Differ. Equ. 2021, 2021, 356. [Google Scholar] [CrossRef]
- Kreyszig, E. Introductory Functional Analysis with Applications; John Wiley Sons: Hoboken, NJ, USA, 1991; Volume 17. [Google Scholar]
- Huo, H.F.; Feng, L.X. Global stability for an HIV/AIDS epidemic model with different latent stages and treatment. Appl. Math. Model. 2013, 37, 1480–1489. [Google Scholar] [CrossRef]
- Alizon, S.; Magnus, C. Modelling the course of an HIV infection: Insights from ecology and evolution. Viruses 2012, 4, 1984–2013. [Google Scholar] [CrossRef] [PubMed]
- Yusuf, T.T.; Benyah, F. Optimal strategy for controlling the spread of HIV/AIDS disease: A case study of South Africa. J. Biol. Dyn. 2012, 6, 475–494. [Google Scholar] [CrossRef] [PubMed]
- Arruda, E.F.; Dias, C.M.; de Magalhã, C.V.; Pastore, D.H.; Thomé, R.C.; Yang, H.M. An optimal control approach to HIV immunology. Appl. Math. 2015, 6, 1115–1130. [Google Scholar] [CrossRef]
- Kumar, S.; Chauhan, R.P.; Osman, M.S.; Mohiuddine, S.A. A study on fractional HIV-AIDs transmission model with awareness effect. Math. Methods Appl. Sci. 2023, 46, 8334–8348. [Google Scholar] [CrossRef]
- Cai, L.; Li, X.; Ghosh, M.; Guo, B. Stability analysis of an HIV/AIDS epidemic model with treatment. J. Comput. Appl. Math. 2009, 229, 313–323. [Google Scholar] [CrossRef]
- Khan, A.; Gómez-Aguilar, J.F.; Khan, T.S.; Khan, H. Stability analysis and numerical solutions of fractional order HIV/AIDS model. Chaos Solitons Fractals 2019, 122, 119–128. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Anjam, Y.N.; Turki Alqahtani, R.; Alharthi, N.H.; Tabassum, S. Unveiling the Complexity of HIV Transmission: Integrating Multi-Level Infections via Fractal-Fractional Analysis. Fractal Fract. 2024, 8, 299. https://doi.org/10.3390/fractalfract8050299
Anjam YN, Turki Alqahtani R, Alharthi NH, Tabassum S. Unveiling the Complexity of HIV Transmission: Integrating Multi-Level Infections via Fractal-Fractional Analysis. Fractal and Fractional. 2024; 8(5):299. https://doi.org/10.3390/fractalfract8050299
Chicago/Turabian StyleAnjam, Yasir Nadeem, Rubayyi Turki Alqahtani, Nadiyah Hussain Alharthi, and Saira Tabassum. 2024. "Unveiling the Complexity of HIV Transmission: Integrating Multi-Level Infections via Fractal-Fractional Analysis" Fractal and Fractional 8, no. 5: 299. https://doi.org/10.3390/fractalfract8050299
APA StyleAnjam, Y. N., Turki Alqahtani, R., Alharthi, N. H., & Tabassum, S. (2024). Unveiling the Complexity of HIV Transmission: Integrating Multi-Level Infections via Fractal-Fractional Analysis. Fractal and Fractional, 8(5), 299. https://doi.org/10.3390/fractalfract8050299









