Synchronization of Fractional Delayed Memristive Neural Networks with Jump Mismatches via Event-Based Hybrid Impulsive Controller
Abstract
1. Introduction
- With comprehensive consideration of discrete, distributed, and leakage delays, combined with jump mismatches, we augment the relevance of FMNNs to practical systems in industry.
- With the aim of achieving control objectives for a controlled network at a lower control cost, we unveil two innovative event-based hybrid impulsive controllers, incorporating both static and dynamic event-triggering mechanisms.
- Leveraging novel Lyapunov functions, we establish a duo of sufficient criteria, theoretically ensuring asymptotic synchronization in the aforestated FMNNs.
2. Model for FMNNs
3. Preliminaries
4. Main Results
4.1. Static Event Trigger Strategy
- 1.
- ;
- 2.
- ;
- 3.
- .
4.2. Dynamic Event Trigger Strategy
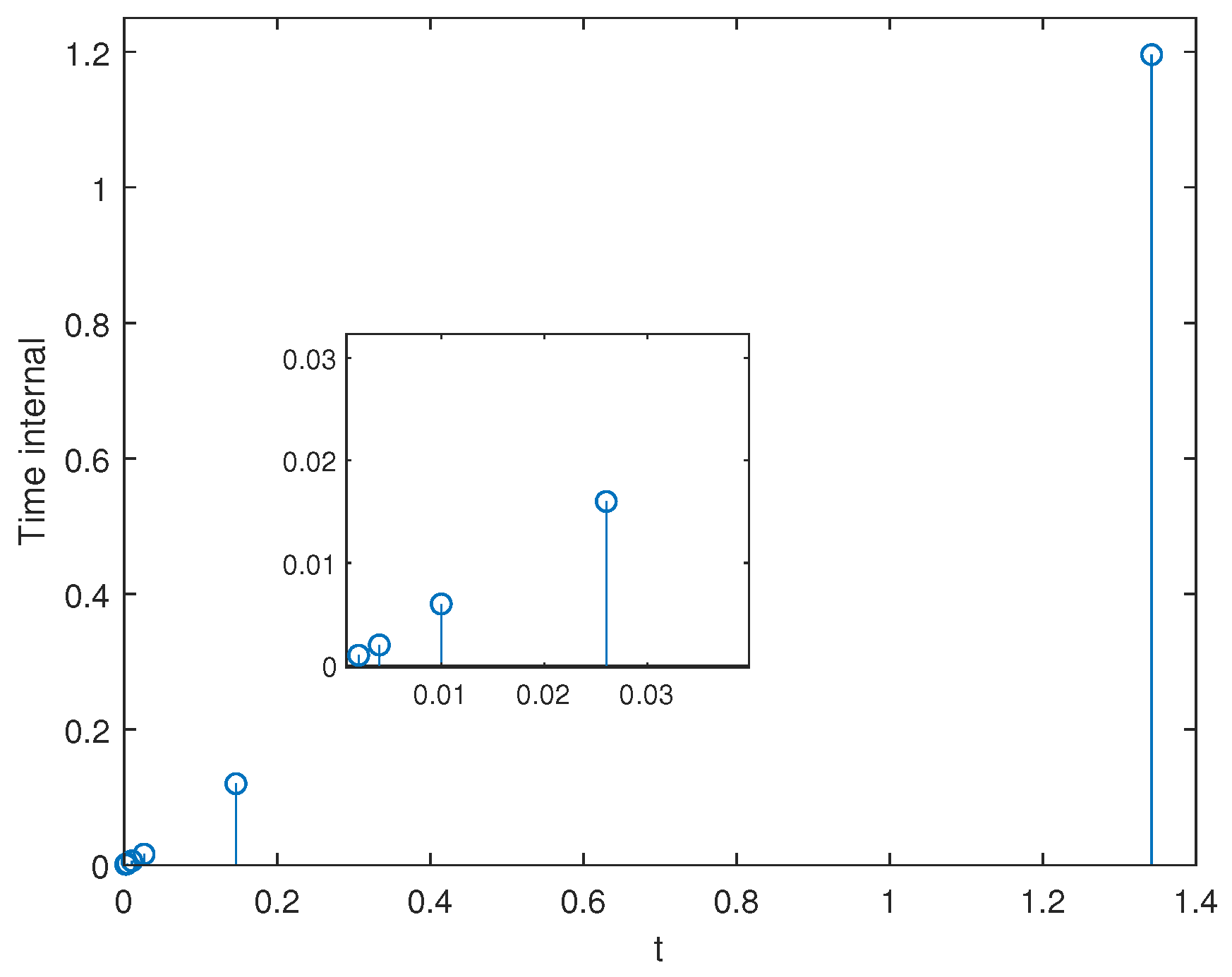
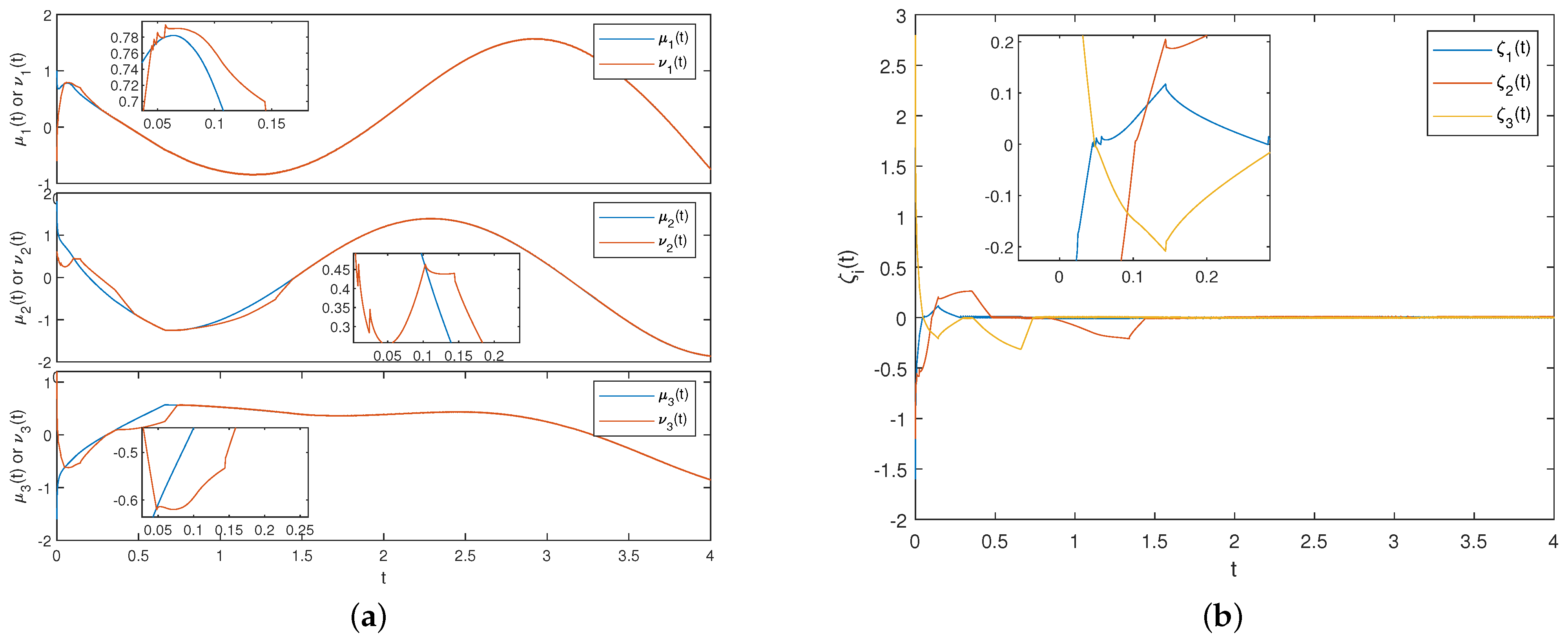
5. Numerical Example
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| MNNs | memristive neural networks; |
| FMNNs | fractional memristive neural networks. |
References
- Qi, F.; Qu, J.; Chai, Y.; Chen, L.; Lopes, A.M. Synchronization of incommensurate fractional-order chaotic systems based on linear feedback control. Fractal Fract. 2022, 6, 221. [Google Scholar] [CrossRef]
- Liang, B.; Zheng, S.; Ahn, C.K.; Liu, F. Adaptive fuzzy control for fractional-order interconnected systems with unknown control directions. IEEE Trans. Fuzzy Syst. 2020, 30, 75–87. [Google Scholar] [CrossRef]
- Udhayakumar, K.; Shanmugasundaram, S.; Kashkynbayev, A.; Janani, K.; Rakkiyappan, R. Saturated and asymmetric saturated impulsive control synchronization of coupled delayed inertial neural networks with time-varying delays. Appl. Math. Model. 2023, 113, 528–544. [Google Scholar] [CrossRef]
- Chen, X.; Liu, Y.; Ruan, Q.; Cao, J. Stabilization of nonlinear time-delay systems: Flexible delayed impulsive control. Appl. Math. Model. 2023, 114, 488–501. [Google Scholar] [CrossRef]
- Li, X.; Rao, R.; Zhong, S.; Yang, X.; Li, H.; Zhang, Y. Impulsive control and synchronization for fractional-order hyper-chaotic financial system. Mathematics 2022, 10, 2737. [Google Scholar] [CrossRef]
- Ji, X.; Lu, J.; Jiang, B.; Shi, K. Distributed Synchronization of Delayed Neural Networks: Delay-Dependent Hybrid Impulsive Control. IEEE Trans. Netw. Sci. Eng. 2021, 9, 634–647. [Google Scholar] [CrossRef]
- Wang, W.; Dong, J.; Xu, D.; Yan, Z.; Zhou, J. Synchronization control of time-delay neural networks via event-triggered non-fragile cost-guaranteed control. Math. Biosci. Eng. 2022, 20, 52–75. [Google Scholar] [CrossRef]
- Yang, A.; Ma, S. Event-triggered control for switched singular systems with asynchronous switching and state jumps. Appl. Math. Comput. 2023, 437, 127543. [Google Scholar] [CrossRef]
- Xie, H.; Zong, G.; Yang, D.; Chen, Y.; Shi, K. Dynamic output feedback L∞ control of switched affine systems: An event-triggered mechanism. Nonlinear Anal. Hybrid Syst. 2023, 47, 101278. [Google Scholar] [CrossRef]
- Wang, J.; Krstic, M. Event-triggered output-feedback backstepping control of sandwich hyperbolic PDE systems. IEEE Trans. Autom. Control 2021, 67, 220–235. [Google Scholar] [CrossRef]
- Wang, L.; Dong, J. Adaptive fuzzy consensus tracking control for uncertain fractional-order multiagent systems with event-triggered input. IEEE Trans. Fuzzy Syst. 2020, 30, 310–320. [Google Scholar] [CrossRef]
- Cao, Y.; Wang, S.; Guo, Z.; Huang, T.; Wen, S. Synchronization of memristive neural networks with leakage delay and parameters mismatch via event-triggered control. Neural Netw. 2019, 119, 178–189. [Google Scholar] [CrossRef] [PubMed]
- Wang, M.; Li, P.; Li, X. Event-triggered delayed impulsive control for input-to-state stability of nonlinear impulsive systems. Nonlinear Anal. Hybrid Syst. 2023, 47, 101277. [Google Scholar] [CrossRef]
- Liang, Z.; Liu, X. Hybrid event-triggered impulsive flocking control for multi-agent systems via pinning mechanism. Appl. Math. Model. 2023, 114, 23–43. [Google Scholar] [CrossRef]
- Li, X.; Li, P. Input-to-state stability of nonlinear systems: Event-triggered impulsive control. IEEE Trans. Autom. Control 2021, 67, 1460–1465. [Google Scholar] [CrossRef]
- Bao, Y.; Zhao, D.; Sun, J.; Wen, G.; Yang, T. Resilient Synchronization of Neural Networks Under DoS Attacks and Communication Delays via Event-Triggered Impulsive Control. IEEE Trans. Syst. Man Cybern. Syst. 2024, 54, 471–483. [Google Scholar] [CrossRef]
- Liu, X.; Chen, L.; Zhao, Y.; Li, H. Event-triggered hybrid impulsive control for synchronization of fractional-order multilayer signed networks under cyber attacks. Neural Netw. 2024, 172, 106124. [Google Scholar] [CrossRef]
- Chua, L. Memristor-the missing circuit element. IEEE Trans. Circuit Theory 1971, 18, 507–519. [Google Scholar] [CrossRef]
- Strukov, D.B.; Snider, G.S.; Stewart, D.R.; Williams, R.S. The missing memristor found. Nature 2008, 453, 80–83. [Google Scholar] [CrossRef]
- Zhang, Y.; Yu, Y.; Cui, X. Dynamical behaviors analysis of memristor-based fractional-order complex-valued neural networks with time delay. Appl. Math. Comput. 2018, 339, 242–258. [Google Scholar] [CrossRef]
- Wang, X.; Yu, Y.; Cai, J.; Zhong, S.; Yang, N.; Shi, K.; Mazumder, P.; Tashi, N. Dynamic pinning synchronization of fuzzy-dependent-switched coupled memristive neural networks with mismatched dimensions on time scales. IEEE Trans. Fuzzy Syst. 2020, 30, 779–793. [Google Scholar] [CrossRef]
- Xu, R.; Zhang, Y. Generalized Gronwall fractional summation inequalities and their applications. J. Inequal. Appl. 2015, 2015, 242. [Google Scholar] [CrossRef]
- Chen, J.; Zeng, Z.; Jiang, P. Global Mittag-Leffler stability and synchronization of memristor-based fractional-order neural networks. Neural Netw. 2014, 51, 1–8. [Google Scholar] [CrossRef]
- Ding, D.; Xiao, H.; Yang, Z.; Luo, H.; Hu, Y.; Zhang, X.; Liu, Y. Coexisting multi-stability of Hopfield neural network based on coupled fractional-order locally active memristor and its application in image encryption. Nonlinear Dyn. 2022, 108, 4433–4458. [Google Scholar] [CrossRef]
- Yu, F.; Yu, Q.; Chen, H.; Kong, X.; Mokbel, A.A.M.; Cai, S.; Du, S. Dynamic analysis and audio encryption application in IoT of a multi-scroll fractional-order memristive Hopfield neural network. Fractal Fract. 2022, 6, 370. [Google Scholar] [CrossRef]
- Jia, T.; Chen, X.; He, L.; Zhao, F.; Qiu, J. Finite-Time Synchronization of Uncertain Fractional-Order Delayed Memristive Neural Networks via Adaptive Sliding Mode Control and Its Application. Fractal Fract. 2022, 6, 502. [Google Scholar] [CrossRef]
- Ding, Z.; Chen, C.; Wen, S.; Li, S.; Wang, L. Lag projective synchronization of nonidentical fractional delayed memristive neural networks. Neurocomputing 2022, 469, 138–150. [Google Scholar] [CrossRef]
- Wu, X.; Liu, S.; Wang, H.; Wang, Y. Stability and pinning synchronization of delayed memristive neural networks with fractional-order and reaction–diffusion terms. ISA Trans. 2023, 136, 114–125. [Google Scholar] [CrossRef] [PubMed]
- Kao, Y.; Li, Y.; Park, J.H.; Chen, X. Mittag–Leffler synchronization of delayed fractional memristor neural networks via adaptive control. IEEE Trans. Neural Netw. Learn. Syst. 2020, 32, 2279–2284. [Google Scholar] [CrossRef]
- You, F.; Tang, H.A.; Wang, Y.; Xia, Z.Y.; Li, J.W. Adaptive Output Synchronization of Coupled Fractional-Order Memristive Reaction-Diffusion Neural Networks. Fractal Fract. 2024, 8, 78. [Google Scholar] [CrossRef]
- Yang, S.Y.; Tang, H.A.; Hu, X.; Xia, Q.; Wang, L.; Duan, S. Adaptive finite-time passivity and synchronization of coupled fractional-order memristive neural networks with multi-state couplings. Neurocomputing 2024, 579, 127380. [Google Scholar] [CrossRef]
- Song, C.; Cao, J.; Abdel-Aty, M. New Results on Robust Synchronization for Memristive Neural Networks with Fractional Derivatives via Linear Matrix Inequality. Fractal Fract. 2022, 6, 585. [Google Scholar] [CrossRef]
- Zhang, S.; Yang, Y.; Li, L.; Wu, D. Quasi-synchronization of fractional-order complex-valued memristive recurrent neural networks with switching jumps mismatch. Neural Process. Lett. 2021, 53, 865–891. [Google Scholar] [CrossRef]
- Zhang, L.; Yang, Y. Lag synchronization for fractional-order memristive neural networks with time delay via switching jumps mismatch. J. Frankl. Inst. 2018, 355, 1217–1240. [Google Scholar] [CrossRef]
- Wu, X.; Liu, S.; Wang, H. Pinning synchronization of stochastic neutral memristive neural networks with reaction–diffusion terms. Neural Netw. 2023, 157, 1–10. [Google Scholar] [CrossRef]
- Wang, F.; Yang, Y.; Hu, M. Asymptotic stability of delayed fractional-order neural networks with impulsive effects. Neurocomputing 2015, 154, 239–244. [Google Scholar] [CrossRef]
- Hu, T.; Park, J.H.; Liu, X.; He, Z.; Zhong, S. Sampled-data-based event-triggered synchronization strategy for fractional and impulsive complex networks with switching topologies and time-varying delay. IEEE Trans. Syst. Man Cybern. Syst. 2021, 52, 3568–3580. [Google Scholar] [CrossRef]

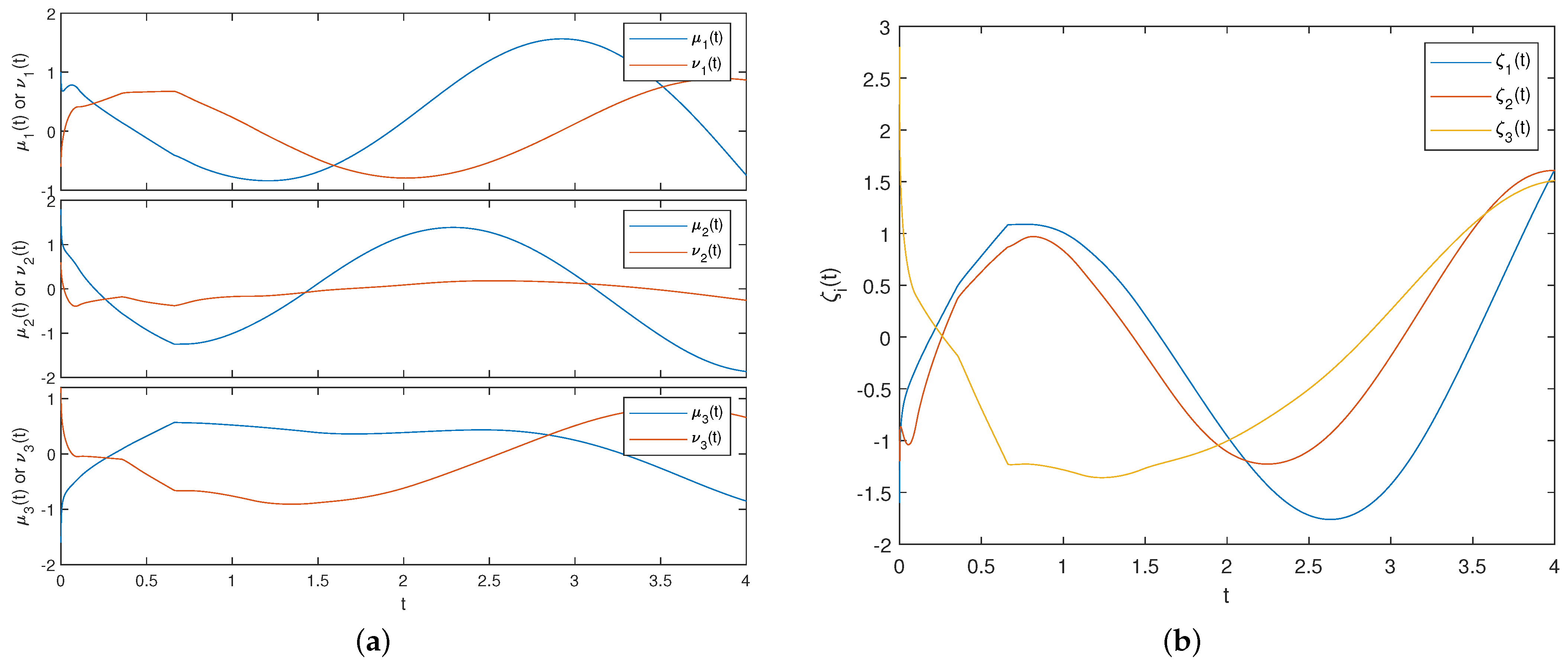
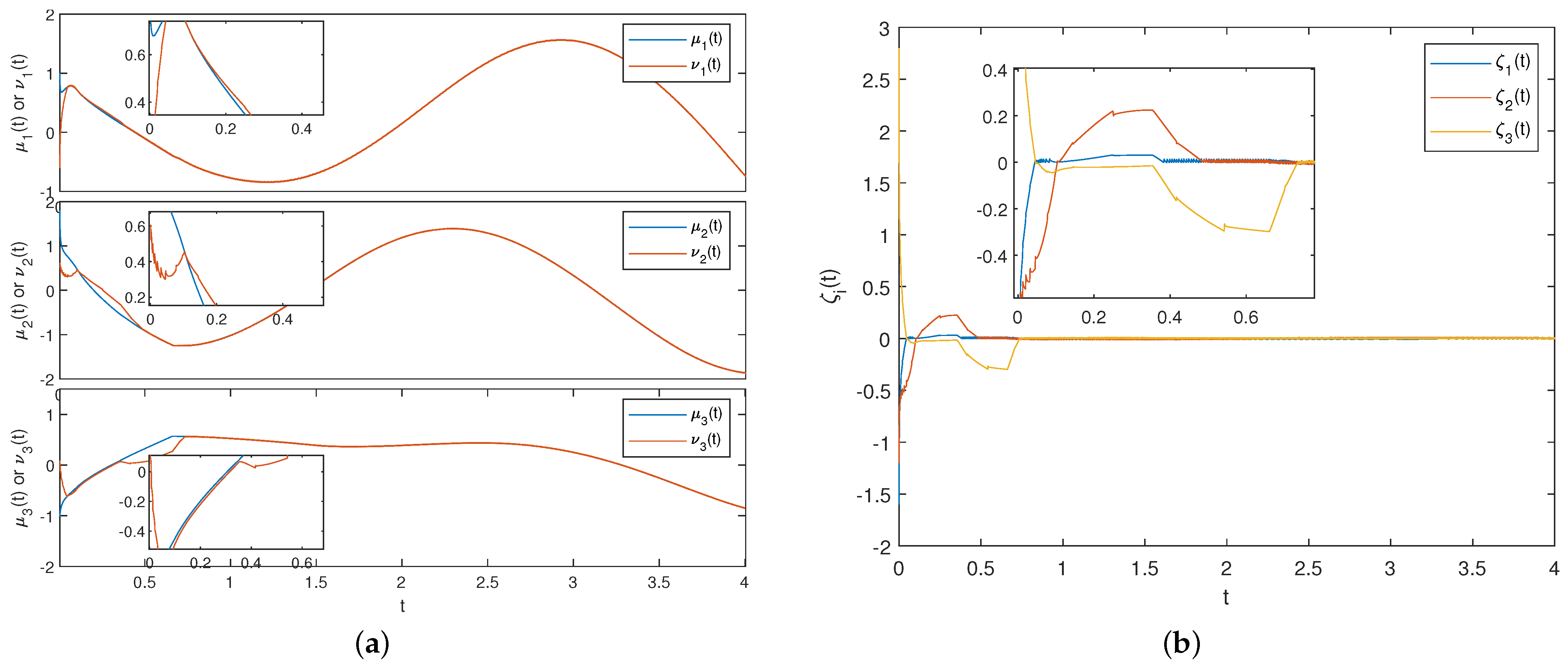

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, H.; Liu, S.; Wu, X.; Sun, J.; Qiao, W. Synchronization of Fractional Delayed Memristive Neural Networks with Jump Mismatches via Event-Based Hybrid Impulsive Controller. Fractal Fract. 2024, 8, 297. https://doi.org/10.3390/fractalfract8050297
Wang H, Liu S, Wu X, Sun J, Qiao W. Synchronization of Fractional Delayed Memristive Neural Networks with Jump Mismatches via Event-Based Hybrid Impulsive Controller. Fractal and Fractional. 2024; 8(5):297. https://doi.org/10.3390/fractalfract8050297
Chicago/Turabian StyleWang, Huiyu, Shutang Liu, Xiang Wu, Jie Sun, and Wei Qiao. 2024. "Synchronization of Fractional Delayed Memristive Neural Networks with Jump Mismatches via Event-Based Hybrid Impulsive Controller" Fractal and Fractional 8, no. 5: 297. https://doi.org/10.3390/fractalfract8050297
APA StyleWang, H., Liu, S., Wu, X., Sun, J., & Qiao, W. (2024). Synchronization of Fractional Delayed Memristive Neural Networks with Jump Mismatches via Event-Based Hybrid Impulsive Controller. Fractal and Fractional, 8(5), 297. https://doi.org/10.3390/fractalfract8050297