Abstract
In recent years, various complex systems and real-world phenomena have been shown to include memory and hereditary properties that change with respect to time, space, or other variables. Consequently, fractional partial differential equations containing variable-order fractional operators have been extensively resorted for modeling such phenomena accurately. In this paper, we consider the two-dimensional fractional cable equation with the Caputo variable-order fractional derivative in the time direction, which is preferable for describing neuronal dynamics in biological systems. A point-wise scheme, namely, the Crank–Nicolson finite difference method, along with a group-wise scheme referred to as the explicit decoupled group method are proposed to solve the problem under consideration. The stability and convergence analyses of the numerical schemes are provided with complete details. To demonstrate the validity of the proposed methods, numerical simulations with results represented in tabular and graphical forms are given. A quantitative analysis based on the CPU timing, iteration counting, and maximum absolute error indicates that the explicit decoupled group method is more efficient than the Crank–Nicolson finite difference scheme for solving the variable-order fractional equation.
Keywords:
variable-order fractional cable equation; finite differences; explicit group methods; stability and convergence; numerical simulations MSC:
35R11; 65M06; 65M12
1. Introduction
The concepts of integral and derivative of the integer order form the backbone of so-called classical calculus. Many quantities such as displacement, velocity, acceleration, jerk, jounce, area and volume can be described precisely based on classical calculus. However, it was discovered that systems of many real-world phenomena cannot be well modeled using classical calculus tools, particularly systems that depict memory effects. This means the case in which the current state of the system depends on all previous ones. For instance, the classical diffusion model is an efficient tool for describing transport processes where the mean square displacement is linear in time , where K is the diffusion constant. However, in complex backgrounds such as porous media and biological systems, it was found that the mean square displacement is no longer linear in time , where is the diffusion exponent. This leads to a new phenomenon known as the anomalous transport process, where the diffusion becomes either slower or faster than the classical model. Obviously, such a process cannot be described adequately by the classical diffusion model. Fractional calculus is a generalization of classical calculus, where the differential and integral operators are allowed to take non-integer values [1]. Due to their non-local property, fractional differential operators serve as powerful tools for modeling complex phenomena that cannot be characterized by classical calculus. In line with that, fractional differential equations have been utilized extensively for modeling seemingly diverse practical problems in widespread fields of science, finance, mechanics, medicine and engineering [2,3]. There are numerous types of fractional-order derivatives that can be found in the literature. The definitions of Riemann–Lioville, Caputo, Grünwald–Letnikov, Riesz, and Hadamard are among the most popular derivatives of fractional calculus. These traditional derivatives are also referred to as power-law type fractional operators. On the other hand, several other kinds of fractional operators that involve Mittag–Leffler and exponential kernel types have been developed recently to overcome the initial singularities of the problems associated with the traditional fractional derivatives. The interested reader may refer to [4] for a full description of the fractional derivatives. Fractional calculus is one of the hottest topics of applied mathematics, where a diverse range of real-world problems can be effectively modeled in the form of fractional differential equations. In 2017, Matlob and Jamali [5] argued that there are no certain rules for selecting the type of fractional derivative suitable for modeling. However, in 2020, Tarasov and Tarasova [6] established a correspondence between the properties of the kernel of the fractional operator and the physical phenomenon under consideration. In the following discussion, some recent applications of fractional-order derivatives are briefly reviewed. In [7], Din et al. investigated the behavior of the climate change phenomenon under the frame of a fractional-order model. The authors employed the Caputo-type fractional derivative and reported that the fractional model generates better results than the integer-order mathematical model. Reyaz et al. [8] utilized the Caputo–Fabrizio fractional derivative to analyze the concentration, temperature, and velocity of a fluid flow with chemical reaction effects and thermal radiation. The authors noticed that the transition between the steady state and the unsteady state of the fluid can be controlled by the fractional-order gamma. In [9], Yang et al. researched the dynamics of the hepatitis B virus (HBV) via a fractional-order biliogical model defined in terms of a Caputo-type fractional derivative. Another fractional epidemic model under the Caputo fractional derivative was presented by Sharif Ullah et al. [10] to study the behavior of the COVID-19 outbreak. Rashid et al. [11] explored childhood diseases and their complications via an SIR model involving the Atangana–Baleanu fractional derivative. In [12], a study on the dynamics of fungicide application was proposed via a fractional mathematical model with the Caputo–Fabrizio operator. In [13], Lauria et al. established a novel intra-hour photovoltaic power forecasting method based on the Caputo-type fractional derivative. In [14], Anwar et al. considered two mathematical fractional models to account for the flow patterns and thermal behavior of a hybrid nanofluid. A comprehensive treatment of the theory, applications, and simulations of fractional derivative-based models can be found in [15].
Roughly speaking, the analytical treatment of fractional derivative-based models that are expressed in terms of fractional partial differential equations (FPDEs) is not an easy task [16]. Therefore, numerical methods have attracted much attention for dealing with FPDEs. The list of numerical methods that are available in the literature includes the finite difference method, finite element method [17,18], finite volume method, spectral method, collocation method, reproducing kernel method, mesh-free method, domain decomposition method, etc.
However, it has been verified that FPDEs with fixed fractional orders are not adequate for describing complex phenomena that exhibit variable memory with respect to time and/or space variables [19]. As a result, a new field of variable-order (VO) fractional calculus has emerged. It was Samko and Ross [20] who paved the way for this interesting field by generalizing the Riemann–Liouville and Marchaud fractional derivatives to their VO sense in 1993. Thereafter, other types of VO fractional differential operators were suggested by Lorenzo, Hartley and Coimbra [21,22,23]. Today, various definitions of VO fractional derivatives with specific meanings are available to handle real-world problems that depict systems with varying memory. The merits of using VO fractional derivatives instead of their corresponding constant-order (CO) fractional derivatives are illustrated in [24]. Another study revealed that it is much easier to describe the physical meaning of VO fractional operators [25]. Consequently, VO FPDEs have attracted the attention of numerous researchers and scholars as accurate models for describing a large variety of phenomena in various branches of science and engineering, such as mechanics, viscoelasticity, anomalous diffusion, wave propagation, control theory, ecology, and many others. Similar to the CO FPDEs, it is difficult to solve VO FPDEs analytically, and numerical techniques are very often resorted to, for instance, see [26,27,28,29]. A profound discussion of the definitions, applications, and numerical simulations of the VO fractional operators can be seen in the insightful review papers [30,31].
In this work, we consider the numerical solution of the non-homogeneous initial-boundary value problem of the two-dimensional variable-order fractional cable equation (VO FCE) in the form,
with the initial-boundary conditions,
Here is the domain, and is its boundary, , and are positive constants. are known functions, and is the unknown function. and is the VO Caputo fractional derivative of u defined as,
The FCE can be viewed as a fundamental biological model that accounts for the voltage difference between the cell membrane and neurons. It was shown that the electrodiffusion of ions in spiny neuronal dendrites follows an anomalous pattern that cannot be captured by the classical cable equation [32]. In 2008, Henry and Langlands [33] introduced the FCE for the first time to study the anomalous diffusion phenomenon in the nerve cell. Since then, FCE has been employed to report on the behavior of different phenomena occurring in several fields, such as neuronal dynamics, control theory, the heterogeneous nature of neuronal tissue, and viscoelastic materials (see [34] and references cited therein). Consequently, the solution of FCE is of practical importance in different fields of application.
In the past few years, several numerical researchers have contributed significantly to solving FCEs since exact analytical solutions are mostly difficult to obtain. Here, we present the recent numerical treatments of the FCE. In [35], Bhrawy and Zaky proposed a spectral collocation method for solving the one-dimensional and two-dimensional VO FCE. In [36], Irandoust-Pakchin et al. generalized the application of the Chebyshev cardinal functions method for solving the one-dimensional VO FCE. In [37], Nagy and Sweilam researched a Crank–Nicolson numerical scheme with stability analysis to solve the one-dimensional VO FCE. In [38], Liu et al. presented finite difference/element approximations, which are formulated utilizing some second-order difference schemes in time and the Galerkin finite element method in space for solving one-dimensional and two-dimensional CO FCE. Stability and convergence analyses were also discussed. In [39], Sweilam and AL-Mekhlafi developed a non-standard compact finite difference scheme to solve the two-dimensional CO FCE. The fractional derivative is defined in the Atangana–Baleanu–Caputo sense, and the truncation error of their method is analyzed. An extended cubic B-Spline collocation method with stability analysis was introduced in [40] to solve the one-dimensional CO FCE. Salama and Ali [41] proposed a fast hybrid method based on a combination of the Laplace transform technique and finite difference approximations to account for the numerical solution of the two-dimensional CO FCE. A meshless numerical scheme with rigorous error analysis for the two-dimensional CO FCE was reported in [42]. Oruç [43] suggested a local hybrid kernel meshless method to deal with the two-dimensional CO FCE. Zheng et al. [44] utilized a finite difference scheme in the temporal direction and a Legendre spectral method in the spatial direction to solve the two-dimensional distributed-order FCE. The theoretical stability and convergence were established in their work. Kumar and Baleanu [45] derived an operational matrix-based numerical method for the solution of the two-dimensional CO FCE. Li and Rui [46] scrutinized an unconditionally stable block-centered finite difference method for solving the two-dimensional CO FCE. Mohebbi and Saffarian [47] applied second-order difference schemes for time discretization and a meshless approach for space discretization in solving the two-dimensional VO FCE. The theoretical stability and convergence have not been investigated. Yin et al. [48] applied the FBT- and FBN- methods proposed in [49] to solve the one-dimensional and two-dimensional CO FCE. The authors gave a detailed numerical analysis of stability and convergence. Sweilam et al. [50] analyzed the two-dimensional FCE and fractional reaction sub-diffusion equation by the weighted average finite difference method. The Sinc–Bernoulli collocation method was considered by Moshtaghi and Saadatmandi [51] to study the one-dimensional CO FCE. Mittal et al. [34] introduced a time–space Jacobi pseudospectral method for the numerical solution of the two-dimensional FCE. Stability, uniqueness, and error analysis were also given in their work. Li and Li [52] solved the two-dimensional CO FCE using a meshless finite point method. Other research work concerned with the numerical analysis of the CO FCE can be seen in [53,54,55,56].
Group-wise iterative methods, usually called explicit group methods, can be thought of as efficient alternatives to their corresponding point-wise iterative methods for solving various types of initial-boundary value problems. In summary, explicit group methods have some salient advantages, such as stability, being easy to implement, forming sparse algebraic systems, accelerating the rate of convergence, reducing arithmetic computations per iteration, and extension to multi-dimensional problems. In [57,58,59,60,61,62], different types of explicit group methods were developed based on standard and skewed difference schemes for solving a variety of CO FPDEs.
Based on the previous discussion, much research has been reported on the CO FCE, whereas numerical works on FCE involving VO fractional derivatives are very few and still far from adequate. In addition, to the best of our knowledge, VO FCE solved by utilizing explicit group methods has not emerged in the literature. Motivated by this, the aim of the current paper is to present a group-wise iterative method, namely the explicit decoupled group method (EDGM) for solving the two-dimensional VO FCE (1). The said method inherits the advantages of the family of explicit group methods for being accurate, stable, efficient, and extendable for multi-dimensional problems. The EDGM is established using Taylor series expansion on a skewed grid obtained by rotating the x-y axes 45° clockwise. Furthermore, we derive a point-wise iterative method, namely, the Crank–Nicolson finite difference method (CN–FDM), as a reference solution algorithm for the VO FCE. The aspects of stability, convergence, and computational complexity in terms of computing time and iteration count are given. The tabulated and graphical results extracted from numerical simulations show that the presented methods have comparable accuracy, while the EDGM results in faster simulations with lower computational complexity compared to the CN–FDM.
The plan of our paper is as follows. We construct the CN–FDM in Section 2 followed by the EDGM in Section 3. Then, Section 4 and Section 5 are devoted to the stability and convergence analyses of the proposed methods, respectively. Some numerical simulations to validate the accuracy and efficiency of the CN–FDM and EDGM are given in Section 6. Finally, the current work ends with a brief conclusion in Section 7.
2. Formulation of the Crank–Nicolson Finite Difference Method (CN–FDM)
In this section, each of the VO time fractional derivatives together with the spatial differential operators in Equation (1) are discretized to construct the CN–FDM. For this purpose, the following notations are defined as,
Here, N, and are positive integers and denote the number of equidistant partitions in time and space directions, respectively. , and are the spatial and temporal step sizes, respectively. In addition, define
as the solution value located at the i-th and j-th coordinates and k-th time level. Obviously, represents the given initial condition, while refers to the unknown solution values for .
The approximate formula for the Caputo VO time fractional derivative () at the time node can be obtained by utilizing the following discretization scheme [63]:
where
and is the local truncation error bounded by,
The right-hand side of Equation (1) can be discretized by applying central difference approximations at the time levels k and , and taking the average as follows:
Omitting the error terms and replacing with its approximation , and upon simplification, the CN–FDM for solving the Dirichlet-type boundary value problem (1)–(3) is obtained as follows:
Let
The fully discrete scheme can be expressed in matrix form as,
where A and B are pentadiagonal matrices defined as,
,
where
In view of the structure of the above matrices, it can be seen that A is a strictly diagonally dominant matrix. This means that the matrix A is non-singular and the fully discrete scheme defined in Equation (7) has a unique solution. Figure 1 depicts the computational molecule of the CN–FDM with . In practice, the CN–FDM is combined with the Gauss–Seidel iterative scheme to generate iterations on all ⧫ points at each time level until convergence is achieved. This point-wise iterative method terminates when the targeted time level N is reached.

Figure 1.
Computational molecule of the CN–FDM with .
In order to accelerate the rate of convergence, a new group-wise iterative method, namely the EDGM, is introduced in the next next section.
3. Formulation of the Explicit Decoupled Group Method (EDGM)
The idea of group-wise iterative methods is to generate iterations on fixed-size groups of points rather than on a single point in point-oriented iterative methods. It has been proven that the iteration matrices of group-wise iterative methods have better spectral properties than those of point-wise iterative methods, which makes the former methods computationally superior to the latter ones. In this section, we present the construction of the EDGM for solving the VO FCE (1). To this end, a new approximation scheme based on the skewed grid for the mentioned equation is derived. This will result in the following skewed CN–FDM of the form,
After simplification and disregarding the error terms and utilizing as an approximation to , the following expression is obtained:
where , .
Next, consider the grid points of the discretized solution domain that are located at the coordinates of , , , . By applying the skewed difference formula (9) to any group of four points located at the said spatial coordinates, the following system of equations is obtained:
where
and
With reference to Figure 2, the computational molecule of the EDGM is obtained by arranging the nodal points of the solution domain into groups of four points. One can easily verify that the execution of Equation (11) corresponds to the solution values located at the ⧫ points, whereas the implementation of Equation (12) corresponds to the solution outcomes placed at the ◊ points. Therefore, iterative computations can be performed independently on either one type of point until convergence is attained. Regardless of the selected point type that takes part in the iterative process, the solution values located at the remaining grid points will be evaluated directly once using the CN–FDM given in Section 2.
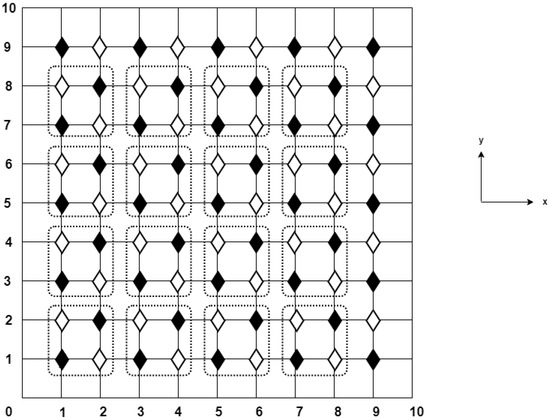
Figure 2.
Computational molecule of the EDGM with .
In this work, the EDGM is combined with the Gauss–Seidel iterative solver to generate iterations at the ⧫ points. Once convergence is achieved, the solution outcomes at the residual ◊ points will be calculated directly once using Equation (7). The prescribed process is terminated when the targeted time level is reached. Compared to the point-wise iterative method presented in Section 2, the EDGM is expected to result in faster simulations since only half of the nodal points are involved in the iteration process, which reduces the computational complexity effectively.
4. Stability Analysis
In this section, the stability of the proposed discrete numerical schemes is investigated via the technique of von Neumann analysis. As a start, the following lemma is introduced.
Lemma 1
([63]). Let , , be the coefficients defined in Equation (7), then the following hold:
- (i)
- (ii)
- .
Suppose that and are the approximate solutions of Equations (7) and (9), respectively. Then, the errors are given by
Similarly, utilizing Equation (14), the round-off error equation for the numerical scheme (9) is in the form
Then, the Fourier series expansions of and are defined as
where and and have the following form:
With the help of the norm and Parseval’s equality, we obtain
Lemma 2.
Suppose that are the solutions of Equation (22) and , then we have
Proof.
To complete the proof, mathematical induction is utilized. First, choose , and we obtain
Since , and are non-negative constants, then
Now, assume that , . We prove it is true for . With the help of Equation (22) and Lemma 1, we obtain
If , then
If , then
Here,
□
Theorem 1.
Given that , the fully discrete numerical scheme (7) is stable.
Proof.
In view of lemma 2 and the Parseval equality, it follows that,
from which we obtain
□
Lemma 3.
Suppose that are the solutions of Equation (24) and , then we have
Proof.
First, putting in Equation (24), we obtain
Next, assume that , . We prove it is true for . With the help of Equation (24) and Lemma 1, we obtain
If , then
If , then
Here,
□
Theorem 2.
Given that , the fully discrete numerical scheme (9) is stable.
Proof.
Utilizing Lemma 3 and Parseval equality, we obtain
From the above result, it immediately follows,
□
5. Convergence Analysis
In this section, we intend to analyze the convergence of the proposed numerical schemes.
Subtracting Equation (7) from Equation (6), the error equation can be obtained as
in which
and is the truncation error at the nodal point . Henceforward, C is a constant that may take various values at different positions. Based on Equation (6), we have
where
The Fourier series expansions of and can be written as
in which
Based on the norm and Parseval’s equality, we have
Next, assume that the solutions of Equation (26) are as follows:
Setting (31) into (26) and simplifying the result, we obtain
where and are as given in Equation (22).
Lemma 4.
Suppose that are the solutions of Equation (32) and , then we have
Proof.
The proof is completed by mathematical induction. First, letting in Equation (31) and observing that , we obtain
Next, suppose that
Setting in Equation (31) and utilizing Lemma 1, we obtain
If , then
If , then
Here,
Therefore, we have
□
Theorem 3.
Given that , the fully discrete numerical scheme (7) is convergent, and the convergence order is .
Proof.
Using Equation (28), we obtain
where as . □
Theorem 4.
The fully discrete numerical scheme (9) is convergent and the convergence order is .
Proof.
The proof can be established in a similar way to Theorem 3. □
6. Numerical Results and Discussion
In this part, we investigate the viability, correctness and efficiency of the proposed group-wise EDGM in comparison to the point-wise CN–FDM presented in Section 2. To this end, two numerical simulations accompanied by their computational outputs in terms of CPU time , number of iterations and maximum absolute error are provided in tabular and graphical forms. The Gauss–Seidel iterative scheme with stopping criteria and the norm is utilized to solve the linear systems. All numerical experiments are conducted using Julia programming language and run on a PC with the configuration: Intel(R) Core(TM) i7-8550U and 8 GB of RAM. In the runs, a uniform grid spacing is used in the horizontal and vertical spatial directions, while the between the exact and numerical solutions is computed as
Example 1.
In the first example, we consider the two-dimensional variable-order fractional cable equation:
with the initial-boundary conditions
where , and the source term is given by
The exact analytical solution of the stated problem is of the form
The considered problem is solved for different choices of and varying spatial and temporal step sizes. The CPU times, iteration numbers, and numerical errors in solving Example 1 are recorded in Table 1 and Table 2. From these tables, it is observed that the EDGM and the CN–FDM can approximate the analytical solution accurately. The results also show that the EDGM outperforms the CN–FDM in terms of iteration counting and CPU timing as well. Figure 3a,b show 2D plots of CPU time when and , respectively, whereas Figure 4a,b show 2D plots of iteration numbers when and . From these figures, it is evident that the EDGM requires fewer iterations and consumes less computing time in handling the fractional problem compared to the CN–FDM. These improvements in time consumption and iteration count indicate that the EDGM is computationally superior to the CN–FDM. Figure 5 presents a graphical representation of the exact solution and the numerical solutions of the proposed methods at y = 0.5, , , and , 0.5, 0.75 and 1. As seen in this figure, the numerical solutions match well with the exact solution of the problem under consideration. The behavior of the numerical errors using the CN–FDM and the EDGM is highlighted in Figure 6 at , , and , from which it is indicated that the numerical solutions are in good agreement with the exact solution.

Table 1.
Comparison of numerical results of the proposed methods for Example 1 at , and various choices of .

Table 2.
Comparison of numerical results of the proposed methods for Example 1 at , and different choices of .
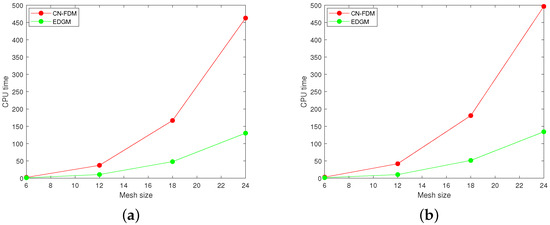
Figure 3.
Graphical comparison of CPU time for the CN–FDM and the EDGM in Example 1. (a) ; (b) .
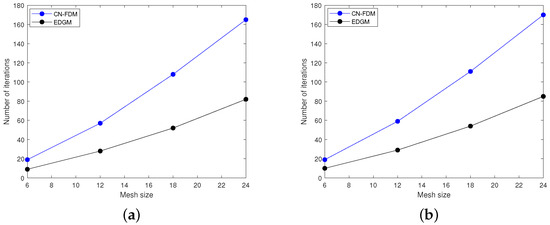
Figure 4.
Graphical comparison of iterations number for the CN–FDM and the EDGM in Example 1. (a) ; (b) .
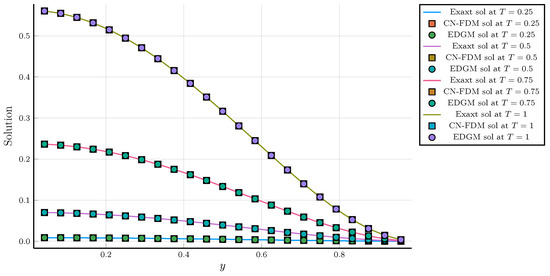
Figure 5.
Graphical comparison of the exact solution and numerical solutions obtained using the CN–FDM and the EDGM in Example 1 at , , and .
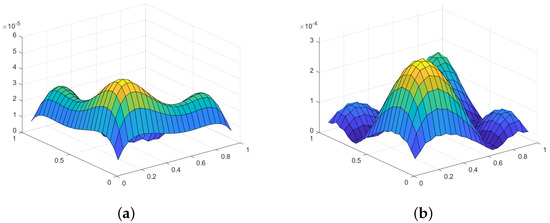
Figure 6.
Graphical representation of absolute errors for the CN–FDM and the EDGM in Example 1 at , and . (a) CN–FDM; (b) EDGM.
Example 2.
In this example, the following two-dimensional variable-order fractional cable equation is considered:
subject to the initial-boundary conditions,
where with the source term defined as,
The exact analytical solution of the current problem is
Table 3 lists the numerical results of solving Example 2 using the EDGM and the CN–FDM for various choices of , h and . The corresponding results show that both EDGM and CN–FDM produce precise numerical solutions, which makes them feasible in terms of accuracy. It is well known that increasing the iteration’s number of a numerical algorithm will result in larger computational complexity, which ultimately leads to slower convergence. Figure 7 and Figure 8 establish a comparison between the EDGM and the CN–FDM in terms of CPU timing and iteration counting, respectively. One can see that the graphs of CPU timing are consistent with those of iteration counting. Obviously, the EDGM provides much efficient simulations in terms of CPU time as well as iteration numbers compared to the CN–FDM. Figure 9 demonstrates a comparison between the exact solution and numerical solutions of the EDGM and CN–FDM at , , , and , 0.5, 0.75 and 1. Figure 10 sketches the maximum errors for the EDGM and the CN–FDM at , , and . As these figures show, the proposed methods generate numerical solutions that are in good agreement with the exact solution of the given variable-order fractional problem.

Table 3.
Comparison of numerical results of the proposed methods for Example 2 at , and various choices of .
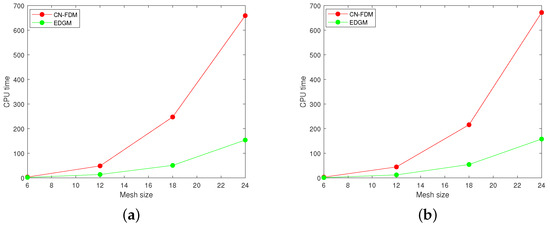
Figure 7.
Graphical comparison of CPU time for the CN–FDM and the EDGM in Example 2. (a) ; (b) .
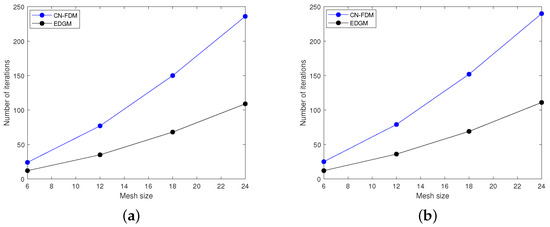
Figure 8.
Graphical comparison of iterations number for the CN–FDM and the EDGM in Example 2. (a) ; (b) .
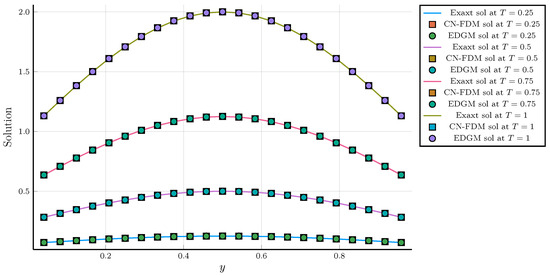
Figure 9.
Graphical comparison of the exact solution and numerical solutions obtained using the CN–FDM and the EDGM in Example 2 at , , and .
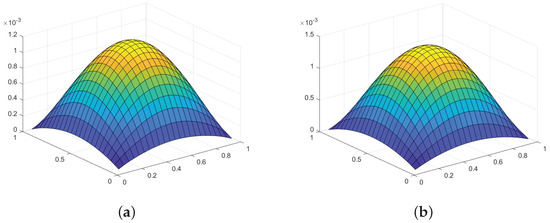
Figure 10.
Graphical representation of absolute errors for the CN–FDM and the EDGM in Example 2 at , and . (a) CN–FDM; (b) EDGM.
In order to quantify the computational efficiency of the EDGM, the improvement percentages in aspects of CPU timing and iteration counting for solving Examples 1 and 2 are reported in Table 3 and Table 4, respectively. For instance, the improvement percentages of CPU timing and iteration counting for Example 1 at indicate that the EDGM has reduced the CPU time approximately by 52.01–79.40% and the number of iterations by 53.91–54.67% compared to the CN–FDM. The improvement percentages of the EDGM for solving Examples 1 and 2 at other values of can be drawn similarly from Table 3 and Table 4.

Table 4.
The improvement percentages of the EDGM compared to the CN–FDM for various choices of in Example 1.
7. Conclusions
In this paper, a point-wise CN–FDM and a group-wise EDGM are designed to deal with the numerical solution of the two-dimensional variable-order fractional cable equation. The CN–FDM and the EDGM are developed based on finite difference approximations derived on the standard and skewed grids, respectively. The stability and convergence of the proposed methods are proved via the technique of von Neumann analysis. The proposed numerical schemes are implemented, and the computational outputs are presented in tabular and graphical forms, from which we observe that the numerical solutions are in good agreement with the exact analytical solutions (see Table 1, Table 2 and Table 3 and Figure 5, Figure 6, Figure 9 and Figure 10). Furthermore, as can be clearly seen from Table 4 and Table 5 and Figure 3, Figure 4, Figure 7 and Figure 8, the EDGM is shown to require cheap computational complexity in terms of CPU timing and iteration counting compared to the CN–FDM. In fact, the obtained numerical results in Table 1 and Table 3 reveal that the EDGM achieves improved percentages 22.14–79.40% in CPU timing and 42.85–55.13% in iteration counting as compared to the CN–FDM. As future works, the EDGM can be constructed based on higher-order discrete schemes to achieve better accuracy. In addition, the EDGM can be implemented on parallel computers and extended to solve other types of high-dimensional variable-order fractional problems.

Table 5.
The improvement percentages of the EDGM compared to the CN–FDM for various choices of in Example 2.
Funding
The author acknowledges the funding support provided by the Deanship of Research Oversight and Coordination (DROC) at King Fahd University of Petroleum & Minerals (KFUPM), Kingdom of Saudi Arabia.
Data Availability Statement
Data is contained within the article.
Conflicts of Interest
The author declares no conflict of interests.
References
- Machado, J.T.; Kiryakova, V.; Mainardi, F. Recent history of fractional calculus. Commun. Nonlinear Sci. Numer. Simul. 2011, 16, 1140–1153. [Google Scholar] [CrossRef]
- Sun, H.; Zhang, Y.; Baleanu, D.; Chen, W.; Chen, Y. A new collection of real world applications of fractional calculus in science and engineering. Commun. Nonlinear Sci. Numer. Simul. 2018, 64, 213–231. [Google Scholar] [CrossRef]
- Dalir, M.; Bashour, M. Applications of fractional calculus. Appl. Math. Sci. 2010, 4, 1021–1032. [Google Scholar]
- Teodoro, G.S.; Machado, J.T.; De Oliveira, E.C. A review of definitions of fractional derivatives and other operators. J. Comput. Phys. 2019, 388, 195–208. [Google Scholar] [CrossRef]
- Matlob, M.A.; Jamali, Y. The concepts and applications of fractional order differential calculus in modeling of viscoelastic systems: A primer. Crit. Rev. Biomed. Eng. 2019, 47, 249–276. [Google Scholar] [CrossRef]
- Tarasov, V.E.; Tarasova, S.S. Fractional derivatives and integrals: What are they needed for? Mathematics 2020, 8, 164. [Google Scholar] [CrossRef]
- Din, A.; Khan, F.M.; Khan, Z.U.; Yusuf, A.; Munir, T. The mathematical study of climate change model under nonlocal fractional derivative. Partial Differ. Equ. Appl. Math. 2022, 5, 100204. [Google Scholar] [CrossRef]
- Reyaz, R.; Mohamad, A.Q.; Lim, Y.J.; Saqib, M.; Shafie, S. Analytical solution for impact of Caputo-Fabrizio fractional derivative on MHD Casson fluid with thermal radiation and chemical reaction effects. Fractal Fract. 2022, 6, 38. [Google Scholar] [CrossRef]
- Yang, X.; Su, Y.; Yang, L.; Zhuo, X. Global analysis and simulation of a fractional order HBV immune model. Chaos Solitons Fractals 2022, 154, 111648. [Google Scholar] [CrossRef]
- Ullah, M.S.; Higazy, M.; Kabir, K.A. Modeling the epidemic control measures in overcoming covid-19 outbreaks: A fractional-order derivative approach. Chaos Solitons Fractals 2022, 155, 111636. [Google Scholar] [CrossRef]
- Rashid, S.; Jarad, F.; Bayones, F.S. On new computations of the fractional epidemic childhood disease model pertaining to the generalized fractional derivative with nonsingular kernel. AIMS Math. 2022, 7, 4552–4573. [Google Scholar] [CrossRef]
- Kumar, P.; Erturk, V.S.; Govindaraj, V.; Kumar, S. A fractional mathematical modeling of protectant and curative fungicide application. Chaos Solitons Fractals X 2022, 8, 100071. [Google Scholar] [CrossRef]
- Lauria, D.; Mottola, F.; Proto, D. Caputo derivative applied to very short time photovoltaic power forecasting. Appl. Energy 2022, 309, 118452. [Google Scholar] [CrossRef]
- Anwar, T.; Kumam, P.; Thounthong, P. A comparative fractional study to evaluate thermal performance of NaAlg–MoS2–Co hybrid nanofluid subject to shape factor and dual ramped conditions. Alex. Eng. J. 2022, 61, 2166–2187. [Google Scholar] [CrossRef]
- Chen, W.; Sun, H.; Li, X. Fractional Derivative Modeling in Mechanics and Engineering; Springer: Beijing, China, 2022. [Google Scholar]
- Zhuang, P.; Liu, F.; Turner, I.; Anh, V. Galerkin finite element method and error analysis for the fractional cable equation. Numer. Algorithms 2016, 72, 447–466. [Google Scholar] [CrossRef]
- Kumar, L.; Sista, S.G.; Sreenadh, K. Galerkin Finite element analysis of time-fractional integro-differential equation of Kirchhoff type for non-homogeneous materials. Math. Methods Appl. Sci. 2024, 74, 2120–2153. [Google Scholar] [CrossRef]
- Guan, Z.; Wang, J.; Liu, Y.; Nie, Y. Unconditional convergence analysis of two linearized Galerkin FEMs for the nonlinear time-fractional diffusion-wave equation. Results Appl. Math. 2023, 19, 100389. [Google Scholar] [CrossRef]
- Tural-Polat, S.N.; Dincel, A.T. Numerical solution method for multi-term variable order fractional differential equations by shifted Chebyshev polynomials of the third kind. Alex. Eng. J. 2022, 61, 5145–5153. [Google Scholar] [CrossRef]
- Samko, S.G.; Ross, B. Integration and differentiation to a variable fractional order. Integral Transform. Spec. Funct. 1993, 1, 277–300. [Google Scholar] [CrossRef]
- Lorenzo, C.F.; Hartley, T.T. Initialization, conceptualization, and application in the generalized (fractional) calculus. Crit. Rev. Biomed. Eng. 2007, 35, 447–553. [Google Scholar] [CrossRef]
- Lorenzo, C.F.; Hartley, T.T. Variable order and distributed order fractional operators. Nonlinear Dyn. 2002, 29, 57–98. [Google Scholar] [CrossRef]
- Coimbra, C.F. Mechanics with variable-order differential operators. Ann. Phys. 2003, 12, 692–703. [Google Scholar] [CrossRef]
- Sun, H.; Chen, W.; Wei, H.; Chen, Y. A comparative study of constant-order and variable-order fractional models in characterizing memory property of systems. Eur. Phys. J. Spec. Top. 2011, 193, 185–192. [Google Scholar] [CrossRef]
- Umarov, S.; Steinberg, S. Variable order differential equations with piecewise constant order-function and diffusion with changing modes. Z. Anal. Ihre Anwendungen 2009, 28, 431–450. [Google Scholar] [CrossRef]
- Zaky, M.A.; Ezz-Eldien, S.S.; Doha, E.H.; Tenreiro Machado, J.A.; Bhrawy, A.H. An efficient operational matrix technique for multidimensional variable-order time fractional diffusion equations. J. Comput. Nonlinear Dyn. 2016, 11, 061002. [Google Scholar] [CrossRef]
- Abdelkawy, M.A.; Zaky, M.A.; Bhrawy, A.H.; Baleanu, D. Numerical simulation of time variable fractional order mobile-immobile advection-dispersion model. Rom. Rep. Phys. 2015, 67, 773–791. [Google Scholar]
- Ali, U.; Naeem, M.; Abdullah, F.A.; Wang, M.K.; Salama, F.M. Analysis and implementation of numerical scheme for the variable-order fractional modified sub-diffusion equation. Fractals 2022, 30, 2240253. [Google Scholar] [CrossRef]
- Salama, F.M.; Fairag, F. On numerical solution of two-dimensional variable-order fractional diffusion equation arising in transport phenomena. AIMS Math. 2024, 9, 340–370. [Google Scholar] [CrossRef]
- Sun, H.; Chang, A.; Zhang, Y.; Chen, W. A review on variable-order fractional differential equations: Mathematical foundations, physical models, numerical methods and applications. Fract. Calc. Appl. Anal. 2019, 22, 27–59. [Google Scholar] [CrossRef]
- Patnaik, S.; Hollkamp, J.P.; Semperlotti, F. Applications of variable-order fractional operators: A review. Proc. R. Soc. A 2020, 476, 20190498. [Google Scholar] [CrossRef]
- Sweilam, N.; Khader, M.; Adel, M. Numerical simulation of fractional cable equation of spiny neuronal dendrites. J. Adv. Res. 2014, 5, 253–259. [Google Scholar] [CrossRef]
- Henry, B.; Langlands, T.; Wearne, S. Fractional cable models for spiny neuronal dendrites. Phys. Rev. Lett. 2008, 100, 128103. [Google Scholar] [CrossRef]
- Mittal, A.K.; Balyan, L.K.; Panda, M.K.; Shrivastava, P.; Singh, H. Pseudospectral analysis and approximation of two-dimensional fractional cable equation. Math. Methods Appl. Sci. 2022, 45, 8613–8630. [Google Scholar] [CrossRef]
- Bhrawy, A.; Zaky, M. Numerical simulation for two-dimensional variable-order fractional nonlinear cable equation. Nonlinear Dyn. 2015, 80, 101–116. [Google Scholar] [CrossRef]
- Irandoust-Pakchin, S.; Abdi-Mazraeh, S.; Khani, A. Numerical solution for a variable-order fractional nonlinear cable equation via Chebyshev cardinal functions. Comput. Math. Math. Phys. 2017, 57, 2047–2056. [Google Scholar] [CrossRef]
- Nagy, A.; Sweilam, N. Numerical simulations for a variable order fractional cable equation. Acta Math. Sci. 2018, 38, 580–590. [Google Scholar] [CrossRef]
- Liu, Y.; Du, Y.; Li, H.; Liu, F.; Wang, Y. Some second-order schemes combined with finite element method for nonlinear fractional cable equation. Numer. Algorithms 2019, 80, 533–555. [Google Scholar] [CrossRef]
- Sweilam, N.; Al-Mekhlafi, S. A novel numerical method for solving the 2-D time fractional cable equation. Eur. Phys. J. Plus 2019, 134, 323. [Google Scholar] [CrossRef]
- Akram, T.; Abbas, M.; Ismail, A.I. Numerical solution of fractional cable equation via extended cubic b-spline. AIP Conf. Proc. 2019, 2138, 030004. [Google Scholar]
- Salama, F.M.; Ali, N.H.M. Fast O(N) hybrid method for the solution of two dimensional time fractional cable equation. Compusoft 2019, 8, 3453–3461. [Google Scholar]
- Nikan, O.; Golbabai, A.; Machado, J.; Nikazad, T. Numerical approximation of the time fractional cable model arising in neuronal dynamics. Eng. Comput. 2022, 38, 155–173. [Google Scholar] [CrossRef]
- Oruç, Ö. A local hybrid kernel meshless method for numerical solutions of two-dimensional fractional cable equation in neuronal dynamics. Numer. Methods Partial Differ. Equ. 2020, 36, 1699–1717. [Google Scholar] [CrossRef]
- Zheng, R.; Liu, F.; Jiang, X.; Turner, I.W. Finite difference/spectral methods for the two-dimensional distributed-order time-fractional cable equation. Comput. Math. Appl. 2020, 80, 1523–1537. [Google Scholar] [CrossRef]
- Kumar, S.; Baleanu, D. Numerical solution of two-dimensional time fractional cable equation with Mittag-Leffler kernel. Math. Methods Appl. Sci. 2020, 43, 8348–8362. [Google Scholar] [CrossRef]
- Li, X.; Rui, H. Stability and convergence based on the finite difference method for the nonlinear fractional cable equation on non-uniform staggered grids. Appl. Numer. Math. 2020, 152, 403–421. [Google Scholar] [CrossRef]
- Mohebbi, A.; Saffarian, M. Implicit rbf meshless method for the solution of two-dimensional variable order fractional cable equation. J. Appl. Comput. Mech. 2020, 6, 235–247. [Google Scholar]
- Yin, B.; Liu, Y.; Li, H.; Zhang, Z. Finite element methods based on two families of second-order numerical formulas for the fractional cable model with smooth solutions. J. Sci. Comput. 2020, 84, 2. [Google Scholar] [CrossRef]
- Yin, B.; Liu, Y.; Li, H.; Zhang, Z. Two families of novel second-order fractional numerical formulas and their applications to fractional differential equations. arXiv 2019, arXiv:1906.01242. [Google Scholar]
- Sweilam, N.; Ahmed, S.; Adel, M. A simple numerical method for two-dimensional nonlinear fractional anomalous sub-diffusion equations. Math. Methods Appl. Sci. 2021, 44, 2914–2933. [Google Scholar] [CrossRef]
- Moshtaghi, N.; Saadatmandi, A. Numerical solution of time fractional cable equation via the sinc-Bernoulli collocation method. J. Appl. Comput. Mech. 2021, 7, 1916–1924. [Google Scholar]
- Li, X.; Li, S. A finite point method for the fractional cable equation using meshless smoothed gradients. Eng. Anal. Bound. Elem. 2022, 134, 453–465. [Google Scholar] [CrossRef]
- Liu, Z.; Cheng, A.; Li, X. A fast-high order compact difference method for the fractional cable equation. Numer. Methods Partial Differ. Equ. 2018, 34, 2237–2266. [Google Scholar] [CrossRef]
- Salama, F.M.; Ali, N.H.M.; Abd Hamid, N.N. Efficient hybrid group iterative methods in the solution of two-dimensional time fractional cable equation. Adv. Differ. Equ. 2020, 2020, 257. [Google Scholar] [CrossRef]
- Khan, M.A.; Alias, N.; Khan, I.; Salama, F.M.; Eldin, S.M. A new implicit high-order iterative scheme for the numerical simulation of the two-dimensional time fractional cable equation. Sci. Rep. 2023, 13, 1549. [Google Scholar] [CrossRef]
- Ali, U.; Naeem, M.; Ganie, A.H.; Fathima, D.; Salama, F.M. Numerical approach for the fractional order cable model with theoretical analyses. Front. Phys. 2023, 11, 1160767. [Google Scholar] [CrossRef]
- Salama, F.M.; Balasim, A.T.; Ali, U.; Khan, M.A. Efficient numerical simulations based on an explicit group approach for the time fractional advection–diffusion reaction equation. Comput. Appl. Math. 2023, 42, 157. [Google Scholar] [CrossRef]
- Abdi, N.; Aminikhah, H.; Sheikhani, A. High-order rotated grid point iterative method for solving 2D time fractional telegraph equation and its convergence analysis. Comput. Appl. Math. 2021, 40, 54. [Google Scholar] [CrossRef]
- Salama, F.M.; Ali, U.; Ali, A. Numerical solution of two-dimensional time fractional mobile/immobile equation using explicit group methods. Int. J. Appl. Comput. Math. 2022, 8, 188. [Google Scholar] [CrossRef]
- Salama, F.M.; Hamid, N.N.A.; Ali, N.H.M.; Ali, U. An efficient modified hybrid explicit group iterative method for the time-fractional diffusion equation in two space dimensions. AIMS Math. 2022, 7, 2370–2392. [Google Scholar] [CrossRef]
- Salama, F.M.; Hamid, N.N.A.; Ali, U.; Ali, N.H.M. Fast hybrid explicit group methods for solving 2D fractional advection-diffusion equation. AIMS Math. 2022, 7, 15854–15880. [Google Scholar] [CrossRef]
- Khan, M.A.; Ali, N.H.M.; Hamid, N.N.A. A new fourth-order explicit group method in the solution of two-dimensional fractional Rayleigh–Stokes problem for a heated generalized second-grade fluid. Adv. Differ. Equ. 2020, 2020, 598. [Google Scholar] [CrossRef]
- Liu, Z.; Li, X. A Crank–Nicolson difference scheme for the time variable fractional mobile–immobile advection–dispersion equation. J. Appl. Math. Comput. 2018, 56, 391–410. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).