Volatility Analysis of Financial Time Series Using the Multifractal Conditional Diffusion Entropy Method
Abstract
1. Introduction
2. Methodology
2.1. Diffusion Entropy Analysis (DEA)
- Transform the series into a diffusion process. Consider the series such that it can be written as:where and is the time scale. The matrix defined ascan be regarded as sub-sequences for any given diffusion time t with initial state . Next, construct a diffusion trajectory for each of these sub-sequences using the stochastic processwhere is the new position of the jth particle in the diffusion process.
- Compute the diffusion entropy. First, partition the x-axis into bin size and assume that represents the number of particles falling in each bin at time t where .
- Determine the optimal bin size B. We note that there is no “best” number of bins, and different bin sizes B reveal different data features. Wider bins are utilized when the density of the underlying data points is low, reducing sampling-related noise. Conversely, narrower bins are employed when the density is high, enhancing the precision of density estimation. Hence, it proves advantageous to adjust the bin size within a histogram. For our calculations, we utilize the Freedman-Diaconis’ rule [15] to determine the bin size B, which is defined as:Freedman-Diaconis’ rule is less sensitive to outliers in data compared to the standard deviation, rendering it more robust. Another approach is the Scott’s rule [16]. It is defined as , where denotes the sample standard deviation. Scott’s rule works best with data that follows a Gaussian distribution.
- We approximate the probability density function (PDF) of a particle falling into a bin at time t using the relative frequency as:At each time t, we calculate the diffusion (Shannon) entropy as follows:Normalizing the diffusion entropy at time t results in:
2.2. Conditional Diffusion Entropy (CDE)
2.3. q-Order Diffusion Entropy Analysis (Q-DEA)
2.4. Multi-Scale Conditional Diffusion Entropy (MS-CDE)
3. Data
4. Results
4.1. q-Order DEA for Dow Jones Industrial Average
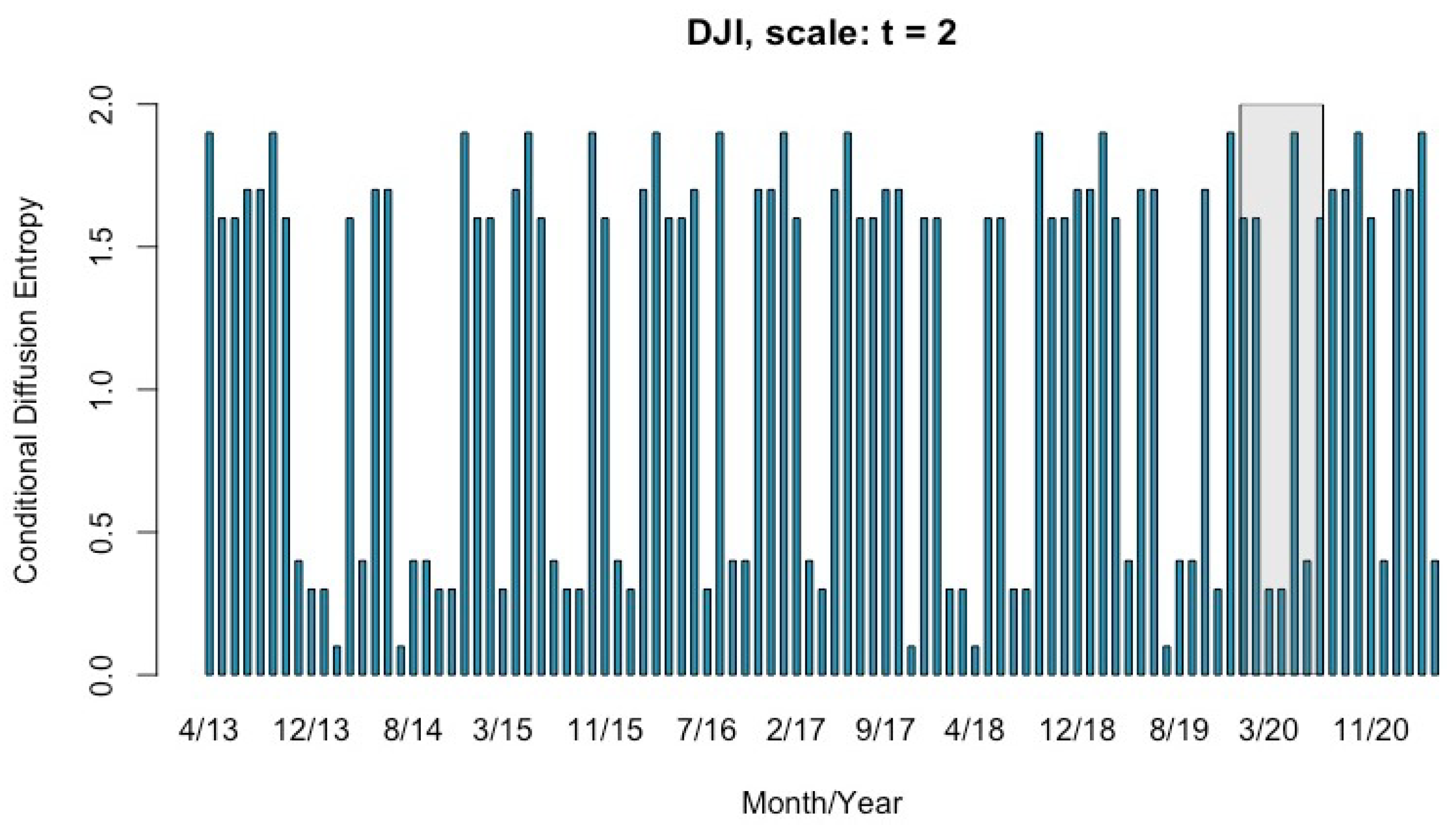
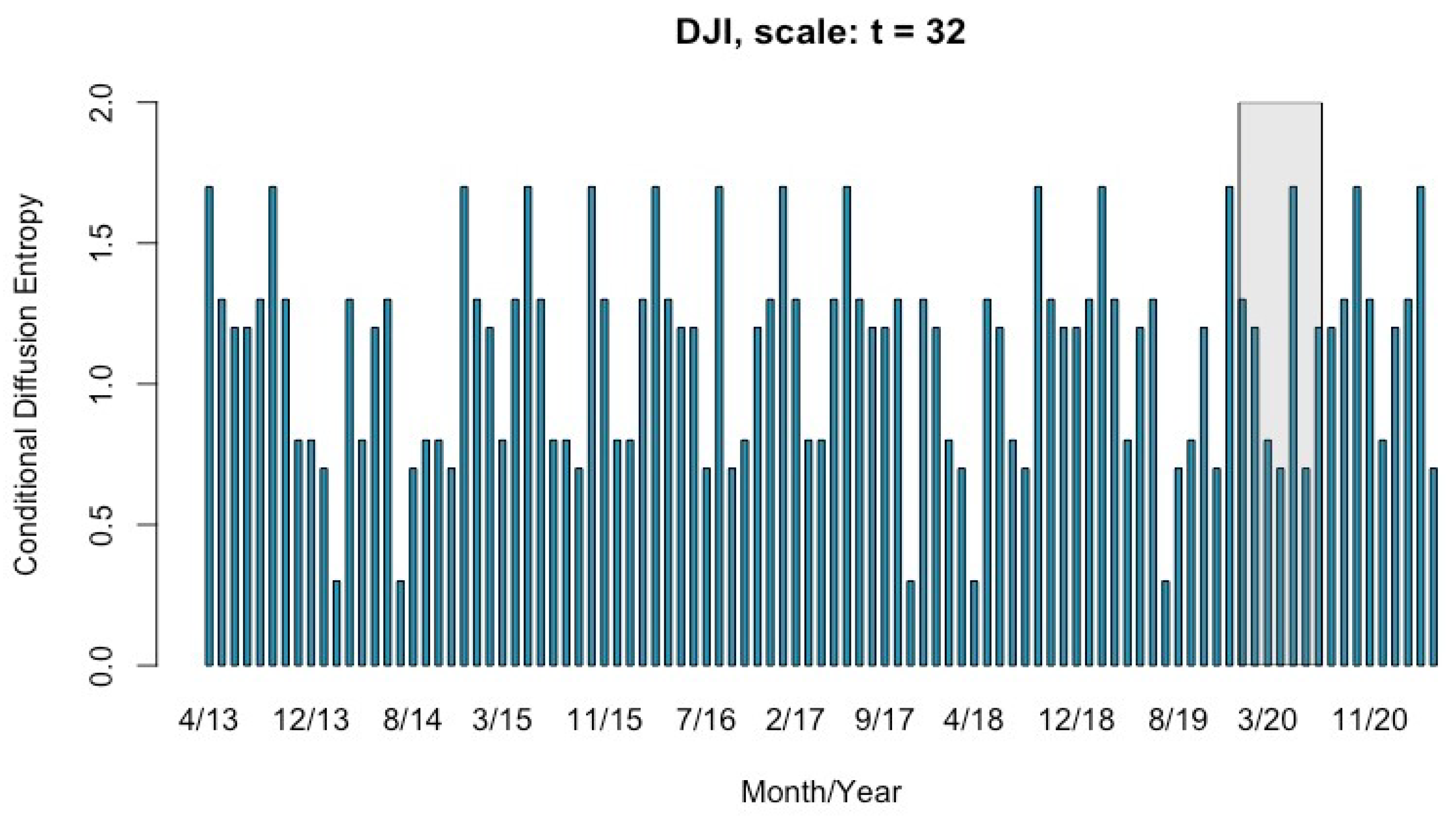
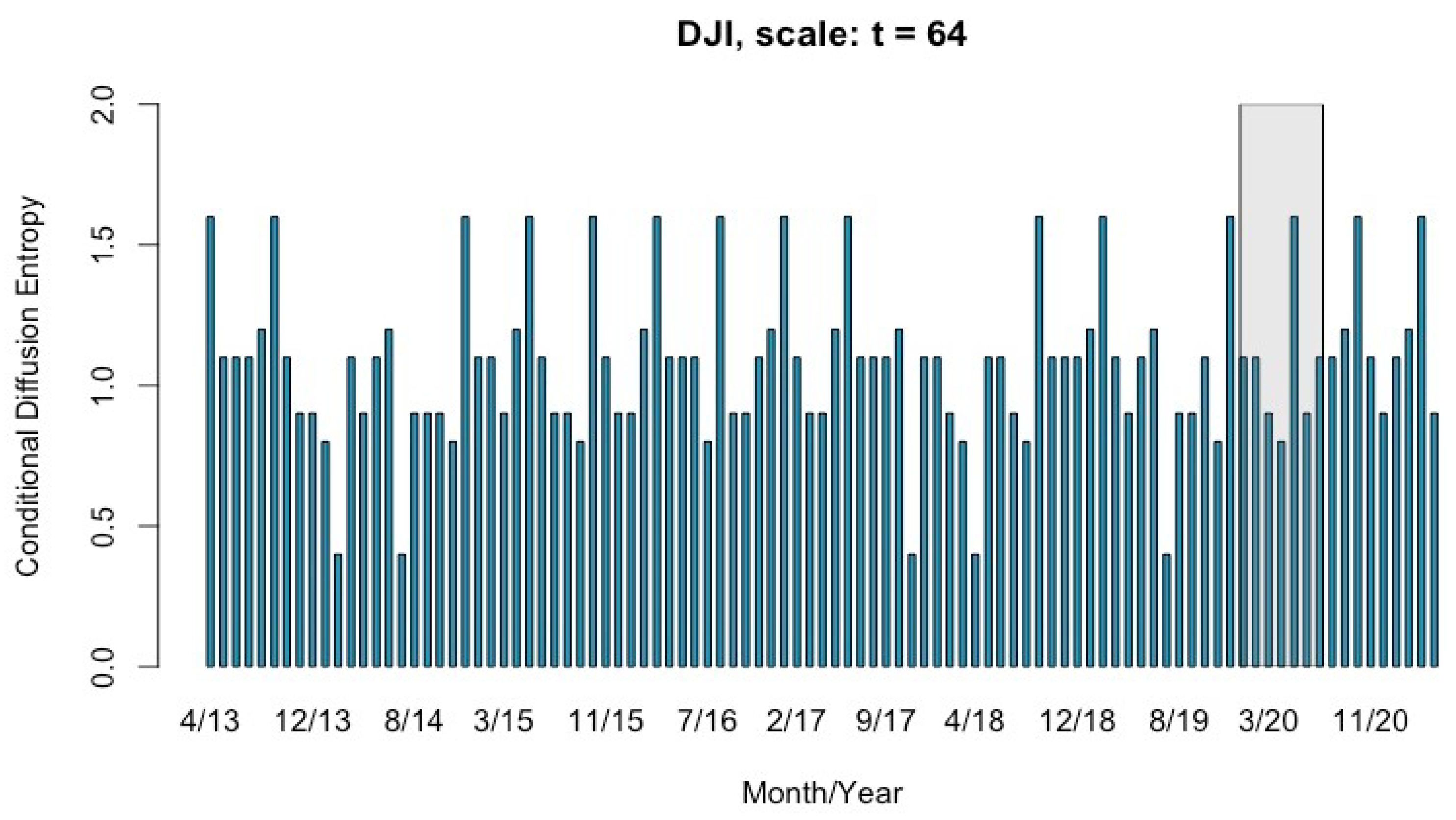
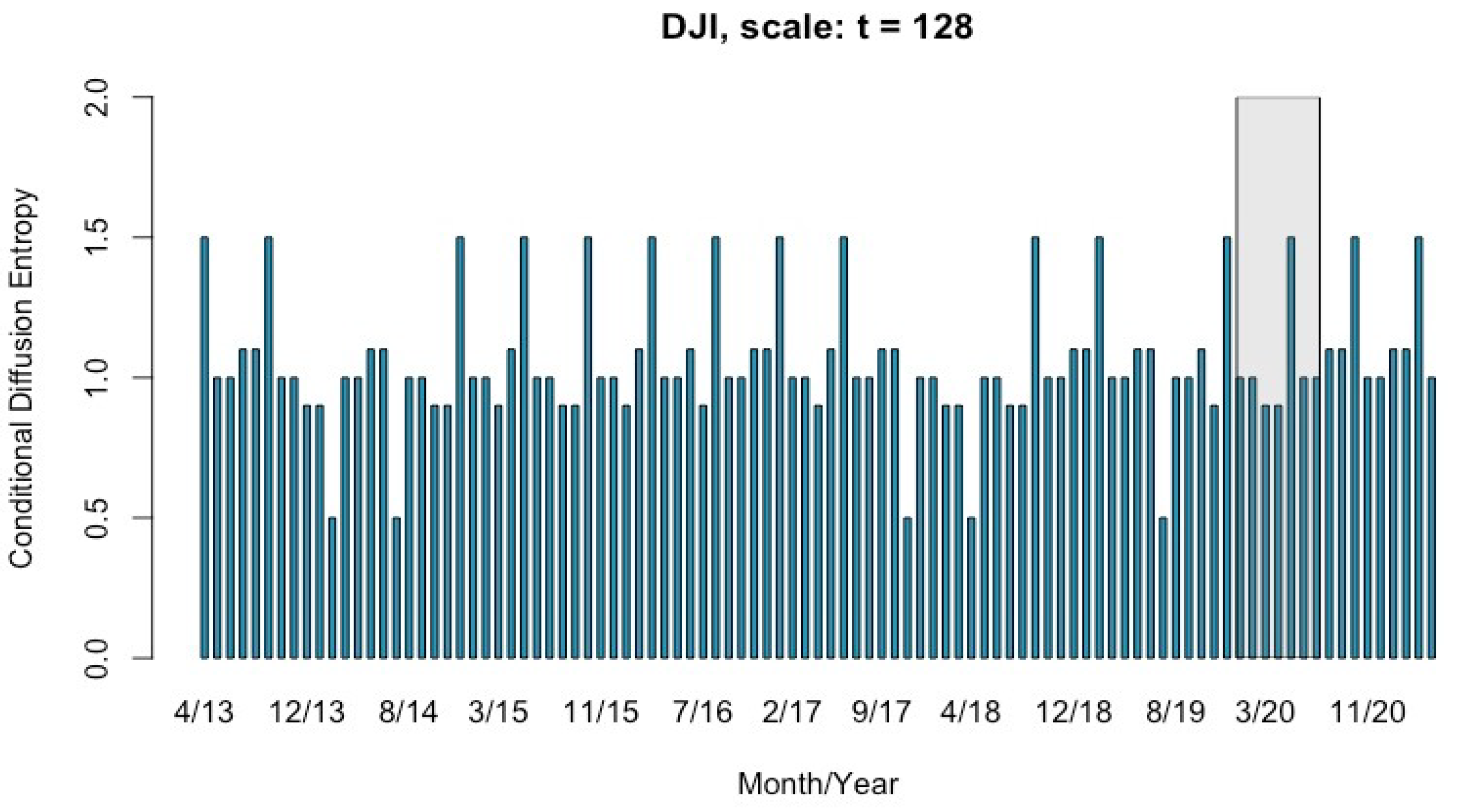
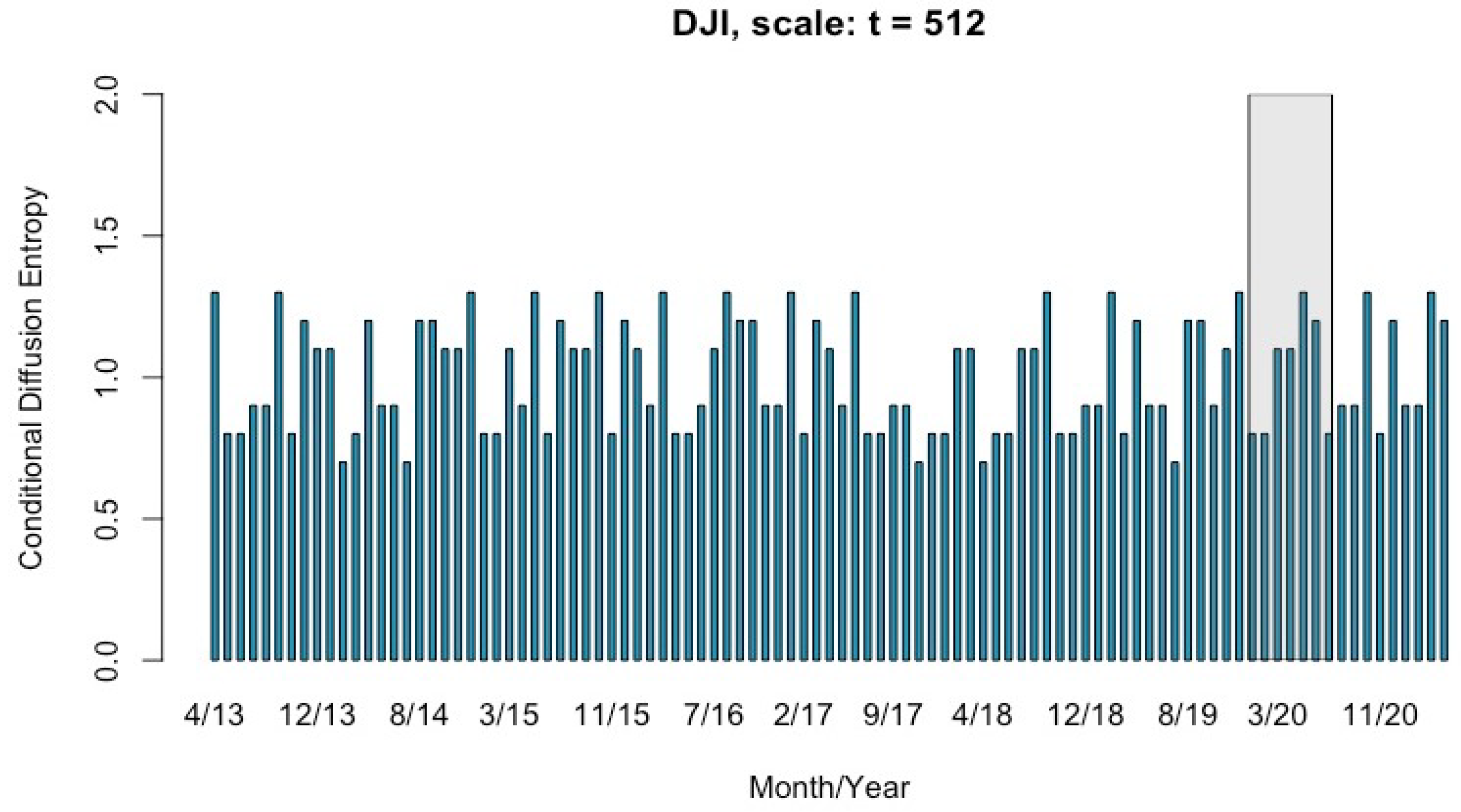
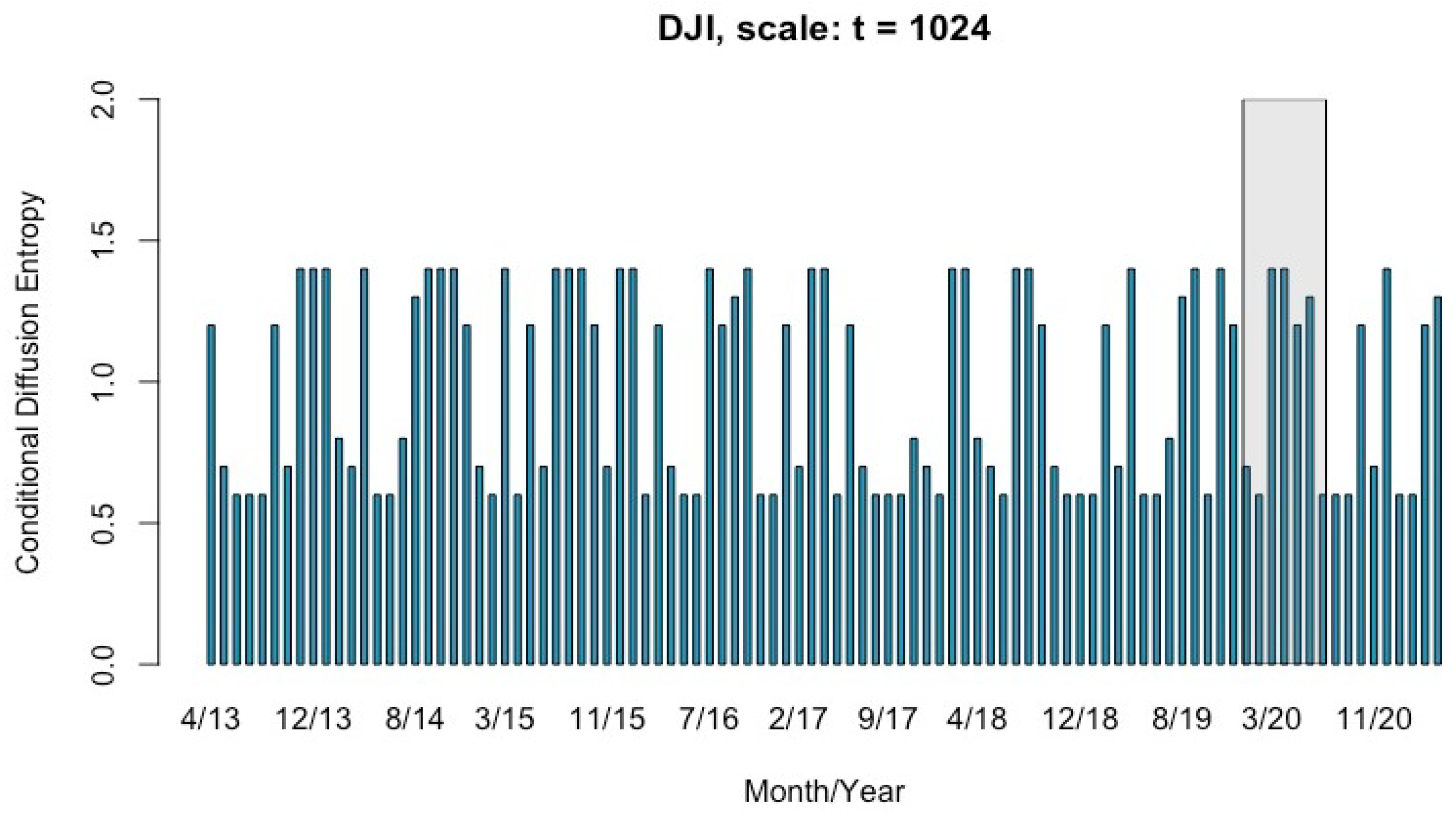
4.2. Multi-Scale Conditional Entropy of DJI from April 2013 to April 2021
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| Acronyms | Definition |
| DJI | Dow Jones Industrial Average |
| SE | Shannon Entropy |
| RE | Rényi Entropy |
| VaR | Vector Autoregression |
| CDE | Conditional Diffusion Entropy |
| MS-CDE | Multi-Scale Conditional Diffusion Entropy |
| Probability Density Function | |
| DEA | Diffusion Entropy Analysis |
| FD | Freedman-Diaconis Rule |
| Q-DEA | q-Order Diffusion Entropy Analysis |
| IQR | Inter quartile Range |
| MFDEA | Multifractal Diffusion Entropy Analysis |
References
- Andreev, B.; Sermpinis, G.; Stasinakis, C. Modelling Financial Markets during Times of Extreme Volatility: Evidence from the GameStop Short Squeeze. Forecasting 2022, 4, 654–673. [Google Scholar] [CrossRef]
- Yamasaki, K.; Muchnik, L.; Havlin, S.; Bunde, A.; Stanley, H.E. Scaling and memory in volatility return intervals in financial markets. Proc. Natl. Acad. Sci. USA 2005, 102, 9424–9428. [Google Scholar] [CrossRef] [PubMed]
- Siokis, F.M. Stock market dynamics: Before and after stock market crashes. Physica A 2012, 391, 1315–1322. [Google Scholar] [CrossRef]
- Wang, F.; Yamasaki, K.; Havlin, S.; Stanley, H.E. Multifactor analysis of multiscaling in volatility return intervals. Phys. Rev. E 2009, 79, 016103. [Google Scholar] [CrossRef] [PubMed]
- Caraiani, P. Modeling the Comovement of Entropy between Financial Markets. Entropy 2018, 20, 417. [Google Scholar] [CrossRef] [PubMed]
- McCauley, J.L. Thermodynamic analogies in economics and finance: Instability of markets. Physica A 2003, 329, 199–212. [Google Scholar] [CrossRef]
- Bentes, S.R.; Menezes, R. Entropy: A new measure of stock market volatility? J. Phys. Conf. Ser. 2012, 394, 012033. [Google Scholar] [CrossRef]
- Zhou, R.; Zhang, J.; Xiong, M.; Yang, F.; Yu, M. Using information entropy to measure bond risk: An empirical investigation. J. Inf. Comput. Sci. 2015, 12, 1089–1100. [Google Scholar] [CrossRef]
- Oh, G.; Kim, H.Y.; Ahn, S.W.; Kwak, W. Analyzing the financial crisis using the entropy density function. Phys. A Stat. Mech. Its Appl. 2015, 419, 464–469. [Google Scholar] [CrossRef]
- Li, S.; Zhuang, Y.; He, J. Stock market stability: Diffusion Entropy Analysis. Phys. A Stat. Mech. Its Appl. 2016, 450, 462–465. [Google Scholar] [CrossRef]
- Scafetta, N.; Grigolini, P. Scaling detection in time series: Diffusion entropy analysis. Phys. Rev. E Stat. Nonlinear Softw. Matter. Phys. 2002, 66, 036130. [Google Scholar] [CrossRef]
- Huang, J.; Shang, P.; Zhao, X. Multifractal diffusion entropy analysis on stock volatility in financial markets. Physica A 2012, 391, 5739–5745. [Google Scholar] [CrossRef]
- Morozov, A.Y. Comment on ’multifractal diffusion entropy analysis on stock volatility in financial markets’ [Physica A. 391 (2012) 5739–5745]. Physica A 2012, 392, 2442. [Google Scholar] [CrossRef]
- Jizba, P.; Korbel, J. Multifractal diffusion entropy analysis: Optimal bin width of probability histograms. Phys. A Stat. Mech. Its Appl. 2014, 413, 438–458. [Google Scholar] [CrossRef]
- Freedman, D.; Diaconis, P. On the histogram as a density estimator: L2 theory. Z. Wahrscheinlichkeitstheorie Verwandte Geb. 1981, 57, 453–476. [Google Scholar] [CrossRef]
- Scott, D.W. On optimal and data-based histograms. Biometrika 1979, 66, 605–610. [Google Scholar] [CrossRef]
- Mariani, M.C.; Kubin, W.; Asante, P.K.; Tweneboah, O.K.; Beccar-Varela, M.P.; Jaroszewicz, S.; Gonzalez-Huizar, H. Self-Similar Models: Relationship between the Diffusion Entropy Analysis, Detrended Fluctuation Analysis and Lévy Models. Mathematics 2020, 8, 1046. [Google Scholar] [CrossRef]
- Mariani, M.C.; Asante, P.K.; Bhuiyan, M.A.M.; Beccar-Varela, M.P.; Jaroszewicz, S.; Tweneboah, O.K. Long-Range Correlations and Characterization of Financial and Volcanic Time Series. Mathematics 2020, 8, 441. [Google Scholar] [CrossRef]
- Jizba, P.; Arimitsu, T. The world according to Rényi: Thermodynamics of multifractal systems. Ann. Phys. 2004, 312, 17–59. [Google Scholar] [CrossRef]
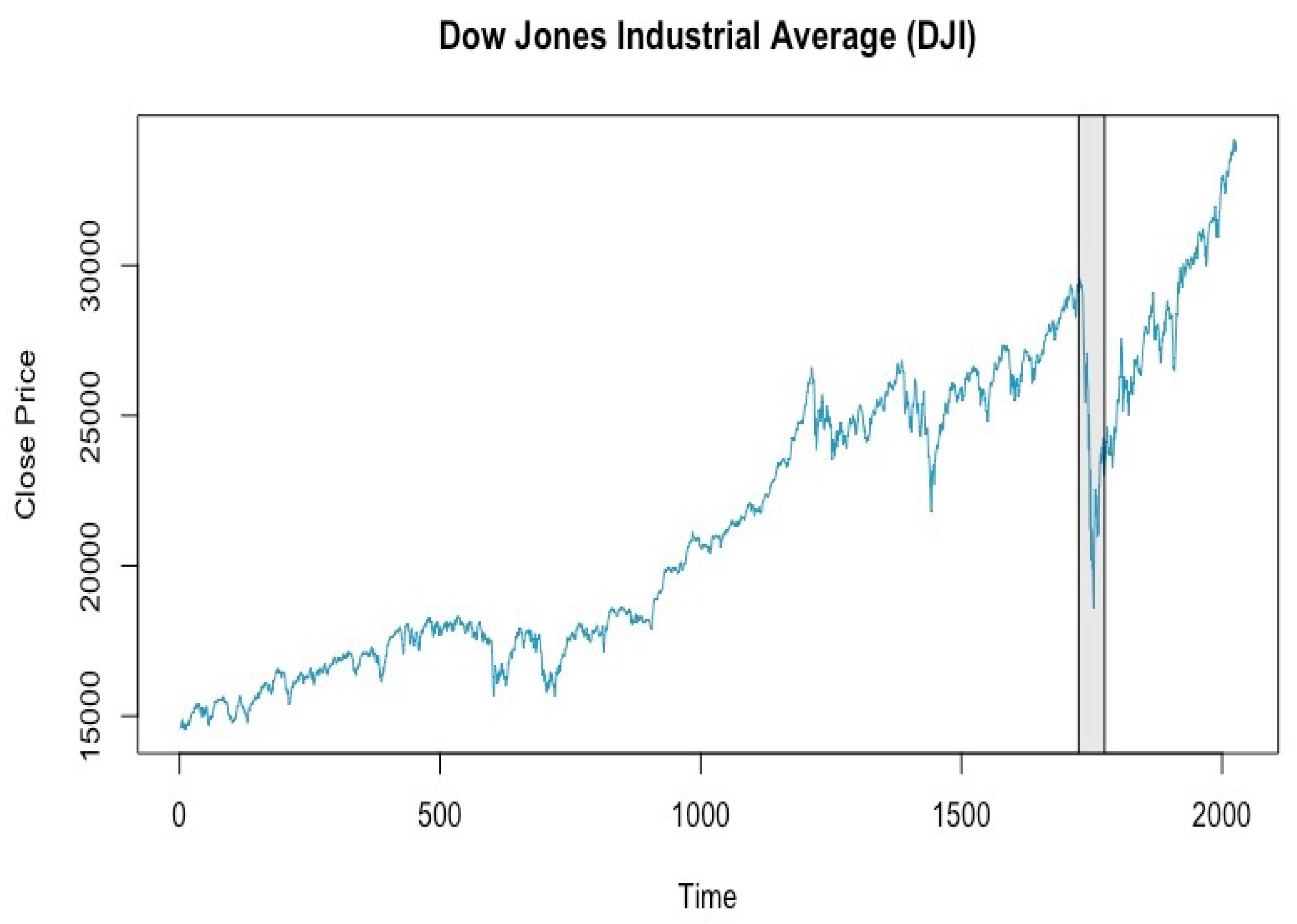





| Data | Start Date | End Date | Median | Mean | Standard Deviation |
|---|---|---|---|---|---|
| 5 April 2013 | 23 April 2021 | 20,812 | 21,555 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mariani, M.C.; Kubin, W.; Asante, P.K.; Tweneboah, O.K. Volatility Analysis of Financial Time Series Using the Multifractal Conditional Diffusion Entropy Method. Fractal Fract. 2024, 8, 274. https://doi.org/10.3390/fractalfract8050274
Mariani MC, Kubin W, Asante PK, Tweneboah OK. Volatility Analysis of Financial Time Series Using the Multifractal Conditional Diffusion Entropy Method. Fractal and Fractional. 2024; 8(5):274. https://doi.org/10.3390/fractalfract8050274
Chicago/Turabian StyleMariani, Maria C., William Kubin, Peter K. Asante, and Osei K. Tweneboah. 2024. "Volatility Analysis of Financial Time Series Using the Multifractal Conditional Diffusion Entropy Method" Fractal and Fractional 8, no. 5: 274. https://doi.org/10.3390/fractalfract8050274
APA StyleMariani, M. C., Kubin, W., Asante, P. K., & Tweneboah, O. K. (2024). Volatility Analysis of Financial Time Series Using the Multifractal Conditional Diffusion Entropy Method. Fractal and Fractional, 8(5), 274. https://doi.org/10.3390/fractalfract8050274








