Abstract
This paper proposes a novel five-dimensional (5D) memristor-based chaotic system by introducing a flux-controlled memristor into a 3D chaotic system with two stable equilibrium points, and increases the dimensionality utilizing the state feedback control method. The newly proposed memristor-based chaotic system has line equilibrium points, so the corresponding attractor belongs to a hidden attractor. By using typical nonlinear analysis tools, the complicated dynamical behaviors of the new system are explored, which reveals many interesting phenomena, including extreme homogeneous and heterogeneous multistabilities, hidden transient state and state transition behavior, and offset-boosting control. Meanwhile, the unstable periodic orbits embedded in the hidden chaotic attractor were calculated by the variational method, and the corresponding pruning rules were summarized. Furthermore, the analog and DSP circuit implementation illustrates the flexibility of the proposed memristic system. Finally, the active synchronization of the memristor-based chaotic system was investigated, demonstrating the important engineering application values of the new system.
1. Introduction
In 1971, Professor Chua first theoretically predicted the existence of components that describe the relationship between charge and magnetic flux from the perspective of circuit theory completeness [1], and defined such components as memristors, which are nonlinear resistors with memory function. The resistance value of a device can change with the history of input current or voltage, that is, it can remember the charge or magnetic flux flowing through it by the change of resistance value. Due to the lack of such devices, the research on memristors and memristor circuits has not attracted widespread attention in the scientific and engineering communities for a long time, until 2008, when Hewlett Packard laboratory developed the first physical model of a nanoscale memristor and provided its memory mechanism from an experimental perspective [2], which has aroused people’s interest in conducting comprehensive research on memristors. Meanwhile, many simple mathematical models with memristor characteristics have been successively reported [3], such as quadratic nonlinear memristor [4], tri-valued memristor model [5], and five-valued memristor model [6]. Considering the unique characteristics of memristors, they have shown great research value and application prospects in engineering fields [7], such as chaotic circuit construction [8,9], chaotic masking secure communication [10], artificial neural networks [11,12], image encryption [13,14], and logic operations [15].
Since memristic systems often exhibit more complex dynamical characteristics, many memristor-based systems have been proposed in recent years [16,17,18,19]. A new 4D chaotic system with double memristors which has infinitely many unstable equilibria was constructed [20]. Dynamical analysis and circuit implementation of a new variable-wing 5D memristor-based hyperchaotic system was derived in [21]. A new memristor-based multi-double-scroll system was achieved by directly embedding a piecewise-nonlinear memristor into Chua’s system [22]. Some complex dynamic behaviors, such as periodic bursting and chaotic bursting, can also be generated in the generalized ternary memristive circuit [23]. The influence of a specific symmetry break on the dynamics of a fourth-order autonomous memristive chaotic circuit was evaluated [24]. A novel conservative memristive system was discovered by introducing the three-terminal memristor into a newly constructed 4D Euler equation [25]. In Ref. [26], a 4D chaotic system was proposed by introducing a memristor to the jerk system. Grid multi-scroll attractors also can be generated in a 4D memristive chaotic system and memristive neural networks [27,28].
Multistability is a common physical phenomenon in nonlinear dynamic systems. When the system parameters remain unchanged and the initial state is changed, the system trajectory may asymptotically approach different stable states, such as equilibrium point, chaos, period, and quasi-period. The special properties of memristors make memristor circuits multi or extremely multi-stable, easily exhibiting the coexistence of multiple or infinite attractors. A 5D memristive chaotic system was introduced by replacing the coupling parameters in the Sprott-B-based 4D chaotic system with a flux-controlled memristor [29], which exhibits extreme multistability phenomena. Liu and Lai devised a new memristive chaotic system with infinite coexisting attractors based on the Sprott-J system [30]. Chang et al. investigated extreme multistability and complex dynamics of a chaotic system based on a smooth bistable bi-local active memristor [31]. Singh et al. found a new 4D memristive hyperchaotic system that has extreme multistability and analyzed a nonlinear active-adaptive projective synchronization control [32]. In Ref. [33], the generation of a novel 4D memristor-based chaotic system characterized by abundant coexisting attractors was investigated. Coexisting attractors or extreme multistability have also been found in the two memristor-based Hopfield neural network [34], fractional-order memristor-based chaotic system [35,36], a pair of coupled memristor-based Duffing oscillators [37], memristor-based double-scroll chaotic system [38], current-controlled memristor-based chaotic circuit [39], and memristor-based time-delay chaotic system [40].
The main contributions and innovations of this paper are as follows.
- (1)
- This paper presents a variable-boostable memristor chaotic system with hidden attractors, and the circuit implementation shows that the newly designed system has feasibility for applications.
- (2)
- The new system contains various interesting dynamic behaviors, such as extreme homogeneous multistabilities, extreme heterogeneous multistabilities, hidden transient state, and complex state transition behavior.
- (3)
- The unstable periodic orbits embedded in the hidden chaotic attractor were explored, and relevant pruning rules are summarized, revealing the symbol encoding mechanism of cycles.
The rest of this article is arranged as follows. Section 2 presents the mathematical model of a 5D memristor-based chaotic system and analyzes its fundamental dynamic properties. In Section 3, various interesting and complex dynamic behaviors of the new system are investigated. Section 4 systematically explores the unstable periodic orbits of the new system. In Section 5, the analog and DSP circuit is designed to implement the memristor-based system. Section 6 discusses the active synchronization control of the new 5D system. Finally, Section 7 concludes this article.
2. The Novel 5D Memristor-Based Chaotic System
In recent years, various mathematical models for memristors have been proposed. In this paper, the following form of cubic nonlinear flux-controlled memristor is adopted to build the new system [41]:
where v and i are the input voltage and output current of the memristor, f and g are two system parameters, and is the state variable. represents the memductance of the flux-controlled memristor; such memristors are not only theoretical models but can also be physically realized in circuits using phase-change materials or nanotechnology, which further proves their feasibility and practicability in the design of physical circuits.
In Ref. [42], a 3D chaotic system with hidden attractors was proposed, and the form of the system is
For the parameter values and the initial values system (2) presents a chaotic attractor with a double-wing shape.
Subsequently, we add a linear feedback term, a nonlinear feedback term, and a flux-controlled memristor to the system (2), where u is the internal state variable of the memristor and x is the input voltage of the memristor. It is worth noting that their incorporation significantly enhances the nonlinear characteristics of chaotic systems, leading to more complex chaotic behaviors. By extending the proposed 3D chaotic system, we obtain a novel 5D memristive chaotic system with richer dynamics than higher-dimensional chaotic systems, as follows:
where , and k are the control parameters. Choosing a sinusoidal voltage source is considered as where and f are the excitation amplitude and frequency, respectively. Taking , the internal initial state of flux-controlled memristor and f is set to 0.05, 0.1, and 0.4 Hz. According to Equation (1), the diagram of memductance and pinched hysteresis loop is displayed in Figure 1.
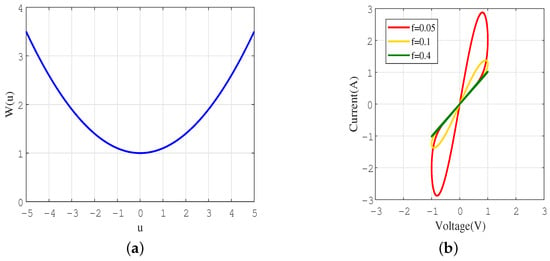
Figure 1.
The characteristic curve of a memristor. (a) Memductance; (b) pinched hysteresis loop for different frequencies.
The parameters of system (3) are fixed as Let the terms on the left-hand side of system (3) be zero, then we can easily find that the system has a line equilibrium
where e is any real constant, according to the category of the hidden attractor, which means that the attractors generated by system (3) are all hidden.
The linearization matrix of system (3) on O is obtained as follows:
Based on the Jacobian matrix (5), the characteristic equation can be calculated by
Thus, the eigenvalues are obtained: , and are both real. It can be concluded that all the equilibrium points located on the line O are unstable saddle points. It is worth noting that the stability of the memristive chaotic circuit cannot be simply determined by the stability of the nonzero eigenvalues of the equilibrium point set O. Under certain parameters, zero eigenvalues also significantly impact the stability of the memristive chaotic circuit.
The symmetry of chaotic systems is an important property. If we perform transformations , the memristive system (3) is invariant, which means that system (3) is symmetric relative to the z-axis in the phase space. Therefore, the limit cycles of the system are either self-symmetric or appear in pairs.
The dissipativity of system (3) can be expressed as follows:
When the following condition is satisfied: , the system is dissipative, which means there may be strange attractors present.
The initial values are set as , and the Ode 45 algorithm is used for numerical integration in Matlab, which reveals the chaotic behaviors characterized by double-wing strange attractors, as shown by the 2D projection of the phase portraits in Figure 2. The corresponding Lyapunov exponents are (see Figure 3a), and the Kaplan–Yorke dimension is Due to the existence of one positive Lyapunov exponent in the system and the system under current parameters is in a chaotic state. The continuous broadband power spectrum shown in Figure 3b also verifies the emergence of chaos.
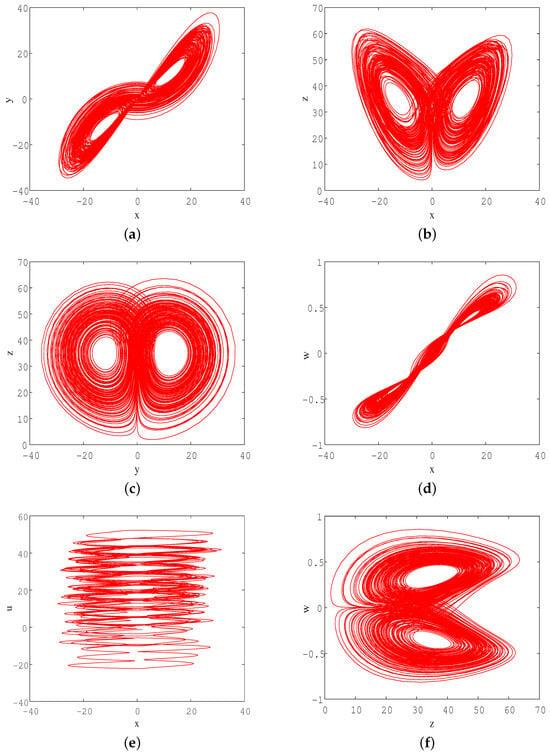
Figure 2.
2D projection of phase portraits in different state space under parameters , the initial values are set as . (a) x–y phase space; (b) x–z phase space; (c) y–z phase space; (d) x–w phase space; (e) x–u phase space; (f) z–w phase space.
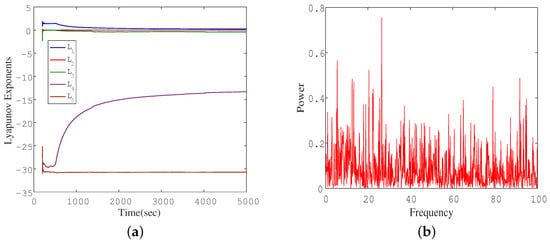
Figure 3.
(a) The Lyapunov exponents spectrum of system (3) for evolution time . (b) A continuous broadband power spectrum.
3. Dynamical Analysis of the Memristor-Based Chaotic System
3.1. Complex Dynamical Behavior Depending on Control Parameter b
When the parameters of system (3) are set as and the initial values are taken the dynamic behavior of the system under different b values is investigated. Figure 4 shows the bifurcation diagram and its corresponding Lyapunov exponents spectrum when b is varied in the interval . It can be seen that system (3) exhibits various states with different b values, such as periodic, quasi-periodic, and chaotic states. When b is in the interval , the system is in a periodic or quasi-periodic state at most positions, except for a few parameters where the system is in a chaotic state. When b, the system has a chaotic status at most positions. However, near , the maximum Lyapunov exponent is approximately zero, which indicates that system (3) is periodic within a small parameter range. Then, when the system eventually becomes a chaotic state, which means that the system indeed produces chaotic attractors with one positive Lyapunov exponent for a wide range of b. Different dynamic behaviors under five b values are summarized in Table 1, and the corresponding 2D projection of phase portraits for some typical values of b in state space are displayed in Figure 5, which indicates the intricate topological structure and rich dynamic properties in the memristor-based system (3).
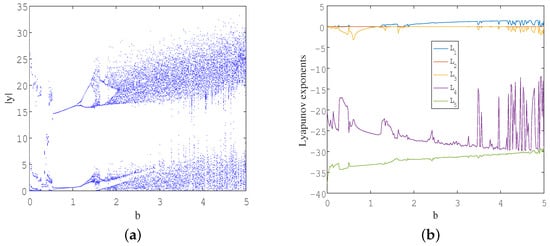
Figure 4.
(a) Bifurcation diagram and (b) Lyapunov exponents spectrum of system (3) versus b under parameters .

Table 1.
Dynamics and Lyapunov exponents for some typical values of b in system (3) with .
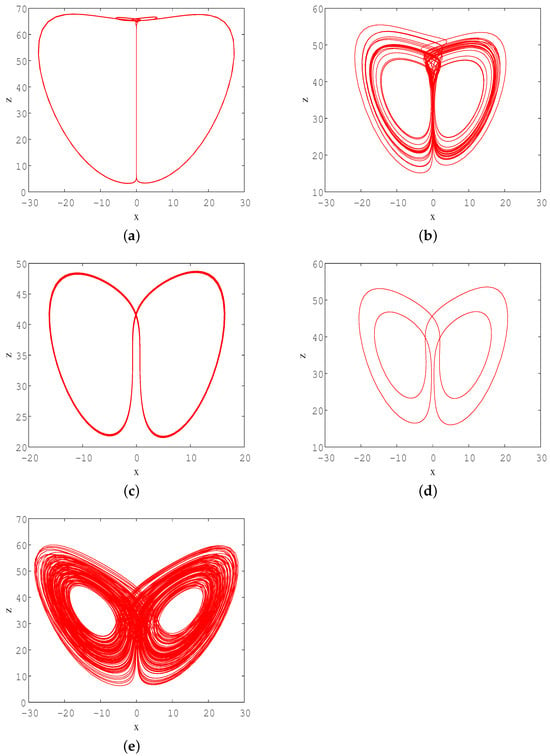
Figure 5.
2D view of phase portraits of system (3), (a) (b) (c) (d) (e) .
3.2. Poincaré Mapping
Poincaré mapping is a very common approach for analyzing dynamic systems. This method analyzes the motion state of the system by selecting an dimensional cross-section in the n-dimensional state space and observing the distribution of the intersection points between the motion trajectory and the cross-section. Suppose there are countless points on the Poincaré section. In that case, the system enters a chaotic state, and the arrangement of points on the Poincaré section generally exhibits certain fractal characteristics. By observing the phase diagrams in Figure 2, we selected the cross-section as , and the corresponding 2D Poincaré mapping is shown in Figure 6a,b. It is obvious that there are many dense points on the cross-section, which further validates the chaotic characteristics of the system. Figure 6c shows the first return map of system (3) with a cross-section for evolution time , where a dense sheet point set with a unimodal structure of two branches is presented.
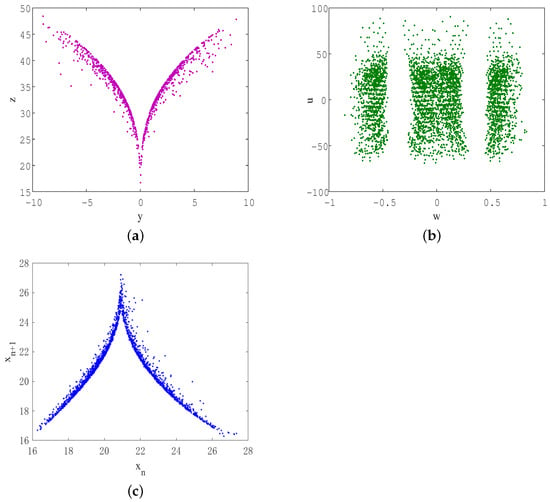
Figure 6.
The 2D Poincaré map with section of system (3): (a) in plane; (b) in plane. (c) The first return map with section . , and the initial values are taken as (1,1,1,1,1).
3.3. Extreme Homogeneous and Heterogeneous Multistabilities
On the other hand, the multistability phenomenon in memristive chaotic systems has broad application prospects in various fields. For instance, in the area of neural networks, multistable systems can simulate the functions of biological neural systems, inspiring the design of efficient artificial neural networks [43]. Moreover, in the domain of secure communications, the complex dynamics of chaotic systems can be utilized for encrypting signals to prevent unauthorized interception or decryption of information [44]. Specifically, homogeneous multistability refers to the ability of a chaotic system to generate coexisting attractors with the same structure but different positions or amplitudes, while heterogeneous multistability refers to the ability of a system to generate several or even infinite coexisting attractors with different structures under the same parameters [45]. Due to the unique memory of memristors on the initial states, in addition to the control parameters that can affect the dynamic behavior of the system, the internal state initial value of the memristor can also have a deep impact on the state of the system. In system (3), when the parameters are taken as and initial values are set as , the system can generate various coexisting chaotic attractors depending on . Figure 7 shows a projection of the chaotic attractors onto the 2D or 3D phase space for seven different whose orbits exhibit a relatively small range of extension in the u direction and are not stationary. Moreover, they shift vertically within the phase space depending on the initial values. This phenomenon indicates that system (3) has the property of homogeneous multistability, which means that under a certain parameter, as the initial value of the memristor changes, the system exhibits extreme multistability phenomena.
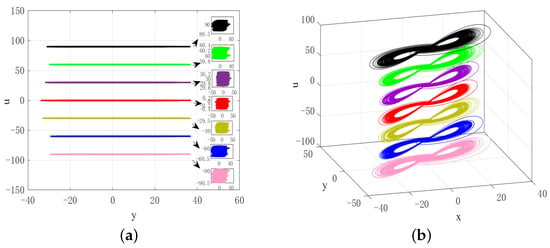
Figure 7.
Phase portraits when (pink), (blue), (yellow), (red), (purple), (green), (black), . (a) In plane, the black rectangular in the subfigure in the right column shows the amplification of the corresponding chaotic attractor, (b) in space.
When the parameters are set as and initial values are set as , system (3) can also present extreme heterogeneous multistability. When is set to 60, 80, 90, 100, and 120, respectively, the phase portraits in the plane, and the space are shown in Figure 8, which reveals the coexisting symmetric limit cycle, asymmetrical limit cycle, quasi-periodic attractor, and chaotic attractors. The coexisting infinitely many attractors with different topological structures confirm the emergence of heterogeneous multistability.
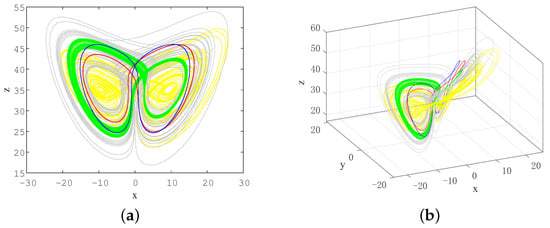
Figure 8.
Phase portraits when (blue), (red), (green), (grey), (yellow), (a) In plane, (b) in space.
3.4. Hidden Transient State and State Transition Behavior
Transient state refers to a special phenomenon where a system is in one state for a short time, but with the evolution of time, it transitions to another state. Here, the hidden transient state and state transition of system (3) depending on the system parameters are discussed. Choosing the parameters the initial condition , and the simulation time . The 2D phase diagram and time-domain waveform of the state variable z are shown in Figure 9. It can be observed that the system turns to another kind of chaos when and there are significant differences in the strange attractors before and after the transfer.
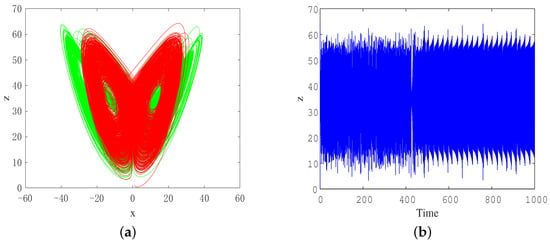
Figure 9.
Transient chaotic transition behavior under parameters . (a) Phase portraits when (red) and (green); (b) time domain waveform about z.
When the parameters are changed to and the initial condition is the system exhibits transient asymptotic convergence and steady-state chaotic behavior, as shown in Figure 10. It can be observed that the time-domain waveform changes from a straight line to disorderly in the vicinity of , and the system has a state transition.
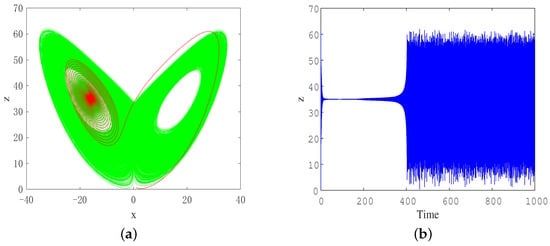
Figure 10.
Transient asymptotic convergence transition behavior under parameters . (a) Phase portraits when (red) and (green); (b) time domain waveform about z.
Similarly, when the parameters are taken and the initial condition is the system has a state transition around , as shown in Figure 11. Obviously, the attractor with quasi-periodic characteristics appears in a short time, and the chaotic attractor appears in a long time, which fully indicates that the system has hidden transient quasi-period under the corresponding parameters and initial values.
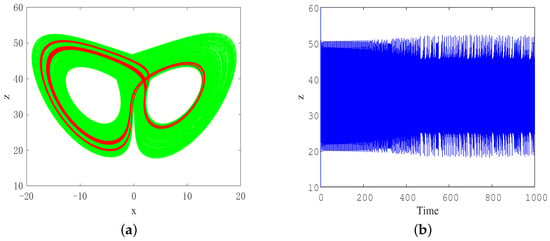
Figure 11.
Transient quasi-periodic transition behavior under parameters . (a) Phase portraits when (red) and (green); (b) time domain waveform about z.
As a result, the hidden transients and state transitions reveal the unpredictability of the new system (3) over long-term evolution. The existence of these dynamic behaviors not only enhances the robustness and adaptability of the system but also lays the foundation for the subsequent in-depth study of synchronous control strategies.
3.5. Offset-Boosting Control
Offset-boosting control refers to the process of adding a constant term to a state variable in a deterministic chaotic system when it only appears once in the system’s equation, resulting in a controllable offset and causing the chaotic signal to change from bipolar to unipolar. Since the derivative of a constant is 0, the form of the differential equation remains unchanged after the introduction of a constant in the variable. Therefore, the offset-boosting control can achieve the mutual conversion of chaotic signals between different polarities by simply changing an additional control constant without changing the basic dynamic characteristics of the system. According to system (3), the state variable w only appears once to the right of the fourth equation in system (3), so it is easy to achieve offset-boosting control of the chaotic attractor. Using the state variable instead of w, where v is the offset increment controller, then system (3) can be rewritten as
Therefore, by changing the size of v within a certain range, the offset-boosting control of the chaotic attractor on the w axis can be achieved. When selecting parameters and the initial values are Figure 12a,b show the phase diagrams and corresponding time series diagrams of three chaotic attractors generated at different positions in the plane when v is and 1, respectively. It can be seen that when , the chaotic signal is on the positive and negative half axes of the w axis; when , the chaotic signal is on the negative half axis of the w axis; when , the chaotic signal is on the positive half axis of the w axis. This indicates that when the offset increment controller v takes a positive value, the attractor shifts towards the negative direction of the w axis; while when the offset increment controller v takes a negative value, the attractor shifts towards the positive direction of the w axis. It can be seen that the memristor-based system (3) belongs to the variable-boostable systems, which is very appropriate in chaos-based applications, because it can be used for amplitude control and reduce the number of components required for signal conditioning [46].
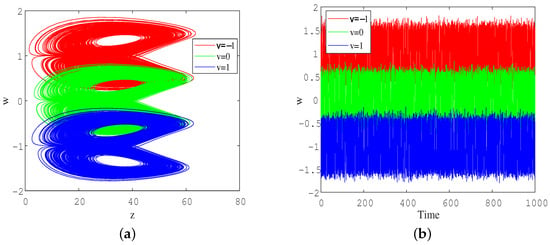
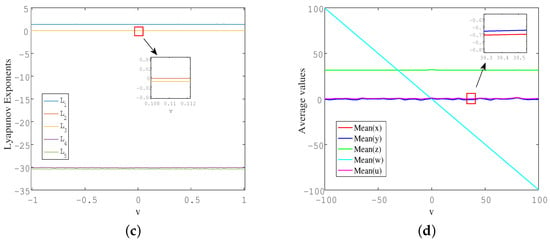
Figure 12.
(a) Phase diagram of chaotic attractors; (b) time series diagram of state variable w; (c) Lyapunov exponents spectrum corresponding to different values of offset-boosting controller v; (d) average values of the state variables.
On the other hand, the Lyapunov exponents spectrum versus v is also calculated, and the five Lyapunov exponents remained almost unchanged, as shown in Figure 12c, indicating that the dynamical state of system (3) did not change with the offset controller v. At the same time, in Figure 12d, the average of the state variable w decreases as the offset v increases, while the average value of the other variables remains unchanged. Furthermore, there is a variable w in the model whose value does not affect the dynamics of the remaining variables. Therefore, system (3) is a four-variable dynamic model whose evolution affects the fifth variable, but not the other way round. In summary, the introduction of the offset v can flexibly shift the position of the attractors in the w direction in the phase space, which has great application value in engineering.
4. Analysis of the Unstable Periodic Orbits via Variational Approach
Unstable periodic orbits play an important role in chaotic systems: according to the periodic orbit theory [47], due to the orbital shadowing effect, the average values of physical quantities in a dynamic system can be calculated by cycle expansions. Thus, it is important not to miss any short cycles as ignoring long cycles has little impact on calculation accuracy. Many numerical calculation methods have been proposed to locate the unstable periodic orbits in chaotic systems. In this section, we employ the variational calculation approach to extract and encode the unstable periodic orbits embedded in the chaotic attractor of the memristor-based system (3).
4.1. Variational Method for Calculations
Strange attractors are composed of numerous unstable periodic densely covered orbits; analyzing periodic orbits can help us better understand the properties of strange attractors. To extract these unsteady periodic orbits, we utilized the variational method in this paper, which has shown its reliability and efficiency [48]. The fundamental physical idea is to make an initial loop guess about the shape of a periodic orbit and then gradually evolve it into a true periodic orbit. The initialization is crucial in variational computation because it determines whether the computed periodic orbits are the ones of interest, which can be achieved in various ways. The following discrete version is expressed by
it can be derived to solve for and , which leads to the period and the position of the cycle. Compared to other numerical methods, as a result of the use of a continuum of points, the variational method has the advantage of numerical stability. The selection of the initial conditions is a crucial factor in ensuring the computation yields the desired trajectory. To accommodate different systems, multiple initialization strategies are used to ensure the flexibility of the method. Especially, when the parameters of system (3) are chosen as the variational method is used here to perform the calculations.
4.2. Symbolic Encoding of Periodic Orbits
We first found the shortest periodic orbit, whose phase diagram projected on the plane is shown in Figure 13a. We can see that the topological structure of the cycle presents a symmetric 8-shape. The Poincaré first return map in Figure 6c exhibits a unimodal structure, which implies the possibility of encoding all short unstable periodic orbits embedded in the strange attractor by symbolic dynamics with two letters. To systematically calculate and classify all short periodic orbits, two-letter symbolic dynamics can be established according to the following rules: we mark orbital segments with as symbol 0, and the orbital segments with as symbol 1; therefore, the cycle in Figure 13a is cycle 01. Utilizing these two basic building blocks, the initial loop guess for calculating other periodic orbits can be constructed accordingly, and their existence can be checked through the variational method.
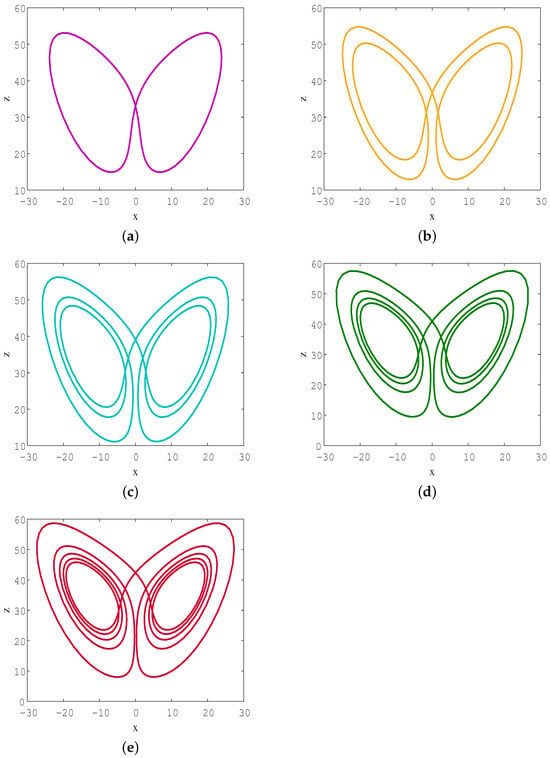
Figure 13.
plane projection of the unstable cycles in system (3) under parameters : (a) cycle 01; (b) 0011; (c) 000111; (d) 00001111; (e) 0000011111.
Through calculations, we also found another four short periodic orbits, which are 0011, 000111, 00001111, and 0000011111, as shown in Figure 13b–e. Table 2 lists the five short periodic orbits, along with their topological lengths, symbol sequences, periods, and five coordinates of a point on the cycle. Figure 14 shows the plane projection of the short periodic orbits with different topological lengths. Through observation, it was found that symbol 0 corresponds to the left half loop on the plane projection, while symbol 1 corresponds to the right half loop. Due to the unclosed projection on the plane of the orbits corresponding to the symbol sequences 0, 1, 001, 0001, etc., these orbits have been pruned. We summarized the pruning rules for the existence of cycles as follows:

Table 2.
Unstable periodic orbits embedded in the hidden chaotic attractor of the memristor-based system (3) for .
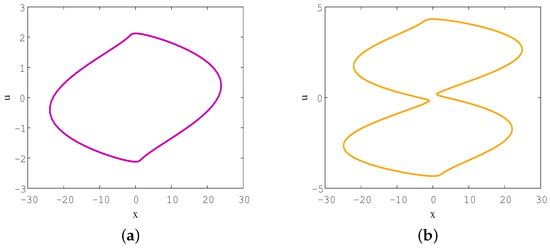
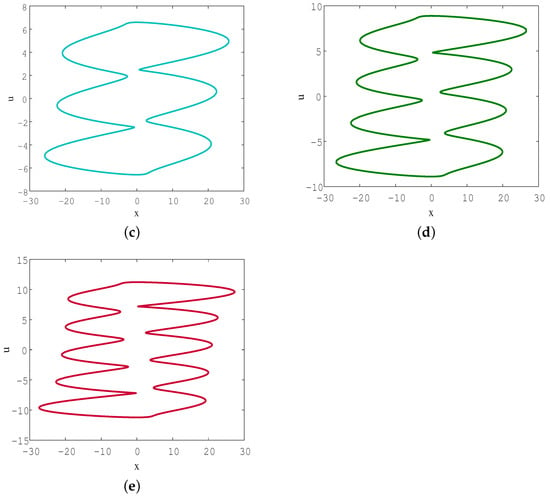
Figure 14.
plane projection of the unstable cycles in system (3) under parameters (a) Cycle 01; (b) 0011; (c) 000111; (d) 00001111; (e) 0000011111.
- (1)
- Periodic orbits with odd topological lengths do not exist due to inconsistent numbers of 0 and 1 in the symbol sequence;
- (2)
- For the periodic orbits with even topological lengths, only those cycles with the same number of 0 and 1 in the symbol sequence may exist.
- (3)
- All symbols 0 or 1 must be arranged consecutively.
Based on the pruning rules mentioned above, all existing periodic orbits are conjugated with themselves. By utilizing 1D symbolic dynamics, we can calculate any complex long periodic orbit. The establishment of symbolic dynamics here indicates that the topological structure of orbits in phase space has a crucial impact on the symbol encoding.
5. Circuit Implementation
5.1. Circuit Simulation
The circuit implementation of a memristor-based chaotic system is very important for engineering applications. In this section, an analog circuit is designed to verify the dynamic behavior of the new memristic chaotic system. The circuit includes circuit components such as capacitors, resistors, operational amplifiers, and analog multipliers. To avoid saturation of the output signal of the operational amplifier, the output level of the chaotic signal is reduced to of the original level, that is, , , , , and . In addition, taking the time scale factor into account, let and Memristic system (3) after scale transformation can be expressed as follows:
where and
The flux-controlled memristor shown in the dashed box in Figure 15b is used to construct a chaotic circuit. The proposed circuit design of system (3) is depicted in Figure 15a. Based on Kirchhoff’s law, the following state equation is obtained:
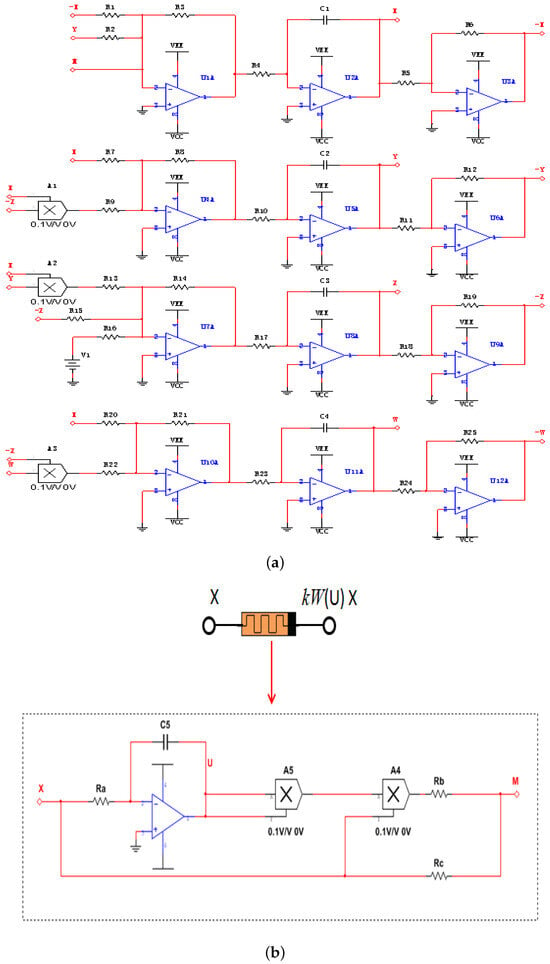
Figure 15.
(a) Circuit implementation of the proposed 5D memristor-based chaotic system. (b) Equivalent circuit of the flux-controlled memristor.
Comparing Equations (10) and (11), it can be concluded that the circuit component parameters in Figure 15 are and
The circuit was simulated using Multisim 14.0 software, and the simulation results are displayed in Figure 16. It is clear that the strange attractors obtained in the analog circuit are in basic agreement with the results of the computer numerical simulation. Affected by the disturbance of the external environment and impurity of precision, the theoretical results and the actual results have a certain degree of error.
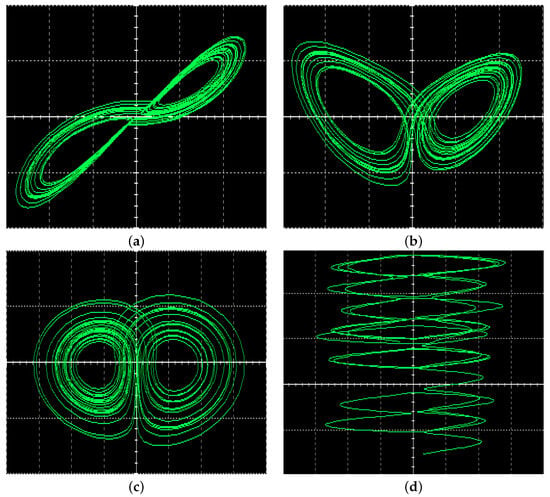
Figure 16.
Multisim software phase diagram for the 5D chaotic system based on memristor: (a) in the plane; (b) in the plane; (c) in the plane; (d) in the plane.
5.2. DSP Implementation
DSP implementation has strong anti-interference capability and high flexibility in system parameter control [49,50]. In this section, we realize the digital circuit of a memristor chaotic system based on DSP technology. The DSP chip TMS320F28335 is used in this paper for its high precision and performance. Additionally, to allow oscilloscopes to better capture the waveform, we used a D/A converter to transform the DSP-generated digital sequences into analog sequences. On the other hand, it is necessary to discretize the continuous memristive chaotic system using a fourth-order Runge–Kutta method and achieve the computation on the DSP chip using C programming, with the waveforms ultimately observed on the oscilloscope. Choosing the parameters and the initial value , the obtained chaotic attractor of the new system is depicted in Figure 17. The results show that the waveforms on the DSP are also in basic agreement with the computer numerical results (Figure 2), which verifies that the system has good flexibility in terms of physical hardware.
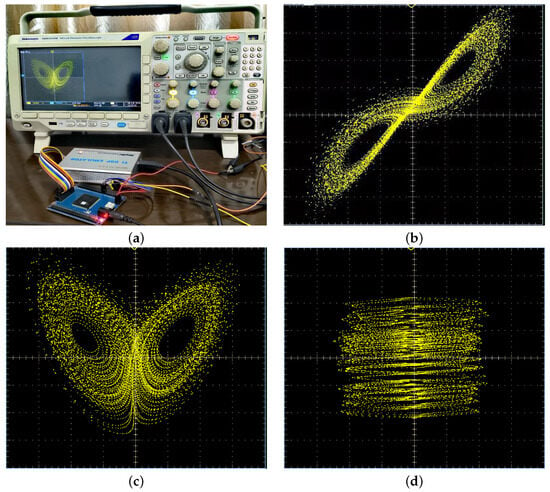
Figure 17.
DSP implementation for the 5D chaotic system based on memristor: (a) DSP experimental platform; (b) in the plane; (c) in the plane; (d) in the plane.
6. Active Synchronization Control of Memristor-Based Chaotic System
Chaos synchronization refers to the process of two or more chaotic systems achieving consistent chaotic motion under coupling or driving, which belongs to specific chaotic control. Chaos synchronization and its application in secure communication and other fields have become a research hotspot in the fields of chaos and control. Many typical chaotic synchronization methods have been proposed [51,52], such as drive-response synchronization method, active–passive synchronization method, adaptive synchronization method, etc. In this section, we use the active control method to achieve complete synchronization of two chaotic systems.
The master and slave systems are described, respectively, as follows:
and
where and are the active controllers. The synchronization errors of the state variable are
Then, one can obtain an error system as
The active controllers are designed as
The errors can be eliminated according to the Routh–Hurwitz stability criterion, and the following active controllers guarantee complete synchronization between the master system (12) and the slave system (13):
In the numerical simulations, we choose the parameters . The initial values of the master and slave systems are taken as and , respectively. Figure 18 displays the time response of the master system (12) and the slave system (13). The error trajectories between the master system and the slave system are shown in Figure 19a, while Figure 19b illustrates the asymptotic convergence of the active controllers to 0. It can be observed that the synchronization errors are asymptotically stable and rapidly achieve synchronization when .
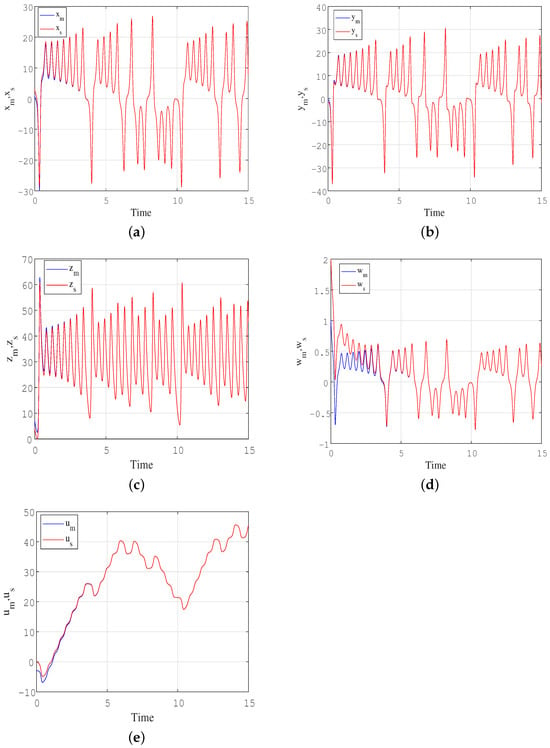
Figure 18.
Coordinates time series of the master system and the slave system showing results of occurrence of synchronization: (a) x variable; (b) y variable; (c) z variable; (d) w variable; (e) u variable.
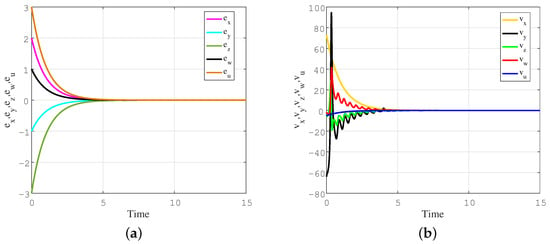
Figure 19.
(a) Synchronization errors evolution between the two memristor-based chaotic systems; (b) time evolution of the active controllers.
Therefore, the research on active synchronization within the proposed memristive chaotic system has significant value for engineering applications. Especially in the secure communication field, the utilization of active synchronization techniques can create synchronized dynamic states between transmitters and receivers, achieving synchronized transmission and decryption of encrypted information. By precisely controlling chaotic synchronization, it is possible to effectively prevent information from being intercepted or tampered with by third parties during transmission, which significantly enhances the security of the communication system.
7. Conclusions
This paper presents a novel 5D memristive chaotic system constructed based on a flux-controlled memristor, which exhibits more complex and richer dynamics than higher-dimensional chaotic systems. Compared to the original system, the novelty of the new system is to have a line equilibrium point, leading to the phenomenon of super-multistability where infinitely many coexisting attractors depend on initial conditions. Additionally, the regularity of unstable periodic orbits in this system is analyzed and discovered for the first time via the variational approach. Specifically, the dynamic characteristics of the system were studied through theoretical analysis and numerical simulation, indicating that the system exhibits extremely complex dynamic behaviors, including hidden transient state and state transition phenomena. At the same time, interesting offset-boosting control was explored using phase portraits and time series diagrams. In particular, by using phase trajectory diagrams based on the initial state changes of memristors, the phenomena of extremely homogeneous and heterogeneous multistability were explored, and an infinite number of coexisting attractors were observed. Moreover, 1D symbolic dynamics was proposed to investigate the unstable periodic orbits in the new system, and the corresponding pruning rules were summarized. Furthermore, the analog and DSP circuit implementation of the memristor-based chaotic system agrees with the numerical simulation results, verifying the flexibility and feasibility of the new system in terms of physical hardware. Finally, active synchronization control for the new system was discussed. The research results presented in this paper provide a theoretical foundation for the application of this system in various engineering fields. For example, in the domain of secure communications, the system can be utilized to develop new encryption algorithms, enhancing the security of data transmission; in the area of signal processing, it can be employed to design sophisticated filters and noise suppression systems, improving the clarity and quality of signals.
Fractional-order chaotic systems can more accurately describe complex nonlinear dynamic behaviors and memory effects by introducing fractional-order calculus. Compared to the integer-order chaotic systems, it has a wider range of dynamic behavior modes and higher model flexibility, thus having more advantages in many practical applications. Therefore, it is very meaningful for us to design the corresponding fractional-order memristor-based systems in our future work. Moreover, determining how to effectively build memristor systems with multi-scroll attractors is also worth further exploration and investigation.
Author Contributions
C.D.: Writing—review and editing, writing—original draft, software, project administration, methodology, investigation, funding acquisition, formal analysis, conceptualization. M.Y.: Writing—review and editing, validation, software, methodology, formal analysis. All authors have read and agreed to the published version of the manuscript.
Funding
This work is supported by the National Natural Science Foundation of China (Grant No. 11647085), Fundamental Research Program of Shanxi Province (Grant No. 202203021221095) and the Graduate Student Innovation Project of Shanxi Province, China (Grant No. 2023KY631).
Data Availability Statement
The data used to support the findings of this study are available from the corresponding author upon request.
Acknowledgments
We thank the anonymous reviewers for their many insightful comments and suggestions, which enhanced the overall quality of our manuscript.
Conflicts of Interest
The authors have no competing interests to declare that are relevant to the content of this article.
References
- Chua, L.O. Memristor-the missing circuit element. IEEE Trans. Circ. Theory 1971, 18, 507–519. [Google Scholar] [CrossRef]
- Strukov, D.B.; Snider, G.S.; Stewart, D.R.; Williams, R.S. The missing memristor found. Nature 2008, 453, 80–83. [Google Scholar] [CrossRef] [PubMed]
- Bao, B.C.; Zou, X.; Liu, Z.; Hu, F. Generalized memory element and chaotic memory system. Int. J. Bifurcat. Chaos 2013, 23, 1350135. [Google Scholar] [CrossRef]
- Bao, B.C.; Xu, J.P.; Liu, Z. Initial state dependent dynamical behaviors in a memristor based chaotic circuit. Chin. Phys. Lett. 2010, 27, 070504. [Google Scholar]
- Wang, X.Y.; Gao, M.; Iu, H.H.C.; Wang, C.H. Tri-valued memristor-based hyper-chaotic system with hidden and coexistent attractors. Chaos Solition Fract. 2022, 159, 112177. [Google Scholar] [CrossRef]
- Huang, L.L.; Liu, S.; Xiang, J.H.; Wang, L.Y. Design and multistability analysis of five-value memristor-based chaotic system with hidden attractors. Chin. Phys. B 2021, 30, 100506. [Google Scholar] [CrossRef]
- Yan, D.W.; Ji’e, M.S.; Wang, L.D.; Duan, S.K. Memristor-based chaotic system with abundant dynamical behaviors and its application. Eur. Phys. J. Plus 2021, 136, 1–27. [Google Scholar] [CrossRef]
- Zhang, X.; Xu, J.; Moshayedi, A.J. Design and FPGA implementation of a hyperchaotic conservative circuit with initial offset-boosting and transient transition behavior based on memcapacitor. Chaos Soliton Frac. 2024, 179, 114460. [Google Scholar] [CrossRef]
- Zhang, J.; Liu, E.; Guo, Y. A new three-dimensional memristor chaotic circuit design and its application in image encryption. J. Supecomput. 2024, 1–31. [Google Scholar] [CrossRef]
- Liu, J.; Xu, R. Adaptive synchronisation of memristor-based neural networks with leakage delays and applications in chaotic masking secure communication. Int. J. Syst. Sci. 2018, 49, 1300–1315. [Google Scholar] [CrossRef]
- Yao, W.; Liu, J.; Sun, Y.; Zhang, J.; Yu, F.; Cui, L.; Lin, H. Dynamics analysis and image encryption application of Hopfield neural network with a novel multistable and highly tunable memristor. Nonlinear Dynam. 2024, 112, 693–708. [Google Scholar] [CrossRef]
- Lai, Q.; Wan, Z.; Zhang, H.; Chen, G. Design and analysis of multiscroll memristive Hopfield neural network with adjustable memductance and application to image encryption. IEEE Trans. Neural Netw. Learn. Syst. 2023, 34, 7824–7837. [Google Scholar] [CrossRef] [PubMed]
- Yao, X.; Chen, X.; Liu, H.; Sun, L.; He, L. Adaptive sliding-mode synchronization of the memristor-based sixth-order uncertain chaotic system and its application in image encryption. Front. Phys. 2022, 10, 863668. [Google Scholar] [CrossRef]
- Lai, Q.; Yang, L.; Chen, G. Design and performance analysis of discrete memristive hyperchaotic systems with stuffed cube attractors and ultraboosting behaviors. IEEE Trans. Ind. Electron. 2023, 71, 7819–7828. [Google Scholar] [CrossRef]
- Vourkas, I.; Sirakoulis, G.C. Emerging memristor-based logic circuit design approaches: A review. IEEE Circ. Syst. Mag. 2016, 16, 15. [Google Scholar] [CrossRef]
- Yu, F.; Zhang, W.; Xiao, X.; Yao, W.; Cai, S.; Zhang, J.; Li, Y. Dynamic analysis and FPGA implementation of a new, simple 5D memristive hyperchaotic Sprott-C system. Mathematics 2023, 11, 701. [Google Scholar] [CrossRef]
- Li, K.; Li, R.; Cao, L.; Feng, Y.; Onasanya, B.O. Periodically intermittent control of memristor-based hyper-chaotic Bao-like system. Mathematics 2023, 11, 1264. [Google Scholar] [CrossRef]
- Wang, Q.; Hu, C.; Tian, Z.; Wu, X.; Sang, H.; Cui, Z. A 3D memristor-based chaotic system with transition behaviors of coexisting attractors between equilibrium points. Results Phys. 2024, 56, 107201. [Google Scholar] [CrossRef]
- Gokyildirim, A.; Yesil, A.; Babacan, Y. Implementation of a memristor-based 4D chaotic oscillator and its nonlinear control. Analog. Integr. Circuits Signal Process. 2022, 110, 91–104. [Google Scholar] [CrossRef]
- Lai, Q.; Wan, Z.; Kengne, L.K.; Kuate, P.D.K.; Chen, C. Two-memristor-based chaotic system with infinite coexisting attractors. IEEE Trans. Circuits Syst. II 2021, 68, 2197–2201. [Google Scholar] [CrossRef]
- Wan, Q.; Li, F.; Yan, Z.; Chen, S.; Liu, J.; Ji, W.; Yu, F. Dynamic analysis and circuit realization of a novel variable-wing 5D memristive hyperchaotic system with line equilibrium. Eur. Phys. J. Spec. Top. 2022, 231, 3029–3041. [Google Scholar] [CrossRef]
- Zhang, S.; Li, C.; Zheng, J.H.; Wang, X.; Zeng, Z.; Peng, X. Generating any number of initial offset-boosted coexisting Chua’s double-scroll attractors via piecewise-nonlinear memristor. IEEE Trans. Ind. Electron. 2022, 69, 7202–7212. [Google Scholar] [CrossRef]
- Yan, S.; Song, Z.; Shi, W.; Shi, W.; Zhao, W.; Ren, Y.; Sun, X. A novel memristor-based dynamical system with chaotic attractor and periodic bursting. Int. J. Bifurc. Chaos 2022, 32, 2250047. [Google Scholar] [CrossRef]
- Kengne, L.K.; Ramadoss, J.; Kengne, J.; Rajagopal, K. Symmetry breaking-induced dynamics for a fourth-order memristor-based chaotic circuit. Circuits Syst. Signal Process. 2022, 41, 3706–3738. [Google Scholar] [CrossRef]
- Wang, Z.; Qi, G. Modeling and analysis of a three-terminal-memristor-based conservative chaotic system. Entropy 2021, 23, 71. [Google Scholar] [CrossRef]
- Li, H.; Yang, Y.; Li, W. Extremely rich dynamics in a memristor-based chaotic system. Eur. Phys. J. Plus 2020, 135, 579. [Google Scholar] [CrossRef]
- Lai, Q.; Chen, Z. Grid-scroll memristive chaotic system with application to image encryption. Chaos Solition Fract. 2023, 170, 113341. [Google Scholar] [CrossRef]
- Lai, Q.; Wan, Z.; Kuate, P.D.K. Generating grid multi-scroll attractors in memristive neural networks. IEEE Trans. Circuits Syst. I 2023, 70, 1324–1336. [Google Scholar] [CrossRef]
- Zhang, G.Z.; Quan, X.; Liu, S. Analysis and FPGA implementation of memristor chaotic system with extreme multistability. Acta Phys. Sin. 2022, 71, 240502. [Google Scholar] [CrossRef]
- Liu, Z.; Lai, Q. A novel memristor-based chaotic system with infinite coexisting attractors and controllable amplitude. Indian J. Phys. 2022, 97, 1159–1167. [Google Scholar] [CrossRef]
- Chang, H.; Li, Y.; Chen, G.; Yuan, F. Extreme multistability and complex dynamics of a memristor-based chaotic system. Int. J. Bifurcat. Chaos 2020, 30, 2030019. [Google Scholar] [CrossRef]
- Singh, P.P.; Rai, A.; Roy, B.K. Memristor-based asymmetric extreme multistable hyperchaotic system with a line of equilibria, coexisting attractors, its implementation and nonlinear active-adaptive projective synchronisation. Eur. Phys. J. Plus 2022, 137, 875. [Google Scholar] [CrossRef]
- Lai, Q.; Chen, Z.; Xu, G.; Liu, F. Analysis and realization of new memristive chaotic system with line equilibria and coexisting attractors. J. Vib. Eng. Technol. 2023, 11, 3493–3505. [Google Scholar] [CrossRef]
- Bao, H.; Hua, M.; Ma, J.; Chen, M.; Bao, B. Offset-control plane coexisting behaviors in two-memristor-based Hopfield neural network. IEEE Trans. Ind. Electron. 2023, 70, 10526–10535. [Google Scholar] [CrossRef]
- Sabarathinam, S.; Papov, V.; Wang, Z.P.; Vadivel, R.; Gunasekaran, N. Dynamics analysis and fractional-order nonlinearity system via memristor-based Chua oscillator. Pramana 2023, 97, 107. [Google Scholar] [CrossRef]
- Wang, M.; Deng, B.; Peng, Y.; Deng, M.; Zhang, Y. Hidden dynamics, synchronization, and circuit implementation of a fractional-order memristor-based chaotic system. Eur. Phys. J. Spec. Top. 2022, 231, 3171–3185. [Google Scholar] [CrossRef]
- Njimah, O.M.; Ramadoss, J.; Telem, A.N.K.; Kengne, J.; Rajagopal, K. Coexisting oscillations and four-scroll chaotic attractors in a pair of coupled memristor-based Duffing oscillators: Theoretical analysis and circuit simulation. Chaos Solition Fract. 2023, 166, 112983. [Google Scholar] [CrossRef]
- Yan, D.; Ji’e, M.; Wang, L.; Duan, S. A novel memristor-based chaotic system with line equilibria and its complex dynamics. Mod. Phys. Lett. B 2021, 35, 2150495. [Google Scholar] [CrossRef]
- Guo, Q.; Wang, N.; Zhang, G. A novel current-controlled memristor-based chaotic circuit. Integration 2021, 80, 20–28. [Google Scholar] [CrossRef]
- Sun, S.; Yan, D.; Ji’e, M.; Du, X.; Wang, L.; Duan, S. Memristor-based time-delay chaotic system with hidden extreme multi-stability and pseudo-random sequence generator. Eur. Phys. J. Spec. Top. 2021, 230, 3481–3491. [Google Scholar] [CrossRef]
- Bao, B.; Hu, W.; Xu, J.; Liu, Z.; Zou, L. Analysis and implementation of memoristor chaotic circuit. Acta Phys. Sin. 2011, 60, 120502. [Google Scholar] [CrossRef]
- Dong, C. Dynamic analysis of a novel 3D chaotic system with hidden and coexisting attractors: Offset boosting, synchronization, and circuit realization. Fractal Fract. 2022, 6, 547. [Google Scholar] [CrossRef]
- Lin, H.; Wang, C.; Yu, F.; Sun, J.; Du, S.; Deng, Z.; Deng, Q. A review of chaotic systems based on memristive Hopfield neural networks. Mathematics 2023, 11, 1369. [Google Scholar] [CrossRef]
- Dong, Q.; Bai, Y.; Zhu, K. A 5-D memristive hyperchaotic system with extreme multistability and its application in image encryption. Phys. Scripta 2024, 99, 035253. [Google Scholar] [CrossRef]
- Huang, L.; Yao, W.; Xiang, J.; Zhang, Z. Heterogeneous and homogenous multistabilities in a novel 4D memristor-based chaotic system with discrete bifurcation diagrams. Complexity 2020, 2020, 2408460. [Google Scholar] [CrossRef]
- Li, C.; Sprott, J.C. Amplitude control approach for chaotic signals. Nonlinear Dynam. 2013, 73, 1335–1341. [Google Scholar] [CrossRef]
- Cvitanović, P.; Artuso, R.; Mainieri, R.; Tanner, G.; Vattay, G.; Whelan, N.; Wirzba, A. Chaos: Classical and Quantum; Niels Bohr Institute: Copenhagen, Denmark, 2016. [Google Scholar]
- Lan, Y.; Cvitanović, P. Variational method for finding periodic orbits in a general flow. Phys. Rev. E 2004, 69, 016217. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.; Mou, J.; Zhang, Y.; Cao, Y. A new hyperchaotic map based on discrete memristor and meminductor: Dynamics analysis, encryption application, and DSP implementation. IEEE Trans. Ind. Electron. 2023, 71, 5094–5104. [Google Scholar] [CrossRef]
- Guo, Z.; Wen, J.; Mou, J. Dynamic analysis and DSP implementation of memristor chaotic systems with multiple forms of hidden attractors. Mathematics 2022, 11, 24. [Google Scholar] [CrossRef]
- Ma, R.R.; Huang, Z.; Xu, H. Fixed-time chaotic stabilization and synchronization of memristor chaotic circuits in noisy environments. J. Korean Phys. Soc. 2024, 84, 90–101. [Google Scholar] [CrossRef]
- Yu, F.; Kong, X.; Yao, W.; Zhang, J.; Cai, S.; Lin, H.; Jin, J. Dynamics analysis, synchronization and FPGA implementation of multiscroll Hopfield neural networks with non-polynomial memristor. Chaos Solition Fract. 2024, 179, 114440. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).