Abstract
In this paper, the discrete octonion linear canonical transform (DOCLCT) is defined. According to the definition of the DOCLCT, some properties associated with the DOCLCT are explored, such as linearity, scaling, boundedness, Plancherel theorem, inversion transform and shift transform. Then, the relationship between the DOCLCT and the three-dimensional (3-D) discrete linear canonical transform (DLCT) is obtained. Moreover, based on a new convolution operator, we derive the convolution theorem of the DOCLCT. Finally, the correlation theorem of the DOCLCT is established.
1. Introduction
The linear canonical transform (LCT) [1,2,3] is a generalized form of the fractional Fourier transform (FrFT). As a linear integral transform with three parameter class, the LCT is more flexible than the FrFT and is a widely used analytical and processing tool in applied mathematics and engineering [4,5,6,7,8]. For analyzing and processing the non-stationary spectrum of finite-duration signals, Pei and Ding [9] proposed the discrete linear canonical transform (DLCT). The DLCT is a very important tool for processing discrete data with a digital camera. Wei et al. [10] studied image encryption using the the random discrete linear canonical transform, which demonstrated that the proposed encryption method is a security-enhanced image encryption scheme. Sun and Li [11] proposed the sliding discrete linear canonical transform and obtained an adaptive method for the computation of the DLCT. Zhang and Li [12] proposed and designed the definition of the DLCT in graph settings. Based on different kinds of DLCTs, several scholars studied many properties and applications [13,14,15,16,17].
Recently, hypercomplex algebras [18,19] are increasingly receiving research interest from scholars. Quaternion algebras are hypercomplex algebras of order 4 and have been widely applied in optical and signal processing [20,21,22]. Urynbassarova et al. [23] extended the DLCT to the quaternion linear canonical transform domain, and proposed the discrete quaternion linear canonical transform (DQLCT). Some properties of the two-dimensional (2-D) DQLCT were derived, such as the shift, modulation, inversion formula and Plancherel theorem. Moreover, they studied the convolution theorem and fast algorithm for the 2-D DQLCT. Based on the 2-D DQLCT, some applications were illustrated by the simulations. Srivastava et al. [24] presented the discrete quadratic-phase Fourier transform. The convolution and correlation theorems for the discrete quadratic-phase Fourier transform were studied.
Octonion algebras [25] are another hypercomplex algebra with order 8 which is the generalized form of the quaternion algebra. Hahn and Snopek [26] proposed the octonion Fourier transform (OFT) and studied the properties. Several applications of the OFT in signal processing were studied in [27,28]. In order to analyze and process the octonion spectrum of finite-duration signals, Błaszczyk [29] exploited the discrete form for the OFT and obtained the discrete octonion Fourier transform (DOFT). According to the DOFT, the analysis of solutions for difference equations and 3-D discrete linear time invariant systems were discussed. Researchers have considered that the linear canonical transform is a general form of the Fourier transform and has good analytical and processing properties [30,31]. We [32] substituted the octonion Fourier kernel function with the octonion linear canonical kernel function and obtained the octonion linear canonical transform (OCLCT). Next, some papers [32,33] discussed many properties and uncertainty principles associated with the OCLCT. Moreover, many scholars [34,35] proposed different transform forms of the OCLCT.
So far, the OCLCT is mainly studied regarding the integral transform of non-stationary continuous signals. As far as we know, the discrete form of the OCLCT has never been published to date. In this paper, in order to study octonion finite-length signals, we propose the discrete octonion linear canonical transform (DOCLCT). The DOCLCT is obtained by replacing the Fourier transform kernel function with the linear canonical transform kernel function based on the octonion algebra setting. Then, several important properties of the DOCLCT are derived, such as linearity, scaling, boundedness, Plancherel theorem inversion transform and shift transform. Moreover, the relation between the DOCLCT and the 3-D DLCT is obtained. The convolution theorem associated with the DOCLCT is presented by a new convolution operator. Finally, the correlation theorem of the DOCLCT is exploited.
This paper is organized as follows: In Section 2, several basic properties of octonion algebra are presented. The definition and the properties of the DOCLCT are obtained in Section 3. In Section 4, the convolution theorem for the DOCLCT is derived. The correlation theorem of the DOCLCT is discussed in Section 5. In Section 6, the conclusions and potential applications are drawn.
2. Preliminaries
This section presents knowledge of octonion algebra [36]. This is the research foundation of this paper.
2.1. Octonion Algebra
Octonion algebra is defined by [36]. An arbitrary can be given by
where . Octonion algebra is a non-associative and non-commutative algebra. Figure 1 presents the multiplication rules of octonion algebra.
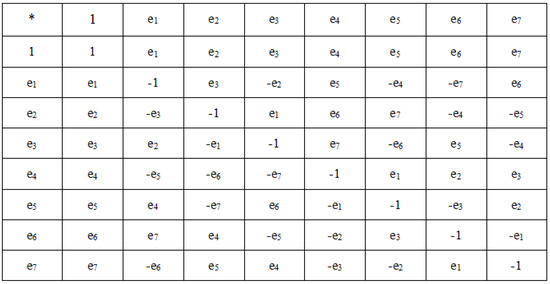
Figure 1.
Multiplication rules in octonion algebra.
The norm of octonion algebra is defined by and . It satisfies for all .
For any octonion algebra, can be represented as
where and are quaternion algebras. That is to say, any octonion algebra can be composed of the sum of two quaternion algebras.
Property 1
([25]). Let . Then, any octonion algebra satisfies the following properties:
Property 2
([25]). For any octonion algebras in the quaternionic form, then the following formulas are right:
According to octonion algebra, we provide the definition of an octonion-valued function. For any octonion-valued function, is defined by
where and are quaternion valued functions. .
For , the norm for the 3-D octonion-valued signal is given by
If , then the norm for the 3-D octonion-valued signal is
2.2. Discrete Linear Canonical Transform
Next, we present the definition of the 3-D DLCT.
Definition 1
([9]). Let be a matrix parameter satisfying (). For any function , the 3-D DLCT is defined by
where the discrete linear canonical transform kernel signal is
where is the periodic sampling interval in the space domain and is the periodic sampling interval in the DLCT domain .
2.3. Discrete Quaternion Linear Canonical Transform
In paper [23], the authors proposed the DQLCT and exploited knowledge about the DQLCT. The DQLCT expands the research scope of the discrete quaternion Fourier transform, and provides a way to solve problems about quaternion non-stationary finite-length signals. Due to the non-commutativity and non-associative properties of quaternion, there are three kinds of DQLCT. The authors of [23] proposed the two-sided DQLCT.
Definition 2
([23]). Let be a matrix parameter satisfying (). The DQLCT of a function is defined by
where the discrete quaternion linear canonical transform kernel signal is
where is the periodic sampling interval in the space domain and is the periodic sampling interval in the DQLCT domain .
The inverse transform of the DQLCT is displayed by
where are inverse matrices.
2.4. Discrete Octonion Fourier Transform
In paper [29], the DOFT of 3-D octonion finite-length signals was given. The DOFT is a very good tool for studying octonion finite-length signals. In the following description, a 3-D octonion finite-length function is equivalent to a 3-D octonion finite-length signal.
Definition 3.
Let a 3-D octonion-valued function be a 3-D finite-length signal and . The DOFT is defined asfollows:
where , , and .
The inverse transform of the DOFT is presented by the following formula [29]:
3. Discrete Octonion Linear Canonical Transform
In this section, based on the DOFT, we extend the 2-D DQLCT to the 3-D discrete octonion linear canonical transform domain. A new transform, the discrete octonion linear canonical transform, is proposed. We can use DOCLCT to solve the problem of non-stationary 3-D octonion finite-length signals.
Definition 4.
The DOCLCT of an octonion-valued signal is defined by
where the kernel signals of the DOCLCT are
and
When (), the DOCLCT reduces to the DOFT.
Properties of the DOCLCT
Next, we present several properties of the DOCLCT.
Theorem 1
(Linearity). For any octonion-valued signals , . Then, the linearity of the DOCLCT is
Proof.
This proof step can be directly obtained by the definition of the DOCLCT. □
Theorem 2
(Scaling). For an octonion-valued signal , . Then, the scaling of the DOCLCT is
where and .
Proof.
According to the definition of the DOCLCT, we have
Let . Then, the above formula becomes
□
Theorem 3.
[Boundedness] Assume that is the even part and is the odd part of a function in the third variable , respectively. Then,
Proof.
According to the Formula (1), the DOCLCT of the function becomes
From the Euler formula, then
where .
Hence, we have the result. □
Theorem 4.
(Plancherel theorem) The Plancherel theorem of the DOCLCT is
Proof.
According to Theorem 3, then
By the Plancherel theorem for the DQLCT [23], we have
In addition, based on the formula
then we have
that is to say
□
Theorem 5
(Inversion transform). The inversion transform of the DOCLCT is obtained as follows:
where and ().
Proof.
According to the definition of the DOCLCT, we have
In addition, by the kernel signals of the DOCLCT, the following formulas hold:
By these three formulas (25), the inverse transform of the DOCLCT can be established. □
The following lemma shows that the DOCLCT can be disassembled by the Euler formula.
Lemma 1.
The DOCLCT can be expressed in another formula:
where
and (). The subscripts e and o indicate a function is either even (e) or odd (o) for an appropriate variable, i.e., is odd for and , and even for .
Proof.
The kernel function of the DOCLCT can be expanded as follows:
By the definition of the DOCLCT, we have the result. □
This lemma eliminates the obstacle caused by the non-commutative and non-associative properties of the DOCLCT.
Next, we give the shift transform of the DOCLCT. There are three forms of the shift function based on three variables, , , and . These three shift functions are independent of each other and are not affected by other remaining variables.
Theorem 6
(Shift transform of the DOCLCT). Let , and denote the DOCLCT of the three shift functions , and , respectively. Then,
where ; ; ; ; ; and , , .
Proof.
We present the proof process for the DOCLCT of the function , and the other two types are obtained according to the same steps.
According to Lemma 1, we have
Then, we can compute the formula:
Let (), hence
where and ().
Let , and
Then, Formula (32) becomes
In addition, we can prove other formulas, such as
By continuing in this way, we have
According to Lemma 1, the first conclusion can be inferred:
where .
4. Convolution Theorem of the DOCLCT
In this section, we first give the definition of the convolution operator associated with the DOCLCT. Then, we obtain the convolution theorem of the DOCLCT by the convolution operator.
Definition 5.
Suppose the real functions and are given; the convolution operator is defined by
where denotes the intervals , .
Lemma 2.
The convolution theorem for the 3-D DLCT is obtained:
Proof.
According to the definition of the 3-D DLCT and the convolution operator, then
Let . Then, the above formula becomes
Since , , . Then, we have
Based on the definition of the 3-D DLCT, we can obtain the proof. □
Next, we obtain the relation between the DOCLCT and the 3-D DLCT. Then, we derive a convolution theorem for the DOCLCT.
Lemma 3.
The relation between the DOCLCT and the 3-D DLCT is given as follows:
where , , , and .
Proof.
According to Definition 1, then
The third equation is based on this fact: .
According to the same method, we can obtain the following two equations:
where (). By the sine and cosine functions, we write the second kernel function of the 3-D DLCT in the cosine and sine forms, respectively.
In Formula (44), if becomes , this multiplies Formula (44) from the right by and according to Figure 1. Hence,
For the convenience of calculation, assume that
By the same steps, we can write in the form
Adding the above two formulas, the following formula is obtained:
Finally, the result can be proven. □
Theorem 7.
The convolution theorem for the DOCLCT is obtained as follows:
where
Proof.
Using Lemma 3, then we have
According to Lemma 2, we obtain
Hence, the result can be obtained. □
5. Correlation Theorem of the DOCLCT
In this section, the correlation operator is presented; then, we obtain the correlation theorem of the DOCLCT.
Definition 6.
Given the real functions and , the correlation operator ⋉ is defined by
Lemma 4.
The correlation theorem for the 3-D DLCT is obtained as follows:
Proof.
The proof process is similar to Lemma 2, so it is omitted. □
According to Lemma 4, we obtain the following theorem:
Theorem 8.
The correlation theorem for the DOCLCT is obtained as follows:
where
Proof.
The proof process is similar to Theorem 7, so it is omitted. □
6. Conclusions
In the present work, the results presented show that the DLCT can be generalized to the case of octonion algebras. We proposed the DOCLCT and studied some basic properties associated with the DOCLCT. Then, according to a new convolution operate, we obtained the convolution theorem of the DOCLCT by the relationship between the DOCLCT and the 3-D DLCT. Finally, the correlation theorem of the DOCLCT was exploited. The properties of the DOCLCT show that they can be used for the analysis of the convolution theorem. The most important contribution of this article is that it provides basic tools for the time–frequency analysis of non-stationary 3-D octonion finite-length signals. The presented results form the foundation of octonion-based signals and system theory.
For applications, the proposed convolution theorem can be used to solve integral equations with special kernels [37]. We can also discuss the design of multiplicative filters with the convolution theorem of the DOCLCT.
We can use the convolution theorem of the DOCLCT in the analysis of some 3-D linear time-invariant systems described in [28]. This hypercomplex generalization of the DOCLCT provides an excellent tool for the analysis of 3-D discrete linear time-invariant systems and 3-D discrete data.
The authors of [38] show how some interesting properties of 1-D complex Gabor filters are extended to 2-D by quaternionic Gabor filters. In parallel, they introduce the corresponding quaternionic Gabor filter-based approach to disparity estimation and texture segmentation. Thus, if one is interested in the development of Gabor filters with values in octonion algebras it is possible to define octonion Gabor filters based on the DOCLCT and to introduce the local octonion phase. This is a theoretical necessity to develop and analyze the DOCLCT.
The DOCLCT is a new concept which allows for the processing of a few gray-scale or color images, as well as images with their local information as one octonion 8-D image in the spectral domain. This concept generalizes the traditional complex and quaternion 2-D DLCTs and can be effectively used for parallel processing up to eight gray-scale images or two color images [39,40]. Surely, the methods presented here are only a first step in using hypercomplex methods in image processing. Detailed work in this area remains in the plan for further action, as well as the further development of this theory.
As a theoretical basis of the frequency-domain definitions of high-dimensional analytic signals, the DOCLCT can be applied in the domain of analytic signals. Other potential applications can be found in noise analysis and image processing, such as the methods presented in [41,42].
Future research will be concerned with extensions of the applications sketched in this paper. Thus, we hope to open a door for future research on high-dimensional signal processing using representations in hypercomplex algebras.
Funding
This work was supported by the National Natural Science Foundation of China (No. 62301474) and the Natural Science Foundation of the Jiangsu Higher Education Institutions of China (No. 23KJB110026).
Data Availability Statement
All the required data are included within the manuscript.
Conflicts of Interest
The author declares no conflicts of interest.
References
- Sun, Y.N.; Qian, W.C. Fast linear canonical transform for nonequispaced Data. Fractal Fract. 2023, 7, 353. [Google Scholar] [CrossRef]
- Yang, Y.N.; Wu, Q.Y.; Jhang, S.T. 2D linear canonical transforms on Lp and applications. Fractal Fract. 2023, 7, 100. [Google Scholar] [CrossRef]
- Chen, Y.; Qu, N. Phase retrieval from linear canonical transforms. Numer. Funct. Anal. Optim. 2022, 43, 1760–1777. [Google Scholar] [CrossRef]
- Wei, D.Y.; Zhang, Y.J.; Li, Y.M. Linear canonical stockwell transform: Theory and applications. IEEE Trans. Signal Process. 2022, 70, 1333–1347. [Google Scholar] [CrossRef]
- Prasad, A.; Kumar, A. Canonical potential and Lp-Sobolev space involving linear canonical Fourier transform. Integral Transform Spec. Funct. 2023, 34, 295–315. [Google Scholar] [CrossRef]
- Prasad, A.; Ansari, Z.A. The wave packet transform in the framework of linear canonical transform. Int. J. Wavelets Multiresolut Inf. Process. 2022, 20, 163–170. [Google Scholar] [CrossRef]
- Shah, F.A.; Tantary, A.Y. Linear canonical ripplet transform: Theory and localization operators. J. Pseudo Differ. Oper. Appl. 2022, 13, 1316–1327. [Google Scholar]
- Gao, W.B.; Li, B.Z. Theories and applications associated with biquaternion linear canonical transform. Math. Methods Appl. Sci. 2023, 46, 13124–13141. [Google Scholar] [CrossRef]
- Pei, S.C.; Ding, J.J. Closed-form discrete fractional and affine Fourier transforms. IEEE Trans. Signal Process. 2000, 48, 1338–1353. [Google Scholar]
- Wei, D.Y.; Wang, R.K.; Li, Y.M. Random discrete linear canonical transform. J. Opt. Soc. Am. A Opt. Image Sci. Vis. 2016, 33, 2470–2476. [Google Scholar] [CrossRef] [PubMed]
- Sun, Y.N.; Li, B.Z. Sliding Discrete Linear Canonical Transform. IEEE Trans. Signal Process. 2018, 66, 4553–4563. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, B.Z. Discrete linear canonical transform on graphs. Digit. Signal Process. 2023, 135, 665–680. [Google Scholar] [CrossRef]
- Koç, A.; Bartan, B.; Ozaktas, H.M. Discrete linear canonical transform based on hyperdifferential operators. IEEE Trans. Signal Process. 2019, 67, 2237–2248. [Google Scholar] [CrossRef]
- Oktem, F.S.; Ozaktas, H. Exact relation between continuous and discrete linear canonical transforms. IEEE Signal Process Lett. 2009, 16, 727–730. [Google Scholar] [CrossRef]
- Shi, J.; Han, M.; Zhang, N.T. Uncertainty principles for discrete signals associated with the fractional Fourier and linear canonical transforms. Signal Image Video Process. 2016, 10, 1519–1525. [Google Scholar] [CrossRef]
- Pei, S.C.; Huang, S.G. Two-dimensional nonseparable discrete linear canonical transform based on CM-CC-CM-CC decomposition. J. Opt. Soc. Am. A Opt. Image Sci. Vis. 2016, 33, 214–227. [Google Scholar] [CrossRef] [PubMed]
- Xu, S.Q.; Feng, L.; Chai, Y.; Cheng, T.L.; He, Y.G. The extrapolation theorem for discrete signals in the offset linear canonical transform domain. Circ. Syst. Signal Process. 2022, 41, 609–620. [Google Scholar] [CrossRef]
- Snopek, K.M. The study of properties of n-D analytic signals and their spectra in complex and hypercomplex domains. Radio Eng. 2012, 21, 29–36. [Google Scholar]
- Sangwine, S.J.; Ell, T.A. Colour image filters based on hypercomplex convolution. IEEE Proc. Vis. Image Signal Process. 2000, 49, 89–93. [Google Scholar] [CrossRef]
- Witten, B.; Shragge, J. Quaternion-based signal processing, stanford exploration project. New Orleans Annu. Meet. 2006, 2006, 2862–2866. [Google Scholar]
- Gao, C.; Zhou, J.; Lang, F.; Pu, Q.; Liu, C. Novel approach to edge detection of color image based on quaternion fractional directional differentation. Adv. Autom. Robot. 2012, 1, 163–170. [Google Scholar]
- Took, C.C.; Mandic, D.P. The quaternion LMS algorithm for adaptive filtering of hypercomplex processes. IEEE Trans. Signal Process. 2009, 57, 1316–1327. [Google Scholar]
- Urynbassarova, D.; Teali, A.A.; Zhang, F. Discrete quaternion linear canonical transform. Digit. Signal Process. 2022, 122, 103361. [Google Scholar] [CrossRef]
- Srivastava, H.M.; Lone, W.Z.; Shah, F.A. Discrete quadratic-phase Fourier transform: Theory and convolution structures. Entropy 2022, 24, 1340. [Google Scholar] [CrossRef] [PubMed]
- Kauhanen, J.; Orelma, H. Cauchy-Riemann operators in octonionic analysis. Adv. Appl. Clifford Algebr. 2018, 1, 1. [Google Scholar] [CrossRef]
- Hahn, S.; Snopek, K. The unified theory of n-dimensional complex and hypercomplex analytic signals. Bull. Pol. Acad. Sci. Tech. Sci. 2011, 56, 167–181. [Google Scholar] [CrossRef]
- Gao, W.B.; Li, B.Z. Octonion short-time Fourier transform for time-frequency representation and its applications. IEEE Trans. Signal Process. 2021, 69, 6386–6398. [Google Scholar] [CrossRef]
- Błaszczyk, Ł. A generalization of the octonion Fourier transform to 3-D octonion-valued signals: Properties and possible applications to 3-D LTI partial differential systems. Multidimens Syst. Signal Process. 2020, 31, 1227–1257. [Google Scholar] [CrossRef]
- Błaszczyk, Ł. Discrete octonion Fourier transform and the analysis of discrete 3-D data. Comput. Appl. Math. 2020, 39, 329. [Google Scholar] [CrossRef]
- Li, X.; Sun, W. Sampling theorems for signals periodic in the linear canonical transform domain. Opt. Commun. 2013, 290, 126–131. [Google Scholar] [CrossRef]
- Chen, X.; Guan, J.; Huang, Y.; Liu, N.; He, Y. Radon-linear canonical ambiguity function-based detection and estimation method for marine target with micromotion. IEEE Trans. Geosci. Remote Sens. 2015, 53, 2225–2240. [Google Scholar] [CrossRef]
- Gao, W.B.; Li, B.Z. The octonion linear canonical transform:Definition and properties. Signal Process. 2021, 188, 108233. [Google Scholar] [CrossRef]
- Gao, W.B.; Li, B.Z. Octonion short-time linear canonical transform. Math. Meth. Appl. Sci. 2023, 1, 321–338. [Google Scholar] [CrossRef]
- Bhat, M.Y.; Dar, A.H. Octonion spectrum of 3D short-time LCT signals. Optik 2021, 261, 169156. [Google Scholar] [CrossRef]
- Bhat, Y.A.; Sheikh, N.A. Octonion offset linear canonical transform. Anal. Math. Phys. 2022, 12, 95. [Google Scholar] [CrossRef]
- Conway, J.H.; Smith, D.A. On Quaternions and Octonions: Their Geometry Arithmetic, and Symmetry; A K Peters Ltd.: Natick, MA, USA, 2003. [Google Scholar]
- Hu, X.X.; Cheng, D.; Kou, K.I. Convolution theorems associated with quaternion linear canonical transform and applications. Signal Process. 2023, 202, 108743. [Google Scholar] [CrossRef]
- Hahn, S.L.; Snopek, K.M. Complex and Hypercomplex Analytic Signals: Theory and Applications; Artech House: Norwood, MA, USA, 2016. [Google Scholar]
- Wang, X.; Wang, C.; Yang, H.; Niu, P. A robust blind color image watermarking in quaternion Fourier transform domain. J. Syst. Softw. 2013, 86, 255–277. [Google Scholar] [CrossRef]
- Alexiadis, D.S.; Sergiadis, G.D. Estimation of motions in color image sequences using hypercomplex Fourier transforms. IEEE Trans. Image Process. 2009, 18, 168–187. [Google Scholar] [CrossRef]
- Sheng, H.D.; Shen, X.J.; Lyu, Y.D.; Shi, Z.N.; Ma, S.Y. Image splicing detection based on Markov features in discrete octonion cosine transform domain. IET Image Process. 2018, 12, 1815–1823. [Google Scholar] [CrossRef]
- Ell, T.; Sangwine, S. Decomposition of 2D hypercomplex Fourier transforms into Pairs of Fourier transforms. In Proceedings of the EUSIPCO, Tampere, Finland, 4–8 September 2000; Volume II. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).