Transient Dynamics of a Fractional Fisher Equation
Abstract
1. Introduction
2. Fractional Fisher Equation
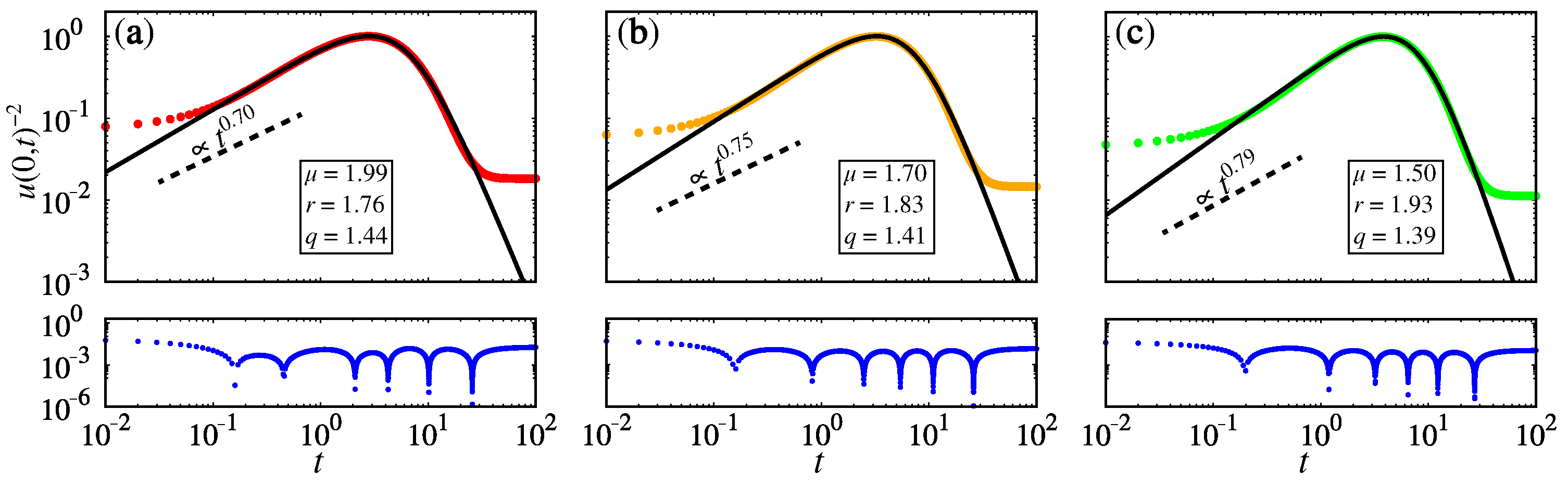
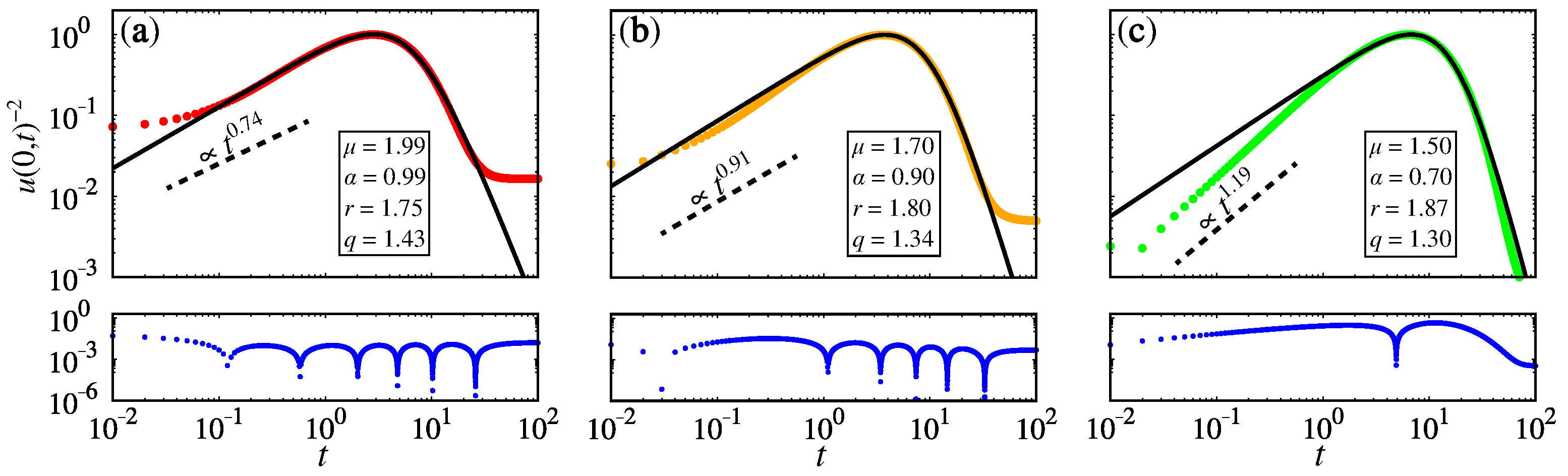
2.1. Time Fractional
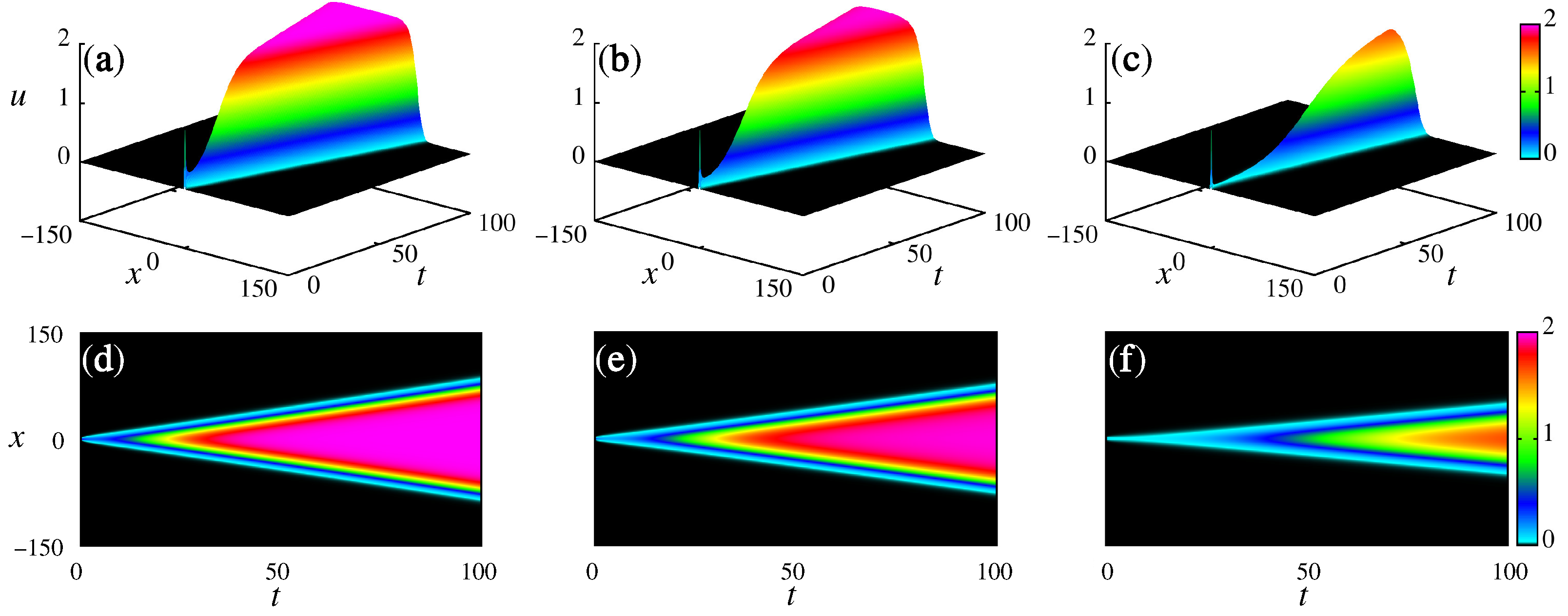
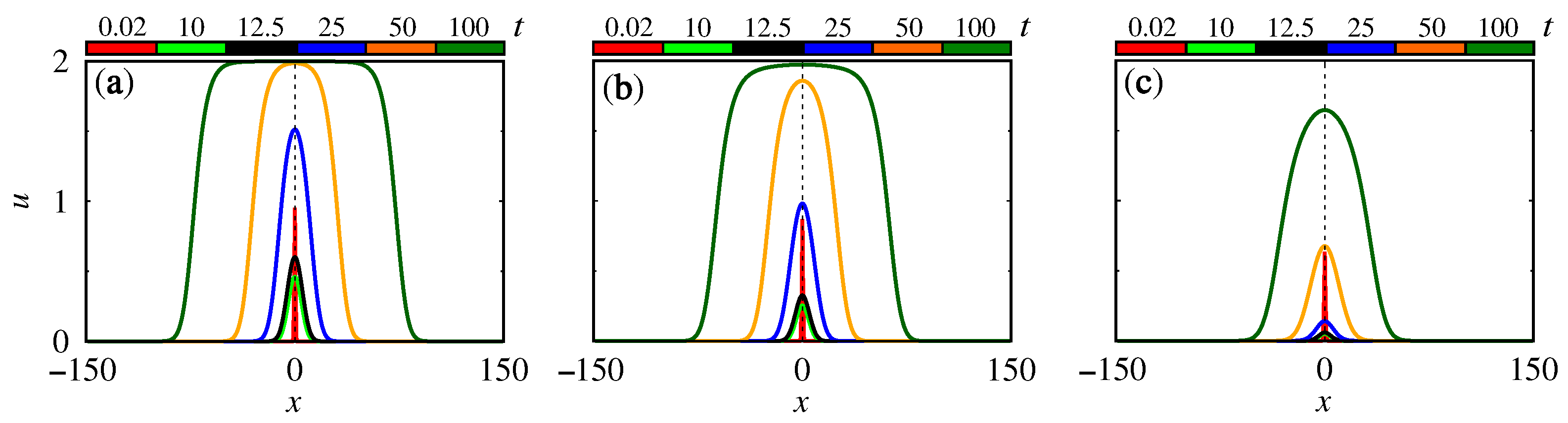
2.2. Space Fractional
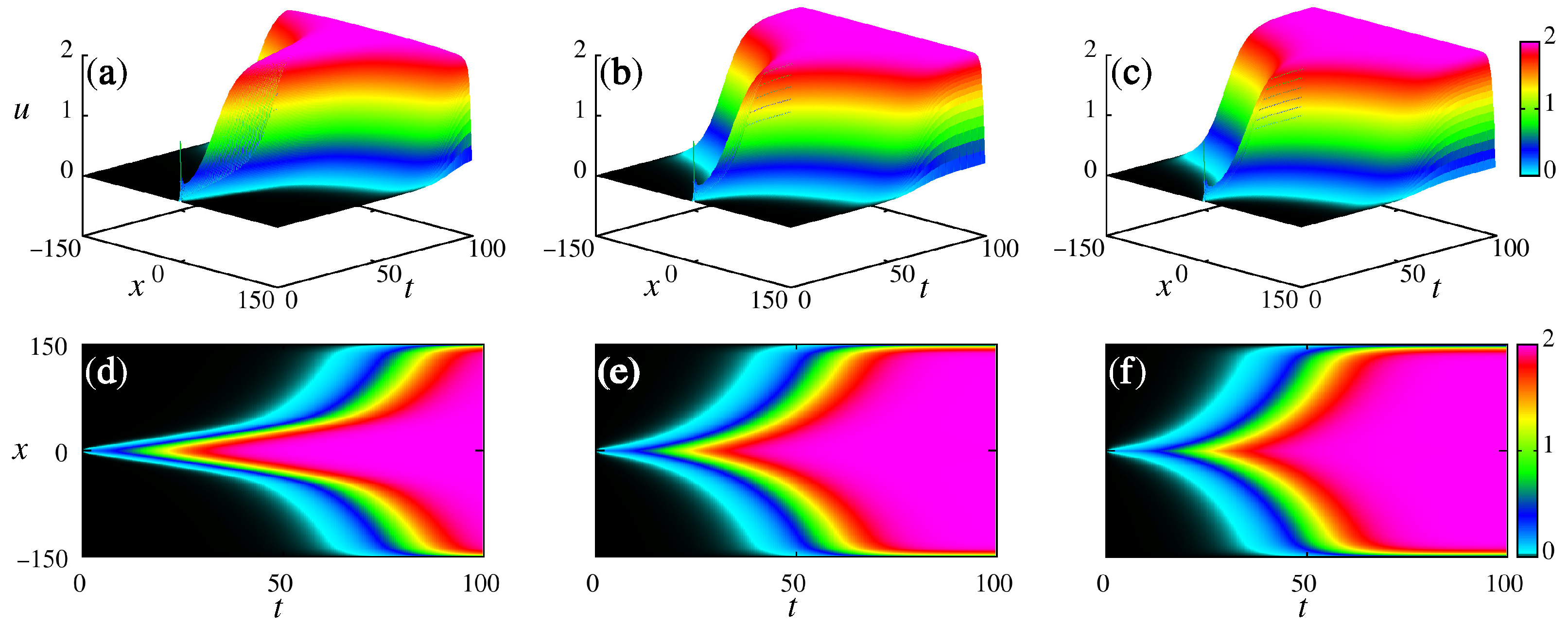
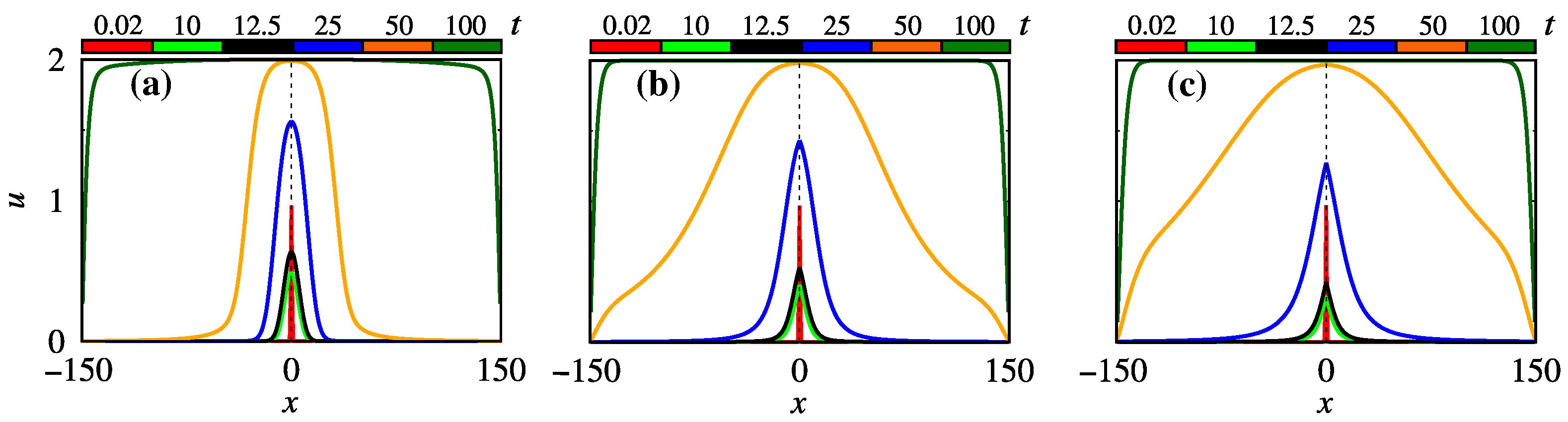
2.3. Time–Space Fractional
3. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhou, Q.; Ekici, M.; Sonmezoglu, A.; Manafian, J.; Khaleghizadeh, S.; Mirzazadeh, M. Exact solitary wave solutions to the generalized Fisher equation. Optik 2016, 127, 12085–12092. [Google Scholar] [CrossRef]
- El-Hachem, M.; McCue, S.W.; Jin, W.; Du, Y.; Simpson, M.J. Revisiting the Fisher–Kolmogorov–Petrovsky–Piskunov equation to interpret the spreading–extinction dichotomy. Proc. R. Soc. A 2019, 475, 20190378. [Google Scholar] [CrossRef] [PubMed]
- Chandraker, V.; Awasthi, A.; Jayaraj, S. A Numerical Treatment of Fisher Equation. Procedia Eng. 2015, 127, 1256–1262. [Google Scholar] [CrossRef]
- Ross, J.; Villaverde, A.F.; Banga, J.R.; Vázquez, S.; Morán, F. A generalized Fisher equation and its utility in chemical kinetics. Proc. Natl. Acad. Sci. USA 2010, 107, 12777–12781. [Google Scholar] [CrossRef] [PubMed]
- Nardini, J.T.; Bortz, D.M. Investigation of a structured Fisher’s equation with applications in biochemistry. SIAM J. Appl. Math. 2018, 78, 1712–1736. [Google Scholar] [CrossRef] [PubMed]
- Kenkre, V. Results from variants of the Fisher equation in the study of epidemics and bacteria. Phys. A Stat. Mech. Appl. 2004, 342, 242–248. [Google Scholar] [CrossRef]
- Wen-Shan, D.; Hong-Juan, Y.; Yu-Ren, S. An exact solution of Fisher equation and its stability. Chin. Phys. 2006, 15, 1414. [Google Scholar] [CrossRef]
- Gazdag, J.; Canosa, J. Numerical solution of Fisher’s equation. J. Appl. Probab. 1974, 11, 445–457. [Google Scholar] [CrossRef]
- Tompson, A.; Dougherty, D. Particle-grid methods for reacting flows in porous media with application to Fisher’s equation. Appl. Math. Model. 1992, 16, 374–383. [Google Scholar] [CrossRef]
- Mavoungou, T.; Cherruault, Y. Numerical study of fisher’s equation by Adomian’s method. Math. Comput. Model. 1994, 19, 89–95. [Google Scholar] [CrossRef]
- Hariharan, G.; Kannan, K.; Sharma, K. Haar wavelet method for solving Fisher’s equation. Appl. Math. Comput. 2009, 211, 284–292. [Google Scholar] [CrossRef]
- Kırlı, E.; Irk, D. Efficient techniques for numerical solutions of Fisher’s equation using B-spline finite element methods. Comput. Appl. Math. 2023, 42, 151. [Google Scholar] [CrossRef]
- Roessler, J.; Hüssner, H. Numerical solution of the 1 + 2 dimensional Fisher’s equation by finite elements and the Galerkin method. Math. Comput. Model. 1997, 25, 57–67. [Google Scholar] [CrossRef]
- Loyinmi, A.; Akinfe, K. Exact solutions to the family of Fisher’s reaction-diffusion equation using Elzaki homotopy transformation perturbation method. Eng. Rep. 2020, 2, e12084. [Google Scholar] [CrossRef]
- Li, W.; Pang, Y. Application of Adomian decomposition method to nonlinear systems. Adv. Differ. Equ. 2020, 2020, 1–17. [Google Scholar] [CrossRef]
- Hariharan, G.; Kannan, K. Haar wavelet method for solving some nonlinear parabolic equations. J. Math. Chem. 2010, 48, 1044–1061. [Google Scholar] [CrossRef]
- Evangelista, L.R.; Lenzi, E.K. An Introduction to Anomalous Diffusion and Relaxation; Springer Nature: Berlin/Heidelberg, Germany, 2023. [Google Scholar]
- Herrmann, R. Fractional Calculus: An Introduction for Physicists; World Scientific: Singapore, 2014. [Google Scholar]
- Guo, B.; Pu, X.; Huang, F. Fractional Partial Differential Equations and Their Numerical Solutions; World Scientific: Singapore, 2015. [Google Scholar]
- Rosseto, M.; Evangelista, L.; Lenzi, E.; Zola, R.; Ribeiro de Almeida, R. Frequency-Dependent Dielectric Permittivity in Poisson–Nernst–Planck Model. J. Phys. Chem. B 2022, 126, 6446–6453. [Google Scholar] [CrossRef]
- Ahmed, H.F. Efficient methods for the analytical solution of the fractional generalized Fisher equation. J. Fract. Calc. Appl. 2019, 10, 85–104. [Google Scholar]
- Hashemi, M.; Baleanu, D. On the Time Fractional Generalized Fisher Equation: Group Similarities and Analytical Solutions. Commun. Theor. Phys. 2016, 65, 11. [Google Scholar] [CrossRef]
- Mirzazadeh, M. A novel approach for solving fractional Fisher equation using differential transform method. Pramana J. Phys. 2016, 86, 957–963. [Google Scholar] [CrossRef]
- Bayrak, M.A.; Demir, A.; Ozbilge, E. On the numerical solution of conformable fractional diffusion problem with small delay. Numer. Methods Partial. Differ. Equ. 2020, 2022, 177–189. [Google Scholar] [CrossRef]
- Majeed, A.; Kamran, M.; Abbas, M.; Singh, J. An Efficient Numerical Technique for Solving Time-Fractional Generalized Fisher’s Equation. Front. Phys. 2020, 8, 1–11. [Google Scholar] [CrossRef]
- Majeed, A.; Kamran, M.; Iqbal, M.K.; Baleanu, D. Solving time fractional Burgers’ and Fisher’s equations using cubic B-spline approximation method. Adv. Differ. Equ. 2020, 2020, 1–15. [Google Scholar] [CrossRef]
- Rashid, S.; Hammouch, Z.; Aydi, H.; Ahmad, A.G.; Alsharif, A.M. Novel Computations of the Time-Fractional Fisher’s Model via Generalized Fractional Integral Operators by Means of the Elzaki Transform. Fractal Fract. 2021, 5, 94. [Google Scholar] [CrossRef]
- Veeresha, P.; Prakasha, D.G.; Baskonus, H.M. Novel simulations to the time-fractional Fisher’s equation. Math. Sci. 2019, 13, 33–42. [Google Scholar] [CrossRef]
- Crank, J. The Mathematics of Diffusion; Oxford University Press: Oxford, UK, 1975. [Google Scholar]
- Picoli, S., Jr.; Mendes, R.S.; Malacarne, L.C.; Lenzi, E.K. Scaling behavior in the dynamics of citations to scientific journals. Europhys. Lett. 2006, 75, 673. [Google Scholar] [CrossRef]
- Picoli, S., Jr.; Mendes, R.S.; Malacarne, L.C.; Santos, R.P.B. q-Distributions in complex systems: A brief review. Braz. J. Phys. 2009, 39, 468–474. [Google Scholar] [CrossRef]
- Tsallis, C. Possible generalization of Boltzmann-Gibbs statistics. J. Stat. Phys. 1988, 52, 479–487. [Google Scholar] [CrossRef]
- Sigalotti, L.D.G.; Ramírez-Rojas, A.; Vargas, C. Tsallis q-Statistics in Seismology. Entropy 2023, 25, 408. [Google Scholar] [CrossRef] [PubMed]
- Murray, J.D. Mathematical Biology: I: An Introduction; Springer: Berlin/Heidelberg, Germany, 2002. [Google Scholar]
- Murray, J.D. Mathematical Biology: II: Spatial Models and Biomedical Applications; Springer: Berlin/Heidelberg, Germany, 2003. [Google Scholar]
- Rahimy, M. Applications of fractional differential equations. Appl. Math. Sci. 2010, 4, 2453–2461. [Google Scholar]
- Evangelista, L.R.; Lenzi, E.K. Fractional Diffusion Equations and Anomalous Diffusion; Cambridge University Press: Cambridge, UK, 2018. [Google Scholar]
- Lenzi, E.; Lenzi, M.; Ribeiro, H.; Evangelista, L. Extensions and solutions for nonlinear diffusion equations and random walks. Proc. R. Soc. A 2019, 475, 20190432. [Google Scholar] [CrossRef]
- Mendez, V.; Fedotov, S.; Horsthemke, W. Reaction-Transport Systems: Mesoscopic Foundations, Fronts, and Spatial Instabilities; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Henry, B.I.; Wearne, S.L. Fractional reaction–diffusion. Phys. Stat. Mech. Appl. 2000, 276, 448–455. [Google Scholar] [CrossRef]
- Henry, B.; Langlands, T.; Wearne, S. Anomalous diffusion with linear reaction dynamics: From continuous time random walks to fractional reaction-diffusion equations. Phys. Rev. E 2006, 74, 031116. [Google Scholar] [CrossRef] [PubMed]
- Guo, X.; Xu, M. Some physical applications of fractional Schrödinger equation. J. Math. Phys. 2006, 47, 082104. [Google Scholar] [CrossRef]
- Gabrick, E.C.; Protachevicz, P.R.; Lenzi, E.K.; Sayari, E.; Trobia, J.; Lenzi, M.K.; Borges, F.S.; Caldas, I.L.; Batista, A.M. Fractional Diffusion Equation under Singular and Non-Singular Kernel and Its Stability. Fractal Fract. 2023, 7, 792. [Google Scholar] [CrossRef]
- Blaszczyk, T.; Bekus, K.; Szajek, K.; Sumelka, W. On numerical approximation of the Riesz–Caputo operator with the fixed/short memory length. J. King Saud Univ. Sci. 2021, 33, 101220. [Google Scholar] [CrossRef]
- Yang, Q.; Liu, F.; Turner, I. Numerical methods for fractional partial differential equations with Riesz space fractional derivatives. Appl. Math. Model. 2010, 34, 200–218. [Google Scholar] [CrossRef]
- Virtanen, P.; Gommers, R.; Oliphant, T.E.; Haberland, M.; Reddy, T.; Cournapeau, D.; Burovski, E.; Peterson, P.; Weckesser, W.; Bright, J.; et al. SciPy 1.0: Fundamental Algorithms for Scientific Computing in Python. Nat. Methods 2020, 17, 261–272. [Google Scholar] [CrossRef]
- Bologna, M.; Tsallis, C.; Grigolini, P. Anomalous diffusion associated with nonlinear fractional derivative Fokker-Planck-like equation: Exact time-dependent solutions. Phys. Rev. E 2000, 62, 2213. [Google Scholar] [CrossRef]
- Tsallis, C.; Lenzi, E. Anomalous diffusion: Nonlinear fractional Fokker–Planck equation. Chem. Phys. 2002, 284, 341–347. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gabrick, E.C.; Protachevicz, P.R.; Souza, D.L.M.; Trobia, J.; Sayari, E.; Borges, F.S.; Lenzi, M.K.; Caldas, I.L.; Batista, A.M.; Lenzi, E.K. Transient Dynamics of a Fractional Fisher Equation. Fractal Fract. 2024, 8, 143. https://doi.org/10.3390/fractalfract8030143
Gabrick EC, Protachevicz PR, Souza DLM, Trobia J, Sayari E, Borges FS, Lenzi MK, Caldas IL, Batista AM, Lenzi EK. Transient Dynamics of a Fractional Fisher Equation. Fractal and Fractional. 2024; 8(3):143. https://doi.org/10.3390/fractalfract8030143
Chicago/Turabian StyleGabrick, Enrique C., Paulo R. Protachevicz, Diogo L. M. Souza, José Trobia, Elaheh Sayari, Fernando S. Borges, Marcelo K. Lenzi, Iberê L. Caldas, Antonio M. Batista, and Ervin K. Lenzi. 2024. "Transient Dynamics of a Fractional Fisher Equation" Fractal and Fractional 8, no. 3: 143. https://doi.org/10.3390/fractalfract8030143
APA StyleGabrick, E. C., Protachevicz, P. R., Souza, D. L. M., Trobia, J., Sayari, E., Borges, F. S., Lenzi, M. K., Caldas, I. L., Batista, A. M., & Lenzi, E. K. (2024). Transient Dynamics of a Fractional Fisher Equation. Fractal and Fractional, 8(3), 143. https://doi.org/10.3390/fractalfract8030143






