Error-Based Switched Fractional Order Model Reference Adaptive Control for MIMO Linear Time Invariant Systems
Abstract
1. Introduction
- This paper proposes an error-based switching mechanism in the design of SFOMRAC schemes for LTI systems. The switching uses the value of the control error to decide whether to use the fractional order or the integer order in the controller parameters adaptive laws. Compared to the previous work [11], the error-based switching is more appealing in practice because it allows for making decisions based on a system signal that can be measured and used as a metric of system performance and stability.
- The SFOMRAC is proposed in this paper for multivariable systems. This is an improvement regarding previous works ([11] and references therein), where only single input, single output systems were considered.
- A complete and thorough analytical proof of stability and convergence of the resulting design is provided in this paper, where the controller will not be limited in advance to switching by a finite amount, as it was in previous works ([11] and some references therein).
- The design and analysis is also carried out for cases when system states are affected by a bounded non-parametric disturbance. This non-ideal case was not addressed in any of the previous works.
- Exhaustive simulation studies are conducted, and numerical results show that the SFOMRAC allows for obtaining a better balance among performance indicator ITAE (Integral of the Time weighted Absolute value of the Error) and control energy ISI (Integral of the Squared Control Signal) for some switching error levels, leading to an improved control strategy compared to the classical non-switched integer-order (MRAC) and fractional-order (FOMRAC) schemes.
2. Basic Concepts
2.1. Notation and Basic Definitions
2.2. Elements of Fractional Calculus
2.3. Analytical Tools
- The function V is convex on and .
- The function V is differentiable on .
3. Problem Statement and Proposed Control Scheme
3.1. Control Problem
3.2. Proposed Control Strategy
3.3. Closed-Loop Description
3.4. Main Results
4. Influence of Controller Parameters in the Resulting Control Energy and System Performance: Simulation Studies
4.1. Performance Indices to Evaluate a Controlled System
4.2. Simulation Details
- If the , then the set of switching error levels to be tested in simulations was selected within a 0.025 difference among them in the whole interval .
- If the , then the set of switching error levels to be tested in simulations was selected within a 0.05 difference among them in the whole interval .
- If the , then the set of switching error levels to be tested in simulations was selected within a 0.125 difference among them in the whole interval .
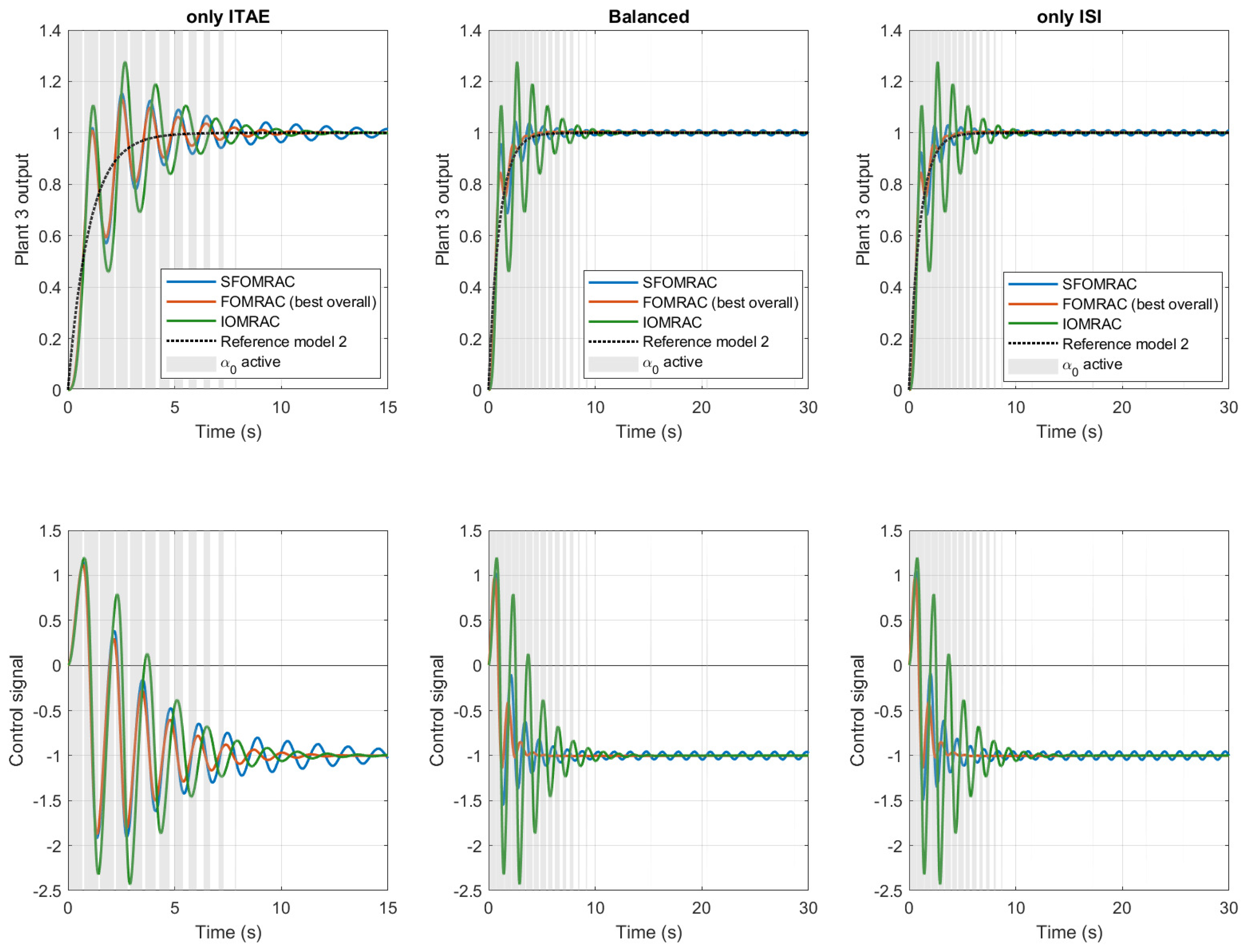
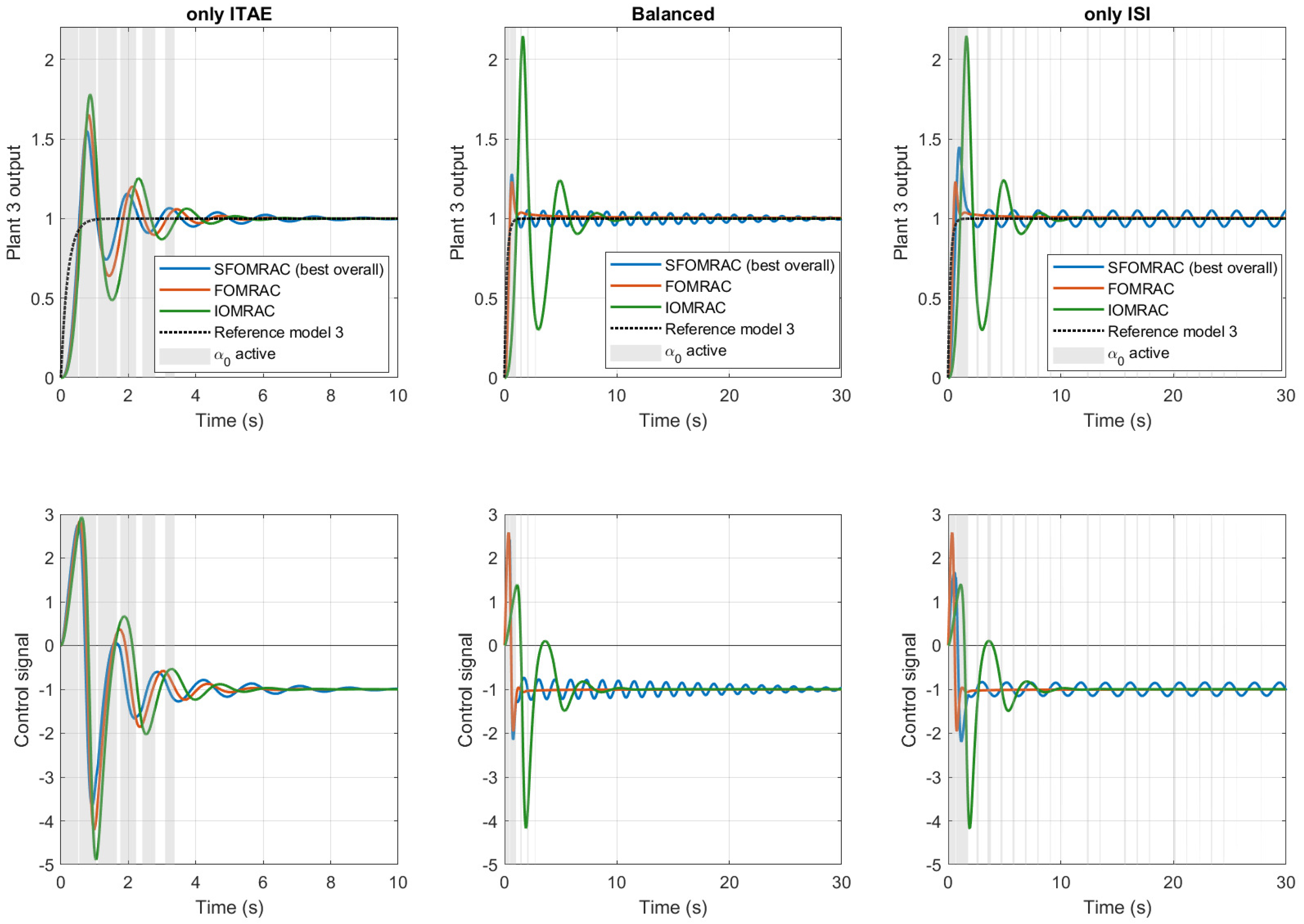
4.3. Analysis of the Results Obtained from Simulation Studies
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations, Volume 204 (North-Holland Mathematics Studies); Elsevier Science Inc.: San Diego, CA, USA, 2006. [Google Scholar]
- Ladaci, S.; Loiseau, J.J.; Charef, A. Fractional order adaptive high-gain controllers for a class of linear systems. Commun. Nonlinear Sci. Numer. Simul. 2008, 13, 707–714. [Google Scholar] [CrossRef]
- Vinagre, B.; Petrás, I.; Podlubny, I.; Chen, Y. Using fractional order adjustment rules and fractional order reference models in model-reference adaptive control. Nonlinear Dyn. 2002, 29, 269–279. [Google Scholar] [CrossRef]
- Suárez, J.; Vinagre, B.; Chen, Y. A fractional adaptation scheme for lateral control of an AGV. J. Vib. Control 2008, 14, 1499–1511. [Google Scholar] [CrossRef]
- Lee, C.; Chang, F. Fractional-order PID controller optimization via improved electromagnetism-like algorithm. Expert Syst. Appl. 2010, 37, 8871–8878. [Google Scholar] [CrossRef]
- Basilio, J.; Oliveira, T.; Ribeiro, J.; Cunha, A. Evaluation of Fractional-Order Sliding Mode Control applied to an energy harvesting system. In Proceedings of the 16th International Workshop on Variable Structure Systems, Rio de Janeiro, Brazil, 11–14 September 2022. [Google Scholar]
- Aguila-Camacho, N.; Duarte-mermoud, M.A. Improving the control energy in model reference adaptive controllers using fractional adaptive laws. IEEE/CAA J. Autom. Sin. 2016, 3, 332–337. [Google Scholar] [CrossRef]
- Afghoul, H.; Krim, F.; Chikouche, D.; Beddar, A. Robust switched fractional controller for performance improvement of single phase active power filter under unbalanced conditions. Front. Energy 2016, 10, 203–212. [Google Scholar] [CrossRef]
- Afghoul, H.; Krim, F.; Beddar, A.; Houabes, M. Switched fractional order controller for grid connected wind energy conversion system. In Proceedings of the 5th International Conference on Electrical Engineering, Boumerdes, Algeria, 29–31 October 2017. [Google Scholar]
- Beddar, A.; Bouzekri, H. Design and real-time implementation of hybrid fractional order controller for grid connected wind energy conversion system. Int. J. Model. Identif. Control 2018, 19, 315–326. [Google Scholar] [CrossRef]
- Aguila-Camacho, N.; García-Bustos, J.E.; Castillo-López, E.I.; Gallegos, J.A.; Travieso-Torres, J.C. Switched Fractional Order Model Reference Adaptive Control for First Order Plants: A Simulation-Based Study. J. Dyn. Syst. Meas. Control-Trans. ASME 2022, 144, 044502. [Google Scholar] [CrossRef]
- Diethelm, K. The Analysis of Fractional Differential Equations: An Application-Oriented Exposition Using Operators of Caputo Type; Springer: Berlin, Germany, 2004. [Google Scholar]
- Gallegos, J.; Aguila-Camacho, N.; Duarte-Mermoud, M. Smooth Solutions to mixed-order fractional differential systems with applications to stability analysis. J. Integral Equations Appl. 2019, 31, 59–84. [Google Scholar] [CrossRef]
- Tuan, H.; Trinh, H. Stability of fractional-order nonlinear systems by Lyapunov direct method. IET Control. Theory Appl. 2018, 12, 2417–2422. [Google Scholar] [CrossRef]
- Tao, G. Adaptive Control Design and Analysis; John Wiley & Sons: Hoboken, NJ, USA, 2003. [Google Scholar]
- Narendra, K.; Annaswamy, A. Stable Adaptive Systems; Dover Publications: Mineola, NY, USA, 2005. [Google Scholar]
- Lavretsky, E.; Gibson, T.E. Projection Operator in Adaptive Systems. arXiv 2012, arXiv:1112.4232. [Google Scholar]
- Valerio, D.; Da Costa, J.S. Ninteger: A non-integer control toolbox for MatLab. In Proceedings of the 1st International Conference on Fractional Differentiation and its Applications (ICFDA), Bordeaux, France, 19–21 July 2004. [Google Scholar]

| Plant 1 | −1 | 1 | Reference model 1 | −0.5 | 0.5 |
| Plant 2 | −10 | 10 | Reference model 2 | −1 | 1 |
| Plant 3 | 1 | 1 | Reference model 3 | −5 | 5 |
| Plant 4 | 10 | 10 | Reference model 4 | −10 | 10 |
| Plant 1: Stable with pole in | |||||||||||
| min | Controller | ||||||||||
| 1 | 0 | 0 | FOMRAC | 1 | 0.1 | - | - | 436.156 | 3435.24 | ||
| 0 | 1 | 0 | SFOMRAC | 10 | 0.5 | 0.0897 | 0.05 | 498.243 | 0.235 | ||
| 0.5 | −0.5 | 0.5 | 0.5 | 0.297 | SFOMRAC | 1 | 0.1 | 0.381 | 0.15 | 459.518 | 918.165 |
| 0.3 | 0.7 | 0.228 | SFOMRAC | 1 | 0.1 | 0.381 | 0.30 | 481.697 | 177.248 | ||
| 0.7 | 0.3 | 0.263 | SFOMRAC | 1 | 0.1 | 0.381 | 0.05 | 444.048 | 2129.20 | ||
| 1 | 0 | 0 | FOMRAC | 1 | 0.1 | - | - | 437.463 | 3403.41 | ||
| 0 | 1 | 0 | SFOMRAC | 10 | 0.5 | 0.161 | 0.05 | 500.033 | 0.346 | ||
| 1 | −1 | 0.5 | 0.5 | 0.297 | SFOMRAC | 1 | 0.1 | 0.461 | 0.15 | 460.725 | 896.975 |
| 0.3 | 0.7 | 0.226 | SFOMRAC | 1 | 0.1 | 0.461 | 0.30 | 480.037 | 219.197 | ||
| 0.7 | 0.3 | 0.264 | SFOMRAC | 1 | 0.1 | 0.461 | 0.10 | 445.614 | 2083.60 | ||
| 1 | 0 | 0 | FOMRAC | 1 | 0.1 | - | - | 438.530 | 3370.86 | ||
| 0 | 1 | 0 | SFOMRAC | 10 | 0.3 | 0.387 | 0.05 | 502.547 | 0.301 | ||
| 5 | −5 | 0.5 | 0.5 | 0.274 | SFOMRAC | 1 | 0.1 | 0.721 | 0.20 | 470.487 | 511.406 |
| 0.3 | 0.7 | 0.201 | SFOMRAC | 1 | 0.1 | 0.721 | 0.30 | 481.916 | 192.159 | ||
| 0.7 | 0.3 | 0.258 | SFOMRAC | 1 | 0.1 | 0.721 | 0.05 | 447.679 | 2008.66 | ||
| 1 | 0 | 0 | FOMRAC | 1 | 0.1 | - | - | 438.661 | 3336.77 | ||
| 0 | 1 | 0 | SFOMRAC | 10 | 0.3 | 0.541 | 0.05 | 503.534 | 0.298 | ||
| 10 | −10 | 0.5 | 0.5 | 0.276 | SFOMRAC | 1 | 0.1 | 0.815 | 0.15 | 465.228 | 765.521 |
| 0.3 | 0.7 | 0.201 | SFOMRAC | 1 | 0.1 | 0.815 | 0.30 | 484.020 | 157.073 | ||
| 0.7 | 0.3 | 0.259 | SFOMRAC | 1 | 0.1 | 0.815 | 0.05 | 448.148 | 1990.14 | ||
| Plant 2: Stable with pole in | |||||||||||
| 1 | 0 | 0 | FOMRAC | 1 | 0.1 | - | - | 435.101 | 3456.47 | ||
| 0 | 1 | 0 | SFOMRAC | 10 | 0.9 | 0.5185 | 0.05 | 497.045 | 0.104 | ||
| 0.5 | −0.5 | 0.5 | 0.5 | 0.317 | SFOMRAC | 1 | 0.1 | 0.352 | 0.15 | 458.488 | 895.718 |
| 0.3 | 0.7 | 0.249 | SFOMRAC | 1 | 0.1 | 0.352 | 0.25 | 475.929 | 262.677 | ||
| 0.7 | 0.3 | 0.273 | SFOMRAC | 1 | 0.1 | 0.352 | 0.05 | 442.999 | 2123.50 | ||
| 1 | 0 | 0 | FOMRAC | 1 | 0.1 | - | - | 436.386 | 3418.62 | ||
| 0 | 1 | 0 | SFOMRAC | 10 | 0.6 | 0.588 | 0.05 | 498.551 | 0.049 | ||
| 1 | −1 | 0.5 | 0.5 | 0.314 | SFOMRAC | 1 | 0.1 | 0.377 | 0.15 | 459.609 | 879.322 |
| 0.3 | 0.7 | 0.244 | SFOMRAC | 1 | 0.1 | 0.377 | 0.30 | 479.012 | 196.760 | ||
| 0.7 | 0.3 | 0.273 | SFOMRAC | 1 | 0.1 | 0.377 | 0.05 | 444.543 | 2077.013 | ||
| 1 | 0 | 0 | FOMRAC | 1 | 0.1 | - | - | 431.396 | 3390.67 | ||
| 0 | 1 | 0 | SFOMRAC | 10 | 0.4 | 0.157 | 0.15 | 499.800 | 0.008 | ||
| 5 | −5 | 0.5 | 0.5 | 0.317 | SFOMRAC | 1 | 0.1 | 0.447 | 0.15 | 462.557 | 788.290 |
| 0.3 | 0.7 | 0.243 | SFOMRAC | 1 | 0.1 | 0.447 | 0.25 | 475.490 | 294.819 | ||
| 0.7 | 0.3 | 0.279 | SFOMRAC | 1 | 0.1 | 0.447 | 0.05 | 446.567 | 2002.01 | ||
| 1 | 0 | 0 | FOMRAC | 1 | 0.1 | - | - | 437.528 | 3387.29 | ||
| 0 | 1 | 0 | SFOMRAC | 10 | 0.5 | 0.311 | 0.05 | 499.963 | 0.009 | ||
| 10 | −10 | 0.5 | 0.5 | 0.321 | SFOMRAC | 1 | 0.1 | 0.524 | 0.15 | 464.131 | 735.770 |
| 0.3 | 0.7 | 0.243 | SFOMRAC | 1 | 0.1 | 0.524 | 0.25 | 477.619 | 250.128 | ||
| 0.7 | 0.3 | 0.281 | SFOMRAC | 1 | 0.1 | 0.524 | 0.05 | 447.013 | 1982.203 | ||
| Plant 3: Unstable with pole in | |||||||||||
| min | Controller | ||||||||||
| 1 | 0 | 0 | FOMRAC | 10 | 0.7 | - | - | 496.808 | 5.841 | ||
| 0 | 1 | 0 | FOMRAC | 10 | 0.8 | - | - | 496.872 | 2.882 | ||
| 0.5 | −0.5 | 0.5 | 0.5 | 0.0001 | FOMRAC | 10 | 0.7 | - | - | 496.808 | 5.841 |
| 0.3 | 0.7 | 0.00014 | FOMRAC | 10 | 0.7 | - | - | 496.808 | 5.841 | ||
| 0.7 | 0.3 | 0.00006 | FOMRAC | 10 | 0.7 | - | - | 496.808 | 5.841 | ||
| 1 | 0 | 0 | FOMRAC | 10 | 0.7 | - | - | 498.921 | 5.706 | ||
| 0 | 1 | 0 | FOMRAC | 10 | 0.9 | - | - | 500.300 | 2.529 | ||
| 1 | −1 | 0.5 | 0.5 | 0.00011 | FOMRAC | 10 | 0.7 | - | - | 498.921 | 5.706 |
| 0.3 | 0.7 | 0.00015 | FOMRAC | 10 | 0.7 | - | - | 498.921 | 5.706 | ||
| 0.7 | 0.3 | 0.00006 | FOMRAC | 10 | 0.7 | - | - | 498.921 | 5.706 | ||
| 1 | 0 | 0 | SFOMRAC | 10 | 0.5 | 0.447 | 0.05 | 502.681 | 7.637 | ||
| 0 | 1 | 0 | SFOMRAC | 10 | 0.8 | 0.553 | 0.05 | 505.226 | 1.105 | ||
| 5 | −5 | 0.5 | 0.5 | 0.00023 | SFOMRAC | 10 | 0.5 | 0.447 | 0.05 | 502.681 | 7.637 |
| 0.3 | 0.7 | 0.00033 | SFOMRAC | 10 | 0.5 | 0.447 | 0.05 | 502.681 | 7.637 | ||
| 0.7 | 0.3 | 0.00014 | SFOMRAC | 10 | 0.5 | 0.447 | 0.05 | 502.681 | 7.637 | ||
| 1 | 0 | 0 | SFOMRAC | 4 | 0.5 | 0.736 | 0.05 | 503.248 | 69.481 | ||
| 0 | 1 | 0 | SFOMRAC | 10 | 0.8 | 0.719 | 0.05 | 506.839 | 0.921 | ||
| 10 | −10 | 0.5 | 0.5 | 0.0017 | SFOMRAC | 6 | 0.5 | 0.684 | 0.05 | 503.395 | 14.353 |
| 0.3 | 0.7 | 0.0014 | SFOMRAC | 6 | 0.5 | 0.684 | 0.05 | 503.395 | 14.353 | ||
| 0.7 | 0.3 | 0.0015 | SFOMRAC | 4 | 0.5 | 0.736 | 0.05 | 503.248 | 69.481 | ||
| Plant 4: Unstable with pole in | |||||||||||
| 1 | 0 | 0 | SFOMRAC | 7 | 0.3 | 0.053 | 0.05 | 497.173 | 52.706 | ||
| 0 | 1 | 0 | SFOMRAC | 10 | 0.8 | 0.491 | 0.35 | 497.227 | 0.346 | ||
| 0.5 | −0.5 | 0.5 | 0.5 | 0.00012 | SFOMRAC | 10 | 0.7 | 0.231 | 0.2 | 497.198 | 0.554 |
| 0.3 | 0.7 | 0.00008 | SFOMRAC | 10 | 0.7 | 0.231 | 0.2 | 497.198 | 0.554 | ||
| 0.7 | 0.3 | 0.00016 | SFOMRAC | 10 | 0.7 | 0.231 | 0.2 | 497.198 | 0.554 | ||
| 1 | 0 | 0 | SFOMRAC | 9 | 0.3 | 0.05 | 0.05 | 498.704 | 28.036 | ||
| 0 | 1 | 0 | SFOMRAC | 10 | 0.8 | 0.51 | 0.5 | 498.761 | 0.286 | ||
| 1 | −1 | 0.5 | 0.5 | 0.00011 | SFOMRAC | 10 | 0.7 | 0.234 | 0.2 | 498.726 | 0.601 |
| 0.3 | 0.7 | 0.00008 | SFOMRAC | 10 | 0.7 | 0.234 | 0.2 | 498.726 | 0.601 | ||
| 0.7 | 0.3 | 0.00014 | SFOMRAC | 10 | 0.7 | 0.234 | 0.2 | 498.726 | 0.601 | ||
| 1 | 0 | 0 | SFOMRAC | 10 | 0.2 | 0.089 | 0.075 | 499.862 | 6.280 | ||
| 0 | 1 | 0 | SFOMRAC | 10 | 0.9 | 0.791 | 0.75 | 500.154 | 0.216 | ||
| 5 | −5 | 0.5 | 0.5 | 0.00026 | SFOMRAC | 10 | 0.4 | 0.157 | 0.15 | 499.900 | 1.609 |
| 0.3 | 0.7 | 0.00023 | SFOMRAC | 10 | 0.4 | 0.157 | 0.15 | 499.900 | 1.609 | ||
| 0.7 | 0.3 | 0.00025 | SFOMRAC | 10 | 0.2 | 0.089 | 0.075 | 499.862 | 6.280 | ||
| 1 | 0 | 0 | SFOMRAC | 10 | 0.2 | 0.162 | 0.15 | 500.00 | 1.399 | ||
| 0 | 1 | 0 | SFOMRAC | 10 | 0.8 | 0.761 | 0.75 | 500.364 | 0.168 | ||
| 10 | −10 | 0.5 | 0.5 | 0.00008 | SFOMRAC | 10 | 0.2 | 0.162 | 0.15 | 500.00 | 1.399 |
| 0.3 | 0.7 | 0.00012 | SFOMRAC | 10 | 0.2 | 0.162 | 0.15 | 500.00 | 1.399 | ||
| 0.7 | 0.3 | 0.00005 | SFOMRAC | 10 | 0.2 | 0.162 | 0.15 | 500.00 | 1.399 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aguila-Camacho, N.; Gallegos, J.A. Error-Based Switched Fractional Order Model Reference Adaptive Control for MIMO Linear Time Invariant Systems. Fractal Fract. 2024, 8, 109. https://doi.org/10.3390/fractalfract8020109
Aguila-Camacho N, Gallegos JA. Error-Based Switched Fractional Order Model Reference Adaptive Control for MIMO Linear Time Invariant Systems. Fractal and Fractional. 2024; 8(2):109. https://doi.org/10.3390/fractalfract8020109
Chicago/Turabian StyleAguila-Camacho, Norelys, and Javier A. Gallegos. 2024. "Error-Based Switched Fractional Order Model Reference Adaptive Control for MIMO Linear Time Invariant Systems" Fractal and Fractional 8, no. 2: 109. https://doi.org/10.3390/fractalfract8020109
APA StyleAguila-Camacho, N., & Gallegos, J. A. (2024). Error-Based Switched Fractional Order Model Reference Adaptive Control for MIMO Linear Time Invariant Systems. Fractal and Fractional, 8(2), 109. https://doi.org/10.3390/fractalfract8020109






