1. Introduction
How to exhibit bifurcation analysis, set up a graph related to Lyapunov exponents, or find a positive topological entropy about higher-dimensional systems with the fractional diffusion coupling under the classical boundary conditions are naturally interesting problems. We can refer the readers to see open problem 2 in [
1] (p. 14) or those in [
2], etc. However, to the best of our knowledge, few researchers have paid their attention to these problems. Thus, how to define the action of fractional diffusion operators on discrete-time dynamical systems, for instance, remains unclear. In this paper, we shall try to answer this question.
We have found that Neimark–Sacker bifurcations can be caused by Turing instability. Thus, a scheme needs to be built about Neimark–Sacker bifurcations in types of discrete-time dynamical systems under linear fractional diffusion coupling with Direchlet/Neumann/periodic-boundary conditions. We explore the complexity induced by the diffusion coupling. Bifurcation analysis is set up and chaotic Turing patterns are shown by the occurrence of positive Lyapunov exponents. Our stimulating model can be viewed as an interesting case study of the following phenomenon: individuals exhibit simple dynamics, but when viewed as a whole, the dynamical behavior of diffusion coupling is very complicated, specifically things such as the existence of fluctuation, limit cycles, and even chaos. This interesting phenomenon was also called Emergence by Holland in [
3]: the diffusion can set up Turing instability and then regular/chaotic patterns in a simple system, and multiple attractive patterns can emerge.
Naturally, there has been some research about some discrete-time dynamical systems by diffusion coupling with classical boundary conditions; for example, p-2 patterns in [
4] for two-dimensional systems and in [
1,
2] for higher-dimensional systems (
). To the best of our knowledge, there few researchers have been concerned with Neimark–Sacker bifurcations analysis on discrete-time dynamical systems with diffusion and delayed coupling under the given classical boundary conditions.
A framework about Hopf bifurcating analysis on high-dimensional discrete-time dynamical systems has been provided by [
5] (pp. 185–187), but it is unknown how to compute formulae (5.50) or (5.51) in [
5] (p. 186). In this paper, we give a clear presentation of this, and regular/chaotic oscillating Turing patterns are the main topics in the present paper.
We investigate the dynamical behavior of discrete-time dynamical systems with the fractional diffusion operator as follows:
under the Neumann-boundary condition:
or the periodic-boundary condition:
and
is defined by the Caputo-like fractional diffusion difference operator, and if
, then:
where
are positive integers and
. This may be a very interesting problem, including the idea about how to define the Caputo-like diffusion difference operator, how to determine its dynamical behavior in discrete-time dynamical systems, etc. Until now, there have been few works concerned with such a question. We investigate some interesting phenomena, i.e., the occurrence of fractional impact on discrete-time dynamical systems.
The single individual model was discussed in [
6], which can be viewed as a model about the nonlinear delayed feedback control on classical chaotic Rulkov maps [
7,
8]. There may exist a delay during processing information in intra-neural communication [
9], information propagation through the cortical network [
10], or simulating the finite transmission velocity through the network node [
11,
12]. For other works related to physical connections with/without delay coupling, we refer the readers to Refs. [
7,
13,
14,
15,
16,
17,
18,
19].
Compared to those discussed in [
6,
20,
21,
22,
23,
24,
25,
26,
27,
28,
29,
30], there occurs a new class of characteristic polynomials in the present as follows:
which is essentially different when compared with those in [
6]. For instance, one can find that there are two pairs of complex conjugate eigenvalues lying on the critical unit circle for
, though when diffusion emerges (
), there is only one pair of complex conjugate eigenvalues with a modulus equal to 1. In fact,
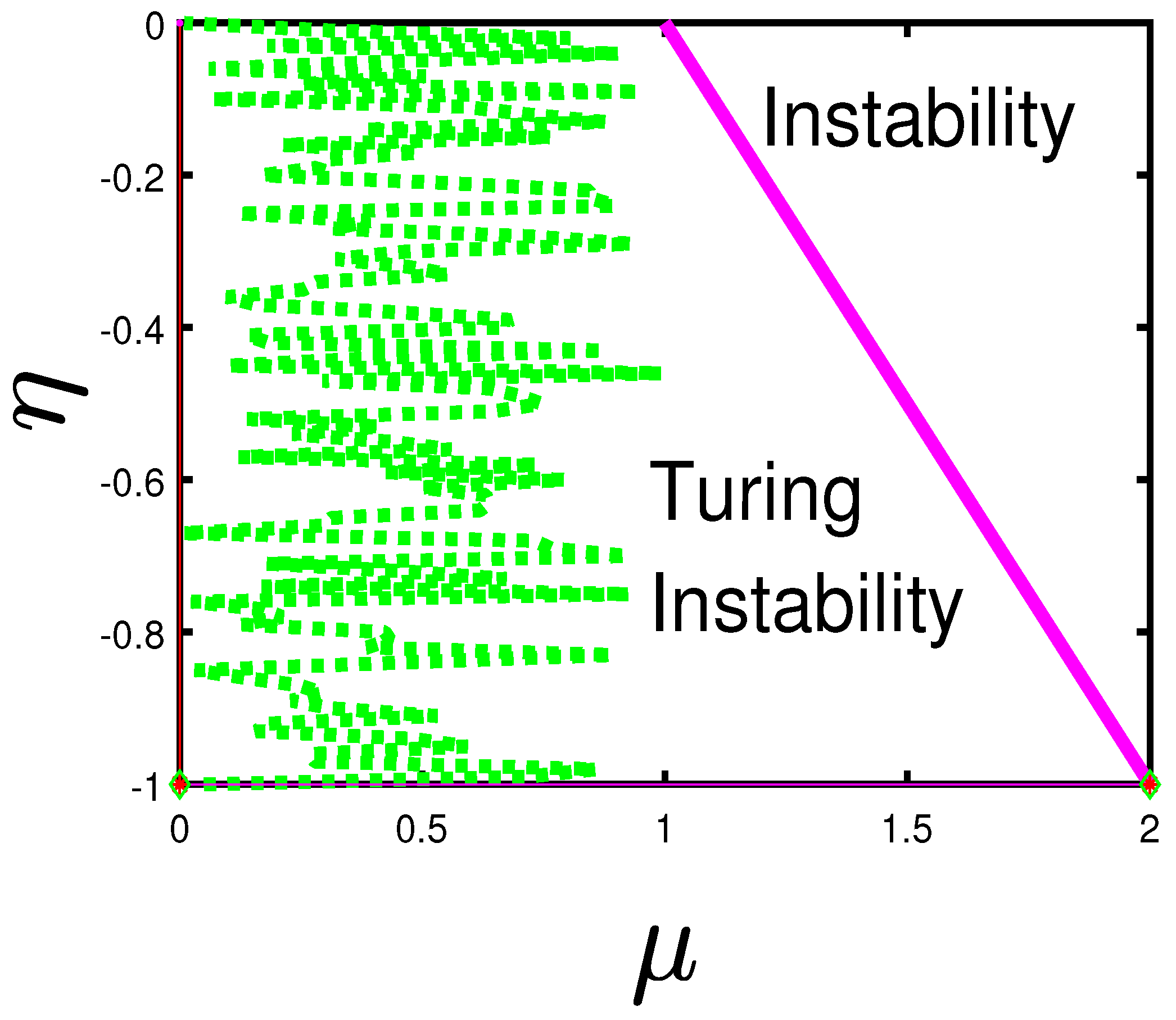
occurs (please see
Figure 1). Moreover, in [
28], it was pointed out that delay can induce a larger stable region (
) [
6] or smaller
and
.This implies that the delayed feedback control may not be an efficient control method, even though it is widely used.
The following is the novelty in this paper:
Build up the framework for Neimark–Sacker bifurcations caused by Turing instability on high-dimensional discrete-time dynamical systems with symmetrical property in the linearized system;
Design bifurcation diagrams and the graphs about Lyapunov exponents;
Introduce the fractional diffusion operator in higher-dimensional discrete dynamical systems.
Now let us list the structure of the rest part of this paper as follows. A framework for Neimark–Sacker bifurcation is presented in
Section 2 for
. Turing instability is analyzed. Eigenvalue problems are also discussed and numerical simulation is shown. Bifurcation diagrams are proposed and regular/chaotic oscillating Turing patterns can be explored by the computation of the largest Lyapunov exponents. Turing instability, including Regular/Chaotic Motions in the given system caused by diffusion and delay, is analyzed. In
Section 3, the fractional diffusion operator in higher-dimensional discrete dynamical systems is introduced and Neimark–Sacker bifurcations caused by Turing instability are analyzed. Further discussion on dynamical behavior caused by the fractional diffusion operator is set up in
Section 4 and the conclusions are drawn in
Section 5.
2. Regular Diffusion Operator : Turing Instability and Neimark–Sacker Bifurcations
By employing the projection technique proposed by Kuznetsov [
5] (p. 182), one can rewrite the given system as:
where
,
, and
where
is a smooth function which can have the following form by the Taylor expansion at the fixed point:
with the components of the vectors
B and
C are listed as follows:
and
According to those results obtained by [
1,
2,
31,
32], we have the following theorem.
Theorem 1. are all the eigenvalues of the matrix N related to Neumann boundary problems Equation (2) [1] and the corresponding eigenvector is where:such that , andwhere N related to (2) has a similar form as defined by [2] (p. 9203). In fact, where except that , and :if or , then , andif and , then Theorem 2. are all the eigenvalues of the matrix N related to Equation (3) and , a standard orthogonal basis can be formed such that and , where N has another form as follows: where except for , if , then:if and , then:and if , then: In addition, if s is odd or t is odd, one can choose , where:and and for . For related works about eigenvalues problems please see Theorem 2.2 [2] (p. 9203). 2.1. Eigenvalue Problems
It is known that there is a unique fixed point
for
without diffusion coupling [
6]. Now let us investigate the linearized system near the synchronized fixed point
, that is:
If we introduce
, then the characteristic matrix of (
6) becomes:
Hence, the characteristic equation, in view of the symmetric property
A and
, is as follows:
where
By choosing the notation
defined as
, and setting up the direct computation or similar analysis as [
6], it is easy to verify that there is a positive root of the polynomial Equation (
8) or Equation (
4) greater than 1 for
. Therefore, the equilibrium becomes unstable if
. Moreover, there can occur a codimension-two bifurcation with 1:1 resonance at
for
, and
is a single eigenvalue at
for
or
.
In what follows, let us begin a study of the characteristic polynomial Equation (
4) for
in detail and all possible higher-codimensional bifurcations. Suppose that
and
, and the diffusion coefficient
. Then,
.
If , then becomes a cubic polynomial Set , . Then, . If , then there exist three real eigenvalues, whereas , there can occur a pair of complex conjugate eigenvalues. One can obtain the following theorem.
Theorem 3. Suppose that:
Then there exists a pair of complex conjugate roots of the polynomial Equation (4) with with modulus equal to 1. Moreover, the transversality condition holds true: . In the case , is a quartic polynomial of a form as It is easy to verify the following theorem.
Theorem 4. If the following hypotheses become valid:
Then there exists a pair of complex conjugate roots of the polynomial Equation (4) with with modulus equal to 1. Furthermore, all roots are single and the transversality condition holds true: . Remark 1. If compared with those in Ref. [17], there are no two pairs of complex conjugate roots with the module equal to 1 at the same time for and the diffusion term . 2.2. Neimark–Sacker Bifurcations
Theorem 5. Suppose that , and
, and
, and
with the single multiplier and there occurs the absence of strong resonances, i.e., , system Equations (1) and (2) at the synchrous fixed point are locally topologically equivalent to the normal form as follows:near the critical value . Moreover, if , the unique stable limit cycle emerges by Neimark–Sacker bifurcations. Otherwise, if , the bifurcating invariant limit cycle is unstable. Proof. It is known that the linear operator has a simple root with one pair of complex eigenvalues denoted by
,
. Moreover, these multipliers are the only eigenvalues lying on the unit circle
. Suppose that
be a complex eigenvector corresponding to the critical eigenvalue
Then:
One can rewrite system Equation (
5) as another form of the following type:
where
and
If we choose
, then:
By introducing the adjoint eigenvector
, we have:
with
and
. The critical real eigenspace
corresponding to
is two-dimensional, spanned by
, i.e.,
. Obviously,
. The real eigenspace
corresponding to all eigenvalues of
other than
is (
)-dimensional. Its validity holds true:
if and only if
or both
and
.
Choose a standard orthogonal basis , for instance. Then, compute the fundamental solution basis of the following homogeneous linear equations , which can be found by the well-known Gram–Schmidt process and unitization. Next, for any vector , we have , where with . We obtain the coordinate on .
In these coordinates, the map Equation (
9) can be written as:
Furthermore, one can obtain that:
where
, which have the following expressions:
Since , we have .
The center manifold
now can be represented [
33] (p. 258) as:
where
, and
and
, which is invertible.
Thus, in the absence of strong resonances, i.e.,
, the restricted map can generically be rewritten as:
A normal form ban be found by further analysis as follows:
, where the direction of bifurcating closed invariant curves is pointed out by the real number
, which could be computed by the formula as follows:
□
Remark 2. A framework for Neimark–Sacker bifurcation in high-dimensional discrete-time systems was proposed by [5] (pp. 185–187). However, it is still unknown how to compute the variable y in the Formulae (5.50) or (5.51) in [5] (p. 186). In this paper, we give a clear presentation. Below, we investigate the case for even t and s and for odd t or odd s with repeated eigenvalues. Using the same technique as earlier we obtain the following theorem.
Theorem 6. Suppose that and, with the single multiplier :
, and ;
, and .
Moreover, since there exists the absence of strong resonances, i.e., , then system Equations (1)–(3) at the unique fixed point is locally topologically equivalent to the normal form as follows:near the critical value . Moreover, if , the stable limit cycle emerges by Neimark–Sacker bifurcations. Otherwise, if , the bifurcating invariant limit cycle is unstable. Remark 3. There can exist multistability, which is a well-known phenomenon discussed in [11,12,34] in high-dimensional systems Equations (1) and (2)) or (1)–(3)). 2.3. Numerical Simulations: Regular/Chaotic Motions Caused by Diffusion and Delay
In this section, we focus on rich dynamic exhibited by system Equation (
1) and (
2). Assume that
,
and
. The initial condition is randomly chosen around the equilibrium
.
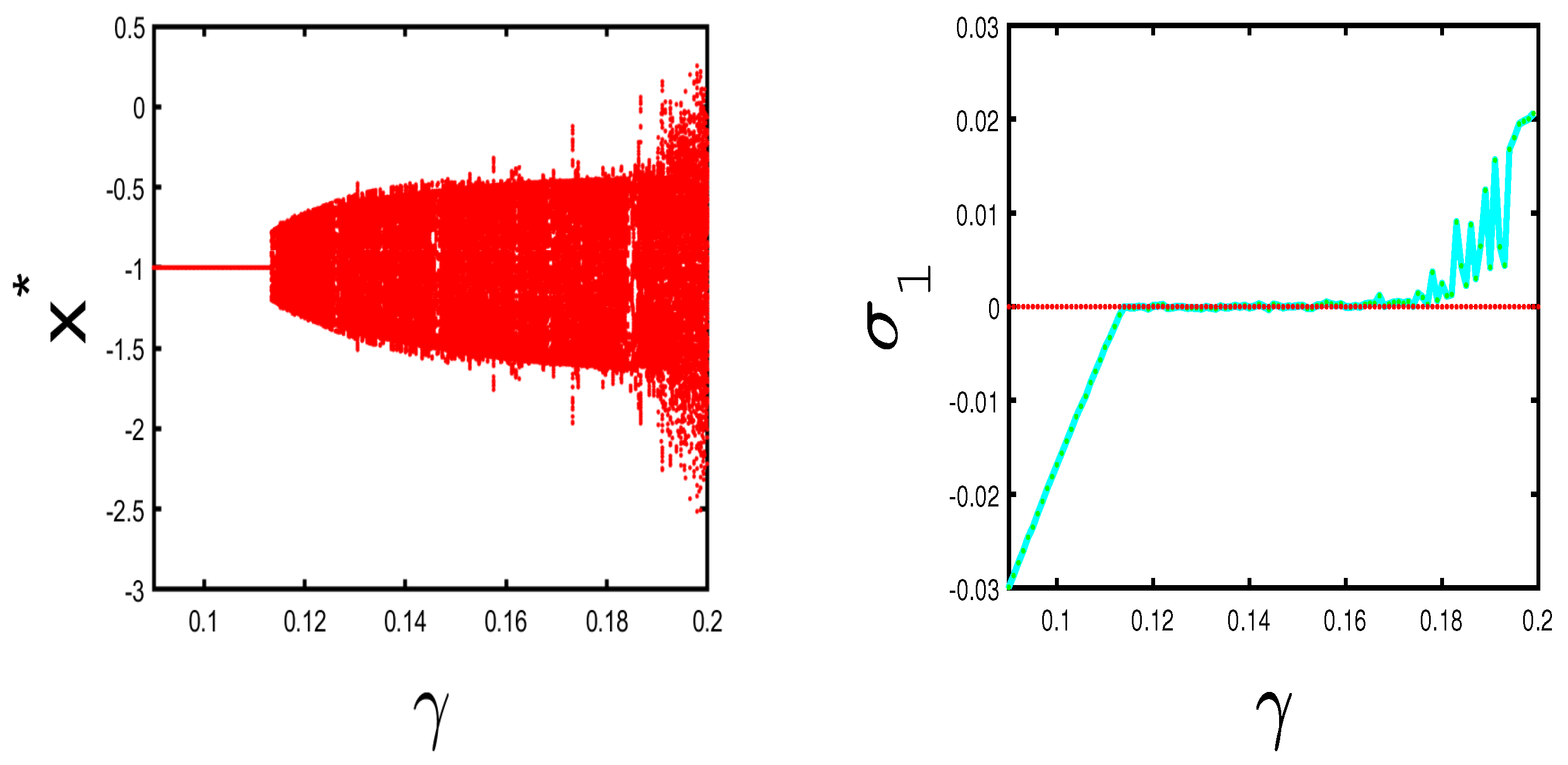
Bifurcation diagrams and the graph related the largest Lyapunov exponent are shown by
Figure 2,
Figure 3 and
Figure 4 as the parameter
,
or
a change their values by
and
,
,
. As the diffusion strength coefficient
has a continuous change, the unique fixed point solution
becomes unstable and there occur aperiodic patterns (invariant limit cycles or Tori (Figure
3ii,iii)) and even chaos (
Figure 2 and
Figure 4), because of the existence of a positive Lyapunov exponent (for the computation of Lyapunov exponents, please see [
26,
35,
36,
37,
38] and the references cited therein). It is also shown by
Figure 4 that there exist two (blue, yellow) separate regions, which implies that there are regular (the blue region in
Figure 4 with the largest Lyapunov exponent
) or irregular (unbounded solutions or chaotic attractors: the yellow region in
Figure 4 with the largest Lyapunov exponent
) motions. It is shown by
Figure 2 that the largest Lyapunov exponent can become positive and that invariant closed curves occur due to Neimark–Sacker bifurcation. Further discussions are needed as to whether invariant chaotic sets like the classical logistic map with
[
39] do or do not exist for sufficiently larger
,
a, or
. As pointed out by Ref. [
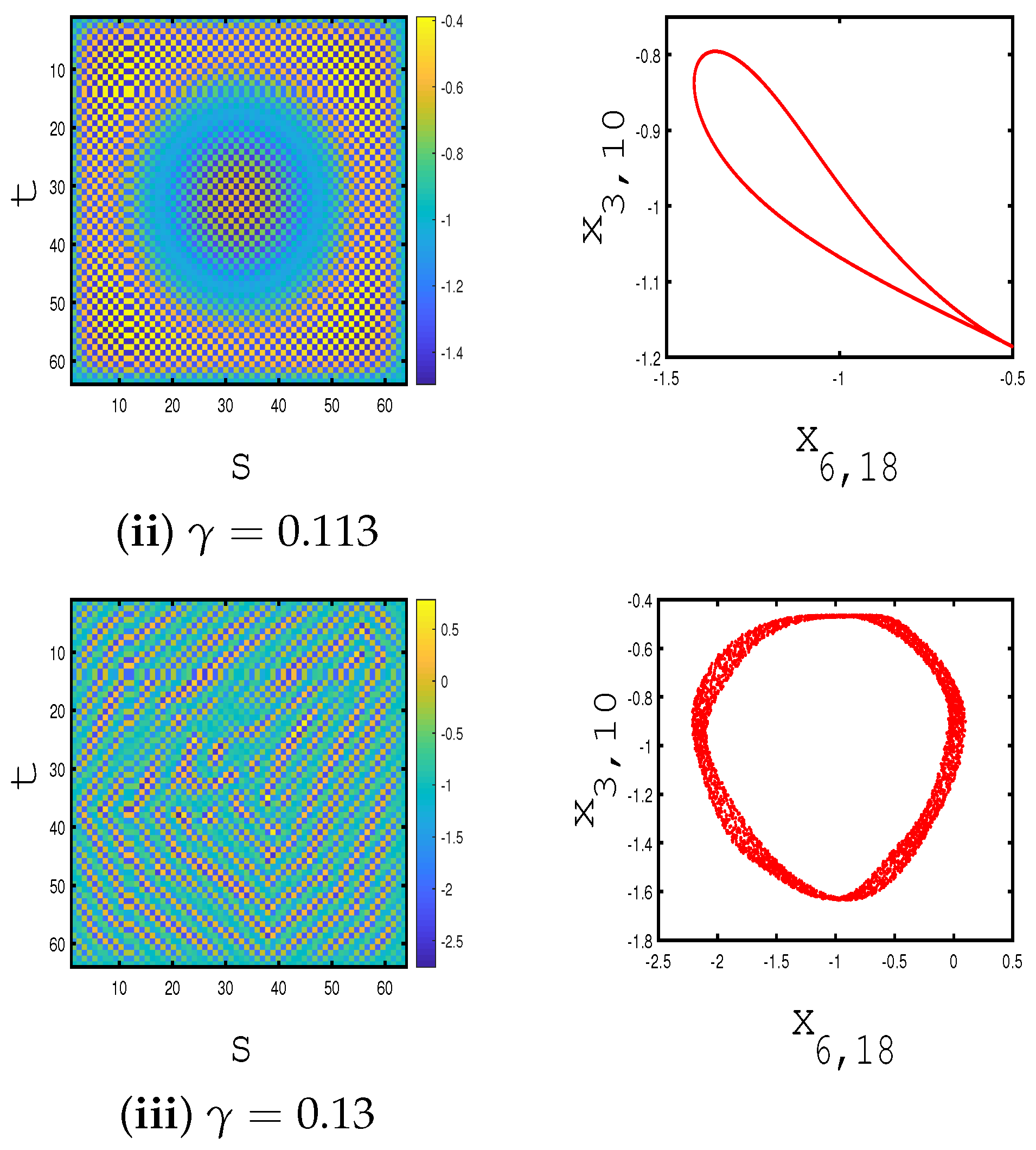
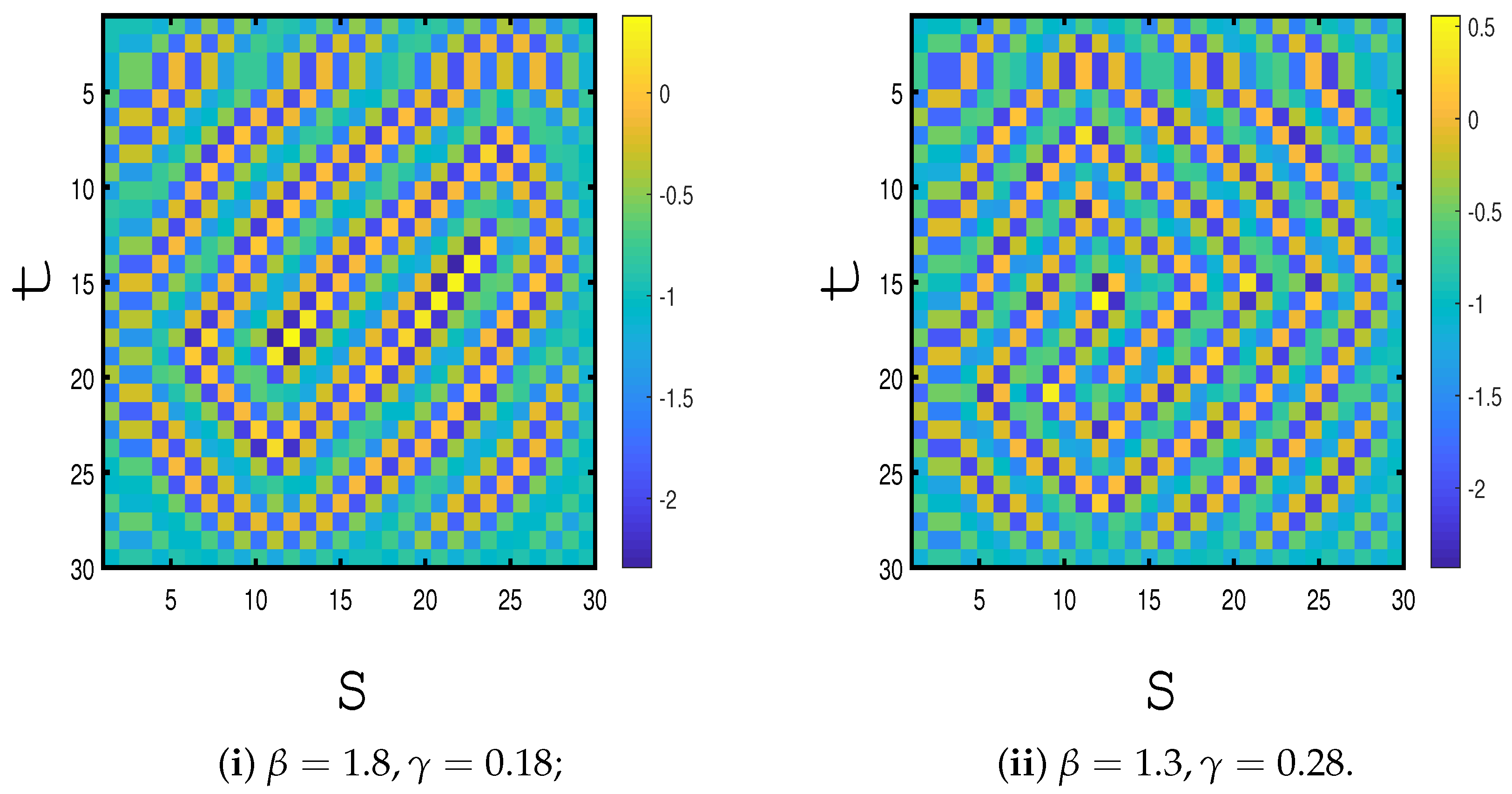
15], symbolic dynamics may help us give a clear understanding about the complexity generated by a given model. Regular/chaotic oscillating Turing patterns can be discovered by
Figure 2 for
and
, and 0.13, respectively. Turing instability [
1,
4,
40] and multistability emerges [
11,
12,
26,
27,
34,
38,
41].
3. Fractional Diffusion Difference Operator : Turing Instability and Neimark–Sacker Bifurcations
Let us introduce the fractional diffusion difference operator with the following properties:
are all the eigenvalues of the operator
and the selection of vectors
is a standard orthogonal basis, such that:
which implies that
M is the matrix representation of the operator
related to Neumann boundary problems Equation (
2) with the symmetrical property;
The symmetrical matrix
is the matrix representation of the operator
related to periodic boundary problems Equation (
3), and
,
) are all the eigenvalues of the operator
or the matrix
.
Moreover, we have the following theorem.
Theorem 7. Suppose that are all the eigenvalues of the fractional diffusion difference operator related to Neumann boundary problems (2). If one choose the corresponding eigenvector where: Then, , where and (for more details about , please see [1]). Theorem 8. Suppose that are all the eigenvalues of the fractional diffusion difference operator related to periodic boundary problems Equation (3) and a selection of vectors is a standard orthogonal basis such that and . In addition, if s is odd or t is odd, one can choose , where , (for more details about , please see [2]). Moreover, one can find that:
(a) Assume that t and s are both even, is the unique largest eigenvalue , and , .
(b) Assume that t and s are both odd, is the largest eigenvalue , the multiplicity is 4, and the case (1) , , or (2) , , or (3) , , or (iv) , , is valid, respectively.
(c) Assume that t is even and s is odd, is the largest eigenvalue , the multiplicity is 2, and (1) , or (2) , become valid, respectively.
(d) Assume that s is even and t is odd, is the largest eigenvalue , the multiplicity is 2, and (1) , or (2) , hold true, respectively.
(e) The single root 0 is the smallest eigenvalue among all .
Rewrite system Equation (
1) as:
where
,
, and:
where
is a smooth function which can have the following form by the Taylor expansion at
and:
and
3.1. Eigenvalue Problems
The linearized system becomes:
Then, by introducing
, the characteristic matrix of (
13) is as follows:
Hence, the characteristic equation, in view of the symmetric property
, is as follows:
where
In the next section, we are interested in the following characteristic polynomial:
for
. Suppose that
and
, and the diffusion coefficient
. Then,
.
If , becomes a cubic polynomial Set , . Then, . If , then there are three real eigenvalues, whereas if , there exists one pair of complex conjugate eigenvalues. Therefore, one can obtain the following theorem.
Theorem 9. Suppose that:
Then, under the assumption that , there exists one pair of complex conjugate roots of the algebraic Formula (16) with modulus equal to 1. Moreover, transversality conditions hold true: . If , is a quartic polynomial of a form as
Theorem 10. Suppose that:
Then, there exists one pair of complex conjugate roots of the algebraic Formula (16) with modulus equal to 1. Moreover, the transversality condition holds true: . 3.2. Neimark–Sacker Bifurcations
Theorem 11. Suppose that , and, with the single multiplier :
, and ;
, and .
Moreover, if there is an absence of strong resonances, i.e., , system Equations (1) and (2) at the unique fixed point is locally topologically equivalent to the normal form as follows:near the critical value . Moreover, if , the unique stable limit cycle emerges by Neimark–Sacker bifurcations. Otherwise, if , the bifurcating invariant limit cycle is unstable. Below, we assume that both t and s are even. Using the same techniques and method as earlier we obtain the following theorem.
Theorem 12. Suppose that and, with the single multiplier :
, and
, and
Moreover, if there is an absence of strong resonances, i.e., , system Equations (1)–(3) at the unique fixed point are locally topologically equivalent to the normal form as follows:near the critical value . Moreover, if , the stable limit cycle emerges by Neimark–Sacker bifurcations. Otherwise, if , the bifurcating invariant limit cycle is unstable. Since the proofs of the above two theorems are similar to the techniques and method in Theorem 5, they are omitted.