Analyzing the Chaotic Dynamics of a Fractional-Order Dadras–Momeni System Using Relaxed Contractions
Abstract
1. Introduction and Preliminaries
2. Basic Definitions
- 1
- ⇔
- 2
- 3
- (i)
- Then ; whenever there is a positive , there is a positive satisfying for each . It can be formulated as
- (ii)
- The sequence is Cauchy provided that, given any , there exists , such that whenever .
- (iii)
- Then U is complete if every Cauchy sequence in U has a limit in U.
- (iv)
- Every convergent sequence in U has a single limit point.
- The condition leads to it indicates is non-decreasing.
- Given any
- We can find and that leads to
- is continuous.
3. Results on Basic Contraction
4. Connecting Fractional Order Dadras–Momeni Chaotic System to Fixed Point Results
- (i)
- (ii)
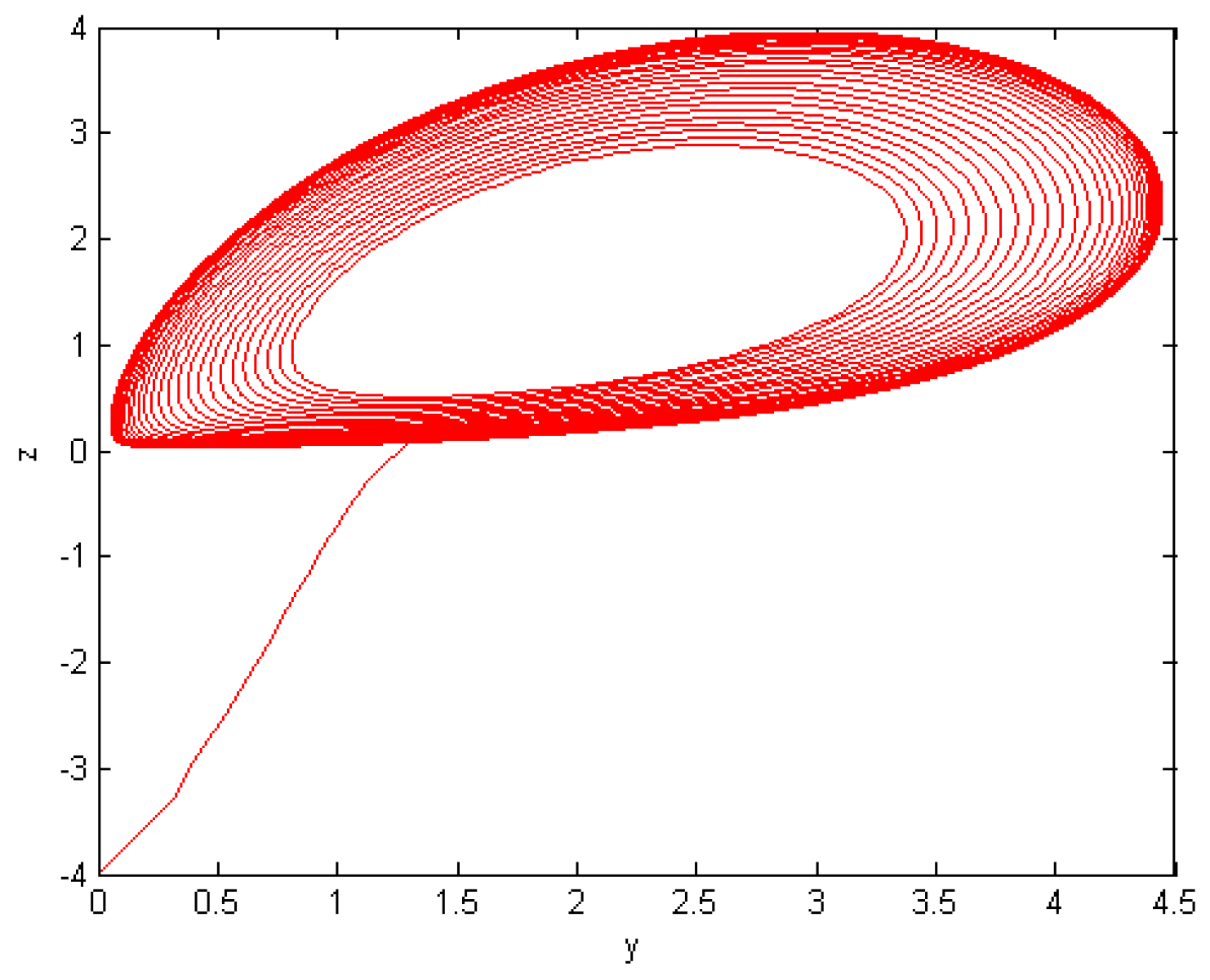
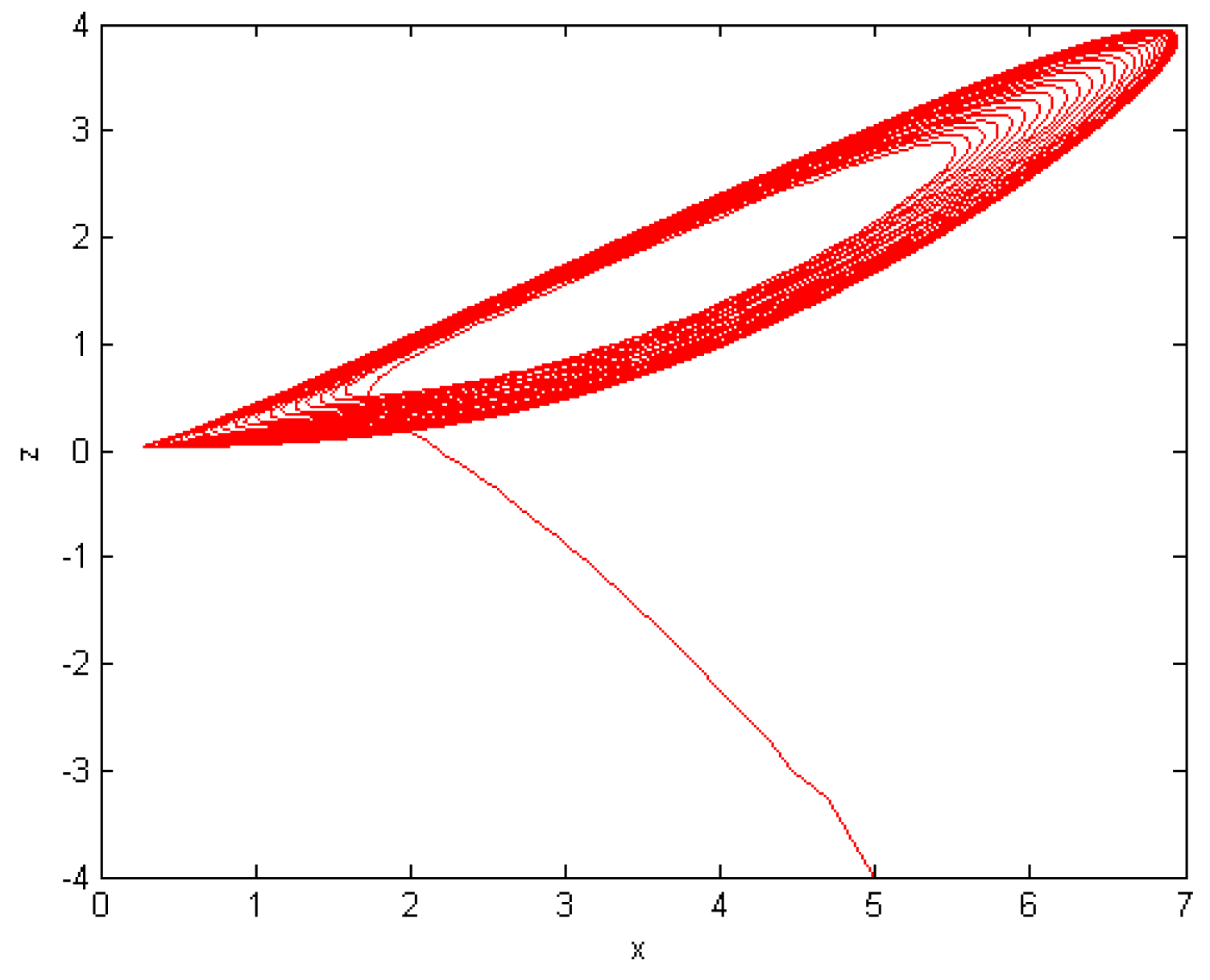
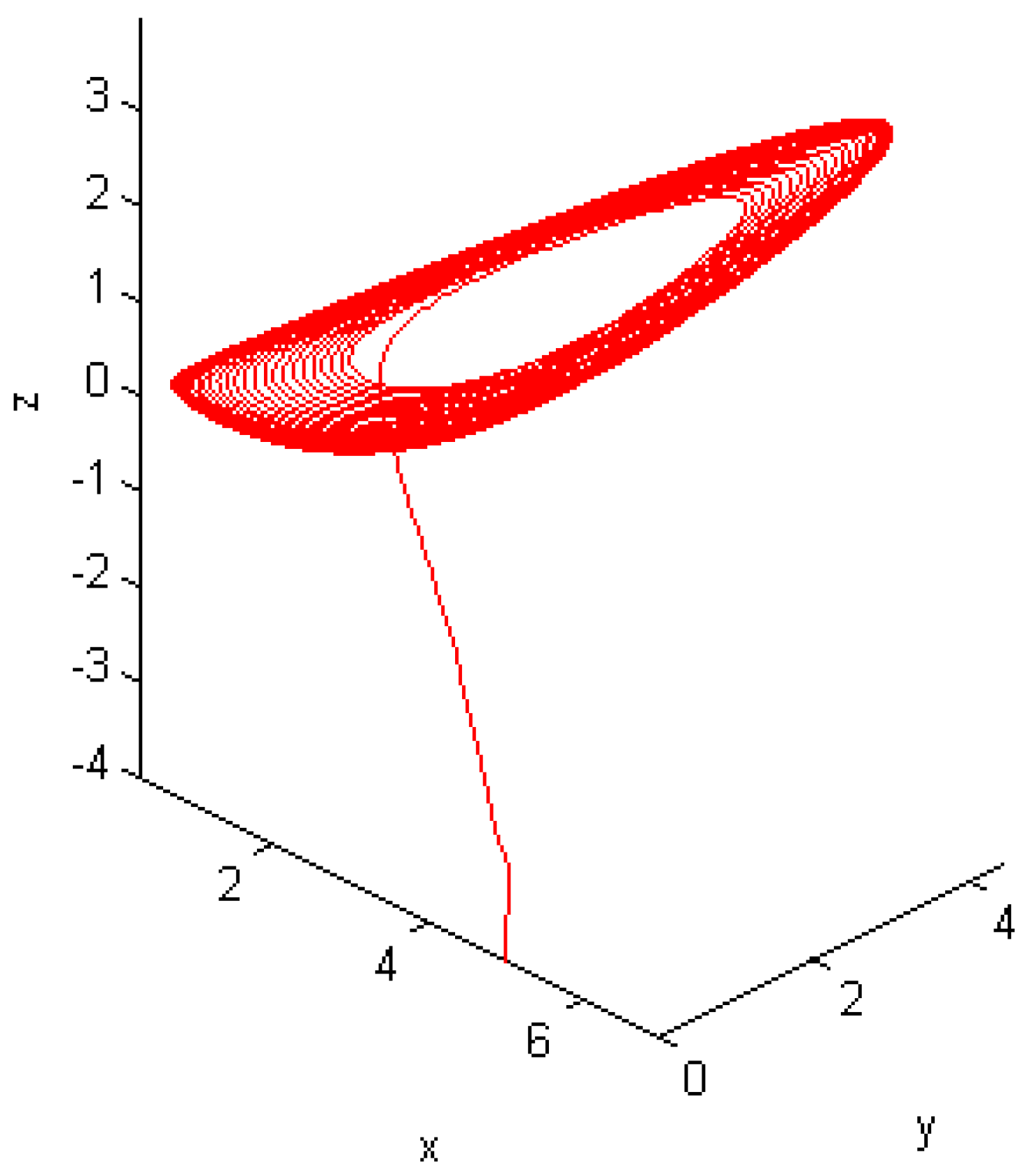
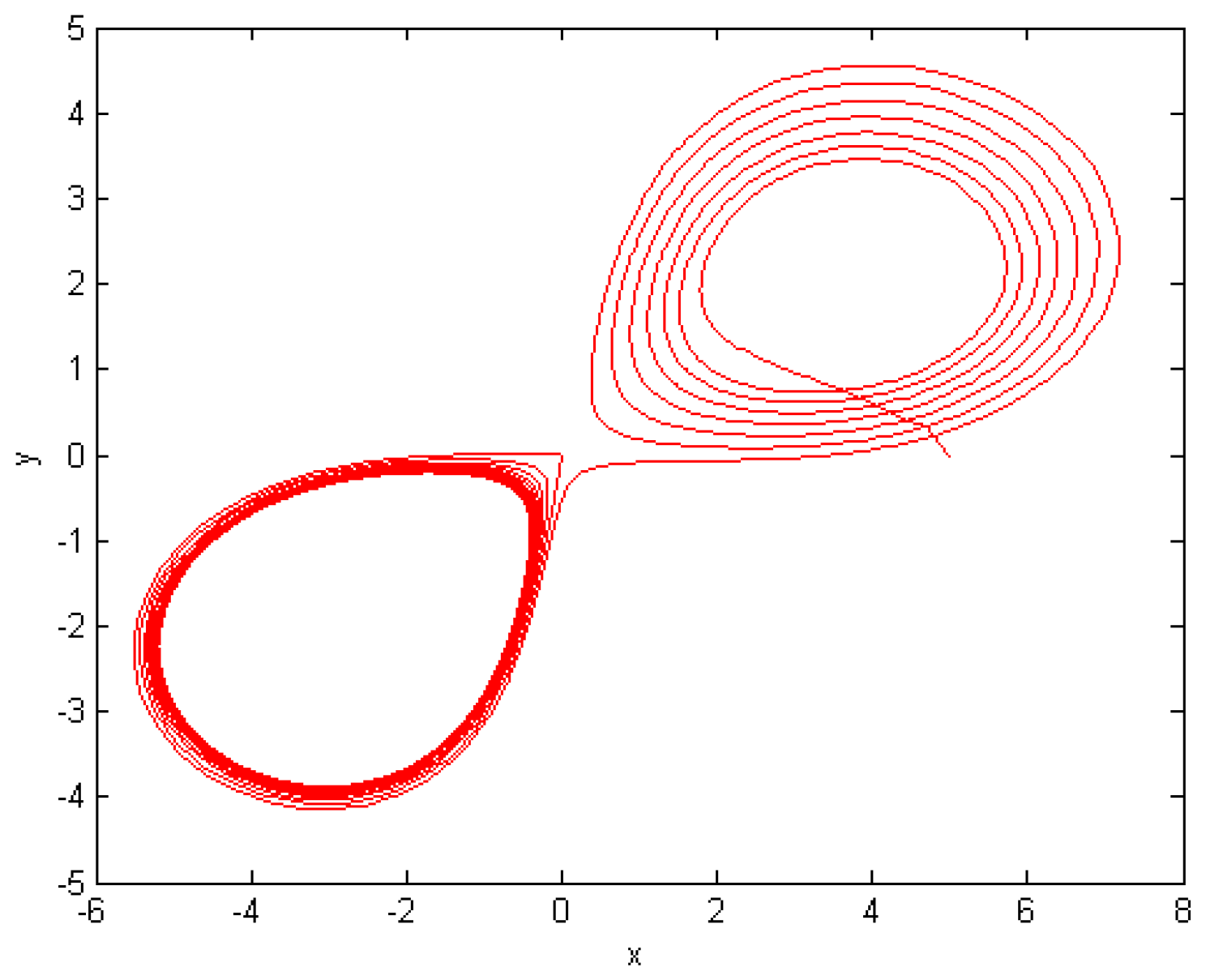
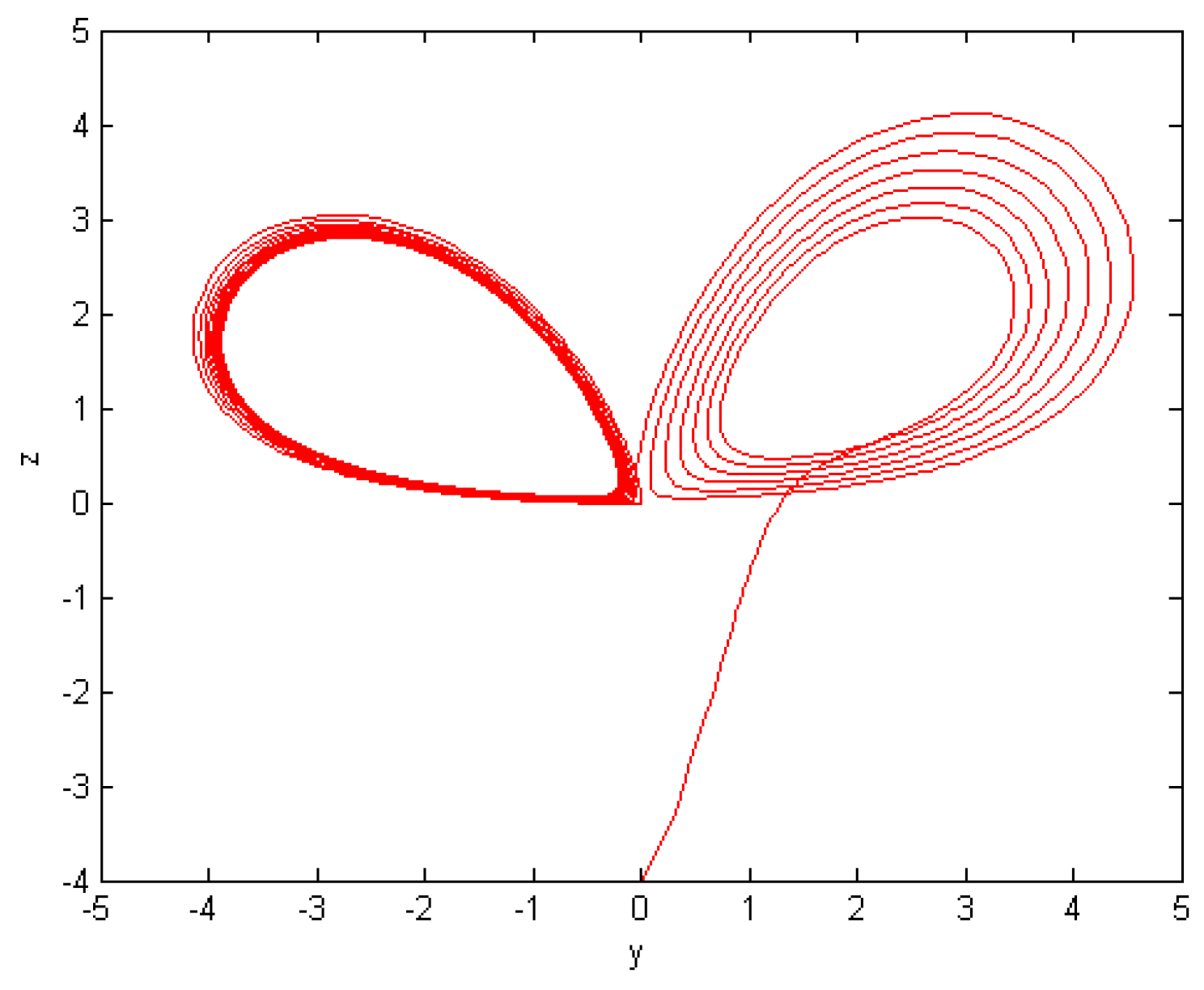
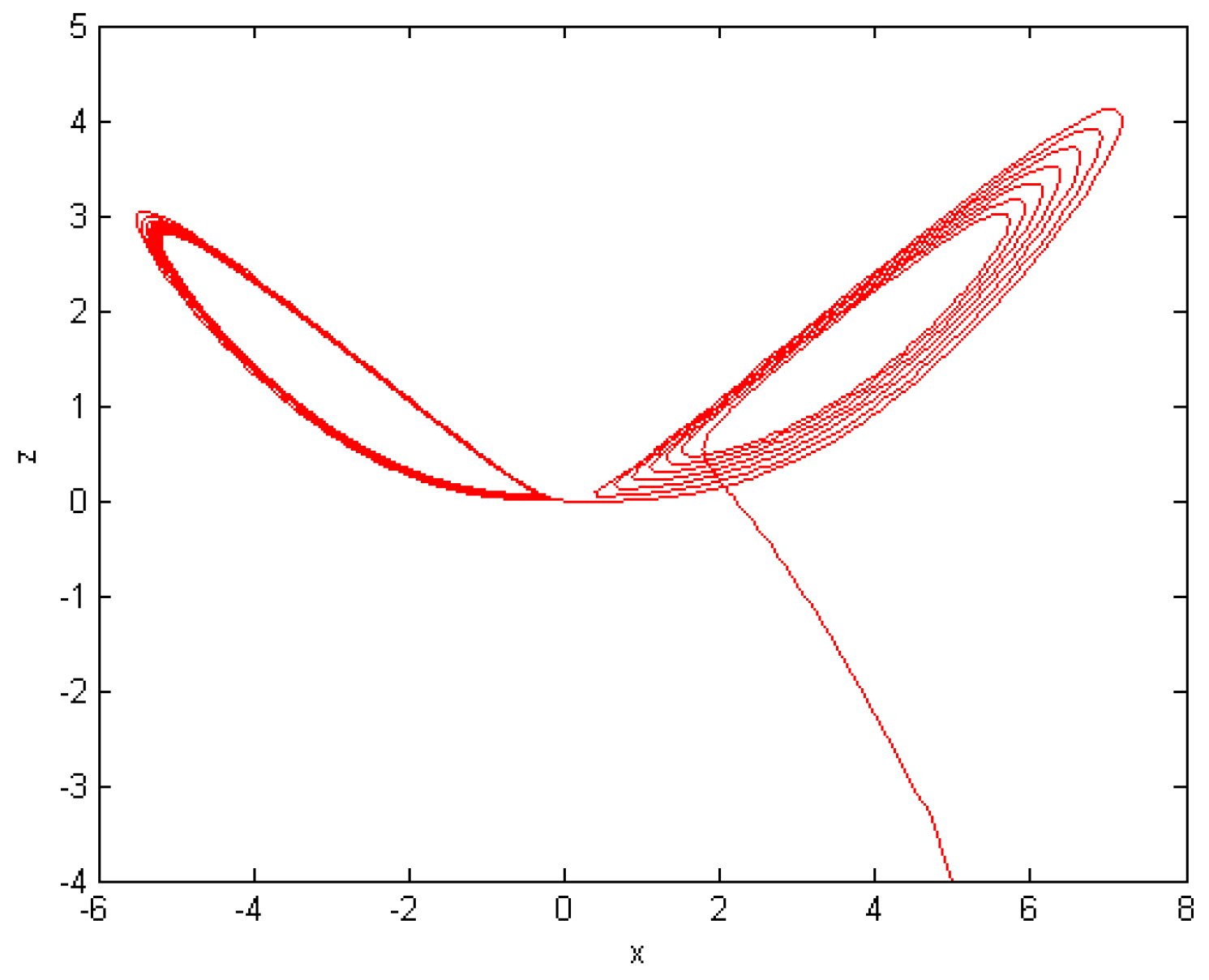
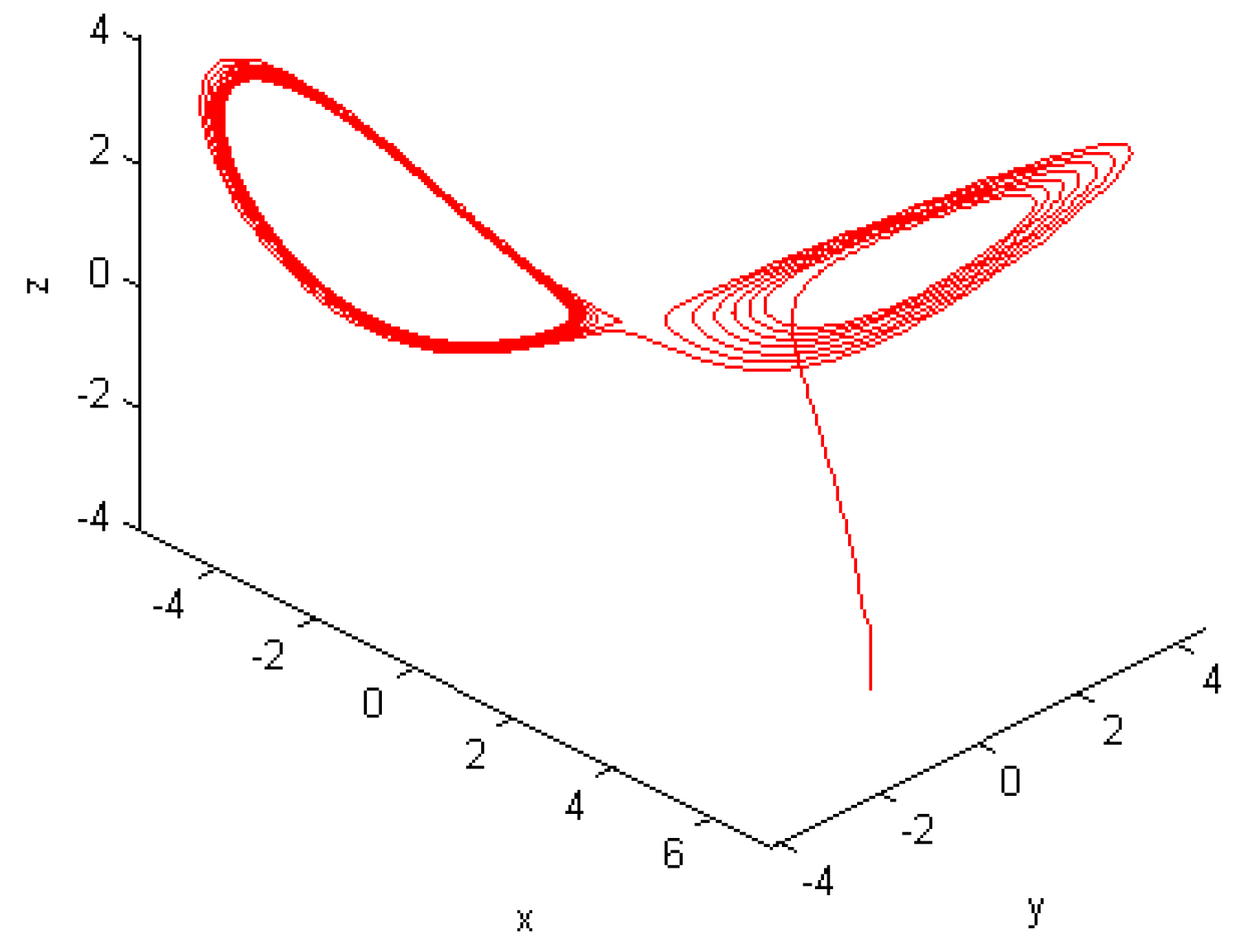
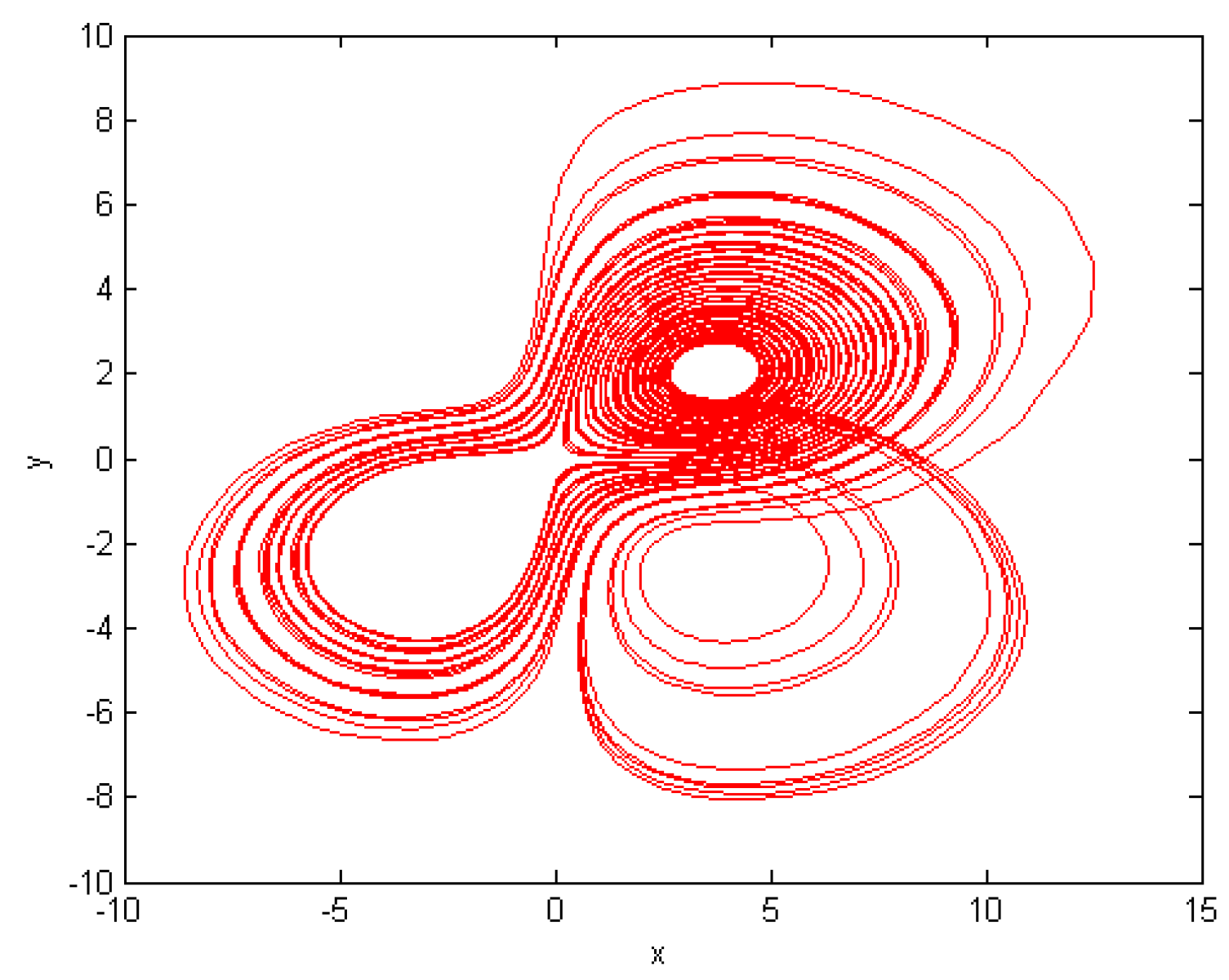
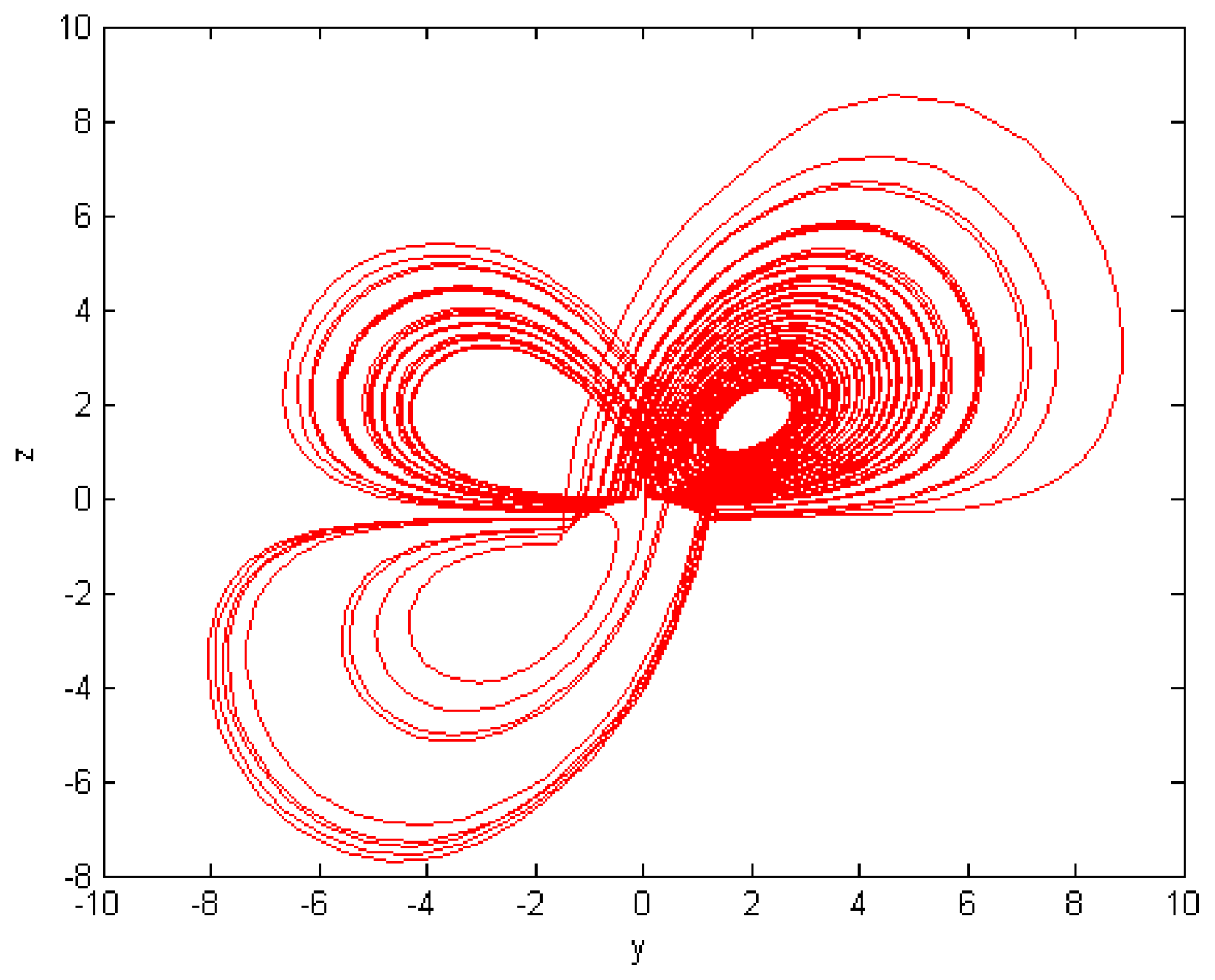
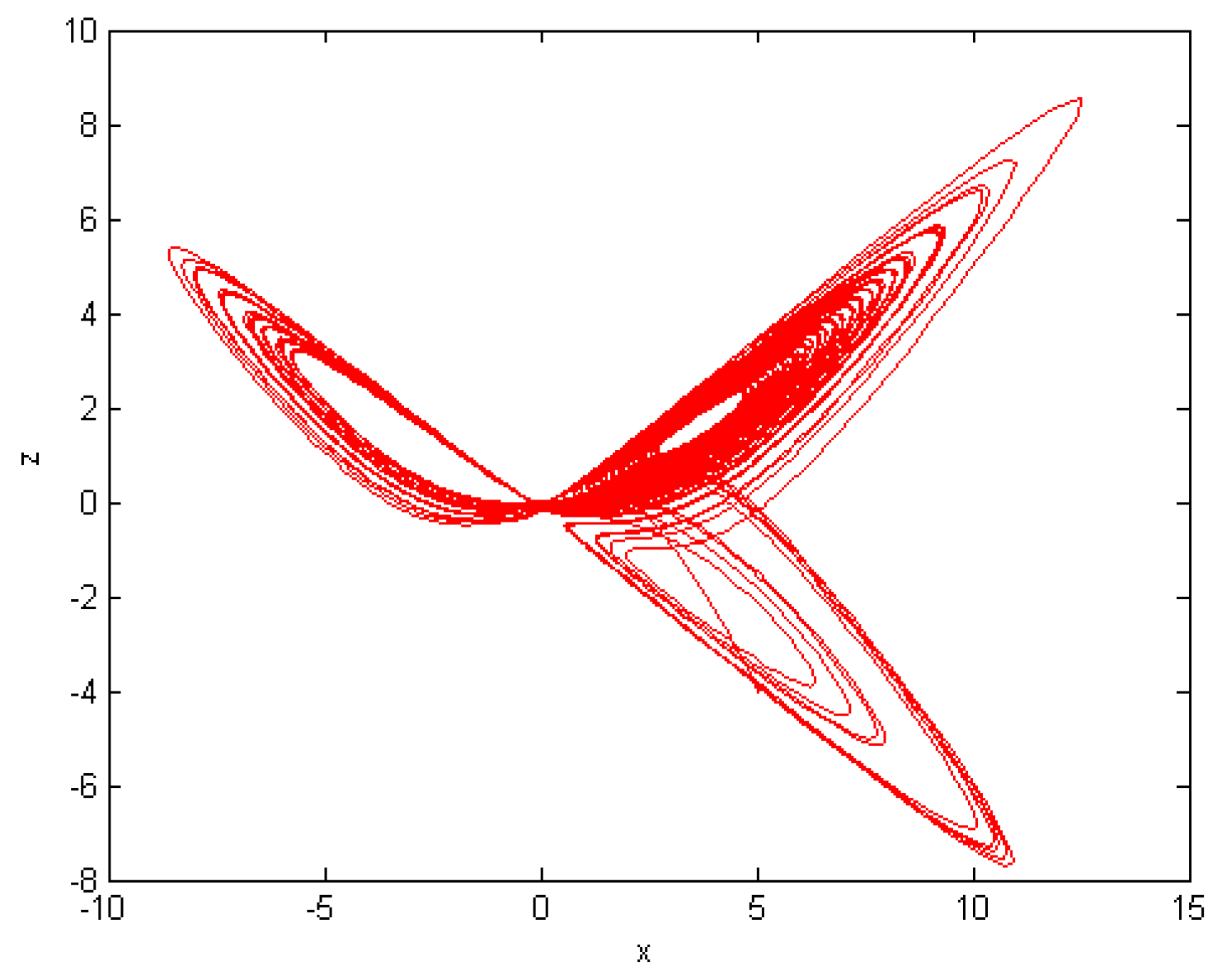
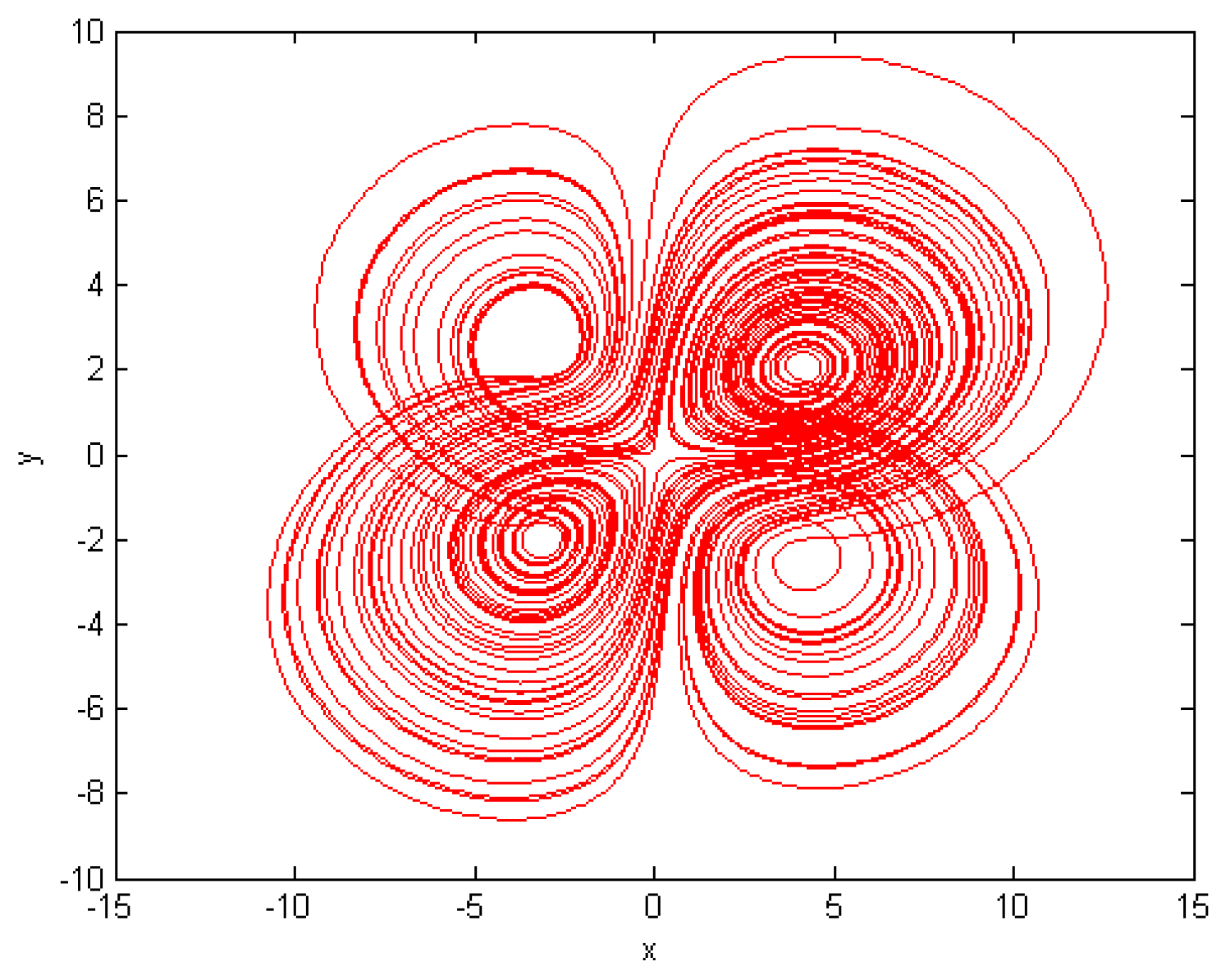
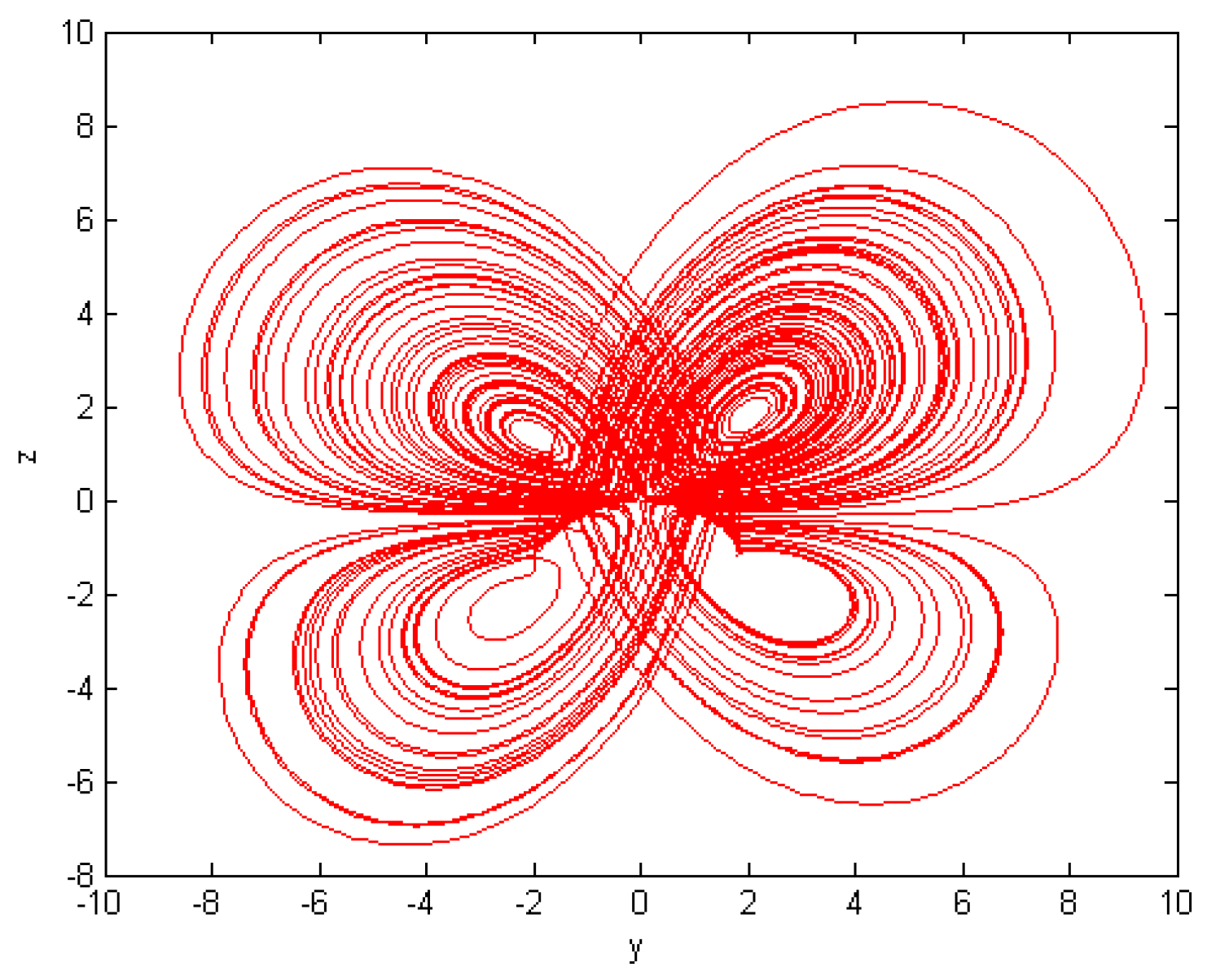
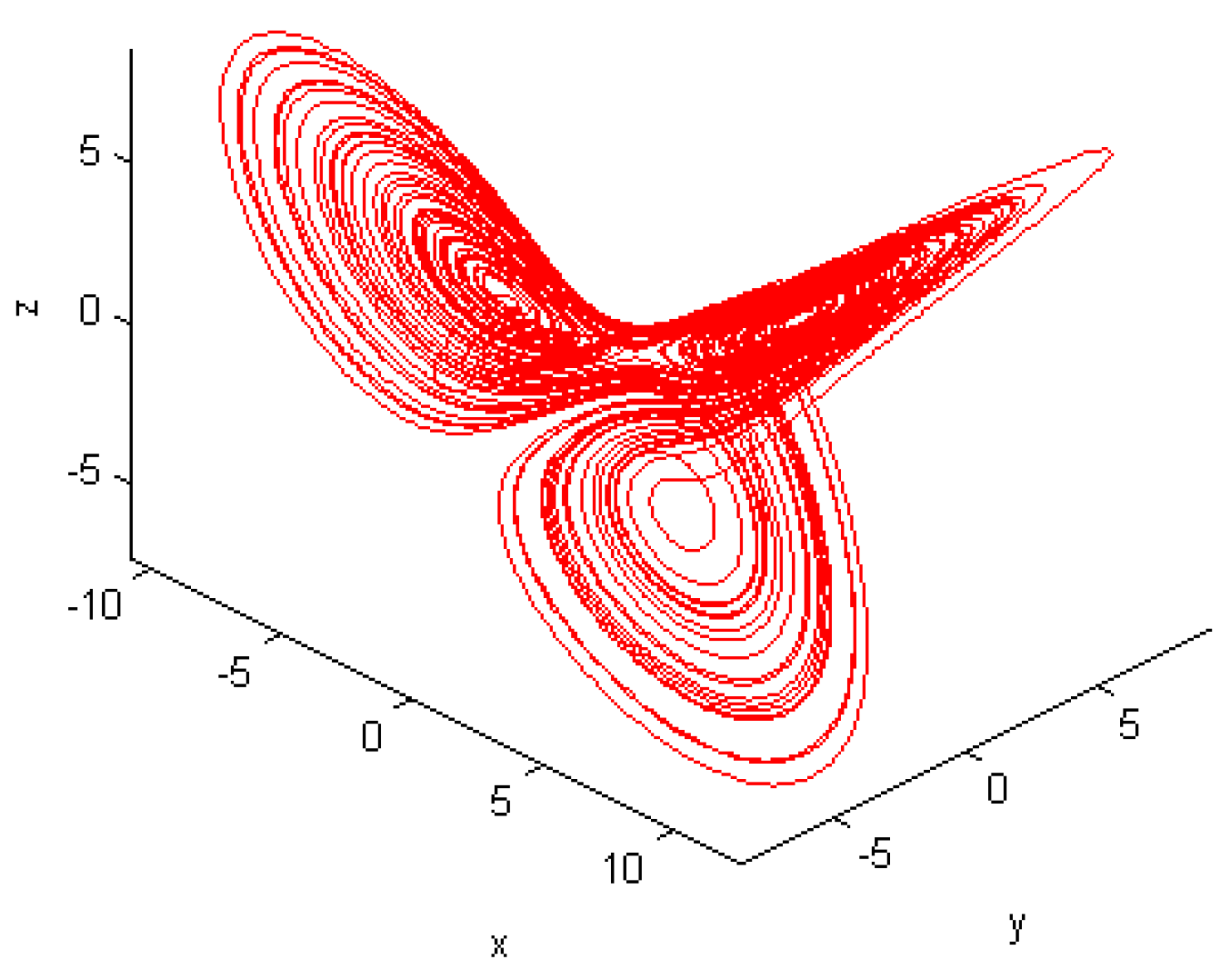
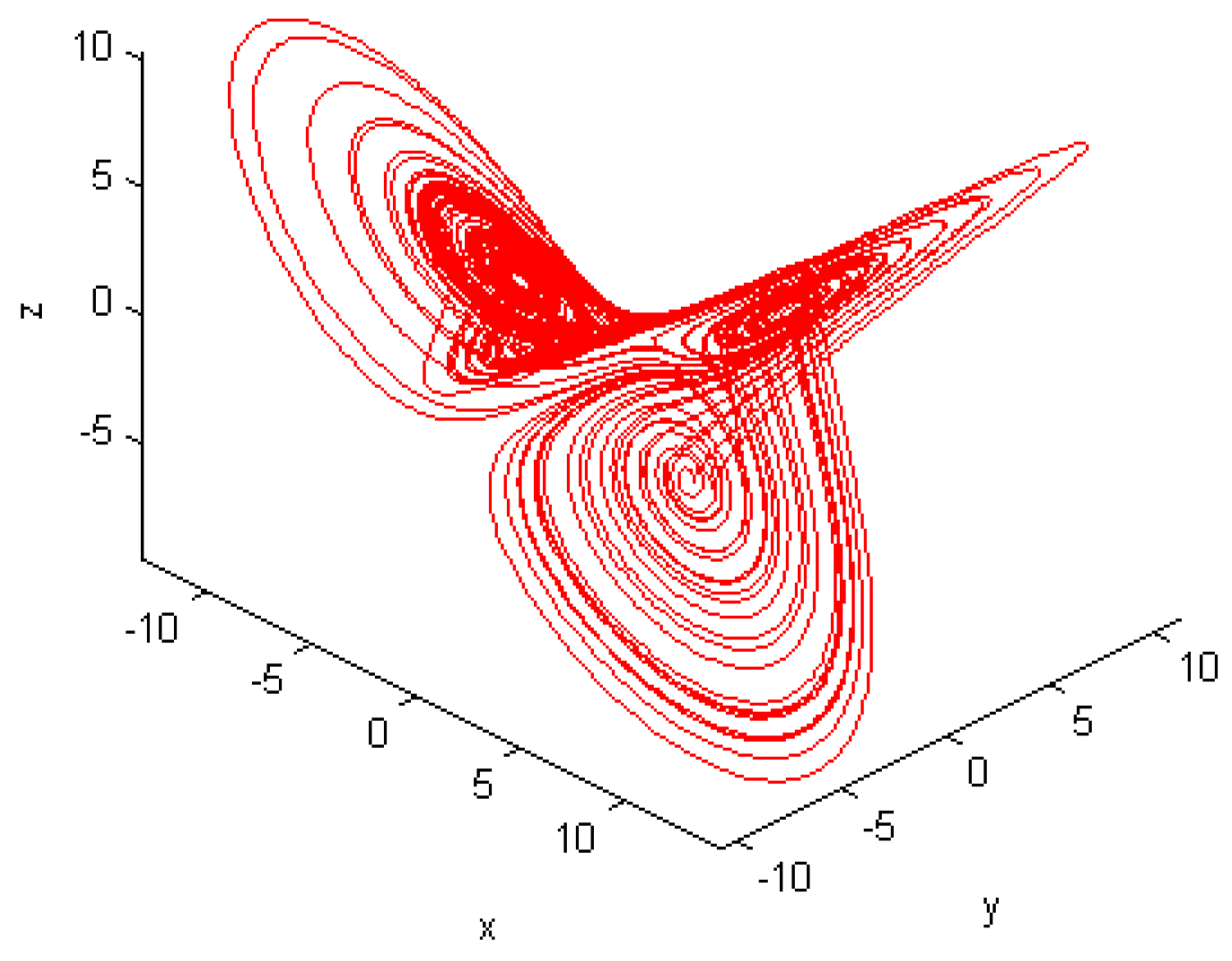
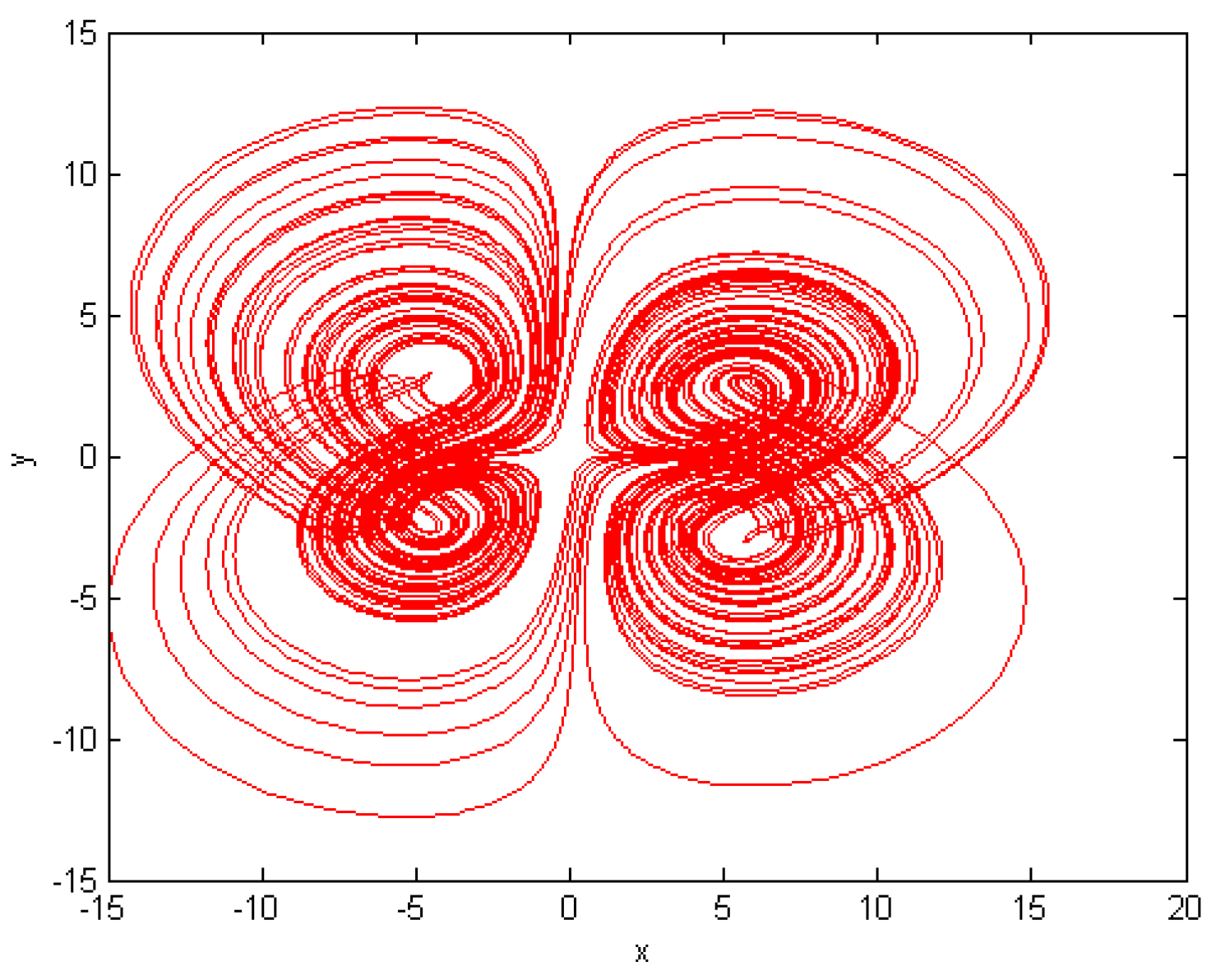
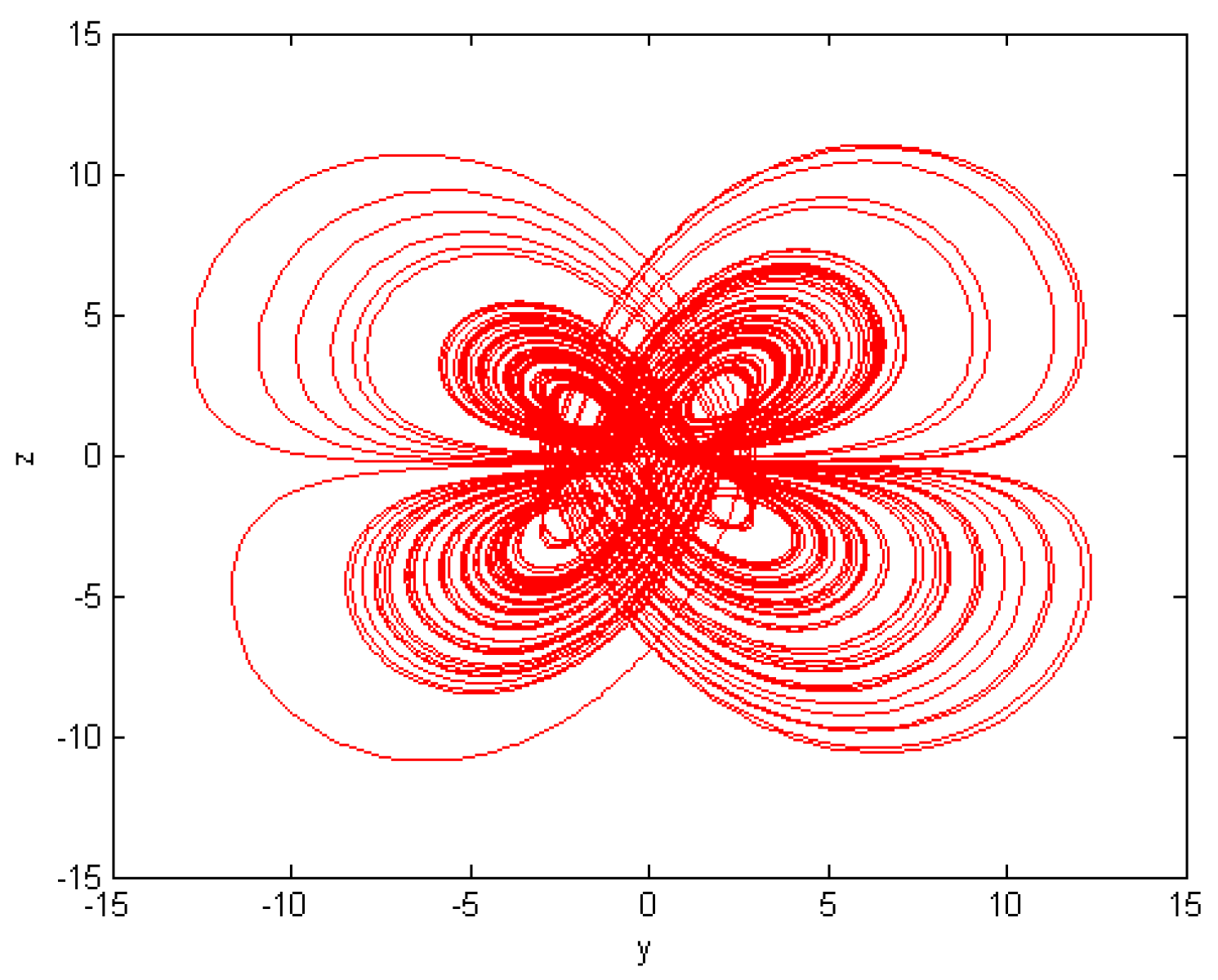
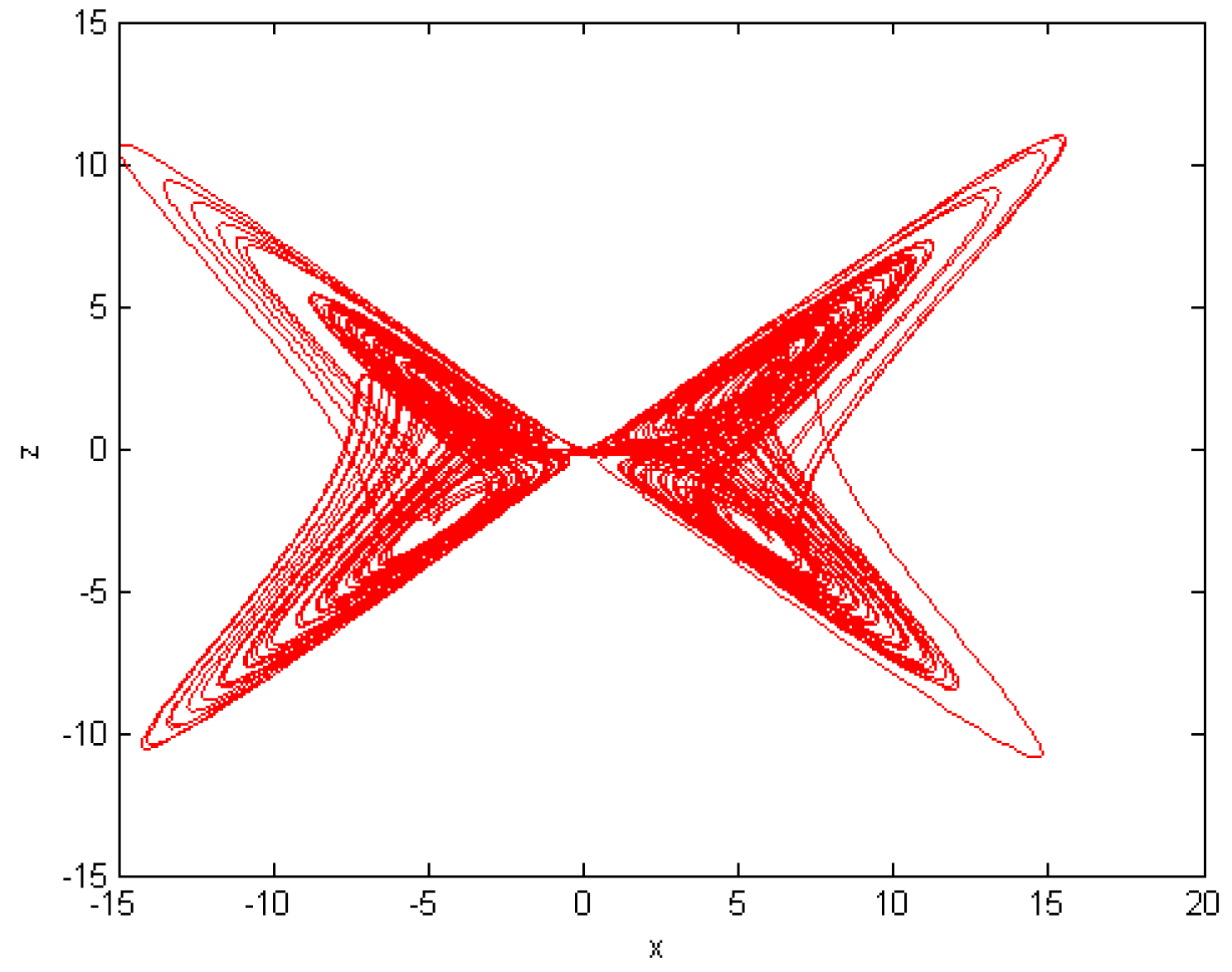
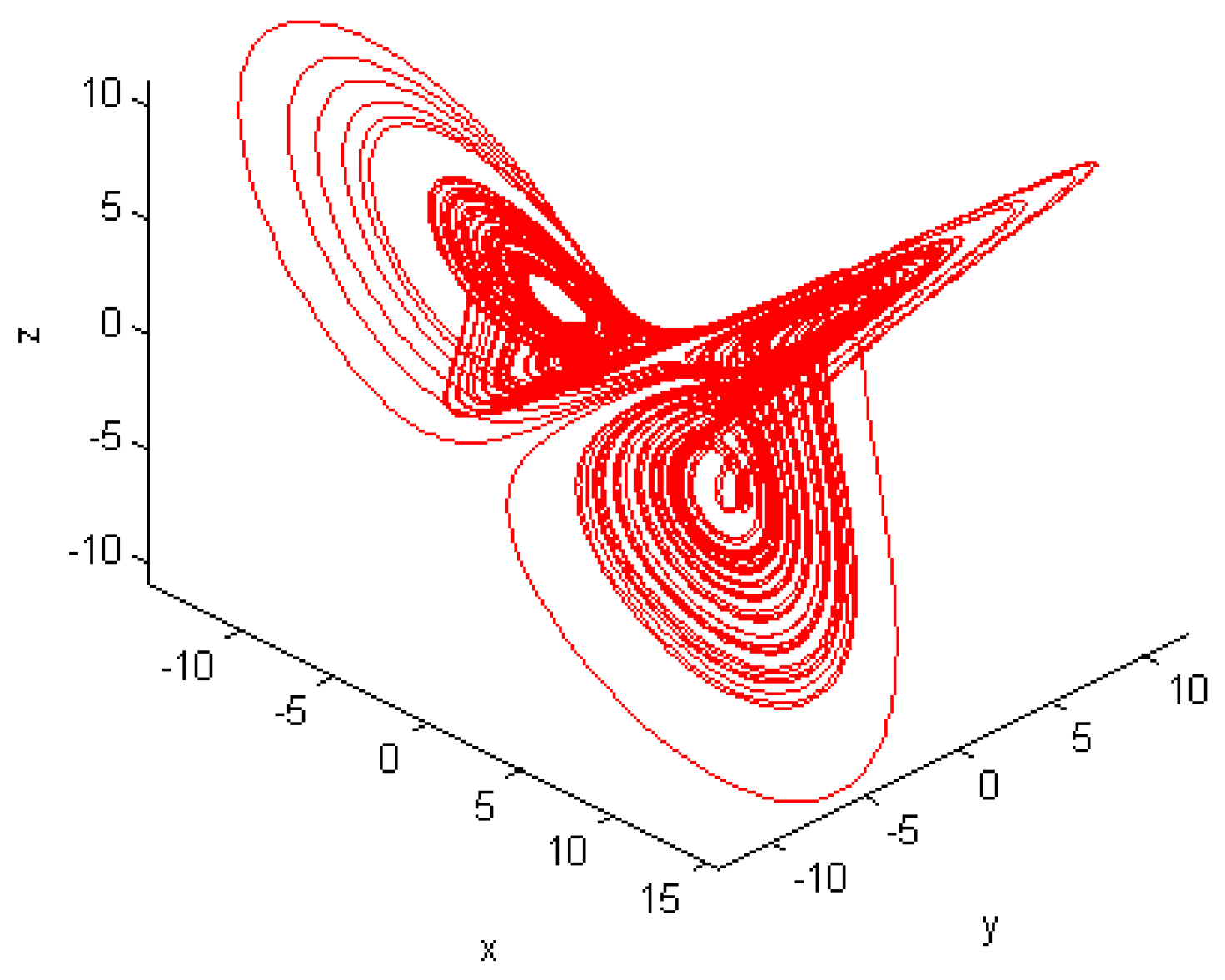
5. Numerical Results
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Banach, S. Sur les opérations dans les ensembles abstraits et leur application aux équations intégrales. Fundam. Math. 1922, 3, 133–181. [Google Scholar] [CrossRef]
- Bakhtin, I.A. The contraction mapping principle in quasi-metric spaces. Funct. Anal. Unianowsk Gos. Ped. Inst. 1989, 30, 26–37. [Google Scholar]
- Czerwik, S. Contraction mappings in b-metric spaces. Acta Math. Inform. Univ. Ostrav. 1993, 1, 5–11. [Google Scholar]
- Kamran, T.; Samreen, M.; UL Ain, Q. A Generalization of b-Metric Space and Some Fixed Point Theorems. Mathematics 2017, 5, 19. [Google Scholar] [CrossRef]
- Mlaiki, N.; Aydi, H.; Souayah, N.; Abdeljawad, T. Controlled Metric Type Spaces and the Related Contraction Principle. Mathematics 2018, 6, 194. [Google Scholar] [CrossRef]
- Abdeljawad, T.; Mlaiki, N.; Aydi, H.; Souayah, N. Double controlled metric type spaces and some fixed point results. Mathematics 2018, 6, 320. [Google Scholar] [CrossRef]
- Younis, M.; Ahmad, H.; Chen, L.; Han, M. Computation and convergence of fixed points in graphical spaces with an application to elastic beam deformations. J. Geom. Phys. 2023, 192, 104955. [Google Scholar] [CrossRef]
- Ahmad, H.; Din, F.U.; Younis, M. A fixed point analysis of fractional dynamics of heat transfer in chaotic fluid layers. J. Comput. Appl. Math. 2025, 453, 116144. [Google Scholar] [CrossRef]
- Younıs, M.; Mutlu, A.; Ahmad, H. Ćirić Contraction with Graphical Structure of Bipolar Metric Spaces and Related Fixed Point Theorems. Hacet. J. Math. Stat. 2024, 1–19. [Google Scholar] [CrossRef]
- Ahmad, H. Analysis of Fixed Points in Controlled Metric Type Spaces with Application. In Recent Developments in Fixed-Point Theory: Theoretical Foundations and Real-World Applications; Springer Nature: Singapore, 2024; pp. 225–240. [Google Scholar]
- Poincaré, H. Sur le problème des trois corps et les équations de la dynamique. Acta Math. 1890, 13, 1–270. [Google Scholar]
- Lorenz, E.N. Deterministic nonperiodic flow. J. Atmos. Sci. 1963, 20, 130–141. [Google Scholar] [CrossRef]
- May, R.M. Simple mathematical models with very complicated dynamics. Nature 1976, 261, 459–467. [Google Scholar] [CrossRef]
- Feigenbaum, M.J. Quantitative universality for a class of nonlinear transformations. J. Stat. Phys. 1978, 19, 25–52. [Google Scholar] [CrossRef]
- Mandelbrot, B.B. The Fractal Geometry of Nature; WH Freeman and Company: New York, NY, USA, 1982. [Google Scholar]
- Liouville, J. Mémoire sur quelques questions de géométrie et de mécanique, et sur un nouveau genre de calcul pour résoudre ces questions. J. De L’École Polytech. 1832, 13, 1–69. [Google Scholar]
- Caputo, M. Linear models of dissipation whose Q is almost frequency independent. II. Geophys. J. Int. 1967, 13, 529–539. [Google Scholar] [CrossRef]
- Caputo, M.; Fabrizio, M. A new definition of fractional derivative without singular kernel. Prog. Fract. Differ. Appl. 2015, 1, 1–3. [Google Scholar]
- Atangana, A.; Baleanu, D. New fractional derivatives with non-local and non-singular kernel, Theory and application to heat transfer model. Therm. Sci. 2016, 20, 763–769. [Google Scholar] [CrossRef]
- Jleli, M.; Samet, B. A new generalization of the Banach contraction principle. J. Inequal. Appl. 2014, 38, 1–8. [Google Scholar] [CrossRef]
- Branciari, A. A fixed point theorem of Banach-Caccioppoli type on a class of generalized metric spaces. Publ. Math. (Debr.) 2000, 57, 31–37. [Google Scholar] [CrossRef]
- Jleli, M.; Karapınar, E.; Samet, B. Further generalizations of the Banach contraction principle. J. Inequal. Appl. 2014, 439, 1–9. [Google Scholar] [CrossRef]
- Ahmad, J.; Al-Mazrooeia, A.E.; Cho, Y.J.; Yang, Y. Fixed point results for generalized θR-contractions. J. Nonlinear Sci. Appl. 2017, 10, 2350–2358. [Google Scholar] [CrossRef]
- Liu, X.; Chang, S.; Xiao, Y.; Zao, L.C. Existence of fixed points for θR-type contraction and θR-type Suzuki contraction in complete metric spaces. Fixed Point Theory Appl. 2016, 8, 1–12. [Google Scholar]
- Hussain, N.; Parvaneh, V.; Samet, B.; Vetro, C. Some fixed point theorems for generalized contractive mappings in complete metric spaces. Fixed Point Theory Appl. 2015, 185, 1–17. [Google Scholar] [CrossRef]
- CvetkoviĆ, M.; Karapinar, E.; PetruŞel, A. Fixed point theorems for basic θ-contraction and applications. Carpathian J. Math. 2024, 40, 3–789. [Google Scholar] [CrossRef]
- Dadras, S.; Momeni, H.R. A novel three-dimensional autonomous chaotic system generating two, three and four-scroll attractors. Phys. Lett. A 2009, 373, 3637–3642. [Google Scholar] [CrossRef]
- Liu, X.; Hong, L.; Dang, H.; Yang, L. Bifurcations and Synchronization of the Fractional-Order Bloch System. Discret. Dyn. Nat. Soc. 2017, 2017, 4694305. [Google Scholar] [CrossRef]






Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ahmad, H.; Din, F.U.; Younis, M.; Guran, L. Analyzing the Chaotic Dynamics of a Fractional-Order Dadras–Momeni System Using Relaxed Contractions. Fractal Fract. 2024, 8, 699. https://doi.org/10.3390/fractalfract8120699
Ahmad H, Din FU, Younis M, Guran L. Analyzing the Chaotic Dynamics of a Fractional-Order Dadras–Momeni System Using Relaxed Contractions. Fractal and Fractional. 2024; 8(12):699. https://doi.org/10.3390/fractalfract8120699
Chicago/Turabian StyleAhmad, Haroon, Fahim Ud Din, Mudasir Younis, and Liliana Guran. 2024. "Analyzing the Chaotic Dynamics of a Fractional-Order Dadras–Momeni System Using Relaxed Contractions" Fractal and Fractional 8, no. 12: 699. https://doi.org/10.3390/fractalfract8120699
APA StyleAhmad, H., Din, F. U., Younis, M., & Guran, L. (2024). Analyzing the Chaotic Dynamics of a Fractional-Order Dadras–Momeni System Using Relaxed Contractions. Fractal and Fractional, 8(12), 699. https://doi.org/10.3390/fractalfract8120699










