Numerical Simulation Based on Interpolation Technique for Multi-Term Time-Fractional Convection–Diffusion Equations
Abstract
1. Introduction
2. Highly Accurate Numerical Algorithm for Equation (1)
2.1. Background Knowledge of the BRICM
2.2. The Differential Matrices
2.3. Approximate Scheme of the Caputo Derivative
2.4. Discrete Scheme of Equation (1)
3. Convergence Analysis
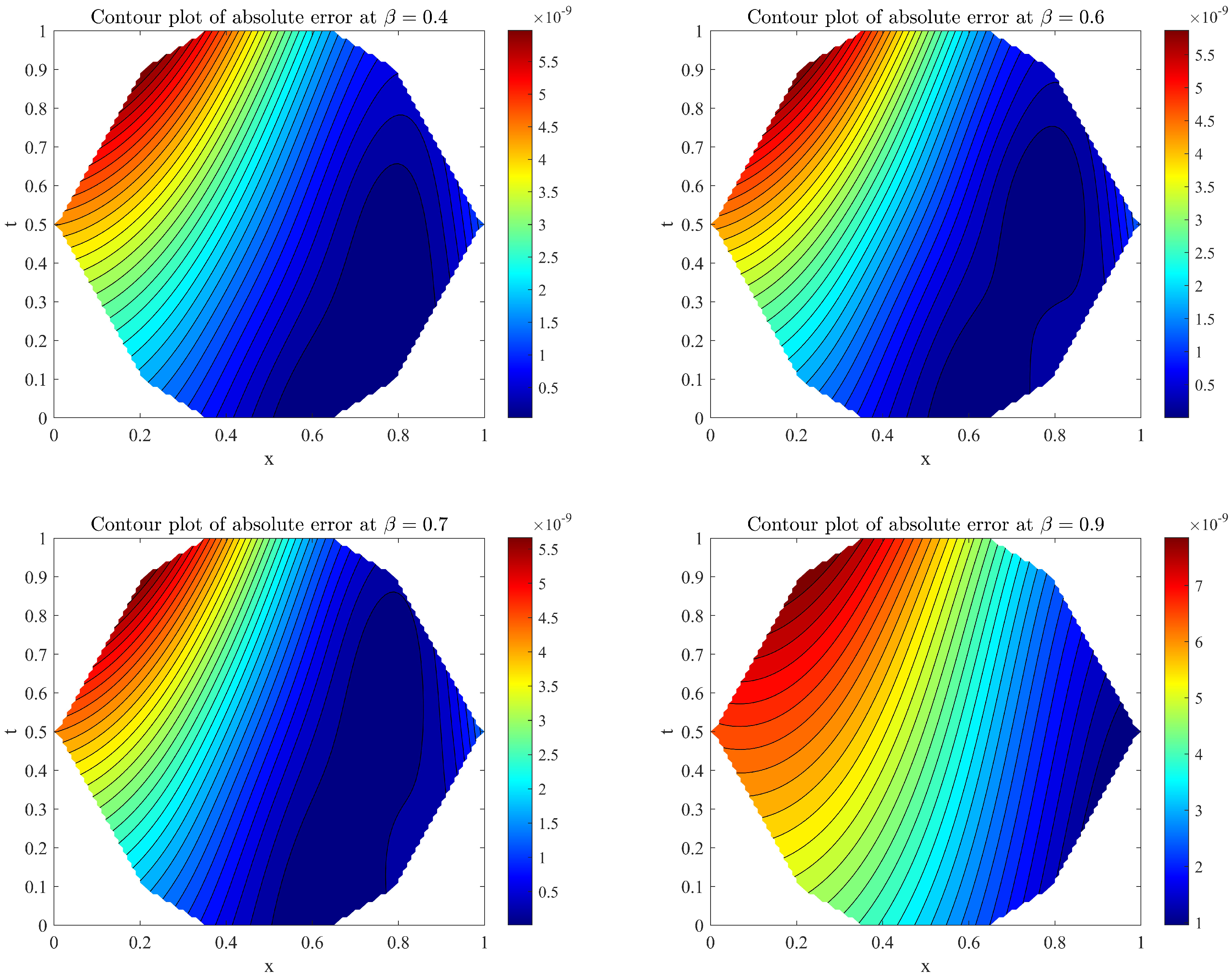
4. Numerical Examples
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Fang, Z.W.; Sun, H.W.; Wang, H. A fast method for variable-order Caputo fractional derivative with applications to time-fractional diffusion equations. Comput. Math. Appl. 2020, 80, 1443–1458. [Google Scholar] [CrossRef]
- Mehandiratta, V.; Mehra, M.; Leugering, G. Optimal control problems driven by time-fractional diffusion equations on metric graphs: Optimality system and finite difference approximation. SIAM J. Control Optim. 2021, 59, 4216–4242. [Google Scholar] [CrossRef]
- Gu, X.M.; Sun, H.W.; Zhao, Y.L.; Zheng, X. An implicit difference scheme for time-fractional diffusion equations with a time-invariant type variable order. Appl. Math. Lett. 2021, 120, 107270. [Google Scholar] [CrossRef]
- Zhang, X.D.; Feng, Y.L.; Luo, Z.Y.; Liu, J. A spatial sixth-order numerical scheme for solving fractional partial differential equation. Appl. Math. Lett. 2025, 159, 109265. [Google Scholar] [CrossRef]
- Huang, C.B.; Chen, H.; An, N. β-robust superconvergent analysis of a finite element method for the distributed order time-fractional diffusion equation. J. Sci. Comput. 2022, 90, 44. [Google Scholar] [CrossRef]
- Zheng, X.C.; Wang, H. Optimal-order error estimates of finite element approximations to variable-order time-fractional diffusion equations without regularity assumptions of the true solutions. IMA J. Numer. Anal. 2021, 41, 1522–1545. [Google Scholar] [CrossRef]
- Feng, L.B.; Zhuang, P.; Liu, F.; Turner, I.; Gu, Y. Finite element method for space-time fractional diffusion equation. Numer. Algorithms 2016, 72, 749–767. [Google Scholar] [CrossRef]
- Liu, F.; Zhuang, P.; Turner, I.; Burrage, K.; Anh, V. A new fractional finite volume method for solving the fractional diffusion equation. Appl. Math. Model. 2014, 38, 3871–3878. [Google Scholar] [CrossRef]
- Li, J.; Liu, F.W.; Feng, L.B.; Turner, I. A novel finite volume method for the Riesz space distributed-order diffusion equation. Comput. Math. Appl. 2017, 74, 772–783. [Google Scholar] [CrossRef]
- Lipnikov, K.N.; Svyatskiy, D.; Vassilevski, Y.V. Interpolation-free monotone finite volume method for diffusion equations on polygonal meshes. J. Comput. Phys. 2009, 228, 703–716. [Google Scholar] [CrossRef]
- Zheng, M.L.; Liu, F.W.; Anh, V.V.; Turner, I. A high-order spectral method for the multi-term time-fractional diffusion equations. Appl. Math. Model. 2016, 40, 4970–4985. [Google Scholar] [CrossRef]
- Jafarzadeh, S.; Larios, A.; Bobaru, F. Efficient solutions for nonlocal diffusion problems via boundary-adapted spectral methods. J. Peridynamics Nonlocal Model. 2020, 2, 85–110. [Google Scholar] [CrossRef]
- Kumbinarasaiah, S. Hermite wavelets approach for the multi-term fractional differential equations. J. Interdiscip. Math. 2021, 24, 1241–1262. [Google Scholar] [CrossRef]
- Delkhosh, M.; Parand, K. A new computational method based on fractional Lagrange functions to solve multi-term fractional differential equations. Numer. Algorithms 2021, 88, 729–766. [Google Scholar] [CrossRef]
- Abd-Elhameed, W.M.; Alsuyuti, M.M. Numerical treatment of multi-term fractional differential equations via new kind of generalized Chebyshev polynomials. Fractal Fract. 2023, 7, 74. [Google Scholar] [CrossRef]
- Tural-Polat, S.N.; Dincel, A.T. Numerical solution method for multi-term variable order fractional differential equations by shifted Chebyshev polynomials of the third kind. Alex. Eng. J. 2022, 61, 5145–5153. [Google Scholar] [CrossRef]
- Hashemi, M.S.; Inc, M.; Hajikhah, S. Generalized squared remainder minimization method for solving multi-term fractional differential equations. Nonlinear Anal. Model. 2021, 26, 57–71. [Google Scholar] [CrossRef]
- Shiralashetti, S.C.; Deshi, A.B. An efficient Haar wavelet collocation method for the numerical solution of multi-term fractional differential equations. Nonlinear Dynam. 2016, 83, 293–303. [Google Scholar] [CrossRef]
- Guo, B.L.; Pu, X.K.; Huang, F.H. Fractional Partial Differential Equations and Their Numerical Solutions; World Scientific: Singapore, 2015. [Google Scholar]
- Hilfer, R. Applications of Fractional Calculus in Physics; World Scientific: Singapore, 2000. [Google Scholar]
- Podlubny, I. Fractional Differential Equations; Academic Press: New York, NY, USA, 1999. [Google Scholar]
- Torkaman, S.; Heydari, M.; Loghmani, G.B. A combination of the quasilinearization method and linear barycentric rational interpolation to solve nonlinear multi-dimensional Volterra integral equations. Math. Comput. Simula. 2023, 208, 366–397. [Google Scholar]
- Liu, H.Y.; Ma, Y.Y.; Li, H.; Zhang, W. Combination of discrete technique on graded meshes with barycentric rational interpolation for solving a class of time-dependent partial integro-differential equations with weakly singular kernels. Comput. Math. Appl. 2023, 141, 159–169. [Google Scholar]
- Fahimi-khalilabad, I.; Irandoust-Pakchin, S.; Abdi-Mazraeh, S. High-order finite difference method based on linear barycentric rational interpolation for Caputo type sub-diffusion equation. Math. Comput. Simula. 2022, 199, 60–80. [Google Scholar] [CrossRef]
- Li, J. Linear barycentric rational collocation method for solving biharmonic equation. Demonstr. Math. 2022, 55, 587–603. [Google Scholar] [CrossRef]
- Yang, M.M.; Ma, W.T.; Ge, Y.B. Barycentric rational interpolation method of the Helmholtz equation with irregular domain. Math. Model. Anal. 2023, 28, 330–351. [Google Scholar] [CrossRef]
- Li, J.; Cheng, Y.L. Barycentric rational interpolation method for solving time-dependent fractional convection-diffusion equation. Electron. Res. Arch. 2023, 31, 4034–4056. [Google Scholar] [CrossRef]
- Berrut, J.P.; Mittelmann, H.D. Lebesgue constant minimizing linear rational interpolation of continuous functions over the interval. Comput. Math. Appl. 1997, 33, 77–86. [Google Scholar] [CrossRef]
- Berrut, J.P. Rational functions for guaranteed and experimentallywell-conditioned global interpolation. Comput. Math. Appl. 1988, 15, 1–16. [Google Scholar] [CrossRef]
- Floater, M.S.; Hormann, K. Barycentric rational interpolation with no poles and high rates of approximation. Numer. Math. 2007, 107, 315–331. [Google Scholar] [CrossRef]
- Klein, G.; Berrut, J.P. Linear rational finite differences from derivatives of barycentric rational interpolants. SIAM J. Numer. Anal. 2012, 50, 643–656. [Google Scholar] [CrossRef]
- Kahaner, D.; Moler, C.; Nash, S. Numerical Methods and Software; Prentice-Hall, Inc.: Hoboken, NJ, USA, 1989. [Google Scholar]
- Fornberg, B. A practical Guide to Pseudospectral Methods; Cambridge University Press: Cambridge, UK, 1998. [Google Scholar]
- Cirillo, E.; Hormann, K.; Sidon, J. Convergence rates of derivatives of Floater-Hormann interpolants for well-spaced nodes. Appl. Numer. Math. 2017, 116, 108–118. [Google Scholar] [CrossRef]
- Hormann, K.; Klein, G.; Marchi, S.D. Barycentric rational interpolation at quasi-equidistant nodes. Dolomit. Res. Notes Approx. 2012, 5, 1–6. [Google Scholar]
- Ravi Kanth, A.S.V.; Garg, N. An implicit numerical scheme for a class of multi-term time-fractional diffusion equation. Eur. Phys. J. Plus 2019, 134, 312. [Google Scholar] [CrossRef]




| CPU Time (s) | |||
|---|---|---|---|
| 4.5310 × | – | 0.1089 | |
| 2.0196 × | 6.6753 | 0.1445 | |
| 1.0301 × | 9.1740 | 0.2182 | |
| 6.4164 × | 11.3796 | 0.2408 |
| Chebyshev Nodes | Equidistant Nodes | Chebyshev Nodes | Equidistant Nodes | |
|---|---|---|---|---|
| 5 × 5 | 4.7064 × | 4.0635 × | 6.0160 × | 4.4925 × |
| 7 × 7 | 3.9313 × | 1.0369 × | 4.4536 × | 1.0910 × |
| 9 × 9 | 2.1562 × | 1.6026 × | 2.3250 × | 1.6524 × |
| 11 × 11 | 6.2475 × | 1.6719 × | 6.5704 × | 1.7065 × |
| I | ||||
|---|---|---|---|---|
| Present Method | Method in [36] | Present Method | Method in [36] | |
| 25 | 1.6819 × | 3.5338 × | 1.6817 × | 3.5334 × |
| 50 | 6.0084 × | 8.8537 × | 5.9549 × | 8.8528 × |
| 100 | 8.6425 × | 2.2146 × | 1.4588 × | 2.2144 × |
| 200 | 2.0880 × | 5.5372 × | 9.5881 × | 5.5365 × |
| Chebyshev Nodes | Equidistant Nodes | Chebyshev Nodes | Equidistant Nodes | |
|---|---|---|---|---|
| 6 × 6 | 4.3316 × | 4.5049 × | 4.3319 × | 4.4997 × |
| 8 × 8 | 1.2194 × | 4.2148 × | 1.2193 × | 4.2113 × |
| 10 × 10 | 2.3307 × | 2.3521 × | 2.3305 × | 2.3506 × |
| 12 × 12 | 3.2037 × | 8.8581 × | 3.2093 × | 8.8541 × |
| 4.3384 × | – | 4.3340 × | – | 4.3298 × | – | |
| 1.2217 × | 6.2045 | 1.2202 × | 6.2049 | 1.2187 × | 6.2053 | |
| 2.3337 × | 8.8686 | 2.3318 × | 8.8677 | 2.3298 × | 8.8669 | |
| 3.2065 × | 11.7579 | 3.2047 × | 11.7572 | 3.2050 × | 11.7546 | |
| 3.4117 × | 3.4003 × | 3.3950 × | 3.3972 × | 3.3953 × | |
| 3.4392 × | 3.3966 × | 3.3948 × | 3.3950 × | 3.3955 × | |
| 6.2334 × | 3.3713 × | 3.3797 × | 3.3795 × | 3.3803 × | |
| 6.8880 × | 3.2667 × | 3.3074 × | 3.3288 × | 3.3408 × |
| 1.6758 × | – | 1.6752 × | – | 1.6778 × | – | |
| 4.0572 × | 4.5885 | 4.0565 × | 4.5883 | 4.0809 × | 4.5828 | |
| 6.4739 × | 7.1918 | 6.4784 × | 7.1903 | 6.5555 × | 7.1801 | |
| 6.5814 × | 10.2819 | 6.6072 × | 10.2747 | 6.7627 × | 10.2491 | |
| 8.3788 × | 2.0286 × | 3.2370 × | 3.2907 × | |
| 8.3758 × | 2.0282 × | 3.2392 × | 3.3036 × | |
| 8.3890 × | 2.0404 × | 3.2777 × | 3.3813 × | |
| 8.4041 × | 2.0540 × | 3.3215 × | 3.2910 × |
| 8.0841 × | – | 9.0868 × | – | 1.1011 × | – | |
| 2.5106 × | 4.1655 | 2.4138 × | 4.2782 | 2.1358 × | 7.7013 | |
| 2.2096 × | 8.2259 | 2.1925 × | 8.1711 | 2.1735 × | 7.9735 | |
| 8.9602 × | 12.3413 | 8.6162 × | 12.4116 | 1.1141 × | 11.8163 | |
| 2.1999 × | 5.2842 × | 4.2828 × | 4.4389 × | 4.4982 × | |
| 3.9612 × | 6.4776 × | 4.6389 × | 4.2809 × | 4.3786 × | |
| 1.2493 × | 1.2395 × | 6.5162 × | 5.2498 × | 4.9184 × | |
| 1.5758 × | 1.0574 × | 3.1175 × | 1.7277 × | 1.3319 × |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Chen, Y.; Wei, L.; Kumar, S. Numerical Simulation Based on Interpolation Technique for Multi-Term Time-Fractional Convection–Diffusion Equations. Fractal Fract. 2024, 8, 687. https://doi.org/10.3390/fractalfract8120687
Zhang X, Chen Y, Wei L, Kumar S. Numerical Simulation Based on Interpolation Technique for Multi-Term Time-Fractional Convection–Diffusion Equations. Fractal and Fractional. 2024; 8(12):687. https://doi.org/10.3390/fractalfract8120687
Chicago/Turabian StyleZhang, Xindong, Yan Chen, Leilei Wei, and Sunil Kumar. 2024. "Numerical Simulation Based on Interpolation Technique for Multi-Term Time-Fractional Convection–Diffusion Equations" Fractal and Fractional 8, no. 12: 687. https://doi.org/10.3390/fractalfract8120687
APA StyleZhang, X., Chen, Y., Wei, L., & Kumar, S. (2024). Numerical Simulation Based on Interpolation Technique for Multi-Term Time-Fractional Convection–Diffusion Equations. Fractal and Fractional, 8(12), 687. https://doi.org/10.3390/fractalfract8120687





