Quadrature Solution for Fractional Benjamin–Bona–Mahony–Burger Equations
Abstract
1. Introduction
2. Model Formulation of the Problem
2.1. Space–Time-Fractional Modified BBME [35,36]
2.2. Time-Fractional BBMBE [35,36]
3. Methods of Solution
3.1. Polynomial Differential Quadrature (PDQ) Technique
3.2. Description of Discrete Singular Convolution DQM (DSCDQM)
- Regularized Shannon kernel (RSK)
- 2.
- Regularized Dirichlet kernel (RDK)
3.3. Generalized Caputo-Kind Fractional Derivative
- Caputo’s Fractional Derivative
3.4. Perturbation Technique [65]
3.5. Iterative Quadrature [68]
4. Numerical Results
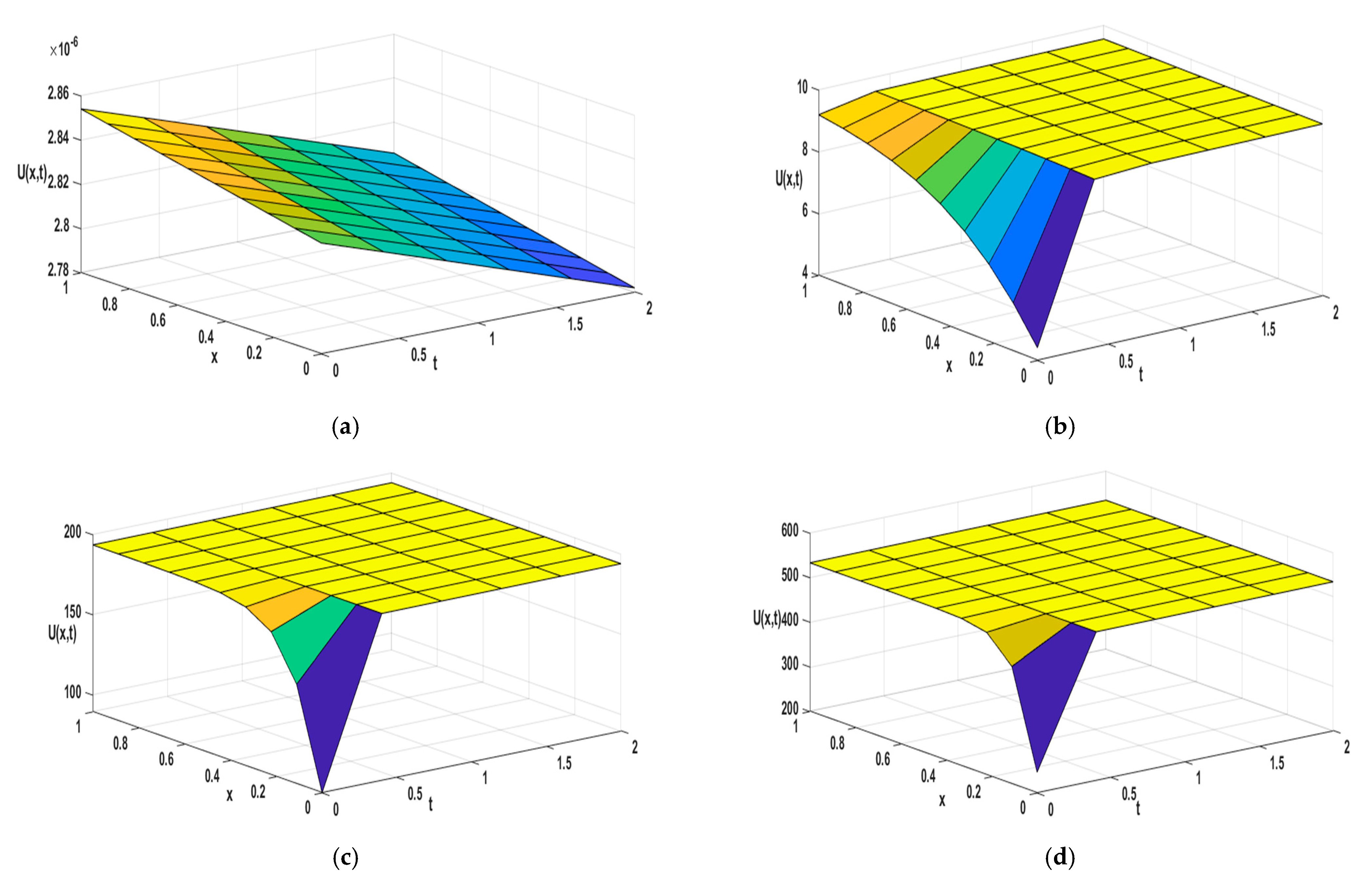
4.1. Consider a 1D Problem of MBBME Along the x-Direction as Follows
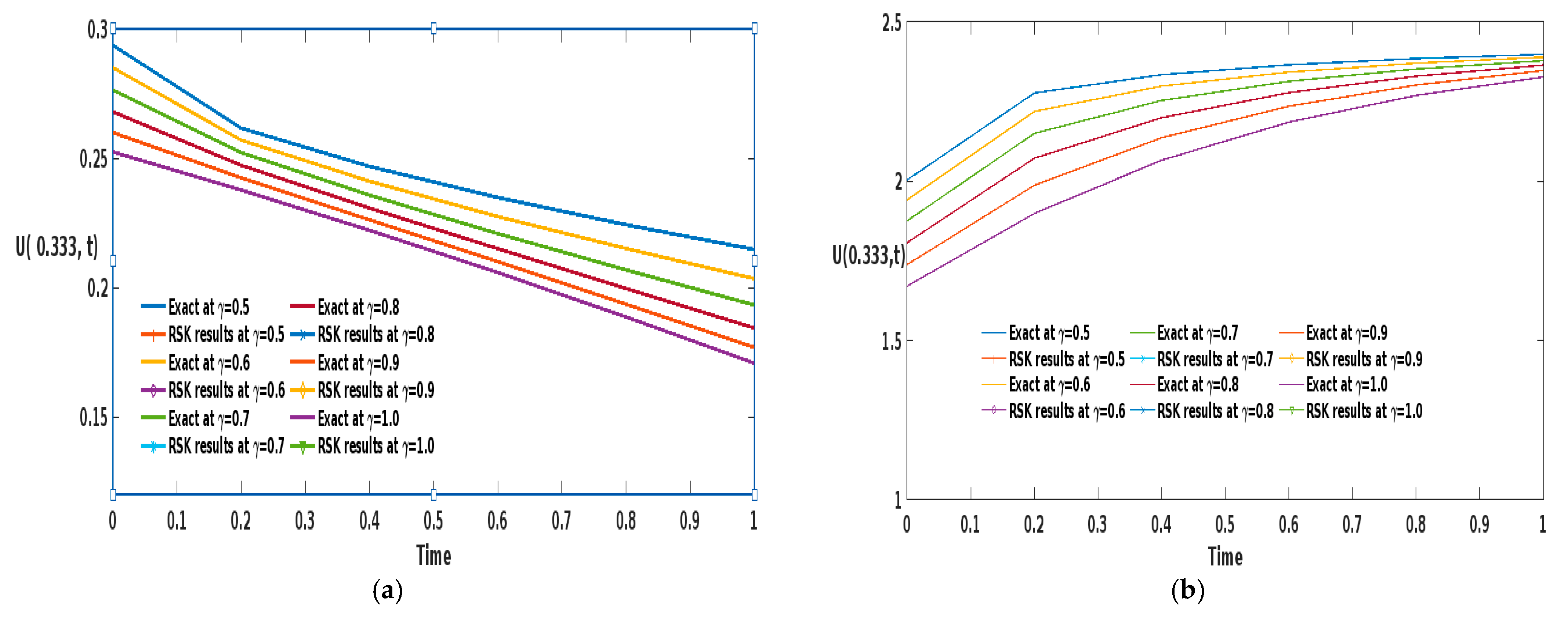
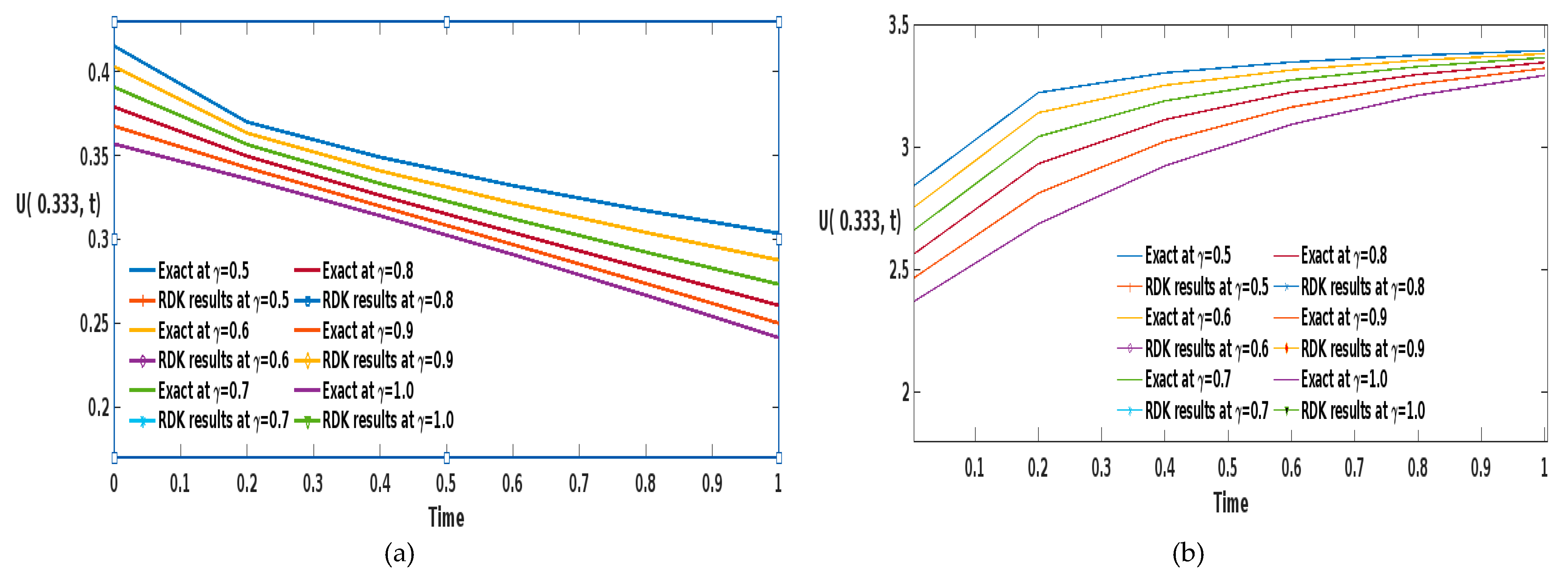
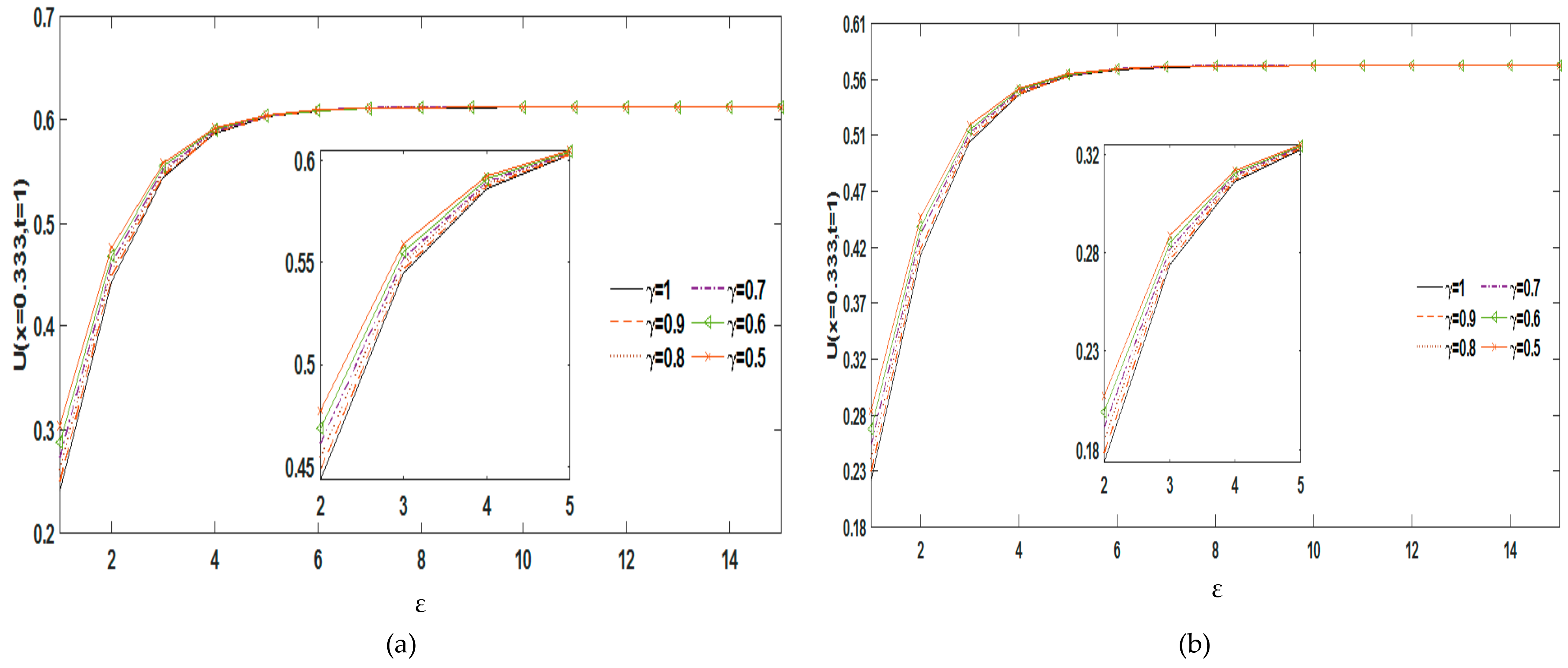
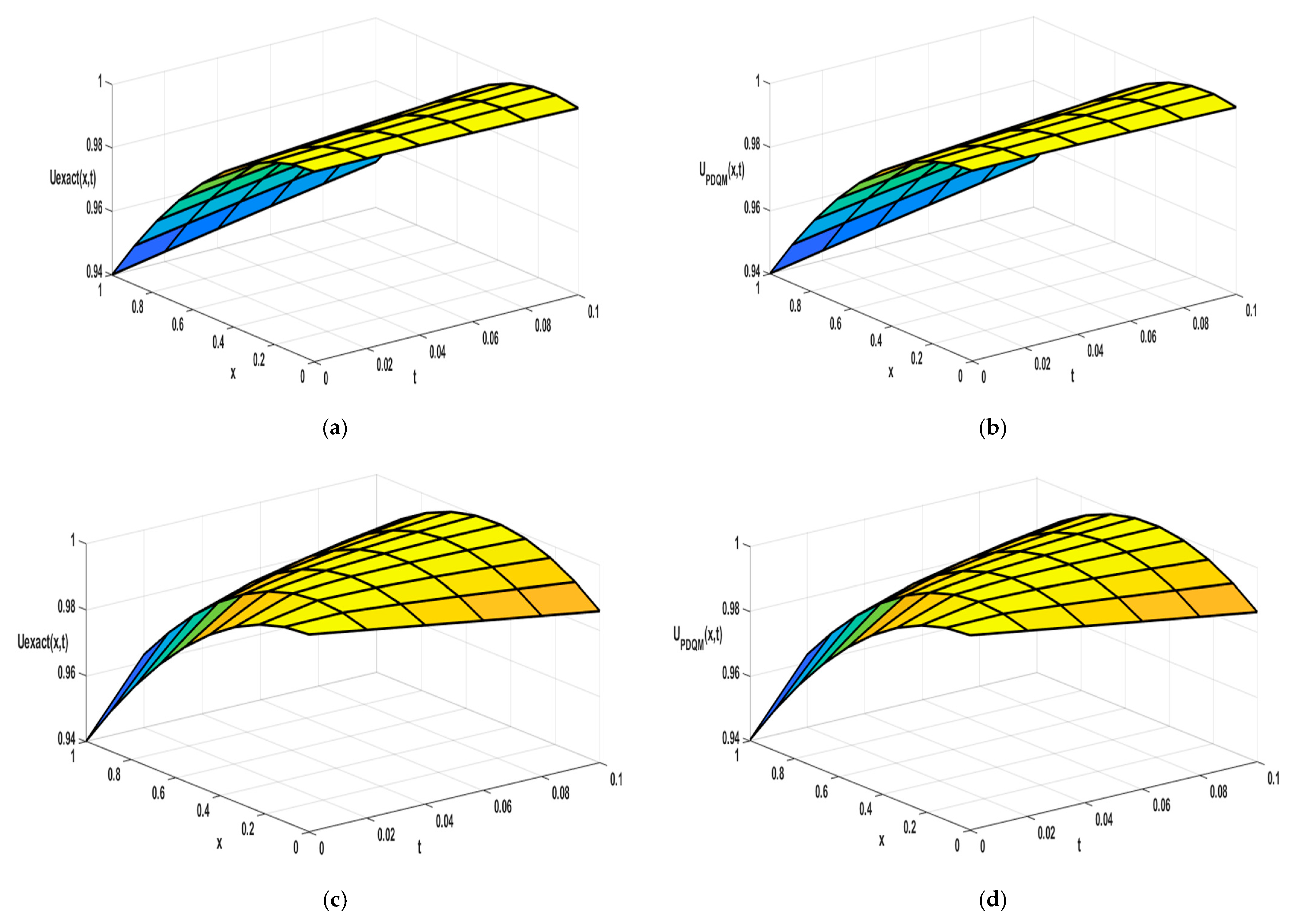
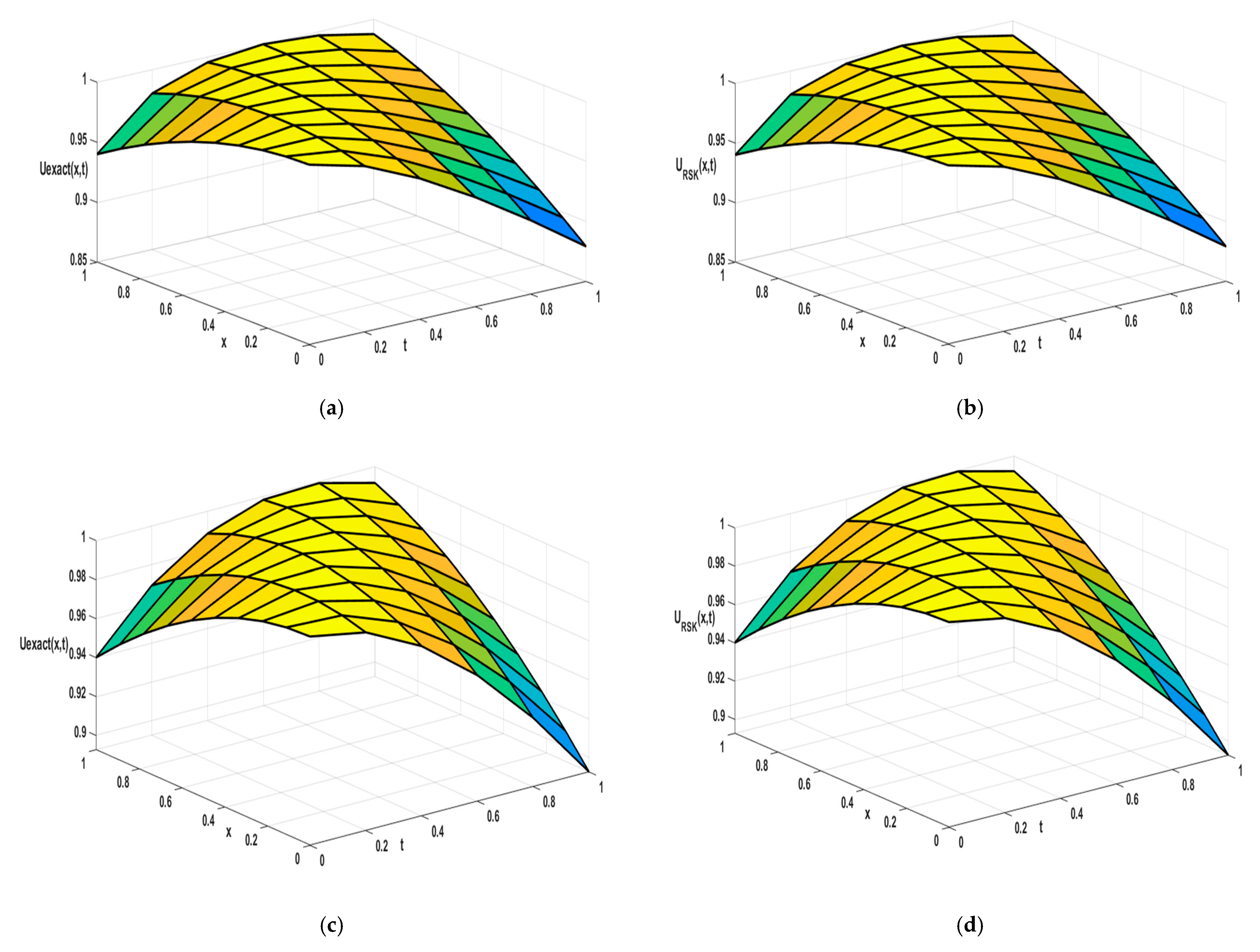
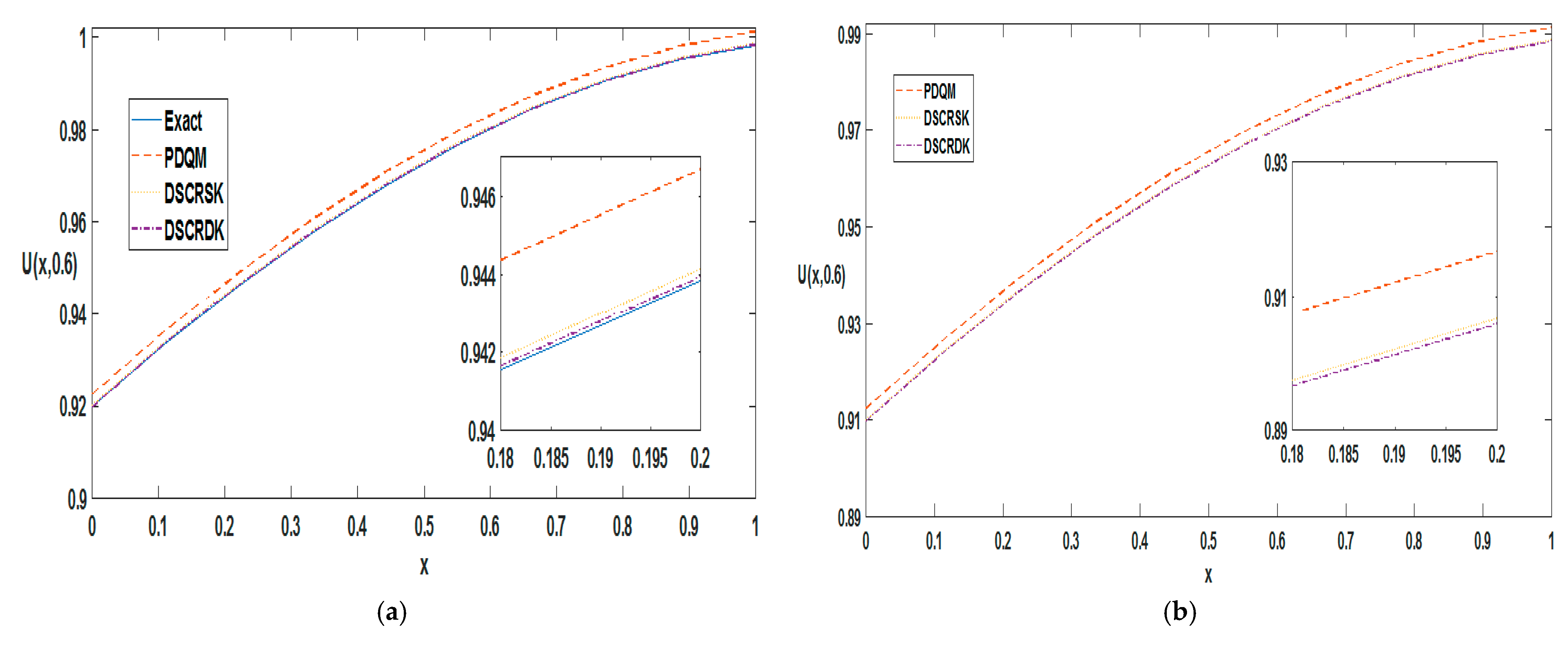
4.2. Consider a Problem Time-Fractional BBM-Burger Equation as Follows
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and applications of fractional differential equations. In North-Holland Mathematics Studies; Elsevier Science: Amsterdam, The Netherlands, 2006; Volume 204, pp. 15–23. [Google Scholar]
- Miller, K.S.; Ross, B. An Introduction to the Fractional Calculus and Fractional Differential Equations; Wiley: New York, NY, USA, 1993. [Google Scholar]
- Podlubny, I. Fractional Differential Equations: An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of Their Solution and Some of Their Applications; Academic Press: Cambridge, MA, USA, 1998; Volume 198. [Google Scholar]
- Gomez-Aguilar, J.F.; Cordova-Fraga, T.; Torres-Jimenez, J.; Escobar-Jimenez, R.F.; Olivares-Peregrino, V.H.; Guerrero-Ramirez, G.V. Nonlocal transport processes and the fractional Cattaneo-Vernotte equation. Math. Probl. Eng. 2016, 2016, 7845874. [Google Scholar] [CrossRef][Green Version]
- Anjum, N.; He, C.; He, J. Two-Scale Fractal Theory for the Population Dynamics. Fractals 2021, 29, 2150182. [Google Scholar] [CrossRef]
- Abel, N.H. Solutions de quelques problems a l’aide d’integrales definies. Werk 1823, 1, 10–14. [Google Scholar]
- Caputo, M. Linera Models of Dissipation Whose q is Almost Frequency Independent. Ann. Geophys. 1966, 19, 383–393. [Google Scholar]
- Euler, L. On transcendental progression that is, those whose general terms cannot be given algebraically. Acad. Sci. Imp. Petropolitanae 1738, 1, 38–57. [Google Scholar]
- Fourier, J. Theorie Analytique de la Chaleur; Gauthier-Villars: Paris, France, 1888; Volume 1. [Google Scholar]
- Laplace, P.S. Theorie Analytique de Probabilities; Courcier: Paris, France, 1812. [Google Scholar]
- Liouville, J. Memory on some questions of geometry and mechanics, and on a new kind of calculation to solve these questions. J. de l’E’cole Pol. Tech. 1832, 13, 1–69. [Google Scholar]
- Ross, B. The development of fractional calculus. 1695–1900. Hist. Math. 1977, 4, 75–89. [Google Scholar] [CrossRef]
- Benjamin, T.B.; Bona, J.L.; Mahony, J.J. Model equations for long waves in nonlinear dispersive systems. Philos. Trans. R. Soc. A 1972, 272, 47–78. [Google Scholar]
- Horton, J.W. Fluctuation spectra of a drift wave soliton gas. Phys. Fluids 1982, 25, 1838–1843. [Google Scholar]
- Islam, S.; Haq, S.; Ali, A. A meshfree method for the numerical solution of the RLW equation. J. Comput. Appl. Math. 2009, 223, 997–1012. [Google Scholar] [CrossRef]
- Kaya, D. A numerical simulation of solitary-wave solutions of the generalized regularized long-wave equation. Appl. Math. Comput. 2004, 149, 833–841. [Google Scholar] [CrossRef]
- Dag, I.; Ozer, M.N. Approximation of RLW equation by least square cubic B-spline finite element method. Appl. Math. Model. 2001, 25, 221–231. [Google Scholar] [CrossRef]
- Dag, I.; Saka, B.; Irk, D. Application of cubic B-splines for numerical solution of the RLW equation. Appl. Math. Comput. 2004, 159, 373–389. [Google Scholar]
- Esen, A.; Kutluay, S. Application of a lumped Galerkin method to the regularized long wave equation. Appl. Math. Comput. 2006, 174, 833–845. [Google Scholar] [CrossRef]
- Gardner, L.R.T.; Gardner, G.A.; Dag, I. A B-spline finite element method for the regularized long wave equation. Commun. Numer. Methods Eng. 1995, 11, 59–68. [Google Scholar] [CrossRef]
- Barati, A. The numerical solution of time fractional generalized Benjamin-Bona-Mahony equation via the Sinc functions. Int. J. Nonlinear Anal. 2023, 14, 2759–2770. [Google Scholar]
- Yaro, D.; Seadawy, A.R.; Dianchen, L.U.; Apeanti, W.O.; Akuamoah, S.W. Dispersive wave solutions of the nonlinear fractional Zakhorov-KuznetsovBenjamin-Bona-Mahony equation and fractional symmetric regularized long wave equation. Results Phys. 2019, 12, 1971–1979. [Google Scholar] [CrossRef]
- Kumar, V. Modified (G’/G)-expansion method for finding traveling wave solutions of the coupled Benjamin–Bona–Mahony-KdV equation. J. Ocean. Eng. Sci. 2019, 4, 252–255. [Google Scholar] [CrossRef]
- Liu, Y. Approximate Solutions of Fractional Nonlinear Equations Using Homotopy Perturbation Transformation Method. In Abstract and Applied Analysis; Hindawi Publishing Corporation: Cairo, Egypt, 2012; p. 752869. [Google Scholar] [CrossRef]
- Ray, S.S.; Das, G. Numerical simulation of time fractional Benjamin-Bona-Mahony-Burger equation describing propagation of long waves on the water surface. J. Ocean. Eng. Sci. 2023, in press. [Google Scholar]
- Dehghan, M.; Shafieeabyaneh, N.; Abbaszadeh, M. Numerical and theoretical discussions for solving nonlinear generalized Benjamin–Bona–Mahony– Burgers equation based on the Legendre spectral element method. Numer. Methods Partial. Differ. Equ. 2021, 37, 360–382. [Google Scholar] [CrossRef]
- Elmandouh, A.; Fadhal, E. Bifurcation of Exact Solutions for the Space-Fractional Stochastic Modified Benjamin–Bona–Mahony Equation. Fractal Fract. 2022, 6, 718. [Google Scholar] [CrossRef]
- Javeeda, S.; Saif, S.; Waheed, A. Dumitru Baleanu, Exact solutions of fractional mBBM equation and coupled system of fractional Boussinesq-Burgers. Results Phys. 2018, 9, 1275–1281. [Google Scholar] [CrossRef]
- Dehghan, M.; Abbaszadeh, M.; Mohebbi, A. The numerical solution of nonlinear high dimensional generalized Benjamin–Bona–Mahony–Burgers equation via the meshless method of radial basis functions. Comput. Math. Appl. 2014, 68, 212–237. [Google Scholar] [CrossRef]
- Oruç, Ö. A new algorithm based on Lucas polynomials for approximate solution of 1D and 2D nonlinear generalized Benjamin–Bona–Mahony–Burgers equation. Comput. Math. Appl. 2017, 74, 3042–3057. [Google Scholar] [CrossRef]
- Dehghan, M.; Abbaszadeh, M.; Mohebbi, A. The use of interpolating element-free Galerkin technique for solving 2D generalized Benjamin–Bona–Mahony–Burgers and regularized long-wave equations on non-rectangular domains with error estimate. J. Comput. Appl. Math. 2015, 286, 211–231. [Google Scholar] [CrossRef]
- Hajiketabi, M.; Abbasbandy, S.; Casas, F. The Lie-group method based on radial basis functions for solving nonlinear high dimensional generalized Benjamin–Bona–Mahony–Burgers equation in arbitrary domains. Appl. Math. Comput. 2018, 321, 223–243. [Google Scholar] [CrossRef]
- Bayarassou, K. Fourth-order accurate difference schemes for solving Benjamin–Bona–Mahony–Burgers (BBMB) equation. Eng. Comput. 2019, 37, 123–138. [Google Scholar] [CrossRef]
- Arora, S.; Jain, R.; Kukreja, V.K. Solution of Benjamin–Bona–Mahony–Burgers equation using collocation method with quintic Hermite splines. Appl. Numer. Math. 2020, 154, 1–16. [Google Scholar] [CrossRef]
- Islam, M.T.; Akbar, M.A.; Azad, M.A. The exact traveling wave solutions to the nonlinear space-time fractional modified Benjamin-Bona-Mahony equation. J. Mech. Cont. Math. Sci. 2018, 13, 56–71. [Google Scholar] [CrossRef]
- Ege, S.M.; Misirli, E. The modified Kudryashov method for solving some fractional-order nonlinear equations. Adv. Differ. Equ. 2014, 2014, 135. [Google Scholar] [CrossRef]
- Guner, O.; Bekir, A. Bright and dark soliton solutions for some nonlinear fractional differential equations. Chin. Phys. B 2016, 25, 030203. [Google Scholar] [CrossRef]
- Kapoor, M.; Joshi, V. A numerical regime for 1-D Burgers’ equation using UAT tension B-spline differential quadrature method. Int. J. Comput. Methods Eng. Sci. Mech. 2021, 22, 181–192. [Google Scholar] [CrossRef]
- Joshi, V.; Kapoor, M.; Bhardwaj, N.; Masud, M.; Al-Amri, J.F. Numerical Approximation of One- and Two-Dimensional Coupled Nonlinear Schrödinger Equation by Implementing Barycentric Lagrange Interpolation Polynomial DQM. Math. Probl. Eng. 2021, 2021, 9968063. [Google Scholar] [CrossRef]
- Castro López, R.; Sun, G.-H.; Camacho-Nieto, O.; Yáñez-Márquez, C.; Dong, S.-H. Analytical traveling-wave solutions to a generalized Gross–Pitaevskii equation with some new time and space varying nonlinearity coefficients and external fields. Phys. Lett. A 2017, 381, 2978–2985. [Google Scholar] [CrossRef]
- Guo, Y.; Li, W.; Dong, S.H. Gaussian solitary solution for a class of logarithmic nonlinear Schrödinger equation in (1 + n) dimensions. Results Phys. 2023, 44, 106187. [Google Scholar] [CrossRef]
- Solaimani, M.; Dong, S.-H. Quantum information entropies of multiple quantum well systems in fractional Schrödinger equations. Int. J. Quant. Chem. 2020, 120, e26113. [Google Scholar] [CrossRef]
- Child, M.S.; Dong, S.H.; Wang, X.G. Quantum states of a sextic potential: Hidden symmetry and quantum monodromy. J. Phys. A 2000, 33, 5653–5661. [Google Scholar] [CrossRef]
- Santana-Carrillo, R.; Velázquez Peto, J.M.; Sun, G.-H.; Dong, S.-H. Quantum information entropy for a hyperbolic double well potential in the fractional Schrödinger equation. Entropy 2023, 25, 988. [Google Scholar] [CrossRef]
- Santana-Carrillo, R.; González-Flores, J.S.; Magana-Espinal, E.; Quezada, L.F.; Sun, G.-H.; Dong, S.-H. Quantum information entropy of hyperbolic potentials in fractional schrödinger equation. Entropy 2022, 24, 1516. [Google Scholar] [CrossRef]
- Ragb, O.; Matbuly, M.S.; Civalek, O. Free vibration of irregular plates via indirect differential quadrature and singular convolution techniques. Eng. Anal. Bound. Elem. 2021, 128, 66–79. [Google Scholar] [CrossRef]
- Ragb, O.; Mohamed, M.; Matbuly, M.S.; Civalek, O. An accurate numerical approach for studying perovskite solar cells. Int. J. Energy Res. 2021, 45, 16456–16477. [Google Scholar] [CrossRef]
- Zayed, E.M.E.; Al-Joudi, S. Applications of an extended (G’/G)-expansion method to find exact solutions of nonlinear PDEs in mathematical physics. Math. Probl. Eng. 2010, 2010, 1–19. [Google Scholar] [CrossRef]
- Shu, C. Differential Quadrature and Its Application in Engineering; Springer-Verlag: Berlin/Heidelberg, Germany, 2000; Volume 360. [Google Scholar]
- Bellman, R.; Kashef, B.; Lee, E.S.; Vasudevan, R. Differential quadrature and splines. Comput. Math. Appl. 1975, 1, 371–376. [Google Scholar] [CrossRef]
- Quan, J.R.; Chang, C.T. New insights in solving distributed system equations by the quadrature method—I. Analysis. Comput. Chem. Eng. 1989, 13, 779–788. [Google Scholar] [CrossRef]
- Quan, J.R.; Chang, C.T. New sightings in involving distributed system equations by the quadrature methods—II. Comput. Chem. Eng. 1989, 13, 717–724. [Google Scholar]
- Shu, C.; Richards, B.E. Application of generalized differential quadrature to solve two-dimensional incompressible Navier-Stokes equations. Int. J. Numer. Methods Fluids 1992, 15, 791–798. [Google Scholar] [CrossRef]
- Wei, G.W. Vibration analysis by discrete singular convolution. J. Sound Vib. 2001, 244, 535–553. [Google Scholar] [CrossRef]
- Wei, G.W.; Zhao, Y.B.; Xiang, Y. Discrete singular convolution and its application to the analysis of plates with internal supports. Part 1: Theory and algorithm. Int. J. Numer. Methods Eng. 2002, 55, 913–946. [Google Scholar] [CrossRef]
- Wang, X.; Xu, S. Free vibration analysis of beams and rectangular plates with free edges by the discrete singular convolution. J. Sound Vib. 2010, 329, 1780–1792. [Google Scholar] [CrossRef]
- Ragb, O.; Wazwaz, A.-M.; Mohamed, M.; Matbuly, M.S.; Salah, M. Fractional differential quadrature techniques for fractional order Cauchy reaction-diffusion equations. Math. Meth. Appl. Sci. 2023, 46, 10216–10233. [Google Scholar] [CrossRef]
- Caputo, M. Linear models of dissipation whose Q is almost frequency independent—II. Geophys. J. Int. 1967, 13, 529–539. [Google Scholar] [CrossRef]
- Weilbeer, M. Efficient Numerical Methods for Fractional Differential Equations and Their Analytical Background; Mathematics; Papierflieger: Clausthal-Zellerfeld, Germany, 2005. [Google Scholar]
- Mustafa, A.; Ragb, O.; Salah, M.; Salama, R.S.; Mohamed, M. Distinctive Shape Functions of Fractional Differential Quadrature for Solving Two-Dimensional Space Fractional Diffusion Problems. Fractal Fract. 2023, 7, 668. [Google Scholar] [CrossRef]
- Xu, Y.; He, Z.; Agrawal, O.P. Numerical and analytical solutions of new generalized fractional diffusion equation. Comput. Math. Appl. 2013, 66, 2019–2029. [Google Scholar] [CrossRef]
- Kumar, P.; Erturk, V.S.; Kumar, A. A new technique to solve generalized Caputo type fractional differential equations with the example of computer virus model. J. Math. Ext. 2021, 15, 1–23. [Google Scholar]
- Hilfer, R. Applications of Fractional Calculus in Physics. World Scientific Publishing Co., Inc.: River Edge, NJ, USA, 2000. [Google Scholar]
- Magin, R.L. Fractional Calculus in Bioengineering; Begell House Publishers: Danbury, CT, USA, 2006. [Google Scholar]
- Samko, S.G.; Kilbas, A.A.; Marichev, O.I. Fractional Integrals and Derivatives, Theory and Applications. Nikolski, S.M., Ed.; Gordon and Breach Science Publishers: Yverdon, Switzerland, 1993. [Google Scholar]
- Nadjafi, J.S.; Ghorbani, A. He’s homotopy perturbation method: An effective tool for solving nonlinear integral and integro-differential equations. Comput. Math. Appl. 2009, 2009, 2379–2390. [Google Scholar] [CrossRef]
- Turyilmazoglu, M. Some issues on HPM and HAM method: A convergence scheme. Math. Comput. Model. 2011, 53, 1929–1936. [Google Scholar] [CrossRef]
- Ragb, O.; Seddek, L.F.; Matbuly, M.S. Iterative differential quadrature solutions for Bratu problem. Comput. Math. Appl. 2017, 74, 249–257. [Google Scholar] [CrossRef]



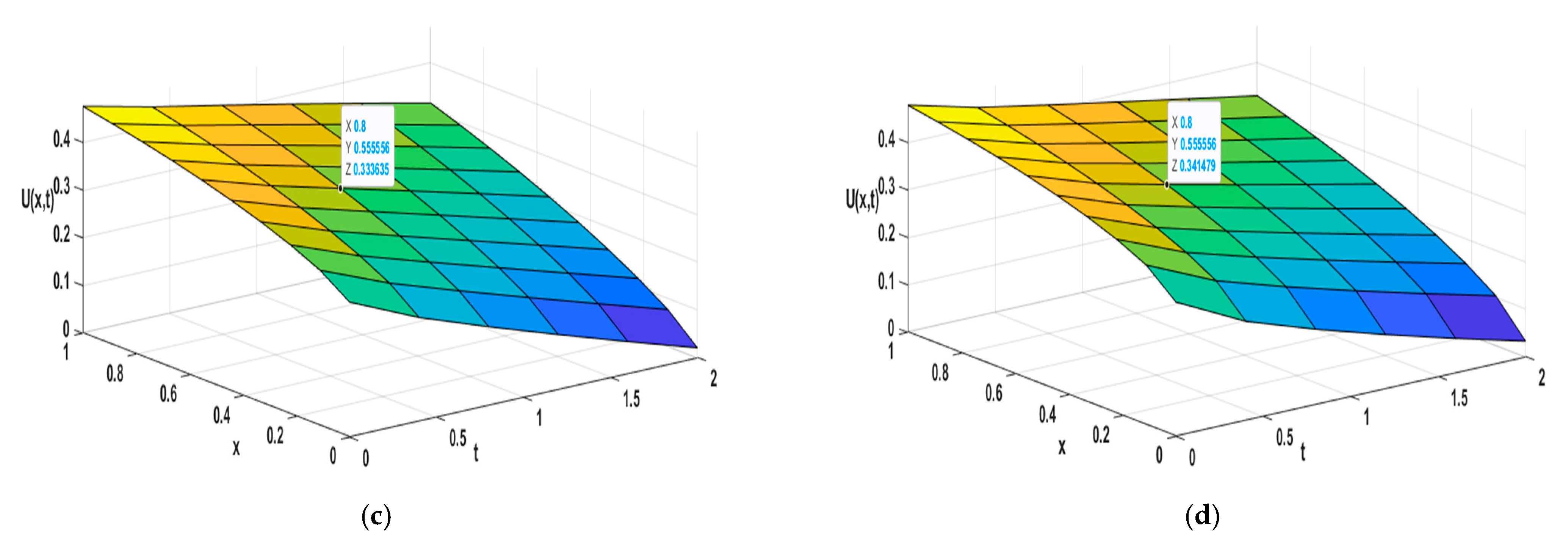
| nx | PDQM + Perturbation | PDQM + Iterative | ||||
|---|---|---|---|---|---|---|
| 4 | 0.33410 | 0.33480 | 0.33525 | 0.32034 | 0.33251 | 0.33283 |
| 7 | 0.33452 | 0.33502 | 0.33582 | 0.33124 | 0.33502 | 0.33612 |
| 10 | 0.33541 | 0.33571 | 0.33601 | 0.33254 | 0.33752 | 0.33798 |
| 13 | 0.33554 | 0.33612 | 0.33675 | 0.33401 | 0.33791 | 0.33851 |
| 16 | 0.33587 | 0.33695 | 0.33725 | 0.33491 | 0.33810 | 0.33881 |
| 19 | 0.33588 | 0.33702 | 0.33790 | 0.33551 | 0.33817 | 0.33925 |
| 22 | 0.33601 | 0.33751 | 0.33851 | 0.33607 | 0.33831 | 0.33934 |
| 25 | 0.33608 | 0.33801 | 0.33908 | 0.33615 | 0.33897 | 0.33955 |
| Exact [35] | 0.33610 | 0.33803 | 0.33936 | 0.33610 | 0.33803 | 0.33936 |
| CPU time | 0.183610 s at 10 × 10 | 0.096258 s at 10 × 10 | ||||
| Grid Size | Bandwidth | DSC-RSK + Perturbation | DSC-RDK + Iterative | ||||||
|---|---|---|---|---|---|---|---|---|---|
| 9 | 3 | - | - | - | - | 0.26846 | 0.26871 | 0.26877 | 0.26985 |
| 5 | 0.26808 | 0.26811 | 0.26821 | 0.26821 | 0.26846 | 0.26871 | 0.26877 | 0.26985 | |
| 7 | 0.26808 | 0.26811 | 0.26821 | 0.26821 | 0.26846 | 0.26871 | 0.26877 | 0.26985 | |
| 9 | 0.26808 | 0.26811 | 0.26821 | 0.26821 | 0.26846 | 0.26871 | 0.26877 | 0.26985 | |
| 11 | 0.26808 | 0.26811 | 0.26821 | 0.26821 | 0.26846 | 0.26871 | 0.26877 | 0.26985 | |
| 15 | 0.26808 | 0.26811 | 0.26821 | 0.26821 | 0.26846 | 0.26871 | 0.26877 | 0.26985 | |
| 19 | 0.26808 | 0.26811 | 0.26821 | 0.26821 | 0.26846 | 0.26871 | 0.26877 | 0.26985 | |
| 10 | 3 | 0.26709 | 0.26813 | 0.26829 | 0.26849 | 0.26814 | 0.26819 | 0.26822 | 0.26838 |
| 5 | 0.26709 | 0.26813 | 0.26829 | 0.26849 | 0.26814 | 0.26819 | 0.26822 | 0.26838 | |
| 7 | 0.26709 | 0.26813 | 0.26829 | 0.26849 | 0.26814 | 0.26819 | 0.26822 | 0.26838 | |
| 9 | 0.26709 | 0.26813 | 0.26829 | 0.26849 | 0.26814 | 0.26819 | 0.26822 | 0.26838 | |
| 11 | 0.26709 | 0.26813 | 0.26829 | 0.26849 | 0.26814 | 0.26819 | 0.26822 | 0.26838 | |
| 15 | 0.26709 | 0.26813 | 0.26829 | 0.26849 | 0.26814 | 0.26819 | 0.26822 | 0.26838 | |
| 19 | 0.26709 | 0.26813 | 0.26829 | 0.26849 | 0.26814 | 0.26819 | 0.26822 | 0.26838 | |
| 11 | 3 | 0.26709 | 0.26813 | 0.26829 | 0.26849 | 0.26814 | 0.26819 | 0.26822 | 0.26838 |
| 5 | 0.26709 | 0.26813 | 0.26829 | 0.26849 | 0.26814 | 0.26819 | 0.26822 | 0.26838 | |
| 7 | 0.26709 | 0.26813 | 0.26829 | 0.26849 | 0.26814 | 0.26819 | 0.26822 | 0.26838 | |
| 9 | 0.26709 | 0.26813 | 0.26829 | 0.26849 | 0.26814 | 0.26819 | 0.26822 | 0.26838 | |
| 11 | 0.26709 | 0.26813 | 0.26829 | 0.26849 | 0.26814 | 0.26819 | 0.26822 | 0.26838 | |
| 15 | 0.26709 | 0.26813 | 0.26829 | 0.26849 | 0.26814 | 0.26819 | 0.26822 | 0.26838 | |
| 19 | 0.26709 | 0.26813 | 0.26829 | 0.26849 | 0.26814 | 0.26819 | 0.26822 | 0.26838 | |
| CPU Time | 0.095582 s. at nx = 10, | 0.096531 s. at nx = 10, | |||||||
| Exact [35] | 0.26834 | ||||||||
| Grid Points nx | |||||||
|---|---|---|---|---|---|---|---|
| 1 | 5 | 10 | 15 | 20 | 30 | 40 | |
| 10 | 0.26820 | 0.26821 | 0.26823 | 0.26823 | 0.26823 | 0.26823 | 0.26823 |
| 11 | 0.26820 | 0.26821 | 0.26823 | 0.26823 | 0.26823 | 0.26823 | 0.26823 |
| 12 | 0.26820 | 0.26821 | 0.26823 | 0.26823 | 0.26823 | 0.26823 | 0.26823 |
| 13 | 0.26820 | 0.26821 | 0.26823 | 0.26823 | 0.26823 | 0.26823 | 0.26823 |
| 14 | 0.26820 | 0.26821 | 0.26823 | 0.26823 | 0.26823 | 0.26823 | 0.26823 |
| 15 | 0.26820 | 0.26821 | 0.26823 | 0.26823 | 0.26823 | 0.26823 | 0.26823 |
| Exact [35] | 0.26834 | ||||||
| CPU Time | 0.072366 s at nx = 10 | ||||||
| Time | ||||||
|---|---|---|---|---|---|---|
| PDQM | DSC-RSK = 2 | DSC-RDK = 1 | PDQM | DSC-RSK = 2 | DSC-RDK = 1 | |
| 0.3 | 5.1778 × 10−4 | 3.5078 × 10−4 | 2.9011 × 10−4 | 5.7120 × 10−4 | 3.6210 × 10−4 | 2.9801 × 10−4 |
| 0.5 | 8.0243 × 10−4 | 3.5241 × 10−4 | 2.9021 × 10−4 | 9.1042 × 10−4 | 3.6201 × 10−4 | 2.9811 × 10−4 |
| 1 | 1.5487 × 10−3 | 3.5277 × 10−4 | 2.9021 × 10−4 | 2.4017 × 10−3 | 3.6251 × 10−4 | 2.9724 × 10−4 |
| 2 | 3.5518 × 10−3 | 3.5188 × 10−4 | 2.9005 × 10−4 | 3.9118 × 10−3 | 3.6280 × 10−4 | 2.9880 × 10−4 |
| 5 | 5.5001 × 10−3 | 3.5001 × 10−4 | 2.9011 × 10−4 | 5.5289 × 10−3 | 3.6291 × 10−4 | 2.9818 × 10−4 |
| 7 | 6.1901 × 10−3 | 3.5002 × 10−4 | 2.9003 × 10−4 | 7.0991 × 10−3 | 3.6292 × 10−4 | 2.9921 × 10−4 |
| 10 | 7.15410 × 10−3 | 3.5012 × 10−4 | 2.9015 × 10−4 | 7.80662 × 10−3 | 3.6294 × 10−4 | 2.9912 × 10−4 |
| Method | Time = 0.2 | Time = 0.4 | Time = 0.6 | Time = 0.8 | Time = 1 | ||
|---|---|---|---|---|---|---|---|
| 1 | 0.9 | PDQM | 0.389721295 | 0.3680463518 | 0.3378722832 | 0.3346095 | 0.3056576 |
| RSK | 0.3876536321 | 0.3640845129 | 0.34574756900 | 0.326278013 | 0.3056760 | ||
| RDK | 0.3870390159 | 0.3619246792 | 0.34522989232 | 0.326552839 | 0.3056886 | ||
| Exact [35] | 0.3872035353 | 0.36711214584 | 0.34683211164 | 0.326103456 | 0.3048345 | ||
| 0.8 | PDQM | 0.3910653065 | 0.3753397944 | 0.35308995183 | 0.335620599 | 0.3180235 | |
| RSK | 0.3901965632 | 0.37030983171 | 0.35153027266 | 0.330488302 | 0.3138299 | ||
| RDK | 0.3909431115 | 0.37069452570 | 0.35823577077 | 0.336317366 | 0.3199452 | ||
| Exact [35] | 0.3930743748 | 0.37260909741 | 0.35297863310 | 0.333601339 | 0.3142535 | ||
| 0.7 | PDQM | 0.3906530165 | 0.37012073090 | 0.37684786559 | 0.352215195 | 0.3128846 | |
| RSK | 0.3986530659 | 0.37702073090 | 0.35269978635 | 0.341211190 | 0.3286423 | ||
| RDK | 0.3986530659 | 0.37702073090 | 0.35699786359 | 0.341211190 | 0.3286423 | ||
| Exact [35] | 0.3981059865 | 0.37769699000 | 0.35912585548 | 0.341445249 | 0.3242833 | ||
| 0.9 | 0.9 | PDQM | 0.3663380120 | 0.34596421740 | 0.3176178900 | 0.314533214 | 0.2873180 |
| RSK | 0.3643942101 | 0.34220197239 | 0.32501543003 | 0.301806701 | 0.2587335 | ||
| RDK | 0.3638174100 | 0.34021507209 | 0.3221424516 | 0.302578696 | 0.2847347 | ||
| 0.8 | PDQM | 0.3675134601 | 0.35198762819 | 0.33018761905 | 0.314872483 | 0.2928942 | |
| RSK | 0.3664874785 | 0.34547018091 | 0.33015780438 | 0.311870659 | 0.2871195 | ||
| RDK | 0.3672891487 | 0.34741258453 | 0.33005416742 | 0.307816138 | 0.3007148 | ||
| 0.7 | PDQM | 0.3671068214 | 0.34792114513 | 0.35267014237 | 0.330101082 | 0.2910412 | |
| RSK | 0.3741014734 | 0.35432142199 | 0.33015871538 | 0.321540739 | 0.3008924 | ||
| RDK | 0.3661240338 | 0.34591012564 | 0.30547823176 | 0.310784533 | 0.2187318 |
| Time | Non-Uniform PDQM | DSCDQM-RSK | Uniform PDQM | DSCDQM-RDK | ||||
|---|---|---|---|---|---|---|---|---|
| RMS | Comput. Time (S) | RMS | Comput. Time (S) | RMS | Comput. Time (S) | RMS | Comput. Time (S) | |
| 1 | 5.2629 × 10−5 | 0.1375 | 5.625× 10−5 | 0.08399 | 6.0666× 10−5 | 0.1374 | 2.1913× 10−5 | 0.08399 |
| 2 | 1.1454 × 10−4 | 0.1556 | 1.224× 10−4 | 0.08495 | 1.3201× 10−4 | 0.1544 | 4.7697× 10−5 | 0.08487 |
| 3 | 1.5468× 10−4 | 0.1640 | 1.653× 10−4 | 0.0944 | 1.7824× 10−4 | 0.1640 | 6.4416× 10−5 | 0.0943 |
| 4 | 2.5786× 10−4 | 0.1782 | 2.755× 10−4 | 0.1153 | 2.9704× 10−4 | 0.1781 | 1.0740× 10−4 | 0.1152 |
| 5 | 7.7367× 10−4 | 0.1832 | 7.251× 10−4 | 0.1173 | 8.8964× 10−4 | 0.1811 | 3.2254× 10−4 | 0.1171 |
| 6 | 7.7812× 10−4 | 0.22108 | 7.551× 10−4 | 0.15603 | 9.1604× 10−4 | 0.2210 | 4.7768× 10−4 | 0.15512 |
| Time | ||||||
|---|---|---|---|---|---|---|
| RKHSM [36] | DSC-RDK = 1 | RKHSM [36] | DSC-RDK = 1 | RKHSM [36] | DSC-RDK = 1 | |
| 0.1 | 5.93 × 10−3 | 1.11 × 10−4 | 4.42 × 10−3 | 1.01 × 10−4 | 5.67 × 10−3 | 1.10 × 10−4 |
| 0.2 | 4.23 × 10−3 | 2.21 × 10−4 | 2.97× 10−3 | 2.11 × 10−4 | 4.57 × 10−3 | 2.01 × 10−4 |
| 0.3 | 2.66 × 10−3 | 2.21 × 10−4 | 1.65 × 10−3 | 2.20 × 10−4 | 3.58 × 10−3 | 2.11 × 10−4 |
| 0.4 | 1.14 × 10−3 | 2.35 × 10−4 | 4.93 × 10−4 | 2.30 × 10−4 | 2.68 × 10−3 | 2.27 × 10−4 |
| 0.5 | 4.91 × 10−4 | 2.01 × 10−4 | 7.94 × 10−4 | 2.01 × 10−4 | 1.88 × 10−3 | 2.00 × 10−4 |
| 0.6 | 1.96 × 10−3 | 2.93 × 10−4 | 1.87 × 10−3 | 2.21 × 10−4 | 1.20 × 10−3 | 2.18 × 10−4 |
| 0.7 | 3.46 × 10−3 | 2.15 × 10−4 | 2.89 × 10−3 | 2.12 × 10−4 | 7.23 × 10−3 | 2.11 × 10−4 |
| 0.8 | 4.98 × 10−3 | 2.98 × 10−4 | 3.87 × 10−3 | 2.54 × 10−4 | 4.35 × 10−4 | 2.43 × 10−4 |
| 0.9 | 6.50 × 10−3 | 2.98 × 10−4 | 4.81 × 10−3 | 2.55 × 10−4 | 5.17 × 10−4 | 2.45 × 10−4 |
| DSC-RSK | DSC-RDK | |||
|---|---|---|---|---|
| nxx nt | L2 Error | L∞ Error | L2 Error | L∞ Error |
| 5 × 5 | 2.7987 × 10−5 | 3.2532 × 10−7 | 1.0557 × 10−5 | 1.2922 × 10−7 |
| 5 × 7 | 3.2589 × 10−5 | 6.3011 × 10−7 | 1.4282 × 10−5 | 3.2888 × 10−7 |
| 5 × 8 | 3.4497 × 10−5 | 9.3029 × 10−7 | 1.8859 × 10−5 | 6.2035 × 10−7 |
| 7 × 5 | 3.5214 × 10−5 | 9.5135 × 10−7 | 1.9551 × 10−5 | 6.3141 × 10−7 |
| 7 × 7 | 3.7213 × 10−5 | 9.7s141 × 10−7 | 1.9851 × 10−5 | 6.5198 × 10−7 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abdelfattah, W.M.; Ragb, O.; Mohamed, M.; Salah, M.; Mustafa, A. Quadrature Solution for Fractional Benjamin–Bona–Mahony–Burger Equations. Fractal Fract. 2024, 8, 685. https://doi.org/10.3390/fractalfract8120685
Abdelfattah WM, Ragb O, Mohamed M, Salah M, Mustafa A. Quadrature Solution for Fractional Benjamin–Bona–Mahony–Burger Equations. Fractal and Fractional. 2024; 8(12):685. https://doi.org/10.3390/fractalfract8120685
Chicago/Turabian StyleAbdelfattah, Waleed Mohammed, Ola Ragb, Mokhtar Mohamed, Mohamed Salah, and Abdelfattah Mustafa. 2024. "Quadrature Solution for Fractional Benjamin–Bona–Mahony–Burger Equations" Fractal and Fractional 8, no. 12: 685. https://doi.org/10.3390/fractalfract8120685
APA StyleAbdelfattah, W. M., Ragb, O., Mohamed, M., Salah, M., & Mustafa, A. (2024). Quadrature Solution for Fractional Benjamin–Bona–Mahony–Burger Equations. Fractal and Fractional, 8(12), 685. https://doi.org/10.3390/fractalfract8120685









