Oscillatory and Asymptotic Criteria for a Fifth-Order Fractional Difference Equation

Abstract

In this paper, using the properties of the conformable fractional difference and fractional sum, we initially establish some oscillatory and asymptotic criteria for a fifth-order fractional difference equation. Several critical inequalities, the Riccati transformation technique, and the integral technique are used in the deduction process. We provide some example to test the results. The established criteria are new results in the study of oscillation, and can be extended to other types of high-order fractional difference equations as well as fractional differential equations with more complicated forms.

1. Introduction

In the theoretical research of differential and difference equations, the study of the qualitative properties of solutions is an important topic. Qualitative properties mainly include oscillation, asymptotic properties, boundedness, stability, and continuous dependence on initial values. Among the research on the qualitative properties of solutions, the study of oscillation is extremely important. The oscillatory theory has extensive applications in economics, ecology, biology, control, engineering, life sciences, and many other fields. For example, in control science, the oscillation and stability theory of differential equations can be used to study the stability and control problems of systems, helping design and optimize control systems to ensure their stable operation. In ecology, the oscillation theory of differential equations can be used to simulate population dynamics and interactions in ecosystems. In economics, oscillation theory can be used to analyze economic cycles and market economic fluctuations. In biology and life sciences, the oscillation theory can be used to study the growth and changes of biological populations, helping predict disease transmission and the stability of ecosystems. In the field of engineering, oscillation theory can be used to analyze and design various oscillation systems, ensuring the stable operation and safety of the equipment.

An equation is oscillatory in the case its solutions are neither positive nor negative when the time variable eventually tends to infinity. As an important topic among qualitative analysis, in the last few decades, there have been extensive research results for the oscillation of various differential and difference equations [1,2,3,4,5] as well as dynamic equations on time scales [6,7,8,9,10,11]. With the rapid development of fractional calculus, the study of the theory and applications of fractional differential equations has been paid much attention by many authors [12,13]. Also, research on oscillation has been extended to fractional differential equations and difference equations [14,15,16,17,18]. Among these research works, we notice that there have been relatively few research results on the oscillation of high-order differential equations and fractional differential equations so far. In [19,20], the authors researched several classes of fourth-order neutral differential equations, and established some valid oscillation criteria for them. In [21], the authors researched the oscillation of the following fourth-order nonlinear delay differential equation

$${\left[r\left(t\right)z\left(t\right)\right]}^{\left(4\right)}+q\left(t\right)x\left(\tau \left(t\right)\right)=0,$$

while in [22,23,24], the following fourth-order nonlinear differential equation with a continuously distributed delay was studied:

$${\left[r\left(t\right){\left(x^{\prime \prime \prime }\left(t\right)\right)}^{\alpha }\right]}^{\prime }+{\int }_a^{b}q(t,\xi )f\left(x\left(g(t,\xi )\right)\right)=0.$$

Usually, the oscillation analysis in the case of high order differential equations, especially high-order fractional differential and difference equations, is more complicated than those of a lower order in the fulfilling process. In general, there are two research methods for the oscillation theory of fractional differential and difference equations. The first method is to find the analytical solutions of the equations, and then to discuss the oscillation of the solutions. The second method is to use Riccati transformation and some inequality and integral techniques to obtain oscillation conditions. In the case the analytical solutions of the equations can not be obtained easily, the Riccati transformation combined with inequality and integral techniques becomes the main tool in the research of oscillation. To the best of our knowledge, there are no research results on the oscillation of fifth-order fractional differential and difference equations so far in the literature.

Motivated by the above analysis, in this paper, we pay attention to research on the oscillatory and asymptotic behaviour of the following fifth-order fractional difference equation:

$${\Delta }^{4\alpha }\left[c\left(n\right){\Delta }^{\alpha }x\left(n\right)\right]+e\left(n\right)g\left(x\left(n\right)\right)=0,n\in [n_0,\infty )\bigcap \mathbb{Z},0<\alpha \le 1,n_0\ge 1,$$

(1)

where ${\Delta }^{\alpha }$ denotes the conformable fractional difference operator, ${\Delta }^{k\alpha }={\Delta }^{\alpha }\dots {\Delta }^{\alpha }$ for k times, g is an odd function satisfying $g\left(x\left(n\right)\right)\ge k{x}^{\gamma }\left(n\right)$ for $x\left(n\right)>0$, $k>0$, $\gamma$ is a positive odd number, and $c\left(n\right)$ and $e\left(n\right)$ are positive functions.

In the following, we denote an interval $[m,n]\bigcap \mathbb{Z}$ by ${[m,n]}_{\mathbb{Z}}$.

Motivated by the definition of the conformable fractional derivative [25], we provide the following definition on the conformable fractional difference and fractional sum.

Definition 1. 

For a function u defined on ${\mathbb{Z}}^{+}$, the conformable fractional difference and fractional sum on ${[m,n]}_{\mathbb{Z}}$ of order α are defined by

$${\Delta }^{\alpha }u\left(n\right)=[u(n+1)-u\left(n\right)]n^{1-\alpha }$$

and

$$I_m^{\alpha }u\left(n\right)=\sum _{s=m}^{n-1}{s}^{\alpha -1}u\left(s\right)$$

respectively, where $m<n.$

Similar to the properties of the conformable fractional derivative and fractional integral, we have the following properties for the conformable fractional difference and fractional sum.

(i)

${\Delta }^{\alpha }u\left(n\right)=n^{1-\alpha }\Delta u\left(n\right),$

(ii)

${\Delta }^{\alpha }\left[I_m^{\alpha }u\left(n\right)\right]=u\left(n\right),$

(iii)

$I_m^{\alpha }\left[{\Delta }^{\alpha }u\left(n\right)\right]=u\left(n\right)-u\left(m\right),$

(iv)

${\Delta }^{\alpha }\left[u\left(n\right)v\left(n\right)\right]=u(n+1){\Delta }^{\alpha }v\left(n\right)+v\left(n\right){\Delta }^{\alpha }u\left(n\right)=u\left(n\right){\Delta }^{\alpha }v\left(n\right)+v(n+1){\Delta }^{\alpha }u\left(n\right),$

(v)

${\Delta }^{\alpha }u\left[v\left(n\right)\right]={\displaystyle \frac{{\displaystyle u\left[v\right(n+1)-u[v\left(n\right)]}}{{\displaystyle v(n+1)-v\left(n\right)}}}{\Delta }^{\alpha }v\left(n\right),$

(vi)

${\Delta }^{\alpha }\left({\displaystyle \frac{{\displaystyle u}}{{\displaystyle v}}}\right)\left(n\right)={\displaystyle \frac{{\displaystyle v\left(n\right){\Delta }^{\alpha }u\left(n\right)-u\left(n\right){\Delta }^{\alpha }v\left(n\right)}}{{\displaystyle v\left(n\right)v(n+1)}}}.$

The conformable fractional calculus has been used in various fields by many authors in the literature [26,27,28].

In the rest of this paper, we propose some lemmas, and then based on certain Riccati transformation, inequality and integral techniques, deduce some new oscillatory and asymptotic criteria to Equation (1) based on the properties of the conformable fractional difference and fractional sum. Some example are presented to test the established results. Finally, we provide some conclusions.

2. Main Results

In order to establish oscillatory and asymptotic criteria for Equation (1), we first provide some lemmas.

Lemma 1. 

Given $n_1>n_0$. If $x\left(n\right)$ is an eventually positive solution to Equation (1) on ${[n_1,\infty )}_{\mathbb{Z}}$, and

$$\underset{n\to \infty }{lim}{I}_{n_0}^{\alpha }\left({\displaystyle \frac{{\displaystyle 1}}{{\displaystyle c\left(n\right)}}}\right)=\infty ,$$

(2)

then one can find $n_2\in {[n_1,\infty )}_{\mathbb{Z}}$, such that ${\Delta }^{4\alpha }\left[c\left(n\right){\Delta }^{\alpha }x\left(n\right)\right]<0,{\Delta }^{3\alpha }\left[c\left(n\right){\Delta }^{\alpha }x\left(n\right)\right]>0,n\in {[n_2,\infty )}_{\mathbb{Z}}$.

Proof. 

By $x\left(n\right)>0,n\in {[n_1,\infty )}_{\mathbb{Z}}$, one can obtain

$${\Delta }^{4\alpha }\left[c\left(n\right){\Delta }^{\alpha }x\left(n\right)\right]=-e\left(n\right)g\left(x\left(n\right)\right)\le -ke\left(n\right)x^{\gamma }\left(n\right)<0,$$

(3)

which means ${\Delta }^{3\alpha }\left[c\left(n\right){\Delta }^{\alpha }x\left(n\right)\right]$ is decreasing on ${[n_1,\infty )}_{\mathbb{Z}}$, and the sign of ${\Delta }^{3\alpha }\left[c\left(n\right){\Delta }^{\alpha }x\left(n\right)\right]$ does not change eventually. We conclude there exists $n_2\in {[n_1,\infty )}_{\mathbb{Z}}$, such that ${\Delta }^{3\alpha }\left[c\left(n\right){\Delta }^{\alpha }x\left(n\right)\right]>0,n\in {[n_2,\infty )}_{\mathbb{Z}}$. Otherwise, one can find $n_3\in {[n_2,\infty )}_{\mathbb{Z}}$ satisfying ${\Delta }^{3\alpha }\left[c\left(n\right){\Delta }^{\alpha }x\left(n\right)\right]<0,n\in {[n_3,\infty )}_{\mathbb{Z}}$. So, ${\Delta }^{2\alpha }\left[c\left(n\right){\Delta }^{\alpha }x\left(n\right)\right]$ is decreasing on ${[n_3,\infty )}_{\mathbb{Z}}$, and

$$\begin{array}{cc}\hfill & {\Delta }^{\alpha }\left[c\left(n\right){\Delta }^{\alpha }x\left(n\right)\right]-{\Delta }^{\alpha }\left[c\left(n_3\right){\Delta }^{\alpha }x\left(n_3\right)\right]=I_{n_3}^{\alpha }\left({\Delta }^{2\alpha }\left[c\left(n\right){\Delta }^{\alpha }x\left(n\right)\right]\right)\hfill \\ \hfill & =\sum _{s=n_3}^{n-1}{s}^{\alpha -1}{\Delta }^{2\alpha }\left[c\left(s\right){\Delta }^{\alpha }x\left(s\right)\right]\hfill \\ \hfill & \le \left(\sum _{s=n_3}^{n-1}{s}^{\alpha -1}\right){\Delta }^{2\alpha }\left[c\left(n_3\right){\Delta }^{\alpha }x\left(n_3\right)\right]\hfill \\ \hfill & \le \left({\int }_{n_3-1}^{n-1}{s}^{\alpha -1}ds\right){\Delta }^{2\alpha }\left[c\left(n_3\right){\Delta }^{\alpha }x\left(n_3\right)\right]\hfill \\ \hfill & =\left({\displaystyle \frac{{(n-1)}^{\alpha }-{(n_3-1)}^{\alpha }}{\alpha }}\right){\Delta }^{2\alpha }\left[c\left(n_3\right){\Delta }^{\alpha }x\left(n_3\right)\right].\hfill \end{array}$$

(4)

It follows that $\underset{n\to \infty }{lim}{\Delta }^{\alpha }\left[c\left(n\right){\Delta }^{\alpha }x\left(n\right)\right]=-\infty$, and then one can find $n_4\in {[n_3,\infty )}_{\mathbb{Z}}$ such that ${\Delta }^{\alpha }\left[c\left(n\right){\Delta }^{\alpha }x\left(n\right)\right]<0$ for $n\in {[n_4,\infty )}_{\mathbb{Z}}$. Furthermore,

$$\begin{array}{c}c\left(n\right){\Delta }^{\alpha }x\left(n\right)-c\left(n_4\right){\Delta }^{\alpha }x\left(n_4\right)=I_{n_4}^{\alpha }\left({\Delta }^{\alpha }\left[c\left(n\right){\Delta }^{\alpha }x\left(n\right)\right]\right)=\sum _{s=n_4}^{n-1}{s}^{\alpha -1}{\Delta }^{\alpha }\left[c\left(s\right){\Delta }^{\alpha }x\left(s\right)\right]\hfill \\ \le \left(\sum _{s=n_4}^{n-1}{s}^{\alpha -1}\right){\Delta }^{\alpha }\left[c\left(n_4\right){\Delta }^{\alpha }x\left(n_4\right)\right]\hfill \\ \le \left({\int }_{n_4-1}^{n-1}{s}^{\alpha -1}ds\right){\Delta }^{\alpha }\left[c\left(n_4\right){\Delta }^{\alpha }x\left(n_4\right)\right]\hfill \\ =\left({\displaystyle \frac{{(n-1)}^{\alpha }-{(n_4-1)}^{\alpha }}{\alpha }}\right){\Delta }^{\alpha }\left[c\left(n_4\right){\Delta }^{\alpha }x\left(n_4\right)\right].\hfill \end{array}$$

(5)

So $\underset{n\to \infty }{lim}c\left(n\right){\Delta }^{\alpha }x\left(n\right)=-\infty$, and one can find $n_5\in {[n_4,\infty )}_{\mathbb{Z}}$ such that $c\left(n\right){\Delta }^{\alpha }x\left(n\right)<0$ on ${[n_5,\infty )}_{\mathbb{Z}}$. Moreover,

$$\begin{array}{c}x\left(n\right)-x\left(n_5\right)=I_{n_5}^{\alpha }\left({\Delta }^{\alpha }x\left(n\right)\right)={\displaystyle \sum _{s=n_5}^{n-1}}{s}^{\alpha -1}{\Delta }^{\alpha }x\left(s\right)\hfill \\ \le \left({\displaystyle \sum _{s=n_5}^{n-1}}{s}^{\alpha -1}{\displaystyle \frac{{\displaystyle 1}}{{\displaystyle c\left(s\right)}}}\right)\left[c\left(n_5\right){\Delta }^{\alpha }x\left(n_5\right)\right]=\left[c\left(n_5\right){\Delta }^{\alpha }x\left(n_5\right)\right]I_{n_5}^{\alpha }\left({\displaystyle \frac{{\displaystyle 1}}{{\displaystyle c\left(n\right)}}}\right).\hfill \end{array}$$

From (2), one can see that $\underset{n\to \infty }{lim}x\left(n\right)=-\infty$, which is a contradiction. So, we have proven ${\Delta }^{3\alpha }\left[c\left(n\right){\Delta }^{\alpha }x\left(n\right)\right]>0$ on ${[n_2,\infty )}_{\mathbb{Z}}$. The proof is complete. □

Lemma 2. 

Assume $x\left(n\right)$ is an eventually a positive solution to Equation (1), and (2) is satisfied, then one can find $\overline{n}$, such that one of the following conclusions is satisfied for $n\in {[\overline{n},\infty )}_{\mathbb{Z}}$.

$$\begin{array}{cc}\left(i\right).\hfill & {\Delta }^{4\alpha }\left[c\left(n\right){\Delta }^{\alpha }x\left(n\right)\right]<0,{\Delta }^{3\alpha }\left[c\left(n\right){\Delta }^{\alpha }x\left(n\right)\right]>0,\hfill \\ \hfill & {\Delta }^{2\alpha }\left[c\left(n\right){\Delta }^{\alpha }x\left(n\right)\right]>0,{\Delta }^{\alpha }\left[c\left(n\right){\Delta }^{\alpha }x\left(n\right)\right]>0,{\Delta }^{\alpha }x\left(n\right)>0,\hfill \end{array}$$

(6)

$$\begin{array}{cc}\left(ii\right).\hfill & {\Delta }^{4\alpha }\left[c\left(n\right){\Delta }^{\alpha }x\left(n\right)\right]<0,{\Delta }^{3\alpha }\left[c\left(n\right){\Delta }^{\alpha }x\left(n\right)\right]>0,\hfill \\ \hfill & {\Delta }^{2\alpha }\left[c\left(n\right){\Delta }^{\alpha }x\left(n\right)\right]<0,{\Delta }^{\alpha }\left[c\left(n\right){\Delta }^{\alpha }x\left(n\right)\right]>0,{\Delta }^{\alpha }x\left(n\right)>0,\hfill \end{array}$$

(7)

$$\begin{array}{cc}\left(iii\right).\hfill & {\Delta }^{4\alpha }\left[c\left(n\right){\Delta }^{\alpha }x\left(n\right)\right]<0,{\Delta }^{3\alpha }\left[c\left(n\right){\Delta }^{\alpha }x\left(n\right)\right]>0,\hfill \\ \hfill & {\Delta }^{2\alpha }\left[c\left(n\right){\Delta }^{\alpha }x\left(n\right)\right]<0,{\Delta }^{\alpha }\left[c\left(n\right){\Delta }^{\alpha }x\left(n\right)\right]>0,{\Delta }^{\alpha }x\left(n\right)<0.\hfill \end{array}$$

(8)

Proof. 

In fact, due to the result of Lemma 1, it holds that ${\Delta }^{4\alpha }\left[c\left(n\right){\Delta }^{\alpha }x\left(n\right)\right]<0,$${\Delta }^{3\alpha }\left[c\left(n\right){\Delta }^{\alpha }x\left(n\right)\right]>0$ eventually. Then, the sign of ${\Delta }^{2\alpha }\left[c\left(n\right){\Delta }^{\alpha }x\left(n\right)\right]$ does not change eventually.

In the case ${\Delta }^{2\alpha }\left[c\left(n\right){\Delta }^{\alpha }x\left(n\right)\right]>0$ for $n\in [n_1,\infty )$, one has

$$\begin{array}{cc}& {\Delta }^{\alpha }\left[c\left(n\right){\Delta }^{\alpha }x\left(n\right)\right]-{\Delta }^{\alpha }\left[c\left(n_1\right){\Delta }^{\alpha }x\left(n_1\right)\right]=\sum _{s=n_1}^{n-1}{s}^{\alpha -1}{\Delta }^{2\alpha }\left[c\left(s\right){\Delta }^{\alpha }x\left(s\right)\right]\hfill \\ & \ge \left({\displaystyle \frac{n^{\alpha }-n_1^{\alpha }}{\alpha }}\right){\Delta }^{2\alpha }\left[c\left(n_1\right){\Delta }^{\alpha }x\left(n_1\right)\right].\hfill \end{array}$$

So $\underset{n\to \infty }{lim}{\Delta }^{\alpha }\left[c\left(n\right){\Delta }^{\alpha }x\left(n\right)\right]=\infty$, which means these exists $n_2>n_1$, such that ${\Delta }^{\alpha }\left[c\left(n\right){\Delta }^{\alpha }x\left(n\right)\right]>0$ for $n\in [n_2,\infty )$. Furthermore,

$$\begin{array}{cc}& c\left(n\right){\Delta }^{\alpha }x\left(n\right)-c\left(n_2\right){\Delta }^{\alpha }x\left(n_2\right)=\sum _{s=n_2}^{n-1}{s}^{\alpha -1}{\Delta }^{\alpha }\left[c\left(s\right){\Delta }^{\alpha }x\left(s\right)\right]\hfill \\ & \ge \left({\displaystyle \frac{n^{\alpha }-n_2^{\alpha }}{\alpha }}\right){\Delta }^{\alpha }\left[c\left(n_2\right){\Delta }^{\alpha }x\left(n_2\right)\right].\hfill \end{array}$$

So, one can derive that $\underset{n\to \infty }{lim}c\left(n\right){\Delta }^{\alpha }x\left(n\right)=\infty$, which means (6) is satisfied.

In the case ${\Delta }^{2\alpha }\left[c\left(n\right){\Delta }^{\alpha }x\left(n\right)\right]<0$ for $n\in [n_1,\infty )$, one can see the sign of ${\Delta }^{\alpha }\left[c\left(n\right){\Delta }^{\alpha }x\left(n\right)\right]$ does not change eventually. We conclude ${\Delta }^{\alpha }\left[c\left(n\right){\Delta }^{\alpha }x\left(n\right)\right]>0$ eventually. Otherwise, there exists $n_2>n_1$, such that ${\Delta }^{\alpha }\left[c\left(n\right){\Delta }^{\alpha }x\left(n\right)\right]<0$ for $n\in [n_2,\infty )$. Then, following in a similar manner as the proof process of Lemma 1, one can obtain $c\left(n\right){\Delta }^{\alpha }x\left(n\right)<0$ and $\underset{n\to \infty }{lim}x\left(n\right)=-\infty$ eventually, which is a contradiction. So, it holds that ${\Delta }^{\alpha }\left[c\left(n\right){\Delta }^{\alpha }x\left(n\right)\right]>0$ eventually. And, furthermore, the sign of ${\Delta }^{\alpha }x\left(n\right)$ does not change eventually. So, either (7) or (8) is satisfied. The proof is complete. □

Lemma 3. 

Assume $x\left(n\right)$ is an eventually positive solution of Equation (1). If (2) and (8) are satisfied, and

$$\underset{n\to \infty }{lim}\sum _{s_5=n_0}^n\left\{{\displaystyle \frac{{\displaystyle s_5^{\alpha -1}}}{{\displaystyle c\left(s_5\right)}}}\sum _{s_4=s_5}^{\infty }\left\{s_4^{\alpha -1}\sum _{s_3=s_4}^{\infty }\left[s_3^{\alpha -1}\sum _{s_2=s_3}^{\infty }\left(s_2^{\alpha -1}\sum _{s_1=s_2}^{\infty }{s}_1^{\alpha -1}e\left(s_1\right)\right)\right]\right\}\right\}=\infty ,$$

(9)

then

$$\underset{n\to \infty }{lim}x\left(n\right)=0.$$

Proof. 

It follows from (8) that ${\Delta }^{\alpha }\left[c\left(n\right){\Delta }^{\alpha }x\left(n\right)\right]>0,{\Delta }^{\alpha }x\left(n\right)<0$ eventually. So, $x\left(n\right)$ is decreasing, while $c\left(n\right){\Delta }^{\alpha }x\left(n\right)$ is increasing eventually. Let $\underset{n\to \infty }{lim}x\left(n\right)={\mu }_1\ge 0$, and $\underset{n\to \infty }{lim}c\left(n\right){\Delta }^{\alpha }x\left(n\right)={\mu }_2\le 0$. We conclude ${\mu }_1=0$. Otherwise, one can find $n^{*}$, such that $x\left(n\right)\ge {\mu }_1>0$ for $n\in {[n^{*},\infty )}_{\mathbb{Z}}$, and

$${\Delta }^{4\alpha }\left[c\left(n\right){\Delta }^{\alpha }x\left(n\right)\right]=-e\left(n\right)g\left(x\left(n\right)\right)\le -ke\left(n\right)x^{\gamma }\left(n\right)\le -k{\mu }_1^{\gamma }e\left(n\right),n\in {[n^{*},\infty )}_{\mathbb{Z}}.$$

(10)

Fulfilling the fractional sum for (10) from n to ∞ fourth times, one can obtain the following statements:

$$\begin{array}{c}{\Delta }^{3\alpha }\left[c\left(n\right){\Delta }^{\alpha }x\left(n\right)\right]\ge \underset{n\to \infty }{lim}{\Delta }^{3\alpha }\left[c\left(n\right){\Delta }^{\alpha }x\left(n\right)\right]+k{\mu }_1^{\gamma }{\displaystyle \sum _{s_1=n}^{\infty }}{s}_1^{\alpha -1}e\left(s_1\right)\ge k{\mu }_1^{\gamma }{\displaystyle \sum _{s_1=n}^{\infty }}{s}_1^{\alpha -1}e\left(s_1\right),\\ {\Delta }^{2\alpha }\left[c\left(n\right){\Delta }^{\alpha }x\left(n\right)\right]\le \underset{n\to \infty }{lim}{\Delta }^{2\alpha }\left[c\left(n\right){\Delta }^{\alpha }x\left(n\right)\right]-k{\mu }_1^{\gamma }{\displaystyle \sum _{s_2=n}^{\infty }}\left(s_2^{\alpha -1}{\displaystyle \sum _{s_1=s_2}^{\infty }}{s}_1^{\alpha -1}e\left(s_1\right)\right)\\ \le -k{\mu }_1^{\gamma }{\displaystyle \sum _{s_2=n}^{\infty }}\left(s_2^{\alpha -1}{\displaystyle \sum _{s_1=s_2}^{\infty }}{s}_1^{\alpha -1}e\left(s_1\right)\right),\\ {\Delta }^{\alpha }[c(n){\Delta }^{\alpha }x\left(n\right)]\ge \underset{n\to \infty }{lim}{\Delta }^{\alpha }\left[c\left(n\right){\Delta }^{\alpha }x\left(n\right)\right]+k{\mu }_1^{\gamma }{\displaystyle \sum _{s_3=n}^{\infty }}\left[s_3^{\alpha -1}{\displaystyle \sum _{s_2=s_3}^{\infty }}\left(s_2^{\alpha -1}{\displaystyle \sum _{s_1=s_2}^{\infty }}{s}_1^{\alpha -1}e\left(s_1\right)\right)\right]\\ \ge k{\mu }_1^{\gamma }{\displaystyle \sum _{s_3=n}^{\infty }}\left[s_3^{\alpha -1}{\displaystyle \sum _{s_2=s_3}^{\infty }}\left(s_2^{\alpha -1}{\displaystyle \sum _{s_1=s_2}^{\infty }}{s}_1^{\alpha -1}e\left(s_1\right)\right)\right],\\ c\left(n\right){\Delta }^{\alpha }x\left(n\right)\le {\mu }_2-k{\mu }_1^{\gamma }{\displaystyle \sum _{s_4=n}^{\infty }}\left\{s_4^{\alpha -1}{\displaystyle \sum _{s_3=s_4}^{\infty }}\left[s_3^{\alpha -1}{\displaystyle \sum _{s_2=s_3}^{\infty }}\left(s_2^{\alpha -1}{\displaystyle \sum _{s_1=s_2}^{\infty }}{s}_1^{\alpha -1}e\left(s_1\right)\right)\right]\right\}\\ \le -k{\mu }_1^{\gamma }{\displaystyle \sum _{s_4=n}^{\infty }}\left\{s_4^{\alpha -1}{\displaystyle \sum _{s_3=s_4}^{\infty }}\left[s_3^{\alpha -1}{\displaystyle \sum _{s_2=s_3}^{\infty }}\left(s_2^{\alpha -1}{\displaystyle \sum _{s_1=s_2}^{\infty }}{s}_1^{\alpha -1}e\left(s_1\right)\right)\right]\right\}.\end{array}$$

Fulfilling the fractional sum for the last inequality on ${[n^{*},n]}_{\mathbb{Z}}$, one has

$$\begin{array}{c}x\left(n\right)-x\left(n^{*}\right)\le \\ -k{\mu }_1^{\gamma }{\displaystyle \sum _{s_5=n^{*}}^{n-1}}\left\{{\displaystyle \frac{s_5^{\alpha -1}}{c\left(s_5\right)}}{\displaystyle \sum _{s_4=s5}^{\infty }}\left\{s_4^{\alpha -1}{\displaystyle \sum _{s_3=s_4}^{\infty }}\left[s_3^{\alpha -1}{\displaystyle \sum _{s_2=s_3}^{\infty }}\left(s_2^{\alpha -1}{\displaystyle \sum _{s_1=s_2}^{\infty }}{s}_1^{\alpha -1}e\left(s_1\right)\right)\right]\right\}\right\}.\end{array}$$

(11)

According to (9) and (11), one has $\underset{n\to \infty }{lim}x\left(n\right)=-\infty ,$ which is a contradiction. So, $\underset{n\to \infty }{lim}x\left(n\right)=0$. The proof is complete. □

Theorem 1. 

Suppose ${\zeta }_1\left(n\right),{\zeta }_2\left(n\right)$ are positive functions, and (2) and (9) hold. If for any sufficiently large $n_4>n_3>n_2>n_1>n_0$,

$$\underset{n\to \infty }{lim}{I}_{n_0}^{\alpha }\left({\displaystyle \frac{{\displaystyle 4\gamma ke\left(n\right)A_2^{\gamma -1}(n_1,n_2,n_3,n_4,n)A_1(n_1,n_2,n_3,n){\zeta }_1^2\left(n\right)-c\left(n\right){\left[{\Delta }^{\alpha }{\zeta }_1\left(n\right)\right]}^2}}{{\displaystyle 4\gamma A_2^{\gamma -1}(n_1,n_2,n_3,n_4,n)A_1(n_1,n_2,n_3,n){\zeta }_1\left(n\right)}}}\right)=\infty ,$$

(12)

and either

$$\underset{n\to \infty }{lim}{I}_{n_0}^{\alpha }e\left(n\right)=\infty$$

(13)

or

$$\underset{n\to \infty }{lim}{I}_{n_0}^{\alpha }\left[\sum _{s_1=n}^{\infty }{s}_1^{\alpha -1}e\left(s_1\right)\right]=\infty$$

(14)

or

$$\underset{n\to \infty }{lim}{I}_{n_0}^{\alpha }\left[{\displaystyle \frac{{\displaystyle 4\gamma A_4^{\gamma -1}(n_3,n_4,n)A_3(n_3,n){\zeta }_2^2\left(n\right)Q_1\left(n\right)-c\left(n\right){\left[{\Delta }^{\alpha }{\zeta }_2\left(n\right)\right]}^2}}{{\displaystyle 4\gamma A_4^{\gamma -1}(n_3,n_4,n)A_3(n_3,n){\zeta }_2\left(n\right)}}}\right]=\infty$$

(15)

holds, where

$$\begin{array}{cc}\hfill & A_1(n_1,n_2,n_3,n)={\displaystyle \frac{(n^{\alpha }-n_3^{\alpha })(n_3^{\alpha }-n_2^{\alpha })(n_2^{\alpha }-n_1^{\alpha })}{{\alpha }^3}},\hfill \\ \hfill & A_2(n_1,n_2,n_3,n_4,n)={\displaystyle \frac{(n_4^{\alpha }-n_3^{\alpha })(n_3^{\alpha }-n_2^{\alpha })(n_2^{\alpha }-n_1^{\alpha })}{{\alpha }^3}}\left[{\Delta }^{3\alpha }\left(c\left(n_4\right){\Delta }^{\alpha }x\left(n_4\right)\right)\right]I_{n_4}\left({\displaystyle \frac{1}{c\left(n\right)}}\right),\hfill \\ \hfill & A_3(n_3,n)={\displaystyle \frac{n^{\alpha }-n_3^{\alpha }}{\alpha }},\hfill \\ \hfill & A_4(n_3,n_4,n)=\left({\displaystyle \frac{n_4^{\alpha }-n_3^{\alpha }}{\alpha }}\right)\left[{\Delta }^{\alpha }\left(c\left(n_4\right){\Delta }^{\alpha }x\left(n_4\right)\right)\right]I_{n_4}\left({\displaystyle \frac{1}{c\left(n\right)}}\right),\hfill \\ \hfill & Q_1\left(n\right)=k\sum _{s_2=n}^{\infty }\left[s_2^{\alpha -1}\sum _{s_1=s_2}^{\infty }{s}_1^{\alpha -1}e\left(s_1\right)\right],\hfill \end{array}$$

then, the solution $x\left(n\right)$ to Equation (1) is oscillatory or $\underset{n\to \infty }{lim}x\left(n\right)=0$.

Proof. 

If $x\left(n\right)$ is a non-oscillatory solution to Equation (1), and without loss of generality, suppose $x\left(n\right)$ is eventually positive, that is, there exists $n_1>n_0$, such that $x\left(n\right)>0$ for ${[n_1,\infty )}_{\mathbb{Z}}$. According to Lemma 2, one can find $\overline{n}\in {[n_1,\infty )}_{\mathbb{Z}}$, such that (6) or (7) or (8) is satisfied for $n\in {[\overline{n},\infty )}_{\mathbb{Z}}$.

Case $\left(i\right)$: Assume (6) is satisfied. Define a Riccati function ${\theta }_1\left(n\right)={\displaystyle \frac{{\displaystyle {\zeta }_1\left(n\right)}}{{\displaystyle x^{\gamma }\left(n\right)}}}{\Delta }^{3\alpha }\left[c\left(n\right){\Delta }^{\alpha }x\left(n\right)\right],$ where ${\zeta }_1\left(n\right)$ is a positive function. Then, ${\theta }_1\left(n\right)\ge 0,n\in {[\overline{n},\infty )}_{\mathbb{Z}}$. Using $x\left(n\right)$ is increasing, and the property $\left(v\right)$, one has

$${\Delta }^{\alpha }{x}^{\gamma }\left(n\right)={\displaystyle \frac{{\displaystyle x^{\gamma }(n+1)-x^{\gamma }\left(n\right)}}{{\displaystyle x(n+1)-x\left(n\right)}}}{\Delta }^{\alpha }x\left(n\right)\ge \gamma x^{\gamma -1}\left(n\right){\Delta }^{\alpha }x\left(n\right).$$

Through the use of the inequality above and the properties of fractional difference and fractional sum, one can deduce that

$$\begin{array}{cc}\hfill & {\Delta }^{\alpha }{\theta }_1\left(n\right)={\displaystyle \frac{{\zeta }_1\left(n\right)}{x^{\gamma }\left(n\right)}}{\Delta }^{\alpha }\left({\Delta }^{3\alpha }\left[c\left(n\right){\Delta }^{\alpha }x\left(n\right)\right]\right)+\left({\Delta }^{\alpha }\left({\displaystyle \frac{{\zeta }_1\left(n\right)}{x^{\gamma }\left(n\right)}}\right)\right){\Delta }^{3\alpha }\left[c(n+1){\Delta }^{\alpha }x(n+1)\right]\hfill \\ \hfill & \le -{\displaystyle \frac{{\zeta }_1\left(n\right)}{x^{\gamma }\left(n\right)}}e\left(n\right)g\left(x\left(n\right)\right)\hfill \\ \hfill & +\left[{\displaystyle \frac{x^{\gamma }\left(n\right){\Delta }^{\alpha }{\zeta }_1\left(n\right)-\gamma x^{\gamma -1}\left(n\right)\left({\Delta }^{\alpha }x\left(n\right)\right){\zeta }_1\left(n\right)}{x^{\gamma }\left(n\right)x^{\gamma }(n+1)}}\right]{\Delta }^{3\alpha }\left[c(n+1){\Delta }^{\alpha }x(n+1)\right]\hfill \\ \hfill & =-{\displaystyle \frac{{\zeta }_1\left(n\right)}{x^{\gamma }\left(n\right)}}e\left(n\right)g\left(x\left(n\right)\right)+{\displaystyle \frac{{\Delta }^{\alpha }{\zeta }_1\left(n\right)}{{\zeta }_1(n+1)}}{\theta }_1(n+1)-\left[{\displaystyle \frac{\gamma x^{\gamma -1}\left(n\right)\left({\Delta }^{\alpha }x\left(n\right)\right){\zeta }_1\left(n\right)}{x^{\gamma }\left(n\right){\zeta }_1(n+1)}}\right]{\theta }_1(n+1)\hfill \\ \hfill & \le -ke\left(n\right){\zeta }_1\left(n\right)+{\displaystyle \frac{{\Delta }^{\alpha }{\zeta }_1\left(n\right)}{{\zeta }_1(n+1)}}{\theta }_1(n+1)-\left[{\displaystyle \frac{\gamma x^{\gamma -1}\left(n\right)\left({\Delta }^{\alpha }x\left(n\right)\right){\zeta }_1\left(n\right)}{x^{\gamma }(n+1){\zeta }_1(n+1)}}\right]{\theta }_1(n+1).\hfill \end{array}$$

For $n_4>n_3>n_2>n_1>\overline{n}$, and $n\in {[n_4,\infty )}_{\mathbb{Z}}$, one can derive that

$$\begin{array}{c}{\Delta }^{2\alpha }[c\left(n\right){\Delta }^{\alpha }x\left(n\right)]={\Delta }^{2\alpha }\left[c\left(n_1\right){\Delta }^{\alpha }x\left(n_1\right)\right]+\sum _{s=n_1}^{n-1}{s}^{\alpha -1}{\Delta }^{3\alpha }\left[c\left(s\right){\Delta }^{\alpha }x\left(s\right)\right]\hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\ge \left[{\int }_{n_1}^n{s}^{\alpha -1}ds\right]{\Delta }^{3\alpha }\left[c\left(n\right){\Delta }^{\alpha }x\left(n\right)\right]\hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}=\left({\displaystyle \frac{n^{\alpha }-n_1^{\alpha }}{\alpha }}\right){\Delta }^{3\alpha }\left[c\left(n\right){\Delta }^{\alpha }x\left(n\right)\right],\hfill \\ {\Delta }^{\alpha }[c\left(n\right){\Delta }^{\alpha }x\left(n\right)]={\Delta }^{\alpha }\left[c\left(n_2\right){\Delta }^{\alpha }x\left(n_2\right)\right]+\sum _{s=n_2}^{n-1}{s}^{\alpha -1}{\Delta }^{2\alpha }\left[c\left(s\right){\Delta }^{\alpha }x\left(s\right)\right]\hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\ge \left({\displaystyle \frac{n^{\alpha }-n_2^{\alpha }}{\alpha }}\right){\Delta }^{2\alpha }\left[c\left(n_2\right){\Delta }^{\alpha }x\left(n_2\right)\right]\hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\ge \left({\displaystyle \frac{n^{\alpha }-n_2^{\alpha }}{\alpha }}\right)\left({\displaystyle \frac{n_2^{\alpha }-n_1^{\alpha }}{\alpha }}\right){\Delta }^{3\alpha }\left[c\left(n_2\right){\Delta }^{\alpha }x\left(n_2\right)\right]\hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\ge \left({\displaystyle \frac{n^{\alpha }-n_2^{\alpha }}{\alpha }}\right)\left({\displaystyle \frac{n_2^{\alpha }-n_1^{\alpha }}{\alpha }}\right){\Delta }^{3\alpha }\left[c\left(n\right){\Delta }^{\alpha }x\left(n\right)\right],\hfill \end{array}$$

$$\begin{array}{c}c\left(n\right){\Delta }^{\alpha }x\left(n\right)=c\left(n_3\right){\Delta }^{\alpha }x\left(n_3\right)+{\displaystyle \sum _{s=n_3}^{n-1}}{s}^{\alpha -1}{\Delta }^{\alpha }\left[c\left(s\right){\Delta }^{\alpha }x\left(s\right)\right]\hfill \\ \ge \left({\displaystyle \frac{n^{\alpha }-n_3^{\alpha }}{\alpha }}\right){\Delta }^{\alpha }\left[c\left(n_3\right){\Delta }^{\alpha }x\left(n_3\right)\right]\hfill \\ \ge \left({\displaystyle \frac{n^{\alpha }-n_3^{\alpha }}{\alpha }}\right)\left({\displaystyle \frac{n_3^{\alpha }-n_2^{\alpha }}{\alpha }}\right)\left({\displaystyle \frac{n_2^{\alpha }-n_1^{\alpha }}{\alpha }}\right){\Delta }^{3\alpha }\left[c\left(n_3\right){\Delta }^{\alpha }x\left(n_3\right)\right]\hfill \\ \ge \left({\displaystyle \frac{n^{\alpha }-n_3^{\alpha }}{\alpha }}\right)\left({\displaystyle \frac{n_3^{\alpha }-n_2^{\alpha }}{\alpha }}\right)\left({\displaystyle \frac{n_2^{\alpha }-n_1^{\alpha }}{\alpha }}\right){\Delta }^{3\alpha }\left[c\left(n\right){\Delta }^{\alpha }x\left(n\right)\right]\hfill \\ \ge \left({\displaystyle \frac{n^{\alpha }-n_3^{\alpha }}{\alpha }}\right)\left({\displaystyle \frac{n_3^{\alpha }-n_2^{\alpha }}{\alpha }}\right)\left({\displaystyle \frac{n_2^{\alpha }-n_1^{\alpha }}{\alpha }}\right){\Delta }^{3\alpha }\left[c(n+1){\Delta }^{\alpha }x(n+1)\right]\hfill \\ \triangleq A_1(n_1,n_2,n_3,n){\Delta }^{3\alpha }\left[c(n+1){\Delta }^{\alpha }x(n+1)\right],\hfill \\ x\left(n\right)=x\left(n_4\right)+{\displaystyle \sum _{s=n_4}^{n-1}}{s}^{\alpha -1}{\displaystyle \frac{c\left(s\right){\Delta }^{\alpha }x\left(s\right)}{c\left(s\right)}}{d}^{\alpha }s\ge \left[c\left(n_4\right){\Delta }^{\alpha }x\left(n_4\right)\right]{\displaystyle \sum _{s=n_4}^{n-1}}{\displaystyle \frac{s^{\alpha -1}}{c\left(s\right)}}\hfill \\ \ge \left({\displaystyle \frac{n_4^{\alpha }-n_3^{\alpha }}{\alpha }}\right)\left({\displaystyle \frac{n_3^{\alpha }-n_2^{\alpha }}{\alpha }}\right)\left({\displaystyle \frac{n_2^{\alpha }-n_1^{\alpha }}{\alpha }}\right)\left[{\Delta }^{3\alpha }\left(c\left(n_4\right){\Delta }^{\alpha }x\left(n_4\right)\right)\right]I_{n_4}\left({\displaystyle \frac{1}{c\left(n\right)}}\right)\hfill \\ \triangleq A_2(n_1,n_2,n_3,n_4,n).\hfill \end{array}$$

Then it follows that

$$\begin{array}{c}{\Delta }^{\alpha }{\theta }_1\left(n\right)\le -ke\left(n\right){\zeta }_1\left(n\right)+{\displaystyle \frac{{\Delta }^{\alpha }{\zeta }_1\left(n\right)}{{\zeta }_1(n+1)}}{\theta }_1(n+1)\hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}-\gamma A_2^{\gamma -1}(n_1,n_2,n_3,n_4,n){\displaystyle \frac{{\zeta }_1\left(n\right)A_1(n_1,n_2,n_3,n){\Delta }^{3\alpha }\left[c(n+1){\Delta }^{\alpha }x(n+1)\right]}{c\left(n\right){\zeta }_1(n+1)x^{\gamma }(n+1)}}{\theta }_1(n+1)\hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}=-ke\left(n\right){\zeta }_1\left(n\right)+{\displaystyle \frac{{\Delta }^{\alpha }{\zeta }_1\left(n\right)}{{\zeta }_1(n+1)}}{\theta }_1(n+1)\hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}-\gamma A_2^{\gamma -1}(n_1,n_2,n_3,n_4,n){\displaystyle \frac{A_1(n_1,n_2,n_3,n){\zeta }_1\left(n\right)}{c\left(n\right){\zeta }_1^2(n+1)}}{\theta }_1^2(n+1)\hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\le {\displaystyle \frac{c\left(n\right){\left[{\Delta }^{\alpha }{\zeta }_1\left(n\right)\right]}^2-4\gamma ke\left(n\right)A_2^{\gamma -1}(n_1,n_2,n_3,n_4,n)A_1(n_1,n_2,n_3,n){\zeta }_1^2\left(n\right)}{4\gamma A_2^{\gamma -1}(n_1,n_2,n_3,n_4,n)A_1(n_1,n_2,n_3,n){\zeta }_1\left(n\right)}}\hfill \end{array}$$

(16)

Fulfilling fractional sum on ${[n_4,n]}_{\mathbb{Z}}$, combining with $\left(iii\right)$, one can derive that

$$\begin{array}{c}{\displaystyle \sum _{s=n_4}^{n-1}}{s}^{\alpha -1}{\displaystyle \frac{{\displaystyle 4\gamma ke\left(s\right)A_2^{\gamma -1}(n_1,n_2,n_3,n_4,s)A_1(n_1,n_2,n_3,s){\zeta }_1^2\left(s\right)-c\left(s\right){\left[{\Delta }^{\alpha }{\zeta }_1\left(s\right)\right]}^2}}{{\displaystyle 4\gamma A_2^{\gamma -1}(n_1,n_2,n_3,n_4,s)A_1(n_1,n_2,n_3,s){\zeta }_1\left(s\right)}}}\hfill \\ \hspace{1em}\hspace{1em}\le -{\displaystyle \sum _{s=n_4}^{n-1}}{s}^{\alpha -1}{\Delta }^{\alpha }{\theta }_1\left(s\right)={\theta }_1\left(n_4\right)-{\theta }_1\left(n\right)\le {\theta }_1\left(n_4\right),\hfill \end{array}$$

which is a contradiction to (12).

Case $\left(ii\right)$: Suppose (7) holds. it follows from fulfilling the fractional sum for (1) on ${[n_1,n]}_{\mathbb{Z}}$ that

$$\begin{array}{c}-{\Delta }^{3\alpha }\left[c\left(n_1\right){\Delta }^{\alpha }x\left(n_1\right)\right]=-{\Delta }^{3\alpha }\left[c\left(n\right){\Delta }^{\alpha }x\left(n\right)\right]-I_{n_1}^{\alpha }\left[e\left(n\right)g\left(x\left(n\right)\right)\right]\le -I_{n_1}^{\alpha }\left[e\left(n\right)g\left(x\left(n\right)\right)\right]\hfill \\ \hspace{1em}\le -k{I}_{n_1}^{\alpha }\left[e\left(n\right)x^{\gamma }\left(n\right)\right]\le -k{x}^{\gamma }\left(n_1\right)I_{n_1}^{\alpha }e\left(n\right).\hfill \end{array}$$

Then

$$I_{n_1}^{\alpha }e\left(n\right)\le {\displaystyle \frac{{\displaystyle {\Delta }^{3\alpha }\left[c\left(n_1\right){\Delta }^{\alpha }x\left(n_1\right)\right]}}{{\displaystyle k{x}^{\gamma }\left(n_1\right)}}},$$

which is a contradiction to (13).

Fulfilling fractional sum for (1) from n to ∞, one can obtain that

$$\begin{array}{c}-{\Delta }^{3\alpha }\left[c\left(n\right){\Delta }^{\alpha }x\left(n\right)\right]=-\underset{n\to \infty }{lim}{\Delta }^{3\alpha }\left[c\left(n\right){\Delta }^{\alpha }x\left(n\right)\right]-{\displaystyle \sum _{s=n}^{\infty }}{s}^{\alpha -1}e\left(s\right)g\left(x\left(s\right)\right)\\ \hspace{1em}\le -{\displaystyle \sum _{s=n}^{\infty }}{s}^{\alpha -1}e\left(s\right)g\left(x\left(s\right)\right)\le -k{\displaystyle \sum _{s=n}^{\infty }}{s}^{\alpha -1}e\left(s\right)x^{\gamma }\left(s\right)\le -k{x}^{\gamma }\left(n\right){\displaystyle \sum _{s=n}^{\infty }}{s}^{\alpha -1}e\left(s\right),\hfill \end{array}$$

and

$$-{\Delta }^{3\alpha }\left[c\left(n\right){\Delta }^{\alpha }x\left(n\right)\right]+k{x}^{\gamma }\left(n\right){\displaystyle \sum _{s=n}^{\infty }}{s}^{\alpha -1}e\left(s\right)\le 0.$$

(17)

Fulfilling fractional sum for (17) on ${[n_1,n]}_{\mathbb{Z}}$, yields

$${\Delta }^{2\alpha }\left[c\left(n_1\right){\Delta }^{\alpha }x\left(n_1\right)\right]-{\Delta }^{2\alpha }\left[c\left(n\right){\Delta }^{\alpha }x\left(n\right)\right]+I_{n_1}^{\alpha }\left[k{x}^{\gamma }\left(n\right){\displaystyle \sum _{s_1=n}^{\infty }}{s}_1^{\alpha -1}e\left(s_1\right)\right]\le 0,$$

which imples

$$I_{n_1}^{\alpha }\left[k{x}^{\gamma }\left(n\right){\displaystyle \sum _{s_1=n}^{\infty }}{s}_1^{\alpha -1}e\left(s_1\right)\right]\le -{\Delta }^{2\alpha }\left[c\left(n_1\right){\Delta }^{\alpha }x\left(n_1\right)\right],$$

and

$$I_{n_1}^{\alpha }\left[{\displaystyle \sum _{s_1=n}^{\infty }}{s}_1^{\alpha -1}e\left(s_1\right)\right]\le -{\displaystyle \frac{{\displaystyle {\Delta }^{2\alpha }\left[c\left(n_1\right){\Delta }^{\alpha }x\left(n_1\right)\right]}}{{\displaystyle k{x}^{\gamma }\left(n_1\right)}}},$$

which is a contradiction to (14).

Fulfilling fractional sum for (17) from n to ∞, yields

$${\Delta }^{2\alpha }\left[c\left(n\right){\Delta }^{\alpha }x\left(n\right)\right]+k{\displaystyle \sum _{s_2=n}^{\infty }}\left[s_2^{\alpha -1}{x}^{\gamma }\left(s_2\right){\displaystyle \sum _{s_1=s_2}^{\infty }}{s}_1^{\alpha -1}e\left(s_1\right)\right]\le \underset{n\to \infty }{lim}{\Delta }^{2\alpha }\left[c\left(n\right){\Delta }^{\alpha }x\left(n\right)\right]\le 0,$$

which means

$${\Delta }^{2\alpha }\left[c\left(n\right){\Delta }^{\alpha }x\left(n\right)\right]+k{x}^{\gamma }\left(n\right){\displaystyle \sum _{s_2=n}^{\infty }}\left[s_2^{\alpha -1}{\displaystyle \sum _{s_1=s_2}^{\infty }}{s}_1^{\alpha -1}e\left(s_1\right)\right]\le 0.$$

Define ${\theta }_2\left(n\right)={\displaystyle \frac{{\displaystyle {\zeta }_2\left(n\right)}}{{\displaystyle x^{\gamma }\left(n\right)}}}{\Delta }^{\alpha }\left[c\left(n\right){\Delta }^{\alpha }x\left(n\right)\right],Q_1\left(n\right)=k{\displaystyle \sum _{s_2=n}^{\infty }}\left[s_2^{\alpha -1}{\displaystyle \sum _{s_1=s_2}^{\infty }}{s}_1^{\alpha -1}e\left(s_1\right)\right]$, where ${\zeta }_2\left(n\right)$ is a positive function. Then, ${\theta }_2\left(n\right)\ge 0,n\in {[\overline{n},\infty )}_{\mathbb{Z}}$, and it holds that

$$\begin{array}{c}{\Delta }^{\alpha }{\theta }_2\left(n\right)={\displaystyle \frac{{\zeta }_2\left(n\right)}{x^{\gamma }\left(n\right)}}{\Delta }^{2\alpha }\left[c\left(n\right){\Delta }^{\alpha }x\left(n\right)\right]+\left({\Delta }^{\alpha }\left({\displaystyle \frac{{\zeta }_2\left(n\right)}{x^{\gamma }\left(n\right)}}\right)\right){\Delta }^{\alpha }\left[c(n+1){\Delta }^{\alpha }x(n+1)\right]\hfill \\ \hspace{1em}\hspace{1em}\le -{\zeta }_2\left(n\right)Q_1\left(n\right)\hfill \\ \hspace{1em}\hspace{1em}+\left[{\displaystyle \frac{x^{\gamma }\left(n\right){\Delta }^{\alpha }{\zeta }_2\left(n\right)-\gamma x^{\gamma -1}\left(n\right)\left({\Delta }^{\alpha }x\left(n\right)\right){\zeta }_2\left(n\right)}{x^{\gamma }\left(n\right)x^{\gamma }(n+1)}}\right]{\Delta }^{\alpha }\left[c(n+1){\Delta }^{\alpha }x(n+1)\right]\hfill \\ \hspace{1em}\hspace{1em}=-{\zeta }_2\left(n\right)Q_1\left(n\right)+{\displaystyle \frac{{\Delta }^{\alpha }{\zeta }_2\left(n\right)}{{\zeta }_2(n+1)}}{\theta }_2(n+1)-\left[{\displaystyle \frac{\gamma x^{\gamma -1}\left(n\right)\left({\Delta }^{\alpha }x\left(n\right)\right){\zeta }_2\left(n\right)}{x^{\gamma }\left(n\right){\zeta }_2(n+1)}}\right]{\theta }_2(n+1)\hfill \\ \hspace{1em}\hspace{1em}\le -{\zeta }_2\left(n\right)Q_1\left(n\right)+{\displaystyle \frac{{\Delta }^{\alpha }{\zeta }_2\left(n\right)}{{\zeta }_2(n+1)}}{\theta }_2(n+1)-\left[{\displaystyle \frac{\gamma x^{\gamma -1}\left(n\right)\left({\Delta }^{\alpha }x\left(n\right)\right){\zeta }_2\left(n\right)}{x^{\gamma }(n+1){\zeta }_2(n+1)}}\right]{\theta }_2(n+1).\hfill \end{array}$$

For $n_4>n_3>n_2>n_1>\overline{n}$, and $n\in {[n_4,\infty )}_{\mathbb{Z}}$, similar as the proof in Case $\left(i\right)$, one has

$$\begin{array}{c}c\left(n\right){\Delta }^{\alpha }x\left(n\right)\ge \left({\displaystyle \frac{n^{\alpha }-n_3^{\alpha }}{\alpha }}\right){\Delta }^{\alpha }\left[c\left(n_3\right){\Delta }^{\alpha }x\left(n_3\right)\right]\hfill \\ \hspace{1em}\hspace{1em}\ge \left({\displaystyle \frac{n^{\alpha }-n_3^{\alpha }}{\alpha }}\right){\Delta }^{\alpha }\left[c\left(n\right){\Delta }^{\alpha }x\left(n\right)\right]\hfill \\ \hspace{1em}\hspace{1em}\ge \left({\displaystyle \frac{n^{\alpha }-n_3^{\alpha }}{\alpha }}\right){\Delta }^{\alpha }\left[c(n+1){\Delta }^{\alpha }x(n+1)\right]\hfill \\ \hspace{1em}\hspace{1em}\triangleq A_3(n_3,n){\Delta }^{\alpha }\left[c(n+1){\Delta }^{\alpha }x(n+1)\right],\hfill \\ x\left(n\right)\ge \left({\displaystyle \frac{n_4^{\alpha }-n_3^{\alpha }}{\alpha }}\right)\left[{\Delta }^{\alpha }\left(c\left(n_4\right){\Delta }^{\alpha }x\left(n_4\right)\right)\right]I_{n_4}\left({\displaystyle \frac{1}{c\left(n\right)}}\right)\triangleq A_4(n_3,n_4,n).\hfill \end{array}$$

Furthermore,

$$\begin{array}{c}{\Delta }^{\alpha }{\theta }_2\left(n\right)\le -{\zeta }_2\left(n\right)Q_1\left(n\right)+{\displaystyle \frac{{\Delta }^{\alpha }{\zeta }_2\left(n\right)}{{\zeta }_2(n+1)}}{\theta }_2(n+1)\hfill \\ \hspace{1em}\hspace{1em}-\gamma A_4^{\gamma -1}(n_3,n_4,n){\displaystyle \frac{{\zeta }_2\left(n\right)A_3(n_3,n){\Delta }^{\alpha }\left[c(n+1){\Delta }^{\alpha }x(n+1)\right]}{c\left(n\right){\zeta }_2(n+1)x^{\gamma }(n+1)}}{\theta }_2(n+1)\hfill \\ \hspace{1em}\hspace{1em}=-{\zeta }_2\left(n\right)Q_1\left(n\right)+{\displaystyle \frac{{\Delta }^{\alpha }{\zeta }_2\left(n\right)}{{\zeta }_2(n+1)}}{\theta }_2(n+1)-\gamma A_4^{\gamma -1}(n_3,n_4,n){\displaystyle \frac{A_3(n_3,n){\zeta }_2\left(n\right)}{c\left(n\right){\zeta }_2^2(n+1)}}{\theta }_2^2(n+1)\hfill \\ \hspace{1em}\hspace{1em}\le {\displaystyle \frac{c\left(n\right){\left[{\Delta }^{\alpha }{\zeta }_2\left(n\right)\right]}^2-4\gamma A_4^{\gamma -1}(n_3,n_4,n)A_3(n_3,n){\zeta }_2^2\left(n\right)Q_1\left(n\right)}{4\gamma A_4^{\gamma -1}(n_3,n_4,n)A_3(n_3,n){\zeta }_2\left(n\right)}}.\hfill \end{array}$$

(18)

Fulfilling fractional sum for (18) on ${[n_4,n]}_{\mathbb{Z}}$, yields

$$\begin{array}{c}{I}_{n_4}^{\alpha }\left[{\displaystyle \frac{{\displaystyle 4\gamma A_4^{\gamma -1}(n_3,n_4,n)A_3(n_3,n){\zeta }_2^2\left(n\right)Q_1\left(n\right)-c\left(n\right){\left[{\Delta }^{\alpha }{\zeta }_2\left(n\right)\right]}^2}}{{\displaystyle 4\gamma A_4^{\gamma -1}(n_3,n_4,n)A_3(n_3,n){\zeta }_2\left(n\right)}}}\right]\hfill \\ \le {\theta }_2\left(n_4\right)-{\theta }_2\left(n\right)\le {\theta }_2\left(n_4\right),\hfill \end{array}$$

which is a contradiction to (15).

Case $\left(iii\right)$: Suppose (8) holds. It follows from Lemma 3 that $\underset{n\to \infty }{lim}x\left(n\right)=0$.

From the analysis above, the proof is complete.

Let $\mathbb{D}=\left\{(n,m)\right|n\ge m\ge n_0\}$, and $\mathcal{B}$ is defined on $\mathbb{D}$, satisfying $\mathcal{B}(n,n)=0,$$\mathcal{B}(n,m)>0,$${\Delta }_m^{\alpha }\mathcal{B}(n,m)\le 0$ for $n>m\ge n_0$. Next, we establish the Philos-type oscillation criteria for Equation (1). □

Theorem 2. 

If (2) and (9) are satisfied, and for any sufficiently large $n_4>n_3>n_2>n_1>n_0$, it holds that

$$\begin{array}{c}\underset{n\to \infty }{lim}sup{\displaystyle \frac{{\displaystyle 1}}{{\displaystyle \mathcal{B}(n,n_0)}}}\{{\displaystyle \sum _{s=n_4}^{n-1}}\{s^{\alpha -1}\mathcal{B}(n,s)\hfill \\ {\displaystyle \frac{{\displaystyle 4\gamma ke\left(s\right)A_2^{\gamma -1}(n_1,n_2,n_3,n_4,s)A_1(n_1,n_2,n_3,s){\zeta }_1^2\left(s\right)-c\left(s\right){\left[{\Delta }^{\alpha }{\zeta }_1\left(s\right)\right]}^2}}{{\displaystyle 4\gamma A_2^{\gamma -1}(n_1,n_2,n_3,n_4,s)A_1(n_1,n_2,n_3,s){\zeta }_1\left(s\right)}}}\left\}\right\}=\infty ,\hfill \end{array}$$

(19)

and either (13) or (14) or

$$\begin{array}{c}\underset{n\to \infty }{lim}sup{\displaystyle \frac{{\displaystyle 1}}{{\displaystyle \mathcal{B}(n,n_0)}}}\{{\displaystyle \sum _{s=n_0}^{n-1}}\{s^{\alpha -1}\mathcal{B}(n,s)\hfill \\ {\displaystyle \frac{{\displaystyle 4\gamma A_4^{\gamma -1}(n_3,n_4,s)A_3(n_3,s){\zeta }_2^2\left(s\right)Q_1\left(s\right)-c\left(s\right){\left[{\Delta }^{\alpha }{\zeta }_2\left(s\right)\right]}^2}}{{\displaystyle 4\gamma A_4^{\gamma -1}(n_3,n_4,s)A_3(n_3,s){\zeta }_2\left(s\right)}}}\left\}\right\}=\infty \hfill \end{array}$$

(20)

holds, where $A_1,A_2,A_3,A_4,Q_1,{\zeta }_1,{\zeta }_2$ are defined as in Theorem 1, then Equation (1) is oscillatory or $\underset{n\to \infty }{lim}x\left(n\right)=0$.

Proof. 

Similar to the proof in Theorem 1. In Case $\left(i\right)$ of Theorem 1, starting from (16), replacing n with s, multiplying $\mathcal{B}(n,s)$ on both sides, and fulfilling fractional sum on ${[n_4,n]}_{\mathbb{Z}}$, one can obtain that

$$\begin{array}{cc}\hfill & {\displaystyle \sum _{s=n_4}^{n-1}}\left\{s^{\alpha -1}\mathcal{B}(n,s){\displaystyle \frac{4\gamma ke\left(s\right)A_2^{\gamma -1}(n_1,n_2,n_3,n_4,s)A_1(n_1,n_2,n_3,s){\zeta }_1^2\left(s\right)-c\left(s\right){\left[{\Delta }^{\alpha }{\zeta }_1\left(s\right)\right]}^2}{4\gamma A_2^{\gamma -1}(n_1,n_2,n_3,n_4,s)A_1(n_1,n_2,n_3,s){\zeta }_1\left(s\right)}}\right\}\hfill \\ \hfill & \le -{\displaystyle \sum _{s=n_4}^{n-1}}\left[s^{\alpha -1}\mathcal{B}(n,s){\Delta }^{\alpha }{\theta }_1\left(s\right)\right]=\mathcal{B}(n,n_4){\theta }_1\left(n_4\right)+{\displaystyle \sum _{s=n_4}^{n-1}}{s}^{\alpha -1}{\theta }_1(s+1){\Delta }_s^{\alpha }\mathcal{B}(n,s)\hfill \\ \hfill & \le \mathcal{B}(n,n_4){\theta }_1\left(n_4\right)\le \mathcal{B}(n,n_0){\theta }_1\left(n_4\right),\hfill \end{array}$$

where the properties $\left(iv\right)$ and $\left(iii\right)$ are used in the last two steps. Moreover,

$$\begin{array}{c}\underset{n\to \infty }{lim}sup{\displaystyle \frac{{\displaystyle 1}}{{\displaystyle \mathcal{B}(n,n_0)}}}\{{\displaystyle \sum _{s=n_4}^{n-1}}\{s^{\alpha -1}\mathcal{B}(n,s)\hfill \\ {\displaystyle \frac{{\displaystyle 4\gamma ke\left(s\right)A_2^{\gamma -1}(n_1,n_2,n_3,n_4,s)A_1(n_1,n_2,n_3,s){\zeta }_1^2\left(s\right)-c\left(s\right){\left[{\Delta }^{\alpha }{\zeta }_1\left(s\right)\right]}^2}}{{\displaystyle 4\gamma A_2^{\gamma -1}(n_1,n_2,n_3,n_4,s)A_1(n_1,n_2,n_3,s){\zeta }_1\left(s\right)}}}\left\}\right\}\hfill \\ \le {\theta }_1\left(n_4\right)+{\displaystyle \sum _{s=n_0}^{n_4}}\left|s^{\alpha -1}{\displaystyle \frac{{\displaystyle 4\gamma ke\left(s\right)A_2^{\gamma -1}(n_1,n_2,n_3,n_4,s)A_1(n_1,n_2,n_3,s){\zeta }_1^2\left(s\right)-c\left(s\right){\left[{\Delta }^{\alpha }{\zeta }_1\left(s\right)\right]}^2}}{{\displaystyle 4\gamma A_2^{\gamma -1}(n_1,n_2,n_3,n_4,s)A_1(n_1,n_2,n_3,s){\zeta }_1\left(s\right)}}}\right|\hfill \\ <\infty ,\hfill \end{array}$$

which is a contradiction to (19).

In Case $\left(ii\right)$ of Theorem 1, replacing n with s in (18), multiplying $\mathcal{B}(n,s)$ on both sides, and fulfilling fractional sum on ${[n_4,n]}_{\mathbb{Z}}$, one can obtain that

$$\begin{array}{cc}\hfill & {\displaystyle \sum _{s=n_4}^{n-1}}\left\{s^{\alpha -1}\mathcal{B}(n,s){\displaystyle \frac{4\gamma ke\left(s\right)A_2^{\gamma -1}(n_1,n_2,n_3,n_4,s)A_1(n_1,n_2,n_3,s){\zeta }_1^2\left(s\right)-c\left(s\right){\left[{\Delta }^{\alpha }{\zeta }_1\left(s\right)\right]}^2}{4\gamma A_2^{\gamma -1}(n_1,n_2,n_3,n_4,s)A_1(n_1,n_2,n_3,s){\zeta }_1\left(s\right)}}\right\}\hfill \\ \hfill & \le -{\displaystyle \sum _{s=n_4}^{n-1}}\left[s^{\alpha -1}\mathcal{B}(n,s){\Delta }^{\alpha }{\theta }_1\left(s\right)\right]=\mathcal{B}(n,n_4){\theta }_1\left(n_4\right)+{\displaystyle \sum _{s=n_4}^{n-1}}{s}^{\alpha -1}{\theta }_1(s+1){\Delta }_s^{\alpha }\mathcal{B}(n,s)\hfill \\ \hfill & \le \mathcal{B}(n,n_4){\theta }_1\left(n_4\right)\le \mathcal{B}(n,n_0){\theta }_1\left(n_4\right),\hfill \end{array}$$

Furthermore,

$$\begin{array}{cc}\hfill & \underset{n\to \infty }{lim}sup{\displaystyle \frac{1}{\mathcal{B}(n,n_0)}}\{{\displaystyle \sum _{s=n_0}^{n-1}}\{s^{\alpha -1}\mathcal{B}(n,s)\hfill \\ \hfill & {\displaystyle \frac{4\gamma A_4^{\gamma -1}(n_3,n_4,s)A_3(n_3,s){\zeta }_2^2\left(s\right)Q_1\left(s\right)-c\left(s\right){\left[{\Delta }^{\alpha }{\zeta }_2\left(s\right)\right]}^2}{4\gamma A_4^{\gamma -1}(n_3,n_4,s)A_3(n_3,s){\zeta }_2\left(s\right)}}\left\}\right\}\hfill \\ \hfill & \le {\theta }_2\left(n_4\right)+{\displaystyle \sum _{s=n_0}^{n_4}}\left|s^{\alpha -1}{\displaystyle \frac{4\gamma A_4^{\gamma -1}(n_3,n_4,s)A_3(n_3,s){\zeta }_2^2\left(s\right)Q_1\left(s\right)-c\left(s\right){\left[{\Delta }^{\alpha }{\zeta }_2\left(s\right)\right]}^2}{4\gamma A_4^{\gamma -1}(n_3,n_4,s)A_3(n_3,s){\zeta }_2\left(s\right)}}\right|<\infty ,\hfill \end{array}$$

which is a contradiction to (20).

As in Case $\left(iii\right)$ of Theorem 1, it holds that $\underset{n\to \infty }{lim}x\left(n\right)=0$, the proof is complete. □

3. Applications

In this part, we provide some applications for the main theorems established in the previous section.

Example 1. 

$${\Delta }^{4\times {\displaystyle \frac{1}{2}}}\left[n^{{\displaystyle \frac{1}{2}}}{\Delta }^{{\displaystyle \frac{1}{2}}}x\left(n\right)\right]+n{x}^3\left(n\right)=0,n\in [1,\infty ).$$

(21)

It can be seen from (1) that $\alpha ={\displaystyle \frac{{\displaystyle 1}}{{\displaystyle 2}}},n_0=1,c\left(n\right)=n^{{\displaystyle \frac{1}{2}}},e\left(n\right)=n,g\left(x\left(n\right)\right)=x^3\left(n\right)$, $k=1,\gamma =3$.

To verify (2), we have $\underset{n\to \infty }{lim}{I}_{n_0}^{\alpha }\left({\displaystyle \frac{{\displaystyle 1}}{{\displaystyle c\left(n\right)}}}\right)=\underset{n\to \infty }{lim}{\displaystyle \sum _{s=n_0}^{n-1}}{\displaystyle \frac{{\displaystyle s^{-\frac{1}{2}}}}{{\displaystyle c\left(s\right)}}}=\underset{n\to \infty }{lim}{\displaystyle \sum _{s=n_0}^{n-1}}{\displaystyle \frac{{\displaystyle 1}}{{\displaystyle s}}}=\infty .$

It is easy to verify (9), (13), and (14). To verify (12), as

$$\underset{n\to \infty }{lim}{A}_1(n_1,n_2,n_3,n)=\underset{n\to \infty }{lim}{A}_2^2(n_1,n_2,n_3,n_4,n)=\infty ,$$

so one can find $n^{*}$ satisfying $A_1(n_1,n_2,n_3,s)>1,A_2^2(n_1,n_2,n_3,n_4,n)>1$ for $n>n^{*}>n_4$. Setting ${\zeta }_1\left(n\right)=n$, it follows that

$$\begin{array}{cc}\hfill & {\displaystyle \sum _{s=n^{*}}^{n-1}}\left\{s^{\alpha -1}{\displaystyle \frac{4\gamma ke\left(s\right)A_2^{\gamma -1}(n_1,n_2,n_3,n_4,s)A_1(n_1,n_2,n_3,s){\zeta }_1^2\left(s\right)-c\left(s\right){\left[{\Delta }^{\alpha }{\zeta }_1\left(s\right)\right]}^2}{4\gamma A_2^{\gamma -1}(n_1,n_2,n_3,n_4,s)A_1(n_1,n_2,n_3,s){\zeta }_1\left(s\right)}}\right\}\hfill \\ \hfill & ={\displaystyle \sum _{s=n^{*}}^{n-1}}\left\{s^{-{\displaystyle \frac{1}{2}}}[s^2-{\displaystyle \frac{s^{-\frac{1}{2}}}{12A_2^2(n_1,n_2,n_3,n_4,s)A_1(n_1,n_2,n_3,s)s}}]\right\}\hfill \\ \hfill & >{\displaystyle \sum _{s=n^{*}}^{n-1}}\left\{s^{-{\displaystyle \frac{1}{2}}}[s^2-{\displaystyle \frac{s^{-\frac{1}{2}}}{12s}}]\right\}\hfill \\ \hfill & ={\displaystyle \sum _{s=n^{*}}^{n-1}}[s^{{\displaystyle \frac{3}{2}}}-{\displaystyle \frac{1}{12}}{s}^{-2}]ds.\hfill \end{array}$$

So, (12) holds. On the other hand, if we let ${\zeta }_2\left(n\right)=n$ in (15), then similar as the process above, one can easily deduce that (15) also holds. So, by using Theorem 1, one can conclude Equation (21) is oscillatory or $\underset{n\to \infty }{lim}x\left(n\right)=0$.

Under some given initial values, one can obtain the values of the solution $x\left(n\right)$ for Equation (21). For example, if we select the initial values as $x\left(1\right)=0,x\left(2\right)=2,x\left(3\right)=0$, $x\left(4\right)=2$, then the solution can be demonstrated in Figure 1.

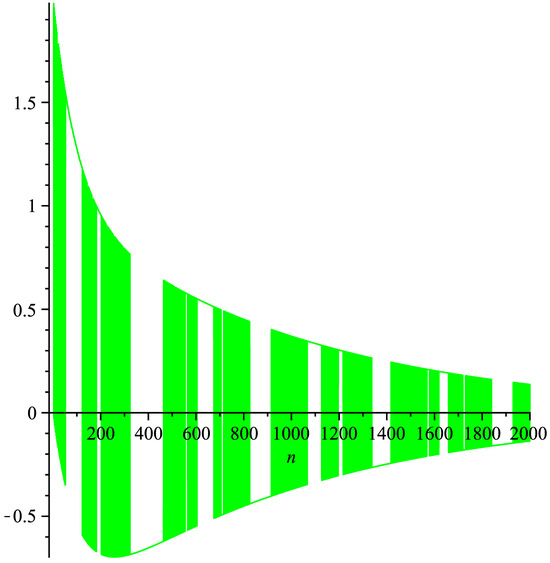
Figure 1. Demonstration of the oscillatory behavior of the solution of (21) when n is large enough.

It can be seen from Figure 1 that the solution of Equation (21) is oscillatory in the case n is large enough.

Example 2. 

$${\Delta }^{4\times {\displaystyle \frac{1}{3}}}\left[n^{{\displaystyle \frac{1}{3}}}{\Delta }^{{\displaystyle \frac{1}{2}}}x\left(n\right)\right]+x^5\left(n\right)=0,t\in [2,\infty ).$$

(22)

According to (1), one has $\alpha ={\displaystyle \frac{{\displaystyle 1}}{{\displaystyle 3}}},n_0=2,c\left(n\right)=n^{{\displaystyle \frac{1}{3}}},e\left(n\right)=1,g\left(x\left(n\right)\right)=x^5\left(n\right)$, $k=1,\gamma =5$.

We will use Theorem 2 to derive the oscillatory and asymptotic behaviour of Equation (22). To this end, it is necessary to verify (2), (9), (13), (14), (19), and (20). Obviously, (2), (9), (13), and (14) can be easily verified. On the other hand, for (19), if we let $\mathcal{B}(n,s)=n-s,{\zeta }_1\left(n\right)=n$, and $n^{*}$ is defined as in Example 1, then one can obtain that

$$\begin{array}{cc}\hfill & {\displaystyle \frac{1}{\mathcal{B}(n,n_0)}}\{{\displaystyle \sum _{s=2}^{n-1}}\{s^{\alpha -1}\mathcal{B}(n,s)\hfill \\ \hfill & {\displaystyle \frac{4\gamma ke\left(s\right)A_2^{\gamma -1}(n_1,n_2,n_3,n_4,s)A_1(n_1,n_2,n_3,s){\zeta }_1^2\left(s\right)-c\left(s\right){\left[{\Delta }^{\alpha }{\zeta }_1\left(s\right)\right]}^2}{4\gamma A_2^{\gamma -1}(n_1,n_2,n_3,n_4,s)A_1(n_1,n_2,n_3,s){\zeta }_1\left(s\right)}}\left\}\right\}\hfill \\ \hfill & ={\displaystyle \frac{1}{(n-2)}}\left\{({\displaystyle \sum _{s=2}^{n^{*}}}+{\displaystyle \sum _{s=n^{*}}^{n-1}})\left\{s^{-{\displaystyle \frac{2}{3}}}(n-s)[5s-{\displaystyle \frac{s^{-1}}{20A_2^4(n_1,n_2,n_3,n_4,n)A_1(n_1,n_2,n_3,s)s}}]\right\}\right\}\hfill \\ \hfill & >{\displaystyle \frac{1}{(n-2)}}\{{\displaystyle \sum _{s=2}^{n^{*}}}{s}^{-{\displaystyle \frac{2}{3}}}(n-s)[5s-{\displaystyle \frac{s^{-1}}{20A_2^4(n_1,n_2,n_3,n_4,n)A_1(n_1,n_2,n_3,s)s}}]\hfill \\ \hfill & +{\displaystyle \sum _{s=n^{*}}^{n-1}}{s}^{\alpha -1}(n-s)(5s-{\displaystyle \frac{s^{-1}}{20s}})\}\hfill \\ \hfill & >{\displaystyle \frac{1}{(n-2)}}\{{\displaystyle \sum _{s=2}^{n^{*}}}{s}^{-{\displaystyle \frac{2}{3}}}(n-s)[5s-{\displaystyle \frac{s^{-1}}{20A_2^4(n_1,n_2,n_3,n_4,n)A_1(n_1,n_2,n_3,s)s}}]\hfill \\ \hfill & +{\displaystyle \sum _{s=n^{*}}^{n-1}}(n-s)s^{{\displaystyle \frac{1}{3}}}\}.\hfill \\ \hfill & As{s}^{{\displaystyle \frac{1}{3}}}>{\int }_{s-1}^s{t}^{{\displaystyle \frac{1}{3}}}dt,s^{{\displaystyle \frac{4}{3}}}<{\int }_s^{s+1}{t}^{{\displaystyle \frac{4}{3}}}dt,then\hfill \\ \hfill & {\displaystyle \sum _{s=n^{*}}^{n-1}}(n-s)s^{{\displaystyle \frac{1}{3}}}>{\displaystyle \frac{3}{4}}n(n^{{\displaystyle \frac{4}{3}}}-{(n^{*}-1)}^{{\displaystyle \frac{4}{3}}})]-[{\displaystyle \frac{3}{7}}({(n+1)}^{{\displaystyle \frac{7}{3}}}-{\left(n^{*}\right)}^{{\displaystyle \frac{7}{3}}}).\hfill \end{array}$$

So furthermore one has

$$\begin{array}{c}{\displaystyle \frac{1}{\mathcal{B}(n,n_0)}}\{{\displaystyle \sum _{s=2}^{n-1}}\{s^{\alpha -1}\mathcal{B}(n,s)\hfill \\ {\displaystyle \frac{4\gamma ke\left(s\right)A_2^{\gamma -1}(n_1,n_2,n_3,n_4,s)A_1(n_1,n_2,n_3,s){\zeta }_1^2\left(s\right)-c\left(s\right){\left[{\Delta }^{\alpha }{\zeta }_1\left(s\right)\right]}^2}{4\gamma A_2^{\gamma -1}(n_1,n_2,n_3,n_4,s)A_1(n_1,n_2,n_3,s){\zeta }_1\left(s\right)}}\left\}\right\}\hfill \\ >{\displaystyle \frac{1}{(n-2)}}\{{\displaystyle \sum _{s=2}^{n^{*}}}{s}^{-{\displaystyle \frac{2}{3}}}(n-s)[5s-{\displaystyle \frac{s^{-1}}{20A_2^4(n_1,n_2,n_3,n_4,n)A_1(n_1,n_2,n_3,s)s}}]\hfill \\ +\frac{3}{4}n(n^{\frac{4}{3}}-{(n^{*}-1)}^{\frac{4}{3}})]-[\frac{3}{7}({(n+1)}^{\frac{7}{3}}-{(n^{*})}^{\frac{7}{3}})\}.\hfill \end{array}$$

From the inequality above, one can deduce that (19) is satisfied. Moreover, if we let ${\zeta }_2\left(n\right)=n$, then following in a similar manner as the analysis above, one can deduce that (20) is also satisfied. So, by using Theorem 2, the solution $x\left(n\right)$ to Equation (22) is oscillatory or $\underset{n\to \infty }{lim}x\left(n\right)=0$.

In (22), if we select the initial values as $x\left(1\right)=-2,x\left(2\right)=0,x\left(3\right)=-2,x\left(4\right)=0$, then, it holds $\underset{n\to \infty }{lim}x\left(n\right)=0$, which can be demonstrated in Figure 2.

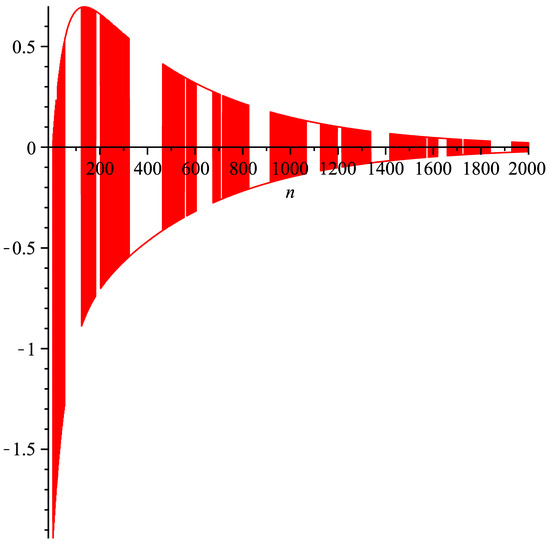
Figure 2. Demonstration of the asymptotic behavior of the solution of (22) when n is large enough.

4. Conclusions

We have successfully established some oscillatory and asymptotic criteria for a fifth-order fractional difference equation through use of the Riccati transformation, inequality technique, and the properties of the conformable fractional difference and fractional sum. The process can be extended to other types of high-order fractional difference equations as well as fractional differential equations, such as fifth-order fractional differential or difference equations with a neutral term, damping term, or impulse term and so on, which is worthy for further research.