Extinction Dynamics and Equilibrium Patterns in Stochastic Epidemic Model for Norovirus: Role of Temporal Immunity and Generalized Incidence Rates
Abstract
1. Introduction
- A1:
- Molluscan shellfish become affected throughout the packing process.
- A2:
- Fresh products are polluted during collecting, manufacturing, or packaging.
- A3:
- Infection may occur in the preparation of ready-for-consumption foods.
1.1. Structure and Life Cycle of Norovirus
- Entry: The norovirus capsid, comprised of structural proteins VP1 and VP2, binds to the host cell surface via interactions with histo-blood group antigens (HBGAs), facilitating viral entry. The capsid is then internalized and disassembled, releasing the positive-sense RNA ((+)RNA)) genome into the cytoplasm.
- Translation and Processing of the Viral Genome: The (+)RNA genome is translated into a polyprotein by host cell mechanisms, a process initiated by the nonstructural protein VPg, which attaches to the 5’ end of the RNA. This polyprotein is subsequently cleaved into six nonstructural proteins by the virus-encoded protease, Pro.
- Replication: The (+)RNA serves as a template for the synthesis of complementary negative sense RNAs, which are then used to produce new copies of genomic and subgenomic (+)RNAs. These steps facilitate the replication of the viral genome and the production of structural protein-encoding RNAs.
- Subgenomic RNA Production: Subgenomic (+)RNAs, which specifically contain ORF2 and ORF3, are synthesized to produce the structural proteins VP1 and VP2.
- Encapsidation and Virion Assembly: Newly synthesized genomic and subgenomic (+)RNAs are packaged into new virions through a process of encapsidation, with the assembly of the capsid proteins VP1 and VP2 around the RNA genome. The newly assembled virions are released from the host cell to initiate further infections. The exact mechanism of virion release remains an area of ongoing research.
1.2. Motivation
1.3. Contribution
2. Norovirus Dynamics: A Mathematical Approach
- (A1)
- with increasing property (i.e., ) and ;
- (A2)
- The function is either constant or monotonic decreasing over the interval and .
3. Well-Posedness of the Model: Existence and Uniqueness of Positive Global Solution
4. Extinction of Norovirus
5. Permanence in the Mean via Stationary Distribution
- (H1)
- ∃ a constant ; for all and ;
- (H2)
- There is a function satisfying for any .
- Case 1.
- If , we obtain
- Case 2.
- If we take a solution from the subset , then we have
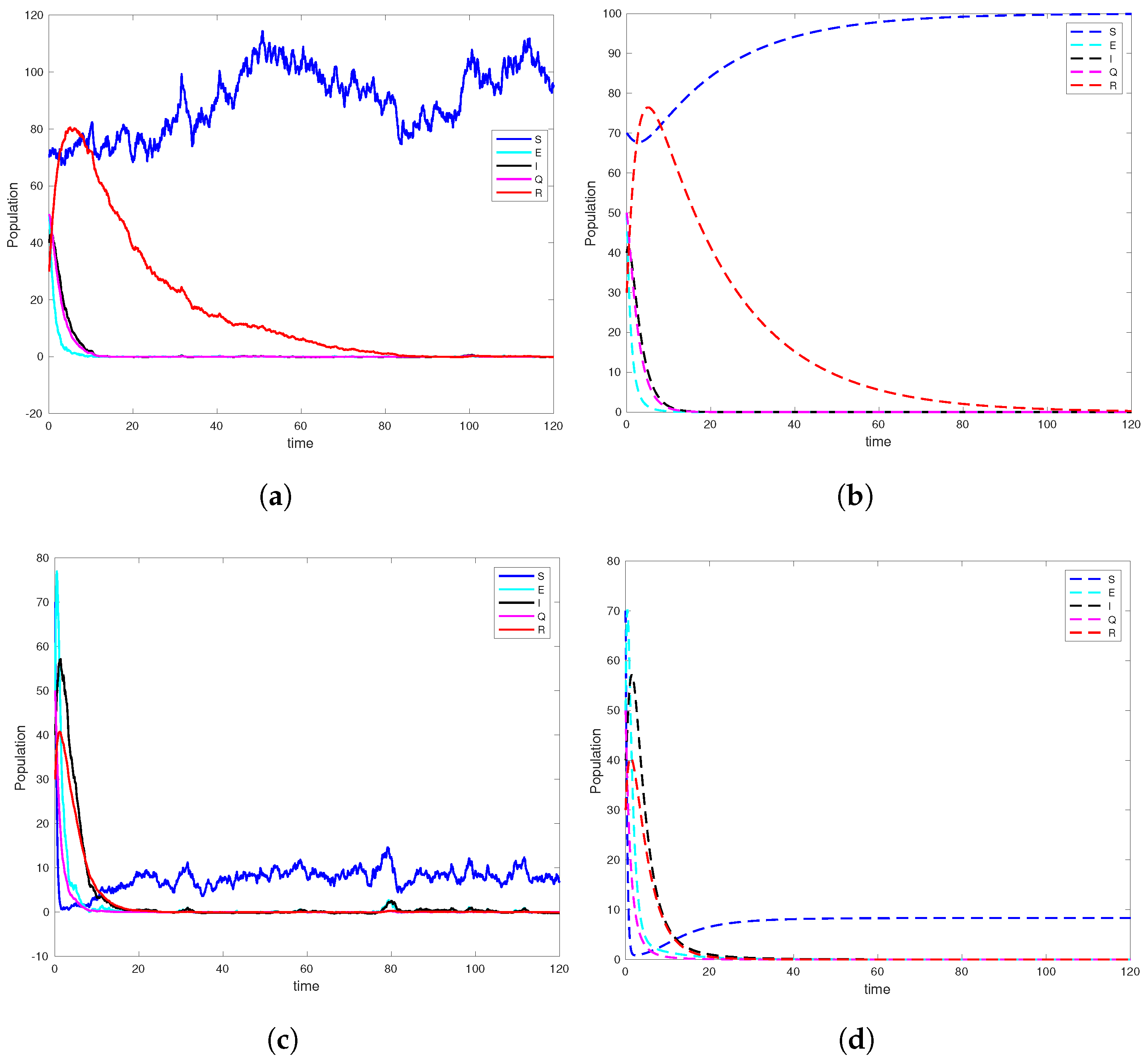
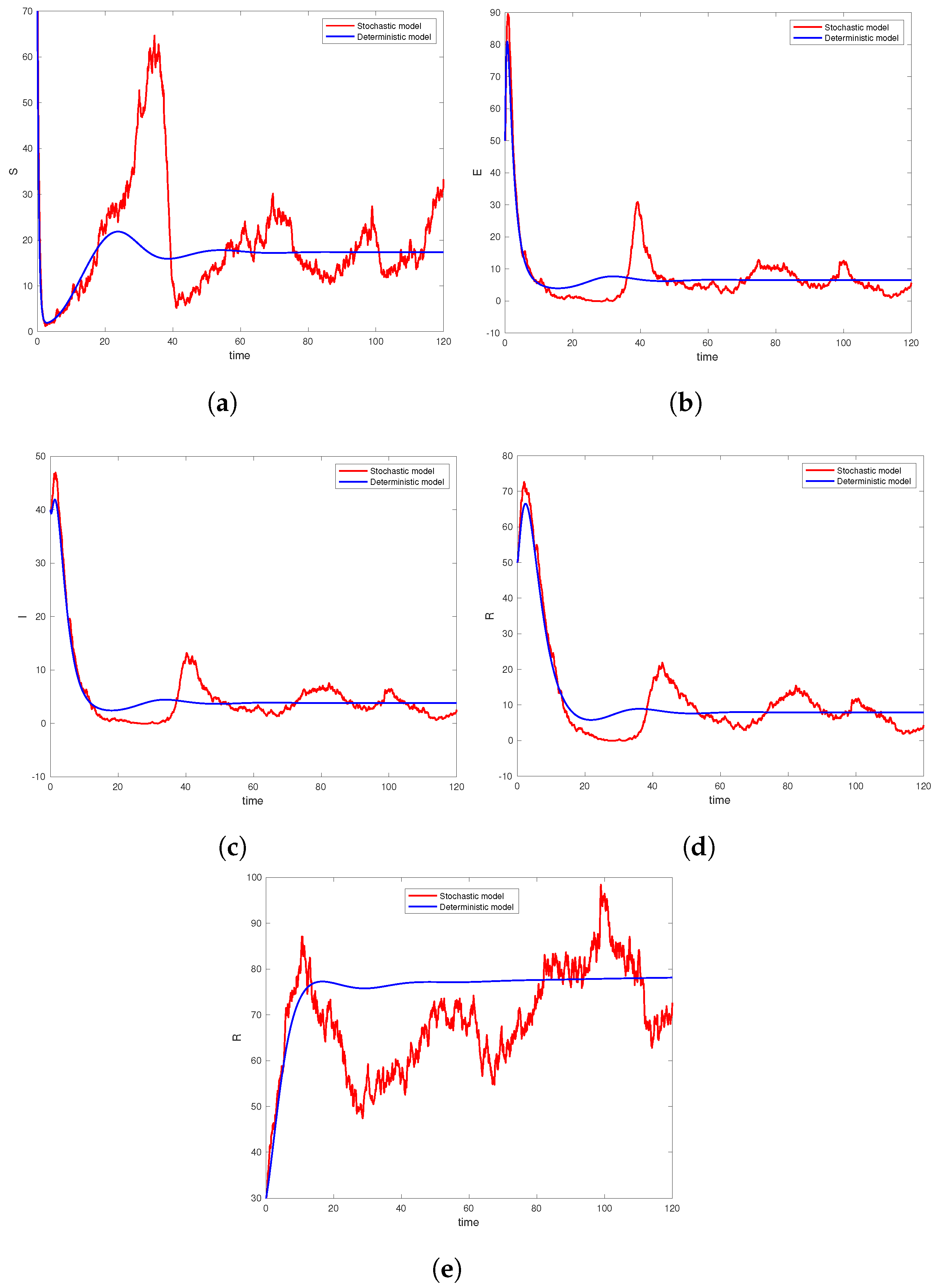
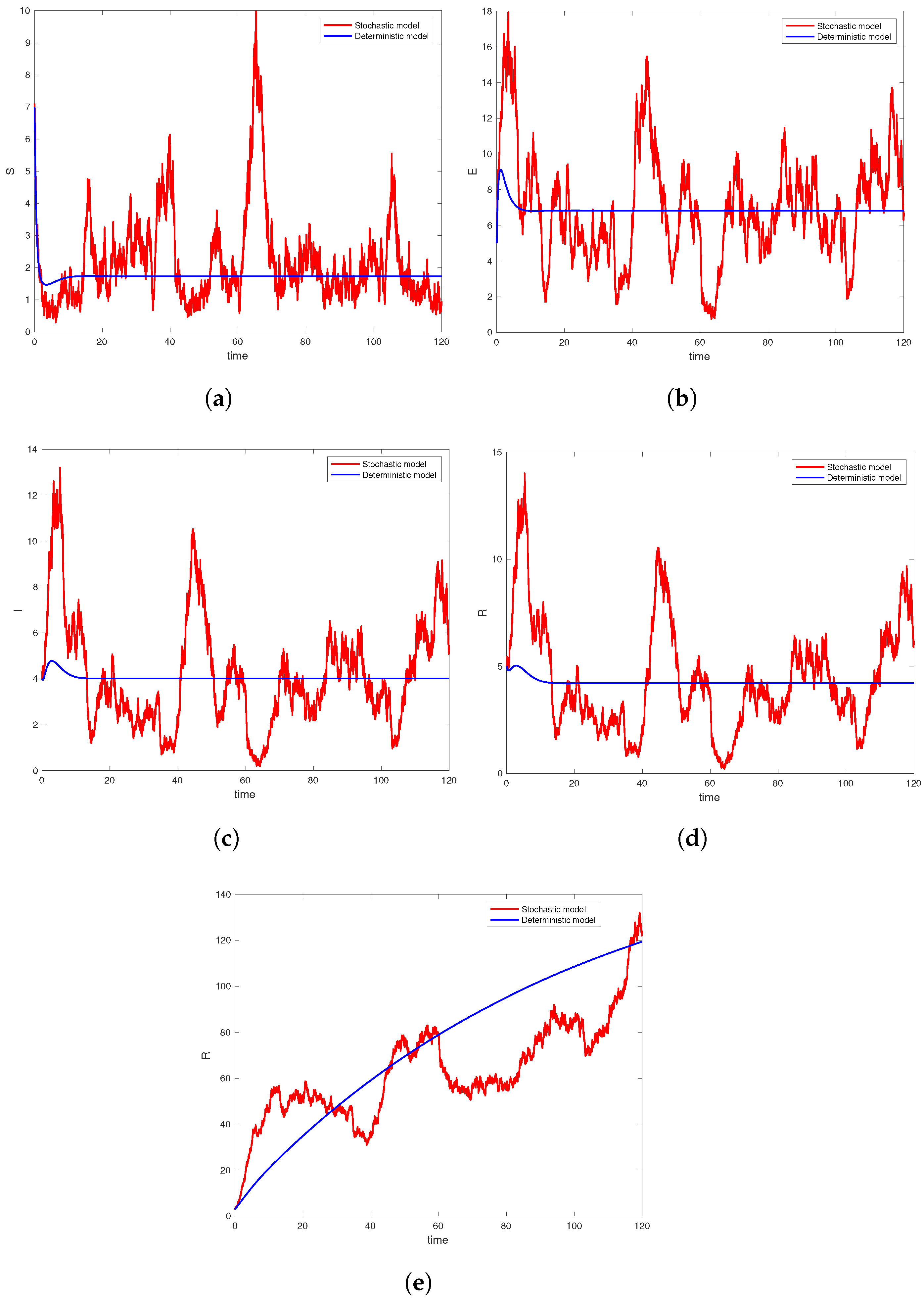
6. Computer Simulation and Illustrative Examples
6.1. Simulation Studies on Epidemic Extinction
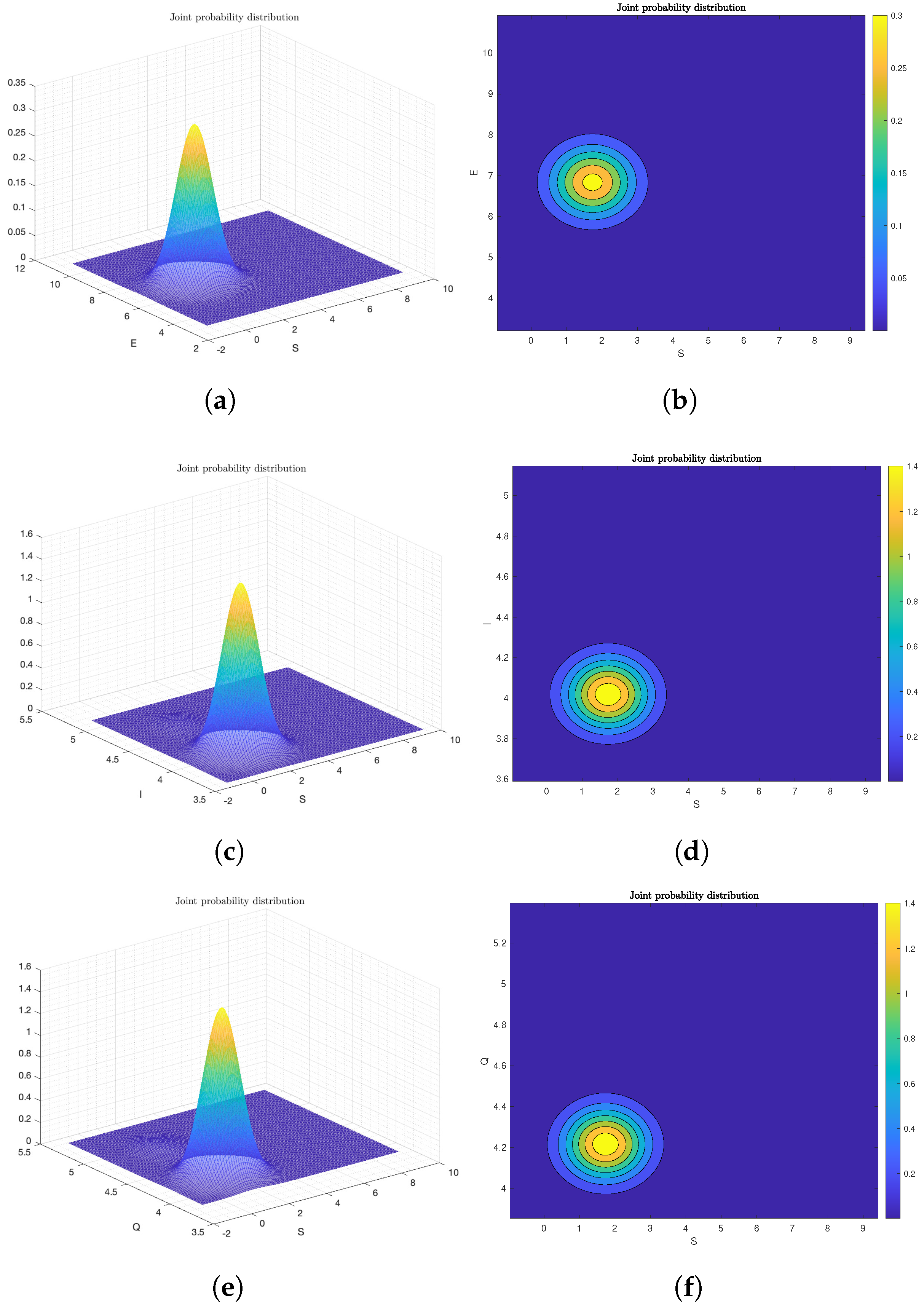
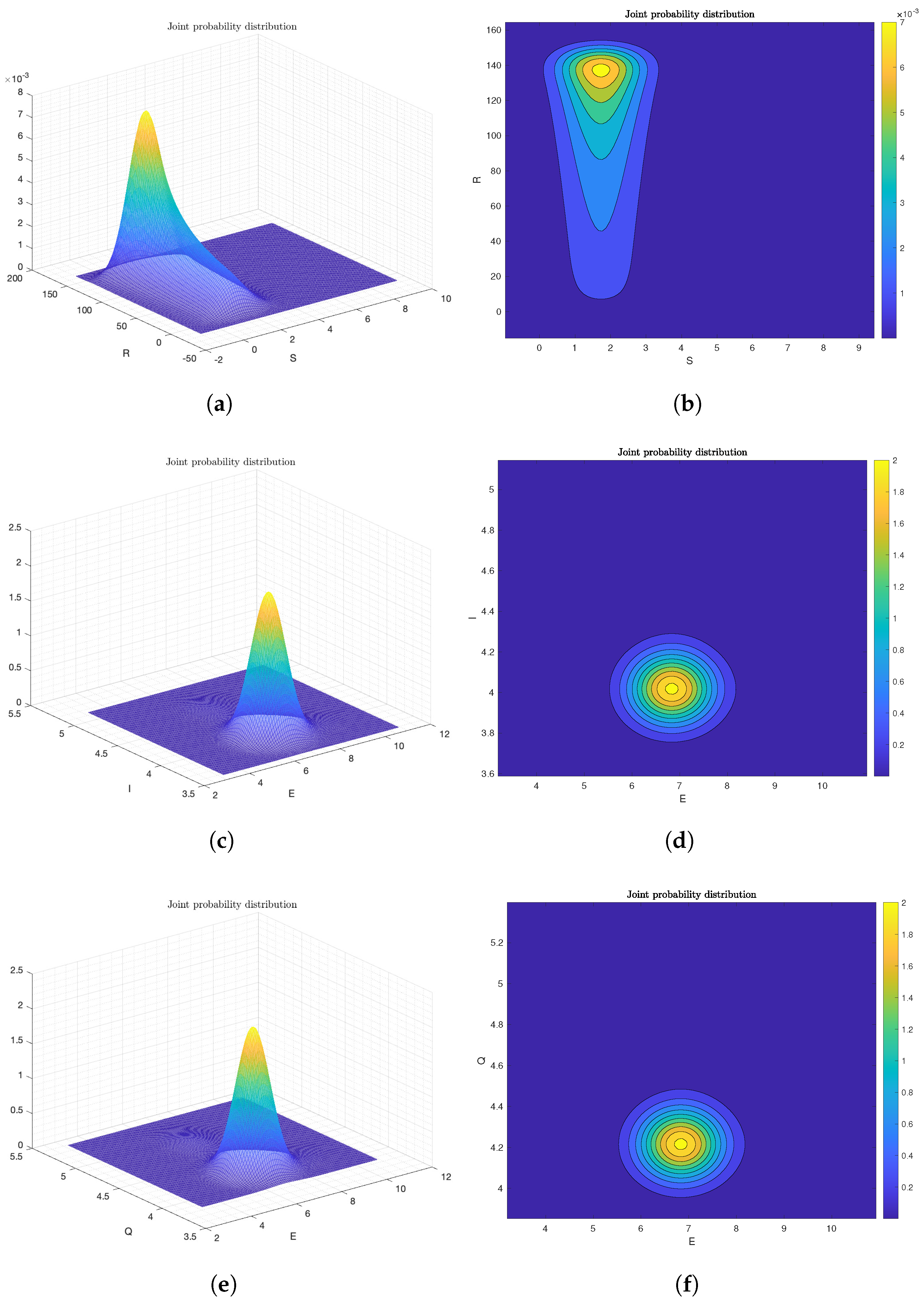
6.2. Numerical Analysis of Ergodicity and Stationary Distribution
Frequency Histogram of System (2)
6.3. The Effect of Probability Density Function
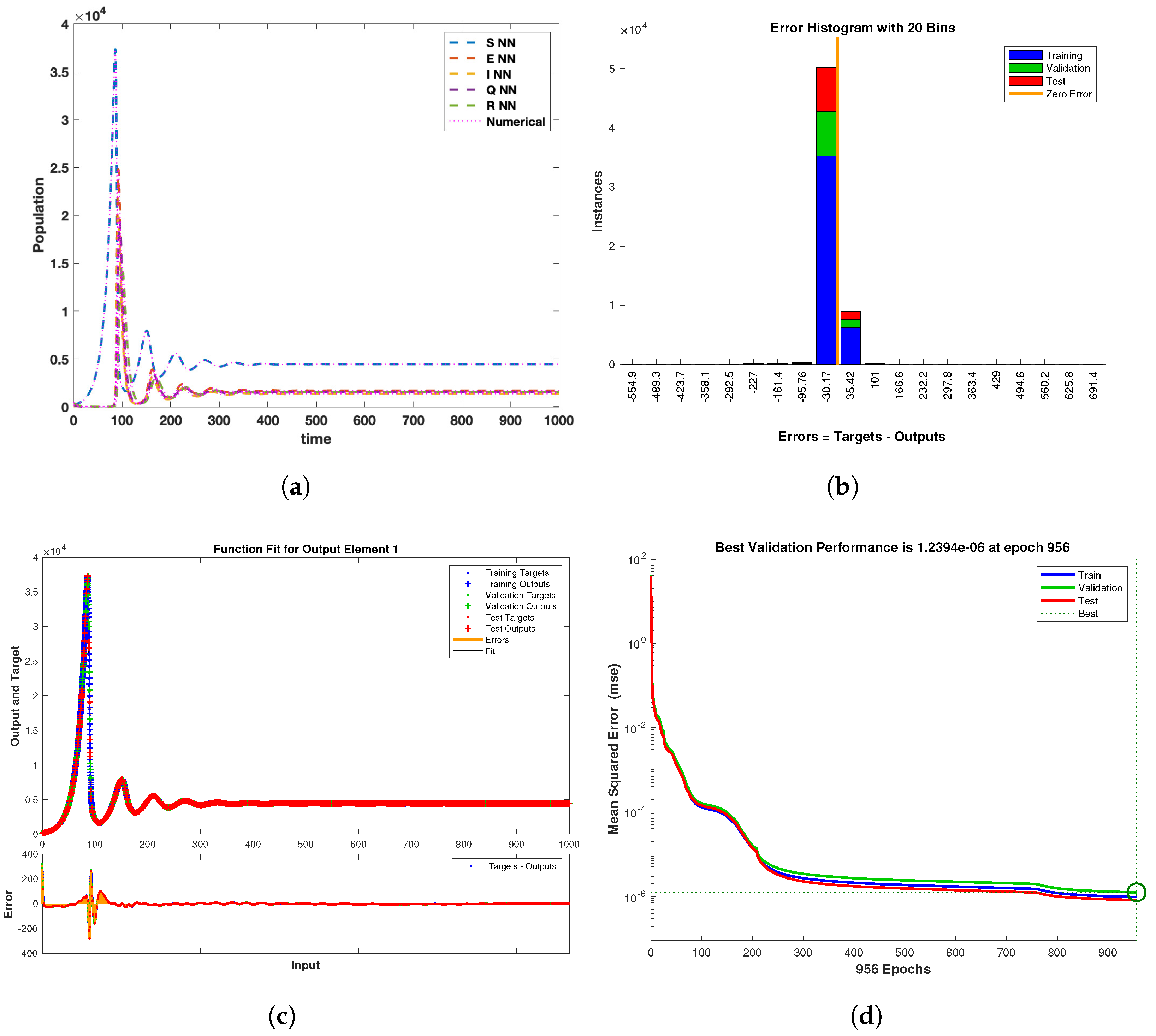
6.4. The LMBNNs Method
7. Conclusions and Future Research Directions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Koopmans, M.; Duizer, E. Foodborne viruses: An emerging problem. Int. J. Food Microbiol. 2004, 90, 23–41. [Google Scholar] [CrossRef] [PubMed]
- Widdowson, M.A.; Sulka, A.; Bulens, S.N.; Beard, R.S.; Chaves, S.S.; Hammond, R.; Salehi, E.D.P.; Swanson, E.; Totaro, J.; Woron, R.; et al. Norovirus and foodborne disease, United States, 1991–2000. Emerg. Infect. Dis. 2005, 11, 95–102. [Google Scholar] [CrossRef] [PubMed]
- Mokhtari, A.; Jaykus, L.A. Quantitative exposure model for the transmission of norovirus in retail food preparation. Int. J. Food Microbiol. 2009, 133, 38–47. [Google Scholar] [CrossRef] [PubMed]
- Bean, N.H.; Goulding, J.S.; Daniels, M.T.; Angulo, F.J. Surveillance for foodborne disease outbreaks—United States, 1988–1992. J. Food Prot. 1997, 60, 1265–1286. [Google Scholar] [CrossRef] [PubMed]
- Ahmed, S.M.; Lopman, B.A.; Levy, K. A systematic review and meta-analysis of the global seasonality of norovirus. PLoS ONE 2013, 8, e75922. [Google Scholar] [CrossRef]
- Marshall, J.A.; Bruggink, L.D. The dynamics of norovirus outbreak epidemics: Recent insights. Int. J. Environ. Res. Public Health 2011, 8, 1141–1149. [Google Scholar] [CrossRef]
- Rohayem, J. Norovirus seasonality and the potential impact of climate change. Clin. Microbiol. Infect. 2009, 15, 524–527. [Google Scholar] [CrossRef]
- Carmona-Vicente, N.; Fernández-Jiménez, M.; Ribes, J.M.; Téllez-Castillo, C.J.; Khodayar-Pardo, P.; Rodríguez-Diaz, J.; Buesa, J. Norovirus infections and seroprevalence of genotype GII. 4-specific antibodiesin a Spanish population. J. Med. Virol. 2015, 87, 675–682. [Google Scholar] [CrossRef]
- Honma, S.; Nakata, S.; Numata, K.; Kogawa, K.; Yamashita, T.; Oseto, M.; Jiang, X.; Chiba, S. Epidemiological study of prevalence of genogroup II human calicivirus (Mexico virus) infections in Japan and Southeast Asia as determined by enzyme- linked immunosorbent assays. J. Clin. Microbiol. 1998, 36, 2481–2484. [Google Scholar] [CrossRef]
- Simmons, K.; Gambhir, M.; Leon, J.; Lopman, B. Duration of immunity to norovirus gastroenteritis. Emerg. Infect. Dis. 2013, 19, 1260–1267. [Google Scholar] [CrossRef]
- Hall, A.J.; Lopman, B.A.; Payne, D.C.; Patel, M.M.; Gastañaduy, P.A.; Vinjé, J.; Parashar, U.D. Norovirus disease in the United States. Emerg. Infect. Dis. 2013, 19, 1198–1205. [Google Scholar] [CrossRef] [PubMed]
- Lai, C.C.; Wang, Y.H.; Wu, C.Y.; Hung, C.H.; Jiang, D.D.S.; Wu, F.T. A norovirus outbreak in a nursing home: Norovirus shedding time associated with age. J. Clin. Virol. 2013, 56, 96–101. [Google Scholar] [CrossRef]
- Murata, T.; Katsushima, N.; Mizuta, K.; Muraki, Y.; Hongo, S.; Matsuzaki, Y. Prolonged norovirus shedding in infants 6 months of age with gastroenteritis. Pediatr. Infect. Dis. J. 2007, 26, 46–49. [Google Scholar] [CrossRef]
- Din, A.; Li, Y.; Khan, T.; Zaman, G. Mathematical analysis of spread and control of the novel corona virus (COVID-19) in China. Chaos Solitons Fractals 2020, 141, 110286. [Google Scholar] [CrossRef]
- Khan, F.M.; Khan, Z.U. Numerical Analysis of Fractional Order Drinking Mathematical Model. J. Math. Tech. Model. 2024, 1, 11–24. [Google Scholar]
- Gaythorpe, K.A.M.; Trotter, C.L.; Lopman, B.; Steele, M.; Conlan, A.J.K. Norovirus transmission dynamics: A modelling review. Epidemiol. Infect. 2018, 146, 147–158. [Google Scholar] [CrossRef] [PubMed]
- Liu, G.; Qi, H.; Chang, Z.; Meng, X. Asymptotic stability of a stochastic May mutualism system. Comput. Math. Appl. 2020, 79, 735–745. [Google Scholar] [CrossRef]
- Tran, K.Q.; Yin, G. Optimal harvesting strategies for stochastic ecosystems. IET Control. Theory Appl. 2017, 11, 2521–2530. [Google Scholar] [CrossRef]
- Ma, T.; Meng, X.; Chang, Z. Dynamics and optimal harvesting control for a stochastic one-predator-two-prey time delay system with jumps. Complexity 2019, 2019, 5342031. [Google Scholar] [CrossRef]
- Din, A. The stochastic bifurcation analysis and stochastic delayed optimal control for epidemic model with general incidence function. Chaos 2021, 31, 31. [Google Scholar] [CrossRef]
- Huo, L.A.; Dong, Y.F.; Lin, T.T. Dynamics of a stochastic rumor propagation model incorporating media coverage and driven by Lévy noise. Chin. Phys. B 2021, 30, 080201. [Google Scholar] [CrossRef]
- Din, A.; Li, Y. Lévy noise impact on a stochastic hepatitis B epidemic model under real statistical data and its fractal–fractional Atangana–Baleanu order model. Phys. Scr. 2021, 96, 124008. [Google Scholar] [CrossRef]
- Wang, L.L.; Huang, N.J. Ergodic stationary distribution of a stochastic nonlinear epidemic model with relapse and cure. Appl. Anal. 2020, 101, 2652–2668. [Google Scholar] [CrossRef]
- Lopman, B.; Simmons, K.; Gambhir, M.; Vinjé, J.; Parashar, U. Epidemiologic implications of asymptomatic reinfection: A mathematical modeling study of norovirus. Am. J. Epidemiol. 2013, 179, kwt287. [Google Scholar] [CrossRef]
- Vanderpas, J.; Louis, J.; Reynders, M.; Mascart, G.; Vandenberg, O. Mathematical model for the control of nosocomial norovirus. J. Hosp. Infect. 2009, 71, 214–222. [Google Scholar] [CrossRef] [PubMed]
- Lee, R.M.; Lessler, J.; Lee, R.A.; Rudolph, K.E.; Reich, N.G.; Perl, T.M.; Cummings, D.A. Incubation periods of viral gastroenteritis: A systematic review. BMC Infect. Dis. 2013, 13, 1. [Google Scholar] [CrossRef] [PubMed]
- Khan, W.A.; Zarin, R.; Zeb, A.; Khan, Y.; Khan, A. Navigating Food Allergy Dynamics via a Novel Fractional Mathematical Model for Antacid-Induced Allergies. J. Math. Tech. Model. 2024, 1, 25–51. [Google Scholar]
- Anderson, R.M.; May, R.M. Infectious Disease of Humans: Dynamics and Control; Oxford University Press: Oxford, UK, 1991. [Google Scholar]
- Li, L.; Bai, Y.P.; Jin, Z. Periodic solutions of an epidemic model with saturated treatment. Nonlinear Dyn. 2014, 76, 1099–1108. [Google Scholar] [CrossRef]
- Zhang, Z.H.; Suo, Y.H. Qualitative analysis of a SIR epidemic model with saturated treatment rate. Appl. Math. Comput. 2010, 34, 177–194. [Google Scholar]
- Ebert, D.; Zschokke-Rohringer, C.D.; Carius, H.J. Dose effects and density-dependent regulation of two microparasites of Daphnia magna. Oecologia 2000, 122, 200–209. [Google Scholar] [CrossRef]
- Song, X.Y.; Neumann, A.U. Global stability and periodic solution of the viral dynamics. J. Math. Anal. Appl. 2007, 329, 281–297. [Google Scholar] [CrossRef]
- Anderson, R.M.; May, R.M. Regulation and stability of host-parasite population interactions: I. Regulatory processes. J. Anim. Ecol. 1978, 47, 219–247. [Google Scholar] [CrossRef]
- Din, A.; Li, Y. Optimizing HIV/AIDS dynamics: Stochastic control strategies with education and treatment. Eur. Phys. J. Plus 2024, 139, 1–19. [Google Scholar] [CrossRef]
- Caraballo, T.; Fatini, M.E.; Pettersson, R.; Taki, R. A stochastic SIRI epidemic model with relapse and media coverage. Discrete Contin. Dyn. Syst. Ser. B 2018, 23, 2483–3501. [Google Scholar] [CrossRef]
- Chen, X.Y.; Cao, J.D.; Park, J.H.; Qiu, J.L. Stability analysis and estimation of domain of attraction for the endemic equilibrium of a SEIQ epidemic model. Nonlinear Dyn. 2017, 87, 975–985. [Google Scholar] [CrossRef]
- Fan, K.G.; Zhang, Y.; Gao, S.J.; Wei, X. A class of stochastic delayed SIR epidemic models with generalized nonlinear incidence rate and temporary immunity. Physica A 2017, 481, 198–208. [Google Scholar] [CrossRef]
- El Fatini, M.; El Khalifi, M.; Gerlach, R.; Laaribi, A.; Taki, R. Stationary distribution and threshold dynamics of a stochastic SIRS model with a general incidence. Phys. A Stat. Mech. Its Appl. 2019, 534, 120696. [Google Scholar] [CrossRef]
- Liu, Q.; Jiang, D.Q.; Hayat, T.; Alsaedi, A.; Ahmad, B. A stochastic SIRS epidemic model with logistic growth and general nonlinear incidence rate. Physica A 2020, 551, 124152. [Google Scholar] [CrossRef]
- Zhang, Y.; Ma, X.; Din, A. Stationary distribution and extinction of a stochastic SEIQ epidemic model with a general incidence function and temporary immunity. AIMS Math 2021, 6, 12359–12378. [Google Scholar] [CrossRef]
- Zhao, Y.N.; Jiang, D.Q. The threshold of a stochastic SIS epidemic model with vaccination. Appl. Math. Comput. 2014, 243, 718–727. [Google Scholar] [CrossRef]
- Khasminskii, R. Stochastic Stability of Differential Equations; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Higham, D.J. An algorithmic introduction to numerical simulation of stochastic differential equations. SIAM Rev. 2001, 43, 525–546. [Google Scholar] [CrossRef]
- Towers, S.; Chen, J.; Cruz, C.; Melendez, J.; Rodriguez, J.; Salinas, A.; Yu, F.; Kang, Y. Quantifying the relative effects of environmental and direct transmission of norovirus. R. Soc. Open Sci. 2018, 5, 170602. [Google Scholar] [CrossRef] [PubMed]
- Assab, R.; Temime, L. The role of hand hygiene in controlling norovirus spread in nursing homes. BMC Infect. Dis. 2016, 16, 395. [Google Scholar] [CrossRef] [PubMed]
- Rushton, S.P.; Sanderson, R.A.; Reid, W.D.; Shirley, M.D.; Harris, J.P.; Hunter, P.R.; O’Brien, S.J. Transmission routes of rare seasonal diseases: The case of norovirus infections. Philos. Trans. R. Soc. B 2019, 374, 20180267. [Google Scholar] [CrossRef] [PubMed]
- Din, A. Optimal control theory of a novel stochastic human norovirus model and vaccine development. Int. J. Mod. Phys. B 2022, 36, 2250238. [Google Scholar] [CrossRef]
- Cui, T.; Din, A.; Liu, P.; Khan, A. Impact of Levy noise on a stochastic Norovirus epidemic model with information intervention. Comput. Methods Biomech. Biomed. Eng. 2023, 26, 1086–1099. [Google Scholar] [CrossRef]
- Din, A.; Li, Y. Stochastic optimal control for norovirus transmission dynamics by contaminated food and water. Chin. Phys. B 2022, 31, 020202. [Google Scholar] [CrossRef]



| Parameters | Meaning |
|---|---|
| The immigration or birth rate of susceptible population | |
| The disease transmission rate for exposing disease | |
| The Natural death rate | |
| The rate of infected from exposed class | |
| The rate of mortality of infected and quarantined individuals because of illness | |
| Rate of quarantine from exposed individuals | |
| Rate of quarantine from infectious individuals | |
| Rate of recovered from quarantined individuals | |
| The susceptible class | |
| The exposed compartment | |
| The infected individuals | |
| Quarantined population | |
| People recovered from the infection |
| Parameters | Case 1 | Case 2 | Case 3 | Source |
|---|---|---|---|---|
| 5.00 | 3.50 | 3.50 | Assumed | |
| 0.001 | 0.50 | 0.30 | Assumed | |
| 0.05 | 0.01 | 0.03 | Assumed | |
| 0.50 | 0.30 | 0.30 | Assumed | |
| 0.05 | 0.30 | 0.30 | Assumed | |
| 0.40 | 0.20 | 0.20 | Assumed | |
| 0.20 | 0.30 | 0.30 | Assumed | |
| 0.50 | 0.40 | 0.10 | Assumed | |
| 0.50 | 1.50 | 0.67 | Assumed | |
| 0.60 | 1.40 | 0.59 | Assumed | |
| 0.50 | 1.20 | 0.50 | Assumed | |
| 0.21 | 1.32 | 0.45 | Assumed | |
| 0.19 | 1.20 | 0.50 | Assumed | |
| 70.0 | 70.0 | 7.00 | Assumed | |
| 50.0 | 50.0 | 5.00 | Assumed | |
| 40.0 | 40.0 | 4.00 | Assumed | |
| 50.0 | 50.0 | 5.00 | Assumed | |
| 50.0 | 50.0 | 3.00 | Assumed |
| Citation | Model Type | Major Work | Advancements Offered by Our Model |
|---|---|---|---|
| [44] | Stochastic | Examined environmental and direct transmissions. | Our model not only uses advanced simulation techniques for more accurate predictions but also incorporates a generalized incidence function and considers temporal immunity, allowing for a more realistic representation of norovirus transmission dynamics under varying environmental conditions. |
| [45] | Stochastic | Focused on hand hygiene’s effect in nursing homes. | Expands to include more diverse control strategies and their effectiveness under stochastic disturbances. |
| [46] | Stochastic | Developed a stochastic model to analyze different transmission routes for norovirus. | Our model further enhances this by incorporating seasonal variations and a broader set of epidemiological data for more accurate predictions. |
| [47] | Stochastic | Explored stochastic modeling for norovirus control with vaccine implementation. | Our model offers a more detailed consideration of environmental factors and temporary immunity in addition to vaccination strategies. |
| [48] | Stochastic | Investigated the effects of Levy noise on norovirus transmission dynamics. | Unlike models focusing only on stochastic disturbances, ours integrates these with practical disease control strategies like vaccination. |
| [49] | Stochastic | Developed a stochastic model for norovirus focusing on transmission through contaminated food and water. | Our model extends by incorporating direct human-to-human interactions and a wider range of environmental influences. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ain, Q.T.; Qiang, X.; Rao, Y.; Shi, X.; Kosari, S.; Kou, Z. Extinction Dynamics and Equilibrium Patterns in Stochastic Epidemic Model for Norovirus: Role of Temporal Immunity and Generalized Incidence Rates. Fractal Fract. 2024, 8, 586. https://doi.org/10.3390/fractalfract8100586
Ain QT, Qiang X, Rao Y, Shi X, Kosari S, Kou Z. Extinction Dynamics and Equilibrium Patterns in Stochastic Epidemic Model for Norovirus: Role of Temporal Immunity and Generalized Incidence Rates. Fractal and Fractional. 2024; 8(10):586. https://doi.org/10.3390/fractalfract8100586
Chicago/Turabian StyleAin, Qura Tul, Xiaoli Qiang, Yongsheng Rao, Xiaolong Shi, Saeed Kosari, and Zheng Kou. 2024. "Extinction Dynamics and Equilibrium Patterns in Stochastic Epidemic Model for Norovirus: Role of Temporal Immunity and Generalized Incidence Rates" Fractal and Fractional 8, no. 10: 586. https://doi.org/10.3390/fractalfract8100586
APA StyleAin, Q. T., Qiang, X., Rao, Y., Shi, X., Kosari, S., & Kou, Z. (2024). Extinction Dynamics and Equilibrium Patterns in Stochastic Epidemic Model for Norovirus: Role of Temporal Immunity and Generalized Incidence Rates. Fractal and Fractional, 8(10), 586. https://doi.org/10.3390/fractalfract8100586









