Fractal Analysis of the Centrifuge Vibrograms

Abstract

This paper presents a new approach to analyzing the components of centrifuge rotor vibrograms using a 2D trajectory fractal analysis based on the Detrended Moving Average method. The method identifies the different noise oscillatory behavior of the rotor depending on the rotation frequencies, ranging from non-stationary unbounded and 1/f pink noise to correlated and uncorrelated noise. Fractal characteristics of the vibrograms were computed for the first time and demonstrated differences for rotation frequencies close to the eigenfrequencies and far from them. This paper also discusses the influence of gyroscopic effects on the natural frequencies of centrifuge oscillations and the excitation of second harmonics when the centrifuge rotates at higher frequencies. The main cause of rotor vibration is identified as the mass imbalance of the rotors, and this paper proposes a vibration classification according to source nodes to diagnose serviceable and faulty technical systems. Finally, the possibility of anisotropy of the vibrogram is discussed, and the oriented fractal scaling components analysis method is applied to pave the way for further investigation.

1. Introduction

In the field of mechanical engineering, the study of centrifugal flywheel control systems is a key area at the intersection of nonlinear science, control theory, and industrial applications.

Centrifuges are used in various industries, in medical applications, and food production for the purification of biological samples (e.g., proteins, DNA), simulation of high gravitational forces for scientific research, drying of wet materials, production of fuel from uranium in nuclear power plants, and analysis of blood and other medical samples in clinical diagnostics. High-speed precision centrifuges must ensure a high degree of mixture separation and trouble-free operation [1]. They have fast-rotating elements in the form of rotors. To ensure a high degree of separation requires high speed and stability. These requirements can be met only if the dynamic characteristics are determined, the knowledge of which makes it possible to determine the stable and unstable zones of rotation of the centrifuge [2,3].

All modern known simulations of centrifuge dynamics are simplified and based on models with a single body [4], which is a rotating rotor, while real centrifuges are practically a multi-mass system [5]. From the single-mass model, it is impossible to obtain the necessary information about the natural frequency spectrum of the centrifuge and the zone of instability [3,6].

The dynamic behavior of the centrifuge is determined by the mass of the body, the way it is fastened, the masses of the rotating parts and, in turn, the way they are connected and the quality of the balancing [7,8,9]. During operation, oscillations of the centrifuge shaft, as a rule, are caused by the imbalance phenomenon, which consists of the displacement of the center of mass relative to the axis of rotation. The findings, especially regarding the role of unbalance in suppressing the sub-synchronous oil whirl and preventing chaos, have direct implications for the design and operation of turbochargers in internal combustion engines. The identification of stable regions at medium-high speeds guides engineers in optimizing rotor assemblies to ensure reliable and efficient performance under various operating conditions. Since the imbalance is the cause of the oscillations, its effect on the shaft oscillations was investigated thoroughly in the literature.

An analytical model for investigating structural vibrations of a high-speed rotor supported by rolling bearings is presented in paper [10]. The results show the appearance of instability in the dynamic response, as the speed of the rotor-bearing system is changed. Authors [11] present a study of the stability of rotor-bearing systems. A comparison of threshold curves obtained using different approaches to dynamic force modeling provides the necessary information about the sensitivity of stability predictions to modeling methods, which allows for informed decisions on bearing design parameters that ultimately affect the stability of the entire rotor system. Period doubling and the mechanism of intermittency have been observed as the routes to instability. The appearance of regions of periodic, sub-harmonic, and chaotic behavior is observed to be strongly dependent on rotor speeds. In paper [1], different models of internal damping are investigated, leading to self-excited vibrations. The removable rotor shaft connection is the main reason for internal damping. The main influence parameters for stability are deduced analytically and numerically. The authors demonstrated instability effects that could occur in real lab centrifuges and which could be hardly simulated by a simple model of the rotor. In the work [12], the pros and cons of the conventional frequency-speed diagram are discussed in relation to the desired rotor dynamic properties. From such diagrams drawn for rotating machines, engineers can understand which modes are likely to be excited by the excitation sources of interest, which speed regions are safe for operation, and so on.

The work [13] expands the scope of traditional rotor dynamics analysis by incorporating the interaction of thrust and radial bearings in a shaft motion simulation. The study’s emphasis on the influence of the shaft diameter and thrust bearing position provides practical guidance for engineers involved in designing turbocharger rotor systems. By considering these factors during the design phase, rotor assemblies can be optimized to mitigate the potential negative effects on both shaft motion and thrust bearing health, thereby contributing to the reliability and longevity of turbocharger components.

In the experimental investigation [14] of a steady-state vibration response of the rotor bearing system with rotor faults such as unbalance, crack, rotor-stator rub and misalignment at sub-critical rotational speeds, the conventional Fourier spectrum (i.e., FFT) was shown to have limitations in exhibiting the whirling nature (i.e., forward/backward whirl) of the rotor faults. The possibility of diagnosing these rotor faults through unique vibration features was exhibited in the full spectrum. The investigation also highlighted the directional nature of higher harmonics, in particular, the 2× component.

Work [15] introduces a novel method for deriving Campbell diagrams for bearing rotor systems, challenging the traditional reliance on linear force coefficients. This approach offers a more accurate representation of the low-amplitude free vibrations of rotor dynamic systems. The practical implication lies in improving the predictive capabilities of analytical tools, enabling engineers to better understand and address potential instabilities in rotor systems. Investigation [16] into the backward whirling characteristics of dual-rotor systems caused by unbalance provides crucial insights for understanding and controlling complex rotor behaviors. The identification of conditions necessary for generating backward whirling and the factors influencing this phenomenon directly inform the design and operational considerations of counter-rotating dual-rotor systems.

Based upon the influence coefficient method, which is widely used in the industry for both rigid and flexible rotor balancing, a new technique, called the relative coefficient method, has been developed for rotor balancing. The steps for measuring the relative coefficients and the examples of rotor balancing are given in the paper [17]. In the study [18], the dynamic characteristics of centrifugal pendulum vibration absorbers that are used to suppress torsional vibrations are investigated both theoretically and experimentally. It is clarified that, although the centrifugal pendulum has remarkable effects in suppressing harmonic vibration, it induces large-amplitude harmonic vibrations, second and third-order superharmonic resonances, and unstable vibrations of the harmonic type under some conditions.

A nonlinear analysis of rotor dynamics was also applied to the study of the behavior of rotating systems (rotors) under nonlinear operating conditions. In this type of analysis, the interactions between the rotating parts, such as shafts, bearings, and other components, are modeled, taking into account their nonlinear behavior and considering effects such as nonlinear stiffness, nonlinear damping, and geometric nonlinearity. The objective is to predict the system’s dynamic response under different operating conditions and to identify potential sources of instability and other dynamic issues. In particular, in [19], the stability of the rotating system was investigated by applying Lyapunov’s method. The effects of the different parameters on the system behavior are investigated, showing that the rotor-AMB system exhibits a variety of nonlinear phenomena such as bifurcations, the coexistence of multiple solutions, jump phenomenon, and sensitivity to initial conditions. The study of the Lyapunov exponent and general dimension of the time series for rotor systems under different working conditions was capable of acting as the quantitative characterization of the fault diagnosis for the rotor system, which can diagnose and monitor the mechanical faults of the rotor system [20]. The results of [21] show that instability and chaos can emerge, as the speed of the rotor-bearing system is varied. The occurrence of period doubling and the mechanism of intermittency, which results in chaos, has been observed. To understand and depict the complex behavior of the system, techniques such as Poincaré maps, phase plots, time displacement responses, and FFT are utilized.

The nonlinear analysis provides a more accurate representation of the system’s behavior compared to linear analysis and is especially useful for the design and optimization of high-speed rotors and other complex rotating systems. One of the methods to access fractal properties of the vibrogram is the detrended moving average (DMA) analysis [22]. The DMA method is useful in the analysis of centrifuge rotors for detecting patterns such as bifurcations, chaos, and other nonlinear behaviors. By removing the trend in the data, DMA provides a more accurate representation of the underlying dynamics of the system, which can help in the understanding of the rotor’s behavior and the identification of potential sources of instability.

Research [23] not only addresses the challenging phenomenon of rotor-stator rub but also introduces a Smoothening Function (SF) to enhance the efficiency of rub detection. The application of the Adaptive Chirp Mode Decomposition (ACMD) method enables the exploration of the instantaneous frequencies of the rubbing rotor, providing a deeper understanding of the system’s dynamic behavior. The considerable reduction in computation time achieved with the SF contributes to the practicality of implementing such models for real-world applications, where efficiency and accuracy are paramount. The initial investigation, presented in [24], illuminates the global structure of nonlinear responses by navigating a two-dimensional parameter space. The revelation of comb-shaped self-similarity structures, alternating between periodic and chaotic responses, underscores the complexity inherent in these mechanical governors. The findings not only contribute to the theoretical understanding of nonlinear systems but also hold practical implications for the design and optimization of mechanical centrifugal governors in real-world applications.

The dynamic characteristics of a centrifuge, like any dynamic system, are its natural frequencies and critical speeds. From the practice of operating machines, it is known that shafts that rotate at certain revolutions, falling into resonance, become dynamically unstable [2,10]. Therefore, there is a need to determine the eigenfrequencies of rotor systems to avoid the appearance of resonance. When the rotor rotates at a fixed angular speed, for most machines, during calculation and design, the task of adjusting the natural frequencies from the angular speed of rotation is set. Whenever possible, the structure is made rigid enough so that the lower natural frequency of oscillation is higher than the angular speed of rotation, and then operation in the pre-resonance mode is guaranteed. But, for many high-speed machines, the necessary high rigidity is unattainable, and the operating mode is allowed to be resonant or in the interval between any two main resonant frequencies. At the same time, in the acceleration and braking modes, transient modes of passing through resonance, which must be passed rather quickly, become dynamically dangerous [1,25,26,27].

Expanding upon the exploration of centrifugal flywheel governors, the research outlined in [28] delves into the realm of fractional calculus. This extension introduces novel concepts such as a speed function and a hierarchical type-2 fuzzy neural network, harnessing them to achieve an accelerated convergence and approximation of elusive nonlinear components. The design of a stabilization controller, grounded in the backstepping framework, not only ensures system stability but also optimizes performance through the minimization of a predefined cost function. Shifting focus to the domain of centrifugal compressors, the study [29] explores the relationship between dynamic pressure and fractal characteristics. By employing entropy measures and fractal analysis, the research sheds light on the intrinsic dynamics of dynamic pressure under various working conditions, particularly identifying and characterizing surge states. This method not only aids in the identification of incipient surges but also establishes a foundation for designing effective surge control strategies critical for the reliable operation of centrifugal compressors.

In response to the increasing prevalence of centrifugal pumps in industrial applications, study [30] introduces an innovative fault diagnosis model. Leveraging Convolutional Neural Networks (CNNs) and fractal dimension features extracted through Empirical Mode Decomposition (EMD), the proposed model demonstrates a high accuracy in diagnosing faults in centrifugal pumps. The integration of advanced computational techniques with fractal analysis showcases the potential for real-time, online monitoring, providing a robust framework for maintaining the stable operation of centrifugal pumps crucial for industrial processes.

In this work, we study the fractal properties of the centrifuge vibrogram in the case of rotating at frequencies from different regions in the spectral domain (close and far from the eigenfrequencies) to unveil and characterize their chaotic properties. For the first time, we apply the detrended moving average analysis to the intrinsic mode functions of the vibrogram projections onto the orthogonal axes, which are obtained from an empirical mode decomposition, and demonstrate its suitability for studying the fractal properties of the oscillations of centrifuges.

2. Materials and Methods

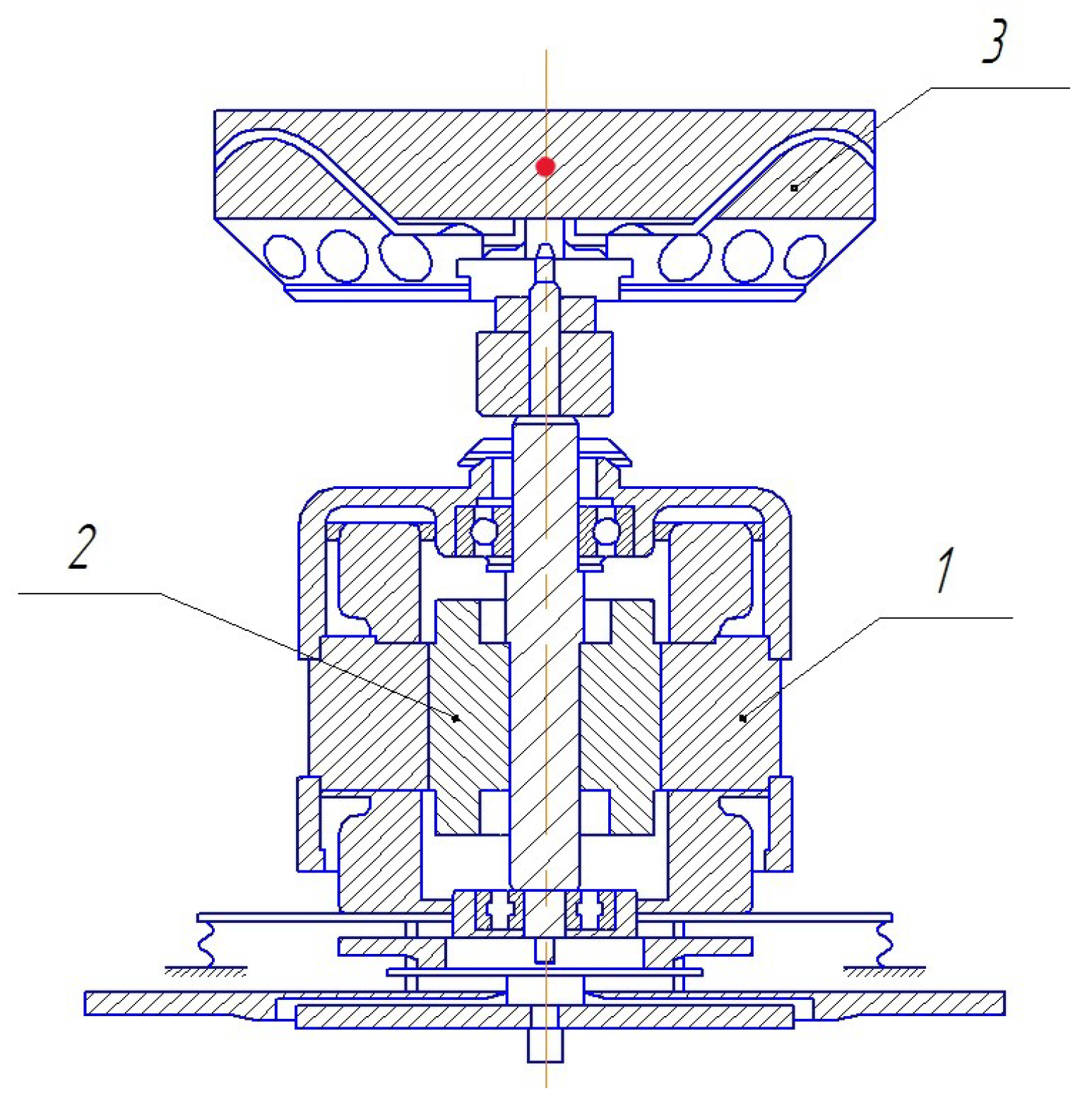
2.1. Measurement of the Centrifuge Vibrogram

The experimental study was conducted at the Institute of Mechanics, Otto von Guericke University of Magdeburg (Germany). The centrifuge body Pico 21 is a cylindrical bowl fixed on three rubber supports that are symmetrically arranged around the circumference. Inside the housing, on its axis, an electric motor is fixed on two supports, on the axis of which the centrifuge rotor is fixed. The centrifuge consists of (Figure 1) a rotor 3 rotating around a vertical axis, which is rotated by an electric motor; the motor rotor (anchor) 2 sits on the same axis, which is fixed in the housing, and the stator and housing 1 are fixed on elastic supports. The specifications of the centrifuge are presented in

Table 1. Specification of the centrifuge.

Parameters of the Centrifuge	Value
Continuous operation time, min	99, in 1 min step
Dimensions (W × D × H), mm	225 × 243 × 352
Maximum acceleration value, g	21,100
Max. centrifuge volume, mL	24 × 2
Max. speed, rpm	14,800
Max. noise, dB	56
Weight, kg	11
Timer, min	1 … 99
Voltage, V	220

.

The dynamic behavior of the centrifuge depends not only on the supports but also on the deformation of the elastic elements, which are the shaft and bearings.

The experimental bench is presented in Figure 2. Displacements of the centrifuge rotor (1) were measured using two Triangulation Displacement Sensors Opto NCDT 2220 (micro-epsilon) ILD 2220-100 lasers (resolution 1.5 $\mathsf{\mu }$m) (2a, 2b), the rays of which were directed at an angle of 90° to the side surface of the rotating laboratory centrifuge rotor to which the mirror tape was attached. The signals were measured (4, 5) using an amplifier type NP-3414 built into the laser. The DS-2000 receives this signal and transmits the expanded signal to the oscillation sensor, and the DS-0227 multi-channel station analyzes it. The results of data processing and the trajectory of the rotating body are displayed on the PC screen.

Shaft vibrations were measured. The centrifuge was accelerated to different operating speeds of revolution, and vibrograms of oscillations were recorded and stored for further analysis. The horizontal displacements and the trajectory of the upper point of the shaft with the fixed rotor of the centrifuge during the rotation of the rotor at different speeds were measured at different frequencies. The rotor runout during the experiments was within an acceptable range for such centrifuges.

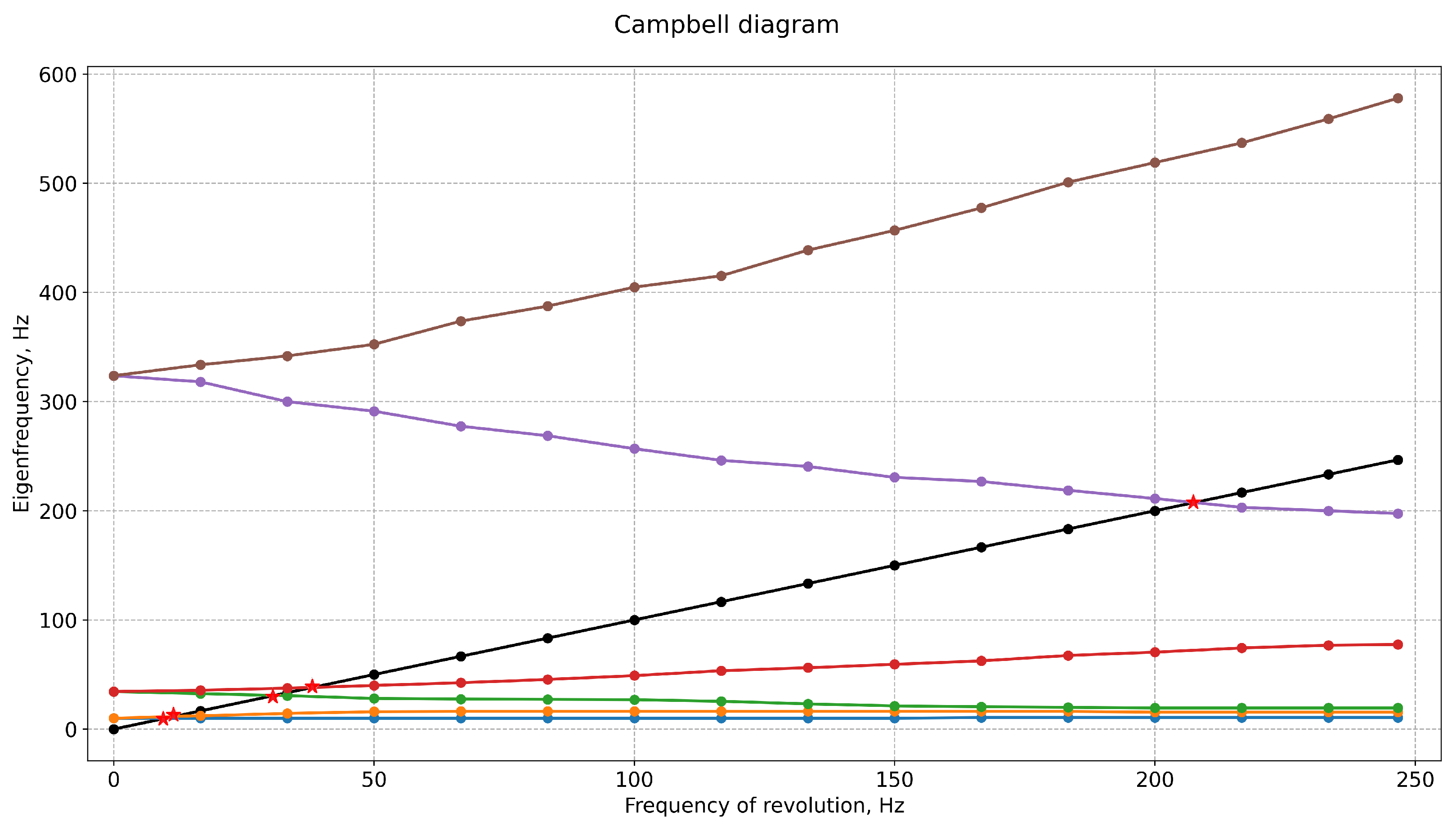
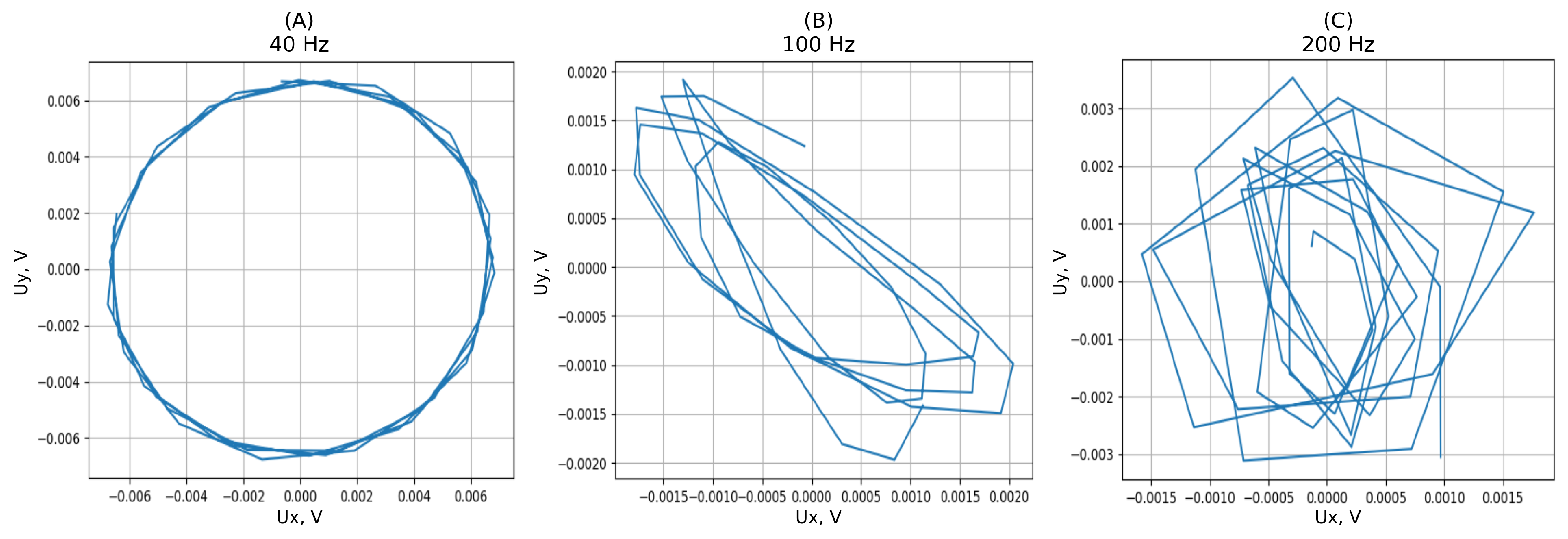
2.2. Study of Rotation at Different Frequencies

To define the critical frequencies, the centrifuge was rotated in frequency ranges between 0 and 14,800 rpm. Based on this, Campbell’s diagram [4,31] was constructed experimentally (Figure 3), which represents the dependence of natural frequencies on the speed of rotation of the rotor, that is, the influence of gyroscopic effects on natural frequencies, since natural frequencies in dynamic systems depend on gyroscopic effects caused by the speed of rotation. The Campbell diagram contains branches of eigenvalues created by the splitting of gyroscopic forces.

The critical speed is found when the forced frequencies coincide with the natural frequencies. The range from zero to the first critical speed is called the subcritical range [32]. The Campbell diagram is used to find critical velocities to avoid large amplitudes. One possibility to avoid high amplitudes for supercritical mechanisms is to pass through critical speeds very quickly during start and stop operations. Forward and backward whirls appear if the movement is in the same direction as the rotation. The forward whirl usually appears by unbalanced rotation, while the backward whirl can be caused by other periodic forces.

The centrifuge was accelerated to various operating speeds, vibrograms of oscillations were recorded, and then, with the help of spectral analysis, resonant frequencies that coincide with the natural frequencies were determined. For rotation frequencies of 100 Hz and 200 Hz, the sampling frequency was 1024 Hz and the recording duration was 2 s; for a rotation frequency of 40 Hz, the sampling frequency was 512 Hz, and the duration of the recording was 4 s. The examples of the shaft movement trajectories are given in Figure 4.

2.3. Analysis of Oscillations

To compute the spectral characteristics of the $x(t)$ and $y(t)$ data, we used the Welch method implemented in Scipy package [33]. To obtain an estimate of the power spectral density of the signal, it first divides the data into overlapping segments, and then computes a modified periodogram for each segment, followed by averaging the periodograms.

Empirical Mode Decomposition (EMD) is one of the most powerful methods to process and analyze the rotating machinery [34]. It is especially suitable for processing nonlinear and non-stationary signals, which is the case when the rotation frequency is approaching the eigenfrequencies. EMD was first introduced and explained in detail in [35], and consists of self-adaptively decomposing the original signal into components called (intrinsic mode functions, IMFs). Each IMF represents the oscillatory component embedded in the signal. As a result of the EMD procedure, the original time series $s(t)$ is decomposed into a sum of the K IMFs $c_k$ and residual $r_k$:

$$s(t)=\sum _{j=0}^K{c}_k+r_K,$$

(1)

Residue $r_k$ represents the main trend in the signal $s(t)$, while IMFs $c_k$-th are variations presented in $s(t)$ in different frequency bands.

In the case of our data, we decomposed both coordinates $x(t)$ and $y(t)$ using the Python package for Empirical Mode Decomposition [36] and used the IMF of 0-th-order $c_0$ for a further analysis of the amplitude envelope detection using the Hilbert transform, to keep the main oscillating component of the original signal. The Hilbert transform provides another signal that is 90° out of phase with the original signal. The combination of the original signal and the Hilbert transformed signal formulate an analytic signal, and its phase and amplitude define, respectively, the instantaneous phase and envelope of the IMF as a function of time.

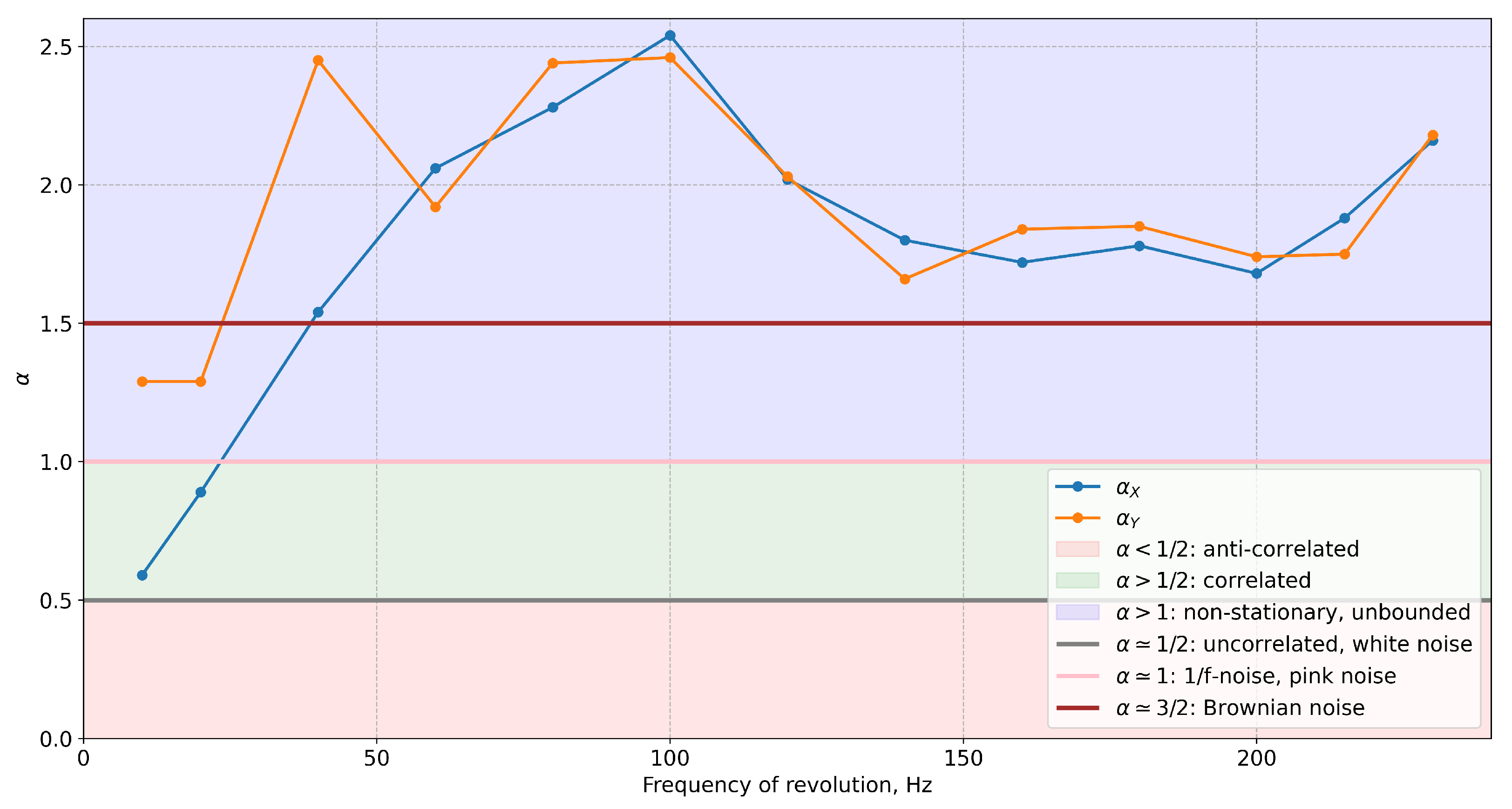
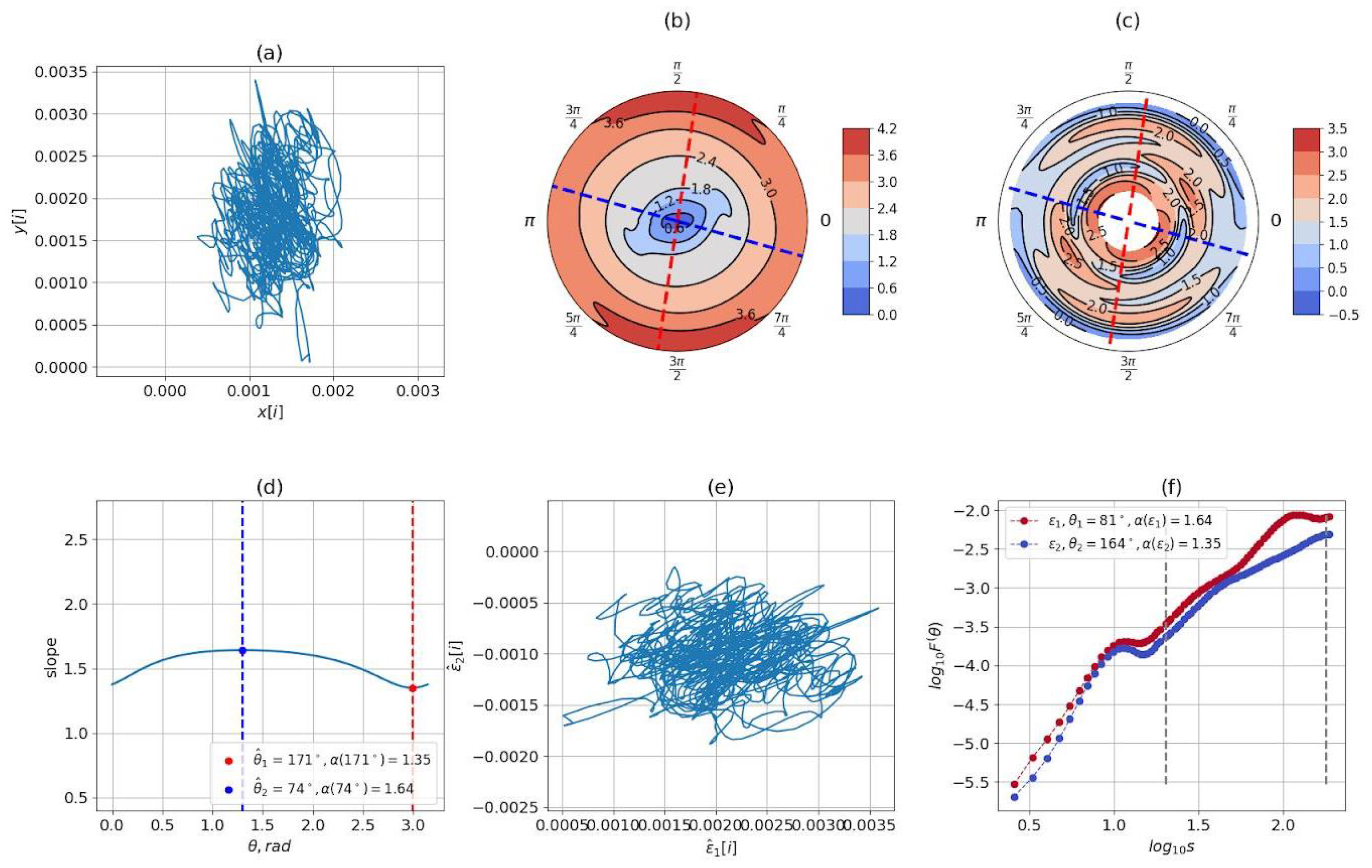
2.4. Detrended Moving Average Analysis

The detrended moving average (DMA) [22] method is a statistical technique commonly used to estimate the scaling exponent of time series data with long-range correlations, such as EEG time series during a cognitive workload [37], seismic time series [38], financial time series [39], etc. The DMA algorithm is widely applied to evaluate the long- and short-term correlations of one- and high-dimensional time series data, both in temporal and spatial domains.

A conventional DMA analysis involves two main steps. In the first step, we integrate the observed time series as follows

$$y[i]=\sum _{j=1}^{i}x[j],$$

(2)

In the next step, we remove the local trend from the time series, which is conducted by fitting a polynomial function to the data and subtracting it from the original data. The degree of the polynomial function used depends on the nature of the trend present in the data. Then, we calculate the so-called fluctuation function, as follows

$$F(s)=\sqrt{\frac{1}{N}\sum _{i=1}^N{\left(y[i]-{\tilde{y}}_{\mathrm{SG}}^{(m,s)}[i]\right)}^2},$$

(3)

where ${\tilde{y}}_{\mathrm{SG}}^{(m,s)}$ represents the m-th-order Savitzky–Golay smoothing filter [40,41] for $\left\{y[i]\right\}$, and s is window length of the Savitzky–Golay filter.

Then, we obtain the double-logarithmic plot of fluctuation function $F(s)$, against scales s. In DMA analysis, the double logarithmic plot is used to identify the scaling behavior of the data. If the data exhibit scaling behavior, the moving averages will exhibit power-law scaling with the time scale. This means that as the time scale increases, the size of the moving averages will increase or decrease in a power-law fashion. To measure the degree of self-similarity or long-range correlation present in the data, the scaling exponent alpha is calculated as the slope of the straight line fitted to the double logarithmic plot.

The scaling exponent is an important parameter in DMA analysis because it can provide insights into the underlying dynamics or processes that generated the time series data. Depending on its value, the meaning of the scaling exponent is interpreted as follows:

•

$\alpha <0.5$ —Long-range anticorrelated signal;

•

$\alpha =0.5$ —Uncorrelated signal;

•

$\alpha >0.5$ —Long-range correlated signal.

In this work, we applied DMA to the envelope (extracted using the Hilbert transform) of the 0-th-order IMF.

3. Results

A spectral analysis of the rotor oscillations made it possible to observe oscillations at the natural frequencies, which correspond to the rotation frequency, as well as at the higher harmonics, which are multiples of the oscillation frequency (Figure 5).

An example of the 0-th-order IMFs for X and Y and their corresponding log-log plots is given in Figure 6 for three rotation frequencies. Based on the empirical analysis of log-log plots, two different scale ranges were selected: from 0.5 to 1.1, and from 1.3 to 2.25, because in each of them, the log-log plot is linear, but with a different slope. Then, these two scaling ranges were used for the computation of the DMA scaling exponent, both for X and Y signals.

The plots in Figure 7 and Figure 8 show the relationship between the scaling exponents ($\alpha$) obtained from DMA and the frequency of rotation of a centrifuge, to describe the fractal characteristics of the motion of the rotor in two dimensions (X and Y). In the short scaling range (Figure 7) from 0.5 to 1.1, for the lower frequencies, the $\alpha$ values are rising, indicating that the fractal properties of the system are changing as the frequency increases. Both ${\alpha }_X$ and ${\alpha }_Y$ start below 1.5, implying a correlated behavior at the lowest frequencies. As the frequency increases, both ${\alpha }_X$ and ${\alpha }_Y$ cross into the non-stationary unbounded range (>1). Toward the higher end of this low-frequency range, the values of $\alpha$ seem to stabilize around the $\alpha$ = 2.0 mark, and demonstrate the synchronous changes for X and Y dimensions across all frequencies. A special mention of ${\alpha }_X$ close to 0.5 at 40 Hz suggests that the oscillations at this frequency demonstrate the white noise-like behavior.

For the long scaling range (Figure 8) from 1.3 to 2.25, the opposite behavior is evident. Here, the $\alpha$ values for ${\alpha }_X$ start well above 1, indicating a non-stationary, unbounded behavior at lower frequencies within this range. As the frequency increases, ${\alpha }_X$ decreases sharply, reaching a 0.5 value at 40 Hz, which again demonstrates the white noise behavior. After that deep dip, ${\alpha }_X$ and ${\alpha }_Y$ then show more non-stationary characteristics between 60 and 160 Hz. Then ${\alpha }_X$ keeps fluctuating around $\alpha$ = 1.0, which suggests the pink noise-like characteristics. ${\alpha }_Y$ drops below 1.0, so marking the shift in the fractal characteristics of the Y component seems to be correlated as the frequency increases. Only at 230 Hz do the Y oscillations show the non-stationary behavior again.

The differences between the two plots at various frequencies suggest that the fractal properties of the rotor’s motion in the X and Y directions are dependent on the frequency of a rotation and exhibit different behaviors at different scaling ranges. The fluctuations and trends in these plots could be due to a variety of physical phenomena in the rotor system, possibly including resonances, damping effects, and the intrinsic properties of the materials being used.

The resulting scaling exponents and fractal properties of oscillations are presented in

Table A1. Scaling exponents for the scaling range from 0.5 to 1.1.

Frequency, Hz	X, IMFO		Y, IMFO
	${\mathit{\alpha }}_{\mathit{X}}$	Property	${\mathit{\alpha }}_{\mathit{Y}}$	Property
10	0.59	Uncorrelated, white noise	1.29	Non-stationary, unbounded
20	0.89	1/f-noise, pink noise	1.29	Non-stationary, unbounded
40	1.54	Non-stationary, unbounded	2.45	Non-stationary, unbounded
60	2.06	Non-stationary, unbounded	1.92	Non-stationary, unbounded
80	2.28	Non-stationary, unbounded	2.44	Non-stationary, unbounded
100	2.54	Non-stationary, unbounded	2.46	Non-stationary, unbounded
120	2.02	Non-stationary, unbounded	2.03	Non-stationary, unbounded
140	1.8	Non-stationary, unbounded	1.66	Non-stationary, unbounded
160	1.72	Non-stationary, unbounded	1.84	Non-stationary, unbounded
180	1.78	Non-stationary, unbounded	1.85	Non-stationary, unbounded
200	1.68	Non-stationary, unbounded	1.74	Non-stationary, unbounded
215	1.88	Non-stationary, unbounded	1.75	Non-stationary, unbounded
230	2.16	Non-stationary, unbounded	2.18	Non-stationary, unbounded

and

Table A2. Scaling exponents for the scaling range from 1.3 to 2.25.

Frequency, Hz	X, IMFO		Y, IMFO
	${\mathit{\alpha }}_{\mathit{X}}$	Property	${\mathbf{\alpha }}_{\mathbf{Y}}$	Property
10	2.40	Non-stationary, unbounded	1.32	Non-stationary, unbounded
20	1.89	Non-stationary, unbounded	0.93	1/f-noise, pink noise
40	0.48	Uncorrelated, white noise	0.80	1/f-noise, pink noise
60	1.33	Non-stationary, unbounded	1.01	1/f-noise, pink noise
80	1.37	Non-stationary, unbounded	1.11	1/f-noise, pink noise
100	1.31	Non-stationary, unbounded	1.60	Non-stationary, unbounded
120	1.08	1/f-noise, pink noise	1.19	1/f-noise, pink noise
140	1.22	1/f-noise, pink noise	1.04	1/f-noise, pink noise
160	1.08	1/f-noise, pink noise	0.94	1/f-noise, pink noise
180	0.90	1/f-noise, pink noise	0.72	Correlated
200	1.17	1/f-noise, pink noise	0.64	Uncorrelated, white noise
215	0.97	1/f-noise, pink noise	0.69	Uncorrelated, white noise
230	1.14	1/f-noise, pink noise	1.05	1/f-noise, pink noise

, respectively, in Appendix A.

4. Discussion

In the results of this research, we applied the new approach of the 2D trajectory fractal analysis to the components of the centrifuge rotor vibrograms. This method demonstrated different noise oscillatory behaviors of the rotor depending on the rotation frequencies, non-stationary unbounded, 1/f pink noise, correlated, and uncorrelated. This analysis supported the traditional spectral analysis of the centrifuge vibrograms.

For the first time, fractal characteristics of the vibrograms demonstrated that the centrifuge has different fractality for different frequencies, which were computed. From the Campbell diagram (see Section 2.3), the following resonant frequencies are defined: 10, 11.6, 30.9, 38.2, and 207.4 Hz. As can be observed, fractal characteristics of the vibrogram are in some cases different for rotation frequencies close to the eigenfrequencies and far from them. In particular, an X-axis oscillation for 40 Hz is uncorrelated white noise, while oscillations for both 20 and 60 Hz demonstrate non-stationary properties. Y-axis oscillations for 200 and 215 Hz have white noise properties, while oscillations at a lower frequency (180 Hz) are correlated, and at a higher frequency (230 Hz) are pink noise.

Using the data obtained in the paper, as well as data provided from the papers [5,42], a new calculation model is used for analyzing the real design and dynamic behavior of the laboratory centrifuge on the example Pico 21 centrifuge with sufficient accuracy. Analytically, based on the use of kinetostatics methods and the use of the parameters of the proposed model, the influence of the gyroscopic effects on the natural frequencies of the centrifuge oscillations was obtained.

Also, when the centrifuge rotates at a higher frequency, we can observe the excitation of the second harmonics, along with the oscillation at the rotation frequency (see, e.g., Figure 5). This effect is found in other experiments [2,43], so our data confirms its presence in our data. The main cause of rotor vibration is the mass imbalance of the rotors. If the system has several rotating rotors, then each rotor excites its own vibration, which has several components, usually two or three. The frequencies of these components are multiples of the rotational frequency of the exciting rotor. The vibration spectrum (its amplitude-frequency composition) allows us to determine the sources and causes of increased vibration, as well as to identify vibrations for serviceable and faulty technical systems, that is, to solve diagnostic problems.

For the convenience of vibration identification, it is classified according to source nodes. So, they distinguish between rotary vibration, bearing vibration, etc. Classification by structural units allows us to directly connect the vibration with its source and creates the possibility of predicting the frequency structure of a vibration, taking into account their design and operation. In the future, it is planned to use the model and methods for determining dynamic characteristics to describe the behavior of other types of centrifuges and systems with rotating bodies at different speeds.

Also, it could be noted that the fractal properties of the vibrograms for X and Y coordinates are mostly different for the same frequencies. This could originate from the fact that the oscillations of the centrifuge during the rotation have different properties in different directions. This suggests the need to study the directional behavior of the oscillations, with the possibility to define the orientation of the prevailing oscillations. Recently, a new method of quantifying the directional fractal properties of the 2D trajectories was proposed [44], allowing for an analysis of oriented fractal scaling components in anisotropic oscillations. To understand whether the anisotropy of the fractal properties is present in the vibrogram and pave the way for further deeper investigation, the OFSCA method was applied to the 0-th-order IMFs of the vibrograms. In Figure 9, the underlying trajectories and the representation of the OFSCA results are given.

In OFSCA, the original 2D trajectory (Figure 9a), which is constructed from X and Y projections, is subject to the decomposition into a sum of two fluctuations. These fluctuations are extracted with the assumption that they could be rotated with respect to the original orthogonal X and Y axes, revealing the anisotropic (oriented) properties of the underlying trajectory. The OFSCA extracts the angles of the fluctuating components (angles of the dotted lines in Figure 9b,c) from the requirements that two components have different scaling exponent values (marked in Figure 9d). These components constitute the alternative representation of the original 2D trajectory (Figure 9e), constructed from components with different fractality and specific angles. The fractal characteristics of the extracted components are analyzed with DMA, and scaling exponents are extracted from the slope of the linear part of the log-log plot (Figure 9f). The oriented components exhibit fractal scaling patterns in oscillating systems that are anisotropic, meaning that they vary depending on the direction of measurement. This may uncover identifying and quantifying fractal-scaling properties in the centrifuge oscillations and analyze how they are affected by the anisotropic properties of the system.

Regarding the limitations of the study, they are twofold. First, we were limited by the experimental design and did not study a broader range of rotation frequencies with higher granularity. We used only a small laboratory centrifuge to demonstrate the applicability of the proposed approach of studying fractal properties. For other types of centrifuges, the other rotation frequencies should be selected, which correspond to the practical applications. In the future, a more detailed study is required to understand the relationship between operating frequencies of rotation, eigenfrequencies, and the frequencies at which the DMA-based fractal characteristics should be measured. Second, from Figure 7 and Figure 8, it is clear that the dependency of the scaling exponents is different for the lower and higher scaling ranges. In the current study, these scaling ranges were empirically optimized to reveal different fractal properties of the rotation. The selection of these ranges for different centrifuges should be formalized depending on the construction and operation of the centrifuge, which is also a subject of future studies.

The results of this study can be used to identify fractal characteristics of vibrations in serviceable and faulty technical systems, solve diagnostic problems, and predict the frequency structure of the vibration. Fractal characteristics of high-speed rotating centrifuges can support the design of new approaches in modeling centrifuge vibrations, taking into account both technological and operational imbalances, as well as fault diagnosis. This will improve health monitoring and quality control policies for centrifuges.

5. Conclusions

The results of the research demonstrate that the new approach of the 2D trajectory fractal analysis applied to the components of the centrifuge rotor vibrograms allows for a better understanding of the noise oscillatory behavior of the rotor. The fractal analysis provides additional information on the traditional spectral analysis of the centrifuge vibrograms. The study also reveals that the centrifuge has different fractality for different frequencies, and the anisotropy of the fractal properties may be present in the vibrogram. This suggests the need to study the directional behavior of the oscillations in future investigations. The new calculation model was used for analyzing the real design and dynamic behavior of the laboratory centrifuge on the example Pico 21 centrifuge with sufficient accuracy. These findings provide valuable insights into the behavior of laboratory centrifuges and could pave the way for future studies on other types of centrifuges and systems with rotating bodies at different speeds.