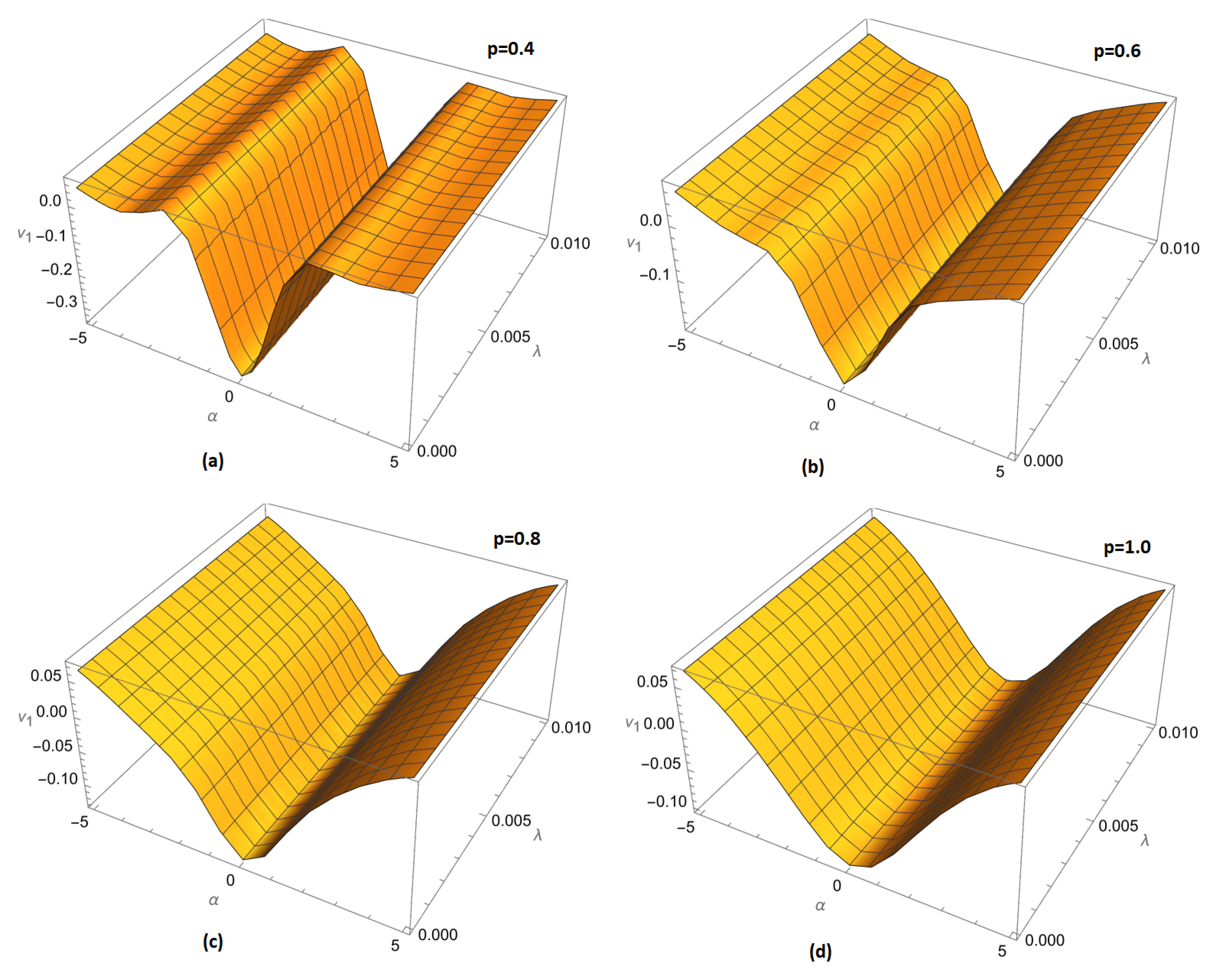
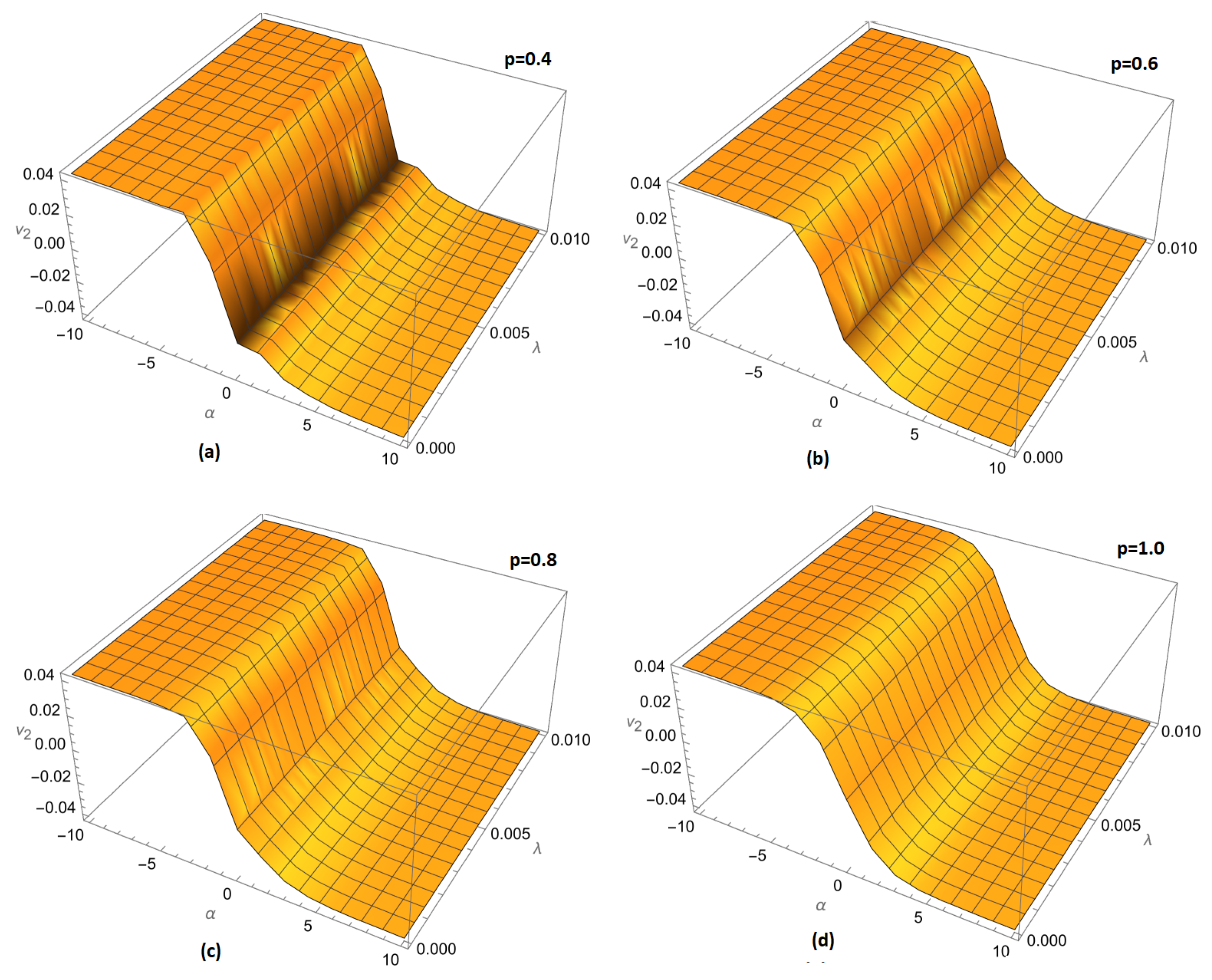
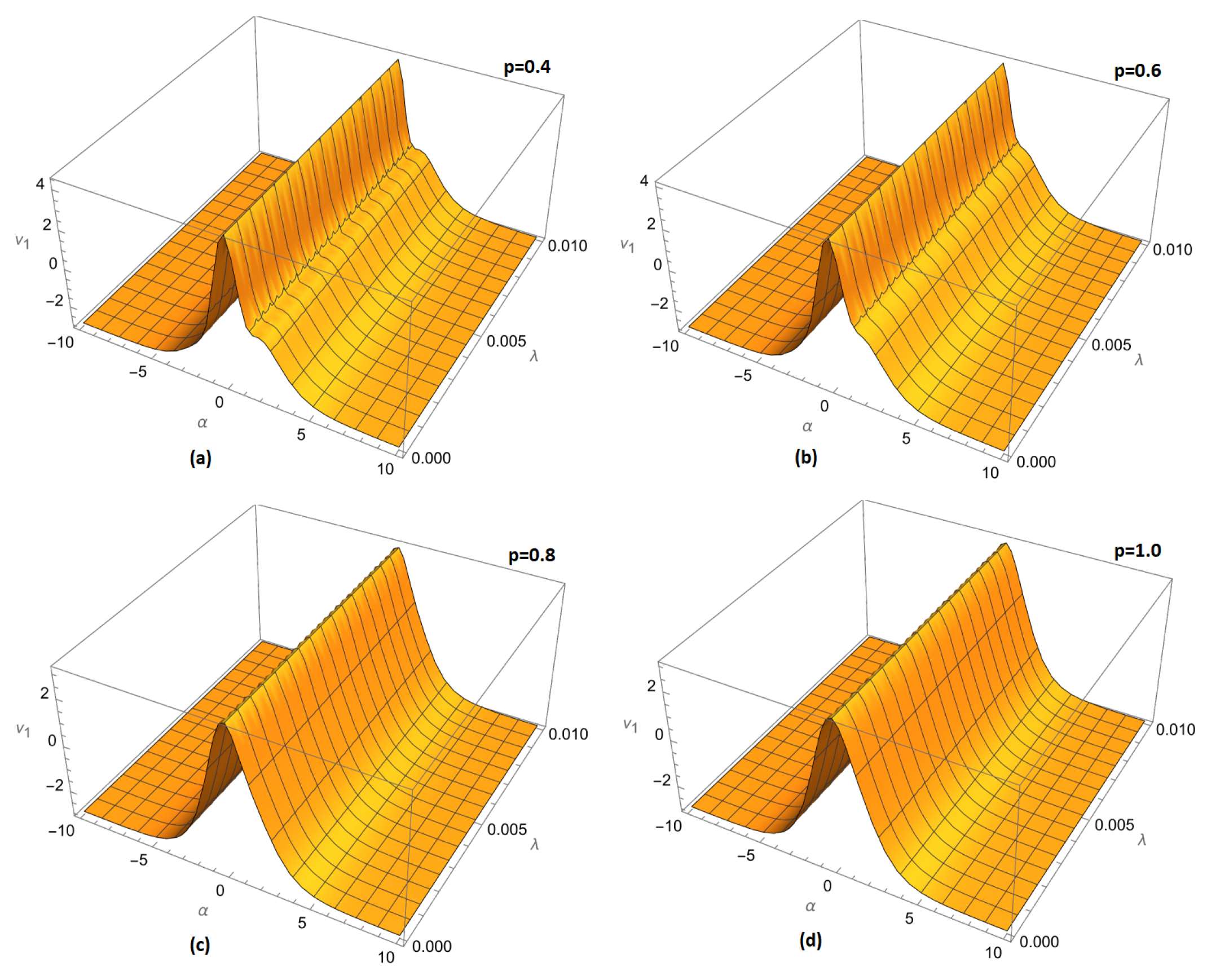
Figure 1.
Variation of fractional order (a) , (b) , (c) and (d) for of example 1 ARPSM solution for .
Figure 1.
Variation of fractional order (a) , (b) , (c) and (d) for of example 1 ARPSM solution for .
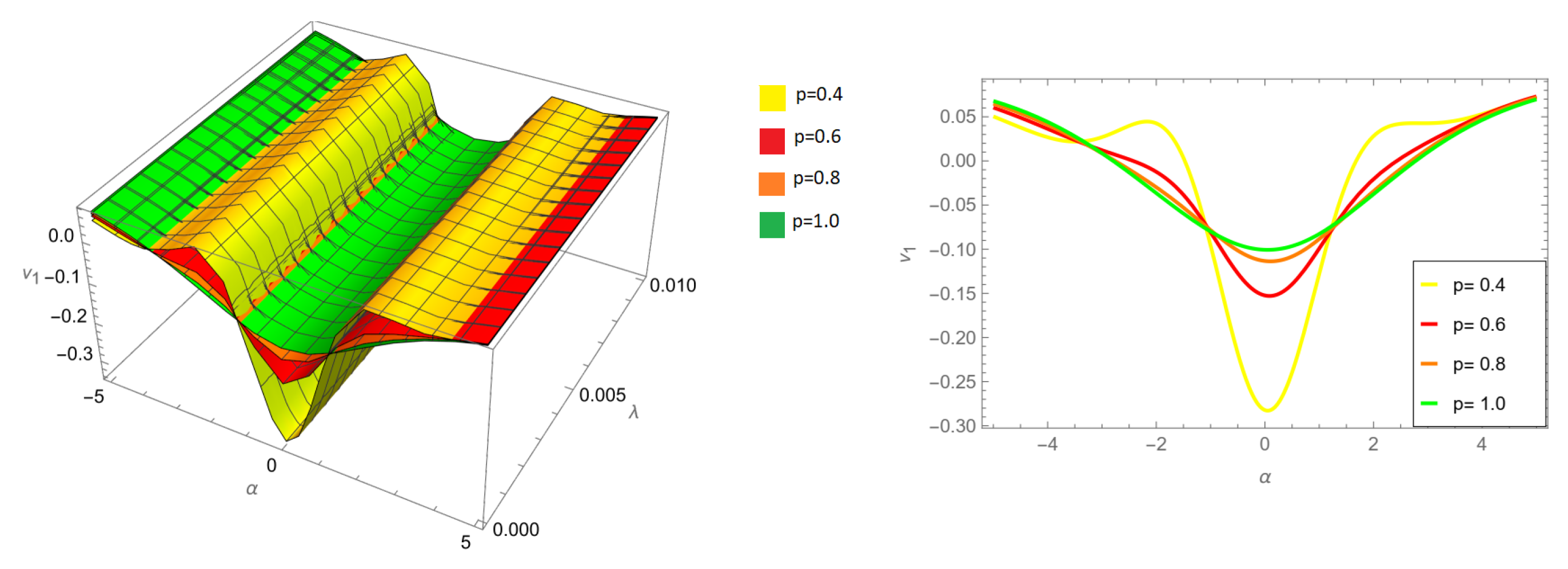
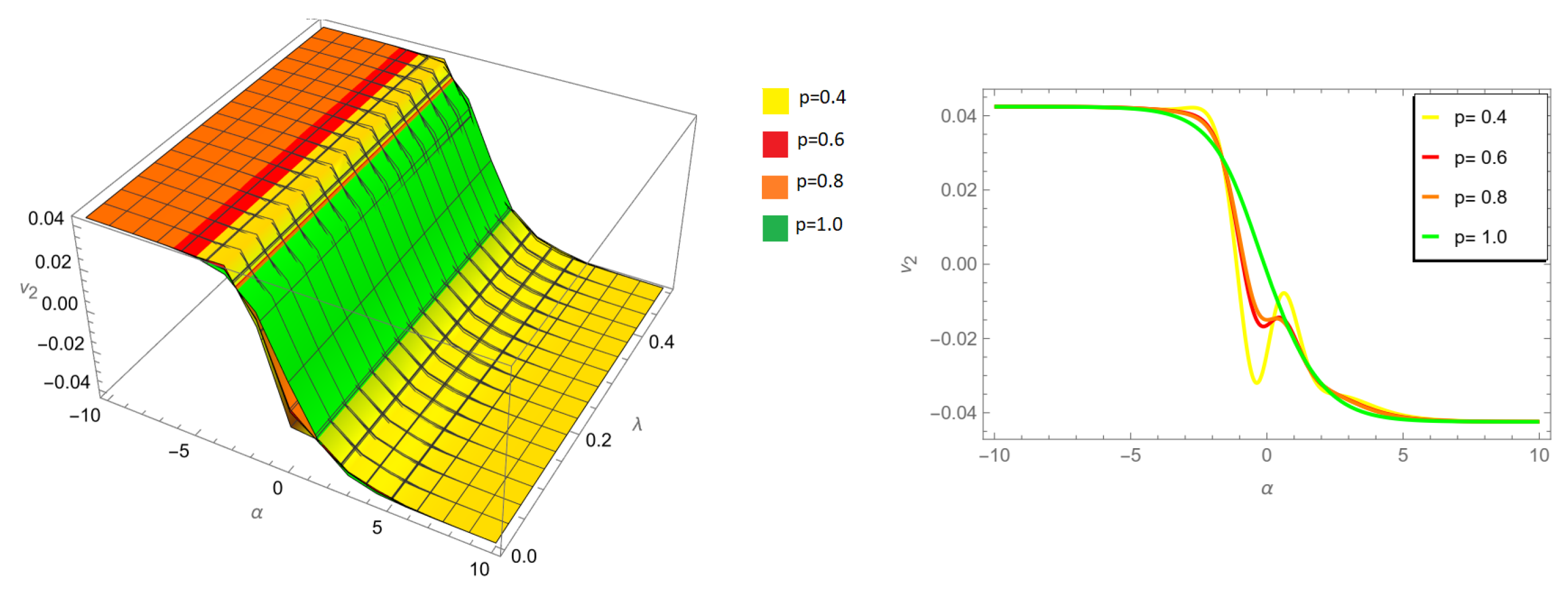
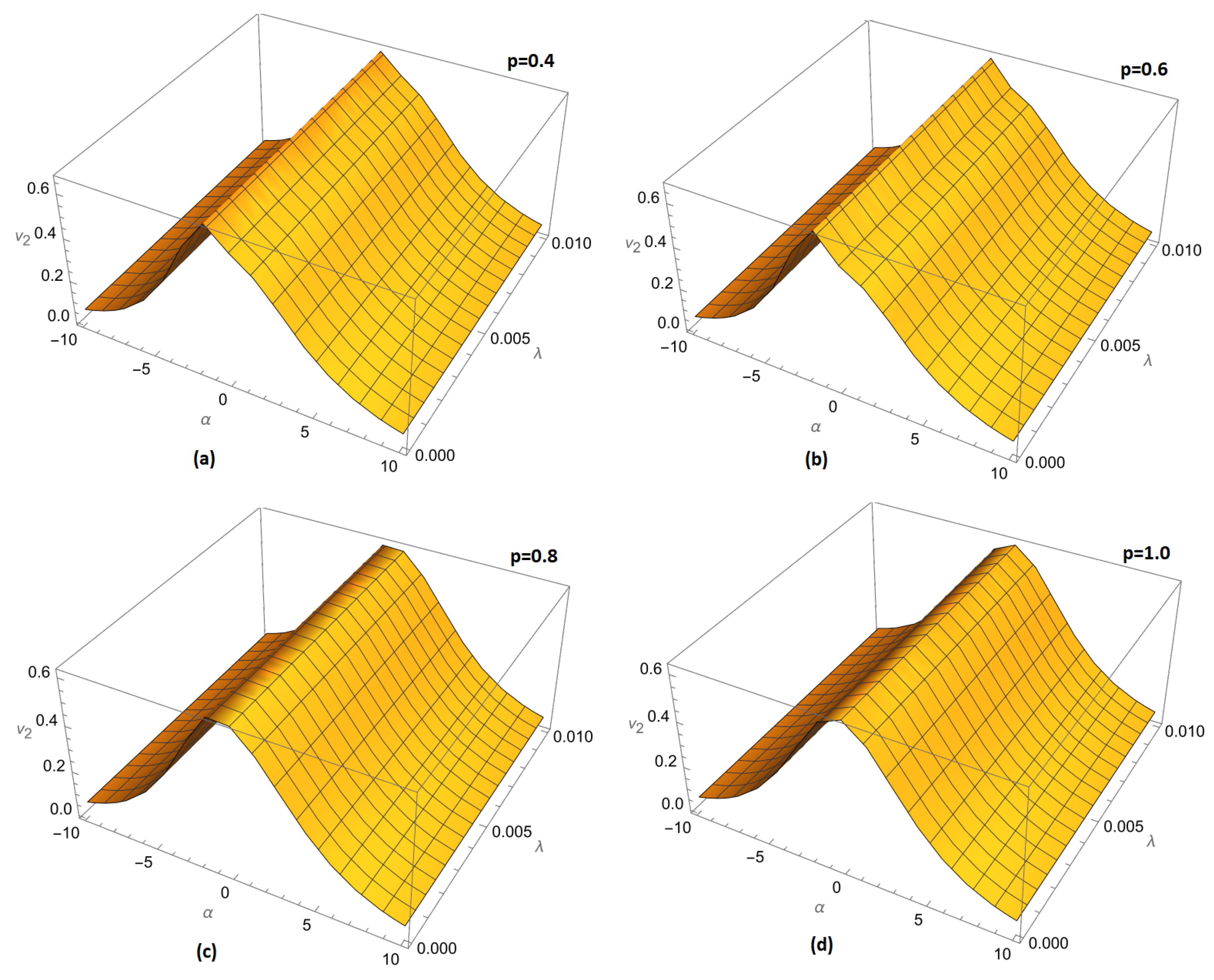
Figure 2.
Three-dimensional and two-dimensional comparison of different fractional orders p for of example 1 ARPSM solution for .
Figure 2.
Three-dimensional and two-dimensional comparison of different fractional orders p for of example 1 ARPSM solution for .
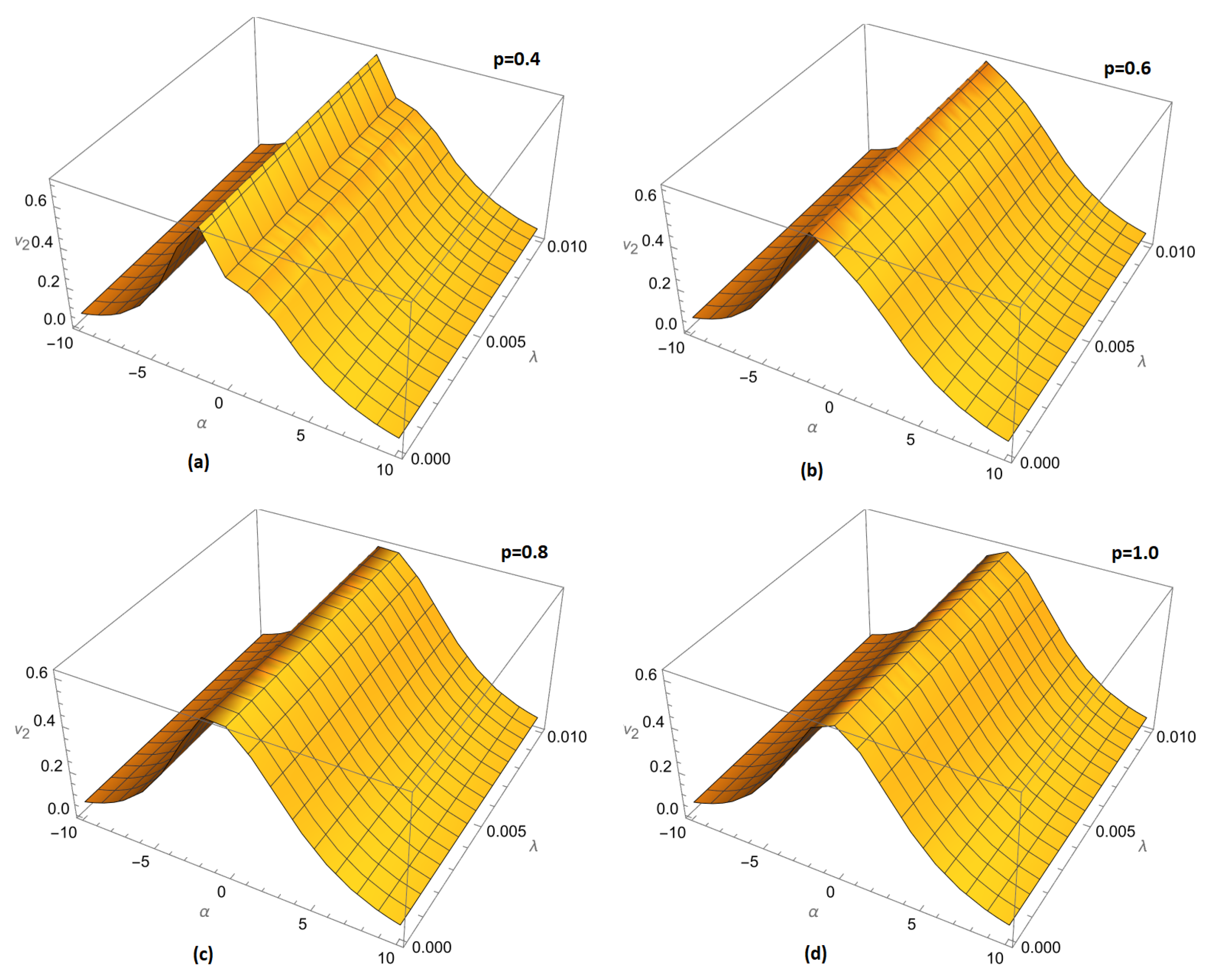
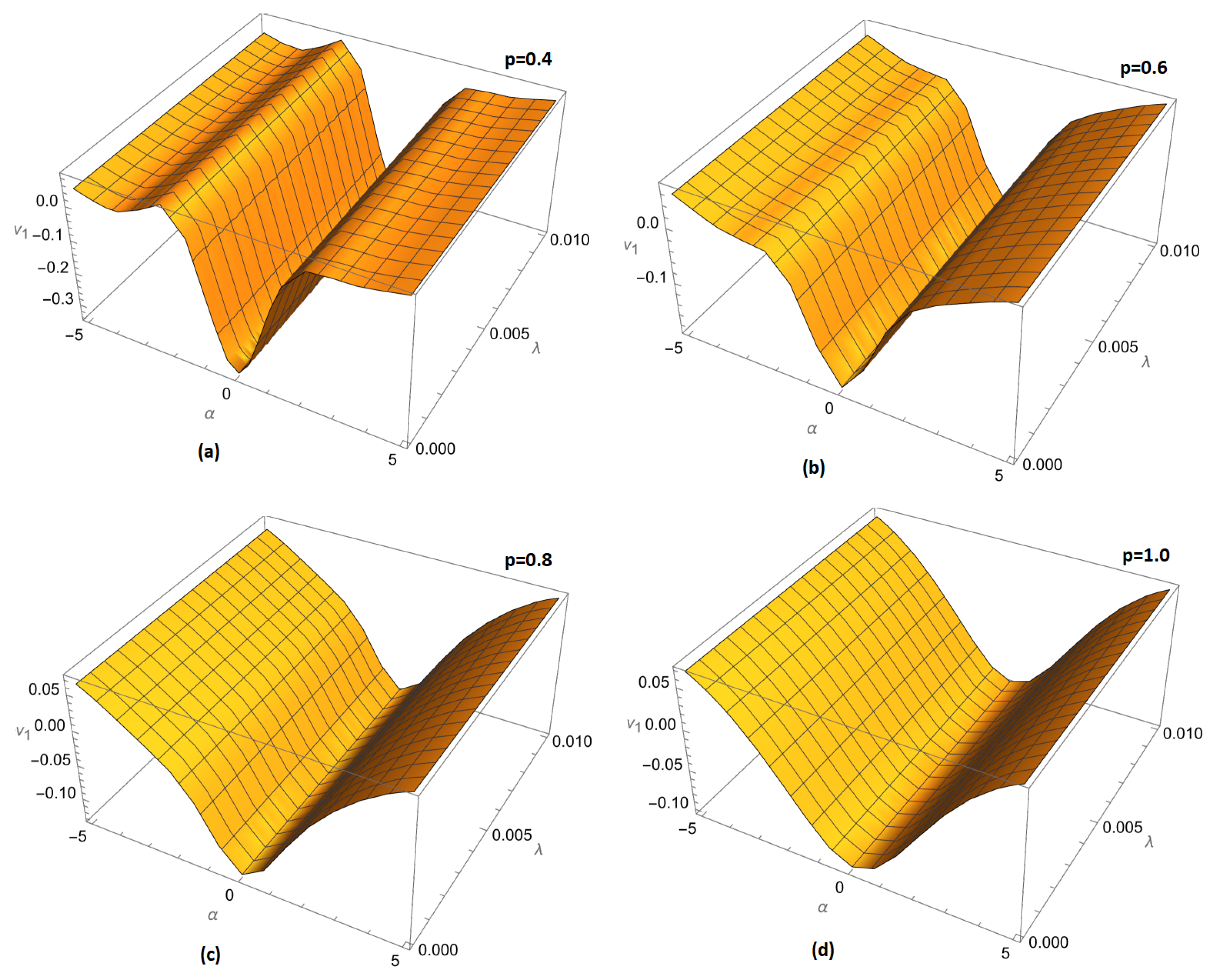
Figure 3.
Variation of fractional order (a) , (b) , (c) and (d) for of example 1 ARPSM solution for for .
Figure 3.
Variation of fractional order (a) , (b) , (c) and (d) for of example 1 ARPSM solution for for .
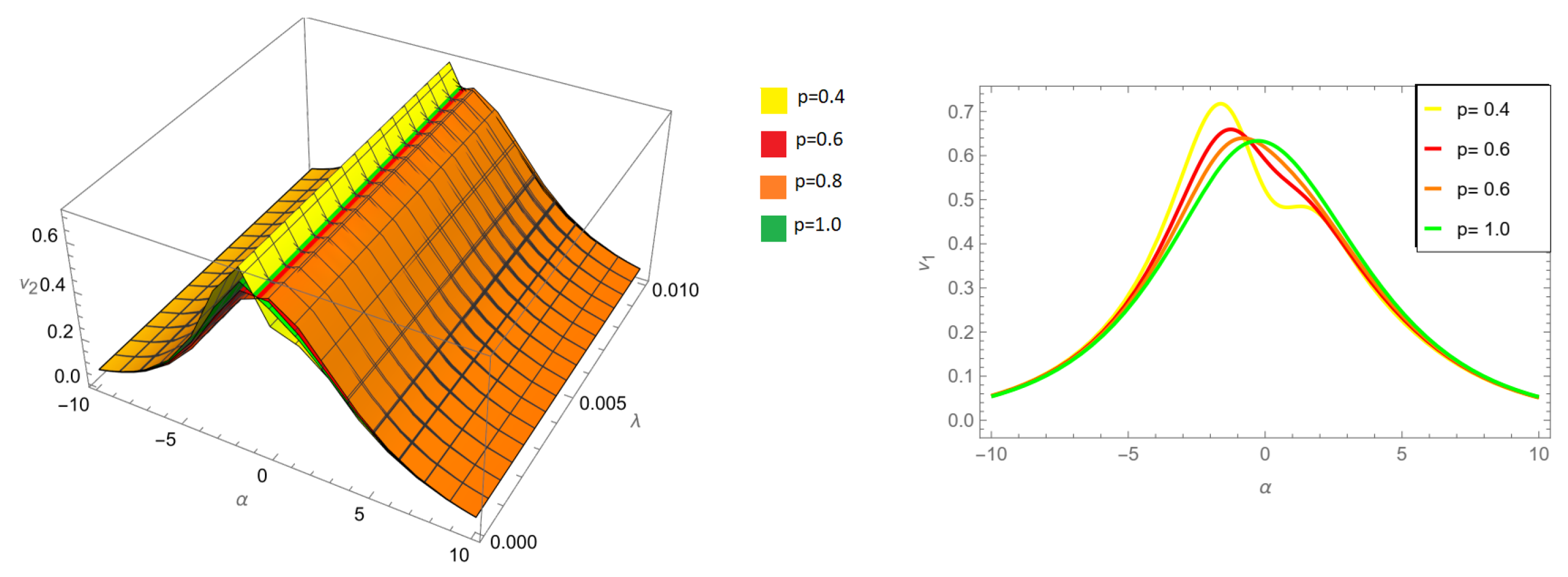
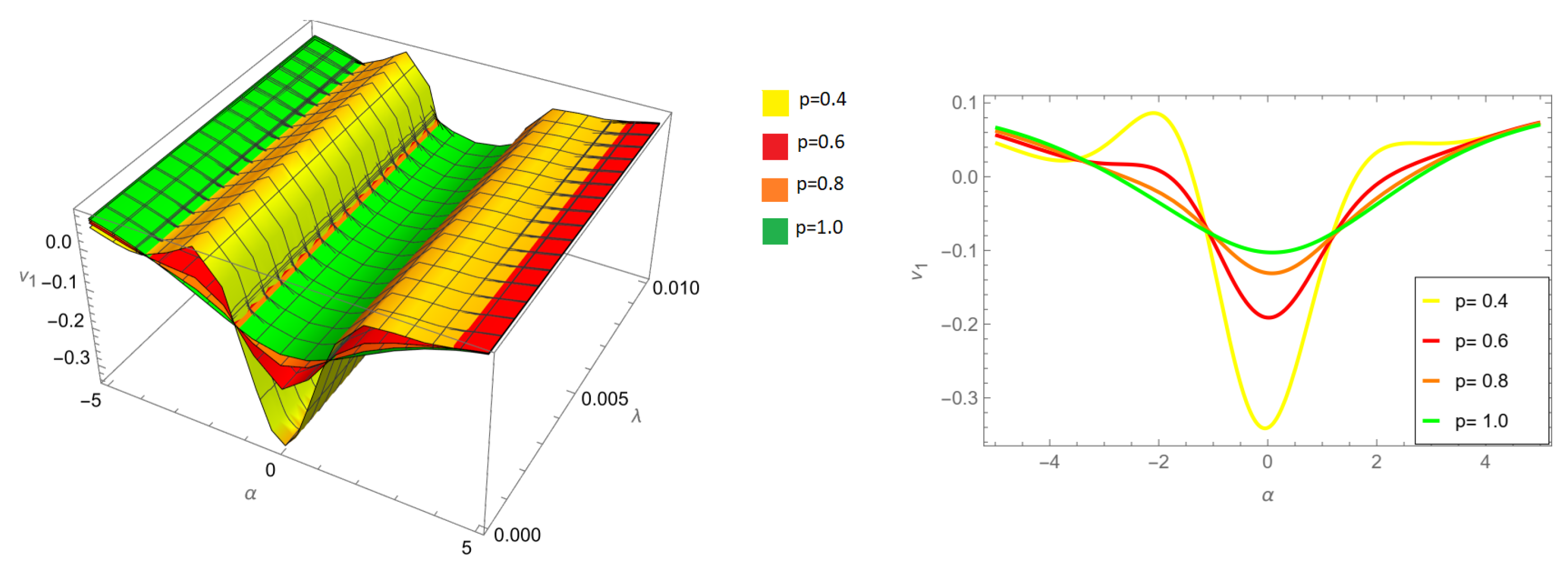
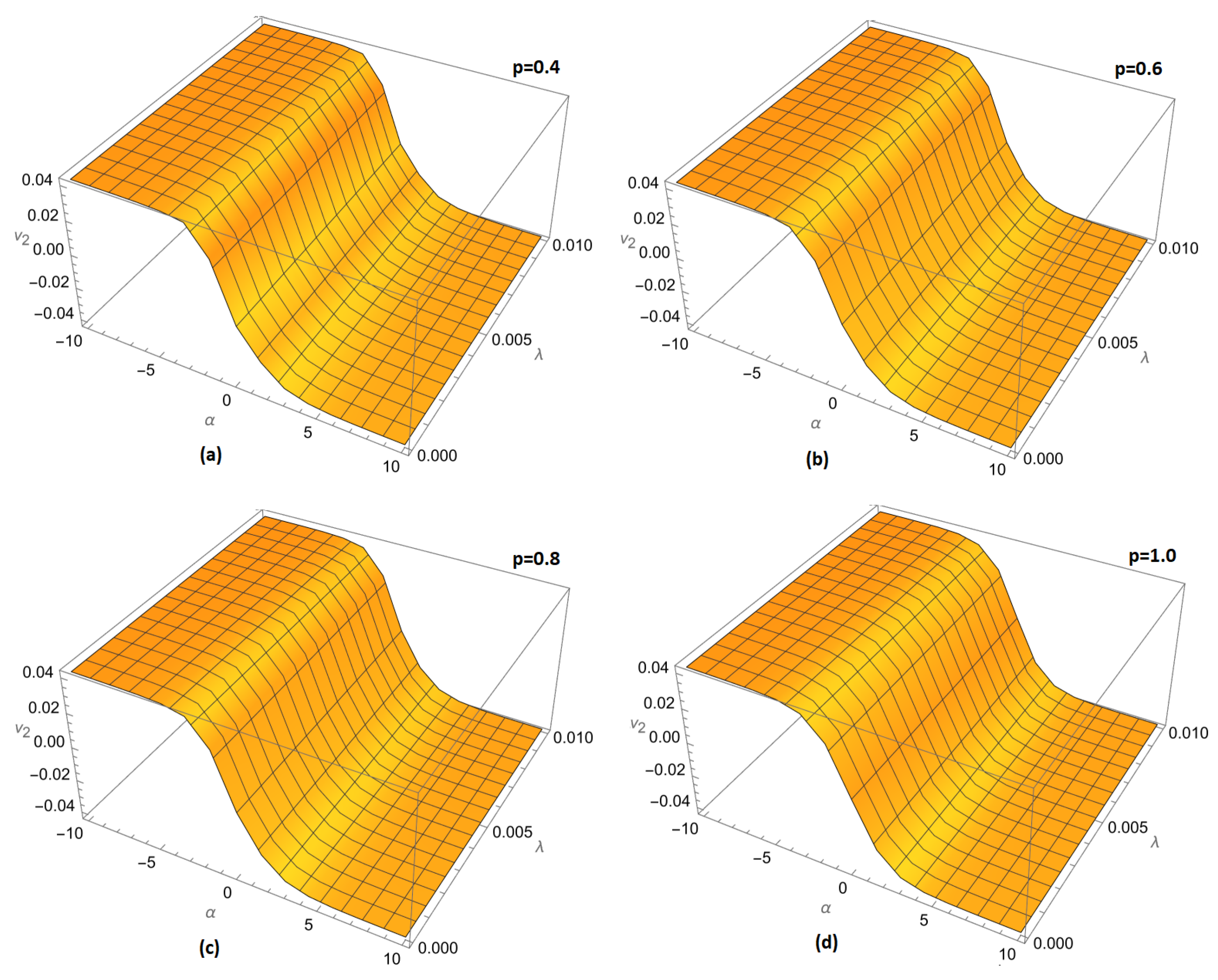
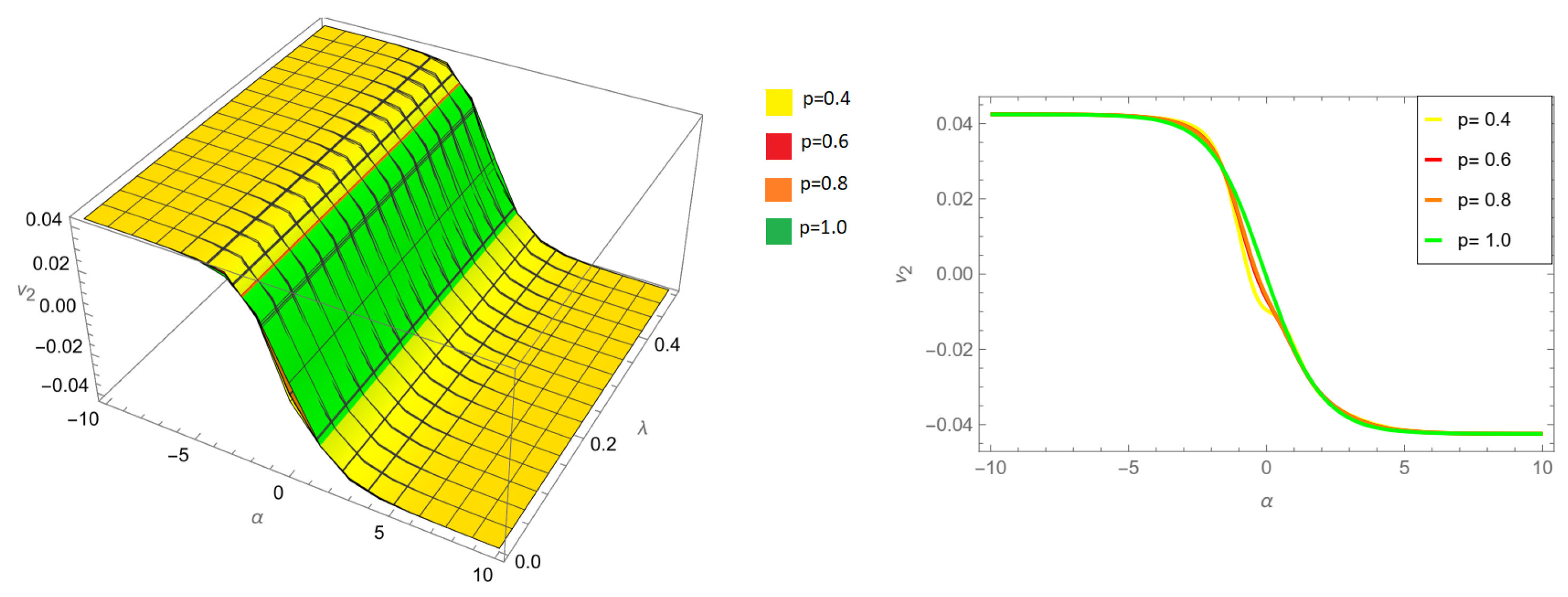
Figure 4.
Three-dimensional and two-dimension comparison of different fractional orders p for of example 1 ARPSM solution for .
Figure 4.
Three-dimensional and two-dimension comparison of different fractional orders p for of example 1 ARPSM solution for .
Figure 5.
Variation of fractional order (a) , (b) , (c) and (d) for of example 2 ARPSM solution for for .
Figure 5.
Variation of fractional order (a) , (b) , (c) and (d) for of example 2 ARPSM solution for for .
Figure 6.
Three-dimensional and two-dimensional comparison of different fractional orders p for of example 2 ARPSM solution for .
Figure 6.
Three-dimensional and two-dimensional comparison of different fractional orders p for of example 2 ARPSM solution for .
Figure 7.
Variation of fractional order (a) , (b) , (c) and (d) for of example 2 ARPSM solution for for .
Figure 7.
Variation of fractional order (a) , (b) , (c) and (d) for of example 2 ARPSM solution for for .
Figure 8.
Three-dimensional and two-dimensional comparison of different fractional orders p for of example 2 ARPSM solution for .
Figure 8.
Three-dimensional and two-dimensional comparison of different fractional orders p for of example 2 ARPSM solution for .
Figure 9.
Variation of fractional order (a) , (b) , (c) and (d) for of example 1 NITM solution for .
Figure 9.
Variation of fractional order (a) , (b) , (c) and (d) for of example 1 NITM solution for .
Figure 10.
Three-dimensional and two-dimensional comparison of different fractional order p for of example 1 NITM solution for .
Figure 10.
Three-dimensional and two-dimensional comparison of different fractional order p for of example 1 NITM solution for .
Figure 11.
Variation of fractional order (a) , (b) , (c) and (d) for of example 1 NITM solution for .
Figure 11.
Variation of fractional order (a) , (b) , (c) and (d) for of example 1 NITM solution for .
Figure 12.
Three-dimensional and two-dimensional comparison of different fractional order p for of example 1 NITM solution for .
Figure 12.
Three-dimensional and two-dimensional comparison of different fractional order p for of example 1 NITM solution for .
Figure 13.
Variation of fractional order (a) , (b) , (c) and (d) for of example 2 NITM solution for .
Figure 13.
Variation of fractional order (a) , (b) , (c) and (d) for of example 2 NITM solution for .
Figure 14.
Three-dimensional and two-dimensional comparison of different fractional order p for of example 2 NITM solution for .
Figure 14.
Three-dimensional and two-dimensional comparison of different fractional order p for of example 2 NITM solution for .
Figure 15.
Variation of fractional order (a) , (b) , (c) and (d) for of example 2 NITM solution for .
Figure 15.
Variation of fractional order (a) , (b) , (c) and (d) for of example 2 NITM solution for .
Figure 16.
Three-dimensional and two-dimensional comparison of different fractional order p for of example 2 NITM solution for .
Figure 16.
Three-dimensional and two-dimensional comparison of different fractional order p for of example 2 NITM solution for .
Table 1.
The comparison of different fractional orders of ARPSM solution of example 1 of for .
Table 1.
The comparison of different fractional orders of ARPSM solution of example 1 of for .
| | | | | | | |
|---|
| 0 | −0.0523823 | −0.0501432 | −0.0500004 | −0.05 | 0.00238228 | 0.000143191 | 4.18800 × |
| 0.1 | −0.052455 | −0.0501279 | −0.0499529 | −0.0499499 | 0.00250508 | 0.00017795 | 3.01163 × |
| 0.2 | −0.052399 | −0.0500107 | −0.0498056 | −0.0498001 | 0.00259898 | 0.000210666 | 5.57137 × |
| 0.3 | −0.0522144 | −0.049792 | −0.0495591 | −0.049551 | 0.00266333 | 0.000241 | 8.07032 × |
| 0.4 | −0.0519019 | −0.0494725 | −0.0492143 | −0.0492039 | 0.00269803 | 0.000268656 | 1.04818 × |
| 0.5 | −0.0514634 | −0.0490532 | −0.0487726 | −0.0487599 | 0.00270358 | 0.000293385 | 1.27803 × |
| 0.6 | −0.0509018 | −0.0485358 | −0.0482357 | −0.0482208 | 0.002681 | 0.000314992 | 1.49424 × |
| 0.7 | −0.0502206 | −0.0479221 | −0.0476057 | −0.0475888 | 0.00263177 | 0.000333328 | 1.69466 × |
| 0.8 | −0.0494241 | −0.0472146 | −0.0468851 | −0.0468663 | 0.00255781 | 0.000348297 | 1.87738 × |
| 0.9 | −0.0485174 | −0.0464159 | −0.0460764 | −0.046056 | 0.0024614 | 0.000359853 | 2.04074 × |
| 1 | −0.0475062 | −0.0455291 | −0.045183 | −0.0451611 | 0.00234507 | 0.000367995 | 2.18338 × |
Table 2.
The comparison of different fractional orders of ARPSM solution of example 1 of for .
Table 2.
The comparison of different fractional orders of ARPSM solution of example 1 of for .
| | | | | | | |
|---|
| 0 | 0.445671 | 0.447209 | 0.447213 | 0.447214 | 0.00154242 | 0.000049447 | 2.71011 × |
| 0.1 | 0.444773 | 0.447045 | 0.447087 | 0.447102 | 0.00232883 | 0.0000562121 | 1.45678 × |
| 0.2 | 0.443671 | 0.446659 | 0.446738 | 0.446766 | 0.00309533 | 0.000107159 | 2.8786 × |
| 0.3 | 0.44237 | 0.446051 | 0.446166 | 0.446209 | 0.00383819 | 0.000157518 | 4.28507 × |
| 0.4 | 0.440876 | 0.445223 | 0.445373 | 0.44543 | 0.004554 | 0.000207031 | 5.66885 × |
| 0.5 | 0.439192 | 0.444176 | 0.444362 | 0.444432 | 0.00523973 | 0.000255447 | 7.02288 × |
| 0.6 | 0.437325 | 0.442915 | 0.443134 | 0.443217 | 0.00589272 | 0.000302527 | 8.34037 × |
| 0.7 | 0.435278 | 0.441441 | 0.441693 | 0.441789 | 0.00651072 | 0.000348047 | 9.61496 × |
| 0.8 | 0.433059 | 0.439759 | 0.440042 | 0.440151 | 0.00709186 | 0.000391798 | 1.08407 × |
| 0.9 | 0.430671 | 0.437872 | 0.438186 | 0.438306 | 0.00763469 | 0.000433591 | 1.20121 × |
| 1 | 0.428121 | 0.435786 | 0.436128 | 0.436259 | 0.00813811 | 0.000473254 | 1.31244 × |
Table 3.
The comparison of different fractional orders of ARPSM solution of example 2 of for .
Table 3.
The comparison of different fractional orders of ARPSM solution of example 2 of for .
| | | | | | | |
|---|
| −0.5 | 2.64509 | 2.64084 | 2.6402 | 2.6401 | 0.00498289 | 0.000740352 | 9.74069 × |
| −0.4 | 2.77074 | 2.76693 | 2.76636 | 2.76627 | 0.00446789 | 0.000659444 | 8.7449 × |
| −0.3 | 2.87068 | 2.86755 | 2.86708 | 2.86701 | 0.00367436 | 0.000536885 | 7.15344 × |
| −0.2 | 2.94305 | 2.94078 | 2.94045 | 2.9404 | 0.00264689 | 0.000379776 | 5.06799 × |
| −0.1 | 2.98648 | 2.98523 | 2.98505 | 2.98503 | 0.00144809 | 0.000197893 | 2.62897 × |
| 0.1 | 2.98387 | 2.98483 | 2.985 | 2.98502 | 0.00115043 | 0.00019213 | 2.61859 × |
| 0.2 | 2.93801 | 2.94002 | 2.94034 | 2.94039 | 0.00238083 | 0.000374625 | 5.05872 × |
| 0.3 | 2.86353 | 2.86646 | 2.86692 | 2.86699 | 0.00345764 | 0.000532689 | 7.14588 × |
| 0.4 | 2.76193 | 2.76559 | 2.76616 | 2.76625 | 0.00431374 | 0.00065646 | 8.73951 × |
| 0.5 | 2.63518 | 2.63934 | 2.63998 | 2.64008 | 0.00489907 | 0.000738729 | 9.73776 × |
Table 4.
The comparison of different fractional orders of ARPSM solution of example 2 of for .
Table 4.
The comparison of different fractional orders of ARPSM solution of example 2 of for .
| | | | | | | |
|---|
| 1 | −0.199922 | −0.196678 | −0.196152 | −0.196061 | 0.00386074 | 0.000617078 | 9.02631 × |
| 1.1 | −0.215516 | −0.212859 | −0.212428 | −0.212354 | 0.0031612 | 0.000505073 | 7.36884 × |
| 1.2 | −0.230353 | −0.228251 | −0.22791 | −0.227852 | 0.00250073 | 0.000398811 | 5.79595 × |
| 1.3 | −0.244428 | −0.24284 | −0.242584 | −0.24254 | 0.00188798 | 0.000299995 | 4.3334 × |
| 1.4 | −0.257742 | −0.256623 | −0.256443 | −0.256413 | 0.00132905 | 0.000209845 | 2.9997 × |
| 1.5 | −0.2703 | −0.269601 | −0.26949 | −0.269472 | 0.000827636 | 0.000129125 | 1.80645 × |
| 1.6 | −0.282113 | −0.281786 | −0.281736 | −0.281728 | 0.000385347 | 0.0000581901 | 7.590282 × |
| 1.7 | −0.293199 | −0.293194 | −0.293196 | −0.293197 | 5.992109 × | 2.955875 × | 1.424832 × |
| 1.8 | −0.303576 | −0.303846 | −0.303891 | −0.3039 | 0.000324097 | 5.45956 × | 9.023568 × |
| 1.9 | −0.313269 | −0.313767 | −0.313849 | −0.313864 | 0.000595754 | 9.72328 × | 1.5282 × |
| 2 | −0.322301 | −0.322986 | −0.323098 | −0.323118 | 0.00081668 | 0.00013153 | 2.03 × |
Table 5.
The comparison of different fractional orders of NITM solution of example 1 of for .
Table 5.
The comparison of different fractional orders of NITM solution of example 1 of for .
| | | | | | | |
|---|
| 0 | −0.0591648 | −0.0500335 | −0.05 | −0.05 | 0.00916479 | 0.0000335001 | 1.680000 × |
| 0.1 | −0.059281 | −0.0500011 | −0.0499505 | −0.0499499 | 0.00933107 | 0.0000512042 | 6.157033 × |
| 0.2 | −0.0591906 | −0.0498684 | −0.0498013 | −0.0498001 | 0.00939052 | 0.0000683243 | 1.208437 × |
| 0.3 | −0.0588959 | −0.0496357 | −0.0495528 | −0.049551 | 0.00934484 | 0.0000846762 | 1.789121 × |
| 0.4 | −0.0584016 | −0.0493039 | −0.0492062 | −0.0492039 | 0.00919779 | 0.00010009 | 2.352063 × |
| 0.5 | −0.0577148 | −0.0488743 | −0.0487627 | −0.0487599 | 0.00895499 | 0.00011441 | 2.891837 × |
| 0.6 | −0.0568445 | −0.0483483 | −0.0482242 | −0.0482208 | 0.0086237 | 0.000127501 | 3.403370 × |
| 0.7 | −0.0558014 | −0.047728 | −0.0475927 | −0.0475888 | 0.00821261 | 0.000139246 | 3.882007 × |
| 0.8 | −0.0545978 | −0.0470158 | −0.0468706 | −0.0468663 | 0.00773151 | 0.000149549 | 4.323579 × |
| 0.9 | −0.0532471 | −0.0462144 | −0.0460608 | −0.046056 | 0.00719103 | 0.000158334 | 4.724447 × |
| 1 | −0.0517634 | −0.0453267 | −0.0451662 | −0.0451611 | 0.00660231 | 0.000165549 | 5.081553 × |
Table 6.
The comparison of different fractional orders of NITM solution of example 1 of for .
Table 6.
The comparison of different fractional orders of NITM solution of example 1 of for .
| | | | | | | |
|---|
| 0 | 0.44128 | 0.447192 | 0.447214 | 0.447214 | 0.00593382 | 0.0000216897 | 3.354094 × |
| 0.1 | 0.439701 | 0.446977 | 0.447102 | 0.447102 | 0.00740105 | 0.000124982 | 6.691626 × |
| 0.2 | 0.437966 | 0.446539 | 0.446766 | 0.446766 | 0.00880056 | 0.000227508 | 1.328656 × |
| 0.3 | 0.436082 | 0.44588 | 0.446208 | 0.446209 | 0.0101265 | 0.000328737 | 1.968883 × |
| 0.4 | 0.434055 | 0.445002 | 0.44543 | 0.44543 | 0.0113743 | 0.000428148 | 2.580538 × |
| 0.5 | 0.431892 | 0.443907 | 0.444432 | 0.444432 | 0.0125402 | 0.000525246 | 3.154696 × |
| 0.6 | 0.429596 | 0.442598 | 0.443217 | 0.443217 | 0.0136218 | 0.000619558 | 3.682926 × |
| 0.7 | 0.427172 | 0.441078 | 0.441789 | 0.441789 | 0.0146174 | 0.000710642 | 4.157401 × |
| 0.8 | 0.424624 | 0.439353 | 0.44015 | 0.440151 | 0.0155266 | 0.000798088 | 4.570989 × |
| 0.9 | 0.421956 | 0.437424 | 0.438305 | 0.438306 | 0.0163496 | 0.000881527 | 4.917337 × |
| 1 | 0.419172 | 0.435299 | 0.436259 | 0.436259 | 0.0170875 | 0.000960626 | 5.190937 × |
Table 7.
The comparison of different fractional orders of NITM solution of example 2 of for .
Table 7.
The comparison of different fractional orders of NITM solution of example 2 of for .
| | | | | | | |
|---|
| −0.5 | 2.64134 | 2.64021 | 2.6401 | 2.6401 | 0.00123342 | 0.000105605 | 2.692781 × |
| −0.4 | 2.76737 | 2.76636 | 2.76627 | 2.76627 | 0.00109926 | 0.0000947386 | 1.500451 × |
| −0.3 | 2.8679 | 2.86709 | 2.86701 | 2.86701 | 0.000896034 | 0.0000774602 | 7.113980 × |
| −0.2 | 2.94104 | 2.94046 | 2.9404 | 2.9404 | 0.000635413 | 0.0000548648 | 2.646464 × |
| −0.1 | 2.98536 | 2.98506 | 2.98503 | 2.98503 | 0.000333511 | 0.0000284636 | 6.657231 × |
| 0.1 | 2.98471 | 2.98499 | 2.98502 | 2.98502 | 0.000314729 | 0.0000283185 | 6.790399 × |
| 0.2 | 2.93977 | 2.94034 | 2.94039 | 2.94039 | 0.000618625 | 0.0000547351 | 2.658594 × |
| 0.3 | 2.86611 | 2.86691 | 2.86699 | 2.86699 | 0.00088236 | 0.0000773546 | 7.124251 × |
| 0.4 | 2.76516 | 2.76615 | 2.76625 | 2.76625 | 0.00108954 | 0.0000946634 | 1.501242 × |
| 0.5 | 2.63885 | 2.63997 | 2.64008 | 2.64008 | 0.00122813 | 0.000105564 | 2.693303 × |
Table 8.
The comparison of different fractional orders of NITM solution of example 2 of for .
Table 8.
The comparison of different fractional orders of NITM solution of example 2 of for .
| | | | | | | |
|---|
| 1 | −0.197541 | −0.196293 | −0.196063 | −0.196061 | 0.00147921 | 0.000231952 | 1.798267 × |
| 1.1 | −0.213538 | −0.21254 | −0.212356 | −0.212354 | 0.00118324 | 0.000185393 | 1.184791 × |
| 1.2 | −0.228756 | −0.227994 | −0.227853 | −0.227852 | 0.000904042 | 0.00014133 | 6.100023 × |
| 1.3 | −0.243186 | −0.242641 | −0.242541 | −0.24254 | 0.000645635 | 0.000100483 | 8.379734 × |
| 1.4 | −0.256824 | −0.256476 | −0.256412 | −0.256413 | 0.000410844 | 0.000063362 | 3.869535 × |
| 1.5 | −0.269674 | −0.269502 | −0.269471 | −0.269472 | 0.000201381 | 0.000030285 | 7.982325 × |
| 1.6 | −0.281746 | −0.28173 | −0.281727 | −0.281728 | 0.000017965 | 0.000013933 | 1.148569 × |
| 1.7 | −0.293058 | −0.293174 | −0.293196 | −0.293197 | 0.000139526 | 0.000023324 | 1.438657 × |
| 1.8 | −0.303629 | −0.303856 | −0.303899 | −0.3039 | 0.000271908 | 0.000043998 | 1.670929 × |
| 1.9 | −0.313484 | −0.313803 | −0.313862 | −0.313864 | 0.000380528 | 0.000060854 | 1.849134 × |
| 2 | −0.322651 | −0.323044 | −0.323116 | −0.323118 | 0.000467126 | 0.000074184 | 1.977937 × |
Table 9.
The comparison of absolute error for of ARPSM and NITM solution of example 1 for .
Table 9.
The comparison of absolute error for of ARPSM and NITM solution of example 1 for .
| Exact | | | ARPSM Error | NITM Error |
|---|
| 0 | −0.05 | −0.0500004 | −0.05 | 4.187999 × | 1.680000 × |
| 0.1 | −0.0499499 | −0.0499529 | −0.0499505 | 3.01163 × | 6.157033 × |
| 0.2 | −0.0498001 | −0.0498056 | −0.0498013 | 5.57137 × | 1.208437 × |
| 0.3 | −0.049551 | −0.0495591 | −0.0495528 | 8.07032 × | 1.789121 × |
| 0.4 | -0.0492039 | -0.0492143 | −0.0492062 | 1.04818 × | 2.352063 × |
| 0.5 | −0.0487599 | -0.0487726 | −0.0487627 | 1.27803 × | 2.891837 × |
| 0.6 | −0.0482208 | -0.0482357 | −0.0482242 | 1.49424 × | 3.403370 × |
| 0.7 | −0.0475888 | -0.0476057 | −0.0475927 | 1.69466 × | 3.882007 × |
| 0.8 | −0.0468663 | −0.0468851 | −0.0468706 | 1.87738 × | 4.323579 × |
| 0.9 | −0.046056 | −0.0460764 | −0.0460608 | 2.04074 × | 4.724447× |
| 1 | −0.0451611 | −0.045183 | −0.0451662 | 2.18338 × | 5.081553 × |
Table 10.
The comparison of absolute error for of ARPSM and NITM solution of example 1 for .
Table 10.
The comparison of absolute error for of ARPSM and NITM solution of example 1 for .
| Exact | | | ARPSM Error | NITM Error |
|---|
| 0 | 0.447214 | 0.447213 | 0.447214 | 2.71011 × | 3.35410 |
| 0.1 | 0.447102 | 0.447087 | 0.447102 | 1.45678 × | 6.69162 × |
| 0.2 | 0.446766 | 0.446738 | 0.446766 | 2.8786 × | 1.32865 × |
| 0.3 | 0.446209 | 0.446166 | 0.446208 | 4.28507 × | 1.96888 × |
| 0.4 | 0.44543 | 0.445373 | 0.44543 | 5.66885 × | 2.58053 × |
| 0.5 | 0.444432 | 0.444362 | 0.444432 | 7.02288 × | 3.15469 × |
| 0.6 | 0.443217 | 0.443134 | 0.443217 | 8.34037 × | 3.68292 × |
| 0.7 | 0.441789 | 0.441693 | 0.441789 | 9.61496 × | 4.15740 × |
| 0.8 | 0.440151 | 0.440042 | 0.44015 | 1.08407 × | 4.57098 × |
| 0.9 | 0.438306 | 0.438186 | 0.438305 | 1.20121 × | 4.91733 × |
| 1 | 0.436259 | 0.436128 | 0.436259 | 1.31244 × | 5.19093 × |
Table 11.
The comparison of absolute error for of ARPSM and NITM solution of example 2 for .
Table 11.
The comparison of absolute error for of ARPSM and NITM solution of example 2 for .
| Exact | | | ARPSM Error | NITM Error |
|---|
| −0.5 | 2.6401 | 2.6402 | 2.6401 | 9.74069 × | 2.692781 × |
| −0.4 | 2.76627 | 2.76636 | 2.76627 | 8.7449 × | 1.500451 × |
| −0.3 | 2.86701 | 2.86708 | 2.86701 | 7.15344 × | 7.113980 × |
| −0.2 | 2.9404 | 2.94045 | 2.9404 | 5.06799 × | 2.646464 × |
| −0.1 | 2.98503 | 2.98505 | 2.98503 | 2.62897 × | 6.657231 × |
| 0.1 | 2.98502 | 2.985 | 2.98502 | 2.61859 × | 6.790399 × |
| 0.2 | 2.94039 | 2.94034 | 2.94039 | 5.05872 × | 2.658594 × |
| 0.3 | 2.86699 | 2.86692 | 2.86699 | 7.14588 × | 7.124251 × |
| 0.4 | 2.76625 | 2.76616 | 2.76625 | 8.73951 × | 1.501242 × |
| 0.5 | 2.64008 | 2.63998 | 2.64008 | 9.73776 × | 2.693303 × |
Table 12.
The comparison of absolute error for of ARPSM and NITM solution of example 2 for .
Table 12.
The comparison of absolute error for of ARPSM and NITM solution of example 2 for .
| Exact | | | ARPSM Error | NITM Error |
|---|
| 1 | −0.196061 | −0.196152 | −0.196063 | 9.02631 × | 1.79826 × |
| 1.1 | −0.212354 | −0.212428 | −0.212356 | 7.36884× | 1.18479 × |
| 1.2 | −0.227852 | −0.22791 | −0.227853 | 5.79595× | 6.10002 × |
| 1.3 | −0.24254 | −0.242584 | −0.242541 | 4.3334 × | 8.37973 × |
| 1.4 | −0.256413 | −0.256443 | −0.256412 | 2.9997 × | 3.86953 × |
| 1.5 | −0.269472 | −0.26949 | −0.269471 | 1.80645 × | 7.98232 × |
| 1.6 | −0.281728 | −0.281736 | −0.281727 | 7.59028 × | 1.14856 × |
| 1.7 | −0.293197 | −0.293196 | −0.293196 | 1.42483 × | 1.43865 × |
| 1.8 | −0.3039 | −0.303891 | −0.303899 | 9.02356 × | 1.67092 × |
| 1.9 | −0.313864 | −0.313849 | −0.313862 | 1.5282 × | 1.84913 × |
| 2 | −0.323118 | −0.323098 | −0.323116 | 2.03 × | 1.97793 × |