Power-Efficient Electronically Tunable Fractional-Order Filter
Abstract
:1. Introduction
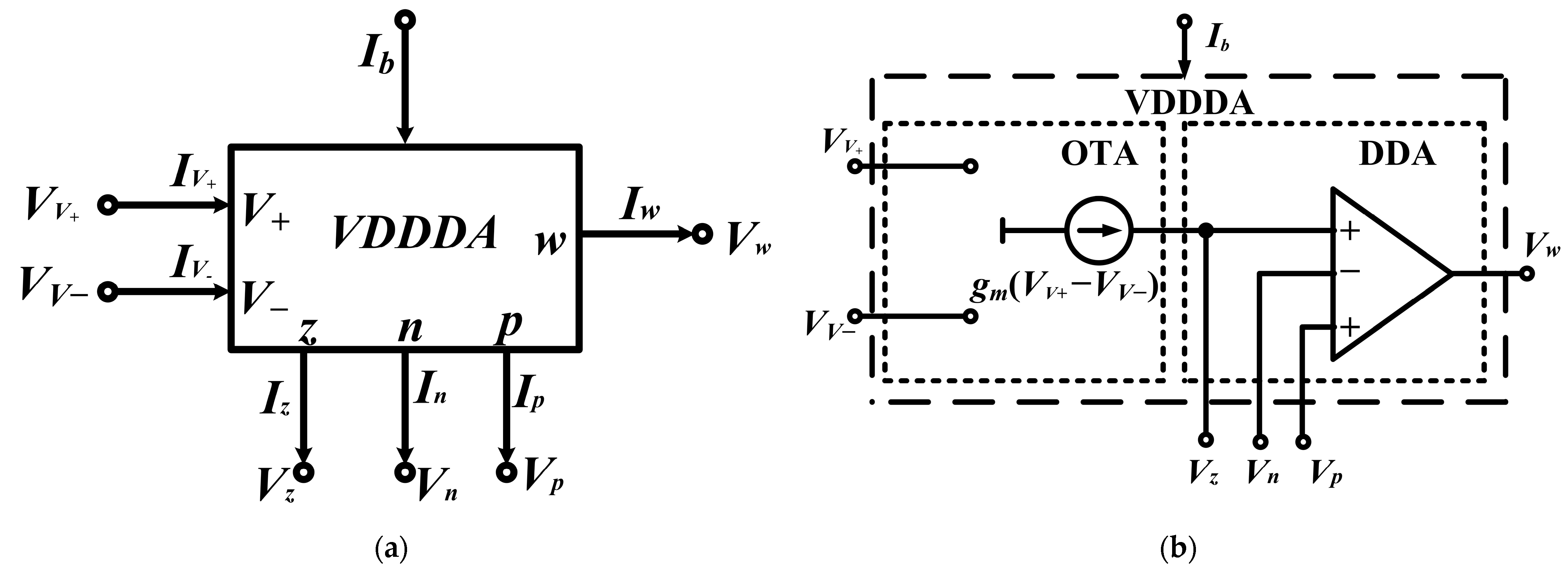
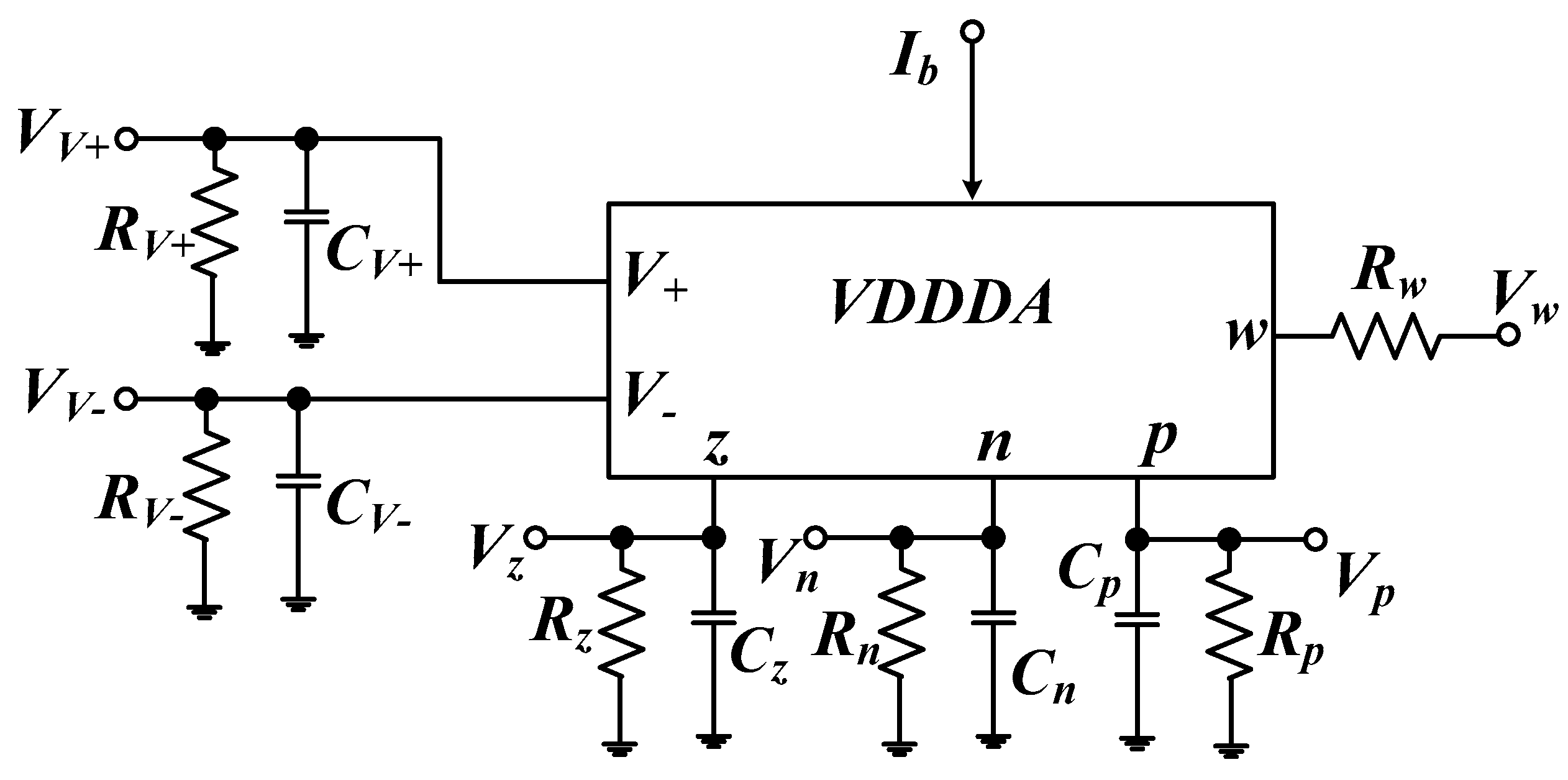
2. Voltage Differencing Differential Difference Amplifier: VDDDA
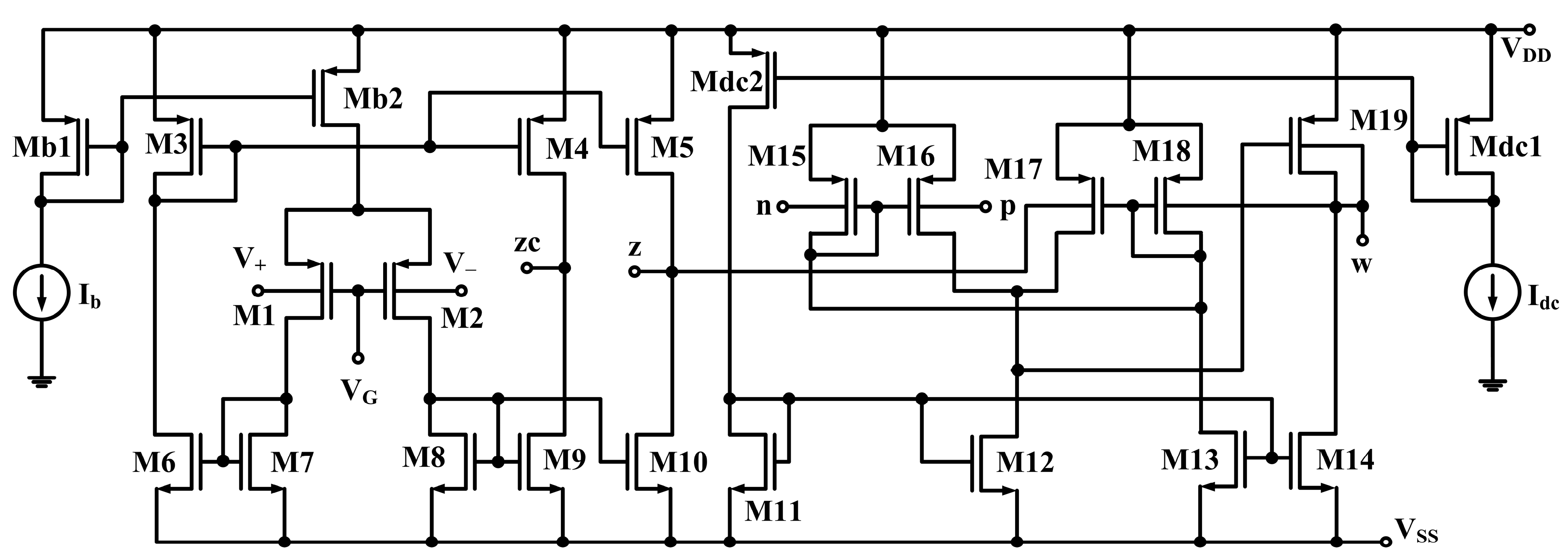
2.1. Proposed VDDDA
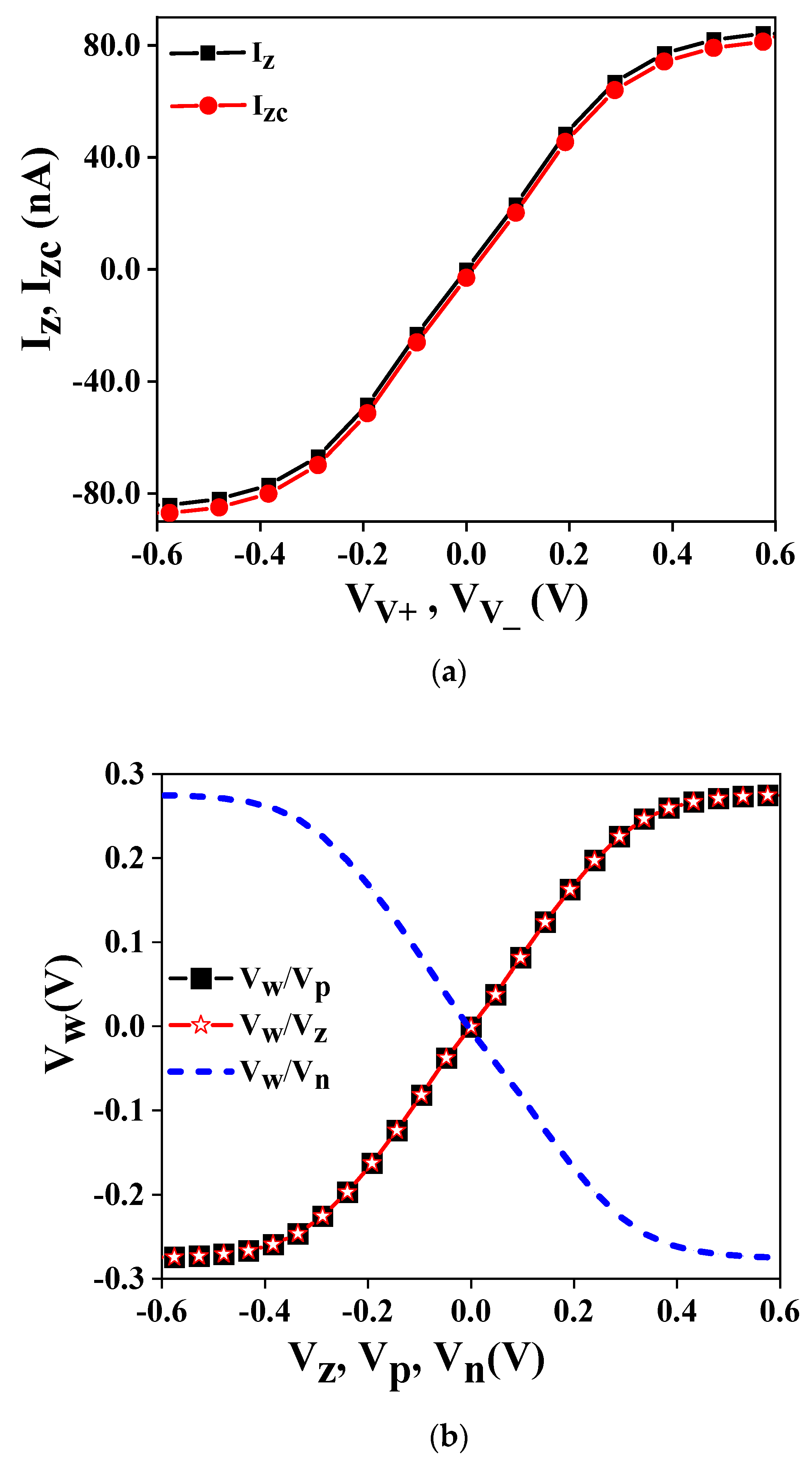
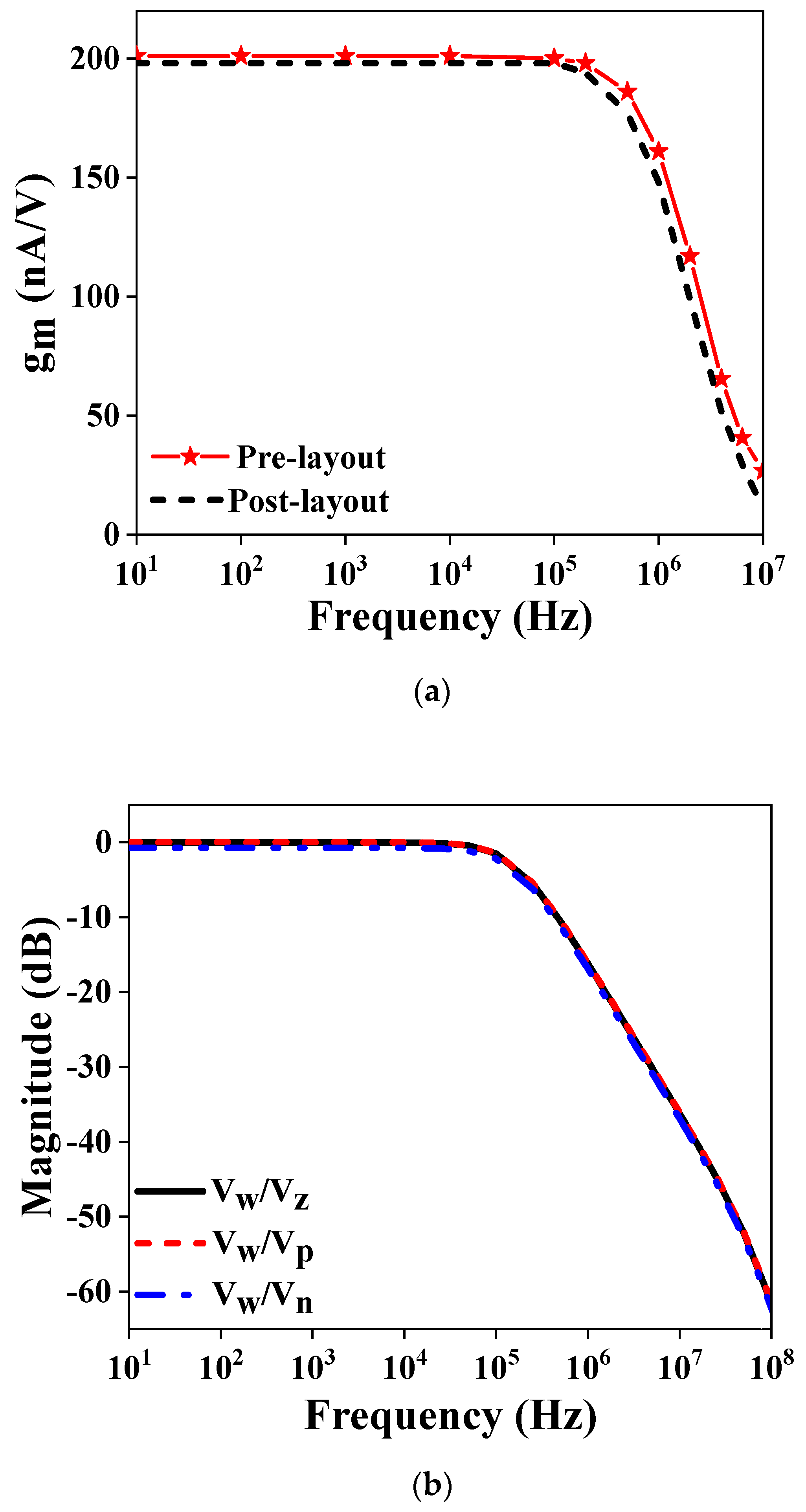
2.2. Simulation Results of VDDDA
3. Fractional-Order Low-Pass Filter (FO-LPF)
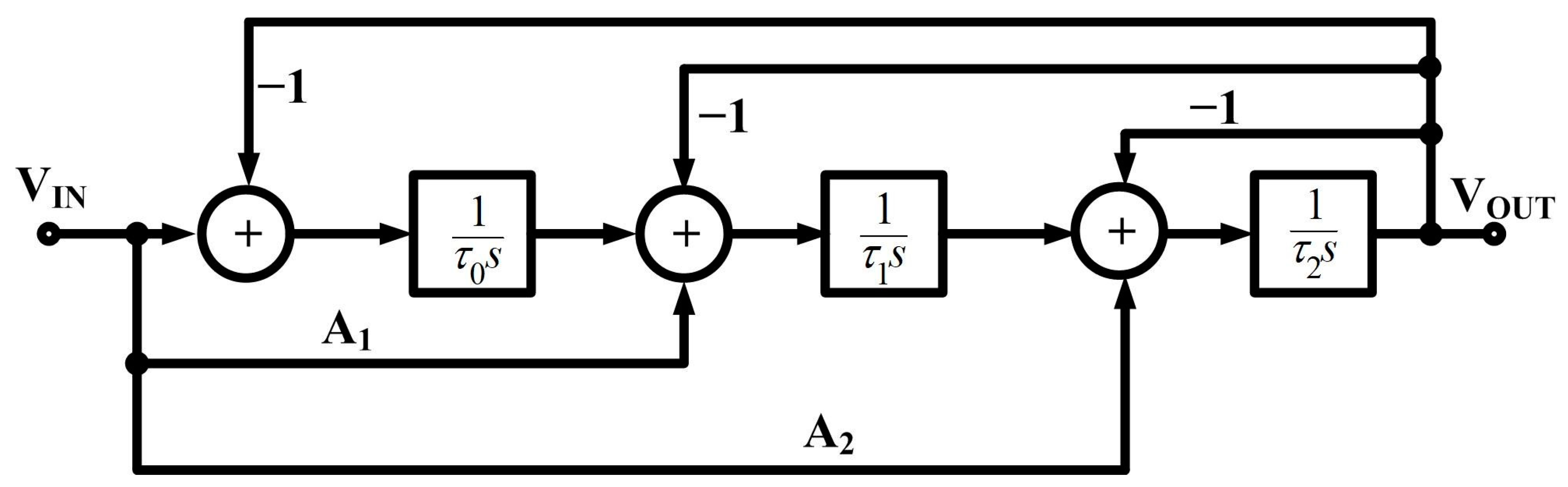
3.1. Basics of FO-LPF of Order 1 + α
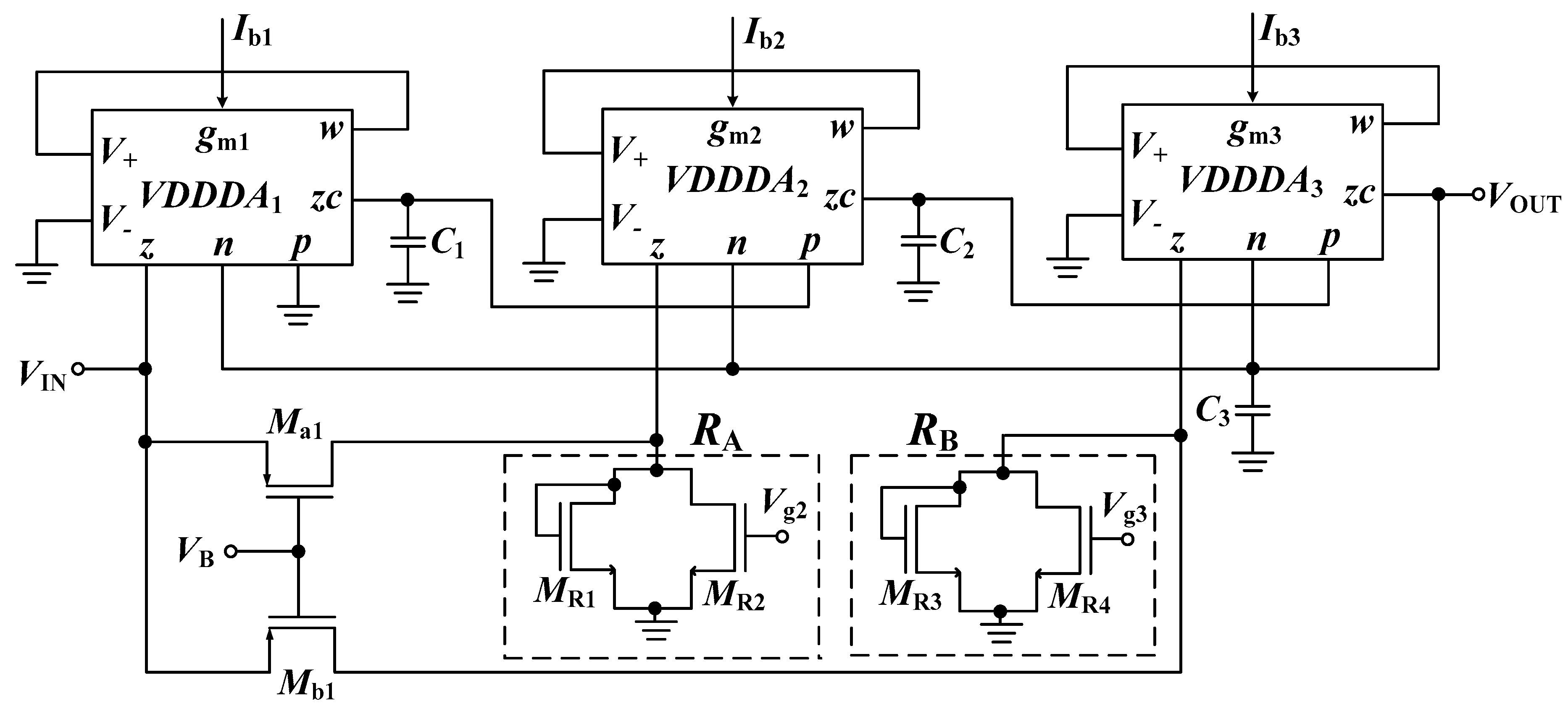
3.2. Proposed FO-LPF Using LV-LP VDDDA
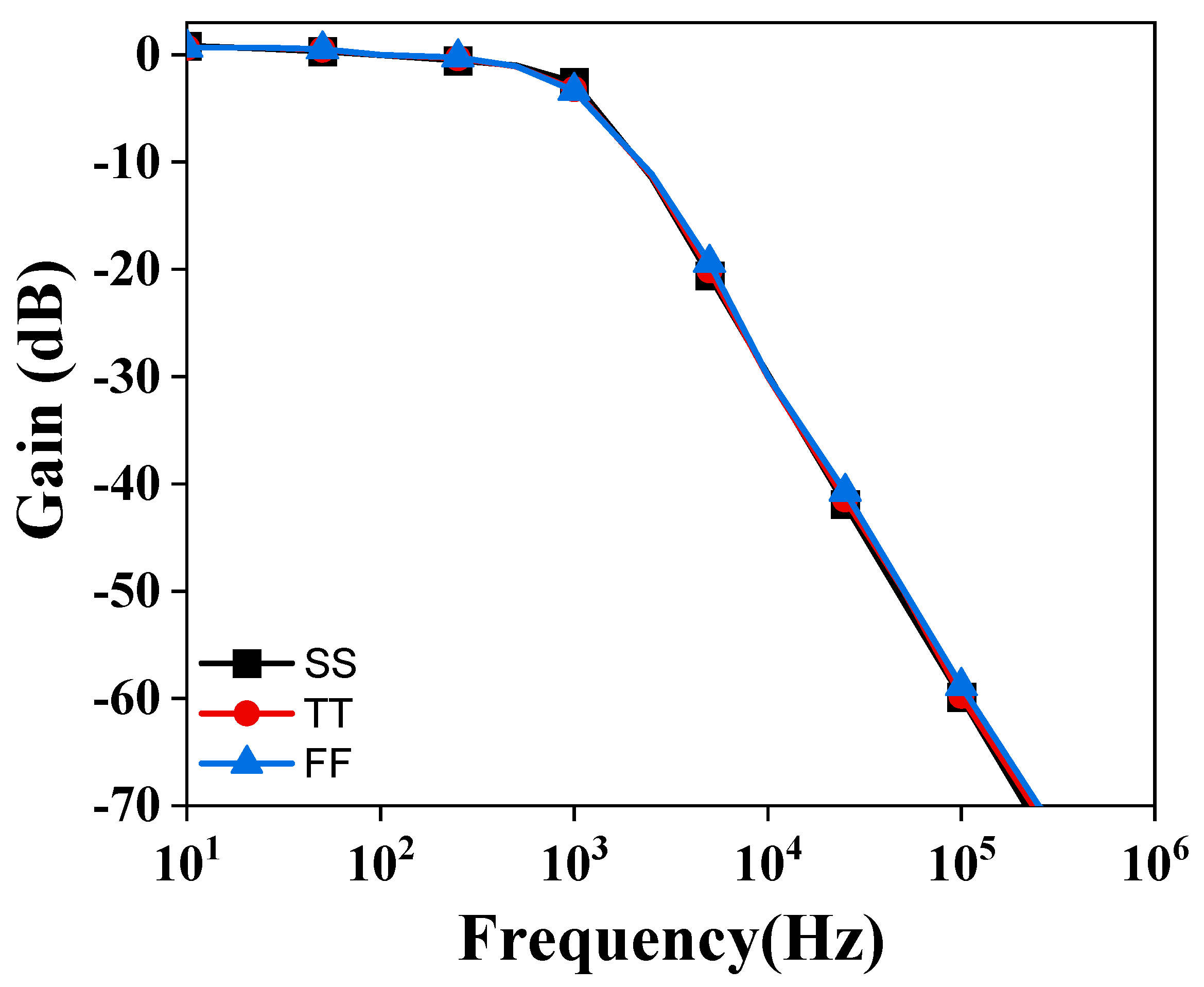
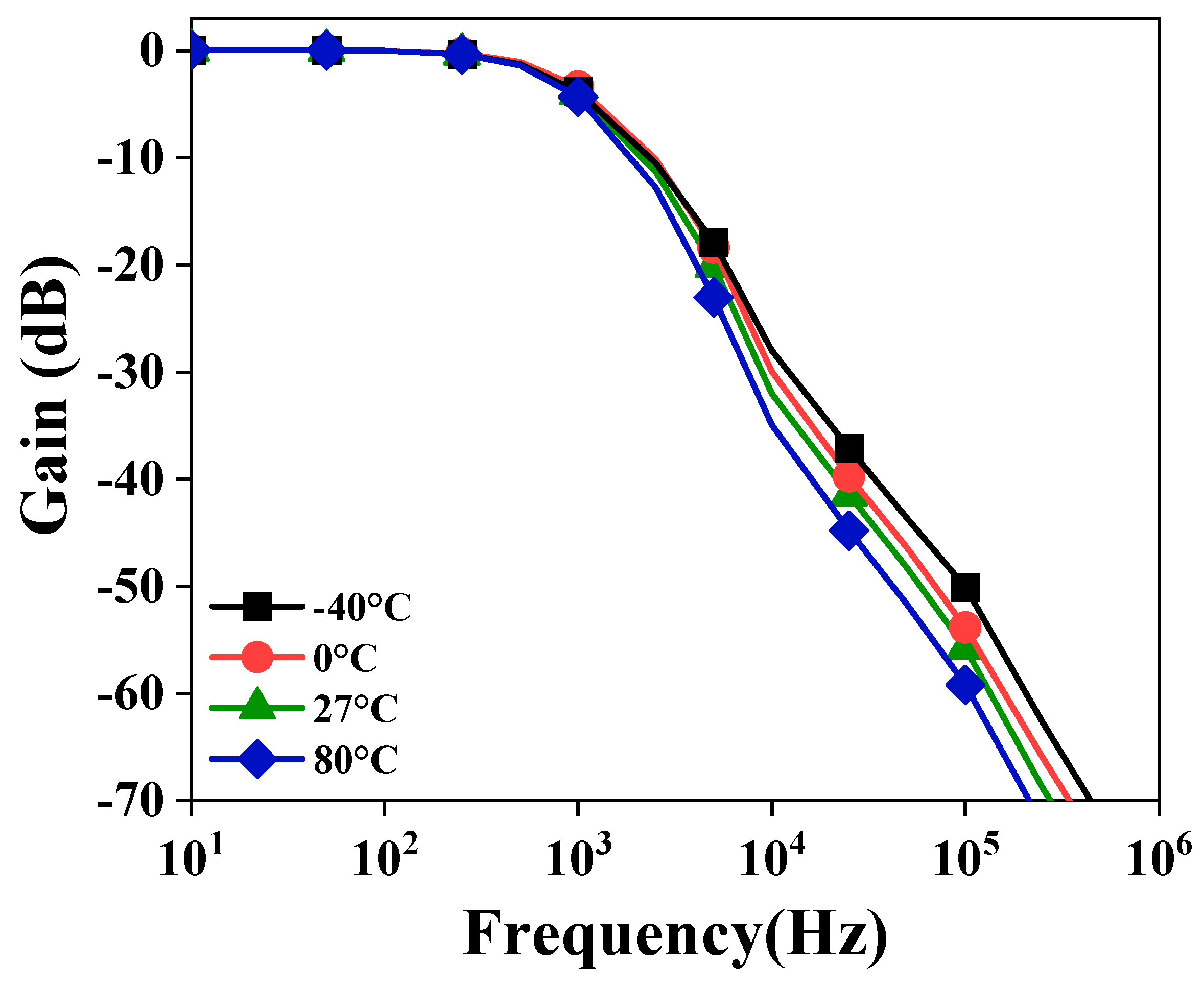
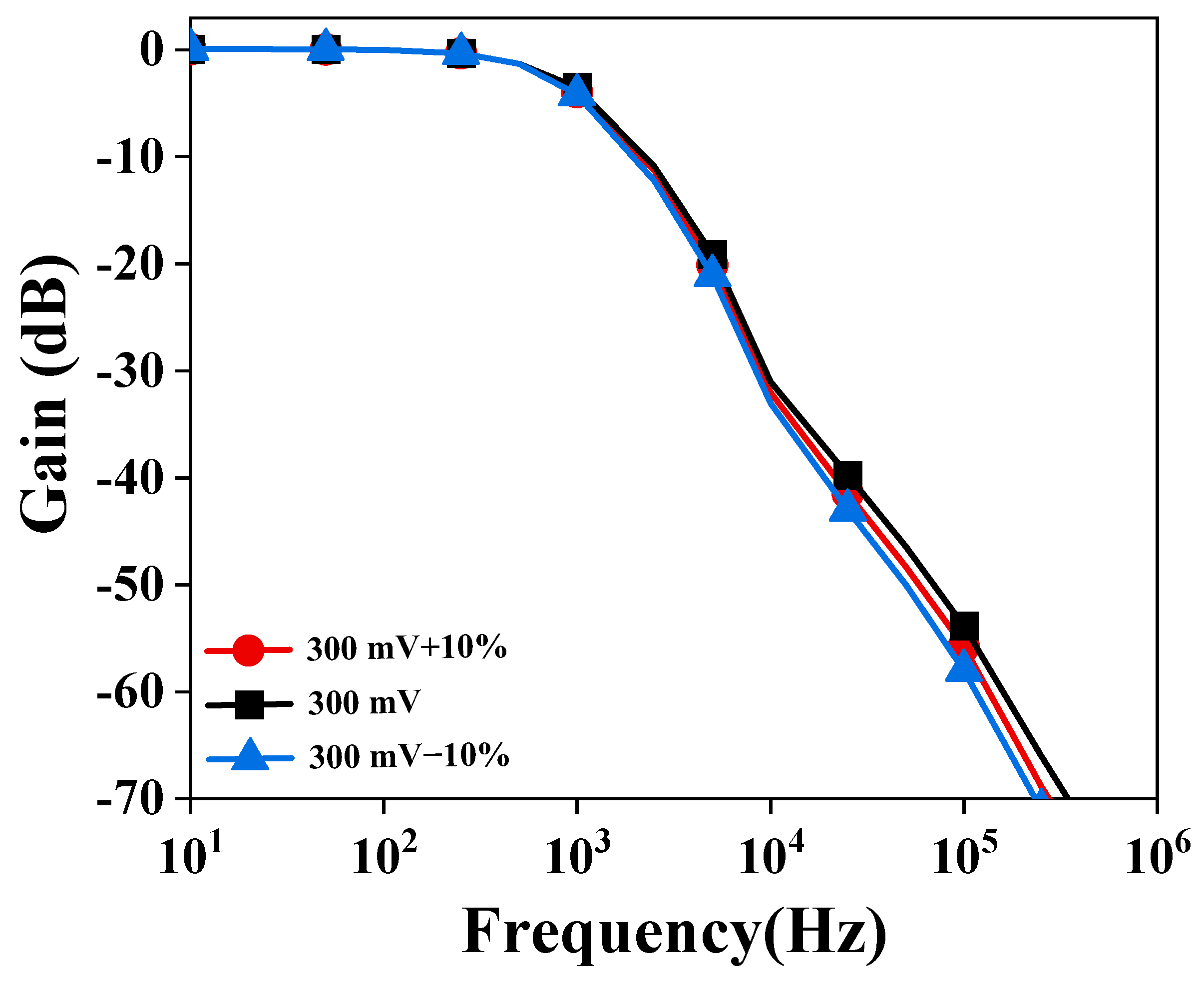
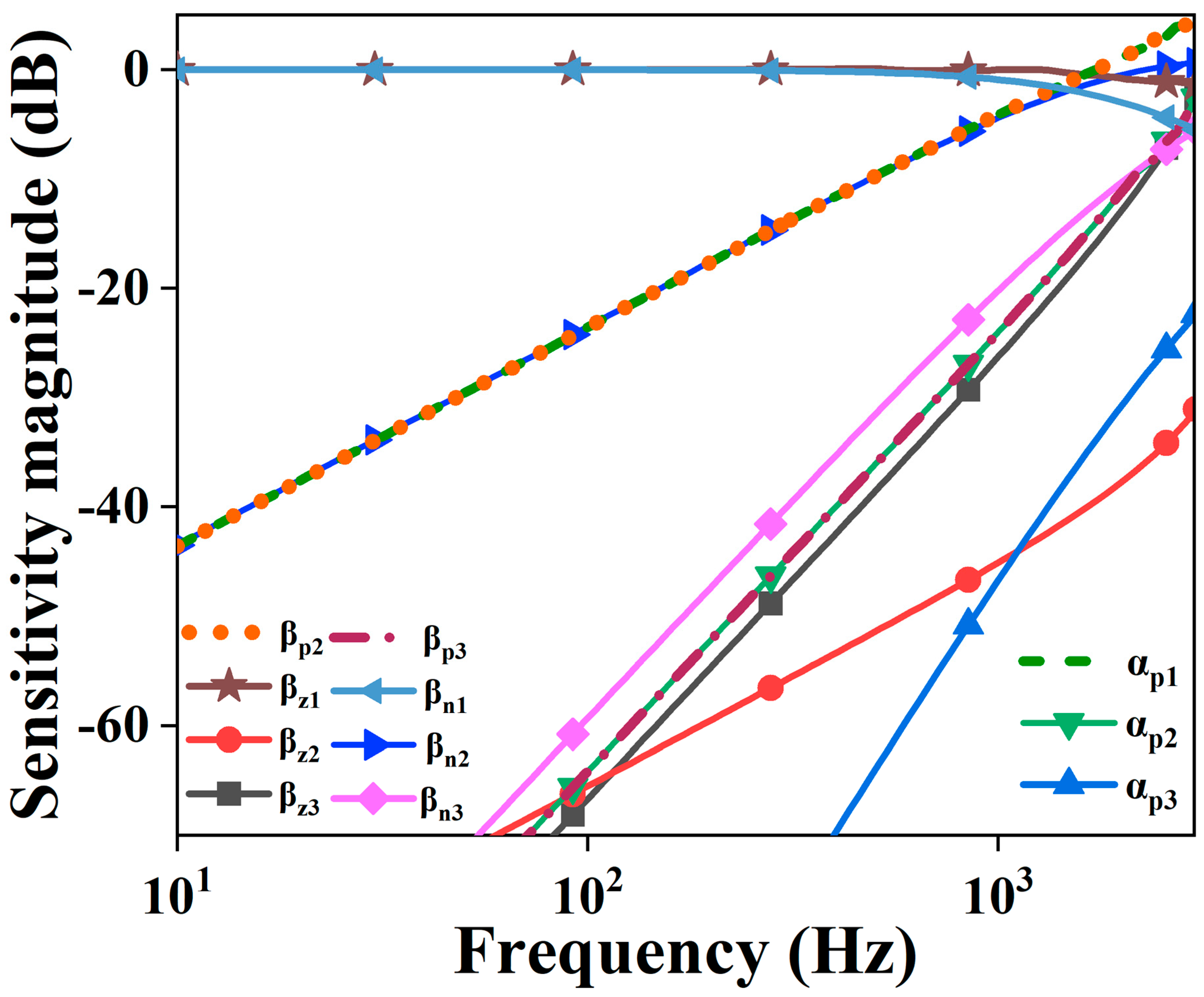
3.3. Effect of Non-Idealities on FO-LPF
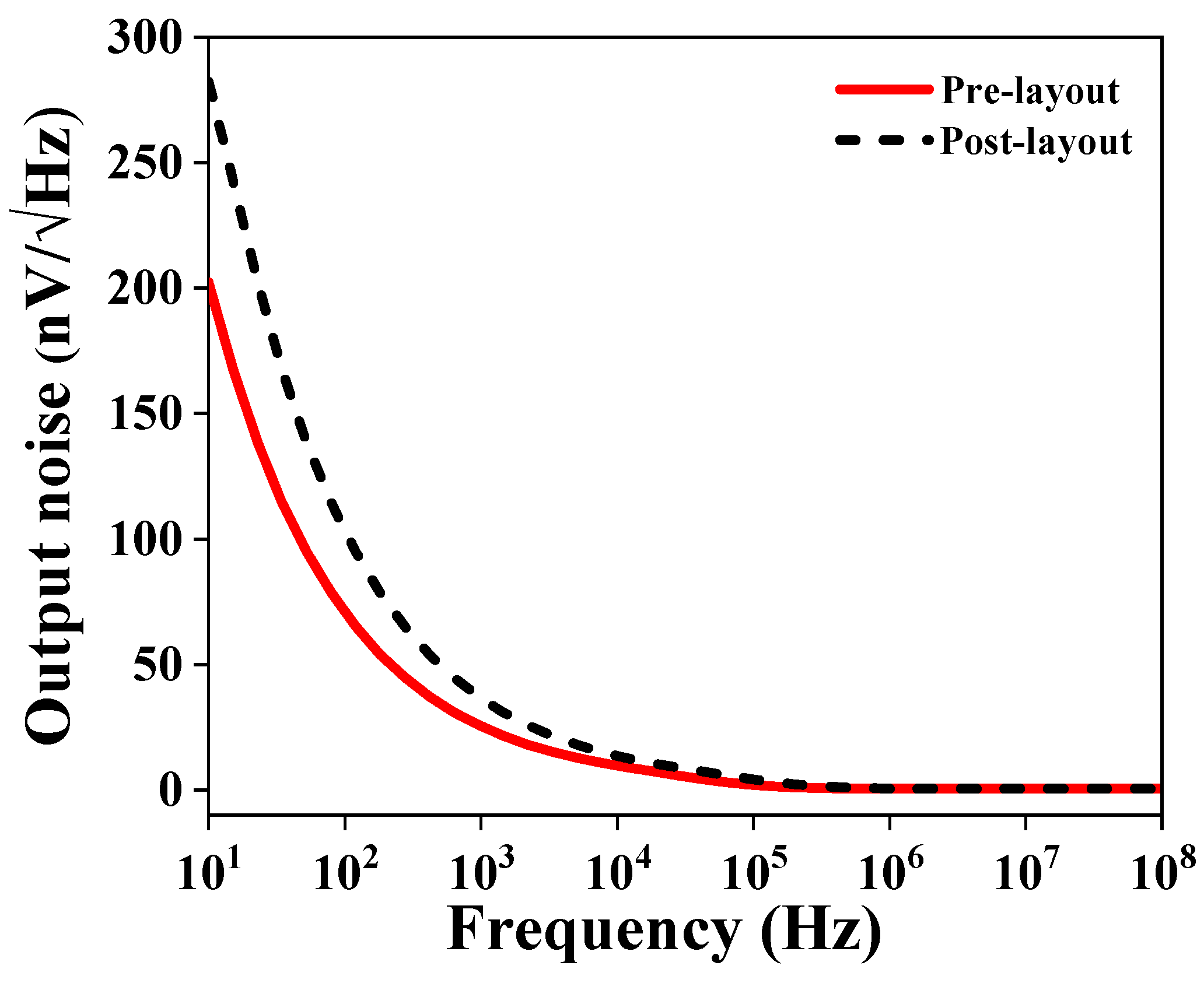
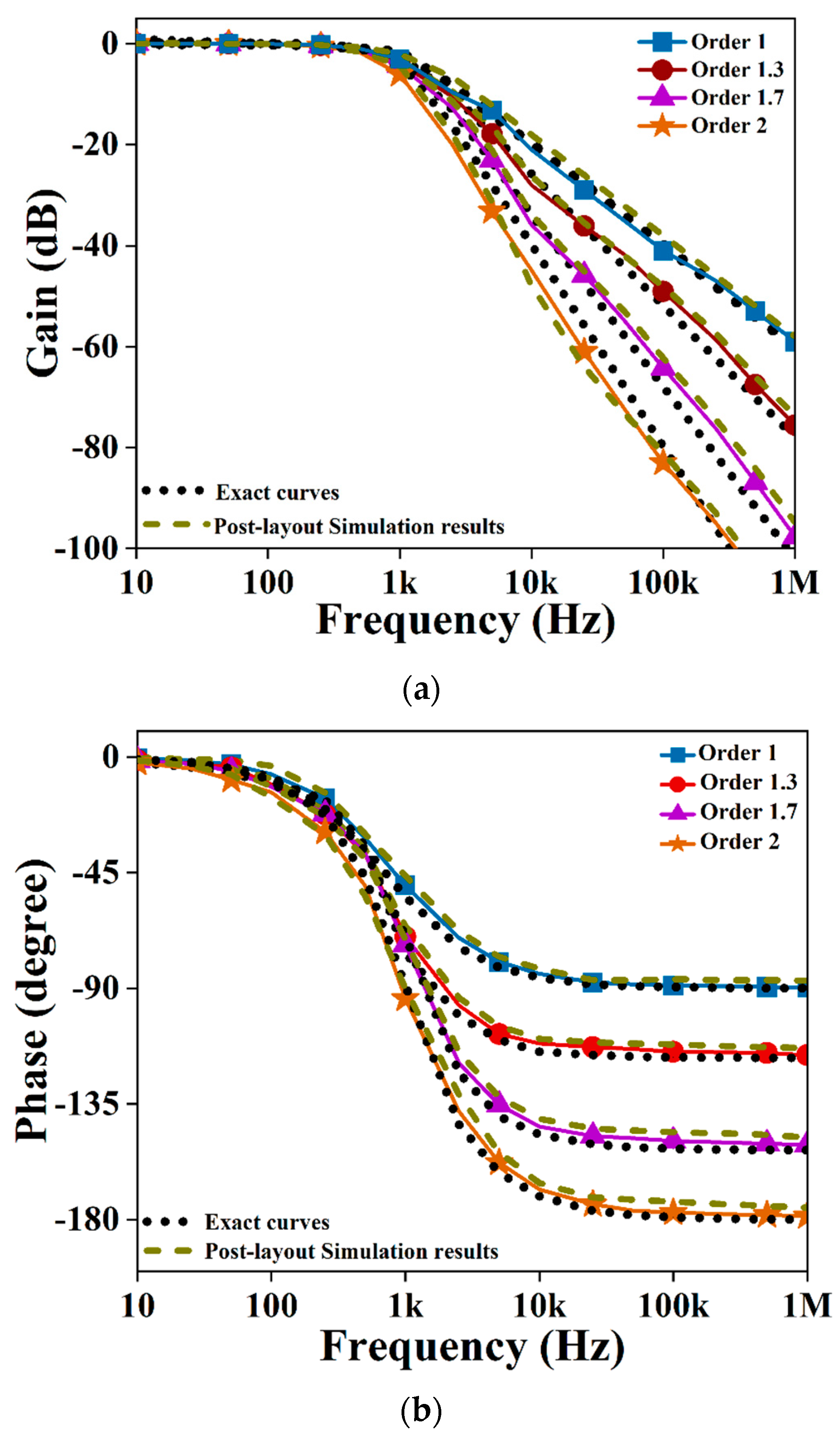
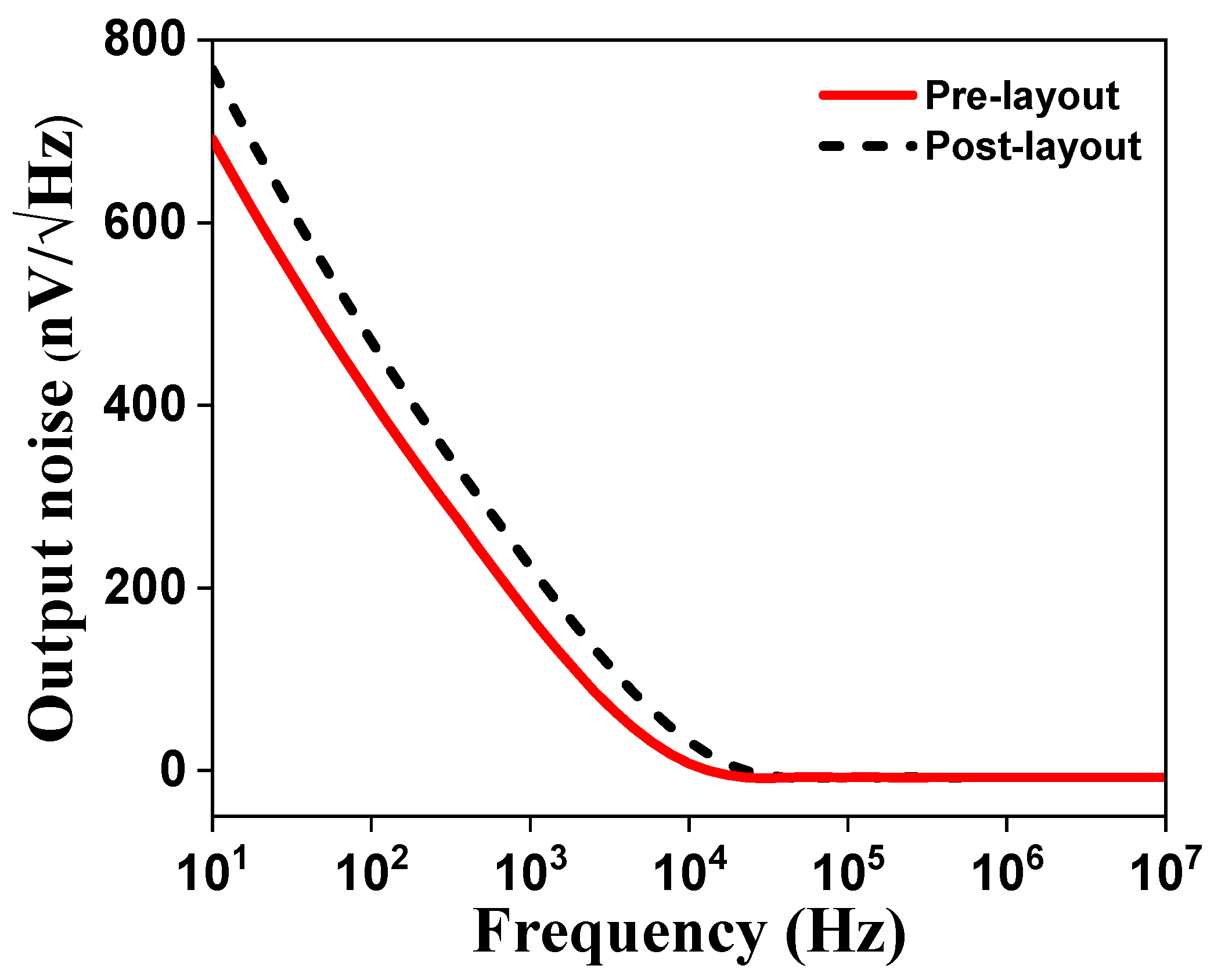
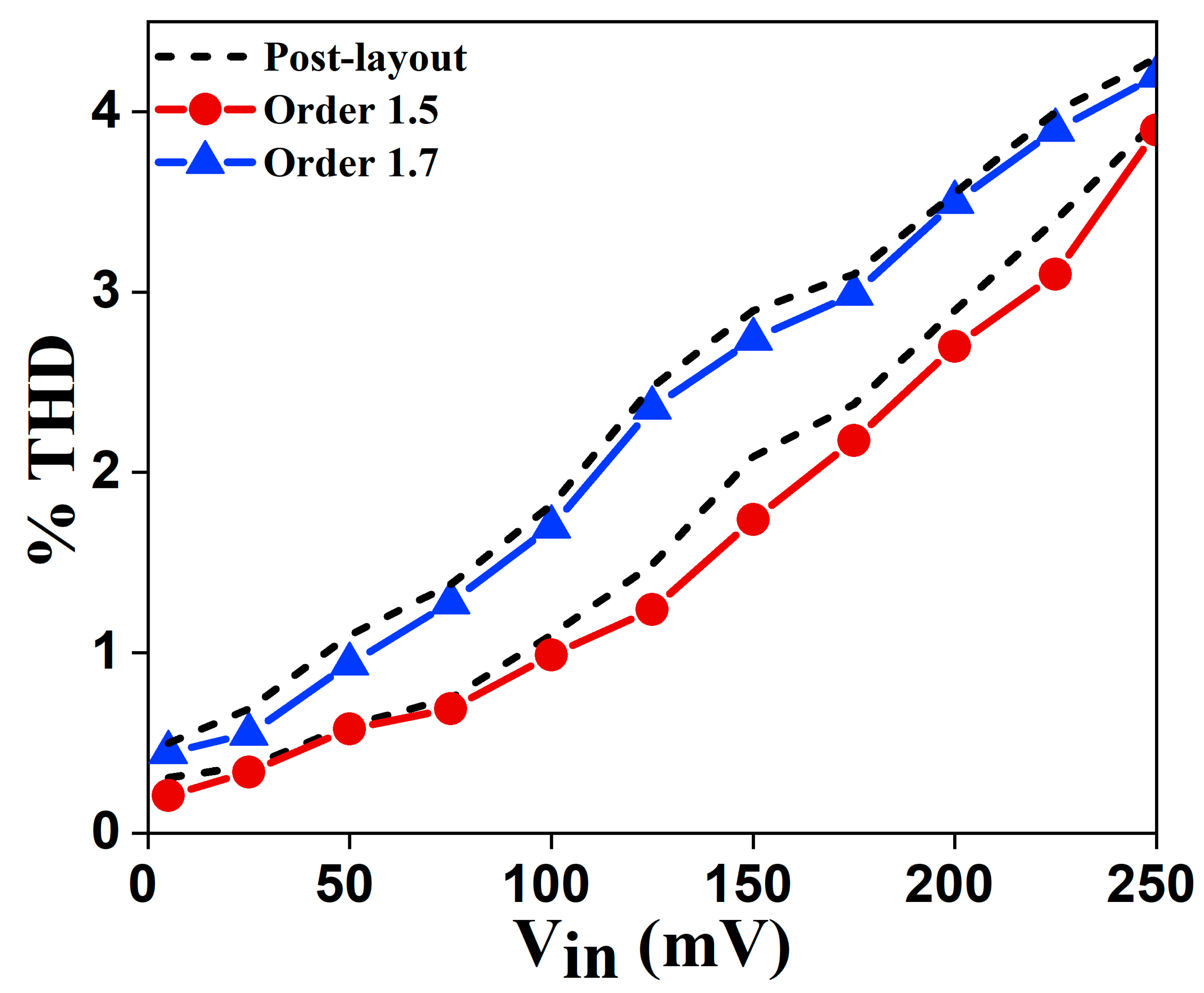
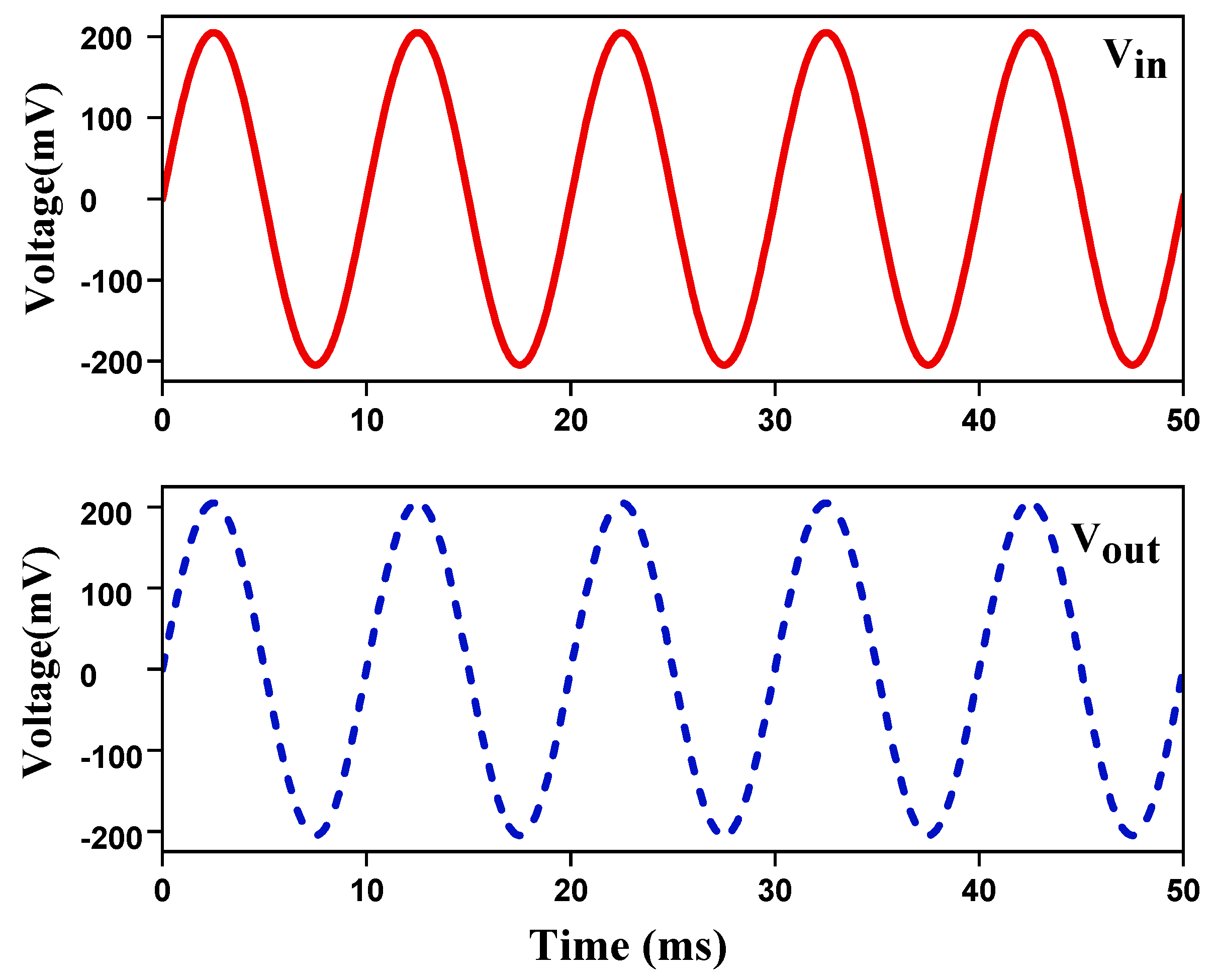
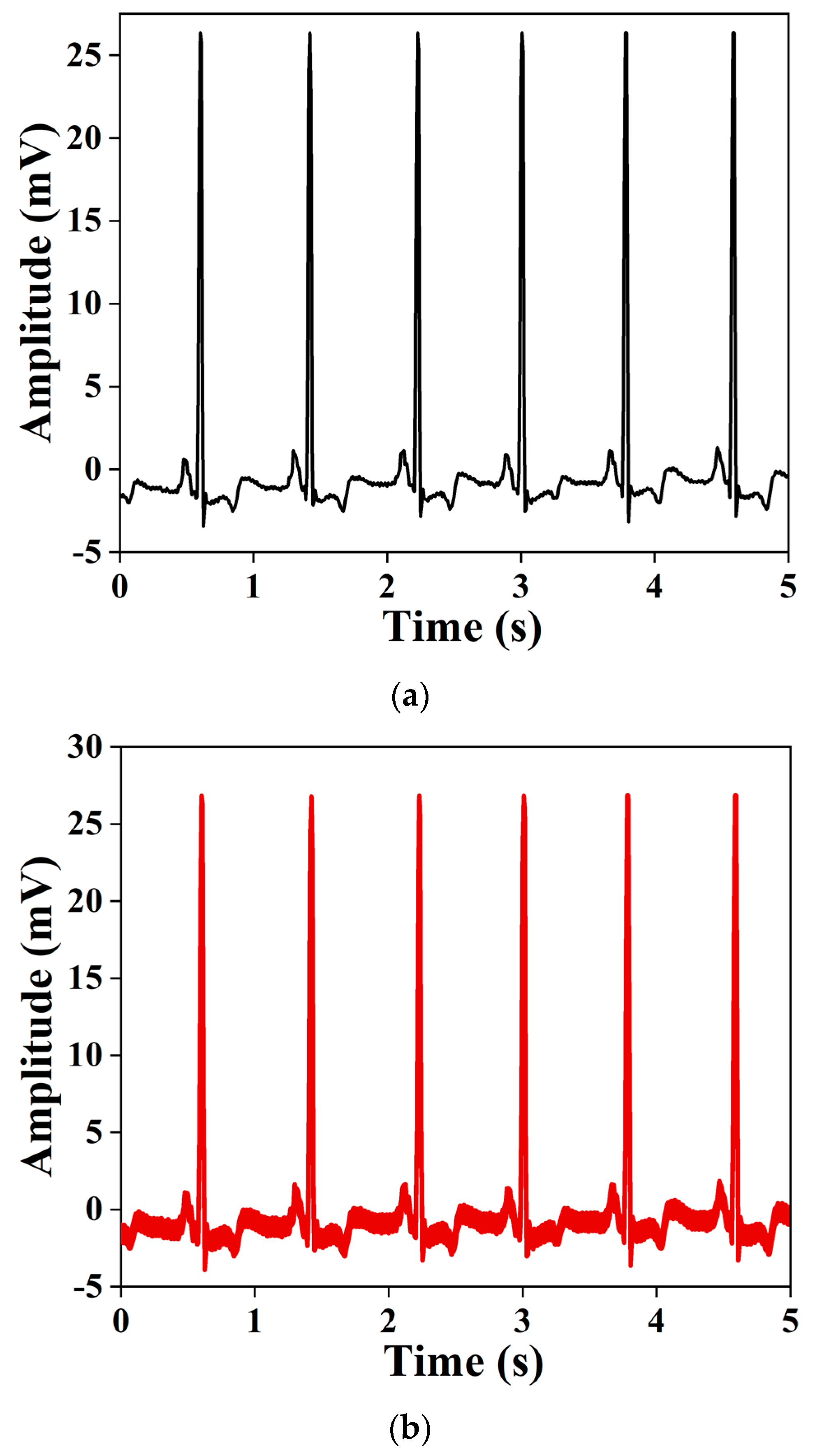
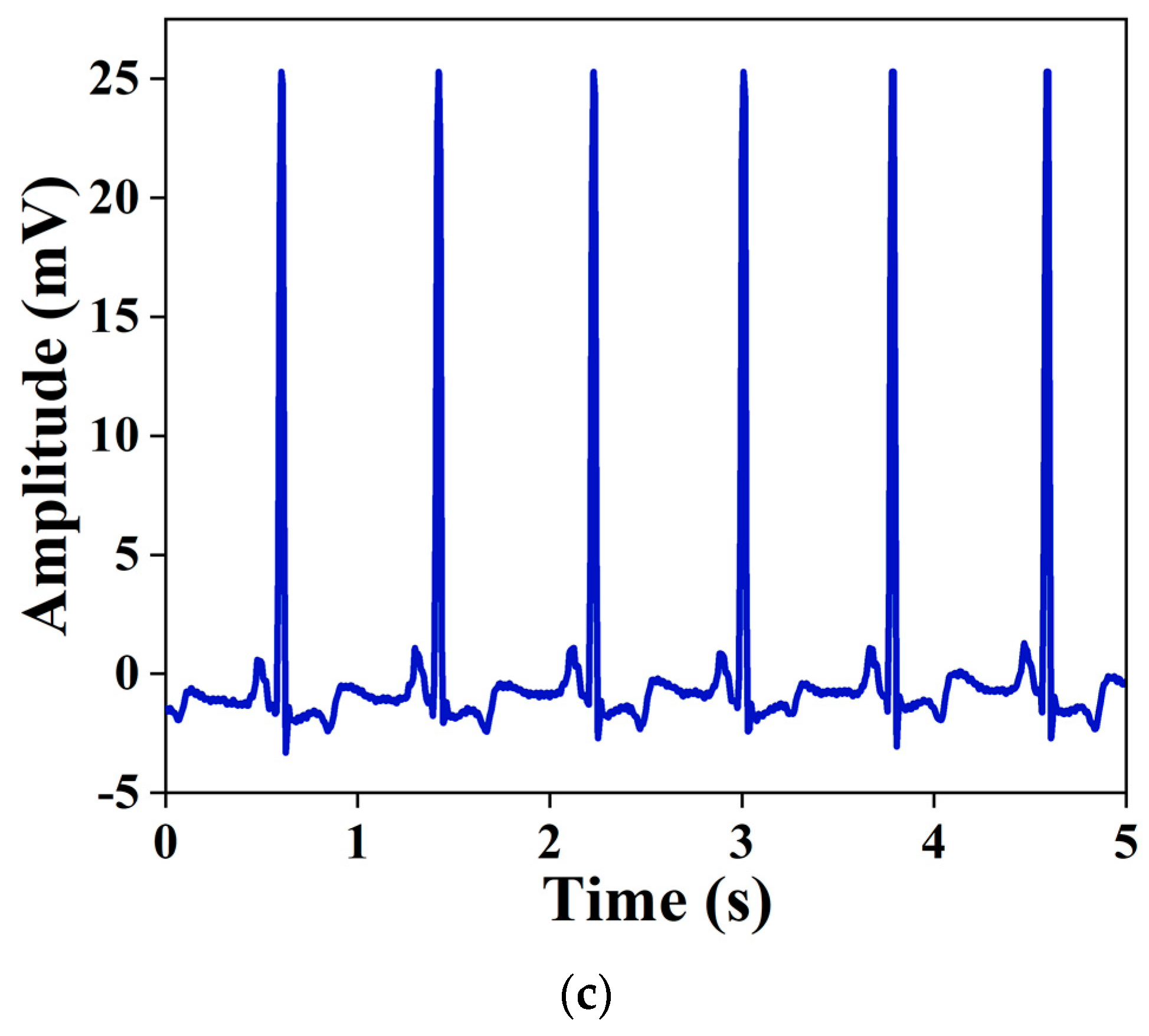
3.4. Simulation Results
4. Comparison
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Shah, D.K.; Chaurasiya, R.B.; Vyawahare, V.A.; Pichhode, K.; Patil, M.D. FPGA implementation of fractional-order chaotic systems. AEU-Int. J. Electron. Commun. 2017, 78, 245–257. [Google Scholar] [CrossRef]
- Elsafty, A.H.; Tolba, M.F.; Said, L.A.; Madian, A.H.; Radwan, A.G. Enhanced hardware implementation of a mixed-order nonlinear chaotic system and speech encryption application. AEU-Int. J. Electron. Commun. 2020, 125, 153347. [Google Scholar] [CrossRef]
- Radwan, A.G.; Khanday, F.A.; Said, L.A. (Eds.) Fractional-Order Design: Devices, Circuits, and Systems; Academic Press: Amsterdam, The Netherlands; Elsevier Science: Amsterdam, The Netherlands, 2021. [Google Scholar]
- Rezazadehshabilouyoliya, V.; Atasoyu, M.; Ozoguz, S. Emulation of a constant phase element by utilizing a lattice structure based fractional-order differentiator. AEU-Int. J. Electron. Commun. 2020, 127, 153418. [Google Scholar] [CrossRef]
- Elwakil, A.S. Fractional-order circuits and systems: An emerging interdisciplinary research area. IEEE Circuits Syst. Mag. 2010, 10, 40–50. [Google Scholar] [CrossRef]
- Koton, J.; Sladok, O.; Salasek, J.; Ushakov, P.A. Current-mode fractional low-and high-pass filters using current conveyors. In Proceedings of the 8th International Congress on Ultra-Modern Telecommunications and Control Systems and Workshops (ICUMT), Lisbon, Portugal, 18–20 October 2016. [Google Scholar]
- Valsa, J.; Dvorak, P.; Friedl, M. Network model of the CPE. Radioengineering 2011, 20, 619–626. [Google Scholar]
- Adhikary, A.; Sen, S.; Biswas, K. Practical realization of tunable fractional order parallel resonator and fractional order filters. IEEE Trans. Circuits Syst. I Reg. Pap. 2016, 63, 1142–1151. [Google Scholar] [CrossRef]
- Abdelaty, A.M.; Soltan, A.; Ahmed, W.A.; Radwan, A.G. Fractional order Chebyshev-like low-pass filters based on integer order poles. Microelectron. J. 2019, 90, 72–81. [Google Scholar] [CrossRef]
- Khalil, N.A.; Said, L.A.; Radwan, A.G.; Soliman, A.M. Generalized two-port network based fractional order filters. AEU-Int. J. Electron. Commun. 2019, 104, 128–146. [Google Scholar] [CrossRef]
- Varshney, G.; Pandey, N.; Pandey, R. Electronically tunable multifunction transadmittance-mode fractional-order filter. Arabian J. Sci. Eng. 2021, 46, 1067–1078. [Google Scholar] [CrossRef]
- Mishra, S.K.; Gupta, M.; Upadhyay, D.K. Active realization of fractional order Butterworth lowpass filter using DVCC. J. King Saud Univ. Eng. Sci. 2020, 32, 158–165. [Google Scholar] [CrossRef]
- Ghoneim, M.; Hesham, R.; Yassin, H.; Madian, A. α-order universal filter realization based on single input multi-output differential voltage current conveyor. Analog Integr. Circuits Signal Process. 2021, 107, 411–422. [Google Scholar] [CrossRef]
- Maundy, B.; Elwakil, A.S.; Freeborn, T.J. On the practical realization of higher-order filters with fractional stepping. Signal Process. 2011, 91, 484–491. [Google Scholar] [CrossRef]
- Verma, R.; Pandey, N.; Pandey, R. CFOA based low pass and high pass fractional step filter realizations. AEU-Int. J. Electron. Commun. 2019, 99, 161–176. [Google Scholar] [CrossRef]
- Tsirimokou, G.; Koumousi, S.; Psychalinos, C. Design of fractional-order filters using current feedback operational amplifiers. J. Eng. Sci. Technol. Rev. 2016, 9, 71–81. [Google Scholar] [CrossRef]
- Langhammer, L.; Dvorak, J.; Jerabek, J.; Koton, J.; Sotner, R. Fractional-order high-pass filter with electronically adjustable parameters. J. Electr. Eng. 2018, 69, 3–13. [Google Scholar]
- Jerabek, J.; Sotner, R.; Dvorak, J.; Polak, J.; Kubanek, D.; Herencsar, N.; Koton, J. Reconfigurable fractional-order filter with electronically controllable slope of attenuation, pole frequency and type of approximation. J. Circuits Syst. Comput. 2017, 26, 1750157. [Google Scholar] [CrossRef]
- Khateb, F.; Kubánek, D.; Tsirimokou, G.; Psychalinos, C. Fractional-order filters based on low-voltage DDCCs. Microelectron. J. 2016, 50, 50–59. [Google Scholar] [CrossRef]
- Kaur, G.; Ansari, A.Q.; Hashmi, M.S. Analysis and investigation of CDBA based fractional-order filters. Analog Integr. Circuits Signal Process. 2020, 105, 111–124. [Google Scholar] [CrossRef]
- Koton, J.; Kubanek, D.; Sladok, O.; Vrba, K.; Shadrin, A.; Ushakov, P. Fractional-order low-and high-pass filters using UVCs. J. Circuits Syst. Comput. 2017, 26, 1750192. [Google Scholar] [CrossRef]
- Herencsar, N.; Sotner, R.; Metin, B.; Koton, J.; Vrba, K. VDDDA-New ‘voltage differencing’ device for analog signal processing. In Proceedings of the 8th International Conference on Electrical and Electronics Engineering (ELECO), Bursa, Turkey, 28–30 November 2013. [Google Scholar]
- Soisang, S.; Jirasereemomkul, K.; Jaikla, W.; Higuchi, K. Voltage-mode multifunctional biquadratic filter using VDDDA. Appl. Mech. Mater. 2015, 781, 155–159. [Google Scholar] [CrossRef]
- Sangyaem, S.; Siripongdee, S.; Jaikla, W.; Khateb, F. Five-inputs single-output voltage mode universal filter with high input and low output impedance using VDDDAs. Optik 2017, 128, 14–25. [Google Scholar] [CrossRef]
- Jaikla, W.; Khateb, F.; Kulej, T.; Pitaksuttayaprot, K. Universal filter based on compact CMOS structure of VDDDA. Sensors 2021, 21, 1683. [Google Scholar] [CrossRef] [PubMed]
- Alagoz, B.B.; Yeroglu, C.; Kavuran, G.; Ates, A. Detection of RR interval alterations in ECG signals by using first order fractional filter. In Proceedings of the 39th International Conference on Telecommunications and Signal Processing (TSP), Vienna, Austria, 27–29 June 2016. [Google Scholar]
- Kulej, T.; Khateb, F.; Kumngern, M. 0.3-V nanopower biopotential low-pass filter. IEEE Access 2020, 8, 119586–119593. [Google Scholar] [CrossRef]
- Khateb, F.; Prommee, P.; Kulej, T. MIOTA-based filters for noise and motion artifact reductions in biosignal acquisition. IEEE Access 2022, 10, 14325–14338. [Google Scholar] [CrossRef]
- Agambayev, A.; Farhat, M.; Patole, S.P.; Hassan, A.H.; Bagci, H.; Salama, K.N. An ultra-broadband single-component fractional-order capacitor using MoS2-ferroelectric polymer composite. Appl. Phys. Lett. 2018, 113, 093505. [Google Scholar] [CrossRef]
- Tu, S.; Jiang, Q.; Zhang, X.; Alshareef, H.N. Solid state MXene based electrostatic fractional capacitors. Appl. Phys. Lett. 2019, 114, 232903. [Google Scholar] [CrossRef]
- Freeborn, T.J.; Maundy, B.; Elwakil, A.S. Field programmable analogue array implementation of fractional step filters. IET Circuits Devices Syst. 2010, 4, 514–524. [Google Scholar] [CrossRef]
- Dvorak, J.; Langhammer, L.; Jerabek, J.; Koton, J.; Sotner, R.; Polak, J. Synthesis and analysis of electronically adjustable fractional-order low-pass filter. J. Circuits Syst. Comput. 2018, 27, 1850032. [Google Scholar] [CrossRef]
- Langhammer, L.; Sotner, R.; Dvorak, J.; Jerabek, J.; Polak, J. Fully-differential tunable fractional-order filter with current followers and current amplifiers. In Proceedings of the 27th International Conference Radioelektronika (RADIOELEKTRONIKA), Brno, Czech Republic, 19–20 April 2017. [Google Scholar]
- Sacu, I.E.; Alci, M. A current mode design of fractional order universal filter. Adv. Electr. Comput. Eng. 2019, 19, 71–78. [Google Scholar] [CrossRef]
- Langhammer, L.; Sotner, R.; Dvorak, J.; Jerabek, J.; Andriukaitis, D. Reconnection–less reconfigurable fractional–order current–mode integrator design with simple control. IEEE Access 2021, 9, 136395–136405. [Google Scholar] [CrossRef]
- Kaur, G.; Ansari, A.Q.; Hashmi, M.S. Complexity reduced design procedure of a fractional order all-pass filter. Wirel. Pers. Commun. 2022, 125, 2515–2535. [Google Scholar] [CrossRef]
- Tasneem, S.; Ranjan, R.K.; Paul, S.K. Low-Frequency Electronically Tunable Fractional Filter and its Implementation as Neural Network. J. Circuits, Syst. Comput. 2023, 2450037. [Google Scholar] [CrossRef]
- Akbari, M.; Hussein, S.M.; Hashim, Y.; Tang, K.T. An enhanced input differential pair for low-voltage bulk-driven amplifiers. IEEE Trans. Very Large Scale Integr. VLSI Syst. 2021, 10, 1601–1611. [Google Scholar] [CrossRef]



| Transistor | W (μm)/L (μm) |
|---|---|
| M1, M2 | 12/0.6 |
| M3–M5, Mb1, Mb2, Mdc1, Mdc2 | 10/0.6 |
| M6, M9, M10 | 7/0.6 |
| M7, M8 | 4/0.6 |
| M11–M14 | 4/0.3 |
| M15–M18 | 10/0.3 |
| M19 | 20/0.3 |
| Order of Filter | 1.3 | 1.5 | 1.7 | 1.9 |
|---|---|---|---|---|
| C1 [pF] | 90 | 90 | 90 | 90 |
| C2 [pF] | 90 | 90 | 90 | 90 |
| C3 [pF] | 30 | 30 | 30 | 30 |
| RA [kΩ] | 2 | 1.67 | 1 | 0.5 |
| RB [kΩ] | 4.6 | 4 | 3.4 | 2.8 |
| gm1 [nS] | 150 | 172 | 190 | 210 |
| gm2 [nS] | 619 | 650 | 652 | 607 |
| gm3 [nS] | 643 | 537 | 485 | 475 |
| Ib1 (nA) | 12.3 | 12.5 | 12.9 | 14.5 |
| Ib2 (nA) | 72 | 74 | 74.1 | 65 |
| Ib3 (nA) | 75 | 53 | 47 | 46 |
| Order of Filter | Slope of Attenuation [dB/dec] | |
|---|---|---|
| Theoretical | Simulated | |
| 1.3 | 26 | 26.04 |
| 1.5 | 30 | 30.57 |
| 1.7 | 34 | 33.64 |
| 1.9 | 38 | 37.61 |
| Pole Frequency | 500 Hz | 1 kHz | 2 kHz |
|---|---|---|---|
| C1 [pF] | 90 | 90 | 90 |
| C2 [pF] | 90 | 90 | 90 |
| C3 [pF] | 30 | 30 | 30 |
| RA [kΩ] | 1.67 | 1.67 | 1.67 |
| RB [kΩ] | 4 | 4 | 4 |
| gm1 [S] | 85.8 n | 172 n | 343 n |
| gm2 [S] | 325 n | 650 n | 1.3 μ |
| gm3 [S] | 269 n | 537 n | 1.07 μ |
| Ib1 (nA) | 5 | 12.5 | 29 |
| Ib2 (nA) | 26 | 74 | 150 |
| Ib3 (nA) | 20 | 53 | 145 |
| Theoretical Pole Frequency | Simulated Pole Frequency |
|---|---|
| 500 Hz | 502 Hz |
| 1 kHz | 1.003 kHz |
| 2 kHz | 2.007 kHz |
| [Ref.] (Year) | Type (Number) of ABB Used | Function Realized | No. of Passive Elements (R, C) | Grounded/Floating Elements | Supply Voltage | Electronic Tunability | Use of LV-LP Technique | Total Power Dissipation (W) |
|---|---|---|---|---|---|---|---|---|
| [6] (2016) | CCII (4), DDCC (1) | LPF | 7, 3 | G | NA | No | No | NA |
| [14] (2011) | OPAMP (2) | LPF | 10, 3 | F | NA | No | No | NA |
| [15] (2018) | CFOA (4) | LPF | 9, 3 | F | ±10 V | No | No | NA |
| [16] (2016) | CFOA (4) | LPF | 10, 3 | F | ±10 V | No | No | NA |
| [17] (2018) | OTA (3), MOCF (1), ACF (2) | LPF | 0, 3 | G | ±1 V | Yes | No | NA |
| [18] (2017) | OTA (3), CF (1), ACA (3) | LPF | 0, 3 | G | NA | Yes | No | NA |
| [19] (2016) | DDCC (5) | LPF | 7, 3 | G | ±0.5 V | No | Yes | 0.185 m |
| [20] (2020) | CDBA (5) | LPF, BPF | 11, 3 | F | ±10 V | No | No | NA |
| [21] (2017) | UVC (4) | LPF | 10, 3 | F | NA | No | No | NA |
| [32] (2018) | MOCF (2), DOCF (1), ACA (5) | LPF | 3, 3 | F | NA | Yes | No | NA |
| [33] (2017) | ACA (5), FD-CF (3) | LPF | 6, 3 | F | NA | Yes | No | NA |
| [34] (2019) | OTA (8), CF (1) | LPF, HPF, BPF, BRF | 0, 3 | G | ±0.75 V | Yes | No | 8.74 μ |
| [35] (2021) | OTA (6), CF (3), ACA (1) | LPF | 0, 1 * | G | ±1.65 V | No | No | 72.6 m |
| [36] (2022) | CDBA (4) | APF | 11, 3 | F | NA | Yes | No | NA |
| [37] (2023) | CFTA (5) | LPF | 2, 3 | G | ±0.9 V | Yes | No | 6.8 m |
| Proposed | VDDDA (3), MOS (6) | LPF | 0, 3 | G | ±0.3 V | Yes | Yes | 663 n |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tasneem, S.; Ranjan, R.K.; Paul, S.K.; Herencsar, N. Power-Efficient Electronically Tunable Fractional-Order Filter. Fractal Fract. 2024, 8, 31. https://doi.org/10.3390/fractalfract8010031
Tasneem S, Ranjan RK, Paul SK, Herencsar N. Power-Efficient Electronically Tunable Fractional-Order Filter. Fractal and Fractional. 2024; 8(1):31. https://doi.org/10.3390/fractalfract8010031
Chicago/Turabian StyleTasneem, Sadaf, Rajeev Kumar Ranjan, Sajal K. Paul, and Norbert Herencsar. 2024. "Power-Efficient Electronically Tunable Fractional-Order Filter" Fractal and Fractional 8, no. 1: 31. https://doi.org/10.3390/fractalfract8010031
APA StyleTasneem, S., Ranjan, R. K., Paul, S. K., & Herencsar, N. (2024). Power-Efficient Electronically Tunable Fractional-Order Filter. Fractal and Fractional, 8(1), 31. https://doi.org/10.3390/fractalfract8010031






