Grey Time Power Model with Caputo Fractional Derivative
Abstract
:1. Introduction
2. Preliminaries
2.1. Caputo Fractional Derivative and Laplace Transform
2.2. Grey Time Power Model and Sequence Smoothness
3. The Construction of the Grey Time Power Model
4. Modeling Method and Process of GM (r, 1, ) Model after Data Transformation
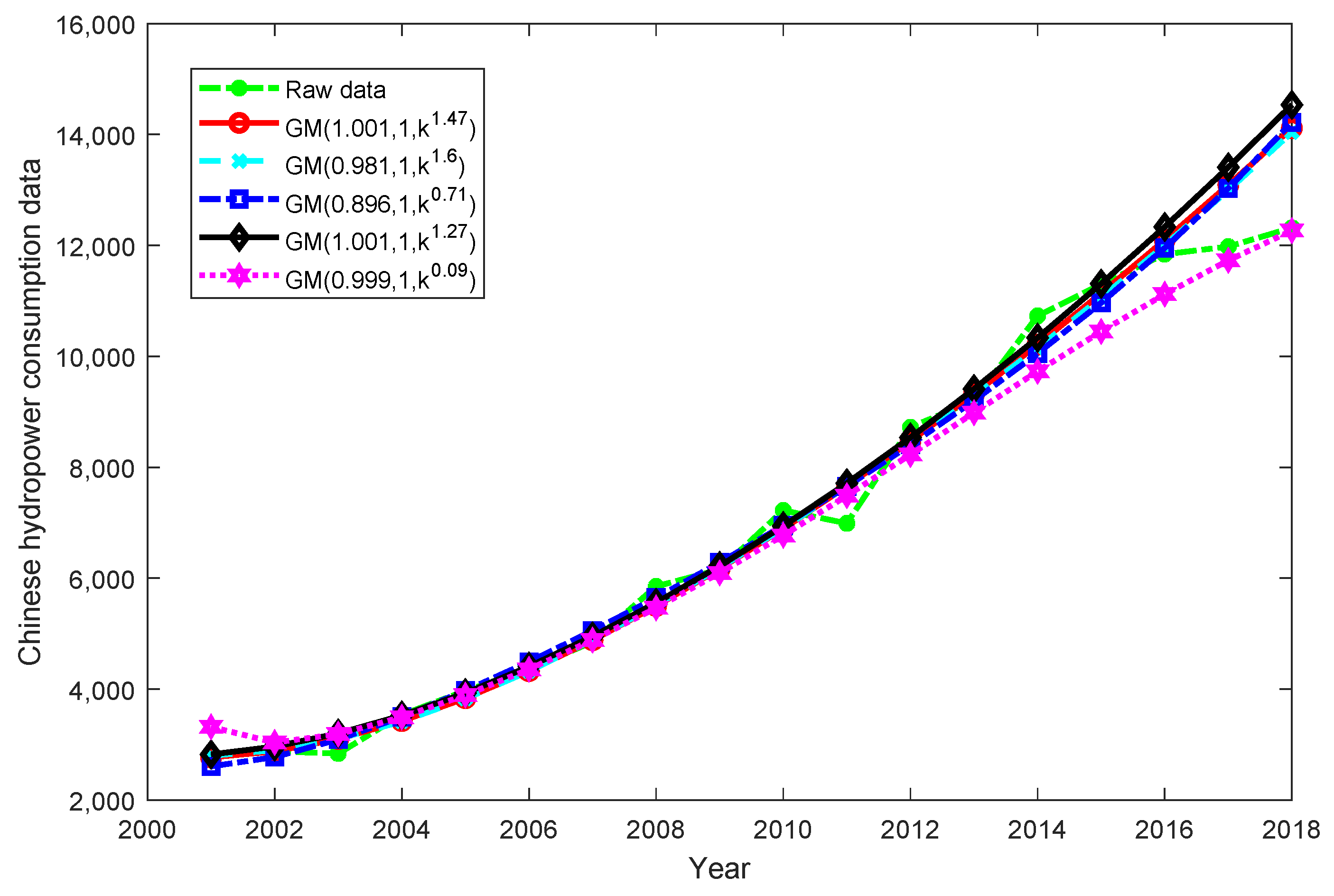
5. Example Application
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Deng, J.L. Grey control system. J. Huazhong Inst. Technol. 1982, 3, 9–18. [Google Scholar]
- Zhu, X.Y.; Dang, Y.G.; Ding, S. Using a self-adaptive grey fractional weighted model to forecast Jiangsu’s electricity consumption in China. Energy 2020, 190, 116417. [Google Scholar] [CrossRef]
- Cao, Y.; Yin, K.D.; Li, X.M. Prediction of direct economic disasters based on the improved GM(1,1) model. J. Grey Syst. 2020, 32, 133–146. [Google Scholar]
- Li, B.; Wei, Y. Optimized grey derivative of GM(1,1). Syst. Eng. 2009, 29, 100–105. [Google Scholar]
- Xie, N.M.; Liu, S.F. Discrete grey forecasting model and its optimization. Appl. Math. Model. 2009, 33, 1173–1186. [Google Scholar] [CrossRef]
- Xie, N.M.; Liu, S.F.; Yang, Y.J.; Yuan, C.Q. On novel grey forecasting model based on non-homogeneous index sequence. Appl. Math. Model. 2013, 37, 5059–5068. [Google Scholar] [CrossRef]
- Cui, J.; Liu, S.F.; Zeng, B. A novel grey forecasting model and its optimization. Appl. Math. Model. 2013, 37, 4399–4406. [Google Scholar] [CrossRef]
- Li, N.; Wang, J.L.; Wu, L.F.; Bentley, Y. Predicting monthly natural gas production in China using a novel grey seasonal model with particle swarm optimization. Energy 2021, 215, 1191–1209. [Google Scholar] [CrossRef]
- Qian, W.Y.; Dang, Y.G.; Liu, S.F. Grey GM (1,1,tα) model with time power term and its application. Syst. Eng. Theory Pract. 2012, 32, 2247–2252. [Google Scholar]
- Wu, Z.H.; Wu, Z.C.; Li, F. Improved grey forecasting model with time power and its modeling mechanism. Control Decis. 2019, 34, 637–641. [Google Scholar]
- Ding, S.; Li, R.J.; Wu, S. Application of a novel structure-adaptative grey model with adjustable time power item for nuclear energy consumption foresting. Appl. Energy 2019, 34, 637–641. [Google Scholar]
- Guo, H.; Xiao, X.P.; Jeffrey, F. Non-equidistance GM (1,1,tα) model with time power and its application. Control Decis. 2015, 30, 1514–1518. [Google Scholar]
- Liu, S.F.; Zhu, C.Y.; Xie, N.M. On discrete grey system forecasting model corresponding with polynomial time-vary sequence. J. Grey Syst. 2013, 25, 1–18. [Google Scholar]
- Luo, D.; Wei, B.L. Grey forecasting model with polynomial term and its optimization. J. Syst. 2017, 29, 58–69. [Google Scholar]
- Wei, B.L.; Xie, N.M.; Hu, A.Q. Optimal solution for novel grey polynomial prediction model. Appl. Math. Model. 2018, 62, 717–727. [Google Scholar] [CrossRef]
- Wei, B.L.; Xie, N.M.; Yang, Y.J. Data-based structure selection for unified discrete grey prediction model. Expert Syst. Appl. 2019, 136, 264–275. [Google Scholar] [CrossRef]
- Shen, Q.Q.; Zhang, Z.J.; Qi, X.C.; Qiu, X.Y. Traffic flow prediction based on fractional seasonal grey model. J. Nantong Univ. Nat. Sci. Ed. 2021, 20, 37–42. [Google Scholar]
- Xu, Z.D.; Dang, Y.G.; Yang, D.L. Discrete grey forecasting model with fractional order polynomial and its application. Control Decis. 2023, 10, 1–7. [Google Scholar]
- Wu, L.F.; Liu, S.F.; Yao, L.G.; Xu, R.T. Using fractional order accumulation to reduce errors from inverse accumulated generating operator of grey model. Soft Comput. 2014, 19, 483–488. [Google Scholar] [CrossRef]
- Yao, T.X.; Wu, L.F.; Liu, S.F.; Cui, W. Non-homogeneous discrete grey model with fractional-order accumulation. Neural Comput. Appl. 2014, 25, 1215–1221. [Google Scholar]
- Zhou, W.J.; Cheng, Y.K.; Ding, S.; Dang, Y.G.; Wang, Z.X. Forecasting Chinese hydropower consumption forecasting by using the repeatability fractional grey time power model. Chin. J. Manag. Sci. 2023, 31, 279–286. [Google Scholar]
- Nie, Y.; Zhou, Y. The scenario research of land use change based on modified GM (1,1). Mathe Pract. Theory 2007, 37, 10–11. [Google Scholar]
- He, B.; Meng, Q. Study on generalization for grey forecasting model. Syst. Eng. Theory Pract. 2002, 9, 137–140. [Google Scholar]
- Cao, C.; Fan, C.J.; Hu, Z.G. Grey forecasting model and its application based on the sine function transformation. J. Math. (PRC) 2013, 33, 697–701. [Google Scholar]
- Zhang, J.; Ran, M.F. Grey modeling based on the transformation of Aarc cotx+B function. Grey Syst. Theory Appl. 2015, 5, 157–164. [Google Scholar] [CrossRef]
- Zhang, J.; Lü, X.; Ran M., F.; Han, G. DGM model based on Anti-cotangent function and its application. J. Grey Syst. 2016, 28, 63–74. [Google Scholar]
- Li, F.Q.; Liu, J.G. Research on data transformation for increasing accuracy of grey forecasting model. Stat. Decis. 2008, 20, 15–17. [Google Scholar]
- Qian, W.Y.; Dang, Y.G. New type of data transformation and its application in GM(1,1) model. Syst. Eng. Electr. 2019, 31, 2879–2881. [Google Scholar]
- Wu, L.F.; Liu, S.F.; Yao, L.G. Grey model with Caputo fractional derivative. Syst. Eng. Theory Pract. 2015, 35, 1311–1315. [Google Scholar]
- Mao, S.H.; Gao, M.Y.; Xiao, X.P.; Zhu, M. A novel fractional grey system model and its application. Appl. Math Model. 2016, 40, 5063–5076. [Google Scholar] [CrossRef]
- Xie, W.L.; Liu, C.X.; Li, W.D.; Wu, W.Z.; Liu, C. Continuous grey model with conformable fractional derivative. Chaos Solit. Fract. 2020, 139, 1–20. [Google Scholar] [CrossRef]
- Kilbas, A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations, 1st ed.; Elsevier: Amsterdam, The Netherlands, 2006; pp. 1–132. [Google Scholar]
- Chen, W.; Sun, H.G.; Li, X.C. Fractional Derivative Modeling of Mechanical and Engineering Problems, 1st ed.; Science Press: Beijing, China, 2010; pp. 68–70. [Google Scholar]
| Model Parameter | r | a | b | c | |
|---|---|---|---|---|---|
| Parameter values | 1.001 | 1.470 | 0.5077 | 0.0978 | 1.2527 |
| Year | GM (1, 1, t) | RFGM (1, 1) | ARLMA | LSSVM | RFGM (1, 1, ) | GM (r, 1, ) |
|---|---|---|---|---|---|---|
| 2016 | 4.104 | 6.124 | 9.508 | 8.424 | 5.161 | 2.160 |
| 2017 | 12.842 | 14.823 | 18.587 | 15.572 | 7.426 | 9.273 |
| 2018 | 19.586 | 21.454 | 28.064 | 24.646 | 1.986 | 14.587 |
| FARE (%) | 4.180 | 3.617 | 5.805 | 3.767 | 3.469 | 3.220 |
| PARE (%) | 12.177 | 14.134 | 18.720 | 16.214 | 4.858 | 8.673 |
| Serial Number | Smooth Ratio of OS | Smooth Ratio of SAT | Stepwise Ratio of OS | Stepwise Ratio of SAT |
|---|---|---|---|---|
| 1 | 1.0380 | 0.8053 | 0.9738 | 0.8053 |
| 2 | 0.5017 | 0.3956 | 0.9825 | 0.8868 |
| 3 | 0.4164 | 0.2187 | 0.9544 | 0.7714 |
| 4 | 0.3301 | 0.1498 | 0.9600 | 0.8349 |
| 5 | 0.2724 | 0.1114 | 0.9586 | 0.8546 |
| 6 | 0.2384 | 0.0847 | 0.9480 | 0.8451 |
| 7 | 0.2322 | 0.0606 | 0.9058 | 0.7758 |
| 8 | 0.1982 | 0.0507 | 0.9463 | 0.8871 |
| 9 | 0.1941 | 0.0373 | 0.8707 | 0.7731 |
| 10 | 0.1573 | 0.0352 | 0.9883 | 0.9804 |
| 11 | 0.1696 | 0.0227 | 0.7583 | 0.6657 |
| 12 | 0.1530 | 0.0184 | 0.8653 | 0.8317 |
| 13 | 0.1547 | 0.0108 | 0.6351 | 0.5949 |
| 14 | 0.1411 | 0.0073 | 0.7003 | 0.6856 |
| 15 | 0.1296 | 0.0041 | 0.5773 | 0.5697 |
| 16 | 0.1160 | 0.0024 | 0.5861 | 0.5836 |
| 17 | 0.1069 | 0 | 0 | 0 |
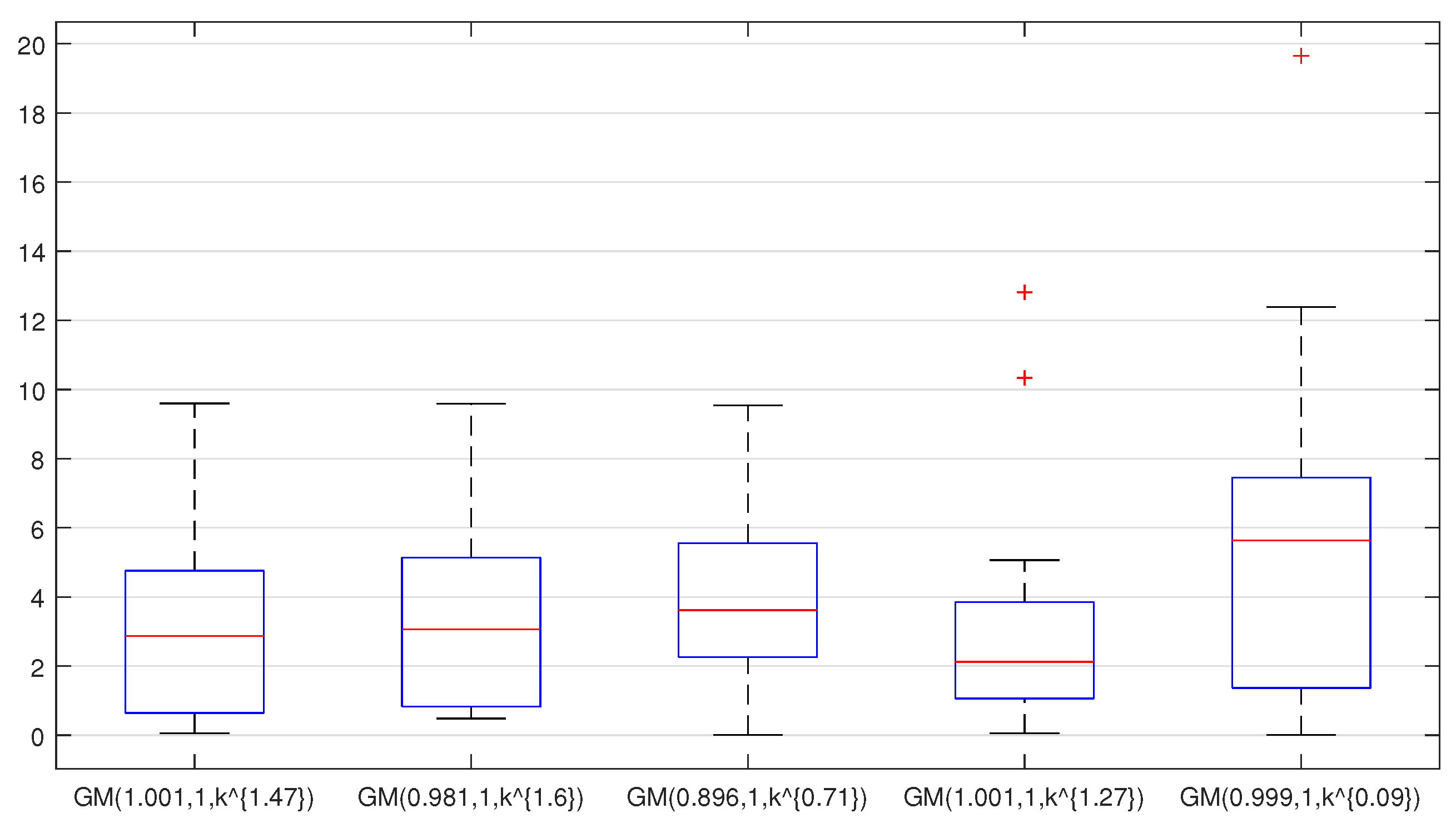
| Year | GM (1.001, 1, ) | GM (1.001, 1, ) | GM (0.981, 1, ) | GM (0.896, 1, ) | GM (0.999, 1, ) |
|---|---|---|---|---|---|
| 2016 | 2.160 | 4.165 | 1.380 | 0.953 | 5.704 |
| 2017 | 9.273 | 11.936 | 8.494 | 8.7825 | 0.051 |
| 2018 | 14.587 | 17.995 | 13.981 | 15.427 | 3.904 |
| FARE (%) | 3.220 | 3.358 | 3.420 | 3.906 | 4.824 |
| PARE (%) | 8.673 | 11.365 | 7.952 | 8.387 | 3.220 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, P.; Gu, C.-Y. Grey Time Power Model with Caputo Fractional Derivative. Fractal Fract. 2024, 8, 25. https://doi.org/10.3390/fractalfract8010025
Hu P, Gu C-Y. Grey Time Power Model with Caputo Fractional Derivative. Fractal and Fractional. 2024; 8(1):25. https://doi.org/10.3390/fractalfract8010025
Chicago/Turabian StyleHu, Pan, and Chuan-Yun Gu. 2024. "Grey Time Power Model with Caputo Fractional Derivative" Fractal and Fractional 8, no. 1: 25. https://doi.org/10.3390/fractalfract8010025
APA StyleHu, P., & Gu, C.-Y. (2024). Grey Time Power Model with Caputo Fractional Derivative. Fractal and Fractional, 8(1), 25. https://doi.org/10.3390/fractalfract8010025





