Forecasting the Active Cases of COVID-19 via a New Stochastic Rayleigh Diffusion Process
Abstract
:1. Introduction
2. The Proposed SRDP
2.1. Definition of the SDE of the SRDP
2.2. The Explicit Form of the SRDP
2.3. Characteristics of the SRDP
2.3.1. The TPDF of the Process
2.3.2. The r-th Conditional and Its Mean Functions
2.4. Remark
3. Inference on the SRDP
3.1. The Model Estimation by Using the ML
3.2. The Model Characteristics Estimation
3.2.1. The MF and CMF Estimation
3.2.2. Confidence Interval
3.3. Optimization via the SA Algorithm
3.3.1. The Objective Function
3.3.2. Bounding the Search Space
- 1.
- Choose the first solution arbitrarily in the obtained bounded subspace.
- 2.
- The initial temperature must be sufficiently high for a good probability in accepting a less good solution to be at least 80% (see [26]).
- 3.
- The cooling process is with being constant. Typically, .
- 4.
- The number of solutions generated at a temperature T is determined by the length L of the chain.
- 5.
- The stopping conditions are indicated when the system reaches the required energy level (freezing temperature), or when an acceptance ratio is reached. In this case, the total number of generated solutions is given. As for the maximal number of iteration, it is fixed to 1000.
4. Numerical Simulation of the SRDP
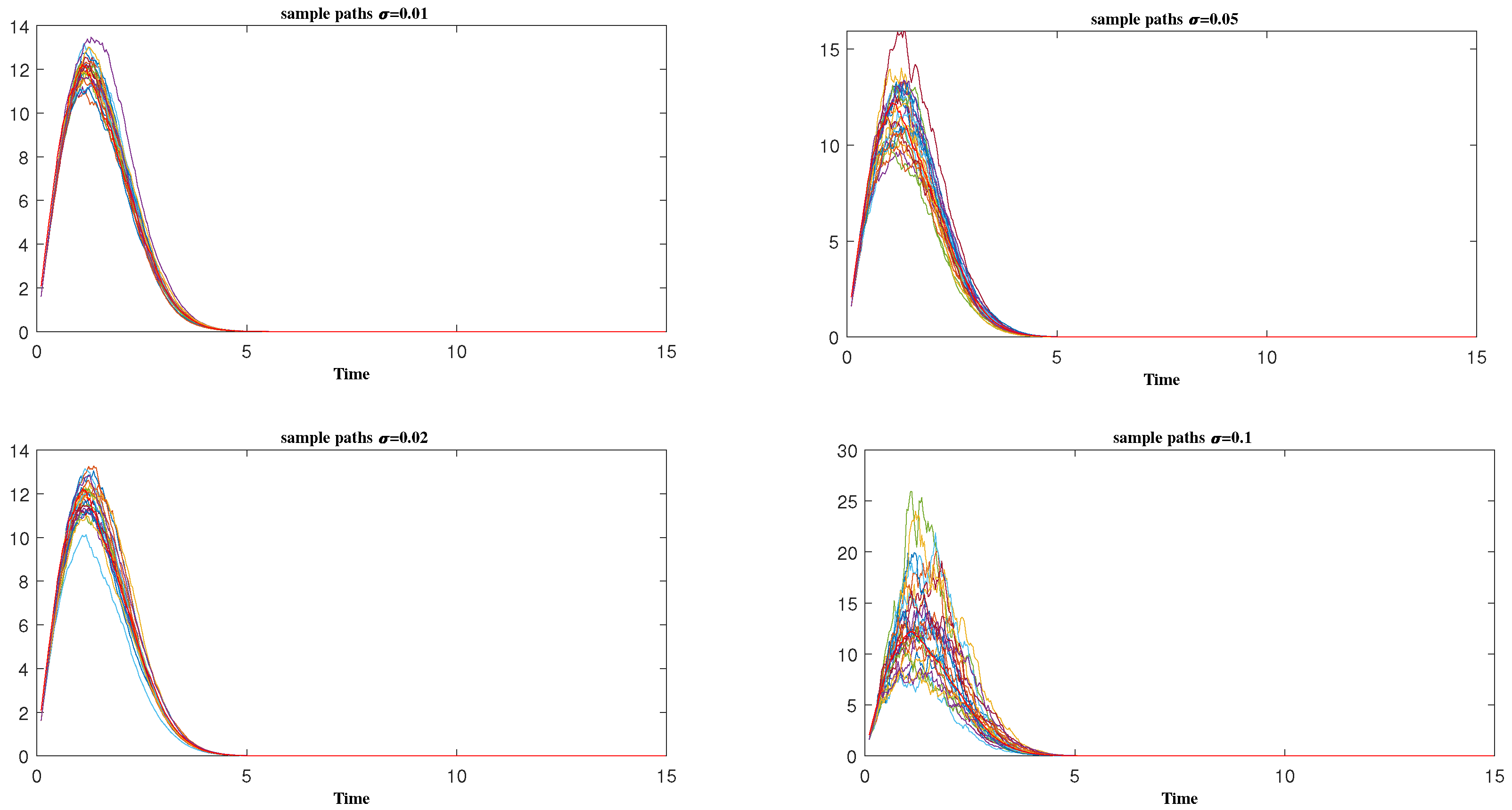
4.1. Simulation of Sample Path of the SRDP
4.2. Parameter Estimation of the SRDP
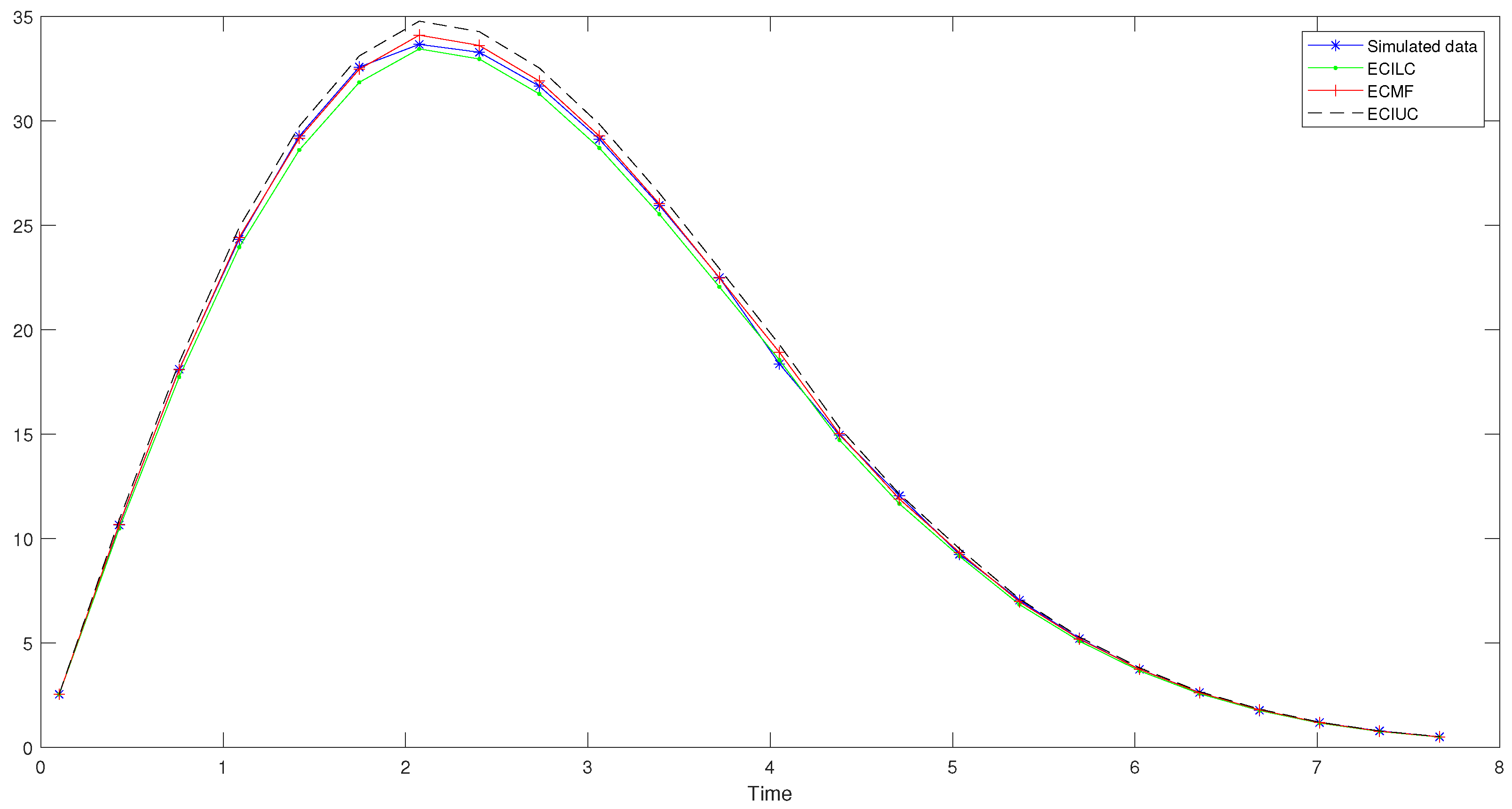
4.3. Prediction Study Using EMF and ECMF
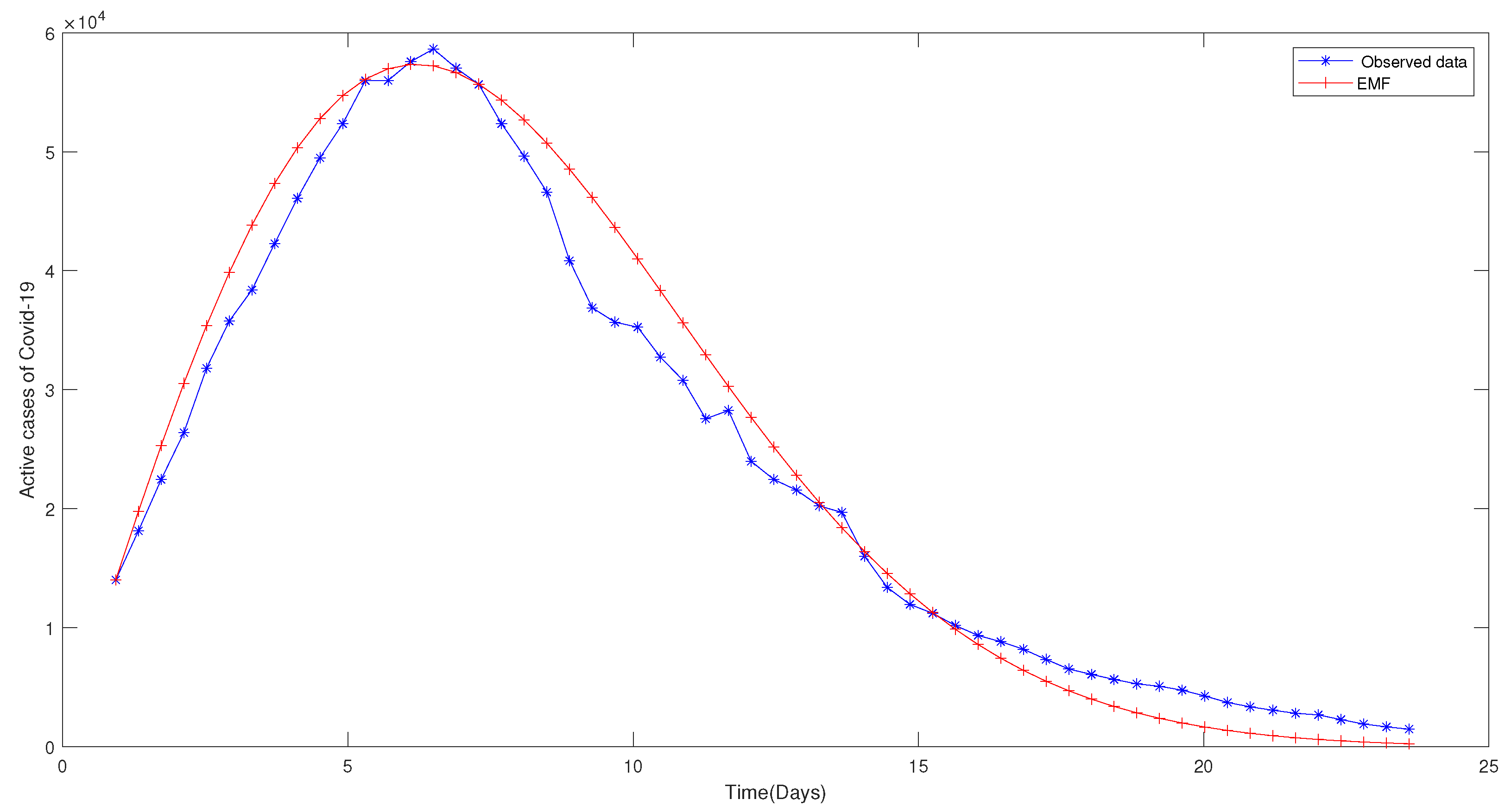
5. Application to Real Data
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Román-Román, P.; Torres-Ruiz, F. A stochastic model related to the Richards-type growth curve. Estimation by means of simulated annealing and variable neighborhood search. Appl. Math. Comput. 2015, 266, 579–598. [Google Scholar] [CrossRef]
- Gutiérrez, R.; Gutiérrez-Sánchez, R.; Nafidi, A. The trend of the total stock of the private car-petrol in Spain: Stochastic modelling using a new gamma diffusion process. Appl. Energy 2009, 86, 18–24. [Google Scholar] [CrossRef]
- Nafidi, A.; Bahij, M.; Achchab, B.; Gutiérrez-Sànchez, R. The stochastic Weibull diffusion process: Computational aspects and simulation. Appl. Math. Comput. 2019, 348, 575–587. [Google Scholar] [CrossRef]
- Nafidi, A.; El-Azri, A.; Gutiérrez-Sànchez, R. The stochastic modified Lundqvist-Korf diffusion process: Statistical and computational aspects and application to modeling of the CO2 emission in Morocco. Stoch. Environ. Res. Risk Assess. 2022, 36, 1163–1176. [Google Scholar] [CrossRef]
- Capocelli, R.M.; Ricciardi, L.M. A diffusion model for population growth in random environment. Theor. Popul. Biol. 1974, 25, 28–41. [Google Scholar] [CrossRef]
- Ricciardi, L.M.; Sacerdote, L.; Sato, S. Diffusion approximation and first-passage-time problem for a model neuron II. Outline of a computation method. Math. Biosci. 1983, 64, 29–44. [Google Scholar] [CrossRef]
- Capocelli, R.; Ricciard, L. Growth with regulationin random environment. Kybernetik 1974, 15, 147–157. [Google Scholar] [CrossRef]
- Giovanis, A.N.; Skaidas, C.H. A Stochastic Logistic Innovation Diffusion Model Studying the Electricity Consumption in Greece and the United States. Technol. Forecast. Soc. Chang. 1999, 61, 235–246. [Google Scholar] [CrossRef]
- Danane, J.; Allali, K.; Hammouch, Z.; Nisar, K.S. Mathematical analysis and simulation of a stochastic COVID-19 Lévy jump model with isolation strategy. Results Phys. 2021, 23, 103994. [Google Scholar] [CrossRef] [PubMed]
- Varotsos, C.A.; Krapivin, V.F. A new model for the spread of COVID-19 and the improvement of safety. Saf. Sci. 2020, 132, 104962. [Google Scholar] [CrossRef]
- Jianguo, S.; Miaomiao, G.; Daqing, J. Threshold Dynamics and the Density Function of the Stochastic Coronavirus Epidemic Model. Fractal Fract. 2022, 6, 245. [Google Scholar]
- Nicola, F. On COVID-19 diffusion in Italy: Data analysis and possible outcome. Vojnoteh. Glas. 2020, 68, 216–224. [Google Scholar]
- Rayleigh, L.F.R.S. XII. On the resultant of a large number of vibrations of the same pitch and of arbitrary phasel. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1880, 10, 73–78. [Google Scholar] [CrossRef]
- Rayleigh, L. Philos. Mag. Lett. 1902, 32, 473.
- Giorno, V.; Nobile, A.; Ricciardi, L.; Sacerdote, L. Some remarks on the Rayleigh process. J. Appl. Probab. 1986, 23, 398–408. [Google Scholar] [CrossRef]
- Bibby, B.M.; Sorensen, M. A hyperbolic diffusion model for stock prices. Financ. Stochast 1996, 1, 25–41. [Google Scholar] [CrossRef]
- Ait-Sahalia, Y. Maximum-likelihood estimation of discretely sampled diffusion: A closed-form approximation approach. Econometrica 2019, 70, 223–262. [Google Scholar] [CrossRef]
- Kloeden, P.; Platen, E. The Numerical Solution of Stochastic Differential Equations; Springer: Berlin/Heidelberg, Germany, 1992. [Google Scholar]
- Chakroune, Y.; Nafidi, A. A new stochastic diffusion process based on the Rayleigh density function. Procedia Comput. Sci. 2022, 201, 758–763. [Google Scholar] [CrossRef]
- Gutiérrez, R.; Gutiérrez-Sánchez, R.; Nafidi, A. Trend analysis and computational statistical estimation in a stochastic Rayleigh model: Simulation and application. Math. Comput. Simul. 2008, 77, 209–217. [Google Scholar] [CrossRef]
- Cho-Hoi, H.; Chi-Fai, L.; Chi-Hei, L. Modelling Foreign Exchange Interventions under Rayleigh Process: Applications to Swiss Franc Exchange Rate Dynamics. Entropy 2022, 24, 888. [Google Scholar]
- Gutiérrez, R.; Gutiérrez-Sánchez, R.; Nafidi, A. The Stochastic Rayleigh diffusion model: Statistical inference and computational aspects. Applications to modelling of real cases. Appl. Math. Comput. 2006, 175, 628–644. [Google Scholar] [CrossRef]
- Arnold, L. Stochastic Differential Equations; John Wiley and Sons: New York, NY, USA, 1973. [Google Scholar]
- Zehna, P. Invariance of maximum likelihood estimators. Ann. Math. Stat. 1996, 37, 744. [Google Scholar] [CrossRef]
- Katsamaki, A.; Skiadas, C. Analytic solution and estimation of parameters on a stochastic exponential model for technology diffusion process. Appl. Stoch. Model. Data Anal 1995, 11, 59–75. [Google Scholar] [CrossRef]
- Kirkpatrick, S.; Gelatt, D.; Vecchi, M. Optimization by simulated annealing. Science 1983, 220, 671–680. [Google Scholar] [CrossRef]
- Gutiérrez-jáimez, R.; Román, P.; Romero, D.; Serrano, J.J.; Torres, F. A new Gompertz-type diffusion process with application to random growth. Math. Biosci. 2007, 208, 147–165. [Google Scholar] [CrossRef]


| N | ||||||
|---|---|---|---|---|---|---|
| 100 | 0.496327 | 0.022891 | 0.004853 | 0.001140 | 0.009778 | 0.049805 |
| 200 | 0.522479 | 0.005428 | 0.013147 | 0.000554 | 0.025162 | 0.102109 |
| 500 | 0.495557 | 0.010547 | 0.014024 | 0.000763 | 0.028301 | 0.072424 |
| MAPE | Interpretation |
|---|---|
| <10 | Highly accurate forecasting |
| 20–30 | Good forecasting |
| 30–50 | Reasonable forecasting |
| >50 | Inaccurate forecasting |
| MAE | RMSE | MAPE |
|---|---|---|
| 0.10925 | 0.17931 | 3.56523 |
| Parameters | ||
|---|---|---|
| estimated values | 0.20174 | 0.02124 |
| i | EMF | ECMF | ECI | |
|---|---|---|---|---|
| 1 | 2.53160 | 02.53160 | 02.53160 | [02.53160 02.53160] |
| 2 | 10.64310 | 10.67555 | 10.67555 | [10.46910 10.88499] |
| 3 | 18.10549 | 18.13428 | 18.07915 | [17.72953 18.43385] |
| 4 | 24.33010 | 24.45975 | 24.42093 | [23.94867 24.90004] |
| 5 | 29.26810 | 29.32107 | 29.16564 | [28.60162 29.73784] |
| 6 | 32.57670 | 32.53200 | 32.47323 | [31.84525 33.11032] |
| 7 | 33.66320 | 34.05875 | 34.10554 | [33.44599 34.77466] |
| 8 | 33.28419 | 34.00826 | 33.61329 | [32.96326 34.27275] |
| 9 | 31.66570 | 32.60080 | 31.90671 | [31.28968 32.53268] |
| 10 | 29.12040 | 30.13244 | 29.26814 | [28.70214 29.84235] |
| 11 | 25.95149 | 26.93398 | 26.02936 | [25.52600 26.54003] |
| 12 | 22.49320 | 23.33262 | 22.48150 | [22.04674 22.92257] |
| 13 | 18.36149 | 19.62098 | 18.91509 | [18.54931 19.28619] |
| 14 | 14.95020 | 16.03638 | 15.00699 | [14.71678 15.30141] |
| 15 | 12.04740 | 12.75082 | 11.88717 | [11.65729 12.12038] |
| 16 | 09.23780 | 09.87071 | 09.32617 | [09.14582 09.50914] |
| 17 | 07.04150 | 07.44401 | 06.96670 | [06.83197 07.10338] |
| 18 | 05.20210 | 05.47186 | 05.17599 | [05.07589 05.27754] |
| 19 | 03.73410 | 03.92209 | 03.72873 | [03.65662 03.80188] |
| 20 | 02.62060 | 02.74225 | 02.61081 | [02.56032 02.66203] |
| 21 | 01.76380 | 01.87084 | 01.78784 | [01.75327 01.82292] |
| 22 | - | 01.24572 | 01.17444 | [01.15173 01.19748] |
| 23 | - | 00.80975 | 00.76449 | [00.74971 00.77949] |
| 24 | - | 00.51394 | 00.49429 | [00.48473 00.50399] |
| COVID-19 Active Cases | EMF | ECMF | ECCB |
|---|---|---|---|
| 14,024 | 14,024 | 14,024 | [14,024 14,024] |
| 18,152 | 19,774 | 19,774 | [18,347 21,281] |
| 22,457 | 25,268 | 23,195 | [21,522 24,963] |
| 26,396 | 30,438 | 27,052 | [25,101 29,114] |
| 31,808 | 35,225 | 30,547 | [28,343 32,875] |
| 35,768 | 39,575 | 35,736 | [33,158 38,460] |
| 38,386 | 43,446 | 39,266 | [36,433 42,259] |
| 42,282 | 46,802 | 41,352 | [38,368 44,504] |
| 46,081 | 49,622 | 44,829 | [41,595 48,246] |
| 49,491 | 51,890 | 48,188 | [44,711 51,860] |
| 52,350 | 53,604 | 51,126 | [47,437 55,022] |
| 55,971 | 54,770 | 53,488 | [49,629 57,565] |
| 55,982 | 55,402 | 56,617 | [52,532 60,932] |
| 57,568 | 55,525 | 56,106 | [52,058 60,382] |
| 58,631 | 55,168 | 57,198 | [53,071 61,558] |
| 57,021 | 54,369 | 57,782 | [53,613 62,186] |
| 55,655 | 53,169 | 55,762 | [51,739 60,012] |
| 52,353 | 51,613 | 54,027 | [50,129 58,144] |
| 49,613 | 49,750 | 50,463 | [46,822 54,309] |
| 46,610 | 47,629 | 47,497 | [44,070 51,117] |
| 40,845 | 45,298 | 44,329 | [41,131 47,708] |
| 36,884 | 42,806 | 38,598 | [35,814 41,540] |
| 35,677 | 40,200 | 34,639 | [32,140 37,279] |
| 35,255 | 37,524 | 33,302 | [30,899 35,840] |
| 32,746 | 34,818 | 32,713 | [30,352 35,206] |
| 30,791 | 32,119 | 30,208 | [28,028 32,510] |
| 27,560 | 29,460 | 28,242 | [26,204 30,394] |
| 28,257 | 26,869 | 25,136 | [23,323 27,052] |
| 23,991 | 24,370 | 25,629 | [23,780 27,582] |
| 22,462 | 21,983 | 21,641 | [20,079 23,290] |
| 21,569 | 19,723 | 20,152 | [18,698 21,688] |
| 20,242 | 17,600 | 19,248 | [17,859 20,715] |
| 19,694 | 15,623 | 17,968 | [16,672 19,338] |
| 16,014 | 13,796 | 17,390 | [16,136 18,716] |
| 13,392 | 12,119 | 14,068 | [13,053 15,140] |
| 11,961 | 10,591 | 11,704 | [10,859 12,596] |
| Prediction | |||
| - | 09,209 | 10,400 | [09,650 11,192] |
| - | 07,966 | 09,707 | [09,007 10,447] |
| - | 06,857 | 08,775 | [08,142 09,444] |
| - | 05,872 | 08,012 | [07,434 08,623] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nafidi, A.; Chakroune, Y.; Gutiérrez-Sánchez, R.; Tridane, A. Forecasting the Active Cases of COVID-19 via a New Stochastic Rayleigh Diffusion Process. Fractal Fract. 2023, 7, 660. https://doi.org/10.3390/fractalfract7090660
Nafidi A, Chakroune Y, Gutiérrez-Sánchez R, Tridane A. Forecasting the Active Cases of COVID-19 via a New Stochastic Rayleigh Diffusion Process. Fractal and Fractional. 2023; 7(9):660. https://doi.org/10.3390/fractalfract7090660
Chicago/Turabian StyleNafidi, Ahmed, Yassine Chakroune, Ramón Gutiérrez-Sánchez, and Abdessamad Tridane. 2023. "Forecasting the Active Cases of COVID-19 via a New Stochastic Rayleigh Diffusion Process" Fractal and Fractional 7, no. 9: 660. https://doi.org/10.3390/fractalfract7090660
APA StyleNafidi, A., Chakroune, Y., Gutiérrez-Sánchez, R., & Tridane, A. (2023). Forecasting the Active Cases of COVID-19 via a New Stochastic Rayleigh Diffusion Process. Fractal and Fractional, 7(9), 660. https://doi.org/10.3390/fractalfract7090660










