A Matrix Transform Technique for Distributed-Order Time-Fractional Advection–Dispersion Problems
Abstract
:1. Introduction
2. Preliminary Notions and Used Notation
- 1.
- ,
- 2.
- ,
- 3.
- 4.
- ,
- 5.
- .
3. Numerical Method
3.1. Matrix Transform Method for Approximating the Riesz-Space Fractional Derivative
3.2. Numerical Scheme Based on the Simpson Formula for Equation (22)
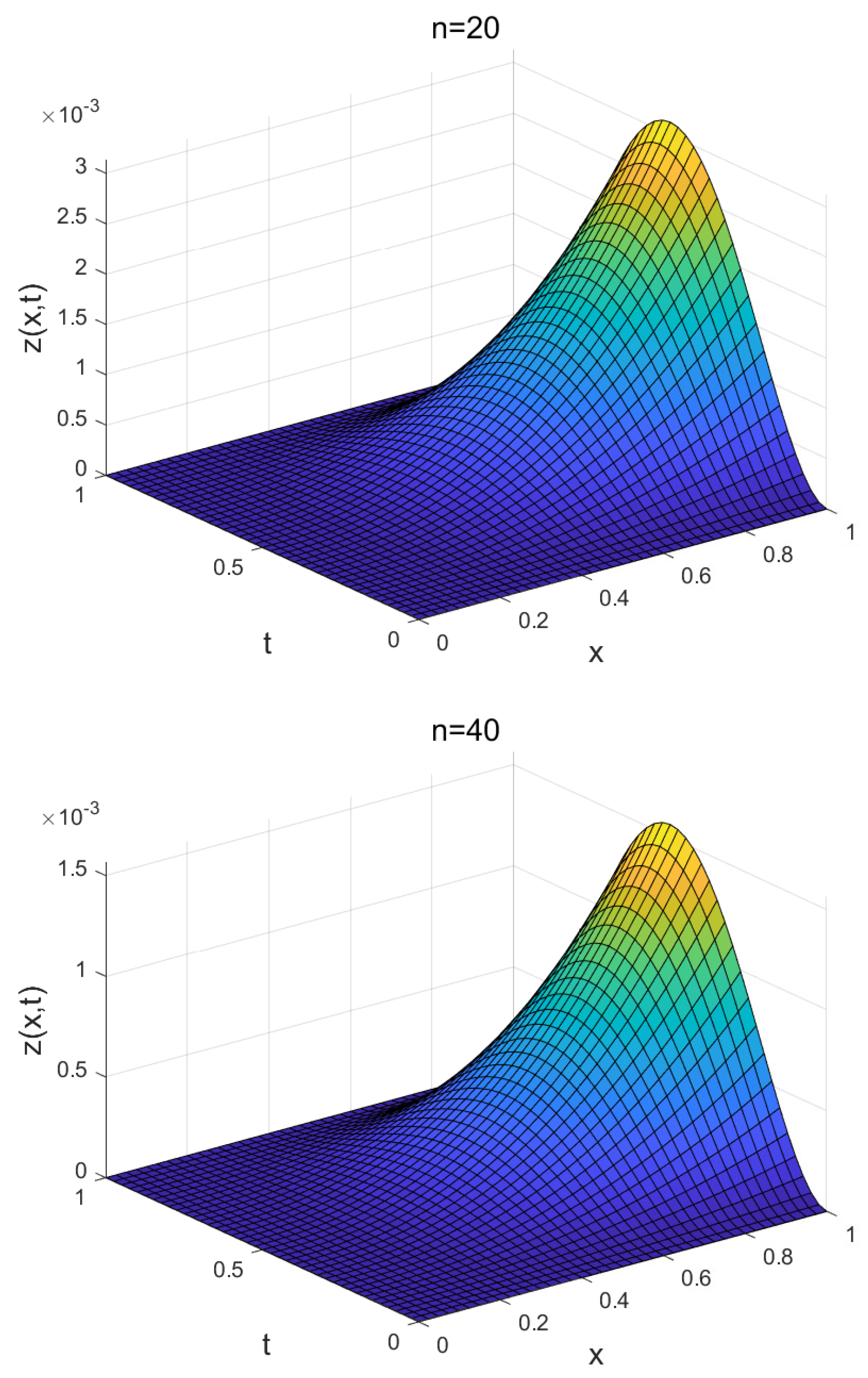
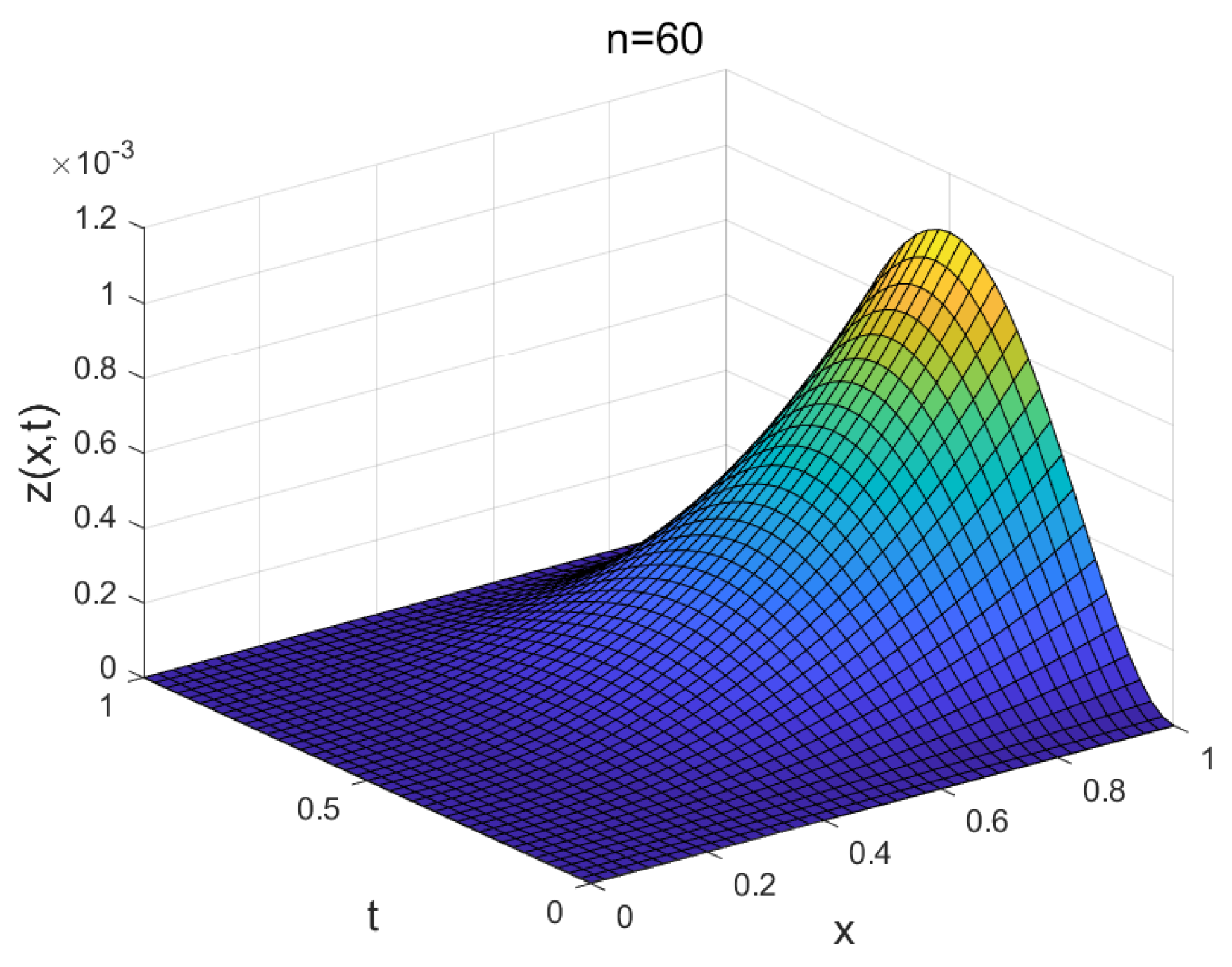
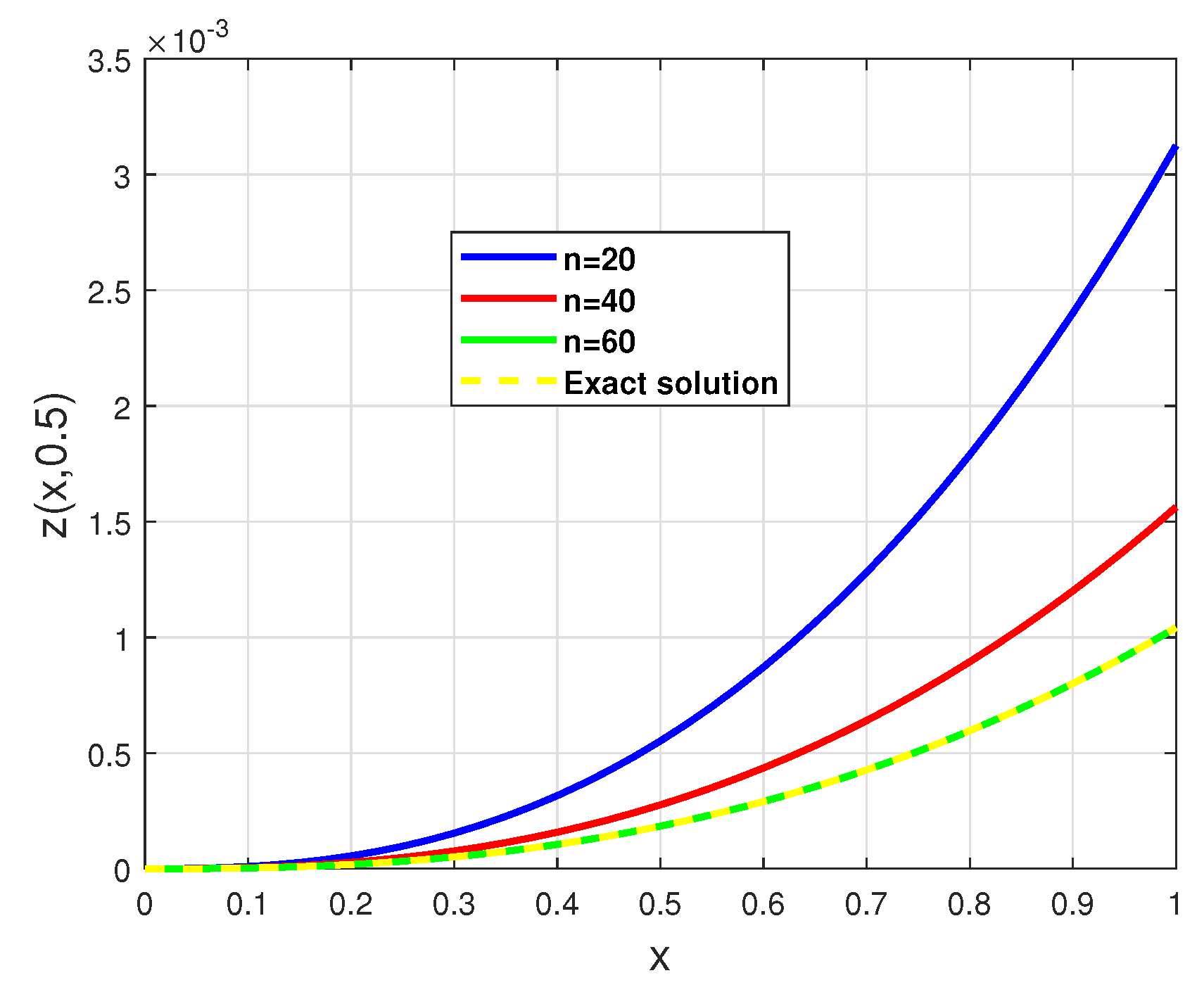
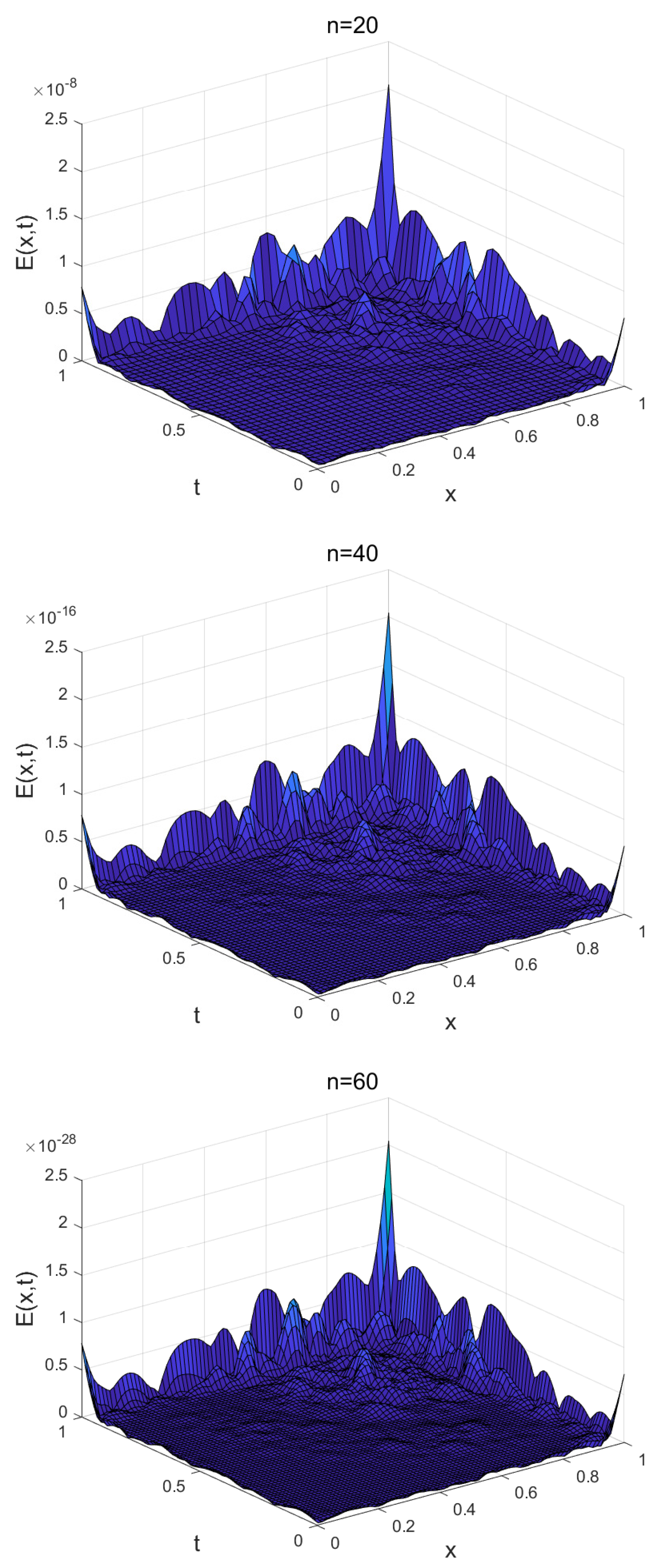
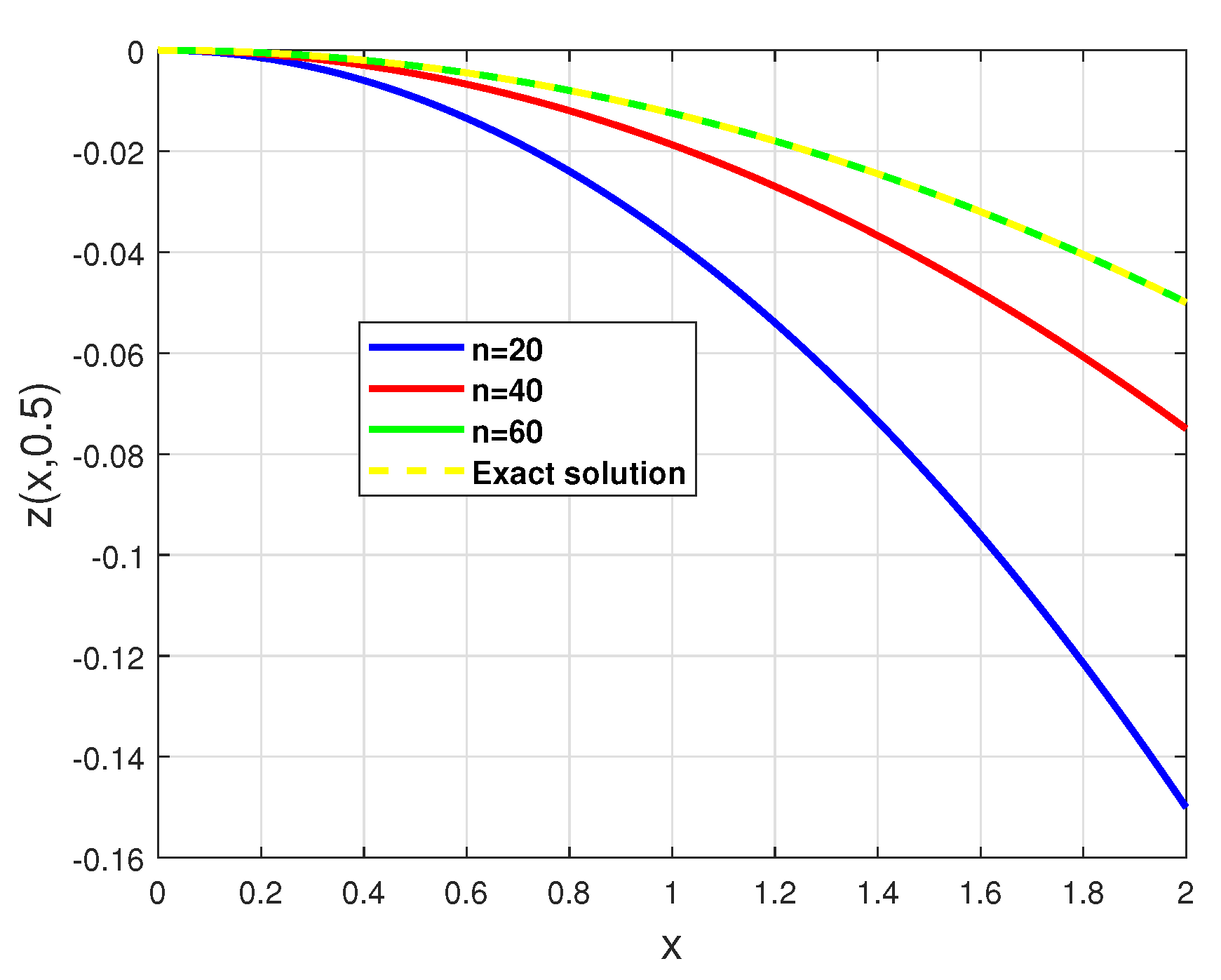
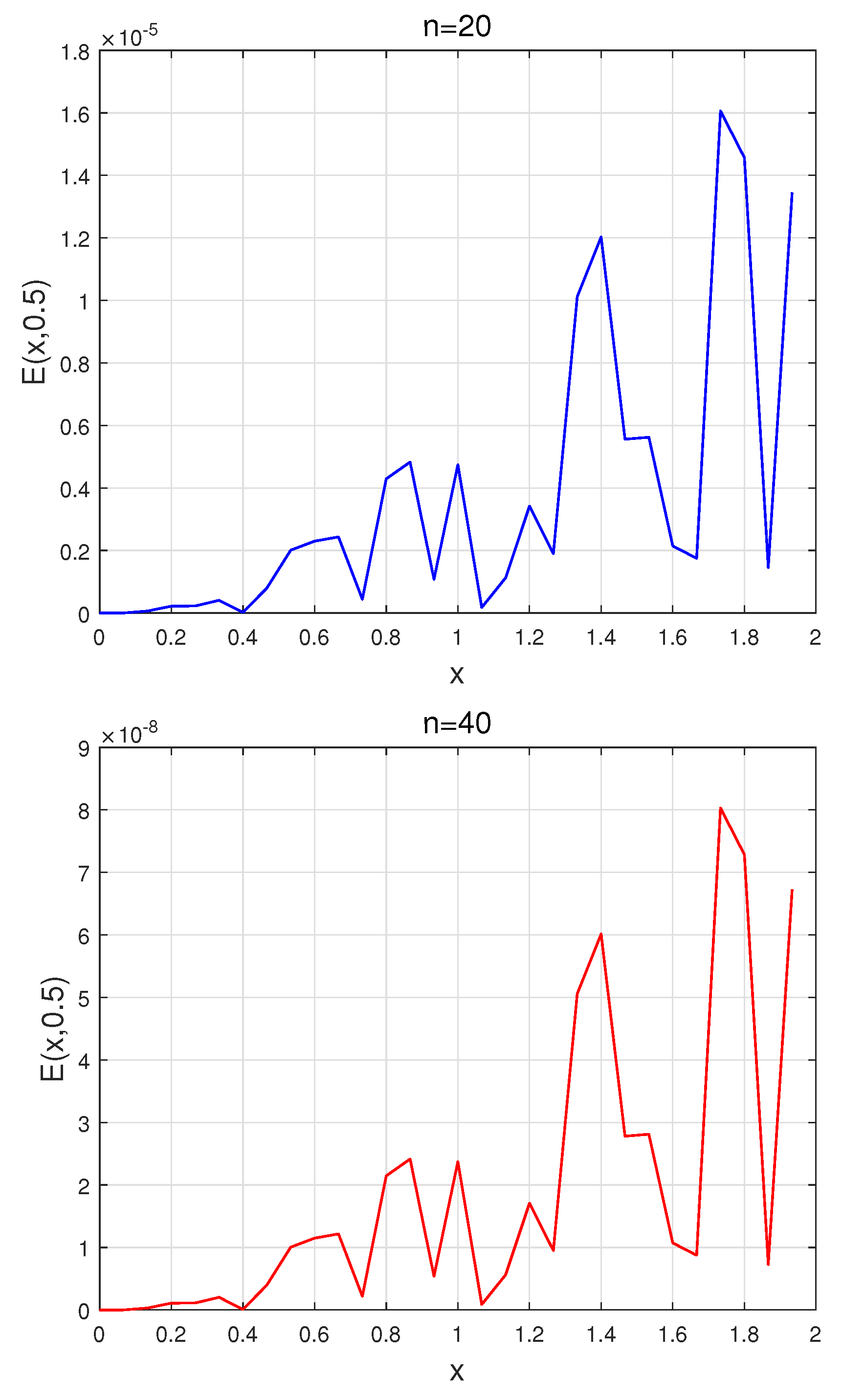
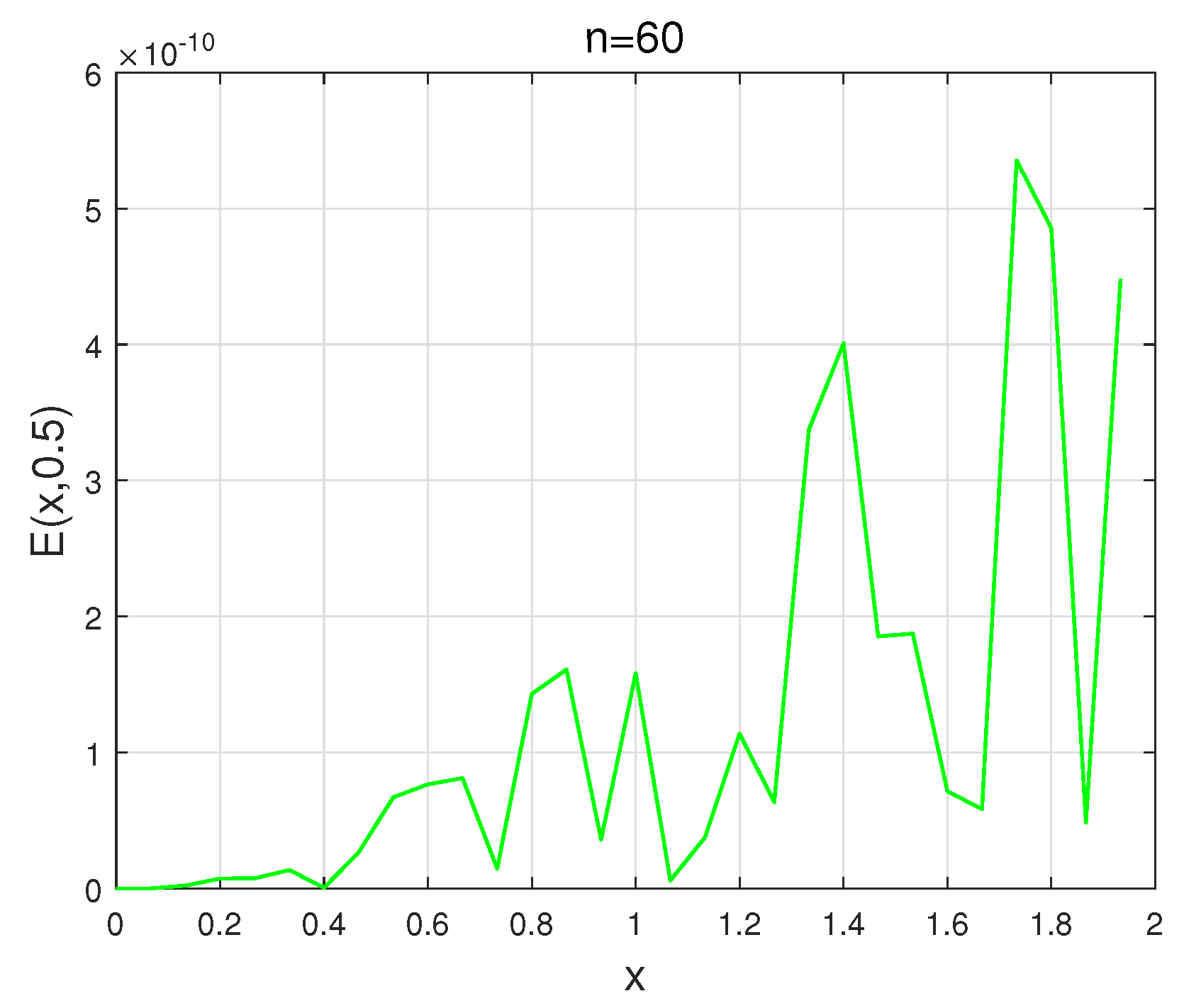
4. Illustrative Examples
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Podulbny, I. Fractional Differential Equations; Academic Press: New York, NY, USA, 1999. [Google Scholar]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations; Elsevier: Amsterdam, The Netherlands, 2006; Volume 204. [Google Scholar]
- Mainardi, F.; Pagnini, G.; Gorenflo, R. Some aspects of fractional diffusion equations of single and distributed order. Appl. Math. Comput. 2007, 187, 295–305. [Google Scholar] [CrossRef]
- Derakhshan, M.; Aminataei, A. New approach for the chaotic dynamical systems involving Caputo-Prabhakar fractional derivative using Adams-Bashforth scheme. J. Differ. Equ. Appl. 2021, 1–17. [Google Scholar] [CrossRef]
- Ata, E.; Kıymaz, I.O. New generalized Mellin transform and applications to partial and fractional differential equations. Int. J. Math. Comput. Eng. 2023, 1, 45–66. [Google Scholar] [CrossRef]
- Jafari, H.; Goswami, P.; Dubey, R.; Sharma, S.; Chaudhary, A. Fractional SZIR Model of Zombies Infection. Authorea 2022. [Google Scholar] [CrossRef]
- Singh, R.; Mishra, J.; Gupta, V.K. The dynamical analysis of a Tumor Growth model under the effect of fractal fractional Caputo-Fabrizio derivative. Int. J. Math. Comput. Eng. 2023, 1, 115–126. [Google Scholar] [CrossRef]
- Qin, S.; Liu, F.; Turner, I.; Vegh, V.; Yu, Q.; Yang, Q. Multi-term time-fractional Bloch equations and application in magnetic resonance imaging. J. Comput. Appl. Math. 2017, 319, 308–319. [Google Scholar] [CrossRef]
- Srivastava, V.; Rai, K. A multi-term fractional diffusion equation for oxygen delivery through a capillary to tissues. Math. Comput. Model. 2010, 51, 616–624. [Google Scholar] [CrossRef]
- Huang, J.; Zhang, J.; Arshad, S.; Tang, Y. A numerical method for two-dimensional multi-term time-space fractional nonlinear diffusion-wave equations. Appl. Numer. Math. 2021, 159, 159–173. [Google Scholar] [CrossRef]
- Lorenzo, C.F.; Hartley, T.T. Variable order and distributed order fractional operators. Nonlinear Dyn. 2002, 29, 57–98. [Google Scholar] [CrossRef]
- Atanackovic, T. A generalized model for the uniaxial isothermal deformation of a viscoelastic body. Acta Mech. 2002, 159, 77–86. [Google Scholar] [CrossRef]
- Zaky, M.A.; Machado, J.T. On the formulation and numerical simulation of distributed-order fractional optimal control problems. Commun. Nonlinear Sci. Numer. Simul. 2017, 52, 177–189. [Google Scholar] [CrossRef]
- Yuttanan, B.; Razzaghi, M. Legendre wavelets approach for numerical solutions of distributed order fractional differential equations. Appl. Math. Model. 2019, 70, 350–364. [Google Scholar] [CrossRef]
- Fardi, M.; Zaky, M.; Hendy, A. Nonuniform difference schemes for multi-term and distributed-order fractional parabolic equations with fractional Laplacian. Math. Comput. Simul. 2023, 206, 614–635. [Google Scholar] [CrossRef]
- Diethelm, K.; Ford, N.J. Numerical analysis for distributed-order differential equations. J. Comput. Appl. Math. 2009, 225, 96–104. [Google Scholar] [CrossRef]
- Ford, N.J.; Luisa Morgado, M.; Rebelo, M. An implicit finite difference approximation for the solution of the diffusion equation with distributed order in time. Electron. Trans. Numer. Anal. 2015, 44, 289–305. [Google Scholar]
- Ye, H.; Liu, F.; Anh, V.; Turner, I. Numerical analysis for the time distributed-order and Riesz space fractional diffusions on bounded domains. IMA J. Appl. Math. 2015, 80, 825–838. [Google Scholar] [CrossRef]
- Yang, X.; Zhang, H.; Xu, D. WSGD-OSC scheme for two-dimensional distributed order fractional reaction–diffusion equation. J. Sci. Comput. 2018, 76, 1502–1520. [Google Scholar] [CrossRef]
- Hu, X.; Liu, F.; Turner, I.; Anh, V. An implicit numerical method of a new time distributed-order and two-sided space-fractional advection-dispersion equation. Numer. Algorithms 2016, 72, 393–407. [Google Scholar] [CrossRef]
- Zaky, M.A.; Machado, J.T. Multi-dimensional spectral tau methods for distributed-order fractional diffusion equations. Comput. Math. Appl. 2020, 79, 476–488. [Google Scholar] [CrossRef]
- Shi, Y.; Liu, F.; Zhao, Y.; Wang, F.; Turner, I. An unstructured mesh finite element method for solving the multi-term time fractional and Riesz space distributed-order wave equation on an irregular convex domain. Appl. Math. Model. 2019, 73, 615–636. [Google Scholar] [CrossRef]
- Moghaddam, B.; Machado, J.T.; Morgado, M. Numerical approach for a class of distributed order time fractional partial differential equations. Appl. Numer. Math. 2019, 136, 152–162. [Google Scholar] [CrossRef]
- Chen, H.; Lü, S.; Chen, W. Finite difference/spectral approximations for the distributed order time fractional reaction–diffusion equation on an unbounded domain. J. Comput. Phys. 2016, 315, 84–97. [Google Scholar] [CrossRef]
- Morgado, M.L.; Rebelo, M.; Ferras, L.L.; Ford, N.J. Numerical solution for diffusion equations with distributed order in time using a Chebyshev collocation method. Appl. Numer. Math. 2017, 114, 108–123. [Google Scholar] [CrossRef]
- Zaky, M.; Doha, E.; Tenreiro Machado, J. A spectral numerical method for solving distributed-order fractional initial value problems. J. Comput. Nonlinear Dyn. 2018, 13, 101007. [Google Scholar] [CrossRef]
- Fei, M.; Huang, C. Galerkin–Legendre spectral method for the distributed-order time fractional fourth-order partial differential equation. Int. J. Comput. Math. 2020, 97, 1183–1196. [Google Scholar] [CrossRef]
- Ilic, M.; Liu, F.; Turner, I.; Anh, V. Numerical approximation of a fractional-in-space diffusion equation (II)–with nonhomogeneous boundary conditions. Fract. Calc. Appl. Anal. 2006, 9, 333–349. [Google Scholar]
- Zhang, H.; Liu, F.; Jiang, X.; Zeng, F.; Turner, I. A Crank–Nicolson ADI Galerkin–Legendre spectral method for the two-dimensional Riesz space distributed-order advection–diffusion equation. Comput. Math. Appl. 2018, 76, 2460–2476. [Google Scholar] [CrossRef]
- Ansari, A.; Derakhshan, M.H. On spectral polar fractional Laplacian. Math. Comput. Simul. 2023, 206, 636–663. [Google Scholar] [CrossRef]
- Li, C.; Zeng, F. Numerical Methods for Fractional Calculus; CRC Press: Boca Raton, FL, USA, 2015; Volume 24. [Google Scholar]
- Salkuyeh, D.K. On the finite difference approximation to the convection–diffusion equation. Appl. Math. Comput. 2006, 179, 79–86. [Google Scholar] [CrossRef]




| 38 | 78 | 159 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Derakhshan, M.; Hendy, A.S.; Lopes, A.M.; Galhano, A.; Zaky, M.A. A Matrix Transform Technique for Distributed-Order Time-Fractional Advection–Dispersion Problems. Fractal Fract. 2023, 7, 649. https://doi.org/10.3390/fractalfract7090649
Derakhshan M, Hendy AS, Lopes AM, Galhano A, Zaky MA. A Matrix Transform Technique for Distributed-Order Time-Fractional Advection–Dispersion Problems. Fractal and Fractional. 2023; 7(9):649. https://doi.org/10.3390/fractalfract7090649
Chicago/Turabian StyleDerakhshan, Mohammadhossein, Ahmed S. Hendy, António M. Lopes, Alexandra Galhano, and Mahmoud A. Zaky. 2023. "A Matrix Transform Technique for Distributed-Order Time-Fractional Advection–Dispersion Problems" Fractal and Fractional 7, no. 9: 649. https://doi.org/10.3390/fractalfract7090649
APA StyleDerakhshan, M., Hendy, A. S., Lopes, A. M., Galhano, A., & Zaky, M. A. (2023). A Matrix Transform Technique for Distributed-Order Time-Fractional Advection–Dispersion Problems. Fractal and Fractional, 7(9), 649. https://doi.org/10.3390/fractalfract7090649









