Study on the Characteristics of Composite Recycled Aggregate Concrete Based on Box–Behnken Design Response Surface Model
Abstract
:1. Introduction
2. Experimental Section
2.1. Raw Materials
2.2. WCP
2.2.1. Screening Test
2.2.2. Oxide Content
2.3. Experimental Design and Methods
2.3.1. Basic Mixing Ratio
2.3.2. BBD Trial Protocol
2.3.3. Compressive Strength Test
2.3.4. SEM Test
- Magnification: 20–3 × 105;
- Acceleration voltage: 0.2–30 kV;
- Beam current: maximum 2 µA and continuously adjustable;
- Moving range of the sample table: X = Y = 50 mm.
3. Response Surface Result Analysis
3.1. Model Establishment
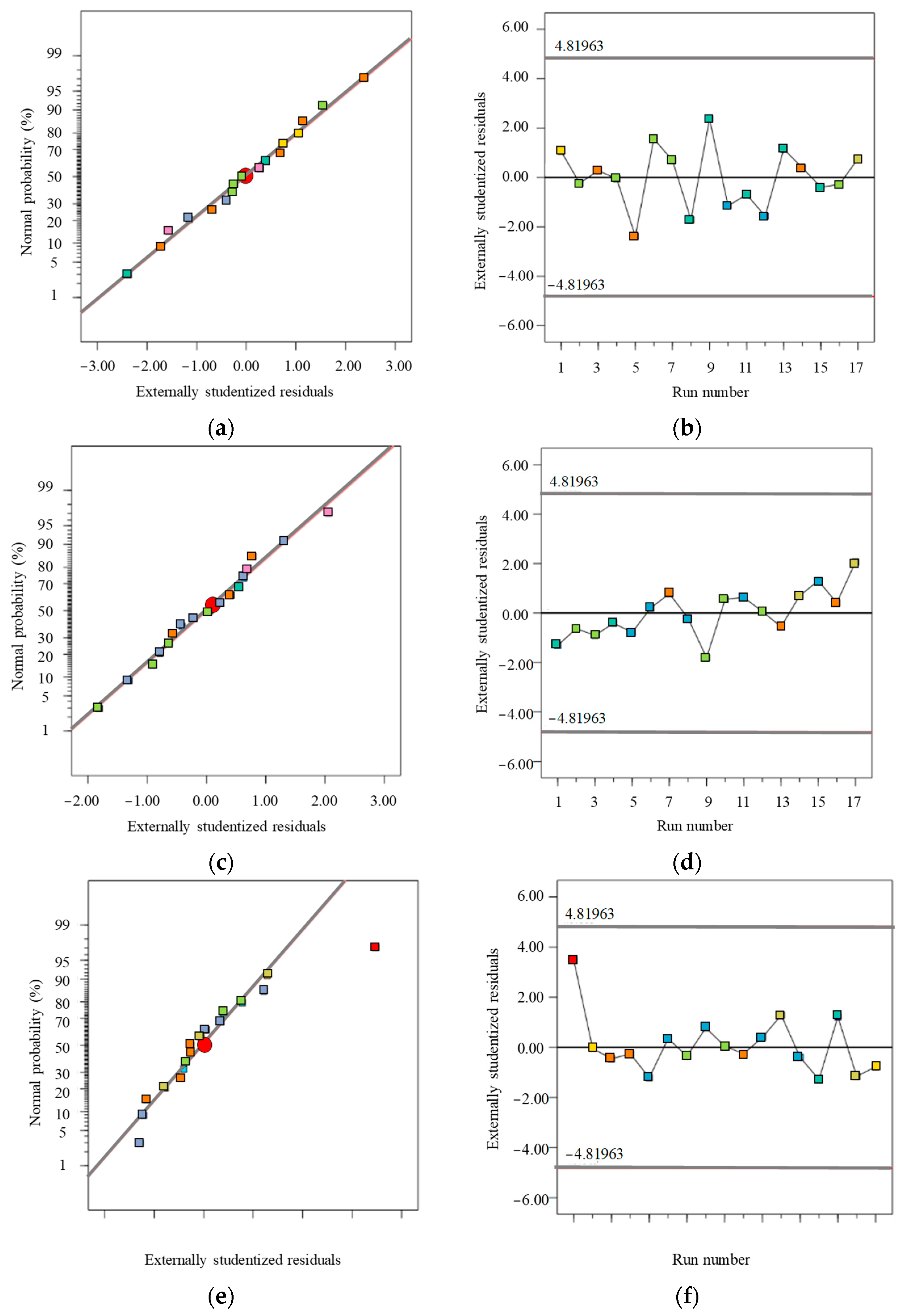
3.2. Model Verification of Response Surface Analysis
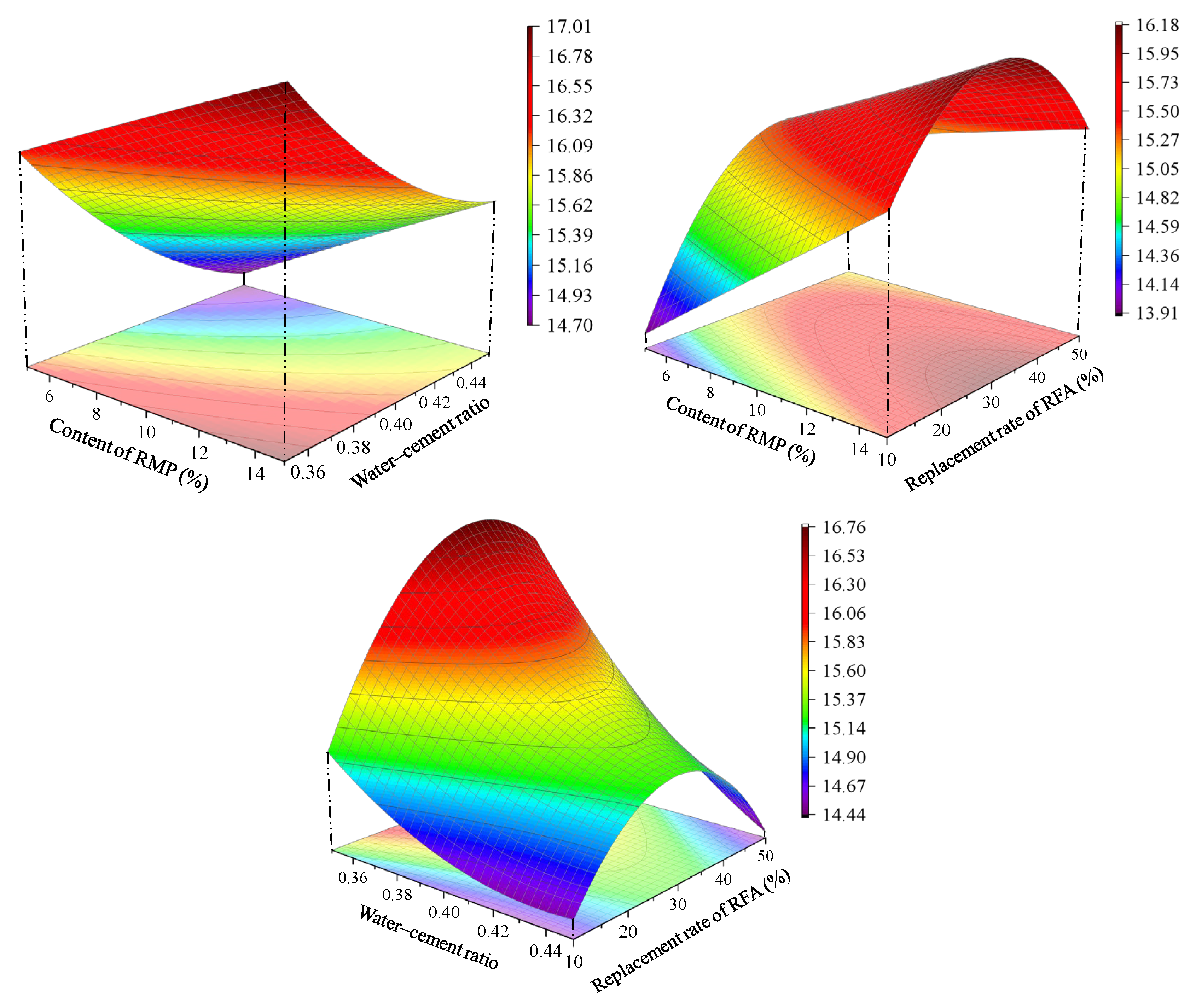
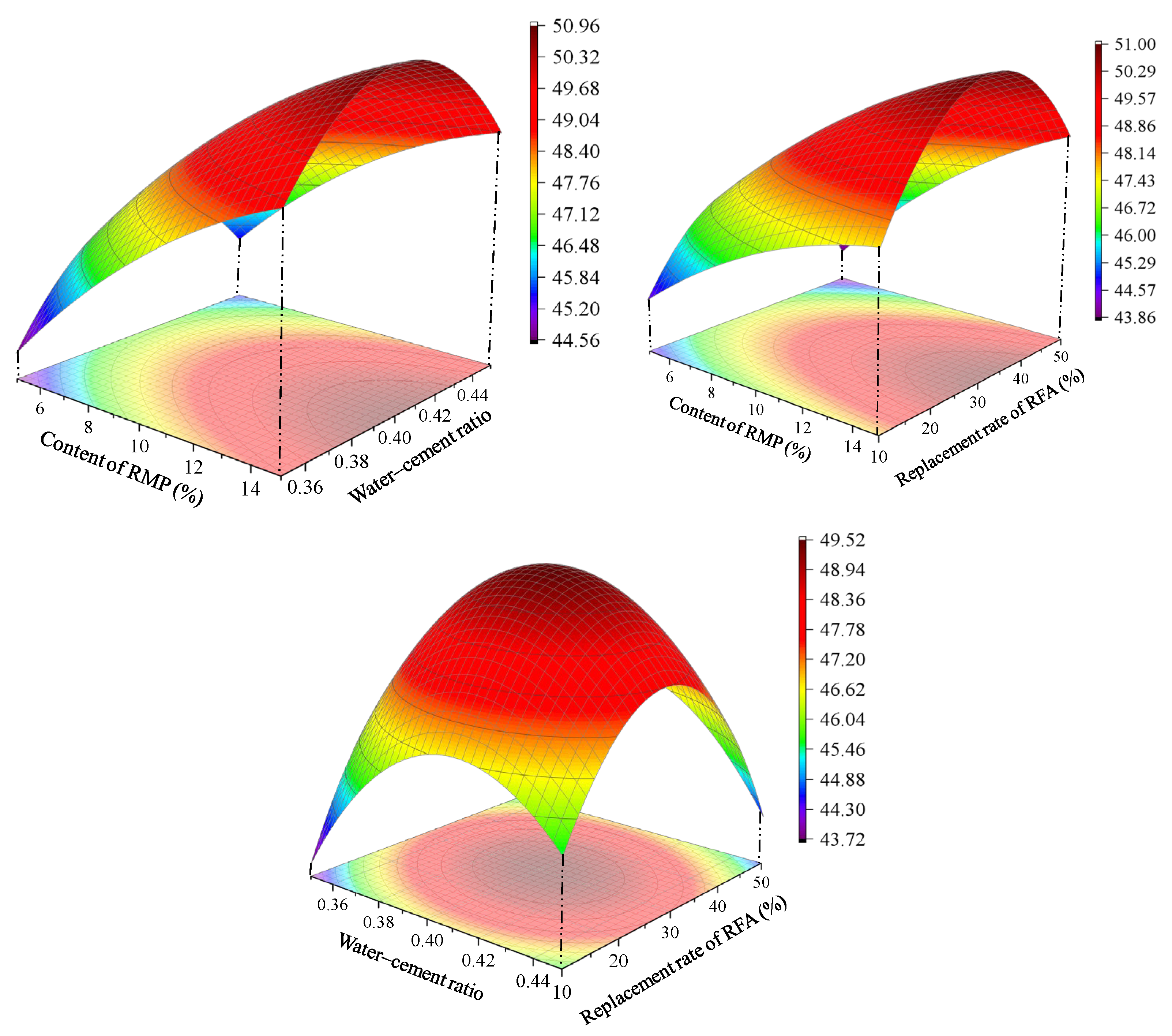
3.3. Analysis of Response Surface Test Results
3.4. Mix Ratio Optimization
4. Microstructure Analysis Based on Fractal Theory
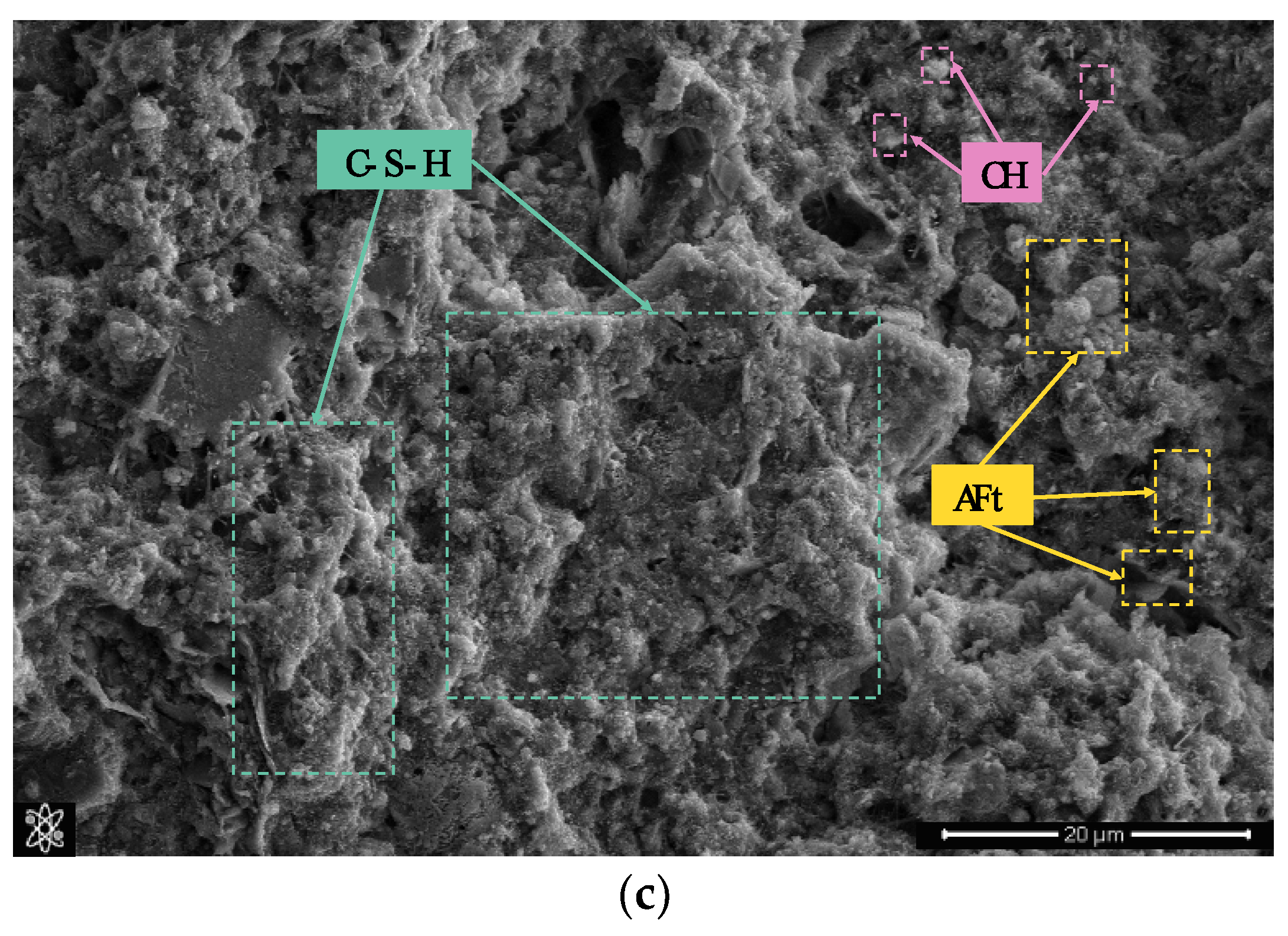
4.1. Surface Microscopic Morphology Changes
4.2. Grayscale Binarization Analysis
4.3. Fractal Dimension Calculation
5. Conclusions
- (1)
- Based on the response surface experimental analysis of compressive strength, it was found that an appropriate amount of WCP is beneficial for improving the short-, middle-, and long-term strength of concrete. The optimal dosage is 15% by mass of the fine aggregate;
- (2)
- The water–cement ratio has a significant impact on the compressive strength of concrete. According to the experimental process used in this study, the optimal water-cement ratio is 0.43;
- (3)
- The replacement of 33% of natural aggregate with RFA does not have a significant effect on compressive strength. This can serve as a guideline for the application of RFA as a substitute for natural aggregate;
- (4)
- Grayscale binarization processing of the concrete matrix revealed that the concrete with singular incorporation of fine aggregate has the largest pore area, while the concrete with dual incorporation of RFA and WCP has the smallest pore area. The fractal dimension of the pores is negatively correlated with compressive strength;
- (5)
- Fractal analysis of the hydration products at three levels demonstrated a positive correlation between the fractal dimension of the hydrated calcium silicate gel and compressive strength. The layered fractal model shows superiority in evaluating the compressive strength of concrete.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Guo, Y.; Liu, Y.; Wang, W.; Zhang, Y.; Wang, Z.; Jiang, L. A study on heat transfer performance of recycled aggregate thermal insulation concrete. J. Build. Eng. 2020, 32, 101797. [Google Scholar] [CrossRef]
- Bidabadi, M.S.; Akbari, M.; Panahi, O. Optimum mix design of recycled concrete based on the fresh and hardened properties of concrete. J. Build. Eng. 2020, 32, 101483. [Google Scholar] [CrossRef]
- Li, L.; Xuan, D.; Sojobi, A.O.; Liu, S.; Chu, S.H.; Poon, C.S. Development of nano-silica treatment methods to enhance recycled aggregate concrete. Cem. Concr. Compos. 2021, 118, 103963. [Google Scholar] [CrossRef]
- Kazmi SM, S.; Munir, M.J.; Wu, Y.F.; Patnaikuni, I.; Zhou, Y.; Xing, F. Axial stress-strain behavior of macro-synthetic fiber reinforced recycled aggregate concrete. Cem. Concr. Compos. 2019, 97, 341–356. [Google Scholar] [CrossRef]
- Liang, C.; Ma, H.; Pan, Y.; Ma, Z.; Duan, Z.; He, Z. Chloride permeability and the caused steel corrosion in the concrete with carbonated recycled aggregate. Constr. Build. Mater. 2019, 218, 506–518. [Google Scholar] [CrossRef]
- Medjigbodo, S.; Bendimerad, A.Z.; Rozière, E.; Loukili, A. How do recycled concrete aggregates modify the shrinkage and self-healing properties? Cem. Concr. Compos. 2018, 86, 72–86. [Google Scholar] [CrossRef]
- Lessly, S.H.; Kumar, S.L.; Jawahar, R.R.; Prabhu, L. Durability properties of modified ultra-high performance concrete with varying cement content and curing regime. Mater. Today Proc. 2021, 45, 6426–6432. [Google Scholar] [CrossRef]
- Hu, L.; He, Z.; Shao, Y.; Cai, X.; Zhang, S. Microstructure and properties of sustainable cement-based materials using combustion treated rice husk ash. Constr. Build. Mater. 2021, 294, 123482. [Google Scholar] [CrossRef]
- Zhang, L.; Gong, H.; Liu, J.; Li, H. Mechanical properties and chloride penetration resistance of copper slag aggregate concrete. Fractal Fract. 2022, 6, 427. [Google Scholar] [CrossRef]
- Kang, S.H.; Hong, S.G.; Moon, J. The use of rice husk ash as reactive filler in ultra-high performance concrete. Cem. Concr. Res. 2019, 115, 389–400. [Google Scholar] [CrossRef]
- Safiuddin, M.; West, J.S.; Soudki, K.A. Hardened properties of self-consolidating high performance concrete including rice husk ash. Cem. Concr. Compos. 2010, 32, 708–717. [Google Scholar] [CrossRef]
- Akono, A.T.; Zhan, M.; Chen, J.; Shah, S.P. Nanostructure of calcium-silicate-hydrates in fine recycled aggregate concrete. Cem. Concr. Compos. 2021, 115, 103827. [Google Scholar] [CrossRef]
- Etxeberria, M.; Gonzalez-Corominas, A. The assessment of ceramic and mixed recycled aggregates for high strength and low shrinkage concretes. Mater. Struct. 2018, 51, 129. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, C.; Zhu, H.; Wu, Q. Reaction kinetics and mechanical properties of a mineral-micropowder/metakaolin-based geopolymer. Ceram. Int. 2022, 48, 14173–14181. [Google Scholar] [CrossRef]
- Mesgari, S.; Akbarnezhad, A.; Xiao, J.Z. Recycled geopolymer aggregates as coarse aggregates for Portland cement concrete and geopolymer concrete: Effects on mechanical properties. Constr. Build. Mater. 2020, 236, 117571. [Google Scholar] [CrossRef]
- Sun, Y.; Li, J.S.; Chen, Z.; Xue, Q.; Sun, Q.; Zhou, Y.; Chen, X.; Liu, L.; Poon, C.S. Production of lightweight aggregate ceramsite from red mud and municipal solid waste incineration bottom ash: Mechanism and optimization. Constr. Build. Mater. 2021, 287, 122993. [Google Scholar] [CrossRef]
- Martinez-Echevarria, M.J.; Lopez-Alonso, M.; Garach, L.; Alegre, J.; Poon, C.S.; Agrela, F.; Cabrera, M. Crushing treatment on recycled aggregates to improve their mechanical behaviour for use in unbound road layers. Constr. Build. Mater. 2020, 263, 120517. [Google Scholar] [CrossRef]
- Awoyera, P.O.; Okoro, U.C. Filler-ability of highly active metakaolin for improving morphology and strength characteristics of recycled aggregate concrete. Silicon 2019, 11, 1971–1978. [Google Scholar] [CrossRef]
- Xu, Y.; Chen, W.; Jin, R.; Shen, J.; Smallbone, K.; Yan, C.; Hu, L. Experimental investigation of photocatalytic effects of concrete in air purification adopting entire concrete waste reuse model. J. Hazard. Mater. 2018, 353, 421–430. [Google Scholar] [CrossRef]
- Xu, G.; Shen, W.; Zhang, B.; Li, Y.; Ji, X.; Ye, Y. Properties of recycled aggregate concrete prepared with scattering-filling coarse aggregate process. Cem. Concr. Compos. 2018, 93, 19–29. [Google Scholar] [CrossRef]
- Kim, J.; Sadowski, Ł. Properties of recycled aggregate concrete designed with equivalent mortar volume method. Struct. Integr. Recycl. Aggreg. Concr. Prod. Fill. Pozzolans 2022, 301, 365–381. [Google Scholar]
- Kumar, R. Effects of high volume dolomite sludge on the properties of eco-efficient lightweight concrete: Microstructure, statistical modeling, multi-attribute optimization through Derringer’s desirability function, and life cycle assessment. J. Clean. Prod. 2021, 307, 127107. [Google Scholar] [CrossRef]
- Sharaky, I.A.; Ghoneim, S.S.; Aziz BH, A.; Emara, M. Experimental and theoretical study on the compressive strength of the high strength concrete incorporating steel fiber and metakaolin. Structures 2021, 31, 57–67. [Google Scholar] [CrossRef]
- Shaheen, N.; Rizwan, S.A.; Khushnood, R.A.; Bier, T.A. Mechanical and energy performance of variably cured effective microorganisms cementitious composite designed via Taguchi. J. Clean. Prod. 2021, 310, 127350. [Google Scholar] [CrossRef]
- Zhang, Q.; Feng, X.; Chen, X.; Lu, K. Mix design for recycled aggregate pervious concrete based on response surface methodology. Constr. Build. Mater. 2020, 259, 119776. [Google Scholar] [CrossRef]
- GB175-2007; General Purpose Portland Cement. State Bureau of Technical Supervision: Beijing, China, 2006. (In Chinese)
- GB/T 14685-2011; Pebbie and Crushed Stone for Building. State Quality of the People’s Republic of China General Administration of Quantity Supervision, Inspection and Quarantine: Beijing, China, 2011. (In Chinese)
- JGJ 52-2006; Quality and Test Method Standard of Ordinary Concrete’s and Gazvel. China Architecture and Building Press: Beijing, China, 2006. (In Chinese)
- JGJ 63-2006; Standard of Water for Concrete. Ministry of Construction, PRC: Beijing, China, 2006. (In Chinese)
- Alkhaly, Y.R.; Hasan, M. Characteristics of reactive powder concrete comprising synthesized rice husk ash and quartzite powder. J. Clean. Prod. 2022, 375, 134154. [Google Scholar] [CrossRef]
- JGJ 55-2011; Specification for Mix Proportion Design of Ordinary Concrete. China Building Industry Press: Beijing, China, 2011. (In Chinese)
- Marzouki, M.; Samet, B.; Tounsi, H. Application of Plackett–Burman and Box-Behnken designs for the optimization of Tunisian dam sediment-based geopolymers. J. Build. Eng. 2022, 50, 104162. [Google Scholar] [CrossRef]
- GB/T 50081-2002; Standard for Test Method of Mechanical Properties on Ordinary Concrete. China Architecture & Building Press: Beijing, China, 2003. (In Chinese)
- He, Z.H.; Zhan, P.M.; Du, S.G.; Liu, B.J.; Yuan, W.B. Creep behavior of concrete containing glass powder. Compos. Part B Eng. 2019, 166, 13–20. [Google Scholar] [CrossRef]
- Kim, Y.J. Quality properties of self-consolidating concrete mixed with waste concrete powder. Constr. Build. Mater. 2017, 135, 177–185. [Google Scholar] [CrossRef]
- Rasheed, M.F.; Rahim, A.; Irfan-ul-Hassan, M.; Ali, B.; Ali, N. Sulfur concrete made with waste marble and slag powders: 100% recycled and waterless concrete. Environ. Sci. Pollut. Res. 2022, 29, 65655–65669. [Google Scholar] [CrossRef]
- Zheng, C.; Lou, C.; Du, G.; Li, X.; Liu, Z.; Li, L. Mechanical properties of recycled concrete with demolished waste concrete aggregate and clay brick aggregate. Results Phys. 2018, 9, 1317–1322. [Google Scholar] [CrossRef]
- Zhang, L.; Dang, F.; Ding, W.; Zhu, L. Quantitative study of meso-damage process on concrete by CT technology and improved differential box counting method. Measurement 2020, 160, 107832. [Google Scholar] [CrossRef]
- Yang, X.; Wang, M. Fractal dimension analysis of aggregate packing process: A numerical case study on concrete simulation. Constr. Build. Mater. 2021, 270, 121376. [Google Scholar] [CrossRef]
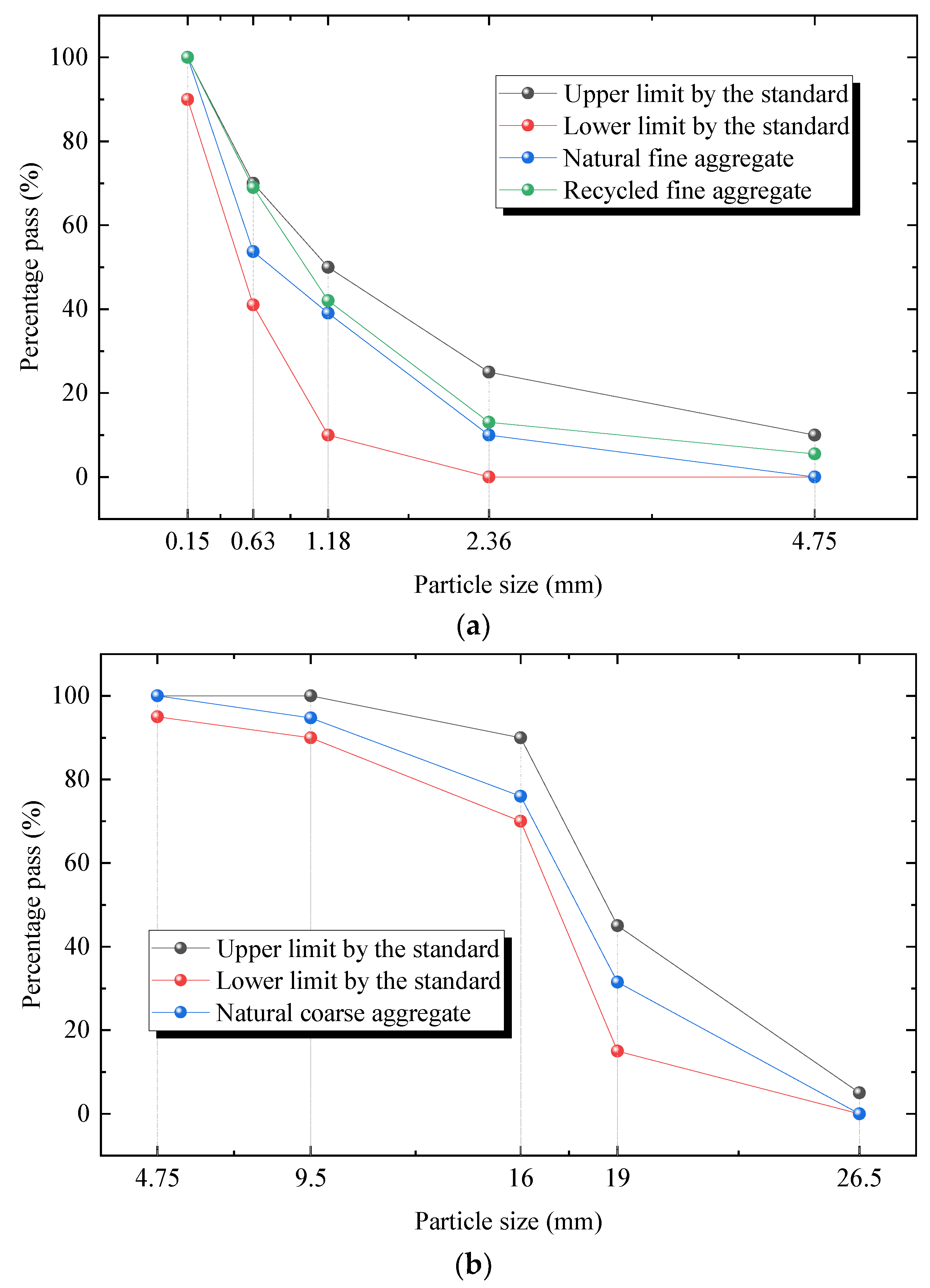









| Type | Performance Density (kg/m3) | Loose Packing Density (kg/m3) | Crushing Value Index (%) | Princess (%) | Water Absorption Rate at 24 h (%) | Moisture Content (%) |
|---|---|---|---|---|---|---|
| NCA | 2670 | 1566 | 18.2 | 18 | 1.1 | 1 |
| NFA | 2530 | 1506 | 13.7 | 7 | 1.4 | 1.77 |
| RFA | 2330 | 1280 | 27 | 5 | 15.4 | 5.8 |
| Water-Reducing Rate (%) | Air Content (%) | pH Level | Density (kg/m3) | Water-Reducing Rate (%) |
|---|---|---|---|---|
| 30 | 2.4 | 7.9 | 1053 | 24 |
| Element | CaO | SiO2 | Fe2O3 | Al2O3 | MgO | Na2O | K2O | P2O5 | TiO2 | ZrO2 | LOI |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Content | 43.73 | 26.55 | 8.19 | 13.18 | 4.99 | 0.75 | 2.21 | 0.05 | 0.03 | 0.03 | 0.29 |
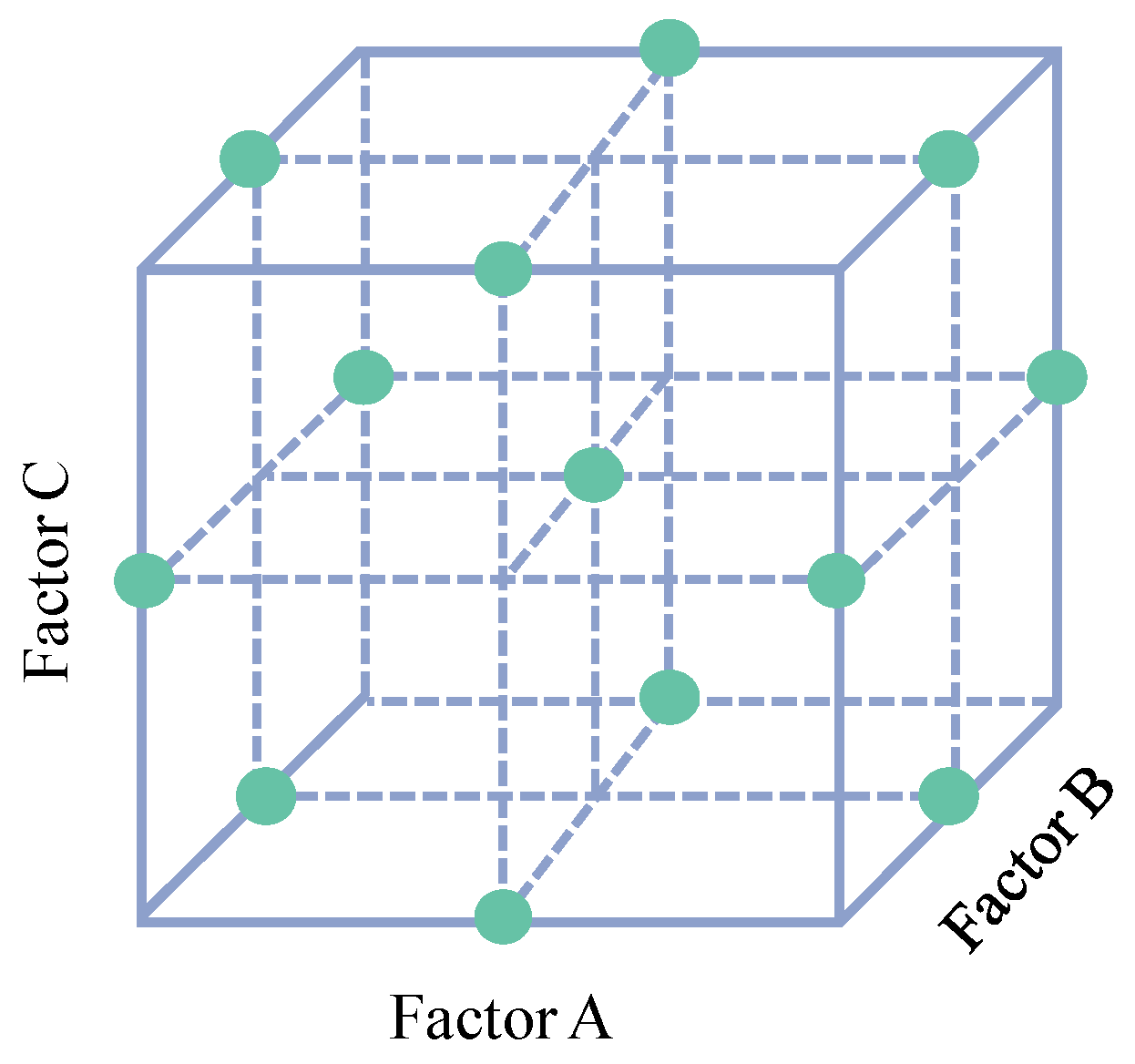
| Number | Variable Factors | Level | ||
|---|---|---|---|---|
| A | Percentage of WCP (%) | 5 | 10 | 15 |
| B | Water–cement ratio | 0.35 | 0.4 | 0.45 |
| C | Aggregate substitution rate (%) | 10 | 30 | 50 |
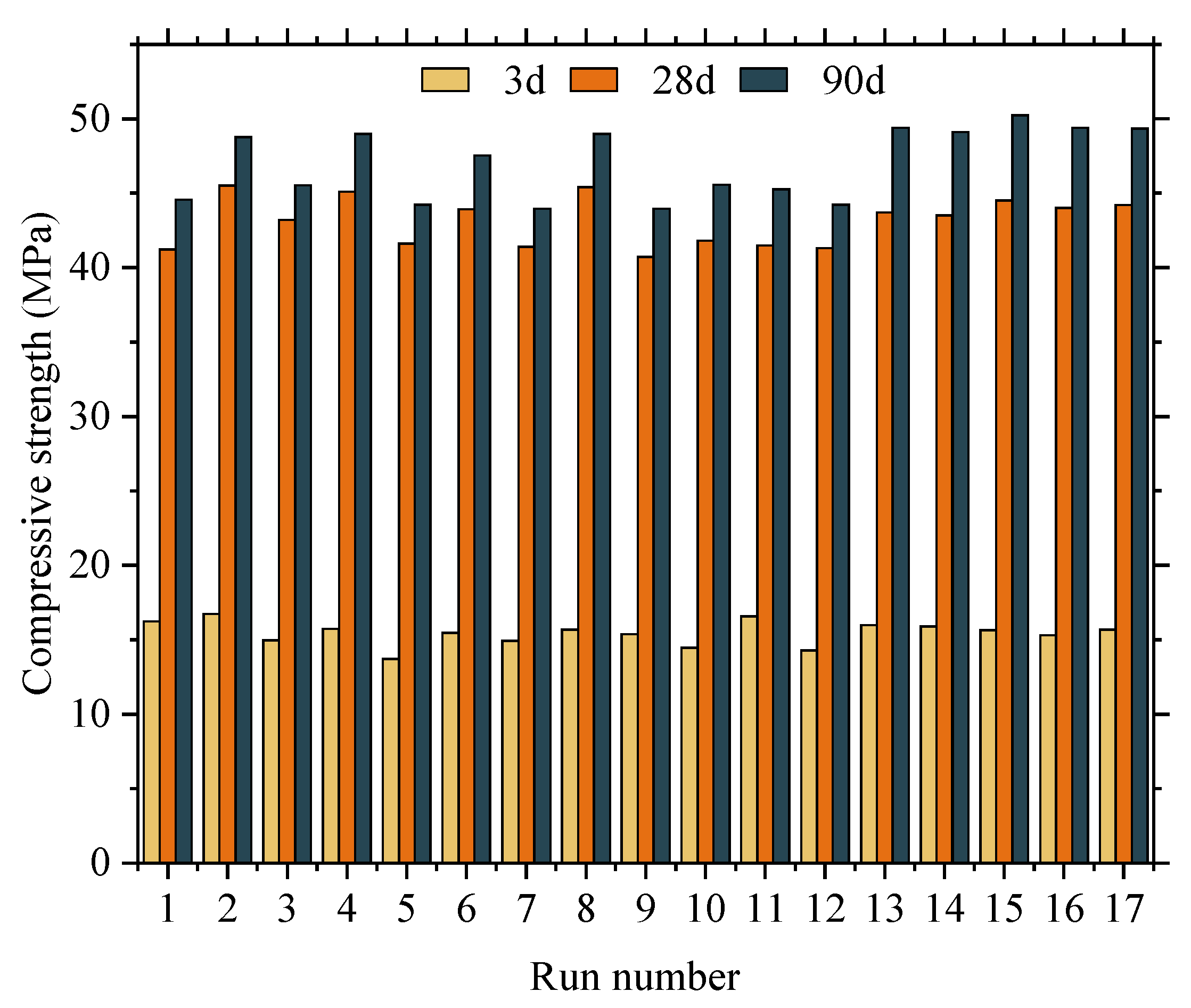
| Number | Cement | Designed Water | NCA | NFA | RFA | Additional Water | WCP | Water Reducer |
|---|---|---|---|---|---|---|---|---|
| 1 | 406 | 142.1 | 1290 | 486.5 | 208.5 | 13.81 | 34.75 | 4.87 |
| 2 | 406 | 142.1 | 1290 | 486.5 | 208.5 | 13.81 | 104.25 | 4.87 |
| 3 | 406 | 182.7 | 1290 | 486.5 | 208.5 | 13.81 | 34.75 | 4.87 |
| 4 | 406 | 182.7 | 1290 | 486.5 | 208.5 | 13.81 | 104.25 | 4.87 |
| 5 | 406 | 162.4 | 1290 | 625.5 | 69.5 | 4.60 | 34.75 | 4.87 |
| 6 | 406 | 162.4 | 1290 | 625.5 | 69.5 | 4.60 | 104.25 | 4.87 |
| 7 | 406 | 162.4 | 1290 | 347.5 | 347.5 | 23.01 | 34.75 | 4.87 |
| 8 | 406 | 162.4 | 1290 | 347.5 | 347.5 | 23.01 | 104.25 | 4.87 |
| 9 | 406 | 142.1 | 1290 | 625.5 | 69.5 | 4.60 | 69.5 | 4.87 |
| 10 | 406 | 182.7 | 1290 | 625.5 | 69.5 | 4.60 | 69.5 | 4.87 |
| 11 | 406 | 142.1 | 1290 | 347.5 | 347.5 | 23.01 | 69.5 | 4.87 |
| 12 | 406 | 182.7 | 1290 | 347.5 | 347.5 | 23.01 | 69.5 | 4.87 |
| 13 | 406 | 162.4 | 1290 | 486.5 | 208.5 | 13.81 | 69.5 | 4.87 |
| 14 | 406 | 162.4 | 1290 | 486.5 | 208.5 | 13.81 | 69.5 | 4.87 |
| 15 | 406 | 162.4 | 1290 | 486.5 | 208.5 | 13.81 | 69.5 | 4.87 |
| 16 | 406 | 162.4 | 1290 | 486.5 | 208.5 | 13.81 | 69.5 | 4.87 |
| 17 | 406 | 162.4 | 1290 | 486.5 | 208.5 | 13.81 | 69.5 | 4.87 |
| Time/d | Prediction Model |
|---|---|
| 3 | Y3d = 28.19619 + 0.0714 × A − 76.24 × B + 0.295325 × 30 + 0.26 × A × B − 0.002525 × A × 30 − 0.355 × B × 30 − 0.00027 × A2 + 88.3 × B2 − 0.001879 × 302 |
| Y3d = 28.19619 + 0.0714 × A − 76.24 × 0.4 + 0.295325 × C + 0.26 × A × 0.4 − 0.002525 × A × C − 0.355 × 0.4 × C − 0.00027 × A2 + 88.3 × 0.42 − 0.001879 × C2 | |
| Y3d = 28.19619 + 0.0714 × 10 − 76.24 × B + 0.295325 × C + 0.26 × 10 × B − 0.002525 × 10 × C − 0.355 × B × C − 0.00027 × 102 + 88.3 × B2 − 0.001879 × C2 | |
| 28 | Y28d = −38.22625 + 0.537 × A + 356.8 × B + 0.34725 × 30 − 2.4 × A × B + 0.00425 × A × 30 − 0.325 × B × 30 + 0.0304 × A2 − 396 × B2 − 0.004163 × 302 |
| Y28d = −38.22625 + 0.537 × A + 356.8 × 0.4 + 0.34725 × C − 2.4 × A × 0.4 + 0.00425 × A × C − 0.325 × 0.4 × C + 0.0304 × A2 − 396 × 0.42 − 0.004163 × C2 | |
| Y28d = −38.22625 + 0.537 × 10 + 356.8 × B + 0.34725 × C − 2.4 × 10 × B + 0.00425 × 10 × C − 0.325 × B × C + 0.0304 × 102 − 396 × B2 − 0.004163 × C2 | |
| 90 | Y90d = −100.97306 + 1.00685 × A + 663.865 × B + 0.643613 × 30 − 0.73 × A × B + 0.00435 × A × 30 − 0.66 × B × 30 − 0.02223 × A2 − 790.3 × B2 − 0.006933 × 302 |
| Y90d = −100.97306 + 1.00685 × A + 663.865 × 0.4 + 0.643613 × C − 0.73 × A × 0.4 + 0.00435 × A × C − 0.66 × 0.4 × C − 0.02223 × A2 − 790.3 × 0.42 − 0.006933 × C2 | |
| Y90d = −100.97306 + 1.00685 × 10 + 663.865 × B + 0.643613 × C − 0.73 × 10 × B + 0.00435 × 10 × C − 0.66 × B × C − 0.02223 × 102 − 790.3 × B2 − 0.006933 × C2 |
| Source | C.V.% | F-Value | p-Value | Significance | R² | Adjusted R² | Predicted R² | Adeq Precision |
|---|---|---|---|---|---|---|---|---|
| 3 d | 1.89 | 12.47 | 0.0016 | significant | 0.9413 | 0.8658 | 0.8565 | 13.8164 |
| 28 d | 0.792 | 39.47 | <0.0001 | significant | 0.9807 | 0.9558 | 0.9057 | 19.5297 |
| 90 d | 0.8093 | 68.75 | <0.0001 | significant | 0.9888 | 0.9744 | 0.9380 | 19.8009 |
| Source | Sum of Squares | Degrees of Freedom | Mean Square | F-Value | p-Value |
|---|---|---|---|---|---|
| A | 1.78 | 1 | 1.78 | 20.88 | 0.0026 |
| B | 3.73 | 1 | 3.73 | 43.79 | 0.0003 |
| C | 0.75 | 1 | 0.75 | 8.82 | 0.0208 |
| AB | 0.01 | 1 | 0.01 | 0.19 | 0.6693 |
| AC | 0.25 | 1 | 0.25 | 3.00 | 0.1270 |
| BC | 0.50 | 1 | 0.50 | 5.92 | 0.0452 |
| Source | Sum of Squares | Degrees of Freedom | Mean Square | F-Value | p-Value |
|---|---|---|---|---|---|
| A | 19.53 | 1 | 19.53 | 167.65 | <0.0001 |
| B | 0.78 | 1 | 0.78 | 6.71 | 0.0360 |
| C | 0.32 | 1 | 0.32 | 2.75 | 0.1414 |
| AB | 1.44 | 1 | 1.44 | 12.36 | 0.0098 |
| AC | 0.72 | 1 | 0.72 | 6.20 | 0.0416 |
| BC | 0.42 | 1 | 0.42 | 3.63 | 0.0986 |
| Source | Sum of Squares | Degrees of Freedom | Mean Square | F-Value | p-Value |
|---|---|---|---|---|---|
| A | 32.12 | 1 | 32.12 | 221.91 | <0.0001 |
| B–B | 0.40 | 1 | 0.40 | 2.83 | 0.1364 |
| C–C | 0.16 | 1 | 0.16 | 1.12 | 0.3246 |
| AB | 0.13 | 1 | 0.13 | 0.92 | 0.3693 |
| AC | 0.75 | 1 | 0.75 | 5.23 | 0.0561 |
| BC | 1.74 | 1 | 1.74 | 12.04 | 0.0104 |
| Test Number | Cement (kg/m3) | Designed Water | NCA | NFA | RFA | Additional Water | WCP | Water Reducer |
|---|---|---|---|---|---|---|---|---|
| 1 | 406 | 172.96 | 1290 | 465.65 | 229.35 | 15.19 | 104.25 | 4.87 |
| Category | NAC | RAC | RAPC | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Level | F1 | F2 | F3 | F1 | F2 | F3 | F1 | F2 | F3 |
| Min | 10 | 10 | 10 | 10 | 1 | 1 | 1 | 1 | 1 |
| Max | 13,456 | 9506 | 59,879 | 28,808 | 6645 | 56,632 | 6700 | 2355 | 154,697 |
| Range | 13,446 | 9496 | 59,869 | 28,798 | 6644 | 56,631 | 6699 | 2354 | 154,696 |
| Mean | 214 | 117 | 283 | 502 | 111 | 283 | 143 | 30 | 428 |
| Sum | 116,662 | 111,834 | 135,580 | 164,679 | 104,010 | 131,062 | 108,894 | 61,593 | 196,621 |
| Category | NAC | RAC | RAPC | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Level | F1 | F2 | F3 | F1 | F2 | F3 | F1 | F2 | F3 |
| Fractal dimension | 1.71 | 1.73 | 1.81 | 1.71 | 1.75 | 1.71 | 1.67 | 1.76 | 1.83 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, H.; Zhang, L.; Liu, J.; Chu, F.; Tian, Y. Study on the Characteristics of Composite Recycled Aggregate Concrete Based on Box–Behnken Design Response Surface Model. Fractal Fract. 2023, 7, 648. https://doi.org/10.3390/fractalfract7090648
Li H, Zhang L, Liu J, Chu F, Tian Y. Study on the Characteristics of Composite Recycled Aggregate Concrete Based on Box–Behnken Design Response Surface Model. Fractal and Fractional. 2023; 7(9):648. https://doi.org/10.3390/fractalfract7090648
Chicago/Turabian StyleLi, Haizhou, Lu Zhang, Jianping Liu, Fujiao Chu, and Yifan Tian. 2023. "Study on the Characteristics of Composite Recycled Aggregate Concrete Based on Box–Behnken Design Response Surface Model" Fractal and Fractional 7, no. 9: 648. https://doi.org/10.3390/fractalfract7090648
APA StyleLi, H., Zhang, L., Liu, J., Chu, F., & Tian, Y. (2023). Study on the Characteristics of Composite Recycled Aggregate Concrete Based on Box–Behnken Design Response Surface Model. Fractal and Fractional, 7(9), 648. https://doi.org/10.3390/fractalfract7090648






