Complex Dynamical Characteristics of the Fractional-Order Cellular Neural Network and Its DSP Implementation
Abstract
:1. Introduction
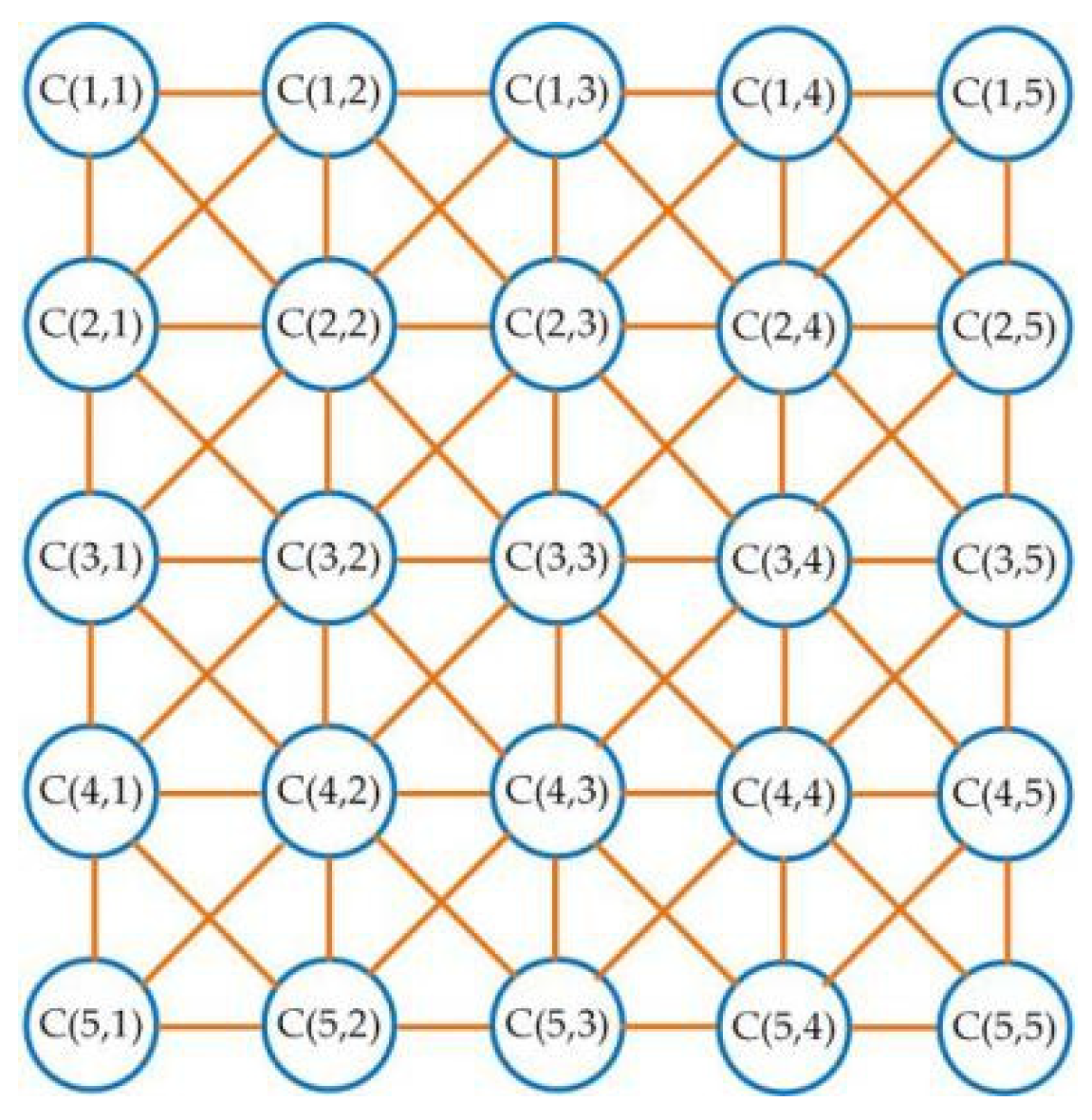
2. CNN System with Hyperbolic Tangent Activation Function
2.1. Adomian Decomposition Method
2.2. Solution of the Fractional-Order CNN System
3. Analysis of Dynamical Characteristics of the CNN System
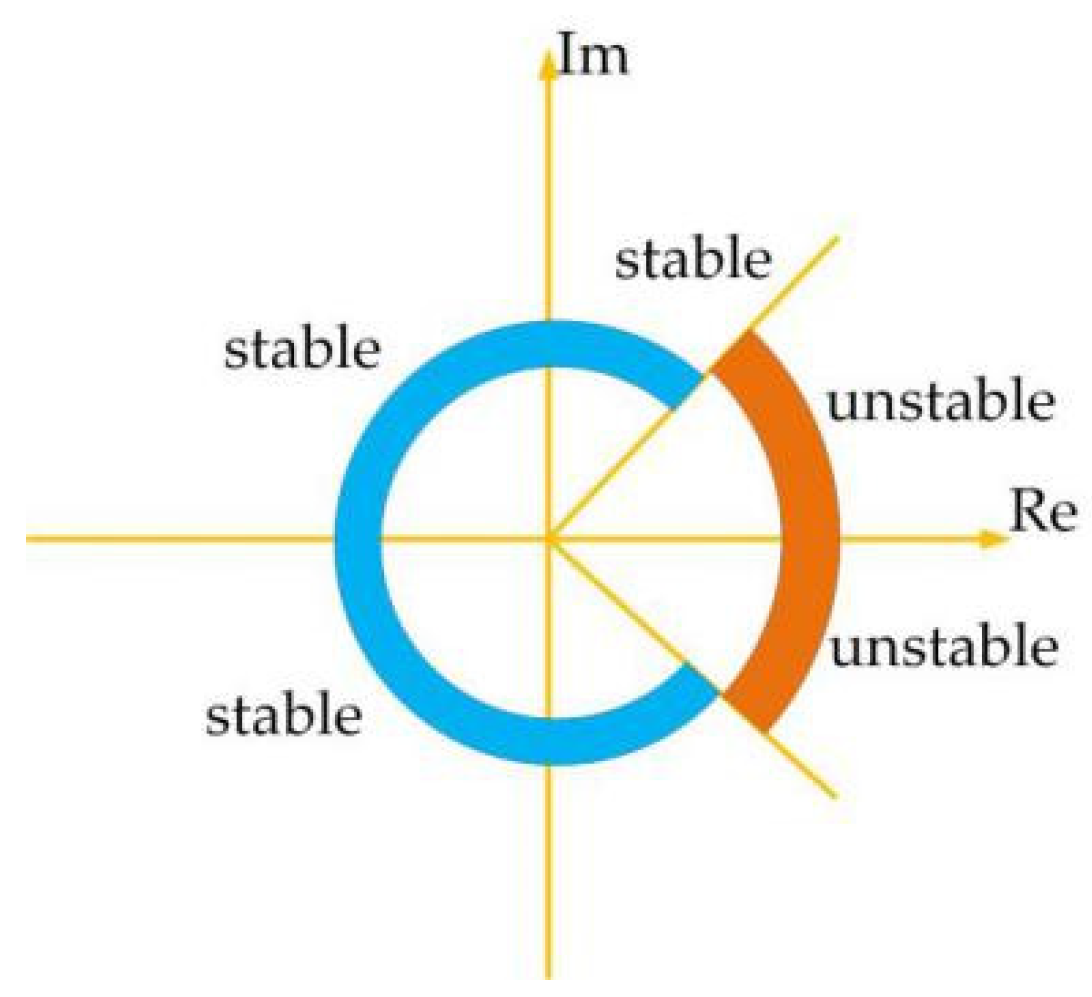
3.1. Stability of Equilibrium Points
3.2. Influence of Different System Parameters
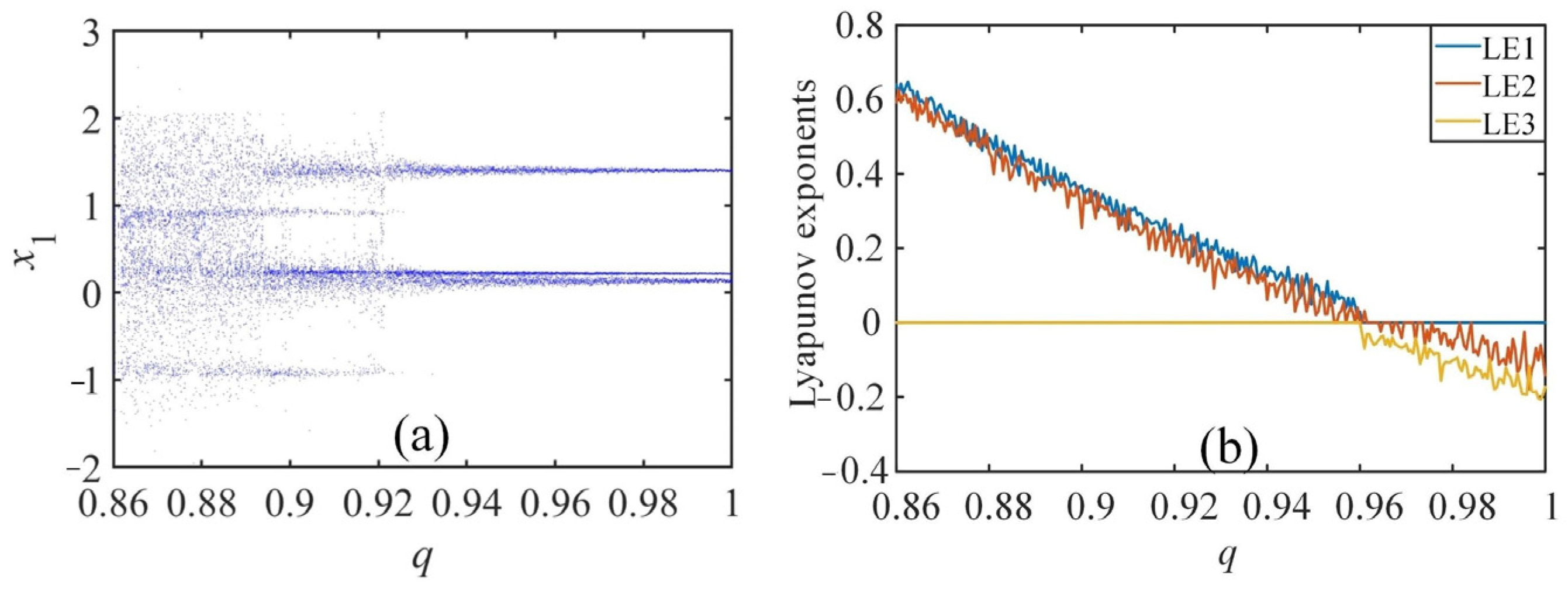
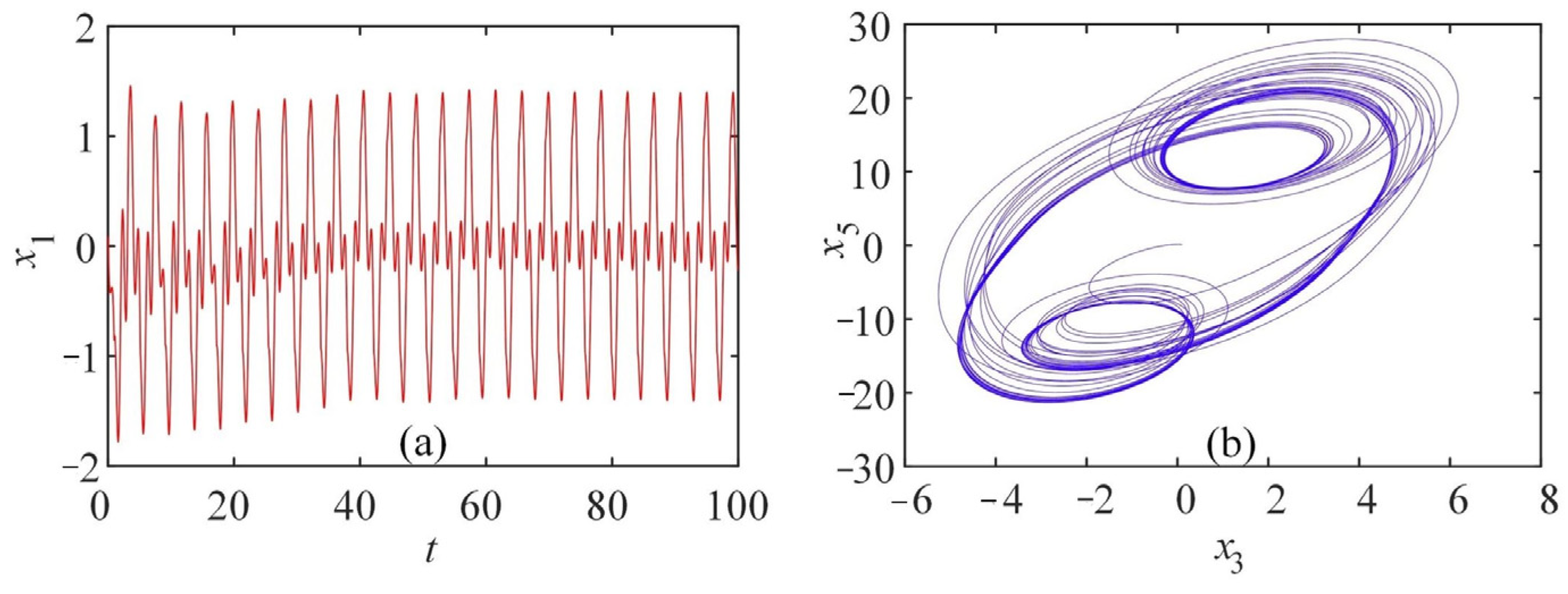
3.2.1. Influence of the Order q
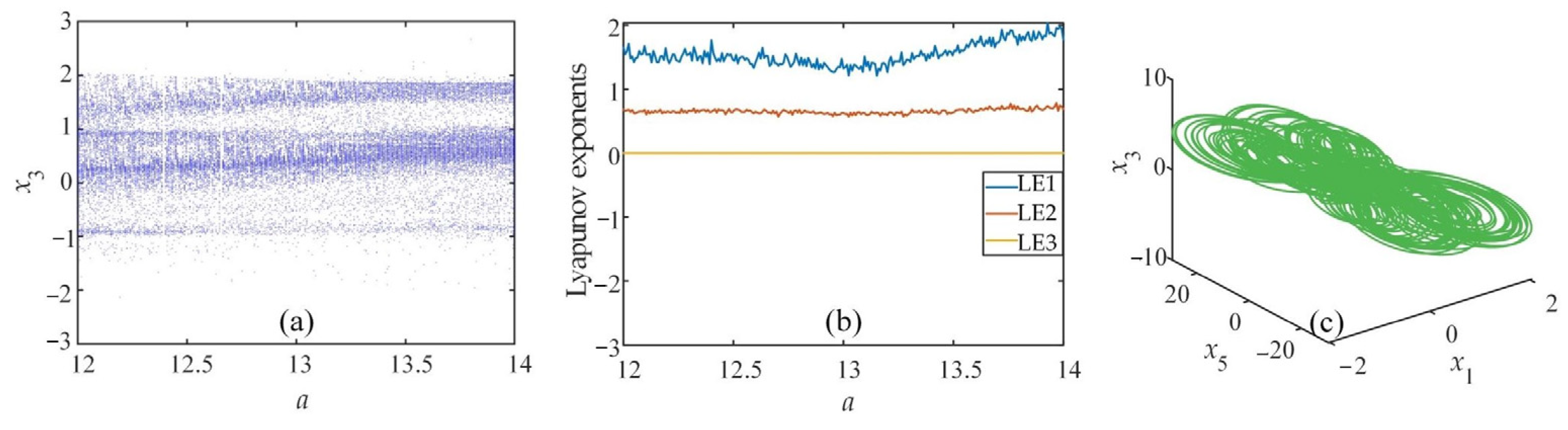
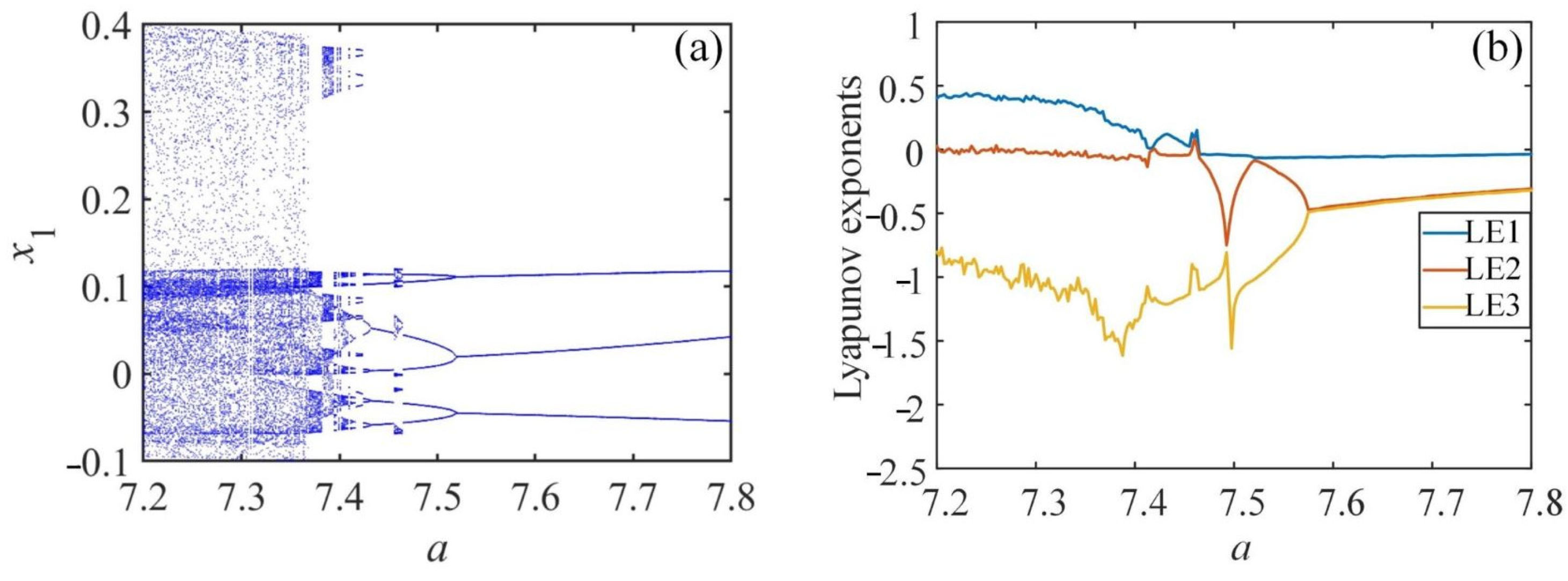
3.2.2. Influence of the Parameter a
3.2.3. Influence of the Parameter b
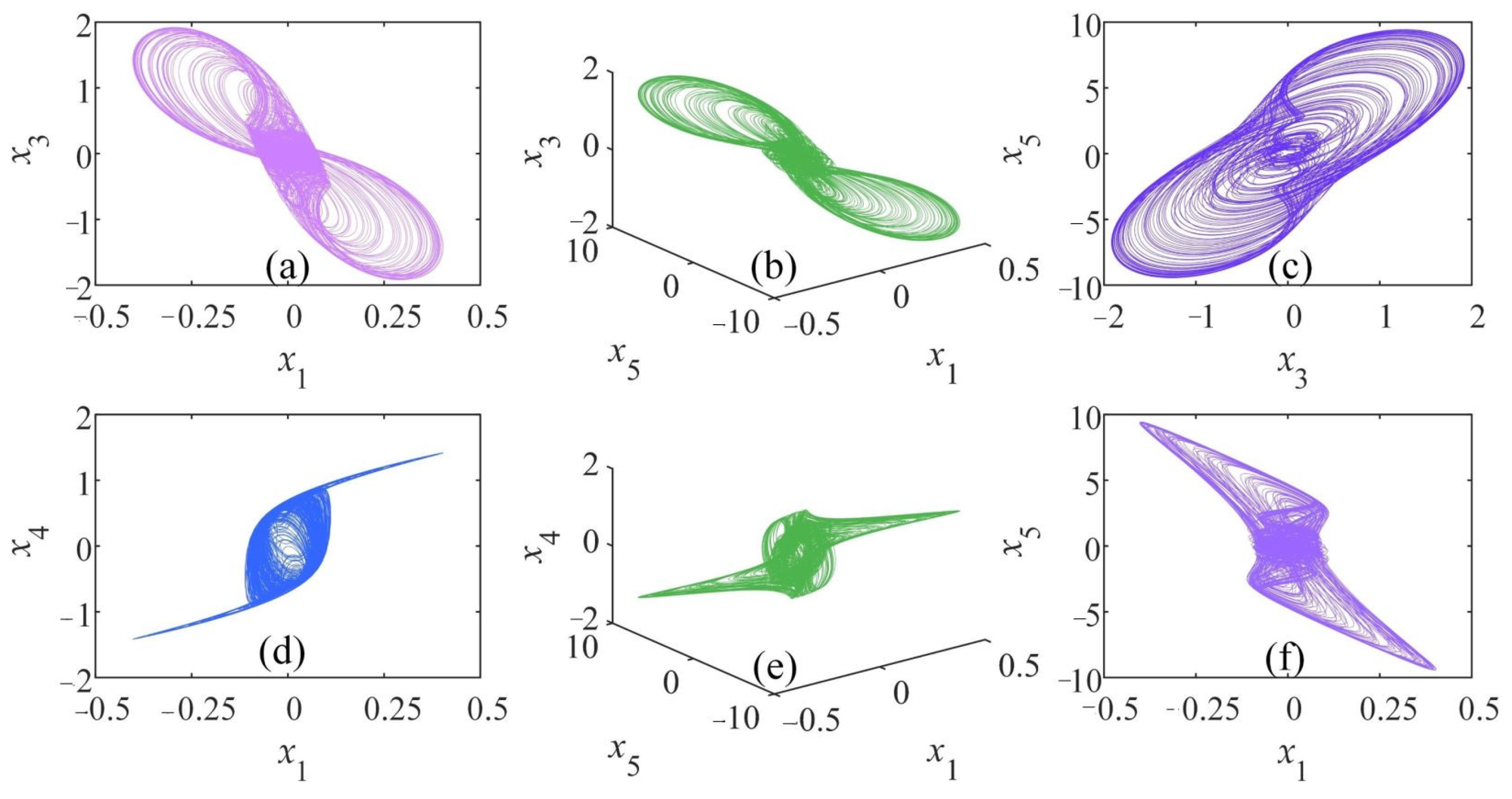
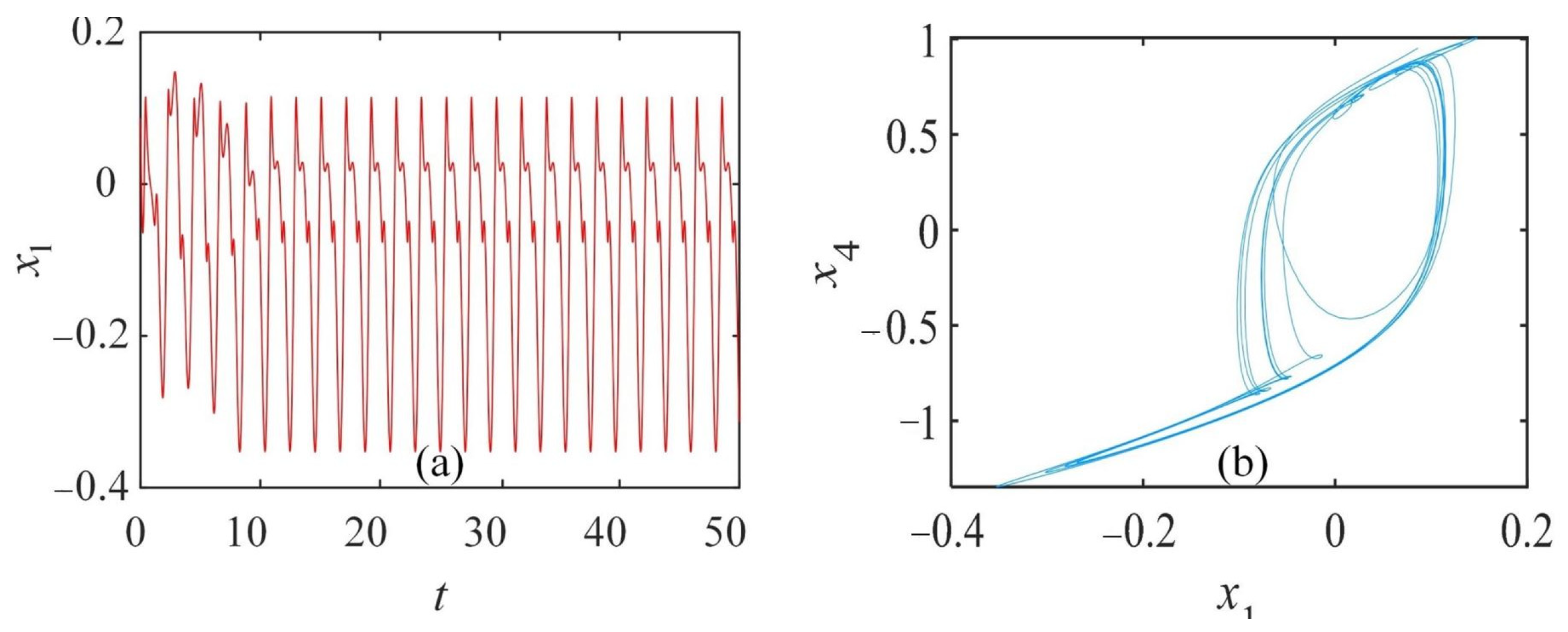
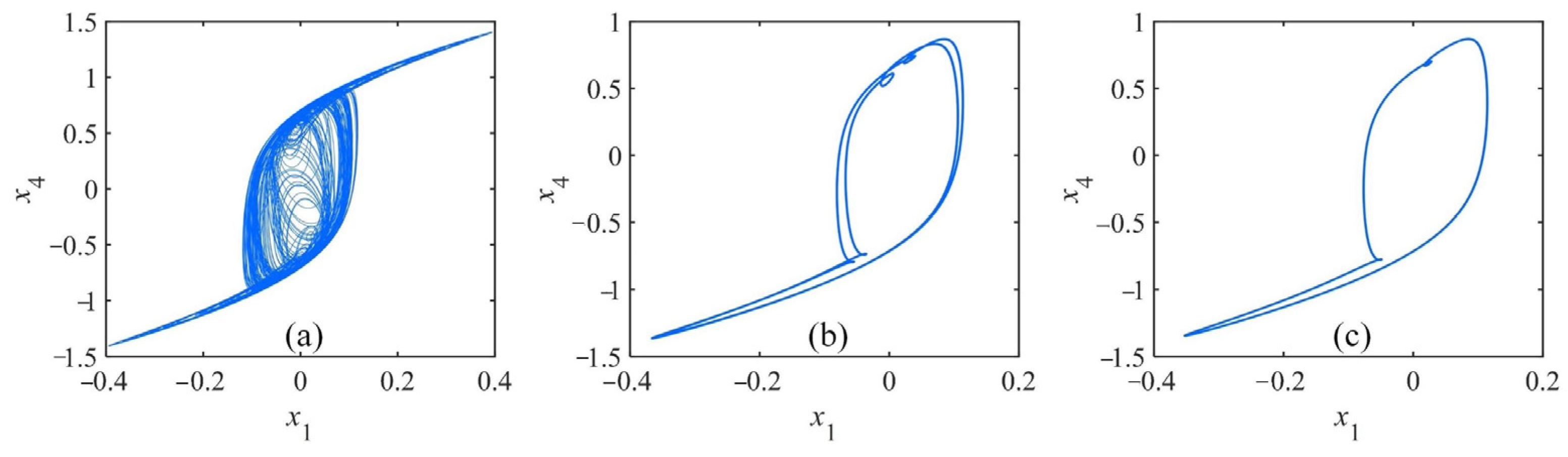
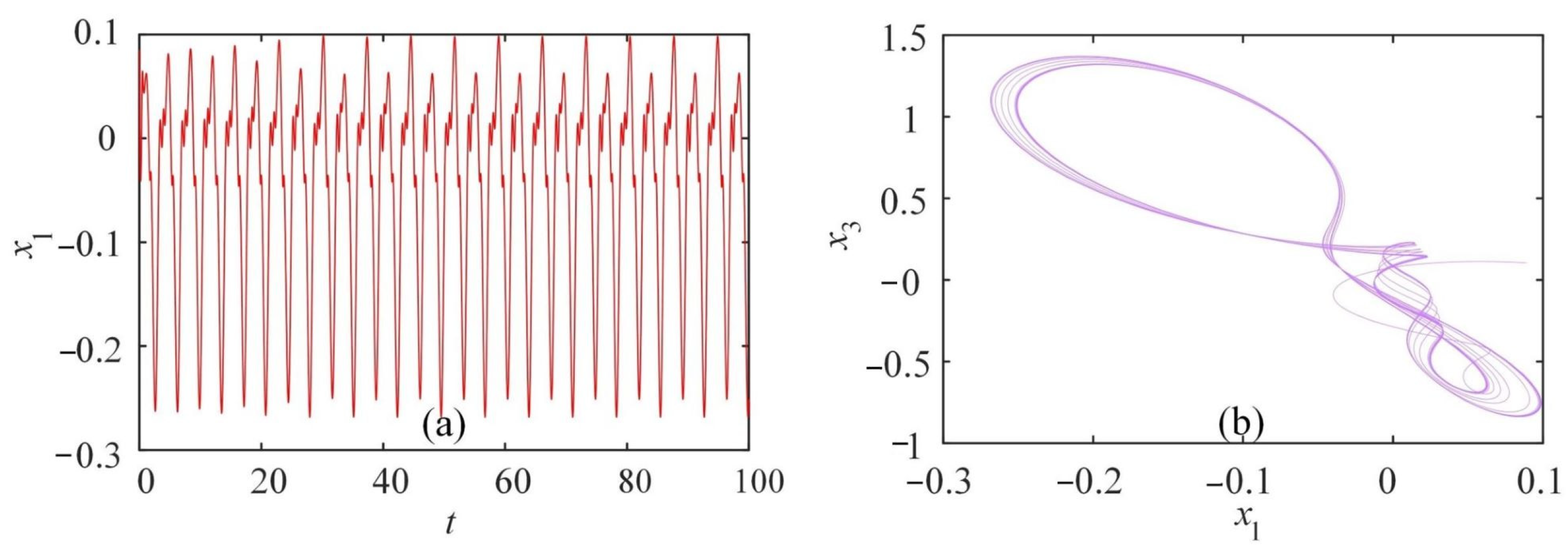
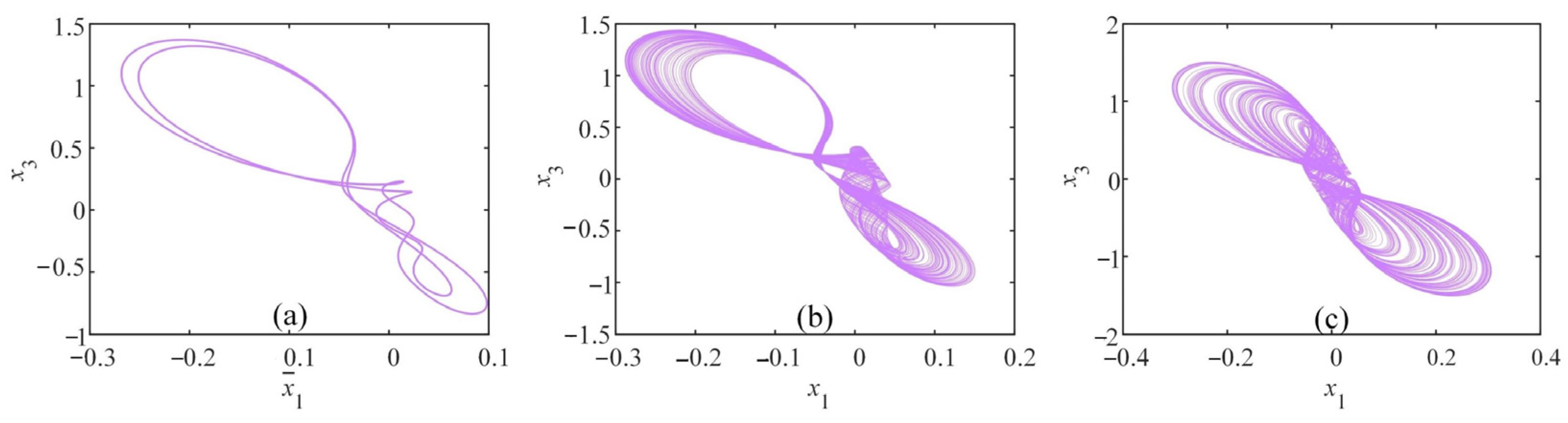
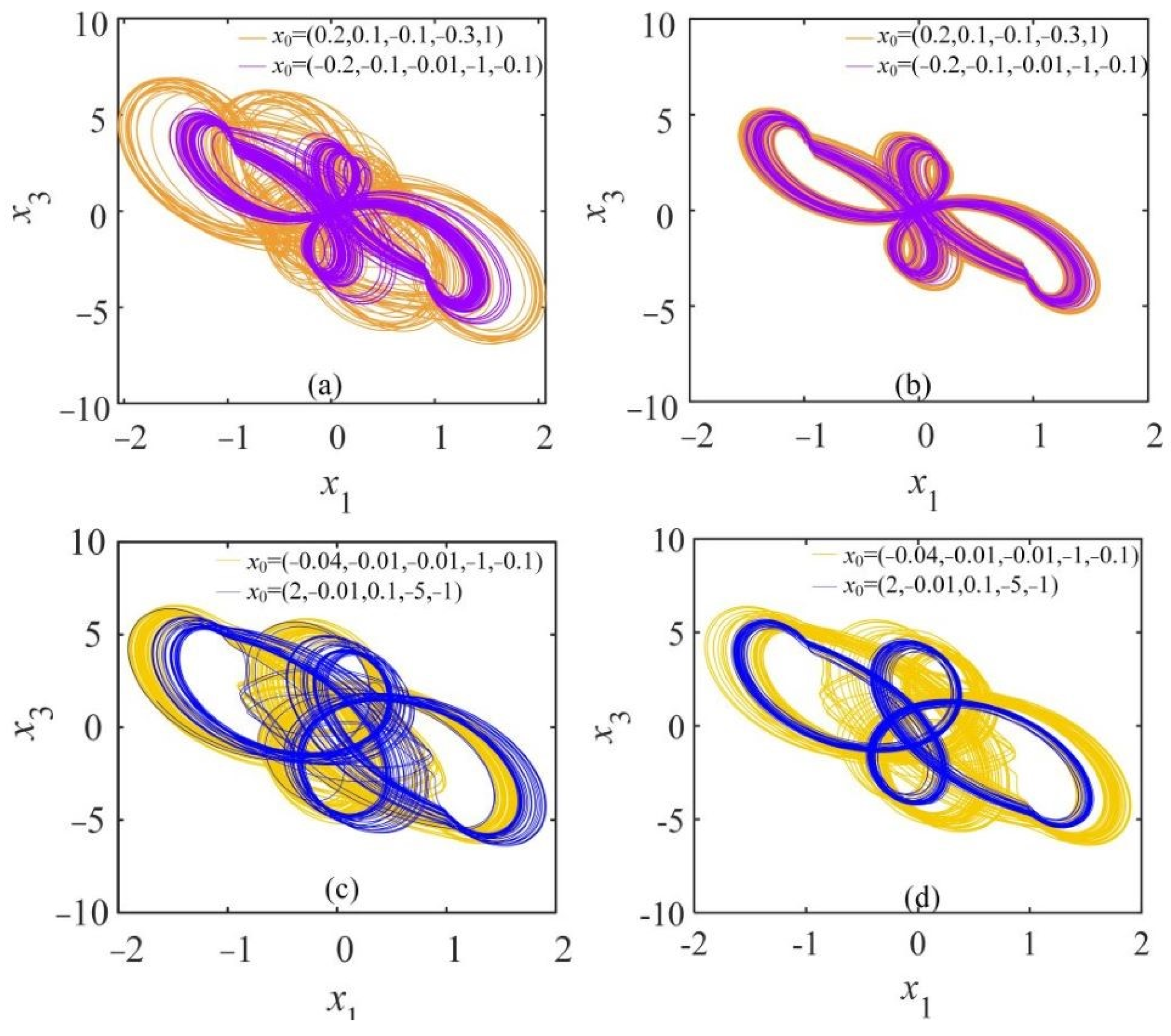
3.3. Coexistence of Attractors
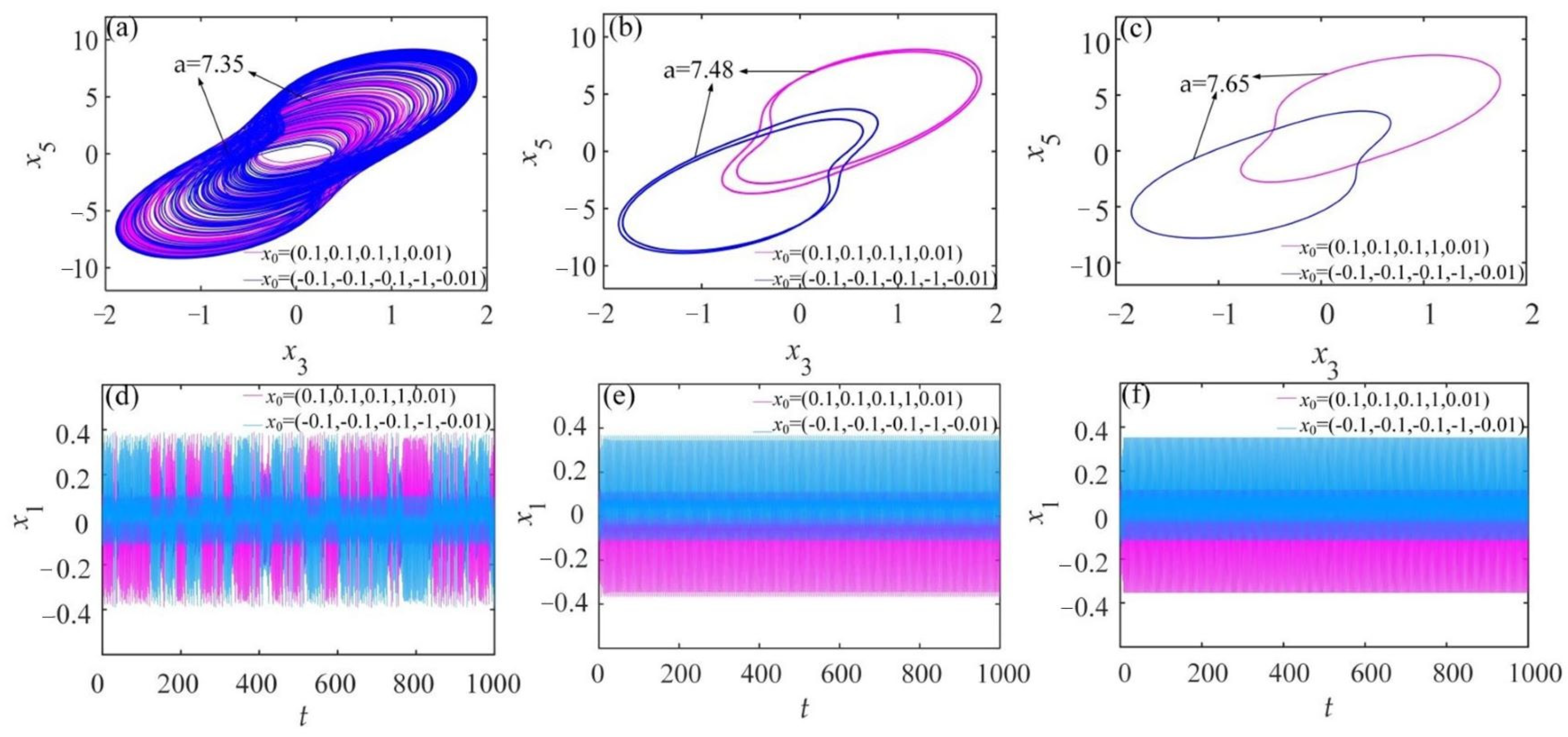
3.3.1. Coexisting Attractors Changing with Template Parameter a
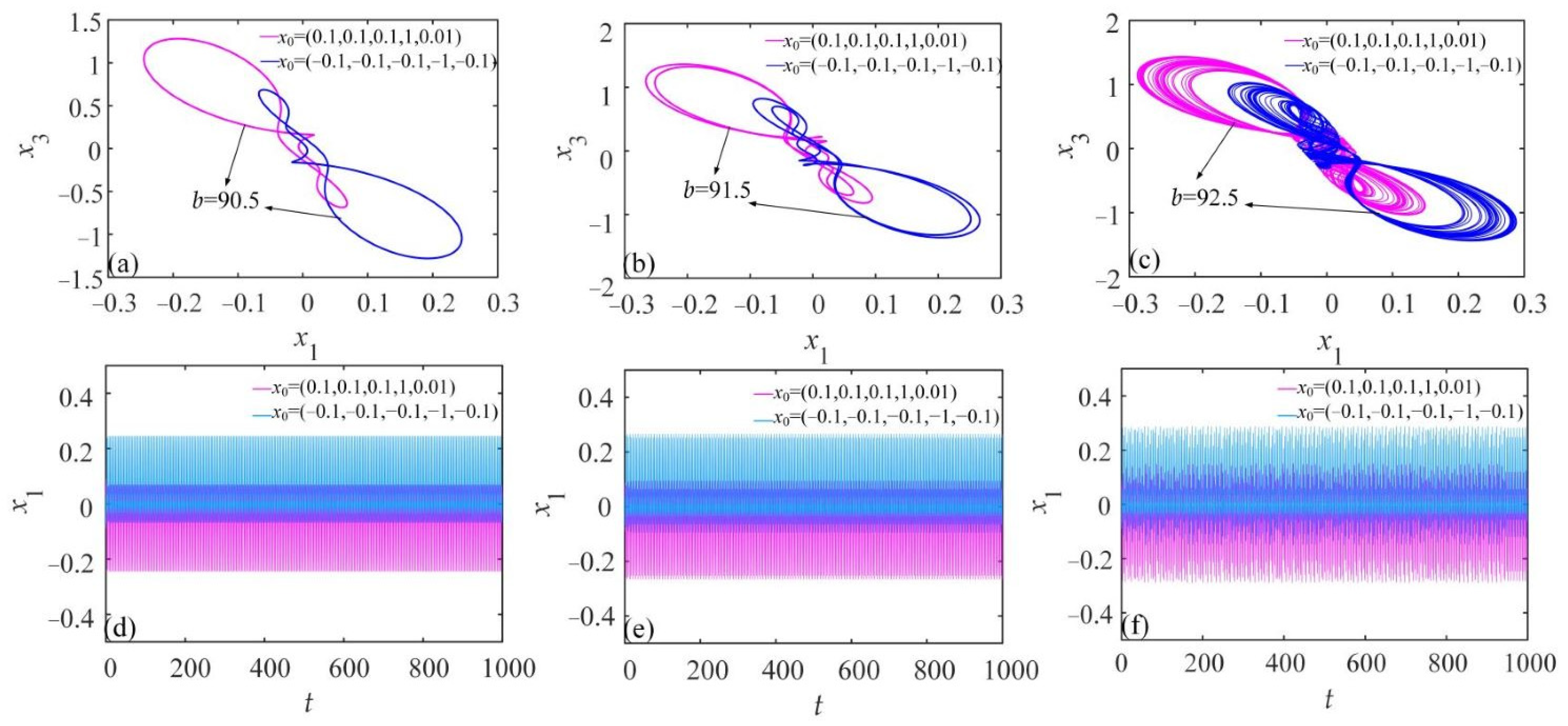
3.3.2. Coexisting Attractors Changing with Template Parameter b
3.3.3. Coexisting Hyperchaotic Attractor with Order q
3.4. State Transition
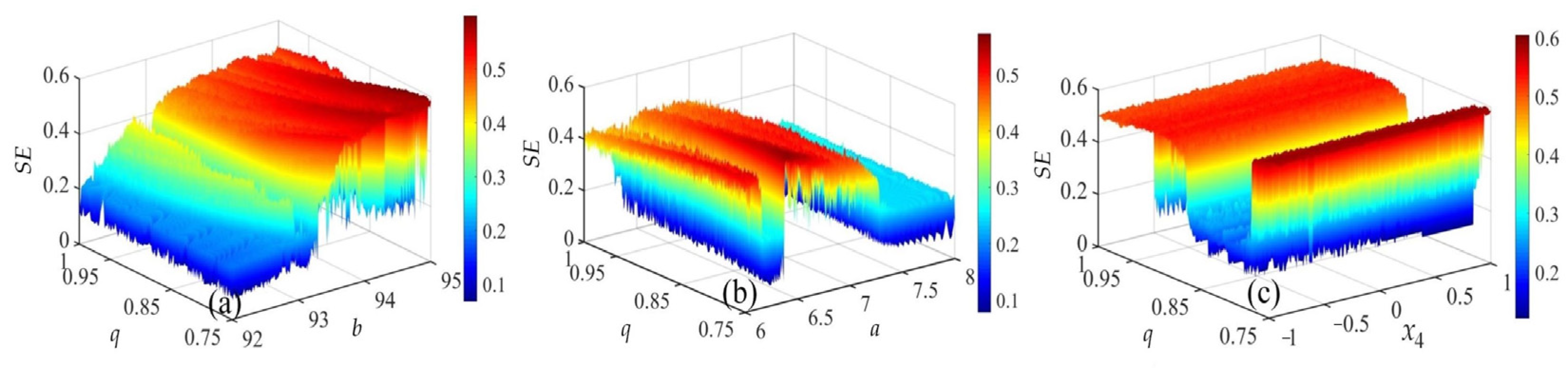
3.5. Complexity of CNN System
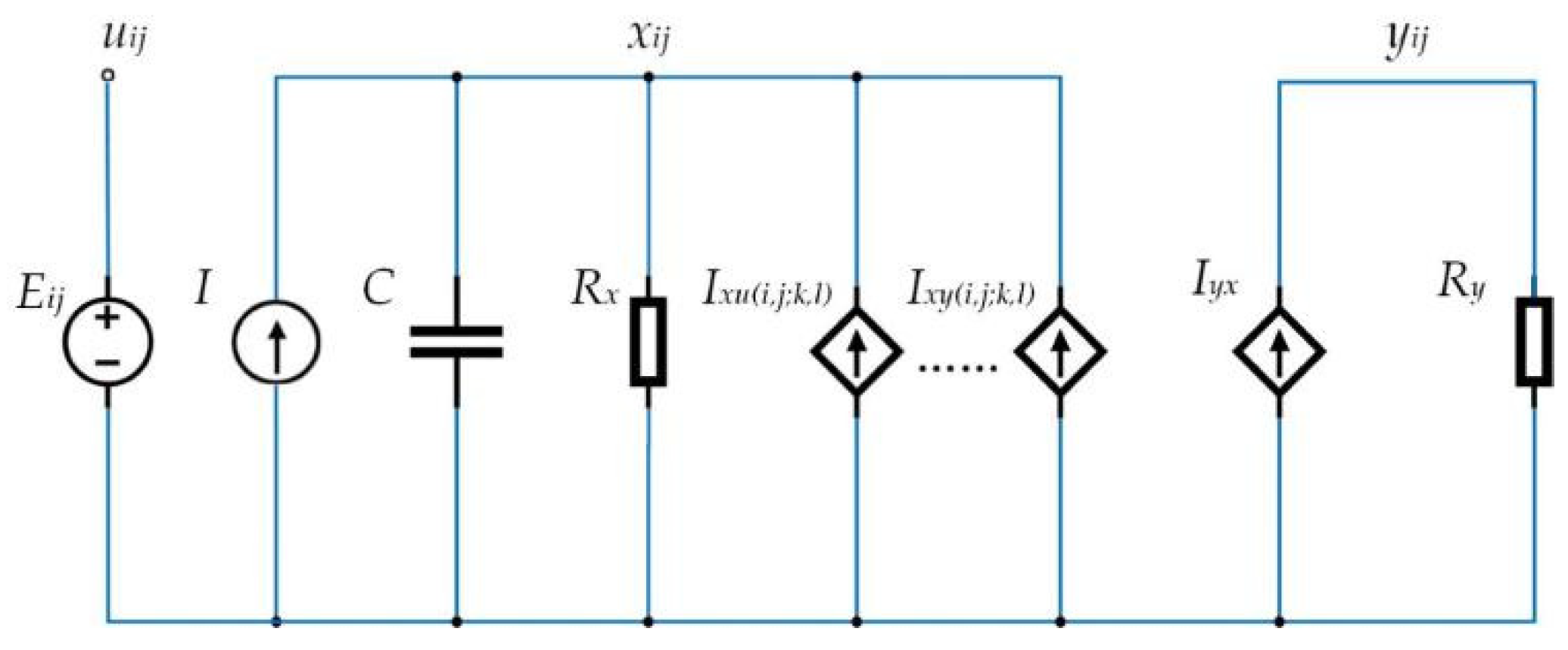
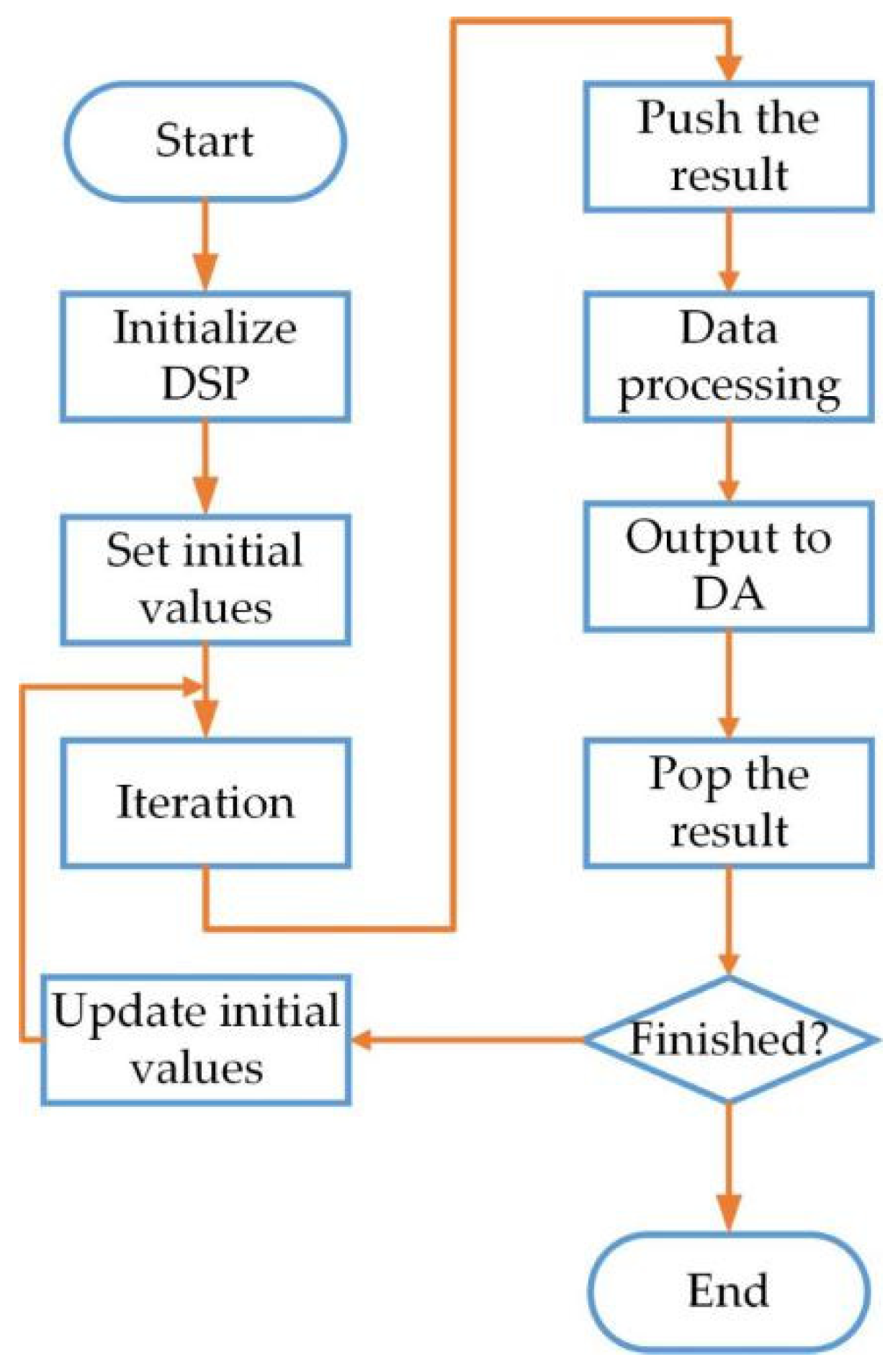
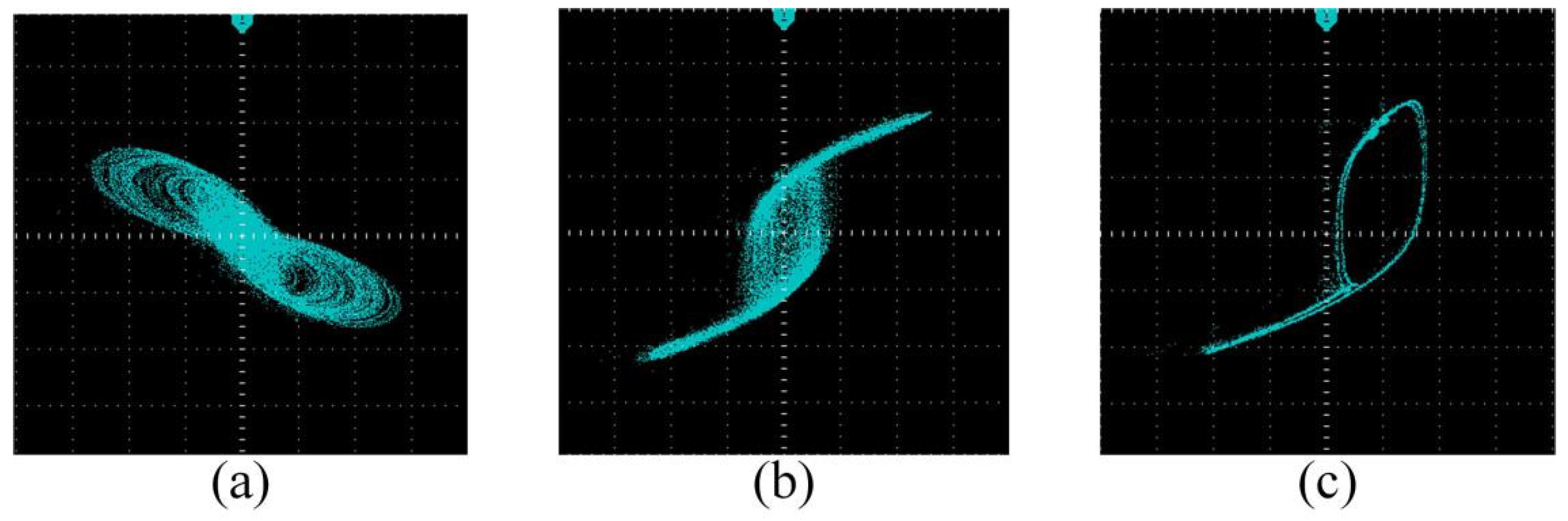
4. DSP Implementation of the Fractional-Order CNN System
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Lin, H.; Wang, C.; Chen, C.; Sun, Y.; Zhou, C.; Xu, C.; Hong, Q. Neural bursting and synchronization emulated by neural networks and circuits. IEEE Trans. Circuits Syst. I Regul. Pap. 2021, 68, 3397–3410. [Google Scholar] [CrossRef]
- Chen, M.; Qi, J.; Xu, Q.; Bao, B. Quasi-period, periodic bursting and bifurcations in memristor-based FitzHugh-Nagumo circuit. AEUE-Int. J. Electron. Commun. 2019, 110, 152840. [Google Scholar] [CrossRef]
- Ma, T.; Mou, J.; Yan, H.; Cao, Y. A new class of hopfield neural network with double memristive synapses and its DSP implementation. Eur. Phys. J. Plus 2022, 137, 1135. [Google Scholar] [CrossRef]
- Ma, J.; Tang, J. A review for dynamics in neuron and neuronal network. Nonlinear Dyn. 2017, 89, 1569–1578. [Google Scholar] [CrossRef]
- Yang, F.; Wang, X. Dynamic characteristic of a new fractional-order chaotic system based on the hopfield neural network and its digital circuit implementation. Phys. Scr. 2021, 96, 035218. [Google Scholar] [CrossRef]
- Chua, L.O.; Yang, L. Cellular neural networks: Theory. IEEE Trans. Circuits Syst. 1988, 35, 1257–1271. [Google Scholar] [CrossRef]
- Di Marco, M.; Forti, M.; Tesi, A. Complex dynamics in nearly symmetric three-cell cellular neural networks. Int. J. Bifurc. Chaos 2002, 12, 1267–1293. [Google Scholar] [CrossRef]
- Makoto, I. RTD-based cellular neural networks with multiple steady states. Int. J. Bifurc. Chaos 2001, 11, 2913–2959. [Google Scholar]
- Chen, F.; Li, J.; Chen, F. Chaos for discrete-time RTD-based cellular neural networks. Int. J. Bifurc. Chaos 2007, 17, 4395–4401. [Google Scholar] [CrossRef]
- Zou, F.; Nossek, J.A. Bifurcation and chaos in cellular neural networks. IEEE Trans. Circuits Syst. I Regul. Pap. 1993, 40, 166–173. [Google Scholar] [CrossRef]
- Wang, L.; Liu, W.; Shi, H.; Zurada, J.M. Cellular neural networks with transient chaos. IEEE Trans. Circuits Syst. II Express Briefs 2007, 54, 440–444. [Google Scholar] [CrossRef]
- Chen, F.; Li, J. Hypechaos in RTD-based cellular neural networks. Int. J. Bifurc. Chaos 2008, 18, 3439–3446. [Google Scholar] [CrossRef]
- Xiu, C.; Zhou, R.; Liu, Y. New chaotic memristive cellular neural network and its application in secure communication system. Chaos Solitons Fractals Interdiscip. J. Nonlinear Sci. Nonequilibrium Complex Phenom. 2020, 141, 110316. [Google Scholar] [CrossRef]
- Gao, X.; Mou, J.; Banerjee, S.; Zhang, Y. Color-gray multi-image hybrid compression-encryption scheme based on BP neural network and knight tour. IEEE Trans. Cybern. 2023, 53, 5037–5047. [Google Scholar] [CrossRef] [PubMed]
- Sha, Y.; Mou, J.; Wang, J.; Banerjee, S.; Sun, B. Chaotic image encryption with Hopfield neural network. Fractals 2023, 31, 2340107. [Google Scholar] [CrossRef]
- Chua, L.O.; Yang, L. Cellular neural networks: Applications. IEEE Trans. Circuits Syst. 1988, 35, 1273–1290. [Google Scholar] [CrossRef]
- Kumar, A.; Das, S.; Yadav, V.K.; Rajeev; Cao, J.; Huang, C. Synchronizations of fuzzy cellular neural networks with proportional time-delay. Aims Math. 2021, 6, 10620–10642. [Google Scholar] [CrossRef]
- Norouzi, B.; Mirzakuchaki, S. An image encryption algorithm based on DNA sequence operations and cellular neural network. Multimed. Tools Appl. 2017, 76, 13681–13701. [Google Scholar] [CrossRef]
- Zhang, R.; Yu, L.; Jiang, D.; Ding, W.; Song, J.; He, K.; Ding, Q. A novel plaintext-related color image encryption scheme based on cellular neural network and Chen’s chaotic system. Symmetry 2021, 13, 393. [Google Scholar] [CrossRef]
- Wang, X.; Su, Y.; Luo, C.; Wang, C. A novel image encryption algorithm based on fractional order 5D cellular neural network and Fisher-Yates scrambling. PLoS ONE 2020, 15, e0236015. [Google Scholar] [CrossRef]
- Du, F.; Lu, J. Finite-time synchronization of fractional-order delayed fuzzy cellar neural networks with parameter uncertainties. IEEE Trans. Fuzzy Syst. 2022, 31, 1769–1779. [Google Scholar] [CrossRef]
- Han, X.; Mou, J.; Xiong, L.; Ma, C.; Liu, T.; Cao, Y. Coexistence of infinite attractors in a fractional-order chaotic system with two nonlinear functions and its DSP implementation. Integration 2021, 81, 43–55. [Google Scholar] [CrossRef]
- Qin, C.; Sun, K.; He, S. Characteristic analysis of fractional-order memristor-based hypogenetic jerk system and its DSP implementation. Electronics 2021, 10, 841. [Google Scholar] [CrossRef]
- Ren, L.; Li, S.; Banerjee, S.; Mou, J. A new fractional-order complex chaotic system with extreme multistability and its implementation. Phys. Scr. 2023, 98, 055201. [Google Scholar] [CrossRef]
- Liu, X.; Mou, J.; Wang, J.; Banerjee, S.; Li, P. Dynamical analysis of a novel fractional-order chaotic system based on memcapacitor and meminductor. Fractal Fract. 2022, 6, 671. [Google Scholar] [CrossRef]
- Can, N.H.; Nikan, O.; Rasoulizadeh, M.N.; Jafari, H.; Gasimov, Y.S. Numerical computation of the time non-linear fractional generalized equal width model arising in shallow water channel. Therm. Sci. 2020, 24 (Suppl. 1), 49–58. [Google Scholar] [CrossRef]
- Salama, F.M.; Ali, N.H.M.; Hamid, N.N.A. Fast O (N) hybrid Laplace transform-finite difference method in solving 2D time fractional diffusion equation. J. Math. Comput. Sci. 2021, 23, 110–123. [Google Scholar] [CrossRef]
- Jassim, H.K.; Shareef, M.A. On approximate solutions for fractional system of differential equations with Caputo-Fabrizio fractional operator. J. Math. Comput. Sci. 2021, 23, 58–66. [Google Scholar] [CrossRef]
- Akram, T.; Abbas, M.; Ali, A. A numerical study on time fractional Fisher equation using an extended cubic B-spline approximation. J. Math. Comput. Sci. 2021, 22, 85–96. [Google Scholar] [CrossRef]
- Kang, Y.-M.; Xie, Y.; Lu, J.-C.; Jiang, J. On the nonexistence of non-constant exact periodic solutions in a class of the Caputo fractional-order dynamical systems. Nonlinear Dyn. 2015, 82, 1259–1267. [Google Scholar] [CrossRef]
- Sun, H.; Abdelwahab, A.; Onaral, B. Linear approximation of transfer function with a pole of fractional power. IEEE Trans. Autom. Control 1984, 29, 441–444. [Google Scholar] [CrossRef]
- Diethelm, K.; Ford, N.J.; Freed, A.D. A predictor-corrector approach for the numerical solution of fractional differential equations. Nonlinear Dyn. 2002, 29, 3–22. [Google Scholar] [CrossRef]
- Adomian, G. A new approach to nonlinear partial differential equations. J. Math. Anal. Appl. 1984, 102, 420–434. [Google Scholar] [CrossRef]
- Tavazoei, M.S.; Haeri, M. Unreliability of frequency-domain approximation in recognising chaos in fractional-order systems. IET Signal Process. 2007, 1, 171–181. [Google Scholar] [CrossRef]
- Ma, C.; Mou, J.; Yang, F.; Yan, H. A fractional-order hopfield neural network chaotic system and its circuit realization. Eur. Phys. J. Plus 2020, 135, 100. [Google Scholar] [CrossRef]
- Ma, T.; Mou, J.; Li, B.; Banerjee, S.; Yan, H. Study on the complex dynamical behavior of the fractional-order hopfield neural network system and its implementation. Fractal Fract. 2022, 6, 637. [Google Scholar] [CrossRef]
- Zheng, Y.; Ji, Z. Predictive control of fractional-order chaotic systems. Chaos Solitons Fractals 2016, 87, 307–313. [Google Scholar] [CrossRef]
- Jahanshahi, H.; Zambrano-Serrano, E.; Bekiros, S.; Wei, Z.; Volos, C.; Castillo, O.; Aly, A.A. On the dynamical investigation and synchronization of variable-order fractional neural networks: The Hopfield-like neural network model. Eur. Phys. J. Spec. Top. 2022, 231, 1757–1769. [Google Scholar] [CrossRef]
- Huang, X.; Zhao, Z.; Wang, Z.; Li, Y. Chaos and hyperchaos in fractional-order cellular neural networks. Neurocomputing 2012, 94, 13–21. [Google Scholar] [CrossRef]
- Ilsang, O.; Yongdai, K. Smooth function approximation by deep neural networks with general activation functions. Entropy 2019, 21, 627. [Google Scholar]
- Han, Q.; Liao, X.; Huang, T.; Peng, J.; Li, C.; Huang, H. Analysis and design of associative memories based on stability of cellular neural networks. Neurocomputing 2012, 97, 192–200. [Google Scholar] [CrossRef]
- Nakagawa, M. On the chaos neuron models with chebyshev type activation functions. J. Phys. Soc. Jpn. 2020, 90, 014001. [Google Scholar] [CrossRef]
- Liu, Y.; Song, Z.; Tan, M. Multiple µ-stability and multiperiodicity of delayed memristor-based fuzzy cellular neural networks with nonmonotonic activation functions. Math. Comput. Simul. 2019, 159, 1–17. [Google Scholar] [CrossRef]
- Amanda, C.M.; Paulo, C.R. Hopfield neural network: The hyperbolic tangent and the piecewise-linear activation functions. Neural Netw. 2012, 34, 42–45. [Google Scholar] [CrossRef]
- Ma, T.; Mou, J.; Al-Barakati, A.A.; Jahanshahi, H.; Li, S. Coexistence behavior of a double-MR-based cellular neural network system and its circuit implementation. Nonlinear Dyn. 2023, 111, 11593–11611. [Google Scholar] [CrossRef]
- Rajput, G.; Raut, G.; Chandra, M.; Vishvakarma, S.K. VLSI implementation of transcendental function hyperbolic tangent for deep neural network accelerators. Microprocess. Microsyst. 2021, 84, 104270. [Google Scholar] [CrossRef]
- Shakiba, F.M.; Zhou, M. Novel analog implementation of a hyperbolic tangent neuron in artificial neural networks. IEEE Trans. Ind. Electron. 2020, 68, 10856–10867. [Google Scholar] [CrossRef]
- Arena, P.; Baglio, S.; Fortuna, L.; Manganaro, G. Chua’s circuit can be generated by CNN cells. IEEE Trans. Circuits Syst. I Fundam. Theory Appl. 1995, 42, 123–125. [Google Scholar] [CrossRef]
- Malik, S.A.; Mir, A.H. FPGA realization of fractional order neuron. Appl. Math. Model. 2020, 81, 372–385. [Google Scholar] [CrossRef]
- Sharma, A.; Rawat, T.K. Design and FPGA implementation of lattice wave fractional order digital differentiator. Microelectron. J. 2019, 88, 67–78. [Google Scholar] [CrossRef]





| Full Name | Abbreviation |
|---|---|
| Cellular neural network | CNN |
| Adomian decomposition method | ADM |
| Lyapunov Exponent spectrum | LEs |
| Spectral entropy | SE |
| Digital signal processing | DSP |
| Frequency-domain method | FDM |
| Predictor-corrector method | PCM |
| a | System State | a | System State |
|---|---|---|---|
| [7.2, 7.36] | Chaos-I | [7.44, 7.46) | Asymptotic Period-II |
| (7.36, 7.4] | Chaos-II | 7.46 | Asymptotic Period-IV |
| (7.4, 7.43) | Asymptotic Period-VI | [7.47, 7.51] | Asymptotic Period-II |
| 7.43 | Asymptotic Period-IV | (7.51, 7.8] | Asymptotic Period-I |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cao, H.; Chu, R.; Cui, Y. Complex Dynamical Characteristics of the Fractional-Order Cellular Neural Network and Its DSP Implementation. Fractal Fract. 2023, 7, 633. https://doi.org/10.3390/fractalfract7080633
Cao H, Chu R, Cui Y. Complex Dynamical Characteristics of the Fractional-Order Cellular Neural Network and Its DSP Implementation. Fractal and Fractional. 2023; 7(8):633. https://doi.org/10.3390/fractalfract7080633
Chicago/Turabian StyleCao, Hongli, Ran Chu, and Yuanhui Cui. 2023. "Complex Dynamical Characteristics of the Fractional-Order Cellular Neural Network and Its DSP Implementation" Fractal and Fractional 7, no. 8: 633. https://doi.org/10.3390/fractalfract7080633
APA StyleCao, H., Chu, R., & Cui, Y. (2023). Complex Dynamical Characteristics of the Fractional-Order Cellular Neural Network and Its DSP Implementation. Fractal and Fractional, 7(8), 633. https://doi.org/10.3390/fractalfract7080633






