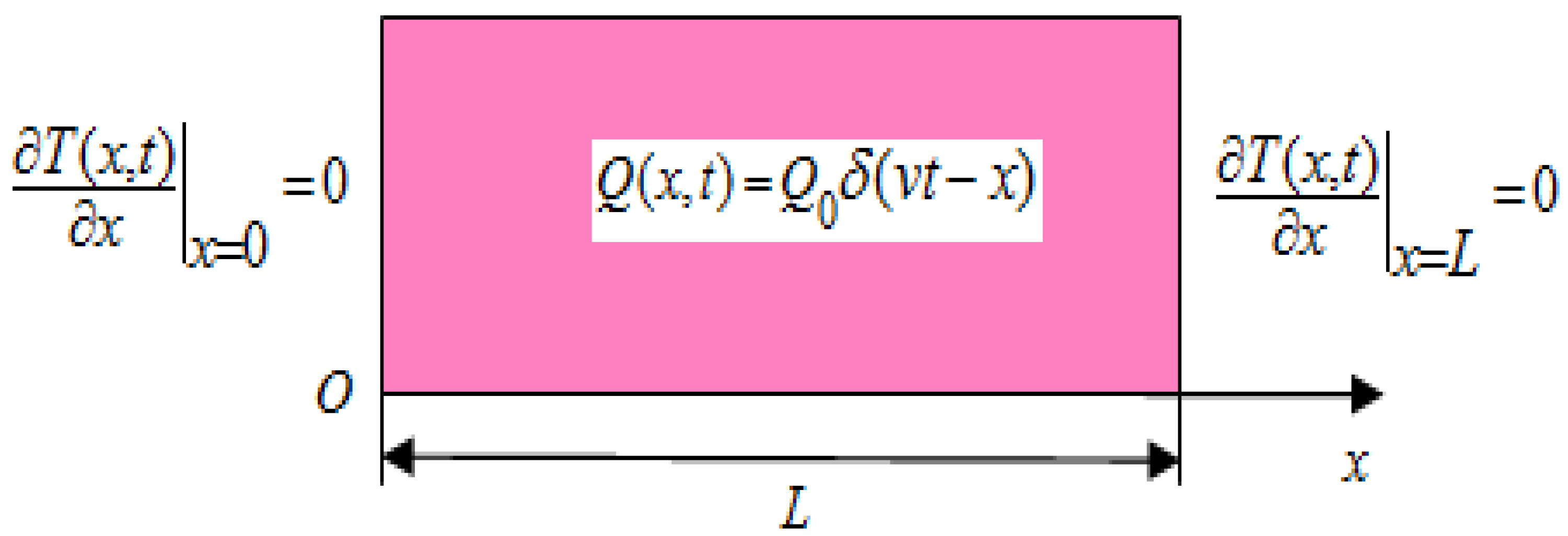1. Introduction
In the field of biological sciences, bioheat transfer is the intriguing and interdisciplinary study of heat transport inside living systems. This intriguing area of research focuses on a variety of processes, including heat transfer inside cells and tissues and the thermoregulatory mechanisms that enable animals to control their body temperatures. Bioheat transfer examines the principles of thermodynamics, fluid mechanics, and physiological processes in order to comprehend the intricate relationship between heat and life.
The way that living tissues work is fundamentally impacted by heat as an energy type. Numerous physiological functions are impacted, including the maintenance of enzymatic reactions and the control of metabolic activity. One must have a complete understanding of the generation, transport, and dissipation of heat within biological systems in order to understand the behavior and operation of such systems. Researchers in this rapidly evolving field employ theoretical models, experimental techniques, and computer simulations to better understand the intricate dynamics of heat transport in biological systems. By combining knowledge from several domains, these interdisciplinary techniques increase the bonds between biologists, physicists, engineers, mathematicians, and medics [
1,
2,
3,
4].
Thermal shock can occur when a biological system’s temperature changes significantly and fast. In the context of bioheat transport, the term “thermal shock” refers to the detrimental effects that sudden temperature fluctuations have on biological tissues and organisms. Understanding the physics and impacts of thermal shock is crucial in many fields, including biomedical engineering, cryobiology, thermal medicine, and thermal therapy [
5,
6].
The fractional integral is a mathematical concept that broadens the definition of the term “integral” to include orders other than integers. It offers a potent tool for exploring and modifying functions across a range of mathematical and scientific fields. Due to its versatility and broad variety of applications, the study of fractional integrals has attracted a lot of attention in recent years [
7,
8].
The area of bioheat transfer investigates how heat moves and is distributed within biological systems. The Pennes bioheat equation and other conventional partial differential equations have been used to model heat transfer in biological tissues. Instantaneous heat conduction and local thermal equilibrium are presupposed in these models [
9,
10,
11,
12,
13].
The concept of differentiation and integration is broadened to encompass non-integer orders through the use of fractional calculus. Because fractional calculus takes into account memory-like effects, non-locality, and long-range interactions, it may be used to represent complex physical processes like bioheat transmission. The fractional integral operator, a crucial tool in fractional calculus, enables the description of heat transfer processes with memory and long-term repercussions. The typical non-local heat conduction behavior observed in biological tissues results from a combination of factors including blood perfusion, capillary networks, and metabolic heat sources. By including non-local heat conduction components into bioheat transfer equations using fractional integral models, more precise estimates of the temperature distribution inside tissues may be achieved. Fractional integral operators can be used to explain events in biological tissues that mimic memory. Understanding these effects, which are the result of prior temperature exposure, is necessary to comprehending thermal responses and adaptive processes. Models can better accurately depict the long-term effects of previous heat exposure on tissue temperature distribution by employing fractional integral operators. Thermal treatments and diagnostic procedures may benefit from the use of fractional integral operators in bioheat transfer models. Treatment planning and optimization may be strengthened by taking non-local and memory-like effects into account. This will result in thermal therapies such as cancer hyperthermia treatments being more successful. Models that take into consideration memory effects can also help in the interpretation of temperature readings and the creation of diagnostic tools [
14,
15,
16,
17,
18].
The mathematical model of heat transfer proposed by Pennes [
19] has been widely studied in different circumstances. Also, different fractional forms of the heat transfer equation in biological tissues have been investigated. We must mention that most of the time, the studied fractional equations were obtained from the classical form in which, the temperature derivative in relation to time was artificially replaced with a fractional derivative. Even if from a mathematical point of view things are correct, there is no physical argument in favor of this construction.
In the present work, the fractional model is built starting from the constitutive equation of the thermal flow. The dimensionless form of Fourier’s law is generalized by proposing a constitutive relationship in which the thermal flow is determined not only by the temperature gradient but also by its history. The choice of the relaxation (damping) function of the heat flux is very important in the formulation of the bio-heat equation with memory.
The solution corresponding to a problem with a fractional operator contains as a parameter the fractional order of the operator. The presence of this parameter in the solution could lead to the optimal choice of the parameter value in order to achieve a solution with a certain property.
On the other hand, fractional models could be useful tools in choosing the mathematical model that leads to values close to the values obtained through experiments. In this way, an analytical model could be associated with a set of experimental values.
In this paper we develop a mathematical model by fractionalization of the temperature gradient by the fractional integral Riemann–Liouville operator. The proposed mathematical model is new in the specialized literature. Another interesting aspect is given by the property of the heat source we considered. The proposed form allows the application, at certain moments of time, of a thermal shock in a specified area of the tissue. This property could have applications in various medical treatments.
Using the Laplace transform (LT), the analytical solution in the Laplace domain for the temperature distribution in the biological tissue is obtained. Numerical values, in the real domain for temperature are determined using the Stehfest numerical algorithm for the inversion of the LT. The analytical solution for the ordinary case () is also determined. The influence of the memory parameter on the temperature distribution is investigated.
2. Materials and Methods
2.1. Statement of the Problem
Heat transfer in a one-dimensional biological tissue with length
, subjected to the moving thermal shocks is considered (
Figure 1).
The governing equations of heat transfer are [
18,
20]:
Fourier’s Law
where
is the Dirac function. The special form of the heat source
shows that at each time instant
, a constant heat source
is applied in the position
. In Equation (1) the parameter
denotes the velocity of the moving heat source.
Along with Equations (1) and (2) the following conditions are considered:
Introducing the dimensionless variables, functions and parameters,
Equations (1) and (2) become
The non-dimensionless forms of the conditions are
2.2. Fractional Mathematical Model
We considered the fractional constitutive equation of the thermal flux
where
is the fractional integral Riemann–Liouville operator [
21,
22,
23]. In Equation (12),
is Gamma function (the Euler integral of the second kind). It is used as a normalization coefficient.
The Laplace transform of the fractional integral operator (11) is given by
where
is the LT of the function
[
24].
For α = 0, the Equation (10) reduces to Equation (7).
Equation (10) can be written as
highlights that time-variation of the thermal flux is significantly influenced by the history of the temperature gradient whose values are scaled by the kernel
of the power law.
2.3. Solution of Stated Problem
2.3.1. Semi-Analytical Solution for the Generalized Bio-Heat Equation
To determine the solution of Equations (6) and (10), the Laplace transform method is used. Applying the LT to Equations (6) and (10) and using the initial value (8) we obtain
Using (16) into Equation (15), we obtain the ordinary differential equation for the transformed temperature
:
A particular solution of the non-homogenous Equation (17) is
where
The general solution of the homogeneous equation associated to Equation (17) is
and the general solution of differential Equation (17) is
Using the boundary condition (18), we get
The analytically expression
of the LT is complicated. Therefore, determining the inverse of this transform using complex analysis is difficult. Even if this inverse transform can be determined, its expression is complicated enough to be useful in numerical calculations. For these reasons, we will determine the values of the inverse Laplace transform using Sthefest’s numerical algorithm [
25].
According with Sthefest’s algorithm, the numerical values of the function
are given by
where
and
denotes the integer value function.
Formula (25) that generates the numerical values of
temperature will be used in
Section 3 of this work.
2.3.2. Solution for the Ordinary Bio-Heat Equation with Moving Thermal Shocks
In this particular case, Functions (20)–(24) have simplified forms. We will analyze these functions in turn.
The inverse LT of Equation (26) is [
26]
On the other hand,
whose inverse LT is
In the considered particular case, function
given by Equation (24) has the following expression:
Let us note that the terms in the expressions of functions
and
are of the form of the function
which is written as
Using the formulas [
26]
we get the inverse Lapace transform of
given by
Now, using (35) and the formula [
26]
we obtain
The last function that must be inverted is
The inverse LT of
is
Finally, the temperature
is given by
In this section, the analytical solution was determined in the Laplace domain for the temperature of the biological tissue, expression given by Equation (24). In particular, in the ordinary case corresponding to
, the expression of the temperature in the real domain given by Equation (40) was determined. The values in the real domain of the temperature (24) will be obtained using Equation (25). The discussion of the numerical results for certain values of the problem parameters in presented in
Section 3 of the paper.
Regarding the particular case , we make a few remarks, namely:
There are many published articles in which the Pennes equation has been investigated considering different forms of heat sources or boundary conditions. We only mention two articles [
27,
28] in which the authors studied the problem of microwave heating of skin tissue together with the effects of surface cooling and blood flow, respectively, three heat transfer models for radiofrequency ablation. The form of the thermal source considered by Wang et al. [
27], allowed the authors to use an elegant method for the integration of the studied partial differential equation. They transformed the initial boundary value problem into a standard heat equation problem. The different form of the thermal source considered by us with respect to Wang et al. [
27] does not allow the comparison of the results of this article with those obtained in Wang et al [
27].
The expression of the heat source with the Dirac distribution in the problem studied by us generates difficulties in the use of classical methods from the theory of partial differential equations. This is one reason why we used the LT to determine the solution. On the other hand, the presence of the fractional integration operator in the equations of the generalized model requires the use of the LT method to determine the analytical solution of the considered problem.
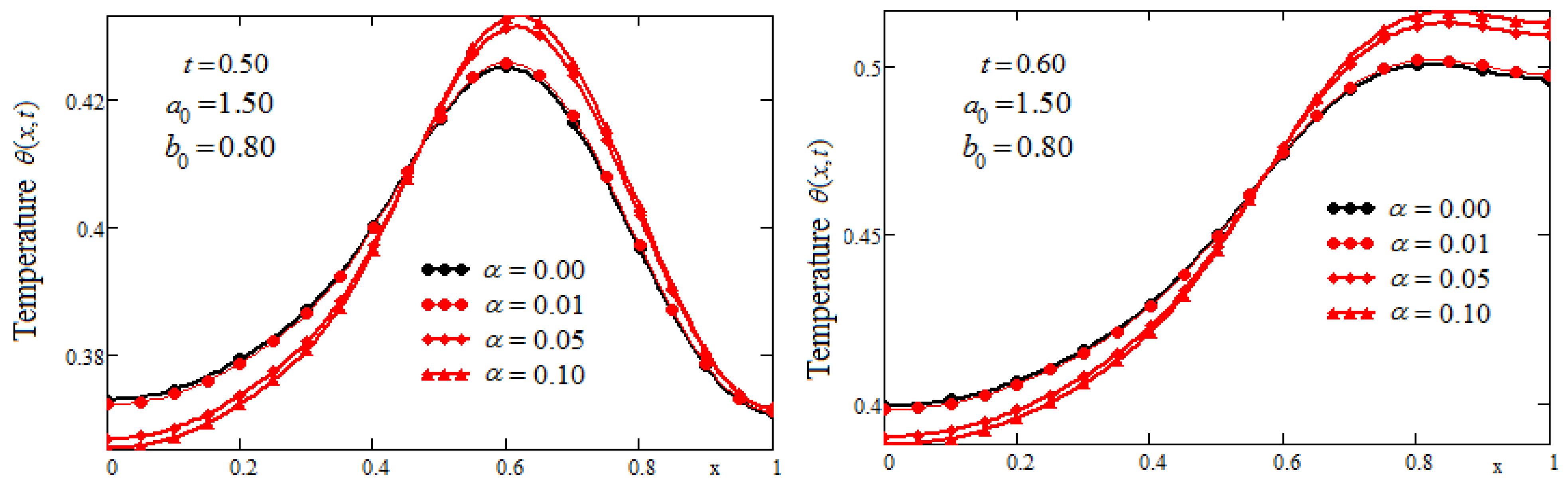
To verify the correctness of the analytical solution (40) we used the form of the general solution (24) and determined its numerical values for alpha tending to zero. The results are presented in
Figure 2. It is observed that when
the graphs of the generalized solution tend to overlap the graph of the analytical solution given by Equation (40). This fact shows the correctness of the solutions determined by us.
3. Numerical Results and Discussions
In this paper, a generalized form of the Pennes equation that models heat transfer in biological tissues is investigated. To analyze the complex thermal diffusion that occurs in such tissues, we have considered the thermal flux defined by a fractional differential equation with the Riemann–Liouville integral operator. In such thermal processes, the thermal flux is influenced not only by the temperature gradient but also by its history. In addition, the heat transfer is studied under the hypothesis of the existence of a mobile heat source that, at every moment, generates a thermal shock in a well-established position in the field of biological tissue. The proposed equation is brought to the non-dimensional form by conveniently choosing dimensionless variables. The analytical solution in the Laplace domain for the dimensional temperature was determined using the LT. Because the expression of the LT of the non-dimensional temperature is complicated, the determination of the inverse LT is difficult to find with complex analysis methods. Therefore, the determination of the temperature values in the real domain was achieved with the help of the Stehfest numerical algorithm.
To analyze the influence of the thermal memory parameter on the heat transfer process, numerical simulations have been carried out. The obtained results are presented in graphical illustrations. In all the cases analyzed, the particular case of Fourier’s law corresponding to the value of the fractional parameter is also presented. In this way, the difference between the classic heat transfer and the one based on the fractional model is highlighted.
Figure 3 has been sketched to highlight the tissue temperature variation for three values of
and two values of the parameter
. Considering the special shape of the heat source, the dimensionless parameter
has a significant influence on the temperature distribution. Let us note that, at a moment of time
t, the thermal shock is applied in the position
in the biological tissue. This is clearly highlighted in
Figure 3 where the maximum temperature is achieved in such positions. It should also be noted that until the thermal shock is applied, the temperature corresponding to the fractional model is higher than that corresponding to the classic model. There is a position in the tissue located after the one in which the temperature has the maximum value, a position after which the temperature corresponding to the classical model becomes higher than that of the generalized model. The convenient choice of the fractional parameter
and the
parameter could lead to optimal heating/cooling of certain tissue areas.
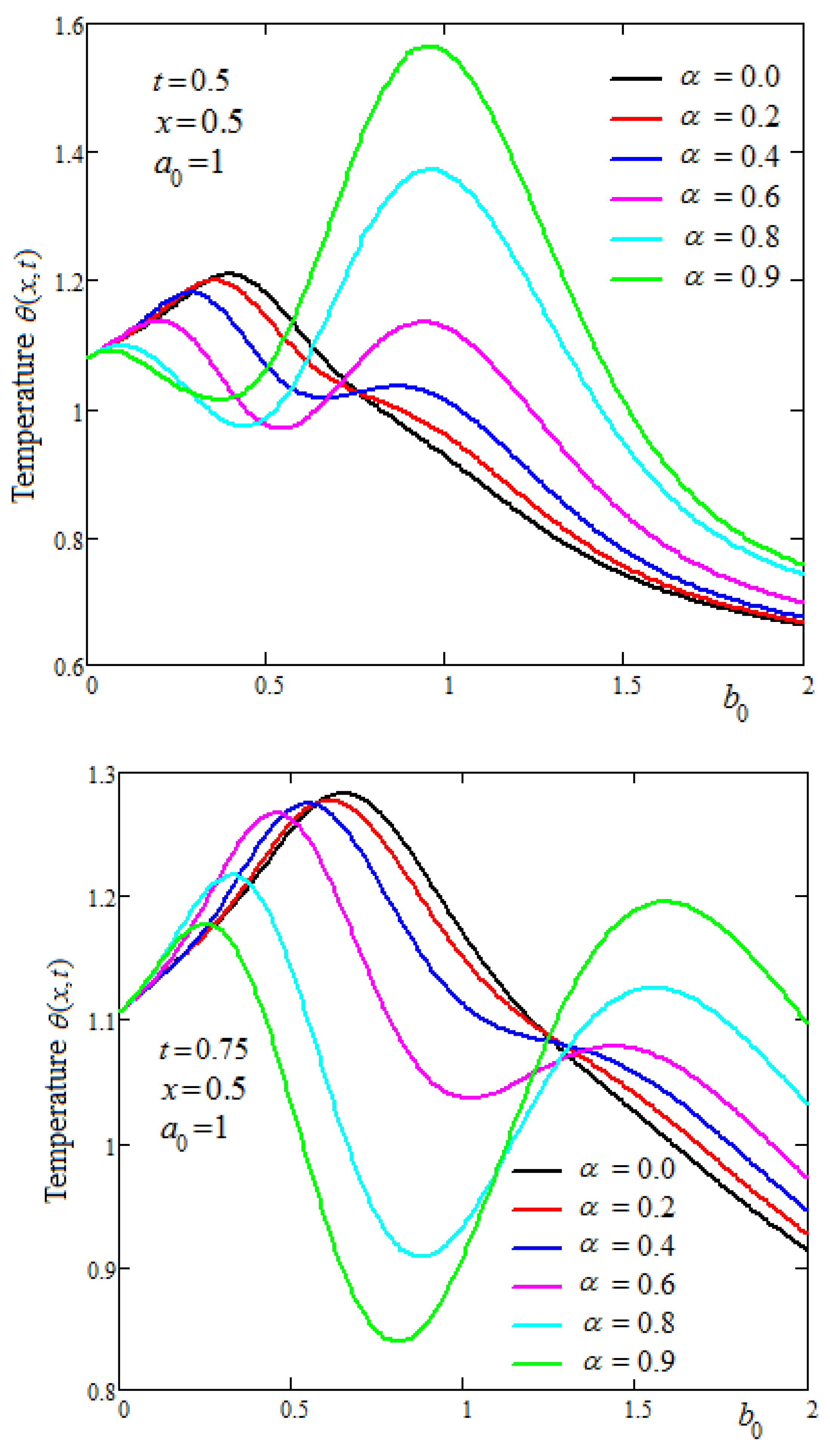
Figure 4 shows the temperature profiles at three time values and for increasing values of the thermal memory parameter
. It is observed that at different values of time, there are areas in the tissue where the temperature has an oscillating character or is increasing or decreasing.
The non-dimensional blood perfusion parameter
gives the behavior of the convective term (−
) in Equation (6), therefore this parameter significantly influences the temperature distribution.
Figure 5 shows profiles of the tissue temperature when the values of the
parameter increase. The temperature values are decreasing with the parameter
because the convective term plays the role of a cooling condition.
The influence of heat source parameter
is shown in
Figure 6. The temperature profiles are drawn in the middle of the biological tissue. Obviously, for different values of the source parameter
, the position of the thermal shock is changed; therefore, the temperature values are oscillating.
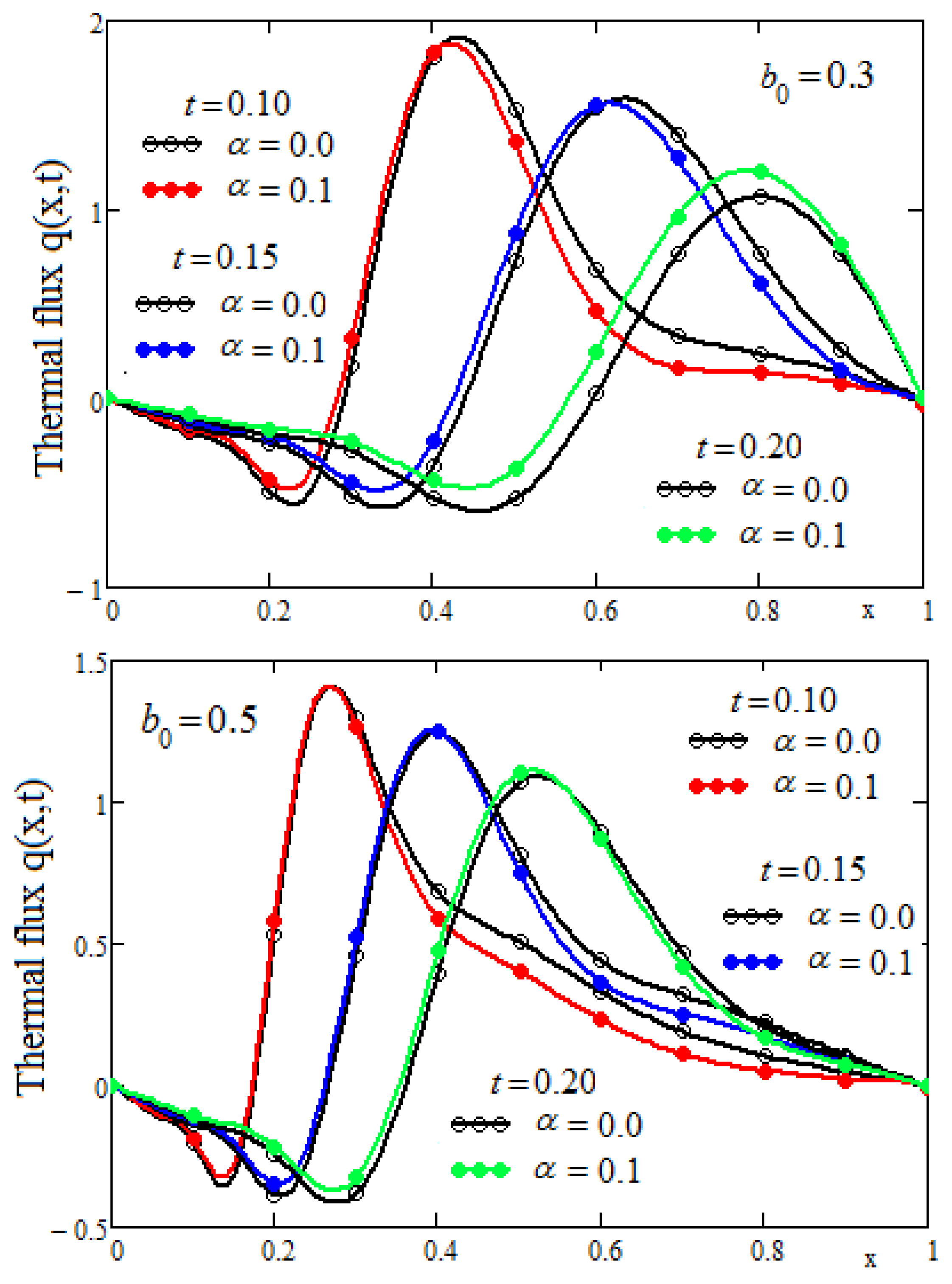
In the final part of this section, we investigate the variation of the thermal flux of the proposed model. It is known that in thermal processes the rate of heat transfer is characterized by thermal flux. Using Equations (16) and (24) we obtain the LT of the thermal flux given by
Values of the thermal flux in the real domain are determined using Stehfest’s algorithm.
Figure 7 shows the heat flux profiles at three moments of time and two values of the heat source parameter
b0. For each time value, the curves corresponding to the classic model (alpha = 0) and the generalized model (alpha = 0.1) were drawn. The numerical data chose were the same as in
Figure 3 to see the correlation between the evolution in space of the thermal flux and of the temperature. Obviously, there is a very good correlation between the graphs in
Figure 3 and
Figure 7. In the intervals in which the thermal flux has negative values, the temperature increases and in the intervals in which the thermal flux has positive values, the temperature decreases.
4. Conclusions
A semi-analytical solution for the time-fractional generalized Pennes bio-heat equation in the presence of a localized moving heat source and a constant metabolic heat generation source has been obtained using the LT and a numerical algorithm for LT inversion.
The mathematical model considered is based on the time-fractional generalized Fourier’s law, which highlights certain aspects of anomalous thermal diffusion. The constitutive equation of the thermal flux is described by the time-fractional Riemann–Liouville integral operator. As a result, the thermal flux is influenced not only by the temperature gradient but also by its historical values.
The thermal source generates a linear thermal shock at every instant at a specified position within the tissue.
Numerical simulations demonstrate that the fractional model is capable of generating higher tissue temperatures than the classical model based on Fourier’s law. By choosing the appropriate parameters for the mobile source that generates the thermal shock, it becomes possible to induce heating or cooling in specified areas of the biological tissue.
Author Contributions
Conceptualization, J.D.C.; Methodology, D.V.; Software, B.A.; Validation, B.L.; Investigation, N.A.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research work was supported by King Saud University through Researchers Supporting Project number: RSPD2023R650, King Saud University Riyadh, Saudi Arabia and Korea Institute of Energy Technology Evaluation and Planning (KETEP) grant funded by the Korea government (MOTIE) (20202020900060, The Development and Application of Operational Technology in Smart Farm Utilizing Waste Heat from Particulates Reduced Smokestack).
Data Availability Statement
Not applicable.
Acknowledgments
The authors extend their appreciation to King Saud University for funding this research through Researchers Supporting Project number: RSPD2023R650, King Saud University Riyadh, Saudi Arabia. This work was supported by Korea Institute of Energy Technology Evaluation and Planning (KETEP) grant funded by the Korea government (MOTIE) (20202020900060, The Development and Application of Operational Technology in Smart Farm Utilizing Waste Heat from Particulates Reduced Smokestack).
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| | Specific heat of tissue |
| | Specific heat of blood |
| | Blood density |
| | Tissue density |
| Arterial blood temperature |
| Local dimensional tissue temperature |
| Blood perfusion rate |
| Dirac distribution |
| Thermal conductivity of tissue |
| Local thermal flux |
| Dimensionless spatial coordinate |
| Spatial coordinate |
| Dimensionless time |
| Time |
| Dimensionless temperature |
| Dimensionless thermal flux |
| Riemann–Liouville fractional integral |
| Fractional order of Riemann–Liouville operator |
| Modified Bessel function of first kind and order |
| LT Laplace transform |
| Heat source due to metabolic heat generation in the tissue |
| Heat source intensity |
References
- Xu, F.; Lu, T.J.; Seffen, K.A.; Ng, E.Y.K. Mathematical modelling of skin bioheat transfer. Appl. Mech. Rev. 2009, 62, 050801. [Google Scholar] [CrossRef]
- Hildebrand, M.; Goslow, G.E.J. Analysis of Vertebrate Structure; Wiley: New York, NY, USA, 2001. [Google Scholar]
- Gokul, K.C.; Gurung, D.B.; Adhikary, P.R. Effect of blood perfusion and metabolism in temperature distribution in human eye. Adv. Appl. Math. Biosci. 2013, 4, 13–23. [Google Scholar]
- Nowakowska, O.; Bulinski, Z. Mathematical modelling of heat transport in section of human arm. Comp. Assist. Meth Eng. Sci. 2015, 22, 347–363. [Google Scholar]
- Ahmed, N.; Shah, N.A.; Ali, F.; Vieru, D.; Zaman, F.D. Analytical Solutions of the Fractional Mathematical Model for the Concentration of Tumor Cells for Constant Killing Rate. Mathematics 2021, 9, 1156. [Google Scholar] [CrossRef]
- Ahmed, N.; Shah, N.A.; Taherifar, S.; Zaman, F.D. Memory effects and of the killing rate on the tumor cells concentration for a one-dimensional cancer model. Chaos Solitons Fractals 2021, 144, 110750. [Google Scholar] [CrossRef]
- Imran, M.A.; Shah, N.A.; Khan, I.; Aleem, M. Applications of non-integer Caputo time fractional derivatives to natural convection flow subject to arbitrary velocity and Newtonian heating. Neural Comput. Appl. 2018, 30, 1589–1599. [Google Scholar] [CrossRef]
- Shah, N.A.; Wakif, A.; El-Zahur, E.R.; Thumma, T.; Yook, S.J.; Ashwinkumar, G.P. Heat transfers Thermodynamic activity of a second-grade ternary nanofluid flow over a vertical plate with Atangana-Baleanu Time-Fractional integral. Alex. Eng. J. 2022, 12, 10045–10053. [Google Scholar] [CrossRef]
- Moaaz, O.; Abouelregal, A.E. Multi-fractional-differential operators for a thermo-elastic magnetic response in an unbounded solid with a spherical hole via the DPL model. AIMS Math. 2022, 8, 5588–5615. [Google Scholar] [CrossRef]
- Durkee, J.W.; Antich, P.P. Exact-solution to the multiregional time dependent bioheat equation with transient heat-sources and boundary-conditions. Phys. Med. Biol. 1991, 36, 345368. [Google Scholar] [CrossRef]
- Deng, Z.; Liu, J. Analytical study on bioheat transfer problems with spatial or transient heating on skin surface or inside biological bodies. J. Biomech. Eng. 2002, 124, 638–649. [Google Scholar] [CrossRef]
- Shih, T.C.; Yuan, P.; Lin, W.L.; Kou, H.S. Analytical analysis of the Pennes bioheat transfer equation with sinusoidal heat flux condition on skin surface. Med. Eng. Phis. 2007, 29, 946–953. [Google Scholar] [CrossRef]
- Zolfaghari, A.; Maerefat, M. A New Simplified Thermoregulatory Bioheat Model for Evaluating Thermal Response of the Human Body to Transient Environment. Build. Environ. 2010, 45, 2068–2076. [Google Scholar] [CrossRef]
- Jiang, X.; Qi, H. Thermal wave model of bioheat transfer with modified Riemann-Liouville fractional derivative. J. Phys. A Math. Theor. 2012, 45, 485101. [Google Scholar] [CrossRef]
- Damor, R.S.; Kumar, S.; Shukla, A.K. Numerical solution of fractional bioheat equation with constant and sinusoidal heat flux coindition on skin tissue. Am. J. Math. Anal. 2013, 1, 20–24. [Google Scholar]
- Ezzat, M.A.; Al-Sowayan, N.S.; Al-Muhiameed, Z.I.A.; Ezzat, S.M. Fractional modelling of Pennes’ bioheat transfer equation. Heat Mass Transf. 2014, 50, 907–914. [Google Scholar] [CrossRef]
- Ferrás, L.L.; Ford, N.J.; Morgado, M.L.; Nóbrega, J.M.; Rebelo, M.S. Fractional Pennes’ Bioheat Equation: Theoretical and Numerical Studies. Fract. Calc. Appl. Anal. 2015, 18, 1080–1106. [Google Scholar] [CrossRef]
- Hristov, J. Bio-Heat Models Revisited: Concepts, Derivations, non-dementalization and Fractionalization Approaches. Front. Phys. 2019, 7, 189. [Google Scholar] [CrossRef]
- Pennes, H.H. Analysis of tissue and arterial blood temperatures in the resting forearm. J. Appl. Phys. 1948, 1, 93–122. [Google Scholar] [CrossRef]
- Talaee, M.R.; Kabiri, A. Exact analytical solution of bioheat equation subjected to intensive moving heat source. J. Mech. Med. Biol. 2017, 17, 1750081. [Google Scholar] [CrossRef]
- Hristov, J. Constitutive fractional modeling. In Mathematical Modelling: Principle and Theory; Contemporary Mathematics; Dutta, H., Ed.; AMS: Vaulx-en-Velin, France, 2023; Volume 786, pp. 37–140. [Google Scholar] [CrossRef]
- Fabrizio, M.; Giogi, C.; Morro, A. Modeling heat Conduction via fractional derivatives. Heat Mass Transf. 2017, 53, 2785. [Google Scholar] [CrossRef]
- Vieru, D.; Fetecau, C.; Ahmed, N.; Shah, N.A. A generalized kinetic model of the advection-dispersion process in a sorbing medium. Math. Model. Nat. Phenom. 2021, 16, 39. [Google Scholar] [CrossRef]
- Eiderman, V. An Introduction to Complex Analysis and the Laplace Transform; Chapman and Hall/CRc: New York, NY, USA, 2021. [Google Scholar]
- Kuznetsov, A. On the convergence of the Gaver-Stehfert algorithm. SIAM J. Numer. Anal. 2013, 51, 2984–2998. [Google Scholar] [CrossRef]
- Roberts, G.E.; Kaufman, H. Table of Laplace Transform; W.B. Saunders Company: Philadelphia, PA, USA, 1996. [Google Scholar]
- Wang, H.; Burgei, W.A.; Zhou, H. Analytical solution of one-dimensional Pennes’bioheat equation. Open Phys. 2020, 18, 1084–1092. [Google Scholar] [CrossRef]
- Tucci, C.; Trujillo, M.; Berjano, E.; Iasiello, M.; Andreozzi, A.; Vanoli, G.P. Pennes’ bioheat equation vs. porous media approach in computer modeling of radiofrequency tumor ablation. Sci. Rep. 2021, 11, 5272. [Google Scholar] [CrossRef] [PubMed]
| Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).