Fractional-Order Models of Damping Phenomena in a Flexible Sensing Antenna Used for Haptic Robot Navigation
Abstract
1. Introduction
2. State of the Art in Modeling Flexible Link Antennae
- Measure, record, and characterize the intrinsic dynamics of the flexible link by extending the model proposed in [19] to fractional order, with the measured motor angle as model input and the measured motor coupling torque as output.
- Consider different effects in the model in terms of damping. In particular, six different model structures will be considered, including internal and external damping, both of integer and fractional orders.
- Analyze the variability in the identified models, as well as the performance of the fitting.
3. Experimental Setup
4. Dynamic Model
- The deflection is small enough with respect to x to approximate by .
- The lateral deflection of the beam (out of the plane) is assumed to be zero.
- The cross-sections of the slender beam remain plane and orthogonal to the beam axis even after deformation. Moreover, rotatory inertia and shear deformation can be neglected because our antenna is very slender.
5. Methods
5.1. Experiment Description
5.2. Identification Methods
- Model with integer-order internal damping (henceforth referred to as type I).
- Model with integer-order external damping (hereafter, type II).
- Model with integer-order internal and external damping (type III).
- Model with fractional-order internal damping (henceforth named type IV).
- Model with fractional-order external damping (type V).
- Model with fractional-order internal and external damping (type VI).
5.3. Model Variability
- Mean square error (MSE) per sampling frequency, defined aswhere and are the experimental and nominal frequency responses, respectively. It should be remarked that for in (26), this index coincides with the cost function J.
- Weighted mean square error (WMSE), defined aswhere is the frequency in rad/s. This error allows more importance to be given to low frequencies. Similarly to MSE, this index coincides with the cost function J with frequency-dependent weights in (26).
- Maximum deviation (MD), defined as
- Mean deviation of resonant peaks (MDR), which measures the mean deviation of each resonance mode of the frequency response of each experiment with respect to that of the nominal one in terms of both magnitude and frequency, defined aswhere and denote the frequency, in rad/s, of each resonant peak () for the experiments and the nominal model, respectively, whereas and represent the magnitude, in dB, of the experimental and the nominal frequency responses, respectively, at the resonance frequency .
6. Results
6.1. Variability in the Model Structure
- With respect to the measured responses plotted in Figure 6, although noisy at certain frequencies (mainly at very low and high frequencies and those corresponding to the anti-resonant peaks), we can confirm that the Welch’s method outperforms the FFT algorithm for estimating experimental frequency responses. Several zero-phase filters were tried on the time-domain experimental data and the Welch’s method configurations, but with poorer results than those shown. Likewise, taking into account the results shown in this figure, it can be said that qualitatively and looking at the fit of resonant peaks (in magnitude, phase, and frequency), the models whose frequency responses are most similar to the experimental ones are models type III and type VI (Figure 6c,f) (integer- and fractional-order models with two and four parameters, respectively). On the other hand, models type I and type IV (see Figure 6a,d) perform better at low frequencies and they excessively dampen high vibration modes because of parameter (it should be recalled that this defines internal damping, which depends on the material of the flexible link). By contrast, models type II and type V (Figure 6b,e) are able to better adjust high frequencies due to the external damping parameter, . Obviously, these preliminary conclusions should be validated in a quantitative manner.
- From Table 3, except for model type III, there are significant differences in the identified nominal model for each of the forms of weighting function , even obtaining values for parameter an order of magnitude higher when the frequency-dependent weights are considered. For the rest of the parameters, the mean values are reduced with the frequency-dependent weighting function, with parameter varying the least of these three, while and are reduced by about 22% and 30%, respectively (except in the cases of the type V and VI models, where is practically unchanged or varies by about 75%, respectively). The differences can be better appreciated in Figure 6, excluding the case of model type III (Figure 6c), where the form of in (26) has no influence (the frequency response of the models is the same). As can be observed, the main discrepancies are found in the resonance and anti-resonance peaks, both in magnitude and in phase (especially in the latter).
- Considering the standard deviation values in Table 3, the parameter with the highest variability for all the identified models is , with its value, except in the case of the model type III, being higher for the case of the frequency-dependent weighting function (note that this parameter does not appear in models type II and type V).
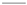 ) is the frequency response of all the experiments, (
) is the frequency response of all the experiments, ( ) is the response of the nominal model obtained with constant weights, and (
) is the response of the nominal model obtained with constant weights, and ( ) is the one for the nominal model with frequency-dependent weights.
) is the one for the nominal model with frequency-dependent weights.
 ) is the frequency response of all the experiments, (
) is the frequency response of all the experiments, ( ) is the response of the nominal model obtained with constant weights, and (
) is the response of the nominal model obtained with constant weights, and ( ) is the one for the nominal model with frequency-dependent weights.
) is the one for the nominal model with frequency-dependent weights.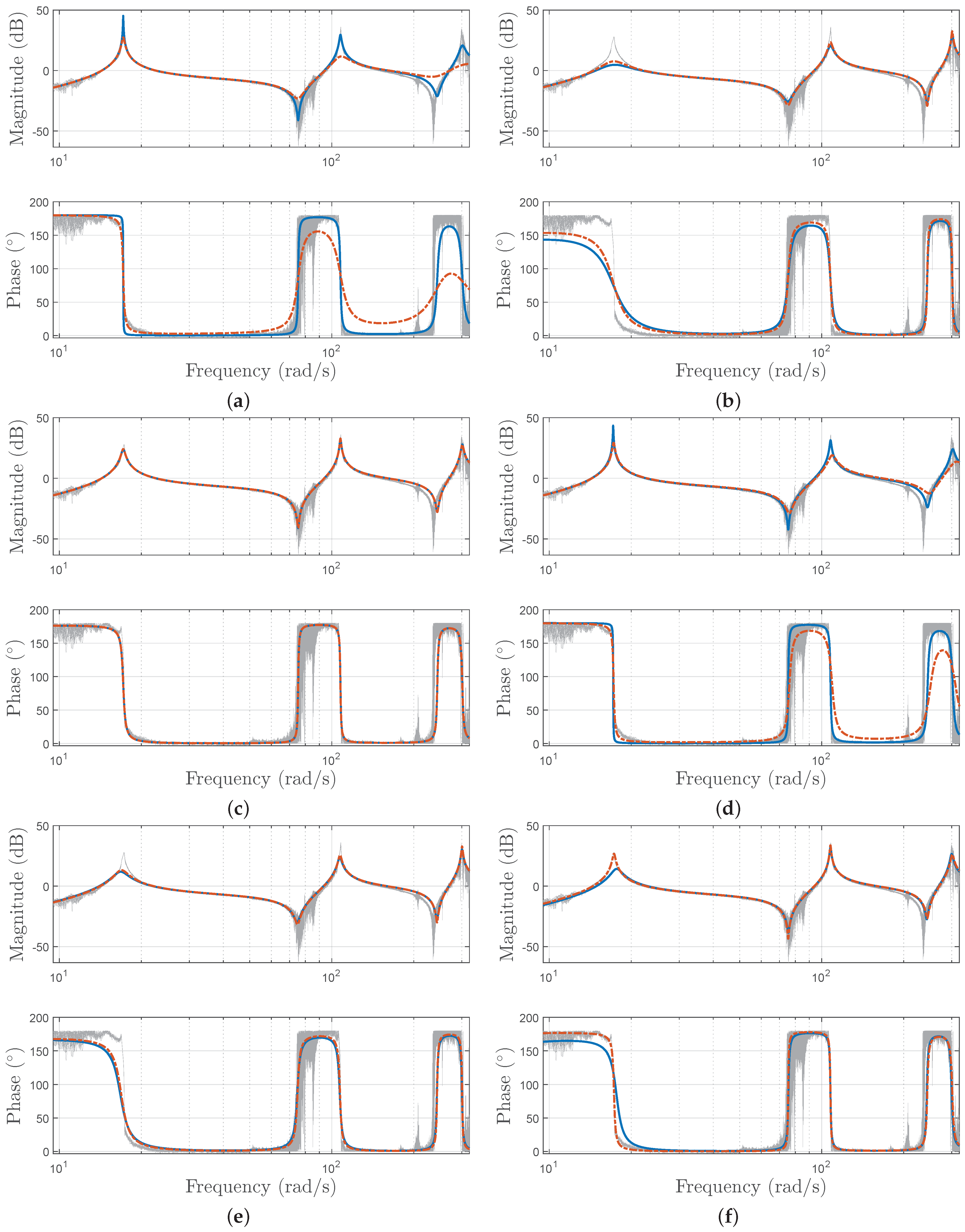
| Model | () | () | |||||||
|---|---|---|---|---|---|---|---|---|---|
| const | -dep | const | -dep | const | -dep | const | -dep | ||
| Type I | Mean | - | - | 1.33 | 10.75 | - | - | - | - |
| Mdn | - | - | 1.32 | 10.71 | - | - | - | - | |
| Std | - | - | 0.09 | 0.34 | - | - | - | - | |
| Min | - | - | 1.19 | 10.19 | - | - | - | - | |
| Max | - | - | 1.46 | 11.42 | - | - | - | - | |
| Type II | Mean | - | - | - | - | - | - | 1.97 | 1.39 |
| Mdn | - | - | - | - | - | - | 1.88 | 1.35 | |
| Std | - | - | - | - | - | - | 0.29 | 0.20 | |
| Min | - | - | - | - | - | - | 1.44 | 1.07 | |
| Max | - | - | - | - | - | - | 2.58 | 1.82 | |
| Type III | Mean | - | - | 0.54 | 0.54 | - | - | 0.20 | 0.20 |
| Mdn | - | - | 0.52 | 0.52 | - | - | 0.20 | 0.20 | |
| Std | - | - | 0.08 | 0.06 | - | - | 0.04 | 0.01 | |
| Min | - | - | 0.36 | 0.42 | - | - | 0.14 | 0.18 | |
| Max | - | - | 0.70 | 0.65 | - | - | 0.29 | 0.23 | |
| Type IV | Mean | 0.832 | 0.679 | 2.49 | 24.45 | - | - | - | - |
| Mdn | 0.831 | 0.678 | 2.46 | 24.59 | - | - | - | - | |
| Std | 0.026 | 0.009 | 0.23 | 1.01 | - | - | - | - | |
| Min | 0.768 | 0.658 | 1.97 | 22.45 | - | - | - | - | |
| Max | - | - | - | - | |||||
| Type V | Mean | - | - | - | - | ||||
| Mdn | - | - | - | - | |||||
| Std | - | - | - | - | |||||
| Min | - | - | - | - | |||||
| Max | - | - | - | - | |||||
| Type VI | Mean | ||||||||
| Mdn | |||||||||
| Std | |||||||||
| Min | |||||||||
| Max | |||||||||
6.2. Fitting Performance
6.2.1. Fitting of Overall Frequency Response
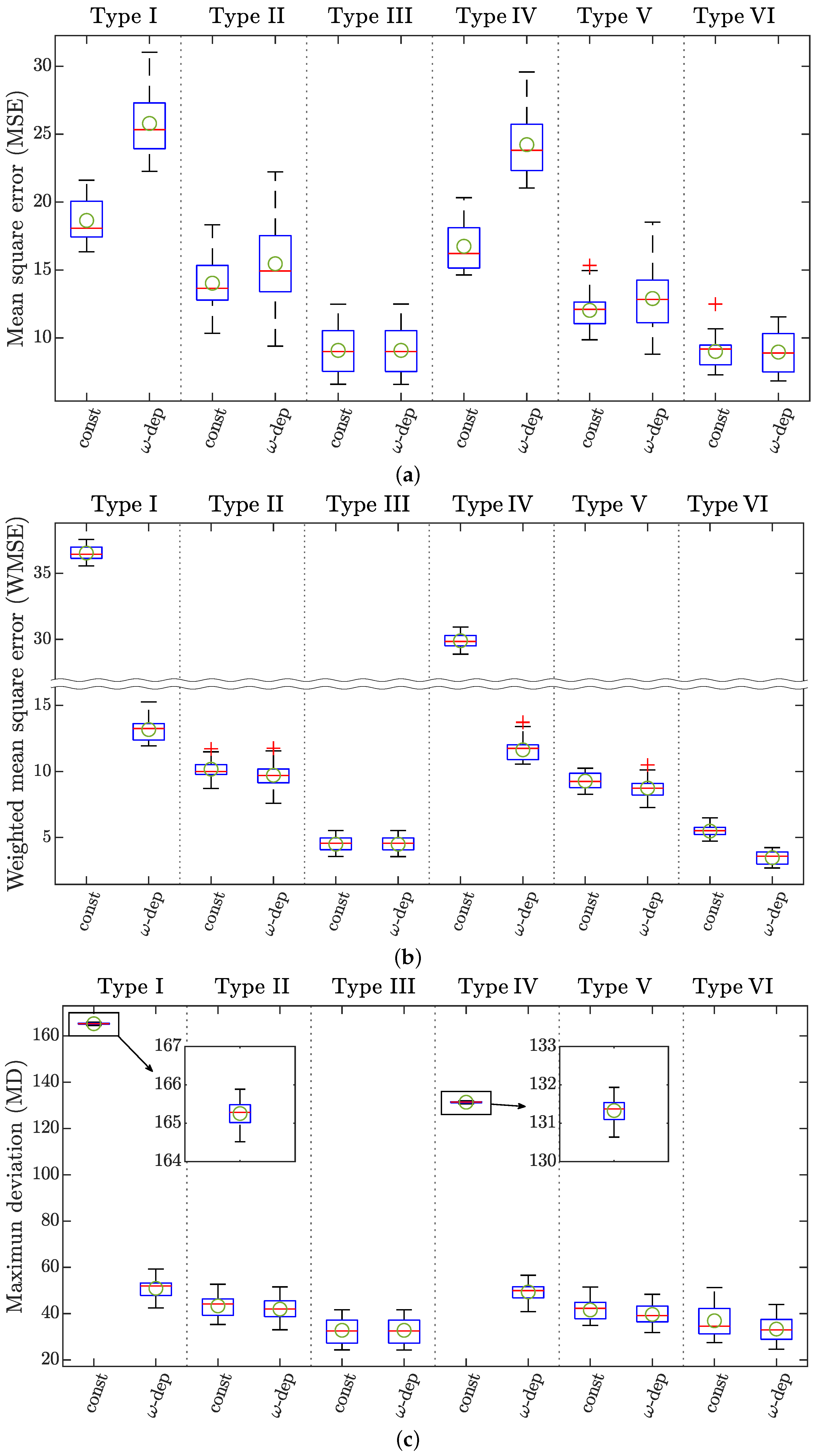
- Considering MSE (Figure 7a), the values obtained for all the models are lower for the constant weighting function, except for type III and type VI, for which there is practically no difference between the two forms of the function. Taking into account that this index is utilized as a cost function for identification (in this paper, the definition of MSE takes the form of the cost function (26) for ), constant weights are expected to show better results. However, it is remarked that there are no differences in model type III because the nominal models for the two weighting functions are the same. Likewise, when comparing all the identified models, models type III and type VI are the ones that perform better, with mean values of MSE of, respectively, and for constant weights, and and for frequency-dependent weights. The standard deviation is lower for the case of type VI. These results confirm the conclusion previously reached by looking at the frequency responses in graphical form. Again, it should be remarked that model type III is of integer order with two parameters, whereas model type VI is a fractional-order four-parameter dynamic model.
- With respect to WMSE (Figure 7b), lower values for each model are obtained with frequency-dependent weights, as is expected (the definition of WMSE takes the form of the cost function (26) for frequency-dependent weights). Additionally, similar to the results obtained with MSE, the models with the worst performance are type I and type IV, whereas models type III and type VI have the best results, with mean values of and for constant weights, and and for frequency-dependent weights, respectively. In contrast with MSE, it is appreciated that frequency-dependent weights provide a better result than constant ones for models type I, IV, and VI. This fact agrees with the results shown in Figure 6f.
- Where MD is concerned (Figure 7c), significant changes were found for the two weighting functions for models type I and IV, but for this index the worst results are obtained for .
6.2.2. Fitting of the Resonant Peaks
- First peak: in frequency, the best model is type VI with a mean deviation of 0 rad/s, followed by type II and type IV, with rad/s. Additionally, model type I gives the best results in magnitude with a mean deviation of dB. As expected, the best models, in this case, were all obtained with frequency-dependent weights, which by definition give more importance to the first resonant peak. Furthermore, except for type II, these models are dependent on internal damping that performs better at low frequencies.
- Second peak: model type IV in frequency and model type VI in magnitude are the best, with constant and frequency-dependent weighting functions with a mean deviation of rad/s and dB, respectively.
- Third peak: for frequency, model type VI with a constant weighting function (deviation value of rad/s), and model type V with frequency-dependent weighting for magnitude (mean deviation of dB) are the best fits. Hence, the models that best adjust the third peak are those that depend on fractional-order external damping.
6.3. Discussion about the Best Identified Models
- When comparing the two forms of cost function (26), the mean values of the damping parameters for model type III are practically equal for constant and frequency-dependent weights. However, the standard deviations of both and are lower for the case of frequency-dependent weights (refer to Table 3). Furthermore, there is a slight improvement in the fit of the resonant peaks for frequency-dependent weights (see Table 4). Concerning model type VI, the standard deviations of the four damping parameters are also lower with frequency-dependent weights. Moreover, as was said, the difference between using the two weighting functions can be observed in Figure 6 and Figure 7.
- For our system, using frequency-dependent weights for identification is preferable for the following reasons. Firstly, the behavior of the sensing antenna is mainly characterized by the first resonance mode. Hence, the accurate fit of the first resonant peak is preferred over the rest. Secondly, as is observed in experimental frequency responses in Figure 6, noise increases as frequency increases. While the noise at the anti-resonances has almost no influence, the noise produced in the third resonance peak substantially affects the fitting performance, as can be seen by comparing the MSE and WMSE indexes. MSE, which gives the same importance to all the frequencies, is more affected by this noise. Therefore, there are no significant differences between the identified models for the two weighting functions in terms of MSE, although their frequency responses are graphically quite different (see, e.g., Figure 6f).
- Where variability in the model structure is concerned (Table 3), the standard deviations of parameters and for model type VI (with percentages of 28% and 7% with respect to the mean value) are higher than those obtained for the parameters of type III (with 11% and 5%). Since model type VI has more parameters, it is expected to have more variability. Nevertheless, model type VI has a fractional-order internal damping that can be approximated to an integer order (mean and median of are practically equal to 1). Meanwhile, the fractional-order external damping has a derivative order close to 0.5. If a model with fewer parameters than type VI is required, it can be set by a model with integer-order internal and fractional-order external dampings (with a number of three parameters). Furthermore, it could be said that integer order performs better in fitting internal damping than fractional order. Taking into account the considered experimental setup (carbon fiber beam in air), the results provide interesting information when compared with the literature (see, e.g., [34] and references therein): (a) means that the beam can be described by classical Kelvin–Voigt damping; and (b) being close to 0.5 indicates that the interaction of the antenna with the environment can also be modeled as in other reference works.
- Regarding the fitting of the overall frequency response (Figure 7), the difference between models type III and type VI in terms of MSE is slight: that of type VI is about 1% lower than the corresponding MSE of type III. However, this difference increases to 23% when considering WMSE. Since the noise of the third resonance peak affects MSE more than WMSE, it is better to use WMSE in our application.
- Taking into account the deviation of resonant peaks in Table 4, the nominal model of type VI (obtained with the frequency-dependent weighting function) performs better than model type III in describing the first two resonance modes of the flexible link. The mean deviation of model type VI is 100% and 77% lower than type III in the frequency and magnitude of the first peak, respectively, and 14% and 44% for the second peak. However, the mean deviation of model type III is a 6% and 24% lower in frequency and magnitude, respectively, than the corresponding values of model type VI for the third peak.
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| DOF | Degrees of freedom |
| FFT | Fast Fourier transform |
| max | Maximum value |
| MD | Maximum deviation |
| mdn | Median |
| MDR | Mean deviation of resonant peaks |
| min | Minimum value |
| MSE | Mean square error |
| PID | Proportional-integral-derivative |
| std | Standard deviation |
| WMSE | Weighted mean square error |
Appendix A
References
- Staudacher, E.; Gebhardt, M.; Durr, V. Antennal movements and mechanoreception: Neurobiology of active tactile sensors. Adv. Insect Physiol. 2005, 32, 49–205. [Google Scholar] [CrossRef]
- Prescott, T.J.; Pearson, M.J.; Mitchinson, B.; Sullivan, J.W.; Pipe, A.G. Whisking with robots from rat vibrissae to biomimetic technology for active touch. IEEE Robot. Autom. Mag. 2009, 16, 42–50. [Google Scholar] [CrossRef]
- Ueno, N.; Svinin, M.; Kaneko, M. Dynamic contact sensing by flexible beam. IEEE/ASME Trans. Mechatron. 1998, 3, 254–264. [Google Scholar] [CrossRef]
- Meirovitch, L. Analytical Methods in Vibrations; Macmillan Series in Applied Mechanics; Macmillan: New York, NY, USA, 1967. [Google Scholar]
- Baker, W.E.; Woolam, W.E.; Young, D. Air and internal damping of thin cantilever beams. Int. J. Mech. Sci. 1967, 9, 743–766. [Google Scholar] [CrossRef]
- Banks, H.T.; Inman, D.J. On Damping Mechanisms in Beams. J. Appl. Mech. 1991, 58, 716–723. [Google Scholar] [CrossRef]
- Li, M. Theory of Fractional Engineering Vibrations; De Gruyter: Berlin, Germany, 2021. [Google Scholar] [CrossRef]
- Mujumdar, A.; Tamhane, B.; Kurode, S. Fractional order modeling and control of a flexible manipulator using sliding modes. In Proceedings of the 2014 American Control Conference, Portland, OR, USA, 4–6 June 2014; pp. 2011–2016. [Google Scholar] [CrossRef]
- Singh, A.P.; Deb, D.; Agarwal, H. On selection of improved fractional model and control of different systems with experimental validation. Commun. Nonlinear Sci. Numer. Simul. 2019, 79, 104902. [Google Scholar] [CrossRef]
- Di Paola, M.; Heuer, R.; Pirrotta, A. Fractional visco-elastic Euler-Bernoulli beam. Int. J. Solids Struct. 2013, 50, 3505–3510. [Google Scholar] [CrossRef]
- Freundlich, J. Transient vibrations of a fractional Kelvin-Voigt viscoelastic cantilever beam with a tip mass and subjected to a base excitation. J. Sound Vib. 2019, 438, 99–115. [Google Scholar] [CrossRef]
- Zhang, G.; Wu, Z.; Li, Y. Nonlinear Dynamic Analysis of Fractional Damped Viscoelastic Beams. Int. J. Struct. Stab. Dyn. 2019, 19, 1950129. [Google Scholar] [CrossRef]
- Agrawal, O.P. Analytical Solution for Stochastic Response of a Fractionally Damped Beam. J. Vib. Acoust 2004, 126, 561–566. [Google Scholar] [CrossRef]
- Liang, Z.f.; Tang, X. Analytical solution of fractionally damped beam by Adomian decomposition method. Appl. Math. Mech. (Engl. Ed.) 2007, 28, 219–228. [Google Scholar] [CrossRef]
- Abu-Mallouh, R.; Abu-Alshaikh, I.; Zibdeh, H.S.; Ramadan, K. Response of Fractionally Damped Beams with General Boundary Conditions Subjected to Moving Loads. Shock Vib. 2012, 19, 321421. [Google Scholar] [CrossRef]
- Alkhaldi, H.; Abualshaikh, I.; Al-Rabadi, A. Vibration Control of Fractionally-Damped Beam Subjected to a Moving Vehicle and Attached to Fractionally-Damped Multiabsorbers. Adv. Math. Phys. 2013, 2013, 232160. [Google Scholar] [CrossRef]
- Behera, D.; Chakraverty, S. Numerical solution of fractionally damped beam by homotopy perturbation method. Open Phys. 2013, 11, 792–798. [Google Scholar] [CrossRef][Green Version]
- Jena, R.; Chakraverty, S.; Jena, S. Dynamic response analysis of fractionally damped beams subjected to external loads using Homotopy Analysis Method (HAM). J. Appl. Comput. Mech. 2019, 5, 355–366. [Google Scholar] [CrossRef]
- Pota, H.R.; Alberts, T.E. Multivariable Transfer Functions for a Slewing Piezoelectric Laminate Beam. J. Dyn. Syst. Meas. Control 1995, 117, 352–359. [Google Scholar] [CrossRef]
- Tzes, A.P.; Yurkovich, S. Application and Comparison of On-Line Identification Methods for Flexible Manipulator Control. Int. J. Robot. Res. 1991, 10, 515–527. [Google Scholar] [CrossRef]
- Valério, D.; Ortigueira, M.D.; da Costa, J.S. Identifying a Transfer Function From a Frequency Response. J. Comput. Nonlinear Dyn. 2008, 3, 021207. [Google Scholar] [CrossRef]
- Pintelon, R.; Guillaume, P.; Rolain, Y.; Schoukens, J.; Van Hamme, H. Parametric identification of transfer functions in the frequency domain—A survey. IEEE Trans. Autom. Control 1994, 39, 2245–2260. [Google Scholar] [CrossRef]
- Ljung, L. System Identification: Theory for the User; Prentice-Hall, Inc.: Hoboken, NJ, USA, 1987. [Google Scholar]
- Valério, D.; da Costa, J.S. An Introduction to Fractional Control; The Institution of Engineering and Technology: Stevenage, UK, 2012; Chapter Fractional Identification; pp. 141–180. [Google Scholar] [CrossRef]
- Yu, W.; Luo, Y.; Chen, Y.; Pi, Y. Frequency domain modelling and control of fractional-order system for permanent magnet synchronous motor velocity servo system. IET Control Theory Appl. 2016, 10, 136–143. [Google Scholar] [CrossRef]
- Tejado, I.; Valério, D.; Pires, P.; Martins, J. Fractional order human arm dynamics with variability analyses. Mechatronics 2013, 23, 805–812. [Google Scholar] [CrossRef]
- Caponetto, R.; Matera, F.; Murgano, E.; Privitera, E.; Xibilia, M.G. Fuel Cell Fractional-Order Model via Electrochemical Impedance Spectroscopy. Fractal Fract. 2021, 5, 21. [Google Scholar] [CrossRef]
- Vinagre, B.M.; Feliu, V.; Feliu, J. Frequency domain identification of a flexible structure with piezoelectric actuators using irrational transfer function models. In Proceedings of the 37th IEEE Conference on Decision and Control (Cat. No.98CH36171), Tampa, FL, USA, 16–18 December 1998; Volume 2, pp. 1278–1280. [Google Scholar] [CrossRef]
- Feliu, V.; Feliu-Talegón, D.; Castillo-Berrio, C. Improved object detection using a robotic sensing antenna with vibration damping control. Sensors 2017, 17, 852. [Google Scholar] [CrossRef] [PubMed]
- Traver, J.E.; Nuevo-Gallardo, C.; Rodríguez, P.; Tejado, I.; Vinagre, B.M. Modeling and Control of IPMC-Based Artificial Eukaryotic Flagellum Swimming Robot: Distributed Actuation. Algorithms 2022, 15, 181. [Google Scholar] [CrossRef]
- Mérida-Calvo, L.; Feliu-Talegón, D.; Vicente Feliu-Batlle, F. Improving the Detection of the Contact Point in Active Sensing Antennae by Processing Combined Static and Dynamic Information. Sensors 2021, 21, 1808. [Google Scholar] [CrossRef]
- Castillo-Berrio, C.F.; Feliu-Batlle, V. Vibration-free position control for a two degrees of freedom flexible-beam sensor. Mechatronics 2015, 27, 1–12. [Google Scholar] [CrossRef]
- Oñate, E. Slender Plane Beams. Euler-Bernoulli Theory. In Structural Analysis with the Finite Element Method Linear Statics: Volume 2. Beams, Plates and Shells; Springer: Dordrecht, The Netherlands, 2013. [Google Scholar] [CrossRef]
- Bagley, R.L.; Torvik, P.J. A Theoretical Basis for the Application of Fractional Calculus to Viscoelasticity. J. Rheol. 1983, 27, 201–210. [Google Scholar] [CrossRef]
- Mainardi, F. Fractional Calculus and Waves in Linear Viscoelasticity. An Introduction to Mathematical Models; Imperial College Press: London, UK, 2010. [Google Scholar]



 ) reference angle and (
) reference angle and ( ) measured angle by the encoder; (b) measured coupling torque.
) measured angle by the encoder; (b) measured coupling torque.
 ) reference angle and (
) reference angle and ( ) measured angle by the encoder; (b) measured coupling torque.
) measured angle by the encoder; (b) measured coupling torque.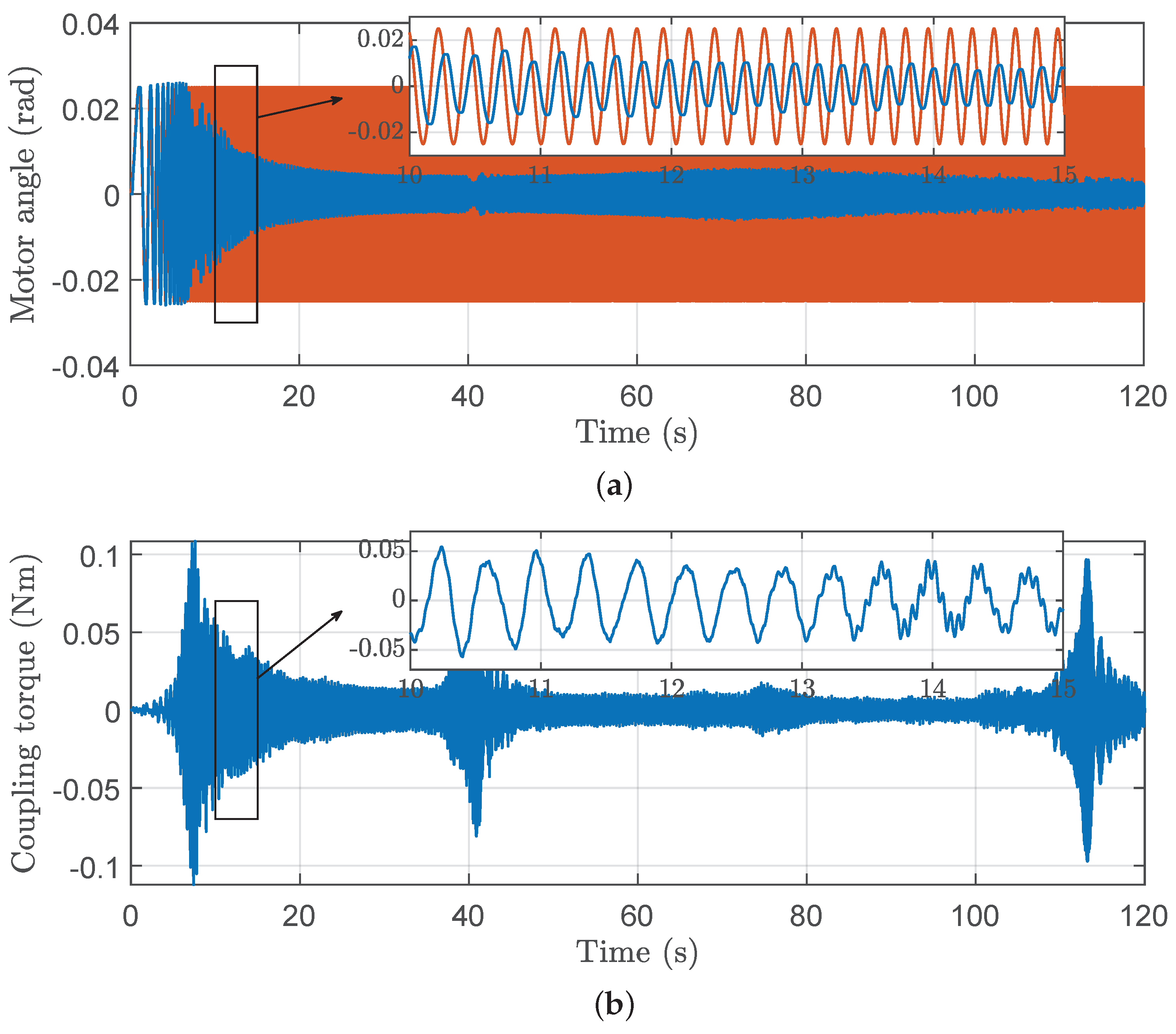
 ) is the frequency response of all the experiments, (
) is the frequency response of all the experiments, ( ) is the response of the nominal model type III, and (
) is the response of the nominal model type III, and ( ) is the one for the nominal model type VI.
) is the one for the nominal model type VI.
 ) is the frequency response of all the experiments, (
) is the frequency response of all the experiments, ( ) is the response of the nominal model type III, and (
) is the response of the nominal model type III, and ( ) is the one for the nominal model type VI.
) is the one for the nominal model type VI.
| Parameter | Value | Unit |
|---|---|---|
| L | m | |
| kg/m | ||
| E | N/m2 | |
| I | m4 |
| Parameter | Model | |||||
|---|---|---|---|---|---|---|
| Type I | Type II | Type III | Type IV | Type V | Type VI | |
| 1 | 0 | 1 | − | 0 | − | |
| − | 0 | − | − | 0 | − | |
| 0 | 1 | 1 | 0 | − | − | |
| 0 | − | − | 0 | − | − | |
| Resonant Peak | Weighting Function | Model | |||||
|---|---|---|---|---|---|---|---|
| Type I | Type II | Type III | Type IV | Type V | Type VI | ||
| Frequency (rad/s) | |||||||
| First | const | ||||||
| -dep | |||||||
| Second | const | ||||||
| -dep | |||||||
| Third | const | ||||||
| -dep | |||||||
| Magnitude (dB) | |||||||
| First | const | ||||||
| -dep | |||||||
| Second | const | ||||||
| -dep | |||||||
| Third | const | ||||||
| -dep | |||||||
| Model | Parameter | Performance Index | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| () | () | WMSE | (rad/s) | (dB) | (rad/s) | (dB) | (rad/s) | (dB) | |||
| Type III | 1 | 1 | |||||||||
| Type VI | |||||||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Haro-Olmo, M.I.; Tejado, I.; Vinagre, B.M.; Feliu-Batlle, V. Fractional-Order Models of Damping Phenomena in a Flexible Sensing Antenna Used for Haptic Robot Navigation. Fractal Fract. 2023, 7, 621. https://doi.org/10.3390/fractalfract7080621
Haro-Olmo MI, Tejado I, Vinagre BM, Feliu-Batlle V. Fractional-Order Models of Damping Phenomena in a Flexible Sensing Antenna Used for Haptic Robot Navigation. Fractal and Fractional. 2023; 7(8):621. https://doi.org/10.3390/fractalfract7080621
Chicago/Turabian StyleHaro-Olmo, María Isabel, Inés Tejado, Blas M. Vinagre, and Vicente Feliu-Batlle. 2023. "Fractional-Order Models of Damping Phenomena in a Flexible Sensing Antenna Used for Haptic Robot Navigation" Fractal and Fractional 7, no. 8: 621. https://doi.org/10.3390/fractalfract7080621
APA StyleHaro-Olmo, M. I., Tejado, I., Vinagre, B. M., & Feliu-Batlle, V. (2023). Fractional-Order Models of Damping Phenomena in a Flexible Sensing Antenna Used for Haptic Robot Navigation. Fractal and Fractional, 7(8), 621. https://doi.org/10.3390/fractalfract7080621









