A Numerical Technique Based on Bernoulli Wavelet Operational Matrices for Solving a Class of Fractional Order Differential Equations

Abstract

In this paper, we present an efficient, new, and simple programmable method for finding approximate solutions to fractional differential equations based on Bernoulli wavelet approximations. Bernoulli Wavelet functions involve advantages such as orthogonality, simplicity, and ease of usage, in addition to the fact that fractional Bernoulli wavelets have exact operational matrices that improve the accuracy of the applied approach. A fractional differential equation was simplified to a system of algebraic equations using the fractional order integration operational matrices of Bernoulli wavelets. Examples are used to demonstrate the technique’s precision.

1. Introduction

The branch of mathematics known as fractional calculus explores the characteristics of derivatives and integrals of non-integer orders (see [1]). Many of the fundamental properties of the differentiation of integer order and the integration of n-fold are preserved because it is an enlargement of classical calculus. Abel used fractional calculus for the first time in 1823 when he applied a derivative of order $1/2$ to the Tautochrone problem’s integral equation solution (see [2,3]). Additionally, fractional calculus and fractional differential equations (FDEs) have recently been discovered in a variety of scientific domains, such as economics [4], medicine [5], dynamics of viscoelastic materials [6], solid mechanics [7], fluid-dynamic traffic models [8], and many other fields. The exact solution is not known for the vast majority of FDEs. So, many scientists have focused their research efforts over the past few years on finding numerical solutions for fractional differential equations. The perturbation approach of homotopy [9,10], the analysis approach of homotopy [11], the variational iteration method [12,13], the differential transform method [14], the Adomian decomposition approach [15,16], the Legendre polynomials technique [17], and the spline functions method [18,19] are examples of these efficient numerical methods. Lately, A lot of interest has been directed to Wavelet theory; wavelets are a unique class of functions with a variety of beneficial properties. Generally, there are three types of wavelet transforms: discrete wavelet transform (DWT), wavelet packet transform (WPT), and continuous wavelet transform (CWT). The continuous wavelet transform (CWT) is a formal tool that offers a comprehensive representation of a signal by allowing the wavelets’ translation and scale parameters to change continuously. The continuous wavelet transform of a function $x\left(t\right)$ at a scale $a>0,a\in {\mathbb{R}}^{+}$ and translational value $b\in \mathbb{R}$ can be represented as follows:

$$X_W(a,b)={\left|a\right|}^{\frac{-1}{2}}\underset{-\infty }{\overset{\infty }{\int }}\omega \left(\frac{t-b}{a}\right)x\left(t\right)dt,$$

where $\omega$ is the mother wavelet, which is a continuous function in both the time and frequency domains. The mother wavelet’s primary job is to serve as a source function for generating daughter wavelets, which are simply translated and scaled replicas of the mother wavelet. Wavelets are characterized by orthogonality, compact support, accuracy in representing polynomials to a definite degree, and the capability to represent functions at various levels of resolution; therefore, a large number of operational matrices based on various wavelet types, such as Legendre wavelets [20,21], Chebyshev wavelets [22] and Bernoulli wavelets [23,24,25] are constructed for the purpose of solving FDEs. The motivation of this study comes from the need for more precious, easily programmable techniques to solve FDEs. Although many studies [23,24,25] used Bernoulli wavelets to solve FDEs, the technique introduced in the current study is a more efficient programmable method, a fact which is proved throughout the presented numerical example. Further, the fact that fractional Bernoulli wavelets have correct operational matrices improves the precision of the method used, and we note that as the order of the Caputo derivative $\alpha$ approaches an integer value, our presented method provides a solution for the integer-order differential equations.

Throughout this work, a novel numerical method for solving the initial and boundary value problems for FDEs is introduced, where the fractional derivatives are specified in the sense of Caputo. The approach is based upon Bernoulli wavelet approximation. The article is structured as follows: In Section 2, we start by providing certain definitions and mathematical foundations for fractional calculus theory, Bernoulli’s polynomials, and wavelets. Section 3 describes our process for creating the operational matrix of fractional integration as well as the algorithm for our proposed method; then, we illustrate convergence analysis and error estimation of the Bernoulli wavelets method. In Section 4, four illustrative examples are augmented with comparative tables and graphs. Finally, we provide the conclusion and recommended future work.

2. Preliminaries

In this section, we provide definitions and mathematical foundations for fractional calculus theory, Bernoulli’s polynomials, and wavelets.

Definition 1.

The factorial function is generalized into the Gamma function, denoted by $\Gamma \left(z\right)$; it is expressed in [26]

$$\Gamma \left(z\right)=\underset{0}{\overset{\infty }{\int }}{t}^{z-1}{e}^{-t}dt,Rez>0,$$

where z is any complex argument with a positive real part and $t\in [0,\infty ]$.

We list some fundamental characteristics of the Γ function below:

$$\begin{array}{c}\Gamma \left(1\right)=\Gamma \left(2\right)=1;\hfill \\ \Gamma (z+1)=z\Gamma \left(z\right);\hfill \\ \Gamma \left(z\right)=(z-1)!;\hfill \\ \Gamma (z+1)=z!.\hfill \end{array}$$

Definition 2.

The exponential function is expanded by the Mittag–Leffler function. The implementation of one-parameter functions comes first [1].

$$E_{\alpha }\left(z\right)=\sum _{k=0}^{\infty }\frac{z^k}{\Gamma (\alpha k+1)},\alpha \in \mathbb{R},z\in \mathbb{C}.$$

Using two parameters, The Mittag–Leffler function is defined as

$$E_{\alpha ,\beta }\left(z\right)=\sum _{k=0}^{\infty }\frac{z^k}{\Gamma (\alpha k+\beta )},$$

where $\alpha >0$, $\beta >0$ and z belongs to the complex plane $\mathbb{C}$.

Definition 3.

As shown by [1], On the common Lebesgue space $L_1[0,1]$, the Riemann–Liouville fractional integral operator $I^{\rho }$ of order ρ defined by

$$I^{\rho }h\left(x\right)=\left\{\begin{array}{cc}\frac{1}{\Gamma \left(\rho \right)}{\int }_0^x{(x-t)}^{\rho -1}h\left(t\right)dt,\hfill & \rho >0,\hfill \\ h\left(x\right),\hfill & \rho =0.\hfill \end{array}\right.$$

For the power function, the Riemann–Liouville fractional integral satisfies

$$I^{\rho }{t}^{\mu }=\frac{\Gamma (\mu +1)}{\Gamma (\mu +\rho +1)}{t}^{\rho +\mu }.$$

Definition 4.

As shown in [1], The Riemann–Liouville fractional derivative of order $\rho >0$ definition is

$$\left(D^{\rho }h\right)\left(x\right)={(\frac{d}{dt})}^m\left(I^{m-\rho }h\right)\left(x\right).m-1\le \rho <m,m\in \mathbb{N}.$$

(1)

Definition 5.

In the perspective of Caputo, the fractional-order derivative is defined as ([1])

$$D_{*}^{\rho }h\left(x\right)=\left\{\begin{array}{c}\frac{1}{\Gamma (m-\rho )}{\int }_0^x{(x-t)}^{m-\rho -1}{h}^{\left(m\right)}\left(t\right)dt,m-1⩽\rho <m,m\in \mathbb{N},\hfill \\ \frac{d^m}{d{x}^m}h\left(x\right),\rho =m\in \mathbb{N}.\hfill \end{array}\right.$$

(2)

The last definition enables one to write

$$D_{*}^{\rho }{x}^k=\left\{\begin{array}{cc}0,\hfill & \mathrm{if}k\in {\mathbb{N}}_{0}andk<\lceil \rho \rceil ,\hfill \\ \frac{\Gamma (k+1)}{\Gamma (k+1-\rho )}{x}^{k-\rho },\hfill & \mathrm{if}k\in {\mathbb{N}}_{0}andk\ge \lceil \rho \rceil ,\hfill \end{array}\right.$$

(3)

where $\mathbb{N}=\{1,2,\dots \}$ and ${\mathbb{N}}_0=\{0,1,2,\dots \}$.

Remark 1.

The differences between the Riemann–Liouville and Caputo formulas for the fractional derivatives lead to the following variants:

$\left(a\right)$ While the Riemann–Liouville fractional derivative of a constant does not equal zero, the Caputo fractional derivative does.

$\left(b\right)$ The commutative property is not satisfied by the fractional derivatives of Riemann–Liouville and Caputo:

$$D_{*}^{\rho }{D}_{*}^{m}f\left(t\right)=D_{*}^{\rho +m}f\left(t\right)\ne D_{*}^m{D}_{*}^{\rho }f\left(t\right)where\rho \in (j-1,j),andj,m\in \mathbb{N},$$

(4)

$$D^{\rho }{D}^{m}f\left(t\right)=D^{\rho +m}f\left(t\right)\ne D^m{D}^{\rho }f\left(t\right)where\rho \in (j-1,j),andj,m\in \mathbb{N},$$

(5)

where the equality holds in (4) and (5) under the following additional conditions:

$$f^{\left(s\right)}\left(0\right)=0,s=j,j+1,\dots ,mfor{D}_{*}^{\rho },$$

and

$$f^{\left(s\right)}\left(0\right)=0,s=0,1,\dots ,mfor{D}^{\rho }.$$

Wavelets

Wavelets are a unique class of functions with a variety of beneficial properties. The mother wavelet is a single function that is used to translate and expand a family of functions called wavelets. When the translation parameter b and the dilation parameter a change continuously, the wavelets illustrated below occurs [27].

$${\psi }_{a,b}\left(t\right)={\left|a\right|}^{\frac{-1}{2}}\psi (\frac{t-b}{a}).a,b\in \mathbb{R},a\ne 0.$$

(6)

If we constrain the parameters a and b to discrete values as $a=a_0^{-k},b=n{b}_0{a}_0^{-k},a_0>1,b_0>1$, where n and k$\in {\mathbb{Z}}^{+}$, the discrete wavelets family is given by

$${\psi }_{k,n}\left(t\right)={\left|a\right|}^{\frac{k}{2}}\psi (a_0^{k}t-n{b}_0),$$

(7)

where ${\psi }_{k,n}\left(t\right)$ form a wavelet basis for $L^2\left(\mathbb{R}\right)$.

Now, we are going to give brief explanation of Chebyshev wavelets, Legendre wavelets, and Bernoulli wavelets.

• Chebyshev Wavelets (CWs) Here, we describe three kinds of Chebyshev wavelets, which are correspondingly named the Chebyshev polynomials [28,29].
  • First Kind Chebyshev Wavelets (FSTCWs): The FSTCWs ${\varrho }_{p,q}^1\left(t\right)={\varrho }^1(l,p,q,x)$ have four arguments, $q=1,2,\dots ,2^{l-1},l$ positive integer and are defined as:

    $${\varrho }_{qp}^1\left(x\right)=\left\{\begin{array}{cc}{2}^{\frac{1}{2}}\breve{X_p}(2^{l}x-2q+1),\hfill & \frac{q-1}{2^{l-1}}\le x<\frac{q}{2^{l-1}};\hfill \\ 0,\hfill & \mathrm{elsewhere},\hfill \end{array}\right.$$

    $$\breve{X_p}=\left\{\begin{array}{cc}\frac{1}{\sqrt{\Pi }},\hfill & p=0;\hfill \\ \sqrt{\frac{2}{\Pi }}{X}_p,\hfill & p>0,\hfill \end{array}\right.$$

    and $p=0,1,\dots ,P-1$, P denotes the first kind Chebyshev polynomials degree and t represents the time. Here $X_p$ are first kind Chebyshev polynomials with degree p. Based on the definition, Chebyshev polynomials are orthogonal with regard to the weight function $w\left(x\right)={(1-x^2)}^{\frac{-1}{2}}$ within $[-1,1]$. The recursive equations are:
    $X_0\left(x\right)=1,X_1\left(x\right)=x,X_{p+1}\left(x\right)=2x{X}_p\left(x\right)-X_{p-1}\left(x\right),p=1,2,3,\dots$
    It needs to be noticed that in Chebyshev wavelets, in order to obtain the orthogonal wavelets, the weight functions have to be dilated and translated as

    $$w_q\left(x\right)=w(2^{l}x-2q+1)={(1-{(2^{l}x-2q+1)}^2)}^{\frac{-1}{2}}.$$
  • Second Kind Chebyshev Wavelets (SNDCWs): The SNDCWs has the following form

    $${\varrho }_{qp}^2\left(x\right)=\left\{\begin{array}{cc}{2}^{\frac{1}{2}}\breve{Y_p}(2^{l}x-2q+1),\hfill & \frac{q-1}{2^{l-1}}\le x<\frac{q}{2^{l-1}};\hfill \\ 0,\hfill & \mathrm{elsewhere},\hfill \end{array}\right.$$

    where

    $$\breve{Y_p}=\sqrt{\frac{2}{\Pi }}{Y}_p,p\ge 0,$$
    $Y_p$ are second kind Chebyshev polynomials with degree p. Based on the definition, Chebyshev polynomials are orthogonal with regard to the weight function $w\left(x\right)=\sqrt{(1-x^2)}$ within $[-1,1]$. The recursive formula is as follows:
    $Y_0\left(x\right)=1,Y_1\left(x\right)=2x,Y_{p+1}\left(x\right)=2x{Y}_p\left(x\right)-Y_{p-1}\left(x\right),p=1,2,3,\dots$
  • Third Kind Chebyshev Wavelets (TRDCWs): The TRDCWs take the following form:

    $${\varrho }_{qp}^3\left(x\right)=\left\{\begin{array}{cc}{2}^{\frac{1}{2}}\breve{Z_p}(2^{l}x-2q+1),\hfill & \frac{q-1}{2^{l-1}}\le x<\frac{q}{2^{l-1}};\hfill \\ 0,\hfill & \mathrm{elsewhere},\hfill \end{array}\right.$$

    where

    $$\breve{Z_p}=\sqrt{\frac{1}{\Pi }}{Z}_p,p\ge 0,$$
    $Z_p$ are third kind Chebyshev polynomials of degree p. Based on the definition, Chebyshev polynomials are orthogonal with regard to the weight function $w\left(x\right)=\sqrt{\frac{1+x}{1-x}}$ within $[-1,1]$. The recursive formula is as follows:
    $Z_0\left(x\right)=1,Z_1\left(x\right)=2x-1,Z_{p+1}\left(x\right)=2x{Z}_p\left(x\right)-Z_{p-1}\left(x\right),p=1,2,3,\dots$
• Legendre Wavelets (LWs) The LWs ${\vartheta }_{q,p}\left(t\right)=\vartheta (l,q,p,x)$ have four arguments, $q=1,2,\dots ,2^{k-1},k$ positive integer, x denotes time, and p is the degree of the Legendre polynomials. They are defined on $[0,1)$ as follows: [30,31,32]

  $${\vartheta }_{qp}\left(x\right)=\left\{\begin{array}{cc}\sqrt{p+\frac{1}{2}}{2}^{\frac{k}{2}}{\zeta }_p(2^{l}x-2q+1),\hfill & \frac{q-1}{2^{l-1}}\le x<\frac{q}{2^{l-1}};\hfill \\ 0,\hfill & \mathrm{elsewhere},\hfill \end{array}\right.$$
  $p=0,1,\dots ,P-1$, ${\zeta }_p$ are the Legendre polynomials of degree p with regard to the weight function $w\left(x\right)=1$ on $[-1,1]$ and fulfill the recurrence equations listed below:
  ${\zeta }_0\left(x\right)=1,{\zeta }_1\left(x\right)=x,{\zeta }_{p+1}\left(x\right)=\frac{2p+1}{p+1}x{\zeta }_p\left(x\right)-\frac{p}{p+1}{\zeta }_{p-1}\left(x\right),p=1,2,3,\dots$
• Bernoulli wavelets
  First, we must grasp what Bernoulli polynomials of order m mean [33]

  $${\beta }_m\left(t\right)=\sum _{i=0}^m\left(\genfrac{}{}{0pt}{}{m}{i}\right){\alpha }_{m-i}{t}^i,$$

  (8)
  ${\alpha }_i$,$i=0,1,2,\dots ,m$ are Bernoulli numbers. These are a set of signed rational numbers discovered in the series expansion of trigonometric functions [34]

  $$\frac{t}{e^t-1}=\sum _{i=0}^{\infty }{\alpha }_i\frac{t^i}{i!},$$

  (9)

  so, we have
  ${\alpha }_0=1$, ${\alpha }_1=\frac{-1}{2}$, ${\alpha }_2=\frac{1}{6}$, ${\alpha }_4=\frac{-1}{30}$, ${\alpha }_{2n+1}=0$, $n=1,2,3,\dots$
  Also, the first polynomials of Bernoulli are
  ${\beta }_0\left(t\right)=1$, ${\beta }_1\left(t\right)=t-\frac{1}{2}$, ${\beta }_2\left(t\right)=t^2-t+\frac{1}{6}$, ${\beta }_3\left(t\right)=t^3-\frac{3}{2}{t}^2+\frac{1}{2}t$, ${\beta }_4\left(t\right)=t^4-2t^3+t^2-\frac{1}{30},\dots$
  Bernoulli polynomials are a complete basis in [0, 1] [35].
  Bernoulli wavelets ${\psi }_{n,m}\left(t\right)=\psi (k,\widehat{n},m,t)$ have four arguments: $\widehat{n}=n-1,n=1,2,3,\dots ,2^{k-1},$ k$\in {\mathbb{Z}}^{+}$, m is the order for Bernoulli polynomials, and t is the normalized time. They are described on $[0,1)$ as follows [28,36]:

  $${\psi }_{n,m}\left(t\right)=\left\{\begin{array}{c}{2}^{\frac{k-1}{2}}\widehat{B_m}(2^{k-1}t-\widehat{n}),\frac{\widehat{n}}{2^{k-1}}\le t<\frac{\widehat{n}+1}{2^{k-1}},\hfill \\ 0,\mathrm{otherwise},\hfill \end{array}\right.$$

  (10)

  here

  $$\widehat{B_m}\left(t\right)=\left\{\begin{array}{c}1,m=0,\hfill \\ \frac{1}{\sqrt{\frac{{(-1)}^{m-1}{(m!)}^2}{(2m!)}{\alpha }_{2m}}}{\beta }_m\left(t\right),m>0,\hfill \end{array}\right.$$

  (11)

  where $m=0,1,2,\dots , M-1$, M is a positive integer number and $n=1,2,\dots ,2^{k-1}$. The coefficient $\sqrt{\frac{{(-1)}^{m-1}{(m!)}^2}{(2m!)}{\alpha }_{2m}}$ is for normality, the dilation parameter is $a=2^{-(k-1)}$, and the translation parameter is $b=\widehat{n}{2}^{-(k-1)}$. The few Bernoulli wavelet basis at $k=1$ and $M=11$ are:

  $$\begin{array}{cc}\hfill {\psi }_{1,0}\left(t\right)& =1,\hfill \\ \hfill {\psi }_{1,1}\left(t\right)& =\sqrt{3}(-1+2t),\hfill \\ \hfill {\psi }_{1,2}\left(t\right)& =\sqrt{5}(1-6t+6t^2),\hfill \\ \hfill {\psi }_{1,3}\left(t\right)& =\sqrt{210}(t-3t^2+2t^3),\hfill \\ \hfill {\psi }_{1,4}\left(t\right)& =10\sqrt{21}(\frac{-1}{30}+t^2-2t^3+t^4),\hfill \\ \hfill {\psi }_{1,5}\left(t\right)& =\sqrt{\frac{462}{5}}(-t+10t^3-15t^4+6t^5),\hfill \\ \hfill {\psi }_{1,6}\left(t\right)& =\sqrt{\frac{1430}{691}}(1-21t^2+105t^4-126t^5+42t^6),\hfill \\ \hfill {\psi }_{1,7}\left(t\right)& =2\sqrt{\frac{143}{7}}(t-7t^3+21t^5-21t^6+6t^7),\hfill \\ \hfill {\psi }_{1,8}\left(t\right)& =\sqrt{\frac{7293}{3617}}(-1+20t^2-70t^4+140t^6-120t^7+30t^8),\hfill \\ \hfill {\psi }_{1,9}\left(t\right)& =\sqrt{\frac{1,939,938}{219,335}}(-3t+20t^3-42t^5+60t^7-45t^8+10t^9),\hfill \\ \hfill {\psi }_{1,10}\left(t\right)& =22\sqrt{\frac{125,970}{174,611}}(\frac{5}{66}-\frac{3t^2}{2}+5t^4-7t^6+\frac{15t^8}{2}-5t^9+t^{10}).\hfill \end{array}$$

3. Materials and Methods

Here, we provide the basic materials we need for our proposed method, like function approximation, the transformation matrix of the Bernoulli wavelet to the Bernoulli polynomials, the fractional integration Bernoulli wavelet operational matrix, and the Riemann–Liouville fractional operational matrix of integration. Then, we provide a concise step-by-step algorithm for our procedure. Finally, we illustrate the Bernoulli wavelets convergence analysis and error estimation.

3.1. Function Approximation

A function $f\left(t\right)$ in $L^2[0,1]$ can be rewritten using Bernoulli functions as

$$f\left(t\right)=\sum _{i=0}^{\infty }{a}_i{\beta }_i\left(t\right),$$

(12)

only the finite terms of the above-mentioned series are actually taken into account; hence,

$$f\left(t\right)=\sum _{i=0}^{M-1}{a}_i{\beta }_i\left(t\right)=A^T\beta ,$$

where $A={[a_0,a_1,\dots ,a_{M-1}]}^T$ and $\beta \left(t\right)={[{\beta }_0\left(t\right),{\beta }_1\left(t\right),\dots ,{\beta }_{M-1}\left(t\right)]}^T$. The elements of A can be calculated using the Bernoulli polynomials’ orthogonality feature as follows.

Let $f_i=\underset{0}{\overset{1}{\int }}f\left(t\right){\beta }_i\left(t\right)dt.$ Using (12), we obtain

$$\begin{array}{cc}\hfill f_i& =\sum _{i=0}^{M-1}{a}_i\underset{0}{\overset{1}{\int }}{\beta }_i\left(t\right){\beta }_j\left(t\right)dt,i,j=0,1,\dots ,M-1,\hfill \\ \hfill & =\sum _{i=0}^{M-1}{a}_i{h}_{ij},\hfill \end{array}$$

where $h_{ij}=\underset{0}{\overset{1}{\int }}{\beta }_i\left(t\right){\beta }_j\left(t\right)dt.$

Therefore,

$$f_i=A^T[h_{0,0},h_{0,1},\dots ,h_{0,M-1},h_{1,0},h_{1,1},\dots ,h_{1,M-1},\dots ,h_{M-1,1},\dots ,h_{M-1,M-1}].$$

3.2. The Bernoulli Wavelet to Bernoulli Polynomials Transformation Matrix

In this subsection, we illustrate how to express the Bernoulli wavelets ${\psi }_{2^{k-1}M\times 1}$ related to the polynomials of Bernoulli ${\beta }_{M\times 1}\left(t\right)$ and the transformation matrix ${\varphi }_{2^{k-1}M\times M}$. The Bernoulli wavelets may be expanded into M-term Bernoulli polynomials as

$${\psi }_{2^{k-1}M\times 1}={\varphi }_{2^{k-1}M\times M}{\beta }_{M\times 1}\left(t\right),$$

where $\varphi$ is the transformation matrix of the Bernoulli wavelet to the Bernoulli polynomials. For example, when $M=3$ and $k=2$, we have

$$\begin{array}{c}\psi \left(t\right)={[{\psi }_{10}\left(t\right),{\psi }_{11}\left(t\right),{\psi }_{12}\left(t\right),{\psi }_{20}\left(t\right),{\psi }_{21}\left(t\right),{\psi }_{22}\left(t\right)]}^T,\hfill \\ \beta \left(t\right)={[{\beta }_0\left(t\right),{\beta }_1\left(t\right),{\beta }_2\left(t\right)]}^T,\hfill \end{array}$$

for $0\le t<\frac{1}{2}$, hence

$$\begin{array}{cc}\hfill {\psi }_{10}\left(t\right)& =\sqrt{2}{\beta }_0\left(t\right),\hfill \\ \hfill {\psi }_{11}\left(t\right)& =\sqrt{6}{\beta }_0\left(t\right)+4\sqrt{(}6){\beta }_1\left(t\right),\hfill \\ \hfill {\psi }_{12}\left(t\right)& =3\sqrt{10}{\beta }_0\left(t\right)+12\sqrt{(}10){\beta }_1\left(t\right)+24\sqrt{(}10){\beta }_2\left(t\right),\hfill \end{array}$$

while for $\frac{1}{2}\le t<1$, we have

$$\begin{array}{cc}\hfill {\psi }_{20}\left(t\right)& =\sqrt{2}{\beta }_0\left(t\right),\hfill \\ \hfill {\psi }_{21}\left(t\right)& =-\sqrt{6}{\beta }_0\left(t\right)+4\sqrt{(}6){\beta }_1\left(t\right),\hfill \\ \hfill {\psi }_{22}\left(t\right)& =3\sqrt{10}{\beta }_0\left(t\right)-12\sqrt{(}10){\beta }_1\left(t\right)+24\sqrt{(}10){\beta }_2\left(t\right).\hfill \end{array}$$

In this case,

$$\varphi =\left\{\begin{array}{cc}{\varphi }_1={\left[a_{ij}\right]}_{6\times 3},\hfill & 0\le t<\frac{1}{2},\hfill \\ {\varphi }_2={\left[b_{ij}\right]}_{6\times 3},\hfill & \frac{1}{2}\le t<1,\hfill \end{array}\right.$$

where

$$\begin{array}{c}\hfill {\varphi }_1=\left[\begin{array}{ccc}\sqrt{2}& 0& 0\\ \sqrt{6}& 4\sqrt{6}& 0\\ 3\sqrt{10}& 12\sqrt{10}& 24\sqrt{10}\\ --& ---& ---\\ 0& 0& 0\\ 0& 0& 0\\ 0& 0& 0\end{array}\right],{\varphi }_2=\left[\begin{array}{ccc}0& 0& 0\\ 0& 0& 0\\ 0& 0& 0\\ --& ---& ---\\ \sqrt{2}& 0& 0\\ -\sqrt{6}& 4\sqrt{6}& 0\\ 3\sqrt{10}& -12\sqrt{10}& 24\sqrt{10}\end{array}\right].\end{array}$$

In general, for arbitrary M and $k=2$, we get

$$\varphi =\left\{\begin{array}{cc}{\varphi }_1={\left[a_{ij}\right]}_{2^{k-1}M\times M},\hfill & 0\le t<\frac{1}{2},\hfill \\ {\varphi }_2={\left[b_{ij}\right]}_{2^{k-1}M\times M},\hfill & \frac{1}{2}\le t<1,\hfill \end{array}\right.$$

with

$$a_{ij}=\frac{1}{2^{\frac{k-1}{2}}}\left\{\begin{array}{c}{2}^i\frac{1}{{\lambda }_{i-1}},i=j,\hfill \\ 2^{j-1}\times \left(\begin{array}{c}i-1\\ i-j\end{array}\right)\times \frac{1}{{\lambda }_{i-1}}\hfill & j<i<M,\hfill \\ 0,otherwise,\hfill \end{array}\right.$$

and

$$b_{ij}=\left\{\begin{array}{c}0,1\le i\le M,j=1,2,3,\dots ,M,\hfill \\ {(-1)}^{i+j-M}{a}_{i-M,j},M+1\le i\le 2^{k-1}M,\hfill \end{array}\right.$$

where ${\lambda }_0=1$, and ${\lambda }_i=\sqrt{\frac{{(-1)}^{i-1}{(i!)}^2}{(2i!)}{\alpha }_{2i}},i=1,2,\dots ,M-1$.

Also, consider the case when $M=3$ and $K=1$, for which we have the following three Bernoulli wavelet basis

$$\begin{array}{cc}\hfill {\psi }_{10}\left(t\right)& =1,\hfill \\ \hfill {\psi }_{11}\left(t\right)& =2\sqrt{3}(t-\frac{1}{2}),\hfill \\ \hfill {\psi }_{12}\left(t\right)& =6\sqrt{5}(t^2-t+\frac{1}{6}),0<t\le 1.\hfill \end{array}$$

(13)

The above set of three basis (13) can be written in terms of the Bernoulli polynomials ${\beta }_0\left(t\right)=1,{\beta }_1\left(t\right)=t-\frac{1}{2},{\beta }_2\left(t\right)=t^2-t+\frac{1}{6}$ as:

$$\begin{array}{cc}\hfill {\psi }_{10}\left(t\right)& ={\beta }_0\left(t\right)=\left[100\right]\beta \left(t\right),\hfill \\ \hfill {\psi }_{11}\left(t\right)& =\left[02\sqrt{3}0\right]\beta \left(t\right),\hfill \\ \hfill {\psi }_{12}\left(t\right)& =\left[006\sqrt{5}\right]\beta \left(t\right),\hfill \end{array}$$

(14)

where $\beta \left(t\right)=\left[{\beta }_0\left(t\right){\beta }_1\left(t\right){\beta }_2\left(t\right)\right]$. The three relations in (14) can be put in the matrix form

$$\left[\begin{array}{c}{\psi }_{10}\left(t\right)\\ {\psi }_{11}\left(t\right)\\ {\psi }_{12}\left(t\right)\end{array}\right]=\left[\begin{array}{ccc}1& 0& 0\\ 0& 2\sqrt{3}& 0\\ 0& 0& 6\sqrt{5}\end{array}\right]\times \left[\begin{array}{c}{\beta }_0\left(t\right)\\ {\beta }_1\left(t\right)\\ {\beta }_2\left(t\right)\end{array}\right],$$

(15)

or

$$\psi \left(t\right)=\Phi \beta \left(t\right),$$

(16)

where $\psi \left(t\right)=\left[{\psi }_{10}\left(t\right){\psi }_{11}\left(t\right){\psi }_{12}\left(t\right)\right]$, and $\Phi$ is the $3\times 3$ transformation matrix.

3.3. Fractional Integration Operational Bernoulli Wavelet Matrix

The operational integration matrix of the Bernoulli wavelet is obtained as follows in this subsection. Let

$$I^q\psi \left(t\right)=P^{\left(q\right)}\psi \left(t\right),$$

(17)

where $P^{\left(q\right)}$ referred to the fractional integration Bernoulli wavelet operational matrix. Using (15) and (17), we get

$$I^q\psi \left(t\right)=I^q\Phi \beta \left(t\right)=\Phi I^q\beta \left(t\right).$$

(18)

Now, the Riemann–Liouville fractional integration of the vector $\beta \left(t\right)=[{\beta }_0\left(t\right),{\beta }_1\left(t\right),\dots ,$ ${\beta }_{M-1}{\left(t\right)]}^T$ is provided by [25]

$$I^q\beta \left(t\right)=F^q\beta \left(t\right),$$

(19)

where $F^q$ is the $M\times M$ Riemann–Liouville fractional operational matrix of integration. From (17)–(19), we get

$$P^{\left(q\right)}\psi \left(t\right)=P^{\left(q\right)}\Phi \beta \left(t\right)=\Phi F^{\left(q\right)}\beta \left(t\right),$$

hence, $p^{\left(q\right)}$ is provided by

$$P^{\left(q\right)}=\Phi F^{\left(q\right)}{\Phi }^{-1}.$$

3.4. Convergence Analysis

Theorem 1

([23]). Using the Bernoulli wavelets approach, the solution of (23) converges to the $\check{x}\left(t\right)$ described in (25).

Proof. 

Assume ${\psi }_{n,m}\left(t\right)$ is the basis of $L^2\left(R\right)$ and $L^2\left(R\right)$ is a Hilbert space. Let

$$\check{x}\left(t\right)\approx \sum _{n=1}^{2^{K-1}}\sum _{m=0}^{M-1}{c}_{n,m}{\psi }_{n,m}\left(t\right),$$

where

$$c_{n,m}=<\check{x}\left(t\right),{\psi }_{n,m}\left(t\right)>.$$

Noting that $<.,.>$ denotes the inner product. Now,

$$\check{u}\left(t\right)\approx \sum _{n=1}^{2^{K-1}}\sum _{m=0}^{M-1}{\zeta }_j\psi \left(t\right),$$

here, we denote

$${\zeta }_j:=<\check{x}\left(t\right),{\psi }_{n,m}\left(t\right)>\mathrm{and}\psi \left(t\right):={\psi }_{n,m}\left(t\right).$$

Let $S_n$ be the partial sums sequence of $\left({\zeta }_j\psi \left(t_j\right)\right)$ and $S_n$ and $S_m$ are arbitrary partial sums with $n\ge m$. We prove $S_n$ is a cauchy sequence in Hilbert space. Let

$$S_n=\sum _{j=1}^n{\zeta }_j\psi \left(t_j\right),$$

so,

$$\begin{array}{cc}\hfill <\check{x}\left(t\right),S_n>& =<\check{x}\left(t\right),\sum _{j=1}^n{\zeta }_j\psi \left(t_j\right)>=\sum _{j=1}^n\overline{{\zeta }_j}<\check{x}\left(t\right),\psi \left(t_j\right)>,\hfill \\ \hfill & =\sum _{j=1}^n\overline{{\zeta }_j}{\zeta }_j=\sum _{j=1}^n\mid {\zeta }_j{\mid }^2.\hfill \end{array}$$

Now, we hope that

$$\Vert S_n-S_m{\Vert }^2=\sum _{j=m+1}^n\mid {\zeta }_j{\mid }^2,\mathrm{for}n>m,$$

(20)

to prove this, since

$$\begin{array}{cc}\hfill \Vert \sum _{j=m+1}^n{\zeta }_j\psi \left(t_j\right){\Vert }^2& =<\sum _{i=m+1}^n{\zeta }_i\psi \left(t_i\right),\sum _{j=m+1}^n{\zeta }_j\psi \left(t_j\right)>,\hfill \\ \hfill & =\sum _{i=m+1}^n\sum _{j=m+1}^n{\zeta }_j\overline{{\zeta }_j}<\psi \left(t_i\right),\psi \left(t_j\right)>,\hfill \\ \hfill & =\sum _{j=m+1}^n\overline{{\zeta }_j}{\zeta }_j=\sum _{j=1}^n\mid {\zeta }_j{\mid }^2.\hfill \end{array}$$

As a consequence, we obtain

$$\Vert S_n-S_m{\Vert }^2=\sum _{j=m+1}^n\mid {\zeta }_j{\mid }^2,\mathrm{for}n>m.$$

(21)

Using Bessel’s inequality, we get that ${\sum }_{j=m+1}^n\mid {\zeta }_j{\mid }^2$ is convergent, and hence, $\Vert S_n-S_m{\Vert }^2\to 0$ as $m,n\to \infty$.

So, $S_n$ is a cauchy sequence, and we can assume that it converges to ${}^{\prime }{s}^{\prime }$. All we need to do now is to prove $\check{x}\left(t\right)=s$, since

$$\begin{array}{cc}\hfill <s-\check{x}\left(t\right),\psi \left(t_j\right)>& =<s,\psi \left(t_j\right)>-<\check{x}\left(t\right),\psi {(}_j)>,\hfill \\ \hfill & =<\underset{n\to \infty }{lim}{S}_n,\psi \left(t_j\right)>-{\zeta }_j=\underset{n\to \infty }{lim}<S_n,\psi \left(t_j\right)>-{\zeta }_j=0,\hfill \end{array}$$

consequently, we have $\check{x}\left(t\right)=s$, and ${\sum }_{j=1}^n{\zeta }_j\psi \left(t_j\right)$ converges to $\check{x}\left(t\right)$. □

3.5. Error Estimation

Taking into consideration that $\check{x}\left(t\right)$ is the approximate solution and $x\left(t\right)$ is the exact solution, the error function $E_n\left(t\right)$ is represented by [23]

$$E_n\left(t\right)=x\left(t\right)-\check{x}\left(t\right),$$

hence

$$\check{x}\left(t\right)=\sum _{n=1}^{2^{K-1}}\sum _{m=0}^{M-1}{c}_{n,m}{\psi }_{n,m}\left(t\right)+H_n\left(t\right)=C^T\psi \left(t\right)+H_n\left(t\right),$$

where, $H_n\left(t\right)$ is the term of perturbation.

$$H_n\left(t\right)=\check{x}\left(t\right)-C^T\psi \left(t\right),$$

(22)

As a result, it is clear that

$$E_n\left(t\right)+C^T\psi \left(t\right)=-H_n\left(t\right).$$

As a result of this convergence theorem and error estimation, the stability of the Bernoulli wavelet approach is established.

4. Results

4.1. Procedure

Here, we will provide a concise step-by-step description of our computational algorithm to solve the FDEs under consideration to enhance the clarity and the understanding of the proposed method.

First, we give an outline of the suggested algorithm as follows:

Consider the following FDE

$$D^{q_1}x\left(t\right)=f(t,x\left(t\right),D^{q_2}x\left(t\right)),n-1<q_1\le n,m-1<q_2\le m,$$

(23)

where $n\ge m$ and the following initial conditions exist:

$x\left(0\right)=x_0$,$x^{\left(1\right)}\left(0\right)=x_1$, $x^{\left(2\right)}\left(0\right)=x_2$,..., $x^{(n-1)}\left(0\right)=x_{n-1}.$

We let

$$D^{n}x\left(t\right)=C^T\psi \left(t\right),$$

(24)

hence,

$$D^{n-1}x\left(t\right)=I^{n-(n-1)}{D}^{n}x\left(t\right)+x^{(n-1)}\left(0\right)=C^T{P}^{\left(1\right)}\psi \left(t\right)+x_{n-1},$$

$$D^{n-2}x\left(t\right)=I^{n-1-(n-2)}{D}^{n-1}x\left(t\right)+x^{(n-2)}\left(0\right)=C^T{P}^{\left(2\right)}\psi \left(t\right)+x_{n-1}t+x_{n-2},$$

⋮

$$x\left(t\right)=C^T{P}^{\left(n\right)}\psi \left(t\right)+\sum _{i=0}^{n-1}{x}_i\frac{t^i}{i!}.$$

(25)

Hence,

$$D^{q_1}x\left(t\right)=C^T{P}^{(n-q_1)}\psi \left(t\right)+I^{-q_1}(\sum _{i=0}^{n-1}{x}_i\frac{t^i}{i!}),$$

(26)

$$D^{q_2}x\left(t\right)=C^T{P}^{(n-q_2)}\psi \left(t\right)+I^{-q_2}(\sum _{i=0}^{n-1}{x}_i\frac{t^i}{i!}).$$

(27)

Substituting from (25)–(27) into (23), we arrive at a set of algebraic equations with a $2^{(k-1)}M$ variable that can be solved for C; then, we substitute in (25) to get the semi-analytic solution. It is to be noted that the obtained solution is more accurate than that of the previous results, which means that our technique using Bernoulli wavelets is more accurate and efficient. As seen below, we provide our algorithm in the following simple and unambiguous phases that may be simply programmed as follows:

• Step 1: Assign the values for k and M to clarify the dimensions of: Bernoulli wavelets ${\psi }_{2^{k-1}M\times 1}$, Bernoulli polynomials ${\beta }_{M\times 1}\left(t\right)$, the transformation matrix ${\varphi }_{2^{k-1}M\times M}$, $C={[C_0,C_1,\dots ,C_{M-1}]}^T$ and $F^q$ the $M\times M$ Riemann–Liouville fractional operational matrix of integration.
• Step 2: Compute the $M\times M$ Riemann–Liouville fractional operational matrix of integration $F^q$.
  For simplicity, if we take $M=3,$ $k=1$, we follow the following
  Stage a:

  $$g\left(i\right)=\frac{\Gamma \left(i\right)}{\Gamma (q+i)},i=1,2,3$$
  Stage b: compute the values $a\left(i\right),b\left(i\right)$ and $c\left(i\right)$, where

  $$\begin{array}{cc}\hfill a\left(i\right)& =\frac{1}{q+i},\hfill \\ \hfill b\left(i\right)& =12[\frac{1}{q+i+1}-\frac{1}{2(q+i)}],\hfill \\ \hfill c\left(i\right)& =180[\frac{1}{q+i+2}-\frac{1}{q+i+1}+\frac{1}{6(q+i)}],i=i,2,3\hfill \end{array}$$
  Stage c: compute the row vectors $h_1,h_2$ and $h_3$, where

  $$\begin{array}{cc}\hfill h_1& =\left[\begin{array}{ccc}g\left(1\right)a\left(1\right),& g\left(1\right)b\left(1\right),& g\left(1\right)c\left(1\right)\end{array}\right],\hfill \\ \hfill h_2& =\left[\begin{array}{ccc}g\left(2\right)a\left(2\right)-\frac{1}{2}g\left(1\right)a\left(1\right),& g\left(2\right)b\left(2\right)-\frac{1}{2}g\left(1\right)b\left(1\right),& g\left(2\right)c\left(2\right)-\frac{1}{2}g\left(1\right)c\left(1\right)\end{array}\right],\hfill \end{array}$$

  $$\begin{array}{cc}\hfill h_3=[g\left(3\right)a\left(3\right)-g\left(2\right)a\left(2\right)+& \frac{1}{6}g\left(1\right)a\left(1\right),g\left(3\right)b\left(3\right)-g\left(2\right)b\left(2\right)+\frac{1}{6}g\left(1\right)b\left(1\right),\hfill \\ \hfill & g\left(3\right)c\left(3\right)-g\left(2\right)c\left(2\right)+\frac{1}{6}g\left(1\right)c\left(1\right)].\hfill \end{array}$$
  Then, the matrix F is of the form

  $$\mathbf{F}=\left[\begin{array}{ccc}{h}_1;& h_2;& h_3\end{array}\right]$$
• Step 3: We construct the transformation matrix $\Phi$. For example, if we take $M=3,$ $k=1,$ as in (15), then we derive the operational matrix of the Bernoulli wavelet of the fractional integration $P^{\left(q\right)}$ from the relation

  $$P^{\left(q\right)}=\Phi F^{\left(q\right)}{\Phi }^{-1}.$$

  (28)
  Example: Taking $q=2,M=3,k=1$, from stage a, we have

  $$g\left(1\right)=0.5000,g\left(2\right)=0.1667,g\left(3\right)=0.0833.$$
  From stage b, we have

  $$\begin{array}{c}\hfill a\left(1\right)=0.3330,a\left(2\right)=0.2500,a\left(3\right)=0.2000,\\ \hfill b\left(1\right)=1,b\left(2\right)=0.9000,b\left(3\right)=0.8000,\\ \hfill c\left(1\right)=1,c\left(2\right)=1.5000,c\left(3\right)=1.7143.\end{array}$$
  Hence, the matrix $F^q$ takes the form

  $${\mathbf{F}}^{\left(\mathbf{2}\right)}=\left[\begin{array}{ccc}0.1667& 0.5000& 0.5000\\ -0.0417& -0.1000& 0\\ 0.0028& 0& -0.0238\end{array}\right].$$
  Finally, $P^{\left(2\right)}$ takes the form

  $$\begin{array}{cc}\hfill P^{\left(2\right)}& =\Phi F^{\left(2\right)}{\Phi }^{-1}=\left[\begin{array}{ccc}0.1667& 0.1443& 0.0373\\ -0.1443& -0.1000& 0\\ 0.0373& 0& -0.0238\end{array}\right],\hfill \end{array}$$

  which can be written as

  $$P^{\left(2\right)}=\left[\begin{array}{ccc}0.1667& 0.1443& 0.0373\\ -0.1443& -0.1000& 0\\ 0.0373& 0& -0.0238\end{array}\right],$$

  which is the same as [25]. Similarly, we can compute $P^{\left(q\right)}$ for any fractional number q. For example, if we take $q=\frac{1}{3}$, we get

  $$P^{\left(\frac{1}{3}\right)}=\left[\begin{array}{ccc}0.8399& 0.2078& -0.0537\\ -0.2078& 0.5039& 0.1787\\ -0.0537& -0.1787& 0.4199\end{array}\right].$$
• Step 4: Substituting from (25)–(28) into (23), we arrive at a set of algebraic equations with a $2^{(k-1)}M$ variable that can be solved for C.
• Step 5: Solve the system of algebraic equations using MATLAB program to compute the unknown vector C.
• Step 6: Substitute for unknown vector C in (25) to obtain the approximated solution.

4.2. Numerical Examples

Four examples are provided in this part to demonstrate the practicality and precision of our technique. In each case, we created a new MATLAB program to handle the test difficulties addressed by this study.

Example 1.

Take into account the FDE [37]

$$D^{2}x\left(t\right)+\frac{1}{2}{D}^{\alpha }x\left(t\right)+x\left(t\right)=f\left(t\right),0<\alpha <1,$$

(29)

where

$$f\left(t\right)=3+t^2(\frac{1}{\Gamma (3-\alpha )}{t}^{-\alpha }+1),$$

under initial conditions $x\left(0\right)=1,$ $x^{\prime }\left(0\right)=0$.

The solution to (29) for $\alpha =0.5000$ is $x\left(t\right)=t^2+1$. Let $D^{2}x\left(t\right)=C^T\psi \left(t\right)$; then, we have

$$Dx\left(t\right)=I^{2-1}{D}^{2}x\left(t\right)+x^{\prime }\left(0\right)=I{C}^T\psi \left(t\right)+0=C^T{P}^{\left(1\right)}\psi \left(t\right),$$

$$x\left(t\right)=IDx\left(t\right)+x\left(0\right)=C^T{P}^{\left(2\right)}\psi \left(t\right)+1,$$

and

$$D^{0.5}x\left(t\right)=C^T{P}^{(2-0.5)}\psi \left(t\right).$$

A linear system of equations with the following structure is then used to represent the problem:

$$C^T\psi \left(t\right)+\frac{1}{2}{C}^T{P}^{\left(\frac{3}{2}\right)}\psi \left(t\right)+C^T{P}^{\left(2\right)}\psi \left(t\right)=A^T\psi \left(t\right),$$

(30)

where $A^T\psi \left(t\right)$ is the approximation to the function $g\left(t\right)$ in terms of the Bernoulli wavelets, where

$$g\left(t\right)=-1+(3+t^2(\frac{1}{\Gamma (3-\alpha )}{t}^{-\alpha }+1))=2+t^2(\frac{1}{\Gamma (3-\alpha )}{t}^{-\alpha }+1),$$

To get the unknown coefficient vector $C=[c_{10},c_{11},c_{12}]$, we solve the resultant linear algebraic equation system obtained from (30) of the form

$$(I+\frac{1}{2}{P}^{{\left(\frac{3}{2}\right)}^T}+P^{{\left(2\right)}^T})C=A.$$

(31)

Now, we compute the operational matrices $P^{\left(1.5\right)}$, $P^{\left(2\right)}$ and the vector A for the unknown coefficient vector C; the system of linear Equation (31) must be solved. For $\alpha =0.5000$ and $M=3,$ $K=1,$ we have

$${\mathbf{P}}^{(\mathbf{1}.\mathbf{5})}=\left[\begin{array}{ccc}0.3009& 0.2234& 0.0320\\ -0.2234& -0.1003& 0.0454\\ 0.0320& -0.0454& -0.0386\end{array}\right],$$

$${\mathbf{P}}^{\left(\mathbf{2}\right)}=\left[\begin{array}{ccc}0.1667& 0.1443& 0.0373\\ -0.1443& -0.1000& -0.0000\\ 0.0373& -0.0000& -0.0238\end{array}\right],$$

and $A={[2.6000,0.5100,0.1100]}^T$.

Substitute for $P^{\left(2\right)}$, $P^{(2-\alpha )}$, and $A^T$ in (31) and solve the resultant algebraic equation system in the unknown coefficient vector $C=[c_{10},c_{11},c_{12}]$. Then, we get $c_{10}=2,$ $c_{11}=4.7000\times {10}^{-15}$, $c_{12}=5.9000\times {10}^{-16}$. Now, substituting in $x\left(t\right)=C^T{P}^{\left(2\right)}\psi \left(t\right)+1$, we obtain the approximated solution

$$\check{x\left(t\right)}=t^2+1.4600\times {10}^{-11}t+1\simeq t^2+1,$$

which is the exact solution. A numerical solution, for this example is investigated in [37] using cubic spline for $n=8$ and $\alpha =0.5000$; the maximum absolute error found was $9.1300\times {10}^{-5}$.

Example 2.

Think about the differential equations of fractional order [38]

$$D^{\alpha }x\left(t\right)=x\left(t\right)+f\left(t\right),1<\alpha <2,$$

(32)

where

$$f\left(t\right)=t^3+(\frac{2}{\Gamma (3-\alpha )}{t}^{2-\alpha }),$$

with initial conditions $x\left(0\right)=0,$ $x^{\prime }\left(0\right)=0$. The solution of (32) for $\alpha =1.9000$ is $x\left(t\right)=t^2$. Let $D^{2}x\left(t\right)=C^T\psi \left(t\right)$; then, we have

$$Dx\left(t\right)=I^{2-1}{D}^{2}x\left(t\right)+x^{\prime }\left(0\right)=I{C}^T\psi \left(t\right)+0=C^T{P}^{\left(1\right)}\psi \left(t\right),$$

$$x\left(t\right)=IDx\left(t\right)+x\left(0\right)=C^T{P}^{\left(2\right)}\psi \left(t\right),$$

and

$$D^{\alpha }x\left(t\right)=C^T{P}^{(2-\alpha )}\psi \left(t\right),$$

the problem is then transformed to the following system of linear algebraic equations:

$$C^T{P}^{\left(2\right)}\psi \left(t\right)+C^T{P}^{(2-\alpha )}\psi \left(t\right)=A^T\psi \left(t\right),$$

(33)

where $f\left(t\right)=A^T\psi \left(t\right)$ is the approximation to $f\left(t\right)$ in terms of Bernoulli wavelets.

Now, we compute the operational matrices $P^{(2-\alpha )}$, $P^{\left(2\right)}$ and the vector A to solve (33) for the unknown vector $C=[c_{10},c_{11},c_{12}]$; for $\alpha =1.9000$ and $M=3,$ $K=1$, we have

$${\mathbf{P}}^{(\mathbf{2}-\mathbf{ff})}=\left[\begin{array}{ccc}0.9556& 0.0788& -0.0295\\ -0.0788& 0.8323& 0.0817\\ -0.0295& -0.0817& 0.7888\end{array}\right],$$

$${\mathbf{P}}^{\left(\mathbf{2}\right)}=\left[\begin{array}{ccc}0.1667& 0.1443& 0.0373\\ -0.1443& -0.1000& -0.0000\\ 0.0373& -0.0000& -0.0238\end{array}\right],$$

and $A={[2.2000,0.4500,0.0150]}^T$.

Substitute $P^{\left(2\right)}$, $P^{(2-\alpha )}$, and $A^T$ in (33) and solve the resulted algebraic equation system in the unknown coefficient vector $C=[c_{10},c_{11},c_{12}]$. Then, we get $c_{10}=2,$ $c_{11}=-1.0900\times {10}^{-14},$ $c_{12}=1.1200\times {10}^{-15}$. Now, substituting in $x\left(t\right)=C^T{P}^{\left(2\right)}\psi \left(t\right),$ we obtain the needed approximated solution

$$\check{x\left(t\right)}=t^2+4.2188\times {10}^{-15}t-3.9516\times {10}^{-16}.$$

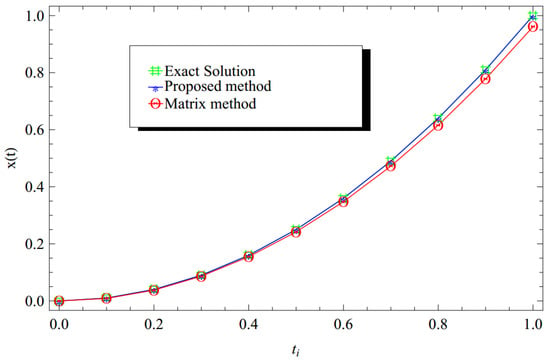
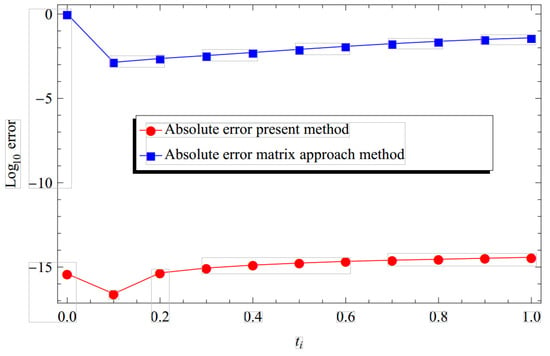
With the evaluation of the approximate solution using our proposed procedure and matrix approach method [38], the computation of the relevant absolute errors and relative errors are illustrated in

Table 1. Evaluation of the approximate solution of Example 2 using the proposed Bernoulli wavelet (with $M=3,k=1$) and matrix approach method [38], and computation of the relevant absolute errors. The CPU elapsed time for our method is 0.240562 s.

t	Exact Solution	Proposed Method	Absolute Error	The Matrix Approach	Absolute Error
		(Bernoulli Wavelet, M = 3, k = 1)		Method [38]
0.0	0.0000	−4.000000000000000$\times {10}^{-16}$	3.951574000000000$\times {10}^{-16}$	0	0
0.1	0.0100	1.000000000000000$\times {10}^{-2}$	2.602085000000000$\times {10}^{-17}$	8.621129726629000$\times {10}^{-3}$	1.378870273371000$\times {10}^{-3}$
0.2	0.0400	4.000000000000000$\times {10}^{-2}$	4.510281000000000$\times {10}^{-16}$	3.768990737059000$\times {10}^{-2}$	2.310092694100000$\times {10}^{-3}$
0.3	0.0900	9.000000000000000$\times {10}^{-2}$	8.743006000000000$\times {10}^{-16}$	8.653940580194799$\times {10}^{-2}$	3.460594198052000$\times {10}^{-3}$
0.4	0.1600	1.600000000000000$\times {10}^{-1}$	1.30451200000000$\times {10}^{-15}$	1.547406970677520$\times {10}^{-1}$	5.259302932248000$\times {10}^{-3}$
0.5	0.2500	2.500000000000017$\times {10}^{-1}$	1.720846000000000$\times {10}^{-15}$	2.419317740052830$\times {10}^{-1}$	8.068225994717000$\times {10}^{-3}$
0.6	0.3600	3.600000000000022$\times {10}^{-1}$	2.164935000000000$\times {10}^{-15}$	3.478600123952930$\times {10}^{-1}$	1.213998760470700$\times {10}^{-2}$
0.7	0.4900	4.900000000000025$\times {10}^{-1}$	2.553513000000000$\times {10}^{-15}$	4.724404482263740$\times {10}^{-1}$	1.755955177362000$\times {10}^{-2}$
0.8	0.6400	6.400000000000028$\times {10}^{-1}$	2.886580000000000$\times {10}^{-15}$	6.158149467974990$\times {10}^{-1}$	2.418505320250100$\times {10}^{-2}$
0.9	0.8100	8.100000000000032$\times {10}^{-1}$	3.330669000000000$\times {10}^{-15}$	7.784088457659700$\times {10}^{-1}$	3.159115420340300$\times {10}^{-2}$
1	1.0000	1.000000000000004	3.774758000000000$\times {10}^{-15}$	9.609838046410990$\times {10}^{-1}$	3.901619535890100$\times {10}^{-2}$

and

Table 2. Evaluation of the approximate solution of Example 2 using the proposed Bernoulli wavelet (with $M=3,k=1$) and matrix approach method [38], and computation of the relevant relative errors. The CPU elapsed time for our method is is 0.230562 s.

t	Exact Solution	Proposed Method	Relative Error	The Matrix Approach	Relative Error
		(Bernoulli wavelet, M = 3, k = 1)		Method [38]
0.1	0.0100	1.000000000000000$\times {10}^{-2}$	0	8.621129726629000$\times {10}^{-3}$	1.378870000000000$\times {10}^{-1}$
0.2	0.0400	4.000000000000050$\times {10}^{-2}$	1.249000000000000$\times {10}^{-14}$	3.768990737059000$\times {10}^{-2}$	5.775230000000000$\times {10}^{-2}$
0.3	0.0900	9.000000000000090$\times {10}^{-2}$	1.002280000000000$\times {10}^{-14}$	8.653940580194799$\times {10}^{-2}$	3.845100000000000$\times {10}^{-2}$
0.4	0.1600	1.600000000000013$\times {10}^{-1}$	8.153200000000000$\times {10}^{-14}$	1.547406970677520$\times {10}^{-1}$	3.287060000000000$\times {10}^{-2}$
0.5	0.2500	2.500000000000017$\times {10}^{-1}$	6.883380000000000$\times {10}^{-15}$	2.419317740052830$\times {10}^{-1}$	3.227290000000000$\times {10}^{-2}$
0.6	0.3600	3.600000000000022$\times {10}^{-1}$	6.167910000000000$\times {10}^{-15}$	3.478600123952930$\times {10}^{-1}$	3.372220000000000$\times {10}^{-2}$
0.7	0.4900	4.900000000000025$\times {10}^{-1}$	5.097960000000000$\times {10}^{-15}$	4.724404482263740$\times {10}^{-1}$	3.583580000000000$\times {10}^{-2}$
0.8	0.6400	6.400000000000028$\times {10}^{-1}$	4.336810000000000$\times {10}^{-15}$	6.158149467974990$\times {10}^{-1}$	3.778910000000000$\times {10}^{-2}$
0.9	0.8100	8.100000000000032$\times {10}^{-1}$	3.837810000000000$\times {10}^{-15}$	7.784088457659700$\times {10}^{-1}$	3.900140000000000$\times {10}^{-2}$
1	1.0000	1.000000000000004	3.552710000000000$\times {10}^{-15}$	9.609838046410990$\times {10}^{-1}$	3.901620000000000$\times {10}^{-2}$

, respectively. To further demonstrate the correctness of the procedure, Figure 1 and Figure 2 compare the approximations to the exact solutions. We can draw the conclusion that results obtained using the current strategy are more accurate than those obtained using the outlined procedure mentioned in [38].

Example 3.

Take the FDE [39]

$$D^{\alpha }x\left(t\right)=-x\left(t\right)+t^2+\frac{2}{\Gamma (3-\alpha )}{t}^{2-\alpha },0<\alpha <1,$$

(34)

under initial conditions $x\left(0\right)=0$. Here, $x\left(t\right)=t^2$ is the exact solution of (34). Let $Dx\left(t\right)=C^T\psi \left(t\right)$; then, we have

$$x\left(t\right)=IDx\left(t\right)+x\left(0\right)=C^T{P}^{\left(1\right)}\psi \left(t\right),$$

and

$$D^{\alpha }x\left(t\right)=C^T{P}^{(1-\alpha )}\psi \left(t\right).$$

The problem is then transformed to the following system of linear algebraic equations

$$C^T{P}^{\left(1\right)}\psi \left(t\right)+C^T{P}^{(1-\alpha )}\psi \left(t\right)=A^T\psi \left(t\right),$$

or,

$$(P^{{(1-\alpha )}^T}+P^{{\left(1\right)}^T})C=A,$$

(35)

here, $f\left(t\right)$ is approximated in terms of the Bernoulli wavelets as

$$f\left(t\right)\simeq A^T\psi \left(t\right).$$

Now, the operational matrices $P^{(1-\alpha )}$, $P^{\left(1\right)}$ and the vector A are calculated to solve (35) for the unknown vector $C=[c_{10},c_{11},c_{12}]$ for five values of $\alpha (\alpha =0.1000,0.2000,0.3000,0.4000,0.5000)$. For $\alpha =0.1000,$ and $M=3,$ $K=1,$ we have

$${\mathbf{P}}^{({\displaystyle 1}-\mathbf{ff})}=\left[\begin{array}{ccc}0.5472& 0.2942& -0.0097\\ -0.2942& 0.0421& 0.1477\\ -0.0097& -0.1477& 0.0250\end{array}\right],$$

$${\mathbf{P}}^{\left(\mathbf{1}\right)}=\left[\begin{array}{ccc}0.5000& 0.2887& 0.0000\\ -0.2887& 0.0000& 0.1291\\ 0& -0.1291& 0\end{array}\right],$$

and $A={[0.7107,0.6071,0.1501]}^T$. Substitute $P^{(1-\alpha )},$ $P^{\left(1\right)},$ and $A^T$ in (35) and solve the resulted system. Then, we get $c_{10}=1,$ $c_{11}=0.5770,$ $c_{12}=-1.0900\times {10}^{-14}$. Now, substituting in $x\left(t\right)=C^T{P}^{\left(1\right)}\psi \left(t\right)$, the approximated solution is given by

$$\check{x\left(t\right)}=t^2+1.200\times {10}^{-10}t-5.8000\times {10}^{-11}.$$

Now, for $\alpha =0.2000$, and $M=3,K=1$, using the same MATLAB program, we obtain

$${\mathbf{P}}^{(\mathbf{1}-\mathbf{ff})}=\left[\begin{array}{ccc}0.5965& 0.2952& -0.0201\\ -0.2952& 0.0942& 0.1650\\ -0.0201& -0.1650& 0.0595\end{array}\right],$$

and $A={[0.7594,0.6382,0.1497]}^T$. Substitute $P^{(1-\alpha )}$, $P^{\left(1\right)}$, and $A^T$ in (35) and solve the resulted system. Then, we get $c_{10}=1,$ $c_{11}=0.5770,$ $c_{12}=-1.2000\times {10}^{-14}$. Now, substituting in $x\left(t\right)=C^T{P}^{\left(1\right)}\psi \left(t\right)$, the approximated solution is given by

$$\check{x\left(t\right)}=t^2+1.2000\times {10}^{-10}t-5.8000\times {10}^{-11}.$$

Now, for $\alpha =0.3000$, and $M=3,$ $K=1,$ we have

$${\mathbf{P}}^{(\mathbf{1}-\mathbf{ff})}=\left[\begin{array}{ccc}0.6474& 0.2907& -0.0304\\ -0.2907& 0.1575& 0.1798\\ -0.0304& -0.1798& 0.1059\end{array}\right],$$

and $A={[0.8129,0.6703,0.1479]}^T$. Substitute $P^{(1-\alpha )},P^{\left(1\right)}$, and $A^T$ in Equation (35) and solve the resulted system. Then, we get $c_{10}=1,$ $c_{11}=0.5770,$ $c_{12}=-7.0100\times {10}^{-15}$. Now, substituting in $x\left(t\right)=C^T{P}^{\left(1\right)}\psi \left(t\right)$, the approximated solution is given by

$$\check{x\left(t\right)}=t^2+1.2000\times {10}^{-10}t-1.2000\times {10}^{-10}.$$

In case of $\alpha =0.4000$ and $M=3,K=1$, we have

$${\mathbf{P}}^{(\mathbf{1}-\mathbf{ff})}=\left[\begin{array}{ccc}0.6995& 0.2796& -0.0401\\ -0.2796& 0.2332& 0.1903\\ -0.0401& -0.1903& 0.1665\end{array}\right],$$

and $A={[0.8714,0.7029,0.1443]}^T$. Substitute $P^{(1-\alpha )}$, $P^{\left(1\right)}$, and $A^T$ in (35) and solve the resulted system. Then, we get $c_{10}=1,$ $c_{11}=0.5770,$ $c_{12}=1.7100\times {10}^{-14}$. Now, substituting in $x\left(t\right)=C^T{P}^{\left(1\right)}\psi \left(t\right)$, the approximated solution is given by

$$\check{x\left(t\right)}=t^2+1.2000\times {10}^{-10}t-5.8000\times {10}^{-11}.$$

Finally, $\alpha =0.5000$, and $M=3,$ $K=1,$ we have

$${\mathbf{P}}^{(\mathbf{1}-\mathbf{ff})}=\left[\begin{array}{ccc}0.7523& 0.2606& -0.0481\\ -0.2606& 0.3224& 0.1942\\ -0.0481& -0.1942& 0.2442\end{array}\right],$$

and $A={[0.9351,0.7354,0.1386]}^T$. Substitute $P^{(1-\alpha )}$, $P^{\left(1\right)}$, and $A^T$ in (37) and solve the resultant system. Then, we get $c_{10}=1,$ $c_{11}=0.5770,$ $c_{12}=-9.3200\times {10}^{-15}$. Now, substituting in $x\left(t\right)=C^T{P}^{\left(1\right)}\psi \left(t\right)$, the approximated solution is given by

$$\check{x\left(t\right)}=t^2+1.2000\times {10}^{-10}t-1.2000\times {10}^{-10}.$$

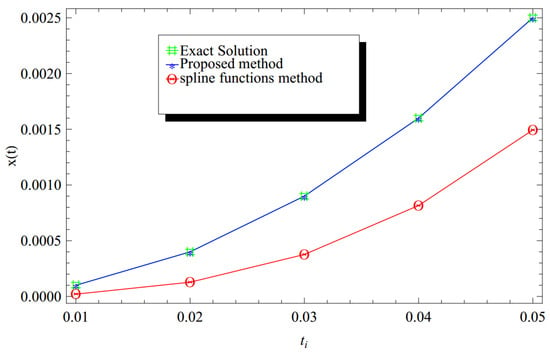
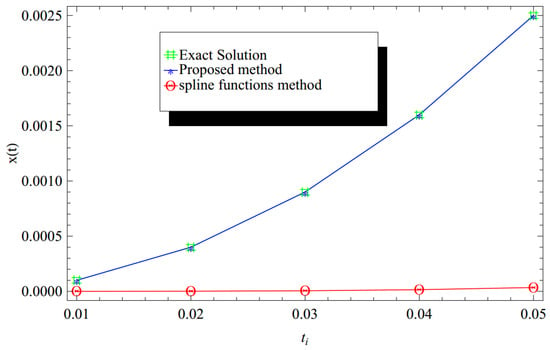
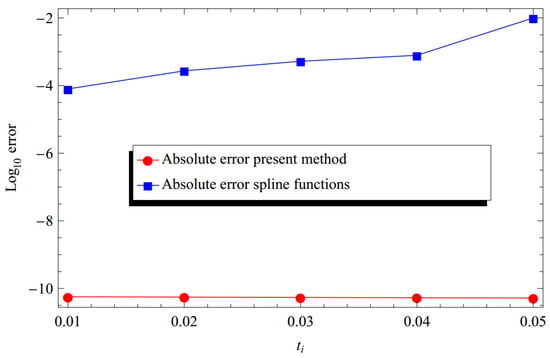
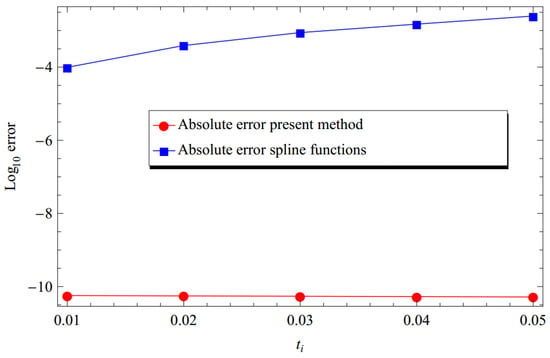
The evaluation of the approximate solution of our proposed method and the spline function’s method of integral form (using h = 0.01 and m = 2 ) [39] and the computation of the relevant absolute errors and relative errors are illustrated throughout

Table 3. Evaluation of the approximate solution of Example 3 using the proposed Bernoulli wavelet (with $M=3,k=1$) and the spline functions method of integral form (using h = 0.01 and m = 2) [39], and computation of the relevant absolute errors. The CPU elapsed time for each $\alpha$ is approximately 2.315821 s.

$\mathit{\alpha }$	t	Exact Solution	Proposed Method	Absolute Error	Spline Functions Method	Absolute Error
			(Bernoulli Wavelet, M = 3, k = 1)		of Integral Form (Using h =
					0.01 and m = 2) [39]
0.1	0.0100	1.000000000000000$\times {10}^{-4}$	9.999994320000000$\times {10}^{-5}$	5.679999999258930$\times {10}^{-11}$	2.048670000000000$\times {10}^{-5}$	7.951300000000000$\times {10}^{-5}$
	0.0200	4.000000000000000$\times {10}^{-4}$	3.999999444000000$\times {10}^{-4}$	5.559999997298980$\times {10}^{-11}$	1.276150000000000$\times {10}^{-4}$	2.723800000000000$\times {10}^{-4}$
	0.0300	9.000000000000000$\times {10}^{-4}$	8.999999456000000$\times {10}^{-4}$	5.440000002115280$\times {10}^{-11}$	3.763020000000000$\times {10}^{-4}$	5.237000000000000$\times {10}^{-4}$
	0.0400	1.600000000000000$\times {10}^{-3}$	1.599999946800000$\times {10}^{-3}$	5.319999996089560$\times {10}^{-11}$	8.158430000000000$\times {10}^{-4}$	7.841600000000000$\times {10}^{-4}$
	0.0500	2.500000000000000$\times {10}^{-3}$	2.499999948000000$\times {10}^{-3}$	5.200000022589910$\times {10}^{-11}$	1.493580000000000$\times {10}^{-3}$	1.000000000000000$\times {10}^{-3}$
0.2	0.0100	1.000000000000000$\times {10}^{-4}$	9.999994320000000$\times {10}^{-5}$	5.679999999258930$\times {10}^{-11}$	3.757990000000000$\times {10}^{-6}$	9.599999999999999$\times {10}^{-5}$
	0.0200	4.000000000000000$\times {10}^{-4}$	3.999999444000000$\times {10}^{-4}$	5.559999997298980$\times {10}^{-11}$	2.939430000000000$\times {10}^{-5}$	3.700000000000000$\times {10}^{-4}$
	0.0300	9.000000000000000$\times {10}^{-4}$	8.999999456000000$\times {10}^{-4}$	5.440000002115280$\times {10}^{-11}$	9.899630000000001$\times {10}^{-5}$	8.000000000000000$\times {10}^{-4}$
	0.0400	1.600000000000000$\times {10}^{-3}$	1.599999946800000$\times {10}^{-3}$	5.319999996089560$\times {10}^{-11}$	2.358220000000000$\times {10}^{-4}$	1.300000000000000$\times {10}^{-3}$
	0.0500	2.500000000000000$\times {10}^{-3}$	2.499999948000000$\times {10}^{-3}$	5.200000022589910$\times {10}^{-11}$	4.644040000000000$\times {10}^{-4}$	2.000000000000000$\times {10}^{-3}$
0.3	0.0100	1.000000000000000$\times {10}^{-4}$	9.999988120000000$\times {10}^{-5}$	1.187999999887950$\times {10}^{-10}$	5.419970000000001$\times {10}^{+01}$	9.899999999999999$\times {10}^{-5}$
	0.0200	4.000000000000000$\times {10}^{-4}$	3.999998824000000$\times {10}^{-4}$	1.175999999963010$\times {10}^{-10}$	6.097229999999999$\times {10}^{-6}$	3.900000000000000$\times {10}^{-4}$
	0.0300	9.000000000000000$\times {10}^{-4}$	8.999998836000000$\times {10}^{-4}$	1.163999999902530$\times {10}^{-10}$	2.365070000000000$\times {10}^{-5}$	8.700000000000000$\times {10}^{-4}$
	0.0400	1.600000000000000$\times {10}^{-3}$	1.599999884800000$\times {10}^{-3}$	1.151999999299960$\times {10}^{-10}$	6.227089999999999$\times {10}^{-5}$	1.500000000000000$\times {10}^{-3}$
	0.0500	2.500000000000000$\times {10}^{-3}$	2.499999886000000$\times {10}^{-3}$	1.139999999781590$\times {10}^{-10}$	1.325200000000000$\times {10}^{-4}$	2.300000000000000$\times {10}^{-3}$
0.4	0.0100	1.000000000000000$\times {10}^{-4}$	9.999994320000000$\times {10}^{-5}$	5.679999999258930$\times {10}^{-11}$	8.838670000000001$\times {10}^{-8}$	9.899999999999999$\times {10}^{-5}$
	0.0200	4.000000000000000$\times {10}^{-4}$	3.999999444000000$\times {10}^{-4}$	5.559999997298980$\times {10}^{-11}$	1.137680000000000$\times {10}^{-6}$	3.900000000000000$\times {10}^{-4}$
	0.0300	9.000000000000000$\times {10}^{-4}$	8.999999456000000$\times {10}^{-4}$	5.440000002115280$\times {10}^{-11}$	5.125250000000000$\times {10}^{-6}$	8.800000000000001$\times {10}^{-4}$
	0.0400	1.600000000000000$\times {10}^{-3}$	1.599999946800000$\times {10}^{-3}$	5.319999996089560$\times {10}^{-11}$	1.500400000000000$\times {10}^{-5}$	1.500000000000000$\times {10}^{-3}$
	0.0500	2.500000000000000$\times {10}^{-3}$	2.499999948000000$\times {10}^{-3}$	5.200000022589910$\times {10}^{-11}$	3.466460000000000$\times {10}^{-5}$	2.500000000000000$\times {10}^{-3}$
0.5	0.0100	1.000000000000000$\times {10}^{-4}$	9.999988120000000$\times {10}^{-5}$	1.187999999887950$\times {10}^{-10}$	1.130950000000000$\times {10}^{-8}$	9.899999999999999$\times {10}^{-5}$
	0.0200	4.000000000000000$\times {10}^{-4}$	3.999998824000000$\times {10}^{-4}$	1.175999999963010$\times {10}^{-10}$	1.907550000000000$\times {10}^{-7}$	3.900000000000000$\times {10}^{-4}$
	0.0300	9.000000000000000$\times {10}^{-4}$	8.999998836000000$\times {10}^{-4}$	1.163999999902530$\times {10}^{-10}$	1.006400000000000$\times {10}^{-6}$	9.000000000000001$\times {10}^{-4}$
	0.0400	1.600000000000000$\times {10}^{-3}$	1.599999884800000$\times {10}^{-3}$	1.151999999299960$\times {10}^{-10}$	3.295210000000000$\times {10}^{-6}$	1.500000000000000$\times {10}^{-3}$
	0.0500	2.500000000000000$\times {10}^{-3}$	2.499999886000000$\times {10}^{-3}$	1.139999999781590$\times {10}^{-10}$	8.303120000000000$\times {10}^{-6}$	2.500000000000000$\times {10}^{-3}$

and

Table 4. Evaluation of the approximate solution of Example 3 using the proposed Bernoulli wavelet (with $M=3,k=1$) and the spline functions method of integral form (using h = 0.01 and m = 2) [39], and computation of the relevant relative errors. The CPU elapsed time for each $\alpha$ is approximately 1.97275 s.

$\mathit{\alpha }$	t	Exact Solution	Proposed Method	Relative Error	Spline Functions Method	Relative Error
			(Bernoulli Wavelet, M = 3, k = 1)		of Integral Form (Using h =
					0.01 and m = 2) [39]
0.1	0.0100	1.000000000000000$\times {10}^{-4}$	9.999994320000000$\times {10}^{-5}$	5.680000000000000$\times {10}^{-7}$	2.048670000000000$\times {10}^{-5}$	7.951330000000000$\times {10}^{-1}$
	0.0200	4.000000000000000$\times {10}^{-4}$	3.999999444000000$\times {10}^{-4}$	1.390000000000000$\times {10}^{-7}$	1.276150000000000$\times {10}^{-4}$	6.809630000000000$\times {10}^{-1}$
	0.0300	9.000000000000000$\times {10}^{-4}$	8.999999456000000$\times {10}^{-4}$	6.044440000000000$\times {10}^{-8}$	3.763020000000000$\times {10}^{-4}$	5.818870000000000$\times {10}^{-1}$
	0.0400	1.600000000000000$\times {10}^{-3}$	1.599999946800000$\times {10}^{-3}$	3.325000000000000$\times {10}^{-8}$	8.158430000000000$\times {10}^{-4}$	4.900980000000000$\times {10}^{-1}$
	0.0500	2.500000000000000$\times {10}^{-3}$	2.499999948000000$\times {10}^{-3}$	2.080000000000000$\times {10}^{-8}$	1.493580000000000$\times {10}^{-3}$	4.025680000000000$\times {10}^{-1}$
0.2	0.0100	1.000000000000000$\times {10}^{-4}$	9.999994320000000$\times {10}^{-5}$	5.680000000000000$\times {10}^{-7}$	3.757990000000000$\times {10}^{-6}$	9.624200000000001$\times {10}^{-1}$
	0.0200	4.000000000000000$\times {10}^{-4}$	3.999999444000000$\times {10}^{-4}$	1.390000000000000$\times {10}^{-7}$	2.939430000000000$\times {10}^{-5}$	9.265139999999999$\times {10}^{-1}$
	0.0300	9.000000000000000$\times {10}^{-4}$	8.999999456000000$\times {10}^{-4}$	6.044440000000000$\times {10}^{-8}$	9.899630000000001$\times {10}^{-5}$	8.900040000000000$\times {10}^{-1}$
	0.0400	1.600000000000000$\times {10}^{-3}$	1.599999946800000$\times {10}^{-3}$	3.325000000000000$\times {10}^{-8}$	2.358220000000000$\times {10}^{-4}$	8.526110000000000$\times {10}^{-1}$
	0.0500	2.500000000000000$\times {10}^{-3}$	2.499999948000000$\times {10}^{-3}$	2.080000000000000$\times {10}^{-8}$	4.644040000000000$\times {10}^{-4}$	8.142380000000000$\times {10}^{-1}$
0.3	0.0100	1.000000000000000$\times {10}^{-4}$	9.999988120000000$\times {10}^{-5}$	1.188000000000000$\times {10}^{-6}$	6.119970000000001$\times {10}^{-7}$	9.938800000000000$\times {10}^{-1}$
	0.0200	4.000000000000000$\times {10}^{-4}$	3.999998824000000$\times {10}^{-4}$	2.940000000000000$\times {10}^{-7}$	6.097229999999999$\times {10}^{-6}$	9.847570000000000$\times {10}^{-1}$
	0.0300	9.000000000000000$\times {10}^{-4}$	8.999998836000000$\times {10}^{-4}$	1.293330000000000$\times {10}^{-7}$	2.365070000000000$\times {10}^{-5}$	9.737209999999999$\times {10}^{-1}$
	0.0400	1.600000000000000$\times {10}^{-3}$	1.599999884800000$\times {10}^{-3}$	7.200000000000000$\times {10}^{-8}$	6.227089999999999$\times {10}^{-5}$	9.610810000000000$\times {10}^{-1}$
	0.0500	2.500000000000000$\times {10}^{-3}$	2.499999886000000$\times {10}^{-3}$	4.560000000000000$\times {10}^{-8}$	1.325200000000000$\times {10}^{-4}$	9.469919999999999$\times {10}^{-1}$
0.4	0.0100	1.000000000000000$\times {10}^{-4}$	9.999994320000000$\times {10}^{-5}$	5.680000000000000$\times {10}^{-7}$	8.838670000000001$\times {10}^{-8}$	9.991160000000000$\times {10}^{-1}$
	0.0200	4.000000000000000$\times {10}^{-4}$	3.999999444000000$\times {10}^{-4}$	1.390000000000000$\times {10}^{-7}$	1.137680000000000$\times {10}^{-6}$	9.971560000000000$\times {10}^{-1}$
	0.0300	9.000000000000000$\times {10}^{-4}$	8.999999456000000$\times {10}^{-4}$	6.044440000000000$\times {10}^{-8}$	5.125250000000000$\times {10}^{-6}$	9.943050000000000$\times {10}^{-1}$
	0.0400	1.600000000000000$\times {10}^{-3}$	1.599999946800000$\times {10}^{-3}$	3.325000000000000$\times {10}^{-8}$	1.500400000000000$\times {10}^{-5}$	9.906230000000000$\times {10}^{-1}$
	0.0500	2.500000000000000$\times {10}^{-3}$	2.499999948000000$\times {10}^{-3}$	2.080000000000000$\times {10}^{-8}$	3.466460000000000$\times {10}^{-5}$	9.861340000000000$\times {10}^{-1}$
0.5	0.01	1.000000000000000$\times {10}^{-4}$	9.999988120000000$\times {10}^{-5}$	1.188000000000000$\times {10}^{-6}$	1.130950000000000$\times {10}^{-8}$	9.998870000000000$\times {10}^{-1}$
	0.02	4.000000000000000$\times {10}^{-4}$	3.999998824000000$\times {10}^{-4}$	2.940000000000000$\times {10}^{-7}$	1.907550000000000$\times {10}^{-7}$	9.995230000000001$\times {10}^{-1}$
	0.03	9.000000000000000$\times {10}^{-4}$	8.999998836000000$\times {10}^{-4}$	1.293330000000000$\times {10}^{-7}$	1.006400000000000$\times {10}^{-6}$	9.988820000000000$\times {10}^{-1}$
	0.04	1.600000000000000$\times {10}^{-3}$	1.599999884800000$\times {10}^{-3}$	7.200000000000000$\times {10}^{-8}$	3.295210000000000$\times {10}^{-6}$	9.979400000000000$\times {10}^{-1}$
	0.05	2.500000000000000$\times {10}^{-3}$	2.499999886000000$\times {10}^{-3}$	4.560000000000000$\times {10}^{-8}$	8.303120000000000$\times {10}^{-6}$	9.966790000000000$\times {10}^{-1}$

, respectively. Additionally, the solutions and absolute errors of the suggested technique compared to the spline function’s method of integral form are in excellent agreement with the exact solution, as demonstrated by Figure 3, Figure 4, Figure 5 and Figure 6.

Example 4.

We explore the linear fractional differential equations in this example [40]:

$$D^{2}x\left(t\right)+D^{1.5}x\left(t\right)+x\left(t\right)=f\left(t\right),$$

(36)

where

$$f\left(t\right)=t^2+2+4\sqrt{\frac{t}{\Pi }},$$

with the initial conditions $x\left(0\right)=0,x^{\prime }\left(0\right)=0$. Here, $x\left(t\right)=t^2$ is the exact solution for (36). We can use our approach as follows:

Let $D^{2}x\left(t\right)=C^T\psi \left(t\right)$; then, we have

$$Dx\left(t\right)=I^{2-1}{D}^{2}x\left(t\right)+x^{\prime }\left(0\right)=I{C}^T\psi \left(t\right)+0=C^T{P}^{\left(1\right)}\psi \left(t\right),$$

$$x\left(t\right)=IDx\left(t\right)+x\left(0\right)=C^T{P}^{\left(2\right)}\psi \left(t\right),$$

and

$$D^{\alpha }x\left(t\right)=C^T{P}^{(2-\alpha )}\psi \left(t\right).$$

The problem is then transformed to the following system of linear algebraic equations:

$$C^T\psi \left(t\right)+C^T{P}^{\left(\frac{1}{2}\right)}\psi \left(t\right)+C^T{P}^{\left(2\right)}\psi \left(t\right)=A^T\psi \left(t\right),$$

or,

$$C^T(I+P^{\left(\frac{1}{2}\right)}+P^{\left(2\right)})=A^T.$$

(37)

Hence, using Bernoulli wavelets, $f\left(t\right)$ is approximately represented as

$$f\left(t\right)\simeq A^T\psi \left(t\right)=[3.80000.8100-0.0220]\psi \left(t\right).$$

For $M=3,K=1$, we have

$${\mathbf{P}}^{(\mathbf{0}.\mathbf{5})}=\left[\begin{array}{ccc}0.7523& 0.2606& -0.0481\\ -0.2606& 0.3224& 0.1942\\ -0.0481& -0.1942& 0.2442\end{array}\right],$$

$${\mathbf{P}}^{\left(\mathbf{2}\right)}=\left[\begin{array}{ccc}0.1667& 0.1443& 0.0373\\ -0.1443& -0.1000& -0.0000\\ 0.0373& -0.0000& -0.0238\end{array}\right],$$

and substitute $P^{\left(2\right)}$, $P^{\left(0.5\right)}$, and $A^T$ in (37) and solve the resulted algebraic equation system in the unknown coefficient vector $C=[c_{10},c_{11},c_{12}]$. Then, we get $c_{10}=2$, $c_{11}=-2.5700\times {10}^{-15}$, $c_{12}=1.3700$ $\times {10}^{-15}$. Now, substituting in $x\left(t\right)=C^T{P}^{\left(2\right)}\psi \left(t\right)$, we obtain the needed approximated solution

$$\check{x\left(t\right)}=t^2+3.4906,$$

which can be approximated to the exact solution $x\left(t\right)=t^2$. The evaluation of the approximate solution using our proposed method and the fractional finite difference method(FFDM) (when $h=0.1$) [40] and the computation of the relevant absolute errors and relative errors are illustrated throughout

Table 5. Evaluation of the approximate solution of Example 4 using the proposed Bernoulli wavelet (with $M=3,k=1$) and the FFDM (when $h=0.1$) [40], and computation of the relevant absolute errors. The CPU elapsed time for our method is 1.681526 s.

t	Exact Solution	Proposed Method	Absolute Error	FFDM [40]	Absolute Error
		(Bernoulli Wavelet, M = 3, k = 1)
0.1	0.0100	1.000000000000349$\times {10}^{-2}$	3.490263633665336$\times {10}^{-15}$	1.000000000000325$\times {10}^{-2}$	3.200560000000000$\times {10}^{-15}$
0.2	0.0400	4.000000000000350$\times {10}^{-2}$	3.490263633665336$\times {10}^{-15}$	4.000000000000937$\times {10}^{-2}$	9.298120000000000$\times {10}^{-15}$
0.3	0.0900	9.000000000000352$\times {10}^{-2}$	3.497202527569243$\times {10}^{-15}$	9.000000000001489$\times {10}^{-2}$	1.480760000000000$\times {10}^{-14}$
0.4	0.1600	1.600000000000035$\times {10}^{-1}$	3.497202527569243$\times {10}^{-15}$	1.600000000000190$\times {10}^{-1}$	1.898480000000000$\times {10}^{-14}$
0.5	0.2500	2.500000000000035$\times {10}^{-1}$	3.497202527569243$\times {10}^{-15}$	2.500000000000235$\times {10}^{-1}$	2.298160000000000$\times {10}^{-14}$
0.6	0.3600	3.600000000000035$\times {10}^{-1}$	3.497202527569243$\times {10}^{-15}$	3.600000000000282$\times {10}^{-1}$	2.803310000000000$\times {10}^{-14}$
0.7	0.4900	4.900000000000034$\times {10}^{-1}$	3.497202527569243$\times {10}^{-15}$	4.900000000000332$\times {10}^{-1}$	3.302910000000000$\times {10}^{-14}$
0.8	0.6400	6.400000000000033$\times {10}^{-1}$	3.441691376337985$\times {10}^{-15}$	6.400000000000382$\times {10}^{-1}$	3.796960000000000$\times {10}^{-14}$
0.9	0.8100	8.100000000000033$\times {10}^{-1}$	3.441691376337985$\times {10}^{-15}$	8.100000000000432$\times {10}^{-1}$	4.296560000000000$\times {10}^{-14}$
1	1.0000	1.000000000000003	3.552713678800501$\times {10}^{-15}$	1.000000000000049	3.99680000000000$\times {10}^{-14}$

and

Table 6. Evaluation of the approximate solution of Example 4 using the proposed Bernoulli wavelet (with $M=3,k=1$) and the FFDM (when $h=0.1$) [40], and computation of the relative errors. The CPU elapsed time for our method is 1.381526 s.

t	Exact Solution	Proposed Method	Relative Error	FFDM [40]	Relative Error
		(Bernoulli Wavelet, M = 3, k = 1)
0.1	0.0100	1.000000000000349$\times {10}^{-2}$	3.490260000000000$\times {10}^{-13}$	1.000000000000325$\times {10}^{-2}$	3.24914$\times {10}^{-13}$
0.2	0.0400	4.000000000000350$\times {10}^{-2}$	8.743010000000000$\times {10}^{-14}$	4.000000000000937$\times {10}^{-2}$	2.341880000000000$\times {10}^{-13}$
0.3	0.0900	9.000000000000352$\times {10}^{-2}$	3.916620000000000$\times {10}^{-14}$	9.000000000001489$\times {10}^{-2}$	1.654540000000000$\times {10}^{-13}$
0.4	0.1600	1.600000000000035$\times {10}^{-1}$	2.203100000000000$\times {10}^{-14}$	1.600000000000190$\times {10}^{-1}$	1.188290000000000$\times {10}^{-13}$
0.5	0.2500	2.500000000000035$\times {10}^{-1}$	1.398880000000000$\times {10}^{-14}$	2.500000000000235$\times {10}^{-1}$	9.414690000000000$\times {10}^{-14}$
0.6	0.3600	3.600000000000035$\times {10}^{-1}$	9.714450000000001$\times {10}^{-15}$	3.600000000000282$\times {10}^{-1}$	7.848660000000000$\times {10}^{-14}$
0.7	0.4900	4.900000000000034$\times {10}^{-1}$	7.023860000000000$\times {10}^{-15}$	4.900000000000332$\times {10}^{-1}$	6.774630000000000$\times {10}^{-14}$
0.8	0.6400	6.400000000000033$\times {10}^{-1}$	5.204170000000000$\times {10}^{-15}$	6.400000000000382$\times {10}^{-1}$	5.967450000000000$\times {10}^{-14}$
0.9	0.8100	8.100000000000033$\times {10}^{-1}$	3.974870000000000$\times {10}^{-15}$	8.100000000000432$\times {10}^{-1}$	5.331810000000000$\times {10}^{-14}$
1	1.0000	1.000000000000003	3.330670000000000$\times {10}^{-15}$	1.000000000000049	4.862780000000000$\times {10}^{-14}$

, respectively.

5. Discussion

This paper presents an easily programmable procedure that leverages the power of the Bernoulli wavelet for highly accurate numerical solutions of initial value fractional differential equations. The innovative approach entails transforming fractional order initial value problems into a set of algebraic equations. Through comprehensive analysis and comparison with widely used methods, the results from various numerical examples and detailed comparative tables convincingly demonstrate the superior accuracy and efficiency of the proposed strategy. Remarkably, this numerical scheme exhibits exceptional precision even when employing a minimal number of basis elements. The numerical examples show absolute and relative errors alongside graphical representations, confirming the remarkable accuracy achieved by the proposed method. Furthermore, the method’s advantages over other techniques are elaborated in Table 2, Table 3, Table 4, Table 5 and Table 6. However, it is essential to acknowledge the study’s current limitations and emphasize the potential for future extensions to address more complex models. For instance, further investigation is warranted to apply the suggested technique to numerically solve more general fractional differential equations, including those with variable coefficients, time-fractional telegraph equations with Dirichlet boundary conditions, and classical fractional-order dynamical systems incorporating nonlinearity.