On Finite-Time Blow-Up Problem for Nonlinear Fractional Reaction Diffusion Equation: Analytical Results and Numerical Simulations

Abstract

The study of the blow-up phenomenon for fractional reaction–diffusion problems is generally deemed of great importance in dealing with several situations that impact our daily lives, and it is applied in many areas such as finance and economics. In this article, we expand on some previous blow-up results for the explicit values and numerical simulation of finite-time blow-up solutions for a semilinear fractional partial differential problem involving a positive power of the solution. We show the behavior solution of the fractional problem, and the numerical solution of the finite-time blow-up solution is also considered. Finally, some illustrative examples and comparisons with the classical problem with integer order are presented, and the validity of the results is demonstrated.

1. Introduction

The study of mathematical models and physical systems has captured the attention of numerous researchers and mathematicians. They strive to develop theoretical frameworks, numerical methods, and analytical tools, particularly in the solvability of partial differential equations (PDEs). These endeavors are still ongoing as researchers are motivated to uncover the underlying mechanisms, especially in the field of fractional partial differential equations [1,2,3,4,5,6,7].

Fractional operators and corresponding differential and integral equations are often chosen because of the memory effects provided by their analytical properties [8,9,10,11,12,13,14,15]. However, when it comes to a mathematical problem, the solution is derived from a real model, the theoretical results of which are often not directly applicable to the given problem. So, problems like the integer case are solved numerically [16,17,18,19].

The scientific community has shown great interest in studying dynamic states, such as the explosion of solutions. Currently, the biggest challenge lies in identifying or estimating the occurrence of finite-time blow-up phenomena [20,21,22,23,24,25]. This area of study is considered highly important, with roots tracing back to the 19th century, when Henri Poincaré and Paul Painlevé highlighted the possibility of finite-time singularities in ordinary differential equations (ODEs). Subsequently, after 50 years, Alan Turing, Grigoriy A. Kolmogorov, Andrei N. Tikhonov, and Vladimir M. Volpert made significant contributions to the understanding of finite-time blow-up in nonlinear PDEs.

All of these factors have motivated our own research on finite-time blow-up phenomena in nonlinear problems. Specifically, we examine the following equation:

$$\left\{\begin{array}{cc}\hfill & {}^C{D}_t^{\alpha }u-a\Delta u=u^p\mathrm{for}(x,t)\in Q\hfill \\ \hfill & u(x,0)=\phi \left(x\right)\mathrm{for}x\in \mathsf{\Omega }\hfill \\ \hfill & u(0,t)=0\mathrm{for}t\in \left[0,T\right]\hfill \\ \hfill & \frac{\partial u}{\partial x}(1,t)=0\mathrm{for}t\in \left[0,T\right].\hfill \end{array}\right.$$

Here, $\alpha$ represents a fractional exponent ranging from 0 to 1, and our goal is to explore the combined effects of time-fractional diffusion, represented by the Caputo fractional derivative ${}^C{D}_t^{\alpha }u$, and a nonlinear reaction term $u^p$. The fractional derivative accounts for the memory effect and the non-local nature of time evolution in the equation, which is crucial for studying finite-time blow-up. To support our research, we present a numerical study utilizing the finite difference scheme and compare it with the classical case to validate our expectations regarding the involvement of the exponent $\alpha$.

2. Formulation of the Problem

This article concerns finite-time blow-up solutions of the fractional nonlinear diffusion equation, which are given as follows:

$$\mathcal{L}u={}^C{D}_t^{\alpha }u-a\Delta u=u^p,$$

(1)

with the initial condition

$$lu=u(x,0)=\phi \left(x\right)\forall x\in \left[0,1\right],$$

(2)

and the mixed boundary conditions

$$u(0,t)=u_x(1,t)=0\forall t\in \left[0,T\right],$$

(3)

where $\phi \in L^2\left(\mathsf{\Omega }\right)$ is a given function and $p\ge 1$, and a is positive constant called the thermal diffusivity.

The topic of existence and uniqueness is not new for scholars. Many of them have treated it differently. The most well known approaches are the Faedo–Galarkin method, the energy inequality method, the linearization method, and other techniques [ 26].

For analyzing the existence of the main problem, we can simply use the same idea as in the article by Oussaeif and Bouziani [27], where the source term is generally given by $f(x,t,v)$

$$\left\{\begin{array}{ccc}{}^C{D}_t^{\alpha }v-a\Delta v=f(x,t,v)& & \forall (x,t)\in Q\\ v(x,0)=0& & \forall x\in \mathsf{\Omega }\\ v(0,t)=0& & \forall t\in \left[0,T\right]\\ v_x(1,t)=0& & \forall t\in \left[0,T\right]\end{array}\right..$$

A positive term f represents a heat source due to an exothermic reaction. Otherwise, the reaction is endothermic. If f depends on the gradient, then convection effects are taken into consideration.

3. Finite-Time Blow-Up Solution

This section is devoted to studying the finite time of explosion solution for the following fractional problem:

$$\begin{array}{cc}\hfill & {}^C{D}_t^{\alpha }u-a\Delta u=u^p,\forall (x,t)\in Q\hfill \\ \hfill & u(x,0)=\phi \left(x\right),\hfill \\ \hfill & \forall x\in \mathsf{\Omega }u(0,t)=0\hfill \\ \hfill & \forall t\in \left[0,T\right]u_x(1,t)=0,\forall t\in \left[0,T\right]\hfill \end{array}$$

3.1. Analytical Estimation

This method was devised by Kaplan in the case of a bounded domain $\mathsf{\Omega }$. Suppose that $p\ge 2$ and that $f=f\left(u\right)=u^p$ is convex. The first eigenfunction ${\phi }_1$ of the Laplacian and the corresponding eigenvalue ${\lambda }_1$ are the solution of the following:

$$\left\{\begin{array}{c}-\Delta \phi ={\lambda }^2\phi \\ \phi \left(0\right)=0\\ {\phi }_x\left(1\right)=0\end{array}\right.;$$

(P)

the solution of the Sturm–Liouville problem is:

$${\phi }_1\left(x\right)=bsin\left(\frac{\pi }{2}x\right);\mathrm{where}\underset{\mathsf{\Omega }}{\int }\phi \left(x\right)dx=1\mathrm{and}{\lambda }_1=\frac{\pi }{2}.$$

Multiplying $\left(1\right)$ by ${\phi }_1$, integrating over $\mathsf{\Omega }$, we arrive at the relation

$$\begin{array}{ccc}\hfill {}^C{D}_t^{\alpha }\underset{\mathsf{\Omega }}{\int }u{\phi }_{1}dx-a\underset{\mathsf{\Omega }}{\int }\Delta u{\phi }_{1}dx& =& \underset{\mathsf{\Omega }}{\int }{u}^p{\phi }_{1}dx,\hfill \\ \hfill {}^C{D}_t^{\alpha }\underset{\mathsf{\Omega }}{\int }u{\phi }_{1}dx-a\underset{\mathsf{\Omega }}{\int }\Delta u{\phi }_{1}dx& =& \underset{\mathsf{\Omega }}{\int }{u}^p{\phi }_{1}dx,\hfill \\ \hfill {}^C{D}_t^{\alpha }\underset{\mathsf{\Omega }}{\int }u{\phi }_{1}dx+a{\lambda }_1\underset{\mathsf{\Omega }}{\int }u{\phi }_{1}dx& =& \underset{\mathsf{\Omega }}{\int }{u}^p{\phi }_{1}dx.\hfill \end{array}$$

By using the Jensen’s inequality, we obtain

$${}^C{D}_t^{\alpha }\underset{\mathsf{\Omega }}{\int }u{\phi }_{1}dx+a{\lambda }_1\underset{\mathsf{\Omega }}{\int }u{\phi }_{1}dx\ge {\left(\underset{\mathsf{\Omega }}{\int }u{\phi }_1\right)}^p.$$

After putting

$$\mathrm{\Pi }\left(t\right)=\underset{\mathsf{\Omega }}{\int }u{\phi }_{1}dx.$$

The differential inequality leads immediately to the following

$${}^C{D}_t^{\alpha }\mathrm{\Pi }+a{\lambda }_1\mathrm{\Pi }\ge {\mathrm{\Pi }}^p.$$

It becomes evident that the estimate of the finite-time blowup depends on the solution of the precedent inequality, but the studies do not have a large field, despite considerable recent and ongoing progress, and are still not sufficient to solve the Bernoulli equation. Therefore, we concentrate on the general idea in the article to obtain an estimation for a finite-time blow-up [ 28].

$$\frac{t^{1-\alpha }}{\mathrm{\Gamma }\left(2-\alpha \right)}{\mathrm{\Pi }}^{\prime }+a{\lambda }_1\mathrm{\Pi }\ge {\mathrm{\Pi }}^p.$$

(4)

So, for solving the equation, we must apply the following variable change

$$y={\mathrm{\Pi }}^{1-p}.$$

(5)

Therefore, it follows from $\left(4\right)$ and $\left(5\right)$ that

$$\begin{array}{ccc}\hfill \frac{t^{1-\alpha }}{\mathrm{\Gamma }\left(2-\alpha \right)\left(1-p\right)}{y}^{\prime }+a{\lambda }_{1}y& =& 1\hfill \\ \hfill y^{\prime }\left(t\right)+a{\lambda }_1\mathrm{\Gamma }\left(2-\alpha \right)\left(1-p\right)t^{-1+\alpha }y\left(t\right)& =& \mathrm{\Gamma }\left(2-\alpha \right)\left(1-p\right)t^{-1+\alpha }.\hfill \end{array}$$

By putting

$$\begin{array}{ccc}\hfill C& =& a{\lambda }_1\mathrm{\Gamma }\left(2-\alpha \right)\left(1-p\right),\hfill \\ \hfill C^{\prime }& =& \mathrm{\Gamma }\left(2-\alpha \right)\left(1-p\right).\hfill \end{array}$$

So, the equation becomes

$$y^{\prime }+C{t}^{-1+\alpha }y=C^{\prime }{t}^{-1+\alpha }.$$

As may be apparent to the reader, we can solve it easily, and we obtain the following solution:

$$y=(B-a{\lambda }_1)exp\left(\frac{-C}{\alpha }{t}^{\alpha }\right)+a{\lambda }_1.$$

Where

$$B=y\left(0\right)={\mathrm{\Pi }}^{1-p}\left(0\right).$$

So, we get

$${\mathrm{\Pi }}^{1-p}=(B-a{\lambda }_1)exp\left(\frac{-C}{\alpha }{t}^{\alpha }\right)+a{\lambda }_1.$$

Then, $\forall t\in \left[0,T\right]$

$$\mathrm{\Pi }\left(t\right)={((B-a{\lambda }_1)exp\left(\frac{-C}{\alpha }{t}^{\alpha }\right)+a{\lambda }_1)}^{\frac{1}{1-p}}.$$

Next, for $\mathrm{\Pi }\to \infty ,$ we give the main result:

$$T^{*}={\left(\frac{\alpha }{a{\lambda }_1\mathrm{\Gamma }\left(2-\alpha \right)\left(1-p\right)}ln\left(1-\frac{{\mathrm{\Pi }}^{1-p}\left(0\right)}{a{\lambda }_1}\right)\right)}^{\frac{1}{\alpha }}.$$

The solution u must blow up. Notice that $\mathrm{\Pi }\left(0\right)\ge 0$, and the initial data are sufficiently large.

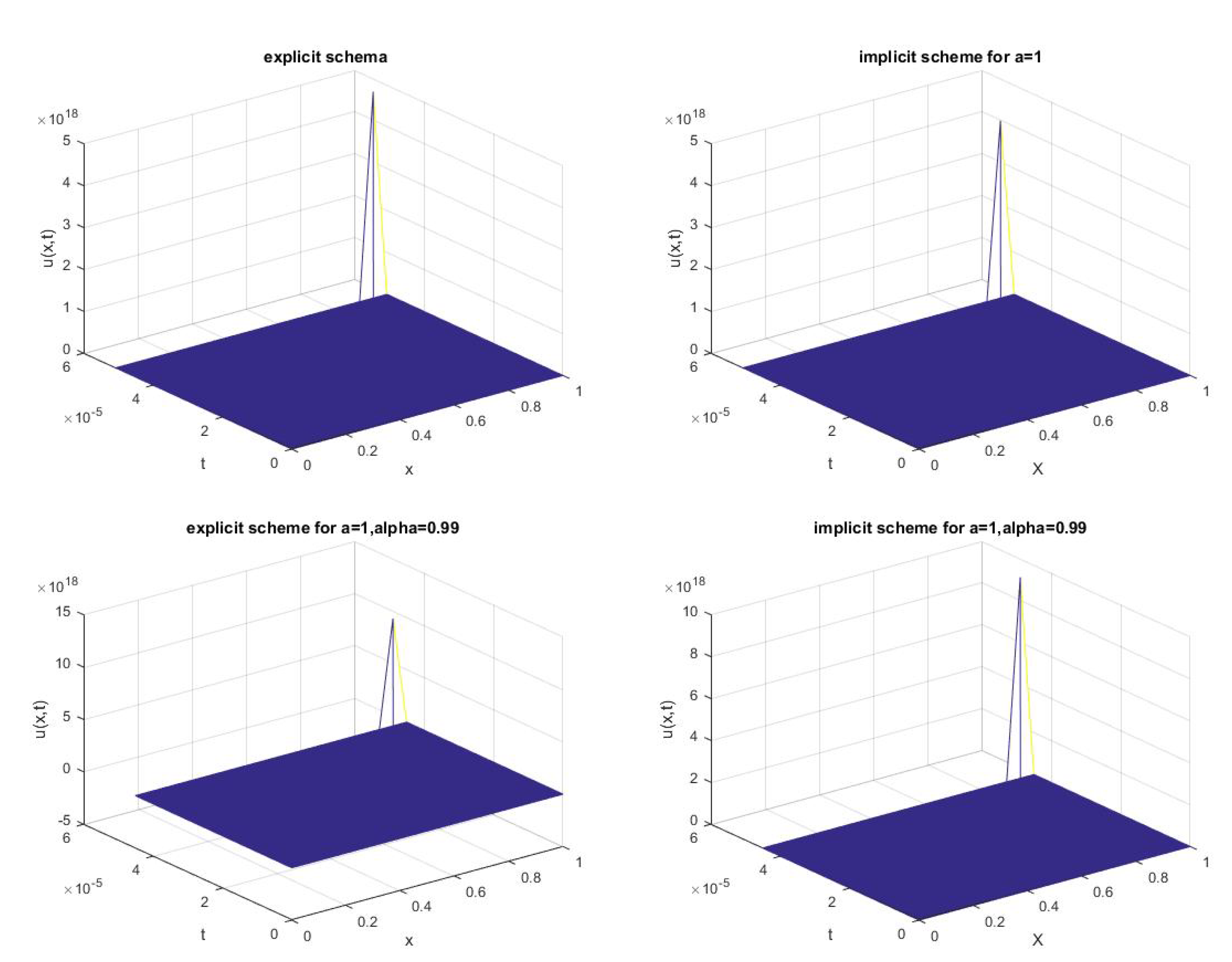
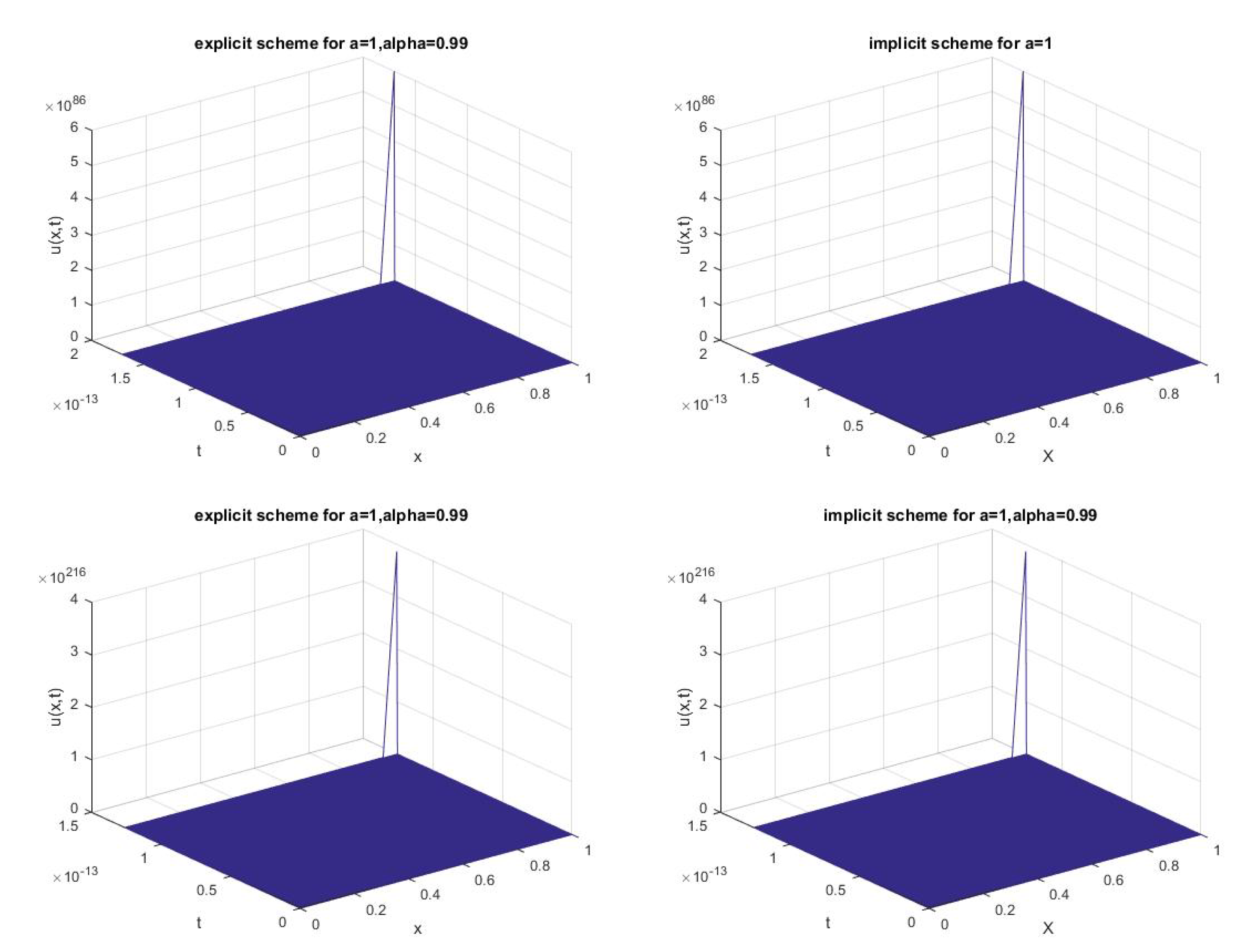
3.2. Numerical Simulation of Explosion Phenomena

Accurately detecting blow-up solutions is a difficult task. Assuming that we can follow the true behavior of the solution with reasonable accuracy, how do we find the blow-up time $T^{*}$? For that reason, the research area is aimed at developing numerical methods that preserve specific properties of fundamental differential equations. Much progress has been made in the field over the past decade.

To establish the numerical approximation scheme, let $\Delta t=\frac{T}{n}$ and $t_k=k\Delta t$, where $k=0,1,\dots ,n$ is the integration time $0\le t_k\le T$. As usual, $\Delta x=\frac{L}{m};$ $x_i=i\Delta x$, where $i=0,\dots ,m$ is the grid size in the spatial direction.

3.2.1. The Explicit Scheme

$$u(x_i,t_{k+1})-u(x_i,t_k)-ru(x_{i-1},t_k)+2ru(x_i,t_k)-ru(x_{i+1},t_k)$$

$$=\Delta t^{\alpha }\mathrm{\Gamma }\left(2-\alpha \right)u^p(x_i,t_k)-\underset{j=1}{\sum ^k}(u(x_i,t_{k-j+1})-u(x_i,t_{k-j}))\times \left[{\left(j+1\right)}^{1-\alpha }-{\left(j\right)}^{1-\alpha }\right].$$

So, we obtain the following scheme:

$$\begin{array}{ccc}\hfill u(x_i,t_{k+1})& =& (1-2r)u(x_i,t_k)+ru(x_{i-1},t_k)+ru(x_{i-1},t_k)\hfill \\ & & -\underset{j=1}{\sum ^k}(u(x_i,t_{k-j+1})-u(x_i,t_{k-j}))\times \left[{\left(j+1\right)}^{1-\alpha }-{\left(j\right)}^{1-\alpha }\right]+\Delta t^{\alpha }\mathrm{\Gamma }\left(2-\alpha \right)u^p(x_i,t_k).\hfill \end{array}$$

3.2.2. The Linear Implicit Scheme

$$\begin{array}{ccc}& & \frac{\Delta t^{-\alpha }}{\mathrm{\Gamma }\left(2-\alpha \right)}\underset{j=0}{\sum ^k}(u(x_i,t_{k-j+1})-u(x_i,t_{k-j}))\times \left[{\left(j+1\right)}^{1-\alpha }-{\left(j\right)}^{1-\alpha }\right]\hfill \\ & & -\frac{u(x_{i-1},t_{k+1})-u(x_i,t_{k+1})+u(x_{i+1},t_{k+1})}{\Delta x^2}\hfill \\ & =& u^p(x_i,t_k).\hfill \end{array}$$

Then, by putting $r=\frac{\Delta t^{\alpha }\mathrm{\Gamma }\left(2-\alpha \right)}{\Delta x^2},$ we get

$$\begin{array}{ccc}& & \underset{j=0}{\sum ^k}(u(x_i,t_{k-j+1})-u(x_i,t_{k-j}))\times \left[{\left(j+1\right)}^{1-\alpha }-{\left(j\right)}^{1-\alpha }\right]\hfill \\ & & -r\left(u(x_{i-1},t_{k+1})-u(x_i,t_{k+1})+u(x_{i+1},t_{k+1})\right)\hfill \\ & =& \Delta t^{\alpha }\mathrm{\Gamma }\left(2-\alpha \right)u^p(x_i,t_k).\hfill \end{array}$$

So, we get

$$\begin{array}{ccc}& & \left(1+r\right)u(x_i,t_{k+1})-ru(x_{i-1},t_{k+1})-ru(x_{i-1},t_{k+1})\hfill \\ & & =\Delta t^{\alpha }\mathrm{\Gamma }\left(2-\alpha \right)u^p(x_i,t_k)+u(x_i,t_k)-\underset{j=1}{\sum ^k}(u(x_i,t_{k-j+1})-u(x_i,t_{k-j}))\times \left[{\left(j+1\right)}^{1-\alpha }-{\left(j\right)}^{1-\alpha }\right].\hfill \end{array}$$

By using the limit condition

$$\begin{array}{cc}\hfill u(x_0,t_{k+1})& =0\hfill \\ \hfill {\displaystyle \frac{u(x_n,t_{k+1})-u(x_{n-1},t_{k+1})}{h}}& =0\Rightarrow u(x_n,t_{k+1})=u(x_{n-1},t_{k+1}).\hfill \end{array}$$

We write the system in the matrix form:

$$A^{n+1}{U}^{n+1}=B^{n+1},$$

(6)

with

$$A=\left(\begin{array}{ccccccc}0& -r& 0& \dots & 0& 0& 0\\ 0& 1+2r& -r& \dots & 0& 0& 0\\ 0& & \dots & & & & ⋮\\ ⋮& & & & & & 0\\ 0& & & & -r& 1+2r& -r\\ 0& & & & 0& 0& 1+r\end{array}\right)$$

$$U^{k+1}=\left(\begin{array}{c}{u}_1^{k+1}\\ u_2^{k+1}\\ \cdots \\ \dots \\ u_{n-1}^{k+1}\\ u_n^{k+1}\end{array}\right)$$

$$B^{k+1}=\left(\Delta t^{\alpha }\mathrm{\Gamma }\left(2-\alpha \right)u^p(x_i,t_k)+u(x_i,t_k)-\underset{j=1}{\sum ^k}(u(x_i,t_{k-j+1})-u(x_i,t_{k-j}))\times \left[{\left(j+1\right)}^{1-\alpha }-{\left(j\right)}^{1-\alpha }\right]\right)$$

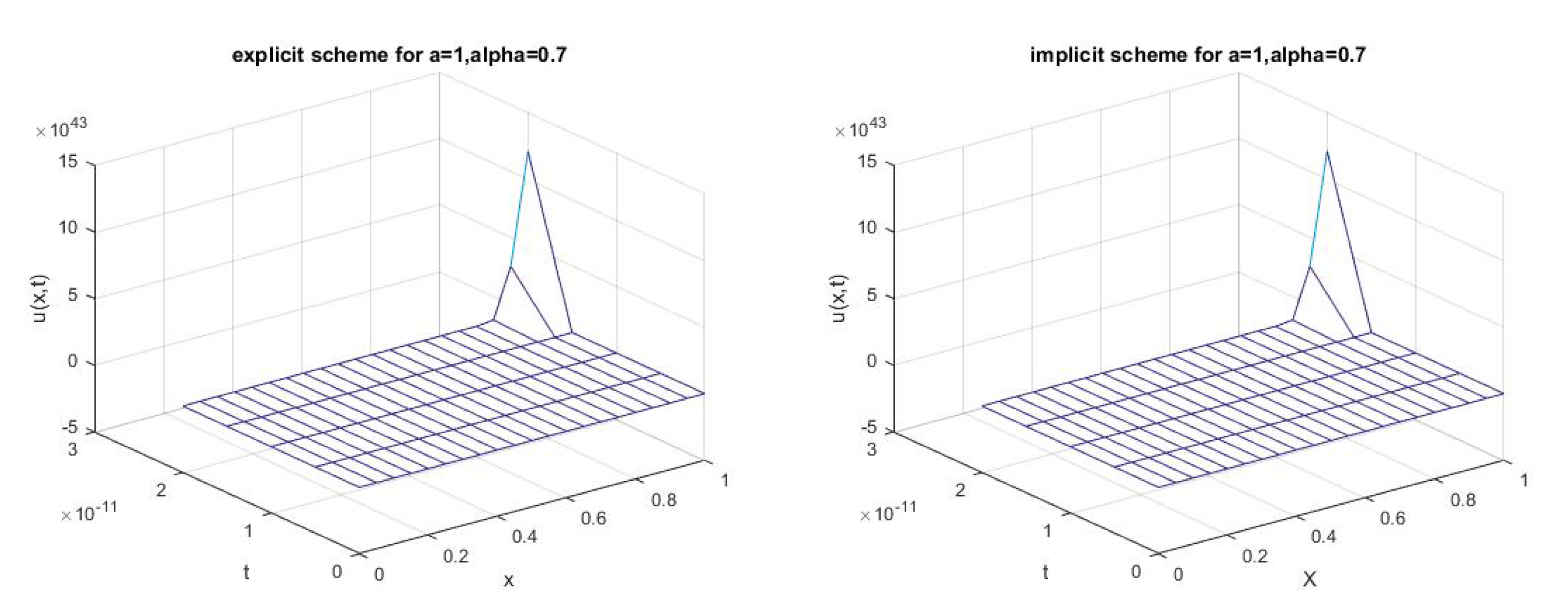
3.3. Numerical Experiment

This is a brief expository presentation of the various approaches to the computational treatment of cases of blow-up problems using two methods: the explicit method and the implicit method. To validate our results, we based them on the following problem:

$$\left\{\begin{array}{ccc}{}^C{D}_t^{\alpha }u-a\Delta u=u^p& & \forall (x,t)\in Q\\ u(x,0)=100sin\left(\frac{\pi }{2}x\right)& & \forall x\in \mathsf{\Omega }\\ u(0,t)=0& & \forall t\in \left[0,T\right]\\ u_x(1,t)=0& & \forall t\in \left[0,T\right]\end{array}\right.$$

(P₂)

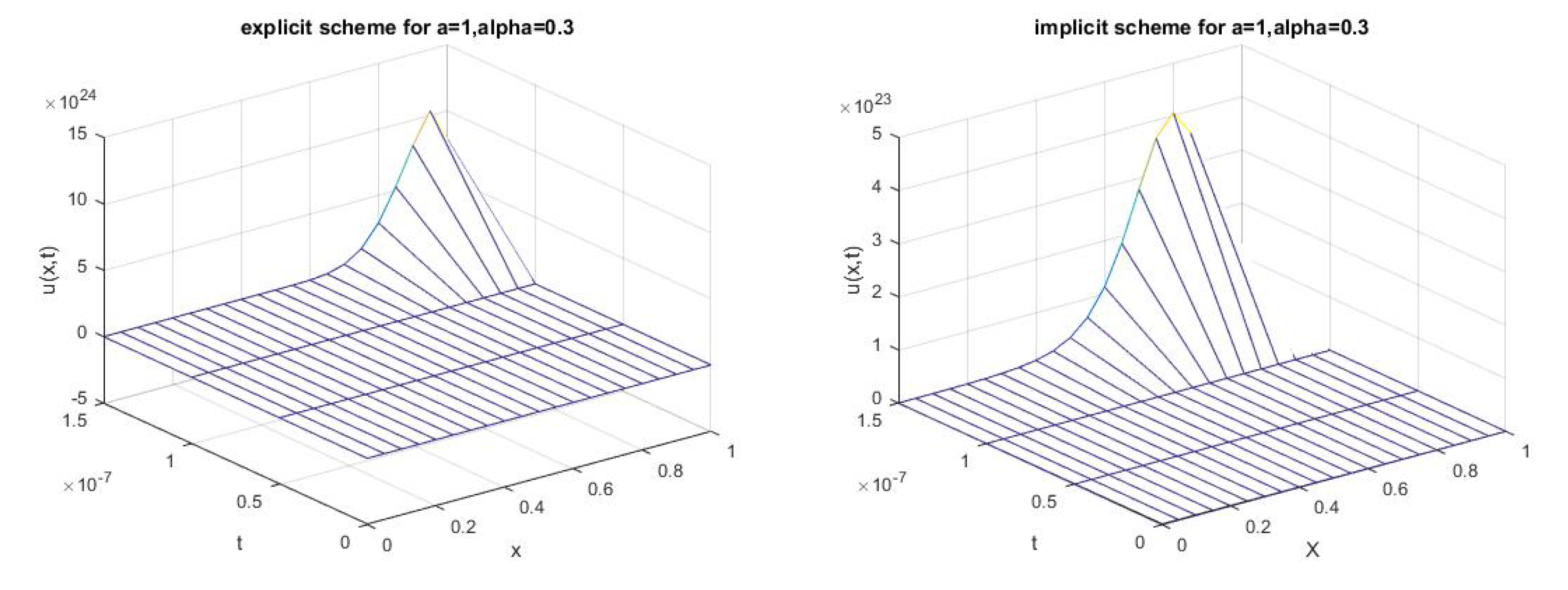
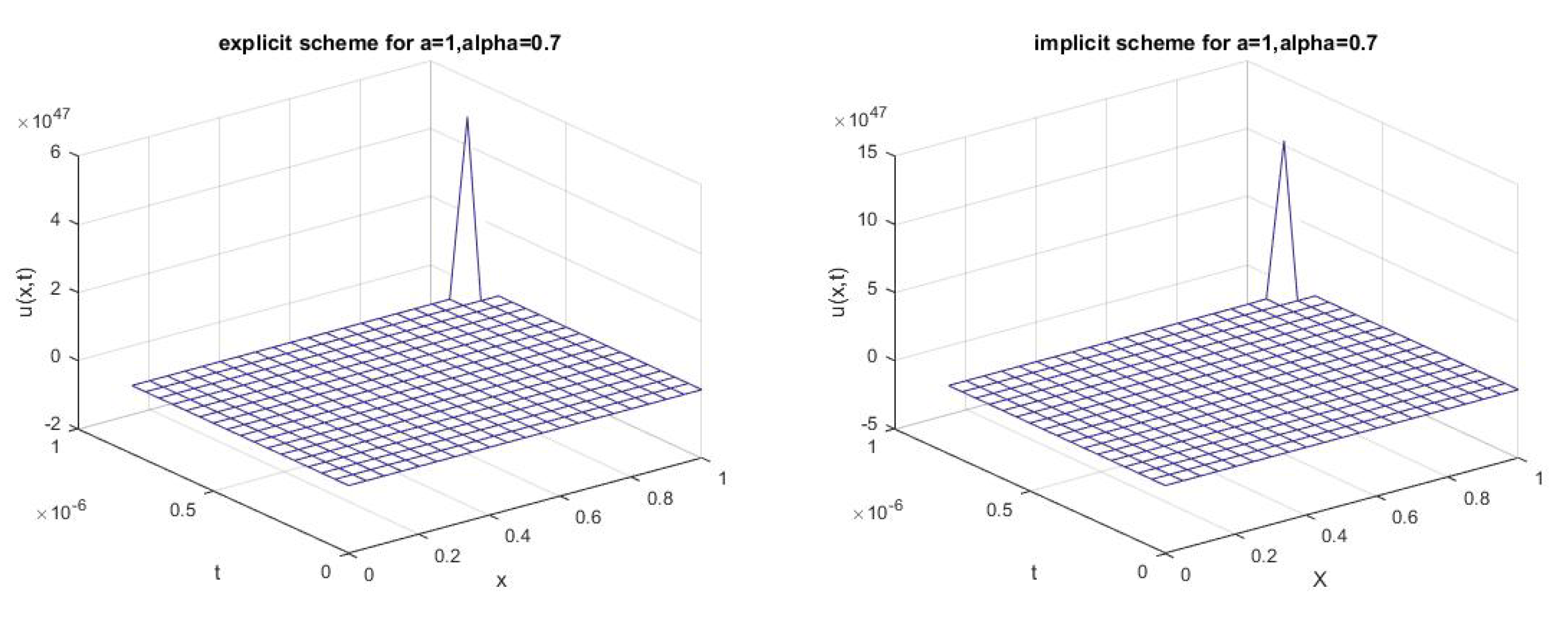
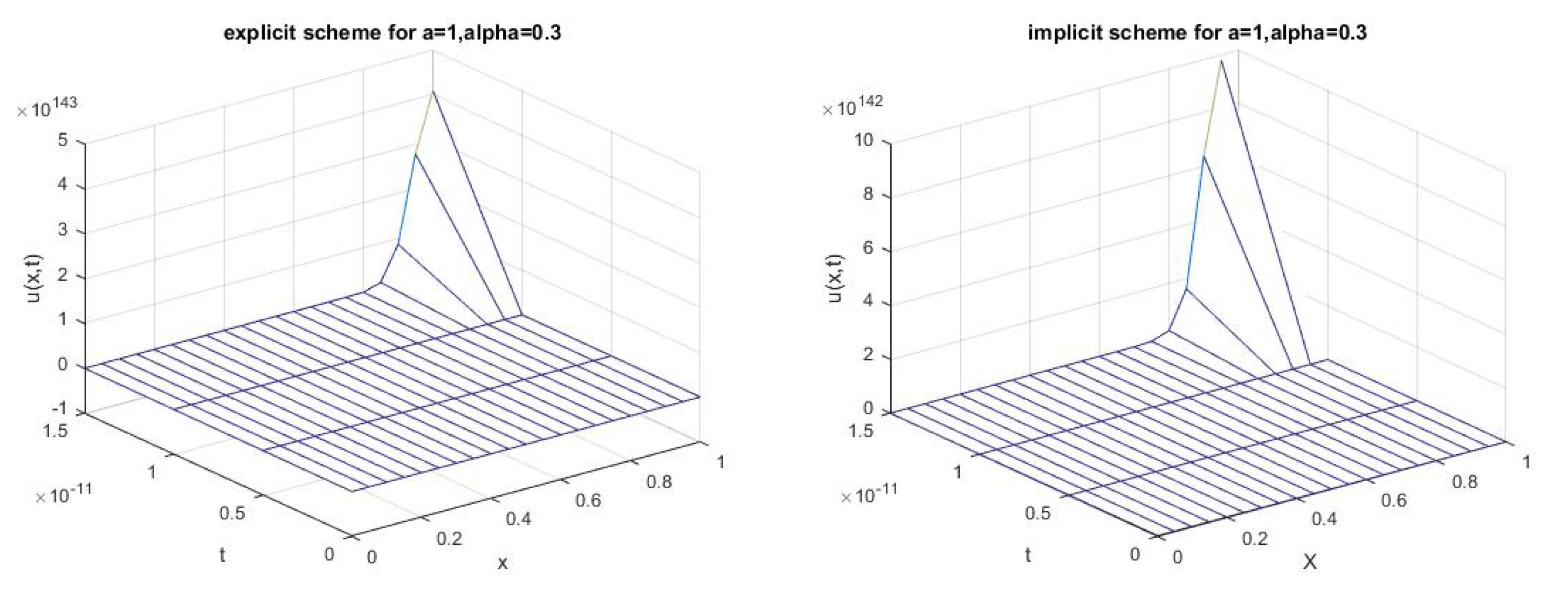
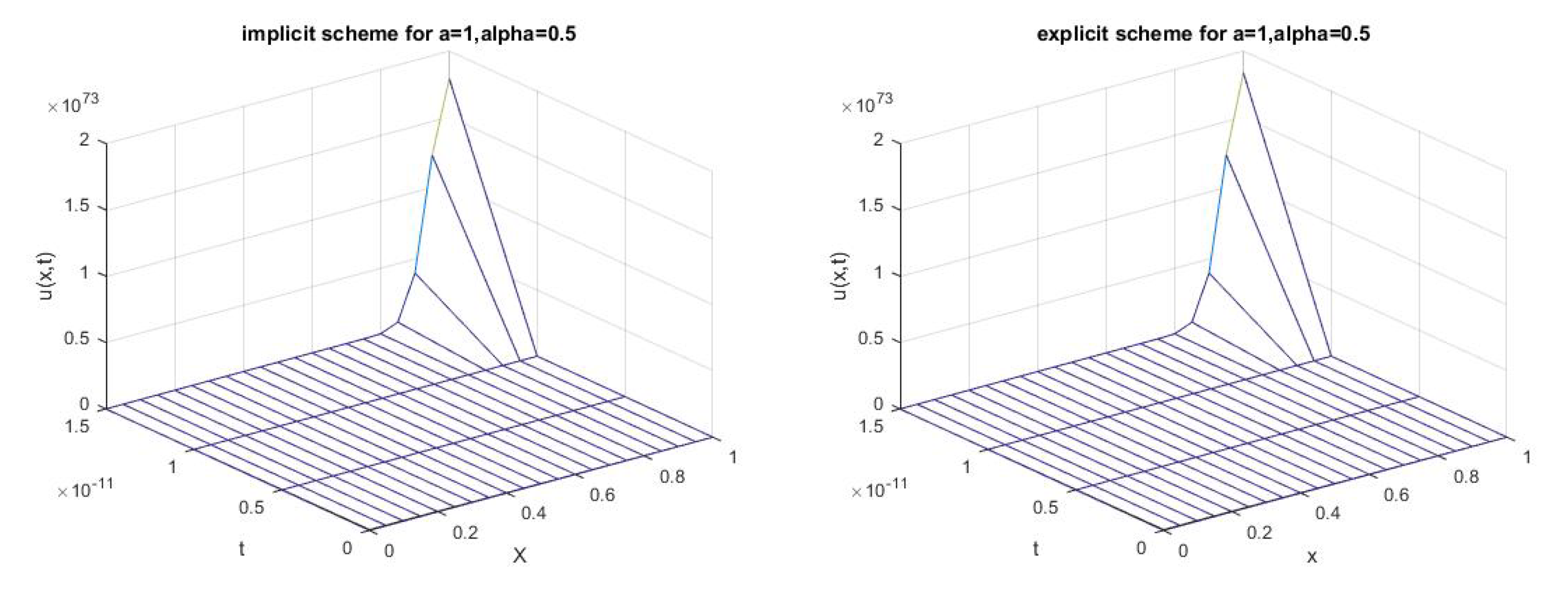
3.3.1. Example 1

By inputting the previous problem $p=3,\alpha =0.3,$ we obtain the following Figure 1:

Then, if we input the problem $\left({\mathrm{P}}_2\right)$ $p=3,\alpha =0.5,$ we obtain the following Figure 2:

Furthermore, we take $p=3,\alpha =0.7$ in the problem (P₂), and we obtain the following Figure 3:

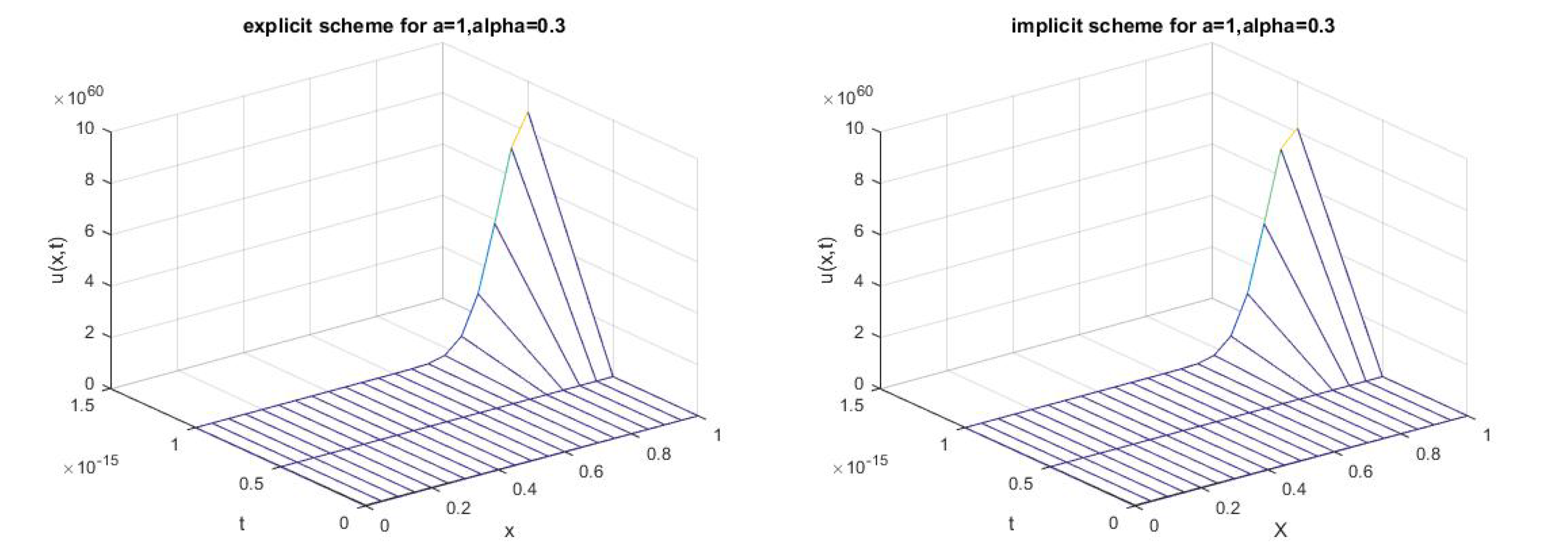
3.3.2. Example 2

By taking $p=5,\alpha =0.3$ in the problem (P₂), we obtain the following Figure 4:

Furthermore, if we take $p=5,\alpha =0.5$ in the problem (P₂), we obtain the following Figure 5:

Then, by putting $p=5,\alpha =0.7$ in the problem (P₂), we obtain the following Figure 6:

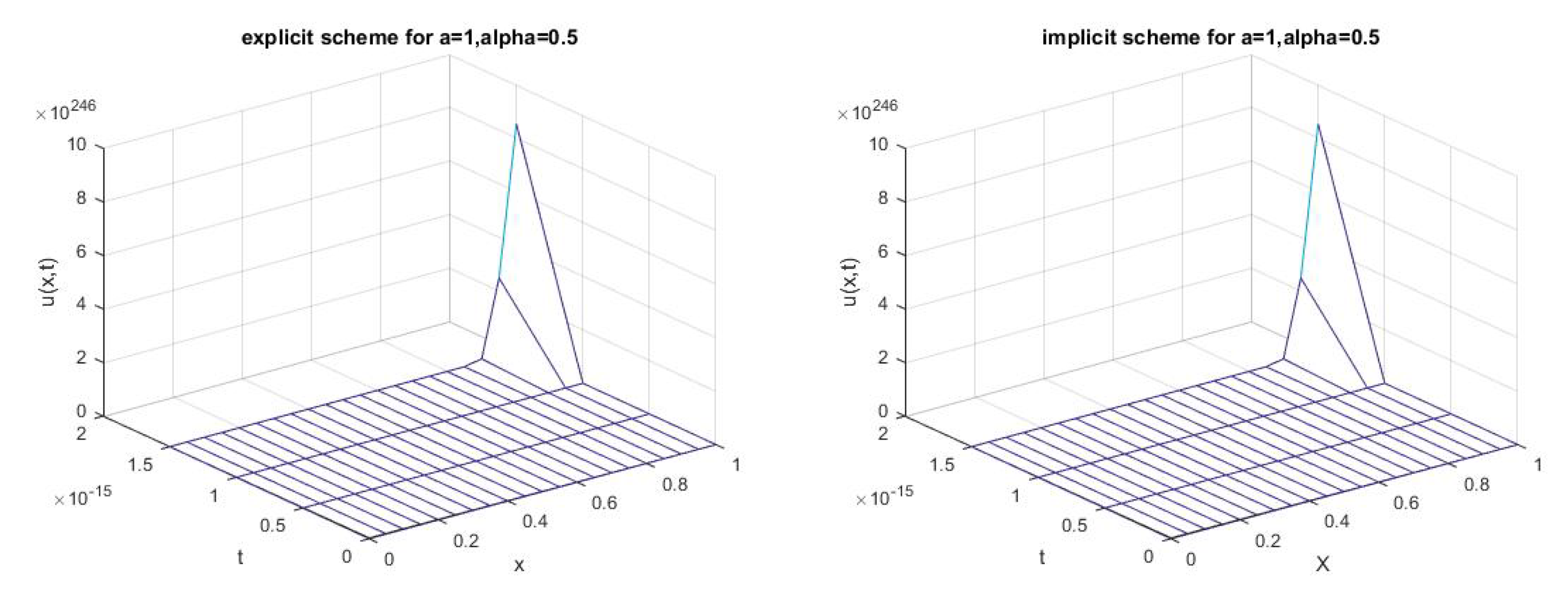
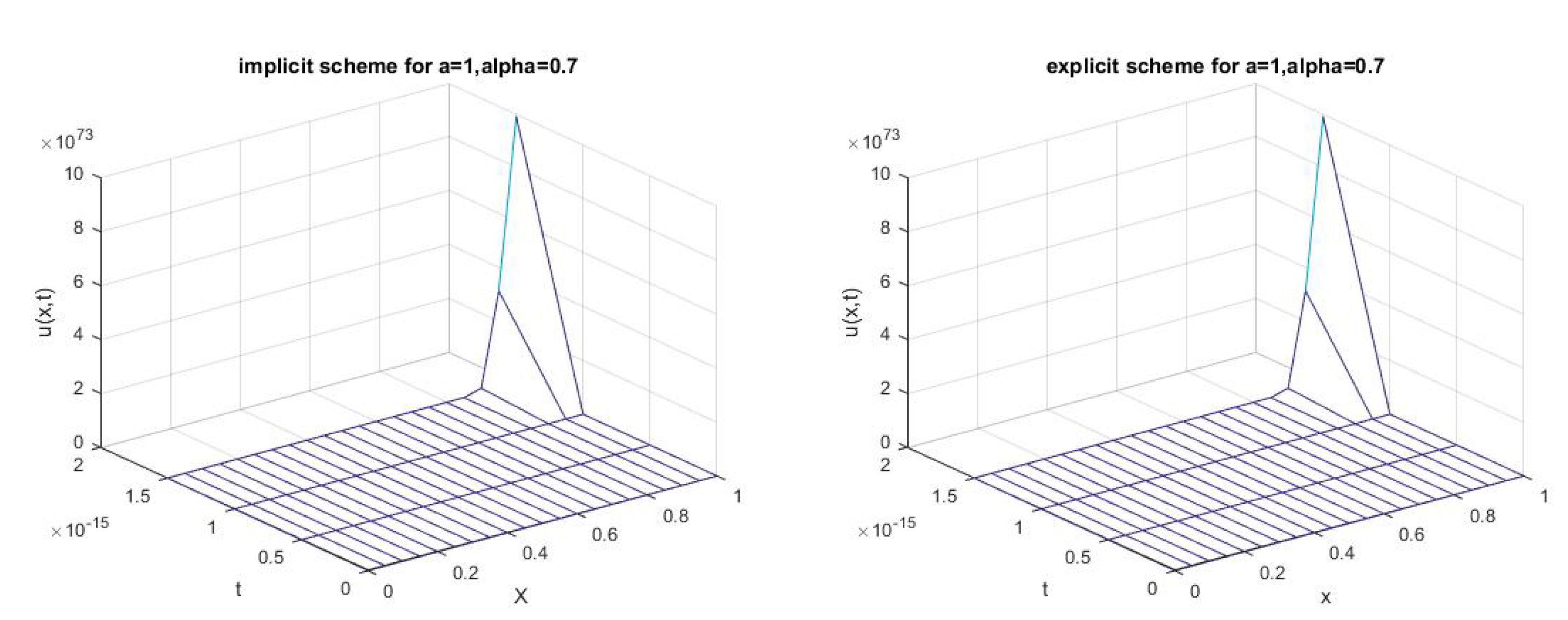
3.3.3. Example 3

By putting $p=7,\alpha =0.3$ in the problem (P₂), we obtain the following Figure 7:

Then, by taking $p=7,\alpha =0.5$ in the problem (P₂), we obtain the following Figure 8:

Furthermore, if we take $p=7,\alpha =0.7$ in the problem (P₂), we obtain the following Figure 9:

4. Comparison Results between Integer and Fractional Problems

This section deals with the comparison of the numerical simulation of the finite-time blow-up solution between the fractional problem (P) where $\alpha \to 1$ and the following classical problem:

$$\left\{\begin{array}{ccc}{u}_t-a\Delta u=u^p& & \forall (x,t)\in Q\\ u(x,0)=\phi \left(x\right)& & \forall x\in \mathsf{\Omega }\\ u(0,t)=0& & \forall t\in \left[0,T\right]\\ u_x(1,t)=0& & \forall t\in \left[0,T\right]\end{array}\right.$$

(P_c)

By using the same eigenvalue problem in the second section and applying the Kaplan method, we obtain that the finite-time blow-up of the classical problem (P_c) is given by

$$T_c^{*}=\frac{ln\left(\frac{1}{a{\lambda }_1{\left(\mathrm{\Pi }(0\right)}^{1-p}}\right)}{\left(p-1\right)a{\lambda }_1}.$$

We know that $\alpha$ has an impact on the finite-time blow-up; this prompted us to investigate a combination between $\alpha$ as a fraction between 0 and 1 $\left(0〈\alpha 〈1\right)$. For this, we plan to add the numerical results to the research as well as the real difference between the fractional and integer time derivatives where $\alpha \to 1$.

We chose $\alpha =\frac{99}{100},$ for the same last example (P₂) where we show the comparison of the finite-time blow-up solution between the fractional problem (P₂) with $\alpha =\frac{99}{100}$ and the following classical problem:

$$\left\{\begin{array}{ccc}{u}_t-a\Delta u=u^p& & \forall (x,t)\in Q\\ u(x,0)=100sin\left(\frac{\pi }{2}x\right)& & \forall x\in \mathsf{\Omega }\\ u(0,t)=0& & \forall t\in \left[0,T\right]\\ u_x(1,t)=0& & \forall t\in \left[0,T\right]\end{array}\right.$$

(P_ce)

For the following different examples:

4.1. Comparison Example 1

By putting $p=3$ in the problem (P₂) and $\alpha =\frac{99}{100}$ in the problem (P_ce), we obtain the following Figure 10:

4.2. Comparison Example 2

For $p=5$, $\alpha \to 1$ and $\alpha =0.99$, we obtain the following Figure 11:

4.3. Comparison Example 3

For $p=7$, $\alpha \to 1$ and $\alpha =0.99$, we obtain the following Figure 12:

5. Conclusions

In this work, we developed some prior findings on the blow-up phenomena in fractional reaction–diffusion problems that incorporate a positive power of the unknown variable in the equation. The finite-time blow-up solution is shown numerically, and the behavior solution of the fractional problem is also shown. This article underscores the pivotal role of the exponent $\alpha$ in defining the finite-time blow-up phenomenon in conjunction with the power p and the initial condition. The interdependence of these factors necessitates careful consideration and analysis when studying nonlinear problems. Finally, to confirm and validate the efficiency of the obtained results, we present some numerical examples and compare them to the classical problem with integer order. Future research should continue to explore and refine our understanding of these relationships, leading to further advancements in the field of fractional partial differential equations and their applications. This would certainly help to implement the finite-time blow-up phenomenon in the financial and economic fields.