Global Stability and Bifurcation Analysis of a Virus Infection Model with Nonlinear Incidence and Multiple Delays

Abstract

In order to investigate the impact of general nonlinear incidence, cellular infection, and multiple time delays on the dynamical behaviors of a virus infection model, a within-host model describing the virus infection is formulated and studied by taking these factors into account in a single model. Qualitative analysis of the global properties of the equilibria is carried out by utilizing the methods of Lyapunov functionals. The existence and properties of local and global Hopf bifurcations are discussed by regarding immune delay as the bifurcation parameter via the normal form, center manifold theory, and global Hopf bifurcation theorem. This work reveals that the immune delay is mainly responsible for the existence of the Hopf bifurcation and rich dynamics rather than the intracellular delays, and the general nonlinear incidence does not change the global stability of the equilibria. Moreover, ignoring the cell-to-cell infection may underevaluate the infection risk. Numerical simulations are carried out for three kinds of incidence function forms to show the rich dynamics of the model. The bifurcation diagrams and the identification of the stability region show that increasing the immune delay can destabilize the immunity-activated equilibrium and induce a Hopf bifurcation, stability switches, and oscillation solutions. The obtained results are a generalization of some existing models.

1. Introduction

Human immunodeficiency virus (HIV) is regarded as one of the major threats to the health of human society and is an important research topic in the field of public health. In recent years, an increasing number of scholars have investigated the dynamic behaviors of HIV infection models by incorporating the different factors that impact the infection procedure. The analysis and understanding of the dynamical behaviors of HIV in the host by modeling HIV infection plays an important role in exploring the mechanism of virus infection. The classical virus infection model is composed of three components: uninfected cells, infected T-cells, and the virus [1]. As the research progresses, improved models have been proposed by many researchers (see [2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17] and the references therein).

During the process of HIV infection, it takes some time for the initial virus to enter the target cells and for the subsequent viral latency, as well as for infected CD4+ T cells to release infectious free virus particles. Moreover, because of the presence of latently infected cells, HIV cannot be completely eradicated and can be reactivated, continuing to replicate even after antiviral therapy. Thus, this may be an important reason for explaining the failure to eradicate HIV virus infection. In addition, time is needed during the activation procedure of latent cells; thus, there exists a time delay for latent cells to be activated and converted to infected cells [15,18]. Motivated by the above facts, dynamical models with intracellular delays and latency have been investigated (see [11,14,15,16,19,20,21] and the references therein).

As we know, the main two primary immunity modes are humoral and cellular immunity, which are dominated by B cells and cytotoxic T lymphocytes (CTLs), respectively. In virus infections, cellular immunity is reduced by CTLs attacking the infected cells, whereas the B-cell immune response is prevalent during viral infections by attacking the viruses. Both modes are regarded as an important path of eliminating or controlling viral gain when HIV invades the human body. The investigation of the two modes of immune response using viral infection models has received attention from many researchers (see [2,4,5,10,19,22,23,24] and the references therein). However, it is not clear which immune response mode is the most effective one. The existing literature on malaria infection shows that the humoral immune response is more effective compared to the cellular immune response [25]. Thus, the humoral immunity response is considered in the current study. Admittedly, an effective immune response requires the combination of humoral and cellular immunity due to the fact that the humoral immune response alone may not eradicate the infection [26].

In addition, viral stimulation of antigens also requires some time to generate an effective humoral immune response. Studies have been conducted that analyzed the effect of humoral immune delay on the equilibrium stability of viral infection models (see [6,16,27,28] and the references therein). The results have shown that the dynamics of the models incorporating immune delays become more complex, and the existence of time delays can destabilize the steady state and result in Hopf bifurcation, or even chaos solutions, in the corresponding models. However, what the dynamics will be when taking both the intracellular delay and immune response delay into account in a single model remains unknown. The answer will be addressed in this study.

Note that most classical models of disease transmission assume a bilinear incidence (see [2,3,4,5,6] and the references therein). Recent theoretical studies have shown that a nonlinear incidence is more realistic, and a general incidence rate may help us gain a unification theory by omitting unessential details. Common nonlinear incidences include saturated incidence [7,8,9,10,11], Beddington–DeAngelis incidence (B-D) [12,13,14,15,16], and Ivlev functional response functions [29,30,31,32,33], among others. For example, Wang et al. [14] considered the following delayed virus infection model with a B-D incidence rate

$$\left\{\begin{array}{c}{T}^{\prime }\left(t\right)=\lambda -d_{1}T\left(t\right)+\gamma T\left(t\right)(1-\frac{T\left(t\right)}{T_{max}})-\frac{\beta T\left(t\right)V\left(t\right)}{1+aT\left(t\right)+bV\left(t\right)},\hfill \\ L^{\prime }\left(t\right)=\frac{\eta e^{-m{\tau }_1}\beta T(t-{\tau }_1)V(t-{\tau }_1)}{1+aT(t-{\tau }_1)+bV(t-{\tau }_1)}-\alpha L\left(t\right)-d_{2}L\left(t\right),\hfill \\ I^{\prime }\left(t\right)=\frac{(1-\eta )e^{-m{\tau }_2\beta T(t-{\tau }_2)V(t-{\tau }_2)}}{1+aT(t-{\tau }_2)+bV(t-{\tau }_2)}+\alpha L\left(t\right)-d_{3}I\left(t\right),\hfill \\ V^{\prime }\left(t\right)=kI(t-{\tau }_3)-d_{4}V\left(t\right),\hfill \end{array}\right.$$

(1)

where $T\left(t\right)$, $L\left(t\right)$, $I\left(t\right)$, and $V\left(t\right)$ denote the concentrations of the uninfected cells, latently infected T-cells, actively infected T-cells, and the virus at time t, respectively. The sufficient condition for the global dynamics of Model (1) was presented utilizing the Lyapunov method. However, whether the delay can lead to bifurcation was not discussed in the paper. For the details of Model (1), one can refer to [14].

Recently, the literature has implied that the HIV infection mode within the host has another important mechanism, i.e., cell-to-cell infection, in addition to virus-to-cell infection. It has been found that cell-to-cell infection is a more potent and efficient way of virus propagation than the virus-to-cell infection mode [34,35,36,37,38]. Motivated by this fact, models incorporating cell-to-cell infection have been proposed and studied by many researchers (see [5,20,39,40,41,42,43,44,45,46,47] and the references therein). Note that only virus-to-cell infection was considered and the B-cell immune response in the host was ignored in Model (1). However, the B-cell immune response plays a key role in the immune response by detecting and eliminating HIV virus particles during infection. Thus, motivated by [6,14,16], we consider a delayed virus infection model incorporating general nonlinear incidence and humoral immunity in line with Model (1). In addition, two infection mechanisms are taken into consideration in the model. Therefore, the model takes the form:

$$\left\{\begin{array}{cc}\hfill T^{\prime }\left(t\right)=& \lambda -{\beta }_{1}f\left(V\left(t\right)\right)T\left(t\right)-{\beta }_{2}g\left(I\left(t\right)\right)T\left(t\right)-d_{1}T\left(t\right),\hfill \\ \hfill L^{\prime }\left(t\right)=& \eta ({\beta }_{1}f\left(V(t-{\tau }_1)\right)T(t-{\tau }_1)+{\beta }_{2}g\left(I(t-{\tau }_1)\right)T(t-{\tau }_1))-\alpha L\left(t\right)-d_{2}L\left(t\right),\hfill \\ \hfill I^{\prime }\left(t\right)=& (1-\eta )({\beta }_{1}f\left(V(t-{\tau }_2)\right)T(t-{\tau }_2)+{\beta }_{2}g\left(I(t-{\tau }_2)\right)T(t-{\tau }_2))\hfill \\ \hfill & +\alpha L(t-{\tau }_3)-d_{3}I\left(t\right),\hfill \\ \hfill V^{\prime }\left(t\right)=& kI(t-{\tau }_4)-pV\left(t\right)B\left(t\right)-d_{4}V\left(t\right),\hfill \\ \hfill B^{\prime }\left(t\right)=& qV(t-{\tau }_5)B(t-{\tau }_5)-d_{5}B\left(t\right),\hfill \end{array}\right.$$

(2)

where $B\left(t\right)$ denotes the concentrations of the B cells at time t. Infected cells in the host stimulate B-cell production at a rate of $qVB$, and free virus particles are cleared by antibodies at a rate of $pVB$. $d_5$ is the mortality rate of the B cells, ${\beta }_1$ is the rate of virus-to-cell infection, ${\beta }_2$ is the rate of cell-to-cell infection, ${\tau }_3$ is the time delay for latent infected cells to become active infected cells, and ${\tau }_5$ is the time delay of the activation of the B-cell immune system. The other parameters have the same meanings as in Model (1) (see [14]). Here, the incidences are assumed to be the nonlinear forms ${\beta }_{1}Tf\left(V\right)$ and ${\beta }_{2}Tg\left(I\right)$, respectively, and $f\left(V\right)$ and $g\left(I\right)$ satisfy the following properties

$$\begin{array}{c}\hfill f\left(0\right)=g\left(0\right)=0,f^{\prime }\left(V\right)>0,g^{\prime }\left(I\right)>0,f^{″}\left(V\right)\le 0,g^{″}\left(I\right)\le 0.\end{array}$$

(3)

In line with (3), one can obtain

$$\begin{array}{c}\hfill f^{\prime }\left(V\right)V\le f\left(V\right)\le f^{\prime }\left(0\right)V,g^{\prime }\left(I\right)I\le g\left(I\right)\le g^{\prime }\left(0\right)I,forI,V\ge 0.\end{array}$$

(4)

Assume that Model (2) satisfies the following initial condition

$$\begin{array}{cc}\hfill & T\left(\theta \right)={\psi }_1\left(\theta \right),L\left(\theta \right)={\psi }_2\left(\theta \right),I\left(\theta \right)={\psi }_3\left(\theta \right),V\left(\theta \right)={\psi }_4\left(\theta \right),B\left(\theta \right)={\psi }_5\left(\theta \right),\hfill \\ \hfill & {\psi }_i\left(\theta \right)\ge 0,\theta \in [-\tau ,0],\tau =max\left\{{\tau }_1,{\tau }_2,{\tau }_3,{\tau }_4,{\tau }_5\right\},i=1,2,3,4,5,\hfill \end{array}$$

(5)

where $({\psi }_1\left(\theta \right),{\psi }_2\left(\theta \right),{\psi }_3\left(\theta \right),{\psi }_4\left(\theta \right),{\psi }_5\left(\theta \right))\in C([-\tau ,0],{\mathbb{R}}_{+}^5)$.

The rest of the paper is organized as follows. In Section 2, we present some basic results, including the existence of equilibria and the positivity and boundedness of the solutions for Model (5). In Section 3, both the global stability of all equilibria of Model (5) and the existence of local and global Hopf bifurcations are investigated. Moreover, the properties of the Hopf bifurcation solutions are analyzed by applying the normal form and center manifold theory. Some numerical simulations are carried out in Section 4. The summary in Section 5 concludes the paper.

2. Preliminary Results

Before analyzing the dynamical behaviors of the model, we first present some preliminary results. According to the results presented in [48], the solution of Model (2) with initial conditions (5) is non-negative. In the following, we show the boundedness of the solution. From the first equation in Model (2), a simple calculation yields

$$\begin{array}{c}\hfill \underset{t\to \infty }{lim\; sup}T\left(t\right)\le T_0=\frac{\lambda }{d_1}.\end{array}$$

We define $P\left(t\right)=\eta T(t-{\tau }_1-{\tau }_3)+(1-\eta )T(t-{\tau }_2)+L(t-{\tau }_3)+I\left(t\right)+\frac{d_3}{2k}V(t+{\tau }_4)+\frac{p{d}_3}{2kq}B(t+{\tau }_4+{\tau }_5).$ The derivation of $P\left(t\right)$ yields

$$\begin{array}{cc}\hfill P^{\prime }\left(t\right)=& \lambda -d_1\eta T(t-{\tau }_1-{\tau }_3)-d_1(1-\eta )T(t-{\tau }_2)-d_{2}L(t-{\tau }_3)-\frac{d_3}{2}I\left(t\right)-\frac{d_3{d}_4}{2k}V(t+{\tau }_4)\hfill \\ & -\frac{p{d}_3{d}_5}{2kq}B(t+{\tau }_4+{\tau }_5)\le \lambda -dP\left(t\right),\hfill \end{array}$$

where $d=min\left\{d_1,d_2,\frac{d_3}{2},d_4,d_5\right\}$. Thus, $\underset{t\to +\infty }{lim\; sup}P\left(t\right)\le \frac{\lambda }{d}$, which implies that $T\left(t\right)$, $L\left(t\right)$, $I\left(t\right)$, $V\left(t\right)$, and $B\left(t\right)$ are bounded. Based on the above analysis, we have the following result.

Theorem 1.

The solutions $\left(T\right(t),L(t),I(t),V(t),B(t\left)\right)$ of Model (2) with initial conditions (5) are non-negative and ultimately bounded for all $t\ge 0$.

Based on the above discussion, it is reasonable to suppose that there exists a positive constant $M>0$ such that $T\le T_0$, L, I, V, $B\le M$ for large t. Thus, in the following, we analyze the dynamic behaviors of Model (2) in a bounded feasible region, which is given by

$$\begin{array}{c}\hfill \mathrm{\Gamma }=\left\{X=(T,L,I,V,B):T\le T_0,L,I,V,B\le M\right\}.\end{array}$$

In the following, we show the existence of equilibria for Model (2), including the infection-free equilibrium $E_0=(T_0,0,0,0,0)$ (i.e., no infection exists), immunity-inactivated equilibrium $E_1=(T_1,L_1,I_1,V_1,0)$ (i.e., the immune response has not been activated), and immunity-activated equilibrium $E_2=(T_2,L_2,I_2,V_2,B_2)$ (i.e., immune response has been activated and coexists with the virus). For convenience, we denote $D_1=\frac{\alpha \eta }{\alpha +d_2}+(1-\eta )$. Obviously, Model (2) always has an infection-free equilibrium $E_0=(T_0,0,0,0,0)$, where $T_0=\frac{\lambda }{d_1}$. This is the only biologically meaningful equilibrium if ${\mathfrak{R}}_0=\frac{T_0{D}_1(k{\beta }_1{f}^{\prime }\left(0\right)+{\beta }_2{d}_4{g}^{\prime }\left(0\right))}{d_3{d}_4}\le 1$, which is the basic reproduction number. It follows from the expression of the basic reproduction number ${\mathfrak{R}}_0$ that neglecting either the virus-to-cell infection or the cell-to-cell infection may underevaluate the infection risk. Any other equilibrium $E_i=(T_i,L_i,I_i,V_i,B_i)$ ($i=1,2$) in Model (2) is determined using the following equations.

$$\begin{array}{cc}\hfill & \lambda =d_{1}T+{\beta }_{1}Tf\left(V\right)+{\beta }_{2}Tg\left(I\right),\hfill \\ \hfill & \eta ({\beta }_{1}Tf\left(V\right)+{\beta }_{2}Tg\left(I\right))=\alpha L+d_{2}L,\hfill \\ \hfill & (1-\eta )({\beta }_{1}Tf\left(V\right)+{\beta }_{2}Tg\left(I\right))=d_{3}I-\alpha L,\hfill \\ \hfill & d_{4}V+pVB=kI,\hfill \\ \hfill & (qV-d_5)B=0.\hfill \end{array}$$

(6)

When $B_1=0$ and $V_1\ne 0$, it follows from (6) that

$$\begin{array}{cc}\hfill & \lambda -d_1{T}_1={\beta }_1{T}_{1}f\left(V_1\right)+{\beta }_2{T}_{1}g\left(I_1\right)=\frac{d_3{I}_1}{D_1},\hfill \\ \hfill & V_1=\frac{k{I}_1}{d_4},L_1=\frac{\eta }{\alpha +d_2}({\beta }_1{T}_{1}f\left(V_1\right)+{\beta }_2{T}_{1}g\left(I_1\right)).\hfill \end{array}$$

(7)

In order to have $T_1>0$ and $I_1>0$ at equilibrium, we must have $I_1\in (0,\frac{\lambda D_1}{d_3})$. From the first equation in (7), we have $T_1=\frac{d_3{I}_1}{D_1({\beta }_{1}f(\frac{k{I}_1}{d_4})+{\beta }_{2}g(I_1))}$, and then substituting $T_1$ into the first equation in (6) yields

$$\begin{array}{c}\hfill -\lambda =-\frac{d_{3}I}{D_1}-\frac{d_1{d}_{3}I}{D_1({\beta }_{1}f\left(\frac{kI}{d_4}\right)+{\beta }_{2}g\left(I\right))}=:H\left(I\right).\end{array}$$

For all $I>0$, it follows from (4) that

$$\begin{array}{c}\hfill H^{\prime }\left(I\right)=-\frac{d_1{d}_3({\beta }_1(f\left(\frac{kI}{d_4}\right)-\frac{kI}{d_4}{f}^{\prime }\left(\frac{kI}{d_4}\right))+{\beta }_2(g\left(I\right)-I{g}^{\prime }\left(I\right)))}{D_1{({\beta }_{1}f\left(V\right)+{\beta }_{2}g\left(\frac{d_{4}V}{k}\right))}^2}-\frac{d_3}{D_1}<0.\end{array}$$

Further, from (3), we have

$$\begin{array}{cc}\hfill \underset{I\to 0^{+}}{lim}H\left(I\right)=& -\frac{d_1{d}_3{d}_4}{k{\beta }_1{D}_1{f}^{\prime }\left(0\right)+{\beta }_2{d}_4{D}_1{g}^{\prime }\left(0\right)}=-\frac{\lambda }{{\mathfrak{R}}_0},\hfill \\ \hfill H\left(\frac{\lambda D_1}{d_3}\right)=& -\lambda -\frac{\lambda d_1}{{\beta }_{1}f\left(\frac{\lambda k{D}_1}{d_3{d}_4}\right)+{\beta }_{2}g\left(\frac{\lambda D_1}{d_3}\right)}<-\lambda .\hfill \end{array}$$

This implies that the immunity-inactivated equilibrium $E_1=(T_1,L_1,I_1,V_1,B_1)$ exists only if ${\mathfrak{R}}_0>1$.

When $B_2\ne 0$, a simple calculation from (6) implies that

$$\begin{array}{c}\hfill \lambda -d_1{T}_2={\beta }_1{T}_{2}f\left(V_2\right)+{\beta }_2{T}_{2}g\left(I_2\right)=\frac{d_3}{D_1}{I}_2,V_2=\frac{d_5}{q},\\ \hfill L_2=\frac{\eta d_3}{\alpha +(1-\eta )d_2}{I}_2,B_2=\frac{k{I}_2-d_4{V}_2}{p{V}_2}=\frac{d_4}{p}({\mathfrak{R}}_1-1),\end{array}$$

(8)

where ${\mathfrak{R}}_1=\frac{kq{D}_1}{d_3{d}_4{d}_5}({\beta }_1{T}_{2}f\left(V_2\right)+{\beta }_2{T}_{2}g\left(I_2\right))$. In order to have $T_2>0$ and $I_2>0$, we must have $I_2\in (0,\frac{\lambda D_1}{d_3})$. From the first equation in (8), we have

$$\begin{array}{c}\hfill T_2=\frac{d_3{I}_2}{D_1({\beta }_{1}f\left(\frac{d_5}{q}\right)+{\beta }_{2}g\left(I_2\right))},\end{array}$$

(9)

then, substituting $T_2$ into the first equation in (6) leads to

$$\begin{array}{c}\hfill 0=\lambda -\frac{d_1{d}_{3}I}{D_1({\beta }_{1}f\left(\frac{d_5}{q}\right)+{\beta }_{2}g\left(I\right))}-\frac{d_{3}I}{D_1}=:F\left(I\right).\end{array}$$

(10)

For all $I>0$, from (4), we can obtain

$$\begin{array}{c}\hfill F^{\prime }\left(I\right)=-\frac{d_1{d}_3{\beta }_{1}f\left(\frac{d_5}{q}\right)+d_1{d}_3{\beta }_2(g\left(I\right)-I{g}^{\prime }\left(I\right))}{D_1{({\beta }_{1}f\left(\frac{d_5}{q}\right)+{\beta }_{2}g\left(I\right))}^2}-\frac{d_3}{D_1}<0.\end{array}$$

Further, from (3), $F\left(0\right)=\lambda >0$ and $F\left(\frac{\lambda D_1}{d_3}\right)=-\frac{\lambda d_1}{{\beta }_{1}f\left(\frac{d_5}{q}\right)+{\beta }_{2}g\left(\frac{\lambda D_1}{d_3}\right)}<0$. Then, there exists a unique $I_2\in (0,\frac{\lambda D_1}{d_3})$ such that $F\left(I_2\right)=0$. This implies that the immunity-activated equilibrium $E_2=(T_2,L_2,I_2,V_2,B_2)$ exists only if ${\mathfrak{R}}_1>1$.

3. Stability and Bifurcation Analysis

3.1. Stability Analysis

Theorem 2.

If ${\mathfrak{R}}_0<1$, the infection-free equilibrium $E_0$ in Model (2) is globally asymptotically stable for ${\tau }_i\ge 0,i=1,2,3,4,5$.

Proof. 

Define the Lyapunov functional ${\mathcal{V}}_1={\mathcal{V}}_{11}+{\mathcal{V}}_{12}$, where

$$\begin{array}{cc}\hfill {\mathcal{V}}_{11}=& D_1{T}_0\phi \left(\frac{T\left(t\right)}{T_0}\right)+\frac{\alpha }{\alpha +d_2}L\left(t\right)+I\left(t\right)+\frac{{\beta }_1{D}_1{T}_0{f}^{\prime }\left(0\right)}{d_4{\mathfrak{R}}_0}V\left(t\right)+\frac{{\beta }_1{D}_1{T}_0{f}^{\prime }\left(0\right)p}{d_{4}q{\mathfrak{R}}_0}B\left(t\right),\hfill \\ \hfill {\mathcal{V}}_{12}=& \frac{\alpha \eta }{\alpha +d_2}{\int }_{t-{\tau }_1}^t({\beta }_{1}f\left(V\left(s\right)\right)T\left(s\right)+{\beta }_{2}g\left(I\left(s\right)\right)T\left(s\right))ds\hfill \\ \hfill & +(1-\eta ){\int }_{t-{\tau }_2}^t({\beta }_{1}f\left(V\left(s\right)\right)T\left(s\right)+{\beta }_{2}g\left(I\left(s\right)\right)T\left(s\right))ds+\alpha {\int }_{t-{\tau }_3}^{t}L\left(s\right)ds\hfill \\ \hfill & +\frac{k{\beta }_1{D}_1{T}_0{f}^{\prime }\left(0\right)}{d_4{\mathfrak{R}}_0}{\int }_{t-{\tau }_4}^{t}I\left(s\right)ds+\frac{{\beta }_1{D}_1{T}_0{f}^{\prime }\left(0\right)p}{d_4{\mathfrak{R}}_0}{\int }_{t-{\tau }_5}^{t}V\left(s\right)B\left(s\right)ds.\hfill \end{array}$$

By calculating the derivative of ${\mathcal{V}}_1$ along the solutions of Model (2) and applying $\lambda =d_1{T}_0$, we obtain

$$\begin{array}{cc}\hfill {\dot{\mathcal{V}}}_1=& d_1{D}_1{T}_0\left(1-\frac{T_0}{T\left(t\right)}\right)\left(1-\frac{T\left(t\right)}{T_0}\right)+D_1({\beta }_1{T}_{0}f\left(V\left(t\right)\right)+{\beta }_2{T}_{0}g\left(I\left(t\right)\right))\hfill \\ \hfill & -d_{3}I\left(t\right)+\frac{k{\beta }_1{D}_1{T}_0{f}^{\prime }\left(0\right)}{d_4{\mathfrak{R}}_0}I\left(t\right)-\frac{{\beta }_1{D}_1{T}_0{f}^{\prime }\left(0\right)}{{\mathfrak{R}}_0}V\left(t\right)-\frac{{\beta }_1{D}_1{T}_0{f}^{\prime }\left(0\right)d_{5}p}{d_{4}q{\mathfrak{R}}_0}B\left(t\right)\hfill \\ \hfill =& d_1{D}_1{T}_0\left(1-\frac{T_0}{T\left(t\right)}\right)\left(1-\frac{T\left(t\right)}{T_0}\right)+{\beta }_1{D}_1{T}_{0}f\left(V\left(t\right)\right)+{\beta }_2{D}_1{T}_{0}g\left(I\left(t\right)\right)\hfill \\ \hfill & -\frac{{\beta }_2{D}_1{T}_0{g}^{\prime }\left(0\right)}{{\mathfrak{R}}_0}I\left(t\right)-\frac{{\beta }_1{D}_1{T}_0{f}^{\prime }\left(0\right)}{{\mathfrak{R}}_0}V\left(t\right)-\frac{{\beta }_1{D}_1{T}_0{f}^{\prime }\left(0\right)d_{5}p}{d_{4}q{\mathfrak{R}}_0}B\left(t\right).\hfill \end{array}$$

Condition (4) implies that

$$\begin{array}{cc}\hfill {\dot{\mathcal{V}}}_1\le & d_1{D}_1{T}_0\left(1-\frac{T_0}{T\left(t\right)}\right)\left(1-\frac{T\left(t\right)}{T_0}\right)+\frac{{\beta }_1{D}_1{T}_0{f}^{\prime }\left(0\right)}{{\mathfrak{R}}_0}V\left(t\right)({\mathfrak{R}}_0-1)\hfill \\ \hfill & +\frac{{\beta }_2{D}_1{T}_0{g}^{\prime }\left(0\right)}{{\mathfrak{R}}_0}I\left(t\right)({\mathfrak{R}}_0-1)-\frac{{\beta }_1{D}_1{T}_0{f}^{\prime }\left(0\right)d_{5}p}{d_{4}q{\mathfrak{R}}_0}B\left(t\right).\hfill \end{array}$$

Since, $\left(1-\frac{T_0}{T\left(t\right)}\right)\left(1-\frac{T\left(t\right)}{T_0}\right)\le 0$, the equality holds if and only if $T=T_0$. Therefore, if ${\mathfrak{R}}_0<1$, then ${\dot{\mathcal{V}}}_1\le 0$. It can be shown that the largest compact invariant set in $\left\{X\in \mathrm{\Gamma }|{\dot{\mathcal{V}}}_1=0\right\}$ is the singleton $E_0$. LaSalle’s invariance principle [49] implies that $E_0$ is globally asymptotically stable when ${\mathfrak{R}}_0<1$. This completes the proof. □

Before the proof of the global stability of the immunity-inactivated equilibrium $E_1$, we present the following result.

Lemma 1.

Define ${\overline{\mathfrak{R}}}_1=\frac{q{V}_1}{d_5}$, then we claim that ${\mathfrak{R}}_1>1$ is equivalent to ${\overline{\mathfrak{R}}}_1>1$.

Proof. 

Obviously, ${\mathfrak{R}}_1=\frac{kq{D}_1}{d_3{d}_4{d}_5}({\beta }_1{T}_{2}f\left(V_2\right)+{\beta }_2{T}_{2}g\left(I_2\right))=\frac{kq{I}_2}{d_4{d}_5}>1$ implies that $\tilde{I}:=\frac{d_4{d}_5}{kq}>0$. and the inequalities ${\overline{\mathfrak{R}}}_1=\frac{q{V}_1}{d_5}=\frac{kq{I}_1}{d_4{d}_5}>1$ are equivalent to the inequality $I_1>\tilde{I}$. From the monotonicity of function $H\left(I\right)$, it follows that ${\overline{\mathfrak{R}}}_1>1$ is equivalent to $H\left(\tilde{I}\right)>0$ for $H\left(I_1\right)=0$.

On the other hand, ${\mathfrak{R}}_1>1$ is equivalent to $I_2>\tilde{I}$. From the monotonicity of function $F\left(I\right)$, we know that ${\mathfrak{R}}_1>1$ is equivalent to $F\left(\tilde{I}\right)>0$ because $F\left(I_2\right)=0$. Note that $H\left(\tilde{I}\right)=F\left(\tilde{I}\right)$, i.e., ${\mathfrak{R}}_1>1$ is equivalent to $H\left(\tilde{I}\right)>0$. Then ${\mathfrak{R}}_1>1$ is equivalent to ${\overline{\mathfrak{R}}}_1>1$. Therefore, the claim is true. □

Theorem 3.

If ${\mathfrak{R}}_1<1<{\mathfrak{R}}_0$, the immunity-inactivated equilibrium $E_1$ in Model (2) is globally asymptotically stable for ${\tau }_i\ge 0,i=1,2,3,4,5$.

Proof. 

We employ a particular function, $\phi \left(x\right)=x-1-lnx$, when $x>0$. Then, $\phi \left(x\right)>0$ and $\phi \left(x\right)=0$ if and only if $x=1$. Define the Lyapunov functional ${\mathcal{V}}_2={\mathcal{V}}_{21}+{\mathcal{V}}_{22}$, where

$$\begin{array}{cc}\hfill {\mathcal{V}}_{21}=& D_1\left(T\left(t\right)-T_1-T_{1}ln\frac{T\left(t\right)}{T_1}\right)+\frac{\alpha }{\alpha +d_2}\left(L\left(t\right)-L_1-L_{1}ln\frac{L\left(t\right)}{L_1}\right)+I\left(t\right)-I_1-I_{1}ln\frac{I\left(t\right)}{I_1}\hfill \\ \hfill & +\frac{{\beta }_1{D}_1{T}_{1}f\left(V_1\right)}{k{I}_1}\left(V\left(t\right)-V_1-V_{1}ln\frac{V\left(t\right)}{V_1}\right)+\frac{{\beta }_1{D}_1{T}_{1}f\left(V_1\right)p}{kq{I}_1}B\left(t\right),\hfill \\ \hfill {\mathcal{V}}_{22}=& \frac{\alpha \eta }{\alpha +d_2}\left({\beta }_1{T}_{1}f\left(V_1\right){\int }_{t-{\tau }_1}^t\left(\frac{T\left(s\right)f\left(V\right(s\left)\right)}{T_{1}f\left(V_1\right)}-1-ln\frac{T\left(s\right)f\left(V\right(s\left)\right)}{T_{1}f\left(V_1\right)}\right)ds\right.\hfill \\ \hfill & \left.+{\beta }_2{T}_{1}g\left(I_1\right){\int }_{t-{\tau }_1}^t\left(\frac{T\left(s\right)g\left(I\right(s\left)\right)}{T_{1}g\left(I_1\right)}-1-ln\frac{T\left(s\right)g\left(I\right(s\left)\right)}{T_{1}g\left(I_1\right)}\right)ds\right)\hfill \\ \hfill & +(1-\eta )\left({\beta }_1{T}_{1}f\left(V_1\right){\int }_{t-{\tau }_2}^t\left(\frac{T\left(s\right)f\left(V\right(s\left)\right)}{T_{1}f\left(V_1\right)}-1-ln\frac{T\left(s\right)f\left(V\right(s\left)\right)}{T_{1}f\left(V_1\right)}\right)ds\right.\hfill \\ \hfill & \left.+{\beta }_2{T}_{1}g\left(I_1\right){\int }_{t-{\tau }_2}^t\left(\frac{T\left(s\right)g\left(I\right(s\left)\right)}{T_{1}g\left(I_1\right)}-1-ln\frac{T\left(s\right)g\left(I\right(s\left)\right)}{T_{1}g\left(I_1\right)}\right)ds\right)\hfill \\ \hfill & +\frac{\alpha \eta }{\alpha +d_2}({\beta }_1{T}_{1}f\left(V_1\right)+{\beta }_2{T}_{1}g\left(I_1\right)){\int }_{t-{\tau }_3}^t\left(L\left(s\right)-L_1-L_{1}ln\frac{L\left(s\right)}{L_1}\right)ds\hfill \\ \hfill & +{\beta }_1{D}_1{T}_{1}f\left(V_1\right){\int }_{t-{\tau }_4}^t\left(I\left(s\right)-I_1-I_{1}ln\frac{I\left(s\right)}{I_1}\right)ds+\frac{{\beta }_1{D}_1{T}_{1}f\left(V_1\right)p}{k{I}_1}{\int }_{t-{\tau }_5}^{t}V\left(s\right)B\left(s\right)ds.\hfill \end{array}$$

From the equilibrium conditions of $E_1$, we have

$$\begin{array}{cc}\hfill & \lambda =d_1{T}_1+{\beta }_1{T}_{1}f\left(V_1\right)+{\beta }_2{T}_{1}g\left(I_1\right),\eta ({\beta }_1{T}_{1}f\left(V_1\right)+{\beta }_2{T}_{1}g\left(I_1\right))=(\alpha +d_2)L_1,\hfill \\ \hfill & (1-\eta )({\beta }_1{T}_{1}f\left(V_1\right)+{\beta }_2{T}_{1}g\left(I_1\right))+\alpha L_1-d_3{I}_1=0,k{I}_1=d_4{V}_1,\hfill \end{array}$$

which leads to

$$\begin{array}{cc}\hfill {\dot{\mathcal{V}}}_2=& d_1{D}_1{T}_1\left(1-\frac{T_1}{T\left(t\right)}\right)\left(1-\frac{T\left(t\right)}{T_1}\right)+{\beta }_1{T}_{1}f\left(V_1\right)[D_1\left(3-\frac{T_1}{T\left(t\right)}+\frac{f\left(V\right(t\left)\right)}{f\left(V_1\right)}-\frac{V\left(t\right)}{V_1}\right.\hfill \\ & \left.-\frac{V_{1}I(t-{\tau }_4)}{V\left(t\right)I_1}\right)+\frac{\alpha \eta }{\alpha +d_2}\left(1-\frac{T(t-{\tau }_1)f\left(V(t-{\tau }_1)\right)L_1}{T_{1}f\left(V_1\right)L\left(t\right)}-\frac{L(t-{\tau }_3)I_1}{L_{1}I\left(t\right)}\right.\hfill \\ & \left.+ln\frac{T(t-{\tau }_1)f\left(V(t-{\tau }_1)\right)L(t-{\tau }_3)}{T\left(t\right)f\left(V\right(t\left)\right)L\left(t\right)}+ln\frac{I(t-{\tau }_4)}{I\left(t\right)}\right)+(1-\eta )\hfill \\ & \times \left(ln\frac{T(t-{\tau }_2)f\left(V(t-{\tau }_2)\right)I(t-{\tau }_4)}{T\left(t\right)f\left(V\right(t\left)\right)I\left(t\right)}-\frac{T(t-{\tau }_2)f\left(V(t-{\tau }_2)\right)I_1}{T_{1}f\left(V_1\right)I\left(t\right)}\right)\hfill \\ & +\frac{p{D}_1}{k{I}_1}\left(V_1-\frac{d_5}{q}\right)B\left(t\right)]+{\beta }_2{T}_{1}g\left(I_1\right)[D_1\left(2-\frac{T_1}{T\left(t\right)}+\frac{g\left(I\right(t\left)\right)}{g\left(I_1\right)}-\frac{I\left(t\right)}{I_1}\right)\hfill \\ & +\frac{\alpha \eta }{\alpha +d_2}\left(1-\frac{T(t-{\tau }_1)g\left(I(t-{\tau }_1)\right)L_1}{T_{1}g\left(I_1\right)L\left(t\right)}-\frac{L\left(t\right)}{L_1}+\frac{L(t-{\tau }_3)}{L_1}-\frac{L(t-{\tau }_3)I_1}{L_{1}I\left(t\right)}\right.\hfill \\ & \left.+ln\frac{T(t-{\tau }_1)g\left(I(t-{\tau }_1)\right)}{T\left(t\right)g\left(I\right(t\left)\right)}\right)+(1-\eta )\left(ln\frac{T(t-{\tau }_2)g\left(I(t-{\tau }_2)\right)}{T\left(t\right)g\left(I\right(t\left)\right)}\right.\hfill \\ & \left.-\frac{T(t-{\tau }_2)g\left(I(t-{\tau }_2)\right)I_1}{T_{1}g\left(I_1\right)I\left(t\right)}\right)+\frac{\alpha \eta }{\alpha +d_2}\left(\frac{L\left(t\right)}{L_1}-\frac{L(t-{\tau }_3)}{L_1}+ln\frac{L(t-{\tau }_3)}{L\left(t\right)}\right)]\hfill \\ \hfill =& d_1{D}_1{T}_1\left(1-\frac{T_1}{T\left(t\right)}\right)\left(1-\frac{T\left(t\right)}{T_1}\right)+\frac{{\beta }_1{D}_1{T}_{1}f\left(V_1\right)p{d}_5}{k{I}_1}({\overline{\mathfrak{R}}}_1-1)B\left(t\right)\hfill \\ & +{\beta }_1{T}_{1}f\left(V_1\right)[D_1\left(-\phi \left(\frac{T_1}{T\left(t\right)}\right)-\phi \left(\frac{V_{1}I(t-{\tau }_4)}{V\left(t\right)I_1}\right)-\phi \left(\frac{f\left(V_1\right)V\left(t\right)}{f\left(V\left(t\right)\right)V_1}\right)\right.\hfill \\ & \left.+\left(\frac{f\left(V\right(t\left)\right)}{f\left(V_1\right)}-\frac{V\left(t\right)}{V_1}\right)\left(1-\frac{f\left(V_1\right)}{f\left(V\right(t\left)\right)}\right)\right)\hfill \\ & +\frac{\alpha \eta }{\alpha +d_2}\left(-\phi \left(\frac{T(t-{\tau }_1)f\left(V(t-{\tau }_1)\right)L_1}{T_{1}f\left(V_1\right)L\left(t\right)}\right)-\phi \left(\frac{L(t-{\tau }_3)I_1}{L_{1}I\left(t\right)}\right)\right)+(1-\eta )\hfill \\ & \times \left(-\phi \left(\frac{T(t-{\tau }_2)f\left(V(t-{\tau }_2)\right)I_1}{T_{1}f\left(V_1\right)I\left(t\right)}\right)\right)]+{\beta }_2{T}_{1}g\left(I_1\right)[D_1\left(-\phi \left(\frac{T_1}{T\left(t\right)}\right)-\phi \left(\frac{g\left(I_1\right)I\left(t\right)}{g\left(I\left(t\right)\right)I_1}\right)\right.\hfill \\ & \left.+\left(\frac{g\left(I\right(t\left)\right)}{g\left(I_1\right)}-\frac{I\left(t\right)}{I_1}\right)\left(1-\frac{g\left(I_1\right)}{g\left(I\right(t\left)\right)}\right)\right)+\frac{\alpha \eta }{\alpha +d_2}\left(-\phi \left(\frac{T(t-{\tau }_1)g\left(I(t-{\tau }_1)\right)L_1}{T_{1}g\left(I_1\right)L\left(t\right)}\right)\right.\hfill \\ & \left.-\phi \left(\frac{L(t-{\tau }_3)I_1}{L_{1}I\left(t\right)}\right)\right)+(1-\eta )\left(-\phi \left(\frac{T(t-{\tau }_2)g\left(I(t-{\tau }_2)\right)I_1}{T_{1}g\left(I_1\right)I\left(t\right)}\right)\right)].\hfill \end{array}$$

It follows from (3) that

$$\begin{array}{c}\hfill \left(\frac{f\left(V\right(t\left)\right)}{f\left(V_1\right)}-\frac{V\left(t\right)}{V_1}\right)\left(1-\frac{f\left(V_1\right)}{f\left(V\right(t\left)\right)}\right)\le 0,\left(\frac{g\left(I\right(t\left)\right)}{g\left(I_1\right)}-\frac{I\left(t\right)}{I_1}\right)\left(1-\frac{g\left(I_1\right)}{g\left(I\right(t\left)\right)}\right)\le 0.\end{array}$$

Moreover, from Lemma 2, we have ${\dot{\mathcal{V}}}_2\le 0$, with equality holding if and only if $T=T_1,L=L_1,I=I_1,V=V_1,B=B_1$, which implies that the largest compact invariant set in $\left\{X\in \mathrm{\Gamma }|{\dot{\mathcal{V}}}_2=0\right\}$ is the singleton $\left\{E_1\right\}$. Hence, the globally asymptotic stability of the unique immunity-inactivated equilibrium $E_1$ follows from LaSalle’s invariance principle [49]. This completes the proof. □

Theorem 4.

If ${\mathfrak{R}}_1>1$, the immunity-activated equilibrium $E_2$ in Model (2) is globally asymptotically stable for ${\tau }_i>0(i=1,2,3,4)$ and ${\tau }_5=0$.

Proof 

Define the Lyapunov functional ${\mathcal{V}}_3={\mathcal{V}}_{31}+{\mathcal{V}}_{32}$, where

$$\begin{array}{cc}\hfill {\mathcal{V}}_{31}=& D_1\left(T\left(t\right)-T_2-T_{2}ln\frac{T\left(t\right)}{T_2}\right)+\frac{\alpha }{\alpha +d_2}\left(L\left(t\right)-L_2-L_{2}ln\frac{L\left(t\right)}{L_2}\right)+I\left(t\right)-I_2-I_{2}ln\frac{I\left(t\right)}{I_2}\hfill \\ & +\frac{{\beta }_1{D}_1{T}_{2}f\left(V_2\right)}{k{I}_2}\left(V\left(t\right)-V_2-V_{2}ln\frac{V\left(t\right)}{V_2}\right)+\frac{{\beta }_1{D}_1{T}_{2}f\left(V_2\right)p}{kq{I}_2}\left(B\left(t\right)-B_2-B_{2}ln\frac{B\left(t\right)}{B_2}\right),\hfill \\ \hfill W_{31}=& \frac{\alpha \eta }{\alpha +d_2}\left({\beta }_1{T}_{2}f\left(V_2\right){\int }_{t-{\tau }_1}^t\left(\frac{T\left(s\right)f\left(V\right(s\left)\right)}{T_{2}f\left(V_2\right)}-1-ln\frac{T\left(s\right)f\left(V\right(s\left)\right)}{T_{2}f\left(V_2\right)}\right)ds\right.\hfill \\ & \left.+{\beta }_2{T}_{2}g\left(I_2\right){\int }_{t-{\tau }_1}^t\left(\frac{T\left(s\right)g\left(I\right(s\left)\right)}{T_{2}g\left(I_2\right)}-1-ln\frac{T\left(s\right)g\left(I\right(s\left)\right)}{T_{2}g\left(I_2\right)}\right)ds\right)\hfill \\ & +(1-\eta )\left({\beta }_1{T}_{2}f\left(V_2\right){\int }_{t-{\tau }_2}^t\left(\frac{T\left(s\right)f\left(V\right(s\left)\right)}{T_{2}f\left(V_2\right)}-1-ln\frac{T\left(s\right)f\left(V\right(s\left)\right)}{T_{2}f\left(V_2\right)}\right)ds\right.\hfill \\ & \left.+{\beta }_2{T}_{2}g\left(I_2\right){\int }_{t-{\tau }_2}^t\left(\frac{T\left(s\right)g\left(I\right(s\left)\right)}{T_{2}g\left(I_2\right)}-1-ln\frac{T\left(s\right)g\left(I\right(s\left)\right)}{T_{2}g\left(I_2\right)}\right)ds\right)\hfill \\ & +\frac{\alpha \eta }{\alpha +d_2}({\beta }_1{T}_{2}f\left(V_2\right)+{\beta }_2{T}_{2}g\left(I_2\right)){\int }_{t-{\tau }_3}^t\left(L\left(s\right)-L_2-L_{2}ln\frac{L\left(s\right)}{L_2}\right)ds\hfill \\ & +{\beta }_1{D}_1{T}_{2}f\left(V_2\right){\int }_{t-{\tau }_4}^t\left(I\left(s\right)-I_2-I_{2}ln\frac{I\left(s\right)}{I_2}\right)ds.\hfill \end{array}$$

By calculating the derivative of ${\mathcal{V}}_3$ along the solutions of Model (2) and using the following equilibrium condition at $E_2$

$$\begin{array}{cc}\hfill & \lambda =d_1{T}_2+{\beta }_1{T}_{2}f\left(V_2\right)+{\beta }_2{T}_{2}g\left(I_2\right),\eta ({\beta }_1{T}_{2}f\left(V_2\right)+{\beta }_2{T}_{2}g\left(I_2\right))=(\alpha +d_2)L_2,\hfill \\ \hfill & (1-\eta )({\beta }_1{T}_{2}f\left(V_2\right)+{\beta }_2{T}_{2}g\left(I_2\right))+\alpha L_2=d_3{I}_2,k{I}_2=(d_4+p{B}_2)V_2,q{V}_2=d_5,\hfill \end{array}$$

we obtain

$$\begin{array}{cc}\hfill {\dot{\mathcal{V}}}_3=& d_1{D}_1{T}_2\left(1-\frac{T_2}{T\left(t\right)}\right)\left(1-\frac{T\left(t\right)}{T_2}\right)+{\beta }_1{T}_{2}f\left(V_2\right)[D_1\left(3-\frac{T_2}{T\left(t\right)}+\frac{f\left(V\right(t\left)\right)}{f\left(V_2\right)}\right.\hfill \\ \hfill & \left.-\frac{I(t-{\tau }_4)V_2}{I_{2}V\left(t\right)}-\frac{V\left(t\right)}{V_2}\right)+\frac{\alpha \eta }{\alpha +d_2}\left(1-\frac{T(t-{\tau }_1)f\left(V(t-{\tau }_1)\right)L_2}{T_{2}f\left(V_2\right)L\left(t\right)}\right.\hfill \\ \hfill & \left.-\frac{L(t-{\tau }_3)I_2}{L_{2}I\left(t\right)}+ln\frac{I(t-{\tau }_4)}{I\left(t\right)}+ln\frac{T(t-{\tau }_1)f\left(V(t-{\tau }_1)\right)L(t-{\tau }_3)}{T\left(t\right)f\left(V\right(t\left)\right)L\left(t\right)}\right)\hfill \\ \hfill & +(1-\eta )\left(ln\frac{T(t-{\tau }_2)f\left(V(t-{\tau }_2)\right)I(t-{\tau }_4)}{T\left(t\right)f\left(V\right(t\left)\right)I\left(t\right)}-\frac{T(t-{\tau }_2)f\left(V(t-{\tau }_2)\right)I_2}{T_{2}f\left(V_2\right)I\left(t\right)}\right)]\hfill \\ \hfill & +{\beta }_2{T}_{2}g\left(I_2\right)[D_1\left(2-\frac{T_2}{T\left(t\right)}+\frac{g\left(I\right(t\left)\right)}{g\left(I_2\right)}-\frac{I\left(t\right)}{I_2}\right)+\frac{\alpha \eta }{\alpha +d_2}\left(1-\frac{L(t-{\tau }_3)I_2}{L_{2}I\left(t\right)}\right.\hfill \\ \hfill & \left.-\frac{T(t-{\tau }_1)g\left(I(t-{\tau }_1)\right)L_2}{T_{2}g\left(I_2\right)L\left(t\right)}+ln\frac{T(t-{\tau }_1)g\left(I(t-{\tau }_1)\right)L(t-{\tau }_3)}{T\left(t\right)g\left(I\right(t\left)\right)L\left(t\right)}\right)\hfill \\ \hfill & +(1-\eta )\left(ln\frac{T(t-{\tau }_2)g\left(I(t-{\tau }_2)\right)}{T\left(t\right)g\left(I\right(t\left)\right)}-\frac{T(t-{\tau }_2)g\left(I(t-{\tau }_2)\right)I_2}{T_{2}g\left(I_2\right)I\left(t\right)}\right)]\hfill \\ \hfill =& d_1{D}_1{T}_2\left(1-\frac{T_2}{T\left(t\right)}\right)\left(1-\frac{T\left(t\right)}{T_2}\right)+{\beta }_1{T}_{2}f\left(V_2\right)[D_1\left(-\phi \left(\frac{T_2}{T\left(t\right)}\right)-\phi \left(\frac{V_{2}I(t-{\tau }_4)}{V\left(t\right)I_2}\right)\right.\hfill \end{array}$$

$$\begin{array}{cc}& \left.-\phi \left(\frac{f\left(V_2\right)V\left(t\right)}{f\left(V\left(t\right)\right)V_2}\right)+\left(\frac{f\left(V\right(t\left)\right)}{f\left(V_2\right)}-\frac{V\left(t\right)}{V_2}\right)\left(1-\frac{f\left(V_2\right)}{f\left(V\right(t\left)\right)}\right)\right)+\frac{\alpha \eta }{\alpha +d_2}\left(-\phi \left(\frac{L(t-{\tau }_3)I_2}{L_{2}I\left(t\right)}\right)\right.\hfill \\ & \left.-\phi \left(\frac{T(t-{\tau }_1)f\left(V(t-{\tau }_1)\right)L_2}{T_{2}f\left(V_2\right)L\left(t\right)}\right)\right)+(1-\eta )\left(-\phi \left(\frac{T(t-{\tau }_2)f\left(V(t-{\tau }_2)\right)I_2}{T_{2}f\left(V_2\right)I\left(t\right)}\right)\right)]\hfill \\ & +{\beta }_2{T}_{2}g\left(I_2\right)[D_1\left(-\phi \left(\frac{T_2}{T\left(t\right)}\right)-\phi \left(\frac{g\left(I_2\right)I\left(t\right)}{g\left(I\left(t\right)\right)I_2}\right)+\left(\frac{g\left(I\right(t\left)\right)}{g\left(I_2\right)}-\frac{I\left(t\right)}{I_2}\right)\left(1-\frac{g\left(I_2\right)}{g\left(I\right(t\left)\right)}\right)\right)\hfill \\ & +\frac{\alpha \eta }{\alpha +d_2}\left(-\phi \left(\frac{T(t-{\tau }_1)f\left(V(t-{\tau }_1)\right)L_2}{T_{2}f\left(V_2\right)L\left(t\right)}\right)-\phi \left(\frac{L(t-{\tau }_3)I_2}{L_{2}I\left(t\right)}\right)\right)\hfill \\ & +(1-\eta )\left(-\phi \left(\frac{T(t-{\tau }_2)f\left(V(t-{\tau }_2)\right)I_2}{T_{2}f\left(V_2\right)I\left(t\right)}\right)\right)].\hfill \end{array}$$

It follows from (3) that

$$\begin{array}{c}\hfill \left(\frac{f\left(V\right(t\left)\right)}{f\left(V_2\right)}-\frac{V\left(t\right)}{V_2}\right)\left(1-\frac{f\left(V_2\right)}{f\left(V\right(t\left)\right)}\right)\le 0,\left(\frac{g\left(I\right(t\left)\right)}{g\left(I_2\right)}-\frac{I\left(t\right)}{I_2}\right)\left(1-\frac{g\left(I_2\right)}{g\left(I\right(t\left)\right)}\right)\le 0.\end{array}$$

Then, ${\dot{\mathcal{V}}}_3\le 0$, with equality holding if and only if $T=T_2,L=L_2,I=I_2,V=V_2$, $B=B_2$, implying that the largest compact invariant set in $\left\{X\in \mathrm{\Gamma }|{\dot{\mathcal{V}}}_3=0\right\}$ is the singleton $\left\{E_2\right\}$. Therefore, the globally asymptotic stability of the unique immunity-activated equilibrium $E_2$ follows from LaSalle’s invariance principle [49]. This completes the proof. □

3.2. Bifurcation Analysis at $E_2$

For ${\tau }_5>0$ and ${\tau }_i=0(i=1,2,3,4)$, Model (2) becomes

$$\left\{\begin{array}{cc}\hfill T^{\prime }\left(t\right)=& \lambda -{\beta }_{1}f\left(V\left(t\right)\right)T\left(t\right)-{\beta }_{2}g\left(I\left(t\right)\right)T\left(t\right)-d_{1}T\left(t\right),\hfill \\ \hfill L^{\prime }\left(t\right)=& \eta ({\beta }_{1}f\left(V\left(t\right)\right)T\left(t\right)+{\beta }_{2}g\left(I\left(t\right)\right)T\left(t\right))-\alpha L\left(t\right)-d_{2}L\left(t\right),\hfill \\ \hfill I^{\prime }\left(t\right)=& (1-\eta )({\beta }_{1}f\left(V\left(t\right)\right)T\left(t\right)+{\beta }_{2}g\left(I\left(t\right)\right)T\left(t\right))+\alpha L\left(t\right)-d_{3}I\left(t\right),\hfill \\ \hfill V^{\prime }\left(t\right)=& kI\left(t\right)-pV\left(t\right)B\left(t\right)-d_{4}V\left(t\right),\hfill \\ \hfill B^{\prime }\left(t\right)=& qV(t-{\tau }_5)B(t-{\tau }_5)-d_{5}B\left(t\right).\hfill \end{array}\right.$$

(11)

We denote $A_1={\beta }_{1}f\left(V_2\right)+{\beta }_{2}g\left(I_2\right)$ and $A_2={\beta }_2{g}^{\prime }\left(I_2\right)T_2,A_3={\beta }_1{f}^{\prime }\left(V_2\right)T_2$. Then, the characteristic equation in Model (11) at $E_2$ is given by

$$\left|\begin{array}{ccccc}{H}_1\left(u\right)& 0& -A_2& -A_3& 0\\ \eta A_1& H_2\left(u\right)& \eta A_2& \eta A_3& 0\\ (1-\eta )A_1& \alpha & H_3\left(u\right)& (1-\eta )A_3& 0\\ 0& 0& k& H_4\left(u\right)& -p{V}_2\\ 0& 0& 0& q{B}_2{e}^{-u{\tau }_5}& H_5\left(u\right)\end{array}\right|=0,$$

where

$$\begin{array}{cc}\hfill H_1\left(u\right)=& -(d_1+A_1+u),H_2\left(u\right)=-(\alpha +d_2+u),H_3\left(u\right)=-(u+d_3-(1-\eta )A_2),\hfill \\ \hfill H_4\left(u\right)=& -(d_4+p{B}_2+u),H_5\left(u\right)=-(u+d_5-q{V}_2{e}^{-u{\tau }_5}).\hfill \end{array}$$

Calculating the corresponding determinant gives

$$\begin{array}{c}\hfill u^5+a_4{u}^4+a_3{u}^3+a_2{u}^2+a_{1}u+a_0+e^{-u{\tau }_5}(b_4{u}^4+b_3{u}^3+b_2{u}^2+b_{1}u+b_0)=0,\end{array}$$

(12)

where

$$\begin{array}{cc}\hfill a_4=& d_1+A_1+\alpha +d_2+d_3+d_4+p{B}_2+d_5-A_2(1-\eta ),\hfill \\ \hfill a_3=& d_5(d_1+A_1+\alpha +d_2+d_3+d_4+p{B}_2)+(d_1+A_1)(\alpha +d_2)+d_3{d}_4+p{B}_2\hfill \\ \hfill & +(d_1+A_1+\alpha +d_2)(d_3+d_4+p{B}_2)-k{A}_3(1-\eta )-A_2\alpha \eta \hfill \\ \hfill & -(\alpha +d_2+d_4+p{B}_2+d_5+d_1)A_2(1-\eta ),\hfill \\ \hfill a_2=& d_5((d_1+A_1)(\alpha +d_2)+d_3(d_4+p{B}_2)+(d_1+A_1+\alpha +d_2)(d_3+d_4+p{B}_2))\hfill \\ \hfill & +d_3(d_4+p{B}_2)(d_1+A_1+\alpha +d_2)+(d_1+A_1)(\alpha +d_2)(d_3+d_4+p{B}_2)\hfill \\ \hfill & -A_2\alpha \eta (d_1+d_4+p{B}_2+d_5)-k{A}_3\alpha \eta -k{A}_3(1-\eta )(d_1+\alpha +d_2+d_5)\hfill \\ \hfill & -A_2(1-\eta )(d_5(d_1+\alpha +d_2+d_4+p{B}_2)+(d_4+p{B}_2)(d_1+\alpha +d_2)+(\alpha +d_2)d_1),\hfill \\ \hfill a_1=& d_5((d_1+A_1)(\alpha +d_2)(d_3+d_4+p{B}_2)+d_3(d_4+p{B}_2)(d_1+A_1+\alpha +d_2))\hfill \\ \hfill & +(d_1+A_1)(\alpha +d_2)d_3(d_4+p{B}_2)-k{A}_3\alpha \eta (d_1+d_5)-A_2\alpha \eta ((d_1+d_5)(d_4+p{B}_2)\hfill \\ \hfill & +d_1{d}_5)-k{A}_3(1-\eta )(d_1(\alpha +d_2)+(\alpha +d_2)d_5+d_1{d}_5)-A_2(1-\eta )(d_1(\alpha +d_2)d_5\hfill \\ \hfill & +(d_1{d}_5+d_1(\alpha +d_2))(d_4+p{B}_2)+(\alpha +d_2)(d_4+p{B}_2)d_5),\hfill \\ \hfill a_0=& (d_1+A_1)(\alpha +d_2)d_3(d_4+p{B}_2)d_5-k{A}_3\alpha \eta d_1{d}_5-k{A}_3(1-\eta )d_1(\alpha +d_2)d_5\hfill \\ \hfill & -(A_2\alpha \eta d_1{d}_5-A_2(1-\eta )d_1(\alpha +d_2)d_5)(d_4+p{B}_2),\hfill \\ \hfill b_4=& -d_5,b_3=-d_5(d_1+A_1+\alpha +d_2+d_3+d_4-A_2(1-\eta )),\hfill \\ \hfill b_2=& d_5(A_2\alpha \eta +k{A}_3(1-\eta )+A_2(1-\eta )(d_1+d_4+\alpha +d_2)-(d_1+A_1)(\alpha +d_2)\hfill \\ \hfill & -d_3{d}_4-(d_1+A_1+\alpha +d_2)(d_3+d_4)),\hfill \\ \hfill b_1=& d_5(k{A}_3\alpha \eta +k{A}_3(1-\eta )(\alpha +d_2+d_1)+A_2\alpha \eta (d_1+d_4)+A_2(1-\eta )(d_1{d}_4\hfill \\ \hfill & +(d_1+d_4)(\alpha +d_2))-d_3{d}_4(d_1+A_1+\alpha +d_2)-(d_1+A_1)(\alpha +d_2)(d_3+d_4)),\hfill \\ \hfill b_0=& d_5(k{A}_3\alpha \eta d_1+k{A}_3(1-\eta )d_1(\alpha +d_2)+A_2\alpha \eta d_1{d}_4\hfill \\ \hfill & +(A_2(1-\eta )d_1{d}_4-(d_1+A_1)d_3{d}_4)(\alpha +d_2)).\hfill \end{array}$$

Assume that ${\tau }_5>0$ and let $u=i\omega (\omega >0)$ in (12). By separating the real and imaginary parts, we can obtain

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{a}_4{\omega }^4-a_2{\omega }^2+a_0=sin\omega {\tau }_5(b_3{\omega }^2-b_1)\omega -cos\omega {\tau }_5(b_4{\omega }^4-b_2{\omega }^2+b_0),\hfill \\ ({\omega }^4-a_3{\omega }^2+a_1)\omega =sin\omega {\tau }_5(b_4{\omega }^4-b_2{\omega }^2+b_0)+cos\omega {\tau }_5(b_3{\omega }^2-b_1)\omega .\hfill \end{array}\right.\end{array}$$

(13)

Squaring and adding these equations yields

$$\begin{array}{c}\hfill {\omega }^{10}+m_4{\omega }^8+m_3{\omega }^6+m_2{\omega }^4+m_1{\omega }^2+m_0=0,\end{array}$$

(14)

where

$$\begin{array}{cc}\hfill m_4=& a_4^2-b_4^2-2a_3,m_3=a_3^2+2a_1+2b_2{b}_4-2a_2{a}_4-b_3^2,\hfill \\ \hfill m_2=& a_2^2+2a_0{a}_4+2b_1{b}_3-2a_1{a}_3-b_2^2-2b_0{b}_4,\hfill \\ \hfill m_1=& a_1^2+2b_0{b}_2-2a_0{a}_2-b_1^2,m_0=a_0^2-b_0^2.\hfill \end{array}$$

(15)

Let $z={\omega }^2>0$. Then, we obtain

$$\begin{array}{cc}\hfill Q\left(z\right)=& z^5+m_4{z}^4+m_3{z}^3+m_2{z}^2+m_{1}z+m_0=0,\hfill \\ \hfill Q^{\prime }\left(z\right)=& 5z^4+4m_4{z}^3+3m_3{z}^2+2m_{2}z+m_1.\hfill \end{array}$$

(16)

From the expression of $m_4$ in (15), one can show that $m_4>0$. Moreover, it can be shown that (16) has at most four positive real roots by applying the relationship between the root and coefficient. Without loss of generality, we assume that $Q\left(z\right)=0$ has four positive real roots $z_1,z_2,z_3$, and $z_4$. Then, (14) has the positive roots ${\omega }_k=\sqrt{z_k}(k=1,2,3,4)$, and thus (12) has a pair of purely imaginary roots $\pm i{\omega }_k$. Then, it follows from (13) that

$$\begin{array}{cc}\hfill & cos\left({\omega }_k{\tau }_5\right)=\frac{{\Theta }_1}{{(b_4{\omega }_k^4-b_2{\omega }_k^2+b_0)}^2+{\omega }_k^2{(b_3{\omega }_k^2-b_1)}^2}\triangleq G_1^k,\hfill \\ \hfill & sin\left({\omega }_k{\tau }_5\right)=\frac{{\Theta }_2}{{(b_4{\omega }_k^4-b_2{\omega }_k^2+b_0)}^2+{\omega }_k^2{(b_3{\omega }_k^2-b_1)}^2}\triangleq G_2^k,\hfill \end{array}$$

where

$$\begin{array}{cc}\hfill {\Theta }_1=& {\omega }_k^2({\omega }_k^4-a_3{\omega }_k^2+a_1)(b_3{\omega }_k^2-b_1)-(b_4{\omega }_k^4-b_2{\omega }_k^2+b_0)(a_4{\omega }_k^4-a_2{\omega }_k^2+a_0),\hfill \\ \hfill {\Theta }_2=& {\omega }_k(a_4{\omega }_k^4-a_2{\omega }_k^2+a_0)(b_3{\omega }_k^2-b_1)+{\omega }_k({\omega }_k^4-a_3{\omega }_k^2+a_1)(b_4{\omega }_k^4-b_2{\omega }_k^2+b_0).\hfill \end{array}$$

Let

$$\begin{array}{c}\hfill {\tau }_{5k}^{\left(j\right)}=\left\{\begin{array}{cc}\frac{arccos\left(G_1^k\right)+2n\pi }{{\omega }_k},\hfill & if{G}_2^k\ge 0,\hfill \\ \frac{2\pi -arccos\left(G_1^k\right)+2n\pi }{{\omega }_k},\hfill & if{G}_2^k<0,\hfill \end{array}\right.\end{array}$$

(17)

where $k=1,2,3,4$, $j=0,1,2,\cdots$.

Let

$$\begin{array}{c}\hfill {\tau }_0=\underset{1\le k\le 4}{min}\left\{{\tau }_{5k}^{\left(0\right)}\right\},{\omega }_0={\omega }_{k_0}.\end{array}$$

(18)

By calculating the derivation of (12) with respect to ${\tau }_5$, we obtain

$$\begin{array}{cc}\hfill & [5u^4+4a_4{u}^3+3a_3{u}^2+2a_{2}u+a_1+e^{-u{\tau }_5}(4b_4{u}^3+3b_3{u}^2+2b_{2}u+b_1)\hfill \\ \hfill & -{\tau }_5{e}^{-u{\tau }_5}(b_4{u}^4+b_3{u}^3+b_2{u}^2+b_{1}u+b_0)]\frac{du}{d{\tau }_5}\hfill \\ \hfill & =u{e}^{-u{\tau }_5}(b_4{u}^4+b_3{u}^3+b_2{u}^2+b_{1}u+b_0),\hfill \end{array}$$

then,

$$\begin{array}{cc}\hfill {\left(\frac{du}{d{\tau }_5}\right)}^{-1}=& \frac{(5u^4+4a_4{u}^3+3a_3{u}^2+2a_{2}u+a_1)e^{u{\tau }_5}}{u(b_4{u}^4+b_3{u}^3+b_2{u}^2+b_{1}u+b_0)}\hfill \\ \hfill & +\frac{4a_4{u}^3+3a_3{u}^2+2a_{2}u+a_1}{u(b_4{u}^4+b_3{u}^3+b_2{u}^2+b_{1}u+b_0)}-\frac{{\tau }_5}{u}.\hfill \end{array}$$

From (13), we have

$$\begin{array}{cc}\hfill & sign\left\{{\left[\frac{d\left(\mathrm{R}eu\right)}{d{\tau }_5}\right]}_{{\tau }_5={\tau }_{5k}^{\left(j\right)}}^{-1}\right\}\hfill \\ \hfill =& sign\left\{\mathrm{Re}{\left[\frac{(5u^4+4a_4{u}^3+3a_3{u}^2+2a_{2}u+a_1)e^{u{\tau }_5}}{u(b_4{u}^4+b_3{u}^3+b_2{u}^2+b_{1}u+b_0)}\right]}_{u=i{\omega }_k}\right.\hfill \\ \hfill & \left.+\mathrm{Re}{\left[\frac{4a_4{u}^3+3a_3{u}^2+2a_{2}u+a_1}{u(b_4{u}^4+b_3{u}^3+b_2{u}^2+b_{1}u+b_0)}\right]}_{u=i{\omega }_k}\right\}\hfill \\ \hfill =& sign\left\{\frac{{\omega }_k^2[5{\omega }_k^8+(4a_4^2-8a_3){\omega }_k^6+3(a_3^2+2a_1-2a_2{a}_4){\omega }_0^4]}{{\omega }_k^2({\omega }_k^2{(b_3{\omega }_k^2-b_1)}^2+{(b_4{\omega }_k^2-b_2{\omega }_k^2+b_0)}^2)}\right.\hfill \\ \hfill & +\frac{{\omega }_k^2[2(a_2^2-2a_1{a}_3+2a_0{a}_4){\omega }_k^2+a_1^2-2a_0{a}_2]}{{\omega }_k^2({\omega }_k^2{(b_3{\omega }_k^2-b_1)}^2+{(b_4{\omega }_k^2-b_2{\omega }_k^2+b_0)}^2)}\hfill \\ \hfill & +\frac{[-4b_4^2{\omega }_k^6+3(2b_2{b}_4-b_3^2){\omega }_k^4]{\omega }_k^2}{{\omega }_k^2({\omega }_k^2{(b_3{\omega }_k^2-b_1)}^2+{(b_4{\omega }_k^2-b_2{\omega }_k^2+b_k)}^2)}\hfill \\ \hfill & \left.+\frac{[2(2b_1{b}_3-b_2^2-2b_0{b}_4){\omega }_k^2-b_1^2+2b_0{b}_2]{\omega }_k^2}{{\omega }_k^2({\omega }_k^2{(b_3{\omega }_k^2-b_1)}^2+{(b_4{\omega }_k^2-b_2{\omega }_k^2+b_0)}^2)}\right\}\hfill \\ \hfill =& sign\left\{\frac{Q^{\prime }\left({\omega }_k^2\right)}{{(b_3{\omega }_k^2-b_1)}^2{\omega }_k^2+{(b_4{\omega }_k^2-b_2{\omega }_k^2+b_0)}^2}\right\}\hfill \\ \hfill =& sign\left\{Q^{\prime }\left({\omega }_k^2\right)\right\},\hfill \end{array}$$

which yields

$$\begin{array}{c}\hfill sign{\left\{\frac{d\left(Reu\right)}{d{\tau }_5}\right\}}_{{\tau }_5={\tau }_{5k}^{\left(j\right)}}=sign{\left\{{\left[\frac{d\left(Reu\right)}{d{\tau }_5}\right]}^{-1}\right\}}_{{\tau }_5={\tau }_{5k}^{\left(j\right)}}=sign\left\{Q^{\prime }\left({\omega }_k^2\right)\right\}.\end{array}$$

Therefore, if $Q^{\prime }\left({\omega }_k^2\right)\ne 0$, a Hopf bifurcation occurs at $E_2$ for ${\tau }_5={\tau }_{5k}^{\left(j\right)}$ and ${\tau }_i=0(i=1,2,3,4)$. Furthermore, Model (2) undergoes a family of periodic solutions for ${\tau }_5={\tau }_{5k}^{\left(j\right)}$. Thus, we have the following results.

Theorem 5.

If ${\mathfrak{R}}_1>1$ and ${\tau }_i=0(i=1,2,3,4)$, the immunity-activated equilibrium $E_2$ is locally asymptotically stable for ${\tau }_5\in [0,{\tau }_0)$ and unstable when ${\tau }_5>{\tau }_0$. Moreover, if $Q^{\prime }\left({\omega }_k^2\right)\ne 0$, Model (2) undergoes a Hopf bifurcation at $E_2$ when ${\tau }_5={\tau }_{5k}^{\left(j\right)}$.

3.3. Direction of Hopf Bifurcations

Based on the above discussion, a Hopf bifurcation occurs when ${\tau }_5={\tau }_0$. In this section, we study the direction of the Hopf bifurcation using the normal theory and center manifold theorem [50]. We always assume that Model (2) undergoes a Hopf bifurcation at $E_2$ for ${\tau }_5={\tau }_{*}$ with ${\tau }_{*}={\tau }_{5k}^{\left(j\right)}$, and $i{\omega }_{*}$ is the corresponding purely imaginary root of the characteristic equation at $E_2$ for ${\tau }_5={\tau }_{*}$. The conditions for the direction and stability of the Hopf bifurcation are summarized in the following theorem.

Theorem 6.

(i) The direction of the Hopf bifurcation is determined by the sign of ${\mu }_2$, i.e., it is a supercritical bifurcation when ${\mu }_2>0$ and a subcritical bifurcation when ${\mu }_2<0$. (ii) The stability of the bifurcated periodic solution is determined by ${\overline{\beta }}_2$, i.e., the periodic solution is stable when ${\overline{\beta }}_2<0$ and unstable when ${\overline{\beta }}_2>0$. (iii) The period of bifurcated periodic solutions is determined by ${\overline{T}}_2$, i.e., the period increases when ${\overline{T}}_2>0$ and decreases when ${\overline{T}}_2<0$.

The detailed calculations of ${\mu }_2$, ${\overline{\beta }}_2$, and ${\overline{T}}_2$ are given in Appendix A.

3.4. Global Hopf Bifurcation

In the following, we explore the global Hopf bifurcation for ${\mathfrak{R}}_1>1$ using the global Hopf bifurcation theorem of functional equations [51]. Throughout this section, we assume that (16) has a unique positive root. The following lemma is obvious from the definition of the positive invariant set in Model (2).

It follows from Theorem 4 that $E_2$ is globally asymptotically stable when ${\tau }_5=0$. As a special case of Model (2), Model (11) has no nonconstant periodic solution for ${\tau }_5=0$. Thus, the following lemma holds.

Lemma 2.

Model (11) has no nonconstant periodic solution when ${\tau }_5=0$.

It follows from the positive invariant set in Model (2) that the following lemma holds.

Lemma 3.

All nontrivial periodic solutions of Model (11) are uniformly bounded.

The following conclusion shows that Model (11) cannot have a ${\tau }_5$-periodic solution.

Lemma 4.

If ${\mathfrak{R}}_1>1$, Model (11) has no nonconstant periodic solutions of period ${\tau }_5$.

Proof. 

Let $U\left(t\right)=\left(T\right(t),L(t),I(t),V(t),B(t\left)\right)$ be a nontrivial ${\tau }_5$-periodic solution of Model (11). Then, $U(t+{\tau }_5)=(T(t+{\tau }_5),L(t+{\tau }_5),I(t+{\tau }_5),V(t+{\tau }_5),B(t+{\tau }_5))=U\left(t\right)$ is also a ${\tau }_5$-periodic solution of the following corresponding model

$$\left\{\begin{array}{cc}\hfill T^{\prime }\left(t\right)=& \lambda -{\beta }_{1}f\left(V\left(t\right)\right)T\left(t\right)-{\beta }_{2}g\left(I\left(t\right)\right)T\left(t\right)-d_{1}T\left(t\right),\hfill \\ \hfill L^{\prime }\left(t\right)=& \eta ({\beta }_{1}f\left(V\left(t\right)\right)T\left(t\right)+{\beta }_{2}g\left(I\left(t\right)\right)T\left(t\right))-\alpha L\left(t\right)-d_{2}L\left(t\right),\hfill \\ \hfill I^{\prime }\left(t\right)=& (1-\eta )({\beta }_{1}f\left(V\left(t\right)\right)T\left(t\right)+{\beta }_{2}g\left(I\left(t\right)\right)T\left(t\right))+\alpha L\left(t\right)-d_{3}I\left(t\right),\hfill \\ \hfill V^{\prime }\left(t\right)=& kI\left(t\right)-pV\left(t\right)B\left(t\right)-d_{4}V\left(t\right),\hfill \\ \hfill B^{\prime }\left(t\right)=& qV\left(t\right)B\left(t\right)-d_{5}B\left(t\right).\hfill \end{array}\right.$$

(19)

It follows from Theorem 4 that Model (19) has no periodic solution when ${\mathfrak{R}}_1>1$. Thus, this contradiction completes the proof of the lemma. □

Let $\mathbb{X}=C([-{\tau }_5,0],{\mathbb{R}}_{+}^5)$ and $W_t=(T_t,L_t,I_t,V_t,B_t)\in \mathbb{X}$, with $W_t=W(t+\theta )$, $t\ge 0$, $\theta \in [-{\tau }_5,0]$. Model (11) is equivalent to the following functional differential equations

$$W_t^{\prime }=F(W_t,{\tau }_5,\mathcal{T}),W_t\in \mathbb{X},(t,{\tau }_5,\mathcal{T})\in {\mathbb{R}}_{+}\times {\mathbb{R}}_{+}\times \mathbb{R},$$

(20)

where

$$F(W_t,{\tau }_5,\mathcal{T})=\left(\begin{array}{c}\lambda -{\beta }_{1}f\left(V\left(t\right)\right)T\left(t\right)-{\beta }_{2}g\left(I\left(t\right)\right)T\left(t\right)-d_{1}T\left(t\right)\\ \eta ({\beta }_{1}f\left(V\left(t\right)\right)T\left(t\right)+{\beta }_{2}g\left(I\left(t\right)\right)T\left(t\right))-\alpha L\left(t\right)-d_{2}L\left(t\right)\\ (1-\eta )({\beta }_{1}f\left(V\left(t\right)\right)T\left(t\right)+{\beta }_{2}g\left(I\left(t\right)\right)T\left(t\right))+\alpha L\left(t\right)-d_{3}I\left(t\right)\\ kI\left(t\right)-pV\left(t\right)B\left(t\right)-d_{4}V\left(t\right)\\ qV(t-{\tau }_5)B(t-{\tau }_5)-d_{5}B\left(t\right)\end{array}\right).$$

The mapping $F:\mathbb{X}\times {\mathbb{R}}_{+}\times {\mathbb{R}}_{+}\to {\mathbb{R}}_{+}^5$ is completely continuous. By restricting F to the subspace of the constant functions in $\mathbb{X}$, we obtain the mapping $\widehat{F}=F{|}_{{\mathbb{R}}_{+}^5\times {\mathbb{R}}_{+}\times {\mathbb{R}}_{+}}\to {\mathbb{R}}_{+}^5$, where

$$\widehat{F}(W,{\tau }_5,\mathcal{T})=\left(\begin{array}{c}\lambda -{\beta }_{1}f\left(V\left(t\right)\right)T\left(t\right)-{\beta }_{2}g\left(I\left(t\right)\right)T\left(t\right)-d_{1}T\left(t\right)\\ \eta ({\beta }_{1}f\left(V\left(t\right)\right)T\left(t\right)+{\beta }_{2}g\left(I\left(t\right)\right)T\left(t\right))-\alpha L\left(t\right)-d_{2}L\left(t\right)\\ (1-\eta )({\beta }_{1}f\left(V\left(t\right)\right)T\left(t\right)+{\beta }_{2}g\left(I\left(t\right)\right)T\left(t\right))+\alpha L\left(t\right)-d_{3}I\left(t\right)\\ kI\left(t\right)-pV\left(t\right)B\left(t\right)-d_{4}V\left(t\right)\\ qV\left(t\right)B\left(t\right)-d_{5}B\left(t\right)\end{array}\right),$$

$$\begin{array}{c}\hfill {\Delta }_{(E_2,{\tau }_5,\mathcal{T})}\left(u\right)=u^5+a_4{u}^4+a_3{u}^3+a_2{u}^2+a_{1}u+a_0+e^{-u{\tau }_5}(b_4{u}^4+b_3{u}^3+b_2{u}^2+b_{1}u+b_0)=0.\end{array}$$

Then, it can be shown that the assumptions (A1)–(A3) in [51] hold. A point $(\widehat{W},\tau ,T)$ is called a stationary solution of (20) if $\widehat{F}(\widehat{W},\tau ,\mathcal{T})=0$. A stationary solution $(\widehat{W},\tau ,\mathcal{T})$ is called a center if $det{\Delta }_{\widehat{W}}\left(im\frac{2\pi }{\mathcal{T}}\right)=0$ for some integer m. A center $(\widehat{W},\tau ,\mathcal{T})$ is said to be isolated if it is the only center in some neighborhood of $(\widehat{W},\tau ,\mathcal{T})$, and it has finite characteristic values of the form $im\frac{2\pi }{\mathcal{T}}$.

Let

$$\begin{array}{cc}\hfill \Sigma \left(F\right)=& Cl\{(W,\tau ,\mathcal{T})\in \mathbb{X}\times R_{+}\times R_{+}|u\mathrm{be}\mathrm{a}\mathcal{T}-\mathrm{periodic}\mathrm{solution}\},\hfill \\ \hfill N\left(F\right)=& \{(\widehat{W},\tau ,\mathcal{T})\in R_{+}^3|F(\widehat{W},\tau ,\mathcal{T})=0\},\hfill \end{array}$$

and $\ell \left(E_2,{\tau }_{5k}^{\left(j\right)},\frac{2\pi }{{\omega }_k}\right)$ be the connected component of $\left(E_2,{\tau }_{5k}^{\left(j\right)},\frac{2\pi }{{\omega }_k}\right)$ in $\Sigma \left(F\right)$. ${\gamma }_m\left(E_2,{\tau }_{5k}^{\left(j\right)},\frac{2\pi }{{\omega }_k}\right)$ is the mth crossing number of $(E_2,{\tau }_{5k}^{\left(j\right)},\frac{2\pi }{{\omega }_k})$ and m is an integer.

Theorem 7.

Assume that ${\mathfrak{R}}_1>1$ and let ${\tau }_{5k}^{\left(j\right)}$ be defined by (17). Then, for each $\tau >{\tau }_{5k}^{\left(j\right)},j=1,2,\cdots$, Model (11) has at least one nontrivial periodic solution.

Proof. 

It follows from [51] that $\left(E_2,{\tau }_{5k}^{\left(j\right)},\frac{2\pi }{{\omega }_k}\right)$ is an isolated center, and there is a smooth curve $u:({\tau }_{5k}^{\left(j\right)}-ϵ,{\tau }_{5k}^{\left(j\right)}+ϵ)\to C$, such that $det{\Delta }_{\left(E_2,{\tau }_{5k}^{\left(j\right)},\frac{2\pi }{{\omega }_k}\right)}\left(u\left(\tau \right)\right)=0$, $|u\left(\tau \right)-i{\omega }_k|<\epsilon$ for all $\tau \in [{\tau }_{5k}^{\left(j\right)}-ϵ,{\tau }_{5k}^{\left(j\right)}+ϵ]$ and $u\left({\tau }_{5k}^{\left(j\right)}\right)=i{\omega }_k$, $\frac{d\mathrm{Re}\left(u\right(\tau \left)\right)}{d\tau }{\mid }_{\tau ={\tau }_{5k}^{\left(j\right)}}\ne 0$. For the positive $\epsilon$, we define ${\Omega }_{(\epsilon ,\frac{2\pi }{{\omega }_k})}=\left\{(\theta ,\mathcal{T}):0<\theta <\epsilon ,\left|\mathcal{T}-\frac{2\pi }{{\omega }_k}\right|<\epsilon \right\}$. For $\tau \in [{\tau }_{5k}^{\left(j\right)}-ϵ,{\tau }_{5k}^{\left(j\right)}+ϵ]\times \partial {\Omega }_{(\epsilon ,\frac{2\pi }{{\omega }_k})}$, a straightforward calculation yields that $det{\Delta }_{\left(E_2,\tau ,\mathcal{T}\right)}(\theta +i\frac{2\pi }{\mathcal{T}})=0$, if and only if $\theta =0$, $\tau ={\tau }_{5k}^{\left(j\right)},\mathcal{T}=\frac{2\pi }{{\omega }_k}$, which verifies the assumption (A4) in [51] for $m=1$. Moreover, if we put

$$\begin{array}{c}\hfill H^{\pm }\left(E_2,{\tau }_{5k}^{\left(j\right)},\frac{2\pi }{{\omega }_k}\right)(\theta ,\mathcal{T})=det\left(\Delta \left(E_2,{\tau }_{5k}^{\left(j\right)}\pm \delta ,\frac{2\pi }{{\omega }_k}\right)\left(\theta +i\frac{2\pi }{\mathcal{T}}\right)\right),\end{array}$$

it follows from $\frac{d\mathrm{Re}\left(u\right)}{d\tau }{|}_{\tau ={\tau }_{5k}^{\left(j\right)}}\ne 0$ that the crossing number

$$\begin{array}{ccc}\hfill {\gamma }_1\left(E_2,{\tau }_{5k}^{\left(j\right)},\frac{2\pi }{{\omega }_k}\right)& =& {deg}_B\left(H^{-}\left(E_2,{\tau }_{5k}^{\left(j\right)},\frac{2\pi }{{\omega }_k}\right),{\Omega }_{(\epsilon ,\frac{2\pi }{{\omega }_k})}\right)-{deg}_B\left(H^{+}\left(E_2,{\tau }_{5k}^{\left(j\right)},\frac{2\pi }{{\omega }_k}\right),{\Omega }_{(\epsilon ,\frac{2\pi }{{\omega }_k})}\right)\hfill \\ & =& \left\{\begin{array}{c}-1,H^{\prime }\left(z_k\right)>0,\hfill \\ 1,H^{\prime }\left(z_k\right)<0,\hfill \end{array}\right.\hfill \end{array}$$

and then, we have

$${\Sigma }_{\left((\widehat{W},\tau ,\mathcal{T})\in \ell \left(E_2,{\tau }_{5k}^{\left(j\right)},\frac{2\pi }{{\omega }_k}\right)\cap N\left(F\right)\right)}{\gamma }_m\left(\widehat{W},\tau ,\mathcal{T}\right)<0.$$

Thus, the connected component $\ell \left(E_2,{\tau }_{5k}^{\left(j\right)},\frac{2\pi }{{\omega }_k}\right)$ in $\Sigma \left(F\right)$ is nonempty. According to Theorem 3.3 [51], we conclude that $\ell \left(E_2,{\tau }_{5k}^{\left(j\right)},\frac{2\pi }{{\omega }_k}\right)$ is unbounded. It follows from Lemma 3 that the projection of $\ell \left(E_2,{\tau }_{5k}^{\left(j\right)},\frac{2\pi }{{\omega }_k}\right)$ onto the W-space is bounded. From Lemma 4, we know that System (11) with $\tau =0$ has no nontrivial periodic solution. Consequently, the projection of $\ell \left(E_2,{\tau }_{5k}^{\left(j\right)},\frac{2\pi }{{\omega }_k}\right)$ onto the $\tau$-space is away from zero, implying that the projection of $\ell \left(E_2,{\tau }_{5k}^{\left(j\right)},\frac{2\pi }{{\omega }_k}\right)$ onto the $\tau$-space is bounded below. From the definition of ${\tau }_{5k}^{\left(j\right)}$, we have $\frac{2\pi }{{\omega }_k}<{\tau }_{5k}^{\left(j\right)}$. For a contradiction, we assume that the projection of $\ell \left(E_2,{\tau }_{5k}^{\left(j\right)},\frac{2\pi }{{\omega }_k}\right)$ onto the $\tau$-space is bounded, which implies that there exists a ${\tau }^{*}>0$ such that the projection of $\ell \left(E_2,{\tau }_{5k}^{\left(j\right)},\frac{2\pi }{{\omega }_k}\right)$ onto the $\tau$-space is included in the interval $(0,{\tau }^{*})$. Noting that $\frac{2\pi }{{\omega }_k}<{\tau }_{5k}^{\left(j\right)}$ and from Lemma 3, we have $\mathcal{T}<{\tau }^{*}$ for $(W,\tau ,\mathcal{T})\in \ell \left(E_2,{\tau }_{5k}^{\left(j\right)},\frac{2\pi }{{\omega }_k}\right)$, which implies that the projection of $\ell \left(E_2,{\tau }_{5k}^{\left(j\right)},\frac{2\pi }{{\omega }_k}\right)$ onto the $\tau$-space is also bounded. Thus, $\ell \left(E_2,{\tau }_{5k}^{\left(j\right)},\frac{2\pi }{{\omega }_k}\right)$ is bounded. This yields a contradiction and completes the proof. □

4. Numerical Simulations

In this section, we demonstrate the above theoretical results through numerical simulations by choosing three different forms of the general incidence function in Model (2). Most of the parameter values come from [6,17,22,31].

Case (a): Choosing a bilinear incidence function, i.e., $f\left(V\right(t\left)\right)=V\left(t\right)$, $g\left(I\right(t\left)\right)=I\left(t\right)$. Let $\lambda =10,{\beta }_1=0.00025,{\beta }_2=0.000065,k=50,q=0.001,\alpha =0.1,d_1=0.1$, $d_2=0.05,d_3=0.7,d_4=2,d_5=1,p=0.6,\eta =0.001$, ${\tau }_1=3,{\tau }_2=1,{\tau }_3=2$, and ${\tau }_4=4,{\tau }_5=7$. A simple calculation gives that ${\mathfrak{R}}_0=0.9018<1$, which means that the infection-free equilibrium $E_0$ is globally asymptotically stable, implying that the infection dies out. By choosing different initial values, we can observe that all the solution trajectories converge to the infection-free equilibrium $E_0$, as shown in Figure 1. Thus, if effective control measures can be taken to decrease the basic reproduction number ${\mathfrak{R}}_0$ to less than 1, the infection will be controlled.

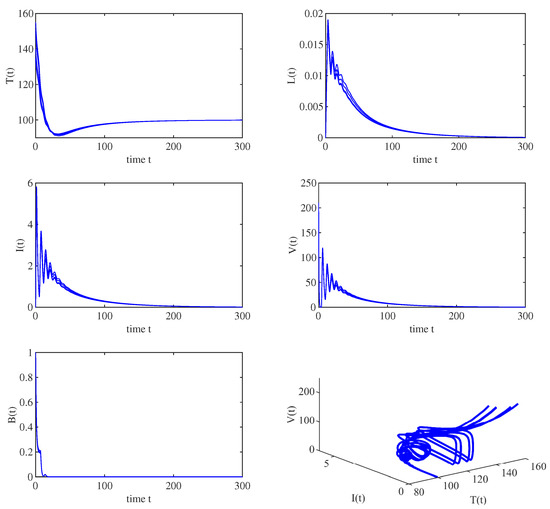
Figure 1. When ${\mathfrak{R}}_0=0.9018<1$, all solution trajectories starting from different initial values converge to the disease-free equilibrium $E_0$, which implies that the infection-free equilibrium $E_0$ is globally asymptotically stable.

When $\lambda =50,{\beta }_1=0.00025$, ${\beta }_2=0.00065,k=30,d_1=0.2$, and the other parameters are the same as those in Figure 1, we have ${\mathfrak{R}}_1=0.6219<1<{\mathfrak{R}}_0=1.5709$. All the solution trajectories starting from different initial values converge to $E_1$, which implies that the immunity-inactivated equilibrium $E_1$ is globally asymptotically stable, as shown in Figure 2. Moreover, when $\lambda =100,{\beta }_1=0.000025,{\beta }_2=0.000065,k=300,d_1=0.1$, ${\tau }_5=0$, and the other parameters are the same as those in Figure 1, ${\mathfrak{R}}_1=4.5504>1$, which implies that the immunity-activated equilibrium $E_2$ is globally asymptotically stable, as shown in Figure 3.

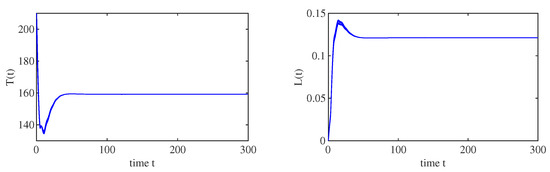
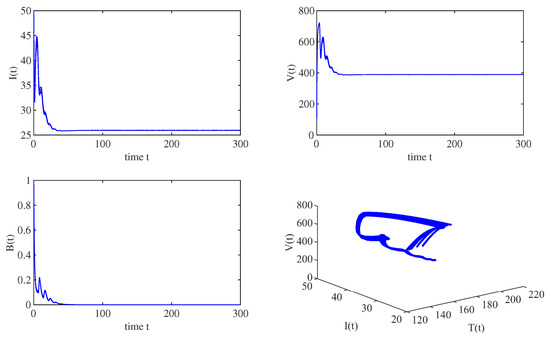
Figure 2. When ${\mathfrak{R}}_1=0.6219<1<{\mathfrak{R}}_0=1.5709$, all solution trajectories starting from different values converge to the immunity-inactivated equilibrium $E_1$, which implies that $E_1$, is globally asymptotically stable.

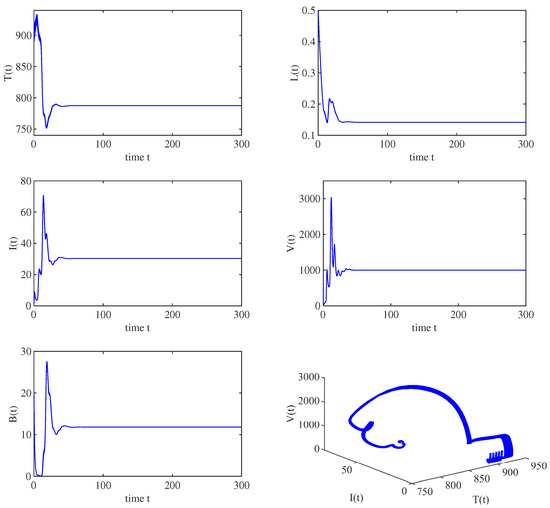
Figure 3. When ${\mathfrak{R}}_1=4.5504>1$, all solution trajectories starting from different initial values converge to the immunity-activated equilibrium $E_2$, which implies that $E_2$ is globally asymptotically stable for ${\tau }_i>0(i=1,2,3,4)$ and ${\tau }_5=0$.

When ${\tau }_5>0$ and ${\tau }_i=0(i=1,2,3,4)$, using the same parameter values as those in Figure 3 and choosing ${\tau }_5$ as the bifurcation parameter, the numerical results indicate that only one positive root of $Q\left(z\right)=0$ exists, i.e., $z=0.1560$. Then, $\omega =0.3950$, and the critical value ${\tau }_0=1.7516$. Figure 4 shows that the immunity-activated equilibrium $E_2$ is locally asymptotically stable when ${\tau }_5=1<{\tau }_0=1.7516$, and a periodic solution bifurcates from an unstable $E_2$ when ${\tau }_5=3>{\tau }_0=1.7516$, as shown in Figure 5, which corresponds to the bifurcation diagram in Figure 6 (left). Furthermore, it follows from Theorem 6 that $c_1\left(0\right)=-2.721296982974015\times {10}^{-4}-2.425211778427851\times {10}^{-4}i$, ${\mu }_2=0.002364569514307$, ${\overline{\beta }}_2=-5.442593965948031\times {10}^{-4}$, and ${\overline{T}}_2=3.590448212830452\times {10}^{-4}$. Thus, the Hopf bifurcation is supercritical and the bifurcated periodic solutions are stable.

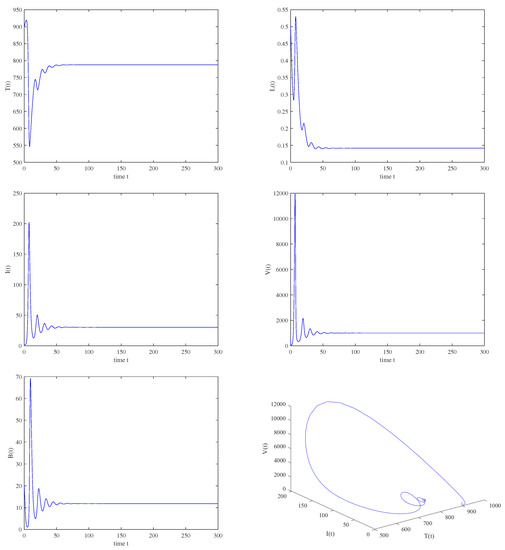
Figure 4. When ${\mathfrak{R}}_1=4.5504>1$, ${\tau }_5=1<{\tau }_0$, ${\tau }_i=0(i=1,2,3,4)$, then $E_2$ is locally asymptotically stable.

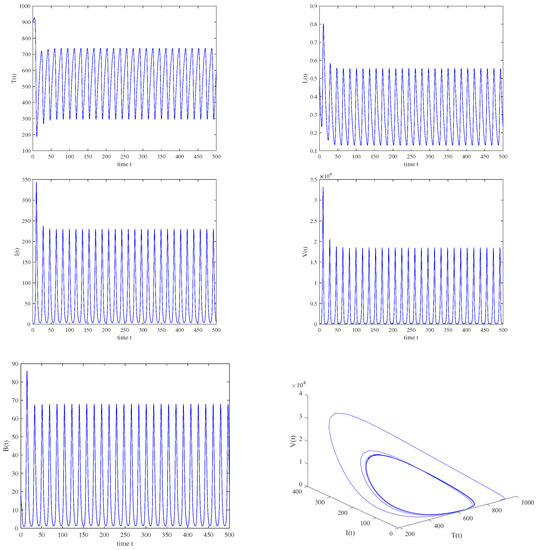
Figure 5. When ${\mathfrak{R}}_1=4.5504>1$, ${\tau }_5=3>{\tau }_0$, ${\tau }_i=0(i=1,2,3,4)$, a stable periodic solution is bifurcated from an unstable equilibrium $E_2$ through the Hopf bifurcation.

Figure 6. On the left is the bifurcation diagram of Model (2) with respect to ${\tau }_5$ when ${\tau }_i=0(i=1,2,3,4)$. On the right is the bifurcation diagram of Model (2) with respect to ${\tau }_5$ when ${\tau }_1=2,{\tau }_2=3,{\tau }_3=6,{\tau }_4=9$ are fixed. It is shown that stability switches occur with intracellular delays.

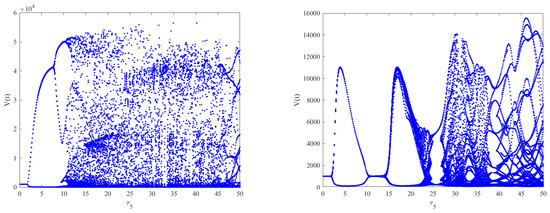
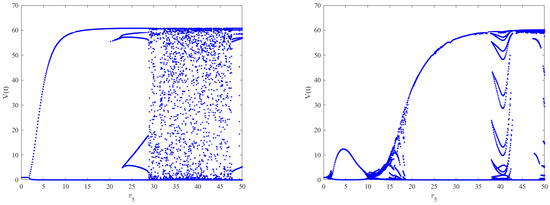
As shown in Figure 6 (left), when ${\tau }_i=0(i=1,2,3,4)$ and by choosing ${\tau }_5$ as the bifurcation parameter, the bifurcation diagram with respect to ${\tau }_5$ shows that the immunity-activated equilibrium is stable for a smaller immune delay (${\tau }_5<{\tau }_0$) and unstable for a larger immune delay, leading to irregular oscillations. However, the theoretical results obtained using Theorems 2–4 show that the intracellular delays ${\tau }_1,{\tau }_2,{\tau }_3$, and ${\tau }_4$ cannot change the global stability of the equilibria. Nevertheless, how the intracellular delays impact the dynamical behaviors of Model (2) also needs to be considered by regarding ${\tau }_5$ as the bifurcation parameter and varying ${\tau }_i(i=1,2,3,4)$.By comparing Figure 6 (left) and Figure 7 (left column), it can be seen that the presence of ${\tau }_1$ has little impact on the dynamics of Model (2) when ${\tau }_1$ increases. However, in Model (2), the phenomenon of stability switches occurs when ${\tau }_2$ appears, except for the Hopf bifurcation and irregular oscillations, as shown in Figure 7 (right column). This indicates that the stability and instability of immunity-activated equilibrium alternate a finite number of times and finally become unstable. A similar phenomenon occurs in the presence of ${\tau }_3$ (left column) and ${\tau }_4$ (right column), as shown in Figure 8. The numerical results show that the immune delay $\left({\tau }_5\right)$ combined with the intracellular delays ${\tau }_2$ and ${\tau }_4$ can lead to more rich and complex dynamical behaviors of Model (2) compared to ${\tau }_1$ and ${\tau }_3$. In order to more clearly compare the effect of intracellular delays ${\tau }_i(i=1,2,3,4)$ combined with the immune delay ${\tau }_5$, we carried out a stability analysis by varying the values of the intracellular delays $0.25\le {\tau }_i(i=1,2,3,4)\le 15$ and the immune delay $0.25\le {\tau }_5\le 50$. The stability region was obtained numerically and the corresponding results are shown in Figure 9. We can see that the combination of ${\tau }_2$ and ${\tau }_4$ with ${\tau }_5$ leads to much richer dynamics. The stability or stability switches are important characteristics from a biological perspective, as they determine whether the eradication of infection is possible in the case of stability regions with the implementation of effective controlling measures. In contrast, it will be difficult to eradicate the infection in unstable regions. Furthermore, in order to investigate the impact of the coexistence of all intracellular delays ${\tau }_i>0(i=1,2,3,4)$ and the immune delay ${\tau }_5$ on the dynamics of Model (2), we fixed ${\tau }_1=2,{\tau }_2=3,{\tau }_3=6$, and ${\tau }_4=9$. The bifurcation diagram shows that stability switches still exist, except for the Hopf bifurcation and complex oscillations in Model (2), as shown in Figure 6 (right).

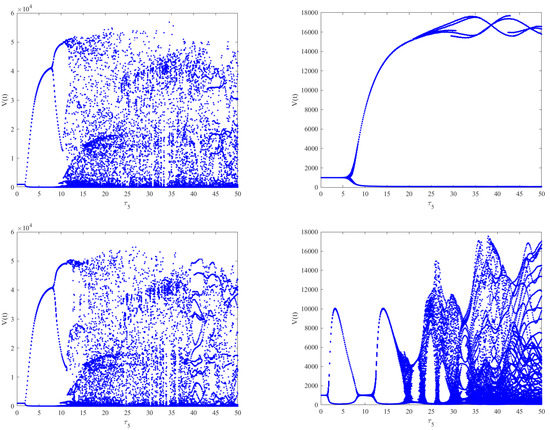
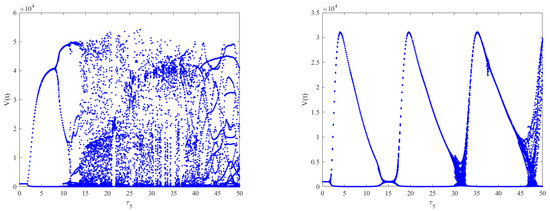
Figure 7. The effect of intracellular time delays ${\tau }_1,{\tau }_2$ on the dynamics of Model (2). The left column shows ${\tau }_1=5,10,15$ from top to bottom, respectively. The right column shows ${\tau }_2=5,10,15$ from top to bottom, respectively. A slight change in the dynamical behaviors can be observed for increasing ${\tau }_1$, while stability switches occur for increasing ${\tau }_2$.

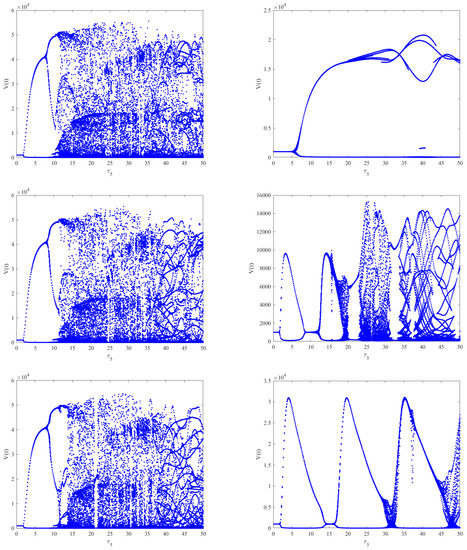
Figure 8. The effect of intracellular time delays ${\tau }_3,{\tau }_4$ on the dynamics of Model (2). The left column shows ${\tau }_3=5,10,15$ from top to bottom, respectively. The right column shows ${\tau }_4=5,10,15$ from top to bottom, respectively. A slight change in the dynamical behaviors can be observed for increasing ${\tau }_3$, while stability switches also occur for increasing ${\tau }_4$.

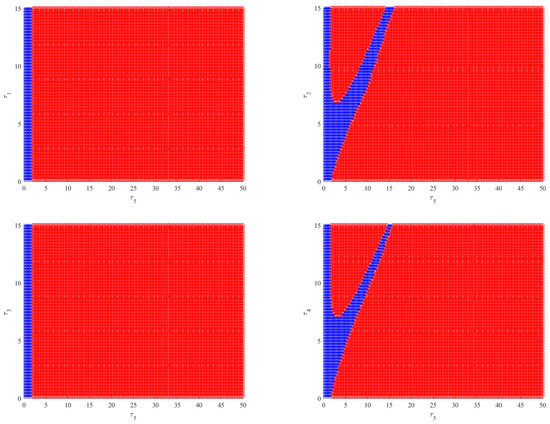
Figure 9. Plots of the stability region by varying the intracellular delays and immune delay. The blue region indicates a stable equilibrium, and the red region represents an unstable equilibrium.

Case (b): Choosing a saturated incidence, i.e., $f\left(V\left(t\right)\right)=\frac{V\left(t\right)}{1+0.1V\left(t\right)}$ and $g\left(I\left(t\right)\right)=\frac{I\left(t\right)}{1+0.4I\left(t\right)}$. Clearly, conditions (3) and (4) are true. When ${\tau }_5>0$, ${\tau }_i=0$ ($i=1,2,3,4$) using the same parameter values as those in Figure 3 and choosing ${\tau }_5$ as the bifurcation parameter. The numerical results indicate that only one positive root of $Q\left(z\right)=0$ exists, i.e., $z=0.1037$, which implies that $\omega =0.3220$ and the critical value ${\tau }_0=2.9134$. Figure 10 shows that the immunity-activated equilibrium $E_2$ is locally asymptotically stable when ${\tau }_5=1<{\tau }_0=2.9134$, and a periodic solution bifurcates from an unstable $E_2$ when ${\tau }_5=3>{\tau }_0=2.9134$, as shown in Figure 11. The corresponding bifurcation diagram with respect to ${\tau }_5$ in the absence of intracellular delays ${\tau }_i=0,(i=1,2,3,4)$ shows that a Hopf bifurcation and periodic oscillations occur in Model (2), as shown in Figure 12 (left). Moreover, the bifurcation diagram with respect to ${\tau }_5$ with intracellular delays ${\tau }_i>0$ ($i=1,2,3,4$) shows that a Hopf bifurcation and periodic solutions also exist, and we can see that the stable interval is longer for ${\tau }_1=2,{\tau }_2=1,{\tau }_3=3,$ and ${\tau }_4=1$, as shown in Figure 12 (right). This implies that different combinations of intracellular delays may be a type of infection control.

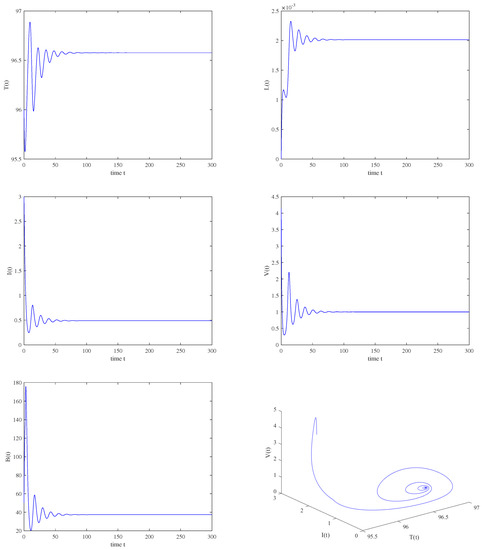
Figure 10. The immunity−activated equilibrium $E_2$ is asymptotically stable when ${\mathfrak{R}}_1=4.5504>1$, ${\tau }_5=1<{\tau }_0$, ${\tau }_i=0(i=1,2,3,4)$.

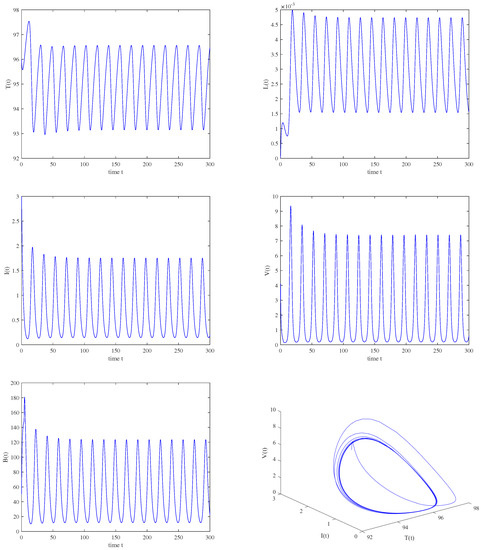
Figure 11. When ${\mathfrak{R}}_1=4.5504>1$, ${\tau }_5=3>{\tau }_0$, ${\tau }_i=0(i=1,2,3,4)$, a periodic solution is bifurcated from the unstable immunity−activated equilibrium $E_2$.

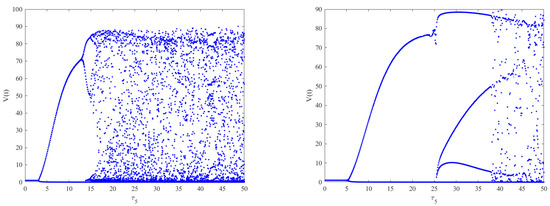
Figure 12. On the left is the bifurcation diagram of Model (2) with respect to ${\tau }_5$ when ${\tau }_i=0(i=1,2,3,4)$. On the right is the bifurcation diagram of Model (2) with respect to ${\tau }_5$ when ${\tau }_1=2,{\tau }_2=1,{\tau }_3=3,{\tau }_4=1$ are fixed. We can see that the stable interval is longer on the right compared to the left, which implies that different combinations of intracellular delays may be a type of infection control.

Case (c): Choosing $f\left(V\left(t\right)\right)=1-e^{-0.05V\left(t\right)}$ and $g\left(I\left(t\right)\right)=1-e^{-0.05I\left(t\right)}$. It is easy to see that the conditions (3) and (4) hold. When ${\tau }_5>0$, ${\tau }_i=0(i=1,2,3,4)$ using the same parameter values as those in Figure 3 and choosing ${\tau }_5$ as the bifurcation parameter. The numerical results indicate that only one positive root of $Q\left(z\right)=0$ exists, i.e., $z=0.1349$. Then, $\omega =0.3673$, and the critical value ${\tau }_0=1.6272$. Figure 13 shows that the immunity-activated equilibrium $E_2$ is locally asymptotically stable when ${\tau }_5=1<{\tau }_0=1.6272$ and a Hopf bifurcation and periodic solution bifurcate from an unstable $E_2$ when ${\tau }_5=3>{\tau }_0=1.6272$, which corresponds to Figure 14. The bifurcation diagram with respect to ${\tau }_5$ without the intracellular delays ${\tau }_i=0(i=1,2,3,4)$ shows that there exist periodic oscillations in Model (2), as shown in Figure 15 (left). Moreover, when ${\tau }_1=2,{\tau }_2=3,{\tau }_3=6,$ and ${\tau }_4=9$ are fixed, as shown in Figure 15 (right), complicated dynamics still occur in Model (2) and the stable interval becomes shorter, which means that the existence of intracellular delays may be detrimental to infection control.

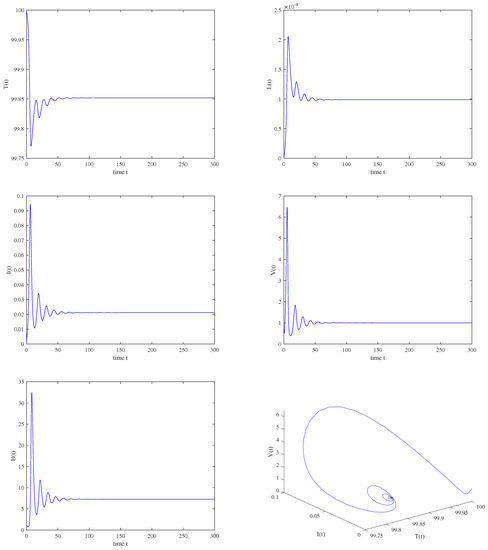
Figure 13. The immunity−activated equilibrium $E_2$ is asymptotically stable when ${\mathfrak{R}}_1=4.5504>1$, ${\tau }_5=1<{\tau }_0$, ${\tau }_i=0(i=1,2,3,4)$.

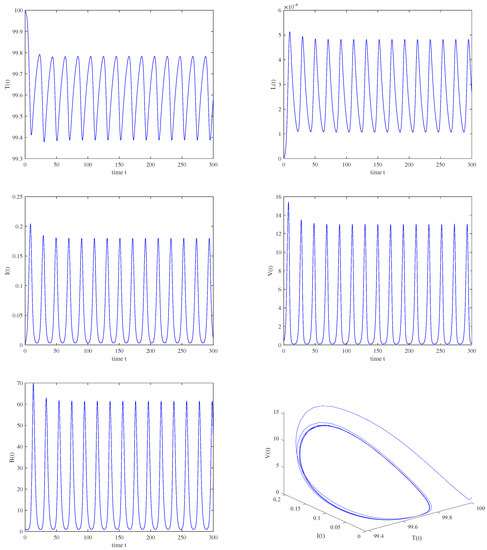
Figure 14. When ${\mathfrak{R}}_1=4.5504>1$, ${\tau }_5=3>{\tau }_0$, ${\tau }_i=0(i=1,2,3,4)$, a periodic solution is bifurcated from an unstable immunity−activated equilibrium $E_2$.

Figure 15. On the left is the bifurcation diagram of Model (2) with respect to ${\tau }_5$ when ${\tau }_i=0(i=1,2,3,4)$. On the right is the bifurcation diagram of Model (2) with respect to ${\tau }_5$ when ${\tau }_1=2,{\tau }_2=3,{\tau }_3=6,{\tau }_4=9$ are fixed. We can see that different oscillations occur, and the stable interval on the right is smaller compared to that on the left.

5. Conclusions

This paper investigated the dynamical behaviors of a class of viral infection models with cell-to-cell infection, general nonlinear incidence, and multiple delays. The aim of this work was to study the effect of intracellular delays and the immune delay on the dynamics of the model. The threshold dynamics of the equilibria were obtained by constructing Lyapunov functionals. It was found that the infection-free equilibrium $E_0$ is globally asymptotically stable when ${\mathfrak{R}}_0<1$, which means that the infection dies out. In addition, the immunity-inactivated equilibrium $E_1$ is globally asymptotically stable when ${\mathfrak{R}}_1<1<{\mathfrak{R}}_0$, which implies that the virus load is insufficient to activate humoral immunity. Moreover, the immunity-activated equilibrium $E_2$ is globally asymptotically stable when ${\mathfrak{R}}_1>1$ in the absence of an immune delay, which means that the virus can coexist with immune cells and reach a balance within the host. By choosing the immune delay as the bifurcation parameter, we found that Model (2) generated a Hopf bifurcation, and periodic oscillations and stability switches occurred, which indicates that the immune delay can destabilize the immunity-activated equilibrium. The properties of the Hopf bifurcation were investigated by applying the normal theory and center manifold theorem. Moreover, the global existence of the Hopf bifurcation was studied. Finally, numerical simulations were carried out to show how the delays impact the dynamics of Model (2).

The obtained results imply that both the intracellular delays and immune delay are responsible for the rich dynamics of the model. However, it follows from the bifurcation diagrams in Figure 6, Figure 7 and Figure 8, Figure 12 and Figure 15 that the immune delay is the main factor for the existence of the Hopf bifurcation and dominates over the intracellular delays in this viral infection model. This implies that the immune system itself has very complicated procedures during virus infection. Moreover, from a biological perspective, stability and stability switches are important, as they determine whether the eradication of infection may be possible in the case of stable regions, whereas it will be difficult in unstable regions. Thus, the stable regions can provide some insights into infection control. In addition, from a mathematical perspective, we can also provide some theoretical suggestions. For example, it was observed in the bifurcation diagrams that the immune delay may be the main reason for the bifurcation, and the model easily reached a stable state for a small immune delay. This indicates that developing effective drugs to decrease the time for activating the immune response system can contribute to infection control. Furthermore, the expression of the basic reproduction number shows that the infection risk will be underevaluated when ignoring either the cell-to-cell infection or virus-to-cell infection. Thus, developing effective drugs for preventing cell-to-cell infection should be considered, except for virus-to-cell infection.

The theoretical analysis of this virus infection model, which incorporates cellular infection, latency, immune response, general nonlinear incidence, and multiple delays, is rare. The investigation of the global stabilities of the corresponding equilibria by applying the Lyapunov method is a generalization of some existing models. Note that only the humoral immune response has been taken into account in this model. However, both the CTL immune response and humoral immune response are the two main immune mechanisms. Also, it takes some time to build up the CTL immune response, so time delays exist during the activation of the CTL immune response. Thus, exploring the dynamics of a model that incorporates both kinds of immune responses and their corresponding immune delays is an interesting project. We leave this for future work.